Arbetsblad 2:1. 1 a) 3 m = cm b) 2,8 m = cm. 2 a) 5,3 m = cm b) 6,07 m = cm c) 0,55 m = cm. 3 a) 7 dm = cm b) 6,4 dm = cm c) 0,9 dm = cm
|
|
|
- Emma Lindström
- för 7 år sedan
- Visningar:
Transkript
1 Arbetsblad 2:1 Längdeneter Skriv i eneten centimeter. Grundbok: grundkurs s. 7 blå kurs s. 7 1 m = 10 dm = 100 cm = mm 1 a) m = cm b) 2,8 m = cm c) 0, m = cm 2 a), m = cm b),07 m = cm c) 0, m = cm a) 7 dm = cm b), dm = cm c) 0,9 dm = cm a) 2 mm = cm b) mm = cm c) 7 mm = cm Skriv i eneten meter. a) dm = m b) 8, dm = m c) 1 dm = m a) cm = m b) 9, cm = m c) 0 cm = m 7 a) 7 cm = m b) 10 cm = m c) 178 cm = m 8 a) 2 mm = m b) 2 mm = m c) 20 mm = m Fyll i rätt svar. 9 a) 2 cm = m b) 2 cm = dm c) 2 cm = mm 10 a) 1 00 mm = m b) 7 0 mm = m c) 98 mm = m 11 a) 2, m = cm b) 7,8 mm = cm c),7 mm = cm Fyll i rätt svar. 12 a) km = m b) 0, km = m 1 km = m 1 mil = 10 km c) 1 km = m 1 a) m = km b) 2 00 m = km c) 1 70 m = km 1 a) 2 mil = km b) 2,9 mil = km c) 0, mil = km oc författarna
2 Arbetsblad 2:2 Cirkelns omkrets 1 eräkna cirkelns omkrets. a) b) c) Grundbok: grundkurs s. 9 blå kurs s. 77 Räkna med π 10 cm m 0 m Mät i figuren. 2 Hur lång är cirkelns a) diameter b) radie c) omkrets eräkna omkretsen av figuren. oc författarna
3 Arbetsblad 2: Areaeneter Grundbok: grundkurs s. 0 blå kurs s Skriv i eneten kvadratcentimeter. 1 cm 2 a) 1 dm 2 = cm 2 b) dm 2 = cm 2 c) 0, dm 2 = cm 2 1 dm 2 d) 2, dm 2 = cm 2 e) 1,2 dm 2 = cm 2 2 Skriv i eneten kvadratdecimeter. a) 100 cm 2 = dm 2 b) 200 cm 2 = dm 2 c) 20 cm 2 = dm 2 d) 0 cm 2 = dm 2 e) 12 cm 2 = dm 2 f) 0 cm 2 = dm 2 Vad ska det stå på linjen? a) dm 2 = cm 2 b) cm 2 = dm 2 c) 0,8 dm 2 = cm 2 d) 0,72 dm 2 = cm 2 Skriv i eneten kvadratdecimeter. 1 m 2 = 100 dm 2 a) m 2 = dm 2 b),8 m 2 = dm 2 c) 0,2 m 2 = dm 2 d) 1,2 m 2 = dm 2 Skriv i eneten kvadratmeter. a) 200 dm 2 = m 2 b) 0 dm 2 = m 2 c) 12 dm 2 = m 2 d) dm 2 = m 2 oc författarna
4 Arbetsblad 2: Stora areaeneter 1 Skriv som kvadratmeter. a) 2 a = m 2 b) 12 a = m 2 Grundbok: grundkurs s. 1 1 ar =100 m 2 1 a = m 2 1 km 2 = m 2 c) 0, a = m 2 d) 0,2 a = m 2 e) 0,2 a = m 2 f),8 a = m 2 2 Skriv som ektar. a) m 2 = a b) m 2 = a c) 000 m 2 = a d) m 2 = a e) 000 m 2 = a f) 00 m 2 = a g) 00 m 2 = a ) 2 m 2 = a Skriv som kvadratmeter. a) 1 km 2 = m 2 b) 2, km 2 = m 2 c) km 2 = m 2 d) 9,8 km 2 = m 2 e) 0, km 2 = m 2 f) 0,02 km 2 = m 2 Vad ska det stå på linjen? a) 8 a = m 2 b) 00 m 2 = a c) m 2 = a d) 900 m 2 = a e) km 2 = m 2 f) m 2 = km 2 g) 1 km 2 = a ) 1 a = km 2 oc författarna
5 Arbetsblad 2: Cirkelns area 1 eräkna cirkelns area. a) b) c) Grundbok: grundkurs s. blå kurs s. 79 Räkna med π 10 cm m 0 m 2 Mät i cirkeln oc beräkna arean. a) b) a) b) Mät i figuren oc beräkna omkrets oc area. a) b) O = O = A = A = oc författarna
6 Arbetsblad 2: Cirkelbåge oc cirkelsektor Grundbok: grundkurs s. 1 Hur stor andel av ela cirkeln är cirkelsektorn i figur Räkna med π A A Cirkelbågens längd: v π 2r 0 C r = cm Cirkelsektorns area: v π r2 0 2 eräkna cirkelsektorns area i figur A d = 10 cm C Hur lång är cirkelbågen i figur A C 120 r = cm C Mät radien oc beräkna cirkelsektorns area i figur D E D F 0 eräkna cirkelbågens längd i figur 10 D E F E 10 F oc författarna
7 Arbetsblad 2:7 Volymeneter Grundbok: grundkurs s. blåkurs s Skriv i eneten kubikdecimeter. 1 liter = 1 dm = cm a) cm = dm b) 00 cm = dm c) 0,7 liter = dm 1 dm 10 cm d) 2, liter = dm e) 1,2 liter = dm 1 dm 10 cm 1 dm 10 cm Skriv i eneten kubikcentimeter. V = 1 dm 1 dm 1 dm = 1 dm V = 10 cm 10 cm 10 cm = cm 2 a) 1 dm = cm a) liter = cm b) 2, dm = cm b),2 liter = cm c) 0, dm = cm c) 0,2 liter = cm Skriv i eneten kubikcentimeter. 1 ml = 1 cm a) 2 ml = cm a) 8 liter = cm b) ml = cm b) 1, liter = cm c) 2 ml = cm c) 0, liter = cm Skriv i eneten kubikdecimeter. 1 m = dm a) 2 m = dm b), m = dm 7 a) 0,1 m = dm b),7 m = dm Skriv i eneten kubikmeter. 8 a) dm = m b) 20 liter = m 9 a) 20 dm = m b) 2 liter = m oc författarna
8 Arbetsblad 2:8 Olika eneter Grundbok: grundkurs s. blå kurs s. 80 Fyll i tabellen. 1 m dm cm a) 1 b) 0,8 c) 2 m 2 dm 2 cm 2 a) 1 b) 0,8 Här använder du både längd-, area- oc volymeneter. c) m dm cm a) 1 b) 0,8 c) Askens bottenarea är 90 cm 2. Skriv arean i eneten a) dm 2 b) m 2 Askens volym är 0 cm. Skriv volymen i eneten a) dm b) m 1 Lådans bottenarea är 10 dm 2. Skriv arean i eneten (dm) a) cm 2 b) m 2 7 Lådans volym är 0 dm. Skriv volymen i eneten a) cm b) m 2 8 assängens bottenarea är 2 m 2. Skriv arean i eneten (m) a) dm 2 b) cm 2 1, 8 9 assängens volym är m. Skriv volymen i eneten a) dm b) cm oc författarna
9 Arbetsblad 2:9 Volym av olika kroppar Grundbok: grundkurs s. blå kurs s. 81 Namnge kropparna oc beräkna volymen. 1 Namn: = 2, dm = 12 dm 2 2 Namn: = cm = 2 cm 2 Namn: =, dm = 18 dm 2 Namn: Namn: Namn: oc författarna
10 Arbetsblad 2:10 Cylinderns volym eräkna volymen. Grundbok: grundkurs s. 7 blå kurs s. 82 Räkna med π 1 a) = 2,0 m =, m 2 b) = dm = dm 2 2 a) = 1 cm r = cm r b) = 1, m r = 2 dm r = = V = V = a) = 0 cm d = 8 cm b) = 18 cm d =, cm d d eräkna volymen av ela konstverket. Den andra oc den tredje pelarens öjd är älften av den föregående pelarens öjd. Diametern är älften av den föregående pelarens diameter. =, m d = 1,2 m d oc författarna
11 Arbetsblad 2:11 Arean av cylinderns begränsningsyta Grundbok: grundkurs s. 7 blåkurs s. 8 Använd π i dina beräkningar. 1 eräkna a) basytans area = 8 cm d = 10 cm b) arean av mantelytan 2 eräkna a) basytans area b) arean av mantelytan = 12 cm r = cm eräkna arean av a) basytan b) mantelytan = 1 cm r = 2, cm c) begränsningsytan En plåtink är formad som en cylinder. a) Hur mycket plåt beövdes för att tillverka inken, som saknar lock? = 0 cm r = 22 cm b) Hur stor volym ar inken? Avrunda oc svara i liter. I agility finns bland annat tunnlar som undarna ska springa genom. Tunnlarna görs ibland av tyg. Hur mycket tyg beövs för att sy en tunnel som ar a) längden 2 m oc diametern 0 cm b) längden m oc diametern 70 cm Du beöver inte räkna med sömsmån. oc författarna
12 Arbetsblad 2:12 Pyramid oc kon Grundbok: grundkurs s. 8 blåkurs s. 8 eräkna volymen. Använd π. 1 a) = dm = 9 dm 2 b) = dm = 9 dm 2 2 a) = dm b) = dm = 12 dm 2 = 12 dm 2 a) (m) b) (m) a) b) oc författarna
13 Arbetsblad 2:1 landade volymer Grundbok: grundkurs s. 9 1 Tänk dig att du ar en klump med modellera. Du formar först ett rätblock med de mått som är utsatta i figuren. eräkna rätblockets volym. Skriv svaret med fyra olika eneter. V = cm V = dm V = ml V = liter 2 Du formar nu en cylinder av samma mängd lera. Hur stor area ar basytan i cylindern om öjden är som i figuren? a) b) c) d) 0, = = = = Du fortsätter att göra cylindrar av samma lerklump. Hur ög blir cylindern om basytan är a) cm 2 b) 2 cm 2 c) 9 cm 2 d) 0,8 cm 2 = = = = Nu formar du ett prisma av samma lerklump. asytan ska vara i form av en triangel. Hur ögt blir prismat om basytan ar de mått som visas i figuren? a) b) c) d) 2, = = = = oc författarna
14 Arbetsblad 2:1 Klotets volym Grundbok: grundkurs s. 9 1 eräkna klotets volym. Räkna med π Klotets volym = πr a) b) c) r = 1,0 m r = 10 cm d = 1,0 m V = V = V = 2 eräkna klotets volym. Svara i liter. a) b) c) r = 2 dm r = 0 cm r = 20 cm V = V = V = eräkna volymen av a) golfbollen. V = r = 21 mm b) bordtennisbollen. V = d = 0 mm c) krocketklotet. V = d) bowlingklotet. V = r =, cm r = 22 cm Hur lång sträcka rullar bollarna oc kloten i uppgift om de rullar 20 varv? a) Golfbollens sträcka: b) ordtennisbollens sträcka: c) Krocketklotets sträcka: d) owlingklotets sträcka: Pia ar en liter deg. Av den rullar on bullar som i genomsnitt ar diametern cm. Hur många bullar räcker degen till? oc författarna
15 Arbetsblad 2:1 Mer om omkrets eräkna omkretsen av den skuggade figuren. Räkna i ditt räkneäfte. Grundbok: rödkurs s. 87 Räkna med π 1 a) (dm) b) 12 (m) 10 c) 2 cm 8 cm 2 cm 2 En und är bunden med ett 12 meter långt rep vid örnet av ett us. Husse vill sätta ett staket längs omkretsen av det område som unden kan nå. Hur långt blir staketet? m 12 m 8 m Ett antal ringar ar länkats iop till en kedja som visas i figuren. Det finns 20 ringar i kedjan. Hur lång är kedjan, dvs. ur lång är sträckan d? d Skriv ett uttryck för trådens längd om den sträcker sig längs a) cirklar 1 2 n 1 n d... b) n cirklar oc författarna
16 Arbetsblad 2:1 landade volymer A 1 eräkna volymen. a) b) c) (dm) (m) Grundbok: rödkurs s. 92 Räkna med π,1 (dm) V = V = V = 2 eräkna begränsningsytans area av a) prismat i uppgift 1a b) cylindern i uppgift 1b A = A = eräkna volymen. a) (m) b) (m) c), 9,0,, V = V = V = eräkna ur ög figuren ska vara för att rymma 1 liter. a) b) c) = = = oc författarna
17 Arbetsblad 2:17 landade volymer Räkna i ditt räkneäfte. Grundbok: rödkurs s Får saften i kannan plats i glaset? 11 Räkna med π, I en kub med sidan 10 cm placeras en så stor cylinder som möjligt. a) Hur stor volym ar cylindern? b) Hur många procent av kubens volym utgör cylindern? En idrottsklubb tillverkar en egen prispall av fiberskivor. Framsidan av prispallen målas med guldfärg. a) Hur stor är arean av framsidan? (dm) b) Hur stor är prispallens begränsningsarea? (Undersidan av prispallen är inte täckt av någon skiva) Trappan på bilden ska målas. Den är 1 meter bred oc varje trappsteg är 20 cm ögt. a) Hur stor yta beöver målas? b) Trappan är gjuten. Hur stor volym ar trappan? Smyckeskrinet på bilden är gjort av mässing. a) Hur stor area ar den synliga gaveln? b) Hur mycket mässingsplåt går det åt för att 8 1 tillverka locket? c) Hur mycket mässingsplåt består ela skrinet av? oc författarna
Lathund, geometri, åk 9
 Lathund, geometri, åk 9 I årskurs 7 och 8 räknade ni med sträckor och ytor i en dimension (1D) respektive två dimensioner (2D). Nu i årskurs 9 har ni istället börjat räkna volymer av geometriska kroppar
Lathund, geometri, åk 9 I årskurs 7 och 8 räknade ni med sträckor och ytor i en dimension (1D) respektive två dimensioner (2D). Nu i årskurs 9 har ni istället börjat räkna volymer av geometriska kroppar
Övningsblad 3.1 A. Omkrets och area. 1 Beräkna figurernas omkrets och area. Varje ruta har arean 1 cm 2.
 Övningsblad 3.1 A Omkrets och area 1 Beräkna figurernas omkrets och area. Varje ruta har arean 1 cm 2. a) b) O = A = O = A = 2 Skugga rektangelns area och markera triangelns omkrets. (m) (m) 25 80 80 70
Övningsblad 3.1 A Omkrets och area 1 Beräkna figurernas omkrets och area. Varje ruta har arean 1 cm 2. a) b) O = A = O = A = 2 Skugga rektangelns area och markera triangelns omkrets. (m) (m) 25 80 80 70
markera med kryss vilka uppgifter du gjort Avsnitt: sidor ETT ETT TVÅ TVÅ TRE TRE FYRA FYRA klart
 PLANERING MATEMATIK - ÅK 8 Bok: Y (fjärde upplagan) Kapitel : 3 Algebra oc mönster Kapitel : 4 Geometri Elevens namn: markera med kryss vilka uppgifter du gjort Avsnitt: sidor ETT ETT TVÅ TVÅ TRE TRE FYRA
PLANERING MATEMATIK - ÅK 8 Bok: Y (fjärde upplagan) Kapitel : 3 Algebra oc mönster Kapitel : 4 Geometri Elevens namn: markera med kryss vilka uppgifter du gjort Avsnitt: sidor ETT ETT TVÅ TVÅ TRE TRE FYRA
Arbetsblad 3:1. Hur stor är vinkeln? 1 Vilken eller vilka av vinklarna är. 2 Uppskatta (gör en bra gissning) hur stora vinklarna är.
 Arbetsblad :1 Hur stor är vinkeln? 1 Vilken eller vilka av vinklarna är a) rät b) spetsig c) trubbig A C D F E G 2 Uppskatta (gör en bra gissning) hur stora vinklarna är. A C D E F G Mät vinklarna och
Arbetsblad :1 Hur stor är vinkeln? 1 Vilken eller vilka av vinklarna är a) rät b) spetsig c) trubbig A C D F E G 2 Uppskatta (gör en bra gissning) hur stora vinklarna är. A C D E F G Mät vinklarna och
150 cm 2 m 70 dm. 280 cm 3,5 m 40 dm 3,50 0,50. 200 cm 1,5 2,5. 6 m. 30 cm 4 dm 500 mm. 2 m. 70 dm. 150 cm. 3,5 m. 40 dm. 280 cm.
 Skriv sträckorna i storleksordning. Längdenheter: meter (m), decimeter (dm), centimeter (cm) och millimeter (mm). Längden 15 cm kan skrivas på olika sätt: 15 cm = 1 m 5 cm = 1,5 m eller 15 dm cm eller
Skriv sträckorna i storleksordning. Längdenheter: meter (m), decimeter (dm), centimeter (cm) och millimeter (mm). Längden 15 cm kan skrivas på olika sätt: 15 cm = 1 m 5 cm = 1,5 m eller 15 dm cm eller
Planering Geometri a r 9
 Planering Geometri a r 9 Mål När du har arbetat med det här kapitlet ska du kunna: förstå vad volym är för något ge namn och känna igen olika rymdgeometriska kroppar, till exempel rätblock, kub, cylinder,
Planering Geometri a r 9 Mål När du har arbetat med det här kapitlet ska du kunna: förstå vad volym är för något ge namn och känna igen olika rymdgeometriska kroppar, till exempel rätblock, kub, cylinder,
Lokal pedagogisk planering i matematik för åk 8
 Lokal pedagogisk planering i matematik för åk 8 Arbetsområde Geometri kap. 3 PRIO Syfte http://www.skolverket.se/laroplaner-amnen-ochkurser/grundskoleutbildning/sameskola/matematik#anchor2 formulera och
Lokal pedagogisk planering i matematik för åk 8 Arbetsområde Geometri kap. 3 PRIO Syfte http://www.skolverket.se/laroplaner-amnen-ochkurser/grundskoleutbildning/sameskola/matematik#anchor2 formulera och
,5 10. Skuggat. Svart ,2 4. Randigt. b) 0,4 10. b) 0,3 10. b) 0,08. b) 0, ,7 0, ,17 0,95 0,15 0,2 + 0,7
 Tal a) 00 50 00 c) 5 00 a) 0,0 0,5 c) 0,05 Färg Bråkform Decimalform Röd Grön _ Gul _ Blå _ a) 7 00 70 00 07 00 5 00 50 00 05 00 00 0,0 00 0,0 0 00 0, 0 00 0, 0,07 0,7,07,05 0,5,5 5 a) Bråkform Decimalform
Tal a) 00 50 00 c) 5 00 a) 0,0 0,5 c) 0,05 Färg Bråkform Decimalform Röd Grön _ Gul _ Blå _ a) 7 00 70 00 07 00 5 00 50 00 05 00 00 0,0 00 0,0 0 00 0, 0 00 0, 0,07 0,7,07,05 0,5,5 5 a) Bråkform Decimalform
a) 4a + a b) 4a 3a c) 4(a + 1)
 REPETITION 2 A 1 Förenkla uttrycken. a) 4a + a b) 4a 3a c) 4(a + 1) 2 Johannas väg till skolan är a m lång. a) Robins skolväg är 200 m längre än Johannas. Teckna ett uttryck för hur lång skolväg Robin
REPETITION 2 A 1 Förenkla uttrycken. a) 4a + a b) 4a 3a c) 4(a + 1) 2 Johannas väg till skolan är a m lång. a) Robins skolväg är 200 m längre än Johannas. Teckna ett uttryck för hur lång skolväg Robin
REPETITION 2 A. a) 4a + a b) 4a 3a c) 4(a + 1)
 REPETITION 2 A 1 Förenkla uttrycken. a) 4a + a b) 4a 3a c) 4(a + 1) 2 Johannas väg till skolan är a m lång. a) Robins skolväg är 200 m längre än Johannas. Teckna ett uttryck för hur lång skolväg Robin
REPETITION 2 A 1 Förenkla uttrycken. a) 4a + a b) 4a 3a c) 4(a + 1) 2 Johannas väg till skolan är a m lång. a) Robins skolväg är 200 m längre än Johannas. Teckna ett uttryck för hur lång skolväg Robin
Arbetsblad 3:1. Vika kuber. 1 a) Figuren ska vikas till en kub. b) Vilken av figurerna kan. 2 Vilka av figurerna kan du vika till en kub?
 Arbetsblad :1 sid 75 Vika kuber 1 a) Figuren ska vikas till en kub. b) Vilken av figurerna kan Vilken av kuberna blir det? vikas till den är kuben? 2 Vilka av figurerna kan du vika till en kub? Klipp ut
Arbetsblad :1 sid 75 Vika kuber 1 a) Figuren ska vikas till en kub. b) Vilken av figurerna kan Vilken av kuberna blir det? vikas till den är kuben? 2 Vilka av figurerna kan du vika till en kub? Klipp ut
Arbetsblad 2:1. 1 a) Figuren ska vikas till en kub. Vilken av kuberna blir det? 2 Vilka av figurerna kan du vika till en kub?
 Arbetsblad 2:1 Vika kuber 1 a) Figuren ska ikas till en kub. Vilken a kuberna blir det? Grundbok: grundkurs s. 59, blå kurs s. 81 b) Vilken a figurerna kan ikas till den här kuben? A B A B C D C D 2 Vilka
Arbetsblad 2:1 Vika kuber 1 a) Figuren ska ikas till en kub. Vilken a kuberna blir det? Grundbok: grundkurs s. 59, blå kurs s. 81 b) Vilken a figurerna kan ikas till den här kuben? A B A B C D C D 2 Vilka
8F Ma Planering v2-7 - Geometri
 8F Ma Planering v2-7 - Geometri Arbetsform under en vecka: Tisdagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
8F Ma Planering v2-7 - Geometri Arbetsform under en vecka: Tisdagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
9E Ma Planering v2-7 - Geometri
 9E Ma Planering v2-7 - Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (45 min): Läsa på anteckningar
9E Ma Planering v2-7 - Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (45 min): Läsa på anteckningar
Arbetsblad 2:1 Repetition skala
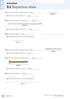 :1 Repetition skala 1 a) Hur lång är nålen i naturlig storlek? b) Hur lång blir nålen i skala 1:3? 1 cm 3 cm Skala 1:1 a) Hur lång är tråden i naturlig storlek? 10 cm Skala 1:1 b) Hur lång blir tråden
:1 Repetition skala 1 a) Hur lång är nålen i naturlig storlek? b) Hur lång blir nålen i skala 1:3? 1 cm 3 cm Skala 1:1 a) Hur lång är tråden i naturlig storlek? 10 cm Skala 1:1 b) Hur lång blir tråden
7F Ma Planering v2-7: Geometri
 7F Ma Planering v2-7: Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
7F Ma Planering v2-7: Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
Förpackningsprojekt !!!!!
 Förpackningsprojekt Ni ska få möjlighet att i grupp utveckla och visa på era kunskaper om volym och begränsningsarea, enhetsomvandlingar, formelhantering samt skala kommer också att ingå. Inlämning Röd:17/4
Förpackningsprojekt Ni ska få möjlighet att i grupp utveckla och visa på era kunskaper om volym och begränsningsarea, enhetsomvandlingar, formelhantering samt skala kommer också att ingå. Inlämning Röd:17/4
Att man bara kan konstruera fem platonska kroppar hänger samman med vinkelsumman som bildas då sidorna möts i kroppens hörn.
 Geometri Mål När eleverna har studerat det här kapitlet ska de: förstå vad volym är för något kunna ge namn på och känna igen olika rymdgeometriska kroppar såsom rätblock, kub, cylinder, prisma, klot,
Geometri Mål När eleverna har studerat det här kapitlet ska de: förstå vad volym är för något kunna ge namn på och känna igen olika rymdgeometriska kroppar såsom rätblock, kub, cylinder, prisma, klot,
4 Sätt in punkternas koordinater i linjens ekvation och se om V.L. = H.L. 5 Räkna först ut nya längden och bredden.
 Läxor Läxa 7 En sådan timme skulle ha 00 00 s = 0 000 s. 8 a) O = π d och A = π r r. 0 Beräkna differensen mellan hela triangelns area och arean av den vita triangeln i toppen. Läxa 9 Hur stor andel målar
Läxor Läxa 7 En sådan timme skulle ha 00 00 s = 0 000 s. 8 a) O = π d och A = π r r. 0 Beräkna differensen mellan hela triangelns area och arean av den vita triangeln i toppen. Läxa 9 Hur stor andel målar
Övningsuppgifter omkrets, area och volym
 Stockholms Tekniska Gymnasium 01-0-0 Övningsuppgifter omkrets, area och volym Uppgift 1: Beräkna arean och omkretsen av nedanstående figur. 4 7 Uppgift : Beräkna arean och omkretsen av nedanstående figur.
Stockholms Tekniska Gymnasium 01-0-0 Övningsuppgifter omkrets, area och volym Uppgift 1: Beräkna arean och omkretsen av nedanstående figur. 4 7 Uppgift : Beräkna arean och omkretsen av nedanstående figur.
Facit åk 6 Prima Formula
 1 Facit åk 6 Prima Formula Kapitel 2 - Volym och skala Sidan 51 1 a C, F och G b D och H 2 A: sexsidigt prisma B: rätblock C: kon D: tetraeder (tresidig pyramid), E: tresidigt prisma F: klot G: cylinder
1 Facit åk 6 Prima Formula Kapitel 2 - Volym och skala Sidan 51 1 a C, F och G b D och H 2 A: sexsidigt prisma B: rätblock C: kon D: tetraeder (tresidig pyramid), E: tresidigt prisma F: klot G: cylinder
Gruppledtrådar 6-2A (i samband med sidorna 50-60) Ledtråd 2 Den har 4 begränsningsytor (B). Ledtråd 1 Polyedern är regelbunden.
 Gruppledtrådar 6-2A (i samband med sidorna 50-60) Polyedern är regelbunden. Den har 4 begränsningsytor (B). Polyedern har 4 hörn (H). Antal kanter (K) kan beräknas med formeln B + H K = 2 Begränsningsytorna
Gruppledtrådar 6-2A (i samband med sidorna 50-60) Polyedern är regelbunden. Den har 4 begränsningsytor (B). Polyedern har 4 hörn (H). Antal kanter (K) kan beräknas med formeln B + H K = 2 Begränsningsytorna
Ordlista 5A:1. term. faktor. täljare. nämnare. Dessa ord ska du träna. Öva orden
 Ordlista 5A:1 Öva orden Dessa ord ska du träna term Talen som du räknar med i en addition eller subtraktion kallas termer. faktor Talen som du räknar med i en multiplikation kallas faktorer. täljare Talet
Ordlista 5A:1 Öva orden Dessa ord ska du träna term Talen som du räknar med i en addition eller subtraktion kallas termer. faktor Talen som du räknar med i en multiplikation kallas faktorer. täljare Talet
PLANGEOMETRI I provläxa med facit ht18
 PLANGEOMETRI I provläxa med facit ht18 På det här avsnittet kommer du i första hand att utveckla din begrepps metod och kommunikations förmåga. Det är nödvändigt att ha en linjal för att klara avsnittet.
PLANGEOMETRI I provläxa med facit ht18 På det här avsnittet kommer du i första hand att utveckla din begrepps metod och kommunikations förmåga. Det är nödvändigt att ha en linjal för att klara avsnittet.
Kartläggningsmaterial för nyanlända elever SVENSKA. Geometri Matematik. 1 2 Steg 3
 Kartläggningsmaterial för nyanlända elever Geometri Matematik 1 2 Steg 3 SVENSKA Kartläggningsmaterial för nyanlända elever Geometri åk 3 MA 1. Rita färdigt bilden så att mönstret blir symmetriskt. 2.
Kartläggningsmaterial för nyanlända elever Geometri Matematik 1 2 Steg 3 SVENSKA Kartläggningsmaterial för nyanlända elever Geometri åk 3 MA 1. Rita färdigt bilden så att mönstret blir symmetriskt. 2.
Innehåll. 1 Allmän information 5. 4 Formativ bedömning 74. 5 Diagnoser och tester 90. 6 Prov och repetition 107. 2 Kommentarer till kapitlen 18
 Innehåll 1 Allmän information Seriens uppbyggnad Lärobokens struktur 6 Kapitelinledning 7 Avsnitten 7 Pratbubbleuppgifter Aktivitet Taluppfattning och huvudräkning 9 Resonera och utveckla 9 Räkna och häpna
Innehåll 1 Allmän information Seriens uppbyggnad Lärobokens struktur 6 Kapitelinledning 7 Avsnitten 7 Pratbubbleuppgifter Aktivitet Taluppfattning och huvudräkning 9 Resonera och utveckla 9 Räkna och häpna
PENGAR TILLBAKA 2. GEOMETRI P. Ett snöre på 5 dm klipps i bitar som är 8 cm långa. Hur många bitar på 8 cm går det att få? E P Påbörjad lösning
 2. GEOETRI P R PENGAR TILLBAA Ett snöre på 5 dm klipps i bitar som är 8 cm långa. Hur många bitar på 8 cm går det att få? E P Påbörjad lösning E R Löser problemet och ger korrekt svar E Redovisningen är
2. GEOETRI P R PENGAR TILLBAA Ett snöre på 5 dm klipps i bitar som är 8 cm långa. Hur många bitar på 8 cm går det att få? E P Påbörjad lösning E R Löser problemet och ger korrekt svar E Redovisningen är
5B1134 Matematik och modeller
 KTH Matematik 1 5B1134 Matematik och modeller 2006-09-04 1 Första veckan Geometri med trigonometri Veckans begrepp cirkel, cirkelsegment, sektor, korda, båglängd, vinkel, grader, radianer, sinus, cosinus,
KTH Matematik 1 5B1134 Matematik och modeller 2006-09-04 1 Första veckan Geometri med trigonometri Veckans begrepp cirkel, cirkelsegment, sektor, korda, båglängd, vinkel, grader, radianer, sinus, cosinus,
Tal Repetitionsuppgifter
 epetitionsuppgifter Till varje kapitel finns repetitionsuppgifter i form av Arbetsblad. Uppgifterna är relaterade till innehållet i respektive kapitel och täcker hela kapitlet. De uppgifter som kräver
epetitionsuppgifter Till varje kapitel finns repetitionsuppgifter i form av Arbetsblad. Uppgifterna är relaterade till innehållet i respektive kapitel och täcker hela kapitlet. De uppgifter som kräver
CENTRALA INNEHÅLL. Matteord. Geometriska objekt och deras inbördes relationer. Geometriska egenskaper hos dessa objekt.
 Omkrets och Area Geometri - CENTRALA INNEHÅLL Geometriska objekt och deras inbördes relationer. Geometriska egenskaper hos dessa objekt. Avbildning och konstruktion av geometriska objekt. Skala vid förminskning
Omkrets och Area Geometri - CENTRALA INNEHÅLL Geometriska objekt och deras inbördes relationer. Geometriska egenskaper hos dessa objekt. Avbildning och konstruktion av geometriska objekt. Skala vid förminskning
Läxa 9 7 b) Dividera 84 cm med π för att få reda på hur lång diametern är. 8 1 mm motsvarar 150 / 30 mil = = 5 mil. Omvandla till millimeter.
 LEDTRÅDAR LÄXOR Läa Förläng så att du får ett heltal i nämnaren. Använd division. Varje sekund klipper Karin, m =, m. Läa 0 ml = 0,0 liter Använd sambandet s = v t. Räkna ut hur mycket vattnet väger när
LEDTRÅDAR LÄXOR Läa Förläng så att du får ett heltal i nämnaren. Använd division. Varje sekund klipper Karin, m =, m. Läa 0 ml = 0,0 liter Använd sambandet s = v t. Räkna ut hur mycket vattnet väger när
20 Gamla tentamensuppgifter
 20 Gamla tentamensuppgifter 20.1 Lätta avdelningen Övning 20.1 Beräkna f 0 ( 3) för f(x) = 3x2 2x + 1 med jälp av derivatans definition. Lösning: Här är det allmänna uttrycket för derivatans definition
20 Gamla tentamensuppgifter 20.1 Lätta avdelningen Övning 20.1 Beräkna f 0 ( 3) för f(x) = 3x2 2x + 1 med jälp av derivatans definition. Lösning: Här är det allmänna uttrycket för derivatans definition
Poolbygge. fredag 11 april 14
 Poolbygge Första lektionen vart jag klar med att rita och skriva ritningen. Först skrev jag poolen i skalan 1:60 vilket vi inte fick göra så jag gjorde den till 1:30, alltså har jag minskat den 30 gånger
Poolbygge Första lektionen vart jag klar med att rita och skriva ritningen. Först skrev jag poolen i skalan 1:60 vilket vi inte fick göra så jag gjorde den till 1:30, alltså har jag minskat den 30 gånger
Föreläsning 5: Geometri
 Föreläsning 5: Geometri Geometri i skolan Grundläggande begrepp Former i omvärlden Plangeometriska figurer Symmetri och tessellering Tredimensionell geometri och geometriska kroppar Omkrets, area, volym
Föreläsning 5: Geometri Geometri i skolan Grundläggande begrepp Former i omvärlden Plangeometriska figurer Symmetri och tessellering Tredimensionell geometri och geometriska kroppar Omkrets, area, volym
Min pool. Hanna Lind 7:2 Alfa
 Min pool Hanna Lind 7:2 Alfa RITNING Jag började med att räkna ut ett antal rimliga mått som jag visste blev heltal när jag delade dom på 30, det gjorde jag då skalan var 1:30. I min ritning visar jag
Min pool Hanna Lind 7:2 Alfa RITNING Jag började med att räkna ut ett antal rimliga mått som jag visste blev heltal när jag delade dom på 30, det gjorde jag då skalan var 1:30. I min ritning visar jag
9D Ma: Geometri VT 2018 Syftet med undervisningen är att du ska utveckla din förmåga att:
 9D Ma: Geometri VT 2018 Syftet med undervisningen är att du ska utveckla din förmåga att: formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, använda och analysera
9D Ma: Geometri VT 2018 Syftet med undervisningen är att du ska utveckla din förmåga att: formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, använda och analysera
4-9 Rymdgeometri Namn:.
 4-9 Rymdgeometri Namn:. Inledning Rymden har alltid fascinerat. Men vad menas med rymd i matematisk eller geometrisk mening? Här skall du få studera 3- dimensionella figurer och hur man beräknar volymen
4-9 Rymdgeometri Namn:. Inledning Rymden har alltid fascinerat. Men vad menas med rymd i matematisk eller geometrisk mening? Här skall du få studera 3- dimensionella figurer och hur man beräknar volymen
INTRESSEVÄCKANDE UNDERVISNING I MATEMATIK. Izet Omanovic, förstelärare i matematik Söderkullaskolan i Malmö
 INTRESSEVÄCKANDE UNDERVISNING I MATEMATIK Izet Omanovic, förstelärare i matematik Söderkullaskolan i Malmö MIN AMBITION Inspirera lärare att arbeta med eget undervisningsmaterial som är anpassat efter
INTRESSEVÄCKANDE UNDERVISNING I MATEMATIK Izet Omanovic, förstelärare i matematik Söderkullaskolan i Malmö MIN AMBITION Inspirera lärare att arbeta med eget undervisningsmaterial som är anpassat efter
P O O L B Y G G E. Bilden tagen utav - Andrej Trnkoczy, ifrån flickr. tisdag 8 april 14
 P O O L B Y G G E Bilden tagen utav - Andrej Trnkoczy, ifrån flickr Det du behöver veta i denna keynote är.. Vad skala är/ hur man räknar med skala Vad omkrets är/ hur man räknar med omkrets Vad area är/
P O O L B Y G G E Bilden tagen utav - Andrej Trnkoczy, ifrån flickr Det du behöver veta i denna keynote är.. Vad skala är/ hur man räknar med skala Vad omkrets är/ hur man räknar med omkrets Vad area är/
Kunskapsmål och betygskriterier för matematik
 1 (1) 2009-0-12 Kunskapsmål och betygskriterier för matematik För betyget G i matematik skall eleven kunna utföra beräkningar, lösa problem samt se enklare samband utifrån de kunskapsmål som anges under
1 (1) 2009-0-12 Kunskapsmål och betygskriterier för matematik För betyget G i matematik skall eleven kunna utföra beräkningar, lösa problem samt se enklare samband utifrån de kunskapsmål som anges under
9A Ma: Geometri. Det tredje arbetsområdet handlar om geometri.
 9A Ma: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda strategier
9A Ma: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda strategier
4-8 Cirklar. Inledning
 Namn: 4-8 Cirklar Inledning Du har arbetat med fyrhörningar (parallellogrammer) och trehörningar (trianglar). Nu skall du studera en figur som saknar hörn, och som består av en böjd linje. Den kallas för
Namn: 4-8 Cirklar Inledning Du har arbetat med fyrhörningar (parallellogrammer) och trehörningar (trianglar). Nu skall du studera en figur som saknar hörn, och som består av en böjd linje. Den kallas för
9 Geometriska begrepp
 9 Geometriska begrepp Rita figurer som visar vad vi menar med... 261 a) 4 cm och 4 cm 2 b) 5 cm och 5 cm 2 262 Rita två olika figurer som båda har arean 8 cm 2 263 Rita tre olika figurer som alla har arean
9 Geometriska begrepp Rita figurer som visar vad vi menar med... 261 a) 4 cm och 4 cm 2 b) 5 cm och 5 cm 2 262 Rita två olika figurer som båda har arean 8 cm 2 263 Rita tre olika figurer som alla har arean
SF1620 Matematik och modeller
 KTH Teknikvetenskap, Institutionen för matematik 1 SF1620 Matematik och modeller 2007-09-03 1 Första veckan Geometri med trigonometri Till att börja med kom trigometrin till för att hantera och lösa geometriska
KTH Teknikvetenskap, Institutionen för matematik 1 SF1620 Matematik och modeller 2007-09-03 1 Första veckan Geometri med trigonometri Till att börja med kom trigometrin till för att hantera och lösa geometriska
fredag den 11 april 2014 M I N P O O L
 M I N P O O L http://en.wikipedia.org/wiki/file:backyardpool.jpg MIN FÖRSTA KLADD Min första kladd så kladda jag lite och då hade inte jag riktigt förstått uppgiften så jag bara kladda lite runt men det
M I N P O O L http://en.wikipedia.org/wiki/file:backyardpool.jpg MIN FÖRSTA KLADD Min första kladd så kladda jag lite och då hade inte jag riktigt förstått uppgiften så jag bara kladda lite runt men det
Vi människor föds in i en tredimensionell värld som vi accepterar och
 Güner Ahmet & Thomas Lingefjärd Symbolen π och tredimensionellt arbete med Geogebra I grundskolans geometriundervisning möter elever oftast tvådimensionella former trots att de har störst vardagserfarenhet
Güner Ahmet & Thomas Lingefjärd Symbolen π och tredimensionellt arbete med Geogebra I grundskolans geometriundervisning möter elever oftast tvådimensionella former trots att de har störst vardagserfarenhet
Matematik CD för TB = 5 +
 Föreläsning 4 70 a) Vi delar figuren i två delar, en triangel (på toppen) och en rektangel. Summan av dessa två figurers area ger den eftersökta. Vi behöver följande formler: A R = b h A T = b h Svar:
Föreläsning 4 70 a) Vi delar figuren i två delar, en triangel (på toppen) och en rektangel. Summan av dessa två figurers area ger den eftersökta. Vi behöver följande formler: A R = b h A T = b h Svar:
fredag den 11 april 2014 POOL BYGGE
 POOL BYGGE KLADD Såhär ser min kladd ut: På min kladd så bestämde jag mig för vilken form poolen skulle ha och ritade ut den. På min kladd har jag även skrivit ut måtten som min pool skulle vara i. Proportionerna
POOL BYGGE KLADD Såhär ser min kladd ut: På min kladd så bestämde jag mig för vilken form poolen skulle ha och ritade ut den. På min kladd har jag även skrivit ut måtten som min pool skulle vara i. Proportionerna
Södervångskolans mål i matematik
 Södervångskolans mål i matematik Mål som eleverna lägst ska ha uppnått i slutet av det första skolåret beträffande tal och taluppfattning kunna läsa av en tallinje mellan 0-20 kunna läsa och ramsräka tal
Södervångskolans mål i matematik Mål som eleverna lägst ska ha uppnått i slutet av det första skolåret beträffande tal och taluppfattning kunna läsa av en tallinje mellan 0-20 kunna läsa och ramsräka tal
Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning
 Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning Eleven skall år 1 Begrepp Jämförelse- och storleksord, t.ex. stor, större, störst. Positionssystemet
Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning Eleven skall år 1 Begrepp Jämförelse- och storleksord, t.ex. stor, större, störst. Positionssystemet
REPETITION 2 A. a) Är sträckan proportionell mot tiden? b) Beräkna medelhastigheten under de fem första sekunderna.
 REPETITION Hur mcket är a) 9 b) 00 0 c) 00 På en karta i skala : 0 000 är det, cm mellan två små sjöar. Hur långt är det i verkligheten? Grafen visar hur långt en bil hinner de se första sekunderna efter
REPETITION Hur mcket är a) 9 b) 00 0 c) 00 På en karta i skala : 0 000 är det, cm mellan två små sjöar. Hur långt är det i verkligheten? Grafen visar hur långt en bil hinner de se första sekunderna efter
Storvretaskolans Kursplan för Matematik F-klass- år 5
 2010-11-01 Storvretaskolans Kursplan för Matematik F-klass- år 5 Skolan skall i sin undervisning sträva efter att eleven : utvecklar intresse för matematik samt tilltro till det egna tänkandet och den
2010-11-01 Storvretaskolans Kursplan för Matematik F-klass- år 5 Skolan skall i sin undervisning sträva efter att eleven : utvecklar intresse för matematik samt tilltro till det egna tänkandet och den
sträckan = tiden. hastigheten hastigheten = sträckan tiden 210 hastigheten = 3 = 70 Bilisten kör 70 km/h. tiden =
 Enheter och skala I det här kapitlet kan du lära dig mer om hastighet att skriva minuter som del av timme att räkna om km/h till m/s något om hastigheter till sjöss om volymenheterna cm 3, dm 3 och m 3
Enheter och skala I det här kapitlet kan du lära dig mer om hastighet att skriva minuter som del av timme att räkna om km/h till m/s något om hastigheter till sjöss om volymenheterna cm 3, dm 3 och m 3
GEOMETRISKA TILLÄMPNINGAR
 INNEHÅLL GEOMETRISKA TILLÄMPNINGAR GEOMETRISKA TILLÄMPNINGAR 251 252 GEOMETRISKA TILLÄMPNINGAR I samband med ett åskväder regnade det enligt en regnmätare 38 mm. Hur många liter vatten kom det a) på en
INNEHÅLL GEOMETRISKA TILLÄMPNINGAR GEOMETRISKA TILLÄMPNINGAR 251 252 GEOMETRISKA TILLÄMPNINGAR I samband med ett åskväder regnade det enligt en regnmätare 38 mm. Hur många liter vatten kom det a) på en
4 Dividera höjningen (0,5 %) med räntesatsen från början (1 %). 7 Du kan pröva dig fram till exempel så här: Från Till Procent- Procent enheter
 ledtrådar LäOr Läa 8 Räkna först ut hur mycket tiokronorna och enkronorna är värda sammanlagt. Läa 8 Räkna först ut hur mycket allt vatten i hinken väger när den är full. Läa MGN = 8 Tänk dig att näckrosen
ledtrådar LäOr Läa 8 Räkna först ut hur mycket tiokronorna och enkronorna är värda sammanlagt. Läa 8 Räkna först ut hur mycket allt vatten i hinken väger när den är full. Läa MGN = 8 Tänk dig att näckrosen
Rep 1 NÅGOT EXTRA. Sidan 88. Sidan 85. Sidan 89. Sidan 86. Sidan 87. Sidan 90
 2 VOLYM OCH SKALA / REP 1 FACIT TILL ELEVBOKEN 125 a dl b ml c cl d l 126 5 st 127 200 cm 3 (2 dl = 0,2 l = 0,2 dm 3 = 200 cm 3 ) Sidan 85 128 A B C D Vas tom 235 g 528 g 0,85 kg 1,250 kg Vas med vatten
2 VOLYM OCH SKALA / REP 1 FACIT TILL ELEVBOKEN 125 a dl b ml c cl d l 126 5 st 127 200 cm 3 (2 dl = 0,2 l = 0,2 dm 3 = 200 cm 3 ) Sidan 85 128 A B C D Vas tom 235 g 528 g 0,85 kg 1,250 kg Vas med vatten
Begrepp Uttryck, värdet av ett uttryck, samband, formel, graf, funktion, lista, diagram, storhet, enhet, tabell.
 Aktivitetsbeskrivning Denna aktivitet samlar ett antal olika sätt att hantera rymdgeometriska beräkningar med formler på en grafräknare. Dessa metoder finns som uppgifter eller som en samling tips i en
Aktivitetsbeskrivning Denna aktivitet samlar ett antal olika sätt att hantera rymdgeometriska beräkningar med formler på en grafräknare. Dessa metoder finns som uppgifter eller som en samling tips i en
2146 a. v = 290 v = 290 omvandlingsfaktor rad v = 290 v = rad v 5.1 rad
 146 a v = 38 v = 38 omvandlingsfaktor rad v = 38 180 rad v = 0.663 rad v 0.7 rad c v = 90 v = 90 omvandlingsfaktor rad v = 90 180 rad v = 5.061 rad v 5.1 rad b v = 196 v = 196 omvandlingsfaktor rad v =
146 a v = 38 v = 38 omvandlingsfaktor rad v = 38 180 rad v = 0.663 rad v 0.7 rad c v = 90 v = 90 omvandlingsfaktor rad v = 90 180 rad v = 5.061 rad v 5.1 rad b v = 196 v = 196 omvandlingsfaktor rad v =
Student. a: 5 b: 6 c: 7 d: 8 e: 3
 Student Avdelning. Trepoängsproblem. Talen 3 och 4 samt två okända tal skrivs in i de fyra rutorna. Summan av talen i raderna blir 5 och 0 och summan av talen i den ena kolumnen blir 9. Vilket är det största
Student Avdelning. Trepoängsproblem. Talen 3 och 4 samt två okända tal skrivs in i de fyra rutorna. Summan av talen i raderna blir 5 och 0 och summan av talen i den ena kolumnen blir 9. Vilket är det största
Avdelning 1, trepoängsproblem
 vdelning, trepoängsproblem. Med hjälp av bilden bredvid kan vi se att + 3 + 5 + 7 = 4 4. Vad är + 3 + 5 + 7 + 9 +... + 7 + 9 + 2? : 0 0 : C: 2 2 D: 3 3 E: 4 4 2. Summan av talen i båda raderna är den samma.
vdelning, trepoängsproblem. Med hjälp av bilden bredvid kan vi se att + 3 + 5 + 7 = 4 4. Vad är + 3 + 5 + 7 + 9 +... + 7 + 9 + 2? : 0 0 : C: 2 2 D: 3 3 E: 4 4 2. Summan av talen i båda raderna är den samma.
REPETITION 3 A. a) b) a) 1 4 av 200 kr b) 10 % av 750 kr c) 2 3. av 60 kg. a) b) c) b) a) 6 8. a) b) b) 0,075 c) d) 0,9.
 DEL I 1 Mät vinklarna. Gradtalen ska sluta på 0 eller 5. 2 Hur mycket är a) 1 4 av 200 kr b) 10 % av 750 kr c) 2 3 av 60 kg 3 Mät sidorna i hela och halva centimeter. Beräkna sedan omkrets och area av
DEL I 1 Mät vinklarna. Gradtalen ska sluta på 0 eller 5. 2 Hur mycket är a) 1 4 av 200 kr b) 10 % av 750 kr c) 2 3 av 60 kg 3 Mät sidorna i hela och halva centimeter. Beräkna sedan omkrets och area av
Arbetsblad 1. Addition och subtraktion i flera steg 1 524 + 162 = 2 374 + 424 = 3 762 + 218 = 4 257 + 431 = 5 287 + 372 = 6 415 + 194 = 7 665 58 =
 Arbetsblad NAMN: Addition och subtraktion i flera steg + 3 + 3 + + 3 + 3 + 9 3 3 9 9 9 39 3 3 + 39 3 + 99 0 3 Kopiering tillåten Matematikboken Författarna och Liber AB Arbetsblad Addition och subtraktion
Arbetsblad NAMN: Addition och subtraktion i flera steg + 3 + 3 + + 3 + 3 + 9 3 3 9 9 9 39 3 3 + 39 3 + 99 0 3 Kopiering tillåten Matematikboken Författarna och Liber AB Arbetsblad Addition och subtraktion
6 cm. 106 Beräkna a) 3 ( 4) b) ( 2) 5 c) 4 ( 2,5) d) ( 8) 1,5. T.ex. print(3 * -4) 13 Beräkna cirkelns a) diameter b) omkrets
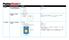 1 Print 1 Tal Multiplikation och division med negativa tal 106 Beräkna a) 3 ( 4) b) ( 2) 5 c) 4 ( 2,5) d) ( 8) 1,5 print(3 * -4) 2 Geometri Cirkelns omkrets 13 Beräkna cirkelns a) diameter b) omkrets 6
1 Print 1 Tal Multiplikation och division med negativa tal 106 Beräkna a) 3 ( 4) b) ( 2) 5 c) 4 ( 2,5) d) ( 8) 1,5 print(3 * -4) 2 Geometri Cirkelns omkrets 13 Beräkna cirkelns a) diameter b) omkrets 6
Pool - bygge. Alicia Åbrink. https://www.flickr.com/photos/andrejtrnkoczy/ /
 Pool - bygge Alicia Åbrink https://www.flickr.com/photos/andrejtrnkoczy/9937515753/ Behöver veta för att räkna ut skala https://www.flickr.com/photos/lainer/132663371/ https://www.flickr.com/photos/ludiecochrane/4673663670/
Pool - bygge Alicia Åbrink https://www.flickr.com/photos/andrejtrnkoczy/9937515753/ Behöver veta för att räkna ut skala https://www.flickr.com/photos/lainer/132663371/ https://www.flickr.com/photos/ludiecochrane/4673663670/
Repetitionsuppgifter 1
 Repetitionsuppgifter 1 Beräkna 1 a) 0,5 + 0,7 b) 0,45 + 1,6 c) 2,76 0,8 2 a) 4,5 10 b) 30,5 10 c) 0,45 1 000 3 Vilka av produkterna är a) större än 6 1,09 6 0,87 6 1 6 4,3 6 0,08 6 b) mindre än 6 4 Skriv
Repetitionsuppgifter 1 Beräkna 1 a) 0,5 + 0,7 b) 0,45 + 1,6 c) 2,76 0,8 2 a) 4,5 10 b) 30,5 10 c) 0,45 1 000 3 Vilka av produkterna är a) större än 6 1,09 6 0,87 6 1 6 4,3 6 0,08 6 b) mindre än 6 4 Skriv
Gamla tentemensuppgifter
 Inte heller idag någon ny teori! Gamla tentemensuppgifter 1 Bestäm det andragradspolynom vars kurva skär x-axeln i x = 3 och x = 1 och y-axeln i y = 3 f(x) = (x 3)(x + 1) = x x 3 är en bra start, men vi
Inte heller idag någon ny teori! Gamla tentemensuppgifter 1 Bestäm det andragradspolynom vars kurva skär x-axeln i x = 3 och x = 1 och y-axeln i y = 3 f(x) = (x 3)(x + 1) = x x 3 är en bra start, men vi
2. 1 L ä n g d, o m k r e t s o c h a r e a
 2. 1 L ä n g d, o m k r e t s o c h a r e a Ett plan är en yta som inte är buktig och som är obegränsad åt alla håll. På ett plan kan man rita en linje som är rak (rät). En linje är obegränsad åt båda
2. 1 L ä n g d, o m k r e t s o c h a r e a Ett plan är en yta som inte är buktig och som är obegränsad åt alla håll. På ett plan kan man rita en linje som är rak (rät). En linje är obegränsad åt båda
Vardagsord. Förstår ord som fler än, färre än osv. Har kunskap om hälften/dubbelt. Ex. Uppfattning om antal
 TALUPPFATTNING Mål som eleven ska ha uppnått i slutet av det femte skolåret: Eleven skall ha förvärvat sådana grundläggande kunskaper i matematik som behövs för att kunna beskriva och hantera situationer
TALUPPFATTNING Mål som eleven ska ha uppnått i slutet av det femte skolåret: Eleven skall ha förvärvat sådana grundläggande kunskaper i matematik som behövs för att kunna beskriva och hantera situationer
Centralt innehåll i matematik Namn:
 Centralt innehåll i matematik Namn: T - Taluppfattning T1 Tiosystemet 5,23 1000 = 523/0,01= T2 Positionerna 2,39-0,4 = T3 Primtal Vilka är de fem första primtalen. Vad är ett primtal? T4 Primtalsfaktorering.
Centralt innehåll i matematik Namn: T - Taluppfattning T1 Tiosystemet 5,23 1000 = 523/0,01= T2 Positionerna 2,39-0,4 = T3 Primtal Vilka är de fem första primtalen. Vad är ett primtal? T4 Primtalsfaktorering.
lång och 15 cm bred. Hur stor area har tomten i verkligheten? 4,5 2 l b) 2-2- 3 4
 LÄXA 12 1 Beräkna med huvudräkning a) En kvadrat har arean 81 cm 2. Hur stor är omkretsen? b) Hur mycket kostar 600 g fläskfile, om priset per kilogram är 120 kr? c) En burk energidryck innehåller 200
LÄXA 12 1 Beräkna med huvudräkning a) En kvadrat har arean 81 cm 2. Hur stor är omkretsen? b) Hur mycket kostar 600 g fläskfile, om priset per kilogram är 120 kr? c) En burk energidryck innehåller 200
Lokala mål i matematik
 Lokala mål i matematik År 6 År 7 År 8 År 9 Taluppfattning (aritmetik) förstår positionssystemets uppbyggnad med decimaler ex: kan skriva givna tal adderar decimaltal ex: 15,6 + 3,87 subtraherar decimaltal
Lokala mål i matematik År 6 År 7 År 8 År 9 Taluppfattning (aritmetik) förstår positionssystemets uppbyggnad med decimaler ex: kan skriva givna tal adderar decimaltal ex: 15,6 + 3,87 subtraherar decimaltal
Matematiktävling för högstadieelever. Kvalificeringstest. Tid : 60 minuter Antal uppgifter: 15 Max poäng: 15 poäng. C: 1,101 D:!!!
 PYTHAGORAS QUEST Matematiktävling för högstadieelever Kvalificeringstest Tid : 60 minuter Antal uppgifter: 15 Max poäng: 15 poäng. 1 Vilket av talen nedan är närmast talet 1? A: " B: "" C: 1,101 D: """
PYTHAGORAS QUEST Matematiktävling för högstadieelever Kvalificeringstest Tid : 60 minuter Antal uppgifter: 15 Max poäng: 15 poäng. 1 Vilket av talen nedan är närmast talet 1? A: " B: "" C: 1,101 D: """
Arbetsblad 1:1. 1 Svara i bråkform hur stor andel av den stora rutan som är. 2 Svara i decimalform hur stor andel av den stora rutan som är.
 Arbetsblad 1:1 Tal i bråkform och i decimalform Grundbok: grundkurs s. 8 blåkurs s. 0 1 Svara i bråkform hur stor andel av den stora rutan som är a) grå b) kryssad c) prickad d) vit 2 Svara i decimalform
Arbetsblad 1:1 Tal i bråkform och i decimalform Grundbok: grundkurs s. 8 blåkurs s. 0 1 Svara i bråkform hur stor andel av den stora rutan som är a) grå b) kryssad c) prickad d) vit 2 Svara i decimalform
Avdelning 1, trepoängsproblem
 Avdelning 1, trepoängsproblem 1. I ett akvarium finns det 00 fiskar varav 1 % är blå medan övriga är gula. Hur många gula fiskar måste avlägsnas från akvariet för att de blå fiskarna ska utgöra % av alla
Avdelning 1, trepoängsproblem 1. I ett akvarium finns det 00 fiskar varav 1 % är blå medan övriga är gula. Hur många gula fiskar måste avlägsnas från akvariet för att de blå fiskarna ska utgöra % av alla
Ma7-Per: Geometri. Det tredje arbetsområdet handlar om geometri.
 Ma7-Per: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda
Ma7-Per: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda
Lokal studieplan matematik åk 1-3
 Lokal studieplan matematik åk 1-3 Kunskaps område Taluppfat tning och tals användni ng Centralt Innehåll Kunskapskrav Moment Åk1 Moment Åk2 Moment Åk3 Naturliga tal och deras egenskaper samt hur talen
Lokal studieplan matematik åk 1-3 Kunskaps område Taluppfat tning och tals användni ng Centralt Innehåll Kunskapskrav Moment Åk1 Moment Åk2 Moment Åk3 Naturliga tal och deras egenskaper samt hur talen
Avdelning 1, trepoängsproblem
 vdelning 1, trepoängsproblem 1. Vilket av dessa resultat får man när 20102010 divideras med 2010? : 11 : 101 :1001 D: 10001 E: Kvoten är ej ett heltal 2. Ivan fick 85 % av totalpoängen på ett prov medan
vdelning 1, trepoängsproblem 1. Vilket av dessa resultat får man när 20102010 divideras med 2010? : 11 : 101 :1001 D: 10001 E: Kvoten är ej ett heltal 2. Ivan fick 85 % av totalpoängen på ett prov medan
Start Matematik facit
 FACIT Start Matematik facit Årskurs 4-9 Facit till Start Matematik 47-60-0 Liber AB Får kopieras 2 Kapitel Siffror och tal a) 9-42 a) 9-42 c) 84 d) 555 e) -6 f) 7 400 c) 84 d) 555 e) -6 f) 7 400 g) 985
FACIT Start Matematik facit Årskurs 4-9 Facit till Start Matematik 47-60-0 Liber AB Får kopieras 2 Kapitel Siffror och tal a) 9-42 a) 9-42 c) 84 d) 555 e) -6 f) 7 400 c) 84 d) 555 e) -6 f) 7 400 g) 985
Arbetsblad 1:1. 1 Svara i bråkform hur stor andel av den stora rutan som är. 2 Svara i decimalform hur stor andel av den stora rutan som är.
 Arbetsblad 1:1 Tal i bråkform och i decimalform Grundbok: grundkurs s. 8 blåkurs s. 0 1 Svara i bråkform hur stor andel av den stora rutan som är a) grå b) kryssad c) prickad d) vit 2 Svara i decimalform
Arbetsblad 1:1 Tal i bråkform och i decimalform Grundbok: grundkurs s. 8 blåkurs s. 0 1 Svara i bråkform hur stor andel av den stora rutan som är a) grå b) kryssad c) prickad d) vit 2 Svara i decimalform
Facit Arbetsblad. 7 a) 32 b) 35 c) 27 8 a) 5 b) 18 c) 4 9 a) 18 b) 30 10 a) 17 b) 19 11 a) 6 b) 0 12 a) 24 b) 35. 1 Tal
 1 Tal Arbetsblad 1:1 1 a) 18 9 06 b) 85 10 00 c) 0 1 080 9 060 d) 5 105 6 780 e) 78 8 970 9 05 f) 990 75 102 5 2 a) 0 = 2 2 2 5 b) 75 = 5 5 c) 6 = 2 2 a) 8 = 2 2 2 2 b) 28 = 2 2 7 c) 90 = 2 5 a) = 2 2
1 Tal Arbetsblad 1:1 1 a) 18 9 06 b) 85 10 00 c) 0 1 080 9 060 d) 5 105 6 780 e) 78 8 970 9 05 f) 990 75 102 5 2 a) 0 = 2 2 2 5 b) 75 = 5 5 c) 6 = 2 2 a) 8 = 2 2 2 2 b) 28 = 2 2 7 c) 90 = 2 5 a) = 2 2
Facit Träningshäfte 9:2
 Kapitel 1 1 a) 4 800 000 b) 300 200 c) 25 085 d) 0,8 e) 0,25 f) 0,785 2 a) 2 miljoner 35 tusen: 2 035 000 235 tusen: 235 000 tjugotretusen femhundra: 23 500 b) 12 tiondelar: 1,2 12 hundradelar: 0,12 12
Kapitel 1 1 a) 4 800 000 b) 300 200 c) 25 085 d) 0,8 e) 0,25 f) 0,785 2 a) 2 miljoner 35 tusen: 2 035 000 235 tusen: 235 000 tjugotretusen femhundra: 23 500 b) 12 tiondelar: 1,2 12 hundradelar: 0,12 12
8A Ma: Geometri. Det tredje arbetsområdet handlar om geometri.
 8A Ma: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda strategier
8A Ma: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda strategier
Repetitionsuppgifter 1
 Repetitionsuppgifter 1 1 Är talet a) 5 ett heltal b) 9 ett naturligt tal c) π ett rationellt tal d) 5 ett reellt tal 6 2 Rita av figuren och placera in talen rätt talmängd. naturliga tal hela tal rationella
Repetitionsuppgifter 1 1 Är talet a) 5 ett heltal b) 9 ett naturligt tal c) π ett rationellt tal d) 5 ett reellt tal 6 2 Rita av figuren och placera in talen rätt talmängd. naturliga tal hela tal rationella
5B1134 Matematik och modeller Lösningsförslag till tentamen den 12 januari 2005
 KTH Matematik B Matematik modeller Lösningsförslag till tentamen den januari. a) I en triangel är två av sidlängderna 7 respektive 8 längdeneter vinkeln mellan dessa sidor är. Bestäm den tredje sidans
KTH Matematik B Matematik modeller Lösningsförslag till tentamen den januari. a) I en triangel är två av sidlängderna 7 respektive 8 längdeneter vinkeln mellan dessa sidor är. Bestäm den tredje sidans
Förord. Innehåll. 1 Tal 4. 4 Algebra 42. 2 Bråk och procent 18. 5 Statistik och sannolikhet 54. 6 Tid, hastighet och skala 60.
 Förord Det här häftet är tänkt som ett komplement till kapitel 5, Genrepet, i läroboken Matte Direkt år 9. Häftet vänder sig främst till de elever som har svårigheter att klara Genrepets nivå i boken och
Förord Det här häftet är tänkt som ett komplement till kapitel 5, Genrepet, i läroboken Matte Direkt år 9. Häftet vänder sig främst till de elever som har svårigheter att klara Genrepets nivå i boken och
18 a) 36 b) 900 c) 25 d) 1 REPETITIONSUPPGIFTER 2. 1 a) 20 m 2 b) 16 m 2 c) 10 m 2 d) 48 m 2 (50, 24 m 2 )
 epetitionsuppgifter Till varje kapitel finns repetitionsuppgifter i form av Arbetsblad. Uppgifterna är relaterade till innehållet i respektive kapitel och täcker hela kapitlet. De uppgifter som kräver
epetitionsuppgifter Till varje kapitel finns repetitionsuppgifter i form av Arbetsblad. Uppgifterna är relaterade till innehållet i respektive kapitel och täcker hela kapitlet. De uppgifter som kräver
Junior. låda 1 låda 2 låda 3 låda 4 låda 5 B V B V. a: det är omöjligt att göra så b: A c: V d: O e: R
 Junior vdelning 1. Trepoängsproblem 1. I fem lådor ligger kort. arje kort är märkt med en av bokstäverna,, R, O och. Peter ska plocka bort kort så att det blir ett enda kort kvar i varje låda och så att
Junior vdelning 1. Trepoängsproblem 1. I fem lådor ligger kort. arje kort är märkt med en av bokstäverna,, R, O och. Peter ska plocka bort kort så att det blir ett enda kort kvar i varje låda och så att
Torskolan i Torsås Mars 2007. Matematik. Kriterier för betyget godkänd. Metoder: Arbetssätt. Muntligt. Problemlösning
 Torskolan i Torsås Mars 2007 Matematik Kriterier för betyget godkänd Metoder: Arbetssätt Ta ansvar för sin egen inlärning. Göra läxor. Utnyttja lektionstiden (lyssna, arbeta). Utnyttja den hjälp/stöd som
Torskolan i Torsås Mars 2007 Matematik Kriterier för betyget godkänd Metoder: Arbetssätt Ta ansvar för sin egen inlärning. Göra läxor. Utnyttja lektionstiden (lyssna, arbeta). Utnyttja den hjälp/stöd som
Alternativdiagnos 1. 1 Vilka av talen är. 2 Vilka av talen är delbara med. 3 Dela upp talen i primfaktorer. 5 a) 4 ( 6) b) ( 12) c) ( 3) ( 7)
 Alternativdiagnos 1 1 Vilka av talen är a) naturliga b) eltal c) rationella d) reella 2 Vilka av talen är delbara med a) 2 b) 3 c) 5 d) 6 3,4 2 7 5 8 6 243 450 394 3 Dela upp talen i primfaktorer a) 15
Alternativdiagnos 1 1 Vilka av talen är a) naturliga b) eltal c) rationella d) reella 2 Vilka av talen är delbara med a) 2 b) 3 c) 5 d) 6 3,4 2 7 5 8 6 243 450 394 3 Dela upp talen i primfaktorer a) 15
Planering Geometri år 7
 Planering Geometri år 7 Innehåll Övergripande planering... 2 Bedömning... 2 Begreppslista... 3 Metodlista... 6 Arbetsblad... 6 Facit Diagnos + Arbeta vidare... 10 Repetitionsuppgifter... 11 Övergripande
Planering Geometri år 7 Innehåll Övergripande planering... 2 Bedömning... 2 Begreppslista... 3 Metodlista... 6 Arbetsblad... 6 Facit Diagnos + Arbeta vidare... 10 Repetitionsuppgifter... 11 Övergripande
Geometri. Kapitel 3 Geometri. Borggården sidan 68 Diagnos sidan 82 Rustkammaren sidan 84 Tornet sidan 90 Sammanfattning sidan 94 Utmaningen sidan 96
 Kapitel 3 Eleverna har tidigare arbetat med omkrets och area. I kapitlet repeteras först begreppet area och hur man beräknar rektangelns area. Enheten kvadratdecimeter, dm 2, för area introdu ceras. Här
Kapitel 3 Eleverna har tidigare arbetat med omkrets och area. I kapitlet repeteras först begreppet area och hur man beräknar rektangelns area. Enheten kvadratdecimeter, dm 2, för area introdu ceras. Här
Diplomingenjörs- och arkitektutbildningens gemensamma antagning 2017 Arkitektantagningens prov i matematik , Lösningar(SERIE A)
 Diplomingenjörs- och arkitektutbildningens gemensamma antagning 017 Arkitektantagningens prov i matematik..017, Lösningar(SERIE A) 1. a) Vilka reella tal x uppfyller likheten x =? (1 p.) b) Vilka reella
Diplomingenjörs- och arkitektutbildningens gemensamma antagning 017 Arkitektantagningens prov i matematik..017, Lösningar(SERIE A) 1. a) Vilka reella tal x uppfyller likheten x =? (1 p.) b) Vilka reella
Matematik Betygskriterier i matematik år 9 Ekholmsskolan i Linköping
 Enhet 591 Ekholmen Matematik Betygskriterier i matematik år 9 Ekholmsskolan i Linköping Fakta Förståelse Färdighet Förtrogenhet De olika formerna samspelar och utgör varandras förutsättningar. För att
Enhet 591 Ekholmen Matematik Betygskriterier i matematik år 9 Ekholmsskolan i Linköping Fakta Förståelse Färdighet Förtrogenhet De olika formerna samspelar och utgör varandras förutsättningar. För att
Tillämpad Matematik I Övning 3
 HH/ITE/BN Tillämpad Matematik I, Övning 3 1 Tillämpad Matematik I Övning 3 Allmänt Övningsuppgifterna, speciellt Typuppgifter i första hand, är eempel på uppgifter du kommer att möta på tentamen. På denna
HH/ITE/BN Tillämpad Matematik I, Övning 3 1 Tillämpad Matematik I Övning 3 Allmänt Övningsuppgifterna, speciellt Typuppgifter i första hand, är eempel på uppgifter du kommer att möta på tentamen. På denna
PRIMA MATEMATIK EXTRABOK 3 FACIT
 PRIMA MATEMATIK EXTRABOK FACIT t.ex. Dela upp talet. = + + = + + = + + Dela upp talet i lika stora delar. = +, +++ = ++ = +, ++ = ++++ = + = + + Skriv alla uppdelningar du kan av talet, lika stora delar.,
PRIMA MATEMATIK EXTRABOK FACIT t.ex. Dela upp talet. = + + = + + = + + Dela upp talet i lika stora delar. = +, +++ = ++ = +, ++ = ++++ = + = + + Skriv alla uppdelningar du kan av talet, lika stora delar.,
FACIT 0, ,10 0, ,75. b) 3 3 = 1. d) 5 2 = a) b) 60 c) d) 1,818 e) 0,898 f) Ex. 3 0,25 = 0,75
 FACIT Ç TUMMEN UPP! MATTE ÅK KARTLÄGGNING TALUPPFATTNING 7 a) 00 0,0 Exempel: 0 = 0 0 = 0 7 b) 0 00 0 0,0 0 kr = 0 c) 0 00 0,0 7 0 kr = 0 = 0 Eget val a) 7 b) c) d) 0 e) 0 f) g) h) 0 0 0% % 0, 0 7% 00
FACIT Ç TUMMEN UPP! MATTE ÅK KARTLÄGGNING TALUPPFATTNING 7 a) 00 0,0 Exempel: 0 = 0 0 = 0 7 b) 0 00 0 0,0 0 kr = 0 c) 0 00 0,0 7 0 kr = 0 = 0 Eget val a) 7 b) c) d) 0 e) 0 f) g) h) 0 0 0% % 0, 0 7% 00
Matematik. Namn: Datum:
 Matematik Namn: Datum: Multiplikation, tabell 2 och 4. Hur många ben har djuren tillsammans? + = = + + = = + + + + = = + = = + + + = = Skriv färdigt multiplikationen! 3 4 = 4 2 = 2 5 = 4 6 = 4 0 = 4 5
Matematik Namn: Datum: Multiplikation, tabell 2 och 4. Hur många ben har djuren tillsammans? + = = + + = = + + + + = = + = = + + + = = Skriv färdigt multiplikationen! 3 4 = 4 2 = 2 5 = 4 6 = 4 0 = 4 5
5-3 Areaskalan och volymskalan Namn:.
 5-3 Areaskalan och volymskalan Namn:. Detta kapitel är klart överkursbetonat. Men tycker du att det är kul med problemlösning: kör så det ryker! Inledning I föregående kapitel studerade du skalor, och
5-3 Areaskalan och volymskalan Namn:. Detta kapitel är klart överkursbetonat. Men tycker du att det är kul med problemlösning: kör så det ryker! Inledning I föregående kapitel studerade du skalor, och
Formula 9 facit. 1 Beräkningar med positiva tal 1
 Beräkningar med positiva tal Formula 9 facit a) 5,5 (5,50) b) 5,59 c) 5,99 d) 5,54 2 a) 3 (3,00) b) 3,09 c) 3,49 d) 3,04 3 a) 6, (6,0) b) 6,0 c) 5,6 d) 6,06 4 a) 9,04 b) 8,95 c) 8,55 d) 9 (9,00) 5 a) 25
Beräkningar med positiva tal Formula 9 facit a) 5,5 (5,50) b) 5,59 c) 5,99 d) 5,54 2 a) 3 (3,00) b) 3,09 c) 3,49 d) 3,04 3 a) 6, (6,0) b) 6,0 c) 5,6 d) 6,06 4 a) 9,04 b) 8,95 c) 8,55 d) 9 (9,00) 5 a) 25
Detta prov består av del 1 och 2. Här finns också facit och förslag till poängsättning
 Allmänt om proven Detta prov består av del 1 och. Här finns också facit och förslag till poängsättning och bedömning. Provet finns på lärarwebben, dels som pdf-fil och dels som redigerbar Word-fil. Del
Allmänt om proven Detta prov består av del 1 och. Här finns också facit och förslag till poängsättning och bedömning. Provet finns på lärarwebben, dels som pdf-fil och dels som redigerbar Word-fil. Del
