Väcker fotboll lika mycket känslor på börsen som på läktaren?
|
|
|
- Håkan Jonasson
- för 8 år sedan
- Visningar:
Transkript
1 ÖREBRO UNIVERSITET Handelshögskolan Nationalekonomi, magisteruppsats Handledare: Mikael Stenkula Examinator: Dan Johansson VT 206 Väcker fotboll lika mycket känslor på börsen som på läktaren? En empirisk studie som undersöker matchresultats påverkan på aktiekursen Författare: Jacob Pelgander Erik Strannelid
2 Abstract The purpose of this paper is to investigate whether or not the outcome of football games affect the share price of football clubs on the stock exchange. By regression and panel analysis we test if the result of a football game has any effect on the abnormal return for ten different football clubs share price. The variables used in the regression are the outcome of the game; wins, draws and losses, the venue, the type of competition and the expectations before the games. The findings show that the share price is affected, more often in a negative way than in a positive. For most clubs losses and draws have a significant negative affect on the share price. Only one of the clubs has a significant positive affect for wins throughout the testing process. European Cup losses has a greater affect than losses in the domestic league in the panel analysis. Key words: Abnormal returns, Football matches, behavioral economics
3 Innehållsförteckning. Inledning Teoretisk bakgrund CAPM Finansiell beteendevetenskap Teori tillämpad på fotbollsklubbar Tidigare studier Data Empirisk modell Resultat Regressionsanalys Paneldataanalys Diskussion Diskussion för regressionsanalys Diskussion för paneldataanalys Brister och begränsningar Slutsatser Referenslista... 30
4 . Inledning Ökad konkurrens inom den Europeiska toppfotbollen har fört med sig ett allt större behov av finansiering från utomstående investerare. Behovet av finansiering har lett till att en del fotbollsklubbar valt att bli offentliga bolag som handlas på börsen. Tottenham Hotspurs var den första klubben att ta steget in på den publika marknaden 983, och sedan dess har många fotbollsklubbar följt i deras fotspår (Peenstra & Scholtens, 2009). Många av de fotbollsklubbar som blev introducerade på börsen har sedan dess blivit uppköpta och åter borttagna från börsen. Då fotbollsklubbar på börsen är en relativt ny företeelse är det av intresse att undersöka hur information om fotbollslagen påverkar aktiekursen. Information om hur bra lagen är ges ungefär en gång i veckan i form av en match mot ett konkurrerande lag, medan information om fotbollsklubbens ekonomiska status ges likt andra företag, i form av kvartalsrapporter och press-meddelanden med mera. Syftet med uppsatsen är att undersöka om det sportsliga resultatet för fotbollsklubbar påverkar klubbarnas aktiekurs. Uppsatsen kommer undersöka sambandet mellan matchresultat och aktiekurser för tio fotbollsklubbar; Juventus FC, SS Lazio, AS Roma, SL Benfica, Sporting Lissabon, FC Porto, Celtic FC, Borussia Dortmund, Olympique Lyon och Manchester United. Det finns ett flertal studier som har undersökt hur matcher påverkar fotbollsklubbars aktiekurs. Danis och Demir (20) undersöker tre börsnoterade lag i Turkiet. De analyserar hur vinst-, förluster-, oavgjorda, hemma-, borta-, liga- och Europamatcher och förväntningar på matchen påverkar kursen. Danis och Demir kommer fram till att en förlust har en signifikant negativ påverkan på den avvikande avkastningen dagen efter match oavsett om matchen spelas hemma, borta, i ligan eller ute i Europa. Vinst har endast en positiv signifikant påverkan på den avvikande avkastningen när vinsten är starkt oväntad. Peenstra och Scholtens (2009) undersöker ett liknande syfte som Danis och Demir men skillnaden är att de gör en paneldataanalys. De använder sig av 274 spelade matcher mellan åren Variablerna som används är vinst, förlust eller oavgjord samt om matchen spelas hemma, borta, i ligan eller i Europa. Peenstra och Scholtens använder också förväntningar på matchen som en förklarande variabel. Resultaten de kommer fram till är att förlust har en signifikant negativ påverkan på aktiekursen, och den är fortsatt signifikant negativ oavsett om matchen är hemma eller borta, i ligan eller ute i Europa. Peenstra och Scholtens resultat visar även att vinst har en signifikant positiv påverkan på aktiekursen.
5 Den effektiva marknadshypotesen säger att prissättningen sker utifrån all tillgänglig information om framtida avkastning samt att investerare agerar rationellt. Förutom ny information om sådant som kan påverka företagets ekonomiska resultat kan priset också påverkas av investerares humör. Det finns många typer av irrationella beslut som kan förklaras med finansiell beteendevetenskap. I de fall som en fotbollsaktie ägs av en fotbollssupporter finns risk att investeraren har en övertro på vad laget i fråga kan prestera. Ett matchresultat antas ha stark påverkan på en supporters humör, vilket kan leda till att investeraren överreagerar på en liten bit information som egentligen har lite eller ingen betydelse för fotbollsklubbens ekonomi. (Gavelin & Sjöberg, 202) För att se hur aktiepriset påverkas dagen efter match tar vi fram ett mått på avvikande avkastning baserat på capital asset pricing model (CAPM). Den metod som används för att undersöka syftet är en regressionsanalys för varje lag och en paneldataanalys för lagen gemensamt. Regressionsanalyserna görs utifrån fyra modeller. I den först modellen tas vinster, oavgjorda och förluster med. Sedan byggs modellen på med hemma- och bortamatcher. Den tredje modellen tar med om matchen spelas i ligan eller ute i Europa och den fjärde och sista modellen tar med förväntningar på matchen i form av odds. Resultatet visar att aktiekursen påverkas av matchresultat. Flera klubbars aktiekurs har signifikant negativ avvikande avkastning dagen efter match vid förlust och oavgjord. En av klubbarna har signifikanta positiva resultat vid vinst. I paneldataanalysen har oavgjord och förlust signifikant negativ påverkan på aktiepriset. Uppsatsens disposition är som följer. I kapitel två tas den finansiella teori upp som ligger till grund för uppsatsen. I kapitel tre tas tidigare studier som undersökt ett liknande syfte upp. I kapitel fyra beskrivs den data som används i uppsatsen. I kapitel fem går vi igenom den empiriska modell som används i uppsatsen. I kapitel sex visas resultaten och i kapitel sju diskuteras dessa resultat. Slutsatserna tas upp i kapitel åtta. 2
6 2. Teoretisk bakgrund 2. CAPM En av de mest grundläggande modellerna inom investeringsteori kallas för Capital asset pricing model (CAPM). CAPM grundas på antaganden om att alla investerare är rationella, har tillgång till samma information, att alla tillgångar handlas offentligt, investerare kan låna till en gemensam riskfri ränta, marknaden är stor och investerare är pris-tagare samt att det inte finns någon skatt eller transaktionskostnader. (Bodie, Kane, & Marcus, 204) Den rationella investeraren vill hitta den kombination av tillgångar som ger högsta möjliga förväntad avkastning till lägsta möjliga risk. I modellen används varians som mått på risk. De optimala kombinationerna av tillgångar hittas längs den effektiva fronten. När lånemarknaden tas in i modellen tillkommer ytterligare placeringsmöjligheter. Investerare kan låna pengar till en riskfri ränta men även placera pengar på banken till samma ränta. Lånemarknaden gör det möjligt att skapa kapitalmarknadslinjen, vilken utgör de effektivaste investeringsmöjligheterna. I figur illustreras effektiva fronten av den positivt lutande delen av den tunna svarta linjen och kapitalmarknadslinjen av den tjocka rätalinjen. (Bodie, Kane, & Marcus, 204) Figur. Kapitalmarknadslinjen En möjlig vidareutveckling på figur är att ersätta x-variabeln varians mot beta. Beta är ett mått på hur väl en tillgång korrelerar med marknaden. Om en tillgångs beta är innebär det att en procents uppgång på marknaden leder till en procents uppgång av tillgångens värde. I Figur 2 används beta istället för varians på x-axeln. Linjen som erhålls kallas Security market line (SML). (Bodie, Kane, & Marcus, 204) 3
7 Figur 2. Security market line Enligt CAPM finns det en förväntad avkastning för en given tillgång baserat på den riskfria räntan, tillgångens korrelation med marknaden samt marknadens avkastning. Den avkastning som inte kan förklaras av beta kommer i fortsättningen av denna uppsats kallas för avvikande avkastning. Avvikande avkastningen erhålls genom att ta den observerade avkastningen minus den förväntade avkastningen. Effektiva marknadshypotesen bygger på att aktier och värdepapper är prissatta utifrån all tillgänglig information som finns. Aktier och andra värdepapper är rationellt prissatta och de framtida förändringarna i kursen är slumpmässiga. Det finns tre olika former av den effektiva marknaden. De tre formerna är svag form, mellanstark form och stark form. Svag form innebär att aktiekurserna förklaras av historiska priser. I den mellanstarka formen så ingår all publik information om bolagen. Stark form innebär att all publik och privat information ingår i aktiekurserna. Stark form är svårt att uppnå då det skulle innebära att det sysslades med insider handel som är olagligt. (Gavelin & Sjöberg, 202) De antaganden som ligger tillgrund för CAPM och effektiva marknadshypotesen kan dock ifrågasättas. Flera studier påvisar att upp- och nedgångar på börsen kan förklaras av andra faktorer än risk och förväntad avkastning. Tidigare studier har även visat att investerares beslut inte alltid är rationella och att investeringsbeslut även styrs av humör eller andra mänskliga faktorer. Hirshleifer och Shumway (2003) hittar i sin studie bevis för att väder har en signifikant påverkan på marknadens avkastning. Andra studier har påvisat samband mellan sportsliga resultat och börsutveckling. Edmans m fl, (2007) hittar bevis för att ett lands börs sjunker när dess landslag blir utslaget från Världsmästerskapen i fotboll. Det finns även empiriska bevis för 4
8 att matchresultat i klubblagsfotboll kan påverka börsen. I Turkiet finns samband mellan börsen och matchresultat för de fotbollsklubbar som anses ha hängivna supportrar (Berument, Ceylan, & Ogut-Eker, 2009). 2.2 Finansiell beteendevetenskap 979 presenterade de två psykologerna Tversky och Kahneman resultatet från en studie som skapade en helt ny gren av ekonomi, nämligen finansiell beteendevetenskap. Grunden för finansiell beteendevetenskap är att traditionell marknadsteori inte tar hänsyn till hur människor faktiskt beter sig och hur de tar beslut. Människors irrationella beteenden kan förklaras av två typer av fel. Vid den första typen av fel saknar investeraren tillräckligt med information för att ta rätt beslut. Den andra typen av fel är att investeraren har rätt information men ändå tar beslut som inte ger dem bästa möjliga utfall. Undersökandet av den andra typen av fel ledde till att Kanheman fick Sveriges Riksbanks pris i ekonomisk vetenskap till Alfred Nobels minne år (Gavelin & Sjöberg, 202) Kahenman och Tversky (979) kom i sin studie fram till att människor uppfattar vinster och förluster på olika sätt. Människor tenderar att vara känsligare för förluster än vinster, vilket innebär att en förlust gör mer ont än vad en vinst gör gott. Ett annat psykologiskt fenomen brukar kallas för spelarens misstag. Det innebär att investeraren tror att en händelse som precis har inträffat har lägre sannolikhet att inträffa igen. Till exempel om det har kommit klave 20 gånger i rad på slantsingling så tror flertalet att krona kommer att dyka upp nästa gång, men sannolikheten ändras inte utan det är fortfarande 50 procents chans att klave kommer igen (Gavelin & Sjöberg, 202). En psykologisk faktor som brukar nämnas i finansiell beteendevetenskap är förankring. Vid förankring fäster en investerare ett värde på en tillgång utan stöd av relevanta fakta. Ett exempel är att investerare håller kvar vid sjunkande aktier för att de anser att aktien egentligen är värd den köpkursen de köpte aktien för. Ett annat irrationellt tankemisstag är mentala konton. Människor tenderar att dela upp sina tillgångar i olika mentala konton. Investeraren gör skillnad mellan olika konton och tar olika stor risk beroende på vad kontot representerar. Andra förekommande beteenden är övertro på sin egen förmåga, överreaktion på ny information, flockbeteende och att investerare söker efter information som bekräftar vad de själva redan tror. (Gavelin & Sjöberg, 202) 5
9 2.3 Teori tillämpad på fotbollsklubbar De teorier som har tagits upp i detta avsnitt försöker förklara hur investerare tänker och agerar på aktiemarknaden. Den finansiella beteendevetenskapen och effektiva marknadshypotesen är två olika teorier om hur investerare fungerar. Uppsatsen avser undersöka hur fotbollsresultat påverkar fotbollsklubbarnas aktiekurser. Finansiella beteendevetenskapen visar att människor inte alltid agerar rationellt utan att det finns förklaringar till att investerare inte är rationella. Dessa förklaringar kan även tillämpas på investerare i fotbollsklubbar. Om det är supportar som är aktieägare kan det finnas övertro och en överreaktion på hur laget och aktiekursen ska gå. En förlust kan till exempel ta hårt vilket innebär att en supporter kan agera irrationellt på aktiemarknaden då den överreagerar på den lilla information som ges vid match. Resultatet från en enskild match i fotboll har inte några direkta ekonomiska effekter på klubben och därför ska inte enskilda matcher påverka klubbens aktiepris enligt den effektiva marknadshypotesen. Det finns givetvis undantag från detta, till exempel i Cup-spel där en enskild match kan innebära avancemang och inkomster till klubben. Matchresultatet från enskilda ligamatcher kan ses som en bit information om hur laget kan förväntas prestera under säsongen men saknar direkt påverkan på klubbens ekonomiska resultat. Det är lagets slutplacering i ligan som avgör vilken ekonomisk kompensation klubben får. Med detta sagt så borde inte enskilda matcher ha en stor påverkan på aktiekursen enligt den effektiva marknadshypotesen, utan det är i slutet av säsongen när investerare vet vilken slutplacering laget får som det borde visas i aktiekursen. Avvikande avkastning för börshandlade fotbollsklubbar dagen efter en match borde därför förklaras av irrationellt beteende snarare än rationalitet och ekonomisk data. Psykologiska effekter kan ha betydelse för fotbollsklubbarnas aktiepris dagen efter match. Om det finns signifikant påverkan på aktiepriset dagen efter en spelad fotbollsmatch så antas det i denna uppsats att det till största del beror på psykologiska effekter. 6
10 3. Tidigare studier Att undersöka hur matchresultat påverkar klubbarnas aktiepriser har undersökts i flera tidigare studier. Forskningen visar resultat som tyder på att matchernas resultat påverkar aktiepriserna. De påverkar olika mycket beroende på vilket/vilka lag som undersöks och även var matchen är spelad. Hakan Danis och Ender Demir (20) undersöker tre klubbar i den turkiska högsta ligan och hur deras matchresultat påverkar aktiekurserna. Tidsperioden sträcker sig från den dagen lagen blev börsnoterade till slutet av säsongen De klubbar som undersöks är Fenerbahce, Galatasaray och Besiktas. De förklarande variabler som används för att undersöka syftet är vinster, oavgjorda, förluster, om matchen spelades hemma eller borta och om den spelades i den inhemska ligan eller ute i Europa. De använder sig även av odds för att få med de förväntningar som finns på matchens resultat. Oddsen räknas om till sannolikheter i syfte att avgöra om matchens resultat var förväntat eller inte. Om sannolikheten för vinst var större än 0,6 och laget vann så räknas det som en förväntad vinst. Metoden som används är en regressionsanalys för vardera lagen där avvikande avkastning är den beroende variabeln. De resultat som Danis och Demir kommer fram till är att en förlust har en signifikant negativ påverkan på den avvikande avkastningen även oavgjord har en signifikant negativ påverkan. Förlust ger signifikant negativ påverkan oavsett om matchen spelas hemma eller borta i cupspel eller i ligan och oavsett vilket det förväntade matchresultatet är. Vinst har en positiv signifikant påverkan på avvikande avkastning för ett av lagen när vinsten var starkt oväntad. Luc Renneboog och Peter Vanbrabant (2000) studerar sambandet mellan matchresultat och aktiekursen för de 7 brittiska lag som var listade på London stock exchange market (LSE) och på alternative investment market (AIM) mellan åren Renneboog och Vanbrabants metod är en paneldataanalys, där de undersöker hur aktiekursen påverkas de fem första dagarna efter match. De förklarande variabler som används i studien är vinster, förluster och oavgjorda men även vilken typ av match som spelas. Syftet med att dela upp matcherna i olika kategorier är att se om det är någon skillnad i påverkan på en vanlig ligamatch mot till exempel en ligamatch som gäller uppflyttning/nedflyttning. Resultaten visar att vinster har en positiv signifikant effekt på avkastningen samt att förlust och oavgjord har en negativ signifikant effekt. De flesta signifikanta resultat infaller dagen efter match. Det finns dock vissa matchresultat som har signifikant påverkan tre eller fyra dagar efter match men dessa resultat har mindre 7
11 påverkan och en lägre signifikansnivå. Alla typer av matcher med signifikanta resultat har signifikanta resultat första dagen efter match. Renneboog och Vanbrabant kommer även fram till att effekten är större när det är en uppflyttnings-/nedflyttningsmatch som spelas än en vanlig ligamatch. Wijtze Peenstra och Bert Scholtens (2009) undersöker i sin artikel 274 spelade fotbollsmatcher mellan åren för att se hur de påverkar aktiekursen. De tar fram den avvikande avkastningen som de använder som beroende variabel. De förklarande variabler som används i studien är vinster, förluster, oavgjorda, liga eller Europamatch och förväntningar på matchresultatet. De använder sig av paneldataanalys för att undersöka deras syfte och resultaten de kommer fram till är att vinster ger en svag positiv avkastning samtidigt som förluster och oavgjorda matcher ger en negativ effekt på den avvikande avkastningen. När förväntningar och om matchen var en liga eller Europamatch tas med i modellen ges liknande svar. Oavsett om förlusten är väntad eller oväntad så ger det en negativ påverkan på avkastningen för både ligamatcher och Europamatcher. Vinsterna ger fortfarande en positiv påverkan oavsett om vinsten var väntad eller oväntad i den inhemska ligan, för Europamatcher ger det en positiv påverkan om vinsten var oväntad. John M. Gandar, Reinhold P. Lamb, Richard A. Zuber & Patrick Yiu (2005) undersöker tio börsnoterade lag i England mellan tidsperioden De använder sig av avvikande avkastning som beroende variabel och sedan variabler som vilken typ av match, om det är hemma eller borta, förväntningar på matchen och även målskillnad som förklarande variabler. De har även med två dummy variabler som beskriver om laget ligger i topp fem eller bland de tre sista då de ligaplaceringarna har en extra ekonomisk betydelse. De använder sig av regressionsanalys för varje enskilt lag samt en paneldataanalys. Gandar m.fl resultat visar knappt på några signifikanta skattningar och hittar därmed inga bevis för att matcher påverkar aktiekursen. Den signifikans de hittar är att vilken typ av match som spelas har betydelse. Cupmatcher har en positiv påverkan på den avvikande avkastningen. Ramzi Benkraiem, Pierre Marques och Waël Louhichi (2009) undersöker 745 matcher utspridda på 8 europeiska lag i sju länder. Syftet är att se hur aktiekursen och handelsvolymen påverkas kring matchdagen, alltså både innan och efter en spelad match. Den beroende variabel som undersöks är den avvikande avkastningen och den avvikande handelsvolymen. De förklarande variablerna som används är vinster, oavgjorda, förluster samt om matchen spelas 8
12 hemma eller borta. Benkraiem m fl använder sig av en regressionsanalys för att undersöka syftet. De finner signifikans att matcher påverkar den avvikande avkastningen och handelsvolymen. Handelsvolymen påverkas både före och efter att matchen har spelats. Dagen efter match finner de signifikanta resultat för avvikande avkastning för matchresultaten förlust och oavgjord. Matchresultatet vinst har däremot signifikanta resultat för avvikande avkastning dagen innan matchen spelas. 9
13 4. Data I detta avsnitt så beskrivs de data som används i uppsatsen. De data som används har hämtats från yahoofinance, worldfootball och oddsportal. Det som undersöks är tio europeiska fotbollslag under tidsperioden Fotbollsklubbarnas resultat är inhämtat från internetsidan worldfootball, oddsen är hämtade från sidan oddsportal och aktiekurserna är hämtade från yahoofinance. De fotbollsklubbar som undersöks är AS Roma, SS Lazio, Juventus FC, FC Porto, SL Benfica, Sporting Lissabon, Borussia Dortmund, Olympique Lyon, Celtic FC och Manchester United. Data för Manchester United går från augusti 202 till slutet 205 på grund av att de inte blev börsnoterade på Nasdaq förrän augusti 202, anledningen till att Manchester United är med i uppsatsen trots att data för hela tidsperioden inte finns är för att Manchester är det enda engelska laget som är börsnoterat. Variablerna som används i denna uppsats motiveras genom de tidigare studier som undersökt en liknande frågeställning. I Danis & Demir (20) så används förutom vinster, oavgjorda och förluster även om det var hemma/bortamatch, Europa/ligamatch och förväntningar på matchen. I denna uppsats kommer liknande variabler att tillämpas. 0
14 Tabell. Deskriptiv statistik Variabel Observationer Medelvärde Standard Min Max avvikelse Vinst ,07 0,26 0 Oavgjord ,03 0,6 0 Förlust ,03 0,6 0 Hemmavinst ,04 0,2 0 Hemmaoavgjord ,0 0, 0 Hemmaförlust ,0 0,09 0 Bortavinst ,03 0,7 0 Bortaoavgjord Bortaförlust Europavinst Europaoavgjord Europaförlust Ligavinst Ligaoavgjord Ligaförlust Förväntad vinst Svagt oväntad vinst Starkt oväntad vinst Förväntad oavgjord Positiv oväntad oavgjord Negativ oväntad oavgjord Förväntad förlust Svagt oväntad förlust Starkt oväntad förlust ,02 0,02 0,0 0,0 0,0 0,06 0,02 0,02 0,04 0,02 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,2 0,3 0, 0,08 0,08 0,24 0,4 0,4 0,2 0,4 0,09 0, 0,09 0,09 0, 0,09 0, Avvikande avkastning ,0027 0,04 0,68 0,64 Den beroende variabeln är klubbarnas avvikande avkastning, alltså avkastningen på klubbarnas aktier när aktiekurserna är jämförda med indexet. Avvikande avkastningen är framräknad genom att skatta ett beta och alfa för varje aktie och sedan använda sig av CAPM för att räkna fram den avvikande avkastningen. Avvikande avkastningen avser nästa handelsdag efter matchen har spelats, om till exempel matchen spelades på söndagen så används den avvikande avkastningen för måndagen. Tabell visar att den avvikande avkastningens medelvärde för de tio lagen gemensamt är -0,027 procent.
15 De förklarande variablerna som används i denna uppsats är vinster, förluster, oavgjorda, hemma, borta, liga, Europa och förväntningar på matcherna. Samtliga förklarande variabler är dummy-variabler. Det innebär att värdena för variablerna är binära och antar antingen värdet 0 eller. I tabell visas deskriptiv statistik över undersökningens variabler. I den andra kolumnen är antalet observationer. Totalt har dagar undersökts för samtliga variabler. Kolumn tre visar medelvärde. För dummy-variablerna visar medelvärdet hur stor andelen av observationerna som antar värdet ett. Till exempel antar variabeln vinst värdet ett 472 antal gånger, då 0,0702 * = 472. I kolumn fyra visas standardavvikelse och i kolumn fem och sex visas min och maxvärde för varje variabel. Den förklarande variabeln vinst inträffar 472 gånger utav de 2553 spelade matcher, alltså är den gemensamma vinstprocenten för lagen 57,6 procent. Oavgjord står för 2,3 procent av matcherna och förluster de resterande 2 procenten. Utav de 2553 spelade matcher så spelades 272 av dessa på hemmaplan och 28 av matcherna på bortaplan. 79,5 procent av matcherna var inhemska ligamatcher och de andra 20,5 procenten var Europamatcher. Under tidsperioden så var det 844 dagar utan match och 2553 matchdagar. Förväntningar på matchen räknas ut med hjälp av odds, genom att räkna ut den inverterade sannolikheten för varje enskild match. Om sannolikheten för vinst är större än 0,6 och laget vinner så räknas matchen som en förväntad vinst. Är sannolikheten för vinst lägre än 0,4 innebär det att laget förväntas förlora, och en sannolikhet mellan 0,6 och 0,4 innebär att matchen förväntas sluta oavgjort. Denna beslutsregel används i Danis & Demir (20) och i Gandar m fl (2005). AS Roma spelade en match mot Genoa CFC den 20 december 205. Oddsen för Romaseger var,53, oddsen för oavgjord var 4,2 och oddsen för Romaförlust var 6,76. Den inverterade sannolikheten för dessa odds är 0,629, 0,229 och 0,42. Då Roma vann matchen och sannolikheten för seger var större än 0,6 blir matchen placerad i kategorin Förväntad vinst(fv). I tabell 2 visas de nio variabler som matcherna delas in i utifrån de förväntningar som finns. 2
16 Tabell 2. Förväntningsvariablerna Förväntat resultat Faktiskt resultat Variabelutfall Vinst Vinst Förväntad vinst (fv) Oavgjord Vinst Svagt oväntad vinst (sov) Förlust Vinst Starkt oväntad vinst (stov) Oavgjord Oavgjord Förväntad oavgjord (fo) Förlust Oavgjord Positiv oväntad oavgjord (Poo) Vinst Oavgjord Negativ oväntad oavgjord (Noo) Förlust Förlust Förväntad förlust (ff) Oavgjord Förlust Svagt oväntad förlust (sof) Vinst Förlust Starkt oväntad förlust (stof) En av svagheterna med datasetet är att Manchester United inte handlades på Nasdaq förrän 202, vilket leder till avsaknad av data och en obalanserad panel. Samtliga fotbollsklubbar i datasetet är börsnoterade bolag men alla fotbollsklubbar handlas inte lika frekvent. Det finns betydande skillnader mellan bolagens handelsvolymer på börsen. En fotbollsklubb som inte handlas frekvent kan ge sämre resultat då handelsvolymen dagen efter match kan vara noll. En annan svaghet är att sannolikhetsnivåerna som avser förväntningar på matchen är godtyckligt valda, men beslutsregeln har används i flera tidigare studier. Därför kommer även beslutsregeln gälla i denna uppsats. Hade andra beslutsregler används så hade resultaten kunnat se annorlunda ut. 3
17 5. Empirisk modell Modellen i denna uppsats bygger på tidigare studiers använda modell. Danis och Demir (20) använder regressionsanalyser för att få fram matchresultats påverkan på den avvikande avkastningen. I denna uppsats kommer en liknande modell att användas både för att räkna ut den avvikande avkastningen för vardera lagen samt regressionsanalyserna för att se hur matchresultaten påverkar aktiekursen. Den avvikande avkastning som används som beroende variabel i denna uppsats räknas ut på följande sätt. I modell räknas avkastningen för varje lag ut, genom att ta den naturliga logaritmen av aktiepriset dag t minus den naturliga logaritmen för aktiepriset dag t-. R t = ln(p t ) ln(p t ) () Avkastningen från modell används sedan i en regression i modell 2 för att estimera fram ett alfa och beta för respektive lag. R it = α i + β i R mt + ε (2) Där R mt står för marknadens avkastning. De estimerade alfa- och betavärdena används sedan i modell 3 för att få fram den avvikande avkastningen. Det är den avvikande avkastningen som används i regressionerna. AR it = R it (α i + β ir mt ) (3) I tabell 3 visas alfa- och betavärdena för varje lag. 4
18 Tabell 3. Alfa- och Betavärdena Lag Alfa Beta Roma -0, ,24 Lazio 0, ,28 Porto -0, ,28 Sporting -0, , Benfica -0, ,34 Dortmund 0, ,44 Juventus -0, ,32 Celtic 0, ,00 Lyon -0, ,3 Manchester United 0, ,48 Efter att den avvikande avkastningen är framräknad görs fyra olika regressionsmodeller för att se hur matchresultat påverkar den avvikande avkastningen. Regressionerna görs med minsta kvadratmetoden. Det finns tre antaganden som ska uppfyllas när minsta kvadratrotsmetoden används. De tre antagandena är att medelvärdet på feltermen ska vara noll, variablerna i regressionen är oberoende av varandra och har samma fördelning samt att extremvärden är osannolika. I modell 4 görs en regression för varje lag för att se hur vinst, oavgjord och förlust påverkar den avvikande avkastningen. AR t = α + β D Vinst + β 2 D Oavgjord + β 3 D Förlust + ε t (4) Hypotesprövningen för samtliga variabler ser ut som följer: H 0 : β = 0 H : β 0 Modell 5 bygger vidare på modell 4 och tillför hemma och bortaplan för att se om den avvikande avkastningen påverkas olika om matchen spelas hemma eller borta AR t = α + β D hv + β 2 D ho + β 3 D hf + β 4 D bv + β 5 D bo + β 6 D bf + ε t (5) Variablerna i modell 5 är avvikande avkastning (AR), hemmavinst (hv), hemmaoavgjord (ho), hemmaförlust (hf), bortavinst (bv), bortaoavgjord (bo) samt bortaförlust (bf). 5
19 I modell 6 undersöks om avvikande avkastningen påverkas olika om matchen är en ligamatch eller Europamatch. AR t = α + β D ev + β 2 D eo + β 3 D ef + β 4 D lv + β 5 D lo + β 6 D lf + ε t (6) Variablerna i modell 6 är Europavinst (ev), Europaoavgjord (eo), Europaförlust (ef), ligavinst (lv), ligaoavgjord (lo) och ligaförlust (lf). I modell 7 tas förväntningarna på matchen med i regressionen. AR t = α + β D fv + β 2 D sov + β 3 D stov + β 4 D fo + β 5 D Poo + β 6 D Noo + β 7 D ff + β 8 D sof + β 9 D stof + ε t (7) Variablerna i modell 7 är förväntad vinst (fv), svagt oväntad vinst (sov), starkt oväntad vinst (stov), förväntad oavgjord (fo), positiv oväntad oavgjord (Poo), negativ oväntad oavgjord (Noo), förväntad förlust (ff), svagt oväntad förlust (sof) och starkt oväntad förlust (stof). Vidare kommer även en panel undersökas. För att se om det finns några generella slutsatser som kan dras för de tio lagen gemensamt. Paneldataregressionerna är samma som modell 4-7 fast för alla lag gemensamt. I regressionen för panelen används fixa effekter för att ta hänsyn till de skillnader som finns mellan fotbollsklubbarna men som är samma över tid. 6
20 6. Resultat 6. Regressionsanalys I tabell 4 visas resultat från regressionen av modell 4 för varje enskilt lag. Fem lag har signifikant negativ avvikande avkastning vid förlust. Tre lag har signifikant negativ avvikande avkastning vid oavgjord och endast ett lag har en positiv signifikant avvikande avkastning vid vinst, vilket betyder att nollhypoteserna förkastas. Vid en Romaförlust är den avvikande avkastningen dagen efter match i genomsnitt -,3 procent. Tabell 4. Regressionsanalys för modell 4 Lag Konstant Vinst Oavgjord Förlust R 2 Roma 0,03 0,02-0,7 -,3*** 0,0047 (0,07) (0,3) (0,42) (0,4) Lazio 0,06-0,4-0,55 -,09*** 0,0045 (0,08) (0,32) (0,46) (0,4) Porto -0,03-0,2-0,49-0,8 0,0005 (0,2) (0,4) (0,79) (,02) Sporting -0,04-0,03 0,03-0,76 0,0003 (0,5) (0,62) (0,9) (0,93) Benfica -0,04-0,3 -,7** -3,9*** 0,009 (0,2) (0,4) (0,79) (0,8) Dortmund 0,04 0,46** -0,98*** -0,97*** 0,03 (0,05) (0,8) (0,3) (0,28) Juventus 0,09-0,24 -,03*** -0,38 0,0044 (0,07) (0,24) (0,36) (0,45) Celtic -0,00-0,0-0, -0, 0,0007 (0,02) (0,06) (0,3) (0,2) Lyon 0,03 0,6 0,32-0,9*** 0,0049 (0,06) (0,23) (0,3) (0,3) Manchester United -0,03 (0,05) -0,03 (0,9) 0,26 (0,3) -0,08 (0,28) 0,0007 Not: Robusta standardfel inom parentes. *, ** och *** anger statistisk signifikans på 0, 5 och procents signifikansnivå. Siffrorna är angivna i procent. I tabell 5 visas resultaten för modell 5 då matcherna delas upp i hemma- och bortamatcher. Endast ett av tio lag har en signifikant positiv avvikande avkastning på hemmavinster. Tre av lagen har signifikant negativ avvikande avkastning på hemmaoavgjord, tre lag har signifikant negativ avvikande avkastning på hemmaförluster. Skattningarna på bortamatcherna visar 7
21 liknande resultat där ett av lagen har en signifikant positiv avvikande avkastning på bortavinst, två av lagen har en signifikant negativ avvikande avkastning på bortaoavgjord dock har ett lag en signifikant positiv avvikande avkastning vid bortaoavgjord. Fem lag har en signifikant negativ avvikande avkastning vid bortaförluster.. Nollhypoteserna förkastas för alla variabler med signifikanta resultat. Tabell 5. Regressionsanalys för modell 5 Lag Konstant Hemmavinst Hemmaoavgjord Hemmaförlust Bortavinst Bortaoavgjord Bortaförlust R 2 Roma 0,03 0,0-0,37 -,5** 0,03 0,02 -,23** 0,0048 (0,07) (0,39) (0,59) (0,70) (0,46) (0,58) (0,5) Lazio 0,06-0,49-0,78-0,79-0,25-0,36 -,24** 0,0047 (0,08) (0,4) (0,68) (0,7) (0,52) (0,62) (0,48) Porto -0,03-0,42-0,55-2,06 0,3-0,45-0,37 0,00 (0,2) (0,53) (,36) (,99) (0,63) (0,97) (,8) Sporting -0,39 0,3 -,75-2,39-0,03,48-0,4 0,0024 (0,5) (0,79) (,35) (,77) (0,99) (,22) (,09) Benfica -0,04-0,82-4,63*** -,55 0,44 0,02-3,66*** 0,044 (0,2) (0,52) (,29) (,72) (0,62) () (0,92) Dortmund 0,04 0,39* -,9** -,26*** 0,54** -0,83** -0,8** 0,036 (0,05) (0,24) (0,48) (0,47) (0,27) (0,4) (0,35) Juventus 0,09-0,22 -,05** -0,7-0,27 -,0** -0,47 0,0044 (0,07) (0,3) (0,53) (0,83) (0,36) (0,48) (0,53) Celtic -0,00-0,57-0, -0,02 0,05-0, -0,6 0,002 (0,02) (0,08) (0,2) (0,2) (0,09) (0,6) (0,5) Lyon 0,03-0,04-0,43 -,4*** 0,47 0,97** -0,66* 0,0085 (0,06) (0,29) (0,45) (0,52) (0,36) (0,42) (0,37) Manchester -0,03-0,6 0,05-0,3 0,8 0,37-0,04 0,006 United (0,05) (0,24) (0,5) (0,45) (0,3) (0,37) (0,35) Not: Robusta standardfel inom parentes. *, ** och *** anger statistisk signifikans på 0, 5 och procents signifikansnivå. Siffrorna är angivna i procent. I tabell 6 visas resultat för modell 6 då matcherna har delats upp i liga- och Europamatcher. Inget av lagen har några signifikanta skattningar på Europavinster. Två lag har en signifikant negativ avvikande avkastning på Europaoavgjorda. Fem lag har signifikant negativ avvikande avkastning på Europaförluster. Ett lag har en signifikant positiv avvikande avkastning på ligavinster. Två lag har signifikant negativ avvikande avkastning på ligaoavgjorda och fyra lag har signifikant negativ avvikande avkastning på ligaförluster.. Nollhypoteserna förkastas för alla variabler med signifikanta resultat. 8
22 Tabell 6. Regressionsanalys för modell 6 Lag Konstant Europavinst Europaoavgjord Europaförlust Ligavinst Ligaoavgjord Ligaförlust R 2 Roma 0,03-0,44-0,96 -,77* 0,04-0,04 -,9*** 0,005 (0,07) (,34) (,09) (0,9) (0,3) (0,45) (0,46) Lazio 0,06-0,05-7, -3,46** -0,47-0,5-0,9** 0,0059 (0,08) (0,79) (0,95) (,44) (0,35) (0,53) (0,42) Porto -0,03 0,8 0,9 -,55-0,9-0,76 0,27 0,000 (0,2) (0,88) (,46) (,32) (0,46) (0,94) (,59) Sporting -0,04-0,0 -,08-0,63-0,03 0,35-0,82 0,0005 (0,5) (,37) (,9) (,62) (0,69) (,03) (,33) Benfica -0,04 0,06-2,22* -4,33*** -0,4 -,34-2* 0,002 (0,2) (0,86) (,22) (,3) (0,45) (,04) (,6) Dortmund 0,04 0,52-2,35*** -3,04*** 0,44** -0,62* -0,20 0,0247 (0,05) (0,4) (0,68) (0,54) (0,2) (0,35) (0,33) Juventus 0,09-0,53-0,9-9,03-0,8 -,08*** -0,24 0,0047 (0,07) (0,57) (0,67) (0,95) (0,26) (0,42) (0,50) Celtic -0,00 0,02-0,07-0,2-0,0-0,2-0,04 0,0009 (0,02) (0,7) (0,23) (0,8) (0,07) (0,5) (0,7) Lyon 0,03 0,4 0,78 -,8*** 0, 0,22-0,58* 0,0068 (0,06) (0,52) (0,72) (0,58) (0,25) (0,34) (0,35) Manchester United -0,03 (0,05) 0,58 (0,48) -0,6 (0,7) -0,00 (0,65) -0,4 (0,2) 0,35 (0,33) -0, (0,3) 0,0026 Not: Robusta standardfel inom parentes. *, ** och *** anger statistisk signifikans på 0, 5 och procents signifikansnivå. Siffrorna är angivna i procent. I tabell 7 visas resultat för modell 7 då förväntningarna på matcherna är med. Tre lag har en negativ signifikant skattning vid förväntade vinster, ett lag har en signifikant positiv skattning vid svagt oväntade vinster, två lag har en signifikant positiv skattning vid starkt oväntade vinster. För variabeln förväntad oavgjord har två lag en signifikant negativ skattning. Ett lag har en signifikant positiv och ett lag har en signifikant negativ skattning på variabeln svagt oväntad oavgjord match. Tre lag har en signifikant negativ skattning på starkt oväntad oavgjord match. För variabeln förväntad förlust har fyra lag en signifikant negativ skattning, variabeln svagt oväntad förlust har tre signifikant negativa skattningar och för variabeln starkt oväntad förlust har två lag en signifikant negativ skattning. Nollhypoteserna förkastas för alla variabler med signifikanta resultat. 9
23 Tabell 7. Regressionsanalys för modell 7 Lag Konstant Förväntad vinst Svagt Starkt oväntad vinst Förväntad oavgjord Positiv oväntad Negativ oväntad Förväntad förlust Svagt oväntad förlust Starkt oväntad förlust R 2 oväntad vinst oavgjord oavgjord Roma 0,03-0,39 0,8 0,59-0,82 0,44-0,27 -,39** -0,64-2,6** 0,0073 (0,07) (0,46) (0,45) (0,7) (0,73) (0,67) (0,76) (0,58) (0,69) (,04) Lazio 0,06 -,9* 0,5-0,5 -,25* 0,27 -,93 -,25*** -0,64 -,4 0,0075 (0,08) (0,62) (0,49) (0,56) (0,7) (0,65) (,58) (0,47) (0,79) (2,04) Porto -0,03-0,2-0,38 0,7-0,48 -,66-0,8 -,5,24 -,59 0,005 (0,2) (0,47) (0,95) (,67) (,59) (,99) (,02) (,4) (,99) (2,5) Sporting -0,04-0,0-0,2 0,34-0,45 0,02 0,64-0,6-0,3 -,88 0,0006 (0,5) (0,82) (,09) (,77) (,4) (,77) (,58) (,26) (,77) (2,7) Benfica -0,04-0,95** 0,84 3,79** -0,2-0,66-3,5*** -2,93*** -2,6* -5,47*** 0,060 (0,2) (0,47) (0,86) (,63) (,43) (,49) (,22) (,3) (,38) (2,) Dortmund 0,04 0,2,02*** 0,93* -0,7 -,92*** -0,82* -0,7 -,5*** -0,6 0,077 (0,05) (0,23) (0,34) (0,49) (0,49) (0,72) (0,48) (0,5) (0,46) (0,49) Juventus 0,09-0,4-0,3-0,6 -,44*** 0,3 -,06* -0, -0,84-0,2 0,006 (0,07) (0,3) (0,43) (0,7) (0,52) (0,9) (0,57) (0,64) (0,73) (,3) Celtic -0,00 0,02-0,07-0,42-0,02-0,07-0,3-0,22-0,07-0,02 0,008 (0,02) (0,07) (0,7) (0,32) (0,43) (0,24) (0,6) (0,9) (0,25) (0,2) Lyon 0,03-0,2 0,39 0,8-0,25 0,78* 0,3-0,85** -0,88* -,39 0,0066 (0,06) (0,38) (0,35) (0,45) (0,5) (0,46) (0,7) (0,4) (0,5) (0,98) Manchester -0,03-0,49* 0,44,02 0,44 0,05 0,25-0,49 0,48-0,05 0,0096 United (0,05) (0,25) (0,3) (0,65) (0,44) (0,48) (0,7) (0,42) (0,5) (0,54) Not: Robusta standardfel inom parentes. *, ** och *** anger statistisk signifikans på 0, 5 och procents signifikansnivå. Siffrorna är angivna i procent. 20
24 Sammanfattningsvis visar resultaten att vissa av lagen saknar signifikanta skattningar, till exempel Celtic, Sporting och Porto. Manchester United har endast en signifikant variabel och den är på tio procents signifikansnivå. Lagen Dortmund, Roma, Lazio, Benfica och Juventus har minst en signifikant variabel i varje modell. Resultaten visar att det finns fler signifikanta resultat som tyder på att den avvikande avkastningen påverkas mer av en förlust än av en vinst. 6.2 Paneldataanalys I tabell 8 visas resultaten för modell 4. Oavgjord och förlust har en signifikant negativ skattning medan vinst har en ickesignifikant skattning. Nollhypoteserna förkastas för variablerna oavgjord och förlust. Vid förlust är den avvikande avkastningen dagen efter match i genomsnitt - 0,97 procent för samtliga fotbollsklubbar i undersökningen. Tabell 8. Paneldataanalys modell 4 Modell 4 Vinst -0,05 (0,08) Oavgjord -0,43* (0,2) Förlust -0,97*** (0,22) Konstant 0,0 (0,0) Observationer R 2 (within) 0,008 Not: Robusta standardfel inom parentes. *, ** och *** anger statistisk signifikans på 0, 5 och procents signifikansnivå. Siffrorna är angivna i procent. I tabell 9 visas resultaten för modell 5. Hemmaoavgjord, hemmaförlust och bortaförlust har signifikant negativa skattningar, de andra variablerna har icke signifikanta skattningar. Nollhypoteserna för hemmaoavgjord, hemmaförlust och bortaförlust förkastas. 2
25 Tabell 9. Paneldataanalys för modell 5 Modell 5 Hemmavinst -0,9 (0,2) Hemmaoavgjord -,0** (0,32) Hemmaförlust -,09*** (0,23) Bortavinst 0,4 (0,) Bortaoavgjord 0,0 (0,27) Bortaförlust -0,92** (0,3) Konstant 0,0 (0,0) Observationer R 2 (within) 0,0024 Not: Robusta standardfel inom parentes. *, ** och *** anger statistisk signifikans på 0, 5 och procents signifikansnivå. Siffrorna är angivna i procent. I tabell 0 visas resultatet för modell 6 där Europaoavgjord, Europaförlust och ligaförlust har signifikant negativa skattningar. De andra variablerna har icke signifikant resultat. Nollhypoteserna förkastas för Europaoavgjord, Europaförlust och Ligaförlust. 22
26 Tabell 0. Paneldataanalys för modell 6 Modell 6 Europavinst (0,) Europaoavgjord -0,79** (0,33) Europaförlust -,8*** (0,5) Ligavinst -0,09 (0,08) Ligaoavgjord -0,32 (0,8) Ligaförlust -0,65*** (0,6) Konstant 0,0 (0,0) Observationer R 2 (within) 0,0023 Not: Robusta standardfel inom parentes. *, ** och *** anger statistisk signifikans på 0, 5 och procents signifikansnivå. Siffrorna är angivna i procent. Både ligaförlust och Europaförlust har signifikanta negativa skattningar vid en procents signifikansnivå, därför görs ett F-test för att se om en av dessa variabler har en större effekt än den andra. F(, 9) = 6.67 Prob > F = Testet visar att de är signifikant skilda från varandra. Detta innebär att Europaförlust har en signifikant större negativ påverkan på aktiekursen än ligaförluster. I tabell visas resultatet för modell 7 där förväntad vinst, förväntad oavgjord, förväntad förlust, svagt oväntad förlust och starkt oväntad förlust har signifikant negativa skattningar. De andra variablerna har icke signifikanta resultat. Nollhypoteserna förkastas för alla variabler med signifikanta resultat. 23
27 Tabell. Paneldataanalys för modell 7 Modell 7 Förväntad vinst -0,26* (0,4) Svagt oväntad vinst 0,2 (0,4) Starkt oväntad vinst 0,33 (0,3) Förväntad oavgjord -0,67*** (0,2) Positiv oväntad oavgjord 0,06 (0,22) Negativ oväntad oavgjord -0,62 (0,36) Förväntad förlust -,02*** (0,2) Svagt oväntad förlust -0,75** (0,24) Starkt oväntad förlust. -,2** (0,45) Konstant 0,0 (0,0) Observationer R 2 (within) 0,0023 Not: Robusta standardfel inom parentes. *, ** och *** anger statistisk signifikans på 0, 5 och procents signifikansnivå. Siffrorna är angivna i procent. 24
28 7. Diskussion 7. Diskussion för regressionsanalys I modell 4 visar fem av lagen signifikant negativa resultat vid förlustmatcher, tre av lagen visar även signifikant negativa resultat vid matchresultatet oavgjort. När hemma-/bortaplan tas med i regressionerna så visas liknande resultat som i den första modellen. Förlust och oavgjorda matcher har fortfarande signifikant negativ påverkan på aktiekursen för flera av lagen. När sedan information om matchen spelades i den inhemska ligan eller ute i Europa så kvarstår de resultat att förluster och oavgjorda har negativ signifikant påverkan på aktiekursen. I modell 7 tas förväntningar på matcherna med, resultaten som visas även där är att förlust och oavgjorda matcher har en signifikant negativ påverkan på aktiekursen oavsett om matchens resultat är oväntad eller inte. Det som är intressant är att tre av lagen får en signifikant negativ skattning när matchen var en förväntad vinst. Resultatet stämmer överens med den tidigare studie som använt en liknande metod. Danis och Demir (20) finner signifikant negativa resultat vid förlust och oavgjord för de tre turkiska lag som de undersöker. Den skillnad i resultat för modell 4 är att vi har ett lag som visar på signifikant positiv påverkan vid vinst. När modellerna för hemma/borta och Europa/ligamatcher jämförs så är resultaten också liknande. Danis och Demirs resultat visar att förlust och oavgjord ger signifikant negativa resultat oavsett om matchen spelas hemma eller borta eller i ligan/ute i Europa vilket även stämmer överens med våra resultat. Dock finns det även skillnader i dessa modeller. I våra resultat visar Dortmund på positiva signifikanta resultat vid ligavinst och vid hemma-/bortavinst. En annan skillnad är att Lyon visar ett signifikant positivt resultat vid bortamatch som slutar oavgjord. I modell 7 får vi också liknande resultat som Danis och Demir. Det som skiljer är att vi får signifikant negativ påverkan för Lazio, Benfica och Manchester för variabeln förväntad vinst. Finansiell beteendevetenskap diskuterar fel investerare gör när investerare inte beter sig rationellt. Felen kan till exempel vara övertro eller överreaktion. Övertro kan vara en förklaring till att signifikanta resultat finns på förluster och oavgjorda men inte på vinster. Investerarna kan vara supportrar och de tror alltid att sitt lag ska vinna. När laget vinner ändras inte aktiekursen då vinsten redan är inräknad i aktiepriset. Dortmund har dock signifikant positiva resultat på vinster vilket skulle kunna bero på att investerarna har lägre och mer realistiska förväntningar på sitt lag. Dortmund saknar signifikanta resultat när matchresultatets utfall är 25
29 det förväntade, det vill säga förväntad vinst, förväntad oavgjord och förväntad förlust. Vilket också tyder på att Dortmund-investerare är mer rationella än andra investerare i de andra fotbollsklubbarna med signifikanta resultat. En annan förklaring till att förlust har mer signifikanta resultat än vinster kan var den så kallade prospect theory. Kahnemann och Tversky (979) kom fram till i sin studie om prospect theory att människor tar förluster hårdare än vad vinster ger glädje. Detta kan överföras till supportrar som då tar en förlorad match mycket hårdare än en vinst, vilket i sin tur kan leda till mer signifikanta resultat vid förlust än vinst. I uppsatsens teoridel nämns överreaktion på information som ett marknadsmisslyckande. Benfica har stora förändringar i avvikande avkastning i jämförelse med övriga lag i vår undersökning. Vid förlust har Benfica -3,9 procent medan övriga lag ligger runt - procent eller lägre. Benficas starkt avvikande avkastning skulle kunna förklaras med överreaktion. Ett enskilt matchresultat borde ha liten betydelse för klubbens ekonomiska resultat. Därför kan vi dra slutsatsen att den avvikande avkastningen, åtminstone till viss del, är känslostyrd. I analysen för varje enskilt lag finns en del ovanliga resultat. Juventus visar endast negativt signifikant resultat vid matchresultat oavgjord och inte vid förlust. Förklaringen till att förlust inte är signifikant negativ för Juventus kan vara att det finns få matcher med resultatet förlust under datainsamlingsperioden. Vissa lag i vår undersökning saknar signifikanta resultat. En förklaring till att lagen visar stor skillnad på antalet signifikanta resultat kan vara att handelsvolymen på dessa aktier skiljer sig åt. Celtic, Porto och Sporting handlas inte lika frekvent som övriga lag och har flera dagar då de inte handlas alls. Detta kan vara en förklaring till att Celtic, Porto och Sporting saknar signifikanta resultat i samtliga modeller. 7.2 Diskussion för paneldataanalys Paneldataanalysens resultat visar på att förlust och oavgjord har signifikant negativ påverkan på den avvikande avkastningen. När modellerna tar med om matchen spelades hemma eller borta så har förlust fortfarande en signifikant negativ påverkan. Hemmaförlusten är signifikanta negativa vid procents signifikansnivå och bortaförlust är signifikant negativ vid 5 procent. Oavgjord har endast signifikant negativ påverkan på hemmamatcher. När Europa- och liga matcher tas med i modellen så visar resultaten att förlust har signifikant negativ påverkan oavsett om förlusten var i ligan eller i Europa och oavgjord har endast signifikant negativ 26
30 påverkan när matchen spelas i Europa. Vinst har inga signifikanta skattningar i modellerna. När förväntningar tas med så har förlust en negativ signifikant påverkan oavsett om förlust var väntad eller oväntad. Det som är lite underligt med resultaten för förväntningarna är att de förväntade vinsterna har en signifikant negativ påverkan på den avvikande avkastningen vilket är resultat som tidigare studier inte har fått. Gandar m.fl. (2005) finner i sin paneldataanalys signifikant påverkan för vilken typ av match som spelas. De finner att en cupmatch ger en positiv effekt på avvikande avkastningen gentemot en ligamatch. Vi finner liknande resultat i vår studie. Efter det genomförda F-testet för att skilja Europaspel från ligaspel, kommer vi fram till att Europaspel har en större påverkan på avvikande avkastningen än ligaspel. Att Europaspel har en större påverkan på aktiekursen beror troligtvis på att de matcherna har en mer direkt påverkan på klubbarnas ekonomi. Europaförlustens större påverkan förklaras alltså inte bara av att matchen är mer känsloladdad utan även av rationellt beteende då klubben faktiskt kan påverkas ekonomiskt. Peenstra och Scholtens (2009) resultat visar att förlust och oavgjord har en signifikant negativ påverkan men även att vinst har en signifikant positiv påverkan på aktiekursen. Även Renneboog och Vanbrabant (2000) resultat visar att förlust och oavgjord har en signifikant negativ påverkan men också att vinst har en positiv signifikant påverkan på den avvikande avkastningen, detta liknar våra resultat förutom att Peenstra och Scholtens samt Renneboog och Vanbrabant får en signifikant positiv skattning för vinst. Förlust ger signifikant negativ påverkan oavsett om matchen spelas i Europa eller i ligan i både Peenstra och Scholtens studie samt i Renneboog och Vanbrabants studie, dessa resultat stämmer överens med de resultat vi får i vår uppsats. En skillnad mellan vår och Renneboog och Vanbrabants studie är urvalet av fotbollsklubbar. Alla fotbollsklubbar i vår undersökning har lag som ofta befinner sig i toppen av tabellen, medan Renneboog och Vanbrabant har 7 lag från Storbritannien vilket ger dem en blandning av topp-, botten- och mittenlag. Resultaten skulle kunna blivit annorlunda om vi haft tillgång till data för lag som vanligtvis befinner sig lägre ner i tabellen. En vunnen match för ett bottenlag är antagligen högre värderad än en vunnen match för ett topplag. Resultaten i paneldataanalysen visar att investerare i de fotbollsklubbarna vi har undersökt reagerar på matchresultat. Vinst saknar signifikant resultat, medan förlust och oavgjord 27
31 påverkar den avvikande avkastningen. Resultatet kan förklaras med både prospect theory eller övertro. Även resultaten av paneldataanalysen när förväntningar tas med stödjer den finansiella beteendevetenskapen om att investerare är känslostyrda. 7.3 Brister och begränsningar Genomgående i de modeller vi har undersökt så är det låga förklaringsgrader vilket kan vara en svaghet i uppsatsen, dock har tidigare studier också haft låga förklaringsgrader vilket mer tyder på att den avvikande avkastningen påverkas lite av matchresultat men även av mycket annat. En svaghet i vår undersökning är urvalet av fotbollsklubbar. Som tidigare nämnts i diskussionen så skulle resultaten för variabeln vinst kunna blivit annorlunda om vi haft tillgång till data för lag som vanligtvis befinner sig lägre ner i tabellen. En vunnen match för ett sämre lag är antagligen högre värderad än en vunnen match för ett bättre lag. Dock så finns det inte så många fotbollsklubbar som idag är börsnoterade vilket försvårar att undersöka lag från varierande liga positioner. 28
Fotbollsklubbars prestationer och deras effekt på aktiekursen
 ÖREBRO UNIVERSITET Handelshögskolan Statistik, kandidatuppsats Handledare: Niklas Karlsson Examinator: Sune Karlsson VT 2016 Fotbollsklubbars prestationer och deras effekt på aktiekursen - En statistisk
ÖREBRO UNIVERSITET Handelshögskolan Statistik, kandidatuppsats Handledare: Niklas Karlsson Examinator: Sune Karlsson VT 2016 Fotbollsklubbars prestationer och deras effekt på aktiekursen - En statistisk
Värdet av ett matchresultat En kvantitativ studie om hur matchresultat påverkar
 Värdet av ett matchresultat En kvantitativ studie om hur matchresultat påverkar börsnoterade fotbollsklubbars aktiepris More than a game A quantitative study of how match results affect the stock price
Värdet av ett matchresultat En kvantitativ studie om hur matchresultat påverkar börsnoterade fotbollsklubbars aktiepris More than a game A quantitative study of how match results affect the stock price
Fotbollsmatcher för hela slanten
 Södertörns högskola Institutionen för ekonomi och företagande Kandidatuppsats 15 hp Företagsekonomi C Vårterminen 2014 et Fotbollsmatcher för hela slanten En eventstudie om hur klubbars matchprestationer
Södertörns högskola Institutionen för ekonomi och företagande Kandidatuppsats 15 hp Företagsekonomi C Vårterminen 2014 et Fotbollsmatcher för hela slanten En eventstudie om hur klubbars matchprestationer
Hur påverkas AIK:s aktiekurs av lagets matchresultat på kort sikt? - en regressionsanalytisk ansats
 Örebro Universitet Handelshögskolan Statistik C, Uppsats Handledare: Niklas Karlsson Examinator: Nicklas Petersson VT 2016 Hur påverkas AIK:s aktiekurs av lagets matchresultat på kort sikt? - en regressionsanalytisk
Örebro Universitet Handelshögskolan Statistik C, Uppsats Handledare: Niklas Karlsson Examinator: Nicklas Petersson VT 2016 Hur påverkas AIK:s aktiekurs av lagets matchresultat på kort sikt? - en regressionsanalytisk
Ekonomisk styrning Delkurs Finansiering
 Ekonomisk styrning Delkurs Finansiering Föreläsning 6 Introduktion till portföljteorin BMA: Kap. 7-8 Jonas Råsbrant jonas.rasbrant@indek.kth.se Föreläsningens innehåll Historisk avkastning för finansiella
Ekonomisk styrning Delkurs Finansiering Föreläsning 6 Introduktion till portföljteorin BMA: Kap. 7-8 Jonas Råsbrant jonas.rasbrant@indek.kth.se Föreläsningens innehåll Historisk avkastning för finansiella
Ekonomisk styrning Delkurs Finansiering
 konomisk styrning Delkurs Finansiering Föreläsning 7 Introduktion till kapitalmarknadsteorin BMA: Kap. 8-9, 13 Jonas Råsbrant jonas.rasbrant@indek.kth.se Föreläsningens innehåll Security Market Line (SML)
konomisk styrning Delkurs Finansiering Föreläsning 7 Introduktion till kapitalmarknadsteorin BMA: Kap. 8-9, 13 Jonas Råsbrant jonas.rasbrant@indek.kth.se Föreläsningens innehåll Security Market Line (SML)
En scatterplot gjordes, och linjär regression utfördes därefter med följande hypoteser:
 1 Uppgiftsbeskrivning Syftet med denna laboration var att utifrån uppmätt data avgöra: (i) Om något samband finnes mellan kroppstemperatur och hjärtfrekvens. (ii) Om någon signifikant skillnad i sockerhalt
1 Uppgiftsbeskrivning Syftet med denna laboration var att utifrån uppmätt data avgöra: (i) Om något samband finnes mellan kroppstemperatur och hjärtfrekvens. (ii) Om någon signifikant skillnad i sockerhalt
Metod och teori. Statistik för naturvetare Umeå universitet
 Statistik för naturvetare -6-8 Metod och teori Uppgift Uppgiften är att undersöka hur hjärtfrekvensen hos en person påverkas av dennes kroppstemperatur. Detta görs genom enkel linjär regression. Låt signifikansnivån
Statistik för naturvetare -6-8 Metod och teori Uppgift Uppgiften är att undersöka hur hjärtfrekvensen hos en person påverkas av dennes kroppstemperatur. Detta görs genom enkel linjär regression. Låt signifikansnivån
Kapitel 12: TEST GÄLLANDE EN GRUPP KOEFFICIENTER - ANOVA
 Kapitel 12: TEST GÄLLANDE EN GRUPP KOEFFICIENTER - ANOVA 12.1 ANOVA I EN MULTIPEL REGRESSION Exempel: Tjänar man mer som egenföretagare? Nedan visas ett utdrag ur ett dataset som innehåller information
Kapitel 12: TEST GÄLLANDE EN GRUPP KOEFFICIENTER - ANOVA 12.1 ANOVA I EN MULTIPEL REGRESSION Exempel: Tjänar man mer som egenföretagare? Nedan visas ett utdrag ur ett dataset som innehåller information
Det här är ett system där vi tjänar pengar på ett av de lagen vi spelar på gör mål, gärna många mål!
 System - Mera Mål! Copyright 2013 Digital Solutions AB www.fotbollspengar.se www.inzideinfo.com www.inthemoneysystem.com Vi vill ha mål, mål, mål mera mål Och mål det kommer det att bli Vi vill ha mål,
System - Mera Mål! Copyright 2013 Digital Solutions AB www.fotbollspengar.se www.inzideinfo.com www.inthemoneysystem.com Vi vill ha mål, mål, mål mera mål Och mål det kommer det att bli Vi vill ha mål,
Multipel Regressionsmodellen
 Multipel Regressionsmodellen Koefficienterna i multipel regression skattas från ett stickprov enligt: Multipel Regressionsmodell med k förklarande variabler: Skattad (predicerad) Värde på y y ˆ = b + b
Multipel Regressionsmodellen Koefficienterna i multipel regression skattas från ett stickprov enligt: Multipel Regressionsmodell med k förklarande variabler: Skattad (predicerad) Värde på y y ˆ = b + b
Effekten av sportsliga prestationer på börsnoterade fotbollsklubbars värdering: prissättning på rationell eller emotionell basis?
 Effekten av sportsliga prestationer på börsnoterade fotbollsklubbars värdering: prissättning på rationell eller emotionell basis? Anton Britschgi < Institutionen för Finansiell Ekonomi och Statistik Svenska
Effekten av sportsliga prestationer på börsnoterade fotbollsklubbars värdering: prissättning på rationell eller emotionell basis? Anton Britschgi < Institutionen för Finansiell Ekonomi och Statistik Svenska
732G71 Statistik B. Föreläsning 1, kap Bertil Wegmann. IDA, Linköpings universitet. Bertil Wegmann (IDA, LiU) 732G71, Statistik B 1 / 20
 732G71 Statistik B Föreläsning 1, kap. 3.1-3.7 Bertil Wegmann IDA, Linköpings universitet Bertil Wegmann (IDA, LiU) 732G71, Statistik B 1 / 20 Exempel, enkel linjär regressionsanalys Ett företag vill veta
732G71 Statistik B Föreläsning 1, kap. 3.1-3.7 Bertil Wegmann IDA, Linköpings universitet Bertil Wegmann (IDA, LiU) 732G71, Statistik B 1 / 20 Exempel, enkel linjär regressionsanalys Ett företag vill veta
Föreläsning 8. NDAB02 Statistik; teori och tillämpning i biologi
 Föreläsning 8 Statistik; teori och tillämpning i biologi 1 Dagens föreläsning o Enkel linjär regression (kap 17.1 17.5) o Skatta regressionslinje (kap 17.2) o Signifikant lutning? (kap 17.3, 17.5a) o Förklaringsgrad
Föreläsning 8 Statistik; teori och tillämpning i biologi 1 Dagens föreläsning o Enkel linjär regression (kap 17.1 17.5) o Skatta regressionslinje (kap 17.2) o Signifikant lutning? (kap 17.3, 17.5a) o Förklaringsgrad
Föreläsning 3. NDAB02 Statistik; teori och tillämpning i biologi
 Föreläsning 3 Statistik; teori och tillämpning i biologi 1 Dagens föreläsning o Inferens om två populationer (kap 8.1 8.) o Parvisa observationer (kap 9.1 9.) o p-värde (kap 6.3) o Feltyper, styrka, stickprovsstorlek
Föreläsning 3 Statistik; teori och tillämpning i biologi 1 Dagens föreläsning o Inferens om två populationer (kap 8.1 8.) o Parvisa observationer (kap 9.1 9.) o p-värde (kap 6.3) o Feltyper, styrka, stickprovsstorlek
Residualanalys. Finansiell statistik, vt-05. Normalfördelade? Normalfördelade? För modellen
 Residualanalys För modellen Johan Koskinen, Statistiska institutionen, Stockholms universitet Finansiell statistik, vt-5 F7 regressionsanalys antog vi att ε, ε,..., ε är oberoende likafördelade N(,σ Då
Residualanalys För modellen Johan Koskinen, Statistiska institutionen, Stockholms universitet Finansiell statistik, vt-5 F7 regressionsanalys antog vi att ε, ε,..., ε är oberoende likafördelade N(,σ Då
Autokorrelation och Durbin-Watson testet. Patrik Zetterberg. 17 december 2012
 Föreläsning 6 Autokorrelation och Durbin-Watson testet Patrik Zetterberg 17 december 2012 1 / 14 Korrelation och autokorrelation På tidigare föreläsningar har vi analyserat korrelationer för stickprov
Föreläsning 6 Autokorrelation och Durbin-Watson testet Patrik Zetterberg 17 december 2012 1 / 14 Korrelation och autokorrelation På tidigare föreläsningar har vi analyserat korrelationer för stickprov
F18 MULTIPEL LINJÄR REGRESSION, FORTS. (NCT
 Stat. teori gk, ht 006, JW F18 MULTIPEL LINJÄR REGRESSION, FORTS. (NCT 1.1, 13.1-13.6, 13.8-13.9) Modell för multipel linjär regression Modellantaganden: 1) x-värdena är fixa. ) Varje y i (i = 1,, n) är
Stat. teori gk, ht 006, JW F18 MULTIPEL LINJÄR REGRESSION, FORTS. (NCT 1.1, 13.1-13.6, 13.8-13.9) Modell för multipel linjär regression Modellantaganden: 1) x-värdena är fixa. ) Varje y i (i = 1,, n) är
Bild 1. Bild 2 Sammanfattning Statistik I. Bild 3 Hypotesprövning. Medicinsk statistik II
 Bild 1 Medicinsk statistik II Läkarprogrammet T5 HT 2014 Anna Jöud Arbets- och miljömedicin, Lunds universitet ERC Syd, Skånes Universitetssjukhus anna.joud@med.lu.se Bild 2 Sammanfattning Statistik I
Bild 1 Medicinsk statistik II Läkarprogrammet T5 HT 2014 Anna Jöud Arbets- och miljömedicin, Lunds universitet ERC Syd, Skånes Universitetssjukhus anna.joud@med.lu.se Bild 2 Sammanfattning Statistik I
Innehåll. Standardavvikelse... 3 Betarisk... 3 Value at Risk... 4 Risknivån i strukturerade produkter... 4
 Del 22 Riskbedömning Innehåll Standardavvikelse... 3 Betarisk... 3 Value at Risk... 4 Risknivån i strukturerade produkter... 4 Vid investeringar i finansiella instrument följer vanligen en mängd olika
Del 22 Riskbedömning Innehåll Standardavvikelse... 3 Betarisk... 3 Value at Risk... 4 Risknivån i strukturerade produkter... 4 Vid investeringar i finansiella instrument följer vanligen en mängd olika
Analytisk statistik. Mattias Nilsson Benfatto, PhD.
 Analytisk statistik Mattias Nilsson Benfatto, PhD Mattias.nilsson@ki.se Beskrivande statistik kort repetition Centralmått Spridningsmått Normalfördelning Konfidensintervall Korrelation Analytisk statistik
Analytisk statistik Mattias Nilsson Benfatto, PhD Mattias.nilsson@ki.se Beskrivande statistik kort repetition Centralmått Spridningsmått Normalfördelning Konfidensintervall Korrelation Analytisk statistik
Aktiekursförändringar och sökfrekvens på internet
 Södertörns högskola Institutionen för samhällsvetenskaper Kandidatuppsats 15 hp Nationalekonomi Vårterminen 2010 Aktiekursförändringar och sökfrekvens på internet Av: Peter Gill Handledare: Stig Blomskog
Södertörns högskola Institutionen för samhällsvetenskaper Kandidatuppsats 15 hp Nationalekonomi Vårterminen 2010 Aktiekursförändringar och sökfrekvens på internet Av: Peter Gill Handledare: Stig Blomskog
, s a. , s b. personer från Alingsås och n b
 Skillnader i medelvärden, väntevärden, mellan två populationer I kapitel 8 testades hypoteser typ : µ=µ 0 där µ 0 var något visst intresserant värde Då användes testfunktionen där µ hämtas från, s är populationsstandardavvikelsen
Skillnader i medelvärden, väntevärden, mellan två populationer I kapitel 8 testades hypoteser typ : µ=µ 0 där µ 0 var något visst intresserant värde Då användes testfunktionen där µ hämtas från, s är populationsstandardavvikelsen
Finansiering. Föreläsning 6 Risk och avkastning BMA: Kap. 7. Jonas Råsbrant
 Finansiering Föreläsning 6 Risk och avkastning BMA: Kap. 7 Jonas Råsbrant jonas.rasbrant@fek.uu.se Föreläsningens innehåll Historisk avkastning för finansiella tillgångar Beräkning av avkastning och risk
Finansiering Föreläsning 6 Risk och avkastning BMA: Kap. 7 Jonas Råsbrant jonas.rasbrant@fek.uu.se Föreläsningens innehåll Historisk avkastning för finansiella tillgångar Beräkning av avkastning och risk
7.5 Experiment with a single factor having more than two levels
 7.5 Experiment with a single factor having more than two levels Exempel: Antag att vi vill jämföra dragstyrkan i en syntetisk fiber som blandats ut med bomull. Man vet att inblandningen påverkar dragstyrkan
7.5 Experiment with a single factor having more than two levels Exempel: Antag att vi vill jämföra dragstyrkan i en syntetisk fiber som blandats ut med bomull. Man vet att inblandningen påverkar dragstyrkan
Anders Lunander, Handelshögskolan vid Örebro universitet (huvudansvarig) Sofia Lundberg, Handelshögskolan vid Umeå universitet
 Slutrapport för projektet Högt anbudspris hög kvalitet? En empirisk analys av relationen mellan anbudspris och bedömning av kvalitet i offentlig upphandling Anders Lunander, Handelshögskolan vid Örebro
Slutrapport för projektet Högt anbudspris hög kvalitet? En empirisk analys av relationen mellan anbudspris och bedömning av kvalitet i offentlig upphandling Anders Lunander, Handelshögskolan vid Örebro
HYPOTESPRÖVNING sysselsättning
 0 självmord 20 40 60 HYPOTESPRÖVNING 4. Se spridningsdiagrammen nedan (A, B och C). Alla tre samband har samma korrelation och samma regressionslinje (r = 0,10, b = 0,15). Vi vill testa om sambandet mellan
0 självmord 20 40 60 HYPOTESPRÖVNING 4. Se spridningsdiagrammen nedan (A, B och C). Alla tre samband har samma korrelation och samma regressionslinje (r = 0,10, b = 0,15). Vi vill testa om sambandet mellan
Linjär regressionsanalys. Wieland Wermke
 + Linjär regressionsanalys Wieland Wermke + Regressionsanalys n Analys av samband mellan variabler (x,y) n Ökad kunskap om x (oberoende variabel) leder till ökad kunskap om y (beroende variabel) n Utifrån
+ Linjär regressionsanalys Wieland Wermke + Regressionsanalys n Analys av samband mellan variabler (x,y) n Ökad kunskap om x (oberoende variabel) leder till ökad kunskap om y (beroende variabel) n Utifrån
ÖverUnder När du tror aktien ska sluta över eller under en viss kurs
 UnderÖver ÖverUnder När du tror aktien ska sluta över eller under en viss kurs Med ÖVER och UNDER kan du på ett nytt och enkelt sätt agera på vad du tror kommer att hända på börsen. När du köper en ÖVER
UnderÖver ÖverUnder När du tror aktien ska sluta över eller under en viss kurs Med ÖVER och UNDER kan du på ett nytt och enkelt sätt agera på vad du tror kommer att hända på börsen. När du köper en ÖVER
Tentamen Metod C vid Uppsala universitet, , kl
 Tentamen Metod C vid Uppsala universitet, 170503, kl. 08.00-12.00 Anvisningar Av rättningspraktiska skäl skall var och en av de tre huvudfrågorna besvaras på separata pappersark. Börja alltså på ett nytt
Tentamen Metod C vid Uppsala universitet, 170503, kl. 08.00-12.00 Anvisningar Av rättningspraktiska skäl skall var och en av de tre huvudfrågorna besvaras på separata pappersark. Börja alltså på ett nytt
Påbyggnad/utveckling av lagen om ett pris Effektiv marknad: Priserna på en finansiell marknad avspeglar all relevant information
 Föreläsning 4 ffektiva marknader Påbyggnad/utveckling av lagen om ett pris ffektiv marknad: Priserna på en finansiell marknad avspeglar all relevant information Konsekvens: ndast ny information påverkar
Föreläsning 4 ffektiva marknader Påbyggnad/utveckling av lagen om ett pris ffektiv marknad: Priserna på en finansiell marknad avspeglar all relevant information Konsekvens: ndast ny information påverkar
CAPM (capital asset pricing model)
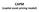 CAPM (capital asset pricing model) CAPM En teoretisk modell för förväntad avkastning i jämvikt, d.v.s. när utbudet av varje tillgång är lika med efterfrågan på motsvarande tillgång. Detta betyder att CAPM
CAPM (capital asset pricing model) CAPM En teoretisk modell för förväntad avkastning i jämvikt, d.v.s. när utbudet av varje tillgång är lika med efterfrågan på motsvarande tillgång. Detta betyder att CAPM
En vinst på planen, en vinst på börsen?
 Nationalekonomiska institutionen Kandidatuppsats 2008-01-23 En vinst på planen, en vinst på börsen? - En undersökning om hur matchresultat påverkar aktiekurser i börsnoterade italienska fotbollslag Handledare:
Nationalekonomiska institutionen Kandidatuppsats 2008-01-23 En vinst på planen, en vinst på börsen? - En undersökning om hur matchresultat påverkar aktiekurser i börsnoterade italienska fotbollslag Handledare:
Analytisk statistik. 1. Estimering. Statistisk interferens. Statistisk interferens
 Analytisk statistik Tony Pansell, Leg optiker Docent, Universitetslektor Analytisk statistik Att dra slutsatser från den insamlade datan. Två metoder:. att generalisera från en mindre grupp mot en större
Analytisk statistik Tony Pansell, Leg optiker Docent, Universitetslektor Analytisk statistik Att dra slutsatser från den insamlade datan. Två metoder:. att generalisera från en mindre grupp mot en större
Logistisk regression och Indexteori. Patrik Zetterberg. 7 januari 2013
 Föreläsning 9 Logistisk regression och Indexteori Patrik Zetterberg 7 januari 2013 1 / 33 Logistisk regression I logistisk regression har vi en binär (kategorisk) responsvariabel Y i som vanligen kodas
Föreläsning 9 Logistisk regression och Indexteori Patrik Zetterberg 7 januari 2013 1 / 33 Logistisk regression I logistisk regression har vi en binär (kategorisk) responsvariabel Y i som vanligen kodas
Två innebörder av begreppet statistik. Grundläggande tankegångar i statistik. Vad är ett stickprov? Stickprov och urval
 Två innebörder av begreppet statistik Grundläggande tankegångar i statistik Matematik och statistik för biologer, 10 hp Informationshantering. Insamling, ordningsskapande, presentation och grundläggande
Två innebörder av begreppet statistik Grundläggande tankegångar i statistik Matematik och statistik för biologer, 10 hp Informationshantering. Insamling, ordningsskapande, presentation och grundläggande
Uppgift 1. Produktmomentkorrelationskoefficienten
 Uppgift 1 Produktmomentkorrelationskoefficienten Både Vikt och Längd är variabler på kvotskalan och således kvantitativa variabler. Det innebär att vi inte har så stor nytta av korstabeller om vi vill
Uppgift 1 Produktmomentkorrelationskoefficienten Både Vikt och Längd är variabler på kvotskalan och således kvantitativa variabler. Det innebär att vi inte har så stor nytta av korstabeller om vi vill
Matematisk statistik, Föreläsning 5
 Matematisk statistik, Föreläsning 5 Ove Edlund LTU 2011-12-09 Ove Edlund (LTU) Matematisk statistik, Föreläsning 5 2011-12-09 1 / 25 Laboration 4 Jobba i grupper med storlek 2 Ove Edlund (LTU) Matematisk
Matematisk statistik, Föreläsning 5 Ove Edlund LTU 2011-12-09 Ove Edlund (LTU) Matematisk statistik, Föreläsning 5 2011-12-09 1 / 25 Laboration 4 Jobba i grupper med storlek 2 Ove Edlund (LTU) Matematisk
Föreläsning 4. NDAB01 Statistik; teori och tillämpning i biologi
 Föreläsning 4 Statistik; teori och tillämpning i biologi 1 Dagens föreläsning o Icke-parametriska test Mann-Whitneys test (kap 8.10 8.11) Wilcoxons test (kap 9.5) o Transformationer (kap 13) o Ev. Andelar
Föreläsning 4 Statistik; teori och tillämpning i biologi 1 Dagens föreläsning o Icke-parametriska test Mann-Whitneys test (kap 8.10 8.11) Wilcoxons test (kap 9.5) o Transformationer (kap 13) o Ev. Andelar
34% 34% 13.5% 68% 13.5% 2.35% 95% 2.35% 0.15% 99.7% 0.15% -3 SD -2 SD -1 SD M +1 SD +2 SD +3 SD
 6.4 Att dra slutsatser på basis av statistisk analys en kort inledning - Man har ett stickprov, men man vill med hjälp av det få veta något om hela populationen => för att kunna dra slutsatser som gäller
6.4 Att dra slutsatser på basis av statistisk analys en kort inledning - Man har ett stickprov, men man vill med hjälp av det få veta något om hela populationen => för att kunna dra slutsatser som gäller
AID:... LÖSNINGSFÖRSLAG TENTA 2013-05-03. Aktiedelen, uppdaterad 2014-04-30
 LÖSNINGSFÖRSLAG TENTA 013-05-03. Aktiedelen, udaterad 014-04-30 Ugift 1 (4x0.5 = oäng) Definiera kortfattat följande begre a) Beta värde b) Security Market Line c) Duration d) EAR Se lärobok, oweroints.
LÖSNINGSFÖRSLAG TENTA 013-05-03. Aktiedelen, udaterad 014-04-30 Ugift 1 (4x0.5 = oäng) Definiera kortfattat följande begre a) Beta värde b) Security Market Line c) Duration d) EAR Se lärobok, oweroints.
Tillämpad statistik (A5), HT15 Föreläsning 11: Multipel linjär regression 2
 Tillämpad statistik (A5), HT15 Föreläsning 11: Multipel linjär regression 2 Ronnie Pingel Statistiska institutionen Senast uppdaterad: 2015-11-23 Faktum är att vi i praktiken nästan alltid har en blandning
Tillämpad statistik (A5), HT15 Föreläsning 11: Multipel linjär regression 2 Ronnie Pingel Statistiska institutionen Senast uppdaterad: 2015-11-23 Faktum är att vi i praktiken nästan alltid har en blandning
Analytisk statistik. Tony Pansell, optiker Universitetslektor
 Analytisk statistik Tony Pansell, optiker Universitetslektor Analytisk statistik Att dra slutsatser från det insamlade materialet. Två metoder: 1. att generalisera från en mindre grupp mot en större grupp
Analytisk statistik Tony Pansell, optiker Universitetslektor Analytisk statistik Att dra slutsatser från det insamlade materialet. Två metoder: 1. att generalisera från en mindre grupp mot en större grupp
Del 1 Volatilitet. Strukturakademin
 Del 1 Volatilitet Strukturakademin Innehåll 1. Implicita tillgångar 2. Vad är volatilitet? 3. Volatility trading 4. Historisk volatilitet 5. Hur beräknas volatiliteten? 6. Implicit volatilitet 7. Smile
Del 1 Volatilitet Strukturakademin Innehåll 1. Implicita tillgångar 2. Vad är volatilitet? 3. Volatility trading 4. Historisk volatilitet 5. Hur beräknas volatiliteten? 6. Implicit volatilitet 7. Smile
Föreläsning 9. NDAB02 Statistik; teori och tillämpning i biologi
 Föreläsning 9 Statistik; teori och tillämpning i biologi 1 (kap. 20) Introduktion I föregående föreläsning diskuterades enkel linjär regression, där en oberoende variabel X förklarar variationen hos en
Föreläsning 9 Statistik; teori och tillämpning i biologi 1 (kap. 20) Introduktion I föregående föreläsning diskuterades enkel linjär regression, där en oberoende variabel X förklarar variationen hos en
ÖVNINGSUPPGIFTER KAPITEL 8
 ÖVNINGSUPPGIFTER KAPITEL 8 SAMPEL KONTRA POPULATION 1. Nedan beskrivs fyra frågeställningar. Ange om populationen är ändlig eller oändlig i respektive fall. Om ändlig, beskriv också vem eller vad som ingår
ÖVNINGSUPPGIFTER KAPITEL 8 SAMPEL KONTRA POPULATION 1. Nedan beskrivs fyra frågeställningar. Ange om populationen är ändlig eller oändlig i respektive fall. Om ändlig, beskriv också vem eller vad som ingår
Analys av medelvärden. Jenny Selander , plan 3, Norrbacka, ingång via den Samhällsmedicinska kliniken
 Analys av medelvärden Jenny Selander jenny.selander@ki.se 524 800 29, plan 3, Norrbacka, ingång via den Samhällsmedicinska kliniken Jenny Selander, Kvant. metoder, FHV T1 december 20111 Innehåll Normalfördelningen
Analys av medelvärden Jenny Selander jenny.selander@ki.se 524 800 29, plan 3, Norrbacka, ingång via den Samhällsmedicinska kliniken Jenny Selander, Kvant. metoder, FHV T1 december 20111 Innehåll Normalfördelningen
Regressions- och Tidsserieanalys - F4
 Regressions- och Tidsserieanalys - F4 Modellbygge och residualanalys. Kap 5.1-5.4 (t.o.m. halva s 257), ej C-statistic s 23. Linda Wänström Linköpings universitet Wänström (Linköpings universitet) F4 1
Regressions- och Tidsserieanalys - F4 Modellbygge och residualanalys. Kap 5.1-5.4 (t.o.m. halva s 257), ej C-statistic s 23. Linda Wänström Linköpings universitet Wänström (Linköpings universitet) F4 1
Skriftlig Tentamen i Finansiell Statistik Grundnivå 7.5 hp, HT2012
 Statistiska Institutionen Patrik Zetterberg Skriftlig Tentamen i Finansiell Statistik Grundnivå 7.5 hp, HT2012 2013-01-18 Skrivtid: 9.00-14.00 Hjälpmedel: Godkänd miniräknare utan lagrade formler eller
Statistiska Institutionen Patrik Zetterberg Skriftlig Tentamen i Finansiell Statistik Grundnivå 7.5 hp, HT2012 2013-01-18 Skrivtid: 9.00-14.00 Hjälpmedel: Godkänd miniräknare utan lagrade formler eller
Gör uppgift 6.10 i arbetsmaterialet (ingår på övningen 16 maj). För 10 torskar har vi värden på variablerna Längd (cm) och Ålder (år).
 Matematikcentrum Matematisk statistik MASB11: BIOSTATISTISK GRUNDKURS DATORLABORATION 4, 21 MAJ 2018 REGRESSION OCH FORTSÄTTNING PÅ MINIPROJEKT II Syfte Syftet med dagens laboration är att du ska bekanta
Matematikcentrum Matematisk statistik MASB11: BIOSTATISTISK GRUNDKURS DATORLABORATION 4, 21 MAJ 2018 REGRESSION OCH FORTSÄTTNING PÅ MINIPROJEKT II Syfte Syftet med dagens laboration är att du ska bekanta
Skolprestationer på kommunnivå med hänsyn tagen till socioekonomi
 1(6) PCA/MIH Johan Löfgren 2016-11-10 Skolprestationer på kommunnivå med hänsyn tagen till socioekonomi 1 Inledning Sveriges kommuner och landsting (SKL) presenterar varje år statistik över elevprestationer
1(6) PCA/MIH Johan Löfgren 2016-11-10 Skolprestationer på kommunnivå med hänsyn tagen till socioekonomi 1 Inledning Sveriges kommuner och landsting (SKL) presenterar varje år statistik över elevprestationer
Läcker företag information?
 NATIONALEKONOMISKA INSTITUTIONEN Uppsala universitet Examensarbete C Författare: Niklas Andersson Handledare: Lennart Berg Termin och år: VT 2011 Datum: 2011-06-07 Läcker företag information? En studie
NATIONALEKONOMISKA INSTITUTIONEN Uppsala universitet Examensarbete C Författare: Niklas Andersson Handledare: Lennart Berg Termin och år: VT 2011 Datum: 2011-06-07 Läcker företag information? En studie
Regressionsanalys av NHL-statistik
 Regressionsanalys av NHL-statistik Av Gustav Hedén gheden@kth.se Examensarbete inom teknisk fysik, grundnivå SA104x KTH Matematisk statistik Handledare Fredrik Armerin 1 Innehållsförteckning Sammanfattning:...
Regressionsanalys av NHL-statistik Av Gustav Hedén gheden@kth.se Examensarbete inom teknisk fysik, grundnivå SA104x KTH Matematisk statistik Handledare Fredrik Armerin 1 Innehållsförteckning Sammanfattning:...
Hur skriver man statistikavsnittet i en ansökan?
 Hur skriver man statistikavsnittet i en ansökan? Val av metod och stickprovsdimensionering Registercentrum Norr http://www.registercentrumnorr.vll.se/ statistik.rcnorr@vll.se 11 Oktober, 2018 1 / 52 Det
Hur skriver man statistikavsnittet i en ansökan? Val av metod och stickprovsdimensionering Registercentrum Norr http://www.registercentrumnorr.vll.se/ statistik.rcnorr@vll.se 11 Oktober, 2018 1 / 52 Det
Medicinsk statistik II
 Medicinsk statistik II Läkarprogrammet termin 5 VT 2013 Susanna Lövdahl, Msc, doktorand Klinisk koagulationsforskning, Lunds universitet E-post: susanna.lovdahl@med.lu.se Dagens föreläsning Fördjupning
Medicinsk statistik II Läkarprogrammet termin 5 VT 2013 Susanna Lövdahl, Msc, doktorand Klinisk koagulationsforskning, Lunds universitet E-post: susanna.lovdahl@med.lu.se Dagens föreläsning Fördjupning
Statistiska Institutionen Gebrenegus Ghilagaber (docent)
 Statistiska Institutionen Gebrenegus Ghilagaber (docent) Lösningsförslag till skriftlig tentamen i FINANSIELL STATISTIK, grundnivå, 7,5 hp, VT09. Onsdagen 3 juni 2009-1 Sannolkhetslära Mobiltelefoner tillverkas
Statistiska Institutionen Gebrenegus Ghilagaber (docent) Lösningsförslag till skriftlig tentamen i FINANSIELL STATISTIK, grundnivå, 7,5 hp, VT09. Onsdagen 3 juni 2009-1 Sannolkhetslära Mobiltelefoner tillverkas
Tentamen Finansiering (2FE253) Lördagen den 8 november 2014, kl. 09:00-13:00
 Tentamen Finansiering (2FE253) Lördagen den 8 november 2014, kl. 09:00-13:00 Skrivtid: 4 timmar (kl. 09:00 13:00) Hjälpmedel: Kalkylator och kursens formelblad OBS! Endast formler som står med på formelbladet
Tentamen Finansiering (2FE253) Lördagen den 8 november 2014, kl. 09:00-13:00 Skrivtid: 4 timmar (kl. 09:00 13:00) Hjälpmedel: Kalkylator och kursens formelblad OBS! Endast formler som står med på formelbladet
Kontrollera att följande punkter är uppfyllda innan rapporten lämnas in: Första sidan är ett försättsblad (laddas ned från kurshemsidan)
 Statistiska institutionen VT 2012 Inlämningsuppgift 1 Statistisk teori med tillämpningar Instruktioner Ett av problemen A, B eller C tilldelas gruppen vid första övningstillfället. Rapporten ska lämnas
Statistiska institutionen VT 2012 Inlämningsuppgift 1 Statistisk teori med tillämpningar Instruktioner Ett av problemen A, B eller C tilldelas gruppen vid första övningstillfället. Rapporten ska lämnas
Föreläsning 9. NDAB01 Statistik; teori och tillämpning i biologi
 Föreläsning 9 Statistik; teori och tillämpning i biologi 1 (kap. 20) Introduktion I föregående föreläsning diskuterades enkel linjär regression, där en oberoende variabel X förklarar variationen hos en
Föreläsning 9 Statistik; teori och tillämpning i biologi 1 (kap. 20) Introduktion I föregående föreläsning diskuterades enkel linjär regression, där en oberoende variabel X förklarar variationen hos en
1/23 REGRESSIONSANALYS. Statistiska institutionen, Stockholms universitet
 1/23 REGRESSIONSANALYS F4 Linda Wänström Statistiska institutionen, Stockholms universitet 2/23 Multipel regressionsanalys Multipel regressionsanalys kan ses som en utvidgning av enkel linjär regressionsanalys.
1/23 REGRESSIONSANALYS F4 Linda Wänström Statistiska institutionen, Stockholms universitet 2/23 Multipel regressionsanalys Multipel regressionsanalys kan ses som en utvidgning av enkel linjär regressionsanalys.
Rättningstiden är i normalfall 15 arbetsdagar, annars är det detta datum som gäller:
 Statistik 2 Provmoment: Ladokkod: Tentamen ges för: TentamensKod: Tentamen SST021 ACEKO16h, ACIVE16h 7,5 högskolepoäng Tentamensdatum: 2018-05-31 Tid: 14.00-19.00 Hjälpmedel: Valfri miniräknare Linjal
Statistik 2 Provmoment: Ladokkod: Tentamen ges för: TentamensKod: Tentamen SST021 ACEKO16h, ACIVE16h 7,5 högskolepoäng Tentamensdatum: 2018-05-31 Tid: 14.00-19.00 Hjälpmedel: Valfri miniräknare Linjal
Det har gång på gång konstaterats att. Förtroende för företagsledningen. har reella ekonomiska konsekvenser för kapitalmarknaden
 Förtroende för företagsledningen har reella ekonomiska konsekvenser för kapitalmarknaden Förtroende för företagsledningen tycks kunna påverka en investerares upplevda risk kopplat till en investering.
Förtroende för företagsledningen har reella ekonomiska konsekvenser för kapitalmarknaden Förtroende för företagsledningen tycks kunna påverka en investerares upplevda risk kopplat till en investering.
OMTENTAMEN I GRUNDLÄGGANDE STATISTIK FÖR EKONOMER
 STOCKHOLMS UNIVERSITET Statistiska institutionen Termeh Shafie OMTENTAMEN I GRUNDLÄGGANDE STATISTIK FÖR EKONOMER 2012-04-16 Skrivtid: 15.00-20.00 Hjälpmedel: Miniräknare utan lagrade formler eller text,
STOCKHOLMS UNIVERSITET Statistiska institutionen Termeh Shafie OMTENTAMEN I GRUNDLÄGGANDE STATISTIK FÖR EKONOMER 2012-04-16 Skrivtid: 15.00-20.00 Hjälpmedel: Miniräknare utan lagrade formler eller text,
Tentamen Finansiering (2FE253) Fredagen den 20 februari 2015, kl. 08:00-12:00
 Tentamen Finansiering (2FE253) Fredagen den 20 februari 2015, kl. 08:00-12:00 Skrivtid: 4 timmar (kl. 08:00 12:00) Hjälpmedel: Kalkylator och kursens formelblad. OBS! Endast formler som står med på formelbladet
Tentamen Finansiering (2FE253) Fredagen den 20 februari 2015, kl. 08:00-12:00 Skrivtid: 4 timmar (kl. 08:00 12:00) Hjälpmedel: Kalkylator och kursens formelblad. OBS! Endast formler som står med på formelbladet
Sänkningen av parasitnivåerna i blodet
 4.1 Oberoende (x-axeln) Kön Kön Längd Ålder Dos Dos C max Parasitnivå i blodet Beroende (y-axeln) Längd Vikt Vikt Vikt C max Sänkningen av parasitnivåerna i blodet Sänkningen av parasitnivåerna i blodet
4.1 Oberoende (x-axeln) Kön Kön Längd Ålder Dos Dos C max Parasitnivå i blodet Beroende (y-axeln) Längd Vikt Vikt Vikt C max Sänkningen av parasitnivåerna i blodet Sänkningen av parasitnivåerna i blodet
F3 Introduktion Stickprov
 Utrotningshotad tandnoting i arktiska vatten Inferens om väntevärde baserat på medelvärde och standardavvikelse Matematik och statistik för biologer, 10 hp Tandnoting är en torskliknande fisk som lever
Utrotningshotad tandnoting i arktiska vatten Inferens om väntevärde baserat på medelvärde och standardavvikelse Matematik och statistik för biologer, 10 hp Tandnoting är en torskliknande fisk som lever
Laboration 2. Omprovsuppgift MÄLARDALENS HÖGSKOLA. Akademin för ekonomi, samhälle och teknik
 MÄLARDALENS HÖGSKOLA Akademin för ekonomi, samhälle och teknik Statistik och kvantitativa undersökningar, A 15 Hp Vårterminen 2017 Laboration 2 Omprovsuppgift Regressionsanalys, baserat på Sveriges kommuner
MÄLARDALENS HÖGSKOLA Akademin för ekonomi, samhälle och teknik Statistik och kvantitativa undersökningar, A 15 Hp Vårterminen 2017 Laboration 2 Omprovsuppgift Regressionsanalys, baserat på Sveriges kommuner
Regressions- och Tidsserieanalys - F1
 Regressions- och Tidsserieanalys - F1 Kap 3: Enkel linjär regression Linda Wänström Linköpings universitet November 4, 2013 Wänström (Linköpings universitet) F1 November 4, 2013 1 / 25 Statistik B, 8 hp
Regressions- och Tidsserieanalys - F1 Kap 3: Enkel linjär regression Linda Wänström Linköpings universitet November 4, 2013 Wänström (Linköpings universitet) F1 November 4, 2013 1 / 25 Statistik B, 8 hp
Oddssättning. - utvärdering av modeller för skattning av matchodds i Svenska Superligan i innebandy
 Örebro universitet Handelshögskolan Statistik C, Uppsats Handledare: Niklas Karlsson Examinator: Nicklas Pettersson VT 2015 Oddssättning - utvärdering av modeller för skattning av matchodds i Svenska Superligan
Örebro universitet Handelshögskolan Statistik C, Uppsats Handledare: Niklas Karlsson Examinator: Nicklas Pettersson VT 2015 Oddssättning - utvärdering av modeller för skattning av matchodds i Svenska Superligan
Hypotesprövning. Andrew Hooker. Division of Pharmacokinetics and Drug Therapy Department of Pharmaceutical Biosciences Uppsala University
 Hypotesprövning Andrew Hooker Division of Pharmacokinetics and Drug Therapy Department of Pharmaceutical Biosciences Uppsala University Hypotesprövning Liksom konfidensintervall ett hjälpmedel för att
Hypotesprövning Andrew Hooker Division of Pharmacokinetics and Drug Therapy Department of Pharmaceutical Biosciences Uppsala University Hypotesprövning Liksom konfidensintervall ett hjälpmedel för att
Instuderingsfrågor till avsnittet om statistik, kursen Statistik och Metod, Psykologprogrammet på KI, T8
 1 Instuderingsfrågor till avsnittet om statistik, kursen Statistik och Metod, Psykologprogrammet på KI, T8 Dessa instuderingsfrågor är främst tänkta att stämma överens med innehållet i föreläsningarna,
1 Instuderingsfrågor till avsnittet om statistik, kursen Statistik och Metod, Psykologprogrammet på KI, T8 Dessa instuderingsfrågor är främst tänkta att stämma överens med innehållet i föreläsningarna,
), beskrivs där med följande funktionsform,
 BEGREPPET REAL LrNGSIKTIG JeMVIKTSReNTA 4,0 3,5 3,0 2,5 2,0 1,5 1,0 0,5 Diagram R15. Grafisk illustration av nyttofunktionen för s = 0,3 och s = 0,6. 0,0 0,0 0,0 0,5 1,0 1,5 2,0 s = 0,6 s = 0,3 Anm. X-axeln
BEGREPPET REAL LrNGSIKTIG JeMVIKTSReNTA 4,0 3,5 3,0 2,5 2,0 1,5 1,0 0,5 Diagram R15. Grafisk illustration av nyttofunktionen för s = 0,3 och s = 0,6. 0,0 0,0 0,0 0,5 1,0 1,5 2,0 s = 0,6 s = 0,3 Anm. X-axeln
Regressions- och Tidsserieanalys - F1
 Regressions- och Tidsserieanalys - F1 Kap 3: Enkel linjär regression Linda Wänström Linköpings universitet May 4, 2015 Wänström (Linköpings universitet) F1 May 4, 2015 1 / 25 Regressions- och tidsserieanalys,
Regressions- och Tidsserieanalys - F1 Kap 3: Enkel linjär regression Linda Wänström Linköpings universitet May 4, 2015 Wänström (Linköpings universitet) F1 May 4, 2015 1 / 25 Regressions- och tidsserieanalys,
1. Lära sig plotta en beroende variabel mot en oberoende variabel. 2. Lära sig skatta en enkel linjär regressionsmodell
 Datorövning 1 Regressions- och tidsserieanalys Syfte 1. Lära sig plotta en beroende variabel mot en oberoende variabel 2. Lära sig skatta en enkel linjär regressionsmodell 3. Lära sig beräkna en skattning
Datorövning 1 Regressions- och tidsserieanalys Syfte 1. Lära sig plotta en beroende variabel mot en oberoende variabel 2. Lära sig skatta en enkel linjär regressionsmodell 3. Lära sig beräkna en skattning
π = proportionen plustecken i populationen. Det numeriska värdet på π är okänt.
 Stat. teori gk, vt 006, JW F0 ICKE-PARAMETRISKA TEST (NCT 13.1, 13.3-13.4) Or dlista till NCT Nonparametric Sign test Rank Teckentest Icke-parametrisk Teckentest Rang Teckentestet är formellt ingenting
Stat. teori gk, vt 006, JW F0 ICKE-PARAMETRISKA TEST (NCT 13.1, 13.3-13.4) Or dlista till NCT Nonparametric Sign test Rank Teckentest Icke-parametrisk Teckentest Rang Teckentestet är formellt ingenting
Strukturakademin Strukturinvest Fondkommission LÅNG KÖPOPTION. Värde option. Köpt köpoption. Utveckling marknad. Rättighet
 Del 11 Indexbevis Innehåll Grundpositionerna... 3 Köpt köpoption... 3 Såld köpoption... 3 Köpt säljoption... 4 Såld säljoption... 4 Konstruktion av Indexbevis... 4 Avkastningsanalys... 5 knock-in optioner...
Del 11 Indexbevis Innehåll Grundpositionerna... 3 Köpt köpoption... 3 Såld köpoption... 3 Köpt säljoption... 4 Såld säljoption... 4 Konstruktion av Indexbevis... 4 Avkastningsanalys... 5 knock-in optioner...
LTH: Fastighetsekonomi 23-24 sep 2008. Enkel och multipel linjär regressionsanalys HYPOTESPRÖVNING
 LTH: Fastighetsekonomi 23-24 sep 2008 Enkel och multipel linjär regressionsanalys HYPOTESPRÖVNING Hypotesprövning (statistisk inferensteori) Statistisk hypotesprövning innebär att man med hjälp av slumpmässiga
LTH: Fastighetsekonomi 23-24 sep 2008 Enkel och multipel linjär regressionsanalys HYPOTESPRÖVNING Hypotesprövning (statistisk inferensteori) Statistisk hypotesprövning innebär att man med hjälp av slumpmässiga
Spelmarknaden Ett test av effektiviteten på den svenska spelmarknaden
 NATIONALEKONOMISKA INSTITUTIONEN Uppsats Fortsättningskurs C Författare: Handledare: Lennart Berg VT 2005 Spelmarknaden Ett test av effektiviteten på den svenska spelmarknaden Ett test av effektiviteten
NATIONALEKONOMISKA INSTITUTIONEN Uppsats Fortsättningskurs C Författare: Handledare: Lennart Berg VT 2005 Spelmarknaden Ett test av effektiviteten på den svenska spelmarknaden Ett test av effektiviteten
BULL & BEAR INTE BARA ATT TUTA OCH KÖRA
 BULL & BEAR INTE BARA ATT TUTA OCH KÖRA En investering i värdepapper kan både öka och minska i värde och det är inte säkert att du får tillbaka hela det investerade kapitalet. Historisk utveckling utgör
BULL & BEAR INTE BARA ATT TUTA OCH KÖRA En investering i värdepapper kan både öka och minska i värde och det är inte säkert att du får tillbaka hela det investerade kapitalet. Historisk utveckling utgör
Bilaga 6 till rapport 1 (5)
 till rapport 1 (5) Bilddiagnostik vid misstänkt prostatacancer, rapport UTV2012/49 (2014). Värdet av att undvika en prostatabiopsitagning beskrivning av studien SBU har i samarbete med Centrum för utvärdering
till rapport 1 (5) Bilddiagnostik vid misstänkt prostatacancer, rapport UTV2012/49 (2014). Värdet av att undvika en prostatabiopsitagning beskrivning av studien SBU har i samarbete med Centrum för utvärdering
Kapitel 15: INTERAKTIONER, STANDARDISERADE SKALOR OCH ICKE-LINJÄRA EFFEKTER
 Kapitel 15: INTERAKTIONER, STANDARDISERADE SKALOR OCH ICKE-LINJÄRA EFFEKTER När vi mäter en effekt i data så vill vi ofta se om denna skiljer sig mellan olika delgrupper. Vi kanske testar effekten av ett
Kapitel 15: INTERAKTIONER, STANDARDISERADE SKALOR OCH ICKE-LINJÄRA EFFEKTER När vi mäter en effekt i data så vill vi ofta se om denna skiljer sig mellan olika delgrupper. Vi kanske testar effekten av ett
STOCKHOLMS UNIVERSITET HT 2008 Statistiska institutionen Linda Wänström. Omtentamen i Regressionsanalys
 STOCKHOLMS UNIVERSITET HT 2008 Statistiska institutionen Linda Wänström Omtentamen i Regressionsanalys 2009-01-08 Skrivtid: 9.00-14.00 Godkända hjälpmedel: Miniräknare utan lagrade formler. Tentamen består
STOCKHOLMS UNIVERSITET HT 2008 Statistiska institutionen Linda Wänström Omtentamen i Regressionsanalys 2009-01-08 Skrivtid: 9.00-14.00 Godkända hjälpmedel: Miniräknare utan lagrade formler. Tentamen består
under en options löptid. Strukturakademin Strukturinvest Fondkommission
 Del 1 Volatilitet Innehåll Implicita tillgångar... 3 Vad är volatilitet?... 3 Volatility trading... 3 Historisk volatilitet... 3 Hur beräknas volatiliteten?... 4 Implicit volatilitet... 4 Smile... 4 Vega...
Del 1 Volatilitet Innehåll Implicita tillgångar... 3 Vad är volatilitet?... 3 Volatility trading... 3 Historisk volatilitet... 3 Hur beräknas volatiliteten?... 4 Implicit volatilitet... 4 Smile... 4 Vega...
Finansiering. Föreläsning 7 Portföljteori och kapitalkostnad BMA: Kap Jonas Råsbrant
 Finansiering Föreläsning 7 Portföljteori och kapitalkostnad BMA: Kap. 8-9 Jonas Råsbrant jonas.rasbrant@fek.uu.se Förväntad avkastning och volatilitet i portföljer Förväntad avkastning och volatilitet
Finansiering Föreläsning 7 Portföljteori och kapitalkostnad BMA: Kap. 8-9 Jonas Råsbrant jonas.rasbrant@fek.uu.se Förväntad avkastning och volatilitet i portföljer Förväntad avkastning och volatilitet
Uppgift a b c d e Vet inte Poäng
 TENTAMEN: Dataanalys och statistik för I2, TMS135 Fredagen den 12 mars kl. 8:45-11:45 på V. Jour: Jenny Andersson, ankn 8294 (mobil:070 3597858) Hjälpmedel: Utdelad formelsamling med tabeller, BETA, på
TENTAMEN: Dataanalys och statistik för I2, TMS135 Fredagen den 12 mars kl. 8:45-11:45 på V. Jour: Jenny Andersson, ankn 8294 (mobil:070 3597858) Hjälpmedel: Utdelad formelsamling med tabeller, BETA, på
STATISTISK POWER OCH STICKPROVSDIMENSIONERING
 STATISTISK POWER OCH STICKPROVSDIMENSIONERING Teori UPPLÄGG Gemensam diskussion Individuella frågor Efter detta pass hoppas jag att: ni ska veta vad man ska tänka på vilka verktyg som finns vilket stöd
STATISTISK POWER OCH STICKPROVSDIMENSIONERING Teori UPPLÄGG Gemensam diskussion Individuella frågor Efter detta pass hoppas jag att: ni ska veta vad man ska tänka på vilka verktyg som finns vilket stöd
732G71 Statistik B. Föreläsning 4. Bertil Wegmann. November 11, IDA, Linköpings universitet
 732G71 Statistik B Föreläsning 4 Bertil Wegmann IDA, Linköpings universitet November 11, 2016 Bertil Wegmann (IDA, LiU) 732G71, Statistik B November 11, 2016 1 / 34 Kap. 5.1, korrelationsmatris En korrelationsmatris
732G71 Statistik B Föreläsning 4 Bertil Wegmann IDA, Linköpings universitet November 11, 2016 Bertil Wegmann (IDA, LiU) 732G71, Statistik B November 11, 2016 1 / 34 Kap. 5.1, korrelationsmatris En korrelationsmatris
Korrelation och autokorrelation
 Korrelation och autokorrelation Låt oss begrunda uttrycket r = i=1 (x i x) (y i y) n i=1 (x i x) 2 n. i=1 (y i y) 2 De kvadratsummor kring de aritmetiska medelvärdena som står i nämnaren är alltid positiva.
Korrelation och autokorrelation Låt oss begrunda uttrycket r = i=1 (x i x) (y i y) n i=1 (x i x) 2 n. i=1 (y i y) 2 De kvadratsummor kring de aritmetiska medelvärdena som står i nämnaren är alltid positiva.
FÖRELÄSNINGSMATERIAL. diff SE. SE x x. Grundläggande statistik 2: KORRELATION OCH HYPOTESTESTNING. Påbyggnadskurs T1. Odontologisk profylaktik
 Grundläggande statistik Påbyggnadskurs T1 Odontologisk profylaktik FÖRELÄSNINGSMATERIAL : KORRELATION OCH HYPOTESTESTNING t diff SE x 1 diff SE x x 1 x. Analytisk statistik Regression & Korrelation Oberoende
Grundläggande statistik Påbyggnadskurs T1 Odontologisk profylaktik FÖRELÄSNINGSMATERIAL : KORRELATION OCH HYPOTESTESTNING t diff SE x 1 diff SE x x 1 x. Analytisk statistik Regression & Korrelation Oberoende
Tentamen i Statistik, STA A13 Deltentamen 2, 5p 21 januari 2006, kl
 Karlstads universitet Institutionen för informationsteknologi Avdelningen för statistik Tentamen i Statistik, STA A13 Deltentamen, 5p 1 januari 006, kl. 09.00-13.00 Tillåtna hjälpmedel: Bifogad formel-
Karlstads universitet Institutionen för informationsteknologi Avdelningen för statistik Tentamen i Statistik, STA A13 Deltentamen, 5p 1 januari 006, kl. 09.00-13.00 Tillåtna hjälpmedel: Bifogad formel-
Turbowarranter. För dig som är. helt säker på hur. vägen ser ut. Handelsbanken Capital Markets
 Turbowarranter För dig som är helt säker på hur vägen ser ut Handelsbanken Capital Markets Hög avkastning med liten kapitalinsats Turbowarranter är ett nytt finansiellt instrument som ger dig möjlighet
Turbowarranter För dig som är helt säker på hur vägen ser ut Handelsbanken Capital Markets Hög avkastning med liten kapitalinsats Turbowarranter är ett nytt finansiellt instrument som ger dig möjlighet
Trefaktorsmodellen. Undersökning på svenska börsnoterade aktiebolag. Av: Nicklas Envall, Patrik Steen Handledare: Ogi Chun
 Södertörns högskola Institutionen för ekonomi och företagande Kandidatuppsats 15hp Företagsekonomi Vårterminen 2014 Trefaktorsmodellen Undersökning på svenska börsnoterade aktiebolag. Av: Nicklas Envall,
Södertörns högskola Institutionen för ekonomi och företagande Kandidatuppsats 15hp Företagsekonomi Vårterminen 2014 Trefaktorsmodellen Undersökning på svenska börsnoterade aktiebolag. Av: Nicklas Envall,
TAMS65 - Föreläsning 11 Regressionsanalys fortsättning Modellval
 TAMS65 - Föreläsning 11 Regressionsanalys fortsättning Modellval Martin Singull Matematisk statistik Matematiska institutionen Innehåll Repetition (t-test för H 0 : β i = 0) Residualanalys Modellval Framåtvalsprincipen
TAMS65 - Föreläsning 11 Regressionsanalys fortsättning Modellval Martin Singull Matematisk statistik Matematiska institutionen Innehåll Repetition (t-test för H 0 : β i = 0) Residualanalys Modellval Framåtvalsprincipen
Föreläsning G60 Statistiska metoder
 Föreläsning 9 Statistiska metoder 1 Dagens föreläsning o Regression Regressionsmodell Signifikant lutning? Prognoser Konfidensintervall Prediktionsintervall Tolka Minitab-utskrifter o Sammanfattning Exempel
Föreläsning 9 Statistiska metoder 1 Dagens föreläsning o Regression Regressionsmodell Signifikant lutning? Prognoser Konfidensintervall Prediktionsintervall Tolka Minitab-utskrifter o Sammanfattning Exempel
F19, (Multipel linjär regression forts) och F20, Chi-två test.
 Partiella t-test F19, (Multipel linjär regression forts) och F20, Chi-två test. Christian Tallberg Statistiska institutionen Stockholms universitet Då man testar om en enskild variabel X i skall vara med
Partiella t-test F19, (Multipel linjär regression forts) och F20, Chi-två test. Christian Tallberg Statistiska institutionen Stockholms universitet Då man testar om en enskild variabel X i skall vara med
Tentamensgenomgång och återlämning: Måndagen 24/2 kl16.00 i B497. Därefter kan skrivningarna hämtas på studentexpeditionen, plan 7 i B-huset.
 Statistiska institutionen Nicklas Pettersson Skriftlig tentamen i Finansiell Statistik Grundnivå 7.5hp, HT2013 2014-02-07 Skrivtid: 13.00-18.00 Hjälpmedel: Godkänd miniräknare utan lagrade formler eller
Statistiska institutionen Nicklas Pettersson Skriftlig tentamen i Finansiell Statistik Grundnivå 7.5hp, HT2013 2014-02-07 Skrivtid: 13.00-18.00 Hjälpmedel: Godkänd miniräknare utan lagrade formler eller
2. Lära sig skatta en multipel linjär regressionsmodell samt plotta variablerna. 4. Lära sig skatta en linjär regressionsmodell med interaktionstermer
 Datorövning 2 Regressions- och tidsserieanalys Syfte 1. Lära sig skapa en korrelationsmatris 2. Lära sig skatta en multipel linjär regressionsmodell samt plotta variablerna mot varandra 3. Lära sig beräkna
Datorövning 2 Regressions- och tidsserieanalys Syfte 1. Lära sig skapa en korrelationsmatris 2. Lära sig skatta en multipel linjär regressionsmodell samt plotta variablerna mot varandra 3. Lära sig beräkna
Lösningsförslag till tentamen på. Statistik och kvantitativa undersökningar STA100, 15 hp. Fredagen den 13 e mars 2015
 MÄLARDALENS HÖGSKOLA Akademin för ekonomi, samhälle och teknik Statistik Lösningsförslag till tentamen på Statistik och kvantitativa undersökningar STA100, 15 hp Fredagen den 13 e mars 015 1 a 13 och 14
MÄLARDALENS HÖGSKOLA Akademin för ekonomi, samhälle och teknik Statistik Lösningsförslag till tentamen på Statistik och kvantitativa undersökningar STA100, 15 hp Fredagen den 13 e mars 015 1 a 13 och 14
Regressionsanalys med SPSS Kimmo Sorjonen (2010)
 1 Regressionsanalys med SPSS Kimmo Sorjonen (2010) 1. Multipel regression 1.1. Variabler I det aktuella exemplet ingår följande variabler: (1) life.sat, anger i vilket utsträckning man är nöjd med livet;
1 Regressionsanalys med SPSS Kimmo Sorjonen (2010) 1. Multipel regression 1.1. Variabler I det aktuella exemplet ingår följande variabler: (1) life.sat, anger i vilket utsträckning man är nöjd med livet;
Kom narmare ÄN NÄRA. Köp aktier i ÖSK.
 Kom narmare ÄN NÄRA Köp aktier i ÖSK. TIDEN ÄR INNE! Tack för att du engagerar dig i ÖSK. Bara att du läser den här texten och tar del av vårt prospekt gör mig glad, även om det är på andra sätt som vi
Kom narmare ÄN NÄRA Köp aktier i ÖSK. TIDEN ÄR INNE! Tack för att du engagerar dig i ÖSK. Bara att du läser den här texten och tar del av vårt prospekt gör mig glad, även om det är på andra sätt som vi
