MAX NORDIN MICHAEL JOHANSSON OSCAR JALDEHAG

Transkript

1 Simulering av synkrotronstrålning från runaway-elektroner i fusionsplasma Kandidatarbete inom Civilingenjörsprogrammet Teknisk fysik och Fysikprogrammet MAX NORDIN MICHAEL JOHANSSON OSCAR JALDEHAG Institutionen för teknisk fysik CHALMERS TEKNISKA HÖGSKOLA GÖTEBORGS UNIVERSITET Göteborg, Sverige 215

2 Sammandrag Runaway-elektroner är ett problem framtidens fusionsreaktorer måste undvika för att fusion ska kunna användas som energikälla. För att förstå runawayelektroners uppkomst studeras den synkrotronstrålning de sänder ut. I det här arbetet har ett datorprogram som simulerar detektorbilder liknande de från en verklig detektor utformats. Metoden som nyttjas bygger på tidigare studier men har förbättras genom att reducera antalet approximationer. Genom att bilda olika fördelningar av runaway-elektroner och beräkna synkrotronstrålningen från dem går det att simulera detektorbilder. Utseendet hos dessa bilder beror främst på fördelningen av elektronernas energi, rörelseriktning och position i rummet. De simulerade bilderna jämförs med tidigare teoretiska och experimentella resultat, och god överensstämmelse påvisas. Den förbättrade modellen introducerar också nya fenomen relaterade till att positionen hos de elektroner som bidrar till detektorbilden inte begränsas. Det visas även att användandet av en realistisk fördelning av elektronhastigheter har särskilt stor inverkan på detektorbilden. Nyckelord: Fusion, Tokamak, Runaway-elektroner, Synkrotronstrålning, Detektorbilder Abstract In order to make fusion a viable energy source several issues have to be tackled. One of these is runaway electrons. By studying the synchrotron radiation emitted by runaway electrons, important information regarding their creation can be obtained. In this study a computer program has been created to simulate images similar to those of a real detector. The approach is built on previous studies in the field, and is generalized by reducing the number of approximations used. By using different distributions of runaway electrons and calculating their synchrotron radiation, a detector image can be generated. The shape of the radiation spot on the image is primarily dependent on the distribution of energy, direction of movement and spatial position of the electrons. The simulated images are compared to previous theoretical and experimental results and match with a high level of accuracy. The improved model even uncovers new phenomena because the detector image is not limited by the spatial positions of the electrons. It is also shown that a realistic distribution of electron velocities has a great impact on the detector image. Keywords: Fusion, Tokamak, Runaway Electrons, Synchrotron Radiation, Detector Images

3 Innehåll 1 Inledning Plasma Fusion Fusion som energikälla Tokamak Runaway-elektroner Synkrotronstrålning Syfte Teori Det toroidala koordinatsystemet Analytisk metod Tillämpning av analytisk metod Metod Antaganden och approximationer Beräkning av synkrotronstrålning Beräkning av detektorbild Rumsliga elektronfördelningar Analytisk distribution av elektronhastigheter i

4 4 Resultat Test av numerisk metod utifrån Pankratov (1996) Jämförelse med Zhou et al. (214) Analytisk fördelning kontra monoenergetisk fördelning Jämförelse med experimentella resultat Diskussion Implementering i MATLAB Analytisk och numerisk lösning Antaganden och approximationer Rumsliga elektronfördelningar Skillnader i Zhou et al. (214) Sammanfattning 47 Referenser 49 ii

5 1 Inledning Kärnfusionsreaktorer kan komma att spela en stor roll för produktionen av elektrisk energi i framtiden. Forskningen inom ämnet har kommit en lång väg sedan starten på 194-talet [1] men det finns fortfarande stora utmaningar att övervinna. I dagens forskningsanordningar har så kallade runaway-elektroner observerats, dessa elektroner har mycket hög energi och kan nå hastigheter nära ljusets. Runaway-elektronerna uppkommer inuti reaktorn och kan orsaka stor skada på reaktorväggarna. Ett användbart sätt att analysera runaway-elektroner är att studera den så kallade synkrotronstrålning de sänder ut. I detta arbete framtas ett numeriskt verktyg som simulerar denna strålning och förhoppningen är en ökad förståelse för runaway-elektroner och hur de uppkommer. Det som följer i detta kapitel är tänkt att ge en kort bakgrund till den fysik som tillämpas i arbetet. 1.1 Plasma Plasma kan definieras på olika sätt och en vanlig definition är följande: Plasma är en kvasineutral gas bestående av laddade och neutrala partiklar som uppvisar ett gemensamt beteende [1]. Att plasmat är kvasineutralt innebär att det innehåller lika många positivt som negativt laddade partiklar, men på mikroskopisk nivå kan skillnader i laddning uppstå. Neutrala partiklar växelverkar på korta avstånd genom kollisioner, men laddade partiklar växelverkar med andra laddade partiklar på långa avstånd genom Coulombkraften. På grund av detta uppvisar plasmat ett gemensamt beteende eftersom många partiklar på långa avstånd påverkar en enskild partikels rörelse mer än enskilda partiklars växelverkan på korta avstånd. Plasma är det absolut vanligaste aggregationstillståndet då 99.9% av universums materia befinner sig i detta tillstånd [2]. På Jorden kan plasma observeras när luften blir joniserad inför ett blixtnedslag eller när plasma från solvinden växelverkar med magnetosfären för att skapa norrsken. Vetenskaplig utveckling har även fört in plasma i vardagen i form av lysrör, neonljus och TV-apparater. Plasma upptäcktes först av William Crookes år 1879 som gav det namnet lysande materia. Han gjorde detta med hjälp av så kallade Crookes-rör, som är ett 1

6 katodstrålrör, vilket även användes av J.J. Thomson för att identifiera elektronen år 1897 och av Wilhelm Röntgen för att upptäcka röntgenstrålningen år Termen plasma myntades av Irving Langmuir [3] när han observerade hur gasen inne i Crookes-röret innehöll ungefär lika många joner som elektroner vilket resulterade i att gasens nettoladdning blev mycket liten. Langmuir kan ha fått namnet plasma ifrån att gasens beteende påminnde honom om blodplasma då gasen transporterar joner och elektroner likt hur blodplasma transporterar röda och vita blodkroppar. Även om det finns många olika varianter av plasma är det en sak de flesta har gemensamt vilket är att det krävs en väldigt hög temperatur för att hålla gasen joniserad. Plasman i jordens jonosfär har en temperatur på cirka 12 K men för de flesta gaser behövs en temperatur på ungefär K [2]. I en vanlig neutral gas byter partiklar rörelseriktning när de kolliderar med andra partiklar. På grund av gasers låga densitet sker denna typ av växelverkan mellan par av partiklar, se Figur 1a. I plasma, som består av laddade partiklar, utsätts partiklarna istället för Coulombväxelverkan där partiklar attraherar eller repellerar varandra beroende på om de har olika eller samma laddning, enligt Figur 1b. N N (a) N 3. + (b) + Figur 1: Skiss över partiklars banor i gas (a) och i plasma (b). I gasen kolliderar de neutrala partiklarna 1 och 2 med varandra och deras banor ändras. Partikel 3s bana korsar banorna för både partikel 1 och 2, men missar båda två och ingen växelverkan sker. I sällsynta situationer kan fler än två partiklar kollidera samtidigt. I plasma är elektroner och joner separerade och växelverkar med varandra enligt Coulombs lag. Det innebär att partiklar med samma laddning repellerar varandra och partiklar med olika laddning attraherar. De två tunga jonerna stöter ifrån varandra och påverkar drastiskt de två lätta elektronernas rörelsebanor. Bild skapad med inspiration från [1]. 2

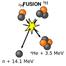
7 1.2 Fusion En viktig utmaning som världen står inför är hur elektrisk energi skall produceras i framtiden. I dagsläget står fossila bränslen för ca 6 % av den totala energiproduktionen i OECD-länderna [4]. För att minska beroendet av fossila bränslen och samtidigt möta den ökande efterfrågan på elektrisk energi krävs en annan källa som kan tillhandahålla storskalig produktion Fusion som energikälla Fusion är processen att slå ihop två atomkärnor till en tyngre kärna. Om slutprodukten väger mindre än summan av de lättare kärnorna frigörs energi enligt Einsteins berömda formel E = mc 2. Reaktioner av detta slag sker i solens centrum men kan teoretiskt även användas här på jorden för att tillverka elektrisk energi. I den enklaste fusionsreaktionen slås två väteatomer ihop till en heliumatom. Ett exempel på detta är reaktionen mellan väteisotoperna deuterium ( 2 H) och tritium ( 3 H) 2 H + 3 H 4 He + n + 17,6 MeV. (1) På grund av att deuterium och tritium båda är positivt laddade och vill stöta bort varandra är sannolikheten att denna reaktion skall ske mycket låg. För att reaktioner skall ske i tillräcklig takt krävs ett plasma med en temperatur i storleksordning 1 miljoner kelvin. Solen, med sin enorma gravitation, har inga problem att innesluta plasma med hög temperatur och högt tryck. Detta är dock huvudproblemet med fusion på jorden; att innesluta ett plasma med sådan hög temperatur kräver en speciell typ av reaktor. Fördelarna med fusion jämfört med andra energikällor är bland annat den låga miljöpåverkan. I fusionsreaktionerna bildas inga växthusgaser som i kol- och oljekraftverk. Neutronerna som bildas i processen absorberas av materialet i reaktorväggen som då kan bli radioaktivt. Därför krävs hantering av radioaktivt avfall, dock inte alls i samma utsträckning som i dagens kärnkraftverk som använder fission. Halveringstiden hos avfall från fusionsreaktorer är ca 1 år [1] vilket kan jämföras med miljontals år för vissa typer av avfall från fissionsreaktorer. Risken för härdsmälta i ett fissionkraftverk beror på att bränsle för flera års energiproduktion förvaras i reaktorn. Detta är inte fallet för fusionsreaktorer; energiinnehållet i bränslet i reaktorn är mycket litet och det krävs att nytt bränsle tillförs hela tiden för att 3

8 hålla igång processen. Deuterium som används i bränslet kan separeras från havsvatten som i princip finns i obegränsade mängder. Tritium har relativt kort halveringstid (12,3 år) och är på grund av det mycket ovanligare. Därför planeras det att istället producera tritium i reaktorn. Neutronerna från reaktion (1) får reagera med litiumplattor på reaktorväggarna för att skapa helium och tritium genom 6 Li + n 4 He + 3 H + 4,8 MeV, (2) 7 Li + n 4 He + 3 H + n 2,5 MeV. (3) I senare generationers reaktorer är det däremot tänkt att reaktorerna endast skall använda deuterium då litium inte är förnybart. En annan tänkbar reaktion som kan komma att användas är den mellan en proton och en boratom under bildandet av tre alfapartiklar: p + 11 B 3 4 He. (4) Fördelen med reaktionen i (4) är att det inte bildas några högenergetiska neutroner som kan göra reaktormaterialen radioaktiva [5]. Än så länge har ingen reaktor byggts som är tillräckligt effektiv för att producera mer elektrisk energi än vad som krävs för att driva produktionen. Den reaktor som än så länge är närmast är forskningsanläggningen JET (Joint European Torus) som har registrerat uteffekt på 16 MW, men för att uppnå denna effekt behövdes 25 MW [1]. En självförsörjande reaktor som producerar mer elektrisk energi än vad som är nödvändigt för att hålla igång fusionsreaktionerna krävs av ett eventuellt kraftverk. Detta hoppas man uppnå med ITER [6] som förväntas vara färdigbyggd kring 22. Om de ekonomiska och teknologiska utmaningarna som hör ihop med fusionsreaktorer kan övervinnas är fusion en god kandidat för storskalig energiproduktion i framtiden Tokamak Det finns olika sorters reaktorer som kan användas för fusion. De två mest framgångsrika är Stellaratorn och Tokamaken. Ordet Tokamak kommer ifrån ryskans toroidal naya kamera s magnitnymi katushkami vilket kan översättas till toroidal kammare med magnetiska spolar. I de båda typerna av reaktorer har plasmat ungefär formen av en torus. Detta är möjligt med ett starkt magnetfält som får 4

9 laddade partiklar att färdas längs med fältlinjerna. Fältet kan delas upp i en poloidal och en toroidal del vilket går att se mer detaljerat i Figur 2. Spolar av koppar eller ett supraledande material genererar det toroidala magnetfältet. På grund av magnetfältets krökning kommer partiklar som enbart befinner sig i ett toroidalt fält att transporteras ut från torusens centrum. Därför behövs också ett poloidalt fält som förhindrar detta. I stellaratorn skapas även detta fält utifrån, medan det i tokamaken skapas med en ström som går genom plasmat. Detta har gjort tokamaken billigare och enklare att konstruera vilket har lett till att den idag är den mest effektiva fusionsreaktorn [1]. Dagens tokamaker har en storradie på någonstans mellan 1 och 3 meter [7, 8], och den nya reaktorn ITER konstrueras för att ha en storradie på 6 meter [6]. Figur 2: Schematisk bild över tokamakens mest grundläggande komponenter. Kring plasmat går det att se spolarna som inducerar det toroidala magnetfältet som håller plasmat i kammaren. De inre spolarna driver plasmaströmmen som tillsammans med de yttre spolarna inducerar det poloidala fältet. Se Figur 5 för en enklare bild av de olika vinklarna. 5

10 1.3 Runaway-elektroner Ett plasma innehåller fria laddade partiklar som till exempel joner och elektroner. Då dessa partiklar befinner sig i ett elektriskt fält kommer de att påverkas av en accelererande kraft och kan nå mycket höga hastigheter. I en vanlig gas bromsas snabba partiklar av en friktionskraft som uppstår när de kolliderar med andra partiklar. I plasma uppstår däremot en effekt där laddade partiklar interagerar med varandra på långa avstånd på grund av Coulombväxelverkan och inte bara med sina närmaste grannar. Friktionskraften i plasmat ökar upp till en viss hastighet för att sedan minska med ökad hastighet, se Figur 3. Anledningen är att snabba partiklar växelverkar under mindre tidsintervall [9]. Detta gör att friktionskraften inte längre kan motverka den accelererande kraften från det elektriska fältet [1]. Elektroner med hastigheter över den kritiska hastigheten, v c, kommer därför att accelereras och påverkas av mindre friktionskraft som leder till att hastigheten springer iväg vilket resulterar i så kallade runaway-elektroner med extremt hög energi. ee D Friktionskraft ee ee c v c Hastighet c Figur 3: Schematiskt samband mellan friktionskraften och hastighet hos elektroner i ett plasma. Ett elektriskt fält E ger upphov till en kraft F = ee som bestämmer den kritiska hastigheten v c. Elektroner med hastigheter v > v c kan accelereras obehindrat och bli runaway-elektroner. E D och E c är Dreicerfältet respektive det kritiska fältet. 6

11 I dagens reaktorer har runaway-elektroner med energi på 3-4 MeV registrerats och i ITER beräknas elektronerna kunna uppnå så mycket som 1 MeV [8]. Problemet med runaway-elektroner är att de har tillräckligt med kinetisk energi att lämna det inneslutande magnetfältet för att sedan slå in i reaktorväggarna och skada väggmaterial och instrument. I den första av två möjliga processer bildas primära runaway-elektroner på grund av att deras hastighet är högre än v c. Ett elektriskt fält, från till exempel förändringar i plasmaströmmen i en tokamak, kan ge upphov till detta. Det till storleken minsta fält som kan bilda primära runaway-elektroner är det kritiska fältet E c (se Figur 3) som beror på plasmats parametrar. Vid ett tillräckligt starkt fält, det så kallade Dreicerfältet, E D, kan alla elektroner bli runaways. I den andra processen skapas sekundära runaway-elektroner genom att runaway-elektroner kolliderar med långsammare elektroner. Då krävs det att runaway-elektronen överför tillräckligt med energi för att göra den långsamma elektronen till en runaway, men fortfarande har tillräckligt med energi kvar för att vara runaway själv. Runawayelektroner kan på så sätt bilda nya runaway-elektroner om de båda har en hastighet över den kritiska efter kollisionen, vilket kan resultera i en snöbollseffekt [2]. 1.4 Synkrotronstrålning För att detektera runaway-elektroner i fusionsplasmor studeras strålningen som de sänder ut. Laddade partiklar kretsar kring magnetiska fältlinjer i cirkulära banor vilket kräver en acceleration riktad mot rörelsens centrum. Denna konstanta acceleration ger upphov till att partiklarna sänder ut strålning vars frekvens beror av cirkelrörelsens frekvens. För icke-relativistiska eller svagt relativistiska partiklar kallas strålningen cyklotronstrålning och skickas ut i alla riktningar. För starkt relativistiska partiklar, så som runaway-elektroner, kallas denna strålning för synkrotronstrålning och strålas istället ut som en kon längs med elektronens hastighetsvektor [2]. Skillnaden går att se i Figur 4. Synkrotronstrålningen skickas ut över ett stort våglängdsintervall och effekten är beroende av flertalet olika plasmaparameterar. Vid fusionsrelevanta plasmaparametrar har synktrotronstrålning högst effekt vid våglängder omkring,5 5 µm [9]. Vanliga detektorer för elektromagnetisk strålning kan användas för att detektera synkrotronstålning i en fusionsreaktor, men på grund av alla instrument som krävs för plasmadiagnostik kan det vara svårt att få plats med en detektor i anslutning till reaktorväggen. 7

12 a a v v (a) (b) Figur 4: Skillnaden mellan cyklotronstrålning (a) och synkrotronstrålning (b). För partiklar med icke-relativistiska eller svagt relativistiska hastigheter skickas strålning ut i alla riktningar medan för starkt relativistiska hastigheter skickas strålning ut som en kon. 1.5 Syfte Runaway-elektroner är ett problem i dagens fusionsreaktorer och bör i framtiden undvikas helt [2] eftersom de kan orsaka skada inuti reaktorn. Studier av synkrotronstrålning kan ge en ökad förståelse för runaway-elektroner och hur de uppkommer. Syftet med detta arbete är att skapa ett verktyg som simulerar synkrotronstrålning från runaway-elektroner i fusionsplasmor. Verktyget som tagits fram är ett datorprogram som givet en distribution av elektroner beräknar detektorbilder som kan jämföras med dem som fås vid riktiga fusionsexperiment. Grunden till arbetet ges av vetenskapliga artiklar inom ämnet där runaway-elektroner har studerats analytiskt [7, 8]. Genom att bygga vidare på dessa analytiska modeller skapas en mer realistisk modell som löses numeriskt i MATLAB. 8

13 2 Teori För att simulera synkrotronstålning från runaway-elektroner i en tokamak krävs beräkningar på ett stort antal elektroner i en toroidal geometri. Varje elektron skall tilldelas en position och en hastighet som beror på det inneslutande magnetfältet. De relativistiska effekterna gör att synkrotronstrålningen sänds ut längs hastighetsriktningen och det går på så sätt att beräkna om strålningen träffar en detektor med given position. I detta avsnitt förklaras den teori som arbetet grundar sig på. Först beskrivs de koordinatsystem som används samt uttryck för magnetfält och elektronhastigheter. Den analytiska lösning som utnyttjas i [7, 8] presenteras också. 2.1 Det toroidala koordinatsystemet För att studera plasmat i en tokamak används ofta ett toroidalt koordinatsystem som definieras enligt x = (R m r cos θ) cos ϕ y = (R m r cos θ) sin ϕ (5) z = r sin θ med den inversa transformen r = tan θ = tan ϕ = y x z 2 + (R m ) 2 x 2 + y 2 z R m x 2 + y 2 där R m är storradien och r är den mindre radien (se Figur 5b), r R m, och θ och ϕ är den poloidala respektive toroidala vinkeln, se Figur 5a. Enhetsvektorerna till detta koordinatsystem är e r = cos θ cos ϕ cos θ sin ϕ sin θ, e θ = sin θ cos ϕ sin θ sin ϕ cos θ, e ϕ = sin ϕ cos ϕ (6), (7) och visas i Figur 6a. Det toroidala koordinatsystemet används för att beskriva så kallade magnetiska (flödes)ytor i ett fusionsplasma. Plasmapartiklar kommer följa 9

14 r R m (a) (b) Figur 5: En torus där den toroidala vinkeln ϕ och den poloidala vinkeln θ är utritade (a) och ungefärliga formen hos tokamakens kammare sett ovanifrån (b). Storradien, R m, och den mindre radien, r, är utritade. dessa ytor som för små värden på r kan antas ha cirkulära tvärsnitt. I Figur 6a visas ett tvärsnitt av en magnetyta med centrum i O m. Eftersom runaway-elektroner har väldigt hög energi följer de inte magnetytorna exakt utan deras rörelsebanor förskjuts ut från origo med ett avstånd δ e, se Figur 6b. Ytorna som elektronerna följer kallas driftytor vars radier benämns r e. y O m r θ R m O y O d r e δ e O m r e θ e ϕ e r z (a) (b) Figur 6: I (a) visas enhetsvektorerna e r, e θ och e ϕ för ett tvärsnitt genom planet ϕ = π/2. Magnetytan (röd) med radie r har centrum i O m. I (b) är elektronens driftyta (blå) med radie r e och centrum i O d utritad. Driftytan är förskjuten med ett avstånd δ e på grund av runaway-elektroners höga energi. 1

15 2.2 Analytisk metod En analytisk metod för att studera runaway-elektroner i en toroidal geometri härleddes av I. M. Pankratov år 1996 [7]. Metoden introducerar användbara ekvationer som, till exempel, beskriver elektronernas position och hastighet. Dessa ekvationer utnyttjas i vårt program för att simulera synkrotronstrålning numeriskt. I detta delavsnitt sammanfattas de viktigaste koncepten i Pankratovs metod. Det resulterande magnetfältet B(r,θ) som går att se i Figur 2 definieras enligt [ ] B r B(r,θ) = e θ e ϕ, (8) 1 r cos θ/r m q(r)r m där B är magnetfältets styrka och q(r) är den så kallade säkerhetsfaktorn vars definition är antalet varv de magnetiska fältlinjerna färdas i den toroidala riktningen per varv i den poloidala riktningen, se Figur 7. Faktorn kallas för säkerhetsfaktor då den bestämmer stabiliteten hos plasmat och för låga värden på q(r) kan oscillationer i plasmat uppstå. Den kan ansättas på olika sätt, som framgår av Figur 8, och har stor inverkan på formen på detektorbilden [8]. Figur 7: Schematisk figur över en magnetisk fältlinje i en torus. I figuren går fältlinjen två toroidala varv per poloidalt varv vilket ger en säkerhetsfaktor q = 2. 11

16 q 2 q 2 q 2 q r (m) r (m) r (m) r (m) (a) (b) (c) (d) Figur 8: Olika säkerhetsfaktorer q(r) från Fig. 6 i [8]. I Figur (a) och (b) är säkerhetsfaktorn konstant och oberoende av plasmats radie och i Figur (c) har säkerhetsfaktorn ett linjärt beroende till plasmats radie. I det experimentellt framtagna radiella beroendet ökar q(r) exponentiellt med plasmats radie, se Figur (d). Elektronernas hastighet och position beskrivs enklast med koordinatsystemet (τ, τ 1, τ 2 ) som definieras enligt τ r = e ϕ + e θ τ = τ q(r)r m τ τ 1 = e r, τ 1 = τ. (9) 1 τ r 2 = e θ e ϕ q(r)r m τ 2 = τ 2 τ 2 Koordinatsystemet (τ, τ 1, τ 2), som inte är normerat, är det som definieras i [7]. För att undvika problem vid implementeringen används istället det normerade systemet (τ, τ 1, τ 2 ). Elektronens hastighet blir v = v τ + v (τ 1 cos α + τ 2 sin α) + (v d + v V )e z (1) där α är gyrovinkeln, v och v är hastighetens parallella respektive vinkelräta komponent med avseende på det inneslutande magnetfältet och accelererande elektriska fältet. Med dessa hastighetskomponenter definieras den så kallade pitchvinkeln, θ p, enligt θ p tan θ p = v v, v v. (11) 12

17 Hastigheten v d är vertikal strömning av elektroner på grund av centrifugalkraften och bestäms av v d = v2 + v2 /2 ω B R m, (12) där α ω B = eb(r,θ) γm e, γ = (1 v2 c 2 ) 1/2, (13) ω B är gyrovinkelfrekvensen och γ är Lorentzfaktorn. Hastigheten v V bestäms av den vertikala komponenten av magnetfältet och är av samma storleksordning som v d. Elektronens position i koordinatsystemet (9) blir R e = R m e R + rτ 1 + v ω B (τ 2 cos α τ 1 sin α) (14) (se Figur 9), där e R = cos ϕe x + sin ϕe y (15) är en enhetsvektor i riktning från origo till magnetytans centrum. y X det R e ˆv Detektor O ϕ Y det x Figur 9: Elektronstrålen (ljusblå) och detektorn (grön) för ett tvärsnitt i detektorplanet (Z = Z det ) sett ovanifrån. Elektronen (punkt) skickar ut strålning i kon (röd) längs med ˆv som är enhetsvektorn i hastighetsriktningen. R e är elektronens positionsvektor och vinkeln är avvikelsen från ϕ = π /2. 13

18 På grund av elektronernas höga energi blir faktorn v ω B r (16) vilket medför att sista termen kan försummas och Ekvation (14) förenklas till R e R m e R + rτ 1. (17) Med hjälp av sinus- och cosinussatserna går det att beräkna plasmats radie r från Figur 6 enligt ( ( ) ) r 2 = re 2 + δe 2 2r e δ e cos π sin 1 δe sin θ (θ π) r e r = (18) re 2 δe 2 sin 2 θ δ e cos θ där förskjutningen av driftytan bestäms av storheten δ e som definieras enligt [8] Detektorns positionsvektor i det kartesiska systemet blir δ e = q(r)γm ec eb. (19) R det = X det e x + Y det e y + Z det e z (2) där Z det oftast sätts till så att detektorn är i samma plan som plasmats centrum, se Figur 9. Synkrotronstrålning skickas ut i en kon med mycket liten öppningsvinkel θ s längs med elektronens hastighetsvektor v. Öppningsvinkeln θ s 1/γ 1 så den försummas. Strålning registreras av detektorn om v (R e R det ) =, (21) det vill säga om elektronens hastighetsvektor är parallell med elektronens positionsvektor sett från detektorn. Om olikheterna v v 1 θ p ξ Y det R m + r cos θ X det 1 η ζ 14 r q(r)r m 1 Z det X det 1 (22)

19 är uppfyllda kan de tre ekvationerna från kryssprodukten i Ekvation (21) förenklas till sin η sin θ + θ p cos (θ α) + ξ (23) och Z det r sin θ [ η cos θ + θ p sin (θ α) + v ] d + v V v [ ] X det + (R m r cos θ) sin, (24) där = ϕ π/2, 1, (25) det vill säga en liten toroidal vinkel som utgår från y-axelns positiva riktning, se Figur 9. Olikheten som representeras av ξ i Ekvation (22) säger att elektronens avstånd till O m projicerad i Z = Z det -planet ska vara mycket mindre än avståndet mellan y-axeln och detektorn om Y det ligger nära R m. Detta innebär att elektroner tar upp en liten del av synfältet sett från detektorn. Den sträcka som elektronen färdas toroidalt för varje poloidalt varv är 2πq(r)R m och 2πr är sträckan för ett poloidalt varv. Olikheten η 1 innebär att den toroidala sträckan elektronen färdas måste vara mycket längre än den poloidala sträckan för att krökningen av elektronbanan inte ska bli för stor. Förenklingen i härledningen av Ekvationerna (23) och (24) består främst av att försumma termer som består av två eller flera små element enligt ξ + ξ 2 ξ. (26) Utöver det som står skrivet i [7] krävs det även att θ p, ξ, η och ζ är av ungefär samma storleksordning och att termen v ω B 1. (27) Dessutom är v d + v V v 1 (28) och flyttar därför bara detektorbilden lite i z-led så den kan försummas. 15

20 2.3 Tillämpning av analytisk metod För elektroner med låga pitchvinklar som uppfyller olikheten θ p r beam, (29) q(r beam )R m där r beam är den största radien bland elektronernas driftytor, kan Ekvation (24) skrivas om så att endast elektroner som uppfyller tan θ = ± X det q(r)r m. (3) träffar detektorn. Detta innebär att endast elektroner längs en strimma av varierande längd kommer registreras. Strimmans form bestäms helt utav vilken typ av säkerhetsfaktor q(r) som används och i [8] ges exempel på strimmans form för de säkerhetsfaktorer presenterade i Figur 8, se avsnitt 4.1 för resultat. Det andra och lite mer allmänna fallet är då r beam θ p, (31) q(r beam )R m vilket resulterar i en större fläck. Om planet z = Z det studeras kan endast elektroner utan vertikal hastighetskomponent (v z = ) kunna träffa detektorn. Från Ekvation (18) fås för θ = och θ = π i Figur 6a att radien på elektronstrålens insida r in respektive utsida r ut i detta plan blir r in = r beam δ beam, θ = r ut = r beam + δ beam, θ = π där δ beam är förskjutningen av driftytan för r beam. Genom att använda radierna i Ekvation (32) tillsammans med vinklarna kan Ekvation (23) reduceras till (32) vilket endast kan gälla för θ p sin α = θ p sin α = r beam δ beam, θ = q(r beam δ beam )R m, (33) r beam + δ beam, θ = π q(r beam + δ beam )R m θ p θ p r beam δ beam, θ = q(r beam δ beam )R m r beam + δ beam, θ = π q(r beam + δ beam )R m (34) 16

21 eftersom sin α 1. Om olikheten för θ = π i Ekvation (34) inte gäller kan den detekterade strålens utsträckning i planet z = Z det beräknas enligt L H = r beam + r e + δ e δ beam +.5R in (χ 2 β 2 1) +.5R ut β 2 2 (35) där variablerna definieras enligt χ 2 = θ 2 p (r beam δ beam ) 2 [q(r beam δ beam )R m ] 2 β 1 = Y det R in X det β 2 = Y det R ut X det (36) R in = R m r beam + δ beam R ut = R m + r e + δ e. Om båda olikheterna i Ekvation (34) gäller ska r e och δ e ersättas med r beam respektive δ beam i Ekvation (35) vilken då ger fläckens maximala utsträckning i planet z = Z det, se avsnitt 4.1 för resultat. 17

22 3 Metod Eftersom syftet är att göra en numerisk beräkning av synkrotronstrålningen krävs ett hjälpmedel för att kunna utföra dessa beräkningar. I MATLAB genereras toroidala koordinater (r,θ,ϕ) för ett stort antal elektroner utifrån olika rumsfördelningar. Elektronerna tilldelas också hastighetskomponenter v och v utifrån fördelningar av energi och pitchvinkel. Givet detta beräknas sedan om synkrotronstrålningen från elektronerna träffar en detektor vars position, tillsammans med värden på andra viktiga parametrar, hämtas från tidigare experiment. Med data från dessa beräkningar simuleras sedan detektorbilder vilka jämförs med bilder från verkliga tokamak-experiment. I kapitlet förklaras först de approximationer som görs i arbetet som inte gjorts i tidigare studier och hur elektronernas hastighet beräknas. Efter det ges en kort sammanfattning om hur programmet beräknar detektorbilden. Kapitlet avslutas sedan med att gå igenom elektronernas fördelning i både positionsrummet och hastighetsrummet. 3.1 Antaganden och approximationer För en numerisk beräkning är det inte nödvändigt att följa den analytiska lösningen efter Ekvation (21), då kryssprodukten kan beräknas direkt i MATLAB. Detta innebär att approximationerna presenterade i Ekvation (22) kan undvikas, vilket ger möjlighet till en mer korrekt lösning. Av samma anledning kan även den sista termen i Ekvation (14) användas, även om dess inverkan på resultatet är liten. En approximation som inte görs i [7], men som är nödvändig här för att beräkningstiderna inte ska bli alltför långa är att kvadraten på parallella hastigheten v ansätts till v 2 v c (37) med syftet att kunna linjarisera en ekvation, se Avsnitt 3.2. I de båda artiklarna [7, 8] nämns inte detektorns utsträckning utan den antas vara en punkt i rummet bestämt av positionsvektorn R det. I den analytiska metoden spelar det ingen roll men i det numeriska fallet, där strålning kommer från ett antal diskreta punkter, kan ingen strålning träffa detektorn. För att undvika detta antas detektorn ha formen av en cirkel i ett yz-plan med mittpunkt i R det. Cirkelns radie sätts till 1.5 cm för att efterlikna en typ av kamera som användes vid de experiment [11, 12] vilka vi jämför våra simulerade detektorbilder med. 18

23 3.2 Beräkning av synkrotronstrålning De toroidala enhetsvektorerna, e r, e θ och e ϕ implementeras i MATLAB enligt definitionen i Ekvation (7). De övriga enhetsvektorerna, τ, τ 1, τ 2 och e R samt gyrovinkelfrekvensen ω B och Lorentzfaktorn γ implementeras också. För att beräkna elektronens fart, v = v, givet en pitchvinkel θ p och en elektronenergi används uttrycket för total energi i det relativistiska fallet: E tot = E kin + E vilo. (38) Genom att bryta ut E kin och använda att E tot = mc 2, där m = γm är den relativistiska massan, och E vilo = m c 2, där m är vilomassan, erhålls ( ) E kin = mc 2 m c 2 = (γ 1) m c 2 1 = 1 v2 /c 1 m c 2. (39) 2 v kan lösas ut ur Ekvation (39): v = c 1 ( ) 2 Ekin m c + 1. (4) 2 För att dela upp v i hastighetskomponenterna v, v, v d och v V behövs Ekvationerna (1), (11), (12) och (13) som tillsammans bildar ekvationssystemet v = v τ + v (τ 1 cos α + τ 2 sin α) + e z (v d + v V ) v = θ p v v d = ( ) v 2 + v2 /ω B R m 2 ω B = eb /m e γ γ = (1 v2 v V = v d c 2 ) 1/2 (41) 19

24 där v V kan ansättas till v d eftersom de är av samma storleksordning (små jämfört med v och v ). Ekvationssystemet kan reduceras till v = v τ + θ p v (τ 1 cos α + τ 2 sin α) + 2v2 + θ2 pv 2 e z 2ω B R m. (42) Denna ekvation kan lösas med MATLAB, men beräkningen är tidskrävande i jämförelse med om ekvationen varit linjär. Här utnyttjas därför approximationen i Ekvation (37) att v 2 v c vilket gör att sista termen i Ekvation (42) ändras och ekvationen blir v = v τ + θ p (τ 1 cos α + τ 2 sin α) θ2 p c e z 2ω B R m. (43) Det som återstår nu är att dela upp högerledet i Ekvation (43) i ortogonala komponenter (förslagsvis de kartesiska) genom att använda definitionerna i Ekvationerna (7) och (9) vilket resulterar i v x v = sin ϕ + r cos ϕ sin θ θ p cos α cos ϕ cos θ q(r)r m r θ p sin α cos ϕ sin θ + θ p sin α sin ϕ q(r)r m v y r = cos ϕ + sin ϕ sin θ θ p cos α sin ϕ cos θ v q(r)r m r θ p sin α sin ϕ sin θ θ p sin α cos ϕ q(r)r m v z r = cos θ + θ p cos α sin θ θ p sin α cos θ θ2 p c v q(r)r m ω B R m som innebär att v kan räknas ut genom (44) v v = v = ( ) 2 vx + v ( vy v ) 2 + ( vz v ) 2. (45) v (vx ) 2 ( ) 2 ( ) 2 /v + vy /v + vz /v Från detta kan de andra hastighetskomponenterna v, v d och v V beräknas enligt Ekvationssystemet (41). 2

25 ˆv S Detektor ˆv S Detektor R e R e (a) Träff. (b) Miss. Figur 1: Schematisk bild som visar hur MATLAB räknar ut om strålningen från en elektron träffar detektorn. Det är avståndet mellan skärningspunkten S och detektorns position som avgör om strålningen träffar eller inte. ˆv är enhetsvektorn i samma riktning som elektronens hastighet v. För att implementera v och R e enligt Ekvation (1) och (14) krävs också ett värde på gyrovinkeln α. Snabbast beräkningstid uppnådes då α slumpades till ett värde på intervallet [,2π]. Alla gyrovinklar blev då lika sannolika och fördelade sig jämt över alla elektroner. I [7] är Ekvation (21) huvudvillkoret för att strålningen ska träffa detektorn. Ekvationen leder i sin tur till villkoren i Ekvation (23) och (24). Dessutom måste olikheterna (22) vara uppfyllda. Eftersom MATLAB arbetar numeriskt kan villkoret (21) testas på ett enklare sätt. Från elektronens position R e följer man hastighetsvektorn v till skärningspunkten, S, i planet där detektorn befinner sig, se Figur 1. Om avståndet mellan S och detektorns position R det är mindre än detektorns radie träffar strålningen detektorn, se Figur 1a. Om avståndet istället är större, som i Figur 1b, missar strålningen. 3.3 Beräkning av detektorbild Utifrån positionerna för de elektroner vars strålning träffat detektorn går det att beräkna detektorbilden. Genom att projicera alla elektroner i ett plan parallellt med detektorns plan erhålls en tvådimensionell bild av elektronerna som tar hänsyn till effekten att en sträcka ser ut att vara längre eller kortare beroende på vilket avstånd den befinner sig från detektorn. Planet ligger vid x = så att elektronernas utsträckning i y- och z-riktning kan uppskattas utifrån projektionens utsträckning. Metoden är illustrerad i Figur

26 Detektor elektron projektion Figur 11: De elektroner vars strålning träffar detektorn projiceras i ett plan (streckad linje) för att få en detektorbild. Avståndet mellan detektorn och planet bestämmer storleken på bilden. För att generera en bild delas projektionsplanet in i ett rutnät, vilket i MATLAB representeras av en matris. Värdet i varje matriselement representerar summan av styrkan på strålningen hos varje elektron i motsvarande ruta. Matrisen kan sedan ritas upp grafiskt för att visa en detektorbild. Matriselementen motsvaras i verkligheten av en pixel i detektorn och värdet av hur mycket ljus som har träffat den pixeln. 3.4 Rumsliga elektronfördelningar För att programmet ska kunna ge något lätthanterligt och användbart räcker det inte med att testa om strålning från enstaka runaway-elektroner träffade detektorn. En fördelning av elektroner likt den som finns i en fusionsreaktor behöver användas, dessa elektronfördelningar kan se ut på olika sätt. Ett sätt är att de toroidala koordinaterna r, θ respektive ϕ för olika elektroner har lika stora avstånd mellan varandra inom ett godtyckligt intervall. Resultatet är att runaway-elektronerna hamnar i skivor, se Figur 12a, där en skiva kan ses från sidan i Figur 13a. Alternativt kan koordinater tas fram slumpvist, se Figur 12b och 13b. Därmed förhindras att mönster från elektronfördelningen avspeglas i detektorbilden. Ytterligare två fördelningar som också slumpar fram koordinater används. I den första har stora radier större sannolikhet. Elektronerna för en godtycklig toroidal vinkel blir då homogent fördelade, se Figur 13d. Denna distribution är användbar vid jämförelse med artiklarna [7, 8] för att se var elektronerna som kan träffa detektorn finns. Den andra, se Figur 13c, har Gaussiskt fördelade radier vilket är mest likt en verklig elektronfördelning i en tokamak [13, 14]. 22

27 (a) (b) Figur 12: Två olika elektronfördelningar sett ovanifrån. Koordinaterna för den toroidala vinkeln väljs med jämna mellanrum (a) eller elektronerna placeras slumpvis där alla toroidala vinklar har lika stor sannolikhet (b). Intervallet de toroidala koordinaterna ligger mellan varieras mellan olika körningar av programmet. För den poloidala vinkeln används mestadels hela intervallet, dvs. [, 2π). Radier upp till,3 m används, så att storleken på en plasmastråle efterliknades [8]. För en korrekt detektorbild behövs ett tillräckligt stort intervall så att inga elektroner som har möjlighet att ses av detektorn ligger utanför. Om intervallet är mycket stort blir det däremot många elektroner som inte ses i detektorn och tar upp onödig beräkningstid. Elektronernas pitchvinklar och detektorns position är faktorer som påverkar valet av toroidala vinklar. Om rumsfördelningen ska ta hänsyn till förskjutning av elektronens driftyta, δ e (se Figur 6b), är det istället driftytans radie, r e, som genereras slumpvist. Med Ekvation (18) omvandlas r e till r, där δ e fås från Ekvation (19) med q(r e ) istället för q(r). Då r beror på θ ökar det poloidala avståndet mellan elektronerna i strålens yttre del, se Figur 14b. Då Ekvation (19) endast gäller för r e > δ e implementerades en alternativ metod som adderar δ e till R m utifrån (6). Denna bevarar det poloidala avståndet mellan elektronerna (se Figur 14c) och fungerar för alla r e. 23

28 (a) (b) (c) (d) Figur 13: De olika typer av rumsliga elektronfördelningar som används. Figurerna visar hur radie och poloidal vinkel fördelar sig. I centrum av varje figur ligger r =. De poloidala koordinaterna valdes med lika stora mellanrum i (a) och slumpades fram i (b), (c) och (d). I (b) hade varje koordinat r och θ lika stor sannolikhet och i (c) användes en gaussisk fördelning för att bestämma radien. Radie slumpades med sannolikhet proportionell mot radiens storlek i (d) så att varje punkt i ett tvärsnitt av torusen har lika stor sannolikhet..3.2 längd (m) längd (m) (a) längd (m) (b) längd (m) (c) Figur 14: Effekten av driftförskjutning med Ekvation (19) (b) och ändrat värde på R m (c) jämfört med avsaknad av förskjutning (a). 24

29 3.5 Analytisk distribution av elektronhastigheter Att beräkna en analytisk hastighetsdistribution av runaway-elektroner i plasma är svårt och har ofta olika begränsningar. En sådan distribution beskriven i [15] kräver att sekundära runaways är många fler än de primära till antalet. Distributionen ger en stationär lösning som är giltig för elektroner med väldigt höga hastigheter. Denna distribution är angiven för det normaliserade rörelsemängdsrummet med axlarna p och p som transformeras från hastighetsrummet genom { p = γv /c p = γv /c, (46) där v och v är de parallella respektive vinkelräta hastighetskomponenterna. Distributionen beror inte bara på de olika hastighetskomponenterna utan även på plasmats egenskaper. Parametrar så som temperatur, elektriskt fält och jonernas nettoladdning har stor påverkan på fördelningen av elektronernas rörelsemängdskomponenter. Dessa parametrars påverkan förklaras först och därefter presenteras distributionen. Den första parametern är Coulomblogaritmen som karaktäriserar växelverkan mellan laddade partiklar i plasmat och bestäms enligt ln Λ 14,9 ln ne + ln T (47) 12 där n e är elektrondensiteten och T är temperaturen givet i kev [16]. För ln Λ 1 är växelverkan på långa avstånd den dominerande effekten [1]. I fusionsplasmor brukar ln Λ ha värden mellan 1-2 [16]. Laddade partiklar i plasma växelverkar med andra laddade partiklar över långa avstånd och vilket ger upphov till små förändringar i partiklarnas färdriktningar. Kollisionstiden, τ, för en partikel är den genomsnittliga tiden mellan två stora förändringar i dess färdriktning. För relativistiska elektroner ges kollisionstiden av τ = 4πε2 m 2 ec 3 e 4 n e ln Λ som används för att bestämma det normaliserade elektriska fältet genom (48) Ē = e E τ m e c. (49) 25

30 Distributionens beroende av det elektriska fältet kan skrivas som Ê = Ē Z eff (5) där Z eff är den effektiva jonladdningen i plasmat (Z eff = 1 för plasma bestående av endast väte). Den sista komponenten som behövs är c Z = 3(Zeff + 5) och alla dessa tillsammans ger distributionen ( n r Ê f AA (p,p ) = 2πc Z p ln Λ exp p ) c Z ln Λ Êp2 2p π (51) (52) där n r är densiteten av runaway-elektroner. Ett exempel på en sådan distribution visas i Figur 15 med plasmaparametrar tagna från [8]. I figuren är distributionen avskuren för p < 5 på grund av att den inte gäller för elektroner med låg energi [9]. I vår MATLAB-rutin används värdet på f AA (p,p )/n r som sannolikheten att en elektron har just parametrarna p och p. log 1 f AA /n r p p 7 Figur 15: En figur som visar distributionen normaliserat mot antalet runaway-elektroner. Parametrarna är T =.55 kev, Z eff = 3 och E =.1 V/m [8]. Då distributionen inte gäller för elektroner med låg energi beräknas inga elektroner med p < 5. 26

31 4 Resultat Hundratals detektorbilder simulerades för att få en överblick av hur formen på bilden varierar. Dessa bilder uppvisar både likheter och skillnader med bilder från andra studier. En upptäckt är att de runaway-elektroner som detekteras har ett större toroidal utsträckning än vad har räknats med tidigare. Effekten av detta är att synkrotronstrålningsfläcken ser större ut på detektorns utsida då elektronerna där befinner sig närmre detektorn. Nytt för det här arbetet är också detektorbilder simulerade för elektroner med energi- och pitchvinkelfördelningar. 4.1 Test av numerisk metod utifrån Pankratov (1996) Sektion 2.3 ger en analytisk beskrivning av var elektroner vars strålning kan träffa detektorn befinner sig. Denna lösning appliceras i [7, 8] och det är därför av intresse att jämföra våra simuleringar med dessa resultat. För låga pitchvinklar ger Ekvation (3) att detektorbilden blir en tunn strimma. Två jämförelser med simulerade bilder går att se i Figur z(m) z(m) y(m) (a) (b) y(m) Figur 16: Jämförelse av formen på detektorbilden för små pitchvinklar. De svarta fläckarna är de simulerade detektorbilderna och de vita linjerna representerar formen för den analytiska lösningen. Säkerhetsfaktorn är konstant i (a) och växer exponentiellt i (b) vilket leder till att linjerna blir böjda. I båda figurerna stämmer det simulerade resultatet väl överens med det analytiska. 27

32 Konstant pitchvinkel på θ p =,1 används för att Ekvation (29) ska gälla. I Figur 16a används en konstant säkerhetsfaktor q = 2 och i Figur 16b används en exponentiell säkerhetsfaktor enligt Figur 8d. Den exponentiella säkerhetsfaktorn resulterar i att formen blir böjd eftersom vinkeln θ för de elektroner som detekteras ändras för olika radier. I båda fallen stämmer den simulerade formen väl överens med linjen för Ekvation (29). När θ p ökar har fler elektroner möjlighet att träffa detektorn. För att hela elektronstrålens horisontella utsträckning ska kunna detekteras måste båda Ekvationerna (33) vara uppfyllda. Med bestämda värden på θ p och r simulerades bilder för olika α. Gyrovinklarna hos de elektroner som detekterades längst in och längst ut på strålen (θ = respektive θ = π) uppskattades på så vis för att jämföra med Ekvationerna (33). I Tabell 1 redovisas en sådan jämförelse för r beam =,4 och en exponentiell säkerhetsfaktor. Tabell 1: Gyrovinklar α som uppfyller Ekvationerna (33) samt de gyrovinklar som kan detektera elektroner längst in respektive ut på elektronstrålen. Värdena från Ekvationerna (33) hamnar ungefär på det i Figur 17a uppmätta intervall. Skillnaden kan bero på avgränsningarna i [7]. Insida Utsida Beräknat värde Uppmätt från Figur 17a,377,33 < α <,38 2,765 2,7 < α < 2,76,182,2 < α <,23 2,96 2,92 < α < 2,97 Ekvationerna (34) undersöktes också på samma vis genom att variera θ p istället för α. Skillnaden mellan värden på θ p då ekvationerna inte uppfylls längre och vad som fås ut ur Figur 17 är mindre än,1. Då endast den första olikheten i Ekvation (34) är uppfyllda kan den totala horisontella utsträckningen av elektroner L H beräknas med Ekvation (35). Denna ekvation visade sig stämma väl med vad som gick att se i de simulerade detektorbilderna då skillnaden var mindre än,5 cm. 28

33 .6.4 z (m) L H y (m) (a) y (m) (b) y (m) (c) Figur 17: I (a) är båda av Ekvationerna (34) uppfyllda och elektroner detekteras i hela planet z =. Då θ p minskas blir fläcken smalare. För (b) är inte längre den första olikheten i Ekvationerna (34) vilket medför att utsträckningen inte blir lika stor åt vänster. Ett fall då (35) kan användas för att beräkna sträckan L H går att se i (c) med en linjär säkerhetsfaktor (Figur 8c). 4.2 Jämförelse med Zhou et al. (214) I sektion III i artikeln av Zhou et al. (214) [8] studeras formen hos synkrotronstrålningsfläcken på detektorn. Teorin som används i artikeln är hämtad från [7], koordinatsystemet (se Figur 6a) och huvudvillkoren (23) och (24) presenteras. Fläckens form beräknas numeriskt med hjälp av dessa ekvationer och några viktiga parametrar från experimentuppställning vid EAST (Experimental Advanced Superconducting Tokamak): storradien, R m = 1,86 m, magnetfältets styrka B = 2 T samt detektorns koordinater, X det = 1,48 m, Y det = 1,85 m och Z det =. Figurer visar hur fläckens form beror på elektronens energi och pitchvinkel, säkerhetsfaktorn, q, värdet på förskjutningen av driftytan, δ e, samt olika radieintervall för elektronstrålen. För att testa vår MATLAB-rutin för flera elektroner med konstant energi och pitchvinkel kördes rutinen för de parametrar som var angivna i [8]. Energi och pitchvinkel med mera varierades på samma sätt som i artikeln för att sedan kunna generera egna figurer att jämföra med artikelns. Elektronernas radiefördelningen antas vara jämn [17], se Figur 13d. 29

34 .2.1 z (m) y (m) (a).4 z (m) z (m) y (m) (b) y (m) (c) Figur 18: Jämförelse mellan Figurerna 5b, 5c och 5d i [8] och det simulerade resultatet. Det gröna området är resultatet i [8] och det svarta är det simulerade resultatet för pitchvinkel θ p =,2 (a),,12 (b) och,19 (c). I [7] visar det sig att olika pitchvinklar ger olika former och i [8] studeras detta ytterligare. Med konstant energi på 3 MeV ges resultaten i Figur 18. Det gröna området är resultatet från [8] och det svarta är det simulerade resultat. Olika typer av säkerhetsfaktorer q(r) definierade i [8] visas i Figur 8. För att testa samtliga säkerhetsfaktorer användes inte bara konstant E = 3 MeV utan även konstant θ p =,2. Det låga värdet på θ p gör det lättare att se skillnaden för olika säkerhetsfaktorer. I Figur 19 jämförs konstant säkerhetsfaktor och en säkerhetsfaktor som växer exponentiellt med radien r. Även ihåliga elektronstrålar med r [15,3]cm studeras i [8]. Övriga parametrar är θ p =,12, E = 3 MeV och säkerhetsfaktorn är den exponentiella från Figur 19b. 3

35 I tidigare jämförelser har inte driftförskjutningen δ e tagits i beaktning. Genom att applicera Ekvation (18) förskjuts elektronerna åt sidan, dock inte lika mycket för alla elektroner, se Figur 14. I Figur 2a och 2b visas resultatet utan respektive med förskjutning av driftytan..3.2 z (m) y (m) (a) z (m) y (m) (b) Figur 19: En figur som jämför Figurerna 6e och 6h i [8] med simulerade bilder som använder samma parametrar. Det gröna området är resultatet i [8] och det svarta är det simulerade för konstant säkerhetsfaktor (a) och exponentiellt växande säkerhetsfaktor (b)..3.2 z (m) (a) y (m) (b) Figur 2: En figur som jämför Figurerna 7b och 7d i [8] med det simulerade resultatet. Det gröna området är resultatet i [8] och det svarta är det simulerade när elektronstrålen är ihålig och förskjutning av driftytan enligt Ekvation (18) har ignorerats (a) och tagits i beaktning (b). 31

36 4.3 Analytisk fördelning kontra monoenergetisk fördelning I [8] simuleras elektroner med rumsfördelning där alla elektroner har samma energi och pitchvinkel. Detta leder till enklare beräkningar men man riskerar att tappa information om detektorbilden eftersom elektroner i en runawaystråle har en energioch pitchvinkelfördelning. För att skapa dessa fördelningar användes en MATLABfunktion som implementerar Ekvation (52). Varje elektron i simuleringen testas för flera värden på energi och pitchvinkel. Hur sannolik en viss energi och pitchvinkel är bestäms av den analytiska fördelningen, se Figur 15, vilket påverkar intensiteten i bilden. Figur 21 visar två simulerade detektorbilder, för monoenergetiska elektroner med konstant θ p =,19 till vänster, och för elektroner med energi- och pitchvinkelfördelning med θ p [;,2] till höger..5 Effekt (g.e.) Effekt (g.e.) z(m) y(m) y(m) Figur 21: Jämförelse mellan en monoenergetisk och en analytisk fördelning. Till vänster: Parametrar som i Figur 5d i [8], speciellt E = 3 MeV och θ p =,19. Till höger: Parametrar som i Figur 5d i [8] men med en analytisk fördelning av energi E [,511; 3] MeV och θ p [;,19]. Notera skillnaden i formen och effekt som bland annat beror på att den analytiska fördelningen har färre elektroner med stor pitchvinkel. 32