Formella metoder. Loop-program som statetransformers. Betrakta följande problem. specifikationen.
|
|
|
- Sandra Jansson
- för 8 år sedan
- Visningar:
Transkript
1 8Att bevisa egenskaper om program Formella metoder... 1 Loop-program som statetransformers... 1 Några exempel... 2 Partiell korrekthet och total korrekthet... 3 Programspecifikation... 3 Hoarelogik och partiell korrekthet... 4 Valid eller ickevalid... 4 Två valida Hoareformler... 5 Några slutledningsregler för Hoareformler... 5 Terminering... 7 Formella metoder Testing can reveal the presence of errors, not their absence. E.W. Djikstra Betrakta följande problem. Syntes Givet en programspecifikation, konstruera ett program som satisfierar specifikationen. Analys Givet ett program konstruera en programspecifikation som beskriver programmet. Verifiering Givet ett program och en programspecifikation visa att programmet satisfierar specifikationen. Ekvivalens och optimering Givet ett program och en programspecifikation konstruera ytterligare ett program som satisfierar samma specifikation, men som är optimal i något avseende. Korrigering (avlusning Givet en programspecifikation och ett program som inte satisfierar specifikationen korrigera programmet så att det satisfierar specifikationen. Samtliga dessa problem är välkända oavgörbara problem. Ändå forskas det mycket på problemen ifråga. Skälet till detta är förstås att det inte bara finns enstaka program utan hela klasser av program där problemen är avgörbara, och där bra metoder formella metoder för att lösa problemen väntar på sin lösning. Dessa sidor utgör en liten introduktion till detta ämne för det fall att programmen är s.k. state transformers (Jag hittar inget bra svenskt namn.. Loopprogram (se kapitel 6 är en enkel klass av just state transformers. tillståndsrummet Loop-program som statetransformers Antag att ett visst loop-programs variabler är x 1, x 2,, x n vilka var och en är tillåtna att antaga godtyckliga värden i N. Det utrymme som programmet kräver man brukar tala om programmets tillståndsrum kan då sägas vara De värden som tupeln N N N = N n ( x 1, x 2,, x n har i olika skeden av programkör- 1
2 2 Att bevisa egenskaper om program ningen sägs vara programmets tillstånd. Om vid en körning av programmet ifråga, det inträffar att programmet stannar, och tupeln ( x 1, x 2,, x n vid start respektive stopp har värdena σ 0 = ( a 10, a 20,, a n0 σ N = ( a 1N, a 2N,, a nm sägs körningen ha σ 0 och σ N som start- respektive sluttillstånd. Observera den omvända konventionen att låta bågar representera tillstånd och noder övergångar. σ 1 q 0 q N En tillståndsövergång q k är här ett programsteg, t ex x 1 x 2, x 1 0 eller x Några enkla exempel illustrerar de just införda begreppen: σ N EXEMPEL 1 Några exempel Betrakta det primitiva loopprogram x = som minskar en varia- bels värde med en enhet. Programvariablerna z x y 0 är x, y, z, så z ggr{ x y programmets tillståndsrum är y++ N 3. En körning där x har värdet 2 vid start ger upphov till följande sekvens av tillståndsövergångar: ( 2,, z x ( 2,, 2 y 0 ( 202,, x y ( 002,, y++ ( 012,, x y ( 112,, ( 122,, y++ EXEMPEL 2 EUKLIDES ALGORITM för beräkning av största gemensamma delare till två positiva naturliga tal kan formuleras som nedan till vänster. Loop-programmet till höger med tre programvariabler, dvs med tillståndsrum N 3, implementerar algoritmen. SGD( x, x = x SGD( x, = SGD( y, x om x < y SGD( x, = SGD( y, x om x > y Sgd x och y i d = Sålänge ( x { Om ( x > så ( x x annars ( y y x d x Här är ett körexempel av loop-programmet: ( 68,, ( 62,, ( 42,, y y x x x y x x y ( 22,, d x ( 222,,
3 Partiell korrekthet och total korrekthet 3 EXEMPEL 3 Partiell korrekthet och total korrekthet Vi skall intressera oss för två aspekter på ett program. Den ena behandlar frågan om programmets output är önskat output (givet av en programspecifikation. Den andra aspekten behandlar även frågan om programmet ifråga stannar. 1 Ett program sägs vara partiellt korrekt om alla dess output är önskade output. 2 Ett program sägs vara totalt korrekt om det stannar (terminerar för varje input och om dess output är önskade output. En seriös diskussion kräver formalisering. Därför ska vi införa en formell apparat för programspecifikation, dvs för beskrivning av input och önskade output. Ett program för beräkning av SGD (som i EXEMPEL 2 till två positiva naturliga tal X, Y skall förslagsvis ha två inputvariabler, säg x, y med initialvärden X, Y, samt en outputvariabel säg d med värdet SGD( X, Y när programmet stannar. Dvs givet (( x = X > 0 ( y = Y > 0 vid start, önskas d = SGD( X, Y vid stopp. Tillsammans utgör dessa två villkor en programspecifikation. Filosofin bakom detta synsätt är att programkonstruktören skall vara fri att utforma programmet efter eget huvud, bara input och output stämmer med de specificerade. Programspecifikation En s.k. programspecifikation EXEMPEL 4 φ = ( previllkor, postvillkor är ett par av logiska utsagor beskrivande programmets start- och stopptillstånd, närmare bestämt programmets inputvariabler vid start och dess outputvariabler vid stopp. I första exemplet nedan ges specifikationer φ beskrivande några mycket enkla program P. (Jfr avsnittet Syntes sid 1. De enklaste loop-programmen och specifikationer av dem: program P specifikation φ x 0 (( x 0, ( x = 0 x++ (( x = X 0, ( x = X+ 1 x ggr { (( x = X 0, ( x = X EXEMPEL 5 I detta exempel presenteras en specifikation φ men inget program. Avsikten är att ge en formell beskrivning av input och output i ett program för division mellan ett naturligt tal X och ett positivt naturligt tal Y. (q och r är outputvariabler vars värden vid stopp är naturliga tal representerande kvoten respektive resten, x och y är inputvariabler. φ = ((( x 0 ( y 0, (( x = qy+ r ( r 0 ( r< ÖVNING 1 Konstruera ett loop-program som satisfierar φ i EXEMPEL 5.
4 4 Att bevisa egenskaper om program Hoarelogik och partiell korrekthet Antag att φ = ( pq, är en programspecifikation och att Du har konstruerat ett program P avsett att satisfiera φ. Om för de igångkörningar av ditt program P som stannar, det gäller att Om p är sann innan P körs igång, så är q sann efter att P har stannat (1 så har Du gjort ett gott jobb. (Det enda man skulle kunna begära ytterligare är att få en garanti på att igångkörda P alltid stannar. Man säger (om (1 stämmer att P är partiellt korrekt m.a.p. φ = ( pq, Notera att (1 är en logisk utsaga som kan vara sann eller falsk. Den är bildad med hjälp av utsagorna p, q samt programmet P. Därför betecknas den med formeln Hoareformel { pp{ q En sådan formel kallas Hoareformel (efter C.A.R. Hoare Begreppet partiell korrekthet kan alltså definieras på följande sätt: DEFINITION P är partiellt korrekt m.a.p. en specifikation φ = ( pq, om { pp{ q är sann för varje körning. Valid eller ickevalid En Hoareformel { pp{ q som är sann vid varje körning av P sägs vara valid, annars ickevalid. Villkoret om partiell korrekthet för ett program P visavi en programspecifikation ( pq, kan således uttryckas som att { pp{ q är valid. Och innebörden i validitet resp. dess motsats ickevaliditet är som nedan: { pp{ q är ickevalid om vid någon körning av P det gäller att 1 p är sann innan P körs, det är sant att P stannar och q är falsk när detta inträffar. { pp{ q är valid om för varje körning av P någon av följande tre punkter gäller 2 p är sann innan P körs, det är sant att P stannar, och q är sann när detta inträffar 3 p är sann innan P körs, och det är falskt att P stannar 4 p är falsk innan P körs EXEMPEL 6 För de enklaste loop-programmen x 0, x++, x ggr { är följande tre formler valida { x 0x 0{ x = 0 { x = X 0x++ { x = X + 1 { x = X 0 ( x ggr { { x = X
5 Partiell korrekthet och total korrekthet 5 Däremot är t ex formeln { x = X 0x++ { x = 1 ickevalid. Om x 0 startas med t ex x = 1 gäller ju punkt 1 ovan. Två valida Hoareformler { pp{ sann { falskp{ q (1 är valid (oberoende av p och P eftersom postvillkoret i detta fall alltid är sant. (En ickevalid formel förutsätter att postvillkoret är falskt efter någon körning av P (se punkt 1. (2 är valid (oberoende av q och P eftersom previllkoret i detta fall alltid är falskt. (En ickevalid formel förutsätter att previllkoret är sant innan någon körning av P (se punkt 1. (1 (2 Några slutledningsregler för Hoareformler S.k. slutledningsregler (eller inferensregler som vanligen skrivs på följande sätt Med PP' menas kör P och sedan P' u u 1, u 2 -- och v v uttrycker att man kan sluta sig till att v är valid om man vet att u är valid (respektive om man vet att u 1 och u 2 båda är valida. Som Du ser används kommatecken istället för och. Tecknet reserverar vi för användning inuti pre- och post-villkoren. Implikationsreglerna p p',{ p' P{ q { pp{ q { p S{ q', q' q { pp{ q (3 (4 Och-regeln { p P{ q',{ pp{ q'' { pp{ q' q'' (5 Eller-regeln { p' P{ q,{ p'' P{ q { p' p'' P{ q (6 { pp{ q,{ qp' { r Sekvensregeln (7 { ppp' { r ovillkorlig (primitiv loop Iterationsreglerna { p P{ p { p ( x ggr{ P { p (8 villkorlig loop { p ( x 0 P{ p (9 { p ( Sålänge ( x 0 { P { p ( x = 0 Vi visar (med ett motsägelseresonemang att den första implikationsregeln (3 är korrekt. Antag tvärtom att p p' och { p' P{ q är valida men att { pp{ q är
6 6 Att bevisa egenskaper om program EXEMPEL 7 ickevalid. Då gäller att q är falskt (10 efter någon körning av P där p var sann innan P startades. Men p p' tillsammans med att p är sann, ger att p' är sann, och validiteten hos { p' P{ q ger då att q är sann efter körningen ifråga, vilket motsäger (10. Av motsägelsen följer att implikationsregeln måste vara korrekt. # På motsvarande sätt kan de övriga reglerna visas vara korrekta. Betrakta divisionsprogrammet nedan: Dividera x med y i q och r = q 0 r x Sålänge r y { Subtrahera y från r q++ Vi bevisar att divisionsprogrammet är partiell korrekt m.a.p. specifikationen dvs att φ = ((( x 0 ( y > 0, (( x = qy+ r ( r 0 ( r< aritmetik {( x 0 ( y> 0 Dividera x med y i q och r{ (( x = qy + r ( r< är sann för varje körning. BEVIS (( x 0 ( y > 0 (( x = 0y + x ( x 0 {( x = 0y + x ( x 0 ( q 0 {( x = qy+ x ( x 0 {( x = qy+ x ( x 0 ( r x {( x = qy+ r ( r 0 sekvens aritmetik {( x = 0y + x ( x 0 ( q 0 ( r x {( x = qy+ r ( r 0 (( x = qy+ r ( r 0 ( r ( ( x = ( q+ 1y+ ( r ( r p är en invariant P = ( Subtrahera y från r ( q++ och p = ( x = qy+ r ( r 0 iteration {( x = ( q+ 1y+ ( r ( r Subtrahera y från r{ ( x = ( q + 1y + r ( r 0 {( x = ( q+ 1y+ ( r ( r 0 q++{( x = qy + r ( r 0 { pp{ p { p ( Sålänge ( r { P { p ( r < EXEMPEL 8 Betrakta specifikationen φ = ( n 0, r 2 n<( r+ 1 tillsammans med följande loop-program. Kvadratrot n i r = r 0 k 0 Sålänge k n { r++ k r.r r
7 Terminering 7 Vi bevisar partiell korrekthet genom att (som i förra exemplet ta ett programsteg i taget, och visa att följande Hoareformel är valid. BEVIS { n 0 Kvadratrot n i r { r 2 n<( r+ 1 2 { n 0 r 0 {( 0 = r 2 ( 0 n {( 0 = r 2 ( 0 n k 0 {( k = r 2 ( k n {( k = r 2 ( k n r++ {( k = ( r 1 2 (( r 1 2 n {( k = ( r 1 2 (( r 1 2 n k r r {( k = r 2 (( r 1 2 n Låt P = ( r++ ( k r r. Då följer av (11 och (12 att {( k = r 2 ( k n P {( k = r 2 (( r 1 2 n Av (13 och iteration följer i sin tur (11 (12 (13 {( k = r 2 ( k n P {( k = r 2 (( r 1 2 n {( k = r 2 Sålänge k n { P {( k = r 2 (( r 1 2 n ( k > n Och av aritmetik: (( k = r 2 ( ( r 1 2 n ( k > n ((( r 1 2 n ( r 2 > n Till sist: {(( r 1 2 n ( r 2 > n r {( r 2 n (( r > n Aritmetik: ((( r 1 2 n ( r 2 > n ( r 2 n<( r Terminering En ideal lösning till en given programspecifikation φ = P sådant att är ett program P är partiellt korrekt m.a.p. φ = ( pq,, och P stannar vid varje körning där p är sann innan P startas. (14 Man säger att P i detta fall är totalt korrekt m.a.p. φ = ( pq,. Eftersom de enda loop-program som överhuvudtaget har någon möjlighet att efter igångkörning vägra att stanna är de som innehåller en eller flera villkorliga loopar, så nöjer vi oss med att diskutera terminering för programavsnitt av typ eller (allmännare ( pq, Sålänge x 0 {B (15 Sålänge villkor {B (16 En garanti för att (15 stannar är att variabeln x minskar med en eller flera enheter vid varje genomgång av repetitionsblocket B. Ty då kommer villkoret x 0 (som är ekvivalent med villkoret x>0 för naturliga tal x förr eller senare att bli falskt. På motsvarande sätt kan man slå fast att (16 stannar, om man lyckas hitta en kvantitet z sådan att 1 z minskar vid varje genomgång av repetitionsblocket B,
8 8 Att bevisa egenskaper om program EXEMPEL 9 EXEMPEL 10 2 z z 0 för något z 0, (OBSERVERA att detta villkor är uppfyllt för varje z vars värden är naturliga tal. eller sådan att 3 z ökar vid varje genomgång av repetitionsblocket B, 4 z z 0 för något z 0. I programavsnittet nedan (som är hämtat från EXEMPEL 8 uppfylls stoppvillkoren 3 och 4 av variabeln k, vilket garanterar terminering. Sålänge k n { r++ k r.r Vad sägs om följande programavsnitt då? Sålänge x är jämn { x x/2 Stoppvillkoret 2 är uppfyllt av variabeln x (ja av varje variabel! Detta gäller oavsett vilket värde som x har vid start. Villkoret 1 däremot uppfylls enbart om x är positiv vid igångkörningen. (Om x har värdet 0 - ett jämnt tal - vid start, så kommer x efter varje genomkörning av repetitionsblocket att ha värdet 0. Dvs då minskar inte x vid genomkörning av repetitionsblocket. Slutsatsen är att programavsnittet ifråga stannar om och endast om det startas med ett positivt x. EXEMPEL 11 Nedanstående loop är tagen från EXEMPEL 2. Sålänge x y { Om x>y så (x x- annars (y y-x Här är det inte lika uppenbart som i de förra exemplen hur man kan hitta en stoppvillkorsuppfyllande kvantitet. Men betrakta x+y. Eftersom vid varje besök i repetitionsblocket den ena av x,y minskar medan den andra lämnas oförändrad, kommer x+y att minska vid varje sådant besök. Därmed är stoppvillkoret 1 uppfyllt av x+y. Och villkoret 2 är ju alltid uppfyllt (av kvantiteter vars värden är naturliga tal. I detta fall är villkoret 2 t.o.m. uppfyllt genom programavsnittets egen försorg. Ty tack vare villkoret x>y i repetitionsblocket kommer x enbart att kunna tilldelas positiva värden av x x-y. Och på motsvarande sätt kommer y enbart att kunna tilldelas ickenegativa värden. Således kommer x+y enbart att kunna tilldelas positiva värden. Slutsats: slingan stannar (ifall den körs igång.
Föreläsning 9: Turingmaskiner och oavgörbarhet. Turingmaskinen. Den maximalt förenklade modell för beräkning vi kommer använda är turingmaskinen.
 Föreläsning 9: Turingmaskiner och oavgörbarhet Turingmaskinen Den maximalt förenklade modell för beräkning vi kommer använda är turingmaskinen. Data är ett oändligt långt band där nollor och ettor står
Föreläsning 9: Turingmaskiner och oavgörbarhet Turingmaskinen Den maximalt förenklade modell för beräkning vi kommer använda är turingmaskinen. Data är ett oändligt långt band där nollor och ettor står
Introduktion till formella metoder Programmeringsmetodik 1. Inledning
 Introduktion till formella metoder Programmeringsmetodik 1. Inledning Fokus på imperativa program (ex. C, Java) program betyder härefter ett imperativt program Program bestäms i en abstrakt mening av hur
Introduktion till formella metoder Programmeringsmetodik 1. Inledning Fokus på imperativa program (ex. C, Java) program betyder härefter ett imperativt program Program bestäms i en abstrakt mening av hur
Turingmaskiner och oavgörbarhet. Turingmaskinen. Den maximalt förenklade modell för beräkning vi kommer använda är turingmaskinen.
 Turingmaskiner och oavgörbarhet Turingmaskinen Den maximalt förenklade modell för beräkning vi kommer använda är turingmaskinen. Data är ett oändligt långt band där nollor och ettor står skrivna: Oändligt
Turingmaskiner och oavgörbarhet Turingmaskinen Den maximalt förenklade modell för beräkning vi kommer använda är turingmaskinen. Data är ett oändligt långt band där nollor och ettor står skrivna: Oändligt
Induktion, mängder och bevis för Introduktionskursen på I
 Induktion, mängder och bevis för Introduktionskursen på I J A S, ht 04 1 Induktion Detta avsnitt handlar om en speciell teknik för att försöka bevisa riktigheten av påståenden eller formler, för alla heltalsvärden
Induktion, mängder och bevis för Introduktionskursen på I J A S, ht 04 1 Induktion Detta avsnitt handlar om en speciell teknik för att försöka bevisa riktigheten av påståenden eller formler, för alla heltalsvärden
DD1350 Logik för dataloger
 DD1350 Logik för dataloger Fö 8 Axiomatiseringar 1 Modeller och bevisbarhet Sedan tidigare vet vi att: Om en formel Φ är valid (sann i alla modeller) så finns det ett bevis för Φ i naturlig deduktion.
DD1350 Logik för dataloger Fö 8 Axiomatiseringar 1 Modeller och bevisbarhet Sedan tidigare vet vi att: Om en formel Φ är valid (sann i alla modeller) så finns det ett bevis för Φ i naturlig deduktion.
1 Duala problem vid linjär optimering
 Krister Svanberg, april 2012 1 Duala problem vid linjär optimering Detta kapitel handlar om två centrala teoretiska resultat för LP, nämligen dualitetssatsen och komplementaritetssatsen. Först måste vi
Krister Svanberg, april 2012 1 Duala problem vid linjär optimering Detta kapitel handlar om två centrala teoretiska resultat för LP, nämligen dualitetssatsen och komplementaritetssatsen. Först måste vi
Lösningar till utvalda uppgifter i kapitel 5
 Lösningar till utvalda uppgifter i kapitel 5 5.3. Vi använder Euklides algoritm och får 4485 = 1 3042 + 1443 3042 = 2 1443 + 156 1443 = 9 156 + 39 156 = 4 39. Alltså är sgd(3042, 4485) = 39. Om vi startar
Lösningar till utvalda uppgifter i kapitel 5 5.3. Vi använder Euklides algoritm och får 4485 = 1 3042 + 1443 3042 = 2 1443 + 156 1443 = 9 156 + 39 156 = 4 39. Alltså är sgd(3042, 4485) = 39. Om vi startar
MÖNSTER OCH TALFÖLJDER
 MÖNSTER OCH TALFÖLJDER FÖRELÄSNINGENS INNEHÅLL OCH SYFTE Genomgång av viktiga matematiska begrepp, uttryck och symboler med anknytning till mönster och talföljder. Skälet till att välja detta innehåll
MÖNSTER OCH TALFÖLJDER FÖRELÄSNINGENS INNEHÅLL OCH SYFTE Genomgång av viktiga matematiska begrepp, uttryck och symboler med anknytning till mönster och talföljder. Skälet till att välja detta innehåll
Introduktion till algoritmer - Lektion 1 Matematikgymnasiet, Läsåret 2014-2015. Lektion 1
 Kattis Lektion 1 I kursen används onlinedomaren Kattis (från http://kattis.com) för att automatiskt rätta programmeringsproblem. För att få ett konto på Kattis anmäler du dig på Programmeringsolympiadens
Kattis Lektion 1 I kursen används onlinedomaren Kattis (från http://kattis.com) för att automatiskt rätta programmeringsproblem. För att få ett konto på Kattis anmäler du dig på Programmeringsolympiadens
MATEMATIKENS SPRÅK. Avsnitt 1
 Avsnitt 1 MATEMATIKENS SPRÅK Varje vetenskap, liksom varje yrke, har sitt eget språk som ofta är en blandning av vardagliga ord och speciella termer. En instruktionshandbok för ett kylskåp eller för en
Avsnitt 1 MATEMATIKENS SPRÅK Varje vetenskap, liksom varje yrke, har sitt eget språk som ofta är en blandning av vardagliga ord och speciella termer. En instruktionshandbok för ett kylskåp eller för en
Sanningsvärdet av ett sammansatt påstående (sats, utsaga) beror av bindeord och sanningsvärden för ingående påståenden.
 MATEMATISK LOGIK Matematisk logik formaliserar korrekta resonemang och definierar formellt bindeord (konnektiv) mellan påståenden (utsagor, satser) I matematisk logik betraktar vi påståenden som antingen
MATEMATISK LOGIK Matematisk logik formaliserar korrekta resonemang och definierar formellt bindeord (konnektiv) mellan påståenden (utsagor, satser) I matematisk logik betraktar vi påståenden som antingen
Om semantisk följd och bevis
 Matematik, KTH Bengt Ek december 2017 Material till kursen SF1679, Diskret matematik: Om semantisk följd och bevis Logik handlar bla om studiet av korrekta slutledningar, dvs frågan om när det är riktigt
Matematik, KTH Bengt Ek december 2017 Material till kursen SF1679, Diskret matematik: Om semantisk följd och bevis Logik handlar bla om studiet av korrekta slutledningar, dvs frågan om när det är riktigt
Booleska variabler och översättning mellan programuttryck och booleska variabler
 Vad är Boolesk algebra Lite förenklat kan man säga att Boolesk algebra är räkneregler konstruerade av den engelske matematikern Gerge Boole för att kunna räkna med logiska uttryck. I den booleska algebran
Vad är Boolesk algebra Lite förenklat kan man säga att Boolesk algebra är räkneregler konstruerade av den engelske matematikern Gerge Boole för att kunna räkna med logiska uttryck. I den booleska algebran
Utsagor (Propositioner) sammansatta utsagor sanningstabeller logisk ekvivalens predikat (öppna utsagor) kvantifierare Section
 Föreläsning 1 Utsagor (Propositioner) sammansatta utsagor sanningstabeller logisk ekvivalens predikat (öppna utsagor) kvantifierare Section 1.1-1.3 i kursboken Definition En utsaga (proposition) är ett
Föreläsning 1 Utsagor (Propositioner) sammansatta utsagor sanningstabeller logisk ekvivalens predikat (öppna utsagor) kvantifierare Section 1.1-1.3 i kursboken Definition En utsaga (proposition) är ett
Några satser ur talteorin
 Några satser ur talteorin LCB 997/2000 Fermats, Eulers och Wilsons satser Vi skall studera några klassiska satser i talteori, vilka är av betydelse bland annat i kodningsteknik och kryptoteknik. De kan
Några satser ur talteorin LCB 997/2000 Fermats, Eulers och Wilsons satser Vi skall studera några klassiska satser i talteori, vilka är av betydelse bland annat i kodningsteknik och kryptoteknik. De kan
Algoritmer, datastrukturer och komplexitet
 Algoritmer, datastrukturer och komplexitet Övningsmästarprovsövning 2 Anton Grensjö grensjo@csc.kth.se 20 november 2017 1 Dagordning 1. Genomgång av uppgiftens lösning 2. Genomgång av bedömningskriterier
Algoritmer, datastrukturer och komplexitet Övningsmästarprovsövning 2 Anton Grensjö grensjo@csc.kth.se 20 november 2017 1 Dagordning 1. Genomgång av uppgiftens lösning 2. Genomgång av bedömningskriterier
A B A B A B S S S S S F F S F S F S F F F F
 Uppsala Universitet Matematiska institutionen Isac Hedén isac distans@math.uu.se Algebra I, 5 hp Vecka 17. Logik När man utför matematiska resonemang så har man alltid vissa logiska spelregler att förhålla
Uppsala Universitet Matematiska institutionen Isac Hedén isac distans@math.uu.se Algebra I, 5 hp Vecka 17. Logik När man utför matematiska resonemang så har man alltid vissa logiska spelregler att förhålla
MMA132: Laboration 2 Matriser i MATLAB
 MMA132: Laboration 2 Matriser i MATLAB Introduktion I den här labben skall vi lära oss hur man använder matriser och vektorer i MATLAB. Det är rekommerad att du ser till att ha laborationshandledningen
MMA132: Laboration 2 Matriser i MATLAB Introduktion I den här labben skall vi lära oss hur man använder matriser och vektorer i MATLAB. Det är rekommerad att du ser till att ha laborationshandledningen
Kapitel 2: De hela talen
 Kapitel 2: De hela talen Divisionsalgoritmen ( a a Z, d Z\{0} q, r Z : d = q + r ) d, 0 r d c 2005 Eric Järpe Högskolan i Halmstad där q kallas kvoten och r kallas principala resten vid heltalsdivision.
Kapitel 2: De hela talen Divisionsalgoritmen ( a a Z, d Z\{0} q, r Z : d = q + r ) d, 0 r d c 2005 Eric Järpe Högskolan i Halmstad där q kallas kvoten och r kallas principala resten vid heltalsdivision.
DD1350 Logik för dataloger. Fö 2 Satslogik och Naturlig deduktion
 DD1350 Logik för dataloger Fö 2 Satslogik och Naturlig deduktion 1 Satslogik En sats(eller utsaga)är ett påstående som kan vara sant eller falskt. I satslogik(eng. propositionallogic) representeras sådana
DD1350 Logik för dataloger Fö 2 Satslogik och Naturlig deduktion 1 Satslogik En sats(eller utsaga)är ett påstående som kan vara sant eller falskt. I satslogik(eng. propositionallogic) representeras sådana
PROV I MATEMATIK Automatateori och formella språk DV1 4p
 UPPSALA UNIVERSITET Matematiska institutionen Salling (070-6527523) PROV I MATEMATIK Automatateori och formella språk DV1 4p 19 mars 2004 SKRIVTID: 15-20. POÄNGGRÄNSER: 18-27 G, 28-40 VG. MOTIVERA ALLA
UPPSALA UNIVERSITET Matematiska institutionen Salling (070-6527523) PROV I MATEMATIK Automatateori och formella språk DV1 4p 19 mars 2004 SKRIVTID: 15-20. POÄNGGRÄNSER: 18-27 G, 28-40 VG. MOTIVERA ALLA
p /\ q r DD1350 Logik för dataloger Kort repetition Fö 3 Satslogikens semantik
 DD1350 Logik för dataloger Fö 3 Satslogikens semantik 1 Kort repetition Satslogik formellt språk för att uttrycka påståenden med variabler och konnektiv /\, \/,, t.ex. p /\ q r 1 Kort repetition Naturlig
DD1350 Logik för dataloger Fö 3 Satslogikens semantik 1 Kort repetition Satslogik formellt språk för att uttrycka påståenden med variabler och konnektiv /\, \/,, t.ex. p /\ q r 1 Kort repetition Naturlig
Algoritmer, datastrukturer och komplexitet
 Algoritmer, datastrukturer och komplexitet Övning 8 Anton Grensjö grensjo@csc.kth.se 12 november 2015 Anton Grensjö ADK Övning 8 12 november 2015 1 / 21 Översikt Kursplanering Ö8: Mästarprov 1, oavgörbarhet
Algoritmer, datastrukturer och komplexitet Övning 8 Anton Grensjö grensjo@csc.kth.se 12 november 2015 Anton Grensjö ADK Övning 8 12 november 2015 1 / 21 Översikt Kursplanering Ö8: Mästarprov 1, oavgörbarhet
Linjära ekvationer med tillämpningar
 UMEÅ UNIVERSITET Institutionen för matematik och matematisk statistik Olof Johansson, Nina Rudälv 2006-10-17 SÄL 1-10p Linjära ekvationer med tillämpningar Avsnitt 2.1 Linjära ekvationer i en variabel
UMEÅ UNIVERSITET Institutionen för matematik och matematisk statistik Olof Johansson, Nina Rudälv 2006-10-17 SÄL 1-10p Linjära ekvationer med tillämpningar Avsnitt 2.1 Linjära ekvationer i en variabel
DD1350 Logik för dataloger. Fö 7 Predikatlogikens semantik
 DD1350 Logik för dataloger Fö 7 Predikatlogikens semantik 1 Kryssprodukt av mängder Om A och B är två mängder så är deras kryssprodukt A B mängden av alla par (a,b), där a A och b B. Ex: A={1,2}, B={3,4},
DD1350 Logik för dataloger Fö 7 Predikatlogikens semantik 1 Kryssprodukt av mängder Om A och B är två mängder så är deras kryssprodukt A B mängden av alla par (a,b), där a A och b B. Ex: A={1,2}, B={3,4},
Hela tal LCB 1999/2000
 Hela tal LCB 1999/2000 Ersätter Grimaldi 4.3 4.5 1 Delbarhet Alla förekommande tal i fortsättningen är heltal. DEFINITION 1. Man säger att b delar a om det finns ett heltal n så att a Man skriver b a när
Hela tal LCB 1999/2000 Ersätter Grimaldi 4.3 4.5 1 Delbarhet Alla förekommande tal i fortsättningen är heltal. DEFINITION 1. Man säger att b delar a om det finns ett heltal n så att a Man skriver b a när
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson LÄSANVISNINGAR VECKA 36 VERSION 1. ARITMETIK FÖR RATIONELLA OCH REELLA TAL, OLIKHETER, ABSOLUTBELOPP ADAMS P.1 Real Numbers and the Real
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson LÄSANVISNINGAR VECKA 36 VERSION 1. ARITMETIK FÖR RATIONELLA OCH REELLA TAL, OLIKHETER, ABSOLUTBELOPP ADAMS P.1 Real Numbers and the Real
Regression med Genetiska Algoritmer
 Regression med Genetiska Algoritmer Projektarbete, Artificiell intelligens, 729G43 Jimmy Eriksson, jimer336 770529-5991 2014 Inledning Hur många kramar finns det i världen givet? Att kunna estimera givet
Regression med Genetiska Algoritmer Projektarbete, Artificiell intelligens, 729G43 Jimmy Eriksson, jimer336 770529-5991 2014 Inledning Hur många kramar finns det i världen givet? Att kunna estimera givet
inte följa någon enkel eller fiffig princip, vad man nu skulle mena med det. All right, men
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Christian Gottlieb Gymnasieskolans matematik med akademiska ögon Induktion Dag 2. Explicita formler och rekursionsformler. Dag mötte vi flera talföljder,
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Christian Gottlieb Gymnasieskolans matematik med akademiska ögon Induktion Dag 2. Explicita formler och rekursionsformler. Dag mötte vi flera talföljder,
de var svåra att implementera och var väldigt ineffektiva.
 OBS! För flervalsfrågorna gäller att flera alternativ eller inget alternativ kan vara korrekt. På flervalsfrågorna kan man bara ha rätt eller fel, dvs frågan måste vara helt korrekt besvarad. Totalt kan
OBS! För flervalsfrågorna gäller att flera alternativ eller inget alternativ kan vara korrekt. På flervalsfrågorna kan man bara ha rätt eller fel, dvs frågan måste vara helt korrekt besvarad. Totalt kan
Kompletteringsmaterial. K2 Något om modeller, kompakthetssatsen
 KTH Matematik Bengt Ek Maj 2008 Kompletteringsmaterial till kursen SF1642, Logik för D1 och IT3: K2 Något om modeller, kompakthetssatsen Vi skall presentera ett enkelt (om man känner till sundhets- och
KTH Matematik Bengt Ek Maj 2008 Kompletteringsmaterial till kursen SF1642, Logik för D1 och IT3: K2 Något om modeller, kompakthetssatsen Vi skall presentera ett enkelt (om man känner till sundhets- och
Algoritmer, datastrukturer och komplexitet
 Algoritmer, datastrukturer och komplexitet Övning 9 Anton Grensjö grensjo@csc.kth.se 9 november 2017 1 Idag Bevis av NP-fullständighet Labbteoriredovisning inför labb 4 2 Teori Teori När vi talar om NP-fullständighet
Algoritmer, datastrukturer och komplexitet Övning 9 Anton Grensjö grensjo@csc.kth.se 9 november 2017 1 Idag Bevis av NP-fullständighet Labbteoriredovisning inför labb 4 2 Teori Teori När vi talar om NP-fullständighet
Multipel tilldelning. Introduktion till programmering D0009E. Föreläsning 6: Iteration. while-satsen. Kom ihåg. Snurror kontra rekursion
 Introduktion till programmering D0009E Föreläsning 6: Iteration Multipel tilldelning Helt ok att tilldela en variabel flera gånger: bruce = bruce, bruce = 7 bruce Output: 7 Som tillståndsdiagram: bruce
Introduktion till programmering D0009E Föreläsning 6: Iteration Multipel tilldelning Helt ok att tilldela en variabel flera gånger: bruce = bruce, bruce = 7 bruce Output: 7 Som tillståndsdiagram: bruce
Komponentvisa operationer,.-notation Multiplikation (*), division (/) och upphöj till (ˆ) av vektorer följer vanliga vektoralgebraiska
 Matlab-föreläsning 3 (4), 17 september, 2015 Innehåll Sekvenser (från förra föreläsningen) Upprepning med for-slingor och while-slingor Villkorssatser med if - then -else - Logik Sekvenser - repetion från
Matlab-föreläsning 3 (4), 17 september, 2015 Innehåll Sekvenser (från förra föreläsningen) Upprepning med for-slingor och while-slingor Villkorssatser med if - then -else - Logik Sekvenser - repetion från
JavaScript del 3 If, Operatorer och Confirm
 JavaScript del 3 If, Operatorer och Confirm Under förra uppgiften så kollade vi på hur användaren kan ge oss information via promt(), vi använde den informationen både för att skriva ut den och för att
JavaScript del 3 If, Operatorer och Confirm Under förra uppgiften så kollade vi på hur användaren kan ge oss information via promt(), vi använde den informationen både för att skriva ut den och för att
Logik och kontrollstrukturer
 Logik och kontrollstrukturer Flödet av instruktioner i ett programmeringsspråk bygger vi upp med hjälp av dess kontrollstrukturer. I C har vi exemplen if, if else, while, do while. Dessutom finns switch
Logik och kontrollstrukturer Flödet av instruktioner i ett programmeringsspråk bygger vi upp med hjälp av dess kontrollstrukturer. I C har vi exemplen if, if else, while, do while. Dessutom finns switch
Programmering i C++ En manual för kursen Datavetenskaplig introduktionskurs 5p
 Programmering i C++ En manual för kursen Datavetenskaplig introduktionskurs 5p Skriven av Michael Andersson Introduktion Programmering I högnivåspråk fokuserar på själv problemet (algoritmen) istället
Programmering i C++ En manual för kursen Datavetenskaplig introduktionskurs 5p Skriven av Michael Andersson Introduktion Programmering I högnivåspråk fokuserar på själv problemet (algoritmen) istället
Grundläggande logik och modellteori
 Grundläggande logik och modellteori Kapitel 6: Binära beslutsdiagram (BDD) Henrik Björklund Umeå universitet 22. september, 2014 Binära beslutsdiagram Binära beslutsdiagram (Binary decision diagrams, BDDs)
Grundläggande logik och modellteori Kapitel 6: Binära beslutsdiagram (BDD) Henrik Björklund Umeå universitet 22. september, 2014 Binära beslutsdiagram Binära beslutsdiagram (Binary decision diagrams, BDDs)
Föreläsning 9: NP-fullständighet
 Föreläsning 9: NP-fullständighet Olika typer av problem: 1. Beslutsproblem: A(x) =Ja. 2. Optimeringsproblem: A(x) =m Vanligen max/min. 3. Konstruktionsproblem: A(x) =En struktur. Vanligen lösningen till
Föreläsning 9: NP-fullständighet Olika typer av problem: 1. Beslutsproblem: A(x) =Ja. 2. Optimeringsproblem: A(x) =m Vanligen max/min. 3. Konstruktionsproblem: A(x) =En struktur. Vanligen lösningen till
Övningshäfte 2: Induktion och rekursion
 GÖTEBORGS UNIVERSITET MATEMATIK 1, MMG200, HT2017 INLEDANDE ALGEBRA Övningshäfte 2: Induktion och rekursion Övning D Syftet är att öva förmågan att utgående från enkla samband, aritmetiska och geometriska,
GÖTEBORGS UNIVERSITET MATEMATIK 1, MMG200, HT2017 INLEDANDE ALGEBRA Övningshäfte 2: Induktion och rekursion Övning D Syftet är att öva förmågan att utgående från enkla samband, aritmetiska och geometriska,
Explorativ övning 7 KOMPLEXA TAL
 Explorativ övning 7 KOMPLEXA TAL Övningens syfte är att bekanta sig med komplexa tal. De komplexa talen, som är en utvidgning av de reella talen, kom till på 1400 talet då man försökte lösa kvadratiska
Explorativ övning 7 KOMPLEXA TAL Övningens syfte är att bekanta sig med komplexa tal. De komplexa talen, som är en utvidgning av de reella talen, kom till på 1400 talet då man försökte lösa kvadratiska
Övningshäfte 2: Komplexa tal (och negativa tal)
 LMA110 VT008 ARITMETIK OCH ALGEBRA DEL Övningshäfte : Komplexa tal (och negativa tal) Övningens syfte är att bekanta sig med komplexa tal och att fundera på några begreppsliga svårigheter som negativa
LMA110 VT008 ARITMETIK OCH ALGEBRA DEL Övningshäfte : Komplexa tal (och negativa tal) Övningens syfte är att bekanta sig med komplexa tal och att fundera på några begreppsliga svårigheter som negativa
Lektion 8: Konstruktion av semantiska tablåer för PTL-formler
 Lektion 8: Konstruktion av semantiska tablåer för PTL-formler Till denna lektion hör uppgift 2, 6 och 0 i lärobokens avsnitt.6 (sid. 255). Lös uppgift 2 genom att konstruera en semantisk tablå. Följande
Lektion 8: Konstruktion av semantiska tablåer för PTL-formler Till denna lektion hör uppgift 2, 6 och 0 i lärobokens avsnitt.6 (sid. 255). Lös uppgift 2 genom att konstruera en semantisk tablå. Följande
Robin Stenwall Lunds universitet
 Robin Stenwall Lunds universitet Vik$gt a) tänka på Innehållet i kursen formell logik förutsätts vara inhämtat (repetera om du är osäker). I allmänhet gäller att kursinnehållet, som ska instuderas på relativt
Robin Stenwall Lunds universitet Vik$gt a) tänka på Innehållet i kursen formell logik förutsätts vara inhämtat (repetera om du är osäker). I allmänhet gäller att kursinnehållet, som ska instuderas på relativt
Likhetstecknets innebörd
 Likhetstecknets innebörd Följande av Görel Sterner översatta och bearbetade text bygger på boken: arithmetic & algebra in elementary school. Portsmouth: Heinemann Elever i åk 1 6 fick följande uppgift:
Likhetstecknets innebörd Följande av Görel Sterner översatta och bearbetade text bygger på boken: arithmetic & algebra in elementary school. Portsmouth: Heinemann Elever i åk 1 6 fick följande uppgift:
Algoritmer, datastrukturer och komplexitet
 Algoritmer, datastrukturer och komplexitet Övning 10 Anton Grensjö grensjo@csc.kth.se 9 november 2017 1 Idag En konstruktionsreduktion Fler bevis av NP-fullständighet 2 Teori Repetition Ett problem tillhör
Algoritmer, datastrukturer och komplexitet Övning 10 Anton Grensjö grensjo@csc.kth.se 9 november 2017 1 Idag En konstruktionsreduktion Fler bevis av NP-fullständighet 2 Teori Repetition Ett problem tillhör
TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter
 TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter Johan Thim 15 augusti 2015 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför
TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter Johan Thim 15 augusti 2015 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför
D. x 2 + y 2 ; E. Stockholm ligger i Sverige; F. Månen är en gul ost; G. 3 2 = 6; H. x 2 + y 2 = r 2.
 Logik Vid alla matematiskt resonemang måste man vara säker på att man verkligen menar det man skriver ner på sitt papper. Därför måste man besinna hur man egentligen tänker. Den vetenskap, som sysslar
Logik Vid alla matematiskt resonemang måste man vara säker på att man verkligen menar det man skriver ner på sitt papper. Därför måste man besinna hur man egentligen tänker. Den vetenskap, som sysslar
Bakgrund. Bakgrund. Bakgrund. Håkan Jonsson Institutionen för systemteknik Luleå tekniska universitet Luleå, Sverige
 Är varje påstående som kan formuleras matematiskt*) alltid antingen sant eller falskt? *) Inom Institutionen för systemteknik Luleå tekniska universitet Luleå, Sverige Exempel: 12 = 13 nej, falskt n! >
Är varje påstående som kan formuleras matematiskt*) alltid antingen sant eller falskt? *) Inom Institutionen för systemteknik Luleå tekniska universitet Luleå, Sverige Exempel: 12 = 13 nej, falskt n! >
En introduktion till predikatlogik
 rasmus.blanck@gu.se FT1200, LC1510 och LGFI52 VT2017 (Premiss 1) (Premiss 2) (Slutsats) Alla människor är dödliga Sokrates är en människa Sokrates är dödlig Detta argument är intuitivt giltigt: Det finns
rasmus.blanck@gu.se FT1200, LC1510 och LGFI52 VT2017 (Premiss 1) (Premiss 2) (Slutsats) Alla människor är dödliga Sokrates är en människa Sokrates är dödlig Detta argument är intuitivt giltigt: Det finns
sanningsvärde, kallas utsagor. Exempel på utsagor från pass 1 är
 PASS 7. EKVATIONSLÖSNING 7. Grundbegrepp om ekvationer En ekvation säger att två matematiska uttryck är lika stora. Ekvationen har alltså ett likhetstecken och två deluttryck på var sin sida om likhetstecknet.
PASS 7. EKVATIONSLÖSNING 7. Grundbegrepp om ekvationer En ekvation säger att två matematiska uttryck är lika stora. Ekvationen har alltså ett likhetstecken och två deluttryck på var sin sida om likhetstecknet.
7, Diskreta strukturer
 Objektorienterad modellering och diskreta strukturer 7, Diskreta strukturer Sven Gestegård Robertz Datavetenskap, LTH 2015 Modeller Matematiska modeller Kontinuerliga modeller Kontinuerliga funktioner
Objektorienterad modellering och diskreta strukturer 7, Diskreta strukturer Sven Gestegård Robertz Datavetenskap, LTH 2015 Modeller Matematiska modeller Kontinuerliga modeller Kontinuerliga funktioner
9. Predikatlogik och mängdlära
 Objektorienterad modellering och diskreta strukturer 9. Predikatlogik och mängdlära Sven Gestegård Robertz Datavetenskap, LTH 2014 Rekaputilation Vi har talat om satslogik naturlig härledning predikatlogik
Objektorienterad modellering och diskreta strukturer 9. Predikatlogik och mängdlära Sven Gestegård Robertz Datavetenskap, LTH 2014 Rekaputilation Vi har talat om satslogik naturlig härledning predikatlogik
Tentamen: Programutveckling ht 2015
 Tentamen: Programutveckling ht 2015 Datum: 2015-11-04 Tid: 09:00-13:00 Sal: Ansvarig: Resultat: Hjälpmedel: Maxpoäng: Betygsgränser: Anslås inom 3 veckor. Inga 40 p 20 p för G, 32 p för VG. Iakttag följande:
Tentamen: Programutveckling ht 2015 Datum: 2015-11-04 Tid: 09:00-13:00 Sal: Ansvarig: Resultat: Hjälpmedel: Maxpoäng: Betygsgränser: Anslås inom 3 veckor. Inga 40 p 20 p för G, 32 p för VG. Iakttag följande:
Diskret matematik: Övningstentamen 1
 Diskret matematik: Övningstentamen 1 1. Bevisa att de reella talen är en icke-uppräknelig mängd.. För två mängder av positiva heltal A och B skriver vi A C B, om det är så att A innehåller ett heltal som
Diskret matematik: Övningstentamen 1 1. Bevisa att de reella talen är en icke-uppräknelig mängd.. För två mängder av positiva heltal A och B skriver vi A C B, om det är så att A innehåller ett heltal som
K2 Något om modeller, kompakthetssatsen
 KTH Matematik Bengt Ek Maj 2005 Kompletteringsmaterial till kursen 5B1928 Logik för D1: K2 Något om modeller, kompakthetssatsen Vi skall presentera ett enkelt (om man känner till sundhets- och fullständighetssatsen
KTH Matematik Bengt Ek Maj 2005 Kompletteringsmaterial till kursen 5B1928 Logik för D1: K2 Något om modeller, kompakthetssatsen Vi skall presentera ett enkelt (om man känner till sundhets- och fullständighetssatsen
Logik för datavetare DVK:Log Tisdagen 28 oktober 2014. Institutionen för dataoch systemvetenskap David Sundgren
 Institutionen för dataoch systemvetenskap David Sundgren Logik för datavetare DVK:Log Tisdagen 28 oktober 2014 Skrivtid: 9 00-13 00. Inga hjälpmedel utom formelsamlingen på nästa sida är tillåtna. För
Institutionen för dataoch systemvetenskap David Sundgren Logik för datavetare DVK:Log Tisdagen 28 oktober 2014 Skrivtid: 9 00-13 00. Inga hjälpmedel utom formelsamlingen på nästa sida är tillåtna. För
Mer om kontinuitet. Kapitel K. K.1 Övre och undre gräns
 Kapitel K Mer om kontinuitet I detta kapitel bevisar vi Sats 3.1, som säger att en kontinuerlig funktion av typen R 2 R på ett kompakt område antar ett största och ett minsta värde. Vi studerar dessutom
Kapitel K Mer om kontinuitet I detta kapitel bevisar vi Sats 3.1, som säger att en kontinuerlig funktion av typen R 2 R på ett kompakt område antar ett största och ett minsta värde. Vi studerar dessutom
Föreläsning 8: Intro till Komplexitetsteori
 Föreläsning 8: Intro till Komplexitetsteori Formalisering av rimlig tid En algoritm som har körtid O(n k ) för någon konstant k är rimligt snabb. En algoritm som har körtid Ω(c n ) för någon konstant c>1
Föreläsning 8: Intro till Komplexitetsteori Formalisering av rimlig tid En algoritm som har körtid O(n k ) för någon konstant k är rimligt snabb. En algoritm som har körtid Ω(c n ) för någon konstant c>1
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 4. b) = 3 1 = 2
 Kapitel.1 101, 102 Exempel som löses i boken 10 a) x= 1 11+ x= 11+ 1 = 2 c) x= 11 7 x= 7 11 = 77 b) x= 5 x 29 = 5 29 = 6 d) x= 2 26 x= 26 2= 1 10 a) x= 6 5+ 9 x= 5+ 9 6= 5+ 5= 59 b) a = 8a 6= 8 6= 2 6=
Kapitel.1 101, 102 Exempel som löses i boken 10 a) x= 1 11+ x= 11+ 1 = 2 c) x= 11 7 x= 7 11 = 77 b) x= 5 x 29 = 5 29 = 6 d) x= 2 26 x= 26 2= 1 10 a) x= 6 5+ 9 x= 5+ 9 6= 5+ 5= 59 b) a = 8a 6= 8 6= 2 6=
Algoritmer, datastrukturer och komplexitet
 Algoritmer, datastrukturer och komplexitet Övning 12 Anton Grensjö grensjo@csc.kth.se 10 december 2015 Anton Grensjö ADK Övning 12 10 december 2015 1 / 19 Idag Idag Komplexitetsklasser Blandade uppgifter
Algoritmer, datastrukturer och komplexitet Övning 12 Anton Grensjö grensjo@csc.kth.se 10 december 2015 Anton Grensjö ADK Övning 12 10 december 2015 1 / 19 Idag Idag Komplexitetsklasser Blandade uppgifter
Robin Stenwall Lunds universitet
 Robin Stenwall Lunds universitet Vik$gt a) tänka på Innehållet i kursen formell logik förutsätts vara inhämtat (repetera om du är osäker). I allmänhet gäller att kursinnehållet, som ska instuderas på relativt
Robin Stenwall Lunds universitet Vik$gt a) tänka på Innehållet i kursen formell logik förutsätts vara inhämtat (repetera om du är osäker). I allmänhet gäller att kursinnehållet, som ska instuderas på relativt
Robin Stenwall Lunds universitet
 Robin Stenwall Lunds universitet Avsnitt 10.3 Några nyttiga ekvivalenser Två sätt att använda tautologa ekvivalenser i första-ordningens logik (1) Satser vars sanningsfuntionella former är tautologt ekvivalenta
Robin Stenwall Lunds universitet Avsnitt 10.3 Några nyttiga ekvivalenser Två sätt att använda tautologa ekvivalenser i första-ordningens logik (1) Satser vars sanningsfuntionella former är tautologt ekvivalenta
Algoritmer, datastrukturer och komplexitet
 Algoritmer, datastrukturer och komplexitet Övning 1 Anton Grensjö grensjo@csc.kth.se 14 september 2015 Anton Grensjö ADK Övning 1 14 september 2015 1 / 22 Översikt Kursplanering F1: Introduktion, algoritmanalys
Algoritmer, datastrukturer och komplexitet Övning 1 Anton Grensjö grensjo@csc.kth.se 14 september 2015 Anton Grensjö ADK Övning 1 14 september 2015 1 / 22 Översikt Kursplanering F1: Introduktion, algoritmanalys
1 Minkostnadsflödesproblem i nätverk
 Krister Svanberg, april 2012 1 Minkostnadsflödesproblem i nätverk Ett nätverk består av en given mängd noder numrerade från 1 till m (där m är antalet noder) samt en given mängd riktade bågar mellan vissa
Krister Svanberg, april 2012 1 Minkostnadsflödesproblem i nätverk Ett nätverk består av en given mängd noder numrerade från 1 till m (där m är antalet noder) samt en given mängd riktade bågar mellan vissa
Föreläsning 9: Talteori
 DD2458, Problemlösning och programmering under press Föreläsning 9: Talteori Datum: 2007-11-13 Skribent(er): Niklas Lindbom och Daniel Walldin Föreläsare: Per Austrin Den här föreläsningen behandlar modulär
DD2458, Problemlösning och programmering under press Föreläsning 9: Talteori Datum: 2007-11-13 Skribent(er): Niklas Lindbom och Daniel Walldin Föreläsare: Per Austrin Den här föreläsningen behandlar modulär
Lösning till tentamensskrivning i Diskret Matematik för CINTE, CL2 och Media 1, SF1610 och 5B1118, onsdagen den 17 augusti 2011, kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning i Diskret Matematik för CINTE, CL och Media, SF60 och 5B8, onsdagen den 7 augusti 0, kl 4.00-9.00. Examinator: Olof Heden Hjälpmedel: Inga
Matematiska Institutionen KTH Lösning till tentamensskrivning i Diskret Matematik för CINTE, CL och Media, SF60 och 5B8, onsdagen den 7 augusti 0, kl 4.00-9.00. Examinator: Olof Heden Hjälpmedel: Inga
Bisektionsalgoritmen. Kapitel Kvadratroten ur 2
 Kapitel 4 Bisektionsalgoritmen Vi ska konstruera lösningar till algebraiska ekvationer av formen f(x) = 0 med hjälp av bisektionsalgoritmen (intervallhalveringsmetoden). På samma gång ska vi se hur man
Kapitel 4 Bisektionsalgoritmen Vi ska konstruera lösningar till algebraiska ekvationer av formen f(x) = 0 med hjälp av bisektionsalgoritmen (intervallhalveringsmetoden). På samma gång ska vi se hur man
LOGIK, MÄNGDER OCH FUNKTIONER
 LOGIK, MÄNGDER OCH FUNKTIONER KOMPLETTERANDE STUDIEMATERIAL TILL MMA121 MATEMATISK GRUNDKURS VÅRTERMINEN 2014 ERIK DARPÖ 1. Utsagor, implikation och ekvivalens En utsaga är en påstående, formulerat med
LOGIK, MÄNGDER OCH FUNKTIONER KOMPLETTERANDE STUDIEMATERIAL TILL MMA121 MATEMATISK GRUNDKURS VÅRTERMINEN 2014 ERIK DARPÖ 1. Utsagor, implikation och ekvivalens En utsaga är en påstående, formulerat med
Formell logik Kapitel 9. Robin Stenwall Lunds universitet
 Formell logik Kapitel 9 Robin Stenwall Lunds universitet Kapitel 9: Introduktion till kvantifiering Vi har hittills betraktat logiska resonemang vars giltighet enbart beror på meningen hos konnektiv som
Formell logik Kapitel 9 Robin Stenwall Lunds universitet Kapitel 9: Introduktion till kvantifiering Vi har hittills betraktat logiska resonemang vars giltighet enbart beror på meningen hos konnektiv som
Likhetstecknets innebörd
 Modul: Algebra Del 5: Algebra som språk Likhetstecknets innebörd Följande av Görel Sterner (2012) översatta och bearbetade text bygger på boken: Carpenter, T. P., Franke, M. L. & Levi, L. (2003). Thinking
Modul: Algebra Del 5: Algebra som språk Likhetstecknets innebörd Följande av Görel Sterner (2012) översatta och bearbetade text bygger på boken: Carpenter, T. P., Franke, M. L. & Levi, L. (2003). Thinking
29 Det enda heltalet n som satisfierar båda dessa villkor är n = 55. För detta värde på n får vi x = 5, y = 5.
 Tentamenskrivning MATA15 Algebra: delprov 1, 6hp Lördagen den 3 november 01 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1 a) Lös den diofantiska ekvationen 9x + 11y 00 b) Ange alla lösningar x, y) sådana
Tentamenskrivning MATA15 Algebra: delprov 1, 6hp Lördagen den 3 november 01 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1 a) Lös den diofantiska ekvationen 9x + 11y 00 b) Ange alla lösningar x, y) sådana
Hur implementera algoritmerna på maskinnivå - datorns byggstenar
 Hur implementera algoritmerna på maskinnivå - datorns byggstenar Binära tal Boolesk logik grindar och kretsar A A extern representation intern representation minnet i datorn extern representation 1000001
Hur implementera algoritmerna på maskinnivå - datorns byggstenar Binära tal Boolesk logik grindar och kretsar A A extern representation intern representation minnet i datorn extern representation 1000001
av envariabelfunktionen g(t) och flervariabelfunktionen t = h(x, y) = x 2 + e y.)
 Lösningsskisser till TATA69 Flervariabelanalys 16-1- 1 Stationära punkter ges av f (4x 3 + 4x, 3y + 6z, z + 6y (,,, dvs (x, y, z (,, eller (x, y, z (, 6, 18 Ur andraderivatorna fås de kvadratiska formerna
Lösningsskisser till TATA69 Flervariabelanalys 16-1- 1 Stationära punkter ges av f (4x 3 + 4x, 3y + 6z, z + 6y (,,, dvs (x, y, z (,, eller (x, y, z (, 6, 18 Ur andraderivatorna fås de kvadratiska formerna
DD1350 Logik för dataloger. Vad är logik?
 DD1350 Logik för dataloger Fö 1 - Introduktion Vad är logik? Vetenskapen som studerar hur man bör resoneraoch dra slutsatser utifrån givna påståenden (=utsagor, satser). 1 Aristoteles (384-322 f.kr) Logik
DD1350 Logik för dataloger Fö 1 - Introduktion Vad är logik? Vetenskapen som studerar hur man bör resoneraoch dra slutsatser utifrån givna påståenden (=utsagor, satser). 1 Aristoteles (384-322 f.kr) Logik
IE1205 Digital Design: F10: Synkrona tillståndsautomater del 2
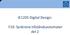 IE1205 Digital Design: F10: Synkrona tillståndsautomater del 2 Sekvensnät Om en och samma insignal kan ge upphov till olika utsignal, är logiknätet ett sekvensnät. Det måste då ha ett inre minne som gör
IE1205 Digital Design: F10: Synkrona tillståndsautomater del 2 Sekvensnät Om en och samma insignal kan ge upphov till olika utsignal, är logiknätet ett sekvensnät. Det måste då ha ett inre minne som gör
Tentamen TMV210 Inledande Diskret Matematik, D1/DI2
 Tentamen TMV20 Inledande Diskret Matematik, D/DI2 208-0-27 kl. 4.00 8.00 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Anton Johansson, telefon: 5325 (alt. Peter Hegarty 070-5705475)
Tentamen TMV20 Inledande Diskret Matematik, D/DI2 208-0-27 kl. 4.00 8.00 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Anton Johansson, telefon: 5325 (alt. Peter Hegarty 070-5705475)
Kvalificeringstävling den 30 september 2008
 SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
Turingmaskinen - en abstrakt datormodell
 Turingmaskinen - en abstrakt datormodell Modeller är viktiga hjälpmedel vid studiet av många fenomen. En bra modell fyller oftast följande krav: Den fångar upp det centrala i sin fysiska motsvarighet Den
Turingmaskinen - en abstrakt datormodell Modeller är viktiga hjälpmedel vid studiet av många fenomen. En bra modell fyller oftast följande krav: Den fångar upp det centrala i sin fysiska motsvarighet Den
Tentamensskrivning i Diskret Matematik för CINTE och CMETE, SF1610, onsdagen den 20 augusti 2014, kl
 1 Matematiska Institutionen KTH Tentamensskrivning i Diskret Matematik för CINTE och CMETE, SF1610, onsdagen den 20 augusti 2014, kl 14.00-19.00. Examinator: Olof Heden Hjälpmedel: Inga hjälpmedel är tillåtna
1 Matematiska Institutionen KTH Tentamensskrivning i Diskret Matematik för CINTE och CMETE, SF1610, onsdagen den 20 augusti 2014, kl 14.00-19.00. Examinator: Olof Heden Hjälpmedel: Inga hjälpmedel är tillåtna
Grundläggande logik och modellteori (5DV102)
 Tentamen 2013-10-31 Grundläggande logik och modellteori (5DV102) M. Berglund och K. Markström Totalt antal uppgifter 11 Maximalt antal poäng 30 Krav för 3 i betyg 14 poäng Krav för 4 i betyg 19 poäng,
Tentamen 2013-10-31 Grundläggande logik och modellteori (5DV102) M. Berglund och K. Markström Totalt antal uppgifter 11 Maximalt antal poäng 30 Krav för 3 i betyg 14 poäng Krav för 4 i betyg 19 poäng,
tidskrift för politisk filosofi nr 2 2006 årgång 10
 tidskrift för politisk filosofi nr 2 2006 årgång 10 Bokförlaget thales lönediskriminering och jämförbarhet av olika arbeten? en diskussion av fem argument för icke-jämförbarhet Stig Blomskog 1. Inledning
tidskrift för politisk filosofi nr 2 2006 årgång 10 Bokförlaget thales lönediskriminering och jämförbarhet av olika arbeten? en diskussion av fem argument för icke-jämförbarhet Stig Blomskog 1. Inledning
Lars-Daniel Öhman Lördag 2 maj 2015 Skrivtid: 9:00 15:00 Hjälpmedel: Miniräknare, lock till miniräknare
 Umeå universitet Tentamen i matematik Institutionen för matematik Introduktion till och matematisk statistik diskret matematik Lars-Daniel Öhman Lördag 2 maj 2015 Skrivtid: 9:00 15:00 Hjälpmedel: Miniräknare,
Umeå universitet Tentamen i matematik Institutionen för matematik Introduktion till och matematisk statistik diskret matematik Lars-Daniel Öhman Lördag 2 maj 2015 Skrivtid: 9:00 15:00 Hjälpmedel: Miniräknare,
TDP015: Lektion 5 - Svar
 TDP015: Lektion 5 - Svar 11 maj 015 1. Huvudsaken här är att det spelar roll vilket initialvärde vi har. Nedan har jag valt beräkningar som slutar när f(x) < ɛ, där ɛ 10 10. Detta behöver ni såklart inte
TDP015: Lektion 5 - Svar 11 maj 015 1. Huvudsaken här är att det spelar roll vilket initialvärde vi har. Nedan har jag valt beräkningar som slutar när f(x) < ɛ, där ɛ 10 10. Detta behöver ni såklart inte
Sekvensnät Som Du kommer ihåg
 Sekvensnät Som Du kommer ihåg Designmetodik Grundläggande designmetodik för tillståndsmaskiner. 1. Analysera specifikationen för kretsen 2. Skapa tillståndsdiagram 3. Ställ upp tillståndstabellen 4. Minimera
Sekvensnät Som Du kommer ihåg Designmetodik Grundläggande designmetodik för tillståndsmaskiner. 1. Analysera specifikationen för kretsen 2. Skapa tillståndsdiagram 3. Ställ upp tillståndstabellen 4. Minimera
Grundläggande logik och modellteori
 Grundläggande logik och modellteori Kapitel 4: Konjunktiv och disjunktiv normalform Henrik Björklund Umeå universitet 15. september, 2014 CNF och DNF Konjunktiv normalform (CNF) Omskrivning av en formel
Grundläggande logik och modellteori Kapitel 4: Konjunktiv och disjunktiv normalform Henrik Björklund Umeå universitet 15. september, 2014 CNF och DNF Konjunktiv normalform (CNF) Omskrivning av en formel
Programmeringsmetodik DV1 Programkonstruktion 1. Moment 4 Om rekursion. PK1&PM1 HT-06 moment 4 Sida 1 Uppdaterad
 Programmeringsmetodik DV1 Programkonstruktion 1 Moment 4 Om rekursion PK1&PM1 HT-06 moment 4 Sida 1 Uppdaterad 2006-10-17 Summera godtyckligt antal tal (* sumupto n Type: int->int Pre: n >= 0, n
Programmeringsmetodik DV1 Programkonstruktion 1 Moment 4 Om rekursion PK1&PM1 HT-06 moment 4 Sida 1 Uppdaterad 2006-10-17 Summera godtyckligt antal tal (* sumupto n Type: int->int Pre: n >= 0, n
Grundläggande logik och modellteori
 Grundläggande logik och modellteori Kapitel 7: SAT-lösare Henrik Björklund Umeå universitet 29. september, 2014 SAT En instans av SAT är en mängd av mängder av literaler. Exempel: {{p, q, r}, {p, q, s},
Grundläggande logik och modellteori Kapitel 7: SAT-lösare Henrik Björklund Umeå universitet 29. september, 2014 SAT En instans av SAT är en mängd av mängder av literaler. Exempel: {{p, q, r}, {p, q, s},
Lösningsanvisningar till de icke obligatoriska workoutuppgifterna
 Lösningsanvisningar till de icke obligatoriska workoutuppgifterna Linjära system 7. (a) Falskt. Kondition är en egenskap hos problemet oberoende av precisionen i beräkningarna. (b) Falskt. Pivotering påverkar
Lösningsanvisningar till de icke obligatoriska workoutuppgifterna Linjära system 7. (a) Falskt. Kondition är en egenskap hos problemet oberoende av precisionen i beräkningarna. (b) Falskt. Pivotering påverkar
Filosofisk logik Kapitel 15. Robin Stenwall Lunds universitet
 Filosofisk logik Kapitel 15 Robin Stenwall Lunds universitet Dagens upplägg Första ordningens mängdlära Naiv mängdlära Abstraktionsaxiomet (eg. comprehension) Extensionalitetsaxiomet Små mängder Ordnade
Filosofisk logik Kapitel 15 Robin Stenwall Lunds universitet Dagens upplägg Första ordningens mängdlära Naiv mängdlära Abstraktionsaxiomet (eg. comprehension) Extensionalitetsaxiomet Små mängder Ordnade
i LabVIEW. Några programmeringstekniska grundbegrepp
 Institutionen för elektroteknik Några programmeringstekniska grundbegrepp 1999-02-16 Inledning Inom datorprogrammering förekommer ett antal grundbegrepp som är i stort sett likadana oberoende om vi talar
Institutionen för elektroteknik Några programmeringstekniska grundbegrepp 1999-02-16 Inledning Inom datorprogrammering förekommer ett antal grundbegrepp som är i stort sett likadana oberoende om vi talar
System.out.println("Jaså du har "+ antalhusdjur+ " husdjur"); if ( antalhusdjur > 5 ) System.out.println("Oj det var många);
 1 Villkor och styrsatser I de program vi sett tidigare har programkörning inneburit att sats efter sats utförts i den ordning de skrivits i källkoden. Vi har inte kunna ändra programmets uppförande beroende
1 Villkor och styrsatser I de program vi sett tidigare har programkörning inneburit att sats efter sats utförts i den ordning de skrivits i källkoden. Vi har inte kunna ändra programmets uppförande beroende
Avsnitt 1, introduktion.
 KTHs Sommarmatematik Introduktion 1:1 1:1 Kvadratkomplettering Avsnitt 1, introduktion. Det här är en viktig teknik som måste tränas in. Poängen med kvadratkomplettering är att man direkt kan se om andragradsfunktionen
KTHs Sommarmatematik Introduktion 1:1 1:1 Kvadratkomplettering Avsnitt 1, introduktion. Det här är en viktig teknik som måste tränas in. Poängen med kvadratkomplettering är att man direkt kan se om andragradsfunktionen
Tommy Färnqvist, IDA, Linköpings universitet. 2 Strukturer 2 2.1 Domäner... 2 2.2 Tolkningar... 3
 Föreläsning 2 Semantik 729G06 Logikdelen Föreläsningsanteckningar i Programmering och logik 27 januari 2014 Tommy Färnqvist, IDA, Linköpings universitet 2.1 Innehåll Innehåll 1 Lite mer syntax 1 2 Strukturer
Föreläsning 2 Semantik 729G06 Logikdelen Föreläsningsanteckningar i Programmering och logik 27 januari 2014 Tommy Färnqvist, IDA, Linköpings universitet 2.1 Innehåll Innehåll 1 Lite mer syntax 1 2 Strukturer
Predikatlogik: Normalformer. Klas Markström
 1 Precis som i satslogik så är det bekvämt att kunna hitta en normalform för meningar. Om vi kan utgå från att alla meningar är på normalform så behöver vi t.e.x. inte bekymra oss om en massa specialfall
1 Precis som i satslogik så är det bekvämt att kunna hitta en normalform för meningar. Om vi kan utgå från att alla meningar är på normalform så behöver vi t.e.x. inte bekymra oss om en massa specialfall
MVE051/MSG Föreläsning 7
 MVE051/MSG810 2016 Föreläsning 7 Petter Mostad Chalmers November 23, 2016 Överblick Deskriptiv statistik Grafiska sammanfattningar. Numeriska sammanfattningar. Estimering (skattning) Teori Några exempel
MVE051/MSG810 2016 Föreläsning 7 Petter Mostad Chalmers November 23, 2016 Överblick Deskriptiv statistik Grafiska sammanfattningar. Numeriska sammanfattningar. Estimering (skattning) Teori Några exempel
Numeriska Metoder och Grundläggande Programmering för P1, VT2014
 Numeriska Metoder och Grundläggande Programmering för P1, VT2014 Föreläsning 2: Styrstrukturer & Programmeringsstrategi (Kap. 3 4 i MATLAB Programming for Engineers, S. Chapman) January 21, 2014 Innehåll:
Numeriska Metoder och Grundläggande Programmering för P1, VT2014 Föreläsning 2: Styrstrukturer & Programmeringsstrategi (Kap. 3 4 i MATLAB Programming for Engineers, S. Chapman) January 21, 2014 Innehåll:
Övningsuppgifter till föreläsning 2 Variabler och uttryck
 Sid 1 (5) Övningsuppgifter till föreläsning 2 Variabler och uttryck Syfte Syftet med övningsuppgifterna är att träna på: Aritmetik, variabler, tilldelning, scanf och printf Generellt Diskutera gärna uppgifterna
Sid 1 (5) Övningsuppgifter till föreläsning 2 Variabler och uttryck Syfte Syftet med övningsuppgifterna är att träna på: Aritmetik, variabler, tilldelning, scanf och printf Generellt Diskutera gärna uppgifterna
, S(6, 2). = = = =
 1 Matematiska Institutionen KTH Lösningar till tentamensskrivning på kursen Diskret Matematik, moment A, för D2 och F, SF161 och SF160, den 17 april 2010 kl 09.00-14.00. Examinator: Olof Heden. DEL I 1.
1 Matematiska Institutionen KTH Lösningar till tentamensskrivning på kursen Diskret Matematik, moment A, för D2 och F, SF161 och SF160, den 17 april 2010 kl 09.00-14.00. Examinator: Olof Heden. DEL I 1.
Kinesiska restsatsen
 Matematik, KTH Bengt Ek juli 2017 Material till kurserna SF1679 och SF1688, Diskret matematik: Kinesiska restsatsen Vi vet att för varje m Z + och varje a Z, ges alla x Z som uppfyller x a (mod m) av x
Matematik, KTH Bengt Ek juli 2017 Material till kurserna SF1679 och SF1688, Diskret matematik: Kinesiska restsatsen Vi vet att för varje m Z + och varje a Z, ges alla x Z som uppfyller x a (mod m) av x
