5B1817 Tillämpad ickelinjär optimering. Metoder för problem utan bivillkor, forts.
|
|
|
- Sandra Andersson
- för 6 år sedan
- Visningar:
Transkript
1 5B1817 Tillämpad ickelinjär optimering Föreläsning 5 Metoder för problem utan bivillkor, forts. A. Forsgren, KTH 1 Föreläsning 5 5B /2007
2 Lösningar För en given metod blir en lösning den bästa punkt metoden kan ge. ˆ Med en metod som använder förstaderivatsinformation blir en lösning typiskt en punkt som uppfyller f(x ) = 0. Exempel: steepest descent. ˆ Med en metod som även använder andraderivatsinformation blir en lösning typiskt en punkt där f(x ) = 0 och 2 f(x ) 0. Exempel: Modifierad Newtonmetod. (Dock behöver man använda även negativa krökningsriktningar för att uppnå detta.) OBS! Vi kan inte med någon av dessa metoder garantera att vi når en lokal minpunkt, om vi inte antar konvexitet eller något motsvarande. Vi kan dock testa om andra ordningens tillräckliga optimalitetsvillkor är uppfyllda om vi använder en andraderivatsmetod. A. Forsgren, KTH 2 Föreläsning 5 5B /2007
3 Gradientbaserade metoder för problem utan bivillkor Betrakta återigen ett ickelinjärt programmeringsproblem utan bivillkor (P ) min f(x) då x IR n, där f C 2. Vi ska nu titta på metoder som använder förstaderivator, liksom steepest-descentmetoden, men på ett bättre sätt. Speciellt kvasi-newtonmetoder och konjugerade gradientmetoden. Båda har motivering från kvadratisk programmering. A. Forsgren, KTH 3 Föreläsning 5 5B /2007
4 Kvasi-Newtonuppdatering En kvasi-newtonmetod beräknar sökriktningen p k ur B k p k = f(x k ), där B k = Bk T 0 och låter B k+1 = B k + C k, där C k är en symmetrisk matris av låg rang, typiskt rang ett eller rang två. Antag att f(x) = 1 2 xt Hx + c T x, där H = H T 0. Då blir f(x k + α k p k ) = f(x k ) + α k Hp k. Alternativt kan vi skriva Hs k = y k, där s k = α k p k och y k = f(x k+1 ) f(x k ). Motiverat av denna kvadratiska modell, krävs i en kvasi-newtonmetod att B k+1 ska uppfylla Kvasi-Newtonvillkoret B k+1 s k = y k, där s k = α k p k och y k = f(x k+1 ) f(x k ). A. Forsgren, KTH 4 Föreläsning 5 5B /2007
5 Kvasi-Newtonmetod Iteration k i en linjesökande kvasi-newtonmetod tar följande form i en given punkt x k med Hessianapproximation B k. ˆ Beräkna sökriktning p k ur B k p k = f(x k ). ˆ Lös approximativt min α 0 f(x k + αp k ), vilket ger α k. ˆ x k+1 x k + α k p k. ˆ s k x k+1 x k, y k f(x k+1 ) f(x k ) ˆ B k+1 B k + C k, där B k+1 s k = y k och B k+1 0 krävs. Olika metoder baseras på olika val av C k och α k. Typiskt har C k rang ett eller rang två. Typiskt väljs B 0 = I. A. Forsgren, KTH 5 Föreläsning 5 5B /2007
6 Symmetriska rang-ett uppdateringen Påstående. Låt B k vara en symmetrisk matris. Låt B k+1 = B k + C k, där C k är symmetrisk med rang ett. Antag att B k+1 s k = y k och (y k B k s k ) T s k 0. Då blir 1 C k = (y (y k B k s k ) T k B k s k )(y k B k s k ) T. s k Bevis. Se Nash och Sofer, Lemma Vi kan skriva B k+1 = B k + γ k w k wk T, där w k = 1. Kvasi-Newtonvillkoret ger B k s k + γ k w k wks T 1 k = y k, dvs w k = γ k wk Ts (y k B k s k ). Då w k = 1 får k vi γ k(y k B k s k ) T s k = y k B k s k, vilket ger γ k = y k B k s k 2. y k B k s k (y k B k s k ) T s k Insättning ger γ k w k wk T = C k. Symmetriska rang-ett uppdateringen är unik. B k+1 0 ej garanterad. A. Forsgren, KTH 6 Föreläsning 5 5B /2007
7 BFGS-uppdateringen Rang-två uppdateringen är inte unik. BFGS-uppdateringen ges av B k+1 = B k 1 s T k B B k s k s T k B k + 1 ks k yk Ts y k yk T. k Påstående. Låt B = Bk T 0, och låt B k+1 vara BFGS-uppdateringen av B k. Då är B k+1 0 om och endast om yks T k > 0. Bevis. Se Nash och Sofer, Lemma Positiv definithet kan garanteras om Wolfe-villkor används i linjesökningen. Då får vi f(x k+1 ) T s k η f(x k ) T s k, vilket ger yks T k (1 η) f(x k ) T s k > 0. Om R k är Choleskyfaktor av B k, dvs B k = RkR T k, kan BFGS-uppdateringen göras som en rang-ett uppdatering av R k till R k+1. A. Forsgren, KTH 7 Föreläsning 5 5B /2007
8 Kvasi-Newtonmetod på kvadratiskt problem Antag att en kvasi-newtonmetod appliceras på ett kvadratisk problem där f(x) = 1 2 xt Hx + c T x, H = H T 0. Antag också att exakt linjesökning utförs samt att {B k } är positivt definita. Då är problemet löst i högst n iterationer och B n = H. Detta innebär att en kvasi-newtonmetod löser sitt kvadratiska modellproblem i ett ändligt antal iterationer, till skillnad från steepest-descentmetoden. Man kan visa ovanstående genom att visa att en kvasi-newtonmetod genererar konjugerade sökriktningar för ett kvadratiskt problem. På ett kvadratiskt problem blir metoden ekvivalent med konjugerade gradientmetoden. A. Forsgren, KTH 8 Föreläsning 5 5B /2007
9 Lösning av ekvationssystem med positivt definit matris Antag att vi vill lösa Hx = c, där H = H T 0. Ekvivalent, minimera f(x) = 1 2 xt Hx + c T x. Alternativ: ˆ Fatoriseringsmetod. Förslag: Choleskyfaktorisering, H = R T R, R högtriangulär. ˆ Iterativ metod. Förslag: Konjugerade gradientmetoden. Struktur hos H avgör vad som är mest effektivt. A. Forsgren, KTH 9 Föreläsning 5 5B /2007
10 Konjugerade riktningar Konjugerade gradientmetoden är en iterativ metod som använder sig av konjugerade sökriktningar. Definition. En mängd vektorer i IR n, {p i }, sägs vara konjugerade med avseende på en positivt definit symmetrisk n n-matris H om p T i Hp j = 0 för i j. Påstående. Konjugerade riktningar är linjärt oberoende. Bevis. Låt p i, i = 1,..., m, vara konjugerade riktningar. Antag att mi=1 γ i p i = 0 för några γ i, i = 1,..., m. Då blir m i=1 γ i p T jhp i = 0 för en godtycklig vektor p j bland de konjugerade riktningarna. Då riktningarna är konjugerade ger detta γ j p T jhp j = 0, och eftersom H 0 och p j 0 får vi γ j = 0. A. Forsgren, KTH 10 Föreläsning 5 5B /2007
11 Konjugerade riktningar, forts. Låt f(x) = 1 2 xt Hx + c T x, där H = H T 0. Låt y = f(y) = m k=1 m k=1 α k p k, där p k, k = 1,..., m är konjugerade. Då blir ( α 2 k 2 pt khp k + α k c T p k ), vilket ger α k = ct p k p T k Hp. k Konjugerade riktningar ger alltså ett separabelt problem. A. Forsgren, KTH 11 Föreläsning 5 5B /2007
12 Linjära konjugerade gradientmetoden Iteration k i konjugerade gradientmetoden tar följande form i en given punkt x k med g k = Hx k + c och p k 1 givna. ˆ β k gt kg k g T k 1 g k 1 ˆ p k g k + β k p k 1. ˆ α k gt kp k p T k Hp k ˆ x k+1 x k + α k p k. ˆ g k+1 g k + α k Hp k. Initialt väljs β 0 = 0. om k 1. = gt kg k p T k Hp. k Då g k = 0 är problemet löst. I praktiken g k < ɛ. A. Forsgren, KTH 12 Föreläsning 5 5B /2007
13 Linjära konjugerade gradientmetoden, forts. Påstående. Antag att {p k } och {g k } genereras med konjugerade gradientmetoden. Då gäller att gkg T l = 0, gkp T l = 0 och p T khp l = 0 för k > l. Bevis. Se Nash och Sofer, Theorem Detta innebär att sökriktningarna {p k } är konjugerade samt att gradienterna {g k } är inbördes ortogonala samt ortogonala mot alla tidigare sökriktningar. En konsekvens är att linjära konjugerade gradientmetoden konvergerar i högst n iterationer. I praktiken behöver H ofta förkonditioneras med en positivt definit matris M som liknar H men där det är lätt att lösa ekvationssystem Mz k = r k. I stället för att lösa Hx = c löser man M 1 Hx = M 1 c. A. Forsgren, KTH 13 Föreläsning 5 5B /2007
14 Ickelinjära konjugerade gradientmetoder Antag nu att f(x) är en ickelinjär (ej nödvändigtvis kvadratisk) funktion. Iteration k i en ickelinjär konjugerad gradientmetod i en punkt x k kan skrivas på följande form. ˆ β k f(x k) T f(x k ) f(x k 1 ) T f(x k 1 ) om k 1. ˆ p k f(x k ) + β k p k 1. ˆ Lös approximativt min α 0 f(x k + αp k ), vilket ger α k. ˆ x k+1 x k + α k p k. Initialt väljs β 0 = 0. Då f(x k ) = 0 är problemet löst. I praktiken f(x k ) < ɛ. Idén är att försöka få bättre metod än steepest descent. A. Forsgren, KTH 14 Föreläsning 5 5B /2007
5B1817 Tillämpad ickelinjär optimering. Optimalitetsvillkor för problem med linjära bivillkor.
 5B1817 Tillämpad ickelinjär optimering Föreläsning 2 Optimalitetsvillkor för problem med linjära bivillkor. A. Forsgren, KTH 1 Föreläsning 2 5B1817 2006/2007 Optimalitetsvillkor för ickelinjära programmeringsproblem
5B1817 Tillämpad ickelinjär optimering Föreläsning 2 Optimalitetsvillkor för problem med linjära bivillkor. A. Forsgren, KTH 1 Föreläsning 2 5B1817 2006/2007 Optimalitetsvillkor för ickelinjära programmeringsproblem
5B1817 Tillämpad ickelinjär optimering. Kvadratisk programmering med olikhetsbivillkor Active-set metoder
 5B1817 Tillämpad ickelinjär optimering Föreläsning 7 Kvadratisk programmering med olikhetsbivillkor Active-set metoder A. Forsgren, KTH 1 Föreläsning 7 5B1817 2006/2007 Kvadratisk programmering med olikhetsbivillkor
5B1817 Tillämpad ickelinjär optimering Föreläsning 7 Kvadratisk programmering med olikhetsbivillkor Active-set metoder A. Forsgren, KTH 1 Föreläsning 7 5B1817 2006/2007 Kvadratisk programmering med olikhetsbivillkor
--x T Kx. Ka = f. K( a a i. = f f i. r i. = a a i. Ke i. a i 1. p i. Ka i. p i Kai α i
 CHALMERS FinitElementmetod M3 illämpad mekanik Föreläsning 18, 15/1 014 91. Lösningen till ekvationssystemet Gradient och konjugerad gradientmetod. a f (1) minimerar den kvadratiska funktionen Π( x) 1
CHALMERS FinitElementmetod M3 illämpad mekanik Föreläsning 18, 15/1 014 91. Lösningen till ekvationssystemet Gradient och konjugerad gradientmetod. a f (1) minimerar den kvadratiska funktionen Π( x) 1
1 Ickelinjär optimering under bivillkor
 Krister Svanberg, maj 2012 1 Ickelinjär optimering under bivillkor Hittills har vi behandlat optimeringsproblem där alla variabler x j kunnat röra sig fritt, oberoende av varann, och anta hur stora eller
Krister Svanberg, maj 2012 1 Ickelinjär optimering under bivillkor Hittills har vi behandlat optimeringsproblem där alla variabler x j kunnat röra sig fritt, oberoende av varann, och anta hur stora eller
Extrempunkt. Polyeder
 Optimum? När man har formulerat sin optimeringsmodell vill man lösa den. Dvs. finna en optimal lösning, x, till modellen. Nästan alltid: Sökmetoder: Stå i en punkt, gå till en annan bättre. Upprepa, tills
Optimum? När man har formulerat sin optimeringsmodell vill man lösa den. Dvs. finna en optimal lösning, x, till modellen. Nästan alltid: Sökmetoder: Stå i en punkt, gå till en annan bättre. Upprepa, tills
1 Konvexa optimeringsproblem grundläggande egenskaper
 Krister Svanberg, april 2012 1 Konvexa optimeringsproblem grundläggande egenskaper Ett optimeringsproblem är i viss mening godartat om det tillåtna området är en konvex mängd och den målfunktion som ska
Krister Svanberg, april 2012 1 Konvexa optimeringsproblem grundläggande egenskaper Ett optimeringsproblem är i viss mening godartat om det tillåtna området är en konvex mängd och den målfunktion som ska
5B1816 Tillämpad mat. prog. ickelinjära problem. Optimalitetsvillkor för problem med ickelinjära bivillkor
 5B1816 Tillämpad mat. prog. ickelinjära problem Föreläsning 3 Optimalitetsvillkor för problem med ickelinjära bivillkor A. Forsgren, KTH 1 Föreläsning 3 5B1816 2005/2006 Optimalitetsvillkor för ickelinjära
5B1816 Tillämpad mat. prog. ickelinjära problem Föreläsning 3 Optimalitetsvillkor för problem med ickelinjära bivillkor A. Forsgren, KTH 1 Föreläsning 3 5B1816 2005/2006 Optimalitetsvillkor för ickelinjära
Institutionen för Matematiska Vetenskaper TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F1/TM1, TMA671 2014-05-26
 Institutionen för Matematiska Vetenskaper Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F/TM, TMA67 4-5-6 DAG: Måndag 6 maj 4 TID: 4. - 8. SAL: V Ansvarig: Ivar Gustafsson, tel: 75-33545 Förfrågningar:
Institutionen för Matematiska Vetenskaper Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F/TM, TMA67 4-5-6 DAG: Måndag 6 maj 4 TID: 4. - 8. SAL: V Ansvarig: Ivar Gustafsson, tel: 75-33545 Förfrågningar:
TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F1/TM1, TMA671 2015-04-18
 Institutionen för Matematiska Vetenskaper Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F/TM, TMA67 5-4-8 DAG: Lördag 8 april 5 TID: 8.3 -.3 SAL: V Ansvarig: Ivar Gustafsson, tel: 75-33545 Förfrågningar:
Institutionen för Matematiska Vetenskaper Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F/TM, TMA67 5-4-8 DAG: Lördag 8 april 5 TID: 8.3 -.3 SAL: V Ansvarig: Ivar Gustafsson, tel: 75-33545 Förfrågningar:
Lösningsförslag till tentamen i SF1861 Optimeringslära för T. Onsdag 25 augusti 2010 kl
 Lösningsförslag till tentamen i SF86 Optimeringslära för T. Onsdag 25 augusti 2 kl. 4. 9. Examinator: Per Enqvist, tel. 79 62 98. (a) Vi har ett nätverksflödesproblem med 5 noder. Låt x = (x 2, x 3, x
Lösningsförslag till tentamen i SF86 Optimeringslära för T. Onsdag 25 augusti 2 kl. 4. 9. Examinator: Per Enqvist, tel. 79 62 98. (a) Vi har ett nätverksflödesproblem med 5 noder. Låt x = (x 2, x 3, x
Institutionen för Matematiska Vetenskaper TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F1, TMA
 Institutionen för Matematiska Vetenskaper Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F, TMA67-8-5 DAG: Onsdag 5 augusti TID: 8.3 -.3 SAL: V Ansvarig: Ivar Gustafsson, tel: 75-33545 Förfrågningar:
Institutionen för Matematiska Vetenskaper Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F, TMA67-8-5 DAG: Onsdag 5 augusti TID: 8.3 -.3 SAL: V Ansvarig: Ivar Gustafsson, tel: 75-33545 Förfrågningar:
1 Duala problem vid linjär optimering
 Krister Svanberg, april 2012 1 Duala problem vid linjär optimering Detta kapitel handlar om två centrala teoretiska resultat för LP, nämligen dualitetssatsen och komplementaritetssatsen. Först måste vi
Krister Svanberg, april 2012 1 Duala problem vid linjär optimering Detta kapitel handlar om två centrala teoretiska resultat för LP, nämligen dualitetssatsen och komplementaritetssatsen. Först måste vi
Lösningsförslag till tentamen i SF1861 Optimeringslära för T. Torsdag 28 maj 2010 kl
 Lösningsförslag till tentamen i SF86 Optimeringslära för T. Torsdag 28 maj 2 kl. 4. 9. Examinator: Per Enqvist, tel. 79 62 98. (a) Inför variablerna x = (x sr, x sm, x sp, x sa, x sd, x gr, x gm, x gp,
Lösningsförslag till tentamen i SF86 Optimeringslära för T. Torsdag 28 maj 2 kl. 4. 9. Examinator: Per Enqvist, tel. 79 62 98. (a) Inför variablerna x = (x sr, x sm, x sp, x sa, x sd, x gr, x gm, x gp,
Lösningar till 5B1762 Optimeringslära för T, 24/5-07
 Lösningar till 5B76 Optimeringslära för T, 4/5-7 Uppgift (a) Först använder vi Gauss Jordans metod på den givna matrisen A = Addition av gånger första raden till andra raden ger till resultat matrisen
Lösningar till 5B76 Optimeringslära för T, 4/5-7 Uppgift (a) Först använder vi Gauss Jordans metod på den givna matrisen A = Addition av gånger första raden till andra raden ger till resultat matrisen
Optimalitetsvillkor. Optimum? Matematisk notation. Optimum? Definition. Definition
 Optimum? När man har formulerat sin optimeringsmodell vill man lösa den Dvs finna en optimal lösning, x, till modellen Nästan alltid: Sökmetoder: Stå i en punkt, gå till en annan (bättre Upprepa, tills
Optimum? När man har formulerat sin optimeringsmodell vill man lösa den Dvs finna en optimal lösning, x, till modellen Nästan alltid: Sökmetoder: Stå i en punkt, gå till en annan (bättre Upprepa, tills
1 LP-problem på standardform och Simplexmetoden
 Krister Svanberg, mars 202 LP-problem på standardform och Simplexmetoden I detta avsnitt utgår vi från LP-formuleringen (2.2) från föreläsning. Denna form är den bäst lämpade för en strömlinjeformad implementering
Krister Svanberg, mars 202 LP-problem på standardform och Simplexmetoden I detta avsnitt utgår vi från LP-formuleringen (2.2) från föreläsning. Denna form är den bäst lämpade för en strömlinjeformad implementering
Lösningar till SF1861/SF1851 Optimeringslära, 24/5 2013
 Lösningar till SF86/SF85 Optimeringslära, 4/5 03 Uppgift (a) Inför de 3 variablerna x ij = kvantitet (i sorten ton) som fabrik nr i åläggs att tillverka av produkt nr j, samt t = tiden (i sorten timmar)
Lösningar till SF86/SF85 Optimeringslära, 4/5 03 Uppgift (a) Inför de 3 variablerna x ij = kvantitet (i sorten ton) som fabrik nr i åläggs att tillverka av produkt nr j, samt t = tiden (i sorten timmar)
Lösningar till tentan i 5B1760 Linjär och kvadratisk optimering, 17 december 2003.
 Lösningar till tentan i 5B7 Linjär och kvadratisk optimering, 7 december 3 Uppgift (a) 3 Vi använder Gauss-Jordans metod för att överföra A 3 5 till trappstegsform 3 7 Addition av ( ) gånger första raden
Lösningar till tentan i 5B7 Linjär och kvadratisk optimering, 7 december 3 Uppgift (a) 3 Vi använder Gauss-Jordans metod för att överföra A 3 5 till trappstegsform 3 7 Addition av ( ) gånger första raden
1 Kvadratisk optimering under linjära likhetsbivillkor
 Krister Svanberg, april 0 Kvadratisk optimering under linjära likhetsbivillkor I detta kapitel behandlas följande kvadratiska optimeringsproblem under linjära likhetsbivillkor: xt Hx + c T x + c 0 då Ax
Krister Svanberg, april 0 Kvadratisk optimering under linjära likhetsbivillkor I detta kapitel behandlas följande kvadratiska optimeringsproblem under linjära likhetsbivillkor: xt Hx + c T x + c 0 då Ax
Lösningar till SF1852 Optimeringslära för E, 16/1 08
 Lösningar till SF8 Optimeringslära för E, 6/ 8 Uppgift (a) Problemet är ett transportproblem, ett specialfall av minkostnadsflödesproblem Nätverket består av 7 st noder A,B,C,P,Q,R,S, alternativt kallade,,,7,
Lösningar till SF8 Optimeringslära för E, 6/ 8 Uppgift (a) Problemet är ett transportproblem, ett specialfall av minkostnadsflödesproblem Nätverket består av 7 st noder A,B,C,P,Q,R,S, alternativt kallade,,,7,
1 Positivt definita och positivt semidefinita matriser
 Krister Svanberg, april 1 1 Positivt definita och positivt semidefinita matriser Inom ickelinjär optimering, speciellt kvadratisk optimering, är det viktigt att på ett effektivt sätt kunna avgöra huruvida
Krister Svanberg, april 1 1 Positivt definita och positivt semidefinita matriser Inom ickelinjär optimering, speciellt kvadratisk optimering, är det viktigt att på ett effektivt sätt kunna avgöra huruvida
Föreläsning 7: Kvadratisk optimering. 4. Kvadratisk optimering under linjära bivillkor
 Föreläsning 7: Kvadratisk optimering 1. Kvadratisk optimering utan bivillkor 2. Positivt definita och semidefinita matriser 3. LDL T faktorisering 4. Kvadratisk optimering under linjära bivillkor 5. Minsta
Föreläsning 7: Kvadratisk optimering 1. Kvadratisk optimering utan bivillkor 2. Positivt definita och semidefinita matriser 3. LDL T faktorisering 4. Kvadratisk optimering under linjära bivillkor 5. Minsta
TNK049 Optimeringslära
 TNK049 Optimeringslära Clas Rydergren, ITN Föreläsning 9 Icke-linjär optimering Konveitet Metoder ör problem utan bivillkor Optimalitetsvillkor ör icke-linjära problem Icke-linjär programmering Non-linear
TNK049 Optimeringslära Clas Rydergren, ITN Föreläsning 9 Icke-linjär optimering Konveitet Metoder ör problem utan bivillkor Optimalitetsvillkor ör icke-linjära problem Icke-linjär programmering Non-linear
TNK049 Optimeringslära
 TNK049 Optimeringslära Clas Rydergren, ITN Föreläsning 3 Problemklassificering Global/lokal optimalitet Konvexitet Generella sökmetoder Agenda Problemklassificering (kap 1.4, 2.1 2.3) Lokalt/globalt optimum
TNK049 Optimeringslära Clas Rydergren, ITN Föreläsning 3 Problemklassificering Global/lokal optimalitet Konvexitet Generella sökmetoder Agenda Problemklassificering (kap 1.4, 2.1 2.3) Lokalt/globalt optimum
Optimering av strålterapi
 Optimering av strålterapi Anders Forsgren Optimeringslära och systemteori Institutionen för matematik KTH Presentation simuleringsteknik 3 oktober 2013 Optimering av strålterapi Gememensamt forskningsprojekt
Optimering av strålterapi Anders Forsgren Optimeringslära och systemteori Institutionen för matematik KTH Presentation simuleringsteknik 3 oktober 2013 Optimering av strålterapi Gememensamt forskningsprojekt
Olinjär optimering med bivillkor: KKT min f (x) då g i (x) 0 för alla i
 Olinjär optimering med bivillkor min då f (x) g i (x) 0 för alla i Specialfall: Konvext problem. Linjära bivillkor: Ax b. Linjära likhetsbivillkor: Ax = b. Inga bivillkor: Hanterat tidigare. Metodprinciper:
Olinjär optimering med bivillkor min då f (x) g i (x) 0 för alla i Specialfall: Konvext problem. Linjära bivillkor: Ax b. Linjära likhetsbivillkor: Ax = b. Inga bivillkor: Hanterat tidigare. Metodprinciper:
Institutionen för Matematik TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F1, TMA DAG: Fredag 30 augusti 2002 TID:
 Institutionen för Matematik Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F, TMA67 22-8-3 DAG: Fredag 3 augusti 22 TID: 8.45-2.45 SAL: V Ansvarig: Ivar Gustafsson, tel: 772 94 (ankn. 94) Förfrågningar:
Institutionen för Matematik Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F, TMA67 22-8-3 DAG: Fredag 3 augusti 22 TID: 8.45-2.45 SAL: V Ansvarig: Ivar Gustafsson, tel: 772 94 (ankn. 94) Förfrågningar:
Crash Course Algebra och geometri. Ambjörn Karlsson c januari 2016
 Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
SF1624 Algebra och geometri
 Föreläsning 16 Institutionen för matematik KTH 5 december 2017 Modul 6 Veckans arbete 1. Idag: Ortonormalt, kap 7.1-7.2 a. Ortogonala och ortonormala baser b. Gram-Schmidts metod c. Ortogonala matriser
Föreläsning 16 Institutionen för matematik KTH 5 december 2017 Modul 6 Veckans arbete 1. Idag: Ortonormalt, kap 7.1-7.2 a. Ortogonala och ortonormala baser b. Gram-Schmidts metod c. Ortogonala matriser
TMV166 Linjär Algebra för M. Tentamen
 MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 8 kl 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Olof Giselsson, ankn
MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 8 kl 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Olof Giselsson, ankn
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Lösningar till tentan i SF1861 Optimeringslära, 1 juni 2017
 Lösningar till tentan i SF86 Optimeringslära, juni 7 Lösningarna är på svenska, utom lösningen av (a som är på engelska (a The considered network is illustrated in FIGURE below, where the supply at the
Lösningar till tentan i SF86 Optimeringslära, juni 7 Lösningarna är på svenska, utom lösningen av (a som är på engelska (a The considered network is illustrated in FIGURE below, where the supply at the
x 1 x 2 T (X) = T ( x 3 x 4 x 5
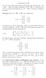 Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
Linjär algebra Föreläsning 10
 Linjär algebra Föreläsning 10 IT-programmet, Chalmers 2006 Samuel Bengmark Repetition Handlade om kvadratiska matriser. Kvadratiska ekvationssystem har: Unik lösning omm Det(A) 0. Har oändligt antal lösningar
Linjär algebra Föreläsning 10 IT-programmet, Chalmers 2006 Samuel Bengmark Repetition Handlade om kvadratiska matriser. Kvadratiska ekvationssystem har: Unik lösning omm Det(A) 0. Har oändligt antal lösningar
CHALMERS Finit Elementmetod M3 Institutionen för tillämpad mekanik. Teorifrågor
 Teorifrågor : Visa att gradienten till en funktion pekar i den riktning derivatan är störst och att riktingen ortogonalt mot gradienten är tangent till funktionens nivåkurva. Visa hur derivatan i godtycklig
Teorifrågor : Visa att gradienten till en funktion pekar i den riktning derivatan är störst och att riktingen ortogonalt mot gradienten är tangent till funktionens nivåkurva. Visa hur derivatan i godtycklig
Institutionen för Matematik. F1 - Linjär algebra och numerisk analys, TMA671 Svar till övningar i Heath s bok och extraövningar
 Institutionen för Matematik Göteborg F1 - Linjär algebra och numerisk analys, TMA671 Svar till övningar i Heath s bok och extraövningar Heath 1: a) -01416 resp -0046 b) -0001593 resp -000051 c) 000165
Institutionen för Matematik Göteborg F1 - Linjär algebra och numerisk analys, TMA671 Svar till övningar i Heath s bok och extraövningar Heath 1: a) -01416 resp -0046 b) -0001593 resp -000051 c) 000165
Approximerande Splines. B-splines. Minsta kvadrat anpassning. Design av kurvor och ytor.
 TANA09 Föreläsning 8 Approximerande Splines B-splines. Minsta kvadrat anpassning. Design av kurvor och ytor. Exempel Parametriska Kurvor. Ritprogram. Beziér kurvor. Design av kurvor och ytor. Tillämpning
TANA09 Föreläsning 8 Approximerande Splines B-splines. Minsta kvadrat anpassning. Design av kurvor och ytor. Exempel Parametriska Kurvor. Ritprogram. Beziér kurvor. Design av kurvor och ytor. Tillämpning
SF1624 Algebra och geometri
 SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
TANA09 Föreläsning 8. Kubiska splines. B-Splines. Approximerande Splines. B-splines. Minsta kvadrat anpassning. Design av kurvor och ytor.
 TANA09 Föreläsning 8 Kubiska splines Approximerande Splines s s s s 4 B-splines. Minsta kvadrat anpassning. Design av kurvor och ytor. x x x x 4 x 5 Exempel Parametriska Kurvor. Ritprogram. Beziér kurvor.
TANA09 Föreläsning 8 Kubiska splines Approximerande Splines s s s s 4 B-splines. Minsta kvadrat anpassning. Design av kurvor och ytor. x x x x 4 x 5 Exempel Parametriska Kurvor. Ritprogram. Beziér kurvor.
Optimeringsproblem. 1 Inledning. 2 Optimering utan bivillkor. CTH/GU STUDIO 6 TMV036c /2015 Matematiska vetenskaper
 CTH/GU STUDIO TMV3c - 1/15 Matematiska vetenskaper Optimeringsproblem 1 Inledning Vi skall söka minsta eller största värdet hos en funktion på en mängd, dvs. vi skall lösa s.k. optimeringsproblem min f(x)
CTH/GU STUDIO TMV3c - 1/15 Matematiska vetenskaper Optimeringsproblem 1 Inledning Vi skall söka minsta eller största värdet hos en funktion på en mängd, dvs. vi skall lösa s.k. optimeringsproblem min f(x)
De optimeringsproblem som kommer att behandlas i denna kurs kan alla (i princip) skrivas. 1 2 xt Hx + c T x. minimera
 Krister Svanberg, mars 2012 1 Introduktion De optimeringsproblem som kommer att behandlas i denna kurs kan alla (i princip) skrivas på följande allmänna form: f(x) (1.1) x F, där x = (x 1,..., x n ) T
Krister Svanberg, mars 2012 1 Introduktion De optimeringsproblem som kommer att behandlas i denna kurs kan alla (i princip) skrivas på följande allmänna form: f(x) (1.1) x F, där x = (x 1,..., x n ) T
SF1624 Algebra och geometri
 SF1624 Algebra och geometri Tjugofemte föreläsningen Mats Boij Institutionen för matematik KTH 10 december, 2009 Tentamens struktur Tentamen består av tio uppgifter uppdelade på två delar, Del A och Del
SF1624 Algebra och geometri Tjugofemte föreläsningen Mats Boij Institutionen för matematik KTH 10 december, 2009 Tentamens struktur Tentamen består av tio uppgifter uppdelade på två delar, Del A och Del
TMV036 Analys och linjär algebra K Kf Bt, del C
 MATEMATIK Chalmers tekniska högskola Tentamen 20-0-, kl. 4.00-8.00 TMV036 Analys och linjär algebra K Kf Bt, del C Telefonvakt: Richard Lärkäng, telefon: 0703-088304 Hjälpmedel: Inga, bara papper och penna.
MATEMATIK Chalmers tekniska högskola Tentamen 20-0-, kl. 4.00-8.00 TMV036 Analys och linjär algebra K Kf Bt, del C Telefonvakt: Richard Lärkäng, telefon: 0703-088304 Hjälpmedel: Inga, bara papper och penna.
TMV166 Linjär algebra för M, vt 2016
 TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
Fö4: Kondition och approximation. Andrea Alessandro Ruggiu
 TANA21/22 HT2018 Fö4: Kondition och approximation Andrea Alessandro Ruggiu Kondition och approximation A.A.Ruggiu 13:e September 2018 1 Konditionstal Kondition och approximation A.A.Ruggiu 13:e September
TANA21/22 HT2018 Fö4: Kondition och approximation Andrea Alessandro Ruggiu Kondition och approximation A.A.Ruggiu 13:e September 2018 1 Konditionstal Kondition och approximation A.A.Ruggiu 13:e September
Föreläsning 5. Approximationsteori
 Föreläsning 5 Approximationsteori Låt f vara en kontinuerlig funktion som vi vill approximera med en enklare funktion f(x) Vi kommer använda två olika approximationsmetoder: interpolation och minstrakvadratanpassning
Föreläsning 5 Approximationsteori Låt f vara en kontinuerlig funktion som vi vill approximera med en enklare funktion f(x) Vi kommer använda två olika approximationsmetoder: interpolation och minstrakvadratanpassning
BEGREPPSMÄSSIGA PROBLEM
 BEGREPPSMÄSSIGA PROBLEM Större delen av de rekommenderade uppgifterna i boken är beräkningsuppgifter. Det är emellertid även viktigt att utveckla en begreppsmässig förståelse för materialet. Syftet med
BEGREPPSMÄSSIGA PROBLEM Större delen av de rekommenderade uppgifterna i boken är beräkningsuppgifter. Det är emellertid även viktigt att utveckla en begreppsmässig förståelse för materialet. Syftet med
Institutionen för Matematik TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F1, TMA DAG: Lördag 26 maj 2001 TID:
 Institutionen för Matematik Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F, TMA67 2-5-26 DAG: Lördag 26 maj 2 TID: 8.45-2.45 SAL: V Ansvarig: Ivar Gustafsson, tel: 772 94 (ankn. 94) Förfrågningar:
Institutionen för Matematik Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F, TMA67 2-5-26 DAG: Lördag 26 maj 2 TID: 8.45-2.45 SAL: V Ansvarig: Ivar Gustafsson, tel: 772 94 (ankn. 94) Förfrågningar:
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F1, TMA671
 Institutionen för Matematik LINJÄR ALGEBRA OCH NUMERISK ANALYS F Göteborg --9 TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F, TMA67 OBS! NYA KURSEN DAG: Tisdag 9 januari TID: 8.45 -.45 SAL: V Ansvarig:
Institutionen för Matematik LINJÄR ALGEBRA OCH NUMERISK ANALYS F Göteborg --9 TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F, TMA67 OBS! NYA KURSEN DAG: Tisdag 9 januari TID: 8.45 -.45 SAL: V Ansvarig:
Institutionen för Matematik TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F1, TMA671 2005-08-26. DAG: Fredag 26 augusti 2005 TID: 8.30-12.
 Institutionen för Matematik Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F, TMA67 5-8-6 DAG: Fredag 6 augusti 5 TID: 8.3-.3 SAL: V Ansvarig: Ivar Gustafsson, tel: 77 94 Förfrågningar: Ivar Gustafsson
Institutionen för Matematik Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F, TMA67 5-8-6 DAG: Fredag 6 augusti 5 TID: 8.3-.3 SAL: V Ansvarig: Ivar Gustafsson, tel: 77 94 Förfrågningar: Ivar Gustafsson
Minsta kvadratmetoden
 Minsta kvadratmetoden där Överbestämda ekvationssystem Det är lämpligt att uppfatta matrisen A som bestående av n kolonnvektorer: A a a a n a a a n a n a n a nn a j a j a nj a a a n j n Då kan vi skriva
Minsta kvadratmetoden där Överbestämda ekvationssystem Det är lämpligt att uppfatta matrisen A som bestående av n kolonnvektorer: A a a a n a a a n a n a n a nn a j a j a nj a a a n j n Då kan vi skriva
Numerisk Analys, MMG410. Exercises 2. 1/33
 Numerisk Analys, MMG410. Exercises 2. 1/33 1. A är en kvadratisk matris vars alla radsummor är noll. Visa att A är singulär. Låt e vara vektorn av ettor. Då är Ae = 0 A har icke-trivialt nollrum. 2/33
Numerisk Analys, MMG410. Exercises 2. 1/33 1. A är en kvadratisk matris vars alla radsummor är noll. Visa att A är singulär. Låt e vara vektorn av ettor. Då är Ae = 0 A har icke-trivialt nollrum. 2/33
Optimeringslära Kaj Holmberg
 Tekniska Högskolan i Linköping TAOP88 Matematiska Institutionen Lösning till tentamen Optimeringslära 9--7 Kaj Holmberg Lösningar Uppgift a: Inför slackvariabler x 5, x 6 och x 7 Starta med slackvariablerna
Tekniska Högskolan i Linköping TAOP88 Matematiska Institutionen Lösning till tentamen Optimeringslära 9--7 Kaj Holmberg Lösningar Uppgift a: Inför slackvariabler x 5, x 6 och x 7 Starta med slackvariablerna
Optimering med bivillkor
 Optimering med bivillkor Vi ska nu titta på problemet att hitta max och min av en funktionen f(x, y), men inte över alla möjliga (x, y) utan bara för de par som uppfyller ett visst bivillkor g(x, y) =
Optimering med bivillkor Vi ska nu titta på problemet att hitta max och min av en funktionen f(x, y), men inte över alla möjliga (x, y) utan bara för de par som uppfyller ett visst bivillkor g(x, y) =
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
LINJÄR ALGEBRA II LEKTION 6
 LINJÄR ALGEBRA II LEKTION 6 JOHAN ASPLUND INNEHÅLL 1 Inre produktrum 1 2 Cauchy-Schwarz olikhet 3 3 Ortogonala projektioner och Gram-Schmidts process 3 4 Uppgifter 4 61:13(a) 4 61:23(a) 4 61:29 5 62:7
LINJÄR ALGEBRA II LEKTION 6 JOHAN ASPLUND INNEHÅLL 1 Inre produktrum 1 2 Cauchy-Schwarz olikhet 3 3 Ortogonala projektioner och Gram-Schmidts process 3 4 Uppgifter 4 61:13(a) 4 61:23(a) 4 61:29 5 62:7
Lösningar till tentan i SF1861 Optimeringslära, 3 Juni, 2016
 Lösningar till tentan i SF86 Optimeringslära, 3 Juni, 6 Uppgift (a) We note that each column in the matrix A contains one + and one, while all the other elements in the column are zeros We also note that
Lösningar till tentan i SF86 Optimeringslära, 3 Juni, 6 Uppgift (a) We note that each column in the matrix A contains one + and one, while all the other elements in the column are zeros We also note that
6.3. Direkta sökmetoder
 6.3. Direkta sökmetoder Förutom de nyss nämnda metoderna för att uppsöka ett minimum av en funktion av en variabel finns det en enkel metod som baserar sig på polynomapproximation av funktionen. Om vi
6.3. Direkta sökmetoder Förutom de nyss nämnda metoderna för att uppsöka ett minimum av en funktion av en variabel finns det en enkel metod som baserar sig på polynomapproximation av funktionen. Om vi
Tentamen TMA946/MAN280 tillämpad optimeringslära
 Tentamen TMA946/MAN80 tillämpad optimeringslära 01081 1. Uppgift: min z 3x 1 + x Då x 1 + x 6 x 1 + x x 1, x 0 Skriv på standardform m.h.aṡlackvariabler min z 3x 1 + x Då x 1 + x s 1 6 x 1 x + s x 1, x,
Tentamen TMA946/MAN80 tillämpad optimeringslära 01081 1. Uppgift: min z 3x 1 + x Då x 1 + x 6 x 1 + x x 1, x 0 Skriv på standardform m.h.aṡlackvariabler min z 3x 1 + x Då x 1 + x s 1 6 x 1 x + s x 1, x,
Lösningar till några övningar inför lappskrivning nummer 3 på kursen Linjär algebra för D, vt 15.
 1 Matematiska Institutionen KTH Lösningar till några övningar inför lappskrivning nummer 3 på kursen Linjär algebra för D, vt 15. 1. Undersök om vektorn (1,, 1, ) tillhör span{(1,, 3, 4), (1, 0, 1, 1),
1 Matematiska Institutionen KTH Lösningar till några övningar inför lappskrivning nummer 3 på kursen Linjär algebra för D, vt 15. 1. Undersök om vektorn (1,, 1, ) tillhör span{(1,, 3, 4), (1, 0, 1, 1),
8 Minsta kvadratmetoden
 Nr, april -, Amelia Minsta kvadratmetoden. Ekvationssystem med en lösning, -fallet Ett linjärt ekvationssystem, som ½ +7y = y = har en entydig lösning om koefficientdeterminanten, här 7, är skild från
Nr, april -, Amelia Minsta kvadratmetoden. Ekvationssystem med en lösning, -fallet Ett linjärt ekvationssystem, som ½ +7y = y = har en entydig lösning om koefficientdeterminanten, här 7, är skild från
2 = 3 = 1. ekvationssystem är beskriven som de vektorer X = 2 0 1 2. 1 1 0 2
 . Tisdagen 35 Igår visade vi att lösningsmängden W R 5 till ekvationssystemet 3x + x 2 + 3x 3 + 2x 4 x 5 = (..) 2x 2 + x 3 + 4x 4 + 2x 5 = 3x 3x 2 + x 3 6x 4 5x 5 = har bas u och u 2 och u 3 där 5 2 6
. Tisdagen 35 Igår visade vi att lösningsmängden W R 5 till ekvationssystemet 3x + x 2 + 3x 3 + 2x 4 x 5 = (..) 2x 2 + x 3 + 4x 4 + 2x 5 = 3x 3x 2 + x 3 6x 4 5x 5 = har bas u och u 2 och u 3 där 5 2 6
Optimering med bivillkor
 Kapitel 9 Optimering med bivillkor 9.1. Optimering med bivillkor Låt f(x) vara en funktion av x R. Vi vill optimera funktionen f under bivillkoret g(x) =C (eller bivllkoren g 1 (x) =C 1,..., g k (x) =C
Kapitel 9 Optimering med bivillkor 9.1. Optimering med bivillkor Låt f(x) vara en funktion av x R. Vi vill optimera funktionen f under bivillkoret g(x) =C (eller bivllkoren g 1 (x) =C 1,..., g k (x) =C
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra, SF1604, den 15 mars 2012 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF604, den 5 mars 202 kl 08.00-3.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF604, den 5 mars 202 kl 08.00-3.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
SF1624 Algebra och geometri Tentamen Torsdag, 17 mars 2016
 SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
1 Grundläggande kalkyler med vektorer och matriser
 Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Lösningar till utvalda uppgifter i kapitel 8
 Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
Laboration 1 i SF1544: Öva på Matlab och konstruera en optimal balk Avsikten med denna laboration är att:
 Laboration 1 i SF1544: Öva på Matlab och konstruera en optimal balk Avsikten med denna laboration är att: - snabbt komma igång med träning på matlabprogrammering (uttnyttja gärna alla schemalagda laborationstillfällen,
Laboration 1 i SF1544: Öva på Matlab och konstruera en optimal balk Avsikten med denna laboration är att: - snabbt komma igång med träning på matlabprogrammering (uttnyttja gärna alla schemalagda laborationstillfällen,
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Tentamen del 1 SF1511, , kl , Numeriska metoder och grundläggande programmering
 KTH Matematik Tentamen del SF5, 28-3-6, kl 8.-., Numeriska metoder och grundläggande programmering Namn:... Personnummer:... Program och årskurs:... Bonuspoäng. Ange dina bonuspoäng från kursomgången HT7-VT8
KTH Matematik Tentamen del SF5, 28-3-6, kl 8.-., Numeriska metoder och grundläggande programmering Namn:... Personnummer:... Program och årskurs:... Bonuspoäng. Ange dina bonuspoäng från kursomgången HT7-VT8
Laboration 1: Optimalt sparande
 Avsikten med denna laboration är att: Laboration 1: Optimalt sparande - snabbt komma igång med träning på matlabprogrammering (uttnyttja gärna alla schemalagda laborationstillfällen, - lösa ett optimeringsproblem
Avsikten med denna laboration är att: Laboration 1: Optimalt sparande - snabbt komma igång med träning på matlabprogrammering (uttnyttja gärna alla schemalagda laborationstillfällen, - lösa ett optimeringsproblem
Analys av jämviktslägen till differentialekvationer
 Analys 360 En webbaserad analyskurs Ordinära differentialekvationer Analys av jämviktslägen till differentialekvationer Anders Källén MatematikCentrum LTH anderskallen@gmail.com Analys av jämviktslägen
Analys 360 En webbaserad analyskurs Ordinära differentialekvationer Analys av jämviktslägen till differentialekvationer Anders Källén MatematikCentrum LTH anderskallen@gmail.com Analys av jämviktslägen
Hjälpmedel: inga Chalmers tekniska högskola Datum: kl Telefonvakt: Peter Hegarty (a) Låt (3p)
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 5 kl 4 8 Tentamen Telefonvakt: Peter Hegarty 766-7787 TMV4/86: Linjär algebra Z/TD Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 5 kl 4 8 Tentamen Telefonvakt: Peter Hegarty 766-7787 TMV4/86: Linjär algebra Z/TD Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt
Linjär Algebra, Föreläsning 9
 Linjär Algebra, Föreläsning 9 Tomas Sjödin Linköpings Universitet Euklidiska rum Vi ska nu införa en extra struktur på vektorrum, en så kallad skalärprodukt, vilken vi kan använda för att definiera längd
Linjär Algebra, Föreläsning 9 Tomas Sjödin Linköpings Universitet Euklidiska rum Vi ska nu införa en extra struktur på vektorrum, en så kallad skalärprodukt, vilken vi kan använda för att definiera längd
Optimeringslära Kaj Holmberg
 Tekniska Högskolan i Linköping Optimering för ingenjörer Matematiska Institutionen Lösning till tentamen Optimeringslära 2018-08-31 Kaj Holmberg Lösningar Uppgift 1 1a: Inför slackvariabler x 5, x 6 och
Tekniska Högskolan i Linköping Optimering för ingenjörer Matematiska Institutionen Lösning till tentamen Optimeringslära 2018-08-31 Kaj Holmberg Lösningar Uppgift 1 1a: Inför slackvariabler x 5, x 6 och
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer III Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer III Innehåll
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Lösningar till SF1861 Optimeringslära, 28 maj 2012
 Lösningar till SF86 Optimeringslära, 28 maj 202 Uppgift.(a) Då det primala problemet P är så är det motsvarande duala problemet D minimera 3x + x 2 då 3x + 2x 2 6 x + 2x 2 4 x j 0, j =, 2. maximera 6 +
Lösningar till SF86 Optimeringslära, 28 maj 202 Uppgift.(a) Då det primala problemet P är så är det motsvarande duala problemet D minimera 3x + x 2 då 3x + 2x 2 6 x + 2x 2 4 x j 0, j =, 2. maximera 6 +
Dagens ämnen. Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer
 Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Iterativa metoder för linjära ekvationssystem
 Iterativa metoder för linjära ekvationssystem Bra för glesa ekvationssystem Finita differensmetoder och FEM ger glesa matriser. Antal nollskilda element är Ç(Æ) om är Æ Æ. I implicita metoder och för tidsoberoende
Iterativa metoder för linjära ekvationssystem Bra för glesa ekvationssystem Finita differensmetoder och FEM ger glesa matriser. Antal nollskilda element är Ç(Æ) om är Æ Æ. I implicita metoder och för tidsoberoende
Institutionen för Matematiska Vetenskaper TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F1, TMA
 Institutionen för Matematiska Vetenskaper Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F, TMA67 009-08-7 DAG: Torsdag 7 augusti 009 TID: 8.30 -.30 SAL: V Ansvarig: Ivar Gustafsson, tel: 77 0
Institutionen för Matematiska Vetenskaper Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F, TMA67 009-08-7 DAG: Torsdag 7 augusti 009 TID: 8.30 -.30 SAL: V Ansvarig: Ivar Gustafsson, tel: 77 0
15 februari 2016 Sida 1 / 32
 TAIU07 Föreläsning 5 Linjära ekvationssystem. Minsta kvadrat problem. Tillämpning: Cirkelpassning. Geometriska objekt. Translationer. Rotationer. Funktioner som inargument. Tillämpning: Derivata. 15 februari
TAIU07 Föreläsning 5 Linjära ekvationssystem. Minsta kvadrat problem. Tillämpning: Cirkelpassning. Geometriska objekt. Translationer. Rotationer. Funktioner som inargument. Tillämpning: Derivata. 15 februari
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 17 april 2010 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
1 De fyra fundamentala underrummen till en matris
 Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
TSRT09 Reglerteori. Sammanfattning av Föreläsning 1. Sammanfattning av Föreläsning 1, forts. Sammanfattning av Föreläsning 1, forts.
 Reglerteori 217, Föreläsning 2 Daniel Axehill 1 / 32 Sammanfattning av Föreläsning 1 TSRT9 Reglerteori Föreläsning 2: Beskrivning av linjära system Daniel Axehill Reglerteknik, ISY, Linköpings Universitet
Reglerteori 217, Föreläsning 2 Daniel Axehill 1 / 32 Sammanfattning av Föreläsning 1 TSRT9 Reglerteori Föreläsning 2: Beskrivning av linjära system Daniel Axehill Reglerteknik, ISY, Linköpings Universitet
Tentamen del 1 SF1546, , , Numeriska metoder, grundkurs
 KTH Matematik Tentamen del 1 SF154, 1-3-3, 8.-11., Numeriska metoder, grundkurs Namn:... Bonuspoäng. Ange dina bonuspoäng från kursomgången läsåret HT15/VT1 här: Max antal poäng är. Gränsen för godkänt/betyg
KTH Matematik Tentamen del 1 SF154, 1-3-3, 8.-11., Numeriska metoder, grundkurs Namn:... Bonuspoäng. Ange dina bonuspoäng från kursomgången läsåret HT15/VT1 här: Max antal poäng är. Gränsen för godkänt/betyg
Numerisk Analys, MMG410. Lecture 8. 1/30
 Numerisk Analys, MMG410. Lecture 8. 1/30 Kort om konditionstal för minstakvadratproblem Antag att x och y löser problemen min x Ax b 2 2 resp. min y (A+F)y (b +f) 2 2 y är alltså lösningen till ett stört
Numerisk Analys, MMG410. Lecture 8. 1/30 Kort om konditionstal för minstakvadratproblem Antag att x och y löser problemen min x Ax b 2 2 resp. min y (A+F)y (b +f) 2 2 y är alltså lösningen till ett stört
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
TENTAMEN I GRUNDKURS I NUMERISKA METODER - DEL 20
 Numerisk Analys - Institutionen för Matematik KTH - Royal institute of technology 2016-05-31, kl 08-11 SF1547+SF1543 TENTAMEN I GRUNDKURS I NUMERISKA METODER - DEL 20 Uppgift 1 Man vill lösa ekvationssystemet
Numerisk Analys - Institutionen för Matematik KTH - Royal institute of technology 2016-05-31, kl 08-11 SF1547+SF1543 TENTAMEN I GRUNDKURS I NUMERISKA METODER - DEL 20 Uppgift 1 Man vill lösa ekvationssystemet
1 som går genom punkten (1, 3) och är parallell med vektorn.
 KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
November 24, Egenvärde och egenvektor. (en likformig expansion med faktor 2) (en rotation 30 grader moturs)
 Fö : November 4, 7 Egenvärde och egenvektor Definition s 9: Låt A resp T : R n R n vara en n n-matris resp en linjär avbildning En icke-trivial vektor v R n kallas en egenvektor till A resp till T med
Fö : November 4, 7 Egenvärde och egenvektor Definition s 9: Låt A resp T : R n R n vara en n n-matris resp en linjär avbildning En icke-trivial vektor v R n kallas en egenvektor till A resp till T med
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. (1 p) (c) Bestäm avståndet mellan A och linjen l.
 SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
