LABORATION 4 RADIOAKTIVT SÖNDERFALL (BIOFYSIK)

Transkript

1 Fysikum FK3005- Experimentella metoder för biofysik Laborationsinstruktion (7 februari 2014) LABORATION 4 RADIOAKTIVT SÖNDERFALL (BIOFYSIK) Mål Laborationen avser att ge allmänna erfarenheter av bakgrundsstrålning, radioaktivt sönderfall, poissonfördelningen och en del apparatur för kärnfysikaliska försök. Materialet i denna övning består av aktiverat silver som innehåller två radioaktiva isotoper. Du skall genom en viktad minsta kvadratanpassning till dina mätdata beräkna halveringstiden för den av isotoperna som har längst halveringstid. Du skall lämna in en utförlig, individuellt författad skriftlig rapport där du presenterar dina mätningar och din dataanalys. Hur analysen görs, och vad som skall presenteras, anges ganska detaljerat i instruktionen för att det skall vara någorlunda enkelt att rätta. Tonvikten ligger alltså inte på att planera mätningar och analys, utan på att genomföra analysen korrekt och att skriva en korrekt rapport.

2 .

3 LABORATION 4: Radioaktivt sönderfall 1 1 Inledning Laborationen avser att ge allmänna erfarenheter av radioaktivt sönderfall, poissonfördelningen 1 och en del av den apparatur som erfordras för kärnfysikaliska försök. Radioaktivt sönderfall sker spontant hos vissa naturligt förekommande isotoper 2 och innebär i allmänhet att atomkärnan omvandlas så att antalet protoner och neutroner där förändras. Ett välbekant exempel är sönderfall av den vanligast förekommande uranisotopen uran-238 som sönderfaller genom att en α-partikel (bestående av två protoner och två neutroner) skickas ut samtidigt som urankärnan omvandlas till torium. I denna laboration skall du studera sönderfallet hos några radioaktiva isotoper hos silver. Silver är normalt inte radioaktivt utan i detta fall måste silvret först bestrålas (vi säger att vi aktiverar silvret) med termiska neutroner. 3 Genom att se hur aktiviteten avtar kan man verifiera den radioaktiva sönderfallslagen och bestämma sönderfallskonstanterna för isotoperna. 2 Lite teori 2.1 Poissonfördelningen och sönderfallslagen Radioaktivt sönderfall är en slumpmässig process. Varje atomkärna sönderfaller, oberoende av andra partiklar, med en viss konstant sannolikhet per tidsenhet, λ. Om kärnan fortfarande inte sönderfallit vid tiden t är λ t sannolikheten för att den kommer att göra det under tiden mellan t och t + t, helt oberoende av hur länge den redan existerat. Detta medför att antalet sönderfall ν bland N stycken partiklar i ett preparat under tidsintervallet t i genomsnitt blir µ = Nλ t. Man kan visa att det faktiska värdet på ν << N sprider sig runt medelvärdet µ enligt poissonfördelningen, dvs att sannolikheten för ν sönderfall i ett intervall t är: 4 P(ν;µ) = e µµν ν! Poissonfördelningen är av stor vikt i fysiken. Medelvärdet µ är lika med variansen, dvs kvadraten av standardavvikelsen, σ = µ. Variabeln ν (här antalet sönderfall) är diskret (ett heltal) till skillnad från normalfördelningens kontinuerliga variabel. Om medelvärdet är stort (åtminstone 12, helst mer) blir poissonfördelningen allt mer lik en normalfördelning till formen, men med det extra villkoret att σ = 1 Poissonfördelningen beskrivs i kapitel 11 i R. Taylor. Se även Appendix B. 2 Ett grundämne kan förekomma i en eller flera olika tunga varianter s.k. isotoper, med olika antal neutroner i kärnan, men med ett fixt antal protoner. 3 En partikel säges vara termisk om den har en kinetisk energi som är av samma storleksordning som energin i de mikroskopiska processer som omfördelar värmenergi mellan olika molekyler, atomer och partiklar. 4 Se Appendix B för en härledning.

4 2 LABORATION 4: Radioaktivt sönderfall µ. Från antalet observerade sönderfall νobs kan man således direkt uppskatta poissonfördelningens medelvärde µ och dessutom kan man uppskatta felet i denna bestämning av µ som ν obs. Det totala antalet kärnor av det sönderfallande ämnet, N, förändras under tiden t i medeltal med µ = Nλ t. Om µ är tillräckligt stort kan vi försumma fluktuationerna i poissonfördelningen för µ och skriva N = N λ t, vilket leder till differentialekvationen dn dt = λn som har lösningen N(t) = N(0)e λt där N(0) är antalet partiklar vid tiden t = 0. Sönderfallskonstanten λ är alltså en egenskap som alla de sönderfallande kärnorna av samma typ har gemensam. Om vi har flera olika populationer av partiklar kommer storleken av de olika populationerna att avta enligt ovan med olika λ och N(0). Aktiviteten n, antalet sönderfall per sekund, erhålles genom derivering och vi finner: n(t) = dn(t) = λn(0)e λt = n(0) e λt dt där n(0) = λn(0) är antalet sönderfall per tidsenhet vid tiden t = 0. Tiden det tar för ett prov att reduceras till 50% av den ursprungliga mängden (alternativt att aktiviteten minskar till hälften) kallas halveringstiden, T 1/2, och är relaterad till sönderfallskonstanten genom sambandet (visa detta): T 1/2 = ln 2 λ Notera att aktiviteten i varje ögonblick kan skrivas: n(t) = λn(t) 2.2 Neutronaktivering och sönderfall av silver Naturligt silver (Ag) består huvudsakligen av c:a 50% Ag och c:a 50% Ag. 5 Om silver bestrålas med termiska neutroner (kinetisk energi omkring 0,025 ev), sker följande reaktioner: Ag + 1 0n Ag + γ Ag + 1 0n Ag + γ De båda bildade silverisotoperna är instabila och sönderfaller till en kadmiumkärna, en elektron och en antielektronneutrino enligt: 5 Siffrorna anger silvrets masstal, dvs totala antalet protoner och neutroner i kärnan, samt atomnumret dvs antalet protoner. Silver definieras genom att atomnumret är 47.

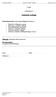
5 LABORATION 4: Radioaktivt sönderfall Ag Cd + e +ν e Ag Cd + e +ν e Antielektronneutrinon (ν e ) är en helt ofarlig, nära viktlös och ickeladdad elementarpartikelsommedljusetshastighetavlägsnarsigfrånpreparatetochlaboratoriet. 6 Elektronerna är elektriskt laddade och har tillräckligt mycket energi för att frigöra sig från preparatet och tränga in i detektorn där de genererar en puls som detekteras. De elektronerna från sönderfallen som missar detektorn absorberas helt i det omgivande stålhöljet. I Fig. 1 visar vi ett exempel på hur en sönderfallskurva kan se ut för silver. I detta fall består sönderfallskurvan av två komponenter. Strax efter aktiveringen domineras sönderfallen av den kortlivade isotopen. Redan efter ett par minuter har denna kortlivade komponent avklingat och den mer långlivade isotopen dominerar fullständigt. Antal sonderfall per tidsenhet Sonderfall av silverisotoperna 108-Ag och 110-Ag Sonderfallskurva Kortlivad komponent Langlivad komponent Tid i minuter Figur 1: Exempel på antal sönderfall för aktiverat silver (heldragen linje) som funktion av tiden. Den prickade linjen anger sönderfallen som härstammar från den kortlivade isotopen och den streckade linjen kommer från den mer långlivade isotopen. I detta sammanhang bör nämnas att man kan visa att summan av två poissonfördelade variabler med medelvärde µ 1 resp. µ 2 också blir poissonfördelad med medelvärdet µ = µ 1 + µ 2, så även om vi som här har två olika populationer av sönderfallande kärnor med olika µ blir totala antalet sönderfall under en kort tidsrymd poissonfördelat. 6 Som ett minne av ditt experiment kommer dessa neutriner att i all framtid fortplanta sig rätlinjigt bort från jorden och ut i universum.

6 4 LABORATION 4: Radioaktivt sönderfall 3 Kärnfysikaliska instrument I denna laboration kommer du att använda elektronik som ofta används i kärnfysikaliska sammanhang. Vi kommer inte att gå igenom utrustningen i detalj utan nöjer oss här med att kort ange funktionen hos de olika delarna (se Fig. 2). Högspänningsmodul Klocka Förstärkare med diskriminator Räknare Spänningsförsörjning för elektroniken ON OFF HV GM Prep. dator Figur 2: Detektorhus med GM-rör och preparathållare. NIM-crate med strömförsörjning och högspänningsaggregat, förstärkare med inbyggd diskriminator, räknare och klocka. Vi har först en ihålig stålcylinder med en öppning och ett inbyggt Geiger-Müller (GM) rör. Röret drivs av högspänning och ger en signal då det träffas, t.ex. av en elektron från en sönderfallande silverkärna. Funktionen beskrivs mer ingående i avsnitt 3.1. Signalerna från GM-röret leds till en förstärkare med inbyggd diskriminator som dels genererar en analog, förstärkt kopia av den inkommande pulsen och dels en standardiserad digital puls om den förstärkta pulsen överskrider en vald tröskelnivå (diskriminatornivå). Tröskelnivån är satt så att man ska undvika att räkna störningar, dvs oönskade signaler. Den digitala pulsen är standardiserad och har en viss bestämd tidslängd och amplitud. Både den analoga och den digitala pulsen kan enkelt studeras med hjälp av ett oscilloskop 7. I denna laboration låter vi den digitala signalen, via en elektronisk anordning, gå vidare till en dator som möjliggör automatisk registrering av antalet digitala pulser från diskriminatorn i på varandra följande tidsintervall. Vi noterar att högspänningsmodulen och förstärkaren sitter monterade i en speciell låda, en s.k. NIM (Nuclear Instrument Modules) crate (sv. back, spjällåda) som ombesörjer strömförsörjningen till modulerna. Craten är uppdelad i 12 spår 7 I mån av tid kommer assistenten att demonstrera detta.

7 LABORATION 4: Radioaktivt sönderfall 5 (eng. slots) och modulerna upptar normalt ett eller två av dessa spår. Högspänningen genereras av en 2-spårsmodul i NIM-craten. Vi kan notera att i NIM-craten sitter ytterliggare två moduler, en räknare(scaler) och en klocka. Dessa används inte i denna laboration, utan antalet digitala pulser per inställt tidsintervall registreras i datorn GM-röret Det gasfyllda urladdningsröret (Geiger-Müller-röret) är en av de enklaste detektorerna för joniserande strålning 9. I Fig. 3 visas hur ett sådant urladdningsrör kan vara 3b 3a տ տ 2 R Förstärkare Högspänning Figur 3: Principskiss över mätning med GM-rör. uppbyggt. Som nämnts tidigare används i urladdningsrören strålningens förmåga att jonisera. Ett rör (höljet) av metall eller glas med metalliserad insida (1) fungerar som katod. Röret är fyllt av en gas med låg densitet. Längs dess axel är spänt en tunn tråd (2) som ges en hög positiv spänning i förhållande till katoden. Mellan tråden (anoden) och katoden uppstår då ett kraftigt elektriskt fält. Infallande joniserande strålning, t.ex. gammafotoner (3a) eller β-partiklar (3b) som sprids 10, åstadkommer par av positivt laddade gasjoner och elektroner (4) i 8 Räknaren och klockan kan användas för enklare mätningar t.ex. för bestämning av bakgrund. Den digitala pulsen leds i detta fall till räknaren som räknar upp ett minnesregister med en enhet varje gång en puls kommer in. Med hjälp av en display på räknaren kan innehållet i minnesregistret läsas av. Till räknaren kan man även ansluta klockan som gör att räknaren registrerar pulser under en viss bestämd tid. I mån av tid kan assistenten demonstrera dessa funktioner för den intresserade 9 Joniserande strålning är ett samlingsbegrepp på strålning som har förmågan att slå ut elektroner ur atomer, vilket förvandlar atomerna till joner. 10 Fotoner med energier över 10 5 ev brukar kallas gamma(fotoner) - jämför röntgenljus med energier mellan 100 och 10 5 ev. β-partiklar är vanliga elektroner (eller positroner). Beteckningarna α (heliumkärnor), β och γ är historiska och härrör från de tre olika sorternas strålning som utsänds av radioaktiva material.

8 6 LABORATION 4: Radioaktivt sönderfall gasen, och dessa accelereras av det elektriska fältet. De ger i sin tur ytterligare jonisation och en urladdning uppstår som innebär att en strömpuls passerar genom röret och resistorn (motståndet) R, och kan registreras som en positiv spänningspuls av förstärkaren (5). Vårt GM-rör är fyllt med argon, neon och några procent släckgas (halogener) som absorberar restelektroner efter att en urladdning ägt rum. Rörets räknehastighet beror av högspänningen. Vid låg spänning ger det nästan inga pulser alls och vid hög spänning kan det generera många oönskade pulser som inte utlöses av att röret träffas av strålning. För ett spänningsintervall mellan dessa lägen ger röret en signal då det träffas, och endast då. Sätts spänningen alltför högt kan röret urladdas kontinuerligt och eventuellt förstöras. I denna laboration skall du inte själv bestämma arbetsspänningen, du skall använda den spänning som redan är inställd. Ändra således inte på den förinställda högspänningen. Observera att GM-rörets fönster är av glimmer med en tjocklek på några tusendels mm och att det är mycket ömtåligt! Mer information om GM-rörets funktion finns i Appendix A. 4 Det experimentella utförandet Vi utsätts ständigt för en låg nivå av naturlig bakgrundsstrålning. Källan för denna strålning är radioaktiva atomkärnor (radionuklider) som skapas och sönderfaller i marken (t.ex. uran och radon från berggrunden) eller strålning av kosmiskt ursprung (myoner, elektroner och gamma-strålning). Denna bakgrundsstrålning kommer naturligtvis också att detekteras av vår apparatur. Det är därför nödvändigt att bestämma dess nivå så att den kan subtraheras från våra mätningar. Bakgrundsstrålningen skall mätas efter sönderfallsmätningen på silver. Det datorprogram som används i detta försök heter Tukan8k och dess funktioner beskrivs kortfattat i Appendix C. Bekanta dig med programmets inställningar och kontroller. Du ska göra en mätning på ett aktiverat silverbleck. Det kan vara bra att öva insättningen av silverblecket (med sin hållare) i stallet under GM-röret några gånger innan mätningarna börjar. För neutronaktiveringen av silverblecken används ett speciellt verktyg med vilket ett silverbleck kan placeras på lämpligt avstånd från neutronkällan 11. Se till att du har ett aktiverat preparat i beredskap i neutronbadet (aktiveringstid ca 15 minuter). Starta räknarprogrammet och välj 5 sekunders intervalltid och 30 minuters totaltid. Innan du sätter i silverblecket kommer bakgrund att registreras. Ta upp det aktiverade silverblecket ur neutronbadet och placera det på preparatspaden så 11 Neutronkällan sitter mitt i en öppen tank med vatten som absorbator (moderator) i preparatrummet.

9 LABORATION 4: Radioaktivt sönderfall 7 nära GM-röret som möjligt. Försök minimera tiden mellan det att blecket tas upp och att det placeras vid GM-röret. Räknarprogrammet fortsätter nu att registrera sönderfallen i silverblecket. När aktiviteten har skjunkit till bakgrundsnivån, tas silverblecket bort och du avslutar programmet. Glöm inte att spara och namnge datafilen - använd dataformatet.lst. Förbered för en ny mätning av enbart bakgrunden med tomt detektorhus men med spade och med öppningen försatt. Starta mätningen och låt den pågå i 6 minuter. 5 Mätvärdesbehandling 1. Rådata. Du har två filer med rådata, en med bakgrunds- och sönderfallsdata och en med bara bakgrundsdata. Det är viktigt att övertyga sig om att det datorprogram som används läser in datafilerna på rätt sätt. Om datafilen är utskriven med filformatet.lst finns två kolumner i varje datafil, den första anger intervallnummer och den andra antal sönderfall per tidsintervall. (Intervall-längden ska vara 5 s). Tänk igenom och notera noggrant vilka delar av sönderfallsdata som ska användas. Observera för filen som innehåller både bakgrunds- och sönderfallsdata att eftersom datatagningen sker kontinuerligt måste en del data tagas bort i skarven mellan bakgrundsnivån och den efterföljande sönderfallsmätningen, alltså från tiden behållaren öppnas och silverblecket sätts på plats. Den punkt som har den högsta räknehastigheten kan vara påverkad av detta och utesluts. Börja därför analysen av sönderfallsdata med den första punkten efter den med högsta räknehastigheten. De båda datafilerna med rådata ska sändas in tillsammans med laborationsrapporten för att den rättande läraren ska kunna kontrollera beräkningarna. 2. Beräkning av bakgrundsräknehastighet. Beräkna bakgrundsräknehastigheten (antalet registrerade händelser per sekund) från filen med enbart bakgrundsdata. Enklaste sättet att göra det är att helt enkelt addera alla bakgrundshändelser från mätningen och dividera med den sammanlagda tiden för bakgrundsmätningen. Beräkna också felet i bakgrundsmätningen, som blir poissonfelet för det totala antalet bakgrundshändelser dividerat med den sammanlagda tiden.

10 8 LABORATION 4: Radioaktivt sönderfall 3. Beräkning av räknehastighet för sönderfallsdata. Beräkna räknehastigheterna per sekund, n(t), för sönderfallsdata. Beräkna också motsvarande poissonfel σ n(t). Räknehastigheterna skall därefter korrigeras för bakgrunden, vilket ger en korrigerad räknehastighet n korr, med nya beräknade fel. Redovisa de formler du använder och redovisa de första fem tidsintervallenmedn korr ochσ nkorr ientabelltillhjälpfördenrättandeläraren. Tabellen ska också innehålla lnn korr med fel (se nästa punkt). 4. Anpassning av den långlivade isotopen. Den bakgrundskorrigerade räknehastigheten beskriver summan av aktiviteterna för den långlivade och den kortlivade silverisotopen (jfr Fig. 1): n korr (t) = n 1 (0)e λ 1t +n 2 (0)e λ 2t Här är n 1 (0) och n 2 (0) raknehastigheten för den långlivade, respektive kortlivade, isotopen vid t = 0. Redovisa ln(n korr ) med felstaplar som funktion av tiden i ett diagram. Eftersom den beräknade räknehastigheten är ett medelvärde av den verkliga räknehastigheten i varje tidsintervall bör man placera värdena i mitten av respektive tidsintervall, dvs första tidpunkten blir 2,5 sekunder, andra 7,5 sekunder osv. Punkterna i diagrammet beskriver nu sönderfallen av två isotoper med olika sönderfallskonstanter (man bör kunna se två distinkta, linjära förlopp i log-diagrammet). Du ska endast beräkna sönderfallskonstanten för den mer långlivade isotopen. Efter tillräckligt lång tid kan man bortse från aktiviteten från den kortlivade isotopen och man kan anta att n korr (t) n 1 (0) e λ 1t. Gör därför en linjär anpassning av ln(n korr ) som funktion av tiden (viktad minsta kvadratanpassning) till den del av kurvan som har högst tid, dvs uteslut de punkter vid lägre tider som synes avvika från den räta linjen. Ange i vilket intervall du utför anpassningen. Bestäm parametrarna λ 1 och n 1 (0) med fel för den långlivade isotopen (observera att den parameter som anpassasärlnn 1 (0)).Etttipsförattförenklaberäkningarnaärattskrivaekvationen ln(n korr ) = lnn 1 (0) λ 1 t som y = a + bt, anpassa parametrarna a och b till data och sedan beräkna de ursprungligen efterfrågade parametrarna med fel. Gör en figur som visar den anpassade räta linjen tillsammans med de punkter (med fel) som den anpassats till. Kontrollera att linjen verkligen ser ut som en anpassning till punkterna! 5. Beräkning av halveringstiden. Härled sambandet mellan sönderfallskonstant och halveringstid. Beräkna halveringstiderna (T 1/2 ) med osäkerhet för den långlivade isotopen och jämför med litteraturvärden. 6. χ 2 -test. Plotta de ursprungliga datapunkterna (inklusive bakgrunden), i linjär skala, med sina felstaplar. Plotta i samma diagram din kurva för antalet sönderfall

11 LABORATION 4: Radioaktivt sönderfall 9 per femsekundersintervall från anpassningen och bakgrundsberäkningen. Beräkna som ett mått på hur väl dina data ansluter sig till din anpassade modell en χ 2 - summa för anpassningen. Gör beräkningen av χ 2 -summan i det tidsintervall där du gjort anpassningen av den långlivade komponenten. Varje term i summan ska vara avvikelsen från modellen i kvadrat, delat med kvadraten på den förväntade spridningen enligt modellen, dvs. variansen. (Enligt modellen blir antalet pulser i ett femsekundersintervall poissonfördelat med ett medelvärde som ges av anpassningen och bakgrundsberäkningen.) Bestäm också det relevanta antalet frihetsgrader. Använd sedan octave-funktionen chi2cdf(chi2obs,ndof) för att bestämma p-värdet (chikvadratsannolikheten). Funktionen ger sannolikheten för ett värde mindre än chi2obs för Ndoffrihetsgrader(integralenavsannolikhetstäthetenfrånnolltillchi2obs) 12. Tänk igenom sambandet mellan den sannolikhet funktionen ger och p-värdet. Ofta anges χ 2, det reducerade chikvadratvärdet. Bestäm ditt χ 2 -värde, och notera att även små avvikelser från förväntansvärdet ett blir betydelsefulla för ett stort antal frihetsgrader (jämför med p-värdet du fick). 6 Redovisning Redovisningen ska vara väl strukturerad och lätt att följa. Den skall innehålla en kort inledning som beskriver syftet med experimentet och en kort sammanfattning av experimentuppställningen och utförandet av mätningarna. Du ska sedan tydligt redogöra för varje steg av databehandlingen och inkludera och förklara alla relevanta tabeller och diagram. De formler du använder ska också redovisas. Dina resultat ska redovisas och diskuteras. Glöm inte att alla tabeller och figurer ska vara numrerade och försedda med förklarande text. De ska också refereras till i den löpande texten. För att den rättande läraren skall kunna kontrollera dina beräkningar skall de båda datafilerna med rådata bifogas. Ange noga vilka delmängder av dessa data du använder, både för bakgrundsdelen och sönderfallsdelen. Det är också viktigt att alla siffror, tabeller och figurer som efterfrågas i avsnitt 5 finns med. 12 I appendix D finns en m-funktion som beräknar samma sak. Du kan utnyttja den om du använder något annat programmeringspaket som inte har funktionen chi2cdf, t.ex. MATLAB. I Taylor finns en tabell över sannolikheter för olika värden på den reducerade chikvadratsumman, men den täcker inte fall med tillräckligt stort antal frihetsgrader.

12 10 LABORATION 4: Radioaktivt sönderfall Appendix A GM-rörets funktion. När joniserande strålning tränger in i GM-röret uppstår en kort strömpuls. Pulsens storlek, som är proportionell mot antalet uppsamlade jonpar, beror av accelerationsspänningen. För låga spänningar växer pulshöjden med spänningen upp till en platå (rekombinationsområdet, område I i figur 3). Först vid platån räcker fältet till för att samla upp alla primära elektroner. Längs platån (område II) är uppsamlingen fullständig och röret fungerar som jonkammare. Vid något ökad spänning börjar stötjonisering förekomma. För måttliga spänningar är stötjonisationen linjär, dvs varje primär elektron ger upphov till ett visst antal enhetsladdningar på anoden. Pulsens storlek blir därför beroende av antalet primärelektroner, som i sin tur beror av strålningstyp (α eller β) och strålningens energi. Detektorn blir energiselekterande och kan fås att skilja på α och β strålning. Därvid fungerar den som en proportionalräknare (område III). Om spänningen ökas ytterligare sprids stötjonisationen längs anoden och pulsens storlek ökar kraftigt. Den inkommande partikelns jonisering fungerar som en startpuls för en jonisationslavin, vars storlek är helt oberoende av startpulsens storlek. Man förlorar energi- och partikelselekteringen, men får den fördelen att pulserna är lika stora och dessutom kraftiga, varför de blir lätta att hantera elektroniskt. Denna typ av urladdningsrör kallas Geiger- Müller-rör (område IV). I detta försök skall urladdningsröret operera i GM-området Antal uppsamlade jonpar N 2 N 1 I Rekombinationsområde II III Antal jonpar från en α-partikel Antal jonpar från en β-partikel Högspänning i volt. IV V Jonkammareområde Proportionalområde Geiger- Müllerområde Urladdningsområde Figur 4: Antalet uppsamlade jonpar som funktion av pålagd spänning.

13 LABORATION 4: Radioaktivt sönderfall 11 Appendix B Härledning av poissonfördelningen. Betrakta ett stort antal kärnor N som alla karakteriseras av sönderfallskonstanten λ. Sannolikheten för att ν givna kärnor sönderfaller under tiden t, medan övriga N ν inte gör det blir (λ t) ν (1 λ t) N ν. Sannolikheten för exakt ν sönderfall blir denna sannolikhet gånger antalet sätt som de ν kärnorna kan väljas. Detta antal ( sätt ges av binomialkoefficienten ( N P(ν) = ν eller P(ν) = ( N ν N ν ) ) (λ t) ν (1 λ t) N ν )(λ t) ν N ν k=0 ( N ν k N! ν!(n ν)!, och vi får: ) ( λ t) k Insättning av uttrycken för binomialkoefficienterna ger M P(ν) = (λ t)ν N! ( λ t) k ν! (N ν k)! k! k=0 Där vi infört hjälpvariabeln M som har värdet N ν. Totala antalet kärnor, N, är mycket större än antalet som sönderfaller under t, dvs vi är intresserade av approximationen N,M. Om vi först låter N med konstant M får vi P(ν) = (λ t)ν ν! M k=0 N ν+k( λ t)k k! Här ser det ut som om termerna blir oändliga pga faktor N ν+k, men detta beror på attn ärenapproximation,ochattn iverklighetenärändligt.detförväntade antalet sönderfall under t är µ = Nλ t som har ett ändligt och välbestämt värde. Då vi approximerar det mycket stora antalet atomer iprovet genom att låta N måste vi samtidigt låta λ t gå mot noll så att produkten µ behåller sitt värde. Om vi utnyttjar detta i uttrycket ovan får vi P(ν) = (Nλ t)ν ν! M ( Nλ t) k k=0 k! = µν ν! M ( µ) k dvs gränsövergången N ; M = konst ger ett väldefinierat resultat som är en ändlig summa av ändliga termer. Nu kan vi slutligen låta också M, vilket ger P(ν;µ) = µν ν! e µ Detta är uttrycket för poisson-sannolikheten för att observera ν sönderfall när medelvärdet av antalet sönderfall är µ. Det gäller alltså om man har ett mycket stort ( oändligt ) antal atomkärnor som var och en har en mycket ( oändligt ) liten sannolikhet att sönderfalla, eller mer allmänt om man har ett mycket stort antal möjligheter att att åstadkomma en händelse, men sannolikheten för att varje enskild möjlighet ger en händelse är mycket liten. k=0 k!

14 12 LABORATION 4: Radioaktivt sönderfall Appendix C Kort introduktion till Tukan8k (MCS-läge) Datainsamlings programmet som skall användas heter Tukan8k. Innan data insamlingen påbörjas bör ni kontrollera att inställningarna i programmet är korrekta. 1. Starta programmet Tips: Om muspekaren hålls stilla över en knapp så får du information om vad knappen gör. 2. Välj Hardware i listan till höger eller i menyn View Go to... Hardware 3. Kontrollera nu följande inställningar i listan mitt på skärmen: a) Mode of running: MCS Om programmet inte är i MCS läge välj Measurement Mode of running i menyn. Välj sedan MCS och OK. Kontrollera nu parametrarna nedan. b) Number of channels: 8192 c) Lower level threshold: < d) Upper level threshold: 7999 e) Dwell time: 5s f) Sweeps count: 1 g) Input signal gating: No gating h) Signal input: Analog (BNC) i) Triggering: Internal j) Advancing: Internal k) Multi-sweeps: No l) Accumulation: Summing m) Stop mode: After current channel update Om någon av parametrarna inte är korrekt inställda, välj Measurement Analyzer parameters i menyn. Därefter kan parametrarnas värden ändras. OBS! Det finns i vissa versioner av Tukan8k ett fel i denna ruta. Signal input (dvs. TTL eller BNC) visas inte korrekt! 4. Om alla värden är korrekt inställda är det dags att välja intervall längd och total mättid. Välj Measurements Analyzer parameters i menyn. Ange att intervall tiden Dwell time skall mätas i sekunder och sedan en lämplig tid. Total mättid

15 LABORATION 4: Radioaktivt sönderfall 13 anges som totalt antal intervall. OBS! Total mättid = (antal intervall) (intervall längd). Exempel: För att få 5 minuters total mättid med en intervall längd om 5 sekunder skall 60 intervall väljas, eftersom 60 5s = 300s. 5. Nu är Tukan8 korrekt inställt och datainsamlingen kan påbörjas. 6. Innan datainsamlingen påbörjas kan det vara bra att tänka på: (a) Tiden som har gått sedan mätningen på börjades visas på skärmen. OBS! X-axeln visar kanal nummer och inte sekunder. (b) Programmet visar alltid kanal 0 t.o.m. Kanal 8191 oavsett hur många kanaler ni har angett. Detta innebär att det kan vara svårt att se era mätdata under mätningen. För att komma till rätta med detta kan ni (före ellerundermätningen)väljascreen Set markersimenyn.härfyllerni i 0 och sedan det antal kanaler ni har valt. Tryck OK, välj sedan Screen Expand on Spectrum i menyn och nu förstoras den intressanta området upp. (I menyn och knapparna där under kan användas för att välja vad som skall visas, t.ex. kan y-axeln visas med logaritmisk skala, Screen Logaritmic scale). Starta datainsamling En datainsamling startas genom att välja Measurement Start (alternativt trycka på GRÖN knapp i raden under menyn). Stoppa datainsamling En datainsamling avbryts/stoppas genom att välja Measurement Stop (alternativt trycka på RÖD knapp i raden under menyn). Förbereda ny datainsamling (rensa gamla mätdata) För att rensa en gammal datainsamling och göra programmet klart för att samla in en ny mätserie välj Measurement Reset (alternativt trycka på VIT knapp i raden under menyn). Spara mätdata När en mätning är klar skall mätdatan sparas. Välj File Export ASCII i menyn. Här finns det tre filformat att välja på (i samtliga fall blir resultatet en text fil):.lst.dat.tab två kolumner, första kolumnen är kanal nummer, andra kolumnen är mätdata en kolumn, bara mätdata en tabell med enbart mätdata Välj det som passar dig bäst, är du osäker välj.lst-format. (Dessa filer kan läsas in i t.ex. Excel eller Octave.)

16 14 LABORATION 4: Radioaktivt sönderfall Appendix D m-funktion för att integrera chikvadratfördelningen % Function to return the integral of the chi2-distribution from % zero to chi2obs for Ndof degrees of freedom. % % Approximates the chi2-value corresponding to the same integrated % probability as a value z sigmas above the mean in the case of % a normal distribution by % % (1-2/(9*Ndof) - z*sqrt(2/(9*ndof)))^3 % % This approximation is only valid for large Ndof % SH/KH function [q]=chi2integral(chi2obs,ndof) if(ndof < 40) disp( chi2integral approximation not valid for less than 40 DOF! ) q=nan; return end z = ((chi2obs/ndof)^(1/3) /(9*Ndof))*sqrt(4.5*Ndof); q = (1+erf(z/sqrt(2)))/2; return