Ljusets diffraktion (180308)
|
|
|
- Ulrika Viklund
- för 6 år sedan
- Visningar:
Transkript
1 Ljusets diffraktion (180308) Innehåll Inledning Inledning... 1 Litteraturhänvisning... 1 Förberedelseuppgifter... 1 Utförande Diffraktionsexperiment med laserljus... 3 Experiment med gitterspektroskop... 4 Diffraktion i N spalter... 5 Appendix 1: Spektroskopet och dess injustering... 7 Appendix : Fraunhoferdiffraktion i ett system av spalter... 8 Fenomenen interferens och diffraktion - som kommer från superpositionsprincipen - är det som verkligen utmärker en vågrörelse. Fysikaliskt behövs inte två olika begrepp, eftersom allt fundamentalt handlar om interferens. Men av tradition brukar man använda ordet interferens när det är två eller ett litet antal vågor som möts i en punkt (t.ex. två-stråleinterferens i tunna skikt) och diffraktion när det är (oändligt) många vågor. Man säger också allmänt att diffraktion är det fenomen som uppstår när en vågfront delvis blockeras av ett hinder, t.ex. när en ljudvåg passerar ett träd eller när en spegel/lins med viss diameter samlar upp en mycket liten del av ljuset från en avlägsen stjärna. I den teoretiska beskrivningen av diffraktion skiljer man på två fall. I det allmänna fallet, som kallas Fresneldiffraktion, tar man hänsyn till att vågfronterna både före och efter aperturen är krökta. I många praktiska situationer kan man emellertid med god approximation anse att vågfronterna är plana (eller, som man också säger, att strålarna är parallella). Detta fall är betydligt enklare att hantera matematiskt och leder till modellen Fraunhoferdiffraktion. Det är viktigt att notera att plana fronter kan uppnås dels approximativt, genom att avstånden från källan till hindret och sedan till betraktelsepunkten är stort, och dels exakt genom att använda avbildande optik. I denna laboration kommer du att studera diffraktionsmönster från en mängd olika aperturer både experimentellt och teoretiskt. En detaljerad laborationsredogörelse är särskilt motiverad i detta fall för att visa att du kan knyta ihop teorin och experimenten. VARNING: Titta aldrig på laserstrålen eller dess reflexer. Litteraturhänvisning Physics for scientists and engineers (sixed edition), Kap 33. Observera att boken inte behandlar det allmänna diffraktionsmönstret från ett system av N spalter utan bara t.ex. specialfallet med två spalter i ekv 33- eller fem spalter i exempel Det allmänna fallet diskuteras i Appendix. Laborationsinstruktioner För E1 1
2 Förberedelseuppgifter Använd länken nedan för att svara på förberedelseuppgifterna. Skriv ut, eller spara i mobilen, dina godkända svar för att visa för handledaren vid laborationens början. Laborationsinstruktioner För E1
3 1. Diffraktionsexperiment med laserljus 1.1 Fraunhoferdiffraktion Eftersom laserljuset består av plana vågfronter kan det användas direkt för att studera Fraunhoferdiffraktion bara diffraktionsmönstret betraktas på en tillräckligt avlägsen skärm. a) Enkelspalt Använd en ställbar spalt och jämför med teorin. Ändras diffraktionsmönstret kvalitativt enligt teorin när spaltvidden ändras? Bestäm spaltvidden för en given spalt, som handledaren delar ut, genom att mäta avstånd i diffraktionsmönstret på skärmen. Gör en enkel feluppskattning av ditt resultat. Vilken är den mest osäkra variabeln? b) Cirkulärt hål Skriv upp den relevanta teoretiska formeln. Jämför mönstret med det från enkelspalten! Använd diffraktionsmönstret för att bestämma ett håls storlek. c) Rektangulärt hål Tag en platta med rektangulärt hål och observera diffraktionsmönstret. Ser du något samband med enkelspaltens diffraktionsmönster? d) Transmissionsgitter Studera kvalitativt några olika gitters diffraktionsmönster. Placera flera gitter efter varandra med ritsorna i olika vinklar. Kan du ange någon enkel princip för det resulterande mönstret? 1. Fresneldiffraktion Detta fall kan enkelt erhållas från föregående uppställning genom att placera en negativ lins mellan lasern och objektet så att vågfronten blir tillräckligt krökt. Fresneldiffraktion är mycket svårare att hantera teoretiskt så vi ska bara kvalitativt titta på några intressanta observationer. a) Cirkulärt hål Använd en irisbländare, variera hålets diameter och observera vad som händer i centrum. b) Cirkulär skiva (kula) Använd en liten kula som hinder och studera diffraktionsmönstret noga. Hur ser det ut i centrum? Laborationsinstruktioner För E1 3
4 . Experiment med gitterspektroskop Injustering Se Appendix 1. Behöver normalt inte göras! Kvalitativt På detta laborationsmoment får du se ett "primitivt" instrument som på enklast möjliga sätt visar principerna för detektion och våglängdsanalys av spektra. Gör du ett bra jobb kommer du ändå att mäta våglängder med bättre än 1 % noggrannhet! I nästa läsperiod får du sedan göra en spektroskopilaboration där du kommer att använda ett modernt och kraftfullt gitterinstrument, men som naturligtvis bygger på samma principer. Belys kollimatorspalten med en spektrallampa och använd ett glest ritsat gitter, med 100 spalter per mm. Titta på den färggranna bilden och försök förklara hur den uppstår. Varför talar man om spektrallinjer och inte t.ex. spektralcirklar eller andra former? Notera att det finns ett spektrum på varje sida om normalen till gitterytan, d.v.s. på varje sida om nollte ordningen. Notera också att för stora diffraktionsvinklar finns det ett överlapp mellan ljus från olika ordningar. Våglängdsbestämning Kvantitativa våglängdsbestämningar görs med hjälp av den s.k. gitterformeln (Appendix ) som säger att maximum för en given våglängd,, och ordning, m, inträffar i en vinkel,, där: asin( ) m Där a är den s.k. gitterkonstanten, d.v.s. avståndet mellan två närliggande spalter. I vårt fall blir a = 1/100 mm. Mät upp vinkeln mellan linjen för nollte ordningen och varje synlig spektrallinje i ordning 1 respektive 4. Beräkna våglängden för varje spektrallinje och identifiera vilket atomslag lampan innehåller genom att jämföra med tabell (t.ex. från TeFyMa). Beräkna avvikelsen i våglängd från tabellvärden och jämför storleken på våglängdsavvikelsen i ordning 1 med ordning 4. Förklara skillnaden. 4 Laborationsinstruktioner För E1
5 3. Diffraktion i N spalter Figur 1. Uppställning för N-spaltsdiffraktion Förberedelse. Diffraktionsobjektet är en glasskiva med fyra objekt som var och ett består av ett antal (N) smala spalter med bredden b och separerade med avståndet a. Flytta glasskivan i sidled så att bägge laserstålarna passerar ett av objekten. Justera vid behov in lasrarna i höjdled så att de bägge mönstren är tydligt separerade på mattglasskivan. Mät avståndet från objektet till glasskärmen. Logga in med din STIL-identitet på datorn. Mappen Nspalt dyker upp på skrivbordet och innehåller länkar till två program: Debut för att se och fånga bilden från kameran samt Nspalt för att simulera diffraktionsmönstret från N spalter enligt Appendix. Registrera diffraktionsmönstret Starta Debutprogrammet, välj "Device" som inputkälla och gå över till "full screen mode" (viktigt!) antingen genom att högerklicka i bilden eller via menyn "View" Ställ in bländaren och fokus på kamera så att du får en skarp bild av linjalen och en bild av den röda lasern som inte är överexponerad. Mät bildens storlek med hjälp av den fasta linjalen på glasskärmen Minimera ströljus genom att släcka alla lampor. Fånga en bild genom att trycka på tangenten "Print Scr". Skärmbilden sparas då som en bitmapbild i datorns klippbord. Analys av diffraktionsmönstret Starta programmet Nspalt och läs in den fångade bilden med menyn Fil / Klistra in bitmap bild (paste) Välj ut mönstret från den röda lasern enligt instruktionen i programmet. Nspalt skapar en intensitetsprofil av det valda tvådimensionella mönstret genom att summera intensiteten i vertikalled. Öppna dialogen N-spalts modellen Ge de data för avbildningen som programmet behöver för att omvandla diffraktionsvinkeln θ till avstånd längs skärmen. Data sparas tills du avslutar Nspalt. Laborationsinstruktioner För E1 5
6 Simulera diffraktionsmönstret genom att ange spaltdata i dialogen. Den röda lasern har våglängen 63,8 nm. OBS, försök tänka igenom vad som ska hända innan du prövar med olika värden så att du testar din förståelse av diffraktionsproblemet snarare än hur snabbt du kan skriva in olika värden! När du har hittat bra spaltdata kan du välja att också visa "diffraktions faktorn" och "interferens faktorn" i samma bild för att tydligt se hur det totala (observerbara) mönstret uppkommer. Om du stänger dialogen kan du med hjälp av menyn Fil / Spara som bitmap spara skärmbilden till en fil för att använda i din rapport Upprepa för alla 4 spaltsystemen Välj systemet med flest antal spalter, registrera mönstret från den gröna lasern och bestäm dess våglängd. Om du hinner kan du ersätta spaltsystemen med ett litet hål och studera mönstret på samma sätt som ovan, men nu med dialogen "Cirkulär apertur" i stället. Vid cirkulär symmetri ersätts sinusfunktionen i enkelspaltmönstret med en Besselfunktion (J 1 (x)). Jämför med uppgift 1.1b ovan och notera den stora skillnaden mellan att visuellt betrakta mönstret, med ögats logaritmiska känslighet, och att mäta fotoelektriskt med en linjär känslighet. 6 Laborationsinstruktioner För E1
7 Appendix 1: Spektroskopet och dess injustering Figur A1-1. Principskiss av spektroskopet. Kollimatorns uppgift är att se till att parallellt ljus (d.v.s. plana vågor) från ingångsspalten träffar transmissionsgittret. Kikarens uppgift är att fokusera parallellt ljus från gittret på ett hårkors, belyst av en liten lampa, så att man i okularet samtidigt ser hårkorset och ett spektrum skarpt. Kikaren är vridbar så att olika delar av diffraktionsmönstret kan betraktas. Vridningen kan mätas på en noggrann vinkelskala. Observera att skalan är graderad i grader och minuter (1' = 1/60 grad). För att bestämma våglängder via vinkelmätningen ställer du först in hårkorset på nollte ordningens spektrallinje (alternativt kan du justera in skalan så att den verkligen visar 0 här) och sedan mäter du diffraktionsvinkeln för de olika spektrallinjerna i de olika ordningarna. Innan du börjar är det tre inställningsmoment som du måste genomföra. Ställ in kikaren för parallella strålar. Tag ut kikaren ur dess fattning. Förskjut okularet tills hårkorset syns skarpt med avslappnat öga. Vrid kikarens fokuseringsratt tills du ser ett mycket avlägset föremål skarpt, dvs. så att mellanbilden faller på hårkorset och båda syns skarpt. Sätt tillbaka kikaren i dess fattning. Den bör nu vara inställd för parallella infallande strålar och skall inte justeras ytterligare. Ställ in kollimatorn för parallella strålar. Ställ kikaren och kollimatorn i linje med varandra. Gör kollimatorspaltens öppning mycket liten. Vrid kollimatorns fokuseringsratt tills du i kikaren ser bilden av kollimatorspalten skarpt i hårkorsets plan. Eftersom kikaren redan var inställd för parallella strålar, så måste detta innebära att kollimatorn nu ger parallellt ljust. Kollimatorspaltens öppning. Då du tittar på ett spektrum kan du lägga märke till att en minskning av kollimatorspalten vidd ger bilden större skärpa men mindre ljus. Speciellt orsakar en alltför stor öppning att detaljer i spektret helt suddas ut. Det gäller alltså att optimera kollimatorspaltens vidd. Laborationsinstruktioner För E1 7
8 Appendix : Fraunhoferdiffraktion i system av spalter Ljusintensiteten som funktion av utträdesvinkeln för ett system av N spalter i Fraunhoferfallet, dvs. med parallella strålar ges av: sin sin N I I( 0) N sin 1 med kbsin och 1 kasin där I(0) = den observerade intensiteten i centrum av mönstret ( = 0). b = spaltvidden a = spaltavstånd (från mitt till mitt) N = antalet spalter k = / Specialfall: sin N 1: I I(0) sin sin sin N : I I(0) I(0) cos sin Diffraktionsmönstret är alltså en produkt av två faktorer. Det är mycket instruktivt att diskutera dessa faktorer var för sig. (sin / ) kan vi kalla enkelspaltfaktorn eftersom den är identisk med resultatet från en ensam spalt. (sin( N) / Nsin ) kan vi kalla interferensfaktorn eftersom den beskriver hur ljus från olika spalter interfererar. Se Figur A-1. Observera att vi dividerat med N innanför parentesen för att få en faktor som antar värden mellan 0 och 1. Det faktum att intensiteten i maxpunkterna ökar med antalet spalter tar vi hand om genom att normera med I(0) som ges av I 0 N där I 0 är bidraget från en ensam spalt. Huvudmaxima (eng. principal maxima) i Figur A-1 uppstår då = m (m = 0, 1,,...) varvid interferensfaktorn har gränsvärdet 1. För att se detta för = 0 gör vi en McLaurinutveckling: sin( N) 1 N ( N)... 1 ( N) när Nsin N Härur följer den s.k. gitterformeln som säger att maximum för en given våglängd inträffar när: 1 m asin m a sin m Vi ser också att intensiteten avtar från maxvärdet till noll då / N dvs att bredden av ett huvudmaximum (/N) minskar ju fler spalter vi har. Vi kan sammanfatta med att säga att ju fler spalter desto högre och smalare blir topparna. 8 Laborationsinstruktioner För E1
9 Bimaxima (eng. secondary maxima) uppstår då täljaren sin(n) = 1 och sin 0. Som framgår av Figur A-1 finns det N - st bimax mellan två huvudmaximum. Om vi studerar de olika fallen i Figur A-1 ser vi också att den relativa intensiteten i bimaxima minskar när N ökar. N = 50 N = 10 N = 5 N = / grader Figur A-1. Interferensfaktorn för ett system med 3, 5, 10 och 50 spalter. När vi har väldigt många spalter talar vi om ett gitter. För gitter brukar man ange antalet ritsor (spalter) per mm. Vanliga värden är 600 eller 100 per mm, vilket innebär att avståndet mellan ritsorna - den s.k. gitterkonstanten a - blir 1666 eller 833 nm. Om gittret är ca 10 cm brett finns det då totalt ca 10 5 spalter. I Figur A- illustreras hur det observerbara mönstret uppstår som en produkt av enkelspaltfaktorn och interferensfaktorn Relativ intensitet / grader Figur A-. Diffraktion i 5 spalter. I figuren visas enkelspaltfaktorn (blå), interferensfaktorn (röd)och produkten (svart) för a = 0 m och b = 10 m. Laborationsinstruktioner För E1 9
Ljusets diffraktion (170310)
 Ljusets diffraktion (170310) Innehåll Inledning Inledning... 1 Litteraturhänvisning... 1 Förberedelseuppgifter... 1 Utförande Diffraktionsexperiment med laserljus... 3 Experiment med gitterspektroskop...
Ljusets diffraktion (170310) Innehåll Inledning Inledning... 1 Litteraturhänvisning... 1 Förberedelseuppgifter... 1 Utförande Diffraktionsexperiment med laserljus... 3 Experiment med gitterspektroskop...
Ljusets böjning och interferens
 Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen ska du studera två centrala vågfenomen: interferens och böjning. Du kommer bl.a. att studera hur ljusvågor böjs när de passerar
Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen ska du studera två centrala vågfenomen: interferens och böjning. Du kommer bl.a. att studera hur ljusvågor böjs när de passerar
Ljudhastighet (vätska & gas) RT v M Intensitet från en punktkälla P I medel 2 4 r Ljudintensitetsnivå I 12 2 LI 10lg med Io 1,0 10 W/m Io Dopplereffek
 Ljudhastighet (vätska & gas) RT v M Intensitet från en punktkälla P I medel 4 r Ljudintensitetsnivå I 1 LI 10lg med Io 1,0 10 W/m Io Dopplereffekt, ljud v v f m m fs v v s Relativistisk Dopplereffekt,
Ljudhastighet (vätska & gas) RT v M Intensitet från en punktkälla P I medel 4 r Ljudintensitetsnivå I 1 LI 10lg med Io 1,0 10 W/m Io Dopplereffekt, ljud v v f m m fs v v s Relativistisk Dopplereffekt,
Ljusets böjning & interferens
 ... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Ljusets böjning & interferens Ljusets vågegenskaper Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen ska
... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Ljusets böjning & interferens Ljusets vågegenskaper Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen ska
Ljusets böjning & interferens
 Ljusets böjning & interferens Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter 3 Appendix Ljusets vågegenskaper Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen
Ljusets böjning & interferens Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter 3 Appendix Ljusets vågegenskaper Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen
Diffraktion och interferens
 Institutionen för Fysik 005-10-17 Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det
Institutionen för Fysik 005-10-17 Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det
Ljusets böjning & interferens
 ... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Ljusets böjning & interferens Ljusets vågegenskaper Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen ska
... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Ljusets böjning & interferens Ljusets vågegenskaper Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen ska
Fysik. Laboration 3. Ljusets vågnatur
 Fysik Laboration 3 Ljusets vågnatur Laborationens syfte: att hjälpa dig att förstå ljusfenomen diffraktion och interferens och att förstå hur olika typer av spektra uppstår Utförande: laborationen skall
Fysik Laboration 3 Ljusets vågnatur Laborationens syfte: att hjälpa dig att förstå ljusfenomen diffraktion och interferens och att förstå hur olika typer av spektra uppstår Utförande: laborationen skall
Diffraktion och interferens
 Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det är just detta fenomen som gör att
Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det är just detta fenomen som gör att
Vinkelupplösning, exempel hålkameran. Vinkelupplösning När är två punkter upplösta? FAF260. Lars Rippe, Atomfysik/LTH 1. Böjning i en spalt
 Kursavsnitt Böjning och interferens Böjning i en spalt bsin m m 1,... 8 9 Böjning i en spalt Böjning i cirkulär öppning med diameter D Böjningsminimum då =m Första min: Dsin 1. 10 11 Vinkelupplösning,
Kursavsnitt Böjning och interferens Böjning i en spalt bsin m m 1,... 8 9 Böjning i en spalt Böjning i cirkulär öppning med diameter D Böjningsminimum då =m Första min: Dsin 1. 10 11 Vinkelupplösning,
Vinkelupplösning, exempel hålkameran. Vinkelupplösning När är två punkter upplösta? FAF260. Lars Rippe, Atomfysik/LTH 1. Böjning i en spalt
 Kursavsnitt Böjning och interferens Böjning i en spalt bsin m m 1,... 8 9 Böjning i en spalt Böjning i cirkulär öppning med diameter D Böjningsminimum då =m Första min: Dsin 1. 10 11 Vinkelupplösning,
Kursavsnitt Böjning och interferens Böjning i en spalt bsin m m 1,... 8 9 Böjning i en spalt Böjning i cirkulär öppning med diameter D Böjningsminimum då =m Första min: Dsin 1. 10 11 Vinkelupplösning,
Diffraktion och interferens
 Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det är just detta fenomen som gör att
Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det är just detta fenomen som gör att
Diffraktion och interferens
 Diffraktion och interferens Laboration i kursen Syfte Laborationen ska ge förståelse för begreppen interferens och diffraktion och hur de karaktäriseras genom experiment. Vidare visar laborationen exempel
Diffraktion och interferens Laboration i kursen Syfte Laborationen ska ge förståelse för begreppen interferens och diffraktion och hur de karaktäriseras genom experiment. Vidare visar laborationen exempel
Interferens och diffraktion
 Laborationsinstruktion Vågrörelselära Interferens och diffraktion VT07 Stockholms Universitet Innehåll Uppgift 1 Diffraktionsförsök med laserljus Uppgift 2 Mäta våglängden med linjal Uppgift 3 Gittrets
Laborationsinstruktion Vågrörelselära Interferens och diffraktion VT07 Stockholms Universitet Innehåll Uppgift 1 Diffraktionsförsök med laserljus Uppgift 2 Mäta våglängden med linjal Uppgift 3 Gittrets
1. Betrakta en plan harmonisk elektromagnetisk våg i vakuum där det elektriska fältet E uttrycks på följande sätt (i SI-enheter):
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Måndagen den 5 maj 2008 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare.
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Måndagen den 5 maj 2008 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare.
Kapitel 36, diffraktion
 Kapitel 36, diffraktion Diffraktionsbegreppet, en variant av interferens Hitta min värden för enkelspalt med vidden a Intensitet för enkelspalt med vidden a Två spalter med vidd a och separation d Många
Kapitel 36, diffraktion Diffraktionsbegreppet, en variant av interferens Hitta min värden för enkelspalt med vidden a Intensitet för enkelspalt med vidden a Två spalter med vidd a och separation d Många
Diffraktion... Diffraktion (Kap. 36) Diffraktion... Enkel spalt. Parallellt monokromatiskt ljus gör att skuggan av rakbladet uppvisar en bandstruktur.
 Diffraktion (Kap. 36) Diffraktion... Fjärilens (Blå Morpho) vingar har en ytstruktur som gör att endast vissa färger (blå) blir synligt under vissa vinklar genom diffraktionseffekter: idag försöker forskare
Diffraktion (Kap. 36) Diffraktion... Fjärilens (Blå Morpho) vingar har en ytstruktur som gör att endast vissa färger (blå) blir synligt under vissa vinklar genom diffraktionseffekter: idag försöker forskare
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi
 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 36-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik Kapitel 36-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Geometrisk optik. Syfte och mål. Innehåll. Utrustning. Institutionen för Fysik 2006-04-25
 Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
5. Elektromagnetiska vågor - interferens
 Interferens i dubbelspalt A λ/2 λ/2 Dal för ena vågen möter topp för den andra och vice versa => mörkt (amplitud = 0). Dal möter dal och topp möter topp => ljust (stor amplitud). B λ/2 Fig. 5.1 För ljusvågor
Interferens i dubbelspalt A λ/2 λ/2 Dal för ena vågen möter topp för den andra och vice versa => mörkt (amplitud = 0). Dal möter dal och topp möter topp => ljust (stor amplitud). B λ/2 Fig. 5.1 För ljusvågor
Laboration 1 Fysik
 Laboration 1 Fysik 2 2015 : Fysik 2 för tekniskt/naturvetenskapligt basår Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen på
Laboration 1 Fysik 2 2015 : Fysik 2 för tekniskt/naturvetenskapligt basår Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen på
Interferens och diffraktion
 Laborationsinstruktion Vågrörelselära Interferens och diffraktion VT11 Stockholms Universitet Innehåll Uppgift 1 Diffraktionsförsök med laserljus Uppgift Mäta våglängden med linjal Uppgift 3 Luftens brytningsindex
Laborationsinstruktion Vågrörelselära Interferens och diffraktion VT11 Stockholms Universitet Innehåll Uppgift 1 Diffraktionsförsök med laserljus Uppgift Mäta våglängden med linjal Uppgift 3 Luftens brytningsindex
Böjning. Tillämpad vågrörelselära. Föreläsningar. Vad är optik? Huygens princip. Böjning vs. interferens FAF260. Lars Rippe, Atomfysik/LTH 1
 Tillämpad vågrörelselära 2 Föreläsningar Vad är optik? F10 och upplösning (kap 16) F11 Interferens och böjning (kap 17) F12 Multipelinterferens (kap 18) F13 Polariserat ljus (kap 20) F14 Reserv / Repetition
Tillämpad vågrörelselära 2 Föreläsningar Vad är optik? F10 och upplösning (kap 16) F11 Interferens och böjning (kap 17) F12 Multipelinterferens (kap 18) F13 Polariserat ljus (kap 20) F14 Reserv / Repetition
Gauss Linsformel (härledning)
 α α β β S S h h f f ' ' S h S h f S h f h ' ' S S h h ' ' f f S h h ' ' 1 ' ' ' f S f f S S S ' 1 1 1 S f S f S S 1 ' 1 1 Gauss Linsformel (härledning) Avbilding med lins a f f b Gauss linsformel: 1 a
α α β β S S h h f f ' ' S h S h f S h f h ' ' S S h h ' ' f f S h h ' ' 1 ' ' ' f S f f S S S ' 1 1 1 S f S f S S 1 ' 1 1 Gauss Linsformel (härledning) Avbilding med lins a f f b Gauss linsformel: 1 a
λ = T 2 g/(2π) 250/6 40 m
 Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
(ii) Beräkna sidoförskjutningen d mellan in- och utgående strålar, uttryckt i vinklarna θ i och tjocklekar t i. (2p)
 Tentamen i Vågrörelselära(FK49) Datum: Onsdag, 4 Augusti,, Tid: 9: - 4: Tillåten Hjälp: Physics handbook eller dylikt och miniräknare Förklara resonemang och uträkningar klart och tydligt. Tentamensskrivningen
Tentamen i Vågrörelselära(FK49) Datum: Onsdag, 4 Augusti,, Tid: 9: - 4: Tillåten Hjälp: Physics handbook eller dylikt och miniräknare Förklara resonemang och uträkningar klart och tydligt. Tentamensskrivningen
Ljudets och ljusets böjning och interferens
 1 Föreredelser Läs i vågläraoken om ljudreflektioner i ett rum (sid 138-140), öjning i en spalt (sid 325-329), öjning i en cirkulär öppning och Bainets princip (sid 329-332), Youngs duelspaltförsök (sid
1 Föreredelser Läs i vågläraoken om ljudreflektioner i ett rum (sid 138-140), öjning i en spalt (sid 325-329), öjning i en cirkulär öppning och Bainets princip (sid 329-332), Youngs duelspaltförsök (sid
Fysik (TFYA14) Fö 5 1. Fö 5
 Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
Tentamen i Fotonik - 2015-08-21, kl. 08.00-13.00
 Tentamen i Fotonik - 2015-08-21, kl. 08.00-13.00 Tentamen i Fotonik 2011 08 25, kl. 08.00 13.00 FAFF25-2015-08-21 FAFF25 2011 08 25 FAFF25 2011 08 25 FAFF25 FAFF25 - Tentamen Fysik för Fysik C och i för
Tentamen i Fotonik - 2015-08-21, kl. 08.00-13.00 Tentamen i Fotonik 2011 08 25, kl. 08.00 13.00 FAFF25-2015-08-21 FAFF25 2011 08 25 FAFF25 2011 08 25 FAFF25 FAFF25 - Tentamen Fysik för Fysik C och i för
Laboration i Geometrisk Optik
 Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson) Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen
Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson) Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen
Geometrisk optik. Laboration
 ... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Geometrisk optik Linser och optiska instrument Avsikten med laborationen är att du ska få träning i att bygga upp avbildande optiska
... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Geometrisk optik Linser och optiska instrument Avsikten med laborationen är att du ska få träning i att bygga upp avbildande optiska
Tentamen i Våglära och optik för F
 Tentamen i Våglära och optik för F FAFF30, 2013 06 03 Skrivtid 8.00 13.00 Hjälpmedel: Läroboken och miniräknare Uppgifterna är inte sorterade i svårighetsgrad Börja varje ny uppgift på ett nytt blad och
Tentamen i Våglära och optik för F FAFF30, 2013 06 03 Skrivtid 8.00 13.00 Hjälpmedel: Läroboken och miniräknare Uppgifterna är inte sorterade i svårighetsgrad Börja varje ny uppgift på ett nytt blad och
FAFF Johan Mauritsson 1. Föreläsningar. Våglära och optik. Världens minsta film. Projekten
 Våglära och optik FAFF30 JOHAN MAURITSSON Föreläsningar F10 Fraunhoferdiffraktion F11 Diffraktionsgitter F12 Fresneldiffraktion F13 Matrisrepresentation av polariserat ljus F14 Polariserat ljus F15 Repetition
Våglära och optik FAFF30 JOHAN MAURITSSON Föreläsningar F10 Fraunhoferdiffraktion F11 Diffraktionsgitter F12 Fresneldiffraktion F13 Matrisrepresentation av polariserat ljus F14 Polariserat ljus F15 Repetition
Elektromagnetiska vågor (Ljus)
 Föreläsning 4-5 Elektromagnetiska vågor (Ljus) Ljus kan beskrivas som bestående av elektromagnetiska vågrörelser, d.v.s. ett tids- och rumsvarierande elektriskt och magnetiskt fält. Dessa ljusvågor följer
Föreläsning 4-5 Elektromagnetiska vågor (Ljus) Ljus kan beskrivas som bestående av elektromagnetiska vågrörelser, d.v.s. ett tids- och rumsvarierande elektriskt och magnetiskt fält. Dessa ljusvågor följer
Interferens och diffraktion
 Laborationsinstruktion Vågrörelselära Interferens och diffraktion v.2.1 VT05 Figur 0 : Bilden visar diffraktion i en spektrometer pga den begränsande apperturen med diametern a. [från Demtröder] Denna
Laborationsinstruktion Vågrörelselära Interferens och diffraktion v.2.1 VT05 Figur 0 : Bilden visar diffraktion i en spektrometer pga den begränsande apperturen med diametern a. [från Demtröder] Denna
Linnéuniversitetet. Naturvetenskapligt basår. Laborationsinstruktion 1 Kaströrelse och rörelsemängd
 Linnéuniversitetet VT2013 Institutionen för datavetenskap, fysik och matematik Program: Kurs: Naturvetenskapligt basår Fysik B Laborationsinstruktion 1 Kaströrelse och rörelsemängd Uppgift: Att bestämma
Linnéuniversitetet VT2013 Institutionen för datavetenskap, fysik och matematik Program: Kurs: Naturvetenskapligt basår Fysik B Laborationsinstruktion 1 Kaströrelse och rörelsemängd Uppgift: Att bestämma
Presentationsmaterial Ljus som vågrörelse - Fysik B. Interferens i dubbelspalt gitter tunna skikt
 Presentationsmaterial Ljus som vågrörelse - Fysik B Interferens i ubbelspalt gitter tunna skikt Syfte och omfattning Detta material behanlar på intet sätt fullstänigt såant som kan ingå i avsnitt me innebören
Presentationsmaterial Ljus som vågrörelse - Fysik B Interferens i ubbelspalt gitter tunna skikt Syfte och omfattning Detta material behanlar på intet sätt fullstänigt såant som kan ingå i avsnitt me innebören
E-I Sida 1 av 6. Diffraktion på grund av spiralstruktur (Total poäng: 10)
 Sida 1 av 6 Diffraktion på grund av spiralstruktur (Total poäng: 10) Inledning Röntgendiffraktionsbilden för DNA (Fig. 1), som togs i Rosalind Franklins laboratorium och blev känd som Photo 51, lade grunden
Sida 1 av 6 Diffraktion på grund av spiralstruktur (Total poäng: 10) Inledning Röntgendiffraktionsbilden för DNA (Fig. 1), som togs i Rosalind Franklins laboratorium och blev känd som Photo 51, lade grunden
Geometrisk optik. Innehåll. Inledning. Litteraturhänvisning. Förberedelseuppgifter. Geometrisk optik
 Geometrisk optik Innehåll Inledning... 1 Litteraturhänvisning... 1 Förberedelseuppgifter... 1 Utförande 1. Undersökning av tunna positiva linser... 3 2. Undersökning av tunna negativa linser... 3 3. Galileikikaren...
Geometrisk optik Innehåll Inledning... 1 Litteraturhänvisning... 1 Förberedelseuppgifter... 1 Utförande 1. Undersökning av tunna positiva linser... 3 2. Undersökning av tunna negativa linser... 3 3. Galileikikaren...
Förklara dessa begrepp: Ackommodera Avbildning, Brytning Brytningslagen Brytningsindex Brytningsvinkel Brännvidd Diffus och regelbunden reflektion
 Förklara dessa begrepp: Ackommodera, ögats närinställning, är förmågan att förändra brytkraften i ögats lins. Ljus från en enda punkt på ett avlägset objekt och ljus från en punkt på ett närliggande objekt
Förklara dessa begrepp: Ackommodera, ögats närinställning, är förmågan att förändra brytkraften i ögats lins. Ljus från en enda punkt på ett avlägset objekt och ljus från en punkt på ett närliggande objekt
Lösningarna inlämnas renskrivna vid laborationens början till handledaren
 Geometrisk optik Förberedelser Läs i vågläraboken om avbildning med linser (sid 227 241), ögat (sid 278 281), färg och färgseende (sid 281 285), glasögon (sid 287 290), kameran (sid 291 299), vinkelförstoring
Geometrisk optik Förberedelser Läs i vågläraboken om avbildning med linser (sid 227 241), ögat (sid 278 281), färg och färgseende (sid 281 285), glasögon (sid 287 290), kameran (sid 291 299), vinkelförstoring
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Tisdagen den 17 juni 2008 kl 9-15
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 1,5 högskolepoäng, FK49 Tisdagen den 17 juni 28 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 1,5 högskolepoäng, FK49 Tisdagen den 17 juni 28 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare
Laboration i Fourieroptik
 Laboration i Fourieroptik David Winge Uppdaterad 30 januari 2015 1 Introduktion I detta experiment ska vi titta på en verklig avbildning av Fouriertransformen. Detta ska ske med hjälp av en bild som projiceras
Laboration i Fourieroptik David Winge Uppdaterad 30 januari 2015 1 Introduktion I detta experiment ska vi titta på en verklig avbildning av Fouriertransformen. Detta ska ske med hjälp av en bild som projiceras
Handledning laboration 1
 : Fysik 2 för tekniskt/naturvetenskapligt basår Handledning laboration 1 VT 2017 Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen
: Fysik 2 för tekniskt/naturvetenskapligt basår Handledning laboration 1 VT 2017 Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen
Föreläsning 3: Radiometri och fotometri
 Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 21 augusti 2008 kl 9-15
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 1 augusti 008 kl 9-15 Hjälpmedel: handbok och räknare. Varje uppgift ger maximalt 4 poäng. Var
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 1 augusti 008 kl 9-15 Hjälpmedel: handbok och räknare. Varje uppgift ger maximalt 4 poäng. Var
för M Skrivtid i hela (1,0 p) 3 cm man bryningsindex i glaset på ett 2. två spalter (3,0 p)
 Tentamen i tillämpad Våglära FAF260, 2016 06 01 för M Skrivtid 08.00 13.00 Hjälpmedel: Formelblad och miniräknare Uppgifterna är inte sorteradee i svårighetsgrad Börja varje ny uppgift på ett nytt blad
Tentamen i tillämpad Våglära FAF260, 2016 06 01 för M Skrivtid 08.00 13.00 Hjälpmedel: Formelblad och miniräknare Uppgifterna är inte sorteradee i svårighetsgrad Börja varje ny uppgift på ett nytt blad
Tentamen i Fotonik , kl
 FAFF25-2015-03-20 Tentamen i Fotonik - 2015-03-20, kl. 14.00-19.15 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2015-03-20 Tentamen i Fotonik - 2015-03-20, kl. 14.00-19.15 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
LABORATION 2 MIKROSKOPET
 LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX 1 (6) LABORATION 2 MIKROSKOPET Att läsa i kursboken: sid. 189-194 Förberedelseuppgifter:
LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX 1 (6) LABORATION 2 MIKROSKOPET Att läsa i kursboken: sid. 189-194 Förberedelseuppgifter:
LJUSETS DIFFRAKTION. 1 Inledning. Ljusets diffraktion
 LJUSETS DIFFRAKTION 1 Inledning I detta arbete åskådliggörs ljusets diffraktion och interferens genom att belysa smala spalter med en laser och granska det mönster som bildas på en skärm bakom spalterna
LJUSETS DIFFRAKTION 1 Inledning I detta arbete åskådliggörs ljusets diffraktion och interferens genom att belysa smala spalter med en laser och granska det mönster som bildas på en skärm bakom spalterna
LABORATION 2 MIKROSKOPET
 LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX (5) Att läsa före lab: LABORATION 2 MIKROSKOPET Synvinkel, vinkelförstoring, luppen och
LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX (5) Att läsa före lab: LABORATION 2 MIKROSKOPET Synvinkel, vinkelförstoring, luppen och
Kapitel 35, interferens
 Kapitel 35, interferens Interferens hos ljusvågor, koherensbegreppet Samband för max och min för ideal dubbelspalt Samband för intensitetsvariation för ideal dubbelspalt Interferens i tunna filmer Michelson
Kapitel 35, interferens Interferens hos ljusvågor, koherensbegreppet Samband för max och min för ideal dubbelspalt Samband för intensitetsvariation för ideal dubbelspalt Interferens i tunna filmer Michelson
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 35-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik Kapitel 35-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Ljusets interferens. Sammanfattning
 HERMODS DISTANSGYMNASIUM Naturvetenskapsprogrammet Emilia Dunfelt Fysik 2 2017-05-06 Ljusets interferens Sammanfattning I försöket undersöks ljusets vågegenskaper med hjälp av gitterekvationen. Två olika
HERMODS DISTANSGYMNASIUM Naturvetenskapsprogrammet Emilia Dunfelt Fysik 2 2017-05-06 Ljusets interferens Sammanfattning I försöket undersöks ljusets vågegenskaper med hjälp av gitterekvationen. Två olika
Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid , ) Retinoskopet
 Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid 345-353, 358-362) Retinoskopet Utvecklat från oftalmoskopi under slutet av 1800-talet. Objektiv metod för att bestämma patientens
Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid 345-353, 358-362) Retinoskopet Utvecklat från oftalmoskopi under slutet av 1800-talet. Objektiv metod för att bestämma patientens
Tentamen i Fotonik , kl
 FAFF25 FAFA60-2016-05-10 Tentamen i Fotonik - 2016-05-10, kl. 08.00-13.00 FAFF25 Fysik för C och D, Delkurs i Fotonik FAFA60 Fotonik för C och D Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling
FAFF25 FAFA60-2016-05-10 Tentamen i Fotonik - 2016-05-10, kl. 08.00-13.00 FAFF25 Fysik för C och D, Delkurs i Fotonik FAFA60 Fotonik för C och D Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling
E-II. Diffraktion på grund av ytspänningsvågor på vatten
 Q Sida 1 av 6 Diffraktion på grund av ytspänningsvågor på vatten Inledning Hur vågor bildas och utbreder sig på en vätskeyta är ett viktigt och välstuderat fenomen. Den återförande kraften på den oscillerande
Q Sida 1 av 6 Diffraktion på grund av ytspänningsvågor på vatten Inledning Hur vågor bildas och utbreder sig på en vätskeyta är ett viktigt och välstuderat fenomen. Den återförande kraften på den oscillerande
FAFA55 HT2016 Laboration 1: Interferens av ljus Nicklas Anttu och August Bjälemark, 2012, Malin Nilsson och David Göransson, 2015, 2016
 Inför Laborationen Laborationen sker i två lokaler: K204 (datorsal) och H226. I början av laborationen samlas ni i H212. Laborationen börjar 15 minuter efter heltimmen som är utsatt på schemat. Ta med
Inför Laborationen Laborationen sker i två lokaler: K204 (datorsal) och H226. I början av laborationen samlas ni i H212. Laborationen börjar 15 minuter efter heltimmen som är utsatt på schemat. Ta med
Laborationskurs i FYSIK B
 Laborationskurs i FYSIK B Labbkursen i fysik består av 6 laborationer. Vid varje labbtillfälle (3 stycken) utförs 2 laborationer. Till alla laborationer skall fullständiga laborationsrapport skrivas och
Laborationskurs i FYSIK B Labbkursen i fysik består av 6 laborationer. Vid varje labbtillfälle (3 stycken) utförs 2 laborationer. Till alla laborationer skall fullständiga laborationsrapport skrivas och
I 1 I 2 I 3. Tentamen i Fotonik , kl Här kommer först några inledande frågor.
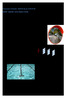 FAFF25-2014-03-14 Tentamen i Fotonik - 2014-03-14, kl. 14.00-19.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2014-03-14 Tentamen i Fotonik - 2014-03-14, kl. 14.00-19.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER
 EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
Diffraktion och interferens Kapitel 35-36
 Diffraktion och interferens Kapitel 35-36 1.3.2016 Natalie Segercrantz Centrala begrepp Huygens princip: Tidsskillnaden mellan korresponderande punkter på två olika vågfronter är lika för alla par av korresponderande
Diffraktion och interferens Kapitel 35-36 1.3.2016 Natalie Segercrantz Centrala begrepp Huygens princip: Tidsskillnaden mellan korresponderande punkter på två olika vågfronter är lika för alla par av korresponderande
Geometrisk optik. Laboration FAFF25/FAFA60 Fotonik 2017
 Avsikten med denna laboration är att du ska få träning i att bygga upp avbildande optiska system, såsom enkla kikare och mikroskop, och på så vis få en god förståelse för dessas funktion. Redogörelsen
Avsikten med denna laboration är att du ska få träning i att bygga upp avbildande optiska system, såsom enkla kikare och mikroskop, och på så vis få en god förståelse för dessas funktion. Redogörelsen
Övning 9 Tenta från Del A. Vägg på avståndet r = 2.0 m och med reflektansen R = 0.9. Lambertspridare.
 Övning 9 Tenta från 2016-08-24 Del A 1.) Du lyser med en ficklampa rakt mot en vit vägg. Vilken luminans får väggen i mitten av det belysta området? Ficklampan har en ljusstyrka på 70 cd och du står 2.0
Övning 9 Tenta från 2016-08-24 Del A 1.) Du lyser med en ficklampa rakt mot en vit vägg. Vilken luminans får väggen i mitten av det belysta området? Ficklampan har en ljusstyrka på 70 cd och du står 2.0
Projekt 6. Fourieroptik Av Eva Danielsson och Carl-Martin Sikström
 Projekt 6. Fourieroptik Av Eva Danielsson och Carl-Martin Sikström Introduktion I detta experiment ska vi titta på en verklig avbildning av fouriertransformen. Detta ska ske med hjälp av en bild som projiceras
Projekt 6. Fourieroptik Av Eva Danielsson och Carl-Martin Sikström Introduktion I detta experiment ska vi titta på en verklig avbildning av fouriertransformen. Detta ska ske med hjälp av en bild som projiceras
Laboration i röntgendiffraktion och laserdiffraktion för E
 Laboration i röntgendiffraktion och laserdiffraktion för E Mats Göthelid Plats: Forum Kista. Samma som för laborationerna i Fysik1. Hiss A våning 8 Uppgifter: Laborationen består av två delar: 1) strukturbestämning
Laboration i röntgendiffraktion och laserdiffraktion för E Mats Göthelid Plats: Forum Kista. Samma som för laborationerna i Fysik1. Hiss A våning 8 Uppgifter: Laborationen består av två delar: 1) strukturbestämning
Kursiverade ord är viktiga begrepp som skall förstås, kunna förklaras och dess relevans i detta sammanhang skall motiveras.
 Holografilab I denna lab kommer ett dubbelexponerat, transmissions hologram göras genom att bygga en holografiuppställning, dubbelexponera och framkalla en holografisk film. Dubbelexponerade hologram används
Holografilab I denna lab kommer ett dubbelexponerat, transmissions hologram göras genom att bygga en holografiuppställning, dubbelexponera och framkalla en holografisk film. Dubbelexponerade hologram används
Laborationer i OPTIK och AKUSTIK (NMK10) Augusti 2003
 TEKNISKA HÖGSKOLAN I LINKÖPING Institutionen för teknik och naturvetenskap Campus Norrköping Igor Zozoulenko Laborationer i OPTIK och AKUSTIK (NMK10) Augusti 2003 Laboration 1: Ljudhastigheten i luft;
TEKNISKA HÖGSKOLAN I LINKÖPING Institutionen för teknik och naturvetenskap Campus Norrköping Igor Zozoulenko Laborationer i OPTIK och AKUSTIK (NMK10) Augusti 2003 Laboration 1: Ljudhastigheten i luft;
Varje laborant ska vid laborationens början lämna renskrivna lösningar till handledaren för kontroll.
 Vätespektrum Förberedelser Läs i Tillämpad atomfysik om atomspektroskopi (sid 147-149), empiriska samband (sid 151-154), och Bohrs atommodell (sid 154-165). Läs genom hela laborationsinstruktionen. Gör
Vätespektrum Förberedelser Läs i Tillämpad atomfysik om atomspektroskopi (sid 147-149), empiriska samband (sid 151-154), och Bohrs atommodell (sid 154-165). Läs genom hela laborationsinstruktionen. Gör
1. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft.
 Problem. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft. (p) Det finns många förklaringar, till exempel Hewitt med insekten
Problem. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft. (p) Det finns många förklaringar, till exempel Hewitt med insekten
LJ-Teknik Bildskärpa
 Bildskärpa - Skärpedjup och fokus - Egen kontroll och fokusjustering - Extern kalibrering Bildskärpa, skärpedjup och fokus Brännpunkt och fokus Medan brännpunkt är en entydig term inom optiken, kan fokus
Bildskärpa - Skärpedjup och fokus - Egen kontroll och fokusjustering - Extern kalibrering Bildskärpa, skärpedjup och fokus Brännpunkt och fokus Medan brännpunkt är en entydig term inom optiken, kan fokus
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 34 - Optik 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Vågrörelselära och optik Kapitel 34 - Optik 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från vänster, sträcka i ljusets riktning = positiv
 Avbildningskvalitet Föreläsning 1 2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Avbildningskvalitet Föreläsning 1 2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Instuderingsfrågor extra allt
 Instuderingsfrågor extra allt För dig som vill lära dig mer, alla svaren finns inte i häftet. Sök på nätet, fråga en kompis eller läs i en grundbok som du får låna på lektion. Testa dig själv 9.1 1 Vilken
Instuderingsfrågor extra allt För dig som vill lära dig mer, alla svaren finns inte i häftet. Sök på nätet, fråga en kompis eller läs i en grundbok som du får låna på lektion. Testa dig själv 9.1 1 Vilken
Polarisation laboration Vågor och optik
 Polarisation laboration Vågor och optik Utförs av: William Sjöström 19940404-6956 Philip Sandell 19950512-3456 Laborationsrapport skriven av: William Sjöström 19940404-6956 Sammanfattning I laborationen
Polarisation laboration Vågor och optik Utförs av: William Sjöström 19940404-6956 Philip Sandell 19950512-3456 Laborationsrapport skriven av: William Sjöström 19940404-6956 Sammanfattning I laborationen
Assistent: Markku Jääskeläinen Laborationen utfördes: 23 februari 2000
 Labrapport: Holografi Assistent: Markku Jääskeläinen Laborationen utfördes: 23 februari 2000 28 februari 2000 Sida 1 Inledning Labrapport: Holografi Teorin för holografi utvecklades redan 1948. Först när
Labrapport: Holografi Assistent: Markku Jääskeläinen Laborationen utfördes: 23 februari 2000 28 februari 2000 Sida 1 Inledning Labrapport: Holografi Teorin för holografi utvecklades redan 1948. Först när
ett uttryck för en våg som beskrivs av Jonesvektorn: 2
 Tentamen i Vågrörelselära(FK49) Datum: Tisdag, 6 Juni, 29, Tid: 9: - 5: Tillåten Hjälp: Physics handbook eller dylikt Förklara resonemang och uträkningar klart och tydligt. Tentamensskrivningen består
Tentamen i Vågrörelselära(FK49) Datum: Tisdag, 6 Juni, 29, Tid: 9: - 5: Tillåten Hjälp: Physics handbook eller dylikt Förklara resonemang och uträkningar klart och tydligt. Tentamensskrivningen består
1. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (1p)
 Problem Energi. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (p) b) Ge en tydlig förklaring av hur frekvens, period, våglängd och våghastighet hänger
Problem Energi. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (p) b) Ge en tydlig förklaring av hur frekvens, period, våglängd och våghastighet hänger
Tentamen i Vågor och Optik 5hp F, Q, kandfys, gylärfys-programm, den 11. juni 2010
 Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 8-13 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 8-13 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
1. Kundts rör. Stående vågor i ett rör med slutna ändar. 2. Ultrajud. Fasförhållande, våglängd och superposition.
 Linköpings Universitetet 2004-04-05 Arno Platau Tekniskt basår, Fysik del 3, FL110, VT 2004 Laboration 1: Ljud 1. Kundts rör. Stående vågor i ett rör med slutna ändar a) Ställ in tongenerator på ca 850
Linköpings Universitetet 2004-04-05 Arno Platau Tekniskt basår, Fysik del 3, FL110, VT 2004 Laboration 1: Ljud 1. Kundts rör. Stående vågor i ett rör med slutna ändar a) Ställ in tongenerator på ca 850
TFEI02: Vågfysik. Tentamen : Lösningsförslag
 160530: TFEI0 1 Uppgift 1 TFEI0: Vågfysik Tentamen 016-05-30: Lösningsförslag a) Ljudintensiteten, I, är ett mått på hur stor effekt, P eff, som transporteras per area. Om vi vet amplituden på vågen kan
160530: TFEI0 1 Uppgift 1 TFEI0: Vågfysik Tentamen 016-05-30: Lösningsförslag a) Ljudintensiteten, I, är ett mått på hur stor effekt, P eff, som transporteras per area. Om vi vet amplituden på vågen kan
Experimentella metoder 2013, Räkneövning 3
 Experimentella metoder 2013, Räkneövning 3 Problem 1: Fem studenter mätte längden av ett rum, deras resultat blev 3,30 m, 2,90 m, 3,70 m, 3,50 m, och 3,10 m. Inga uppgifter om mätnoggrannheten är kända.
Experimentella metoder 2013, Räkneövning 3 Problem 1: Fem studenter mätte längden av ett rum, deras resultat blev 3,30 m, 2,90 m, 3,70 m, 3,50 m, och 3,10 m. Inga uppgifter om mätnoggrannheten är kända.
Tentamen i Vågor och Optik 5hp F, Q, kandfys, gylärfys-programm, den 15. mars 2010
 Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 14-19 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 14-19 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
Hjälpmedel: Typgodkänd räknare, Physics Handbook, Mathematics Handbook.
 CHALMERS TEKNISKA HÖGSKOLA 2009-01-13 Teknisk Fysik 14.00-18.00 Sal: V Tentamen i Optik för F2 (FFY091) Lärare: Bengt-Erik Mellander, tel. 772 3340 Hjälpmedel: Typgodkänd räknare, Physics Handbook, Mathematics
CHALMERS TEKNISKA HÖGSKOLA 2009-01-13 Teknisk Fysik 14.00-18.00 Sal: V Tentamen i Optik för F2 (FFY091) Lärare: Bengt-Erik Mellander, tel. 772 3340 Hjälpmedel: Typgodkänd räknare, Physics Handbook, Mathematics
Optik, F2 FFY091 TENTAKIT
 Optik, F2 FFY091 TENTAKIT Datum Tenta Lösning Svar 2005-01-11 X X 2004-08-27 X X 2004-03-11 X X 2004-01-13 X 2003-08-29 X 2003-03-14 X 2003-01-14 X X 2002-08-30 X X 2002-03-15 X X 2002-01-15 X X 2001-08-31
Optik, F2 FFY091 TENTAKIT Datum Tenta Lösning Svar 2005-01-11 X X 2004-08-27 X X 2004-03-11 X X 2004-01-13 X 2003-08-29 X 2003-03-14 X 2003-01-14 X X 2002-08-30 X X 2002-03-15 X X 2002-01-15 X X 2001-08-31
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi
 1 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus kan ses so elektroagnetiska vågor so rör sig fraåt. När vi ritar strålar
1 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus kan ses so elektroagnetiska vågor so rör sig fraåt. När vi ritar strålar
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 7 poäng, FyL2 Tisdagen den 19 juni 2007 kl 9-15
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 7 poäng, FyL2 Tisdagen den 19 juni 2007 kl 9-15 Hjälpmedel: Handbok, kopior av avsnitt om Fouirertransformer och Fourieranalys
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 7 poäng, FyL2 Tisdagen den 19 juni 2007 kl 9-15 Hjälpmedel: Handbok, kopior av avsnitt om Fouirertransformer och Fourieranalys
Observera också att det inte går att både se kanten på fönstret och det där ute tydligt samtidigt.
 Om förstoringsglaset Du kan göra mycket med bara ett förstoringsglas! I många sammanhang i det dagliga livet förekommer linser. Den vanligast förekommande typen är den konvexa linsen, den kallas också
Om förstoringsglaset Du kan göra mycket med bara ett förstoringsglas! I många sammanhang i det dagliga livet förekommer linser. Den vanligast förekommande typen är den konvexa linsen, den kallas också
M = den svängande fjäderns massa K = den svängande fjäderns fjäderkonstant A = dimensionslös konstant
 UPPGIFT 1: SLINKY SPRING Tid: 50 min. Materiel: Fjäder, plåt, linjal, kronometer, stativ och klämmor. Beskrivning: En "slinky spring" på horisontellt underlag sträcks ut sträckan x under inflytande av
UPPGIFT 1: SLINKY SPRING Tid: 50 min. Materiel: Fjäder, plåt, linjal, kronometer, stativ och klämmor. Beskrivning: En "slinky spring" på horisontellt underlag sträcks ut sträckan x under inflytande av
Vågfysik. Geometrisk optik. Knight Kap 23. Ljus. Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion)
 Vågfysik Geometrisk optik Knight Kap 23 Historiskt Ljus Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion) Hooke, Huyghens (~1660): ljus är ett slags vågor Young
Vågfysik Geometrisk optik Knight Kap 23 Historiskt Ljus Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion) Hooke, Huyghens (~1660): ljus är ett slags vågor Young
Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från vänster, sträcka i ljusets riktning = positiv
 Avbildningskvalitet Föreläsning 1-2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Avbildningskvalitet Föreläsning 1-2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Diffraktion och interferens
 Göteborgs universitet Februari 2016 Chalmers tekniska högskola 10 sidor + bilaga Jan Swenson 1994 Christian Karlsson 2002 Mats Halvarsson 2015 Nils Odebo Länk 2016 O2 Diffraktion och interferens Interferens
Göteborgs universitet Februari 2016 Chalmers tekniska högskola 10 sidor + bilaga Jan Swenson 1994 Christian Karlsson 2002 Mats Halvarsson 2015 Nils Odebo Länk 2016 O2 Diffraktion och interferens Interferens
Interferens och difraktion
 Interferens och difraktion Lab 2 i Vågrörelselära och Optik Stockholms Universitet, VT14 Kontakt: olga.bylund@fysik.su.se Instruktioner för Lab 2: Tre experiment ingåri lab 2: Difraktionsförsök med laserljus,
Interferens och difraktion Lab 2 i Vågrörelselära och Optik Stockholms Universitet, VT14 Kontakt: olga.bylund@fysik.su.se Instruktioner för Lab 2: Tre experiment ingåri lab 2: Difraktionsförsök med laserljus,
Tentamen i Fotonik , kl
 FAFF25-2013-08-26 Tentamen i Fotonik - 2013-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2013-08-26 Tentamen i Fotonik - 2013-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Diffraktion och interferens
 Göteborgs universitet Januari 2015 Chalmers tekniska högskola 11 sidor + bilaga Jan Swenson 1994 Christian Karlsson 2002 Mats Halvarsson 2015 O2 Diffraktion och interferens Interferens med C 60-molekyler.
Göteborgs universitet Januari 2015 Chalmers tekniska högskola 11 sidor + bilaga Jan Swenson 1994 Christian Karlsson 2002 Mats Halvarsson 2015 O2 Diffraktion och interferens Interferens med C 60-molekyler.
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
LABORATION 1 AVBILDNING OCH FÖRSTORING
 LABORATION 1 AVBILDNING OCH FÖRSTORING Personnummer Namn Laborationen godkänd Datum Labhandledare 1 (6) LABORATION 1: AVBILDNING OCH FÖRSTORING Att läsa före lab: Vad är en bild och hur uppstår den? Se
LABORATION 1 AVBILDNING OCH FÖRSTORING Personnummer Namn Laborationen godkänd Datum Labhandledare 1 (6) LABORATION 1: AVBILDNING OCH FÖRSTORING Att läsa före lab: Vad är en bild och hur uppstår den? Se
Vågrörelselära & Kvantfysik, FK2002 1 december 2011
 Räkneövning 6 Vågrörelselära & Kvantfysik, FK2002 december 20 Problem 36.23 Avståndet mellan två konvexa linser i ett mikroskop, l = 7.5 cm. Fokallängden för objektivet f o = 0.8 cm och för okularet f
Räkneövning 6 Vågrörelselära & Kvantfysik, FK2002 december 20 Problem 36.23 Avståndet mellan två konvexa linser i ett mikroskop, l = 7.5 cm. Fokallängden för objektivet f o = 0.8 cm och för okularet f
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
