Interferens och diffraktion

Transkript

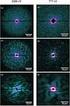
1 Laborationsinstruktion Vågrörelselära Interferens och diffraktion v.2.1 VT05 Figur 0 : Bilden visar diffraktion i en spektrometer pga den begränsande apperturen med diametern a. [från Demtröder] Denna laborationshandledning finns som pdf fil på ftp://ulf.physto.se/ och är i färg.

2 Fundamentalt Denna labbinstruktions teoriavsnitt är endast ett komplement till kurslitteraturen. Allmänt Då en eller flera vågrörelser överlagras uppstår ibland vissa fenomen som benämns interferens och/eller diffraktion. Någon verklig åtskillnad mellan dessa två begrepp finns inte och det har inte visat sig vara nödvändigt. Vanligtvist talar man om interferense då ett fåtal (ex. två) vågrörelser överlagras och om diffraktion då det gäller ett stort antal. (Att tala om diffraktion i en enkelspalt kommer av att man tänker sig ett stort antal vågor, Huygens-Fresnel principen, utgår från olika delar av spalten.) För diffraktionsfenomenet skiljer man på två fall: Diffraktion Fraunhoferdiffraktion ( Far-field diffraction ) Antar en infallande plan våg (parallella strålar) på obstaklet/hindret. Diffraktionsmönstret observeras på - avstånd. Fresneldiffraktion ( Near-field diffraction) Antingen strålningskällan eller observationsplatsen är ej att approximeras med att vara på - långt avstånd. Fraunhoferdiffraktionen är enklare att beskriva pga approximationen avstånd. Vanligtvist arrangerar man mha linser så att Fraunhoferdiffraktion i praktiken gäller. I dessa laborationer ingår bara Fraunhoferdiffraktion. Ett villkor för att få mätbar/observerbar interferens/diffraktion är att de överlagrade vågrörelserna är någorlunda koherenta. Det betyder att de olika vågorna måste svänga med så gott som samma frekvens och ha konstant fasskillnad sinsemellan. Om vågorna inte har samma frekvens eller om deras fasskillnad förändras godtyckligt med tiden kan man inte observera något stationärt diffraktions- eller interferensmönster, ljuskällorna sägs då vara icke-koherenta. Enkelspalt Intensitetsuttrycket bakom en enkelspalt vid Fraunhoferdiffraktion är 2 sin u I SP = I 0 där 2 u π b sinθ = λ u (1) b : spaltbredden θ: böjningsvinkeln λ: ljusets våglängd 2

3 Genom deriveringen I 2sin u( u cosu sin u) SP = I = u u fås villkoren som vinklarna θ m ska uppfylla för minimum och maximum intensitet. minima: maxima: m λ = b sinθ [ u = ±π,±2π, ±3π, ] m =1, 2, 3, m u = tanu θ = 0 [ u = 0 ] Huvudmaxima ( m + 1 ) λ = b sinθ m =1, 2, 3, Sidomaxima m 2 (approximativt) Figur 1 Intensitetvariationen bakom en enkelspalt vid Fraunhoferdiffraktion är plottad för två värden på spaltbredden b. Våglängden är densamma som för en HeNe-laser. Intensiteten för första sidomaximum är ~ 4,7 % av huvud/central-maximum. Dubbelspalt Intensitetsuttrycket bakom en dubbelspalt vid Fraunhoferdiffraktion är: 2 π a sinθ I 4 I cos φ φ = (2) = SP a : avståndet mellan spalterna I SP : samma intensitet som för tidigare enkelspalt λ 3

4 Den första faktorn I SP beskriver diffraktionsmönstret från en av spalterna. Faktorn cos 2 φ beskriver intensitetsfördelningen av strålningen från två koherenta källor på avståndet a från varandra och faktorn 4 kommer av att elektriska fältet är dubbelt så stort jämfört med vad en punkt från en spalt åstadkommer. Genom derivera ovan uttryck (2) map φ och θ fås villkoren för minima och maxima: Interferensmaxima φ = n π n λ = a sinθ n = 1, 2, 3, Interferensminima u = m π m λ = b sinθ n m = 1, 2, 3, m Figur 2 Visar de olika termerna som ingår i uttrycket för intensiteten bakom en dubbelspalt ( Ekv. 2 ) Diffraktionsgitter Diffraktionsgitter finns i två varianter: transmissionsgitter och reflektionsgitter. Den senare varianten är vanligast ty den ger mer intensitet. Ett transmissionsgitter består av N spalter med bredden b. Avståndet mellan spalterna kallas gitterkonstanten och betecknas med d. Gittrets totala längd är B = N d. Observera att det är underförstått att N = antalet belysta spalter. Intensitetsfördelningen i den transmitterade/reflekterade strålen är vid vinkelrätt infall: I = I I = I 2 sin ( N φ) 2 sin φ ; SP i SP π d sinθ φ = λ I SP beskriver diffraktionsmönstret från enskild spalt medan I i beskriver intensitetsfördelningen från N koherenta ljuskällor på avstånd d från varandra. Liksom för en dubbelspalt kommer faktorn I SP att modulera interferensmönstret. Pga limes φ 0 sin(nφ)/φ =N ökar intensiteten för huvudmaxima kvadratiskt med antalet belysta spalter. 4

5 Figur 3 Intensiteten från ett transmissionsgitter med fem belysta spalter. Intensiteten från en enkelspalt ( I SP ) är inlagd som jämförelse. Genom derivering av interferensfaktorn I i fås villkoren för: N φ = k π interferensminimum k λ = N d sinθ k k n N, n = heltal diffraktionsminima interferensmaximum (precis som tidigare för enkelspalt) m λ = b sinθ m =1, 2, 3, Det förekommer två slag: m huvudmaxima (principal maxima) sidomaxima (subsidiary maximum) I allmänhet observeras inte sidomaxima pga sin låga intensitet jämfört med huvudmaxima. Ofta kallas därför endas huvudmaxima för interferensmaxima. Det finns N-2 stycken sidomaxima mellan två närliggande huvudmaxima. Interferensmaxima sker när φ och θ uppfyller N φ = k π k = n N, n = heltal k λ = N d sinθ k 6

6 Kan även skrivas om som: φ = n π n λ = d sinθ k n = spektrallinjens ordning (heltal) Antalet interferensmaxima med relativt hög intensitet (huvudmaxima) som ligger inom centrala maxima för diffraktionsmönstret bestäms av förhållandet d/b, nämligen 2 d/b+1 stycken. [ d = gitterkonstanten (avst. mellan spalterna), b = spaltbredden ] Gitterekvationen som är använd ( n λ = d sinθ n ) är ett specialfall då ljuset kommer in vinkelrätt mot gittret. Mer allmänt är gitterformeln ( the grating equation) : n λ = d (sinθ ± sinθ ) i n = diffraktionsordningen (heltal) θ i = infallsvinkeln Plustecken används om θ i och θ n ligger på samma sida om gitternormalen. n Koherensgrad Intensitetsuttrycket ovan härleddes under förutsättning att den infallande strålningen är en plan våg. För att framställa en plan ljusvåg måste man använda en laser eller en punktformig ljuskälla i kombination med en kollimerande lins. Är ljuskällan däremot utbredd erhåller man med en lins i princip en plan våg från varje punkt i ljuskällan. För att erhålla den resulterande intensitetsfördelningen måste man summera bidragen från hela ljuskällan. Om ljuskällan är tillräckligt liten approximeras intensitetsfördelningen väl av formler härledda för en plan våg. Man brukar säga att ljuset är koherent. Ökas ljuskällans bredd blir approximationen sämre och man talar om lägre koherensgrad. Upplösning En bild av två föremål sägs vara upplöst om man kan uppfatta ett intensitetsminimum mellan de två bilderna. Gränsen för ett optiskt instruments upplösning sätts av de diffraktionsfenomen som alltid uppstår. Diffraktionsmönstrets utseende bestäms av de begränsningar som instrumentet inför i strålknippet från det avbildade föremålet. En väsentlig storhet för diffraktionsmönstret är vinkelavståndet ( θ ) mellan huvudmaximum och 7

7 första minimum. För en oändligt lång spalt gäller θ = λ / b och för en cirkulär apertur θ 1.22 λ / d, där b är spaltbredden och d den cirkulära öppningens diameter. Observera att diffraktionsfenomen uppstår för alla begränsningar. Öppningarna behöver alltså inte vara små för att man ska vara tvungen att ta hänsyn till diffraktionsfenomen. Figur 4 Rayleighs upplösnings kriterium. Streckade linjen är den sammanlagda intensiteten. Praktiskt mäts upplösningen genom att betrakta eller fotografera två bilder som ligger nära varandra och vars avstånd kan varieras. För att teoretiskt kunna beräkna ett instruments upplösning används lord Rayleighs kriterium: Två punkter är upplösta om den enas huvudmaxima faller i den andres första diffraktionsminimum. Överlappen mellan de två mönstrena från två punktformiga ljuskällor har då ett minimum (på 8/π 2 ~81% av maxima) mellan de bådas huvudmaxima. Praktiskt mäts en upplösning som är sämre. Detta beror på att föremål och optiska element inte är ideala och dels på att hänsyn endas tas till de begränsningar av strålknippet som har störst betydelse för mönstrets utseende. Vi ska i det följande skilja på begrepp vilka båda ofta båda kallas för upplösningsförmåga. - upplösningsförmåga - upplösningsgräns Upplösningsgräns avståndet eller vinkelavståndet mellan två föremål vars bilder är nätt och jämt upplöst. ( mkt litet tal) Upplösningsförmåga / Resolving power λ Definierat som R = λ Används för spektrometrar och spektrografer. λ är våglängdsskillnaden för upplösta spektrallinjer. Gittrets upplösningsförmåga Gittrets teoretiska upplösningsförmåga är λ R = = n N λ n spektralordningen N antalet belysta ritsor 8

8 Det ligger nära till hands att tolka detta uttryck som att det krävs många gitterritsor för att få en hög upplösningsförmåga. Det är ej helt sant ty n är en funktion av N. Gitterekvationen för vinkelrätt infallande ljus på ett transmissionsgitter ( n λ = d sinθ ) och gittrets totala belysta bredd B = N d kan användas till att uttrycka upplösningsförmågan som n Gittrets totala belysta bredd begränsar upplösningsförmågan B sinθ R = n. λ Figur 5 Transmissionsgitter med förklaringar till införda beteckningar i texten. För en given belyst gitterbredd B kan hög upplösning fås genom användandet av stor ritstäthet och plocka ut första spektralordningen ( n = 1 ) eller genom att använda gles ritstäthet och plocka ut en högre spektralordning. Av intensitetsskäl och tekniska orsaker är det senare som används när man tillverkar ett högupplösande gitter. Från figur 5 framgår att upplösningsförmågan, R, är lika med vägskillnaden mellan randstrålarna uttryckt i antalet våglängder. Detta är ett resultat som gäller generellt. För ett dispergerande element ( prisma eller gitter ) bestäms bildens (spektrallinjens) utseende av begränsningen av strålknippet efter det dispergerande elementet. Bildens intensitetsfördelning är ett diffraktionsmönster. Om hänsyn bara tas till knippets utbredning i horisontell led och kallar dess bredd för B blir avståndet mellan huvudmaxima och första minimum θ = λ / B. Med hjälp av definitionen på dispersionen, D = dθ / dλ, erhålls D λ = θ = λ / B för två upplösta linjer med våglängden λ och λ+dλ. Detta kan omformas till ett allmänt uttryck för upplösningsförmågan: λ R = = D B'. λ n För det fall som illustreras i figur 5 är D = och gittrets effektiva bredd d cosθ B =B cosθ. Upplösningsförmågan blir: R = n B d = n N 9

9 Uppgift 1 Diffraktionsförsök med laserljus Med en ståltråd placerad i strålgången på en Helium-Neon laser fås ett liknande mönster som från en enkelspalt med samma bredd (b). Diffraktionsminima för en enkelspalt sker vid de vinklar θ som uppfyller mλ = bsin( θ m ) m =1, 2, 3, Figur 6 Uppställning och förklaring till symboler. Vid små vinklar kan approximationen sin(θ m ) X m /Z användas. Ex. vid Z = 2 m och X = 8 cm ger approximationen ett fel på mindre än 0,03%. Avståndet mellan närliggande diffraktionsminima blir med approximationen: X = X m -X m-1 = m λ z ( m 1) λ z b b = λ z b Liten spaltöppning / smal tråd ger glesare mönster! Utförande Placera en tråd i laserns strålgång och ett papper vinkelrätt mot strålen några meter bort. Markera på papperet centralmaximum och så många diffraktionsminima som möjligt. HeNe laserns våglängd är 632,8 nm i luft. Redogörelse Beräkna ståltrådens bredd med feluppskattning. Ange de största felkällorna. Jämför med ev given tjocklek för tråden, mät med ev mikrometerskruv. 10

10 Meassuring the Wavelength of Light with a Ruler [ A.L Schawlow, Am.J.of Phy. 33,1965 ] 11

11 Uppgift 2 Mäta våglängden med linjal Läs föregående artikeln av A.L Schawlow och återupprepa försöket. Figur 7 En möjlig uppställning till Schawlows försök. En HeNe-laser stråle stryker tippen på en ritsad stållinjal. Interferensmaxima inträffar när följande approximativa villkor är uppfyllt: y 2 1 n nλ = 2 2 x0 y 2 0 d Avståndet fr. linjalspets till tavla är x 0. y n är avståndet från det n:te maxima till origo, definierat som (y 0 -y 0 )/2. Origo markerar vart förlängningen av linjalen träffar tavlan. Nollte ordningen (y 0 ) sammanfaller med reflektionen från linjalen och kan urskiljas gm att den är starkare än de andra ordningarna. Välj infallsvinkeln (α) så att ingen negativ ordning förekommer mellan den obrutna laserstrålen (-y 0 ) och nollte ordningen (y 0 ). Om en negativ ordning syns mellan y 0 och y 0 så är den svagare än dessa båda. En felidentifiering av -y 0 och y 0 kommer att förstöra hela försöket. Stållinjalerna har både mm- och tum- skala. En tum (inch) är exakt 25,4 mm. Finare graderingar kan förekomma vid linjalens ände. Var observant! Tumskalan kommer i 1/16-delar och ev. 1/32-delar. Tag upp data för både mm och tum skala. Redogörelse Våglängden på lasern beräknas mha Matlab för både mm- och tum-skala. Visa att gitterformeln är n λ= d sinθ för ett transmissionsgitter. n 12

12 Uppgift 3 Gittrets upplösningsförmåga I en spektrometer placeras ett transmissionsgitter. Du ska variera antalet belysta spalter på detta gitter och se hur det påverkar gittrets upplösningsförmåga. En natriumlampa (Na) har två gula spektrallinjer vid 589,592 och 588,995 nm i luft. Så gott som allt synligt ljus kommer från dessa två linjer. ( De kallas natrium-dubletten, ofta benämnda D 1 =589,592 och D 2 =588,995 nm. ) Inverkan av belysta gitterbredden, B, på upplösningen av dessa två studeras. Figur 8 Spektrometern med transmissionsgitter. Ljuskällan är en spektrallampa innehållande förgasad Natrium. I ställningen sitter ett skjutmått som används till att begränsa antalet belysta ritsor på gittret. Under okularet sitter en liten lampa med sladd som används till att belysa ett hårkors. Den används vid upplinjeringen av gittret. Bilden av den belysta spalten (=objektet) kommer, för olika våglängder, att hamna på olika ställen efter passagen igenom gittret. Eftersom spalten är liten och smal kommer bilden att likna ett sträck/linje. Därav namnet spektrallinje. Ställ in kikaren och kollimatorn Spektrometern som används är ett vinkelmätningsinstrument. Kollimerat (parallellt) ljus från en belyst spalt får passera ett dispergerande element ( ex ett gitter/prisma ). Olika spektrallinjer observeras genom en kikare och vinkeln θ i gitterekvationen n λ = d sinθ läses av för första och andra ordningen (n). I kikaren finns en glödlampa som belyser ett hårkors. Denna används för att ställa in kikaren på -avstånd (autokollimering) samt att få gittret vinkelrätt mot strålgången.. 1 ) Justera okularet (längst ut på kikaren )så att hårkorset syns skarpt i kikaren. Okularet har hål i dess sida för att släppa fram ljuset. Fixera sedan okularet med skruven ovanpå. Rör ej okularet sedan. 2 ) Ställ en plan spegel framför kikaren. Ljustera mha kikarens ratt på sidan så att hårkorsets spegelreflex syns skarpt. Fortsätt ljustera spegeln så att reflexen faller tillbaka på hårkorsets. Spegeln står på en platta som kan tiltas mha skruvar undertill. Flyttas huvudet när hårkorset betraktas så ska inte de två bilderna röra på sig i förhållande till varandra,( inställningen sägs då vara parallaxfri). Rör sedan inte kikarens inställning. Kikaren är nu inställd på -avstånd. 13

13 3 ) Kollimatorn (närmast lampan) kan skjutas in/ut i längdriktningen. Ljustera denna tills dess att den belysta spalten syns skarpt genom kikaren. Spalten kan ändras med skruven på sidan. Ställ in en mycket smal spalt och försök att ljustera kollimatorn så att skrovligheten på spaltens sidor syns skarpt. Rör sedan inte kollimatorns inställning. Kollimatorn är nu inställd på att projicera bilden av spalten på -avstånd. Parallellt ljus faller således på gittret. 4 ) Vrid kikaren så att hårkorset syns mitt i den belysta spalten. Fixera kikaren mha skruven på spektrometerns sida. Placera ett transmissionsgitter i mitten av plattan. Gittrets ritsor ska vara parallella med spalten. Ritsade ytan ska vara vänd mot kikaren. Det är viktigt att gittret står i mitten. Ljustera gittret så att reflexen av det belysta hårkorset faller tillbaka på densamma. Reflexen är svag. Rör bara gittret, ej kikarens inställning. Gittret står nu mot strålgången. Rör sedan ej gittret. 5 ) Placera ett skjutmått i en ställning. Den kommer att användas som en bländare till att begränsa den belysta bredden (B) på gittret. Bländarens öppning ska vara parallell med gittrets ritsor. Mätningen Lossa kikarens fixeringsskruv och vrid in första ordningens spektrallinjer (n=1) av gula natriumdubbletten. Bredden på den belysta spalten kan behövas minska för att dubbletten ska synas upplöst i två linjer. För in skjutmåttet (=bländaren) mellan gittret och kollimatorn, så nära gittret som möjligt. Rubba inte gittret! Justera sedan bländaröppningen till dess att Na-dubbletten nätt och jämt är upplöst. Läs av bländaröppningens bredd. Vrid bländaröppningen 90 och observera ev. skillnad på upplösningen. Gör om ovan försök i andra ordningen. Beräkna, för båda ordningarna, den teoretiskt minsta belysta bredden B TEORI som krävs för att dubbletten ska vara upplöst. Ritstätheten på gittret brukar stå angivet i antal ritsor/mm. Gitterkonstanten fås även från kommande uppgift 4. Redogörelse Redogör för dina observationer i första och andra ordningen och dess överensstämmelse med teorin. 14

14 Uppgift 4 Våglängdsbestämning Med kännedom om våglängden för kvicksilvers (Hg) ena gula linje beräknas gitterkonstanten. Därefter bestäms våglängden för Hg s gröna spektrallinje med hjälp av denna gitterkonstant.. Vinkelbestämningen Spektrallinjerna syns på båda sidor om noll grader. Dvs vid ex ± 31,14. Vinkelbestämningen av θ sker genom att gradskivan läses av vid båda bilderna av samma spektrallinje. Skillnaden mellan de avlästa värdena är då 2θ. Avläsning sker på båda sidors nonier. Samma person läser av båda nonier. Två avläsningar av samma nonie krävs för att bestämma en vinkel θ. Figur 9 Nonierna är indelade i grader och minuter. En minut är 1/60 grad. Gradmarkeringarna är på ½ grad så att bara 30 minuter-sträck räcker! Avläsning sker med samma princip som hos ett skjutmått. Denna nonie visar 81,5 13 dvs 81,72. Plattan som innehåller skalan är roterbar för upprepning av vinkelavläsningen vid annan del av skalan. Detta kompenserar för variationer i skalans gradering och möjliggör fler oberoende mätningar av vinkeln θ. När en spektrallinje har vridits in ska hårkorset ligga mitt i den avbildade spalten/linjen. Liten spaltöppning är att föredra, intensiteten minskas dock. För båda Hg-linjerna bestäms vinkeln i första och andra ordningen. Hg s gula spektrallinjer har tabellvärdena 5769,59 Å och 5790,654 Å. Utförande Mät θ för någon av Hg s gula spektrallinje. Mät upp vinkelskillnaden 2θ i första ordningen. Rotera gradskivan. Mät upp vinkelskillnaden 2θ i första ordningen. Rotera gradskivan. Mät upp vinkelskillnaden 2θ i andra ordningen. Rotera gradskivan. Mät upp vinkelskillnaden 2θ i andra ordningen. Du ska nu ha 16 nonie-avläsningar nedskrivna. Rubbas gittret måste allt göras om. 15

15 Gå över till att göra samma sak för Hg s gröna spektrallinje Totalt ska du ha 32 uppskrivna nonier-avläsningar. Redogörelse Beräkna gitterkonstanten utgående från någon av kvicksilvers gula spektrallinje. Våglängden för kvicksilvers gröna spektrallinje beräknas mha ovan framtagna gitterkonstant. Jämför med tabulerade värden från P.H. Uppgift 5 Luftens brytningsindex vid normalt lufttryck En kyvett placerad i en Michelsoninterferometer evacueras. När luften släpps på så räknas antalet fransar som ändras i mönstret och luftens brytningsindex bestäms från optiska vägskillnaden i de bägge armarna. Läs på efterföljande sida om Michelsoninterferometern. Både speglarna och beamsplittern är känsliga för repningar och fingeravtryck. Rör aldrig ytan på dessa. Lasern kan ge polariserat ljus. Undvik brewstervinkel hos beamsplittern. De handhållna pumparna klarar inte av att pumpa ner mer än till ~50 mbar så formeln måste modifieras på lämpligt sätt. Att antaga att brytningsindex varierar linjärt med trycket är en god approximation. Uppgift Ställ in MI så att ringmönstret framträder. Placera kyvetten i en av armarnas strålgång. Evakuera luften ur kyvetten mha den handdrivna pumpen. Släpp långsamt in luften samtidigt som ringarnas antal räknas. Bestäm luftens brytningsindex vid normalt lufttryck. Redogörelse Jämför ditt beräknade brytningsindex med det tabulerade i P.H för den specifika våglängden på lasern (633,8 nm). 16

16 ( Ulf Sassenberg har skrivit detta stycke ) 17

17 18

18 Uppgift 6 Kvartsvåglängdsplatta i Michelsoninterferometer Ringmönstret observeras när en kvartsvåglängdsplatta, placerad i en av armarna till Michelsoninterferometern, vrids. Fig 10 Michelsoninterferometern som används i laborationen. En λ/4 platta är placerad i en av armarna på interferometern. Utförande Ställ in MI så att ringmönstret framträder. Placera kvartsplattan i en av armarnas strålgång. Vrid plattan och observera mönstret. Från föregående uppgift vet du hur ringarna ändras då optiska vägskillnaden ökar mellan de båda armarna. Du kan således se vilken riktning i den dubbelbrytande plattan som har den långsammaste axeln. Vad händer när λ/4-plattan vrids runt 180? Redogörelse Förklara dina observationer. Muntlig redogörelse till laborationsassistenten. 19