Innehåll. Förord 1. Kapitel Grafik Övningsuppgifter Lösningsförslag... 26
|
|
|
- Malin Dahlberg
- för 9 år sedan
- Visningar:
Transkript
1 Innehåll Förord 1 Kapitel Grafik Övningsuppgifter Lösningsförslag
2 9.1 Grafik Ingenting som handlar om grafik är förstås inkluderat i ANSI C. Däremot finns möjligheter att knyta bibliotek innehållande grafiska rutiner till ett vanligt C-program. En del av dessa, som till exempel OpenGL, Allegro eller det som Windows erbjuder, är i denna situation alltför komplicerade. Vi ska därför, här istället, använda ett enklare system, som en gång i tiden skapades av Borland. Våra grafikprogram kommer att öppna en extra konsol, ett svart fönster, i vilket våra alster kommer att presenteras. Detta fönster kan användas antingen i textmod eller i grafikmod. I textmod, så som vi hittills använt konsolen, kan man bara, som namnet säger, skriva text. Till sitt förfogande har man ju då de 256 ascii-tecknen. Att några av dessa kallas semigrafiska och har utseendet av hörn och streck är en helt annan historia. I grafisk mod delas skärmen in i ett antal pixlar. Vi kommer framöver att använda en grafisk drivrutin vid namn VGA och då delas skärmen historiskt in i 480 rader med 640 pixlar på varje. En pixel pekas ut på samma sätt som en punkt i ett koordinatsystem. Med den skillnaden att origo ligger i skärmens övre vänstra hörn och att y-axeln är riktat nedåt, se figur 9.1. Ett enkelt exempel leder oss in i grafikens värld
3 Figur 9.1: Exempel 1. 1 #include <graphics.h> 2 void main(void) { 3 int gd=detect,gm; 4 initgraph(&gd,&gm,""); 5 line(0,0,639,479); 6 closegraph(); 7 } 1 Om inget annat bestämts kommer ett program att från början hamna i textmod. För att få programmet att arbeta i grafisk mod, måste man först initiera grafiken. Detta görs med hjälp av funktionen initgraph. Denna funktion, liksom alla andra som hanterar grafik når vi genom #include <grahics.h> 3 Variabeln gd är en förkortning av graphic driver. Den får sitt värde genom initgraph, som tar reda på vilket grafikkort och drivrutiner som finns tillgängliga och väljer själv den bästa upplösningen. Detta sker då variabeln har tilldelats värdet DETECT. Variabeln gm är en förkortning för graphic mode. 4 Förutom de två parametrarna, som ska hålla reda på graphic driver och graphic mode finns en tredje parameter, som här alltid ska vara en tom sträng, "". 5 Nu är det bara att sätta igång och rita! Med funktionen line drar man en rät linje mellan två pixlar på skärmen. I detta exempel det 4
4 9.1 Grafik längsta streck som går att dra. Från (0, 0), uppe i vänstra hörnet, till (639,479), nere i högra. 6 Den ordningssamme släcker ner grafiken och övergår till textmod, med closegraph, innan programexekveringen avbryts. Maskrosor Nedan följer nu ett antal exempel, som alla åstadkommer någon form av grafisk output och som går igenom de grafiska funktioner vi kommer att behöva framöver. För dig, som vill få en total överblick över de grafiska funktioner, som systemet innehåller rekommenderar vi en titt på hemsidan. Exempel 2. 1 #include <graphics.h> 2 #include <time.h> 3 #include <math.h> 4 #define PI void blomma(int x, int y, int r) { 6 int k,x1,y1; 7 for(k=0;k<=360;k=k+15) { 8 x1=(int)(r sin(k PI/180.0)+x); 9 y1=(int)(r cos(k PI/180.0)+y); 10 line(x,y,x1,y1); 11 } 12 } 13 int main(void){ 14 int gd=detect,gm,k,x,y,r; 15 srand(time(0)); 16 initgraph(&gd,&gm,""); 17 setcolor(yellow); 18 for(k=1;k<=50;k++){ 19 x=rand()%640; 20 y=rand()%480; 21 r=rand()%50+20; 22 blomma(x,y,r); 23 } 24 } 5
5 16 Grafiken initieras. 17 Om inget annat sägs är ritfärgen (den färg som används till alla linjer, cirklar och text) vit, WHITE. I det system som vi ska använda finns endast 16 färger, se tabell 9.2 nedan. Färgernas namn finns fördefinierade i graphics.h. Kom ihåg att de måste skrivas med versaler. Det skulle gå lika bra att skriva dem som tal, mellan 0 och 15, men detta är ju inte speciellt självdokumenterande, så undvik det. WHITE är alltså inget annat än konstanten 15. För att ändra aktuell ritfärg använder man funktionen setcolor. Eftersom vi ska rita maskrosor så är det lämpligt att välja gul färg Denna rutin kommer att rita 50 maskrosor i olika storlekar på slumpmässiga ställen. I funktionsanropet blomma(x,y,r) anger x och y blommans centrum i koordinatsystemet och r kronbladens längd Tittar vi sedan på funktionen blomma, så innehåller den en loop, som exekveras i 24 varv. I varje varv ritas ett kronblad. För övrigt ingår en del matematik. Det är vanligt med trigonometriska beräkningar i samband med grafikprogrammering. nr färg nr färg 0 BLACK 8 DARKGRAY 1 BLUE 9 LIGHTBLUE 2 GREEN 10 LIGHTGREEN 3 CYAN 11 LIGHTCYAN 4 RED 12 LIGHTRED 5 MAGENTA 13 LIGHTMAGENTA 6 BROWN 14 YELLOW 7 LIGHTGRAY 15 WHITE Figur 9.2: Standardfärgerna 6
6 9.1 Grafik Måla I detta program vill vi dela in skärmen i ett rutnät och fylla var och en av rutorna med en slumpmässigt vald färg. Om vi nu ska tänka i de banor som vi talade om senast att dela upp en programmeringsuppgift i ett antal mindre, så kan det vara lämpligt att ha en funktion som ritar rutnätet och en som sköter målandet. Då blir det inte mycket över till main. Exempel 3. 1 #include <graphics.h> 2 #include <stdlib.h> 3 void rutnat(void){ 4 int k; 5 for(k=0;k<=630;k=k+10) 6 line(k,0,k,470); 7 for(k=0;k<=470;k=k+10) 8 line(0,k,630,k); 9 } 10 void mala(void){ 11 int k,m,farg; 12 for(k=5;k<=625;k=k+10) 13 for(m=5;m<=465;m=m+10){ 14 farg=rand()%15; 15 setfillstyle(solid FILL,farg); 16 floodfill(k,m,white); 17 } 18 } 19 int main(void){ 20 int gd=detect,gm; 21 initgraph(&gd,&gm,""); 22 rutnat(); 23 mala(); 24 closegraph(); 25 } Huvudfunktionen, main, blir kort och koncis. Efter initiering exekveras funktionen rutnat och därefter funktionen mala. 7
7 3-9 Funktionen rutnat är indelad i två rutiner, for-loopar en som ritar vertikala streck och en som ritar horisontella När vi nu ska måla en ruta måste vi finna en koordinat (x,y), som vi vet ligger inuti rutan. Genom denna dubbelloop kommer x och y att anta värden (5,5),(5,15)...(5,465),(15,5)...(625,465) Var och en av dessa punkter ligger mitt inuti en ruta. 14 Vi slumpar fram en färg genom ett tal mellan 0 och 14. Vi undviker 15 som är WHITE och som ju används för ritandet av själva nätet. 15 Innan vi kan måla, måste vi bestämma vilken färg och vilken pensel vi vill ha. Detta klaras av med hjälp av funktionen setfillstyle. Första parametern anger fyllnadsmönstret - penseln. SOLID_FILL ger ett 100 procentig mättnad av vald färg. Andra mönster, som finns tillgängliga, hittar du i tabell 9.3 nedan. Även här kan tal användas i stället för namnen. 16 Själva målandet görs sedan med funktionen floodfill. De första två parametrarna är koordinaten till en punkt som ligger inuti den yta som ska målas. WHITE anger här vilken färg som används för gränsen. Vi har ju ritat nätet med vit färg så inget annat än WHITE, kan ge önskat resultat. Random walk Hur kan en slumpmässig vandring på skärmen se ut? Programmet nedan inför endast två nyheter. Exempel 4. 1 #include <graphics.h> 2 int main(void) { 3 int gd=vga,gm=vgahi,k; 4 initgraph(&gd,&gm,""); 5 setcolor(yellow); 6 moveto(320,240); 7 for(k=1;k<=100;k++) 8 lineto(rand()%640,rand()%480); 9 closegraph(); 10 } 8
8 9.1 Grafik 3 Som alternativ till, att låta datorn ta reda på vilken grafikkvalitet som ska användas, kan vi själva ange det. De värden som datorn ändå upptäcker med DETECT, på de flesta system är gd=vga och gm=vgahi. 5 Ritfärgen sätts till gul 6 På samma sätt som det i textmod finns en cursor, finns i grafisk mode, en aktuell punkt. Den är dock inte synlig och placeras i punkten (0, 0) vid initiering av grafiken. Med hjälp av funktionen moveto kan cursorn flyttas omkring på skärmen, här till skärmens centrum. 7-8 Vår vandring består av 100 etapper och startar i (320,240). Funktionen line kräver fyra parametrar, koordinaterna för start- och slutpunkten. Funktionen lineto dock endast två, koordinaterna för slutpunkten. Som startpunkt i lineto används nämligen cursorns placering. Observera att efter att linjen ritas uppdateras aktuell placering av cursorn till linjens slutpunkt. 8 Koordinaterna till lineto bestäms med hjälp av random, vilket ger en slumpmässig vandring. nr Mönster nr Mönster 0 EMPTY_FILL 7 HATCH_FILL 1 SOLID_FILL 8 XHATCH_FILL 2 LINE_FILL 9 INTERLEAVE_FILL 3 LTSLASH_FILL 10 WIDE_DOT_FILL 4 SLASH_FILL 11 CLOSE_DOT_FILL 5 BKSLASH_FILL 12 USER_FILL 6 LTBKSLASH_FILL Figur 9.3: Fyllnadsmönster Snögubbe Snart är vintern här och vad kan passa bättre än att rita en snögubbe? 9
9 Exempel 5. 1 #include <graphics.h> 2 int main(void) { 3 int gd=detect,gm,k; 4 initgraph(&gd,&gm,""); 5 setcolor(white); 6 setbkcolor(lightgray); 7 cleardevice(); 8 setfillstyle(solid FILL,WHITE); 9 circle(320,400,75); 10 floodfill(320,400,white); 11 fillellipse(320,275,50,50); 12 fillellipse(320,185,40,40); 13 setfillstyle(close DOT FILL,BLUE); 14 bar(305,105,335,150); 15 bar(290,148,350,152); 16 closegraph(); 17 } 5 Först sätter vi ritfärgen till vit, men det är ju onödigt eftersom den WHITE är default. 6-7 Anropet setbkcolor(lightgray) fyller hela skärmen med en ljusgrå färg, när anropet cleardevice, som rensar skärmen, exekveras. 8 Eftersom snögubbar är vita väljer vi WHITE, som målarfärg. 9 Den undre av de tre snöbollarna skapar vi genom att först rita en ofylld cirkel. Funktionen circle har tre parametrar centrumkoordinaterna x och y och radien r. 10 Vi målar sedan cirkeln vit genom floodfill Ett annat och kanske något enklare sätt att skapa en fylld cirkel kan åstadkommas med funktionen fillellipse. Funktionen har fyra parametrar centrumkoordinater, radie i x-led och radie i y- led. I matematiken kallas diametrarna till en ellips för storaxel och lillaxel. Väljer vi de två sista parametrarna lika, får vi en fylld cirkel. Fyllningen bestäms av senaste setfillstyle. Eftersom formen för objektet är känd behöver ingen gränsfärg anges. 10
10 9.1 Grafik När nu de tre snöbollarna är på plats är det dags för stormhatten. Med funktionen bar kan man direkt rita en fylld rektangel. De fyra parametrarna bestäms av rektangelns övre vänstra hörn och nedre högra. Eftersom vi inte vill ha en vit hatt ändrar vi fyllnadsfärgen och även fyllnadsstilen. Vi passar på att experimentera med CLOSE_DOT_FILL. 15 Med samma teknik kan vi sedan fixa till cylinderhattens brätte. nr Teckensnitt 0 DEFAULT_FONT 1 TRIPLEX_FONT 2 SMALL_FONT 3 SANS_SERIF_FONT 4 GOTHIC_FONT Figur 9.4: Teckensnitt Text Att skriva på skärmen i grafisk mod är inte lika enkelt som i textmod. Man kan inte använda printf, utan istället funktionerna outtext och outtextxy. De är dessa funktioner som detta exempel bland annat handlar om. Exempel 6. 1 #include <conio.h> 2 #include <graphics.h> 3 #include <dos.h> 4 void nasta(void) { 5 delay(1000); 6 cleardevice(); 7 } H En liten enkel funktion som fördröjer exekveringen i 1 sekund = 1000 millisekunder. Funktionen delay som inte tillhör ANSI C når man genom dos.h. 11
11 1 int main(void) { 2 int gd=detect,gm,x,y,k; 3 initgraph(&gd,&gm,""); 4 settextstyle(triplex FONT,HORIZ DIR,3); 5 moveto(100,100); 6 outtext("hej"); 7 nasta(); 8 for(k=1;k<=10;k++){ 9 settextstyle(sans SERIF FONT,HORIZ DIR,k); 10 x=100; y=100; 11 outtextxy(x,y,"hej"); 12 nasta(); 13 } 14 line(320,0,320,479); 15 line(0,240,639,240); 16 setcolor(lightcyan); 17 settextstyle(default FONT,HORIZ DIR,4); 18 settextjustify(center TEXT,CENTER TEXT); 19 outtextxy(320,240,"programmering"); 20 nasta(); 21 closegraph(); 22 } 4 Första funktionen som vi inte känner igen från tidigare. I det grafiska systemet finns fem teckensnitt, som kan användas för utskrift av text i grafisk mod. Utskriften kan göras i antingen horisontell eller vertikal riktning och i tio olika storlekar (1 10). Med hjälp av funktionen settextstyle väljes dessa tre parametrar. De tillgängliga teckensnitten presenteras i tabell 9.4 ovan och även de två riktningarna i tabell För att skriva ut en text på en bestämd plats på skärmen kan man först flytta cursorn till aktuell plats med moveto och därefter skriva ut texten med outtext( Önskad text ). Mer om den angivna koordinaten senare Denna slinga skriver ut ordet HEJ tio gånger och använder sig av teckensnittet SANS_SERIF. För varje gång ökas storleken med 1. Observera att vi förstås anropar funktionen settextstyle med 12
12 9.2 Övningsuppgifter alla dess parametrar varje gång, även om det bara är storleken som ska ändras. 11 Som ett alternativ till kombinationen move och outtext för att placera text på skärmen kan outtextxy användas. Funktionen inrymmer förutom själva texten då också x- och y-koordinat för var den ska hamna. 28 Funktionen settextjustify bestämmer hur texten ska placeras i förhållande till de angivna koordinaterna. I tabellen nedan anges de tre möjligheterna för varje riktning och i programmet demonstreras ett av dessa val i relation till ett ritat hårkors nr Riktningar 0 HORITZ_DIR 1 VERT_DIR Figur 9.5: Riktningar vid utskrift av text Rikt nr Justering horiz 0 LEFT_TEXT 1 CENTER_TEXT 2 RIGHT_TEXT vert 0 BOTTOM_TEXT 1 CENTER_TEXT 2 TOP_TEXT Figur 9.6: Textens placering i förhållande till (x,y) 9.2 Övningsuppgifter Uppgift 9-1. Spiralerna En spiral ritas på skärmen. Spiralen ska ha någon av de två formerna i figur 9.7 eller figur 9.8. Exekveringen inleds med en fråga, vars svar ska 13
13 Figur 9.7: Den kvadratiska spiralen bestämma vilken. Teori: Båda spiralerna utgår från en pixel i skärmens centrum (finns fyra att välja mellan) och växer sedan, tills den just når utanför skärmen. För den runda spiralen startar man med en given radie och en vinkel. I en loop ökas vinkeln med ett konstant steg. Radiens längd ökas på samma sätt genom addition av en konstant. Du får själv prova ut lämpliga värden på dessa två konstanter. De nya koordinaterna bestäms med hjälp av trigonometri varefter en linje dras mellan den nya och den gamla punkten. Observera att, hur rund en datorgenererad cirkel eller båge än tycks vara är den alltid uppbyggd av ett antal raka streck! För den kvadratiska spiralen gäller helt andra idéer. Spiralens första och andra streck är lika långa (exempelvis 4 pixels). Därefter ökas strecklängden (lika mycket varje gång) och används två gånger. Detta fortgår sedan i en loop tills stoppkriteriet är uppfyllt. Den färdigritade spiralen ska stanna på skärmen tills ENTER trycks ned. 14
14 9.2 Övningsuppgifter Figur 9.8: Så som vi i första hand tänker oss en spiral Uppgift 9-2. Byn I den här uppgiften ska du måla en tavla! På tavlan ska finnas röda stugor och hängbjörkar, tillsammans en liten svensk sommarby. Teori: I figur 9.9 ser du hur huset ska se ut. En röd stuga, med tegelrött tak och två fönster. Alla hus på tavlan ska vara identiska, endast skalan med vilket husen ritas och placeringen varieras. På samma sätt ser vi att trädet består av en ellips (bladverket) och en rektangel (stammen). I detta program spelar slumpen stor roll. Med hjälp av rand-funktionen bestämmer programmet objektens placering och skala. Som ett ledvärde kan sägas att husets höjd är 80 pixels och bredd är 90 pixels i skalan 1 : 1. Skalan ska sedan slumpas fram mellan 1 : 2 (litet hus) och 3 : 2 (stort hus), ett slumptal i intervallet [ ] hur åstadkommer vi det? Den här uppgiften har du möjlighet att ge din egen utformning. Det enda viktiga är att där finns hus och träd. Egentligen borde det vara så att små hus och träd befinner sig närmare horisonten och kanske delvis skymds av närmare placerade hus, men det får bli en annan gång. 15
15 Figur 9.9: En datorgenererad by Antalet hus och träd ska vara hårdkodade konstanter i programmet. Rita först 50 träd, därefter 30 hus och till sist 15 träd, som alltså kommer i förgrunden. Genom funktionen srand ser man till att två tavlor aldrig blir lika. Varken hus eller träd behöver i sin helhet hamna på skärmen. Tavlan ska stanna på skärmen tills ENTER trycks ned. Figur 9.10: De studsande bollarna 16
16 9.2 Övningsuppgifter Uppgift 9-3. Animering Denna uppgift är en enkel introduktion till att få föremål att röra sig på skärmen att animera. Teori: Det hela går helt enkelt till så här: Bilden ritas ut på skärmen. Förblir där under en kort stund. Bilden tas bort genom att rita om den med bakgrundsfärgen. Bestämma nya x- och y-koordinater Rita om figuren på den nya platsen. I uppgiften ska två gula ringar sväva fritt på skärmen. När de når kanten, den vita ramen, studsar de enligt lagen: infallsvinkeln är lika med reflektionsvinkeln. Alla vinklar som förekommer är en multipel av 45, vilket betyder att absolutbeloppet av x- och y-koordinaternas förändring, att x och y mellan två uppritningar alltid är lika stora. De två ringarna tänks sväva i olika plan och kommer aldrig i beröring med varandra. Färger och radier kan väljas fritt. Lämpligen kan ringarnas radie sättas till 20 pixels. Programmet stannar efter 10 studsar för den ena bollen. På samma sätt har ringarnas utgångsläge hårdkodats. Med hjälp av delay-funktionen kan förloppet bromsas in. Vilket värde (i ms) delay ska ges beror av bland annat processor och grafikkort. Prova dig fram. Uppgift 9-4. Kastparabeln Från gymnasiet har du kunskaper om kastparabeln eller hur? Nu är det dags att visa förloppet på dataskärmen. Använd samma animeringsteknik som den som beskrevs i uppgift 9.2 Teori: Från fysikboken hämtar vi två formler: x = v 0 t sinα y = v 0 t cosα gt2 2 17
17 Figur 9.11: Kanonkulan på väg mot sitt mål v 0 är utgångshastigheten i m/s, t är den tid i s som gått sedan utkastet skedde och α är utkastvinkeln i grader. g är accelerationen, 9.81m/s 2, duger bra. x och y ger koordinaterna i m för var objektet befinner sig vid given tid. Det är all teori, det återstår dock en del intrimning. Modellen ska skalas så att objektet landar ungefär i skärmens nedre högra hörn då utgångshastigheten är 32m/s med utkastvinkeln 45. Tiden t startar med 0 vid utkastet och stegar fram i loopen. Vilket steg kan vara lämpligt? Dessutom ska programmet inledas med en dialog liknade denna: Utgångshastighet (m/s) : Utkastvinkel (grader) : Ta bort (ja=1) (nej=0) : Upprepa (ja=1) (nej=0) : Antal upprepningar : Svarar man nej på frågan om TA BORT kommer gamla objekt att stanna kvar på skärmen. Svara på frågan UPPREPA ska man bara kunna göra om frågan TA BORT har besvarats med ja. Att upprepa innebär att kastandet sker ett givet antal gånger i följd. Den sista bilden ska ligga kvar tills man trycker på ENTER. Det är inte så viktigt var objektet stannar, antingen då periferin når y- 18
18 9.2 Övningsuppgifter koordinaten 479 eller då objektets centrum gör det. Objektet är en fylld cirkel med radien 10 pixels. Figur 9.12: Din klocka behöver inte ha några siffror Uppgift 9-5. Klockan En gammal hederlig programmeringsuppgift att skapa en klocka med roterande visare. Skriv ett program som simulerar en klocka sekund för sekund från 12 : 00 till 13 : 00 Teori: Under programmets exekvering ska alltså varje sekund från 12 : 00 till 13 : 00 visas. Detta betyder att sekundvisaren kommer att snurra 60 varv, minutvisaren ett varv och att timvisaren kommer att vrida sig 30. Samma animeringsteknik som i uppgift 9.2 används. De tre visarna ges olika färg och består av endast en linje. Alla tre visarna ritas om varje sekund. I loopen måste man alltså hela tiden hålla reda på var alla tre visarna befinner sig. Även i detta program behövs delay-funktionen för att man ska hinna se visarna, framför allt sekundvisaren. Det går dock inte att få klockan att gå rätt genom att försöka justera in argumentet för delay. En framkomlig väg för att få klockan att gå rätt är i stället att läsa av datorns interna klocka. Men det klarar vi inte ännu. 19
19 Bilden ska stanna kvar på skärmen tills ENTER trycks ned. Figur 9.13: Sex skott från en darrig hand Uppgift 9-6. Måltavlan Denna uppgift är kanske lite väl lekfull. Hur som helst, här handlar det om att på skärmen rita en måltavla med tio ringar i glada färger. Sex skott ska skjutas mot tavlan, resultatet beräknas och presenteras. Teori: För att skjutandet inte ska bli helt slumpmässigt inleds exekveringen med frågan: Hur stadig. Svaret på denna fråga, ett tal mellan 0 och 100, anger hur stadig vår skytt är på handen. Talet 0 kommer att ge alla skott mitt i prick. Ju högre talet sedan väljes desto ostadigare blir vår skytt. De koordinater i vilket skottet hamnar bestäms av två, så kallade normalfördelade slumptal. Här är formlerna som du direkt kan använda: x = 320+v 2 lnr 2 cos(2πr 1 ) y = 240+v 2 lnr 4 cos(2πr 3 ) v är det inmatade talet (variansen) och r 1...r 4 är alla reella slumptal i intervallet [0, 1). Den yttersta ringen ska ha radien 200 pixels och centrum ska ligga i (320, 240), (för att formlerna ovan ska fungera). Radien minskas redan 20
20 9.2 Övningsuppgifter med 20 pixel för varje ny ring. Poängen bestäms av den högsta ringens poäng i vilken någon del av skottet hamnar. Figur 9.14: En typisk lördagspromenad Uppgift 9-7. Den vandrande teknologen Denna uppgift simulerar promenaden hem för en teknolog, en vanlig lördag. Längst ned i vänstra hörnet ligger krogen (gul). Högst upp i högra hörnet ligger studentens lya (ljusröd). Dessutom finns ett antal hus (vita) som vår student ska passera. Figur 9.15: De åtta riktningarna Teori: Alla hus har dimensionerna 30x30 pixels. De åtta vita husen kan placeras var som helst på skärmen. Dessutom är hela området (skärmen) omsluten av en vit mur. Studenten börjar sin marsch i (15,464), i en slumpmässigt (av åtta möjliga, se figur 9.15), vald riktning. Promenaden 21
21 fortsätter sedan tills teknologen stöter på en vit pixel (går in i väggen). Då slumpas en ny riktning fram (bland de åtta) och promenaden fortsätter. Promenaden lämnar spår efter sig i form av ljusblå, LIGHTCYAN, streck. Hela promenaden är över när han når hemmet, träffar på en röd pixel. Promenadens totala längd presenteras, där vi antar att en pixel är 1m i kvadrat. Observera att de diagonala stegen då måste bli 2m. Figur 9.16: Skymda linjer Uppgift 9-8. Skymda linjer Skymda linjer är ett begrepp i computer graphics, det handlar om de streck som inte syns i en bild på grund av att de ligger bakom andra ytor. Denna uppgift vill ge en första inblick i problematiken kring hidden lines, även om den bara handlar om 2D-grafik. Teori: Mitt på skärmen placeras en rektangel med måtten 320x240. Nu ska ett antal linjesegment ritas in på skärmen. Normalt slumpas ändpunkterna fram och markeras på skärmen. När sedan linjen ritas in ska den del som eventuellt ligger bakom rektangeln inte synas. Det finns nu två olika sätt att angripa detta problem. Antingen bestämmer man ekvationen för den linje som går genom de två punkterna och sedan bestäms skärningspunkterna mellan denna linje och de fyra linjerna som bildar rektangeln. Den del, eller delar av linjen, som ligger utanför rektangeln kan sedan ritas in. 22
22 9.2 Övningsuppgifter Ett annat och kanske det enklaste sättet är att i stället för line-funktionen använda putpixel, som placerar ut en pixel i taget. Den här metoden fungerar enkelt så länge man rör sig med vågräta och lodräta streck. För att klara vilket streck som helst bör du följa följande algoritm, skriven i pseudokod. Det två framslumpade punkterna har koordinaterna (x 1,y 1 ) och (x 2,y 2 ) m tilldelas det största värdet av x 2 x 1 och y 2 y 1 dx = (x 2 x 1 )/m dy = (y 2 y 1 )/m x = dx+0.5 y = dy+0.5 I en loop som snurrar m varv markeras nu en pixel i taget med koordinaterna x och y. För varje varv ökas sedan x med dx och y med dy Till detta kommer, att se upp med, när (x,y) ligger innanför rektangeln. Figur 9.17: Den roterande kvadraten 23
23 Uppgift 9-9. Rotation Att flytta, skala och rotera grafiska objekt på skärmen är andra viktiga funktioner för den som vill lära sig mer om datorgrafik. I denna uppgift ska vi rotera en kvadrat, dels runt sin egen mittpunkt och dessutom, kanske, kring skärmens mittpunkt. Teori: När vi ska rotera en kvadrat kring sitt eget centrum handlar det om att bestämma vilka nya koordinater de fyra hörnpunkterna får efter vridningen. Hörnet (x 1,y 1 ) kommer att hamna i (x 2,y 2 ) då kvadraten vrids vinkeln α. Här har du formlerna x 2 = x 1 cosα y 1 sinα y 2 = x 1 sinα y 1 cosα Dessa formler fungerar direkt om kvadratens centrum ligger i origo, eftersom formlerna är till för att rotera en punkt vinkeln α kring punkten (0,0). Att flytta en kvadrat på skärmen innebär bara att lägga till (eller subtrahera) samma värde till samtliga x-koordinater och ett annat till samtliga y-koordinater. Att rotera en kvadrat kring sin centrumpunkt, som inte ligger i origo innebär alltså att: flytta rotationspunkten till origo och låta hörnpunkterna följa med rotera den med formlerna ovan flytta tillbaka rotationspunkten och hörnpunkterna. rita ut kvadraten i sitt nya läge. Att sedan rotera den kring skärmens mittpunkt är samma sak fast med en annan rotationspunkt. Uppgift Skalbaggarna Så till ett klassiskt problem. Man skulle kunna säga ett program med många buggar. I vart och ett av en kvadrats fyra hörn sitter en kärlekskrank skalbagge. Med kärlekskrank avses här, längtan efter sällskap. Skalbaggarna startar därför, i samma ögonblick och med samma, 24
24 9.2 Övningsuppgifter Figur 9.18: Detta mönster bilar skalbaggarna hastighet närmandet till en granne. A promenerar mot B, B mot C, C mot D och D mot A. Uppgiften består nu i att på datorskärmen visa denna promenad tills minst två skalbaggar möts. Teori: Hela skeendet delas in i ett antal ögonblick. Under varje ögonblick hinner skalbaggen en viss, bestämt sträcka, ett steg utefter en rät linje. Denna linje bestäms av de två skalbaggarnas placering vid ögonblickets början. I programmet håller du reda på de fyra skalbaggarnas placering i form av skärmkoordinater (x och y). Ge dem en startposition, som verkligen bildar hörnen i en kvadrat. Du kommer att behöva två uppsättningar koordinater för varje skalbagge en där skalbaggen befinner sig just nu och en där skalbaggen kommer att hamna efter den lilla förflyttningen. I en loop bestämmer du nu i varje varv, för varje par av skalbaggar, se figur 9.19, avståndet mellan två skalbaggar. Eftersom du bestämt steget, som en konstant i början av programmet kan du nu med hjälp av likformighet beräkna x och y, och sedan den plats där skalbaggen kom- 25
25 Figur 9.19: Triangeln som ger dig en idé om hur beräkningarna görs mer att hamna. När skalbaggens nya position är bestämd, kan en linje dras mellan den gamla punkten och den nya. När de nya positionerna är bestämda för samtliga fyra insekter, kan linjer dras också mellan skalbaggarna. Loopen exekveras, för enkelhets skull, ett bestämt antal varv, tillräckligt många för att inget mer kommer att hända på skärmen. 9.3 Lösningsförslag Uppgift 9-1. Spiralerna 1 #include <stdio.h> 2 #include <graphics.h> 3 #include <math.h> 4 #include <conio.h> 5 int main(void){ 6 int graphdriver=detect,graphmode,v,x,y,typ; 7 int langd=0,delta=3,steg=0; 8 float r,pi= ; 9 printf("rund=1 Kantig=2 : "); 10 scanf("%d",&typ); 11 initgraph(&graphdriver,&graphmode,""); 12 moveto(320,240); H I en brytningstid mellan hela koden i main eller att dela upp i flera funktioner inleder vi här med det förra. Det hade gått alldeles 26
26 9.3 Lösningsförslag utmärkt att låta en funktion ta hand om den runda spiralen och en annan om den kvadratiska Här ställs frågan om vilken spiral som ska ritas Grafiken initieras och cursorn flyttas till skärmens centrum, där ritandet ska börja. 1 if (typ==1) { 2 r=1; v=0; 3 do{ 4 x=(int)(320+r cos(pi v/180.0)); 5 y=(int)(240+r sin(pi v/180.0)); 6 lineto(x,y); 7 r+=0.1; v+=10; 8 } while (x>=0 && x<=639 && y>=0 && y<=479); 9 } H Här hanteras den runda spiralen. 2 Radien r startar med värdet 1 pixel och vinkeln v med En do-loop som inte avbryts förrän vi når skärmens kanter med ritandet. 4-5 x och y ökas med x- respektive y-komposanten av den vektor, som har längden r och bildar vinkeln v med den positiva x-axeln. Beräkningarna sker i float, men resultatet huggs av till int för att passa parametrarna i lineto. Utför man inte denna konvertering får man under kompileringen en varning, som man i och för sig kan överse med. 6 Vi drar en linje till den just beräknade punkten, från den plats där cursorn befinner sig. Vi vet att systemet därefter uppdaterar cursorns placering till (x, y). Om vi varit riktigt noggranna hade vi testat att (x,y) ligger på skärmen, innan vi drar strecket. Nu är det i och för sig tillåtet att rita utanför skärmen även om det inte ger någon synlig effekt. 7 För att få effekten av en spiral ökar vi radien inför nästa varv samtidigt med vinkeln. Hur stor ökningar vi ska göra av r och v testar vi ut genom att köra programmet för olika värden. 27
27 1 else { 2 x=320; y=240; moveto(x,y); 3 while (x<639 && x>0 && y<479 && y>0) { 4 steg++; 5 if(steg%2==0) langd++; 6 switch (steg%4) { 7 case 1: x=x+langd delta; break; 8 case 2: y=y+langd delta; break; 9 case 3: x=x langd delta; break; 10 case 0: y=y langd delta; break; 11 } 12 lineto(x,y); 13 } 14 } 15 closegraph(); 16 } H Som utlovats, en helt annan strategi för den fyrkantiga spiralen. Linjerna som successivt kommer att öka i längd kan ritas i fyra olika riktningar. Denna gång snurrar vi i en while-loop och håller samtidigt reda på i vilken av fyra moder vi befinner oss. 2 x och y ges startvärden och cursorn flyttas till skärmens mitt En loop med samma avbrottskriterier, som för den andra spiralen. 4 Varvräknaren steg, som vi måste ha för att hålla reda på i vilken mod vi befinner, ökas med 1. 5 Om antalet tagna steg är jämnt är det dags att ändra längden, langd, av det streck som ska ritas Vi ser att beroende på steg%4 kommer antingen x eller y att ökas eller minskas med ett antal pixels, som i sin tur beror på langd och konstanten delta, som här är 2 och bestämmer hur tät spiralen kommer att bli. 12 När den nya punkten är beräknad kan linjen ritas ut. 28
28 9.3 Lösningsförslag Uppgift 9-2. Byn 1 #include <graphics.h> 2 #include <time.h> 3 void trad(int n){ 4 int k,x,y; 5 float skala; 6 for(k=1;k<=n;k++){ 7 x=rand()%640; 8 y=rand()%480; 9 skala=(rand()%11+5.0)/10; 10 setcolor(lightgreen); 11 setfillstyle(solid FILL,GREEN); 12 fillellipse(x,y,(int)(skala 20),(int)(skala 40)); 13 setcolor(brown); 14 setfillstyle(solid FILL,BROWN); 15 bar((int)(x skala 6),(int)(y+skala 30), 16 (int)(x+skala 6),(int)(y+skala 60)); 17 } 18 } H Här har vi delat upp programmet i två funktioner förutom main. En som ritar träd och en som ritar hus. Trädet består som vi tidigare sagt av en grön ellips, bladverket, och en brun rektangel, stammen. 3 Indata till funktionen trad är n som anger hur många träd som ska ritas Denna loop åstadkommer ett träd per varv. 7-8 Bestämmer trädets placering på skärmen. Vi behöver inte ta hänsyn till att trädet, i sin helhet, får plats. (x,y) används som centrum för ellipsen som utgör bladverket. 9 Här beräknar vi med hjälp av slumpen den skala vi ska använda, ett tal i intervallet Färger sätts och bladverket ritas. För skalan 1 : 1 använder vi konstanterna 20 och Färger sätts och stammen ritas. Det krävs lite eftertanke för att få stammen rätt placerad i förhållande till bladverket. Stammen i skala 1 : 1 har dimensionerna pixels. 29
29 1 void hus(int n){ 2 int x,y,k; 3 float skala; 4 for(k=1;k<=n;k++){ 5 x=rand()%640; 6 y=rand()%480; 7 skala=(rand()%11+5.0)/10; 8 setfillstyle(solid FILL,RED); 9 bar(x,y,(int)(x+80 skala),(int)(y+60 skala)); 10 setfillstyle(solid FILL,LIGHTRED); 11 bar((int)(x 12 skala),(int)(y 20 skala), 12 (int)(x+92 skala),y); 13 setfillstyle(solid FILL,WHITE); 14 bar((int)(x+10 skala),(int)(y+10 skala), 15 (int)(x+30 skala),(int)(y+50 skala)); 16 bar((int)(x+50 skala),(int)(y+10 skala), 17 (int)(x+70 skala),(int)(y+50 skala)); 18 setfillstyle(solid FILL,BLUE); 19 bar((int)(x+13 skala),(int)(y+13 skala), 20 (int)(x+27 skala),(int)(y+47 skala)); 21 bar((int)(x+53 skala),(int)(y+13 skala), 22 (int)(x+67 skala),(int)(y+47 skala)); 23 } 24 } H Tekniken för att rita huset är den samma. Funktionen hus har n som indata, ett värde som anger hur många hus som ska ritas Ett varv i denna loop skapar en röd liten stuga. 8-9 Först ritas den röda väggen Sedan är det takets tur Två vita rektanglar som fönsterkarmar Avslutas med två mörkblå rektanglar över de vita som själva fönstren. 30
30 9.3 Lösningsförslag 1 int main(void) { 2 srand(time(0)); 3 int gd=vga,gm=vgahi; 4 initgraph(&gd,&gm,""); 5 setbkcolor(lightgray); 6 cleardevice(); 7 trad(50); 8 hus(30); 9 trad(15); 10 closegraph(); 11 } H Huvudfunktionen har nu bara att anropa våra tidigare skrivna funktioner för att vår sommartavla ska bli fullständig. 5-6 Vi väljer ljusgrå som bakgrundsfärg, som träder i kraft i samband med cleardevice. Uppgift 9-3. Animering 1 #include <graphics.h> 2 #include <dos.h> 3 int main(void){ 4 int gd=vga,gm=vgahi,ax,ay,bx,by,ariktx; 5 int arikty,briktx,brikty,studs=0; 6 initgraph(&gd,&gm,""); 7 ax=20; ay=240; ariktx=1; arikty=1; 8 bx=618; by=240; briktx= 1; brikty=1; 9 moveto(0,0); lineto(639,0); lineto(639,479); 10 lineto(0,479); lineto(0,0); 4-10 Deklaration och initiering av variabler, initiering av grafiken och uppritande av ramen. 31
31 1 while (studs<10) { 2 setcolor(yellow); 3 circle(ax,ay,20); 4 circle(bx,by,20); 5 delay(1); 6 setcolor(black); 7 circle(ax,ay,20); circle(bx,by,20); 8 ax=ax+ariktx; bx=bx+briktx; 9 ay=ay+arikty; by=by+brikty; 10 if (ax==618) {ariktx= 1; studs++;} 11 if (ax==21) {ariktx=1; studs++;} 12 if (ay==458) {arikty= 1; studs++;} 13 if (ay==21) {arikty=1; studs++;} 14 if (bx==618) briktx= 1; 15 if (bx==21) briktx=1; 16 if (by==458) brikty= 1; 17 if (by==21) brikty=1; 18 } 19 closegraph(); 20 } 1-18 Programmet består av en enda loop som exekveras till antalet studsar hos den ena ringen har blivit 10. Den ena ringens placering bestäms av ax och ay och den andra av koordinaterna bx och by. 2-5 Vi sätter ritfärgen till YELLOW, ritar ut de båda cirklarna, väntar 1 ms. 6-7 Vi ställer om färgen till BLACK (samma färg som bakgrunden) och ritar cirklarna igen. Nu är de borta! 8-9 Koordinaterna ändras med en pixel i både x- och y-led. I vilken riktning förflyttningen av den första cirkeln sker, avgörs av värdet hos ariktx och arikty. Dessa värden ställs om varje gång cirkeln studsar mot ramen. Inledningsvis har de båda värdena 1 och cirkeln förflyttar sig därför snett ned åt höger För att avgöra om första cirkeln nått ramen. Beroende på om det är en lodrät eller vågrät vägg som nåtts ställs antingen ariktx eller arikty om, samtidigt som antalet studsar räknas upp. 32
32 9.3 Lösningsförslag Samma för den andra cirkeln men nu räknar vi inte studsar. Uppgift 9-4. Kastparabeln 1 #include <graphics.h> 2 #include <math.h> 3 #include <dos.h> 4 int main() { 5 int graphdriver=detect,graphmode,a,v0,tabort; 6 int upprepa,antal=1,fordroj,varv; 7 float x,y,t,pi= ; 8 printf("utgångshastighet : "); 9 scanf("%d",&v0); 10 printf("utgångsvinkel : "); 11 scanf("%d",&a); 12 printf("ta bort (j=1) (n=0) : "); 13 scanf("%d",&tabort); 14 if (tabort) { 15 printf("upprepa (j=1) (n=0) : "); 16 scanf("%d",&upprepa); 17 if (upprepa) { 18 printf("antal upprepningar : "); 19 scanf("%d",&antal); 20 } 21 } 22 printf("fördröjning (ms) : "); 23 scanf("%d",&fordroj); 24 initgraph(&graphdriver,&graphmode,""); 9-24 Nästan halva programmet består av kod för att läsa in alla uppgifter. 16 Variabeln tabort ska ha värdet 0 eller 1. Då tabort är 1 blir villkoret i if-satsen sant. 33
33 1 for (varv=1; varv<=antal; varv++) { 2 cleardevice(); 3 t=0; x=1.0; y=1.0; 4 while (y>=0) { 5 if (tabort) { 6 setcolor(black); 7 setfillstyle(solid FILL,BLACK); 8 fillellipse((int)(7 x),(int)( y),10,10); 9 } 10 t+=0.02; 11 x=v0 t cos(a pi/180); 12 y=v0 t sin(a pi/180) 9.81 t t/2; 13 setcolor(yellow); 14 setfillstyle(solid FILL,YELLOW); 15 fillellipse((int)(7 x),(int)( y),10,10); 16 delay(fordroj); 17 } 18 } 19 setcolor(lightred); 20 settextstyle(triplex FONT, HORIZ DIR, 4); 21 settextjustify(center TEXT,CENTER TEXT); 22 outtextxy(320,240,"klart"); 23 closegraph(); 24 } 1-18 Variabeln antal har minst värdet 1 vilket betyder att for-loopen kommer att göra minst ett varv vi kommer att kasta föremålet minst en gång. 2-3 Vi börjar med att rensa skärmen, sätta tiden till 0 och föremålets utgångsläge till (1,1). 4 Så länge centrum för föremålet håller sig ovanför marken kommer denna while-loop att exekveras. 5-9 Om föremålet ska tas bort, innan den ritas ut igen i nytt läge, så måste vi rita ut en svartmålad cirkelskiva på den plats där föremålet just nu befinner sig. 10 Tiden stegas fram med 2 hundradels sekunder. Ett värde vi experimenterat oss fram till De fysikaliska formlerna, översatta till C, ger värden till de nya koordinaterna (x, y). 34
34 9.3 Lösningsförslag Föremålet ritas ut på den nya platsen. 16 Innan vi går vidare med nästa varv i while-loopen väntar vi fordroj millisekunder. En tid som inte är direkt kopplad till t i formlerna När simuleringen är klar skrivs texten KLART ut i ljusrött, mitt på skärmen. Uppgift 9-5. Klockan 1 #include <graphics.h> 2 #include <dos.h> 3 #include <math.h> 4 int main(void){ 5 int gd=vga,gm=vgahi,v,k,min,sek,x,y; 6 float pi= ; 7 float sekv,sekx,seky,minv,minx,miny,timv,timx,timy; 8 char tid[3]; 9 initgraph(&gd,&gm,""); 10 setfillstyle(solid FILL,RED); 11 fillellipse(320,240,220,220); 12 setfillstyle(solid FILL,BLACK); 13 fillellipse(320,240,180,180); 14 settextstyle(default FONT,HORIZ DIR,2); 15 settextjustify(center TEXT,CENTER TEXT); 16 v=60; 17 setbkcolor(red); 18 for (k=1;k<=12;k++) { 19 x=(int)( cos(v pi/180)); 20 y=(int)( sin(v pi/180)); 21 itoa(k,tid,10); 22 outtextxy(x,480 y,tid); 23 v =30; 24 } Urtavlan kommer på plats. Först målar vi en stor röd cirkelskiva, inuti den en mindre svart cirkelskiva Vi överarbetar urtavlan något, genom att placera ut siffror runt om. I loopen räknar vi ut (x,y) som centrum för siffran med hjälp av trigonometri. 35
35 21 Med hjälp av funktionen itoa översätter vi ett heltal till en sträng. 22 Siffran skrivs ut. I rad 15 har vi bestämt att texten ska centreras kring (x,y). 23 Vinkeln v justeras inför nästa varv. 1 for (k=0;k<=3600;k++) { 2 if (k>0) { 3 setcolor(black); 4 line(320,240,(int)sekx,(int)(480 seky)); 5 line(320,240,(int)minx,(int)(480 miny)); 6 line(320,240,(int)timx,(int)(480 timy)); 7 } 8 min=k/60; 9 sek=k%60; 10 sekv=90 sek 6; 11 minv=90 min 6 sek 0.1; 12 timv=90 min 0.5 sek/120.0; 13 sekx= cos(sekv pi/180); 14 seky= sin(sekv pi/180); 15 minx= cos(minv pi/180); 16 miny= sin(minv pi/180); 17 timx= cos(timv pi/180); 18 timy= sin(timv pi/180); 19 setcolor(lightred); 20 line(320,240,(int)sekx,(int)(480 seky)); 21 setcolor(yellow); 22 line(320,240,(int)minx,(int)(480 miny)); 23 setcolor(lightcyan); 24 line(320,240,(int)timx,(int)(480 timy)); 25 delay(10); 26 } 27 getch(); 28 closegraph(); 29 } 1-26 Klockan ska nu ticka fram en timme. Ett varv i denna loop motsvarar en sekund. Tiden för att exekvera ett varv i loopen kommer dock att ta betydligt kortare tid än en sekund och därför kommer klockan 36
36 9.3 Lösningsförslag inte att gå rätt. Det är klart, att om man successivt ökar fördröjningen, kommer klockan att gå allt bättre (sekx,seky) är yttersta spetsen på sekundvisaren. Med dessa och motsvarande variabler för de andra visarna kan vi nu ta bort dem, genom att rita med BLACK 8-9 Vi vet hur många sekunder det hittills gått och kan därför dela upp den tiden i minuter och sekunder Nu kan vi ta reda på vilka vinklar visarna har. Vi mäter dessa vinklar mot positiva x-axeln, som vanligt. Klockan 3 för timvisaren, motsvarar alltså 0. 1 sekund för sekundvisaren innebär en förändring av vinkeln med 6. Eftersom visarna hos en klocka går medurs, subtraherar vi denna vinkel från tidigare Med hjälp av trigonometri kan vi nu beräkna de ny koordinaterna för de tre visarnas yttersta spetsar Så är det dags att rita ut dem. Alla i olika färger. Uppgift 9-6. Måltavlan Diskussion: Lösningen till Måltavlan innehåller tre funktioner: ringar, som ritar ut måltavlan, slump, som tar fram ett slumptal i intervallet [0...1] och skjut, som skjuter ett skott mot tavlan. 1 #include <graphics.h> 2 #include <stdio.h> 3 #include <math.h> 4 #include <dos.h> 5 void ringar(void){ 6 int farg,k; 7 farg=0; 8 for(k=10;k>=1;k ){ 9 circle(320,240,20 k); 10 farg++; 11 setfillstyle(solid FILL,farg); 12 floodfill(320,240,white); 13 } 14 } 37
37 8-13 De 10 ringarna ritas med början utifrån. Varje ny ring, som är mindre än tidigare täcker delvis den gamla. Ringarnas färger väljs med nummer, från 10 och nedåt. Observera att vi här, enbart för omväxlingens skull, använder circle och floodfill i stället för fillellipse 1 float slump(void){ 2 return (float)rand()/32768; 3 } 2 rand kan som högst ge tal 32767, vilket betyder att funktionen returnerar ett värde i intervallet int skjut(float var){ 2 float x,y,avstand; 3 int r; 4 char strang[10]; 5 x=sqrt( 2 log(slump())) cos( slump()); 6 x=320+var x; 7 y=sqrt( 2 log(slump())) cos( slump()); 8 y=240+var y; 9 setfillstyle(solid FILL,BLACK); 10 fillellipse((int)x,(int)y,12,12); 11 avstand=sqrt(pow(x 320,2)+pow(y 240,2)) 12; 12 if (avstand<0) avstand=0; 13 r=10 (int)(avstand/20); 14 if (r<0) r=0; 15 itoa(r,strang,10); 16 outtextxy((int)x,(int)y,strang); 17 return 10 int(avstand/20); 18 } 5-8 Med hjälp av den givna formeln kan vi nu räkna ut i vilken punkt (x, y), med måltavlans centrum som origo, skottet skulle ha träffat 38
38 9.3 Lösningsförslag om variansen varit 1. Men nu är variansen, darrigheten, var och vi multiplicerar därför x respektive y med detta tal Vi målar ut den svarta prick, som föreställer skottet. 11 Vi räknar med hjälp av avståndsformeln ut avståndet från måltavlans centrum till närmaste punkten på skottets periferi. 12 Om skottet träffat mitt i prick, eller ganska nära, kan faktiskt formeln ovan ge negativt värde. Något vi i så fall justerar till Vi räknar ut resultatet i poäng. Hamnar man utanför tavlan kan man inte få sämre än 0 poäng Vi skriver in resultatet inuti kulhålet. 17 Poängen skickas till main. 1 int main(void){ 2 int gd=vga,gm=vgahi,k,sum; 3 float var; 4 printf("hur stadig: "); scanf("%f",&var); 5 srand(time(0)); 6 initgraph(&gd,&gm,""); 7 settextjustify(center TEXT,CENTER TEXT); 8 ringar(); 9 sum=0; 10 for(k=1;k<=6;k++){ 11 delay(1500); 12 sum+=skjut(var); 13 } 14 delay(2000); 15 closegraph(); 16 printf("slutresultat: %d ",sum); 17 getch(); 18 } 4 Programmet tar emot uppgift om hur stadig skytten är på handen. 8 Måltavlan ritas ut De sex skotten fyras av. Mellan varje skott låter vi det gå 1.5 sekunder. Det enda indata skjut behöver är måttet av skyttens stabilitet. 16 Resultatet skrivs ut under vanlig textmode. 39
39 Uppgift 9-7. Den vandrande teknologen 1 #include <graphics.h> 2 #include <math.h> 3 #include <dos.h> 4 #include <time.h> 5 int main(void){ 6 int graphdriver=detect,graphmode,manx,many,klart; 7 int deltax,deltay; 8 long int diagonal=0,ortogonal=0; 9 float stracka; 10 initgraph(&graphdriver,&graphmode,""); 11 setfillstyle(solid FILL,WHITE); 12 bar(30,30,60,60); bar(100,120,130,150); 13 bar(200,310,230,340); bar(420,100,450,130); 14 bar(500,320,530,350); bar(0,360,30,390); 15 bar(210,0,240,30); bar(609,150,639,180); 16 setfillstyle(solid FILL,YELLOW); 17 bar(0,449,30,479); 18 setfillstyle(solid FILL,LIGHTRED); 19 bar(609,0,639,30); 20 setcolor(white); 21 moveto(0,0); lineto(0,479); lineto(639,479); 22 lineto(639,0); lineto(0,0); 23 manx=15; many=464; klart=0; srand(time(0)); 24 do { 25 deltax=rand()%3 1; 26 deltay=rand()%3 1; 27 }while (deltax==0 && deltay==0); Åtta vita hus, ett gult och ett rött ritas ut i form av fyllda kvadrater på skärmen En ram runt campus ritas ut. 23 Teknologens startpunkt sätts. Flaggan klart sätts till false En slumpmässig riktning plockas fram. Av de nio möjligheterna är det en, (0,0), teknologen står still, som vi inte accepterar. 40
40 9.3 Lösningsförslag 1 while (klart==0) { 2 if (getpixel(manx+deltax,many+deltay)==white) 3 do { 4 deltax=rand()%3 1; 5 deltay=rand()%3 1; 6 } while (deltax==0 && deltay==0); 7 else { 8 putpixel(manx,many,lightcyan); 9 manx+=deltax; 10 many+=deltay; 11 if (deltax!=0 && deltay!=0) 12 diagonal++; 13 else 14 ortogonal++; 15 putpixel(manx,many,red); 16 } 17 klart=getpixel(manx+deltax,many+deltay)==lightred; 18 delay(1); 19 } 20 setcolor(lightred); 21 settextstyle(triplex FONT, HORIZ DIR, 4); 22 settextjustify(center TEXT,CENTER TEXT); 23 outtextxy(320,240,"hemma"); 24 closegraph(); 25 stracka=sqrt(2) diagonal+ortogonal; 26 printf("framme efter %7.0f meter",stracka); 27 } 1-19 När denna loop har exekverats klart har teknologen hittat hem. Men innan dess väntar en lång förvirrad promenad. 2-6 Med hjälp av getpixel kan man ta reda på vilken färg som finns i angiven pixel. deltax och deltay är ju teknologens förflyttningar i varje steg i x- respektive y-led. Om nästa steg innebär att teknologen skulle ha gått in i väggen, så ändrar vi istället hans riktning Om han befinner sig på annan plats är det bara att stega på i tidigare vald riktning. 8 Han ger ett ljusblått spår ifrån sig i den pixel han nu kommer att lämna. 41
41 9-10 Därefter räknar vi ut var teknologen kommer att hamna efter nästa steg Om steget han just tog var diagonalt räknas det för sig, eftersom det är lite längre. Dessa två variabler ska användas senare för att beräkna hela promenadens längd. 15 Det kommer inte att synas så bra, men den pixel där teknologen befinner sig, är röd. 17 Här tar vi reda på om teknologen är hemma och slår i så fall om flaggan. 18 Sedan väntar vi 1 ms, innan det är dags att ta nästa steg Mitt på skärmen hamnar nu texten HEMMA Vi beräknar och skriver ut hur lång promenaden blev. Uppgift 9-8. Skymda linjer 1 #include <graphics.h> 2 #include <stdio.h> 3 int main(void){ 4 int gd=vga,gm=vgahi,linje; 5 int x1,y1,x2,y2,k,antal=1,val; 6 float m,x,y,dx,dy; 7 printf("egna linjer (1)\n"); 8 printf("slumpade (2)\n"); 9 printf("val : "); 10 scanf("%d",&val); 11 if (val==2) { 12 printf("antal : "); 13 scanf("%d",&antal); 14 } 15 initgraph(&gd,&gm,""); 16 moveto(160,120); lineto(480,120); lineto(480,360); 17 lineto(160,360); lineto(160,120); 18 setfillstyle(solid FILL,LIGHTRED); 19 setcolor(yellow); 7-14 Tar emot indata. Man har möjlighet att, antingen själv ange en linje man vill ha ritad, eller att låta slumpen sköta jobbet. 42
42 9.3 Lösningsförslag Ritar ut rektangeln, under vilken linjerna ska vara dolda Bestämmer färger inför vad som komma ska. 1 for(linje=1;linje<=antal;linje++) { 2 if (val==2) { 3 x1=rand()%640; y1=rand()%480; 4 x2=rand()%640; y2=rand()%480; 5 setcolor(yellow); 6 } 7 else { 8 printf("x1 : "); scanf("%d",&x1); 9 printf("y1 : "); scanf("%d",&y1); 10 printf("x2 : "); scanf("%d",&x2); 11 printf("y2 : "); scanf("%d",&y2); 12 } 13 m=abs(x2 x1); 14 if (abs(y2 y1)>m) m=abs(y2 y1); 15 dx=(x2 x1)/m; dy=(y2 y1)/m; 16 x=x1+0.5; y=y1+0.5; 17 for (k=1;k<m;k++){ 18 if (x<160 x>480 y<120 y>360) 19 putpixel((int)x,(int)y,yellow); 20 x+=dx; y+=dy; 21 } 22 setcolor(lightred); 23 fillellipse(x1,y1,2,2); 24 fillellipse(x2,y2,2,2); 25 } 26 closegraph(); 27 } 1-25 Ett varv i loopen för varje linje Skapar data för linjen som ska ritas. Segmentets ändpunkter (x 1,y 1 ) och (x 2,y 2 ) m antar den största skillnaden mellan antingen x 1 och x 2 eller y 1 och y Hjälpvariabeln m används nu för att bestämma dx och dy. Antingen dx eller dy kommer att bli 1 och den andra < För varje varv i loopen markeras först en punkt på den blivande linjen. Därefter ökas koordinaterna x och y. När loopen har ex- 43
43 ekverats klart har vi ritat en linje mellan (x 1,y 1 ) och (x 1,y 1 ), med eventuellt uppehåll, då vi passerar rektangeln Linjens ändpunkter förses med en röda cirklar. Uppgift 9-9. Rotation 1 #include <graphics.h> 2 #include <dos.h> 3 #include <math.h> 4 int main(void){ 5 int gd=vga,gm=vgahi,val,varv=0; 6 float x1,y1,x2,y2,x3,y3,x4,y4,xc,yc,xt; 7 float a,ar,pi= ,dx,dy,v=0; 8 printf("rotation kring sin egen mittpunkt (1)\n"); 9 printf("dessutom kring skärmens mittpunkt (2)\n"); 10 printf("val: "); 11 scanf("%d",&val); 12 initgraph(&gd,&gm,""); 13 x1=480; y1=220; x2=520; y2=220; x3=520; y3=260; 14 x4=480; y4=260; xc=500; yc=240; a=10; Figur 9.20: I A roterar kvadraten runt sin egen mittpunkt (indata 1). I B roterar kvadraten kring skärmens centrum. C kombinerar A och B (indata 2). 44
44 9.3 Lösningsförslag 8-11 Här bestäms vilken typ av rotation som ska ske Startkoordinaterna för kvadratens hörn bestäms. Även för kvadratens centrum, (x c,y c ), som ju hade kunnat räknas ut. a håller reda på, i grader, med hur stor vinkel kvadraten ska roteras i varje steg, här do { 2 varv++; 3 setcolor(black); 4 line((int)x1,(int)y1,(int)x2,(int)y2); 5 line((int)x2,(int)y2,(int)x3,(int)y3); 6 line((int)x3,(int)y3,(int)x4,(int)y4); 7 line((int)x4,(int)y4,(int)x1,(int)y1); 8 if (val==2) { 9 v+=2 pi/180; 10 dx=xc ( cos(v)); dy=yc ( sin(v)); 11 x1 =dx; y1 =dy; x2 =dx; y2 =dy; x3 =dx; y3 =dy; 12 x4 =dx; y4 =dy; xc =dx; yc =dy; 13 } 14 x1 =xc; x2 =xc; x3 =xc; x4 =xc; 15 y1 =yc; y2 =yc; y3 =yc; y4 =yc; 16 ar=pi a/180; 17 xt=x1 cos(ar) y1 sin(ar); 18 y1=x1 sin(ar)+y1 cos(ar); x1=xt; 19 xt=x2 cos(ar) y2 sin(ar); 20 y2=x2 sin(ar)+y2 cos(ar); x2=xt; 21 xt=x3 cos(ar) y3 sin(ar); 22 y3=x3 sin(ar)+y3 cos(ar); x3=xt; 23 xt=x4 cos(ar) y4 sin(ar); 24 y4=x4 sin(ar)+y4 cos(ar); x4=xt; 25 x1+=xc; x2+=xc; x3+=xc; x4+=xc; 26 y1+=yc; y2+=yc; y3+=yc; y4+=yc; 27 setcolor(yellow); 28 line((int)x1,(int)y1,(int)x2,(int)y2); 29 line((int)x2,(int)y2,(int)x3,(int)y3); 30 line((int)x3,(int)y3,(int)x4,(int)y4); 31 line((int)x4,(int)y4,(int)x1,(int)y1); 32 delay(40); 33 } while (varv<180); 34 closegraph(); 35 } 45
45 1-33 Denna do-loop kommer att exekveras 180 gånger. Varje varv skapar en filmruta. 3-7 Tar bort kvadraten från skärmen, genom att rita med svart färg på svart bakgrund Denna gren av programmet utförs endast om val är 2, om kvadraten ska roteras kring skärmens centrum. v har valts till 2 och r = 180. Skärmens centrum har koordinaterna (320, 240) Förflyttningen av kvadraten i x- respektive y-led bestäms. x och y påverkar de fem punkterna (x 1,y 1 )...(x c,y c ) Kvadraten flyttas, så att centrum hamnar i origo Kvadraten roteras nu runt sin egen centrumpunkt. Vi använder formeln för att räkna ut hörnens nya koordinater Kvadraten flyttas tillbaka Kvadraten ritas ut med gul färg 32 Exekveringen stannar upp i 40 ms innan nästa varv påbörjas Uppgift Skalbaggarna 1 #include <graphics.h> 2 #include <math.h> 3 #include <dos.h> 4 int main(void){ 5 int gd=vga,gm=vgahi,k,l,medkvadrat; 6 float koord[5][2]={{80,0},{559,0}, 7 {559,479},{80,479},{80,0}}; 8 float koord2[5][2],steg[4]; 9 float h,t,n,t1,t2; 10 initgraph(&gd,&gm,""); 11 moveto(( )/2,0); 12 linerel(479,0); linerel(0,479); 13 linerel( 479,0); linerel(0, 479); 14 setcolor(lightcyan); 15 steg[0]=2; steg[1]=2; steg[2]=2; steg[3]=2; 16 medkvadrat=1; 46
PROGRAMMERING A C++ GOTOXY, TEXTCOLOR och GRAPHICS.h. Kompendium med lektionsanteckningar och övningsuppgifter. Stefan Sundin
 PROGRAMMERING A C++ DEL 2 av 2. GOTOXY, TEXTCOLOR och GRAPHICS.h Kompendium med lektionsanteckningar och övningsuppgifter Stefan Sundin Torsbergsgymnasiet Bollnäs GOTOXY och TEXTCOLOR Att styra färg och
PROGRAMMERING A C++ DEL 2 av 2. GOTOXY, TEXTCOLOR och GRAPHICS.h Kompendium med lektionsanteckningar och övningsuppgifter Stefan Sundin Torsbergsgymnasiet Bollnäs GOTOXY och TEXTCOLOR Att styra färg och
TAIU07 Matematiska beräkningar med Matlab
 TAIU07 Matematiska beräkningar med Matlab Laboration 3. Linjär algebra Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion 2 En Komet Kometer rör sig enligt ellipsformade
TAIU07 Matematiska beräkningar med Matlab Laboration 3. Linjär algebra Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion 2 En Komet Kometer rör sig enligt ellipsformade
C++ Slumptalsfunktioner + switch-satsen
 C++ Slumptalsfunktioner + switch-satsen Veckans avsnitt består av ett antal lite udda funktioner man kan ha nytta av när man skriver program. Det är en slumptalsgenerator och lite annat smått och gott.
C++ Slumptalsfunktioner + switch-satsen Veckans avsnitt består av ett antal lite udda funktioner man kan ha nytta av när man skriver program. Det är en slumptalsgenerator och lite annat smått och gott.
Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen.
 Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
4-8 Cirklar. Inledning
 Namn: 4-8 Cirklar Inledning Du har arbetat med fyrhörningar (parallellogrammer) och trehörningar (trianglar). Nu skall du studera en figur som saknar hörn, och som består av en böjd linje. Den kallas för
Namn: 4-8 Cirklar Inledning Du har arbetat med fyrhörningar (parallellogrammer) och trehörningar (trianglar). Nu skall du studera en figur som saknar hörn, och som består av en böjd linje. Den kallas för
Funktioner. Räta linjen
 Sidor i boken 14-143, 145-147 Funktioner. Räta linjen Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter
Sidor i boken 14-143, 145-147 Funktioner. Räta linjen Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter
Matematik med Scratch
 Matematik med Scratch Projekten är indelade efter svårighetsgrad. Ganska enkelt Lite svårare Innehåll Sprajten räknar... 2 Rita geometriska figurer... 3 Stämpla mönster av sprajtar... 6 Rita och räkna
Matematik med Scratch Projekten är indelade efter svårighetsgrad. Ganska enkelt Lite svårare Innehåll Sprajten räknar... 2 Rita geometriska figurer... 3 Stämpla mönster av sprajtar... 6 Rita och räkna
Institutionen för matematik och datavetenskap Karlstads universitet. GeoGebra. ett digitalt verktyg för framtidens matematikundervisning
 Karlstads GeoGebrainstitut Institutionen för matematik och datavetenskap Karlstads universitet Mats Brunström Maria Fahlgren GeoGebra ett digitalt verktyg för framtidens matematikundervisning Invigning
Karlstads GeoGebrainstitut Institutionen för matematik och datavetenskap Karlstads universitet Mats Brunström Maria Fahlgren GeoGebra ett digitalt verktyg för framtidens matematikundervisning Invigning
TANA17 Matematiska beräkningar med Matlab
 TANA17 Matematiska beräkningar med Matlab Laboration 1. Linjär Algebra och Avbildningar Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion I denna övning skall
TANA17 Matematiska beräkningar med Matlab Laboration 1. Linjär Algebra och Avbildningar Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion I denna övning skall
Lösningar till uppgifterna sätts ut på kurssidan på nätet i dag kl 19.00. Tentamen i Programmering C, Fri, Kväll, 041211.
 1(8) ÖREBRO UNIVERSITET INSTITUTIONEN FÖR TEKNIK Lösningar till uppgifterna sätts ut på kurssidan på nätet i dag kl 19.00. Denna tenta kommer att vara färdigrättad Ti 14/12 och kan då hämtas på mitt tjänsterum,
1(8) ÖREBRO UNIVERSITET INSTITUTIONEN FÖR TEKNIK Lösningar till uppgifterna sätts ut på kurssidan på nätet i dag kl 19.00. Denna tenta kommer att vara färdigrättad Ti 14/12 och kan då hämtas på mitt tjänsterum,
Användarhandledning Version 1.2
 Användarhandledning Version 1.2 Innehåll Bakgrund... 2 Börja programmera i Xtat... 3 Allmänna tips... 3 Grunderna... 3 Kommentarer i språket... 4 Variabler... 4 Matematik... 5 Arrayer... 5 på skärmen...
Användarhandledning Version 1.2 Innehåll Bakgrund... 2 Börja programmera i Xtat... 3 Allmänna tips... 3 Grunderna... 3 Kommentarer i språket... 4 Variabler... 4 Matematik... 5 Arrayer... 5 på skärmen...
BMI = (vikt i kg) / (längd i m) 2. Lösningsförslag
 HI1024 TEN2 2013-10-28 Betygsgränser: Fx-8, E-9, D-11, C-12, B-14, A-16 (MAX-18) Generella rättningsnormer: Mycket dåliga variabelnamn ger -1p totalt på provet vid andra tillfället Inga eller dåliga kommentarer
HI1024 TEN2 2013-10-28 Betygsgränser: Fx-8, E-9, D-11, C-12, B-14, A-16 (MAX-18) Generella rättningsnormer: Mycket dåliga variabelnamn ger -1p totalt på provet vid andra tillfället Inga eller dåliga kommentarer
Lösningar Heureka 2 Kapitel 3 Rörelse i två dimensioner
 Lösningar Heureka Kapitel 3 Rörelse i två dimensioner Andreas Josefsson Tullängsskolan Örebro Lösningar Fysik Heureka:Kapitel 3 3.1) Enligt figuren: nordliga förflyttningen: 100+00-100=00m Östliga förflyttningen:
Lösningar Heureka Kapitel 3 Rörelse i två dimensioner Andreas Josefsson Tullängsskolan Örebro Lösningar Fysik Heureka:Kapitel 3 3.1) Enligt figuren: nordliga förflyttningen: 100+00-100=00m Östliga förflyttningen:
Tynker gratisapp på AppStore
 Tynker gratisapp på AppStore Innehåll Använda appen 2 Koordinatsystemet 6 Rita rektanglar i koordinatsystemet 7 Rita ellipser i koordinatsystemet 9 Rita trianglar i koordinatsystemet 11 Skapa mönster med
Tynker gratisapp på AppStore Innehåll Använda appen 2 Koordinatsystemet 6 Rita rektanglar i koordinatsystemet 7 Rita ellipser i koordinatsystemet 9 Rita trianglar i koordinatsystemet 11 Skapa mönster med
Om ellipsen och hyperbelns optiska egenskaper
 Om ellipsen och hyperbelns optiska egenskaper Anders Källén MatematikCentrum LTH anderskallen@gmail.com Sammanfattning Ellipser och hyperbler är, liksom parabeln, s.k. kägelsnitt, dvs kurvor som uppkommer
Om ellipsen och hyperbelns optiska egenskaper Anders Källén MatematikCentrum LTH anderskallen@gmail.com Sammanfattning Ellipser och hyperbler är, liksom parabeln, s.k. kägelsnitt, dvs kurvor som uppkommer
Sphero SPRK+ Appen som används är Sphero Edu. När appen öppnas kommer man till denna bild.
 Sphero SPRK+ Appen som används är Sphero Edu När appen öppnas kommer man till denna bild. Klicka på 3D-modeller för att se delarna på Sphero Klicka här för att ansluta Sphero till ipad Programmet för att
Sphero SPRK+ Appen som används är Sphero Edu När appen öppnas kommer man till denna bild. Klicka på 3D-modeller för att se delarna på Sphero Klicka här för att ansluta Sphero till ipad Programmet för att
Kvalificeringstävling den 30 september 2008
 SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
Lär dig programmera! Prova på programmering med enkla exempel! Björn Regnell www.bjornregnell.se
 Lär dig programmera! Prova på programmering med enkla exempel! Björn Regnell www.bjornregnell.se Mål Så enkelt som möjligt: låg tröskel Ett riktigt programmeringsspråk: inget tak Roliga uppgifter som går
Lär dig programmera! Prova på programmering med enkla exempel! Björn Regnell www.bjornregnell.se Mål Så enkelt som möjligt: låg tröskel Ett riktigt programmeringsspråk: inget tak Roliga uppgifter som går
3.0. Tips och Trix Sida 1 av 18
 3.0 https://beta.scratch.mit.edu/ Tips och Trix 2018-08-31 Sida 1 av 18 Innehåll Starta nytt program 3 Scenens koordinatsystem 3 Centrumpunkt / rotationspunkt 4 Sprajtens inställningar 5 Placering i Z-led
3.0 https://beta.scratch.mit.edu/ Tips och Trix 2018-08-31 Sida 1 av 18 Innehåll Starta nytt program 3 Scenens koordinatsystem 3 Centrumpunkt / rotationspunkt 4 Sprajtens inställningar 5 Placering i Z-led
9-1 Koordinatsystem och funktioner. Namn:
 9- Koordinatsystem och funktioner. Namn: Inledning I det här kapitlet skall du lära dig vad ett koordinatsystem är och vilka egenskaper det har. I ett koordinatsystem kan man representera matematiska funktioner
9- Koordinatsystem och funktioner. Namn: Inledning I det här kapitlet skall du lära dig vad ett koordinatsystem är och vilka egenskaper det har. I ett koordinatsystem kan man representera matematiska funktioner
4-4 Parallellogrammer Namn:..
 4-4 Parallellogrammer Namn:.. Inledning Hittills har du arbetat bl.a. med linjer och vinklar. En linje är ju någonting som bara har en dimension, längd. Men när två linjer skär varandra och det bildas
4-4 Parallellogrammer Namn:.. Inledning Hittills har du arbetat bl.a. med linjer och vinklar. En linje är ju någonting som bara har en dimension, längd. Men när två linjer skär varandra och det bildas
Föreläsning 5-6 Innehåll. Exempel på program med objekt. Exempel: kvadratobjekt. Objekt. Skapa och använda objekt Skriva egna klasser
 Föreläsning 5-6 Innehåll Exempel på program med objekt Skapa och använda objekt Skriva egna klasser public class DrawSquare { public static void main(string[] args) { SimpleWindow w = new SimpleWindow(600,
Föreläsning 5-6 Innehåll Exempel på program med objekt Skapa och använda objekt Skriva egna klasser public class DrawSquare { public static void main(string[] args) { SimpleWindow w = new SimpleWindow(600,
Föreläsning 5-6 Innehåll
 Föreläsning 5-6 Innehåll Skapa och använda objekt Skriva egna klasser Datavetenskap (LTH) Föreläsning 5-6 HT 2017 1 / 32 Exempel på program med objekt public class DrawSquare { public static void main(string[]
Föreläsning 5-6 Innehåll Skapa och använda objekt Skriva egna klasser Datavetenskap (LTH) Föreläsning 5-6 HT 2017 1 / 32 Exempel på program med objekt public class DrawSquare { public static void main(string[]
Tänk nu att c är en flaggstång som man lutar och som dessutom råkar befinna sig i ett koordinatsystem.
 Detta tänker jag att man redan vet: sin α= b c och cosα=a c och alltså också att för vinkeln. b=c sin α och a=c cos α Hypotenusan gånger antingen sinus eller cosinus Del 1 Tänk nu att c är en flaggstång
Detta tänker jag att man redan vet: sin α= b c och cosα=a c och alltså också att för vinkeln. b=c sin α och a=c cos α Hypotenusan gånger antingen sinus eller cosinus Del 1 Tänk nu att c är en flaggstång
UPPGIFT 2 KVADRATVANDRING
 UPPGIFT 1 LYCKOTAL Lyckotal är en serie heltal, som hittas på följande sätt. Starta med de naturliga talen: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13... Sök upp det första talet i serien, som är större
UPPGIFT 1 LYCKOTAL Lyckotal är en serie heltal, som hittas på följande sätt. Starta med de naturliga talen: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13... Sök upp det första talet i serien, som är större
diverse egenskapspaletter
 OBJEKTORIENTERADE RITPROGRAM Det fi nns två typer av ritprogram. Ett objektbaserat program ritar i form av matematiska kurvor med noder och styrnoder medan ett pixelbaserat program ritar genom att fylla
OBJEKTORIENTERADE RITPROGRAM Det fi nns två typer av ritprogram. Ett objektbaserat program ritar i form av matematiska kurvor med noder och styrnoder medan ett pixelbaserat program ritar genom att fylla
2D1339 Programkonstruktion för F1, ht 2003
 2D1339 Programkonstruktion för F1, ht 2003 Kontrollskrivning 1 Onsdag 19/11 2003 kl 9.15 10.00 Endast ett svar är rätt på varje fråga! Om mer än ett svar givits blir det noll poäng på frågan. Alla skriftliga
2D1339 Programkonstruktion för F1, ht 2003 Kontrollskrivning 1 Onsdag 19/11 2003 kl 9.15 10.00 Endast ett svar är rätt på varje fråga! Om mer än ett svar givits blir det noll poäng på frågan. Alla skriftliga
Aktivitetsbank. Matematikundervisning med digitala verktyg II, åk 1-3. Maria Johansson, Ulrica Dahlberg
 Aktivitetsbank Matematikundervisning med digitala, åk 1-3 Maria Johansson, Ulrica Dahlberg Matematik: Grundskola åk 1-3 Modul: Matematikundervisning med digitala Aktivitetsbank till modulen Matematikundervisning
Aktivitetsbank Matematikundervisning med digitala, åk 1-3 Maria Johansson, Ulrica Dahlberg Matematik: Grundskola åk 1-3 Modul: Matematikundervisning med digitala Aktivitetsbank till modulen Matematikundervisning
NATIONELLT KURSPROV I MATEMATIK KURS B VÅREN Del I, 10 uppgifter utan miniräknare 3. Del II, 9 uppgifter med miniräknare 6
 freeleaks NpMaB vt2001 1(8) Innehåll Förord 1 NATIONELLT KURSPROV I MATEMATIK KURS B VÅREN 2001 2 Del I, 10 uppgifter utan miniräknare 3 Del II, 9 uppgifter med miniräknare 6 Förord Skolverket har endast
freeleaks NpMaB vt2001 1(8) Innehåll Förord 1 NATIONELLT KURSPROV I MATEMATIK KURS B VÅREN 2001 2 Del I, 10 uppgifter utan miniräknare 3 Del II, 9 uppgifter med miniräknare 6 Förord Skolverket har endast
TAIU07 Matematiska beräkningar med Matlab
 TAIU07 Matematiska beräkningar med Matlab Datorlektion 2. Villkor och Repetition 1 Logiska uttryck Uppgift 1.1 Låt a=3 och b=6 Vad blir resultatet av testerna ab? Uppgift 1.2 Låt a, b,
TAIU07 Matematiska beräkningar med Matlab Datorlektion 2. Villkor och Repetition 1 Logiska uttryck Uppgift 1.1 Låt a=3 och b=6 Vad blir resultatet av testerna ab? Uppgift 1.2 Låt a, b,
Lösningar till tentauppgifterna sätts ut på kurssidan på nätet idag kl
 1(10) ÖREBRO UNIVERSITET INSTITUTIONEN FÖR TEKNIK Lösningar till tentauppgifterna sätts ut på kurssidan på nätet idag kl 13.00. Denna tenta kommer att vara färdigrättad Må 22/3 och kan då hämtas på mitt
1(10) ÖREBRO UNIVERSITET INSTITUTIONEN FÖR TEKNIK Lösningar till tentauppgifterna sätts ut på kurssidan på nätet idag kl 13.00. Denna tenta kommer att vara färdigrättad Må 22/3 och kan då hämtas på mitt
Lösningar till uppgifterna sätts ut på kurssidan på nätet i dag kl 13.00. Omtentamen i Programmering C, Fri, Kväll, 050108.
 1(8) ÖREBRO UNIVERSITET INSTITUTIONEN FÖR TEKNIK Lösningar till uppgifterna sätts ut på kurssidan på nätet i dag kl 13.00. Denna tenta kommer att vara färdigrättad Fr 14/1 och kan då hämtas på mitt tjänsterum,
1(8) ÖREBRO UNIVERSITET INSTITUTIONEN FÖR TEKNIK Lösningar till uppgifterna sätts ut på kurssidan på nätet i dag kl 13.00. Denna tenta kommer att vara färdigrättad Fr 14/1 och kan då hämtas på mitt tjänsterum,
Känguru 2014 Student sida 1 / 8 (gymnasiet åk 2 och 3)
 Känguru 2014 Student sida 1 / 8 NAMN GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Felaktigt svar ger minus 1/4 poäng av uppgiftens totala poängantal.
Känguru 2014 Student sida 1 / 8 NAMN GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Felaktigt svar ger minus 1/4 poäng av uppgiftens totala poängantal.
Den räta linjens ekvation
 Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Introduktion till programmering D0009E. Föreläsning 5: Fruktbara funktioner
 Introduktion till programmering D0009E Föreläsning 5: Fruktbara funktioner 1 Retur-värden Funktioner kan både orsaka en effekt och returnera ett resultat. Hittills har vi ej definierat några egna funktioner
Introduktion till programmering D0009E Föreläsning 5: Fruktbara funktioner 1 Retur-värden Funktioner kan både orsaka en effekt och returnera ett resultat. Hittills har vi ej definierat några egna funktioner
Matematik 3 Digitala övningar med TI-82 Stats, TI-84 Plus och TI-Nspire CAS
 Matematik 3 Digitala övningar med TI-8 Stats, TI-84 Plus och TI-Nspire CAS Matematik 3 digitala övningar med TI-8 Stat, TI-84 Plus och TI Nspire CAS Vi ger här korta instruktioner där man med fördel kan
Matematik 3 Digitala övningar med TI-8 Stats, TI-84 Plus och TI-Nspire CAS Matematik 3 digitala övningar med TI-8 Stat, TI-84 Plus och TI Nspire CAS Vi ger här korta instruktioner där man med fördel kan
Börja koda. Vad är programmering? Installera Processing
 Börja koda Vad är programmering? En dator är uppbyggd kring ett antal delar som samverkar för att du skall kunna använda program, spela spel och titta på bilder. Den viktigaste delen är processorn eller
Börja koda Vad är programmering? En dator är uppbyggd kring ett antal delar som samverkar för att du skall kunna använda program, spela spel och titta på bilder. Den viktigaste delen är processorn eller
UPPGIFT 1 V75 FIGUR 1.
 UPPGIFT 1 V75 FIGUR 1. Varje lördag året om spelar tusentals svenskar på travspelet V75. Spelet går ut på att finna sju vinnande hästar i lika många lopp. Lopp 1: 5 7 Lopp 2: 1 3 5 7 8 11 Lopp 3: 2 9 Lopp
UPPGIFT 1 V75 FIGUR 1. Varje lördag året om spelar tusentals svenskar på travspelet V75. Spelet går ut på att finna sju vinnande hästar i lika många lopp. Lopp 1: 5 7 Lopp 2: 1 3 5 7 8 11 Lopp 3: 2 9 Lopp
y º A B C sin 32 = 5.3 x = sin 32 x tan 32 = 5.3 y = tan 32
 6 Trigonometri 6. Dagens Teori Vi startar med att repetera lite av det som ingått i tidigare kurser angående trigonometri. Här följer en och samma rätvinkliga triangel tre gånger. Med en sida och en vinkel
6 Trigonometri 6. Dagens Teori Vi startar med att repetera lite av det som ingått i tidigare kurser angående trigonometri. Här följer en och samma rätvinkliga triangel tre gånger. Med en sida och en vinkel
NAMN KLASS/GRUPP. Poängsumma: Känguruskutt: UPPGIFT 1 2 3 4 5 6 7 8 9 10 SVAR UPPGIFT 11 12 13 14 15 16 17 18 19 20 SVAR
 Känguru 2010 Junior (gymnasiet åk 1) sida 1 / 6 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara
Känguru 2010 Junior (gymnasiet åk 1) sida 1 / 6 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara
Den räta linjens ekvation
 Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Programmering i C, 7,5 hp
 Programmering i C, 7,5 hp Föreläsning 4 VÄLKOMNA! 31 switch-satsen Antag att vi har en heltalsvariabel a som skall styra programflödet Antag vidare att a kan anta tex 5 olika värden 1,2,3,4,5 printf( Mata
Programmering i C, 7,5 hp Föreläsning 4 VÄLKOMNA! 31 switch-satsen Antag att vi har en heltalsvariabel a som skall styra programflödet Antag vidare att a kan anta tex 5 olika värden 1,2,3,4,5 printf( Mata
3.3 for-satsen. Programmering, grundkurs, 8.0 hp, Elektro, KTH, hösten 2010. Föreläsning 3
 Föreläsning 3 3.3 for-satsen I programmering talar man om tre sätt på vilket ett programflöde kan vara beskaffat: 1. Saker kan hända efter varandra, i sekvens. 2. Flödet kan innebära att ett val görs,
Föreläsning 3 3.3 for-satsen I programmering talar man om tre sätt på vilket ett programflöde kan vara beskaffat: 1. Saker kan hända efter varandra, i sekvens. 2. Flödet kan innebära att ett val görs,
Här hittar du ett exempel på ritprogrammet: https://scratch.mit.edu/projects/82515788/
 Termin 1 Block 4 Ritprogram Nu kommer du att få skapa ett ritprogram där du sedan kan göra egna konstverk! Programmet låter dig rita med olika färgpennor, sudda med suddgummi och måla med stämplar som
Termin 1 Block 4 Ritprogram Nu kommer du att få skapa ett ritprogram där du sedan kan göra egna konstverk! Programmet låter dig rita med olika färgpennor, sudda med suddgummi och måla med stämplar som
Lösningar till tentauppgifterna sätts ut på kurssidan på nätet idag kl 19. Omtentamen i Programmering C, 5p, fristående, kväll, 040110.
 1(8) ÖREBRO UNIVERSITET INSTITUTIONEN FÖR TEKNIK Lösningar till tentauppgifterna sätts ut på kurssidan på nätet idag kl 19. Denna tenta kommer att vara färdigrättad On 14/1-04 och kan då hämtas på mitt
1(8) ÖREBRO UNIVERSITET INSTITUTIONEN FÖR TEKNIK Lösningar till tentauppgifterna sätts ut på kurssidan på nätet idag kl 19. Denna tenta kommer att vara färdigrättad On 14/1-04 och kan då hämtas på mitt
Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Kapitel 2 Vägg/golv... 3
 2014.02.21 1 Vägg/golv Kapitel 2 Kapitel Innehåll... Sida Kapitel 2 Vägg/golv... 3 Yttervägg... 3 Golv... 8 Anpassa vägg till platta på mark... 12 Innervägg... 14 Hur ser väggarna ut?... 19 Ångra/göra
2014.02.21 1 Vägg/golv Kapitel 2 Kapitel Innehåll... Sida Kapitel 2 Vägg/golv... 3 Yttervägg... 3 Golv... 8 Anpassa vägg till platta på mark... 12 Innervägg... 14 Hur ser väggarna ut?... 19 Ångra/göra
Provet består av Del I, Del II, Del III samt en muntlig del och ger totalt 76 poäng varav 28 E-, 24 C- och 24 A-poäng.
 Del I Del II Provtid Hjälpmedel Uppgift 1-10. Endast svar krävs. Uppgift 11-15. Fullständiga lösningar krävs. 10 minuter för del I och del II tillsammans. Formelblad och linjal. Kravgränser Provet består
Del I Del II Provtid Hjälpmedel Uppgift 1-10. Endast svar krävs. Uppgift 11-15. Fullständiga lösningar krävs. 10 minuter för del I och del II tillsammans. Formelblad och linjal. Kravgränser Provet består
i=1 β i a i. (Rudolf Tabbe.) i=1 b i a i n
 Årgång 48, 1965 Första häftet 2505. Låt M = {p 1, p 2,..., p k } vara en mängd med k element. Vidare betecknar M 1, M 2,..., M n olika delmängder till M, alla bestående av tre element. Det gäller alltså
Årgång 48, 1965 Första häftet 2505. Låt M = {p 1, p 2,..., p k } vara en mängd med k element. Vidare betecknar M 1, M 2,..., M n olika delmängder till M, alla bestående av tre element. Det gäller alltså
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs B, kapitel 2
 Kapitel.1 101, 10 Exempel som löses i boken. 103 Testa genom att lägga linjalen lodrätt och föra den över grafen. Om den på något ställe skär grafen i mer än en punkt så visar grafen inte en funktion.
Kapitel.1 101, 10 Exempel som löses i boken. 103 Testa genom att lägga linjalen lodrätt och föra den över grafen. Om den på något ställe skär grafen i mer än en punkt så visar grafen inte en funktion.
Dagens föreläsning. Repetition. Repetition - Programmering i C. Repetition - Vad C består av. Repetition Ett första C-program
 Dagens föreläsning Programmeringsteknik för Ingenjörer VT05 Föreläsning 3-4 Repetition Datatyper Uttryck Operatorer Satser Algoritmer Programmeringsteknik VT05 2 Repetition Repetition - Programmering i
Dagens föreläsning Programmeringsteknik för Ingenjörer VT05 Föreläsning 3-4 Repetition Datatyper Uttryck Operatorer Satser Algoritmer Programmeringsteknik VT05 2 Repetition Repetition - Programmering i
Veckoblad 1, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Programmeringsolympiaden 2011 Kvalificering
 Programmeringsolympiaden 2011 Kvalificering TÄVLINGSREGLER Tävlingen äger rum på ett av skolan bestämt datum under sex timmar effektiv tid. Tävlingen består av sex uppgifter som samtliga ska lösas genom
Programmeringsolympiaden 2011 Kvalificering TÄVLINGSREGLER Tävlingen äger rum på ett av skolan bestämt datum under sex timmar effektiv tid. Tävlingen består av sex uppgifter som samtliga ska lösas genom
Vad är programmering Jonas Lindemann
 Vad är programmering Jonas Lindemann Vad är en dator? Består av e1 antal delar som samverkar Processorn U7ör instruk:oner (addera, skriv :ll minne, fly1a minne ) Minnet Lagrar de instruk:oner som skall
Vad är programmering Jonas Lindemann Vad är en dator? Består av e1 antal delar som samverkar Processorn U7ör instruk:oner (addera, skriv :ll minne, fly1a minne ) Minnet Lagrar de instruk:oner som skall
Agenda. Arrayer deklaration, åtkomst Makron Flerdimensionella arrayer Initiering Strängar Funktioner och arrayer. Övningar nu och då
 Agenda Arrayer deklaration, åtkomst Makron Flerdimensionella arrayer Initiering Strängar Funktioner och arrayer Övningar nu och då 1 Motivering I de flesta problem ingår att hantera multipla data I de
Agenda Arrayer deklaration, åtkomst Makron Flerdimensionella arrayer Initiering Strängar Funktioner och arrayer Övningar nu och då 1 Motivering I de flesta problem ingår att hantera multipla data I de
GeoGebra i matematikundervisningen - Inspirationsdagar för gymnasielärare. Karlstads universitet 19-20 april
 GeoGebra i matematikundervisningen - Inspirationsdagar för gymnasielärare Karlstads universitet 19-0 april Exempel på elevaktiviteter framtagna i skolutvecklingsprojektet IKT och lärande i matematik 1
GeoGebra i matematikundervisningen - Inspirationsdagar för gymnasielärare Karlstads universitet 19-0 april Exempel på elevaktiviteter framtagna i skolutvecklingsprojektet IKT och lärande i matematik 1
Repetitionsprov på algebra, p-q-formeln samt andragradsfunktioner
 Repetitionsprov på algebra, p-q-formeln samt andragradsfunktioner Del B Utan miniräknare Endast svar krävs! 1. Lös ekvationen (x + 3)(x 2) = 0 Svar: (1/0/0) 2. Förenkla uttrycket 4(x 3)(x + 3) så långt
Repetitionsprov på algebra, p-q-formeln samt andragradsfunktioner Del B Utan miniräknare Endast svar krävs! 1. Lös ekvationen (x + 3)(x 2) = 0 Svar: (1/0/0) 2. Förenkla uttrycket 4(x 3)(x + 3) så långt
Iteration while-satsen
 Datatypen double TDA143 I1 Programmerade system Föreläsning 3 (OH-bilder 3) Iteration while-satsen Christer Carlsson I en dator kan man inte lagra hur stora eller hur små tal som helst. De enkla datatyperna,
Datatypen double TDA143 I1 Programmerade system Föreläsning 3 (OH-bilder 3) Iteration while-satsen Christer Carlsson I en dator kan man inte lagra hur stora eller hur små tal som helst. De enkla datatyperna,
Lösningar till utvalda uppgifter i kapitel 1
 Lösningar till utvalda uppgifter i kapitel. Vi utnyttjar definitionen av skalärprodukt som ger att u v u v, där α är (minsta) vinkeln mellan u v. I vårt fall så får vi 7 =. Alltså är den sökta vinkeln
Lösningar till utvalda uppgifter i kapitel. Vi utnyttjar definitionen av skalärprodukt som ger att u v u v, där α är (minsta) vinkeln mellan u v. I vårt fall så får vi 7 =. Alltså är den sökta vinkeln
Trigonometri. Sidor i boken 26-34
 Sidor i boken 6-34 Trigonometri Definition: Gren av matematiken som studerar samband mellan vinklar och sträckor i planet (och rymden). Det grundläggande trigonometriska problemet är att beräkna alla sidor
Sidor i boken 6-34 Trigonometri Definition: Gren av matematiken som studerar samband mellan vinklar och sträckor i planet (och rymden). Det grundläggande trigonometriska problemet är att beräkna alla sidor
Sidor i boken f(x) = a x 2 +b x+c
 Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Laboration 1: Figurer i hierarki
 Laboration 1: Figurer i hierarki Bakgrund Två grundläggande tekniker i objektorienterad konstruktion är arv och komposition. Mål Laborationen har flera avsikter: 1. Ge kunskaper i hur program kan organiseras
Laboration 1: Figurer i hierarki Bakgrund Två grundläggande tekniker i objektorienterad konstruktion är arv och komposition. Mål Laborationen har flera avsikter: 1. Ge kunskaper i hur program kan organiseras
HI1024, Programmering, grundkurs, 8hp KTH STH TENTAMEN. HI1024:TEN2 - Praktisk tentamen Tid: Fredagen den 21 oktober 2011,
 KTH STH TENTAMEN HI1024:TEN2 - Praktisk tentamen Tid: Fredagen den 21 oktober 2011, 8.15-13.15 Gamla kurskoder: HI1900, 6E2950, etc. Examinator: Johnny Panrike Rättande lärare: Nicklas Brandefelt, Johnny
KTH STH TENTAMEN HI1024:TEN2 - Praktisk tentamen Tid: Fredagen den 21 oktober 2011, 8.15-13.15 Gamla kurskoder: HI1900, 6E2950, etc. Examinator: Johnny Panrike Rättande lärare: Nicklas Brandefelt, Johnny
Lab5 för prgmedcl04 Grafik
 Lab5 för prgmedcl04 Grafik Viktigt läs detta först:den här labblydelsen är ganska lång, detta betyder inte att labben tar lång tid.en hel del av lydelsen är anvisning om hur man går tillväga för att kunna
Lab5 för prgmedcl04 Grafik Viktigt läs detta först:den här labblydelsen är ganska lång, detta betyder inte att labben tar lång tid.en hel del av lydelsen är anvisning om hur man går tillväga för att kunna
En kort text om programmering i C.
 En kort text om programmering i C C skapades 1972 av Brian Ritchie och Dennis Kerighan på Bell Labs i USA Det blev det språk som är mest använt genom tiderna Det finns många olika språk Pascal, FORTH,
En kort text om programmering i C C skapades 1972 av Brian Ritchie och Dennis Kerighan på Bell Labs i USA Det blev det språk som är mest använt genom tiderna Det finns många olika språk Pascal, FORTH,
Mitt hus och jag steg för steg instruktioner
 Mitt hus och jag steg för steg instruktioner Till den här uppgiften behöver du ett foto på dig själv, ditt hus, en karta och en huvudlös figur. Se till att alla bilder ligger på samma ställe på din dator
Mitt hus och jag steg för steg instruktioner Till den här uppgiften behöver du ett foto på dig själv, ditt hus, en karta och en huvudlös figur. Se till att alla bilder ligger på samma ställe på din dator
Dagens föreläsning. Repetition. Repetition - Programmering i C. Repetition - Vad C består av. Repetition Ett första C-program
 Dagens föreläsning Programmeringsteknik för Ingenjörer VT05 Föreläsning 3-4 Repetition Datatyper Uttryck Operatorer Satser Algoritmer Programmeringsteknik för ingenjörer, VT06 2 Repetition Repetition -
Dagens föreläsning Programmeringsteknik för Ingenjörer VT05 Föreläsning 3-4 Repetition Datatyper Uttryck Operatorer Satser Algoritmer Programmeringsteknik för ingenjörer, VT06 2 Repetition Repetition -
Tentaupplägg denna gång
 Några tips på vägen kanske kan vara bra. 2014-10-30.kl.08-13 Tentaupplägg denna gång TIPS1: Läs igenom ALLA uppgifterna. Välj den du känner är lättast först. Det kan gärna ta 10-20 minuter. Försök skriva
Några tips på vägen kanske kan vara bra. 2014-10-30.kl.08-13 Tentaupplägg denna gång TIPS1: Läs igenom ALLA uppgifterna. Välj den du känner är lättast först. Det kan gärna ta 10-20 minuter. Försök skriva
Polygoner. Trianglar på tre sätt
 Polygoner Trianglar på tre sätt Man kan skriva in punkter antingen via punktverktyget eller genom att skriva punktens namn och koordinater i inmatningsfältet. Då man ritar månghörningar lönar det sig att
Polygoner Trianglar på tre sätt Man kan skriva in punkter antingen via punktverktyget eller genom att skriva punktens namn och koordinater i inmatningsfältet. Då man ritar månghörningar lönar det sig att
Introduktion till programmering SMD180. Föreläsning 5: Fruktbara funktioner
 Introduktion till programmering Föreläsning 5: Fruktbara funktioner 1 Retur-värden Funktioner kan både orsaka en effekt och returnera ett resultat. Hittills har vi ej definierat några egna funktioner med
Introduktion till programmering Föreläsning 5: Fruktbara funktioner 1 Retur-värden Funktioner kan både orsaka en effekt och returnera ett resultat. Hittills har vi ej definierat några egna funktioner med
Vi börjar med en penna som ritar när du drar runt den på Scenen.
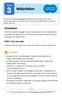 Nivå 3 Målarlådan All Code Clubs must be registered. Registered clubs appear on the map at codeclubworld.org - if your club is not on the map then visit jumpto.cc/ccwreg to register your club. Introduktion
Nivå 3 Målarlådan All Code Clubs must be registered. Registered clubs appear on the map at codeclubworld.org - if your club is not on the map then visit jumpto.cc/ccwreg to register your club. Introduktion
Ordlista 1B:1. modell. hel timme. halv timme. timvisare. Dessa ord ska du träna. Öva orden. När du bygger efter en ritning, får du en modell.
 Ordlista 1B:1 Öva orden Dessa ord ska du träna modell När du bygger efter en ritning, får du en modell. hel timme På en timme går timvisaren ett steg på klockan. halv timme På en halvtimme går minutvisaren
Ordlista 1B:1 Öva orden Dessa ord ska du träna modell När du bygger efter en ritning, får du en modell. hel timme På en timme går timvisaren ett steg på klockan. halv timme På en halvtimme går minutvisaren
Uppgifter till praktiska tentan, del A. (7 / 27)
 Uppgifter till praktiska tentan, del A. (7 / 27) I. Sortering/Sökning: III II. Representation/Omvandling/format/protokoll: II III. Strukturering: II I alla problem, där bokstäver förekommer, antar vi att
Uppgifter till praktiska tentan, del A. (7 / 27) I. Sortering/Sökning: III II. Representation/Omvandling/format/protokoll: II III. Strukturering: II I alla problem, där bokstäver förekommer, antar vi att
Känguru 2018 Student gymnasieserien i samarbete med Jan-Anders Salenius (Brändö gymnasium)
 sida 0 / 9 NAMN GRUPP Poäng: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Ett rätt svar ger 3, 4 eller 5 poäng. I varje uppgift är exakt ett svar korrekt. Felaktigt
sida 0 / 9 NAMN GRUPP Poäng: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Ett rätt svar ger 3, 4 eller 5 poäng. I varje uppgift är exakt ett svar korrekt. Felaktigt
HI1024 Programmering, grundkurs TEN
 HI1024 Programmering, grundkurs TEN2 2015-01-08 KTH STH Haninge 13.15-18.00 Tillåtna hjälpmedel: En A4 handskriven på ena sidan med egna anteckningar Kursboken C PROGRAMMING A Modern Approach K. N. King
HI1024 Programmering, grundkurs TEN2 2015-01-08 KTH STH Haninge 13.15-18.00 Tillåtna hjälpmedel: En A4 handskriven på ena sidan med egna anteckningar Kursboken C PROGRAMMING A Modern Approach K. N. King
Att prova på en enkel Applet och att lära sig olika sätt att hämta data från tangentbordet. Du får även prova på att skapa din första riktiga klass.
 Datateknik A, Syfte: Att prova på en enkel Applet och att lära sig olika sätt att hämta data från tangentbordet. Du får även prova på att skapa din första riktiga klass. Att läsa: Lektion 2 Uppgifter:
Datateknik A, Syfte: Att prova på en enkel Applet och att lära sig olika sätt att hämta data från tangentbordet. Du får även prova på att skapa din första riktiga klass. Att läsa: Lektion 2 Uppgifter:
Undersökande arbetssätt i matematik 1 och 2
 Matematik Gymnasieskola Modul: Matematikundervisning med digitala verktyg Del 6: Undersökande arbetssätt med matematisk programvara Undersökande arbetssätt i matematik 1 och 2 I texten Undersökande arbetssätt
Matematik Gymnasieskola Modul: Matematikundervisning med digitala verktyg Del 6: Undersökande arbetssätt med matematisk programvara Undersökande arbetssätt i matematik 1 och 2 I texten Undersökande arbetssätt
Programmering i Scratch 2.0
 Programmering i Scratch 2.0 Version 1.3 Anders Berglund @andersberglund_ anders.h.berglund@stockholm.se Mälarhöjdens skola 2017 Del 1 Vad är Scratch? Scratch är ett visuellt programmeringsspråk som går
Programmering i Scratch 2.0 Version 1.3 Anders Berglund @andersberglund_ anders.h.berglund@stockholm.se Mälarhöjdens skola 2017 Del 1 Vad är Scratch? Scratch är ett visuellt programmeringsspråk som går
Mathematica. Utdata är Mathematicas svar på dina kommandon. Här ser vi svaret på kommandot från. , x
 Mathematica Första kapitlet kommer att handla om Mathematica det matematiska verktyg, som vi ska lära oss hantera under denna kurs. Indata När du arbetar med Mathematica ger du indata i form av kommandon
Mathematica Första kapitlet kommer att handla om Mathematica det matematiska verktyg, som vi ska lära oss hantera under denna kurs. Indata När du arbetar med Mathematica ger du indata i form av kommandon
Välkommen till Kängurutävlingen Matematikens hopp 17 mars Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Börja med att kopiera källkoden till din scheme-katalog (som du skapade i Laboration 1).
 Laboration 3 Grafiska figurer I den här laborationen skall du konstruera ett schemeprogram som kan rita rektanglar, punkter, cirklar, linjer och bilder som består utav en eller flera av nyss nämnda figurer.
Laboration 3 Grafiska figurer I den här laborationen skall du konstruera ett schemeprogram som kan rita rektanglar, punkter, cirklar, linjer och bilder som består utav en eller flera av nyss nämnda figurer.
OOP Tentamen
 DVS SU/KTH 1 (6) OOP OOP Tentamen 2010-01-15 15.00 20.00 Avser kurserna: DSK1:OOP GES:OOP ID1013 Anvisningar Skriv namn och personnummer på varje inlämnat blad. Påbörja varje ny uppgift på nytt blad. Skriv
DVS SU/KTH 1 (6) OOP OOP Tentamen 2010-01-15 15.00 20.00 Avser kurserna: DSK1:OOP GES:OOP ID1013 Anvisningar Skriv namn och personnummer på varje inlämnat blad. Påbörja varje ny uppgift på nytt blad. Skriv
GeoGebra i matematikundervisningen - Inspirationsdagar för gymnasielärare. Karlstads universitet 19-20 april. Liten introduktionsguide för nybörjare
 GeoGebra i matematikundervisningen - Inspirationsdagar för gymnasielärare 19-20 april Liten introduktionsguide för nybörjare GeoGebra 0 Introduktionsövningar till GeoGebra När man startar GeoGebra är det
GeoGebra i matematikundervisningen - Inspirationsdagar för gymnasielärare 19-20 april Liten introduktionsguide för nybörjare GeoGebra 0 Introduktionsövningar till GeoGebra När man startar GeoGebra är det
Programmera i C Varför programmera i C när det finns språk som Simula och Pascal??
 Programmera i C Varför programmera i C när det finns språk som Simula och Pascal?? C är ett språk på relativt låg nivå vilket gör det möjligt att konstruera effektiva kompilatorer, samt att komma nära
Programmera i C Varför programmera i C när det finns språk som Simula och Pascal?? C är ett språk på relativt låg nivå vilket gör det möjligt att konstruera effektiva kompilatorer, samt att komma nära
Introduktion till algoritmer - Lektion 1 Matematikgymnasiet, Läsåret 2014-2015. Lektion 1
 Kattis Lektion 1 I kursen används onlinedomaren Kattis (från http://kattis.com) för att automatiskt rätta programmeringsproblem. För att få ett konto på Kattis anmäler du dig på Programmeringsolympiadens
Kattis Lektion 1 I kursen används onlinedomaren Kattis (från http://kattis.com) för att automatiskt rätta programmeringsproblem. För att få ett konto på Kattis anmäler du dig på Programmeringsolympiadens
RÖRELSE. - Mätningar och mätinstrument och hur de kan kombineras för att mäta storheter, till exempel fart, tryck och effekt.
 RÖRELSE Inledning När vi går, springer, cyklar etc. förflyttar vi oss en viss sträcka på en viss tid. Ibland, speciellt när vi har bråttom, tänker vi på hur fort det går. I det här experimentet undersöker
RÖRELSE Inledning När vi går, springer, cyklar etc. förflyttar vi oss en viss sträcka på en viss tid. Ibland, speciellt när vi har bråttom, tänker vi på hur fort det går. I det här experimentet undersöker
3. Välj den sprajt (bild) ni vill ha som fallande objekt, t ex en tårta, Cake. Klicka därefter på OK.
 Moment 2: Klonspel Instruktioner för deltagare Idag ska du få lära dig om: Kloner - kopior av samma figur (sprajt) Variabler - ett värde, exempelvis antal poäng Slumptal - slå en tärning för att välja
Moment 2: Klonspel Instruktioner för deltagare Idag ska du få lära dig om: Kloner - kopior av samma figur (sprajt) Variabler - ett värde, exempelvis antal poäng Slumptal - slå en tärning för att välja
Föreläsning 9. Repetition och exempelproblem
 Föreläsning 9 Repetition och exempelproblem /* Calculation of distance when travelling at speed 25 m/s */ #include int distance,speed,time; speed = 25; printf("hur lang tid? "); scanf("%d", &time);
Föreläsning 9 Repetition och exempelproblem /* Calculation of distance when travelling at speed 25 m/s */ #include int distance,speed,time; speed = 25; printf("hur lang tid? "); scanf("%d", &time);
Känguru Student (gymnasiet åk 2 och 3) sida 1 / 6
 Känguru Student (gymnasiet åk 2 och 3) sida 1 / 6 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara
Känguru Student (gymnasiet åk 2 och 3) sida 1 / 6 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara
Föreläsning 3. Iteration while-satsen
 Föreläsning 3 Iteration while-satsen Datatypen double I en dator kan man inte lagra hur stora eller hur små tal som helst. De enkla datatyperna, som används för att lagra tal (t.ex. int och double), har
Föreläsning 3 Iteration while-satsen Datatypen double I en dator kan man inte lagra hur stora eller hur små tal som helst. De enkla datatyperna, som används för att lagra tal (t.ex. int och double), har
Föreläsning 2 Programmeringsteknik och C DD1316. Mikael Djurfeldt
 Föreläsning 2 Programmeringsteknik och C DD1316 Mikael Djurfeldt Föreläsning 2 Programmeringsteknik och C Python introduktion Utskrift Inläsning Variabler Datatyp Aritmetiska operatorer Omvandling
Föreläsning 2 Programmeringsteknik och C DD1316 Mikael Djurfeldt Föreläsning 2 Programmeringsteknik och C Python introduktion Utskrift Inläsning Variabler Datatyp Aritmetiska operatorer Omvandling
Matematik CD för TB = 5 +
 Föreläsning 4 70 a) Vi delar figuren i två delar, en triangel (på toppen) och en rektangel. Summan av dessa två figurers area ger den eftersökta. Vi behöver följande formler: A R = b h A T = b h Svar:
Föreläsning 4 70 a) Vi delar figuren i två delar, en triangel (på toppen) och en rektangel. Summan av dessa två figurers area ger den eftersökta. Vi behöver följande formler: A R = b h A T = b h Svar:
Fönster och dörr. Kapitel 3 - Fönster och dörr... 3
 25.05.2009 Kapitel 3... 1 Kapitel Innehåll... Sida Kapitel 3 -... 3 Fönster...3 Placera med gitter...5 Hur ser fasaden ut?...5 Öppningsbara fönster...7 Relativ positionering...7 Se på 3D-modell...9 Ytterdörrar...9
25.05.2009 Kapitel 3... 1 Kapitel Innehåll... Sida Kapitel 3 -... 3 Fönster...3 Placera med gitter...5 Hur ser fasaden ut?...5 Öppningsbara fönster...7 Relativ positionering...7 Se på 3D-modell...9 Ytterdörrar...9
Svar och arbeta vidare med Student 2008
 Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Programmering. Den första datorn hette ENIAC.
 Programmering Datorn är bara en burk. Den kan inget själv. Hur får man den att göra saker? Man programmerar den. Människor som funderar ut program som fungerar. Datorn förstår bara ettor och nollor och
Programmering Datorn är bara en burk. Den kan inget själv. Hur får man den att göra saker? Man programmerar den. Människor som funderar ut program som fungerar. Datorn förstår bara ettor och nollor och
Programmeringsuppgift Game of Life
 CTH/GU STUDIO TMV06a - 0/0 Matematiska vetenskaper Programmeringsuppgift Game of Life Analys och Linär Algebra, del A, K/Kf/Bt Inledning En cellulär automat är en dynamisk metod som beskriver hur komplicerade
CTH/GU STUDIO TMV06a - 0/0 Matematiska vetenskaper Programmeringsuppgift Game of Life Analys och Linär Algebra, del A, K/Kf/Bt Inledning En cellulär automat är en dynamisk metod som beskriver hur komplicerade
Föreläsning 8 SLUMPTAL, SIMULERING + INTRODUKTION TILL VEKTORER
 Föreläsning 8 SLUMPTAL, SIMULERING + INTRODUKTION TILL VEKTORER Från laboration 3 till 4 I laboration 3 har du implementerat klasser implementerat metoder i klasserna I laboration 4 kommer du att implementera
Föreläsning 8 SLUMPTAL, SIMULERING + INTRODUKTION TILL VEKTORER Från laboration 3 till 4 I laboration 3 har du implementerat klasser implementerat metoder i klasserna I laboration 4 kommer du att implementera
Moment Viktiga exempel Övningsuppgifter
 Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Fler exempel på optimering Exempel 1. Utifrån en rektangulär pappskiva med bredden 7 dm och längden 11 dm, vill man åstadkomma en kartong utan lock,
Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Fler exempel på optimering Exempel 1. Utifrån en rektangulär pappskiva med bredden 7 dm och längden 11 dm, vill man åstadkomma en kartong utan lock,
C++ Funktioner 1. int summa( int a, int b) //funktionshuvud { return a+b; //funktionskropp } Värmdö Gymnasium Programmering B ++ Datainstitutionen
 C++ Funktioner 1 Teori När programmen blir större och mer komplicerade är det bra att kunna dela upp programmet i olika delar som gör specifika saker, vilket kan göra programmet mer lättläst. Ett sätt
C++ Funktioner 1 Teori När programmen blir större och mer komplicerade är det bra att kunna dela upp programmet i olika delar som gör specifika saker, vilket kan göra programmet mer lättläst. Ett sätt
KS övning 1. Problem 1. Beräkna Problem 2. Förenkla. (x 1 3 y
 KS övning 1 Problem 1. Beräkna 48 1 3 Problem 2. Förenkla 6 1 3 (x 1 3 y 1 3 )(x 2 3 +x 1 3 y 1 3 +y 2 3 ) Problem 3. I ABC är AB = 15 cm och AC = 12 cm. En rät linje parallell med BC träffar AB i D och
KS övning 1 Problem 1. Beräkna 48 1 3 Problem 2. Förenkla 6 1 3 (x 1 3 y 1 3 )(x 2 3 +x 1 3 y 1 3 +y 2 3 ) Problem 3. I ABC är AB = 15 cm och AC = 12 cm. En rät linje parallell med BC träffar AB i D och
