Elevers och lärares erfarenheter
|
|
|
- Niklas Samuelsson
- för 8 år sedan
- Visningar:
Transkript
1 Elevers och lärares erfarenheter Avsikten med detta kapitel är att jämföra erfarenheter från grundskolan och gymnasieskolan utifrån den översyn av matematikundervisningen i skolan som gjordes inom Utbildningsdepartementet 1986 och utifrån Skolverkets rapporter från den Nationella utvärderingen, NU Drygt 0 slumpvis utvalda skolor med ca 000 elever i åk 9 deltog i NU. Förutom elevernas kunskaper och färdigheter undersöktes både elevernas och lärarnas syn på matematik och matematikundervisning presenterade en arbetsgrupp vid Utbildningsdepartementet en översyn av undervisningen i matematik i svensk skola. Arbetsgruppens slutsatser sammanfattades i diskussionsmaterialet Matematik för alla (Utbildningsdepartementet 1986). Där redovisas intervjuer med matematik- och yrkeslärare i gymnasieskolan om övergången från grund- till gymnasieskola. Olika brister i elevernas kunnande påpekades liksom de stora skillnaderna i kunskaper mellan olika högstadieskolors elever. Man var också bekymrad över den stora spridningen i kunskaper mellan elever från samma högstadieskola. Många elever har så dåliga kunskaper i matematiken som språk och i allmän ordkunskap att de inte förstår instruktioner och förutsättningar i ett problem som ska lösas med matematiska hjälpmedel. (s ) Lärarna framhöll att åtskilliga elever hade utvecklat en inställning till matematik som var mycket olycklig. Många elever betraktar ämnet som ett "pluggämne", där man före prov läser in några formler som man sedan kan glömma bort. (s. 21) Hur stämmer beskrivningen av elevernas matematikkunskaper och av deras ämnesuppfattning med dina erfarenheter? Många elever tycks betrakta matematiken som ett pluggämne a) Hur har denna uppfattning uppstått? b) Hur kan man undvika att eleverna utvecklar en sådan uppfattning av matematikämnet?
2 Vad händer under lektionerna? Gymnasieinspektörernas rapporter från 1980 visade att en stor del av undervisningstiden gick åt till tyst räkning och att liten tid användes till att resonera kring matematikens natur eller roll, att förebygga missuppfattningar eller att diskutera tankeformer och begreppsbildning. Vid undersökningen 1986 fanns inga tecken på att tiden användes på annat sätt på grundskolans mellan- och högstadium. Man frågade sig om eleverna inte skulle få bättre kunskaper om en rejäl del av undervisningstiden användes till att prata matematik, att diskutera olika lösningar av problem och konstruktion av problem. (DsU 1986: s 29) Enligt Lpo 94 och Lpf 94 skall lärare och elever tillsammans planera vad som skall göras under lektionerna. Eleverna kan då bli engagerade och motiverade att ta ansvar för sin inlärning. Om de får arbeta i mindre grupper finns det goda möjligheter att deras förmåga och lust att engagera sig och att kommunicera matematik förbättras. Eleverna behöver öva sig i att kunna följa ett matematiskt resonemang, att kunna uttrycka sig, förklara och argumentera i matematik. Hur ofta används olika arbetsformer enligt lärarna. Procentuella andelar (N= 1). NU, åk 9. Tabell 4, s. (Skolverket, 199) Arbetsform I stort sett varje lektion Någon gång varje vecka Någon gång varje månad Mycket sällan eller aldrig Huvudräkning. Gemensam och/eller enskild Överslagsräkning. Gemensam och/eller enskild Gemensam genomgång med klassen under Din ledning Enskild "tyst räkning" Eleverna redovisar lösningar och tankesätt för klassen Eleverna arbetar tillsammans två och två eller i mindre grupper 0 18 Eleverna konstruerar egna matematikuppgifter 0 20 Klassen diskuterar olika problem och lösningar tillsammans
3 Hur ofta används olika arbetsformer enligt eleverna. Procentuella andelar (N = 9 00) NU, åk 9. Tabell, s 4. (Skolverket, 199) Arbetsform Hur ofta arbetar du tillsammans med någon kamrat på matematiklektionerna? Hur ofta arbetar ni tillsammans ( eller fler) i smågrupper när ni löser matematikuppgifter? Hur ofta diskuterar ni matematikuppgifter gemensamt i undervisningsgruppen tillsammans med läraren? Hur ofta planerar ni tillsammans med läraren vad ni ska göra på lektionerna i matematik? Hur ofta arbetar du med andra matematikuppgifter än de som finns i läroboken? Hur ofta har läraren gemensamma genomgångar med er? I stort sett varje lektion 9 4 Någon gång varje vecka Någon gång varje månad Mycket sällan eller aldrig Varför har vi hemuppgifter? Enligt NU-rapporten ger så gott som alla högstadielärare hemuppgifter - de flesta någon gång per vecka. Det vanligaste är att alla elever får samma hemuppgifter, men det förekommer också att eleverna får olika många uppgifter och att dessa är av olika slag. Över hälften av lärarna i grundskolan ger hemuppgifter ur andra källor än läroboken. Som exempel nämns tidningar, men även uppgifter gjorda av elever. Hur stämmer resultaten i tabellerna med dina erfarenheter? Välj ut ett matematikavsnitt och försök att beskriva hur ofta du brukar använda de olika arbetsformerna som finns i tabellen. Vad har dina elever för erfarenheter av och önskemål om olika arbetsformer? Utgå från och jämför gärna med resultaten i tabellen. Vilka förslag har dina elever för att öka sitt intresse för och utbyte av matematikutbildningen?
4 En fråga som inte ställts är i vilket syfte lärarna ger hemuppgifterna och hur eleverna ställer sig. Syftet är kanske att befästa vissa färdigheter, men det finns lärare som använder hemuppgifter för att stimulera och aktivera eleverna och ge dem en bakgrund inför vad som skall tas upp vid senare lektioner. Eleverna kan t ex få i uppgift att ta fram fakta så att de kan beskriva problem och beräkningar som gjorts tidigare och utvidga dem med hjälp av ny information. Man försöker ge eleverna en utgångspunkt i form av "det här vet vi, och vad tillför den nya informationen i relation till den vi hade tidigare?". Flertalet elever har gjort sina hemuppgifter, men vad de får ut av hemarbete får vi inte veta i studien. Som lärare borde vi fråga "Vad har du lärt, eller vad har du förstått genom detta?" Glädjen när eleverna förstår I diskussionen om nya betyg har det framförts att antalet prov borde skäras ner. Kan man få en bättre bild av elevernas kunskaper genom kontinuerlig uppföljning - där man antecknar framsteg och inte de fel som det är naturligt att en människa gör medan hon lär sig? Enligt NU-rapporten anser tre av fyra elever att diagnoser är bra. Hur prov och diagnoser används enligt rapporten visas i nedanstående diagram. Andel lärare (%) Förekomst av prov och diagnoser årskurs 9 (N prov = 2, N diagn = ). (NU, åk 9, s ). (Skolverket, 199) Prov Diagnoser Antal
5 Nedan redovisas elevernas svar på frågor om den undervisning de fått under sin skoltid. Jämför denna tabell med tabellen på sidan 11 som beskriver vilka arbetsformer som används under lektionerna. Elevernas svar på några frågor om undervisningen. Procentuella andelar (N = 9 00) NU, åk 9. Tabell 1, s 29. (Skolverket, 199) Påstående Alla i undervisningsgruppen ska räkna samma uppgifter Det är viktigt att alla räknar alla uppgifter i läroboken Jag tycker att det är bra med prov i matematik, så jag får visa vad jag kan Det är bra med diagnoser, så jag får veta om jag behöver arbeta mer med något i matematiken Jag har fått arbeta med för många lätta uppgifter i matematik på lågstadiet på mellanstadiet på högstadiet Jag har fått arbeta med för många svåra uppgifter i matematik på lågstadiet på mellanstadiet på högstadiet Jag skulle vilja lära mig mer matematik i skolan Jag har fått lära mig mycket i matematik som jag tycker är onödigt Jag tror att jag kommer att ha nytta av den matematik som jag lärt mig helt i stort sett delvis inte alls Hur vill du/dina elever att hemuppgifter skall användas i skolarbetet? Vad skall de ha för syfte, innehåll och omfattning? Hur skall de kunna stimulera till arbete och lärande? Vad anser dina elever om prov/diagnoser i matematik? Vilka andra sätt tycker du/de att det finns att ta reda på vad elever kan? Välj ut någon fråga som du vill ha svar på och undersök hur dina elever svarar. Jämför resultaten med siffrorna i tabellerna.
6 Nästan en femtedel av eleverna har haft stora eller mycket stora problem att förstå lärarens förklaringar i matematik på högstadiet. Liknande resultat har nyligen presenterats av Svensson (199). Motsvarande andel för låg- och mellanstadiet är ungefär en tiondel. I tabellen nedan har eleverna gett sin syn på den egna insatsen. Enligt lärarna är det största glädjeämnet när eleverna förstår och får "aha-upplevelser". Andra saker som nämns är att få arbeta med målmedvetna eller duktiga elever och att få bidra till ökat självförtroende i matematik hos eleverna. Hälften av lärarna har också angett svårigheter i matematikundervisningen. En tredjedel nämner omotiverade elever och elever som inte förstår matematiken trots ansträngningar från både elev och lärare. Annat som nämns är svårigheter att hinna med kursen, heterogena elevgrupper, brist på resurser och brist på disciplin. I fråga om mål som det är svårt att förverkliga på högstadiet är det vanligaste svaret "att individualisera undervisningen". Hälften av de 0% som svarat på frågan har nämnt detta. Ungefär en av fem nämner svårigheter att motivera eleverna för matematikämnet och att vardagsanknyta matematiken. Annat som nämns som svårt att förverkliga är att lära eleverna baskunskaper och att ändra en del elevers negativa inställning till ämnet. Elevernas svar på några påståenden rörande den egna motivationen. Procentuella andelar (N = 9 00). NU, åk 9. Tabell 2, s 0. (Skolverket, 199) Påstående helt i stort sett delvis inte alls För det mesta ger jag upp när jag får en svår uppgift 4 Jag skulle ha kunnat vara bättre i matematik om jag ansträngt mig mer Jag har gjort mitt allra bästa för att lära mig matematik på lågstadiet på mellanstadiet på högstadiet Jag är nöjd med det jag presterat i matematik på lågstadiet på mellanstadiet på högstadiet
7 Är matematik det svåraste ämnet? Ca 000 gymnasielever i åk 1 har 1984 och 1989 svarat på frågor om sin grundskoletid. De fick bland annat frågan om de upplevde problem med matematik under sin högstadietid, och i så fall med vad. Svaren utföll ungefär likadant 1989 som Andelen elever som anser sig ha haft stora eller mycket stora problem på högstadiet varierar i olika undervisningssituationer, mellan 2% och 12%. Störst problem säger de sig ha haft med "Att tala i grupp eller i klassen" och med "räkning" (11%). Gymnasieeleverna svarade också på frågan hur pass säkra de kände sig i situationer då de behövde räkna, läsa, skriva eller tala i grupp. 20% av eleverna kände sig osäkra eller mycket osäkra när de skulle räkna. När det gällde att läsa och skriva var det endast 4% som kände sig osäkra. Det framgår inte huruvida situationerna då de behövde räkna gällde skolan eller livet utanför. Välj ett exempel på en egen, särskilt framgångrik undervisningsinsats. Varför blev resultatet så lyckat? Jämför gärna med motsvarande exempel från några kollegor. Välj ett exempel på en misslyckad undervisningsinsats. Varför blev den så misslyckad? Jämför och diskutera gärna med några kollegor. Idag studerar alla elever matematik i gymnasiet. Man kan anta att andelen elever med sämre förkunskaper ökat jämfört med tidigare. Hur hjälper man bäst de elever som uppger sig ha problem? Enligt informationschefen på kronofogdemyndigheten i Göteborg, Rosén (1994), har många problem med privatekonomin. Bristande kunskaper leder till ekonomiska svårigheter och innebär allvarliga störningar i privatlivet. I kronofogdemyndighetens register finns nästan personer. Vet eleverna om detta? I grundskolan arbetar eleverna i par eller i mindre grupper i stort sett varje lektion enligt 0% av lärarna. Hur ofta sker det i din klass? Hur stora grupper? Vilka ämnesområden? På mellanstadiet är det inte ovanligt att eleverna får konstruera egna uppgifter. På högstadiet låter var femte lärare eleverna göra det någon gång varje månad. Vilka erfarenheter har du? Hur gör dina kollegor? Vilka erfarenheter har grundskolans elever av miniräknare och datorer, och vad möter de i gymnasieskolan? Skolverkets rapport nr 1, Matematik i åk 9 ger ytterligare underlag.
8 Litteratur Andersson, K. (1988). Läroboken en autolots. Nämnaren 1(1), Björk, L-E. & Brolin, H. (1990). Matematiken och de nya verktygen. Nämnaren 1(-4), 6-6. Emanuelsson, G. & Johansson, B. (1989). Vad ska en matematiklärare kunna? Nämnaren (1), 2 -. Emanuelsson, G. & Johansson, B. (199). Matematikämnets didaktik - ett växande vetenskapsområde. Nämnaren 22(1), Garmannslund, K. (1984). Kan ikke jenter regne? Nämnaren (4), 2-4. Grevholm, B. & Areskoug, M. (198). Vems matematik? Nämnaren 14(1), 2-. Johansson, B. (1991). Forskning och utvecklingsarbete i matematikdidaktik i Sverige. Nämnaren 18(/4), 4-. Löthman, A. (1991). Perspektiv på matematikundervisning. Nämnaren 18(2), 6-8. Pettersson, A. (1994). Högstadieelevers syn på matematiken. Nämnaren 21(1), 4-. Sjögren, P. (1992). En matematikers syn på svensk skolmatematik. Nämnaren 19(), Svensson, A. (199). Högstadiets matematik skrämmer. Nämnaren 22(2), Wahlund, B. (1986). Vi valde bort matten - fick räkna ändå! Nämnaren 12(4), 0-2. Alexandersson, C. (198). Stabilitet och förändring. En empirisk studie av förhållandet mellan skolkunskaper och vardagsvetande. Göteborg Studies in Educational Sciences, nr. Carlesson, L. (1968). Matematik för vår tid. En presentation och ett debattinlägg. Stockholm: Bokförlaget Prisma. Emanuelsson, G., Johansson, B., Rosén, B. & Ryding, R. (1992). Dokumentation av :e Matematikbiennalen, Göteborg januari Institutionen för ämnesdidaktik, Göteborgs universitet. Emanuelsson, G., Johansson, B., Rosén, B. & Ryding, R. (1994). Dokumentation av 8:e Matematikbiennalen, Göteborg januari Institutionen för ämnesdidaktik, Göteborgs universitet. Grevholm, B. (199). Naturvetenskap och teknik i Sverige. Kan forskningsinformation stimulera? Stockholm: Verket för Högskoleservice. Johansson, B. (199). Matematikdidaktik - nordiskt samarbete i historisk belysning. NOMAD 1 (1), -61. Löthman, A. (1990). Perspektiv på matematikundervisningen. En pilotstudie på Komvux och grundskolans högstadium angående elevers och lärares uppfattningar av undervisningsprocessen. Rapport från Pedagogiska institutionen, Uppsala universitet, 11. Nilsson, M. (199). Matematikundervisning i gymnasieskolan. Del I- III. Lärarhögskolan i Malmö. Pettersson, A. (1990). Att utvecklas i matematik. En studie av elever med olika prestationsutveckling. Stockholm Institute of Education. Studies in Education and Psychology No 2. Skolverket (199a). Den nationella utvärderingen av grundskolan våren Matematik åk 9. Huvudrapport. Skolverkets rapport nr 1. Stockholm: Liber distribution. Skolverket (199b). Attityder till skolan. Skolbildsundersökningen 199/94. Skolverkets rapport Nr 2. Stockholm: Liber distribution. SOU 1992:94. Skola för bildning. Betänkande av läroplanskommittén. Stockholm: Allmänna förlaget. Utbildningsdepartementet. (1986). Matematik för alla. Sammanfattning av rapporten Matematik i skolan. Utbildningsdepartementet och Liber Utbildningsförlaget. Wyndhamn, J. (1988). Tankeform och problemmiljö. Skolan som kontext för tänkande i elementärmatematik. SIC 26, University of Linköping: Studies in Communication. Alrø, H. og Skovsmose, O. (199). Det var ikke meningen! - Om kommunikation i matematikundervisningen. NOMAD 1(2), Cockcroft, W. H.(Chairman). (1982). Mathematics Counts: Report of the Committee of Inquiry into the Teaching of Mathematics in Schools. London: H.M.S.O. Damerow, P. et al (Eds.) (1986). Mathematics for all. Unesco. Grouws, D.A. (Ed.) (1992). Handbook of research on mathematics teaching and learning. A project of the National Council of Teachers of Mathematics, NCTM. New York: MacMillan. National Council for Teaching Mathematics, NCTM (1991). Professional Standards for Teaching Mathematics. Reston, Va.: Author.
Matematik - ett kärnämne
 Matematik - ett kärnämne Elevers och lärares erfarenheter Att utgå från elevers kunnande Elevens och lärarens ansvar Utvärdering av kunskaper Undersökande aktiviteter Matematik i samverkan Att utgå från
Matematik - ett kärnämne Elevers och lärares erfarenheter Att utgå från elevers kunnande Elevens och lärarens ansvar Utvärdering av kunskaper Undersökande aktiviteter Matematik i samverkan Att utgå från
Aha-upplevelser och tidsbrist
 maria nordlund Aha-upplevelser och tidsbrist Vad är det som är glädjen och vad är svårigheten med att undervisa i matematik? Här redovisas några av de upplevelser som lärarna i åk 5 och 9 redovisade i
maria nordlund Aha-upplevelser och tidsbrist Vad är det som är glädjen och vad är svårigheten med att undervisa i matematik? Här redovisas några av de upplevelser som lärarna i åk 5 och 9 redovisade i
Matematikundervisning genom problemlösning
 Matematikundervisning genom problemlösning En studie om lärares möjligheter att förändra sin undervisning Varför problemlösning i undervisningen? Matematikinlärning har setts traditionell som en successiv
Matematikundervisning genom problemlösning En studie om lärares möjligheter att förändra sin undervisning Varför problemlösning i undervisningen? Matematikinlärning har setts traditionell som en successiv
Figur 1: Påverkan som processer. Vad tycker elever om matematik och matematikundervisning?
 Modul: Problemlösning Del 1: Matematiska problem Känsla för problem Lovisa Sumpter När vi arbetar med matematik är det många faktorer som påverkar det vi gör. Det är inte bara våra kunskaper i ämnet som
Modul: Problemlösning Del 1: Matematiska problem Känsla för problem Lovisa Sumpter När vi arbetar med matematik är det många faktorer som påverkar det vi gör. Det är inte bara våra kunskaper i ämnet som
Matematik är ett ämne som många människor, både barn och vuxna
 Mikaela Thorén Motivation för matematik Författaren ger här en bild av vilka faktorer som kan påverka elevers motivation för att lära matematik. Artikeln bygger på författarens examensarbete som belönades
Mikaela Thorén Motivation för matematik Författaren ger här en bild av vilka faktorer som kan påverka elevers motivation för att lära matematik. Artikeln bygger på författarens examensarbete som belönades
Matematikundervisningens dilemma
 Matematikundervisningens dilemma Om jag låter blicken gå runt i klassrummet i så kommer att jag se att eleverna skiljer sig åt i ett flertal avseenden, såsom utseende, personlighet, social och biologisk
Matematikundervisningens dilemma Om jag låter blicken gå runt i klassrummet i så kommer att jag se att eleverna skiljer sig åt i ett flertal avseenden, såsom utseende, personlighet, social och biologisk
Matematikpolicy Västra skolområdet i Linköping
 Matematikpolicy Västra skolområdet i Linköping Syfte Denna matematikpolicy är framtagen i syfte att underlätta och säkerställa arbetet med barns och elevers matematiska utveckling på förskolorna och skolorna
Matematikpolicy Västra skolområdet i Linköping Syfte Denna matematikpolicy är framtagen i syfte att underlätta och säkerställa arbetet med barns och elevers matematiska utveckling på förskolorna och skolorna
Betyg på kvaliteter i kunnandet
 Betyg på kvaliteter i kunnandet Bengt Johansson I tidigare nummer har vi beskrivit och diskuterat arbetet med nytt betygssystem. Skolverket har nu fastställt betygskriterier för alla ämnen i grundskolan.
Betyg på kvaliteter i kunnandet Bengt Johansson I tidigare nummer har vi beskrivit och diskuterat arbetet med nytt betygssystem. Skolverket har nu fastställt betygskriterier för alla ämnen i grundskolan.
Det finns flera aspekter av subtraktion som lärare bör ha kunskap om, en
 Kerstin Larsson Subtraktion Vad är egentligen subtraktion? Vad behöver en lärare veta om subtraktion och subtraktionsundervisning? Om elevers förståelse av subtraktion och om elevers vanliga missuppfattningar?
Kerstin Larsson Subtraktion Vad är egentligen subtraktion? Vad behöver en lärare veta om subtraktion och subtraktionsundervisning? Om elevers förståelse av subtraktion och om elevers vanliga missuppfattningar?
Vad innebär det att undervisa i algebra i årskurs 1 3? Vart ska dessa
 Åsa Brorsson Algebra för lågstadiet I denna artikel beskriver en lärare hur hon arbetar med algebra redan i de tidiga skolåren. Det är ett arbete som hjälper elever att förstå likhetstecknets betydelse,
Åsa Brorsson Algebra för lågstadiet I denna artikel beskriver en lärare hur hon arbetar med algebra redan i de tidiga skolåren. Det är ett arbete som hjälper elever att förstå likhetstecknets betydelse,
Vad gör vi åt Skolverkets lägesbeskrivning och handlingsplan?
 Vad gör vi åt Skolverkets lägesbeskrivning och handlingsplan? Skolverket har nyss överlämnat sin fördjupade anslagsframställning 1994/95-1996/97 till regeringen. Här publicerars några valda avsnitt ur
Vad gör vi åt Skolverkets lägesbeskrivning och handlingsplan? Skolverket har nyss överlämnat sin fördjupade anslagsframställning 1994/95-1996/97 till regeringen. Här publicerars några valda avsnitt ur
OBS! Vik och riv försiktigt! TRENDS IN INTERNATIONAL MATHEMATICS AND SCIENCE STUDY. Elevenkät. Årskurs 4. TIMSS 2015 Skolverket Stockholm
 OBS! Vik och riv försiktigt! TRENDS IN INTERNATIONAL MATHEMATICS AND SCIENCE STUDY Elevenkät Årskurs 4 TIMSS 2015 Skolverket 106 20 Stockholm IEA, 2014 Instruktioner I det här häftet finns frågor om dig
OBS! Vik och riv försiktigt! TRENDS IN INTERNATIONAL MATHEMATICS AND SCIENCE STUDY Elevenkät Årskurs 4 TIMSS 2015 Skolverket 106 20 Stockholm IEA, 2014 Instruktioner I det här häftet finns frågor om dig
Matematikundervisning och självförtroende i årskurs 9
 KATARINA KJELLSTRÖM Matematikundervisning och självförtroende i årskurs 9 I förra numret av Nämnaren beskrev vi elevernas kunskaper i och attityder till matematik enligt nationella utvärderingen 2003.
KATARINA KJELLSTRÖM Matematikundervisning och självförtroende i årskurs 9 I förra numret av Nämnaren beskrev vi elevernas kunskaper i och attityder till matematik enligt nationella utvärderingen 2003.
Verksamhetsrapport. Skolinspektionen. efter kvalitetsgranskning av undervisningen i matematik kurs 3c vid IT-gymnasiet Södertörn i Huddinge kommun
 Bilaga 1 Verksam hetsrapport 2015-02-18 Dnr 400-2014:2725 efter kvalitetsgranskning av undervisningen i matematik kurs 3c vid IT-gymnasiet Södertörn i Huddinge kommun 1 (8) Innehåll Inledning Bakgrundsuppgifter
Bilaga 1 Verksam hetsrapport 2015-02-18 Dnr 400-2014:2725 efter kvalitetsgranskning av undervisningen i matematik kurs 3c vid IT-gymnasiet Södertörn i Huddinge kommun 1 (8) Innehåll Inledning Bakgrundsuppgifter
Uppdrag till Statens skolverk att stärka undervisningen i matematik, naturvetenskap och teknik
 Regeringsbeslut I:4 2011-03-31 U2011/2229/G Utbildningsdepartementet Statens skolverk 106 20 Stockholm Uppdrag till Statens skolverk att stärka undervisningen i matematik, naturvetenskap och teknik Regeringens
Regeringsbeslut I:4 2011-03-31 U2011/2229/G Utbildningsdepartementet Statens skolverk 106 20 Stockholm Uppdrag till Statens skolverk att stärka undervisningen i matematik, naturvetenskap och teknik Regeringens
Utvecklingsarbete i Falu kommun en angelägenhet på alla nivåer i skolförvaltningen
 Utvecklingsarbete i Falu kommun en angelägenhet på alla nivåer i skolförvaltningen Förutsättningar Mellanstor kommun (55 000 inv) 60 kommunala förskolor 25 kommunala grundskolor 3 kommunala gymnasieskolor
Utvecklingsarbete i Falu kommun en angelägenhet på alla nivåer i skolförvaltningen Förutsättningar Mellanstor kommun (55 000 inv) 60 kommunala förskolor 25 kommunala grundskolor 3 kommunala gymnasieskolor
PDA422 MATEMATIKDIDAKTIK II, 15 HÖGSKOLEPOÄNG Didactics of Mathematics II, 15 higher education credits
 Utbildningsvetenskapliga fakulteten PDA422 MATEMATIKDIDAKTIK II, 15 HÖGSKOLEPOÄNG Didactics of Mathematics II, 15 higher education credits Avancerad nivå. Second cycle 1. Fastställande Kursplanen är fastställd
Utbildningsvetenskapliga fakulteten PDA422 MATEMATIKDIDAKTIK II, 15 HÖGSKOLEPOÄNG Didactics of Mathematics II, 15 higher education credits Avancerad nivå. Second cycle 1. Fastställande Kursplanen är fastställd
Matematikundervisning för framtiden
 Matematikundervisning för framtiden Matematikundervisning för framtiden De svenska elevernas matematikkunskaper har försämrats över tid, både i grund- och gymnasieskolan. TIMSS-undersökningen år 2003 visade
Matematikundervisning för framtiden Matematikundervisning för framtiden De svenska elevernas matematikkunskaper har försämrats över tid, både i grund- och gymnasieskolan. TIMSS-undersökningen år 2003 visade
Historiskt perspektiv i klassrummet
 Historiskt perspektiv i klassrummet Mikael Holmquist I de nya kursplaneförslagen betonas matematikens idéhistoria. Här redogörs för några observationer från ett arbete i påbyggnadsutbildningen i matematikdidaktik,
Historiskt perspektiv i klassrummet Mikael Holmquist I de nya kursplaneförslagen betonas matematikens idéhistoria. Här redogörs för några observationer från ett arbete i påbyggnadsutbildningen i matematikdidaktik,
Nationella diagnosmaterial för skolår 2 och 7
 Nationella diagnosmaterial för skolår 2 och 7 Astrid Pettersson I mars 1996 skickades Skolverkets diagnostiska material ut till skolorna. Här beskrivs syfte, innehåll och hur man kan använda materialen
Nationella diagnosmaterial för skolår 2 och 7 Astrid Pettersson I mars 1996 skickades Skolverkets diagnostiska material ut till skolorna. Här beskrivs syfte, innehåll och hur man kan använda materialen
Matematiklyftet. Malmöbiennetten 2013. Nationellt centrum för Matematikutbildning Göteborgs Universitet. Anette Jahnke
 Matematiklyftet Malmöbiennetten 2013 Nationellt centrum för Matematikutbildning Göteborgs Universitet Anette Jahnke #malyft Matematiklyftet Matematiklyftet Fortbildning av alla lärare som undervisar i
Matematiklyftet Malmöbiennetten 2013 Nationellt centrum för Matematikutbildning Göteborgs Universitet Anette Jahnke #malyft Matematiklyftet Matematiklyftet Fortbildning av alla lärare som undervisar i
Handledarutbildning inom Matematiklyftet. Catarina Wästerlid Utbildningstillfälle 1 17 oktober-2016
 Handledarutbildning inom Matematiklyftet Catarina Wästerlid Utbildningstillfälle 1 17 oktober-2016 1. Efter genomgången utbildning ska matematikhandledaren ha goda kunskaper om Matematiklyftets bakgrund
Handledarutbildning inom Matematiklyftet Catarina Wästerlid Utbildningstillfälle 1 17 oktober-2016 1. Efter genomgången utbildning ska matematikhandledaren ha goda kunskaper om Matematiklyftets bakgrund
Motivation för matematik
 Matematik, Specialpedagogik Grundskola åk 1 3 Modul: Inkludering och delaktighet lärande i matematik Del 6: Matematikängslan och motivation Motivation för matematik Karolina Muhrman och Joakim Samuelsson,
Matematik, Specialpedagogik Grundskola åk 1 3 Modul: Inkludering och delaktighet lärande i matematik Del 6: Matematikängslan och motivation Motivation för matematik Karolina Muhrman och Joakim Samuelsson,
+ + åk 1-3 åk 4-6 åk 7-9. annan utbildning: Tänk på den skola där du har huvuddelen av din tjänstgöring när en specifik skola efterfrågas
 1 Var har du huvuddelen av din tjänstgöring? Ange ett alternativ. Grundskola: åk 1-3 åk 4-6 åk 7-9 Gymnasieskola: studie-/högskoleförberedande program yrkesförberedande program/yrkesprogram annan utbildning:
1 Var har du huvuddelen av din tjänstgöring? Ange ett alternativ. Grundskola: åk 1-3 åk 4-6 åk 7-9 Gymnasieskola: studie-/högskoleförberedande program yrkesförberedande program/yrkesprogram annan utbildning:
måndag, 2010 oktober 11
 Har du inte räknat färdigt än? Vad är matematik? Var och hur används matematik? Vad är matematikkunnande? Varför ska vi lära oss matematik? Vad är matematik? Nationalencyklopedin En abstrakt och generell
Har du inte räknat färdigt än? Vad är matematik? Var och hur används matematik? Vad är matematikkunnande? Varför ska vi lära oss matematik? Vad är matematik? Nationalencyklopedin En abstrakt och generell
Samhället och skolan förändras och matematikundervisningen som den
 Saman Abdoka Elevens bakgrund en resurs De senaste tjugo åren har inneburit stora förändringar för såväl samhälle som skolmatematik. Ur en lång erfarenhet av att undervisa i mångkulturella klassrum ger
Saman Abdoka Elevens bakgrund en resurs De senaste tjugo åren har inneburit stora förändringar för såväl samhälle som skolmatematik. Ur en lång erfarenhet av att undervisa i mångkulturella klassrum ger
Undervisa i matematik genom problemlösning
 Modul: Problemlösning Del 1: Matematikundervisning genom problemlösning Undervisa i matematik genom problemlösning Maria Larsson, Mälardalens högskola Att hjälpa barn att bli bättre problemlösare är inte
Modul: Problemlösning Del 1: Matematikundervisning genom problemlösning Undervisa i matematik genom problemlösning Maria Larsson, Mälardalens högskola Att hjälpa barn att bli bättre problemlösare är inte
De senaste årens resultat från internationella kunskapsundersökningar
 M. Däcker, F. Hollsten, E. Kaminski & L. Rådvall Undervisningen har betydelse elevers kunskaper om algebraiska uttryck Inom ramen för Stockholmsprojektet har fyra lärare på högstadiet och gymnasiet undersökt
M. Däcker, F. Hollsten, E. Kaminski & L. Rådvall Undervisningen har betydelse elevers kunskaper om algebraiska uttryck Inom ramen för Stockholmsprojektet har fyra lärare på högstadiet och gymnasiet undersökt
Erik Östergren lärarutbildningen, 5hp HT 2015
 Kurslitteratur Matematik ett kärnämne (Nämnaren Tema) Diverse artiklar All kurslitteratur kommer att finnas tillgänglig på Studentportalen. Kurshemsida http://studentportalen.uu.se Undervisning 20 lektionstillfällen.
Kurslitteratur Matematik ett kärnämne (Nämnaren Tema) Diverse artiklar All kurslitteratur kommer att finnas tillgänglig på Studentportalen. Kurshemsida http://studentportalen.uu.se Undervisning 20 lektionstillfällen.
Matematiklyftet utveckling av kompetensutvecklingskultur och undervisningskultur. Peter Nyström Nationellt centrum för matematikutbildning
 Matematiklyftet utveckling av kompetensutvecklingskultur och undervisningskultur Peter Nyström Nationellt centrum för matematikutbildning Frågan är Hur (hvordan) utvecklar man bäst kvalitet i matematikundervisning
Matematiklyftet utveckling av kompetensutvecklingskultur och undervisningskultur Peter Nyström Nationellt centrum för matematikutbildning Frågan är Hur (hvordan) utvecklar man bäst kvalitet i matematikundervisning
Olikheter i klassen tillgång eller problem?
 Olikheter i klassen tillgång eller problem? Om undervisning i åldersblandad klass Ulla Runesson Åldersblandad undervisning har blivit allt vanligare de senaste åren. Vad finns det för möjligheter och begränsningar
Olikheter i klassen tillgång eller problem? Om undervisning i åldersblandad klass Ulla Runesson Åldersblandad undervisning har blivit allt vanligare de senaste åren. Vad finns det för möjligheter och begränsningar
Att utforska matematiken tillsammans strategier för inkluderande klassrumssamtal
 Att utforska matematiken tillsammans strategier för inkluderande klassrumssamtal - implementering av Talk Moves i en svensk kontext Lisa Dimming, Marita Lundström, Margareta Engvall & Karin Forslund Frykedal
Att utforska matematiken tillsammans strategier för inkluderande klassrumssamtal - implementering av Talk Moves i en svensk kontext Lisa Dimming, Marita Lundström, Margareta Engvall & Karin Forslund Frykedal
OBS! Vik och riv försiktigt! TRENDS IN INTERNATIONAL MATHEMATICS AND SCIENCE STUDY. Elevenkät. Årskurs 8. TIMSS 2015 Skolverket Stockholm
 OBS! Vik och riv försiktigt! TRENDS IN INTERNATIONAL MATHEMATICS AND SCIENCE STUDY Elevenkät Årskurs 8 TIMSS 2015 Skolverket 106 20 Stockholm IEA, 2014 Instruktioner I det här häftet finns frågor om dig
OBS! Vik och riv försiktigt! TRENDS IN INTERNATIONAL MATHEMATICS AND SCIENCE STUDY Elevenkät Årskurs 8 TIMSS 2015 Skolverket 106 20 Stockholm IEA, 2014 Instruktioner I det här häftet finns frågor om dig
Innehållet Aktiviteten utgår från verkligheten, den bygger på det som finns på platsen.
 Denna text kommer från inledningen till boken Att lära in matematik ute 2 och boken Learning in the Outdoor Classroom. Här beskriver vi vad vi utomhuspedagogik är och vad vi uppnår med detta arbetssätt.
Denna text kommer från inledningen till boken Att lära in matematik ute 2 och boken Learning in the Outdoor Classroom. Här beskriver vi vad vi utomhuspedagogik är och vad vi uppnår med detta arbetssätt.
Verksamhetsrapport. Skolinspektionen. efter kvalitetsgranskning av undervisningen i matematik kurs 3c vid Westerlundska gymnasiet i Enköpings kommun
 Bilaga 1 Verksam hetsrapport 2015-03-13 efter kvalitetsgranskning av undervisningen i matematik kurs 3c vid Westerlundska gymnasiet i Enköpings kommun - 2015-03-13 1 (10) Innehåll Inledning Bakgrundsuppgifter
Bilaga 1 Verksam hetsrapport 2015-03-13 efter kvalitetsgranskning av undervisningen i matematik kurs 3c vid Westerlundska gymnasiet i Enköpings kommun - 2015-03-13 1 (10) Innehåll Inledning Bakgrundsuppgifter
Sammanfattning Rapport 2010:13. Undervisningen i matematik i gymnasieskolan
 Sammanfattning Rapport 2010:13 Undervisningen i matematik i gymnasieskolan 1 Sammanfattning Skolinspektionen har granskat kvaliteten i undervisningen i matematik på 55 gymnasieskolor spridda över landet.
Sammanfattning Rapport 2010:13 Undervisningen i matematik i gymnasieskolan 1 Sammanfattning Skolinspektionen har granskat kvaliteten i undervisningen i matematik på 55 gymnasieskolor spridda över landet.
Provmoment: Tentamen Matematik och matematikdidaktik, 3 hp, tillfälle 1
 Matematik med didaktisk inriktning för grundlärare i förskoleklass och grundskolans a rskurs 1-3, III, VT18 7,5 högskolepoäng Provmoment: Tentamen Matematik och matematikdidaktik, 3 hp, tillfälle 1 Ladokkod:
Matematik med didaktisk inriktning för grundlärare i förskoleklass och grundskolans a rskurs 1-3, III, VT18 7,5 högskolepoäng Provmoment: Tentamen Matematik och matematikdidaktik, 3 hp, tillfälle 1 Ladokkod:
Eva Mettävainio, lågstadielärare undervisar på Smedskolan (F-3) i Pajala.
 455 b Matematikinlärning med miniräknare Eva Mettävainio, lågstadielärare undervisar på Smedskolan (F-3) i Pajala. Miniräknaren ska användas i skolan, det står i vår kursplan för matematik (Utbildningsdepartementet,
455 b Matematikinlärning med miniräknare Eva Mettävainio, lågstadielärare undervisar på Smedskolan (F-3) i Pajala. Miniräknaren ska användas i skolan, det står i vår kursplan för matematik (Utbildningsdepartementet,
Verksamhetsrapport. Skoitnst.. 7.1,ktion.en
 Skoitnst.. 7.1,ktion.en Bilaga 1 Verksamhetsrapport Verksamhetsrapport efter kvalitetsgranskning av undervisningen i matematik kurs 3c vid den fristående gymnasieskolan JENSEN gymnasium Uppsala i Uppsala
Skoitnst.. 7.1,ktion.en Bilaga 1 Verksamhetsrapport Verksamhetsrapport efter kvalitetsgranskning av undervisningen i matematik kurs 3c vid den fristående gymnasieskolan JENSEN gymnasium Uppsala i Uppsala
Umeå Universitet NMD Naturvetenskapernas och matematikens Didaktik. Studieguide till Matematik för F 3, kurs 2 Ht MN023
 Umeå Universitet NMD Naturvetenskapernas och matematikens Didaktik Studieguide till Matematik för F 3, kurs 2 Ht 2014 6MN023 Kursnamn: Matematik för åk F 3, kurs 2, 7,5 hp Termin: H 14 Kurskod: 6MN023
Umeå Universitet NMD Naturvetenskapernas och matematikens Didaktik Studieguide till Matematik för F 3, kurs 2 Ht 2014 6MN023 Kursnamn: Matematik för åk F 3, kurs 2, 7,5 hp Termin: H 14 Kurskod: 6MN023
Träff 1 Introduktion till Laborativ Matematik
 Träff 1 Introduktion till Laborativ Matematik Tid: Onsdagen den 29 augusti kl 17.30-20.00 Skolinspektionen (2009). Undervisningen i matematik utbildningens innehåll och ändamålsenlighet. Skolinspektionens
Träff 1 Introduktion till Laborativ Matematik Tid: Onsdagen den 29 augusti kl 17.30-20.00 Skolinspektionen (2009). Undervisningen i matematik utbildningens innehåll och ändamålsenlighet. Skolinspektionens
Spridningen är vanligtvis stor i en klass när det gäller vad elever tycker om,
 Kerstin Johnsson & Jonas Bergman Ärlebäck Godissugen! En tankeavslöjade aktivitet för att introducera området funktioner I den här artikeln diskuteras en aktivitet som introducerar funktioner i åk 8 genom
Kerstin Johnsson & Jonas Bergman Ärlebäck Godissugen! En tankeavslöjade aktivitet för att introducera området funktioner I den här artikeln diskuteras en aktivitet som introducerar funktioner i åk 8 genom
Matematikvisionen Ht 2002- vt 2006
 Matematikvisionen Ht 2002- vt 2006 Sammanfattning av Utbildningsförvaltningens satsning på kompetensutveckling av matematiklärare på gymnasiet i projektet Nollvisionen/Matematikvisionen. Nollvisionen MaA
Matematikvisionen Ht 2002- vt 2006 Sammanfattning av Utbildningsförvaltningens satsning på kompetensutveckling av matematiklärare på gymnasiet i projektet Nollvisionen/Matematikvisionen. Nollvisionen MaA
Ny kursplan i matematik
 Ny kursplan i matematik Läroplanskommitténs förslag till ny kursplan i matematik för grundskolan presenteras på följande sidor. Bengt Johansson och Göran Emanuelsson, som tagit fram underlag till förslaget,
Ny kursplan i matematik Läroplanskommitténs förslag till ny kursplan i matematik för grundskolan presenteras på följande sidor. Bengt Johansson och Göran Emanuelsson, som tagit fram underlag till förslaget,
30-40 år år år. > 60 år år år. > 15 år
 1 av 14 2010-11-02 16:21 Namn: Skola: Epostadress: 1. Kön Kvinna Man 2. Ålder < 30 år 30-40 år 41-50 år 51-60 år > 60 år 3. Har varit verksam som lärare i: < 5 år 6-10 år 11-15 år > 15 år 4. Har du en
1 av 14 2010-11-02 16:21 Namn: Skola: Epostadress: 1. Kön Kvinna Man 2. Ålder < 30 år 30-40 år 41-50 år 51-60 år > 60 år 3. Har varit verksam som lärare i: < 5 år 6-10 år 11-15 år > 15 år 4. Har du en
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Hur viktigt har följande varit för ditt val av gymnasieutbildning?
 1 Vilket år är du född? 2 Går du i grundskolan, gymnasieskolan eller går du inte i skolan? Grundskolan Gymnasieskolan Går inte i grund- eller gymnasieskola. Du behöver inte svara på fler frågor. Viktigt,
1 Vilket år är du född? 2 Går du i grundskolan, gymnasieskolan eller går du inte i skolan? Grundskolan Gymnasieskolan Går inte i grund- eller gymnasieskola. Du behöver inte svara på fler frågor. Viktigt,
En stadieindelad timplan i grundskolan och närliggande frågor
 Utbildningsförvaltningen Grundskoleavdelningen Tjänsteutlåtande Dnr 1.6.1-7608/2016 Sida 1 (10) 2016-10-07 Handläggare Elisabeth Forsberg-Uvemo Telefon: 08-50833010 Annika Risel Telefon: 08-50833607 Till
Utbildningsförvaltningen Grundskoleavdelningen Tjänsteutlåtande Dnr 1.6.1-7608/2016 Sida 1 (10) 2016-10-07 Handläggare Elisabeth Forsberg-Uvemo Telefon: 08-50833010 Annika Risel Telefon: 08-50833607 Till
Reviderad kursplan för grundskolan och förskoleklassen
 Reviderad kursplan för grundskolan och förskoleklassen Bengt Johansson & Göran Emanuelsson Kursplan och betygskriterier för VG och MVG diskuteras nu inom Skolverket. I mars granskas ett första förslag
Reviderad kursplan för grundskolan och förskoleklassen Bengt Johansson & Göran Emanuelsson Kursplan och betygskriterier för VG och MVG diskuteras nu inom Skolverket. I mars granskas ett första förslag
Skolenkäten hösten 2018
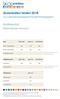 Skolenkäten hösten 2018 Huvudmannarapport/Skolenhetsrapport Enkätresultat Vänersborgs kommun Elever Total antal Antal svar Svarsfrekvens Årskurs 5 grundskola 463 433 94% Årskurs 9 grundskola 393 310 79%
Skolenkäten hösten 2018 Huvudmannarapport/Skolenhetsrapport Enkätresultat Vänersborgs kommun Elever Total antal Antal svar Svarsfrekvens Årskurs 5 grundskola 463 433 94% Årskurs 9 grundskola 393 310 79%
Nationell utvärdering där matematiken
 KATARINA KJELLSTRÖM & ASTRID PETTERSSON Matematiken i den nationella utvärderingen De nationella utvärderingarna i matematik har alltsedan starten varit förlagda till PRIM-gruppen vid Lärarhögskolan i
KATARINA KJELLSTRÖM & ASTRID PETTERSSON Matematiken i den nationella utvärderingen De nationella utvärderingarna i matematik har alltsedan starten varit förlagda till PRIM-gruppen vid Lärarhögskolan i
När vi tänker på någon situation eller händelse där multiplikation
 Maria Flodström & Lina Johnsson Framställningen av multiplikation påverkar taluppfattningen Multiplikation i läromedel för årskurs 1 3 Här ger 2011 års Göran Emanuelssonstipendiater sin analys av hur multiplikation
Maria Flodström & Lina Johnsson Framställningen av multiplikation påverkar taluppfattningen Multiplikation i läromedel för årskurs 1 3 Här ger 2011 års Göran Emanuelssonstipendiater sin analys av hur multiplikation
Identification Label. Student ID: Student Name: Elevenkät Avancerad Matematik. Skolverket Bo Palaszewski, Projektledare Stockholm
 Identification Label Student ID: Student Name: Elevenkät Avancerad Matematik Skolverket Bo Palaszewski, Projektledare 106 20 Stockholm International Association for the Evaluation of Educational Achievement
Identification Label Student ID: Student Name: Elevenkät Avancerad Matematik Skolverket Bo Palaszewski, Projektledare 106 20 Stockholm International Association for the Evaluation of Educational Achievement
Projektbeskrivning. Gymnasieskolans mål och Högskolans förkunskapskrav. En jämförande studie om matematikundervisningen.
 Projektbeskrivning Gymnasieskolans mål och Högskolans förkunskapskrav. En jämförande studie om matematikundervisningen. Bakgrund KTH och LHS har ett regeringsuppdrag att tillsammans utveckla nya inriktningar
Projektbeskrivning Gymnasieskolans mål och Högskolans förkunskapskrav. En jämförande studie om matematikundervisningen. Bakgrund KTH och LHS har ett regeringsuppdrag att tillsammans utveckla nya inriktningar
Podsändningar i skolan
 Podsändningar i skolan Tomas Bergqvist, Brian Hudson, Johan Lithner and Krister Lindwall. UFM 1, Umeå Universitet. Sammanfattning: Elva klasser från olika delar av Sverige deltog under läsåret 2007 i ett
Podsändningar i skolan Tomas Bergqvist, Brian Hudson, Johan Lithner and Krister Lindwall. UFM 1, Umeå Universitet. Sammanfattning: Elva klasser från olika delar av Sverige deltog under läsåret 2007 i ett
Lära matematik med datorn. Ulrika Ryan, projektledare för Matematik för den digitala generationen Byskolan, Södra Sandby
 Lära matematik med datorn Ulrika Ryan, projektledare för Matematik för den digitala generationen Byskolan, Södra Sandby Innehåll Varför undervisar jag som jag gör? Lärarens roll i det digitala klassrummet
Lära matematik med datorn Ulrika Ryan, projektledare för Matematik för den digitala generationen Byskolan, Södra Sandby Innehåll Varför undervisar jag som jag gör? Lärarens roll i det digitala klassrummet
Variation i matematikundervisningen
 Stefan Löfwall Karlstads universitet Variation i matematikundervisningen Idag diskuterar man mycket behovet av att variera matematikundervisningen. Inte minst betonas detta i Skolverkets rapport Lusten
Stefan Löfwall Karlstads universitet Variation i matematikundervisningen Idag diskuterar man mycket behovet av att variera matematikundervisningen. Inte minst betonas detta i Skolverkets rapport Lusten
/////// // ///////// / // /
 Utvärdering matematikämnet hösten 2010 Dessa grupper är inskrivna: Åk 7 Petra & Malins grupp Åk 8 Malins grupp Åk 9 Petras grupp Åk 7 Jörgens grupp Åk 8 Jonas & Petras grupp Åk 9 Jonas grupp Åk 7 Evas
Utvärdering matematikämnet hösten 2010 Dessa grupper är inskrivna: Åk 7 Petra & Malins grupp Åk 8 Malins grupp Åk 9 Petras grupp Åk 7 Jörgens grupp Åk 8 Jonas & Petras grupp Åk 9 Jonas grupp Åk 7 Evas
WORKSHOP PLANERING AV UNDERVISNING. Peter Fredriksson & Lena Knutsson Göteborgs Universitet, Idpp
 WORKSHOP PLANERING AV UNDERVISNING Peter Fredriksson & Lena Knutsson Göteborgs Universitet, Idpp Allmänna råd Lärare bör vid planeringen av undervisningen tydliggöra vilka delar av ämnets syfte (förmågor)
WORKSHOP PLANERING AV UNDERVISNING Peter Fredriksson & Lena Knutsson Göteborgs Universitet, Idpp Allmänna råd Lärare bör vid planeringen av undervisningen tydliggöra vilka delar av ämnets syfte (förmågor)
Pedagogisk planering i matematik; Tal i bråkform, decimalform och procentform. Ur Lgr 11 Kursplan i matematik.
 Pedagogisk planering i matematik; Tal i bråkform, decimalform och procentform. Ur Lgr 11 Kursplan i matematik. Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl
Pedagogisk planering i matematik; Tal i bråkform, decimalform och procentform. Ur Lgr 11 Kursplan i matematik. Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl
Statens skolverk 106 20 Stockholm
 Utbildningsdepartementet Regeringsbeslut I:44 2012-03-29 Statens skolverk 106 20 Stockholm U2011/4343/S U2011/7370/GV (delvis) U2012/2103/GV Uppdrag att svara för utbildning Regeringens beslut Regeringen
Utbildningsdepartementet Regeringsbeslut I:44 2012-03-29 Statens skolverk 106 20 Stockholm U2011/4343/S U2011/7370/GV (delvis) U2012/2103/GV Uppdrag att svara för utbildning Regeringens beslut Regeringen
Constanta Olteanu, Linnéuniversitetet och Anna-Lena Ekdahl, Högskolan i Jönköping
 Modul: Algebra Del 3: Bedömning för utveckling av undervisningen i algebra Intervju Constanta Olteanu, Linnéuniversitetet och Anna-Lena Ekdahl, Högskolan i Jönköping I en undervisning kan olika former
Modul: Algebra Del 3: Bedömning för utveckling av undervisningen i algebra Intervju Constanta Olteanu, Linnéuniversitetet och Anna-Lena Ekdahl, Högskolan i Jönköping I en undervisning kan olika former
UTBILDNINGSVETENSKAPLIGA FAKULTETSNÄMNDEN. Avancerad nivå/second Cycle
 UTBILDNINGSVETENSKAPLIGA FAKULTETSNÄMNDEN SPPS30, Matematiksvårigheter-orsaker och pedagogiska konsekvenser, 15,0 högskolepoäng Disabilities in Mathematics - Causes and Educational Consequenses, 15.0 higher
UTBILDNINGSVETENSKAPLIGA FAKULTETSNÄMNDEN SPPS30, Matematiksvårigheter-orsaker och pedagogiska konsekvenser, 15,0 högskolepoäng Disabilities in Mathematics - Causes and Educational Consequenses, 15.0 higher
NOKflex. Smartare matematikundervisning
 NOKflex Smartare matematikundervisning Med NOKflex får du tillgång till ett heltäckande interaktivt matematikläromedel som ger stöd både för elevens individuella lärande och för lärarledd undervisning.
NOKflex Smartare matematikundervisning Med NOKflex får du tillgång till ett heltäckande interaktivt matematikläromedel som ger stöd både för elevens individuella lärande och för lärarledd undervisning.
Undervisningen i matematik. i gymnasieskolan
 Undervisningen i matematik i gymnasieskolan 55 skolor 150 lektioner 150 lärare Grundskolan: 66 lärare Huvudresultat Flertalet elever får inte den undervisning de har rätt till Flertalet lärare har otillräckliga
Undervisningen i matematik i gymnasieskolan 55 skolor 150 lektioner 150 lärare Grundskolan: 66 lärare Huvudresultat Flertalet elever får inte den undervisning de har rätt till Flertalet lärare har otillräckliga
Räcker kunskaperna i matematik?
 Bilaga 2 Räcker kunskaperna i matematik? LARS BRANDELL Bakgrund Ett viktigt underlag för regeringens uppdrag till NCM har varit Högskoleverkets rapport Räcker kunskaperna i matematik? (Högskoleverket,
Bilaga 2 Räcker kunskaperna i matematik? LARS BRANDELL Bakgrund Ett viktigt underlag för regeringens uppdrag till NCM har varit Högskoleverkets rapport Räcker kunskaperna i matematik? (Högskoleverket,
Matematik Jag är... Jag går i årskurs... Det är roligt med matematik. Namn Antal % A. flicka B. pojke Total
 Matematik 2011 Jag är... A. flicka 127 50 B. pojke 127 50 Jag går i årskurs... A. 3 29 11,4 B. 4 13 5,1 C. 5 30 11,8 D. 6 18 7,1 E. 7 51 20,1 F. 8 38 15 G. 9 75 29,5 Det är roligt med matematik. 50 19,7
Matematik 2011 Jag är... A. flicka 127 50 B. pojke 127 50 Jag går i årskurs... A. 3 29 11,4 B. 4 13 5,1 C. 5 30 11,8 D. 6 18 7,1 E. 7 51 20,1 F. 8 38 15 G. 9 75 29,5 Det är roligt med matematik. 50 19,7
Är svenska elever dåliga i algebra och geometri?
 Är svenska elever dåliga i algebra och geometri? Lena Adolfsson I förra numret gavs en sammanfattande beskrivning av TIMSS-projektets studie av svenska 13-åringars kunskaper i matematik. I denna artikel
Är svenska elever dåliga i algebra och geometri? Lena Adolfsson I förra numret gavs en sammanfattande beskrivning av TIMSS-projektets studie av svenska 13-åringars kunskaper i matematik. I denna artikel
LPP för årskurs 2, Matte V.46-51 HT12
 LPP för årskurs 2, Matte V.46-51 HT12 Värdegrund och uppdrag Skolan ska vara öppen för skilda uppfattningar och uppmuntra att de förs fram. Den ska framhålla betydelsen av personliga ställningstaganden
LPP för årskurs 2, Matte V.46-51 HT12 Värdegrund och uppdrag Skolan ska vara öppen för skilda uppfattningar och uppmuntra att de förs fram. Den ska framhålla betydelsen av personliga ställningstaganden
Lärarutbildning i matematik - möjligheter och begränsningar
 Lärarutbildning i matematik - möjligheter och begränsningar Lisen Häggblom Åbo Akademi, Vasa Lärarutbildningen är en stor utbildning - komplex - har politiskt intresse - många vill vara experter på utbildning
Lärarutbildning i matematik - möjligheter och begränsningar Lisen Häggblom Åbo Akademi, Vasa Lärarutbildningen är en stor utbildning - komplex - har politiskt intresse - många vill vara experter på utbildning
Förstärkt tillsyn av skolors arbete med bedömning
 1 (11) Förstärkt tillsyn av skolors arbete med bedömning och betygssättning Uppdraget Regeringen har i beslut 1 24 november 2011 givit Skolinspektionen i uppdrag att närmare granska hur väl betygssättningen
1 (11) Förstärkt tillsyn av skolors arbete med bedömning och betygssättning Uppdraget Regeringen har i beslut 1 24 november 2011 givit Skolinspektionen i uppdrag att närmare granska hur väl betygssättningen
Miniräknaren metodiskt hjälpmedel
 Miniräknaren metodiskt hjälpmedel Mellanstadielärare Elisabeth Rystedt har i ett enskilt arbete på en av kurserna i matematikämnets didaktik, vid Göteborgs universitet, gjort en sammanställning av hur
Miniräknaren metodiskt hjälpmedel Mellanstadielärare Elisabeth Rystedt har i ett enskilt arbete på en av kurserna i matematikämnets didaktik, vid Göteborgs universitet, gjort en sammanställning av hur
2014-03-30. Mer matematik i högstadiet
 2014-03-30 Mer matematik i högstadiet Mer matematik i högstadiet Vi vill se mer kunskap i skolan, så att alla elever har möjlighet att nå kunskapsmålen. Alla ska få den grund som behövs för att kunna förverkliga
2014-03-30 Mer matematik i högstadiet Mer matematik i högstadiet Vi vill se mer kunskap i skolan, så att alla elever har möjlighet att nå kunskapsmålen. Alla ska få den grund som behövs för att kunna förverkliga
Variationer i matematik en inspirationskälla för pedagoger
 OVANÅKERS KOMMUN Projektbeskrivning 2007-08-23 Variationer i matematik en inspirationskälla för pedagoger Organisation av nätverk och förnyat arbetssätt från förskola till gymnasiet Bakgrund Våra grundskolor
OVANÅKERS KOMMUN Projektbeskrivning 2007-08-23 Variationer i matematik en inspirationskälla för pedagoger Organisation av nätverk och förnyat arbetssätt från förskola till gymnasiet Bakgrund Våra grundskolor
I vilken skolform/vilket program går barnet på adressetiketten? 2 Hur viktiga är följande aspekter för dig och ditt barn vid val av skola?
 Frågorna 1 7 ska besvaras utifrån ett specifikt barn och avse barnets nuvarande förhållanden. På enkätens framsida framgår vilket barn svaren ska gälla. 1 I vilken skolform/vilket program går barnet på
Frågorna 1 7 ska besvaras utifrån ett specifikt barn och avse barnets nuvarande förhållanden. På enkätens framsida framgår vilket barn svaren ska gälla. 1 I vilken skolform/vilket program går barnet på
Skolenkäten hösten 2018
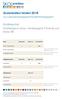 Skolenkäten hösten 2018 Huvudmannarapport/Skolenhetsrapport Enkätresultat Vendestigens skola, Vendestigens Förskola och Skola AB Elever Total antal Antal svar Svarsfrekvens Årskurs 5 grundskola 9 9 100%
Skolenkäten hösten 2018 Huvudmannarapport/Skolenhetsrapport Enkätresultat Vendestigens skola, Vendestigens Förskola och Skola AB Elever Total antal Antal svar Svarsfrekvens Årskurs 5 grundskola 9 9 100%
+ + Grundskola åk Var har du huvuddelen av din tjänstgöring? Grundskola åk 4-6. Ange ett alternativ. Grundskola åk 7-9
 1 Var har du huvuddelen av din tjänstgöring? Ange ett alternativ. Grundskola åk 1-3 Grundskola åk 4-6 Grundskola åk 7-9 Gymnasieskola NV, SP, TE, ES, B Gymnasieskola Övriga program 2 Arbetar du på en kommunal
1 Var har du huvuddelen av din tjänstgöring? Ange ett alternativ. Grundskola åk 1-3 Grundskola åk 4-6 Grundskola åk 7-9 Gymnasieskola NV, SP, TE, ES, B Gymnasieskola Övriga program 2 Arbetar du på en kommunal
Anvisningar för ansökan om bedömning av reell kompetens för grundläggande och/eller särskild behörighet
 Malmö högskola / Gemensamt verksamhetsstöd Studentcentrum 1(5) Mars 2015 Anvisningar för ansökan om bedömning av reell kompetens för grundläggande och/eller särskild behörighet Reell kompetens vad är det?
Malmö högskola / Gemensamt verksamhetsstöd Studentcentrum 1(5) Mars 2015 Anvisningar för ansökan om bedömning av reell kompetens för grundläggande och/eller särskild behörighet Reell kompetens vad är det?
Reell kompetens - Behörig på annat sätt!
 1 (5) Reell kompetens - Behörig på annat sätt! Beskriv så noggrant som möjligt de förutsättningar du har för att klara högskolestudier genom att göra uppgifterna nedan. Skriva alltid namn och personnummer
1 (5) Reell kompetens - Behörig på annat sätt! Beskriv så noggrant som möjligt de förutsättningar du har för att klara högskolestudier genom att göra uppgifterna nedan. Skriva alltid namn och personnummer
Lgr 11 matriser i Favorit matematik 4 6
 Lgr 11 matriser i Favorit matematik 4 6 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla förmågan att De matematiska förmågor
Lgr 11 matriser i Favorit matematik 4 6 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla förmågan att De matematiska förmågor
Affektiva faktorer, attityder, kön och social bakgrund i högskolans matematikundervisning. Översikt. Matematik väcker känslor
 Affektiva faktorer, attityder, kön och social bakgrund i högskolans matematikundervisning Föreläsning i kursen Matematikdidaktik för högskolan Matematikcentrum, Lunds universitet Gerd Brandell Översikt
Affektiva faktorer, attityder, kön och social bakgrund i högskolans matematikundervisning Föreläsning i kursen Matematikdidaktik för högskolan Matematikcentrum, Lunds universitet Gerd Brandell Översikt
Uppskattning av överslag
 Uppskattning av överslag Barbara Reys, Robert Reys & Göran Emanuelsson Här kommer en uppföljande artikel när det gäller taluppfattning och de verktyg som utvecklas för att hantera olika aspekter av taluppfattning.
Uppskattning av överslag Barbara Reys, Robert Reys & Göran Emanuelsson Här kommer en uppföljande artikel när det gäller taluppfattning och de verktyg som utvecklas för att hantera olika aspekter av taluppfattning.
Ansvar för matematiklärande Effekter av undervisningsansvar i det flerspråkiga klassrummet. Åse Hansson. Åse Hansson.
 Ansvar för matematiklärande Effekter av undervisningsansvar i det flerspråkiga klassrummet Åse Hansson Åse Hansson ase.hansson@ped.gu.se Göteborgs universitet Institutionen för didaktik och pedagogisk
Ansvar för matematiklärande Effekter av undervisningsansvar i det flerspråkiga klassrummet Åse Hansson Åse Hansson ase.hansson@ped.gu.se Göteborgs universitet Institutionen för didaktik och pedagogisk
Sammanställning av studentutvärdering samt utvärdering kurs vid institutionen för naturvetenskapernas och matematikens didaktik
 Sid 1 (7) studentutvärdering samt utvärdering kurs vid institutionen för naturvetenskapernas och matematikens didaktik Kurskod ( er): 6MN043 Ifall kursen i allt väsentligt samläses med andra kurser kan
Sid 1 (7) studentutvärdering samt utvärdering kurs vid institutionen för naturvetenskapernas och matematikens didaktik Kurskod ( er): 6MN043 Ifall kursen i allt väsentligt samläses med andra kurser kan
Enhet / skola: Lindens skola i Lanna Åk: 1
 Skolområde Väster Lokal Pedagogisk Planering Enhet / skola: Lindens skola i Lanna Åk: 1 Avsnitt / arbetsområde: Ämnen som ingår: Tema: Undersöka med Hedvig Svenska/svenska som andraspråk, matematik, bild,
Skolområde Väster Lokal Pedagogisk Planering Enhet / skola: Lindens skola i Lanna Åk: 1 Avsnitt / arbetsområde: Ämnen som ingår: Tema: Undersöka med Hedvig Svenska/svenska som andraspråk, matematik, bild,
Lära matematik med datorn
 Lära matematik med datorn Ulrika Ryan Matematik för den digitala generationen Malmö högskola, Lunds Universitet, Göteborgs Universitet och NCM 3 gymnasieskolor och 2 grundskolor i Lunds kommun Matematik
Lära matematik med datorn Ulrika Ryan Matematik för den digitala generationen Malmö högskola, Lunds Universitet, Göteborgs Universitet och NCM 3 gymnasieskolor och 2 grundskolor i Lunds kommun Matematik
Bedömning av muntliga prestationer
 Modul: Bedömning för lärande och undervisning i matematik Del 6: Muntliga bedömningssituationer Bedömning av muntliga prestationer Karin Rösmer, Karin Landtblom, Gunilla Olofsson och Astrid Pettersson,
Modul: Bedömning för lärande och undervisning i matematik Del 6: Muntliga bedömningssituationer Bedömning av muntliga prestationer Karin Rösmer, Karin Landtblom, Gunilla Olofsson och Astrid Pettersson,
I uppdraget ingår även följande åtgärder.
 Regeringsbeslut 1:2 2009-02-19 U2009/914/G U2008/6186/G Utbildningsdepartementet Statens skolverk 106 20 STOCKHOLM Uppdrag till Statens skolverk att genomföra utvecklingsinsatser inom matematik, naturvetenskap
Regeringsbeslut 1:2 2009-02-19 U2009/914/G U2008/6186/G Utbildningsdepartementet Statens skolverk 106 20 STOCKHOLM Uppdrag till Statens skolverk att genomföra utvecklingsinsatser inom matematik, naturvetenskap
Varför undervisar ni matematiklärare på lågstadiet om klockan? Det var
 Christel Svedin & Christina Svensson Möjligheter med analog klocka i geometriundervisning På Dammfriskolan i Malmö ledde lärares ifrågasättande av slentrianmässigt förekommande material och innehåll i
Christel Svedin & Christina Svensson Möjligheter med analog klocka i geometriundervisning På Dammfriskolan i Malmö ledde lärares ifrågasättande av slentrianmässigt förekommande material och innehåll i
Publiceringsår Skolenkäten. Resultat våren 2018
 Publiceringsår 2018 Skolenkäten Resultat våren 2018 2 (15) Innehållsförteckning Inledning... 3 Var sjunde elev i årskurs nio känner sig inte trygg i skolan...4 Försämring avseende upplevd trygghet...4
Publiceringsår 2018 Skolenkäten Resultat våren 2018 2 (15) Innehållsförteckning Inledning... 3 Var sjunde elev i årskurs nio känner sig inte trygg i skolan...4 Försämring avseende upplevd trygghet...4
BAKGRUNDSANALYS FÖR UTVECKLINGSPLAN I MATEMATIK
 UTBILDNINGSFÖRVALTNINGEN PERSONALAVDELNINGEN FOU-ENHETEN BILAGA SID 1 (7) 2012-11-21 BAKGRUNDSANALYS FÖR UTVECKLINGSPLAN I MATEMATIK Matematikundervisning i Sverige Skolämnet matematik och undervisningen
UTBILDNINGSFÖRVALTNINGEN PERSONALAVDELNINGEN FOU-ENHETEN BILAGA SID 1 (7) 2012-11-21 BAKGRUNDSANALYS FÖR UTVECKLINGSPLAN I MATEMATIK Matematikundervisning i Sverige Skolämnet matematik och undervisningen
LMA110, Matematik för lärare 1 30 högskolepoäng
 Gäller fr.o.m. vt 11 LMA110, Matematik för lärare 1 30 högskolepoäng Mathematics 1 for Teachers in Secondary School, 30 higher education credits Grundnivå/First Cycle 1. Fastställande Kursplanen är fastställd
Gäller fr.o.m. vt 11 LMA110, Matematik för lärare 1 30 högskolepoäng Mathematics 1 for Teachers in Secondary School, 30 higher education credits Grundnivå/First Cycle 1. Fastställande Kursplanen är fastställd
Kursplanen i ämnet matematik
 DISKUSSIONSUNDERLAG FÖR GRUNDSKOLAN Diskutera Kursplanen i ämnet matematik Läsåret 2011/12 införs en samlad läroplan för var och en av de obligatoriska skolformerna grundskolan, grundsärskolan, sameskolan
DISKUSSIONSUNDERLAG FÖR GRUNDSKOLAN Diskutera Kursplanen i ämnet matematik Läsåret 2011/12 införs en samlad läroplan för var och en av de obligatoriska skolformerna grundskolan, grundsärskolan, sameskolan
Prata matematik. Bengt Drath. Stöpenskolan i Skövde kommun
 Prata matematik Bengt Drath Högskolan i Skövde Stöpenskolan i Skövde kommun Matematikkunnande Vad ingår i begreppet matematikkunnande? eller som elever skulle tänka: Hur skall en duktig elev i matte vara?
Prata matematik Bengt Drath Högskolan i Skövde Stöpenskolan i Skövde kommun Matematikkunnande Vad ingår i begreppet matematikkunnande? eller som elever skulle tänka: Hur skall en duktig elev i matte vara?
Under en följd av år har svenska elevers bristande matematikkunskaper
 Madeleine Löwing Elevers kunskaper i aritmetik en kartläggning med utgångspunkt i Diamant-diagnoserna Elever som kommer från förskoleklass verkar väl förberedda för vidare lärande i matematik när de kommer
Madeleine Löwing Elevers kunskaper i aritmetik en kartläggning med utgångspunkt i Diamant-diagnoserna Elever som kommer från förskoleklass verkar väl förberedda för vidare lärande i matematik när de kommer
Matematiklektionen i fokus. Några klassrum öppnar dörren
 Matematiklektionen i fokus Några klassrum öppnar dörren Brister i matematikundervisningen Lusten att lära med fokus på matematik (Skolverkets rapport nr 221) Den dominerande undervisningen är genomgång
Matematiklektionen i fokus Några klassrum öppnar dörren Brister i matematikundervisningen Lusten att lära med fokus på matematik (Skolverkets rapport nr 221) Den dominerande undervisningen är genomgång
Muntlig kommunikation på matematiklektioner
 LÄRARPROGRAMMET Muntlig kommunikation på matematiklektioner Enkätundersökning med lärare som undervisar i årskurs 7-9 Margareta Olsson Examensarbete 15hp Höstterminen 2008 Handledare: Maria Bjerneby Häll
LÄRARPROGRAMMET Muntlig kommunikation på matematiklektioner Enkätundersökning med lärare som undervisar i årskurs 7-9 Margareta Olsson Examensarbete 15hp Höstterminen 2008 Handledare: Maria Bjerneby Häll
Digitalisering i skolan
 Digitalisering i skolan 1 Frågeblanketten läses maskinellt. Vi ber dig därför att: Använda bläckpenna Markera dina svar med kryss, så här: Om du svarat fel täck hela rutan med det felaktiga krysset, så
Digitalisering i skolan 1 Frågeblanketten läses maskinellt. Vi ber dig därför att: Använda bläckpenna Markera dina svar med kryss, så här: Om du svarat fel täck hela rutan med det felaktiga krysset, så
Bengt Drath. Högskolan i Skövde Stöpenskolan i Skövde kommun
 Prata matematik Bengt Drath Högskolan i Skövde Stöpenskolan i Skövde kommun Matematikkunnande tikk Vad ingår i begreppet matematikkunnande? eller som elever skulle tänka: Hur skall en duktig elev i matte
Prata matematik Bengt Drath Högskolan i Skövde Stöpenskolan i Skövde kommun Matematikkunnande tikk Vad ingår i begreppet matematikkunnande? eller som elever skulle tänka: Hur skall en duktig elev i matte
RAPPORT Attityder till skolan
 RAPPORT 479 19 Attityder till skolan 18 Publikationen finns att ladda ner som kostnadsfri PDF från Skolverkets webbplats: skolverket.se/publikationer ISSN: 13-2421 ISRN: SKOLV-R-479-SE Omslagsbild: Elke
RAPPORT 479 19 Attityder till skolan 18 Publikationen finns att ladda ner som kostnadsfri PDF från Skolverkets webbplats: skolverket.se/publikationer ISSN: 13-2421 ISRN: SKOLV-R-479-SE Omslagsbild: Elke
