Kursinformation. Kurslitteratur: H. Anton och C. Rorres: Elementary Linear Algebra, 10:e upplagan. Wiley 2011 (betecknas A nedan).
|
|
|
- Lucas Fredriksson
- för 6 år sedan
- Visningar:
Transkript
1 Uppsala Universitet Matematiska Institutionen Bo Styf Linjär algebra II, 5 hp ES, KandFy, Q, X Kursinformation. Undervisning: 17 föreläsningar och 10 lektioner (om vardera 2 45 minuter). Under föreläsningarna går vi igenom teorin och demonstrerar hur den tillämpas på praktisk problemlösning. Lektionerna ägnas åt redovisninguppgifterna (se nedan) samt, i mån av tid, ytterligare problemgenomgång. Kurslitteratur: H. Anton och C. Rorres: Elementary Linear Algebra, 10:e upplagan. Wiley 2011 (betecknas A nedan). Innehåll: Vi läser kapitel , , , , i A. Närmare detaljer framgår av nedanstående lektionsanvisningar. Examination: Kursen avslutas med en skriftlig tentamen. Som betyg på kursen används beteckningarna U (underkänd), 3 (godkänd), 4 (icke utan beröm godkänd) och 5 (med beröm godkänd). Maxpoängen på tentan är 40. Betygskraven är; 18 (25, 32) poäng för betyg 3 (4, 5). Kurshemsida: Material som delas ut på föreläsningarna, och mer, kan återfinnas här. Besök sidan varje dag så att du inte missar något. Lärare: Cecilia Karlsson: Cecilia.Karlsson@math.uu.se. Lektioner för KandFy, Q2. Jonathan Nilsson: Jonathan.Nilsson@math.uu.se. Lektioner för X2B. Bo Styf: styf@math.uu.se, Föreläsningar. Lektioner för ES3A. Katja Trinajstic: Katja.Trinajstic@math.uu.se. Lektioner för ES3B, X2A. Preliminär föreläsningsplan: 1
2 Föreläsning Innehåll Kapitel i A 1-4 Vektorrum, delrum, linjärt beroende, bas, dimension, basbyte, nollrum, rang Inre produkter, vinkel, ortogonalitet, ON-baser, Gram-Schmidt, ortogonala matriser Egenvärden, egenvektorer, diagonalisering, system av differentialekvationer, ON-diagonalisering. 5.4, Allmänna linjära transformationer, kärna och rang, dimensionssatsen, 8.1 isomorfier, 8.2 sammansättningar, inversa transformationen, 8.3 matriser för linjära transformationer, 8.4 similaritet Kvadratiska former, kägelsnitt och andragradsytor Ägnas åt tentamensförberedelser. 4 8 Lektioner med kryssproblem (redovisningsuppgifter): Till var och en av de tio lektionerna hör två problem som du skall försöka lösa. När du kommer till lektionen skall du, på en krysslista som tillhandahålls av läraren, kryssa i de problem som du, helt eller delvis, har lyckats lösa. Lösningarna skall sedan redovisas och betygsättas på lektionen enligt följande: Klassen kommer, på lämpligt sätt, att indelas i grupper om två personer. Dessa grupper kommer att vara intakta under hela kursen. Om, till exempel, klassen består av 30 studenter så får vi femton grupper; A B C D E F G H I K L M N P Q. Innan lektionens början lottar läraren ut åtta av dessa grupper, säg A C E F G H K N. Dessa grupper skall presentera lösningar på kryssproblemen. Lösningarna, som skall presenteras både skriftligt och muntligt, skall granskas och betygssättas av de återstående grupperna, i detta fall alltså B D I L M P Q. Antag att en ytterligare lottning, som görs av läraren innan lektionsstart, utfaller så att A E F G H K N skall betygsättas av I L B Q M D respektive P. Gruppen C, som blev över, betygsätts av läraren, som betecknas med X. Efter en omflyttning kommer vi då att ha åtta par av grupper A-I C-X E-L F-B G-Q H-M K-D och N-P, som förhoppningsvis kan genomföra redovisningen utan att störa varandra alltför mycket. Hur redovisningen/betygsättningen i detalj skall gå till är något vi får diskutera. En modell kan vara: Antag att A skall betygsättas av I. Medlemmarna, I1, och I2, av grupp I har på förhand delat upp problemen så att, säg, I1 betygsätter problem 2 och I2 betygsätter problem 1. I förväg har var och en av I1 och I2 (liksom A1 och A2) gjort betygsmallar för de problem man lyckats lösa. Om, till exempel, var och en av I1 och I2 lyckats lösa båda problemen har båda gruppmedlemmarna, vid lektionens början, två betygsmallar liggande framför sig (eller lagrad i minnet). Betyget (eller poängen) på en lösning är någon av siffrorna 0, 1, 2, 3, 4. För att lektionerna ska kunna fungera effektivt måste du uppmärksamma följande: 2
3 Gör, innan lektionen, en lättläst skriftlig lösning, på A4-ark, av varje problem som du, helt eller delvis, kan lösa (varje problem du tänker kryssa alltså). Använd inte rödpenna (men ta gärna med en rödpenna till lektionen)! Överst på varje ark skall din klass, lektionsnummer, problemnummer och grupptillhörighet, samt lösningssidan anges. Exempelvis: X2A Lektion 1 Problem 1 Trazan Apansson A1 - sid 2 av 2 På lösningens första ark ska sidhuvudet vara (typ) X2A Lektion 1 Problem 1 Trazan Apansson A1 - sid 1 av 2 Betyg Här betyder A1 att Trazan Apansson är medlem nummer ett (av två) av grupp A. Efter A1 - har utrymme lämnats för att skriva in beteckningen på betygsättaren om det blir så att Trazan Apansson ska redovisa sin lösning av problem 1. Om så blir fallet och I2 (den andra medlemmen av grupp I) ska sätta betyg, så fyller I2 i detta så att sidhuvudet på första arket, till exempel, blir X2A Lektion 1 Problem 1 Trazan Apansson A1 - I2 sid 1 av 2 Betyg 4 Skriv bara på arkets ena sida. Lämna ordentligt med utrymme för kommentarer på varje sida. Börja nytt problem på nytt ark. Gör, innan lektionen, en betygsmall till varje problem som du, helt eller delvis, kan lösa. Annars kommer betygsättningen att ta för lång tid. Det är också mycket intressant att jämföra sin betygsmall med andras. Givetvis kan man inte betygsätta ett problem som man inte, åtminstone delvis, lyckats lösa, så det kan uppkomma en del udda situationer, exempelvis att en student får betygsätta två problem eller att läraren får hoppa in. Redovisningen, i vårt exempel, börjar med att I2 tittar på lösningarna till problem 1, som A1 och A2 gjort. Om A1, enligt I2, har en sämre lösning än A2 så ber I2 A1 att redovisa lösningen av problem 1. A1 överlämnar sin skriftliga lösning till I2 och går sedan igenom lösningen muntligt. Under redovisningen noterar I2 (och även I1) lösningens förtjänster och brister och ställer frågor till A1 om något är oklart. I2 skriver, med rött, in kommentarer till lösningen. När redovisningen är klar bestämmer I2 ett betyg som skrivs in i sidhuvudet på första arket av lösningen. I2 överlämnar sedan A1:s skriftliga, vid det här laget röd-kommenterade, lösning av problem 1, till läraren. De inlämnade papperen återlämnas när läraren har gått igenom dem. Likadant gör man förstås med det andra problemet. För att underlätta för läraren skall grupp I se till att sidhuvudet på första arket med lösningen ser ut ungeför som ovan. Läraren ska direkt i sidhuvudet se lektionsnumret (1, 2, 3,... ), gruppen (ES3A, X2B e.t.c), vem som redovisade (i detta fall A1), vem som betygsatte (i detta fall I2) och vilket betyg som satts (i detta fall 4). Det är inte nödvändigt att skriva in några namn, A1 respektive I2 räcker. Ett mer eller mindre optimalt sidhuvud på första arket är alltså 3
4 X2A Lektion 1 Problem 1 A1 - I2 sid 1 av 2 Betyg 4 Hela redovisningen skall vara avklarad på maximalt en halvtimme. Det är mycket viktigt att vi har ordentligt med tid för frågor och problemdemonstration. Om du kryssat minst 50%, respektive minst 80%, av redovisningsuppgifterna får du 1, respektive 2, bonuspoäng. Dessa kommer att adderas till skrivningspoängen vid ordinarie tentamen. Betyget du får på kursen kommer bara att bero på hur du lyckas på sluttentan. Betygen du får (eller ger) under lektionerna kommer inte att vägas in på något sätt. Givetvis kommer din aktivitet (eller brist på aktivitet) under lektionerna att i hög grad påverka ditt kursbetyg. Har du två bonuspoäng ligger du mycket bra till! Bonuspoängen adderas till skrivningspoängen vid ordinarie tentamen i oktober 2011 men ej vid något annat tentamenstillfälle. 4
5 Lektionsanvisningar Inför lektionerna 1 och 2 Till lektion nr 1 bör du förbereda (dvs försöka lösa) följande uppgifter: avs.4.1, s : 1-3, 6, 10, 12, 15, avs.4.2, s : 1-3, 6, 7, 9-12, 15, avs.4.3, s.199: 1, 3, 4, 9, avs.4.4, s : 1-5, 9-11, avs.4.5, s : 1-3, 5-9, 12. Till lektion nr 2 bör du förbereda (dvs försöka lösa) följande uppgifter: avs.4.6, s : 2-5, avs.4.7, s : 5-8, 12, avs.4.8, s.246: 2-3. Extraövningar till lektionerna 1 och Delrummet M av R 4 spänns upp av vektorerna u 1 = (1, 1, 0, 1), u 2 = (2, 1, 1, 1), u 3 = (0, 3, 1, 3), u 4 = (1, 2, 3, 1), u 5 = (1, 1, 2, 4). För vilka värden av den reella konstanten a tillhör vektorn v = (4, a + 3, 5, a 4) delrummet M? Finn en bas i M bland de givna vektorerna u 1,..., u 5. Bestäm även, för a = 2, koordinaterna för vektorn v i den bas du valde. 2. Visa att om M och N är delrum till ett vektorrum V så är även M N ett delrum till V. Två delrum till R 4 är och Bestäm en bas i M N. M = span{(1, 2, 0, 1), ( 1, 1, 3, 2), (2, 7, 3, 1)} N = span{(0, 1, 2, 3), (0, 2, 4, 6), (1, 3, 1, 6), (1, 5, 3, 0)} 3. N är det delrum till R 4 som spänns upp av vektorerna u 1 = (1, 0, 1, 1), u 2 = (2, 1, 1, 1) och u 3 = (1, 1, 2, 1), d.v.s. N = span{u 1, u 2, u 3 }. (a) Avgör om vektorerna v = (0, 2, 2, 11) och w = (2, 1, 2, 1) tillhör N. (b) För vilka värden av den reella konstanten a tillhör vektorn u = (2 a, 1 2a, 2, 1) det linjära höljet N? 5
6 (c) Beskriv det linjära höljet N som en lösningsmängd till ett homogent linjärt ekvationssystem i 4 obekanta. (Obs: om du föredrar det, kan du först lösa del (c) och därefter delarna (a) och (b) av uppgiften.) 4. För vilka värden på den reella konstanten b är vektorerna v 1 = (1, 0, 1, 1) v 2 = (2, 1, 1, 1) och v 3 = (1, 2 + b, 1 b, 2) i R 4 linjärt oberoende? 5. Delrummet M till R 4 ges av Finn en bas i M. M = {(x 1, x 2, x 3, x 4 ) R 4 x 1 x 3 + 2x 4 = 0 och x 1 x 2 + x 3 x 4 = 0}. 6. L är ett linjärt rum, u, v, w är tre linjärt oberoende vektorer i L. Låt a vara en reell konstant. M är det delrum till L som spänns upp av vektorerna g 1 = u+(a+1)v +w g 2 = u+(3 a)v +aw och g 3 = au + 2v + (2 a)w, M = span{g 1, g 2, g 3 }. Bestäm dim M för varje värde av den reella konstanten a. 7. Bestäm en bas i det linjära höljet M av v 1 = (1, 1, 2, 1), v 2 = ( 1, 1, 2, 1), v 3 = (2, 1, 0, 1), v 4 = (3, 2, 2, 0), v 5 = (1, 0, 2, 2), v 6 = (0, 1, 4, 3) och ange koordinaterna för de givna vektorerna i denna bas. 8. E = {e 1, e 2, e 3 } är en bas i vektorrummet V. Inför en ny bas B = {b 1, b 2, b 3 } genom b 1 = 2e 1 + e 2 + e 3 b 2 = e 1 + e 2 e 3 b 3 = 2e 1 + 3e 2 e 3 Bestäm koordinaterna för vektorn u = 3e 1 2e 2 + e 3 i basen B och bestäm koordinaterna för vektorn v = 3b 1 2b 2 + b 3 i basen E. Bestäm även koordinaterna för v u i baserna B och E. Ange basbytesmatriserna T be och T eb. Facit: 1. a = 2. u = (u 1, u 2, u 4 ) utgör en bas i M (t.ex.). Om a = 2 : v = u 1 + 2u 2 + u 4 = ( 1, 2, 1) u. 2. T.ex (1, 5, 3, 0). 3. (a) v N, w / N, (b) a = 1, (c) N = {(y 1, y 2, y 3, y 4 ) R 4 y 1 y 2 y 3 = 0} 4. b v 1 = (1, 2, 1, 0), v 2 = ( 2, 3, 0, 1) (t.ex.) 6. dim M = 3 om a 6, 1, dim M = 2 om a = 6 och dim M = 1 om a = 1. 6
7 7. T.ex. {v 1, v 3 } är en bas i M och v 2 = v 1 ; v 4 = v 1 + v 3 ; v 5 = v 3 v 1 ; v 6 = 2v 1 v u = 7 4 b 1 4b b 3, v = 10e 1 + 4e 2 + 4e 3 och v u = 19 4 b 1 + 2b b 3 = 7e 1 + 6e 2 + 3e 3 7
8 Inför lektionerna 3 och 4 Till lektionerna 3 och 4 bör du förbereda (dvs försöka lösa) följande uppgifter: avs.6.1, s.343: 3-6, 9-13, 16, 19, avs.6.2, s : 1-11, 15-18, avs.6.3, s : 3-9, 16, 18, 20, 22, 23, avs.7.1, s : 1-3, 6-9, 13. Extraövningar till lektionerna 3 och Använd Gram-Schmids metod för att ortogonalisera: (1, 1, 1), (1, 0, 2), ( 1, 2, 1) i E Bestäm en ON-bas i M = span{(2, 1, 1, 1), (2, 2, 0, 3), (0, 1, 1, 2), (1, 0, 0, 1)} som ett delrum i E M är ett delrum till E 4 som definieras genom M = {(x 1, x 2, x 3, x 4 ) E 4 x 1 + x 2 + x 4 = 0 och x 1 + 2x 2 + x 3 + 2x 4 = 0}. (a) Finn en ON-bas i M. (b) Finn en ON-bas i det ortogonala komplementet M. (c) Skriv vektorn u = (1, 1, 2, 0) E 4 som en summa u = u 1 + u 2 med u 1 M och u 2 M. (d) P : E 4 E 4 är den ortogonala projektionen av E 4 på M. Finn P :s matris i standardbasen i E 4. (Gör denna uppgift inför lektion 4!) Obs: Kunde du först lösa del (d) och därefter, med hjälp av denna lösning, del (c) av uppgiften? 4. Bestäm den ortogonala projektionen av u = (1, 1, 2) på linjära höljet M av (2, 1, 0), (1, 1, 2), (1, 0, 2) och använd den för att finna avståndet från u till M. 5. Låt u = (1/ 3, 1/ 3, 1/ 3) E 3. Bestäm en ON-bas B i E 3 sådan att u har koordinatvektorn (u) B = (0, 1, 0) i basen B. 6. Låt M = span{(1, 1, 1, 1), (1, 1, 0, 0)} och låt proj M : E 4 E 4 vara ortogonala projektionen på M. Bestäm standardmatrisen för proj M. Vad blir proj M (1, 2, 3, 5)? Bestäm även avståndet från (1, 2, 3, 5) till M. 7. Rummet P 2 (av alla polynom med grad högst 2) förses med den inre produkten u, v = 1 1 u(x)v(x) dx. Bestäm med Gram-Schmidt s metod, utgående från basen 1, x, x 2, en ONbas i P 2. Visa 2 1 att a 0 + a 1 x + a 2 x 2, b 0 + b 1 x + b 2 x 2 = (3a 0 + a 2 )(3b 0 + b 2 ) a 1b a 2b 2 45
9 Låt M = span{1 + x x 2 }. Bestäm ON-baser i M och M. 8. Låt M = {x E 4 x 1 + x 3 + x 4 = x 2 x 3 + x 4 = 0}. (a) Bestäm standardmatrisen P för ortogonala projektionen på M och standardmatrisen Q för ortogonala projektionen på M. (b) Beräkna proj M (1, 2, 3, 4) och proj M (1, 2, 3, 4). (1, 2, 3, 4) till M respektive M. Beräkna även de båda avstånden från (c) Låt F vara projektionen på M parallellt med N = span{(1,0,1,-1),(1,2,0,-1)} och låt G vara projektionen på N parallellt med M. Bestäm standardmatriserna A och B för F respektive G (d.v.s F (x) = Ax och G(x) = Bx). (d) Beräkna F (1, 2, 3, 4) och G(1, 2, 3, 4). Facit: 1. (1, 1, 1), (0, 1, 1), ( 2, 1, 1). 2. T. ex. 1 (1, 0, 0, 1), ( 1, 1, 1, 1), 1 (1, 5, 3, 1). 6 3.(a). e 1 = 1 2 (0, 1, 0, 1), e 2 = 1 10 ( 2, 1, 2, 1). (t.ex.) 3.(b). e 3 = 1 2 (1, 0, 1, 0), e 4 = 1 10 (1, 2, 1, 2). (t.ex.) 3.(c). u = u 1 + u 2 med u 1 = (1, 0, 1, 1) M och u 2 = (0, 1, 1, 1) M. 3.(d). A = Projektionen är 1 21 (5, 11, 34) och avståndet är 8/ T.ex v 1 = (1, 0, 1)/ 2, v 2 = u och v 3 = ( 1, 2, 1)/ proj M har standardmatrisen proj M (1, 2, 3, 5) = (3, 3, 2, 2)/2. Avståndet är
10 7. ON-basen i P 2 (som Gram-Schmidt frambringar) är {1, 5 3 x, 2 (3x2 1)}. En ON-bas i M { } { 15 3 är 13 (1 + x x2 ). En ON-bas i M är 7 (1 2x), } 3/364(9 4x 35x 2 ). 8. (a) P = P 2 = Q = I P = Q 2 = (b) proj M (1, 2, 3, 4) = ( 5, 3, 4, 1)/3 och proj M (1, 2, 3, 4) = (8, 3, 5, 11)/ respektive (c) A = A 2 = B = I A = B 2 = Avstånden är (d) F (1, 2, 3, 4) = ( 26, 36, 5, 31), G(1, 2, 3, 4) = (27, 38, 8, 27) = (1, 2, 3, 4) F (1, 2, 3, 4). 10
11 Inför lektionerna 5 och 6 Till lektionerna 5 och 6 bör du förbereda följande uppgifter: avs.5.1, s : 1-8, 12, 14, 19, 22, avs.5.2, s : 1, 2, 6, 7, 17, 19, 21, avs.5.4, s.332: 1-9, avs.7.2, s : 7, 9, 10, 12. Extraövningar inför lektionerna 5 och 6 1. Den linjära avbildningen F : R 3 R 3 har i standardbasen matrisen A = a 2 a 3, där a är en reell konstant. För vilka värden på konstanten a är avbildningen F diagonaliserbar? För varje sådan a bestäm en bas i R 3 bestående av egenvektorer till F. 2. Bestäm samtliga egenvärden och egenvektorer till A = Facit: 1. F är diagonaliserbar omm a = 1. Om a = 1 : en bas av egenvektorer till F : u 1 = (1, 1, 0), u 2 = (2, 0, 1), u 3 = ( 1, 1, 1). (t.ex.) 2. Egenvärden: 0, 4. Egenvektorer för 0: (1, 0, 1, 0, 0, 0, 0, 0), (1, 0, 0, 0, 1, 0, 0, 0), (1, 0, 0, 0, 0, 0, 1, 0), (0, 1, 0, 1, 0, 0, 0, 0), (0, 1, 0, 0, 0, 1, 0, 0), (0, 1, 0, 0, 0, 0, 0, 1); egenvektorer för 4: (1, 1, 1, 1, 1, 1, 1, 1), (1, 0, 1, 0, 1, 0, 1, 0). 11
12 Inför lektionerna 7 och 8 Till lektionerna 7 och 8 bör du förbereda följande uppgifter: avs.8.1, s : 2-5, 9, 10, 12, 13, 15, 16, 18, 19, 22, 31, 32, avs.8.2, s : 1-6, 13, 17, avs.8.3, s : 1-6, 13, 21, avs.8.4, s : 1, 3, 4, 6-8, 10, 12, avs.8.5, s : 2-5, 12, 13. Extraövningar till lektionerna 7 och 8 1. För vilka värden på den reella konstanten a finns en linjär operator på R 3 vars nollrum spänns upp av vektorerna (1, 0, 1), (1, 1 a, a) samtidigt som värderummet spänns upp av vektorerna (1, 1, 1) och (1, 1 a, 1)? Ge exempel på en sådan linjär operator i de fall sådana existerar. 2. Låt F vara den linjära operatorn på R 3 som har standardmatrisen A = och låt M vara delrummet till R 3 som spänns upp av vektorn (1, 2, 3). Delrummet N till R 3 definieras genom N = {u R 3 F (u) M}. (i) Visa att N är ett delrum till R 3 (ii) Bestäm en bas i N. 3. Vi ser vektorerna i R 2 som kolonnmatriser. Avbildningen F : R 2 M 22 definieras genom ( ) F (x) = b x T 1, där b = och x R 2 1 (a) Visa att F är linjär. (b) Bestäm F :s matris med avseende på standardbaserna i R 2 och M 22. (c) Bestäm en bas i N(F ) och en bas i V (F ). 4. Låt n vara ett positivt heltal. Mängden Q av alla kvadratiska former q : R n R utgör ett delrum till funktionsrummet över R n (vektorrummet av alla funktioner f : R n R). Låt M vara det linjära rummet av alla n n-matriser och betrakta avbildningen F : M Q som ges av F (A) = q A, där q A (x) = x T Ax (x ses som en kolonnmatris). 12
13 (a) Visa att F är linjär. (b) Bestäm dimensionerna av N(F ), V (F ) och Q. Facit: 1. Antag att F har standardmatrisen A. Av dimensionssatsen, d.v.s dim(n(f ))+dim(v (F )) = 3, följer att endera har vi dim(n(f )) = 1 eller dim(v (F )) = 1. Detta inträffar då a = 1 respektive då a = 2 (då a / {1, 2} finns ingen operator F av önskat slag). I det första fallet (a = 1) gäller N(F ) = span{(1, 0, 1)}, V (F ) = span{(1, 0, 1), (0, 1, 0)}. Vektorerna (x 1, x 2, x 3 ) i A:s radrum måste då uppfylla x 1 + x 3 = 0 så en bas i radrummet är t.ex (1, 0, 1) och (0, 1, 0). Om A = ( har vi därför en operator F som uppfyller kraven. ) = I det andra fallet (a = 2) gäller V (F ) = span{(1, 1, 1)}, N(F ) = span{(1, 0, 1), (0, 1, 1)}. Vektorerna (x 1, x 2, x 3 ) i A:s radrum måste då uppfylla x 1 + x 3 = 0 och x 2 + x 3 = 0 så en bas i radrummet är t.ex (1, 1, 1). Om A = ( ) = får vi därför en operator F med N(F ) och V (F ) enligt ovan (i) Om u, v N, k R så får vi F (ku + v) = kf (u) + F (v) M ty F (u) M, F (v) M och M är ett delrum. (ii) Då x N F (x) = (s, 2s, 3s) för något s R följer att N utgörs av lösningarna till det på matrisform skrivna ekvationssystemet s s s s s Av den sista matrisen framgår att N = {(x 1, x 2, x 3 ) x 1 = s, x 3 = x 2 + s} vilket betyder att N = span{(1, 0, 1), (0, 1, 1)}. 3. (a) F (ku + v) = b (ku + v) T = k b u T + b v T = k F (u) + F (v). 13
14 (b) [F ] = (c) N(F ) = { 0} {( 1 0 V (F ) = span 1 0 ), ( )} 14
15 Inför lektion 9 Till lektion 9 bör du förbereda följande uppgifter: avs.7.3, s : 1-4, 6, 9, 14,
16 Inför lektion 10 Lektion 10 ägnas åt tentamensförberedelser. 16
17 Blandade övningar 1. Visa att det finns en unik inre produkt i R 2 på formen x, y = c 11 x 1 y 1 + c 12 x 1 y 2 + c 21 x 2 y 1 + c 22 x 2 y 2, sådan att b 1 = (3, 2) och b 2 = (4, 3) utgör en ON-bas i R 2 med avseende på denna inre produkt. Bestäm även alla 2 2-matriser A sådana att x, y = (Ax) (Ay). Facit: 1. Den unika inre produkten är x, y = 13x 1 y 1 18x 1 y 2 18x 2 y x 2 y 2. De sökta matriserna ges av A = P M, där P är en godtycklig ortogonalmatris, ( ) ( ) M = B = och B = (b b 2 ) =
Kursinformation. Kurslitteratur: H. Anton och C. Rorres: Elementary Linear Algebra, 9:e upplagan. Wiley, 2005 (betecknas A nedan).
 Uppsala Universitet Matematiska Institutionen Bo Styf Linjär algebra II, 5 hp ES, KandFy, Q, X 20010-08-31 Kursinformation. Undervisning: 17 föreläsningar och 8 lektioner (om vardera 2 45 minuter). Under
Uppsala Universitet Matematiska Institutionen Bo Styf Linjär algebra II, 5 hp ES, KandFy, Q, X 20010-08-31 Kursinformation. Undervisning: 17 föreläsningar och 8 lektioner (om vardera 2 45 minuter). Under
Kursinformation. Kurslitteratur: H. Anton och C. Rorres: Elementary Linear Algebra, 10:e upplagan. Wiley 2011 (betecknas A nedan).
 Uppsala Universitet Matematiska Institutionen Bo Styf Linjär algebra och geometri I, 5 hp ES1, KandMa1, MatemA 2012-08-31 Kursinformation. Undervisning: 20 föreläsningar och 10 lektioner (om vardera 2
Uppsala Universitet Matematiska Institutionen Bo Styf Linjär algebra och geometri I, 5 hp ES1, KandMa1, MatemA 2012-08-31 Kursinformation. Undervisning: 20 föreläsningar och 10 lektioner (om vardera 2
Kryssproblem (redovisningsuppgifter).
 Uppsala Universitet Matematiska Institutionen Bo Styf Linjär algebra II, 5 hp ES, KandFy, Q, X -8- Kryssproblem (redovisningsuppgifter. Till var och en av de åtta lektionerna hör tre problem som du skall
Uppsala Universitet Matematiska Institutionen Bo Styf Linjär algebra II, 5 hp ES, KandFy, Q, X -8- Kryssproblem (redovisningsuppgifter. Till var och en av de åtta lektionerna hör tre problem som du skall
Linjär algebra och geometri I
 UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Jörgen Östensson Vårterminen 2010 Kurslitteratur Linjär algebra och geometri I för X, geo, frist, lärare H. Anton, C. Rorres, Elementary Linear Algebra (Application
UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Jörgen Östensson Vårterminen 2010 Kurslitteratur Linjär algebra och geometri I för X, geo, frist, lärare H. Anton, C. Rorres, Elementary Linear Algebra (Application
Linjär algebra F1, Q1, W1. Kurslitteratur
 UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Linjär algebra för F1, Q1, W1 Kurslitteratur Höstterminen 2006 Eriksson Lind Persson Tengstrand, Algebra för universitet och högskolor, Band II (Linjär Algebra),
UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Linjär algebra för F1, Q1, W1 Kurslitteratur Höstterminen 2006 Eriksson Lind Persson Tengstrand, Algebra för universitet och högskolor, Band II (Linjär Algebra),
Linjär algebra och geometri I
 UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Anders Johansson Linjär algebra och geometri I för Energi, Ma-kand., Frist. Höstterminen 2010 Kurslitteratur H. Anton, C. Rorres, Elementary Linear Algebra
UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Anders Johansson Linjär algebra och geometri I för Energi, Ma-kand., Frist. Höstterminen 2010 Kurslitteratur H. Anton, C. Rorres, Elementary Linear Algebra
UPPSALA UNIVERSITET Matematiska institutionen Styf. Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 2004
 UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
Linjär algebra och geometri 1
 UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Ryszard Rubinsztein Oswald Fogelklou Linjär algebra och geometri 1 för K1, W1, KandKe1 Höstterminen 2008 Kurslitteratur H.Anton, C.Rorres, Elementary Linear
UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Ryszard Rubinsztein Oswald Fogelklou Linjär algebra och geometri 1 för K1, W1, KandKe1 Höstterminen 2008 Kurslitteratur H.Anton, C.Rorres, Elementary Linear
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
Linjär algebra och geometri 1
 UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Ryszard Rubinsztein Oswald Fogelklou Linjär algebra och geometri 1 för K1, W1, KandKe1 Höstterminen 2009 Kurslitteratur H.Anton, C.Rorres, Elementary Linear
UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Ryszard Rubinsztein Oswald Fogelklou Linjär algebra och geometri 1 för K1, W1, KandKe1 Höstterminen 2009 Kurslitteratur H.Anton, C.Rorres, Elementary Linear
Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA
 UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Ryszard Rubinsztein Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA 007 08 16 Skrivtid:
UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Ryszard Rubinsztein Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA 007 08 16 Skrivtid:
TMV142/186 Linjär algebra Z/TD
 MATEMATIK Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Chalmers tekniska högskola Datum: 2018-08-27 kl 1400 1800 Tentamen Telefonvakt: Anders Hildeman ank 5325 TMV142/186 Linjär algebra Z/TD Skriv
MATEMATIK Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Chalmers tekniska högskola Datum: 2018-08-27 kl 1400 1800 Tentamen Telefonvakt: Anders Hildeman ank 5325 TMV142/186 Linjär algebra Z/TD Skriv
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 17 april 2010 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
1. (a) (1p) Undersök om de tre vektorerna nedan är linjärt oberoende i vektorrummet
 1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. t 2
 SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
SF1624 Algebra och geometri Tentamen Torsdag, 9 juni 2016
 SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
Prov i matematik F2, X2, ES3, KandFys2, Lärare, Frist, W2, KandMat1, Q2 LINJÄR ALGEBRA II
 UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Bo Styf Prov i matematik F, X, ES, KandFys, Lärare, Frist, W, KandMat1, Q LINJÄR ALGEBRA II 010 08 4 Skrivtid: 1400 1900 Tillåtna hjälpmedel:
UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Bo Styf Prov i matematik F, X, ES, KandFys, Lärare, Frist, W, KandMat1, Q LINJÄR ALGEBRA II 010 08 4 Skrivtid: 1400 1900 Tillåtna hjälpmedel:
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
SF1624 Algebra och geometri
 Föreläsning 16 Institutionen för matematik KTH 5 december 2017 Modul 6 Veckans arbete 1. Idag: Ortonormalt, kap 7.1-7.2 a. Ortogonala och ortonormala baser b. Gram-Schmidts metod c. Ortogonala matriser
Föreläsning 16 Institutionen för matematik KTH 5 december 2017 Modul 6 Veckans arbete 1. Idag: Ortonormalt, kap 7.1-7.2 a. Ortogonala och ortonormala baser b. Gram-Schmidts metod c. Ortogonala matriser
LINJÄR ALGEBRA II LEKTION 3
 LINJÄR ALGEBRA II LEKTION 3 JOHAN ASPLUND INNEHÅLL Basbyten Kolonnrum, radrum och nollrum 3 Linjära avbildningar från R n till R m 4 Uppgifter 3 46:3 3 47:a 3 48:3a 4 48:a 4 49:9 4 40:7a,b BASBYTEN Om
LINJÄR ALGEBRA II LEKTION 3 JOHAN ASPLUND INNEHÅLL Basbyten Kolonnrum, radrum och nollrum 3 Linjära avbildningar från R n till R m 4 Uppgifter 3 46:3 3 47:a 3 48:3a 4 48:a 4 49:9 4 40:7a,b BASBYTEN Om
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra, SF1604, den 15 mars 2012 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF604, den 5 mars 202 kl 08.00-3.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF604, den 5 mars 202 kl 08.00-3.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
x + y + z + 2w = 0 (a) Finn alla lösningar till ekvationssystemet y + z+ 2w = 0 (2p)
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Examination: En skriftlig tentamen den XX mars samt möjlighet till en omtentamen. Tider och lokaler meddelas senare.
 Kursprogram till Linjär algebra II, SF1604, för D1, vt10. Kursledare och föreläsare: Olof Heden Lindstedtsvägen 25 rum 3641 Tel:790 62 96 (mobil: 0730 547 891) e-post: olohed@math.kth.se Övningar: grupp
Kursprogram till Linjär algebra II, SF1604, för D1, vt10. Kursledare och föreläsare: Olof Heden Lindstedtsvägen 25 rum 3641 Tel:790 62 96 (mobil: 0730 547 891) e-post: olohed@math.kth.se Övningar: grupp
Crash Course Algebra och geometri. Ambjörn Karlsson c januari 2016
 Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
TMV166 Linjär Algebra för M. Tentamen
 MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 3 6 kl. 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Tony Stillfjord,
MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 3 6 kl. 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Tony Stillfjord,
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF1624 Algebra och geometri Tentamen Torsdag, 17 mars 2016
 SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng.
 ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
Lösning till tentamensskrivning på kursen Linjär algebra, SF1604, den 12 mars 2013 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF1604, den 12 mars 2013 kl 14.00-19.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF1604, den 12 mars 2013 kl 14.00-19.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
SF1624 Algebra och geometri
 Föreläsning 10 Institutionen för matematik KTH 21 november 2016 Dagens och veckans ämnen Idag: Allmänna vektorrum, baser, koordinater, kap 4.1-4.4: Vektorrum och delrum, igen Bas, igen Koordinater med
Föreläsning 10 Institutionen för matematik KTH 21 november 2016 Dagens och veckans ämnen Idag: Allmänna vektorrum, baser, koordinater, kap 4.1-4.4: Vektorrum och delrum, igen Bas, igen Koordinater med
(1, 3, 2, 5), (0, 2, 0, 8), (2, 0, 1, 0) och (2, 2, 1, 8)
 1 Matematiska Institutionen KTH Tentamen på kursen SF1604 (och B1109, för D1, Mars 9, 008, kl: 9:00-14:00 Inga hjälpmedel ät tillåtna 1 poäng totalt eller mer ger minst omdömet Fx 1 poäng totalt eller
1 Matematiska Institutionen KTH Tentamen på kursen SF1604 (och B1109, för D1, Mars 9, 008, kl: 9:00-14:00 Inga hjälpmedel ät tillåtna 1 poäng totalt eller mer ger minst omdömet Fx 1 poäng totalt eller
8(x 1) 7(y 1) + 2(z + 1) = 0
 Matematiska Institutionen KTH Lösningsförsök till tentamensskrivningen på kursen Linjär algebra, SF60, den juni 0 kl 08.00-.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Matematiska Institutionen KTH Lösningsförsök till tentamensskrivningen på kursen Linjär algebra, SF60, den juni 0 kl 08.00-.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Lösningar till några övningar inför lappskrivning nummer 3 på kursen Linjär algebra för D, vt 15.
 1 Matematiska Institutionen KTH Lösningar till några övningar inför lappskrivning nummer 3 på kursen Linjär algebra för D, vt 15. 1. Undersök om vektorn (1,, 1, ) tillhör span{(1,, 3, 4), (1, 0, 1, 1),
1 Matematiska Institutionen KTH Lösningar till några övningar inför lappskrivning nummer 3 på kursen Linjär algebra för D, vt 15. 1. Undersök om vektorn (1,, 1, ) tillhör span{(1,, 3, 4), (1, 0, 1, 1),
LINJÄR ALGEBRA II LEKTION 6
 LINJÄR ALGEBRA II LEKTION 6 JOHAN ASPLUND INNEHÅLL 1 Inre produktrum 1 2 Cauchy-Schwarz olikhet 3 3 Ortogonala projektioner och Gram-Schmidts process 3 4 Uppgifter 4 61:13(a) 4 61:23(a) 4 61:29 5 62:7
LINJÄR ALGEBRA II LEKTION 6 JOHAN ASPLUND INNEHÅLL 1 Inre produktrum 1 2 Cauchy-Schwarz olikhet 3 3 Ortogonala projektioner och Gram-Schmidts process 3 4 Uppgifter 4 61:13(a) 4 61:23(a) 4 61:29 5 62:7
TMV166 Linjär algebra för M, vt 2016
 TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
Kursprogram kursen ETE325 Linjär Algebra, 8 hp, vt 2016.
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Vladimir Tkatjev Kursprogram kursen ETE325 Linjär Algebra, 8 hp, vt 2016. Kursperiod: 18 januari 18 maj Examinator och föreläsare: Vladimir Tkatjev: B-huset,
LINKÖPINGS UNIVERSITET Matematiska Institutionen Vladimir Tkatjev Kursprogram kursen ETE325 Linjär Algebra, 8 hp, vt 2016. Kursperiod: 18 januari 18 maj Examinator och föreläsare: Vladimir Tkatjev: B-huset,
Kursprogram kursen ETE325 Linjär Algebra, 8 hp, vt 2015.
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Vladimir Tkatjev Kursprogram kursen ETE325 Linjär Algebra, 8 hp, vt 2015. Kursperiod: 19 januari 21 maj Examinator och föreläsare: Vladimir Tkatjev: B-huset,
LINKÖPINGS UNIVERSITET Matematiska Institutionen Vladimir Tkatjev Kursprogram kursen ETE325 Linjär Algebra, 8 hp, vt 2015. Kursperiod: 19 januari 21 maj Examinator och föreläsare: Vladimir Tkatjev: B-huset,
Tentamen i ETE305 Linjär algebra , 8 13.
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk ( p) ( p) ( p) ( p) ( p) ( p) Tentamen i ETE Linjär algebra, 8. Inga hjälpmedel. Ej räknedosa. Resultatet meddelas vi e-post. För godkänt räcker
LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk ( p) ( p) ( p) ( p) ( p) ( p) Tentamen i ETE Linjär algebra, 8. Inga hjälpmedel. Ej räknedosa. Resultatet meddelas vi e-post. För godkänt räcker
Tentamen TMV140 Linjär algebra Z
 Tentamen TMV40 Linjär algebra Z 307 kl. 08.30 2.30 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, 0703 088 304 Hjälpmedel: Inga, ej heller räknedosa För godkänt
Tentamen TMV40 Linjär algebra Z 307 kl. 08.30 2.30 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, 0703 088 304 Hjälpmedel: Inga, ej heller räknedosa För godkänt
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
Uppgifter, 2015 Tillämpad linjär algebra
 Geometri. Uppgifter, 25 Tillämpad linjär algebra. Uppgift. Låt (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av linjära
Geometri. Uppgifter, 25 Tillämpad linjär algebra. Uppgift. Låt (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av linjära
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. (1 p) (c) Bestäm avståndet mellan A och linjen l.
 SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
3 1 = t 2 2 = ( 1) ( 2) 1 2 = A(t) = t 1 10 t
 SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
LINKÖPINGS TEKNISKA HÖGSKOLA Matematiska institutionen Ulf Janfalk 29 augusti 2018
 LINKÖPINGS TEKNISKA HÖGSKOLA Matematiska institutionen 29 augusti 2018 Kursinformation Linjär Algebra för I1 och Ii1. Examinator: Kurshemsida: http://courses.mai.liu.se/gu/tata31/ Kurslitteratur: Janfalk,
LINKÖPINGS TEKNISKA HÖGSKOLA Matematiska institutionen 29 augusti 2018 Kursinformation Linjär Algebra för I1 och Ii1. Examinator: Kurshemsida: http://courses.mai.liu.se/gu/tata31/ Kurslitteratur: Janfalk,
Linjär algebra HT 2016, kurskoder 5MA160 och 6MA036
 Sid 1 (7) Linjär algebra HT 2016, kurskoder 5MA160 och 6MA036 Kurslitteratur Anton H., Rorres, C., Elementary Linear Algebra with Supplemental Applications. 11th ed. Wiley & Sons (2014) ISBN 978-1-118-67745-2
Sid 1 (7) Linjär algebra HT 2016, kurskoder 5MA160 och 6MA036 Kurslitteratur Anton H., Rorres, C., Elementary Linear Algebra with Supplemental Applications. 11th ed. Wiley & Sons (2014) ISBN 978-1-118-67745-2
29 november, 2016, Föreläsning 21. Ortonormala baser (ON-baser) Gram-Schmidt s ortogonaliseringsprocess
 29 november, 2016, Föreläsning 21 Tillämpad linjär algebra Innehåll: Ortonormala baser (ON-baser) Gram-Schmidt s ortogonaliseringsprocess Minsta-kvadratmetoden - exempel 1. Uppgift. Tentamen 19/1-15, uppgift
29 november, 2016, Föreläsning 21 Tillämpad linjär algebra Innehåll: Ortonormala baser (ON-baser) Gram-Schmidt s ortogonaliseringsprocess Minsta-kvadratmetoden - exempel 1. Uppgift. Tentamen 19/1-15, uppgift
Tentamen i Linjär algebra , 8 13.
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk Kurskod: ETE5 Provkod: TEN Tentamen i Linjär algebra 5 8, 8. Inga hjälpmedel. Ej räknedosa. Resultatet meddelas vi e-post. För godkänt räcker
LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk Kurskod: ETE5 Provkod: TEN Tentamen i Linjär algebra 5 8, 8. Inga hjälpmedel. Ej räknedosa. Resultatet meddelas vi e-post. För godkänt räcker
Lösning av tentamensskrivning på kursen Linjär algebra, SF1604, för CDATE, CTFYS och vissa CL, tisdagen den 20 maj 2014 kl
 1 Matematiska Institutionen, KTH Lösning av tentamensskrivning på kursen Linjär algebra, SF1604, för CDATE, CTFYS och vissa CL, tisdagen den 20 maj 2014 kl 08.00-13.00. Examinator: Olof Heden. OBS: Inga
1 Matematiska Institutionen, KTH Lösning av tentamensskrivning på kursen Linjär algebra, SF1604, för CDATE, CTFYS och vissa CL, tisdagen den 20 maj 2014 kl 08.00-13.00. Examinator: Olof Heden. OBS: Inga
Kursprogram till kursen Linjär algebra II, 5B1109, för F1, ht00.
 Kursprogram till kursen Linjär algebra II, 5B1109, för F1, ht00. Kursledare och föreläsare: Olof Heden Lindstedtsvägen 25 rum 3641 Tel:790 62 96 (hem: 08-716 80 34) e-post: olohed@math.kth.se Mottagningstid:
Kursprogram till kursen Linjär algebra II, 5B1109, för F1, ht00. Kursledare och föreläsare: Olof Heden Lindstedtsvägen 25 rum 3641 Tel:790 62 96 (hem: 08-716 80 34) e-post: olohed@math.kth.se Mottagningstid:
LINJÄR ALGEBRA II LEKTION 8+9
 LINJÄR ALGEBRA II LEKTION 8+9 JOHAN ASPLUND Innehåll. Kvadratiska former. Allmänna linjära avbildningar Matriser för allmänna linjära avbildningar. Uppgifter Extrauppgift från tenta Extrauppgift från tenta
LINJÄR ALGEBRA II LEKTION 8+9 JOHAN ASPLUND Innehåll. Kvadratiska former. Allmänna linjära avbildningar Matriser för allmänna linjära avbildningar. Uppgifter Extrauppgift från tenta Extrauppgift från tenta
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
LINKÖPINGS TEKNISKA HÖGSKOLA Matematiska institutionen Ulf Janfalk 18 september 2014
 LINKÖPINGS TEKNISKA HÖGSKOLA Matematiska institutionen 18 september 2014 Kursinformation Linjär Algebra för I1 och Ii1. Examinator: Kurslitteratur: Janfalk, Ulf: Linjär algebra, 2014 Examination: Efter
LINKÖPINGS TEKNISKA HÖGSKOLA Matematiska institutionen 18 september 2014 Kursinformation Linjär Algebra för I1 och Ii1. Examinator: Kurslitteratur: Janfalk, Ulf: Linjär algebra, 2014 Examination: Efter
kvivalenta. Ange rangen för A samt en bas för kolonnrummet för A. och U =
 MATEMATIK Hjälpmedel: utdelad ordlista, ej räknedosa Chalmers tekniska högskola Datum: 9-- kl 8 Tentamen Telefonvakt: Aron Lagerberg tel 76-786 Linjär Algebra Z (tmv4) Skriv tentamenskod tydligt på samtliga
MATEMATIK Hjälpmedel: utdelad ordlista, ej räknedosa Chalmers tekniska högskola Datum: 9-- kl 8 Tentamen Telefonvakt: Aron Lagerberg tel 76-786 Linjär Algebra Z (tmv4) Skriv tentamenskod tydligt på samtliga
Del 1: Godkäntdelen. TMV142 Linjär algebra Z
 MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 130313 kl 0830 1230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV142 Linjär algebra Z Tentan
MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 130313 kl 0830 1230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV142 Linjär algebra Z Tentan
(a) Bestäm för vilka värden på den reella konstanten c som ekvationssystemet är lösbart. (b) Lös ekvationssystemet för dessa värden på c.
 UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 202-2-3 DEL A Betrakta punkterna A = (2, 2) och B = (6, 4) och linjen (, 3) + t(2, ) i planet (a) Det finns exakt en punkt P på linjen så att triangeln
SF624 Algebra och geometri Lösningsförslag till tentamen 202-2-3 DEL A Betrakta punkterna A = (2, 2) och B = (6, 4) och linjen (, 3) + t(2, ) i planet (a) Det finns exakt en punkt P på linjen så att triangeln
A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)
![A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p) A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)](/thumbs/93/112249032.jpg) SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
Vektorerna är parallella med planet omm de är vinkelräta mot planets normal, dvs mot
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Linjär algebra I, vt 12 Vecko PM läsvecka 4
 Linjär algebra I, vt 12 Vecko PM läsvecka 4 Lay: 2.8-2.9, 4.1-4.6 Underrum i R n, dimension och rang. Vektorrum. Innehållet i avsnitten 2.8 och 2.9 täcks av kapitel 4, men presenterar begreppen på ett
Linjär algebra I, vt 12 Vecko PM läsvecka 4 Lay: 2.8-2.9, 4.1-4.6 Underrum i R n, dimension och rang. Vektorrum. Innehållet i avsnitten 2.8 och 2.9 täcks av kapitel 4, men presenterar begreppen på ett
16.7. Nollrum, värderum och dimensionssatsen
 170 16 LINJÄRA AVBILDNINGAR 16.7. Nollrum, värderum och dimensionssatsen Definition 16.33. Låt F : V W vara en linjär avbildning. 1. Nollrummet till F definierar vi som mängden av alla u V, vilkas bild
170 16 LINJÄRA AVBILDNINGAR 16.7. Nollrum, värderum och dimensionssatsen Definition 16.33. Låt F : V W vara en linjär avbildning. 1. Nollrummet till F definierar vi som mängden av alla u V, vilkas bild
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604 för D, den 5 juni 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF164 för D, den 5 juni 21 kl 9.- 14.. Examinator: Olof Heden. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen.
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF164 för D, den 5 juni 21 kl 9.- 14.. Examinator: Olof Heden. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen.
A = x
 Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
SF1624 Algebra och geometri Bedömningskriterier till tentamen Fredagen den 22 oktober, 2010
 SF1624 Algebra och geometri Bedömningskriterier till tentamen Fredagen den 22 oktober, 2010 Allmänt gäller följande: Om lösningen helt saknar förklarande text till beräkningar och formler ges högst två
SF1624 Algebra och geometri Bedömningskriterier till tentamen Fredagen den 22 oktober, 2010 Allmänt gäller följande: Om lösningen helt saknar förklarande text till beräkningar och formler ges högst två
x 1 x 2 T (X) = T ( x 3 x 4 x 5
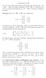 Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
SF1624 Algebra och geometri
 SF1624 Algebra och geometri Tjugofemte föreläsningen Mats Boij Institutionen för matematik KTH 10 december, 2009 Tentamens struktur Tentamen består av tio uppgifter uppdelade på två delar, Del A och Del
SF1624 Algebra och geometri Tjugofemte föreläsningen Mats Boij Institutionen för matematik KTH 10 december, 2009 Tentamens struktur Tentamen består av tio uppgifter uppdelade på två delar, Del A och Del
SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 2014
 SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 214 Skrivtid: 14.-19. Tillåtna hjälpmedel: inga Examinator: Roy Skjelnes Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 214 Skrivtid: 14.-19. Tillåtna hjälpmedel: inga Examinator: Roy Skjelnes Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
SF1624 Algebra och geometri
 Föreläsning 6 Institutionen för matematik KTH 11 november 2016 Feedback Innan vi börjar: En liten feedback-övning Vad menas med rangen av en matris? Vad menas med ett homogent linjärt ekvationssystem?
Föreläsning 6 Institutionen för matematik KTH 11 november 2016 Feedback Innan vi börjar: En liten feedback-övning Vad menas med rangen av en matris? Vad menas med ett homogent linjärt ekvationssystem?
. b. x + 2 y 3 z = 1 3 x y + 2 z = a x 5 y + 8 z = 1 lösning?
 Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
Chalmers tekniska högskola Datum: kl Telefonvakt: Linnea Hietala MVE480 Linjär algebra S
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
Facit/lösningsförslag
 Facit/lösningsförslag 06-08- Låt l vara linjen med parameterform x, y, z 0 s, mellan planet x y z och planet z 0 och låt l vara skärningslinjen a) Skriv l på parameterform b) Beräkna avståndet mellan l
Facit/lösningsförslag 06-08- Låt l vara linjen med parameterform x, y, z 0 s, mellan planet x y z och planet z 0 och låt l vara skärningslinjen a) Skriv l på parameterform b) Beräkna avståndet mellan l
KTH, Matematik. Del I. (totalt 15 poäng, inklusive bonuspoäng). (1) Betrakta följande mängder i R 3 :
 KTH, Matematik Tentamen i Linjär algebra, SF64, för F och D, den 3:e juni, 9 OBS Svaret skall motiveras och lösningen skrivas, ordentligt och klart Inga hjälpmedel är tillåtna Betg enligt följande tabell:
KTH, Matematik Tentamen i Linjär algebra, SF64, för F och D, den 3:e juni, 9 OBS Svaret skall motiveras och lösningen skrivas, ordentligt och klart Inga hjälpmedel är tillåtna Betg enligt följande tabell:
Chalmers tekniska högskola Datum: Våren MVE021 Linjär algebra I
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: Våren 6 Övningstentamen Telefonvakt: Thomas Bäckdahl ankn 8 MVE Linjär algebra I Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: Våren 6 Övningstentamen Telefonvakt: Thomas Bäckdahl ankn 8 MVE Linjär algebra I Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt
1. (a) Bestäm alla värden på c som gör att matrisen A(c) saknar invers: 1 0 1. 1 c 1
 ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
17. Övningar ÖVNINGAR Låt F och G vara avbildningar på rummet, som i basen e = {e 1,e 2,e 3 } ges av. x 1 x 2 2x 2 + 3x 3 2x 1 x 3
 192 17 ÖVNINGAR 17. Övningar 17.1. Låt F och G vara avbildningar på rummet, som i basen e = {e 1,e 2,e 3 } ges av F(eX) = ey = e x 1 x 2 2x 2 + 3x 3 2x 1 x 3, G(eX) = e x 1 x 2 x 2 2 x 2 + x 3 Undersök
192 17 ÖVNINGAR 17. Övningar 17.1. Låt F och G vara avbildningar på rummet, som i basen e = {e 1,e 2,e 3 } ges av F(eX) = ey = e x 1 x 2 2x 2 + 3x 3 2x 1 x 3, G(eX) = e x 1 x 2 x 2 2 x 2 + x 3 Undersök
Uppgifter, 2014 Tillämpad linjär algebra
 Geometri. Uppgifter, 24 Tillämpad linjär algebra. Uppgift. Låt A = (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av
Geometri. Uppgifter, 24 Tillämpad linjär algebra. Uppgift. Låt A = (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av
6.1 Skalärprodukt, norm och ortogonalitet. TMV141 Linjär algebra E VT 2011 Vecka 6. Lärmål 6.1. Skalärprodukt. Viktiga begrepp
 6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng. Använd bifogat formulär för dessa 6 frågor.
 TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
DN1230 Tillämpad linjär algebra Tentamen Onsdagen den 29 maj 2013
 TILLÄMPAD LINJÄR ALGEBRA, DN123 1 DN123 Tillämpad linjär algebra Tentamen Onsdagen den 29 maj 213 Skrivtid: 8-13 Tillåtna hjälpmedel: inga Examinator: Anna-Karin Tornberg Betygsgränser: Betyg A B C D E
TILLÄMPAD LINJÄR ALGEBRA, DN123 1 DN123 Tillämpad linjär algebra Tentamen Onsdagen den 29 maj 213 Skrivtid: 8-13 Tillåtna hjälpmedel: inga Examinator: Anna-Karin Tornberg Betygsgränser: Betyg A B C D E
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
Linjär Algebra, Föreläsning 8
 Linjär Algebra, Föreläsning 8 Tomas Sjödin Linköpings Universitet Linjärkombinationer (repetition) Låt v 1, v 2,..., v n vara vektorer i ett vektorrum V. Givet skalärer λ 1, λ 2,..., λ n R så kallas λ
Linjär Algebra, Föreläsning 8 Tomas Sjödin Linköpings Universitet Linjärkombinationer (repetition) Låt v 1, v 2,..., v n vara vektorer i ett vektorrum V. Givet skalärer λ 1, λ 2,..., λ n R så kallas λ
där β R. Bestäm de värden på β för vilka operatorn är diagonaliserbar. Ange även för respektive av dessa värden en bas av egenvektorer till F.
 MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Examinator: Lars-Göran Larsson TENTAMEN I MATEMATIK MMA9 Linjär algebra Datum: 7 januari 04 Skrivtid:
MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Examinator: Lars-Göran Larsson TENTAMEN I MATEMATIK MMA9 Linjär algebra Datum: 7 januari 04 Skrivtid:
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Problemsamling i Linjär Algebra II. Erik Darpö
 Problemsamling i Linjär Algebra II Erik Darpö ii Notation Inklusion Samma som A B Matriserna A och B är radekvivalenta I n Enhetsmatrisen av storlek n n R n Vektorrummet av alla kolonnvektorer av storlek
Problemsamling i Linjär Algebra II Erik Darpö ii Notation Inklusion Samma som A B Matriserna A och B är radekvivalenta I n Enhetsmatrisen av storlek n n R n Vektorrummet av alla kolonnvektorer av storlek
2x + y + 3z = 1 x 2y z = 2 x + y + 2z = 1
 ATM-Matematik Sören Hector 7 46686 Mikael Forsberg 734 433 Matematik med datalogi, mfl. Linjär algebra ma4a 3 5 Skrivtid: :-5:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa.
ATM-Matematik Sören Hector 7 46686 Mikael Forsberg 734 433 Matematik med datalogi, mfl. Linjär algebra ma4a 3 5 Skrivtid: :-5:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa.
LINJÄR ALGEBRA OCH DIFFERENTIALEKVATIONER, M0031M VT-16
 LINJÄR ALGEBRA OCH DIFFERENTIALEKVATIONER, M0031M VT-16 Denna kurs innehåller fyra olika delar: komplexa tal, linjär algebra, differentialekvationer och en laboration i Matlab. Vi börjar med en introduktion
LINJÄR ALGEBRA OCH DIFFERENTIALEKVATIONER, M0031M VT-16 Denna kurs innehåller fyra olika delar: komplexa tal, linjär algebra, differentialekvationer och en laboration i Matlab. Vi börjar med en introduktion
