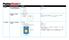
hlager 2: 75 m 3 15 km 17 km h Lager 3: 100 m 3 hlager 5: 100 m 3 15 km 22 km 17 km 17 km 14 km Lager 1: 50 m 3

Transkript

1 MATEMATIKUPPGIFTER I INTRÄDESFÖRHÖRET 2000 Uppgift 1 En långtradarchaufför skall frakta virke från olika lager till fabriken (se nedanstående bild). Hur lönar det sig för chauffören att frakta virket, med tanke på att köra så få kilometer som möjligt, då han startar från fabriken? Det ryms maximalt 50 m 3 virke på långtradaren. Lös uppgiften genom att pröva dig fram. hlager 4: 75 m 3 15 km FABRIK g 24 km 18 km 17 km h Lager 3: 100 m 3 16 km hlager 5: 100 m 3 22 km 17 km 17 km 14 km h Lager 1: 50 m 3 15 km hlager 2: 75 m 3 Uppgift 2 a) Beräkna med hjälp av kartan (skalan 1:10 000) arean av den triangelformade strandtomten. b) På kartan har också ritats den planerade sommarstugevägen. För att få vägen i körbart skick för personbilstrafik måste den 3,2 m breda vägen få ett tio centimeter tjockt gruslager. Gör en uppskattning av mängden grus som behövs. Uppgift 3 a) Vid en renovering av en bostad skall vardagsrummets rektangulära golv som är 5,15 m långt och 4,15 m brett, beläggas med parkett. Hur många bitar av parkett behövs om en bit har storleken 2085 mm x 188 mm och man för säkerhets skull skaffar 5% extra parkett? b) Vid en annan renovering köptes plastmatta, som kostade 60 mk/m 2, parkett som kostade 210 mk/m 2 samt andra tillbehör, som kostade 2300 mk. Hur många kvadratmeter köptes av vartdera golvmaterialet ifall inköpena kostade sammanlagt mk och golvmaterialet skulle räcka till 100 m 2 golv.

2 Uppgift 4 a) Av priset på papper utgjorde råmaterialet 35%, övriga kostnader 55% samt tillverkarens vinst 10%. Med hur många procent ändras priset på papper och i vilken riktning, om råvarukostnaderna sjunker med 4%, de övriga kostnaderna ökar med 6% medan vinsten fortfarande utgör 10% av priset? b) Av priset på papper utgör 35% råmaterialkostnader och av råmaterialkostnaderna är cellulosans andel 60%. Med hur många procent stiger priset på papper, ifall cellulosapriset går upp med 6% och cellulosans prisstegring i sin helhet överförs till papperspriset? Uppgift 5 Träets fuktighetskvot u beräknas med hjälp av följande formel: mu mo u = 100% mo där m u = träbitens massa, som färsk m o = träbitens massa, torkad Med en träbits torr-rådensitet menas den densitet, som man får, när man väger träbiten torr och mäter volymen färsk. a) Fuktighetskvoten för en färsk träbit är 45% och densiteten är 725 kg/m 3. Vilken torrrådensitet har träbiten om den är 20,0 mm hög, 100,0 mm bred och 200,0 mm lång? b) Vilken massa skulle ovan nämnda träbit ha, ifall bitens fuktighetskvot varit 18%? Uppgift 6 Tallens övre diameter d 6,0 (på 6 m:s höjd) beror av brösthöjdsdiametern d 1,3 (på 1,3 m:s höjd) enligt ekvationen d a d + b 6,0 = 1, 3 I ett bestånd såg förhållandet ut som nedan bifogade graf visar. a) Bestäm konstanterna a och b. b) Vilken övre höjd har en tall vars brösthöjdsdiameter är 21 centimeter? d 6,0 (cm) x A (26, 18) x B (8, 6) d 1,3 (cm)

3 MATEMATIKUPPGIFTER I INTRÄDESFÖRHÖRET Bröderna Kalle, Ville och Pelle hade alla varsitt 4 ha stort markområde. a) Kalles område har formen av en rektangel med längden 250 meter. Beräkna områdets bredd. b) Villes område är kvadratiskt. Beräkna områdets sida. c) Pelles område har formen av en cirkel. Beräkna områdets radie. 2. Hur högt är trädet enligt mätningar gjorda efter skissen, om avståndet AB är 23 m? A B 3. En tallplanta var 0,30 m lång då den planterades en vår. Plantan växte under de följande växtperioderna lika mycket varje växtperiod. Om plantan växte under den fjärde växtperioden med 1/6 av den totallängd den hade efter föregående växtperiod, så hur lång var plantan efter åttonde växtperioden? 4. Massan av en stock var från början 210 kg. Vid detta tillfälle var dess fuktighetskvot 20 % (fuktighetskvoten = massan av den mängd vatten som finns i stocken i förhållande till stockens torrmassa). Vid lagring av stocken avdunstade 20 % av vattnet. Vilken var stockens fuktighetskvot nu? 5. En kund köpte från ett hyvleri rundstockar av två olika storlekar. Stockarna hade formen av räta cirkelcylindrar, de mindre stockarnas diametrar var 15 cm, deras volym var 130 dm 3 /st. och priset var 260 mk/st., medan de större stockarnas diametrar var 25 cm, deras volym 260 dm 3 /st. och pris 400 mk/st. Fastvolymen av hela stockpartiet var 52

4 m 3 (fastvolym = trävolymen) och priset mk. Hur mycket köpte kunden av respektive stockstorlek? 6. I ett kontinuerligt växande skogsbestånd (i ett sådant bestånd finns träd i alla diameterklasser) beror trädenas stamantal Y d per hektar av diameterklassen d enligt följande: Y d = , 2 d a) Hur många stammar finns det per hektar i diameterklassen 30 cm? b) I vilken diameterklass finns det 150 stammar per hektar? (Trädens diametrar anges med 1 cm:s noggrannhet, t.ex. i diameterklassen 30 cm finns träd med diametrar 29,5 cm 30,49 cm.)

5 Svar: kortast 463 km 2 Svar: a) 1,43 ha b) (65 70) m 3 3 Svar: a) 59 bitar b) 42 m 2 plastmatta resp. 58 m 2 parkett 4 Svar: a) +2,1 % b) 1,26 % 5 Svar: a) 500 kg/m 3 b) 2,36 kg 6 Svar: a) a = b = 2/3 b) cm Svar: a) 160 m b) 200 m c) 112,8 m 2 Svar: 19,3 m 3 Svar: 1,1 m 4 Svar: 16% 5 Svar: st med d = 15 cm och st med d = 25 cm 6 Svar: a) 13 st b) diameterklassen 16 cm