Lösningsförslag till Problem i kapitel 5 i Mobil Radiokommunikation
|
|
|
- Elin Blomqvist
- för 9 år sedan
- Visningar:
Transkript
1 Lösningsförslag till Problem i kapitel 5 i obil Radiokommunikation 5. Rayleighfädande kanal med medelsignalenergin/bit Ws. AVGB med spektraltätheten N / W/Hz. ottagare som fungerar tillfredsställande med ett signalbrusförhållande [γ ] db > 4 db. a) Bråkdel av tiden som [γ ] db < 4 db. b) insta antal valdiversitetskanaler för att bråkdelen av tiden som [γ ] db < 4 db, efter sammanvägning, skall bli mindre än,. γ N 5 Ws W/Hz Lägsta SNR γ 4/,5 som mottagaren klarar. a) Bestäm hur stor del av tiden som Γ < γ. Kanalen är rayleighfädande signalbrusförhållandet Γ är exponentialfördelat: P Γ (γ) e γ/γ för γ för γ < P(Γ < γ ) P Γ (γ ) e γ /γ e,5/5,49 d.v.s. [SNR] db < 4 db under 5 % av tiden. b) Fördelningsfunktionen för en godtycklig gren i är P Γi (γ) e γ/γ för γ för γ < γ 5 Fördelningsfunktionen för diversitetssystemets resulterande Γ är P Γ (γ) P(Γ < γ) P(Γ < γ,γ < γ,,,γ < γ) {oberoende grenar} (P(Γ i < γ)) P Γi (γ) e γ/γ för γ för γ < I vårt fall är γ γ 4/,5 och P(Γ < γ ) P Γ (γ ) e γ /γ 4
2 e,5/5 4 varav 3,5 välj Ett diversitetssystem med okorrelerade och rayleighfördelade grenar, var och en med samma medel-snr, γ. Beskrivning av tre olika sammanvägningsmetoder samt approximativ fördelningsfunktion för signalbrusförhållandet för var och en efter sammanvägning om antalet grenar,, är stort. Ledning: Summan av ett stort antal grenar är approximativt normalfördelad. I Valdiversitet - välj bästa gren. F Γ (γ) P(Γ i < γ) e γ/γ II Optimalviktsdiversitet - sammanväger samtliga grenar med optimalvikt. edelvärdet av signalbrusförhållandet, Γ i, i varje gren är γ. edelvärdet av summan av grenars signalbrusförhållande, alla med samma fördelning, är γ. Variansen för varje gren vid rayleighfördelning är γ. Variansen för grenar är γ. Centrala gränsvärdessatsen ger då att resulterande γ är normalfördelat enligt γ N γ, γ med fördelningsfunktionen III F Γ (γ) Φ γ γ γ Likaviktsdiversitet - sammanväger samtliga grenar med samma vikt. Den sammanvägda enveloppen ges då av uttrycket (5.) på sidan 86: A A i i där A i är rayleighfördelad medan den resulterande signalens SNR ges av (5.) på samma sida:
3 γ A N N Då är stort är A i i z A i i, enligt centrala gränsvärdessatsen, approximativt normalfördelad med, se (.54) och (.55) på sidan 74: E[A i ] σ π σ Ai σ π 4 och z N σ π, σ π 4 Vi kan nu skriva. γ g(z) där N z N γ z. Täthetsfunktionen för γ blir: p Γ (γ) df Γ (γ) dγ df Z(g(z)) dz p Z(z) g (z) p Z(z) z N Nγ z dz dg(z) df Z(g(z)) dz dg(z) dz σ Z π exp N Fördelningsfunktionen: P Γ (γ) γ p Γ (x) dx N γ σ Z N γ m Z N x v substitution: x v N dx v N 3
4 N σ Z π N γ v exp v m Z σ Z N v dv σ Z π N γ exp v m Z σ Z dv v m Z t σ Z σ Z dt dv σ Z π N γ m Z σ Z e t / dt Φ N γ m E Z b σ Z Φ N γ σ π σ π 4 γ σ N Φ N γ σ N π N σ N π 4 Φ γ γ π 4 γ π Rayleighfädande kanal på vilken sänds datameddelanden med BPSK. edelsignalbrusförhållandet γ 3/. a) Felsannolikheten utan diversitet. b) Antalet diversitetskanaler om felsannolikheten skall minska till 5. Sammanvägningsmetoden är optimalviktsdiversitet. c) Felsannolikheten för en kanal enbart störd av AVGB och med samma signalbrusförhållande. a) γ 3/ 9,95. Eftersom γ kan vi använda (4.39) på sidan 54: 4
5 P f 4γ 4 9,95 b) Enligt (5.4) på sidan 95 ges villkoret för bitfelssannolikheten vid optimalviktsdiversitet och PSK vid SNR > av följande olikhet: P fd Pröva olika värden på,5 4γ < 5 P fd 5.4 Välj 4. c) Enligt (4.) på sidan 47 är bitfelssannolikheten vid AVGB: Paketradiosystem där paketlängden koherenstiden varje paket upplever kanalen som konstant, d.v.s. långsam flat rayleighfädning. Paketen mottas korrekt om [SNR] db > db γ mot. edel-[snr] db [γ ] db db i basstationen. a) Sannolikheten att meddelandet tas emot korrekt. b) Sannolikheten att, om det finns ytterligare en basstation med medel- [SNR] db 5 db, ett av meddelandena tas emot korrekt., 4,7 4 3, 5 4 8,6 7 P PSK Q γ Q 9,95 Q 6,37,3 SNR i den första basstationen kallas Γ. a) P{Γ > γ mot } γ mot p(γ) dγ e γ/γ dγ e γ/γ γ γmot γ mot e γ mot/γ exp / / e, 9 % 5
6 5.5 b) För den andra kanalen med medel-[snr] db 5 db gäller på samma sätt att P{Γ > γ mot } exp /,79 5/ Om kanalerna är oberoende gäller: P{max(Γ,Γ ) > γ mot } P{max(Γ,Γ ) < γ mot } P{(Γ < γ mot ) (Γ < γ mot )} P{Γ < γ mot } P{Γ < γ mot } (,95)(,79) +,79 +,95,95,79, % Ett valdiversitetssystem för mottagning av meddelanden modulerade med DPSK. Kanalen är utsatt för långsam rayleighfädning. edelsignalbrusförhållandet i varje gren är [γ ] db db. Bitfelssannolikheten för en, två och tre oberoende diversitetsgrenar. Diversitetssystemets bitfelssannolikhet ges av uttrycket (5.35) på sidan 95: P fd där för fallet DPSK P e (γ) P DPSK, fixt γ, ges av uttrycket (4.3) på sidan 47: medan täthetsfunktionen, p(γ), för SNR i valdiversitetssystemet ges av (5.7) på sidan 8: I P e (γ )p(γ ) dγ P e (γ) P DPSK e /N e γ p(γ ) γ exp γ γ exp γ γ P fd e γ e γ γ/γ dγ exp γ + dγ γ γ 6
7 γ + exp γ + γ γ γ + γ γ + γ ( + ),45 ; jämför även med uttrycket (4.35) på sidan 53. II P fd e γ e γ γ/γ e γ/γ dγ exp γ γ + exp γ γ + γ γ γ dγ γ Jämför detta resultat med det, för stora värden på SNR, angivna approximativa uttrycket (5.44) på sidan 97: III 3 γ γ + exp γ γ + γ + γ γ + exp γ γ + γ. γ + γ + + 7, P fd γ 7,5 3 P fd e γ 3 e γ γ/γ e γ/γ dγ γ 3 exp γ γ + γ e γ/γ + e γ/γ dγ γ 3 exp γ γ + exp γ γ + + exp γ γ + 3 γ γ γ dγ 3 γ γ γ + γ γ + + γ γ ,75 3. Jämför detta resultat med det, för stora värden på SNR, angivna approximativa uttrycket (5.44) på sidan 97: 7
8 P fd 3 γ 3 3, Ett två-kanals valdiversitetssystem med icke-koherent FSK. Båda kanalerna är utsatta för långsam flat rayleighfädning och har lika stor medeleffekt. inskningen i medeleffekt i förhållande till ett system utan diversitet om felhalten uppgår till 4. I Utan diversitet edelsignalbrusförhållandet γ fås av (4.39) på sidan 54: P varav γ 4 f γ 4 II ed två-kanals valdiversitet Diversitetssystemets bitfelssannolikhet ges av uttrycket (5.35) på sidan 95: P fd P e (γ )p(γ ) dγ där för fallet icke-koherent FSK P e (γ) P IK, uttrycket (4.7) på sidan 48: fixt γ, ges av P e (γ) P IK e /N e γ / medan täthetsfunktionen, p(γ), för SNR i valdiversitetssystemet ges av (5.7) på sidan 8: p(γ ) γ exp γ γ exp γ γ Bitfelshalten kan nu tecknas:. P fd e γ/ e γ γ/γ e γ/γ dγ exp γ γ + exp γ γ + 4 γ γ γ dγ 8
9 5.7 varav γ 97 [γ ] db,9 db, d.v.s. 4,9 7, db lägre medelsignalbrusförhållande än utan diversitet. Jämför även med det approximativa uttrycket (5.46) på sidan 97 gällande för γ : varav γ 73, [γ ] db,4 db, d.v.s. en skillnad på,5 db i förhållande till det mer exakta uttrycket. Flat rayleighfädande paketrundradiosystem. edelsignalbrusförhållandet i mottagaren är [γ ] db 45 db medan korrekt mottagning minst kräver 3 db γ mot. Koherenstiden paketlängden paketen upplever kanalen som konstant. a) Sannolikheten att ett paket tas emot korrekt. b) Sannolikheten att ett paket tas emot korrekt om det finns ytterligare en oberoende antenn med medel-[snr] db 4 db och att endast en antenn behöver ta emot meddelandet korrekt. γ γ γ + exp γ γ + γ + γ γ + 4 exp γ γ + 4 γ γ + γ P fd γ γ - 4 a) Signalbrusförhållandet i huvudmottagaren kallas Γ. P{Γ > γ mot } γ mot p(γ) dγ e γ/γ dγ γ γ mot e γ/γ γmot e γ mot /γ exp 3/ 97 % 45/ b) För den andra antennen med medel-[snr] db 4 db gäller på samma sätt att P{Γ > γ mot } exp 3/,95 4/ Om kanalerna är oberoende gäller: 9
10 5.8 P{max(Γ,Γ ) > γ mot } P{max(Γ,Γ ) < γ mot } P{(Γ < γ mot ) (Γ < γ mot )} P{Γ < γ mot } P{Γ < γ mot } (,969)(,95) +,95 +,969,95,969,997 99,7 %. En kanal med långsam flat rayleighfädning modulerad med icke-koherent FSK medan datatakten är 36 kbit/s. Bitfelssannolikheten är 7 3. Antalet valdiversitetsgrenar för att nedbringa felhalten till 6. Enligt (5.7) sidan 8 är täthetsfunktionen vid valdiversitet med grenar: p(γ ) γ exp γ γ exp γ γ edelsignalbrusförhållandet γ fås enligt (4.39) på sidan 54:. P f γ 7 3 varav γ 43. Enligt (4.36) sidan 53 är bitfelssannolikheten vid fixt SNR P e (γ ) e γ /. Enligt (5.35) på sidan 95 kan vi nu teckna bitfelssannolikheten för diversitetsarrangemanget: P fd P e (γ)p(γ) dγ γ e γ/ e γ/γ e γ/γ dγ γ e γ/ γ/γ e γ/γ i i e γ/γ i dγ i γ ( ) i i exp γ + γ + i γ dγ
11 i γ ( ) i i γ + + i γ exp γ γ + + i γ 5.9 Kravet är att P fd 6. ed γ 43 provar vi olika värden på. 3 4 Välj 4! En radiokommunikationslänk utsatt för flat rayleighfädning. För önskad överföringskvalitet krävs att [SNR] db [γ mot ] db db. edel- [SNR] db är db. För att uppnå tidstillgängligheten 98 %, är systemet kompletterat med ett frekvensvaldiversitetsarrangemang där tillgänglig effekt delas mellan ett antal olika frekvenskanaler. i γ ( ) i i a) Antal diversitetskanaler för att uppnå tidstillgänglighetskravet. b) Största möjliga tidstillgänglighet. a) ed är medelsignalbrusförhållandet i den enda kanalen γ. γ γ + + i P fd γ P fd γ + γ P fd 3 γ + γ γ P fd 4 γ + 3 γ γ + 6 γ Enligt (.6) på sidan 76 är tidstillgängligheten: T till P{Γ > γ mot } γ mot e γ/γ dγ e γ mot/γ exp /,95 γ / ed är medelsignalbrusförhållandet i var och en av de två
12 kanalerna γ. Tidstillgängligheten blir 5 T till P{Γ > γ mot } P{Γ γ mot } P{Γ,Γ γ mot } P{Γ γ mot } P{Γ γ mot } exp γ mot γ exp,967 5 ed 3 är medelsignalbrusförhållandet i var och en av de tre kanalerna γ T till exp γ mot γ. Tidstillgängligheten blir b) Allmänt kan tidstillgängligheten för det angivna frekvensvaldiversitetsarrangemanget tecknas: T till ( e, ) Pröva olika värden på : 3 exp 3 4 T till ( e,4 ) 4,988 5 T till ( e,5 ) 5,996 6 T till ( e,6 ) 6,996 7 T till ( e,7 ) 7,998 8 T till ( e,8 ) 8,995 7 ger maximal tidstillgänglighet 99, % 3,98 98 %
Lösningsförslag till Problem i kapitel 7 i Mobil Radiokommunikation
 Lösningsförslag till Problem i kapitel 7 i Mobil adiokommunikation 7. 7. Två lognormalt fördelade stokastiska variabler X och Y med log-standardavvikelserna σ logx och σ logy. Att den stokastiska variabeln
Lösningsförslag till Problem i kapitel 7 i Mobil adiokommunikation 7. 7. Två lognormalt fördelade stokastiska variabler X och Y med log-standardavvikelserna σ logx och σ logy. Att den stokastiska variabeln
Lösningsförslag till Problem i kapitel 6 i Mobil Radiokommunikation
 Lösningsförslag till Problem i kapitel 6 i Mobil Radiokommunikation 6. En NMT 9 mobiltelefon med sändning och mottagning via MHz åtskilda kanaler. Mottagare och sändare åtskilda av duplexfilter. Telefonen
Lösningsförslag till Problem i kapitel 6 i Mobil Radiokommunikation 6. En NMT 9 mobiltelefon med sändning och mottagning via MHz åtskilda kanaler. Mottagare och sändare åtskilda av duplexfilter. Telefonen
SF1901 Sannolikhetsteori och statistik I
 SF1901 Sannolikhetsteori och statistik I Jimmy Olsson Föreläsning 4 7 november 2017 1 / 29 Idag Förra gången Viktiga kontinuerliga fördelningar (Kap. 3.6) Fördelningsfunktion (Kap. 3.7) Funktioner av stokastiska
SF1901 Sannolikhetsteori och statistik I Jimmy Olsson Föreläsning 4 7 november 2017 1 / 29 Idag Förra gången Viktiga kontinuerliga fördelningar (Kap. 3.6) Fördelningsfunktion (Kap. 3.7) Funktioner av stokastiska
Kap 2. Sannolikhetsteorins grunder
 Kap 2. Sannolikhetsteorins grunder Olika händelser och deras mängbetäckningar Sats 2.7 Dragning utan återläggning av k element ur n (utan hänsyn till ordning) kan ske på ( n ) olika sätt k För två händelser
Kap 2. Sannolikhetsteorins grunder Olika händelser och deras mängbetäckningar Sats 2.7 Dragning utan återläggning av k element ur n (utan hänsyn till ordning) kan ske på ( n ) olika sätt k För två händelser
LINKÖPINGS UNIVERSITET EXAM TAMS 27 / TEN 2
 LINKÖPINGS UNIVERSITET Matematiska institutionen EXAM TAMS 27 / TEN 2 augusti 218, klockan 8.-12. Examinator: Jörg-Uwe Löbus (Tel: 79-62827) Tillåtna hjälpmedel är en räknare, formelsamling i matematisk
LINKÖPINGS UNIVERSITET Matematiska institutionen EXAM TAMS 27 / TEN 2 augusti 218, klockan 8.-12. Examinator: Jörg-Uwe Löbus (Tel: 79-62827) Tillåtna hjälpmedel är en räknare, formelsamling i matematisk
Väntevärde och varians
 TNG6 F5 19-4-216 Väntevärde och varians Exempel 5.1. En grupp teknologer vid ITN slår sig ihop för att starta ett företag som utvecklar datorspel. Man vet att det är 8% chans för ett felfritt spel som
TNG6 F5 19-4-216 Väntevärde och varians Exempel 5.1. En grupp teknologer vid ITN slår sig ihop för att starta ett företag som utvecklar datorspel. Man vet att det är 8% chans för ett felfritt spel som
SF1901 Sannolikhetsteori och statistik I
 SF1901 Sannolikhetsteori och statistik I Jimmy Olsson Föreläsning 7 15 november 2017 1 / 28 Lite om kontrollskrivning och laborationer Kontrollskrivningen omfattar Kap. 1 5 i boken, alltså Föreläsning
SF1901 Sannolikhetsteori och statistik I Jimmy Olsson Föreläsning 7 15 november 2017 1 / 28 Lite om kontrollskrivning och laborationer Kontrollskrivningen omfattar Kap. 1 5 i boken, alltså Föreläsning
Grundläggande matematisk statistik
 Grundläggande matematisk statistik Kontinuerliga fördelningar Uwe Menzel, 8 www.matstat.de Begrepp fördelning Hur beter sig en variabel slumpmässigt? En slumpvariabel (s.v.) har en viss fördelning, d.v.s.
Grundläggande matematisk statistik Kontinuerliga fördelningar Uwe Menzel, 8 www.matstat.de Begrepp fördelning Hur beter sig en variabel slumpmässigt? En slumpvariabel (s.v.) har en viss fördelning, d.v.s.
Laboration 4: Stora talens lag, Centrala gränsvärdessatsen och enkla punktskattningar
 LUNDS TEKNISKA HÖGSKOLA MATEMATIKCENTRUM MATEMATISK STATISTIK DATORLABORATION 4 MATEMATISK STATISTIK, FÖR I/PI, FMS 121/2, HT-3 Laboration 4: Stora talens lag, Centrala gränsvärdessatsen och enkla punktskattningar
LUNDS TEKNISKA HÖGSKOLA MATEMATIKCENTRUM MATEMATISK STATISTIK DATORLABORATION 4 MATEMATISK STATISTIK, FÖR I/PI, FMS 121/2, HT-3 Laboration 4: Stora talens lag, Centrala gränsvärdessatsen och enkla punktskattningar
Tentamen i Trådlös Internet-access
 Mittuniversitetet Inst. för IT och Medier, ITM Stefan Pettersson 005-04-30 Tentamen i Trådlös Internet-access Tid: Kl 9.00-14.00. Hjälpmedel: Valfri miniräknare. Bifogad formelsamling. Ansvarig lärare:
Mittuniversitetet Inst. för IT och Medier, ITM Stefan Pettersson 005-04-30 Tentamen i Trådlös Internet-access Tid: Kl 9.00-14.00. Hjälpmedel: Valfri miniräknare. Bifogad formelsamling. Ansvarig lärare:
SF1911: Statistik för bioteknik
 SF1911: Statistik för bioteknik Föreläsning 6. TK 14.11.2016 TK Matematisk statistik 14.11.2016 1 / 38 Lärandemål Stokastiska modeller för kontinuerliga datatyper Fördelningsfunktion (cdf) Sannolikhetstäthetsfunktion
SF1911: Statistik för bioteknik Föreläsning 6. TK 14.11.2016 TK Matematisk statistik 14.11.2016 1 / 38 Lärandemål Stokastiska modeller för kontinuerliga datatyper Fördelningsfunktion (cdf) Sannolikhetstäthetsfunktion
FACIT: Tentamen L9MA30, LGMA30
 Göteborgs Universitetet GU Lärarprogrammet 06 FACIT: Matematik för lärare, åk 7-9, Sannolikhetslära och statistik, Matematik för gymnasielärare, Sannolikhetslära och statistik 07-0-04 kl..0-.0 Examinator
Göteborgs Universitetet GU Lärarprogrammet 06 FACIT: Matematik för lärare, åk 7-9, Sannolikhetslära och statistik, Matematik för gymnasielärare, Sannolikhetslära och statistik 07-0-04 kl..0-.0 Examinator
Föreläsning 5. Funktioner av slumpvariabler. Ett centralt resultat.
 Föreläsning 5. Funktioner av slumpvariabler. Ett centralt resultat. Jesper Rydén Matematiska institutionen, Uppsala universitet jesper.ryden@math.uu.se 1MS008, 1MS777 vt 2016 Ytterligare begrepp Viktiga
Föreläsning 5. Funktioner av slumpvariabler. Ett centralt resultat. Jesper Rydén Matematiska institutionen, Uppsala universitet jesper.ryden@math.uu.se 1MS008, 1MS777 vt 2016 Ytterligare begrepp Viktiga
Matematisk statistik TMS063 Tentamen
 Matematisk statistik TMS63 Tentamen 8-8- Tid: 4:-8: Tentamensplats: SB Hjälpmedel: Bifogad formelsamling och tabell samt Chalmersgodkänd räknare. Kursansvarig: Olof Elias Telefonvakt/jour: Olof Elias,
Matematisk statistik TMS63 Tentamen 8-8- Tid: 4:-8: Tentamensplats: SB Hjälpmedel: Bifogad formelsamling och tabell samt Chalmersgodkänd räknare. Kursansvarig: Olof Elias Telefonvakt/jour: Olof Elias,
Matematisk statistik 9hp Föreläsning 7: Normalfördelning
 Matematisk statistik 9hp Föreläsning 7: Normalfördelning Anna Lindgren 29+3 september 216 Anna Lindgren anna@maths.lth.se FMS12/MASB3 F7: normalfördelning 1/18 Kovarians, C(X, Y) Repetition Normalfördelning
Matematisk statistik 9hp Föreläsning 7: Normalfördelning Anna Lindgren 29+3 september 216 Anna Lindgren anna@maths.lth.se FMS12/MASB3 F7: normalfördelning 1/18 Kovarians, C(X, Y) Repetition Normalfördelning
Kapitel 7 Samplingfördelningar och Centrala gränsvärdessatsen
 Sannolikhetslära och inferens II Kapitel 7 Samplingfördelningar och Centrala gränsvärdessatsen 1 Statistikor och samplingfördelningar I Kapitel 6 studerades metoder för att bestämma sannolikhetsfördelningen
Sannolikhetslära och inferens II Kapitel 7 Samplingfördelningar och Centrala gränsvärdessatsen 1 Statistikor och samplingfördelningar I Kapitel 6 studerades metoder för att bestämma sannolikhetsfördelningen
Föreläsning 4: Konfidensintervall (forts.)
 Föreläsning 4: Konfidensintervall forts. Johan Thim johan.thim@liu.se 3 september 8 Skillnad mellan parametrar Vi kommer nu fortsätta med att konstruera konfidensintervall och vi kommer betrakta lite olika
Föreläsning 4: Konfidensintervall forts. Johan Thim johan.thim@liu.se 3 september 8 Skillnad mellan parametrar Vi kommer nu fortsätta med att konstruera konfidensintervall och vi kommer betrakta lite olika
SF1901: Övningshäfte
 SF1901: Övningshäfte 24 september 2013 Uppgifterna under rubriken Övning kommer att gås igenom under övningstillfällena. Uppgifterna under rubriken Hemtal är starkt rekommenderade och motsvarar nivån på
SF1901: Övningshäfte 24 september 2013 Uppgifterna under rubriken Övning kommer att gås igenom under övningstillfällena. Uppgifterna under rubriken Hemtal är starkt rekommenderade och motsvarar nivån på
Stokastiska vektorer och multivariat normalfördelning
 Stokastiska vektorer och multivariat normalfördelning Johan Thim johanthim@liuse 3 november 08 Repetition Definition Låt X och Y vara stokastiska variabler med EX µ X, V X σx, EY µ Y samt V Y σy Kovariansen
Stokastiska vektorer och multivariat normalfördelning Johan Thim johanthim@liuse 3 november 08 Repetition Definition Låt X och Y vara stokastiska variabler med EX µ X, V X σx, EY µ Y samt V Y σy Kovariansen
SF1901 Sannolikhetsteori och statistik I
 SF1901 Sannolikhetsteori och statistik I Jimmy Olsson Föreläsning 6 13 november 2017 1 / 29 Idag Förra gången Mer om väntevärden och varianser (Kap. 5.2 5.3) Beroendemått (Kap. 5.4) Summor, linjärkombinationer
SF1901 Sannolikhetsteori och statistik I Jimmy Olsson Föreläsning 6 13 november 2017 1 / 29 Idag Förra gången Mer om väntevärden och varianser (Kap. 5.2 5.3) Beroendemått (Kap. 5.4) Summor, linjärkombinationer
(a) Anta att Danmarksprojektet inte lyckas hålla budgeten. Vad är då sannolikheten att Sverigeprojektet inte heller lyckas hålla budgeten? Motivera!
 TENTAMEN: Statistik och sannolikhetslära (LMA10) Tid och plats: 08:30-1:30 den augusti 016, SB Hjälpmedel: Typgodkänd miniräknare, formelblad Betygsgränser: 3: 1 poäng, 4: 18 poäng, 5: 4 poäng. Maximalt
TENTAMEN: Statistik och sannolikhetslära (LMA10) Tid och plats: 08:30-1:30 den augusti 016, SB Hjälpmedel: Typgodkänd miniräknare, formelblad Betygsgränser: 3: 1 poäng, 4: 18 poäng, 5: 4 poäng. Maximalt
Introduktion till statistik för statsvetare
 "Det finns inget så praktiskt som en bra teori" November 2011 Repetition Vad vi gjort hitills Vi har börjat med att studera olika typer av mätningar och sedan successivt tagit fram olika beskrivande mått
"Det finns inget så praktiskt som en bra teori" November 2011 Repetition Vad vi gjort hitills Vi har börjat med att studera olika typer av mätningar och sedan successivt tagit fram olika beskrivande mått
Hemtenta 2 i Telekommunikation
 Hemtenta 2 i Telekommunikation Tentamen omfattar 4*4=16 poäng. För godkänt krävs minst 8 poäng. Individuell Inlämning senast 2005-10-07 till Jan-Åke Olofsson jan-ake.olofsson@tfe.umu.se eller Björn Ekenstam,
Hemtenta 2 i Telekommunikation Tentamen omfattar 4*4=16 poäng. För godkänt krävs minst 8 poäng. Individuell Inlämning senast 2005-10-07 till Jan-Åke Olofsson jan-ake.olofsson@tfe.umu.se eller Björn Ekenstam,
Blandade problem från elektro- och datateknik
 Blandade problem från elektro- och datateknik Sannolikhetsteori (Kapitel 1-10) E1. En viss typ av elektroniska komponenter anses ha exponentialfördelade livslängder. Efter 3000 timmar brukar 90 % av komponenterna
Blandade problem från elektro- och datateknik Sannolikhetsteori (Kapitel 1-10) E1. En viss typ av elektroniska komponenter anses ha exponentialfördelade livslängder. Efter 3000 timmar brukar 90 % av komponenterna
0 om x < 0, F X (x) = c x. 1 om x 2.
 Avd. Matematisk statistik TENTAMEN I SF193 SANNOLIKHETSLÄRA OCH STATISTIK FÖR 3-ÅRIG Media TIMEH MÅNDAGEN DEN 16 AUGUSTI 1 KL 8. 13.. Examinator: Gunnar Englund, tel. 7974 16. Tillåtna hjälpmedel: Läroboken.
Avd. Matematisk statistik TENTAMEN I SF193 SANNOLIKHETSLÄRA OCH STATISTIK FÖR 3-ÅRIG Media TIMEH MÅNDAGEN DEN 16 AUGUSTI 1 KL 8. 13.. Examinator: Gunnar Englund, tel. 7974 16. Tillåtna hjälpmedel: Läroboken.
SF1901: Sannolikhetslära och statistik
 SF1901: Sannolikhetslära och statistik Föreläsning 6. Normalfördelning, Centrala gränsvärdessatsen, Approximationer Jan Grandell & Timo Koski 06.02.2012 Jan Grandell & Timo Koski () Matematisk statistik
SF1901: Sannolikhetslära och statistik Föreläsning 6. Normalfördelning, Centrala gränsvärdessatsen, Approximationer Jan Grandell & Timo Koski 06.02.2012 Jan Grandell & Timo Koski () Matematisk statistik
LINKÖPINGS UNIVERSITET EXAM TAMS 27 / TEN 2
 LINKÖPINGS UNIVERSITET Matematiska institutionen EXAM TAMS 7 / TEN 8 maj 18, klockan 8.-1. Examinator: Jörg-Uwe Löbus Tel: 79-687 Tillåtna hjälpmedel är en räknare, formelsamling i matematisk statistik
LINKÖPINGS UNIVERSITET Matematiska institutionen EXAM TAMS 7 / TEN 8 maj 18, klockan 8.-1. Examinator: Jörg-Uwe Löbus Tel: 79-687 Tillåtna hjälpmedel är en räknare, formelsamling i matematisk statistik
(a) på hur många sätt kan man permutera ordet OSANNOLIK? (b) hur många unika 3-bokstavskombinationer kan man bilda av OSANNO-
 Tentamenskrivning för TMS6, Matematisk Statistik. Onsdag fm den 1 maj, 217. Examinator: Marina Axelson-Fisk. Tel: 1-7724996 Tillåtna hjälpmedel: typgodkänd miniräknare, tabell- och formelhäfte (bifogas).
Tentamenskrivning för TMS6, Matematisk Statistik. Onsdag fm den 1 maj, 217. Examinator: Marina Axelson-Fisk. Tel: 1-7724996 Tillåtna hjälpmedel: typgodkänd miniräknare, tabell- och formelhäfte (bifogas).
Matematisk statistik 9 hp Föreläsning 6: Linjärkombinationer
 Matematisk statistik 9 hp Föreläsning 6: Linjärkombinationer Anna Lindgren 27+28 september 2016 Anna Lindgren anna@maths.lth.se FMS012/MASB03 F6: linjärkombinationer 1/21 sum/max/min V.v./var Summa av
Matematisk statistik 9 hp Föreläsning 6: Linjärkombinationer Anna Lindgren 27+28 september 2016 Anna Lindgren anna@maths.lth.se FMS012/MASB03 F6: linjärkombinationer 1/21 sum/max/min V.v./var Summa av
FINGERÖVNINGAR I SANNOLIKHETSTEORI MATEMATISK STATISTIK AK FÖR I. Oktober Matematikcentrum Matematisk statistik
 FINGERÖVNINGAR I SANNOLIKHETSTEORI MATEMATISK STATISTIK AK FÖR I Oktober Matematikcentrum Matematisk statistik CENTRUM SCIENTIARUM MATHEMATICARUM LUNDS TEKNISKA HÖGSKOLA MATEMATIKCENTRUM MATEMATISK STATISTIK
FINGERÖVNINGAR I SANNOLIKHETSTEORI MATEMATISK STATISTIK AK FÖR I Oktober Matematikcentrum Matematisk statistik CENTRUM SCIENTIARUM MATHEMATICARUM LUNDS TEKNISKA HÖGSKOLA MATEMATIKCENTRUM MATEMATISK STATISTIK
SF1901: Sannolikhetslära och statistik. Flera stokastiska variabler.
 SF1901: Sannolikhetslära och statistik Föreläsning 5. Flera stokastiska variabler. Jan Grandell & Timo Koski 31.01.2012 Jan Grandell & Timo Koski () Matematisk statistik 31.01.2012 1 / 30 Flerdimensionella
SF1901: Sannolikhetslära och statistik Föreläsning 5. Flera stokastiska variabler. Jan Grandell & Timo Koski 31.01.2012 Jan Grandell & Timo Koski () Matematisk statistik 31.01.2012 1 / 30 Flerdimensionella
SF1901: Sannolikhetslära och statistik
 SF1901: Sannolikhetslära och statistik Föreläsning 4. Funktioner av s.v:er, Flera stokastiska variabler. Marginell sannolikhetsfunktion och -täthetsfunktion. Oberoende sv:er, Maximum och minimum av oberoende
SF1901: Sannolikhetslära och statistik Föreläsning 4. Funktioner av s.v:er, Flera stokastiska variabler. Marginell sannolikhetsfunktion och -täthetsfunktion. Oberoende sv:er, Maximum och minimum av oberoende
Omtentamen i Trådlös Internet-access
 Mittuniversitetet Inst. för IT och medier, ITM Stefan Pettersson 005-06-0 Omtentamen i Trådlös Internet-access Tid: 08.00-13.00. Hjälpmedel: Valfri miniräknare. Bifogad formelsamling. Ansvarig lärare:
Mittuniversitetet Inst. för IT och medier, ITM Stefan Pettersson 005-06-0 Omtentamen i Trådlös Internet-access Tid: 08.00-13.00. Hjälpmedel: Valfri miniräknare. Bifogad formelsamling. Ansvarig lärare:
Del I. Uppgift 1 För händelserna A och B gäller att P (A) = 1/4, P (B A) = 1/3 och P (B A ) = 1/2. Beräkna P (A B). Svar:...
 Avd. Matematisk statistik TENTAMEN I SF9/SF94/SF95/SF96 SANNOLIKHETSTEORI OCH STATISTIK, ONSDAGEN DEN 4:E OKTOBER 08 KL 8.00 3.00. Examinator för SF94/SF96: Tatjana Pavlenko, 08-790 84 66 Examinator för
Avd. Matematisk statistik TENTAMEN I SF9/SF94/SF95/SF96 SANNOLIKHETSTEORI OCH STATISTIK, ONSDAGEN DEN 4:E OKTOBER 08 KL 8.00 3.00. Examinator för SF94/SF96: Tatjana Pavlenko, 08-790 84 66 Examinator för
Lösningsförslag till Problem i kapitel 3 i Mobil Radiokommunikation
 Lösningsförslag till Problem i kapitel 3 i Mobil Radiokommunikation 3.1 En mottagarantenn med 50 Ω matningsimpedans och 10 db antennförstärkning befinner sig i ett fält med styrkan 75 dbµv/m vid frekvensen
Lösningsförslag till Problem i kapitel 3 i Mobil Radiokommunikation 3.1 En mottagarantenn med 50 Ω matningsimpedans och 10 db antennförstärkning befinner sig i ett fält med styrkan 75 dbµv/m vid frekvensen
DIGITAL KOMMUNIKATION
 EN KOR SAMMANFANING AV EORIN INOM DIGIAL KOMMUNIKAION Linjär kod En binär linjär kod kännetecknas av att summan av två kodord också är ett kodord. Ett specialfall är summan av ett kodord med sig själv
EN KOR SAMMANFANING AV EORIN INOM DIGIAL KOMMUNIKAION Linjär kod En binär linjär kod kännetecknas av att summan av två kodord också är ett kodord. Ett specialfall är summan av ett kodord med sig själv
Samplingfördelningar 1
 Samplingfördelningar 1 Parametrar och statistikor En parameter är en konstant som karakteriserar en population eller en modell. Exempel: Populationsmedelvärdet Parametern p i binomialfördelningen 2 Vi
Samplingfördelningar 1 Parametrar och statistikor En parameter är en konstant som karakteriserar en population eller en modell. Exempel: Populationsmedelvärdet Parametern p i binomialfördelningen 2 Vi
Fördelningsfunktionen för en kontinuerlig stokastisk variabel. Täthetsfunktionen för en kontinuerlig och en diskret stokastisk variabel.
 Övning 1 Vad du ska kunna efter denna övning Diskret och kontinuerlig stokastisk variabel. Fördelningsfunktionen för en kontinuerlig stokastisk variabel. Täthetsfunktionen för en kontinuerlig och en diskret
Övning 1 Vad du ska kunna efter denna övning Diskret och kontinuerlig stokastisk variabel. Fördelningsfunktionen för en kontinuerlig stokastisk variabel. Täthetsfunktionen för en kontinuerlig och en diskret
(x) = F X. och kvantiler
 Föreläsning 5: Matstat AK för M, HT-8 MATEMATISK STATISTIK AK FÖR M HT-8 FÖRELÄSNING 5: KAPITEL 6: NORMALFÖRDELNINGEN EXEMPEL FORTKÖRARE Man har mätt hastigheten på 8 bilar som passerade en korsning i
Föreläsning 5: Matstat AK för M, HT-8 MATEMATISK STATISTIK AK FÖR M HT-8 FÖRELÄSNING 5: KAPITEL 6: NORMALFÖRDELNINGEN EXEMPEL FORTKÖRARE Man har mätt hastigheten på 8 bilar som passerade en korsning i
Fysiska lagret. Kanal. Problem är att kanalen har vissa begränsningar: Kanalen är analog Kanalen är bandbreddsbegränsad och är oftast störd (av brus)
 Fysiska lagret Sändare Digital information Kanal Mottagare Problem är att kanalen har vissa begränsningar: Kanalen är analog Kanalen är bandbreddsbegränsad och är oftast störd (av brus) Kanalens kapacitet
Fysiska lagret Sändare Digital information Kanal Mottagare Problem är att kanalen har vissa begränsningar: Kanalen är analog Kanalen är bandbreddsbegränsad och är oftast störd (av brus) Kanalens kapacitet
MS-A0509 Grundkurs i sannolikhetskalkyl och statistik Sammanfattning, del I
 MS-A0509 Grundkurs i sannolikhetskalkyl och statistik Sammanfattning, del I G. Gripenberg Sannolikheter Slumpvariabler Centrala gränsvärdessatsen Aalto-universitetet 8 januari 04 3 Tvådimensionella slumpvariabler
MS-A0509 Grundkurs i sannolikhetskalkyl och statistik Sammanfattning, del I G. Gripenberg Sannolikheter Slumpvariabler Centrala gränsvärdessatsen Aalto-universitetet 8 januari 04 3 Tvådimensionella slumpvariabler
Tentamen den 11 april 2007 i Statistik och sannolikhetslära för BI2
 Tentamen den april 7 i Statistik och sannolikhetslära för BI Uppgift : Låt händelserna A, B, C och D vara händelser i samband med ett försök. a) Anta att P(A)., P(A B)., P(A B).6. Beräkna sannolikheten
Tentamen den april 7 i Statistik och sannolikhetslära för BI Uppgift : Låt händelserna A, B, C och D vara händelser i samband med ett försök. a) Anta att P(A)., P(A B)., P(A B).6. Beräkna sannolikheten
MS-A0509 Grundkurs i sannolikhetskalkyl och statistik Sammanfattning, del I
 MS-A0509 Grundkurs i sannolikhetskalkyl och statistik Sammanfattning, del I G. Gripenberg Aalto-universitetet 28 januari 2014 G. Gripenberg (Aalto-universitetet) MS-A0509 Grundkurs i sannolikhetskalkyl
MS-A0509 Grundkurs i sannolikhetskalkyl och statistik Sammanfattning, del I G. Gripenberg Aalto-universitetet 28 januari 2014 G. Gripenberg (Aalto-universitetet) MS-A0509 Grundkurs i sannolikhetskalkyl
Summor av slumpvariabler
 1/18 Summor av slumpvariabler Måns Thulin Uppsala universitet thulin@math.uu.se Statistik för ingenjörer 9/2 2011 2/18 Dagens föreläsning Parkeringsplatsproblemet Räkneregler för väntevärden Räkneregler
1/18 Summor av slumpvariabler Måns Thulin Uppsala universitet thulin@math.uu.se Statistik för ingenjörer 9/2 2011 2/18 Dagens föreläsning Parkeringsplatsproblemet Räkneregler för väntevärden Räkneregler
(b) Bestäm sannolikheten att minst tre tåg är försenade under högst tre dagar en given vecka.
 Avd. Matematisk statistik TENTAMEN I SF1901, SF1905 SANNOLIKHETSTEORI OCH STATISTIK, MÅNDAGEN DEN 11 JANUARI 2016 KL 14.00 19.00. Kursledare för CINEK2: Thomas Önskog, tel: 08 790 84 55 Kursledare för
Avd. Matematisk statistik TENTAMEN I SF1901, SF1905 SANNOLIKHETSTEORI OCH STATISTIK, MÅNDAGEN DEN 11 JANUARI 2016 KL 14.00 19.00. Kursledare för CINEK2: Thomas Önskog, tel: 08 790 84 55 Kursledare för
Tentamen MVE301 Sannolikhet, statistik och risk
 Tentamen MVE30 Sannolikhet, statistik och risk 207-06-0 kl. 8:30-3:30 Examinator: Johan Jonasson, Matematiska vetenskaper, Chalmers Telefonvakt: Ivar Simonsson, telefon: 03-7725348 Hjälpmedel: Valfri miniräknare.
Tentamen MVE30 Sannolikhet, statistik och risk 207-06-0 kl. 8:30-3:30 Examinator: Johan Jonasson, Matematiska vetenskaper, Chalmers Telefonvakt: Ivar Simonsson, telefon: 03-7725348 Hjälpmedel: Valfri miniräknare.
Uppgift 1. P (A) och P (B) samt avgör om A och B är oberoende. (5 p)
 Avd. Matematisk statistik TENTAMEN I SF90, SF905, SANNOLIKHETSTEORI OCH STATISTIK, MÅNDAGEN DEN 8:E AUGSTI 204 KL 08.00 3.00. Kursledare: Tatjana Pavlenko, 08-790 84 66 Tillåtna hjälpmedel: Formel- och
Avd. Matematisk statistik TENTAMEN I SF90, SF905, SANNOLIKHETSTEORI OCH STATISTIK, MÅNDAGEN DEN 8:E AUGSTI 204 KL 08.00 3.00. Kursledare: Tatjana Pavlenko, 08-790 84 66 Tillåtna hjälpmedel: Formel- och
Matematisk statistik TMS064/TMS063 Tentamen
 Matematisk statistik TMS64/TMS63 Tentamen 29-8-2 Tid: 4:-8: Tentamensplats: SB Hjälpmedel: Bifogad formelsamling och tabell samt Chalmersgodkänd räknare. Kursansvarig: Olof Elias Telefonvakt/jour: Olof
Matematisk statistik TMS64/TMS63 Tentamen 29-8-2 Tid: 4:-8: Tentamensplats: SB Hjälpmedel: Bifogad formelsamling och tabell samt Chalmersgodkänd räknare. Kursansvarig: Olof Elias Telefonvakt/jour: Olof
Avd. Matematisk statistik
 Avd. Matematisk statistik TENTAMEN I SF1901, SANNOLIKHETSTEORI OCH STATISTIK, ONSDAGEN DEN 28:E OKTOBER 2015 KL 8.00 13.00. Kursledare: Tatjana Pavlenko, 08-790 84 66, Björn Olof Skytt 08-790 86 49. Tillåtna
Avd. Matematisk statistik TENTAMEN I SF1901, SANNOLIKHETSTEORI OCH STATISTIK, ONSDAGEN DEN 28:E OKTOBER 2015 KL 8.00 13.00. Kursledare: Tatjana Pavlenko, 08-790 84 66, Björn Olof Skytt 08-790 86 49. Tillåtna
Några extra övningsuppgifter i Statistisk teori
 Statistiska institutionen Några extra övningsuppgifter i Statistisk teori 23 JANUARI 2009 2 Sannolikhetsteorins grunder 1. Tre vanliga symmetriska tärningar kastas. Om inte alla tre tärningarna visar sexa,
Statistiska institutionen Några extra övningsuppgifter i Statistisk teori 23 JANUARI 2009 2 Sannolikhetsteorins grunder 1. Tre vanliga symmetriska tärningar kastas. Om inte alla tre tärningarna visar sexa,
Matematisk statistik 9hp Föreläsning 5: Summor och väntevärden
 Matematisk statistik 9hp Föreläsning 5: Summor och väntevärden Anna Lindgren 20+21 september 2016 Anna Lindgren anna@maths.lth.se FMS012/MASB03 F5: väntevärden 1/18 2D stokastisk variabel Tvådim. stokastisk
Matematisk statistik 9hp Föreläsning 5: Summor och väntevärden Anna Lindgren 20+21 september 2016 Anna Lindgren anna@maths.lth.se FMS012/MASB03 F5: väntevärden 1/18 2D stokastisk variabel Tvådim. stokastisk
Föreläsning 5, FMSF45 Summor och väntevärden
 Föreläsning 5, FMSF45 Summor och väntevärden Stas Volkov 2017-09-19 Stanislav Volkov s.volkov@maths.lth.se FMSFF45 F5: väntevärden 1/18 2D stokastisk variabel Tvådimensionella stokastisk variabel (X, Y)
Föreläsning 5, FMSF45 Summor och väntevärden Stas Volkov 2017-09-19 Stanislav Volkov s.volkov@maths.lth.se FMSFF45 F5: väntevärden 1/18 2D stokastisk variabel Tvådimensionella stokastisk variabel (X, Y)
Två parametrar: µ (väntevärdet) och σ (standardavvikelsen) µ bestämmer normalfördelningens läge
 Lunds tekniska högskola Matematikcentrum Matematisk statistik Matematisk statistik AK för ekosystemteknik, FMSF75 OH-bilder 28-9-3 Normalfördelningen, X N(µ, σ) f(x) = e (x µ)2 2σ 2, < x < 2π σ.4 N(2,).35.3.25.2.5..5
Lunds tekniska högskola Matematikcentrum Matematisk statistik Matematisk statistik AK för ekosystemteknik, FMSF75 OH-bilder 28-9-3 Normalfördelningen, X N(µ, σ) f(x) = e (x µ)2 2σ 2, < x < 2π σ.4 N(2,).35.3.25.2.5..5
FÖRELÄSNING 7:
 FÖRELÄSNING 7: 2016-05-10 LÄRANDEMÅL Normalfördelningen Standardnormalfördelning Centrala gränsvärdessatsen Konfidensintervall Konfidensnivå Konfidensintervall för väntevärdet då variansen är känd Samla
FÖRELÄSNING 7: 2016-05-10 LÄRANDEMÅL Normalfördelningen Standardnormalfördelning Centrala gränsvärdessatsen Konfidensintervall Konfidensnivå Konfidensintervall för väntevärdet då variansen är känd Samla
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen DEL A
 SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 16-8-18 DEL A 1. Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x och y =
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 16-8-18 DEL A 1. Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x och y =
P(ξ > 1) = 1 P( 1) = 1 (P(ξ = 0)+P(ξ = 1)) = 1 0.34. ξ = 2ξ 1 3ξ 2
 Lösningsförslag TMSB18 Matematisk statistik IL 101015 Tid: 12.00-17.00 Telefon: 101620, Examinator: F Abrahamsson 1. Varje dag levereras en last med 100 maskindetaljer till ett företag. Man tar då ett
Lösningsförslag TMSB18 Matematisk statistik IL 101015 Tid: 12.00-17.00 Telefon: 101620, Examinator: F Abrahamsson 1. Varje dag levereras en last med 100 maskindetaljer till ett företag. Man tar då ett
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF625 Envariabelanalys Lösningsförslag till tentamen 206-0- DEL A. Betrakta funktionen f som ges av f(x) = x 2 arctan x. A. Bestäm definitionsmängden till f. B. Bestäm de intervall där f är växande respektive
SF625 Envariabelanalys Lösningsförslag till tentamen 206-0- DEL A. Betrakta funktionen f som ges av f(x) = x 2 arctan x. A. Bestäm definitionsmängden till f. B. Bestäm de intervall där f är växande respektive
TAMS79: Föreläsning 4 Flerdimensionella stokastiska variabler
 TAMS79: Föreläsning 4 Flerdimensionella stokastiska variabler Johan Thim (johan.thim@liu.se) 1 november 18 Vi fokuserar på två-dimensionella variabler. Det är steget från en dimension till två som är det
TAMS79: Föreläsning 4 Flerdimensionella stokastiska variabler Johan Thim (johan.thim@liu.se) 1 november 18 Vi fokuserar på två-dimensionella variabler. Det är steget från en dimension till två som är det
1.1 Gradienten i kroklinjiga koordinatsystem
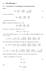 1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
Föreläsning 7: Stokastiska vektorer
 Föreläsning 7: Stokastiska vektorer Johan Thim johanthim@liuse oktober 8 Repetition Definition Låt X och Y vara stokastiska variabler med EX = µ X, V X = σx, EY = µ Y samt V Y = σy Kovariansen CX, Y definieras
Föreläsning 7: Stokastiska vektorer Johan Thim johanthim@liuse oktober 8 Repetition Definition Låt X och Y vara stokastiska variabler med EX = µ X, V X = σx, EY = µ Y samt V Y = σy Kovariansen CX, Y definieras
SF1901: Sannolikhetslära och statistik
 SF1901: Sannolikhetslära och statistik Föreläsning 4. Väntevärde och varians, funktioner av s.v:er, flera stokastiska variabler. Jan Grandell & Timo Koski 10.09.2008 Jan Grandell & Timo Koski () Matematisk
SF1901: Sannolikhetslära och statistik Föreläsning 4. Väntevärde och varians, funktioner av s.v:er, flera stokastiska variabler. Jan Grandell & Timo Koski 10.09.2008 Jan Grandell & Timo Koski () Matematisk
Kurssammanfattning MVE055
 Obs: Detta är enbart tänkt som en översikt och innehåller långt ifrån allt som ingår i kursen (vilket anges exakt på hemsidan). Fullständiga antaganden i satser kan saknas och fel kan förekomma så kontrollera
Obs: Detta är enbart tänkt som en översikt och innehåller långt ifrån allt som ingår i kursen (vilket anges exakt på hemsidan). Fullständiga antaganden i satser kan saknas och fel kan förekomma så kontrollera
Kapitel 9 Egenskaper hos punktskattare
 Sannolikhetslära och inferens II Kapitel 9 Egenskaper hos punktskattare 1 Egenskaper hos punktskattare En skattare är en funktion av stickprovet och således en slumpvariabel. En bedömning av kvaliteten
Sannolikhetslära och inferens II Kapitel 9 Egenskaper hos punktskattare 1 Egenskaper hos punktskattare En skattare är en funktion av stickprovet och således en slumpvariabel. En bedömning av kvaliteten
Tentamen MVE300 Sannolikhet, statistik och risk
 Tentamen MVE300 Sannolikhet, statistik och risk 205-08-8 kl. 8.30-3.30 Examinator: Johan Jonasson, Matematiska vetenskaper, Chalmers Telefonvakt: Johan Jonasson, telefon: 0706-985223 03-7723546 Hjälpmedel:
Tentamen MVE300 Sannolikhet, statistik och risk 205-08-8 kl. 8.30-3.30 Examinator: Johan Jonasson, Matematiska vetenskaper, Chalmers Telefonvakt: Johan Jonasson, telefon: 0706-985223 03-7723546 Hjälpmedel:
Tentamen TEN1, HF1012, 29 maj Matematisk statistik Kurskod HF1012 Skrivtid: 14:00-18:00 Lärare och examinator : Armin Halilovic
 Tentamen TEN, HF, 9 maj 9 Matematisk statistik Kurskod HF Skrivtid: 4:-8: Lärare och examinator : Armin Halilovic Hjälmedel: Bifogat formelhäfte ("Formler och tabeller i statistik ") och miniräknare av
Tentamen TEN, HF, 9 maj 9 Matematisk statistik Kurskod HF Skrivtid: 4:-8: Lärare och examinator : Armin Halilovic Hjälmedel: Bifogat formelhäfte ("Formler och tabeller i statistik ") och miniräknare av
MS-A0509 Grundkurs i sannolikhetskalkyl och statistik Övning 3 Vecka 4, 19 23.1.2015
 MS-A0509 Grundkurs i sannolikhetskalkyl och statistik Övning 3 Vecka 4, 19 23.1.2015 Gripenberg I1. Vi antar att antalet telefonsamtal som kommer till ett servicenummer under en tidsperiod med längden
MS-A0509 Grundkurs i sannolikhetskalkyl och statistik Övning 3 Vecka 4, 19 23.1.2015 Gripenberg I1. Vi antar att antalet telefonsamtal som kommer till ett servicenummer under en tidsperiod med längden
Sannolikheten för att barnet skall få blodgrupp A0 A0 1/2 AA 1 AB 1/2 Övriga 0
 Avd. Matematisk statistik TENTAMEN I SF191, SANNOLIKHETSTEORI OCH STATISTIK, ONSDAGEN DEN 1:A JUNI 216 KL 8. 13.. Kursledare: Thomas Önskog, 8-79 84 55 Tillåtna hjälpmedel: Formel- och tabellsamling i
Avd. Matematisk statistik TENTAMEN I SF191, SANNOLIKHETSTEORI OCH STATISTIK, ONSDAGEN DEN 1:A JUNI 216 KL 8. 13.. Kursledare: Thomas Önskog, 8-79 84 55 Tillåtna hjälpmedel: Formel- och tabellsamling i
Avd. Matematisk statistik
 Avd. Matematisk statistik TENTAMEN I SF1913 MATEMATISK STATISTIK FÖR IT OCH ME ONSDAGEN DEN 12 JANUARI 2011 KL 14.00 19.00. Examinator: Camilla Landén, tel. 7908466. Tillåtna hjälpmedel: Formel- och tabellsamling
Avd. Matematisk statistik TENTAMEN I SF1913 MATEMATISK STATISTIK FÖR IT OCH ME ONSDAGEN DEN 12 JANUARI 2011 KL 14.00 19.00. Examinator: Camilla Landén, tel. 7908466. Tillåtna hjälpmedel: Formel- och tabellsamling
Laboration 4: Stora talens lag, Centrala gränsvärdessatsen och enkla punktskattningar
 LUNDS TEKNISKA HÖGSKOLA MATEMATIKCENTRUM MATEMATISK STATISTIK DATORLABORATION 4 MATEMATISK STATISTIK, AK FÖR I, FMS 120, HT-00 Laboration 4: Stora talens lag, Centrala gränsvärdessatsen och enkla punktskattningar
LUNDS TEKNISKA HÖGSKOLA MATEMATIKCENTRUM MATEMATISK STATISTIK DATORLABORATION 4 MATEMATISK STATISTIK, AK FÖR I, FMS 120, HT-00 Laboration 4: Stora talens lag, Centrala gränsvärdessatsen och enkla punktskattningar
TAMS79: Föreläsning 6. Normalfördelning
 TAMS79: Föreläsning 6 Normalfördelningen Johan Thim (johan.thim@liu.se 3 november 018 Normalfördelning Definition. Låt µ R och > 0. Om X är en stokastisk variabel med täthetsfunktion f X ( = 1 ( ep ( µ,
TAMS79: Föreläsning 6 Normalfördelningen Johan Thim (johan.thim@liu.se 3 november 018 Normalfördelning Definition. Låt µ R och > 0. Om X är en stokastisk variabel med täthetsfunktion f X ( = 1 ( ep ( µ,
Repetitionsföreläsning
 Slumpförsök Repetitionsföreläsning Föreläsning 15 Sannolikhet och Statistik 5 hp Med händelser A B... avses delmängder av ett utfallsrum. Slumpförsök = utfallsrummet + ett sannolikhetsmått P. Fredrik Jonsson
Slumpförsök Repetitionsföreläsning Föreläsning 15 Sannolikhet och Statistik 5 hp Med händelser A B... avses delmängder av ett utfallsrum. Slumpförsök = utfallsrummet + ett sannolikhetsmått P. Fredrik Jonsson
Exempel. Kontinuerliga stokastiska variabler. Integraler i stället för summor. Integraler i stället för summor
 Kontinuerliga stokastiska variabler Exempel En stokastisk variabel är kontinuerlig om den kan anta vilka värden som helst i ett intervall, men sannolikheten för varje enskilt utfall är noll: P(X = x) =.
Kontinuerliga stokastiska variabler Exempel En stokastisk variabel är kontinuerlig om den kan anta vilka värden som helst i ett intervall, men sannolikheten för varje enskilt utfall är noll: P(X = x) =.
SF1901: Sannolikhetslära och statistik
 SF1901: Sannolikhetslära och statistik Föreläsning 5. Kovarians, korrelation, väntevärde och varians för summor av s.v.:er, normalfördelning (del 1) Jan Grandell & Timo Koski 15.09.2008 Jan Grandell &
SF1901: Sannolikhetslära och statistik Föreläsning 5. Kovarians, korrelation, väntevärde och varians för summor av s.v.:er, normalfördelning (del 1) Jan Grandell & Timo Koski 15.09.2008 Jan Grandell &
Kapitel 5 Multivariata sannolikhetsfördelningar
 Sannolikhetslära och inferens II Kapitel 5 Multivariata sannolikhetsfördelningar 1 Multivariata sannolikhetsfördelningar En slumpvariabel som, när slumpförsöket utförs, antar exakt ett värde sägs vara
Sannolikhetslära och inferens II Kapitel 5 Multivariata sannolikhetsfördelningar 1 Multivariata sannolikhetsfördelningar En slumpvariabel som, när slumpförsöket utförs, antar exakt ett värde sägs vara
a) Beräkna sannolikheten att en följd avkodas fel, det vill säga en ursprungliga 1:a tolkas som en 0:a eller omvänt, i fallet N = 3.
 Avd. Matematisk statistik TENTAMEN I SF1901 SANNOLIKHETSTEORI OCH STATISTIK, TISDAGEN DEN 14:E MARS 017 KL 08.00 13.00. Examinator: Thomas Önskog, 08 790 84 55. Tillåtna hjälpmedel: Formel- och tabellsamling
Avd. Matematisk statistik TENTAMEN I SF1901 SANNOLIKHETSTEORI OCH STATISTIK, TISDAGEN DEN 14:E MARS 017 KL 08.00 13.00. Examinator: Thomas Önskog, 08 790 84 55. Tillåtna hjälpmedel: Formel- och tabellsamling
Kapitel 4. Kontinuerliga slumpvariabler och deras sannolikhetsfördelningar. Sannolikhetslära och inferens II
 Sannolikhetslära och inferens II Kapitel 4 Kontinuerliga slumpvariabler och deras sannolikhetsfördelningar 1 Kontinuerliga slumpvariabler En slumpvariabel som kan anta alla värden på något intervall sägs
Sannolikhetslära och inferens II Kapitel 4 Kontinuerliga slumpvariabler och deras sannolikhetsfördelningar 1 Kontinuerliga slumpvariabler En slumpvariabel som kan anta alla värden på något intervall sägs
Tentamen i matematisk statistik (9MA241/9MA341, STN2) kl 08-12
 LINKÖPINGS UNIVERSITET MAI Johan Thim Tentamen i matematisk statistik (9MA21/9MA31, STN2) 212-8-2 kl 8-12 Hjälpmedel är: miniräknare med tömda minnen och formelbladet bifogat. Varje uppgift är värd 6 poäng.
LINKÖPINGS UNIVERSITET MAI Johan Thim Tentamen i matematisk statistik (9MA21/9MA31, STN2) 212-8-2 kl 8-12 Hjälpmedel är: miniräknare med tömda minnen och formelbladet bifogat. Varje uppgift är värd 6 poäng.
Kunna definiera laplacetransformen för en kontinuerlig stokastisk variabel. Kunna definiera z-transformen för en diskret stokastisk variabel.
 Övning 2 Vad du ska kunna efter denna övning Kunna definiera laplacetransformen för en kontinuerlig stokastisk variabel. Kunna definiera z-transformen för en diskret stokastisk variabel. Kunna beräkna
Övning 2 Vad du ska kunna efter denna övning Kunna definiera laplacetransformen för en kontinuerlig stokastisk variabel. Kunna definiera z-transformen för en diskret stokastisk variabel. Kunna beräkna
TMS136. Föreläsning 4
 TMS136 Föreläsning 4 Kontinuerliga stokastiska variabler Kontinuerliga stokastiska variabler är stokastiska variabler som tar värden i intervall av den reella axeln Det kan handla om längder, temperaturer,
TMS136 Föreläsning 4 Kontinuerliga stokastiska variabler Kontinuerliga stokastiska variabler är stokastiska variabler som tar värden i intervall av den reella axeln Det kan handla om längder, temperaturer,
Del I. Uppgift 1 Låt A och B vara två oberoende händelser. Det gäller att P (A) = 0.4 och att P (B) = 0.3. Bestäm P (B A ). Svar:...
 Avd. Matematisk statistik EXEMPELTENTAMEN I SANNOLIKHETSTEORI OCH STATISTIK, Tillåtna hjälpmedel: Formel- och tabellsamling i Matematisk statistik (utdelas vid tentamen). Tentamen består av två delar,
Avd. Matematisk statistik EXEMPELTENTAMEN I SANNOLIKHETSTEORI OCH STATISTIK, Tillåtna hjälpmedel: Formel- och tabellsamling i Matematisk statistik (utdelas vid tentamen). Tentamen består av två delar,
SF1625 Envariabelanalys Tentamen Måndagen den 11 januari 2016
 SF625 Envariabelanalys Tentamen Måndagen den januari 206 Skrivtid: 08:00-3:00 Tillåtna hjälpmedel: inga Examinator: Lars Filipsson Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
SF625 Envariabelanalys Tentamen Måndagen den januari 206 Skrivtid: 08:00-3:00 Tillåtna hjälpmedel: inga Examinator: Lars Filipsson Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
Tentamen i Matematisk Statistik, 7.5 hp
 Tentamen i Matematisk Statistik, 7.5 hp Distanskurs 15 januari, 2011 kl. 9.00 13.00 Maxpoäng: 30p. Betygsgränser: 12p: betyg G, 21p: betyg VG. Hjälpmedel: Miniräknare samt formelsamling som medföljer tentamenstexten.
Tentamen i Matematisk Statistik, 7.5 hp Distanskurs 15 januari, 2011 kl. 9.00 13.00 Maxpoäng: 30p. Betygsgränser: 12p: betyg G, 21p: betyg VG. Hjälpmedel: Miniräknare samt formelsamling som medföljer tentamenstexten.
Statistisk analys av komplexa data
 Statistisk analys av komplexa data Trunkerade data och Tobitregression Bertil Wegmann Avdelning statistik, IDA, Linköpings universitet November 10, 2015 Bertil Wegmann (statistik, LiU) Trunkerade data
Statistisk analys av komplexa data Trunkerade data och Tobitregression Bertil Wegmann Avdelning statistik, IDA, Linköpings universitet November 10, 2015 Bertil Wegmann (statistik, LiU) Trunkerade data
Övning 1(a) Vad du ska kunna efter denna övning. Problem, nivå A. Redogöra för begreppen diskret och kontinuerlig stokastisk variabel.
 Övning 1(a) Vad du ska kunna efter denna övning Redogöra för begreppen diskret och kontinuerlig stokastisk variabel. Definiera fördelningsfunktionen för en stokastisk variabel. Definiera frekvensfunktionen
Övning 1(a) Vad du ska kunna efter denna övning Redogöra för begreppen diskret och kontinuerlig stokastisk variabel. Definiera fördelningsfunktionen för en stokastisk variabel. Definiera frekvensfunktionen
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF1625 Envariabelanalys Lösningsförslag till tentamen 215-1-27 DEL A 4 1. Betrakta funktionen f som ges av f(x) = 1 + x + (x 2). 2 A. Bestäm definitionsmängden till f. B. Bestäm alla intervall där f är
SF1625 Envariabelanalys Lösningsförslag till tentamen 215-1-27 DEL A 4 1. Betrakta funktionen f som ges av f(x) = 1 + x + (x 2). 2 A. Bestäm definitionsmängden till f. B. Bestäm alla intervall där f är
Stokastiska vektorer
 TNG006 F2 9-05-206 Stokastiska vektorer 2 Kovarians och korrelation Definition 2 Antag att de sv X och Y har väntevärde och standardavvikelse µ X och σ X resp µ Y och σ Y Då kallas för kovariansen mellan
TNG006 F2 9-05-206 Stokastiska vektorer 2 Kovarians och korrelation Definition 2 Antag att de sv X och Y har väntevärde och standardavvikelse µ X och σ X resp µ Y och σ Y Då kallas för kovariansen mellan
LINKÖPINGS UNIVERSITET EXAM TAMS 15 / TEN 1
 LINKÖPINGS UNIVERSITET Matematiska institutionen EXAM TAMS 5 / TEN januari 08, klockan 4.00-8.00 Examinator: Jörg-Uwe Löbus (Tel: 0709-6087) Tillåtna hjälpmedel är en räknare, formelsamling i matematisk
LINKÖPINGS UNIVERSITET Matematiska institutionen EXAM TAMS 5 / TEN januari 08, klockan 4.00-8.00 Examinator: Jörg-Uwe Löbus (Tel: 0709-6087) Tillåtna hjälpmedel är en räknare, formelsamling i matematisk
FÖRELÄSNING 8:
 FÖRELÄSNING 8: 016-05-17 LÄRANDEMÅL Konfidensintervall för väntevärdet då variansen är okänd T-fördelningen Goodness of fit-test χ -fördelningen Hypotestest Signifikansgrad Samla in data Sammanställ data
FÖRELÄSNING 8: 016-05-17 LÄRANDEMÅL Konfidensintervall för väntevärdet då variansen är okänd T-fördelningen Goodness of fit-test χ -fördelningen Hypotestest Signifikansgrad Samla in data Sammanställ data
Föreläsning 5, Matematisk statistik 7.5hp för E Linjärkombinationer
 Föreläsning 5, Matematisk statistik 7.5hp för E Linjärkombinationer Stas Volkov Stanislav Volkov s.volkov@maths.lth.se FMSF20 F5: linjärkombinationer 1/20 sum/max/min V.v./var Summa av två oberoende, Z
Föreläsning 5, Matematisk statistik 7.5hp för E Linjärkombinationer Stas Volkov Stanislav Volkov s.volkov@maths.lth.se FMSF20 F5: linjärkombinationer 1/20 sum/max/min V.v./var Summa av två oberoende, Z
1. För tiden mellan två besök gäller. V(X i ) = 1 λ 2 = 25. X i Exp (λ) E(X i ) = 1 λ = 5s λ = 1 5
 LÖSNINGAR TILL Matematisk statistik Tentamen: 29 7 kl 8 3 Matematikcentrum FMSF45 Matematisk statistik AK för D,I,Pi,F, 9 h Lunds universitet MASB3 Matematisk statistik AK för fysiker, 9 h. För tiden mellan
LÖSNINGAR TILL Matematisk statistik Tentamen: 29 7 kl 8 3 Matematikcentrum FMSF45 Matematisk statistik AK för D,I,Pi,F, 9 h Lunds universitet MASB3 Matematisk statistik AK för fysiker, 9 h. För tiden mellan
MS-A0509 Grundkurs i sannolikhetskalkyl och statistik Exempel, del I
 MS-A Grundkurs i sannolikhetskalkyl och statistik Exempel, del I G Gripenberg Aalto-universitetet januari G Gripenberg (Aalto-universitetet) MS-A Grundkurs i sannolikhetskalkyl och statistikexempel, del
MS-A Grundkurs i sannolikhetskalkyl och statistik Exempel, del I G Gripenberg Aalto-universitetet januari G Gripenberg (Aalto-universitetet) MS-A Grundkurs i sannolikhetskalkyl och statistikexempel, del
Matematisk statistik för B, K, N, BME och Kemister
 Matematisk statistik för B, K, N, BME och Kemister Föreläsning 3 Johan Lindström 4 september 7 Johan Lindström - johanl@maths.lth.se FMSF7/MASB F3 /3 fördelningsplot log- Johan Lindström - johanl@maths.lth.se
Matematisk statistik för B, K, N, BME och Kemister Föreläsning 3 Johan Lindström 4 september 7 Johan Lindström - johanl@maths.lth.se FMSF7/MASB F3 /3 fördelningsplot log- Johan Lindström - johanl@maths.lth.se
Diversitetsavstånd CDMA2000/450
 Diversitetsavstånd CDMA2000/450 Av: Carl Elofsson Per Ängskog Mats Nilsson Introduktion Inom skogsindustrin växer behovet av att kunna ha en snabb och säker datauppkoppling till de maskiner som arbetar
Diversitetsavstånd CDMA2000/450 Av: Carl Elofsson Per Ängskog Mats Nilsson Introduktion Inom skogsindustrin växer behovet av att kunna ha en snabb och säker datauppkoppling till de maskiner som arbetar
Avd. Matematisk statistik
 Avd. Matematisk statistik TENTAMEN I SF194 SANNOLIKHETSTEORI OCH STATISTIK, MÅNDAG 1 AUGUSTI 019 KL 8.00 13.00. Examinator: Björn-Olof Skytt, 08-790 86 49. Tillåtna hjälpmedel: Formel- och tabellsamling
Avd. Matematisk statistik TENTAMEN I SF194 SANNOLIKHETSTEORI OCH STATISTIK, MÅNDAG 1 AUGUSTI 019 KL 8.00 13.00. Examinator: Björn-Olof Skytt, 08-790 86 49. Tillåtna hjälpmedel: Formel- och tabellsamling
Demonstration av laboration 2, SF1901
 KTH 29 November 2017 Laboration 2 Målet med dagens föreläsning är att repetera några viktiga begrepp från kursen och illustrera dem med hjälp av MATLAB. Laboration 2 har följande delar Fördelningsfunktion
KTH 29 November 2017 Laboration 2 Målet med dagens föreläsning är att repetera några viktiga begrepp från kursen och illustrera dem med hjälp av MATLAB. Laboration 2 har följande delar Fördelningsfunktion
Stokastiska Processer F2 Föreläsning 1: Repetition från grundkursen
 Stokastiska Processer F2 Föreläsning 1: Repetition från grundkursen Denna föreläsning kommer mest att vara en repetition av stoff från grundkursen. Längden på detta dokument kan tyckas vara oproportionerligt
Stokastiska Processer F2 Föreläsning 1: Repetition från grundkursen Denna föreläsning kommer mest att vara en repetition av stoff från grundkursen. Längden på detta dokument kan tyckas vara oproportionerligt
Armin Halilovic: EXTRA ÖVNINGAR
 ABSOLUTBELOPP Några exempel som du har gjort i gymnasieskolan: a) = b) 0 =0 c) 5 = 5 Alltså x 0 et av ett tal x är lika med själva talet x om talet är positivt eller lika med 0 et av x är lika med det
ABSOLUTBELOPP Några exempel som du har gjort i gymnasieskolan: a) = b) 0 =0 c) 5 = 5 Alltså x 0 et av ett tal x är lika med själva talet x om talet är positivt eller lika med 0 et av x är lika med det
Avd. Matematisk statistik
 Avd. Matematisk statistik TENTAMEN I SF90/SF9 SANNOLIKHETSTEORI OCH STATISTIK, ONSDAG 5 JUNI 09 KL 4.00 9.00. Examinator: Björn-Olof Skytt, 08-790 86 49. Tillåtna hjälpmedel: Formel- och tabellsamling
Avd. Matematisk statistik TENTAMEN I SF90/SF9 SANNOLIKHETSTEORI OCH STATISTIK, ONSDAG 5 JUNI 09 KL 4.00 9.00. Examinator: Björn-Olof Skytt, 08-790 86 49. Tillåtna hjälpmedel: Formel- och tabellsamling
Avd. Matematisk statistik
 Avd. Matematisk statistik TENTAMEN I SF1922/SF1923/SF1924 SANNOLIKHETSTEORI OCH STATISTIK, TISDAG 28 MAJ 2019 KL 8.00 13.00. Examinator för SF1922/SF1923: Tatjana Pavlekno, 08-790 86 44. Examinator för
Avd. Matematisk statistik TENTAMEN I SF1922/SF1923/SF1924 SANNOLIKHETSTEORI OCH STATISTIK, TISDAG 28 MAJ 2019 KL 8.00 13.00. Examinator för SF1922/SF1923: Tatjana Pavlekno, 08-790 86 44. Examinator för
Finansiell Statistik (GN, 7,5 hp,, HT 2008) Föreläsning 3
 Finansiell Statistik (GN, 7,5 hp,, HT 2008) Föreläsning 3 Kontinuerliga sannolikhetsfördelningar (LLL Kap 7 & 9) Department of Statistics (Gebrenegus Ghilagaber, PhD, Associate Professor) Financial Statistics
Finansiell Statistik (GN, 7,5 hp,, HT 2008) Föreläsning 3 Kontinuerliga sannolikhetsfördelningar (LLL Kap 7 & 9) Department of Statistics (Gebrenegus Ghilagaber, PhD, Associate Professor) Financial Statistics
