Förord... sidan 2. Sena faser i lågmassiva stjärnors liv... sidan 3 Avståndet till Planetariska Nebulosor... sidan 4 Kattögenebulosan...
|
|
|
- Axel Vikström
- för 8 år sedan
- Visningar:
Transkript
1
2
3 Innehåll ESA/ESOs Övningsserie i Astronomi 3 Förord Förord... sidan 2 Introduktion Sena faser i lågmassiva stjärnors liv... sidan 3 Avståndet till Planetariska Nebulosor... sidan 4 Kattögenebulosan... sidan 5 Uppgifter Uppgift 1... sidan 7 Uppgift 2... sidan 7 Uppgift 3... sidan 7 Förstoringsmetoden... sidan 8 Uppgift 4... sidan 10 Uppgift 5... sidan 10 Uppgift 6... sidan 10 Uppgift 7... sidan 10 Uppgift 8... sidan 10 Radialpassningsmetoden... sidan 11 Uppgift 9... sidan 13 Uppgift sidan 13 Uppgift sidan 13 Innehåll Ytterligare Läsning Vetenskapliga artiklar... sidan 14 Lärarens Guide Lärarens Guide... sidan 16 1
4 Förord ESA/ESOs Övningsserie i Astronomi 3 Mätning av avståndet till Kattögenebulosan Astronomi är en lättillgänglig och visuell vetenskap, vilket gör den idealisk i undervisningssyfte. De senaste åren har NASA 1, ESA 2, Hubble Space Telescope och ESOs 3 teleskop på La Silla- och Paranalobservatorierna i Chile presenterat allt djupare och mer spektakulära bilder av universum. Hubble och ESOs teleskop har inte bara gett fantastiska bilder, de är även ovärderliga instrument för astronomer. Teleskopen har en mycket bra rums/vinkel-upplösning (bildskärpa), vilket ger astronomer möjlighet att blicka längre ut i universum än någonsin tidigare och låter dem svara på gamla, hittills obesvarade frågor. Att analysera sådana observationer, vilket ofta är ett sofistikerat och detaljerat arbete, är ibland tillräckligt enkelt för att gymnasiestudenter själva ska kunna utföra det. Denna serie av uppgifter är framtagen av den europeiska partnern i Hubbleprojektet, ESA (European Space Agency), som har 15% av observationstiden med Hubble, tillsammans med ESO (the European Southern Observatory). Förord Figur 1: NASA/ESAs Hubble Space Telescope NASA/ESAs Hubble Space Telescope har presenterat spektakulära vyer av universum från sin bana runt jorden. 2
5 Introduktion Sena faser i lätta stjärnors liv Kattögenebulosan (NGC 6543) är en så kallad planetarisk nebulosa. Trots sitt namn har planetariska nebulosor ingenting att göra med planeter. Termen introducerades under 1800-talet då dessa objekt mer såg ut som planeter genom dåtidens små teleskop. Planetariska nebulosor skapas under lätta stjärnors, som till exempel solens, dödsryckningar när stjärnan sakta kastar ut sina yttre lager. Figur 3: Albert Einstein Einsteins berömda ekvation E = Mc 2 visar relationen mellan massa and energi. Ljuset som strålas ut från de flesta stjärnor är en biprodukt av den termonukleära fusionsprocessen, känd som väteförbränning, där fyra vätekärnor bildar en heliumkärna. En sådan fusion kan endast ske i kärnan av en stjärna där gigantiska gravitationella krafter trycker upp temperaturen till runt 10 7 K. I dessa höga temperaturer finns där tillräckligt med energi för att överkomma de elektrostatiska repulsiva krafterna, som agerar mellan protoner vilka har samma laddning, så att fyra kärnor (protoner) kan sammansmälta och skapa en ny kärna, helium (se fig. 2) och därmed frigöra ännu mer energi. Massan av en heliumkärna är endast 99,3% av massan hos de fyra ursprungliga vätekärnorna. Fusionsprocessen konverterar de kvarvarande 0,7% till en viss mängd energi - mestadels ljus - som kan beräknas ur Einsteins berömda ekvation, E = Mc 2. Eftersom c 2 är ett stort nummer betyder det att även en liten mängd materia kan konverteras till en fantastisk mängd energi. Resten av massan på 0,7% involverad i en fusionsreaktion kan verka liten, men när man betraktar den totala mängden reaktioner är massan (och därför energin) som är involverad rejäl. Den utstrålade energin balancerar kraften från gravitationen och stjärnan förblir lugn i ett stabilt jämviktsläge i mer än 90% av sitt liv (solen kommer att stanna i sitt nuvarande stabila tillstånd i ytterligare 5 miljarder år). Introduktion Figur 2: Väteförbränning Den enklaste mekanismen för "tillverkning" av energi startar i fusionen av fyra vätekärnor till en heliumkärna. Processen har flera steg men här visas det samlade resultatet. När väteförådet i kärnan tar slut och väteförbränningen inte längre är möjlig komprimerar de gravitationella krafterna stjärnans kärna. Temperaturen i kärnan ökar då till 100 miljoner K och heliumkärnorna i kärnan börjar sammansmälta för att bilda tyngre ämnen som kol detta är processen heliumförbränning. Vid denna tiden sväller de yttre lagren av stjärnan för en stjärna med solens storlek skulle skalet i denna fasen nå ända ut till jordens nuvarande bana. Material från djupt inom den lätta stjärnan förs gång på gång upp till ytan under denna sena del av dess liv och berikar de yttre lagren med andra ämnen än väte under en process som kallas "dredge-up" (ungefär muddra upp). Lagren skickas slutligen ut i rymden, ibland som ett sfäriskt skal, men oftast i en asymmetrisk form, och bildar en kokong runt 3
6 Introduktion Figur 4: Sena faser i en lågmassiv stjärnas liv När en stjärna når sin sista fas i livet börjar den förbränna tyngre och tyngre grundämnen. Vid denna tid börjar stjärnan kasta ut stoft och gas och därigenom bilda en planetarisk nebulosa. Introduktion den döende stjärnan (se fig. 4). Det ultravioletta ljuset från den centrala kärnan av den döende stjärnan lyser upp det utsända materialet och framhäver strukturen i de spektakulära planetariska nebulosorna vi ser i våra teleskop. Planetariska nebulosor är väldigt kortlivade med astronomiska mått mätt. Åldern av flera välkända planetäriska nebulosor varav en är Kattögenebulosan (NGC 6543) är endast runt tusen år och de blir generellt inte mer än femtio tusen år. Efter detta tonar de bort och in i de interstellära mediet och berikar detta med tyngre grundämnen som blir tillgängligt för nästa generations stjärnor. Solen är en vanlig lågmassiv stjärna och den kommer troligvis att sluta sitt liv som en spektakulär planetarisk nebulosa. Jorden kommer inte att kunna uppehålla något liv när detta händer, men vi har ungefär 5000 miljoner år på oss innan detta blir vårt allvarligaste miljö-problem. Avstånd till Planetariska Nebulosor I denna uppgift ska vi mäta avståndet till Kattögenebulosan. Studierna av fysiska egenskaper som storleken, massan, ljusstyrkan och åldern av planetariska nebulosor är omöjliga utan korrekta avståndsmätningar till nebulosan. Faktiskt är astronomi i allmänhet beroende av avståndsmätningar. Det är inte lätt att mäta avståndet till planetariska nebulosor. Även om de formas från så kallade lågmassiva stjärnor kan begynnelsemassan variera så mycket som med en faktor 10, vilket ger de individuella planetariska nebulosorna väldigt olika egenskaper. Eftersom alla planetariska nebulosor inte har samma storlek eller ljusstyrka är det inte möjligt att använda sådana generaliseringar för att uppskatta deras avstånd. Emellanåt kan dock observationer göras som tillåter en direkt bestämning av avståndet till en planetarisk nebulosa. Så är fal-let med Kattögenebulosan. 4
7 Introduktion Kattögenebulosan Kattögenebulosan ligger i stjärnbilden Draco och är en av de mest komplexa planetariska nebulosor som någonsin setts. Bilder från Hubble avslöjar förvånansvärt komplexa strukturer som till exempel koncentriska skal av gas, höghastighetsjets av gas och ovanliga knutar av gas. Man tror att centralstjärnan faktiskt är en dubbelstjärna eftersom de dynamiska effekterna av två stjärnor som går i bana runt varandra enklast förklarar nebulosans ovanligt kom-plexa struktur. Analyser av olika delar av nebulosan, som visas i fig. 6, har gjorts flera gånger tidigare. Det är känt att flera av de mest framträdande särdragen har en annan ålder än den centrala delen av nebulosan. Mätningarna som vi ska göra i denna övning kommer inte att fokusera på dessa särdrag utan på lillaxeln på ellipsoiden som kallas E25. Introduktion Figur 5: Kattögenebulosan. Denna färgbild av Kattögenebulosan, NGC 6543, tagen med Hubbles Wide Field and Planetary Camera 2 är en sammansättning av tre bilder tagna med olika våglängd. Joniserat kväve (658,4 nm) visas som rött, dubbelt joniserat syre (500,7 nm) visas som grönt och neutralt syre (630,0 nm) visas som blått. Bildens skala är indikerad. Delen som kallas E25 är ellipsoiden närmast centralstjärnan. 5
8 Introduktion Introduktion Figur 6: Geometrisk 3D-modell av Kattögenebulosan Den allmänna bipolära strukturen hos nebulosan är illustrerad här. Den inre ellipsoiden, som kallas E25, är markerad med gult. Anpassad från Reed et al. (1999). 6
9 Uppgifter I de följande två uppgifterna är t den förflutna tiden mellan två observationer. Uppgift 1 Finn en relation mellan vinkelförflyttningen, a, tiden, t, och vinkelhastigheten av förflyttningen, ω. Vinkelhastigheten mäts i enheter av vinkel per tidsenhet. Det är viktigt att denna vinkel mäts i radianer. Uppgift 2 Finn en relation mellan den linjära förflyttningen, l, tiden, t, och hastigheten i den linjära förflyttningens riktning, v t. Denna hastighet kallas tangentialhastighet. Tangentialhastigheten mäts i km/s. Uppgift 3 av olika särdrag i denna relativt avlägsna nebulosa inom synliga våglängder. Detta gör en detaljerad beskrivning av nebulosan möjlig. Att mäta expansionparallaxen längs lillaxeln på E25 motsvarar en bestämning av vinkelhastigheten, ω, vinkelrät mot synriktningen. Lite mer information behövs för att beräkna avståndet till nebulosan: den tangentiella hastigheten längs lillaxeln på E25. Turligt nog har denna hastighet erhållits av en grupp astronomer (Miranda & Solf, 1992), vilka kombinerade spektroskopiska metoder 1 med en kinetisk modell av nebulosans expansion. Gruppens slutsats var att den tangentiala hastigheten längs E25s lillaxel är 16,4 km/s, vilket motsvarar ungefär km/h. När den tangentiala hastigheten är given behöver vi bara bestämma vinkelhastigheten. Du kommer använda två olika metoder, förstorings metoden och radialpassningsmetoden, för att göra detta. Uppgifter Med hjälp av approximationen för små vinklar, som finns i Matematiska Verktyg, finner vi relationen mellan avståndet, D, den linjära förflyttningen, l, och vinkelförflyttningen, a. D = l/a Använd denna ekvation för att finna relationen mellan avståndet, D, tangentielhastigheten, v t, och vinkelhastigheten ω. Kattögenebulosan avbildades två gånger av Hubble, först den 18:e september 1994 och sen igen den 17:e augusti Om de två bilderna visas på en dator omväxlande i snabb takt (en teknik som kallas "blinkning") är det möjligt att se att Kattögenebulosan har expanderat under intervallet mellan de två bilderna. Denna vinkelexpansion är inte tillräckligt stor för att man ska kunna se den endast genom att titta på två papperskopior av bilderna men det är fortfarande möjligt att bestämma expansionen i enheter av vinkel per tidsenhet vilket du kommer se själv om en stund. Användningen a av denna effekt, känd som expansionsparallax, är inte så ovanlig i astronomi. Den är oftare använd på bilder tagna med radioteleskop men här gör Hubbles höga upplösning det möjligt att bestämma expansionsparallaxen b 1 Spektroskopiska mätningar delar in ljus i dess olika färger (till exempel med ett prisma). Ljuset kan sedan bli undersökt för att finna olika dopplerskift skapade av källans rörelse och den motsvarande radialhastigheten (mot eller bort från oss) kan härledas. I detta fall har kunskapen om radialhastigheten kombinerats med en modell av den övergripande expansionsrörelsen (åt alla håll) för att härleda den tangentiella hastigheten. 7
10 Uppgifter Förstoringsmetoden Storleken av expansionen på Hubbles bilder är mindre än en pixel (bildelement) så dessa mätningar kräver en ganska sofistikerad teknik. Förstoringsmetoden tar bilden från 1994 och förstorar den tills den precis passar med bilden från Fig. 7 visar subtraktionsmetoden. Notera att bilden från 1994 inte är förstorad. I varje bild av de nio i fig. 8 har bilden från 1994 förstorats med olika faktorer, F, (detta är siffran i övre högra hörnet på de nio små bilderna) och bilden från 1997 subtraheras från den förstorade bilden från där t är den förflutna tiden mellan de två bilderna och d är avståndet i radianer från centralstjärnan i nebulosan till delen vi vill mäta på (i detta fallet E25s lillaxel). ω är mätt i radianer per tidsenhet. Följande uppgifter tar dig igenom beräkningar av de olika parametrarna i detta uttryck. Efteråt kommer du kunna beräkna ω och sedan avståndet till Kattögenebulosan. Uppgifter Ju mer lika bilderna är, desto mindre struktur kommer att dyka upp i den resulterande bilden. Vi ska leta efter den jämnaste bilden och förstoringsfaktorn i hörnet på bilden är den som beskriver expansionen av Kattögenebulosan från 1994 till Notera att eftersom expansionsparallaxen inte är densamma för alla delar ska vi leta efter den bild där "vår" del E25s lillaxel försvinner. När förstoringsfaktorn är bestämd kan ω beräknas från detta uttryck Figur 7: För att belysa expansionen behövs en speciell bildbehandling Den första bilden (fig. 7a) togs 1994, den andra (fig. 7b) togs Endast en örnögd observatör skulle kunna se någon skillnad mellan de två bilderna utan en dator. Bildbehandlingen subtraherar en bild från den andra. Den sista bilden kallas den resulterande bilden (fig. 7c). 8
11 Uppgifter Uppgifter Figur 8: De nio resulterande bilderna Dessa bilder är resultatet av förstoringar av bilden från 1994 och sen en subtraktion av bilden från Förstoringsfaktorn, F, är indikerad i varje bild (från Reed et al.,1999). 9
12 Uppgifter Uppgift 4 Bestäm i vilken av de nio bilderna i fig. 8 som E25s lillaxel försvinner. Du kan bestämma att två bilder är lika bra och ta ett medelvärde på förstoringfaktorerna. Uppgift 5 Beräkna tiden mellan datumen som de två bilderna togs och konvertera tiden till sekunder. Varför spelar det ingen roll att du inte vet den exakta tiden på dagen som bilderna togs Uppgifter Uppgift 6 Hitta E25s lillaxel i fig. 5. Mät avståndet, d, från centralstjärnan i nebulosan till E25s lillaxel i enheter av millibågsekunder. Gör om detta avstånd till radianer med hjälp av konverteringsfaktorn som ges i Matematiska Verktyg. Uppgift 7 Nu har du allt du behöver för att beräkna expansionsparallaxen, ω, med hjälp av förstoringsmetoden. Uppgift 8 Som tidigare nämnts har tangentialhastigheten, v t, hos E25s lillaxel redan uppmätts av en grupp astronomer till 16,4 km/s. Beräkna avståndet till Kattögenebulosan. Innan du kan jämföra dina resultat med de från Reed et al. ska du beräkna avståndet med hjälp av radialpassningsmetoden. 10
13 Uppgifter Radialpassningsmetoden Om vi mäter pixelvärdet på de pixlar som ligger på en linje genom centralstjärnan i fig. 5 får vi en kurva som i fig. 9. Topparna och dalarna motsvarar ljusa och mörka områden längs linjen och visar intensiteten på ljuset som kommer från olika ryggar och knutar i nebulosan. Skillnaden mellan kurvorna gjorda från de två bilderna från 1994 och 1997 kan användas till att mäta nebulosans expansion. Oturligt nog är skillnaden mellan särdragen i de två bilderna så liten (mindre än en pixel) att vi inte enkelt kan repetera denna mätning här. Du måste lita på de olika mätningarna av ω från vetenskapsmännen och använda detta för att bestämma avståndet till Kattögenebulosan igen. Vetenskapsmännen mätte ω på flera olika platser i E25 (och också på flera andra punkter i nebulosan). Dessa mätningar är indikerade i fig. 10. Mätningarna är gjorda i millibågsekunder/år och de måste konverteras till rätt enheter. Uppgifter Figur 9: Intensitetsprofiler Två exempel på hur intensitetsmätningar längs en linje genom nebulosan ser ut på bilderna från 1994 respektive Linjen vi använt här är den vid klockan 12 i fig
14 Uppgifter Uppgifter Figur 10: ω och Radiala Intensitetsprofiler De resulterande ω från försiktigt passade radiala profiler längs linjerna visade i figuren. ω är mätt i millibågsekunder/år (från Reed et al., 1999). 12
15 Uppgifter Uppgift 9 Identifiera E25s lillaxel i fig. 10. Avläs ω vid rätt "diamanter" var noggrann så du matchar rätt siffra till rätt "diamant"! Ta ett medel på de ω som du hittar i figuren och beräkna avståndet till Kattögenebulosan som innan. Uppgift 10 Den kinematiska åldern (den tid som passerat sedan expansionen av nebulosan startade), T, av den inre kärnan av nebulosan kan härledas från de tidigare beräknade värdena (om man antar att expansionshastigheten är konstant): T = d/ω Värdet på d fick du i uppgift 6. Beräkna den kinematiska åldern, T, för båda värdena av ω som du fått fram. Uppgift 11 Resultatet från Reed et al. på avståndet till Kattögenebulosan är parsec. Detta resultat togs fram inte bara med hjälp av E25 utan också a) genom att mäta andra strukturer med förstoringsmetoden, b) genom att använda alla olika "diamanterna" i radialpassningsmetoden och slutligen c) genom att använda en tredje metod som kallas profilmetoden. Jämför dina resultat med Reed et al's. Fundera över var du har kunnat påverka resultaten genom de val du gjort. Gör om beräkningarna med en aning varierade parametrar. Du kan till exempel använda en annan resulterande bild i förstoringmetoden eller välja andra diamanter i radialpassningsmetoden. Gör små ändringar i parametrarna och du kommer troligen att se stora skillnader i resultaten. Denna övning visar både svårigheten i att få noggranna mätningar på avstånd och styrkan i de astronomiska verktygen. Uppgifter 13
16 Ytterligare läsning Vetenskapliga artiklar Reed, Darren S., Balick, B., Hajian, Arsen R., Klayton, Tracy L., Giovanardi, S., Casertano, S., Panagia, N., Terzian, Y. 1999, AJ, 118, : Hubble Space Telescope Measurements of the Expansion of NGC 6543: Parallax Distance and Nebular Evolution Miranda, L.F., Solf, J. 1992, A&A, 260, : Long-slit spectroscopy of the planetary nebula NGC Collimated bipolar ejections from a precessing central source Se också länkar på: Ytterligare läsning 14
17 Kolofon EUROPEAN SOUTHERN OBSERVATORY Education and Public Relations Service ESA/ESOs övningsserie i astronomi Övning 3: Mätning av avståndet till Kattögenebulosan 2 a upplagan ( ) Producerad av: Hubble European Space Agency Information Centre och European Southern Observatory: (Pdf-versioner av detta material och relaterade internetlänkar finns på denna adress) Postadress: European Southern Observatory Karl-Schwarzschild-Str. 2 D Garching bei München Tyskland Colophon Telefon: (eller ) Fax: (eller ) info@astroex.org Text av: Anne Værnholt Olesen, Lars Lindberg Christensen, Jean-Marc Brauer, och Arntraud Bacher Grafik och layout: Martin Kornmesser Översättning: Martin Lundqvist Svensk Korrekturläsning: Britt Sjöberg Koordination: Lars Lindberg Christensen och Richard West Varma tack till Darren Reed och Arsen Hajian för tillförsel av data, och till Nina Troelsgaard Jensen, Frederiksberg Seminarium, för kommentarer. 15
18 Lärarens Guide Kort Summering Vi mäter Kattögenebulosans expansions vinkelhastighet genom en omsorgsfull undersökning av två bilder från Hubble tagna 1994 och Med hjälp av mätningar av den tangentiella hastigheten från en tidig vetenskaplig artikel är det möjligt att bestämma avståndet till nebulosan. Vi härleder också avståndet genom att se hur mycket radiala intensitetsprofiler av framträdande drag i de två bilderna ändras från 1994 till I denna övning gör studenterna färre mätningar än i övning 1 och 2 men blir introducerade till två olika metoder en "traditionell" och en "mindre traditionell" för beräkningar av avstånd till astro-nomiska objekt. I den ursprungliga artikeln använder astronomerna tre olika metoder men den tredje kräver mycket avancerade datorprogram och det är inte möjligt att här upprepa denna beräkning/mätning. Uppgift 1 och 2 Lärarens Guide Genom att använda ekvationen "avstånd = hastighet tid" finner vi: a = ω t l = v t t Uppgift 3 Genom att använda figur 6 i Matematiska Verktyg med b = l och c = D får vi: D = l / a = v t /ω Uttrycket för ω: d är vinkelavståndet till delen i bilden från F är förstoringsfaktorn. F d är vinkelavståndet till delen i bilden från 1997 så (F-1)d är skillnaden i vinkel mellan bilden från 1994 och bilden från Dividera med den förflutna tiden för att få vinkelhastigheten. Uppgift 4 Den bästa förstoringfaktorn är 1,00275 som är medeltalet av 1,0025 och 1,0030. F = 1,00275 ger det resultat som är närmast det i den vetenskapliga artikeln. Uppgift 5 Tiden som förflutit mellan den 18:e september 1994 till den 17:e augusti 1997 (datumen finns på sidan 7) kan enkelt beräknas. Notera att 1996 är ett skottår. t = 3 år + 1 dag 32 dagar = 1064 dagar = 9, s Med fyra signifikanta siffror gör en dag mer eller mindre ingen urskiljbar skillnad. Uppgift 6 Från en utskriven bild med storleken 149 x 146 mm fås: 44 mm motsvarar 10 bågsekunder så 1 bågsekund är 4,4 mm En direkt mätning av avståndet från centralstjärnan till E25s lillaxel ger: 17,5 mm motsvarar d = 3,98 bågsekunder = 1, radianer (genom att använda konverteringsfaktorn given i rutan i Matematiska Verktyg). 16
19 Lärarens Guide Uppgift 7 Beräkning av ω med hjälp av förstoringsmetoden: ω = (F-1) d/t = (1, ) 1, /(9, ) = 5, radianer/s Uppgift 8 Alltså blir avståndet: D = v t /ω = 16,4/(5, ) = 2, km = 922 pc Uppgift 9 Beräkning av ω och avståndet D till Kattögenebulosan med hjälp av radialpassningsmetoden. Tyvärr så finns det en viss frihet i valet av punkter här - och därför möjligheter att skjuta resultatet i önskad riktning. Ett medel över 12 mätpunkter (i toppen och botten av ellipsoiden) ger: topp 3,55 3,09 3,23 3,94 4,15 2,71 botten 2,82 3,45 6,06 2,67 3,40 3,45 ω _ genomsnitt (mas/år) 3,54 Lärarens Guide ω _ genomsnitt (rad/s)),45 x D (km),01 x D (parsec) 976 ω = 3,54 mas/år = 3, , / ( ) radianer/s = 5, radianer/s Uppgift 10 T = d/ω = (1, )/(5, ) = 3, s = 1060 år Med värdet på ω från radialpassningmetoden: T = 3, s = 1123 år Uppgift 11 Reed et al s resultat är D = 1001 ± 269 pc, T = 1039 ± 259 år. Notera att båda metoderna lämnar ganska mycket utrymme för omedvetna justeringar. Det kan vara en bra idé att låta studenterna utföra en mer formell max/min-analys. Även om det är många beslut som ska tas under mätningarna och beräkningarna är det fortfarande inte möjligt att få helt orimliga resultat. 17
20
Universums tidskalor - från stjärnor till galaxer
 Universums tidskalor - från stjärnor till galaxer Fysik och Kemidagarna 2017 Prof. Peter Johansson Institutionen för Fysik, Helsingfors Universitet Matematisk-naturvetenskapliga fakulteten/ Peter Johansson/
Universums tidskalor - från stjärnor till galaxer Fysik och Kemidagarna 2017 Prof. Peter Johansson Institutionen för Fysik, Helsingfors Universitet Matematisk-naturvetenskapliga fakulteten/ Peter Johansson/
Uppgifter. Uppgifter. Uppgift 2. Uppgift 1
 Uppgift 1 Uppgift 2 Det första målet är att beräkna vinkeldiametern på ringen, det vill säga ringens apparenta diameter sedd från jorden i bågsekunder. Detta är vinkel a. De relativa positionerna för stjärnorna
Uppgift 1 Uppgift 2 Det första målet är att beräkna vinkeldiametern på ringen, det vill säga ringens apparenta diameter sedd från jorden i bågsekunder. Detta är vinkel a. De relativa positionerna för stjärnorna
Vilken av dessa nivåer i väte har lägst energi?
 Vilken av dessa nivåer i väte har lägst energi? A. n = 10 B. n = 2 C. n = 1 ⱱ Varför sänds ljus av vissa färger ut från upphettad natriumånga? A. Det beror på att ångan är mättad. B. Det beror på att bara
Vilken av dessa nivåer i väte har lägst energi? A. n = 10 B. n = 2 C. n = 1 ⱱ Varför sänds ljus av vissa färger ut från upphettad natriumånga? A. Det beror på att ångan är mättad. B. Det beror på att bara
Förord... Sidan 2. Supernovor... Sidan 3 Supernova 1987A... Sidan 4 Avståndet till Stora Magellanska Molnet... Sidan 4 Ringen...
 Innehåll ESA/ESOs Övningsserie i Astronomi 1 Förord Förord... Sidan 2 Introduktion Supernovor... Sidan 3 Supernova 1987A... Sidan 4 Avståndet till Stora Magellanska Molnet... Sidan 4 Ringen... Sidan 5
Innehåll ESA/ESOs Övningsserie i Astronomi 1 Förord Förord... Sidan 2 Introduktion Supernovor... Sidan 3 Supernova 1987A... Sidan 4 Avståndet till Stora Magellanska Molnet... Sidan 4 Ringen... Sidan 5
Introduktion. Stjärnor bildas, producerar energi, upphör producera energi = stjärnor föds, lever och dör.
 Stjärnors födelse Introduktion Stjärnor består av gas i jämvikt: Balans mellan gravitation och tryck (skapat av mikroskopisk rörelse). Olika källor till tryck i olika utvecklingsskeden. Stjärnor bildas,
Stjärnors födelse Introduktion Stjärnor består av gas i jämvikt: Balans mellan gravitation och tryck (skapat av mikroskopisk rörelse). Olika källor till tryck i olika utvecklingsskeden. Stjärnor bildas,
Solens energi alstras genom fusionsreaktioner
 Solen Lektion 7 Solens energi alstras genom fusionsreaktioner i dess inre När solen skickar ut ljus förlorar den också energi. Det måste finnas en mekanism som alstrar denna energi annars skulle solen
Solen Lektion 7 Solens energi alstras genom fusionsreaktioner i dess inre När solen skickar ut ljus förlorar den också energi. Det måste finnas en mekanism som alstrar denna energi annars skulle solen
Universums expansion och storskaliga struktur Ulf Torkelsson
 1 Hubbles lag Föreläsning 13/5 Universums expansion och storskaliga struktur Ulf Torkelsson Den amerikanske astronomen Vesto M. Slipher upptäckte redan på 1910-talet att ljuset från praktiskt taget alla
1 Hubbles lag Föreläsning 13/5 Universums expansion och storskaliga struktur Ulf Torkelsson Den amerikanske astronomen Vesto M. Slipher upptäckte redan på 1910-talet att ljuset från praktiskt taget alla
Stjärnors död samt neutronstjärnor. Planetära nebulosan NGC (New General Catalogue) Kattöganebulosan
 Stjärnors död samt neutronstjärnor Planetära nebulosan NGC (New General Catalogue) 65 43 Kattöganebulosan Introduktion En stjärna lever huvuddelen av sitt liv i huvudserien. Förutsättningen för detta är
Stjärnors död samt neutronstjärnor Planetära nebulosan NGC (New General Catalogue) 65 43 Kattöganebulosan Introduktion En stjärna lever huvuddelen av sitt liv i huvudserien. Förutsättningen för detta är
Orienteringskurs i astronomi Föreläsning 1, Bengt Edvardsson
 Orienteringskurs i astronomi Föreläsning 1, 2014-09-01 Bengt Edvardsson Innehåll: Korta frågor och svar Anteckningarna är en hjälp vid läsningen av boken men definierar inte kursen. Första föreläsningen
Orienteringskurs i astronomi Föreläsning 1, 2014-09-01 Bengt Edvardsson Innehåll: Korta frågor och svar Anteckningarna är en hjälp vid läsningen av boken men definierar inte kursen. Första föreläsningen
Dramatik i stjärnornas barnkammare av Magnus Gålfalk (text och bild)
 AKTUELL FORSKNING Dramatik i stjärnornas barnkammare av Magnus Gålfalk (text och bild) Där stjärnor föds, djupt inne i mörka stoftmoln, händer det märkliga och vackra saker. Med hjälp av ett teleskop och
AKTUELL FORSKNING Dramatik i stjärnornas barnkammare av Magnus Gålfalk (text och bild) Där stjärnor föds, djupt inne i mörka stoftmoln, händer det märkliga och vackra saker. Med hjälp av ett teleskop och
Varje uppgift ger maximalt 3 poäng. För godkänt krävs minst 8,5 poäng och
 Institutionen för Fysik Göteborgs Universitet LÖSNINGAR TILL TENTAMEN I FYSIK A: MODERN FYSIK MED ASTROFYSIK Tid: Lördag 3 augusti 008, kl 8 30 13 30 Plats: V Examinator: Ulf Torkelsson, tel. 031-77 3136
Institutionen för Fysik Göteborgs Universitet LÖSNINGAR TILL TENTAMEN I FYSIK A: MODERN FYSIK MED ASTROFYSIK Tid: Lördag 3 augusti 008, kl 8 30 13 30 Plats: V Examinator: Ulf Torkelsson, tel. 031-77 3136
Edwin Hubbles stora upptäckt 1929
 Edwin Hubbles stora upptäckt 1929 Edwin Hubble Edwin Hubbles observationer av avlägsna galaxer från 1929. Moderna observationer av avlägsna galaxer. Bild: Riess, Press and Kirshner (1996) Galaxerna rör
Edwin Hubbles stora upptäckt 1929 Edwin Hubble Edwin Hubbles observationer av avlägsna galaxer från 1929. Moderna observationer av avlägsna galaxer. Bild: Riess, Press and Kirshner (1996) Galaxerna rör
Kosmologi. Ulf Torkelsson Teoretisk fysik CTH/GU
 Kosmologi Ulf Torkelsson Teoretisk fysik CTH/GU Program Universums expansion, observationer Universums expansion, teori Universums geometri Universums expansion och sammansättning Exotisk materia Andromedagalaxen
Kosmologi Ulf Torkelsson Teoretisk fysik CTH/GU Program Universums expansion, observationer Universums expansion, teori Universums geometri Universums expansion och sammansättning Exotisk materia Andromedagalaxen
Astronomi. Vetenskapen om himlakropparna och universum
 Astronomi Vetenskapen om himlakropparna och universum Solsystemet Vi lever på planeten jorden (Tellus) och rör sig i en omloppsbana runt en stjärna som vi kallar solen. Vårt solsystem består av solen och
Astronomi Vetenskapen om himlakropparna och universum Solsystemet Vi lever på planeten jorden (Tellus) och rör sig i en omloppsbana runt en stjärna som vi kallar solen. Vårt solsystem består av solen och
Från Big Bang till universums acceleration
 Från Big Bang till universums acceleration Rahman Amanullah Forskare vid Oskar Klein Center, Stockholms universitet http://okc.albanova.se/blog/ Hur vet vi att det vi vet är sant? Lånad av Per-Olof Hulth
Från Big Bang till universums acceleration Rahman Amanullah Forskare vid Oskar Klein Center, Stockholms universitet http://okc.albanova.se/blog/ Hur vet vi att det vi vet är sant? Lånad av Per-Olof Hulth
Innehåll. Innehåll. Verktyg. Astronomiska Verktyg. Matematiska Verktyg
 Innehåll Verktyg Magnituder... sidan 2 Apparent magnitud... sidan 2 Absolut magnitud... sidan 3 Olika färger, olika magnituder... sidan 3 Från B-V färgindex till temperatur... sidan 4 Avståndsekvationen...
Innehåll Verktyg Magnituder... sidan 2 Apparent magnitud... sidan 2 Absolut magnitud... sidan 3 Olika färger, olika magnituder... sidan 3 Från B-V färgindex till temperatur... sidan 4 Avståndsekvationen...
Kosmologi. Universums utveckling. MN Institutionen för astronomi. Av rättighetsskäl är de flesta bilder från Wikipedia, om inte annat anges
 Kosmologi Universums utveckling MN Institutionen för astronomi Av rättighetsskäl är de flesta bilder från Wikipedia, om inte annat anges Upplägg Inledning vad ser vi på himlen? Galaxer och galaxhopar Metoder
Kosmologi Universums utveckling MN Institutionen för astronomi Av rättighetsskäl är de flesta bilder från Wikipedia, om inte annat anges Upplägg Inledning vad ser vi på himlen? Galaxer och galaxhopar Metoder
En rundvandring i rymden
 En rundvandring i rymden Solen Vår närmsta och därmed bäst studerade stjärna. Solytan är ca 5700 grader varm, men den tunna gasen som omger solen (koronan) är över en miljon grader. Ett av världens bästa
En rundvandring i rymden Solen Vår närmsta och därmed bäst studerade stjärna. Solytan är ca 5700 grader varm, men den tunna gasen som omger solen (koronan) är över en miljon grader. Ett av världens bästa
Relativitetsteorins grunder, våren 2016 Räkneövning 6 Lösningar
 elativitetsteorins grunder, våren 2016 äkneövning 6 Lösningar 1. Gör en Newtonsk beräkning av den kritiska densiteten i vårt universum. Tänk dig en stor sfär som innehåller många galaxer med den sammanlagda
elativitetsteorins grunder, våren 2016 äkneövning 6 Lösningar 1. Gör en Newtonsk beräkning av den kritiska densiteten i vårt universum. Tänk dig en stor sfär som innehåller många galaxer med den sammanlagda
Från nebulosor till svarta hål stjärnors födelse, liv och död
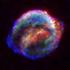 Från nebulosor till svarta hål stjärnors födelse, liv och död Stjärnor Stjärnor är enorma glödande gasklot. Vår sol är en typisk stjärna. Dess diameter är 1 400 000 km och dess massa är 2. 10 30 kg. Temperaturen
Från nebulosor till svarta hål stjärnors födelse, liv och död Stjärnor Stjärnor är enorma glödande gasklot. Vår sol är en typisk stjärna. Dess diameter är 1 400 000 km och dess massa är 2. 10 30 kg. Temperaturen
Kosmologi - läran om det allra största:
 Kosmologi - läran om det allra största: Dikter om kosmos kunna endast vara viskningar. Det är icke nödvändigt att bedja, man blickar på stjärnorna och har känslan av att vilja sjunka till marken i ordlös
Kosmologi - läran om det allra största: Dikter om kosmos kunna endast vara viskningar. Det är icke nödvändigt att bedja, man blickar på stjärnorna och har känslan av att vilja sjunka till marken i ordlös
Fenomenala rymdbilder - en utställning i Kungsträdgården
 Fenomenala rymdbilder - en utställning i Kungsträdgården Rymdstyrelsen, som är en myndighet under Utbildningsdepartemenet, har i samarbete med Stockholms stad producerat utställningen Fenomenala rymdbilder
Fenomenala rymdbilder - en utställning i Kungsträdgården Rymdstyrelsen, som är en myndighet under Utbildningsdepartemenet, har i samarbete med Stockholms stad producerat utställningen Fenomenala rymdbilder
1755: Immanuel Kant, The Universal Natural History and Theories of the Heavens.
 Galaxer 1750: Thomas Wright (1711-1786) föreslår i An original theory or new hypothesis of the universe att vår egen galax, Vintergatan är en gigantisk roterande skiva av stjärnor, planeter, nebulosor,
Galaxer 1750: Thomas Wright (1711-1786) föreslår i An original theory or new hypothesis of the universe att vår egen galax, Vintergatan är en gigantisk roterande skiva av stjärnor, planeter, nebulosor,
Översiktskurs i astronomi Lektion 7: Solens och stjärnornas energiproduktion samt utveckling
 Översiktskurs i astronomi Lektion 7: Solens och stjärnornas energiproduktion samt utveckling Upplägg Energiprocesser i stjärnor Energitransport i stjärnor Solens uppbyggnad Solfläckar Solliknande stjärnors
Översiktskurs i astronomi Lektion 7: Solens och stjärnornas energiproduktion samt utveckling Upplägg Energiprocesser i stjärnor Energitransport i stjärnor Solens uppbyggnad Solfläckar Solliknande stjärnors
Astronomin och sökandet efter liv där ute. Sofia Feltzing Professor vid Lunds universitet
 Astronomin och sökandet efter liv där ute Sofia Feltzing Professor vid Lunds universitet Sofia Feltzings vanliga forskning 250 miljoner år Drakes ekvation!"#"$" "%"!"#$%& "&"'()*" "%""+," "%"+$&%""+-%$&."+,"
Astronomin och sökandet efter liv där ute Sofia Feltzing Professor vid Lunds universitet Sofia Feltzings vanliga forskning 250 miljoner år Drakes ekvation!"#"$" "%"!"#$%& "&"'()*" "%""+," "%"+$&%""+-%$&."+,"
LÖSNING TILL TENTAMEN I STJÄRNORNA OCH VINTERGATAN, ASF010
 Teoretisk fysik och mekanik Institutionen för Fysik och teknisk fysik Chalmers &Göteborgs Universitet LÖSNING TILL TENTAMEN I STJÄRNORNA OCH VINTERGATAN, ASF010 Tid: 25 augusti 2010, kl 8 30 13 30 Plats:
Teoretisk fysik och mekanik Institutionen för Fysik och teknisk fysik Chalmers &Göteborgs Universitet LÖSNING TILL TENTAMEN I STJÄRNORNA OCH VINTERGATAN, ASF010 Tid: 25 augusti 2010, kl 8 30 13 30 Plats:
Innehåll. Innehåll. ESA/ESOs Övningsserie i Astronomi 4. Förord. Introduktion. Uppgifter. Extrauppgifter. Ytterligare Läsning.
 Innehåll ESA/ESOs Övningsserie i Astronomi 4 Förord Förord... sidan 2 Introduktion Stjärnor... sidan 3 Väteförbränning... sidan 3 Stjärnhopar... sidan 3 Klotformiga stjärnhopar... sidan 3 Den klotformiga
Innehåll ESA/ESOs Övningsserie i Astronomi 4 Förord Förord... sidan 2 Introduktion Stjärnor... sidan 3 Väteförbränning... sidan 3 Stjärnhopar... sidan 3 Klotformiga stjärnhopar... sidan 3 Den klotformiga
Till exempel om vi tar den första kol atomen, så har den: 6 protoner, 12 6=6 neutroner, 6 elektroner; atommassan är också 6 men masstalet är 12!
 1) Till exempel om vi tar den första kol atomen, så har den: 6 protoner, 12 6=6 neutroner, 6 elektroner; atommassan är också 6 men masstalet är 12! Om vi tar den tredje kol atomen, så är protonerna 6,
1) Till exempel om vi tar den första kol atomen, så har den: 6 protoner, 12 6=6 neutroner, 6 elektroner; atommassan är också 6 men masstalet är 12! Om vi tar den tredje kol atomen, så är protonerna 6,
Astronomi. Hästhuvudnebulosan. Neil Armstrong rymdresenär.
 Hästhuvudnebulosan Astronomi Neil Armstrong rymdresenär. Illustration av vår galax Vintergatan. Av naturliga själ har vi aldrig sett vår galax ur detta perspektiv. Vilka är vi jordbor egentligen? Var i
Hästhuvudnebulosan Astronomi Neil Armstrong rymdresenär. Illustration av vår galax Vintergatan. Av naturliga själ har vi aldrig sett vår galax ur detta perspektiv. Vilka är vi jordbor egentligen? Var i
VARFÖR MÖRK ENERGI HAR EN ANMÄRKNINGSVÄRT LITET VÄRDE. Ahmad Sudirman
 VARFÖR MÖRK ENERGI HAR EN ANMÄRKNINGSVÄRT LITET VÄRDE Ahmad Sudirman CAD, CAM och CNC Teknik Utbildning med kvalitet (3CTEQ) STOCKHOLM, 9 januari 2014 1 VARFÖR MÖRK ENERGI HAR EN ANMÄRKNINGSVÄRT LITET
VARFÖR MÖRK ENERGI HAR EN ANMÄRKNINGSVÄRT LITET VÄRDE Ahmad Sudirman CAD, CAM och CNC Teknik Utbildning med kvalitet (3CTEQ) STOCKHOLM, 9 januari 2014 1 VARFÖR MÖRK ENERGI HAR EN ANMÄRKNINGSVÄRT LITET
Hertzsprung-Russell-diagrammet Ulf Torkelsson
 1 Stjärnors temperatur Föreläsning 26/2 Hertzsprung-Russell-diagrammet Ulf Torkelsson Om vi antar att en stjärna strålar som en svartkropp så kan vi bestämma dess temperatur genom att studera dess spektrum.
1 Stjärnors temperatur Föreläsning 26/2 Hertzsprung-Russell-diagrammet Ulf Torkelsson Om vi antar att en stjärna strålar som en svartkropp så kan vi bestämma dess temperatur genom att studera dess spektrum.
Orienteringskurs i astronomi Föreläsning 5,
 Orienteringskurs i astronomi Föreläsning 5, 2014-09-15 Bengt Edvardsson Med litet mer detaljer än vad jag hann med på föreläsningen. Kap 6. Solen är en stjärna. För Solen gäller (sid. 145): I kärnan är
Orienteringskurs i astronomi Föreläsning 5, 2014-09-15 Bengt Edvardsson Med litet mer detaljer än vad jag hann med på föreläsningen. Kap 6. Solen är en stjärna. För Solen gäller (sid. 145): I kärnan är
Inspirationsdag i astronomi. Innehåll. Centret för livslångt lärande vid Åbo Akademi Vasa, 24 mars 2011
 Inspirationsdag i astronomi Centret för livslångt lärande vid Åbo Akademi Vasa, 24 mars 2011 Länkar m.m.: www.astronomi.nu/vasa110324 Magnus Näslund Stockholms observatorium Institutionen för astronomi
Inspirationsdag i astronomi Centret för livslångt lärande vid Åbo Akademi Vasa, 24 mars 2011 Länkar m.m.: www.astronomi.nu/vasa110324 Magnus Näslund Stockholms observatorium Institutionen för astronomi
Introduktion till Kosmologi
 Introduktion till Kosmologi Astropartikelfysik Från det allra minsta till det allra största Från http://www.quarkstothecosmos.org/ Universum inom vår horistont Gravitationskraften finns överallt! Einsteins
Introduktion till Kosmologi Astropartikelfysik Från det allra minsta till det allra största Från http://www.quarkstothecosmos.org/ Universum inom vår horistont Gravitationskraften finns överallt! Einsteins
Geometrisk optik. Syfte och mål. Innehåll. Utrustning. Institutionen för Fysik 2006-04-25
 Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
bubblor Spiralen runt R Sculptoris: Våra nya observationer med ALMA bjöd på en rejäl överraskning. För 1 800 år sedan drabbades stjärnan
 Jättarna som blåser bubblor avstjärnstoft av Sofia Ramstedt Möt de röda jättestjärnorna som blåser liv i galaxen. Sofia Ramstedt forskar om AGB-stjärnor, döende solar som skapar himlens vackraste nebulosor
Jättarna som blåser bubblor avstjärnstoft av Sofia Ramstedt Möt de röda jättestjärnorna som blåser liv i galaxen. Sofia Ramstedt forskar om AGB-stjärnor, döende solar som skapar himlens vackraste nebulosor
Alla svar till de extra uppgifterna
 Alla svar till de extra uppgifterna Fö 1 1.1 (a) 0 cm 1.4 (a) 50 s (b) 4 cm (b) 0,15 m (15 cm) (c) 0 cm 1.5 2 m/s (d) 0 cm 1.6 1.2 (a) A nedåt, B uppåt, C nedåt, D nedåt 1.7 2,7 m/s (b) 1.8 Våglängd: 2,0
Alla svar till de extra uppgifterna Fö 1 1.1 (a) 0 cm 1.4 (a) 50 s (b) 4 cm (b) 0,15 m (15 cm) (c) 0 cm 1.5 2 m/s (d) 0 cm 1.6 1.2 (a) A nedåt, B uppåt, C nedåt, D nedåt 1.7 2,7 m/s (b) 1.8 Våglängd: 2,0
Solen och andra stjärnor 19 juli 2006. Stefan Larsson. Dagens text: Kap 3 Från Aristoteles till stjärnspektra
 Solen och andra stjärnor 19 juli 2006 Stefan Larsson Dagens text: Kap 3 Från Aristoteles till stjärnspektra Aristotle s Perfect Spheres Epicykler Att beskriva planeternas banor med enkla cirklar fungerar
Solen och andra stjärnor 19 juli 2006 Stefan Larsson Dagens text: Kap 3 Från Aristoteles till stjärnspektra Aristotle s Perfect Spheres Epicykler Att beskriva planeternas banor med enkla cirklar fungerar
Solsystemet samt planeter och liv i universum
 Solsystemet samt planeter och liv i universum Kap. 7-8, Solsystemet idag och igår Kap. 9.2, Jordens inre Kap. 10, Månen Kap 17, asteroider, kometer Kap 30, Liv i universum Jordens inre Medeltäthet ca 5500
Solsystemet samt planeter och liv i universum Kap. 7-8, Solsystemet idag och igår Kap. 9.2, Jordens inre Kap. 10, Månen Kap 17, asteroider, kometer Kap 30, Liv i universum Jordens inre Medeltäthet ca 5500
FINALTÄVLING SVENSKA FYSIKERSAMFUNDET
 FYSIKTÄVLINGEN FINALTÄVLING 24 april 1999 SVENSKA FYSIKERSAMFUNDET 1. Estimate, by using generally known properties of a typical car, the energy content of one litre of petrol. Some typical data for a
FYSIKTÄVLINGEN FINALTÄVLING 24 april 1999 SVENSKA FYSIKERSAMFUNDET 1. Estimate, by using generally known properties of a typical car, the energy content of one litre of petrol. Some typical data for a
Redan på 1600-talet upptäckte Johannes Kepler att planeternas banor
 Thomas Lingefjärd & Sture Sjöstedt Heltalspunkter på ellipsen Att undersöka matematiska samband har alltid varit en drivkraft inom matematiska vetenskaper och ibland leder en sådan undersökning fram till
Thomas Lingefjärd & Sture Sjöstedt Heltalspunkter på ellipsen Att undersöka matematiska samband har alltid varit en drivkraft inom matematiska vetenskaper och ibland leder en sådan undersökning fram till
Science Night Rymden nu och framåt Aktuell forskning om rymden som utgångspunkt för intresseskapande fysik.
 Science Night Rymden nu och framåt Aktuell forskning om rymden som utgångspunkt för intresseskapande fysik. Nobelpriser i fysik 2017 Liv i rymden En app för att hitta på stjärnhimlen Nobelpriset i fysik
Science Night Rymden nu och framåt Aktuell forskning om rymden som utgångspunkt för intresseskapande fysik. Nobelpriser i fysik 2017 Liv i rymden En app för att hitta på stjärnhimlen Nobelpriset i fysik
Final i Wallenbergs Fysikpris
 Final i Wallenbergs Fysikpris 26-27 mars 2010. Teoriprov Lösningsförslag 1. a) Vattens värmekapacitivitet: Isens värmekapacitivitet: Smältvärmet: Kylmaskinen drivs med spänningen och strömmen. Kylmaskinens
Final i Wallenbergs Fysikpris 26-27 mars 2010. Teoriprov Lösningsförslag 1. a) Vattens värmekapacitivitet: Isens värmekapacitivitet: Smältvärmet: Kylmaskinen drivs med spänningen och strömmen. Kylmaskinens
Atomens historia. Slutet av 1800-talet trodde man att man hade en fullständig bild av alla fysikaliska fenomen.
 Atomfysik ht 2015 Atomens historia Atom = grekiskans a tomos som betyder odelbar Filosofen Demokritos, atomer. Stort motstånd, främst från Aristoteles Trodde på läran om de fyra elementen Alla ämnen bildas
Atomfysik ht 2015 Atomens historia Atom = grekiskans a tomos som betyder odelbar Filosofen Demokritos, atomer. Stort motstånd, främst från Aristoteles Trodde på läran om de fyra elementen Alla ämnen bildas
v F - v c kallas dispersion
 Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
Planeter Stjärnor Galaxer Uppgifter
 Planeter Stjärnor Galaxer Uppgifter 2 Vårt sätt att indela tiden 2.1 Använd Den Svenska Almanackan för två på varandra följande år och räkna antalet dygn från vårdagjämning till höstdagjämning och från
Planeter Stjärnor Galaxer Uppgifter 2 Vårt sätt att indela tiden 2.1 Använd Den Svenska Almanackan för två på varandra följande år och räkna antalet dygn från vårdagjämning till höstdagjämning och från
Fotoelektriska effekten
 Fotoelektriska effekten Bakgrund År 1887 upptäckte den tyska fysikern Heinrich Hertz att då man belyser ytan på en metallkropp med ultraviolett ljus avges elektriska laddningar från ytan. Noggrannare undersökningar
Fotoelektriska effekten Bakgrund År 1887 upptäckte den tyska fysikern Heinrich Hertz att då man belyser ytan på en metallkropp med ultraviolett ljus avges elektriska laddningar från ytan. Noggrannare undersökningar
Stjärnors födslar och död
 Stjärnors födslar och död Stjärnors egenskaper Uppkomst Avstånd Rörelse Skenbar ljusstyrka Färg temperatur Energiproduktion Verklig ljusstyrka Utveckling Ovanliga stjärnor Slutstadier Rymden är inte bara
Stjärnors födslar och död Stjärnors egenskaper Uppkomst Avstånd Rörelse Skenbar ljusstyrka Färg temperatur Energiproduktion Verklig ljusstyrka Utveckling Ovanliga stjärnor Slutstadier Rymden är inte bara
Kosmologi efter elektrosvagt symmetribrott
 Kosmologi efter elektrosvagt symmetribrott Den teoretiska grunden för modern kosmologi Einsteins allmänna relativitetsteori 1907 inser Einstein att man kan lokalt göra sig kvitt med gravitation genom att
Kosmologi efter elektrosvagt symmetribrott Den teoretiska grunden för modern kosmologi Einsteins allmänna relativitetsteori 1907 inser Einstein att man kan lokalt göra sig kvitt med gravitation genom att
Översiktskurs i astronomi Hösten 2009
 Översiktskurs i astronomi Hösten 2009 Upplägg Formell information Vår r plats i Universum Grundläggande astronomiska begrepp Formell information I Lärare (idag): Erik Zackrisson Lärare påp resten av kursen:
Översiktskurs i astronomi Hösten 2009 Upplägg Formell information Vår r plats i Universum Grundläggande astronomiska begrepp Formell information I Lärare (idag): Erik Zackrisson Lärare påp resten av kursen:
Kosmologin söker svar bl.a. på: Hur uppkom universum? Hur gammalt är universum? Hur är materian och energin fördelad?
 7 Kosmologi Kosmologin söker svar bl.a. på: Hur uppkom universum? Hur gammalt är universum? Hur är materian och energin fördelad? Hur uppkom elementarpartiklarna? Hur uppkom grundämnena? Hurdan är universums
7 Kosmologi Kosmologin söker svar bl.a. på: Hur uppkom universum? Hur gammalt är universum? Hur är materian och energin fördelad? Hur uppkom elementarpartiklarna? Hur uppkom grundämnena? Hurdan är universums
Kort introduktion till POV-Ray, del 1
 Kort introduktion till POV-Ray, del 1 Kjell Y Svensson, 2004-02-02,2007-03-13 Denna serie av artiklar ger en grundläggande introduktion och förhoppningsvis en förståelse för hur man skapar realistiska
Kort introduktion till POV-Ray, del 1 Kjell Y Svensson, 2004-02-02,2007-03-13 Denna serie av artiklar ger en grundläggande introduktion och förhoppningsvis en förståelse för hur man skapar realistiska
Innehållsförteckning. Innehållsförteckning 1 Rymden 3. Solen 3 Månen 3 Jorden 4 Stjärnor 4 Galaxer 4 Nebulosor 5. Upptäck universum med Cosmonova 3
 1 Innehållsförteckning Innehållsförteckning 1 Rymden 3 Upptäck universum med Cosmonova 3 Solen 3 Månen 3 Jorden 4 Stjärnor 4 Galaxer 4 Nebulosor 5 2 Rymden Rymden, universum utanför jorden, studeras främst
1 Innehållsförteckning Innehållsförteckning 1 Rymden 3 Upptäck universum med Cosmonova 3 Solen 3 Månen 3 Jorden 4 Stjärnor 4 Galaxer 4 Nebulosor 5 2 Rymden Rymden, universum utanför jorden, studeras främst
Solsystemet. Lektion 15 (kap 7-8)
 Solsystemet Lektion 15 (kap 7-8) Solsystemet Består av nio stora planeter varav de flesta har en eller flera månar Mängder av småplaneter eller asteroider, kometer och meteoroider Interplanetariskt stoft
Solsystemet Lektion 15 (kap 7-8) Solsystemet Består av nio stora planeter varav de flesta har en eller flera månar Mängder av småplaneter eller asteroider, kometer och meteoroider Interplanetariskt stoft
OBS: Alla mätningar och beräknade värden ska anges i SI-enheter med korrekt antal värdesiffror. Felanalys behövs endast om det anges i texten.
 Speed of light OBS: Alla mätningar och beräknade värden ska anges i SI-enheter med korrekt antal värdesiffror. Felanalys behövs endast om det anges i texten. 1.0 Inledning Experiment med en laseravståndsmätare
Speed of light OBS: Alla mätningar och beräknade värden ska anges i SI-enheter med korrekt antal värdesiffror. Felanalys behövs endast om det anges i texten. 1.0 Inledning Experiment med en laseravståndsmätare
att båda rör sig ett varv runt masscentrum på samma tid. Planet
 Tema: Exoplaneter (Del III, banhastighet och massa) Det vi hittills tittat på är hur man beräknar radien och avståndet till stjärnan för en exoplanet. Omloppstiden kunde vi exempelvis få fram genom att
Tema: Exoplaneter (Del III, banhastighet och massa) Det vi hittills tittat på är hur man beräknar radien och avståndet till stjärnan för en exoplanet. Omloppstiden kunde vi exempelvis få fram genom att
Bengt Edlén, atomspektroskopist
 83 Solkoronans gåta Om mannen som lyckades lösa den och samtidigt bevisa att strax utanför solens yta är temperaturen 2 miljoner grader och inte 6 000 som man tidigare trott. Bengt Edlén, atomspektroskopist
83 Solkoronans gåta Om mannen som lyckades lösa den och samtidigt bevisa att strax utanför solens yta är temperaturen 2 miljoner grader och inte 6 000 som man tidigare trott. Bengt Edlén, atomspektroskopist
Polarisation. Abbas Jafari Q2-A. Personnummer: april Laborationsrapport
 Polarisation Laborationsrapport Abbas Jafari Q2-A Personnummer: 950102-9392 22 april 2017 1 Innehåll 1 Introduktion 2 2 Teori 2 2.1 Malus lag............................. 3 2.2 Brewstervinklen..........................
Polarisation Laborationsrapport Abbas Jafari Q2-A Personnummer: 950102-9392 22 april 2017 1 Innehåll 1 Introduktion 2 2 Teori 2 2.1 Malus lag............................. 3 2.2 Brewstervinklen..........................
Universum. Stjärnbilder och Världsbilder
 Universum Stjärnbilder och Världsbilder Stjärnor Stjärngrupp, t.ex. Karlavagnen Stjärnbild, t.ex. Stora Björnen Polstjärnan Stjärnor livscykel -Protostjärna - Huvudseriestjärna - Röd jätte - Vit dvärg
Universum Stjärnbilder och Världsbilder Stjärnor Stjärngrupp, t.ex. Karlavagnen Stjärnbild, t.ex. Stora Björnen Polstjärnan Stjärnor livscykel -Protostjärna - Huvudseriestjärna - Röd jätte - Vit dvärg
Vi ser Vintergatan som ett dimmaktigt bälte över himmelen.
 6 Galaxer Galaxerna är de synliga "byggstenarna" av universum. Man räknar med att det finns 170 miljarder galaxer i den observerbara delen av universum, dvs. inom ca 14 miljarder ljusår. Galaxernas storlek
6 Galaxer Galaxerna är de synliga "byggstenarna" av universum. Man räknar med att det finns 170 miljarder galaxer i den observerbara delen av universum, dvs. inom ca 14 miljarder ljusår. Galaxernas storlek
Vad skall vi gå igenom under denna period?
 Ljus/optik Vad skall vi gå igenom under denna period? Vad är ljus? Ljuskälla? Reflektionsvinklar/brytningsvinklar? Färger? Hur fungerar en kikare? Hur fungerar en kamera/ ögat? Var använder vi ljus i vardagen
Ljus/optik Vad skall vi gå igenom under denna period? Vad är ljus? Ljuskälla? Reflektionsvinklar/brytningsvinklar? Färger? Hur fungerar en kikare? Hur fungerar en kamera/ ögat? Var använder vi ljus i vardagen
Konsten att "se" det osynliga. Om indirekta metoder att upptäcka exoplaneter
 ASTA02 - Lennart Lindegren - 19 okt 2011 Konsten att "se" det osynliga. Om indirekta metoder att upptäcka exoplaneter De allra flesta hittills funna exoplaneter har upptäckts med indirekta metoder. Vad
ASTA02 - Lennart Lindegren - 19 okt 2011 Konsten att "se" det osynliga. Om indirekta metoder att upptäcka exoplaneter De allra flesta hittills funna exoplaneter har upptäckts med indirekta metoder. Vad
Trappist-1-systemet Den bruna dvärgen och de sju kloten
 Trappist--systemet Den bruna dvärgen och de sju kloten Trappist- är en sval dvärgstjärna, en brun dvärg, som man nyligen upptäckte flera planeter kring. För tillfället känner man till sju planeter i omloppsbana
Trappist--systemet Den bruna dvärgen och de sju kloten Trappist- är en sval dvärgstjärna, en brun dvärg, som man nyligen upptäckte flera planeter kring. För tillfället känner man till sju planeter i omloppsbana
Vår galax Vintergatan sedd från sidan. Vår galax Vintergatan sedd uppifrån
 Livet. Detta ord berör hela jorden oavsett religion. I första hand hänvisar jag läsaren till följande länkar: Svarta hålets hemlighet, Vad händer i ett svart hål?, Resan genom det svarta hålet, Livet och
Livet. Detta ord berör hela jorden oavsett religion. I första hand hänvisar jag läsaren till följande länkar: Svarta hålets hemlighet, Vad händer i ett svart hål?, Resan genom det svarta hålet, Livet och
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 36-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik Kapitel 36-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Astrofysikaliska räkneövningar
 Astrofysikaliska räkneövningar Stefan Bergström, Ylva Pihlström Ulf Torkelsson 23 november 2004 Uppgifter 1. Dubbelstjärnesystemet VV Cephei har en period P = 20.3 år. Stjärnorna har massorna M 1 M 2 20
Astrofysikaliska räkneövningar Stefan Bergström, Ylva Pihlström Ulf Torkelsson 23 november 2004 Uppgifter 1. Dubbelstjärnesystemet VV Cephei har en period P = 20.3 år. Stjärnorna har massorna M 1 M 2 20
Vår galax, Vintergatan
 Vår galax, Vintergatan Vår plats i Vintergatan Ca 1785 (William Herschel) till ca 1920 (Jacobus Kapteyn): Solen i galaxens centrum, p.g.a. stjärnor jämt fördelade i Vintergatan i synligt ljus. Herschels
Vår galax, Vintergatan Vår plats i Vintergatan Ca 1785 (William Herschel) till ca 1920 (Jacobus Kapteyn): Solen i galaxens centrum, p.g.a. stjärnor jämt fördelade i Vintergatan i synligt ljus. Herschels
Snabba atomer och lysande stjärnor. Hur spektrallinjer berättar om exciterade atomers livstider och den kemiska sammansättningen hos stjärnor.
 343 Snabba atomer och lysande stjärnor Hur spektrallinjer berättar om exciterade atomers livstider och den kemiska sammansättningen hos stjärnor. Atomspektroskopi en Lundatradition Undersökningar av atomernas
343 Snabba atomer och lysande stjärnor Hur spektrallinjer berättar om exciterade atomers livstider och den kemiska sammansättningen hos stjärnor. Atomspektroskopi en Lundatradition Undersökningar av atomernas
CYGNUS. Länktips! Kallelse: Årsmöte 15 mars 2012
 CYGNUS Medlemsblad för Östergötlands Astronomiska Sällskap Nr 2, 2011 Innehåll Länktips! Kallelse till Årsmötet Sammanfattning av Gösta Gahms föredrag under Höstmötet 1 2 Vårens program 3 ÖAS webbplats
CYGNUS Medlemsblad för Östergötlands Astronomiska Sällskap Nr 2, 2011 Innehåll Länktips! Kallelse till Årsmötet Sammanfattning av Gösta Gahms föredrag under Höstmötet 1 2 Vårens program 3 ÖAS webbplats
Hemsida. Upplägg. Jordbanans lutning. Himlens fä. Solnedgång. Översiktskurs i astronomi Lektion 2: Grundlä. grundläggande astronomi.
 Översiktskurs i astronomi Lektion 2: Grundlä Grundläggande astronomi Hemsida www.astro.su.se/~ ez/kurs/oversiktskurs09.htm /kurs/oversiktskurs09.htm www.astro.su.se/~ez Upplä Upplägg Mer grundlä grundläggande
Översiktskurs i astronomi Lektion 2: Grundlä Grundläggande astronomi Hemsida www.astro.su.se/~ ez/kurs/oversiktskurs09.htm /kurs/oversiktskurs09.htm www.astro.su.se/~ez Upplä Upplägg Mer grundlä grundläggande
Upptäckten av gravitationsvågor
 Upptäckten av gravitationsvågor Peter Johansson Institutionen för Fysik Helsingfors Universitet Fysikersamfundet i Finland - Årsmöte Helsingfors, 16.03.2016 Gravitationsvågor som ett fenomen förutspåddes
Upptäckten av gravitationsvågor Peter Johansson Institutionen för Fysik Helsingfors Universitet Fysikersamfundet i Finland - Årsmöte Helsingfors, 16.03.2016 Gravitationsvågor som ett fenomen förutspåddes
BFL122/BFL111 Fysik för Tekniskt/ Naturvetenskapligt Basår/ Bastermin Föreläsning 10 Relativitetsteori den 26 april 2012.
 Föreläsning 10 Relativa mätningar Allting är relativt är ett välbekant begrepp. I synnerhet gäller detta när vi gör mätningar av olika slag. Många mätningar består ju i att man jämför med någonting. Temperatur
Föreläsning 10 Relativa mätningar Allting är relativt är ett välbekant begrepp. I synnerhet gäller detta när vi gör mätningar av olika slag. Många mätningar består ju i att man jämför med någonting. Temperatur
Kalla Vindar ( och Heta Galaxkärnor) Susanne Aalto Rymd och Geovetenskap Chalmers
 Kalla Vindar ( och Heta Galaxkärnor) Susanne Aalto Rymd och Geovetenskap Chalmers Herschel Space Observatory Massa: ca 3400 kg vid uppskjutning Dimensioner: 7.5m hög, 4m 4m tvärsnitt Våglängder: Infrarött
Kalla Vindar ( och Heta Galaxkärnor) Susanne Aalto Rymd och Geovetenskap Chalmers Herschel Space Observatory Massa: ca 3400 kg vid uppskjutning Dimensioner: 7.5m hög, 4m 4m tvärsnitt Våglängder: Infrarött
Översiktskurs i astronomi Lektion 3: Ljus och teleskop
 Översiktskurs i astronomi Lektion 3: Ljus och teleskop Upplägg Ljus och spektra Elektromagnetisk strålning Våglängd vid frekvens Teleskop och detektorer Seeing Reflektor- och refraktorteleskop CCD-chip
Översiktskurs i astronomi Lektion 3: Ljus och teleskop Upplägg Ljus och spektra Elektromagnetisk strålning Våglängd vid frekvens Teleskop och detektorer Seeing Reflektor- och refraktorteleskop CCD-chip
Översiktskurs i astronomi Våren Formell information I. Formell information II. Formell information IV. Formell information III
 Översiktskurs i astronomi Våren 2009 Upplägg Formell information Vår r plats i Universum Grundläggande astronomiska begrepp Formell information I Lärare: Erik Zackrisson ez@astro.su.se 08-5537 8556 Kurshemsida:
Översiktskurs i astronomi Våren 2009 Upplägg Formell information Vår r plats i Universum Grundläggande astronomiska begrepp Formell information I Lärare: Erik Zackrisson ez@astro.su.se 08-5537 8556 Kurshemsida:
DE SJU SYMMETRISKA UNIVERSUM. Ahmad Sudirman
 DE SJU SYMMETRISKA UNIVERSUM Ahmad Sudirman CAD,CAM och CNC Teknik Utbildning med kvalitet (3CTEQ) STOCKHOLM, den 13 november 2011 1 DE SJU SYMMETRISKA UNIVERSUM Copyright 2011 Ahmad Sudirman* Stockholm
DE SJU SYMMETRISKA UNIVERSUM Ahmad Sudirman CAD,CAM och CNC Teknik Utbildning med kvalitet (3CTEQ) STOCKHOLM, den 13 november 2011 1 DE SJU SYMMETRISKA UNIVERSUM Copyright 2011 Ahmad Sudirman* Stockholm
Föreläsning 3: Radiometri och fotometri
 Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
Översiktskurs i astronomi Lektion 7: Solens och stjärnornas energiproduktion samt utveckling
 Översiktskurs i astronomi Lektion 7: Solens och stjärnornas energiproduktion samt utveckling Frågor från n förra f gången g I Hur långt är det mellan asteroiderna i huvudbältet? För stora asteroider (>1
Översiktskurs i astronomi Lektion 7: Solens och stjärnornas energiproduktion samt utveckling Frågor från n förra f gången g I Hur långt är det mellan asteroiderna i huvudbältet? För stora asteroider (>1
Miniräknare, formelsamling
 Umeå Universitet TENTAMEN Linje: Kurs: Hjälpmedel: Fysik B Miniräknare, formelsamling Lärare: Joakim Lundin Datum: 09-10-29 Tid: 9.00-15.00 Kod:... Grupp:... Poäng:... Betyg U G VG... Tentamen i Fysik
Umeå Universitet TENTAMEN Linje: Kurs: Hjälpmedel: Fysik B Miniräknare, formelsamling Lärare: Joakim Lundin Datum: 09-10-29 Tid: 9.00-15.00 Kod:... Grupp:... Poäng:... Betyg U G VG... Tentamen i Fysik
λ = T 2 g/(2π) 250/6 40 m
 Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Observera att uppgifterna inte är ordnade efter svårighetsgrad!
 TENTAMEN I FYSIK FÖR n, 13 APRIL 2010 Skrivtid: 8.00-13.00 Hjälpmedel: Formelblad och räknare. Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och försedda med svar. Kladdblad
TENTAMEN I FYSIK FÖR n, 13 APRIL 2010 Skrivtid: 8.00-13.00 Hjälpmedel: Formelblad och räknare. Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och försedda med svar. Kladdblad
RÖRELSE. - Mätningar och mätinstrument och hur de kan kombineras för att mäta storheter, till exempel fart, tryck och effekt.
 RÖRELSE Inledning När vi går, springer, cyklar etc. förflyttar vi oss en viss sträcka på en viss tid. Ibland, speciellt när vi har bråttom, tänker vi på hur fort det går. I det här experimentet undersöker
RÖRELSE Inledning När vi går, springer, cyklar etc. förflyttar vi oss en viss sträcka på en viss tid. Ibland, speciellt när vi har bråttom, tänker vi på hur fort det går. I det här experimentet undersöker
BFL122/BFL111 Fysik för Tekniskt/ Naturvetenskapligt Basår/ Bastermin Föreläsning 13 Kärnfysik 2 den 4 maj Föreläsning 13.
 Föreläsning 13 Sönderfallslagen Låt oss börja med ett tankeexperiment (som man med visst tålamod också kan utföra rent praktiskt). Säg att man kastar en tärning en gång. Innan man kastat tärningen kan
Föreläsning 13 Sönderfallslagen Låt oss börja med ett tankeexperiment (som man med visst tålamod också kan utföra rent praktiskt). Säg att man kastar en tärning en gång. Innan man kastat tärningen kan
Gull! Astrofysikk, kärnfysik, kvantmekanik og relativitetsteori i vardagen? Jonas Persson Institutt for Fysikk, NTNU
 Gull! Astrofysikk, kärnfysik, kvantmekanik og relativitetsteori i vardagen? Jonas Persson Institutt for Fysikk, NTNU 2 Periodiska systemet 3 Periodiska systemet för astrofysiker 4 Periodiska systemet -
Gull! Astrofysikk, kärnfysik, kvantmekanik og relativitetsteori i vardagen? Jonas Persson Institutt for Fysikk, NTNU 2 Periodiska systemet 3 Periodiska systemet för astrofysiker 4 Periodiska systemet -
Supersymmetri. en ny värld av partiklar att upptäcka. Johan Rathsman, Lunds Universitet. NMT-dagar, Lund, Symmetrier i fysik
 en ny värld av partiklar att upptäcka, Lunds Universitet NMT-dagar, Lund, 2014-03-10 1 i fysik 2 och krafter 3 ska partiklar och krafter 4 på jakt efter nya partiklar Newtons 2:a lag i fysik Newtons andra
en ny värld av partiklar att upptäcka, Lunds Universitet NMT-dagar, Lund, 2014-03-10 1 i fysik 2 och krafter 3 ska partiklar och krafter 4 på jakt efter nya partiklar Newtons 2:a lag i fysik Newtons andra
Solen och andra stjärnor 24 juli Stefan Larsson. Mer kap 3 Stjärnors egenskaper
 Solen och andra stjärnor 24 juli 2006 Stefan Larsson Mer kap 3 Stjärnors egenskaper Spectralklasser Vilka spektrallinjer som finns i en stjärnas spektrum och hur starka de är beror i första hand på temperaturen
Solen och andra stjärnor 24 juli 2006 Stefan Larsson Mer kap 3 Stjärnors egenskaper Spectralklasser Vilka spektrallinjer som finns i en stjärnas spektrum och hur starka de är beror i första hand på temperaturen
Einstein's svårbegripliga teori. Einstein's första relativitetsteori, den Speciella, förklaras så att ALLA kan förstå den
 Einstein's svårbegripliga teori Einstein's första relativitetsteori, den Speciella, förklaras så att ALLA kan förstå den Speciella relativitetsteorin, Allmänt Einsten presenterade teorin 1905 Teorin gäller
Einstein's svårbegripliga teori Einstein's första relativitetsteori, den Speciella, förklaras så att ALLA kan förstå den Speciella relativitetsteorin, Allmänt Einsten presenterade teorin 1905 Teorin gäller
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 32 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik Kapitel 32 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Fysik (TFYA14) Fö 5 1. Fö 5
 Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
Instuderingsfrågor Atomfysik
 Instuderingsfrågor Atomfysik 1. a) Skriv namn och laddning på tre elementarpartiklar. b) Vilka elementarpartiklar finns i atomkärnan? 2. a) Hur många elektroner kan en atom högst ha i skalet närmast kärnan?
Instuderingsfrågor Atomfysik 1. a) Skriv namn och laddning på tre elementarpartiklar. b) Vilka elementarpartiklar finns i atomkärnan? 2. a) Hur många elektroner kan en atom högst ha i skalet närmast kärnan?
Ett expanderande universum Ulf Torkelsson
 Kosmologins postulat Föreläsning 25/5 Ett expanderande universum Ulf Torkelsson När man bygger upp en kosmologisk modell antar man att universum är homogent, det vill säga att det ser likadant ut överallt,
Kosmologins postulat Föreläsning 25/5 Ett expanderande universum Ulf Torkelsson När man bygger upp en kosmologisk modell antar man att universum är homogent, det vill säga att det ser likadant ut överallt,
Övning 1 Dispersion och prismaeffekt
 Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
Lösningsförslag - tentamen. Fysik del B2 för tekniskt / naturvetenskapligt basår / bastermin BFL 122 / BFL 111
 Linköpings Universitet Institutionen för Fysik, Kemi, och Biologi Avdelningen för Tillämpad Fysik Mike Andersson Lösningsförslag - tentamen Torsdagen den 27:e maj 2010, kl 08:00 12:00 Fysik del B2 för
Linköpings Universitet Institutionen för Fysik, Kemi, och Biologi Avdelningen för Tillämpad Fysik Mike Andersson Lösningsförslag - tentamen Torsdagen den 27:e maj 2010, kl 08:00 12:00 Fysik del B2 för
Materiens Struktur. Lösningar
 Materiens Struktur Räkneövning 5 Lösningar 1. Massorna för de nedan uppräknade A = isobarerna är 27 Co 28 Ni 29 Cu 30 Zn 31 Ga 63,935812u 63,927968u 63,929766u 63,929146u 63,936827u Tabell 1: Tabellen
Materiens Struktur Räkneövning 5 Lösningar 1. Massorna för de nedan uppräknade A = isobarerna är 27 Co 28 Ni 29 Cu 30 Zn 31 Ga 63,935812u 63,927968u 63,929766u 63,929146u 63,936827u Tabell 1: Tabellen
Kapitel: 32 Elektromagnetiska vågor Maxwells ekvationer Hur accelererande laddningar kan ge EM-vågor
 Kapitel: 3 lektromagnetiska vågor Maxwells ekvationer Hur accelererande laddningar kan ge M-vågor genskaper hos M-vågor nergitransport i M-vågor Det elektromagnetiska spektrat Maxwell s ekvationer Kan
Kapitel: 3 lektromagnetiska vågor Maxwells ekvationer Hur accelererande laddningar kan ge M-vågor genskaper hos M-vågor nergitransport i M-vågor Det elektromagnetiska spektrat Maxwell s ekvationer Kan
Tentamen Relativitetsteori , 27/7 2019
 KOD: Tentamen Relativitetsteori 9.00 14.00, 27/7 2019 Hjälpmedel: Miniräknare, linjal och bifogad formelsamling. Observera: Samtliga svar ska lämnas på dessa frågepapper. Det framgår ur respektive uppgift
KOD: Tentamen Relativitetsteori 9.00 14.00, 27/7 2019 Hjälpmedel: Miniräknare, linjal och bifogad formelsamling. Observera: Samtliga svar ska lämnas på dessa frågepapper. Det framgår ur respektive uppgift
I once saw Einstein on a train which whistled past our station. - Your clock ticks much too slow, I yelled. - Ach, nein. That's time dilation
 I once saw Einstein on a train which whistled past our station. - Your clock ticks much too slow, I yelled. - Ach, nein. That's time dilation - Gordon Judge Om man åker fortare än ljuset, svartnar det
I once saw Einstein on a train which whistled past our station. - Your clock ticks much too slow, I yelled. - Ach, nein. That's time dilation - Gordon Judge Om man åker fortare än ljuset, svartnar det
Mörk materia och det tidiga universum Joakim Edsjö Stockholms Universitet
 Mörk materia och det tidiga universum Joakim Edsjö edsjo@physto.se Stockholms Universitet Introduktion till kosmologi Mörk materia Den kosmologiska bakgrundsstrålningen Supernovor och universums geometri
Mörk materia och det tidiga universum Joakim Edsjö edsjo@physto.se Stockholms Universitet Introduktion till kosmologi Mörk materia Den kosmologiska bakgrundsstrålningen Supernovor och universums geometri
Relativitetsteorins grunder, våren 2016 Räkneövning 1 Lösningar
 > < Relativitetsteorins grunder, våren 2016 Räkneövning 1 Lösningar 1. En myon (en elementarpartikel som liknar elektronen, men är 200 ggr tyngre) bildas i atmosfären på L 0 = 2230 m:s höjd ovanför jordytan.
> < Relativitetsteorins grunder, våren 2016 Räkneövning 1 Lösningar 1. En myon (en elementarpartikel som liknar elektronen, men är 200 ggr tyngre) bildas i atmosfären på L 0 = 2230 m:s höjd ovanför jordytan.
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 14 Harmonisk oscillator 1 Vågrörelselära och optik 2 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator:
Vågrörelselära och optik Kapitel 14 Harmonisk oscillator 1 Vågrörelselära och optik 2 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator:
