Innehåll. Innehåll. ESA/ESOs Övningsserie i Astronomi 4. Förord. Introduktion. Uppgifter. Extrauppgifter. Ytterligare Läsning.
|
|
|
- Per-Olof Pettersson
- för 8 år sedan
- Visningar:
Transkript
1
2
3 Innehåll ESA/ESOs Övningsserie i Astronomi 4 Förord Förord... sidan 2 Introduktion Stjärnor... sidan 3 Väteförbränning... sidan 3 Stjärnhopar... sidan 3 Klotformiga stjärnhopar... sidan 3 Den klotformiga stjärnhopen M12... sidan 6 Hertzsprung-Russell-diagrammet... sidan 6 Stellär evolution i H-R-diagrammet... sidan 6 B-V Färgindex... sidan 8 H-R-diagrammet är nyckeln till en hop... sidan 8 Uppgifter Observationer, datareduktion och analys... sidan 9 Tips till bildanalys... sidan 9 Uppgift 1 B-Band träning... sidan 9 Uppgift 2 B-Band kalibrering... sidan 9 Uppgift 3 B-Band magnituder... sidan 9 Uppgift 4 V-Band träning... sidan 9 Uppgift 5 V-Band kalibrering... sidan 9 Uppgift 6 V-Band magnituder... sidan 10 Uppgift 7 Färgindex... sidan 10 Uppgift 8 Yttemperaturer... sidan 10 Uppgift 9 H-R-diagram... sidan 10 Uppgift 10 Huvudserieanpassning... sidan 10 Uppgift 11 Avstånd till M12... sidan 10 Uppgift 12 Extinktionkorrektion... sidan 10 Uppgift sidan 10 Utvecklingen av klotformiga stjärnhopar... sidan 15 Uppgift sidan 16 Uppgift sidan 16 Uppgift sidan 16 Innehåll Extrauppgifter Uppgift sidan 17 Uppgift sidan 18 Ytterligare Läsning Vetenskapliga artiklar... sidan 19 Lärarens Guide Lärarens Guide... sidan 21 1
4 Förord ESA/ESOs Övningsserie i Astronomi 4 Mätning av en klotformig stjärnhops avstånd och ålder Astronomi är en lättillgänglig och visuell vetenskap, vilket gör den idealisk i undervisningssyfte. De senaste åren har NASA 1, ESA 2, Hubble Space Telescope och ESOs 3 teleskop på La Silla- och Paranalobservatorierna i Chile presenterat allt djupare och mer spektakulära bilder av universum. Hubble och ESOs teleskop har inte bara gett fantastiska bilder, de är även ovärderliga instrument för astronomer. Hubble och ESOs teleskop har inte bara gett fantastiska bilder, de är även ovärderliga instrument för astronomer. Teleskopen har en mycket bra rums/vinkel-upplösning (bildskärpa), vilket ger astronomer möjlighet att blicka längre ut i universum än någonsin tidigare och låter dem svara på gamla, hittills obesvarade frågor. Att analysera sådana observationer, vilket ofta är ett sofistikerat och detaljerat arbete, är ibland tillräckligt enkelt för att gymnasiestudenter själva ska kunna utföra det. Förord Denna serie av uppgifter är framtagen av den europeiska partnern i Hubbleprojektet, ESA (European Space Agency), som har 15% av observationstiden med Hubble, tillsammans med ESO (the European Southern Observatory). Figur 1: ESOs Very Large Telescope ESOs Very Large Telescope (VLT) på Paranalobservatoriet (Atacama, Chile) är världens största och mest avancerade teleskop. Med dess suveräna optiska upplösning och oöverträffade spegelarea producerar VLT mycket skarpa bilder och can uppfatta ljus från universums mest avlägsna och ljussvaga objekt. 2
5 Introduktion Stjärnor En stjärna är en gigantisk boll av självlysande gas med fysiska egenskaper som massa, temperatur och radie. Av intresse för astronomerna är också dess avstånd från jorden. Den närmsta och mest studerade stjärnan är givetvis vår sol. Väteförbränning Ljuset som strålas ut från de flesta stjärnor är en biprodukt av termonukleära fusionsprocesser i stjärnans inre kärna. En normal sol-lik stjärna består av ungefär 74% väte, 25% helium och 1% är en blandning mellan övriga grundämnen. Den vanligaste fusionsprocessen i sol-lika stjärnor är väteförbränning där fyra vätekärnor sammansmälter till en heliumkärna. Processen sker i flera steg illustrerade i fig. 2. I det första steget sammansmälter två protoner och bildar deuterium, en form av tungt väte. Detta är en mycket ovanlig händelse även i en stjärnas täta kärna, där temperaturen är flera miljoner grader. Detta är orsaken till att alla sol-lika stjärnor inte exploderar i en okontrollerbar härdsmälta när fusionsprocessen startar, utan förblir i denna stabila fas av sina liv i flera miljarder år. När stjärnorna är stabila är deras yttemperatur, radie och luminositet nästan konstanta. Kärnreaktionerna i kärnan genererar precis tillräckligt med energi för att hålla en balans mellan det utåtriktade termiska trycket och de inåtriktade gravitationella krafterna. Massan av en heliumkärna är endast 93,7% av massan hos de fyra ursprungliga vätekärnorna. Fusionsprocessen konverterar 7% av massan till energi - mestadels ljus. Mängden energi kan beräknas ur Einsteins berömda ekvation, E = Mc 2. Eftersom c 2 är ett stor siffra betyder det att även en liten mängd materia kan konverteras till en fantastisk mängd energi. Resten av massan på 7% involverad i en fusionsreaktion kan verka liten, men när man betraktar den totala mängden reaktioner är massan (och därför energin) som är involverad rejäl. Stjärnhopar Termen "stjärnhop" används för två olika typer av grupper av stjärnor: Öppna stjärnhopar och klotformiga stjärnhopar. Öppna stjärnhopar är lösa samlingar av ett hundratal till några få tusen relativt unga stjärnor. Dessa är typiskt ett fåtal hundra miljoner år gamla, en bråkdel av de miljardtals år det tar för en stjärna att utvecklas. Dessa hopar finns i disken på vår galax, Vintergatan, och innehåller ofta moln av gas och stoft där nya stjärnor föds. Den typiska diametern på en öppen stjärnhop är ungefär 30 ljusår (10 parsec). Introduktion Figur 2: Väteförbränning Den enklaste formen av energiproduktion i stjärnor sker genom fusion av fyra vätekärnor som bildar en heliumkärna. Processen har flera steg men här visas bara det totala resultatet. Klotformiga stjärnhopar de äldsta strukturerna i Vintergatan Några få hundra kompakta, sfäriska hopar kallade klotformiga stjärnhopar existerar i Vintergatans disk och halo och är gravitationellt bundna till vår galax. Varje klotformig stjärnhop består av en sfärisk grupp av upp till en miljon stjärnor vilken typiskt är 100 ljusår i diameter. De flesta klotformiga stjärnhopar är väldigt gamla och bildades troligen redan före galaxen bildades för 12 miljarder år sedan, när majoriteten av den protogalaktiska materien samlades till disken. 3
6 Introduktion Figur 3: Pleiaderna (Messier 45) i stjärnbilden Oxen (Taurus) Detta är en av de mest berömda stjärnhoparna på himlen. Pleiaderna kan ses med blotta ögat även i de mest upplysta städerna. Det är en av de ljusstarkaste och närmaste öppna hoparna. Pleiaderna innehåller mer än 3000 stjärnor, befinner sig ungefär 400 ljusår bort och är endast 13 ljusår i diameter (med tillstånd av Bruno Stampfer och Rainer Eisendle). Introduktion Många klotformiga hopar har troligtvis blivit förstörda över de miljardtals år som de levt, genom återkommande kollisioner med varandra eller med Vintergatan. De överlevande klotformiga stjärnhoparna är äldre än någon annan struktur i Vintergatan. Den astrofysikaliska studien av klotformiga stjärnhopar är en viktig del av forskningsintresset i det internationella astronomiska samfundet. Figur 4: Vintergatan Denna illustration ger en överblick av Vintergatan. De olika komponenterna av detta komplicerade system av stjärnor, gas och stoft är markerade. Diskens plan ligger längs den centrala horisontella linjen. De klotformiga stjärnhoparna är fördelade i en sfärisk halo runt galaxens centrum. Man tror att fördelningen är relaterad till det faktum att dessa hopar av stjärnor bildades tidigt i galaxens historia. 4
7 Introduktion Dessa hopar av stjärnor är viktiga, inte bara för att de är värdefulla testplatser för teorier i stjärnstruktur och evolution, utan också för att de är ett av de få objekt i galaxen som man kan bestämma relativt exakta åldrar för. På grund av deras långa liv ger de en väldigt värdefull lägre gräns för Universums ålder. Spridningen i deras åldrar och korrelationen mellan en hops ålder och kemiska sammansättning gör dessa system till ovärderliga sonder in i processerna för galaxfödslar. Alla stjärnor samlade i en klotformig stjärnhop delar en gemensam historia och skiljer sig enbart från varandra i massa. Därför är klotformiga stjärnhopar ideala platser att studera stjärnors evolution. I de följande uppgifterna kommer du bestämma några egenskaper hos en speciell klotformig stjärnhop, Messier 12. Introduktion Figur 5: De yttre regionerna av den klotformiga stjärnhopen M12 Denna tvåfärgsbild är konstruerad från observationer genom ett blått (B) och ett grönt (V) filter med ESOs Very Large Telescope (VLT). B-bilden visas i blått och V-bilden som rött i denna sammansatta bild. Några av stjärnorna är klart ljusare i B- bilden (ses som blåaktiga stjärnor) medan andra är ljusare i V-bilden (ses som gulaktiga stjärnor). 5
8 Introduktion Introduktion Den klotformiga stjärnhopen M12 Den klotformiga stjärnhopen Messier 12 (eller M12), också kallad NGC 6218, upptäcktes 1764 av Charles Messier och kom att bli det 12:e Messierobjektet. Likt många andra klotformiga stjärnhopar beskrev Messier denna som en "nebulosa utan stjärnor", en konsekvens av den låga upplösningsförmågan hos hans teleskop. William Herschel var den förste att upplösa hopen i enskilda stjärnor år M12 ligger i stjärnbilden Ormbäraren (Ophiuchus) och kan ses med en vanlig kikare på mörka platser. Den visuella magnituden av hela den klotformiga stjärnhopen är 6,7 (läs om magnituder på sidan 2 i Astronomiska Verktyg) och den ljusstarkaste stjärnan i hopen har en visuell magnitud på 12. NGC (New General Catalog) publicerades Den listar öppna och klotformiga stjärnhopar, diffusa och planetariska nebulosor, supernovarester, galaxer av alla typer och även några felaktiga noteringar som inte korresponderar till något objekt alls. Hertzsprung-Russell-diagrammet Ett diagram som visar luminositeten L (eller den absoluta magnituden M) mot yttemperaturen T för stjärnor kallas ett Hertzsprung-Russelldiagram (kort: H-R-diagram). Fig. 6 visar ett generellt exempel som är konstruerat från observationer av stjärnor i närliggande hopar där avstånden är kända (från HIPPARCOS mätningar). Yttemperaturen kan härledas från det uppmätta värdet på dess färg (m B -m V ) (se Astronomiska Verktyg). Figur 6: Ett Hertzsprung-Russell-diagram över närliggande stjärnor H-R-diagrammet visar relationen mellan yttemperaturen och luminositeten hos stjärnorna. Notera den framträdande huvudserien och de olika regionerna där röda jättar och vita dvärgar dominerar. Platsen för solen är markerad och så även den rutt som en stjärna med en solmassa kommer följa under de olika faserna av sitt liv. Solens position i diagrammet är bestämd utifrån dess yttemperatur på 5800 K och dess absoluta magnitud på +4,8. Genom att titta på H-R-diagrammet är det klart att mätningarna av (L, T) för olika stjärnor bildar ett underligt mönster när de plottas i diagrammet. Stjärnorna koncentreras runt specifika områden (markerade i figuren). H-R-diagrammet är nyckeln till förståelsen om hur stjärnor utvecklas med tiden. Olika stjärnor kommer - beroende på sin massa - att flytta sig genom diagrammet längs specifika rutter. Stellär evolution i H-R-diagrammet Stjärnor tillbringar den längsta tiden av sina liv på huvudserien och bränner sakta väte i en stabil jämvikt. Detta är uppenbart anledningen till att de flesta stjärnor ligger på huvudserien, en nästan rät linje från det övre vänstra till det nedra högra hörnet i diagrammet. När väteförrådet i stjärnans kärna tar slut är inte väteförbränning längre möjligt. Detta är slutet för stjärnans tid på huvudserien och jämvikten mellan gastryck och gravitationell kontraktion i stjärnans kärna är inte längre stabil. Vätefusion äger nu rum i ett omgivande skal medan kärnan börjar krympa. När kärnan kontraherar så ökar trycket och den centrala temperaturen så att heliumkärnor i kärnan börjar sammansmälta och 6
9 Introduktion bilda tyngre grundämnen. Denna cykel kan upprepas med tyngre och tyngre grundämnen allt eftersom de lättare tar slut i kärnan. Under denna fas av en stjärnas liv är den en röd jätte. Sådana stjärnor finns i H-R-diagrammet vid sidan av huvudserien upp mot höger hörn. Högre central temperatur gör att stjärnans yttre skal expanderar och kyls ner och som en konsekvens sjunker yttemperaturen. Hela stjärnan blir väldigt stor och på grund av den lägre yttemperaturen sänder den ut det mesta av sitt ljus vid längre våglängder och blir därför röd. Trots sin låga yttemperatur, T, har alla röda jättar en hög luminositet, L, på grund av sin stora radie, R. Detta kan ses i Stefan-Boltzmanns strålningslag för svartkroppsstrålning: stjärnans skal (se ESA/ESOs övning i astronomi 3). Den kollapsade kärnan är väldigt het (vit) och stjärnan är mycket liten. En sådan stjärna kallas mycket passande för vit dvärg och är det normala slutstadiet av en sol-lik stjärnas liv. För att göra en grov uppskattning av relationen mellan luminositet, L, och yttemperatur, T, för alla huvudseriestjärnor så låt oss titta på huvudseriestjärnorna (fig. 6). Den nästan raka linjen som huvudserien utgör spänner över ungefär en storleksordning i temperatur: ( ) K. Luminositeten sträcker sig över ungefär sex storleksordningar: ( L sol ). Vi kan därför grovt uppskatta att: L T 6 för huvudseriestjärnorna. L = σ4πr 2 T 4 där σ är Stefan-Boltzmanns konstant. Typiska värden för röda jättar är R ~ 10 2 R sol, T ~ (3..4)10 3 K, så L är runt 10 3 L sol. När de senare fusionsprocesserna i stjärnors kärnor inte längre kan upprätthållas, kollapsar kärnan igen. Åter igen ökar temperaturen i kärnan och nu kastas stjärnans yttre skal ut. En så kallad planetarisk nebulosa bildas från resterna av För att ge några exempel: En tung stjärna på huvudserien med en yttemperatur på runt T stjärna = 1, K har en luminositet på ungefär L stjärna = (10/5,8) 6 L sol, eller ungefär 26 gånger solens luminositet (solens luminositet har standardvärdet 1 på luminositetsskalan). En lätt stjärna med T stjärna = 3, K har en luminositet på bara cirka 5% av solens luminositet. Introduktion a b Figur 7: Typiskt Hertzsprung-Russell-diagram för en klotformig stjärnhop Efter miljardtals år av evolution visar en klotformig stjärnhops H-R-diagram en kort huvudserie (HS) i den nedre högra delen. Ett område som kallas Röda Jättegrenen börjar vid HS och sträcker sig mot det övre högra hörnet i diagrammet. Punkten där HS viker av och röda jättegrenen ansluter kallas Turn-off-punkt. 7
10 Introduktion B-V Färgindex: En ledtråd till yttemperaturen. All information som kan fås från en stjärna finns i den strålning vi får från den. Som förklarat i Astronomiska Verktyg kan olika filter och färgsystem användas för att mäta en stjärnas ljusstyrka. I denna övning använder vi en B-bild och en V-bild. I din analys av dessa bilder kommer du att ta reda på de apparenta magnituderna, m B och m V, för ett urval av stjärnor i hopen. Sen kan du beräkna värdet på m B -m V (färgindexet B-V). Slutligen kommer du kunna bestämma stjärnornas yttemperaturer (se Astronomiska Verktyg). Introduktion H-R-diagrammet är nyckeln till en hop En stjärnhop är en grupp av stjärnor. En hops liv bestäms av livet hos de olika typerna av stjärnor inom den. Observationer av klotformiga stjärnhopar visar att det finns väldigt lite gas och stoft i dem och därför föds nya stjärnor sällan i en sådan hop. Stjärnorna vi ser i en klotformig stjärnhop är alla "vuxna" och har evolverat på olika sätt beroende på sin massa. De flesta lätta stjärnorna befinner sig på huvudserien, på grund av att lätta stjärnor förbrukar sin energi väldigt långsamt. De förbränner lugnt sitt väte och kommer fortsätta att göra så i miljardtals år till. De kommer därför att stanna länge på huvudserien. Tunga stjärnor i hopen har i motsats till lätta redan konverterat vätet i sina kärnor och blivit röda jättar. Detta hände för länge sedan så idag finns det inga heta stjärnor som fyller ut den övre delen av huvudserien (se fig. 7). Dessa stjärnor finns nu i det diagonala område som börjar vid huvudserien och sträcker sig mot det övre högra hörnet av diagrammet. Detta område kallas Jättegrenen. Punkten där huvudserien och jättegrenen möts kallas turn-off-punkten och är en viktig ledtråd till hopens ålder. I de följande uppgifterna kommer du mäta koordinaterna för denna punkt i ditt diagram och bestämma åldern för M12. 8
11 Uppgifter Observationer, datareduktion och analys Den klotformiga stjärnhopen M12 studerades den 18 juni 1999 med FORS1 instrumentet på ANIU (UT1) på VLT vid ESOs observatorium i Paranal (Chile). Till denna övning har vi valt bilder av stjärnhopens yttre delar där antalet stjärnor är mindre. Exponeringarna togs genom ett blått filter (B-band) och genom ett grönt filter (V-band för visuellt). För att observera och reducera data (processen då störningen från instrument och andra faktorer tas bort från datan) krävs stora teleskop och sofistikerade datorprogram. För astronomer börjar det intressanta analyseringen av data efter detta. I denna övning har data redan samlats in och reducerats. Vi har förenklat analysen en aning genom att välja en grupp med stjärnor som kan anses representera populationen i hela stjärnhopen. Tips för analysen av bilderna För att analysera bilderna måste B och V magnituderna för varje stjärna mätas noga. Fel som görs i början av denna övning kommer att påverka de slutliga resultaten. De 45 stjärnorna delas in i sex grupper: 1 Fem stjärnor nr. 1 till 5 träningsstjärnor 2 Fyra stjärnor nr. 6 till 9 kalibreringsstjärnor 3-6 De återstående stjärnorna delas in i fyra grupper (A, B, C och D) för att reducera arbetet och ge tillräckligt med tid för noggranna mätningar. För att göra mätningarna så noggranna som möjligt föreslår vi följande procedur: Sätt måttstock (se Fig. 8-9 nedan) på stjärnan och flytta den fram och tillbaks. Hitta punkterna där värdena är för höga och för låga. Placera sedan måttstocken i mitten mellan dessa värden och läs av. Upprepa detta några gånger och beräkna ett medelvärde. Låt olika personer i varje grupp mäta varje stjärna minst två gånger och beräkna medelvärden för dessa mätningar. Mellan mätningarna upprepa träningen ovan för att förvissa dig om att de utförs konsistent på samma sätt. Uppgift 1 B-band, träning För träningsstjärnorna (nr. 1 till 5) är magnituderna givna i tabellen (Fig. 10).? Använd dessa för att träna dig på att använda måttstocken genom att göra mätningar i B-bilden (Fig 8) och jämför dem med tabellen. Förvissa dig om att du får samma resultat. Uppgift 2 B-band, kalibrering Varje grupp skall göra kalibreringen (nr. 6-9) självständigt. Mätningarna kan sedan kalibreras med resultaten från andra grupper.? Mät kalibreringsstjärnorna i B-bilden (Fig. 8). Lägg till dessa värden i tabellen och jämför resultaten med andra gruppers. Om där finns skillnader, titta en gång till på dessa stjärnor och på träningsstjärnorna. Uppgift 3 B-band, magnituder? Mät den blå magnituden (m B) för varje märkt stjärna i ytan som du tilldelats (A, B, C eller D) i Fig. 8 och lägg till mätningarna i tabellen. Uppgift 4 V-band, träning? Öva genom att göra mätningar i V-bilden (Fig. 9) och jämför med de som är givna i tabellen. Förvissa dig om att resultaten är desamma. Uppgift 5 V-band, kalibrering? Mät kalibreringsstjärnorna i V-bilden (Fig. 9), skriv in i tabellen och jämför resultaten med andra gruppers. Om där finns skillnader, titta på dessa stjärnor och på kalibreringsstjärnorna igen. Uppgifter 9
12 Uppgifter Uppgifter Uppgift 6 V-band, magnituder? Mät den gröna magnituden (m V) för varje märkt stjärna i ytan som du tilldelats (A, B, C eller D) i Fig. 9 och lägg till mätningarna i tabellen. Uppgift 7 Färgindex? Beräkna värdet på m B m V för varje stjärna och för in resulatet i tabellen. Uppgift 8 Yttemperaturer? Använd diagrammet, Fig 3 i Astronomiska Verktyg, för att omvandla värdena på m B m V till yttemperaturer, T, för stjärnorna och lägg till resultatet i tabellen. Uppgift 9 H-R-diagrammet Huvudserien för stjärnhopen Hyaderna har plottats som referens i diagrammet (Fig. 10). Observera att den absoluta magnituden, M V, har mätts för Hyaderna.? Plotta den apparenta magnituden (m V) mot den beräknade yttemperaturen (T) tillhörande M12 stjärnorna i samma diagram. Uppgift 10 Huvudserieanpassning: Avståndsmodul och stoft som försvagar det stjärnljus som passerar genom detta. Stoft och gas färgar också stjärnljuset rött genom en process som kallas Rayleigh-spridning (som är mest effektiv vid korta våglängder, dvs. blått ljus). Dessa två processer går under namnet "interstellär extinktion". Vi vill att du korrigerar för en del av den påverkan som extinktionen gör på stjärnljuset (den gör magnituden av de observerade stjärnorna för hög och därför blir det beräknade avståndet för stort) 1. Den korrigerade avståndsmodulen m- M är: m M A, där A är en korrektionsfaktor för extinktionen. Detta förändrar avståndsekvationen något: D=10 (m-m-a+5)/5 För M12 har A bestämts till 57 magnituder (i V-bandet, vilket vi använder för att bestämma m M) av Harris et al.?? Beräkna det nya avståndet med korrigeringen för interstellär extinktion. Skiljer sig det korrigerade avståndet från det okorrigerade i uppgift 11? För stjärnorna i M12 känner vi nu (m V, T) och från Hyades mätningarna känner vi (M V, T) för en standard huvudserie. Avståndsmodulen (se Astronomiska Verktyg ) för M12 är förskjutningen längs den vertikala axeln mellan de två plottade huvudserierna.? Beräkna avståndsmodulen m V M V for M12. Uppgift 11 Avståndet till M12? Använd avståndsmodulen och avståndsekvationen (se Astronomiska Verktyg ) för att bestämma avståndet D till M12. Uppgift 12 Extinktionskorrektion Avståndet du precis har beräknat är inte helt korrekt eftersom vår galax innehåller mycket gas 10? Diskutera skillnaderna och vad denna korrektion (en av många som astronomer använder dagligen) innebär för vår förståelse om storleken på Universum. Uppgift 13 Vetenskapsmän har tidigare beräknat avståndet till stjärnhopen till D = 4900 parsec med den ursprungliga mycket större datamängden. Om ditt svar skilljer sig med mindre än 20% från detta värde har du gjort mycket noggranna mätningar, goda beräkningar och du kan vara mycket stolt över ditt resultat! 1 Detta är som tidigare nämnts en förenkling eftersom där också finns en liten påverkan från extinktionen på B-V termen.
13 Figure 8: Bilden på B-Bandet
14 Figur 9: Bilden av V-Bandet
15 Uppgifter Figur 10: Värdetabell Stjärna Forskarens värde ESA/ESO's mätningar/beräkningar B V B-V T B V B-V 1 18,82 17, ,70 17, ,02 18, ,00 18, ,32 18, ,30 18, ,96 19, ,90 19, , , T Uppgifter 13
16 Uppgifter Figur 11: Diagram för plottning Resultatet av mätningarna i uppgift 1-9 ska plottas här. Den kalibrerade huvudserien för Hyaderna är tagen från ESAs satellit HIPPARCOS (från de Bruijne et al., 2001). Uppgifter 14
17 Uppgifter Om ditt resultat har större fel kan det finnas flera skäl till detta. Några orsaker kan vara: Är dina mätningar av magnituderna tillräckligt noggranna? Kan du komma på någon mer sofistikerad metod för reducering av data och passning till huvudserien? Finns det andra sätt att förbättra dina resultat? Utvecklingen av klotformiga stjärnhopar Formen på huvudserien är i stort sett samma för alla klotformiga stjärnhopar, oavsett deras ålder. Den metod som används ovan för att anpassa huvudserien kan också användas för andra Uppgifter Figur 12: Utvecklingen av en teoretisk stjärnhop Denna serie av H-R diagram har skapats genom att beräkna hur ekvationerna för klotformade stjärnhopar påverkar en grupp stjärnor med tiden. I 12a ligger de största och mest ljusstarka stjärnorna längs huvudserien (T>10000K) medan de mindre stjärnorna fortfarande är i inledningsskedet av väteförbränningen (låg temperatur, låg luminositet). I 12b har de största stjärnorna förbrukat det mesta av vätet i kärnan och förbränningen fortsätter i ett yttre skal. Deras luminositet minskar och de blir rödare, de har rört sig bort från huvudserien, jättegrenen uppstår och turn-off-punkten blir synlig. Stjärnor som inte är heta och luminösa är kvar i den övre delen av huvudserien. I 12c-e är den övre delen av huvudserien i stort sett övergiven, medan populationen i jättegrenen har ökat. Nedre delen av huvudserien visar en en stor population av stjärnor med massor nära solens och yttemperaturer mellan 4000 K och 8000 K. Dessa stjärnor kommer att vara i denna fas i ytterligare miljardtals år (omarbetat från R. Kippenhahn). 15
18 Uppgifter Uppgifter stjärnhopar med annan ålder för att bestämma deras avstånd. Emellertid visar observationer av olika H-R diagram för olika stjärnhopar att den övre delen av huvudserien ändrar form beroende på stjärnhopens ålder (se Fig. 12). I äldre stjärnhopar har de mest luminösa stjärnorna utvecklats och rört sig till jättegrenen. Detta resulterar i att den övre delen av huvudserien blir kortare och kopplingen mellan huvudserien och jättegrenen (turn-off-punkten) rör sig nedåt, liknande ett ljus som brinner. Därför måste vi tillägga att turn-off-punktens position är en viktig ledtråd för att bestämma stjärnhopens ålder. Uppgift 14 Turn-off-punkten: från magnituder till luminositet? Bestäm den apparenta magnituden för en stjärna vid turn-off-punkten för M12. Beräkna luminositeten för denna stjärna relativt solens luminositet genom att använda formeln som ges i Astronomiska Verktyg. Turn-off-punkt: från luminositet till massa När luminositeten är känd kan vi bestämma massan på stjärnan genom att använda mass-luminositets-relationen. För stjärnor på huvudserien finns det en observerad korrelation mellan massa och luminositet, där luminositet och massa uttrycks relativt värdena för solen (L sol = W, M sol = kg): Turn-off-punkt: från massa till ålder Livstiden t av en stjärnas huvudseriefas beror på dess luminositet och massa. En stjärna med högre luminositet förbränner mer väte varje sekund än en stjärna med låg luminositet. Alltså minskar massan hos en stjärna med hög luminositet snabbare än en stjärna med låg luminositet och ju lägre luminositet desto längre kan stjärnan brinna. För två stjärnor med olika massa har den tyngre mer material att förbränna, så vi ser att stjärnans livstid är direkt proportionell mot dess massa och omvänt proportionell mot dess luminositet. Genom att använda mass-luminositetsrelationen finner vi livstiden som funktion av massan: t M -2,8 Uppgift 16? Ta massan härledd i uppgift 15 och uppskatta åldern av den klotformiga stjärnhopen relativt till solens uppskattade ålder när den kommer lämna huvudserien, 8, år. Som slutsats kan sägas att hela Universum måste vara äldre än åldern framräknad i uppgift 16. Bestämning av diametern L = M 3,8 Uppgift 15? Omvandla den i uppgift 14 härledda luminositeten till en massa relativt solens massa. För att bestämma M12 diameter behöver vi veta dess vinkeldiameter. I fig. 13 ser man att det finns många stjärnor i hopens centrum. Diskutera vilka stjärnor som tillhör de yttre delarna av hopen. 16
19 Extrauppgifter Extrauppgifter Figur 13: Överblicksbild av en klotformig stjärnhop Denna bild visar M12. Varje sida av bilden motsvarar 25 grader (från Digitized Sky Survey). Uppgift 17?? Mät vinkeldiametern, a, på M12 i centimeter och konvertera värdet till radianer (se "Matematiska Verktyg"). Beräkna sen diametern, d (se approximationen för små vinklar på sidan 8 i "Matematiska Verktyg"). Som avstånd kan du antingen använda det du själv har fått fram eller forskarnas värde på D=4900 parsec. Bestämning av det totala antalet stjärnor För att uppskatta det totala antalet stjärnor, N, i den klotformiga stjärnhopen måste vi göra några antaganden: 1. Hopen består av en blandning av alla typer av stjärnor men vi antar att medelstjärnan är sol-lik, det vill säga att en stjärnas absoluta magnitud är densamma som solens. 2. Vi antar att varje stjärna bidrar till den tota- 17
20 Extrauppgifter la luminositeten på hela hopen. I verkligheten skymmer stoft och andra stjärnor helt eller delvis en del andra stjärnor. Uppgift 18 M12s absoluta magnitud är M hop = 7,32 Hopens totala luminositet mätt i mått av solens luminositet beräknas från L hop /L sol = 2,512 (M_sol-M_hop) Kom ihåg: M sol = 4,8. Extrauppgifter Eftersom L hop N L sol och genom att använda antagande 1, är värdet på L hop /L sol lika med N. På grund av antagande 2 kan vi emellertid förvänta oss att det riktiga värdet av N är lite högre än L hop /L sol. 18
21 Ytterligare läsning Vetenskapliga artiklar de Bruijne, J.H.J., Hoogerneerf, R., and de Zeeuw, P.T., 2001, A&A, 367, : A Hipparcos study of the Hyades open cluster. Cragin, M., Lucyk, J., Rappaport, B.: The Deep Sky Field Guide to Uranometria , Willmann-Bell, Inc. Harris, W.E.: Catalog of parameters for Milky Way Globular Clusters, Revised: June 1999 ( Rosenberg, A., Saviane, I., Piotto, G., Aparicio,A., 1999, AJ, 118, : Galactic Globular Cluster Relative Ages Chaboyer, B., Demarque, P., Sarajedini, A., 1996, ApJ, : Globular Cluster Ages and the Formation of the Galactic Halo Läs mer om interstellär extinktion på: Se även länkar på: Ytterligare läsning 19
22 Colophon ESA/ESOs övningsserie i astronomi Övning 4: Mätning av en klotformig stjärnhops avstånd och ålder 2 a upplagan ( ) EUROPEAN SOUTHERN OBSERVATORY Education and Public Relations Service Producerad av: Hubble European Space Agency Information Centre och European Southern Observatory: (Pdf-versioner av detta material och relaterade internetlänkar finns på denna adress) Colophon Postadress: European Southern Observatory Karl-Schwarzschild-Str. 2 D Garching bei München Tyskland Telefon: (eller ) Fax: (eller ) info@astroex.org Text av: Arntraud Bacher, Jean-Marc Brauer, Rainer Gaitzsch, och Lars Lindberg Christensen Grafik och layout: Martin Kornmesser Översättning: Martin Lundqvist Svensk Korrekturläsning: Britt Sjöberg Koordination: Lars Lindberg Christensen och Richard West Varma tack till Jesper Sollerman för reduktionen av originaldatan, till Nina Troelsgaard Jensen, Frederiksberg Seminarium, för kommentarer, och till Jos de Bruijne för att han delat med sig av sin magnifika Hipparcos-data. Och vi vill också tacka de många människor som förbättrade den andra versionen av denna övning: Anne Vœrnholt Olesen, Ole Hjort Rasmussen, Helle och Henrik Stub, Danmark; Johann Penzl, Tyskland; Thibaut Plisson, USA; Marina Rejkuba och Manuela Zoccali, ESO. 20
23 Lärarens Guide Kort sammanfattning Vi mäter blå (m B ) och gröna (m V ) magnituder av utvalda stjärnor i de yttre regionerna av en klotformig stjärnhop visad i bilder från VLT. Vi konverterar (m B -m V ) till stjärnornas yttemperaturer (T) och plottar m V som funktion av T i ett Hertzsprung-Russell-diagram. Hopens huvudserie som ses i det plottade diagrammet jämförs med en avståndskalibrerad standardhuvudserie från den närliggande hopen Hyaderna. Avståndet till hopen kan bestämmas genom huvudserieanpassning och användning av avståndsmodulen. Hopens ålder, som råkar sammanfalla med en lägre gräns på Universums ålder, kan uppskattas från positionen på turn-off-punkten på huvudserien. Denna lärarguide innehåller lösningar till problemen tillsammans med kommentarer och diskussioner om gjorda approximationer och förenklingar och även ett ytterligare betraktande om stjärnors livscykler. Målet är att maximera användbarheten av övningarna och assistera läraren under förberedelserna. Mer om stjärnors liv En stjärnas livstid är den tid som den stannar på huvudserien. Vi uppskattar solens livstid och sen en stjärnas livstid i förhållande till solens. En protostjärna formas från interstellär materia. Normalt består denna materia av 74% väte, 25% helium och 1% tunga grundämnen. När den inre temperaturen i en protostjärna når ett antal miljoner kelvin kan den börja förbränna väte och blir en huvudseriestjärna. Fyra vätekärnor sammansmälter och bildar en heliumkärna. Eftersom massan av en heliumkärna bara är 99,3% av massan hos fyra vätekärnor konverteras den resterande massan (7%) till energi. For varje kilo stjärnmateria konverteras 007 kg till energi. Från Einsteins lag (E=Mc 2 ) kan vi beräkna den konverterade energin till 6, J/kg. (c är ljushastigheten, m/s). Lärarens Guide Solens luminositet är L sol =3, W (W = J/s). Från detta beräknar vi massan av väte som förbränns varje sekund: M = 3, / (6, ) = 6, kg/s Stjärnan kommer att lämna huvudserien när ungefär 11% av vätemassan är uppbränd eftersom kärnan då blir instabil. Om vi tar solens totala massa M sol = 2, kg kan vi uppskatta massan på det väte som är möjligt att förbränna under stjärnans livstid: = 1, kg. Genom att dela massan med massförlusten per sekund kan vi uppskatta solens totala livstid på huvudserien till: 2, s = 8, år, 1 år = s = 3, s (eller mer än 8 miljarder år). Observationer av solen visar att den är ungeför 4 miljarder år gammal, så att man kan förvänta sig att den ska finnas kvar på huvudserien i ytterligare 4 miljarder år. När vi vet solens livstid kan vi beräkna livstiden av vilken stjärna som helst mätt i solens livslängd. En stjärnas livstid beror på dess massa. Vi kommer att förenkla de komplexa argumenten för att få en enkel men användbar formel: Förrådet av väte som en stjärna har är proportionellt mot dess massa och t är omvänt proportionellt mot dess luminositet så: t M/L 21
24 Lärarens Guide Hastigheten med vilken en stjärna gör sig av med sin energi ökar kraftigt med dess massa. Experimentella resultat för huvudseriestjärnor ges ungefär av: L = M 3,8, den så kallade mass-luminositets relationen. Exponenten 3,8 är en kompromiss. Den kommer av den approximativa genomsnittet av stjärnmassor ( ) M sol. Så i slutsatsen vi drar (approximativt): t M/L = M/M 3,8 = M 2,8 ; ser vi att tunga stjärnor evolverar mycket snabbare än solen och lättare stjärnor saktare. Några exempel: En tung stjärna med ungefär 10 solmassor kommer ha en livstid på ungefär t=0016 t sol, eller ungefär 13 miljoner år. En lätt stjärna med ungefär 6 solmassor kommer ha en livstid på ungefär t=4,2 t sol eller 34 miljarder år. Detta är en mycket högre ålder än Universums egen ålder, därför har ingen lätt stjärna i Universum ännu lämnat huvudserien. Urval av stjärnor Lärarens Guide Den klotformiga stjärnhopen M12 innehåller ungefär stjärnor. Bilden använd i denna övning togs med FORS1 vid ANIU (UT1 av VLT). Den täcker endast en liten del av de yttre regionerna av hopen, valda för att undvika de tätaste delarna av hopen där stjärnorna verkar överlappa varandra. Vi har valt 45 stjärnor som är representativa för hopens population. Storleken på detta urval betyder att arbetsbelastningen på studenterna är rimlig och att deras mätningar kommer vara jämförbara med vetenskapliga resultat som är baserade på ett mycket större urval av stjärnor. En bild på M12 tagen från Digitized Sky Survey (DSS) används för extrauppgifterna. Analys av bilden Vi föreslår att varje grupp använder en overhead med måttstocken på. Vi har inkluderat måttstocken på varje bild så det går att kontrollera att inte kopieringen har ändrat skalan och studenterna bör kontrollera att deras genomskinliga måttstock stämmer överens med den på bilderna. Vi föreslår att arbetet delas upp mellan olika grupper av studenter och vi har delat upp bilderna i sex delar (träning, kalibrering, A, B, C och D). Magnituderna är givna för de fem träningsstjärnorna. Dess stjärnor kan användas för att öva i att använda måttstocken och få riktiga och repeterbara resultat. De fyra kalibreringsstjärnorna kan sen mätas av varje grupp och användas för att kalibrera mätningarna mellan grupperna. För att reducera felen föreslår vi att varje stjärna ska mätas två gånger av varje grupp och att ett medelvärde tas. Det är väldigt viktigt att öva med måttstocken innan man börjar med de riktiga mätningarna. Att göra mätningarna är inte bara att placera måttstocken över bilden utan en stjärna med magnituden 18,5 ska vara helt inom den rätta cirkeln och bakgrundshimlen ska bara precis röra vid kanten. Studenterna ska mäta varje stjärna på detta viset. Om mätningarna hela tiden är över eller under det rätta värdet kan en korrektion göras genom att addera eller subtrahera en passande konstant. Fig. 3 i Astronomiska Verktyg används för att konvertera färgindexet B-V till temperatur. Ett set av tabeller som kan skrivas ut finns med men användandet av kalkylprogram (till exempel Excel) rekommenderas för att förenkla beräkningarna och visningen av B-V färgindex. Uppgift 1-8 Forskarnas och även våra egna mätningar finns i en tabell (se fig. 1). 22
25 Lärarens Guide Forskarens värde ESA/ESO's mätningar/beräkningar Stjärna B V B-V T B V B-V T 1 18,82 17, ,70 17, ,02 18, ,00 18, ,32 18, ,30 18, ,96 19, ,90 19, , , ,94 18, ,00 18, ,80 19, ,80 19, ,06 18, ,00 18, ,20 18, ,10 18, ,99 18, ,00 18, , , ,32 16, ,20 16, ,18 18, ,10 18, ,53 18, ,60 18, , , ,31 18, ,30 18, ,57 17, ,70 17, ,95 18, ,90 18, ,48 16, ,50 16, ,66 18, ,60 18, ,77 19, ,80 19, ,52 18, ,50 18, ,50 18, ,50 18, ,23 17, ,30 17, , , ,04 18, ,90 18, ,76 17, ,80 18, ,88 18, ,90 18, ,27 17, ,30 17, ,14 17, ,20 17, ,84 19, ,80 19, ,62 17, ,60 17, ,92 19, ,90 19, , , ,82 17, ,80 18, ,95 18, ,80 18, ,33 18, ,30 18, , , ,92 19, ,90 19, ,29 18, ,30 18, ,91 17, ,00 16,90 1, ,19 18, ,20 18, ,42 18, ,30 18, ,36 18, ,30 18, ,12 17, ,20 17,20 1, Lärarens Guide Figur 1: Lösningar till uppgift 1 till 8 Tabellen ger stjärnornas nummer och forskarnas värden på B, V, B-V. Våra egna mätningar är också indikerade. 23
26 Lärarens Guide Figur 2: Hertzsprung- Russell-diagram av M12 Diagrammet visar våra mätningar (rött) tillsammans med forskarnas resultat (blått). Lärarens Guide Uppgift 9-13 Den nedre delen av diagrammet (fig. 3) är ganska kort och resultaten är väldigt känsliga för lutningen av den bäst passande linjen dragen mellan datapunkterna. För att förenkla processen och undvika missvisande resultat antar vi att formen på huvudserien är ungefär densamma för alla stjärnhopar, oavsett ålder, och alltså att alla huvudserier är parallella. Därför kan vi använda lutningen av referenshuvudserien från Hyaderna som guide. Värdet på D beror på positionen av huvudserie-linjen i diagrammet. Harris ger m V -M V = 14,02 för M12. Vi uppmätte 13,9. Harris ger värdet på D hop = 4,9 kpc. Detta värde är framtaget genom att inkludera den interstellära extinktionen mellan oss och M12 (57 magnituder) i avståndsekvationen för M12, så m-m = 5 log D Vi beräknar D=10 (m-m+5)/5 = 10 3,78 = 6,026 kpc utan korrektion för interstellär extinktion och D= 10 (m-m- 57+5)/5 = 10 3,666 = 4,634 kpc med korrektion för interstellär extinktion. För de följande beräkningarna använder vi det extinktionskorrigerade avståndet, 4,634 kpc. Uppgift I våra mätningar har en stjärna vid turn-off-punkten en apparent magnitud på 18,7. Forskare har mätt turn-off-punkten att vara 18,3 (Rosenberg et.al.). Vi beräknar nu (L hop /L sol ) = (D hop /D sol ) 2 (I hop /I sol ) Beräkning av ration (I hop /I sol ): Eftersom I sol är mycket större än I cl blir ration ett väldigt litet tal så vi beräknar I sol /I hop och tar sen inversen av värdet för de fortsatta beräkningarna (I sol /I hop ) = 10 (m_hop m_sol)/2,5 = 10 (18,7 ( 26,5))/2,5 = 10 18,08 = 1, så (I hop /I sol ) = 8,
27 Lärarens Guide Figure : Hertzsprung-Russelldiagram av M12 och stjärnhopen Hyaderna Detta diagram inkluderar H-R diagrammet för Hyaderna (övre delen) tillsammans med det av M12, med författarens värden. Linjerna representerar interpolationen av stjärnorna på huvudserien. Lärarens Guide 25
28 Lärarens Guide Fortsatta beräkningar: (D hop /D sol ) = (4634 3, ) / 1, = 9, (L hop /L sol ) = (D hop /D sol ) 2 (I hop /I sol ) = (9, ) 2 8, = 0.76 (M hop /M sol ) = (L hop /L sol ) 1/3,8 = 93 (t hop /t sol ) = (M hop /M sol ) -2,8 = 1,224 t hop = 1,224 t sol = 1,224 8, = år En alternativ och något enklare metod för att bestämma hopars åldrar finns. Den är empirisk (baserad på mätningar) och därför mindre intuitiv. Den består av att applicera följande observerade relation: M V (TO) = 2,70 log 10 (t) + 1,41, Lärarens Guide där M V (TO) är den absoluta magnituden för turn-off-punkten och t hopens ålder i miljarder år. Eftersom M V (TO) = m V (TO) (m V (TO) M V (TO) ) = m V (TO) (m V M V ) (avståndsmodulen är densamma för hela hopen) får vi: m V (TO) (m V M V ) = 2,7 log (t) + 1,41, vilket reduceras till: [(m_v(to) - (m_v M_V)) 1,41) / 2,7] t = 10 Resulterande åldrar från beräkningar av olika set av turn-off-magnitud och avstånd genom att använda den först föreslagna metoden och genom att använda den andra föreslagna metoden beskriven ovan: Text i fet stil är den bästa uppskattningen från litteraturen. Olika metoder för bestämning av klotformiga stjärnhopars ålder beskrivs av Chaboyer et. al, vilka finner åldrar mellan 11, år och 15, år för M12. Uppmätt Turn-off- Ålder, metod 1 Ålder, metod 2 Beräknat avstånd [pc] magnitud [mv] [miljarder år] [miljarder år] 18, , 0 18, , , , 8 15, 2 18, , 0 11, 6 18, , 7 12, 8 18, , 0 13, 5 18, (ext. ej inkl. ) 6, 8 18, 0 26
29 Lärarens Guide Extrauppgifter Uppgift 17 d = D hop a = , = 17,76 pc Hopen slutar där dess densitet når bakgrundsstjärnornas densitet. cm Radianer 4, 8 Vinkeldiameter, a 3, 0 grader 2,2 radianer ,833 x Värdet på vinkeldiametern, a, korresponderar till = 13,2 bågminuter. I atlasen Uranometria 2000 är vinkeldiametern noterad till 14,5 bågminuter. Uppgift 18 L hop /L sol = 2,512 (M_sol M_hop) = 2,512 4,8 ( 7,32) ~ 7500 Det totala antalet stjärnor i M12 är ungefär enligt Carl Grillmair (SIRTF Science Center, privat kommunikation, 2002). Lärarens Guide 27
30 Lärarens Guide Figur 4: Måttstock Denna måttstock behöver bli kopierad på overheadfilm och använd för mätningarna i uppgift 1 till 6. Lärarens Guide
31
32
Introduktion. Stjärnor bildas, producerar energi, upphör producera energi = stjärnor föds, lever och dör.
 Stjärnors födelse Introduktion Stjärnor består av gas i jämvikt: Balans mellan gravitation och tryck (skapat av mikroskopisk rörelse). Olika källor till tryck i olika utvecklingsskeden. Stjärnor bildas,
Stjärnors födelse Introduktion Stjärnor består av gas i jämvikt: Balans mellan gravitation och tryck (skapat av mikroskopisk rörelse). Olika källor till tryck i olika utvecklingsskeden. Stjärnor bildas,
Stjärnors födslar och död
 Stjärnors födslar och död Stjärnors egenskaper Uppkomst Avstånd Rörelse Skenbar ljusstyrka Färg temperatur Energiproduktion Verklig ljusstyrka Utveckling Ovanliga stjärnor Slutstadier Rymden är inte bara
Stjärnors födslar och död Stjärnors egenskaper Uppkomst Avstånd Rörelse Skenbar ljusstyrka Färg temperatur Energiproduktion Verklig ljusstyrka Utveckling Ovanliga stjärnor Slutstadier Rymden är inte bara
Översiktskurs i astronomi Lektion 7: Solens och stjärnornas energiproduktion samt utveckling
 Översiktskurs i astronomi Lektion 7: Solens och stjärnornas energiproduktion samt utveckling Upplägg Energiprocesser i stjärnor Energitransport i stjärnor Solens uppbyggnad Solfläckar Solliknande stjärnors
Översiktskurs i astronomi Lektion 7: Solens och stjärnornas energiproduktion samt utveckling Upplägg Energiprocesser i stjärnor Energitransport i stjärnor Solens uppbyggnad Solfläckar Solliknande stjärnors
Universums tidskalor - från stjärnor till galaxer
 Universums tidskalor - från stjärnor till galaxer Fysik och Kemidagarna 2017 Prof. Peter Johansson Institutionen för Fysik, Helsingfors Universitet Matematisk-naturvetenskapliga fakulteten/ Peter Johansson/
Universums tidskalor - från stjärnor till galaxer Fysik och Kemidagarna 2017 Prof. Peter Johansson Institutionen för Fysik, Helsingfors Universitet Matematisk-naturvetenskapliga fakulteten/ Peter Johansson/
Innehåll. Innehåll. Verktyg. Astronomiska Verktyg. Matematiska Verktyg
 Innehåll Verktyg Magnituder... sidan 2 Apparent magnitud... sidan 2 Absolut magnitud... sidan 3 Olika färger, olika magnituder... sidan 3 Från B-V färgindex till temperatur... sidan 4 Avståndsekvationen...
Innehåll Verktyg Magnituder... sidan 2 Apparent magnitud... sidan 2 Absolut magnitud... sidan 3 Olika färger, olika magnituder... sidan 3 Från B-V färgindex till temperatur... sidan 4 Avståndsekvationen...
Stjärnors död samt neutronstjärnor. Planetära nebulosan NGC (New General Catalogue) Kattöganebulosan
 Stjärnors död samt neutronstjärnor Planetära nebulosan NGC (New General Catalogue) 65 43 Kattöganebulosan Introduktion En stjärna lever huvuddelen av sitt liv i huvudserien. Förutsättningen för detta är
Stjärnors död samt neutronstjärnor Planetära nebulosan NGC (New General Catalogue) 65 43 Kattöganebulosan Introduktion En stjärna lever huvuddelen av sitt liv i huvudserien. Förutsättningen för detta är
Uppgifter. Uppgifter. Uppgift 2. Uppgift 1
 Uppgift 1 Uppgift 2 Det första målet är att beräkna vinkeldiametern på ringen, det vill säga ringens apparenta diameter sedd från jorden i bågsekunder. Detta är vinkel a. De relativa positionerna för stjärnorna
Uppgift 1 Uppgift 2 Det första målet är att beräkna vinkeldiametern på ringen, det vill säga ringens apparenta diameter sedd från jorden i bågsekunder. Detta är vinkel a. De relativa positionerna för stjärnorna
Från nebulosor till svarta hål stjärnors födelse, liv och död
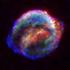 Från nebulosor till svarta hål stjärnors födelse, liv och död Stjärnor Stjärnor är enorma glödande gasklot. Vår sol är en typisk stjärna. Dess diameter är 1 400 000 km och dess massa är 2. 10 30 kg. Temperaturen
Från nebulosor till svarta hål stjärnors födelse, liv och död Stjärnor Stjärnor är enorma glödande gasklot. Vår sol är en typisk stjärna. Dess diameter är 1 400 000 km och dess massa är 2. 10 30 kg. Temperaturen
Förord... sidan 2. Sena faser i lågmassiva stjärnors liv... sidan 3 Avståndet till Planetariska Nebulosor... sidan 4 Kattögenebulosan...
 Innehåll ESA/ESOs Övningsserie i Astronomi 3 Förord Förord... sidan 2 Introduktion Sena faser i lågmassiva stjärnors liv... sidan 3 Avståndet till Planetariska Nebulosor... sidan 4 Kattögenebulosan...
Innehåll ESA/ESOs Övningsserie i Astronomi 3 Förord Förord... sidan 2 Introduktion Sena faser i lågmassiva stjärnors liv... sidan 3 Avståndet till Planetariska Nebulosor... sidan 4 Kattögenebulosan...
LÖSNING TILL TENTAMEN I STJÄRNORNA OCH VINTERGATAN, ASF010
 Teoretisk fysik och mekanik Institutionen för Fysik och teknisk fysik Chalmers &Göteborgs Universitet LÖSNING TILL TENTAMEN I STJÄRNORNA OCH VINTERGATAN, ASF010 Tid: 25 augusti 2010, kl 8 30 13 30 Plats:
Teoretisk fysik och mekanik Institutionen för Fysik och teknisk fysik Chalmers &Göteborgs Universitet LÖSNING TILL TENTAMEN I STJÄRNORNA OCH VINTERGATAN, ASF010 Tid: 25 augusti 2010, kl 8 30 13 30 Plats:
Astronomi. Vetenskapen om himlakropparna och universum
 Astronomi Vetenskapen om himlakropparna och universum Solsystemet Vi lever på planeten jorden (Tellus) och rör sig i en omloppsbana runt en stjärna som vi kallar solen. Vårt solsystem består av solen och
Astronomi Vetenskapen om himlakropparna och universum Solsystemet Vi lever på planeten jorden (Tellus) och rör sig i en omloppsbana runt en stjärna som vi kallar solen. Vårt solsystem består av solen och
Universums expansion och storskaliga struktur Ulf Torkelsson
 1 Hubbles lag Föreläsning 13/5 Universums expansion och storskaliga struktur Ulf Torkelsson Den amerikanske astronomen Vesto M. Slipher upptäckte redan på 1910-talet att ljuset från praktiskt taget alla
1 Hubbles lag Föreläsning 13/5 Universums expansion och storskaliga struktur Ulf Torkelsson Den amerikanske astronomen Vesto M. Slipher upptäckte redan på 1910-talet att ljuset från praktiskt taget alla
Solens energi alstras genom fusionsreaktioner
 Solen Lektion 7 Solens energi alstras genom fusionsreaktioner i dess inre När solen skickar ut ljus förlorar den också energi. Det måste finnas en mekanism som alstrar denna energi annars skulle solen
Solen Lektion 7 Solens energi alstras genom fusionsreaktioner i dess inre När solen skickar ut ljus förlorar den också energi. Det måste finnas en mekanism som alstrar denna energi annars skulle solen
Stjärnors struktur och utveckling Ulf Torkelsson
 Föreläsning 22/4 Stjärnors struktur och utveckling Ulf Torkelsson 1 Observationer av stjärnhopar I allmänhet är det svårt att säga något om stjärnutvecklingen direkt från observationer av stjärnor i vår
Föreläsning 22/4 Stjärnors struktur och utveckling Ulf Torkelsson 1 Observationer av stjärnhopar I allmänhet är det svårt att säga något om stjärnutvecklingen direkt från observationer av stjärnor i vår
Orienteringskurs i astronomi Föreläsning 1, Bengt Edvardsson
 Orienteringskurs i astronomi Föreläsning 1, 2014-09-01 Bengt Edvardsson Innehåll: Korta frågor och svar Anteckningarna är en hjälp vid läsningen av boken men definierar inte kursen. Första föreläsningen
Orienteringskurs i astronomi Föreläsning 1, 2014-09-01 Bengt Edvardsson Innehåll: Korta frågor och svar Anteckningarna är en hjälp vid läsningen av boken men definierar inte kursen. Första föreläsningen
Hertzsprung-Russell-diagrammet Ulf Torkelsson
 1 Stjärnors temperatur Föreläsning 26/2 Hertzsprung-Russell-diagrammet Ulf Torkelsson Om vi antar att en stjärna strålar som en svartkropp så kan vi bestämma dess temperatur genom att studera dess spektrum.
1 Stjärnors temperatur Föreläsning 26/2 Hertzsprung-Russell-diagrammet Ulf Torkelsson Om vi antar att en stjärna strålar som en svartkropp så kan vi bestämma dess temperatur genom att studera dess spektrum.
Dramatik i stjärnornas barnkammare av Magnus Gålfalk (text och bild)
 AKTUELL FORSKNING Dramatik i stjärnornas barnkammare av Magnus Gålfalk (text och bild) Där stjärnor föds, djupt inne i mörka stoftmoln, händer det märkliga och vackra saker. Med hjälp av ett teleskop och
AKTUELL FORSKNING Dramatik i stjärnornas barnkammare av Magnus Gålfalk (text och bild) Där stjärnor föds, djupt inne i mörka stoftmoln, händer det märkliga och vackra saker. Med hjälp av ett teleskop och
Stjärnors spektralklasser; dubbelstjärnor Ulf Torkelsson
 1 Spektralklasser Föreläsning 15/4 Stjärnors spektralklasser; dubbelstjärnor Ulf Torkelsson I början på 1900-talet upprättade Annie Jump Cannon vid Harvard-observatoriet ett klassifikationssystem för stjärnspektra.
1 Spektralklasser Föreläsning 15/4 Stjärnors spektralklasser; dubbelstjärnor Ulf Torkelsson I början på 1900-talet upprättade Annie Jump Cannon vid Harvard-observatoriet ett klassifikationssystem för stjärnspektra.
Solen och andra stjärnor 24 juli Stefan Larsson. Mer kap 3 Stjärnors egenskaper
 Solen och andra stjärnor 24 juli 2006 Stefan Larsson Mer kap 3 Stjärnors egenskaper Spectralklasser Vilka spektrallinjer som finns i en stjärnas spektrum och hur starka de är beror i första hand på temperaturen
Solen och andra stjärnor 24 juli 2006 Stefan Larsson Mer kap 3 Stjärnors egenskaper Spectralklasser Vilka spektrallinjer som finns i en stjärnas spektrum och hur starka de är beror i första hand på temperaturen
Relativitetsteorins grunder, våren 2016 Räkneövning 6 Lösningar
 elativitetsteorins grunder, våren 2016 äkneövning 6 Lösningar 1. Gör en Newtonsk beräkning av den kritiska densiteten i vårt universum. Tänk dig en stor sfär som innehåller många galaxer med den sammanlagda
elativitetsteorins grunder, våren 2016 äkneövning 6 Lösningar 1. Gör en Newtonsk beräkning av den kritiska densiteten i vårt universum. Tänk dig en stor sfär som innehåller många galaxer med den sammanlagda
Förord... Sidan 2. Supernovor... Sidan 3 Supernova 1987A... Sidan 4 Avståndet till Stora Magellanska Molnet... Sidan 4 Ringen...
 Innehåll ESA/ESOs Övningsserie i Astronomi 1 Förord Förord... Sidan 2 Introduktion Supernovor... Sidan 3 Supernova 1987A... Sidan 4 Avståndet till Stora Magellanska Molnet... Sidan 4 Ringen... Sidan 5
Innehåll ESA/ESOs Övningsserie i Astronomi 1 Förord Förord... Sidan 2 Introduktion Supernovor... Sidan 3 Supernova 1987A... Sidan 4 Avståndet till Stora Magellanska Molnet... Sidan 4 Ringen... Sidan 5
Inspirationsdag i astronomi. Innehåll. Centret för livslångt lärande vid Åbo Akademi Vasa, 24 mars 2011
 Inspirationsdag i astronomi Centret för livslångt lärande vid Åbo Akademi Vasa, 24 mars 2011 Länkar m.m.: www.astronomi.nu/vasa110324 Magnus Näslund Stockholms observatorium Institutionen för astronomi
Inspirationsdag i astronomi Centret för livslångt lärande vid Åbo Akademi Vasa, 24 mars 2011 Länkar m.m.: www.astronomi.nu/vasa110324 Magnus Näslund Stockholms observatorium Institutionen för astronomi
En rundvandring i rymden
 En rundvandring i rymden Solen Vår närmsta och därmed bäst studerade stjärna. Solytan är ca 5700 grader varm, men den tunna gasen som omger solen (koronan) är över en miljon grader. Ett av världens bästa
En rundvandring i rymden Solen Vår närmsta och därmed bäst studerade stjärna. Solytan är ca 5700 grader varm, men den tunna gasen som omger solen (koronan) är över en miljon grader. Ett av världens bästa
Översiktskurs i astronomi Lektion 7: Solens och stjärnornas energiproduktion samt utveckling
 Översiktskurs i astronomi Lektion 7: Solens och stjärnornas energiproduktion samt utveckling Frågor från n förra f gången g I Hur långt är det mellan asteroiderna i huvudbältet? För stora asteroider (>1
Översiktskurs i astronomi Lektion 7: Solens och stjärnornas energiproduktion samt utveckling Frågor från n förra f gången g I Hur långt är det mellan asteroiderna i huvudbältet? För stora asteroider (>1
Vilken av dessa nivåer i väte har lägst energi?
 Vilken av dessa nivåer i väte har lägst energi? A. n = 10 B. n = 2 C. n = 1 ⱱ Varför sänds ljus av vissa färger ut från upphettad natriumånga? A. Det beror på att ångan är mättad. B. Det beror på att bara
Vilken av dessa nivåer i väte har lägst energi? A. n = 10 B. n = 2 C. n = 1 ⱱ Varför sänds ljus av vissa färger ut från upphettad natriumånga? A. Det beror på att ångan är mättad. B. Det beror på att bara
Kosmologi. Ulf Torkelsson Teoretisk fysik CTH/GU
 Kosmologi Ulf Torkelsson Teoretisk fysik CTH/GU Program Universums expansion, observationer Universums expansion, teori Universums geometri Universums expansion och sammansättning Exotisk materia Andromedagalaxen
Kosmologi Ulf Torkelsson Teoretisk fysik CTH/GU Program Universums expansion, observationer Universums expansion, teori Universums geometri Universums expansion och sammansättning Exotisk materia Andromedagalaxen
1755: Immanuel Kant, The Universal Natural History and Theories of the Heavens.
 Galaxer 1750: Thomas Wright (1711-1786) föreslår i An original theory or new hypothesis of the universe att vår egen galax, Vintergatan är en gigantisk roterande skiva av stjärnor, planeter, nebulosor,
Galaxer 1750: Thomas Wright (1711-1786) föreslår i An original theory or new hypothesis of the universe att vår egen galax, Vintergatan är en gigantisk roterande skiva av stjärnor, planeter, nebulosor,
Kosmologi. Universums utveckling. MN Institutionen för astronomi. Av rättighetsskäl är de flesta bilder från Wikipedia, om inte annat anges
 Kosmologi Universums utveckling MN Institutionen för astronomi Av rättighetsskäl är de flesta bilder från Wikipedia, om inte annat anges Upplägg Inledning vad ser vi på himlen? Galaxer och galaxhopar Metoder
Kosmologi Universums utveckling MN Institutionen för astronomi Av rättighetsskäl är de flesta bilder från Wikipedia, om inte annat anges Upplägg Inledning vad ser vi på himlen? Galaxer och galaxhopar Metoder
Edwin Hubbles stora upptäckt 1929
 Edwin Hubbles stora upptäckt 1929 Edwin Hubble Edwin Hubbles observationer av avlägsna galaxer från 1929. Moderna observationer av avlägsna galaxer. Bild: Riess, Press and Kirshner (1996) Galaxerna rör
Edwin Hubbles stora upptäckt 1929 Edwin Hubble Edwin Hubbles observationer av avlägsna galaxer från 1929. Moderna observationer av avlägsna galaxer. Bild: Riess, Press and Kirshner (1996) Galaxerna rör
Vi ser Vintergatan som ett dimmaktigt bälte över himmelen.
 6 Galaxer Galaxerna är de synliga "byggstenarna" av universum. Man räknar med att det finns 170 miljarder galaxer i den observerbara delen av universum, dvs. inom ca 14 miljarder ljusår. Galaxernas storlek
6 Galaxer Galaxerna är de synliga "byggstenarna" av universum. Man räknar med att det finns 170 miljarder galaxer i den observerbara delen av universum, dvs. inom ca 14 miljarder ljusår. Galaxernas storlek
Astrofysikaliska räkneövningar
 Astrofysikaliska räkneövningar Stefan Bergström, Ylva Pihlström Ulf Torkelsson 23 november 2004 Uppgifter 1. Dubbelstjärnesystemet VV Cephei har en period P = 20.3 år. Stjärnorna har massorna M 1 M 2 20
Astrofysikaliska räkneövningar Stefan Bergström, Ylva Pihlström Ulf Torkelsson 23 november 2004 Uppgifter 1. Dubbelstjärnesystemet VV Cephei har en period P = 20.3 år. Stjärnorna har massorna M 1 M 2 20
Varje uppgift ger maximalt 3 poäng. För godkänt krävs minst 8,5 poäng och
 Institutionen för Fysik Göteborgs Universitet LÖSNINGAR TILL TENTAMEN I FYSIK A: MODERN FYSIK MED ASTROFYSIK Tid: Lördag 3 augusti 008, kl 8 30 13 30 Plats: V Examinator: Ulf Torkelsson, tel. 031-77 3136
Institutionen för Fysik Göteborgs Universitet LÖSNINGAR TILL TENTAMEN I FYSIK A: MODERN FYSIK MED ASTROFYSIK Tid: Lördag 3 augusti 008, kl 8 30 13 30 Plats: V Examinator: Ulf Torkelsson, tel. 031-77 3136
Fenomenala rymdbilder - en utställning i Kungsträdgården
 Fenomenala rymdbilder - en utställning i Kungsträdgården Rymdstyrelsen, som är en myndighet under Utbildningsdepartemenet, har i samarbete med Stockholms stad producerat utställningen Fenomenala rymdbilder
Fenomenala rymdbilder - en utställning i Kungsträdgården Rymdstyrelsen, som är en myndighet under Utbildningsdepartemenet, har i samarbete med Stockholms stad producerat utställningen Fenomenala rymdbilder
Astronomin och sökandet efter liv där ute. Sofia Feltzing Professor vid Lunds universitet
 Astronomin och sökandet efter liv där ute Sofia Feltzing Professor vid Lunds universitet Sofia Feltzings vanliga forskning 250 miljoner år Drakes ekvation!"#"$" "%"!"#$%& "&"'()*" "%""+," "%"+$&%""+-%$&."+,"
Astronomin och sökandet efter liv där ute Sofia Feltzing Professor vid Lunds universitet Sofia Feltzings vanliga forskning 250 miljoner år Drakes ekvation!"#"$" "%"!"#$%& "&"'()*" "%""+," "%"+$&%""+-%$&."+,"
Laborationsuppgift om Hertzsprung-Russell-diagrammet
 Laborationsuppgift om Hertzsprung-Russell-diagrammet I denna uppgift kommer du att tillverka ett HR-diagram för stjrärnorna i Orions stjärnbild och dra slutsatser om stjärnornas egenskaper. HR-diagrammet
Laborationsuppgift om Hertzsprung-Russell-diagrammet I denna uppgift kommer du att tillverka ett HR-diagram för stjrärnorna i Orions stjärnbild och dra slutsatser om stjärnornas egenskaper. HR-diagrammet
Orienteringskurs i astronomi Föreläsning 5,
 Orienteringskurs i astronomi Föreläsning 5, 2014-09-15 Bengt Edvardsson Med litet mer detaljer än vad jag hann med på föreläsningen. Kap 6. Solen är en stjärna. För Solen gäller (sid. 145): I kärnan är
Orienteringskurs i astronomi Föreläsning 5, 2014-09-15 Bengt Edvardsson Med litet mer detaljer än vad jag hann med på föreläsningen. Kap 6. Solen är en stjärna. För Solen gäller (sid. 145): I kärnan är
Kosmologi - läran om det allra största:
 Kosmologi - läran om det allra största: Dikter om kosmos kunna endast vara viskningar. Det är icke nödvändigt att bedja, man blickar på stjärnorna och har känslan av att vilja sjunka till marken i ordlös
Kosmologi - läran om det allra största: Dikter om kosmos kunna endast vara viskningar. Det är icke nödvändigt att bedja, man blickar på stjärnorna och har känslan av att vilja sjunka till marken i ordlös
2 H (deuterium), 3 H (tritium)
 Var kommer alla grundämnen ifrån? I begynnelsen......var universum oerhört hett. Inom bråkdelar av en sekund uppstod de elementarpartiklar som alla grund- ämnen består av: protoner, neutroner och elektroner.
Var kommer alla grundämnen ifrån? I begynnelsen......var universum oerhört hett. Inom bråkdelar av en sekund uppstod de elementarpartiklar som alla grund- ämnen består av: protoner, neutroner och elektroner.
Mätning av stjärnors avstånd:
 4 Stjärnor Stjärnor är gasklot. Hög temperatur gasen i form av plasma, dvs. med fria elektroner och joner. Stjärnornas energi produceras (i normala fall) med kärnreaktioner (fusion). För att bli en stjärna
4 Stjärnor Stjärnor är gasklot. Hög temperatur gasen i form av plasma, dvs. med fria elektroner och joner. Stjärnornas energi produceras (i normala fall) med kärnreaktioner (fusion). För att bli en stjärna
Geometrisk optik. Syfte och mål. Innehåll. Utrustning. Institutionen för Fysik 2006-04-25
 Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
Trappist-1-systemet Den bruna dvärgen och de sju kloten
 Trappist--systemet Den bruna dvärgen och de sju kloten Trappist- är en sval dvärgstjärna, en brun dvärg, som man nyligen upptäckte flera planeter kring. För tillfället känner man till sju planeter i omloppsbana
Trappist--systemet Den bruna dvärgen och de sju kloten Trappist- är en sval dvärgstjärna, en brun dvärg, som man nyligen upptäckte flera planeter kring. För tillfället känner man till sju planeter i omloppsbana
CO i en spiralgalax. Vintergatans spiralmönster. Vintergatans uppbyggnad. Spiralgalaxen M 83. Den neutrala vätgasens v. fördelning f Vintergatan
 Översiktskurs i astronomi Lektion 10: Vintergatan och andra galaxer Upplägg I Vintergatan Vår plats i Vintergatan Vintergatans uppbyggnad Stjärnhopar Population I, II & III Differentiell rotation Mörk
Översiktskurs i astronomi Lektion 10: Vintergatan och andra galaxer Upplägg I Vintergatan Vår plats i Vintergatan Vintergatans uppbyggnad Stjärnhopar Population I, II & III Differentiell rotation Mörk
Astronomi. Hästhuvudnebulosan. Neil Armstrong rymdresenär.
 Hästhuvudnebulosan Astronomi Neil Armstrong rymdresenär. Illustration av vår galax Vintergatan. Av naturliga själ har vi aldrig sett vår galax ur detta perspektiv. Vilka är vi jordbor egentligen? Var i
Hästhuvudnebulosan Astronomi Neil Armstrong rymdresenär. Illustration av vår galax Vintergatan. Av naturliga själ har vi aldrig sett vår galax ur detta perspektiv. Vilka är vi jordbor egentligen? Var i
Vår galax, Vintergatan
 Vår galax, Vintergatan Vår plats i Vintergatan Ca 1785 (William Herschel) till ca 1920 (Jacobus Kapteyn): Solen i galaxens centrum, p.g.a. stjärnor jämt fördelade i Vintergatan i synligt ljus. Herschels
Vår galax, Vintergatan Vår plats i Vintergatan Ca 1785 (William Herschel) till ca 1920 (Jacobus Kapteyn): Solen i galaxens centrum, p.g.a. stjärnor jämt fördelade i Vintergatan i synligt ljus. Herschels
Från Big Bang till universums acceleration
 Från Big Bang till universums acceleration Rahman Amanullah Forskare vid Oskar Klein Center, Stockholms universitet http://okc.albanova.se/blog/ Hur vet vi att det vi vet är sant? Lånad av Per-Olof Hulth
Från Big Bang till universums acceleration Rahman Amanullah Forskare vid Oskar Klein Center, Stockholms universitet http://okc.albanova.se/blog/ Hur vet vi att det vi vet är sant? Lånad av Per-Olof Hulth
Grundläggande fakta om stjärnor
 Grundläggande fakta om stjärnor På ASAKs (Astronomiska Sällskapet Aquila i Kristianstads) hemsida på Internet finns en månadsguide till Kristianstadtraktens natthimmel (du hittar den genom att i den blå
Grundläggande fakta om stjärnor På ASAKs (Astronomiska Sällskapet Aquila i Kristianstads) hemsida på Internet finns en månadsguide till Kristianstadtraktens natthimmel (du hittar den genom att i den blå
Planeter Stjärnor Galaxer Uppgifter
 Planeter Stjärnor Galaxer Uppgifter 2 Vårt sätt att indela tiden 2.1 Använd Den Svenska Almanackan för två på varandra följande år och räkna antalet dygn från vårdagjämning till höstdagjämning och från
Planeter Stjärnor Galaxer Uppgifter 2 Vårt sätt att indela tiden 2.1 Använd Den Svenska Almanackan för två på varandra följande år och räkna antalet dygn från vårdagjämning till höstdagjämning och från
Orienteringskurs i astronomi Föreläsning 9, Bengt Edvardsson
 Orienteringskurs i astronomi Föreläsning 9, 2014-10-13 Bengt Edvardsson Innehåll: Vintegatan Utseende Delar Rörelser, gas Rörelser, stjärnor Det kosmiska kretsloppet Mörk material Vår galax, Vintergatan
Orienteringskurs i astronomi Föreläsning 9, 2014-10-13 Bengt Edvardsson Innehåll: Vintegatan Utseende Delar Rörelser, gas Rörelser, stjärnor Det kosmiska kretsloppet Mörk material Vår galax, Vintergatan
Introduktion till Kosmologi
 Introduktion till Kosmologi Astropartikelfysik Från det allra minsta till det allra största Från http://www.quarkstothecosmos.org/ Universum inom vår horistont Gravitationskraften finns överallt! Einsteins
Introduktion till Kosmologi Astropartikelfysik Från det allra minsta till det allra största Från http://www.quarkstothecosmos.org/ Universum inom vår horistont Gravitationskraften finns överallt! Einsteins
Översiktskurs i astronomi Lektion 3: Ljus och teleskop
 Översiktskurs i astronomi Lektion 3: Ljus och teleskop Upplägg Ljus och spektra Elektromagnetisk strålning Våglängd vid frekvens Teleskop och detektorer Seeing Reflektor- och refraktorteleskop CCD-chip
Översiktskurs i astronomi Lektion 3: Ljus och teleskop Upplägg Ljus och spektra Elektromagnetisk strålning Våglängd vid frekvens Teleskop och detektorer Seeing Reflektor- och refraktorteleskop CCD-chip
FINALTÄVLING SVENSKA FYSIKERSAMFUNDET
 FYSIKTÄVLINGEN FINALTÄVLING 24 april 1999 SVENSKA FYSIKERSAMFUNDET 1. Estimate, by using generally known properties of a typical car, the energy content of one litre of petrol. Some typical data for a
FYSIKTÄVLINGEN FINALTÄVLING 24 april 1999 SVENSKA FYSIKERSAMFUNDET 1. Estimate, by using generally known properties of a typical car, the energy content of one litre of petrol. Some typical data for a
Innehållsförteckning. Innehållsförteckning 1 Rymden 3. Solen 3 Månen 3 Jorden 4 Stjärnor 4 Galaxer 4 Nebulosor 5. Upptäck universum med Cosmonova 3
 1 Innehållsförteckning Innehållsförteckning 1 Rymden 3 Upptäck universum med Cosmonova 3 Solen 3 Månen 3 Jorden 4 Stjärnor 4 Galaxer 4 Nebulosor 5 2 Rymden Rymden, universum utanför jorden, studeras främst
1 Innehållsförteckning Innehållsförteckning 1 Rymden 3 Upptäck universum med Cosmonova 3 Solen 3 Månen 3 Jorden 4 Stjärnor 4 Galaxer 4 Nebulosor 5 2 Rymden Rymden, universum utanför jorden, studeras främst
VARFÖR MÖRK ENERGI HAR EN ANMÄRKNINGSVÄRT LITET VÄRDE. Ahmad Sudirman
 VARFÖR MÖRK ENERGI HAR EN ANMÄRKNINGSVÄRT LITET VÄRDE Ahmad Sudirman CAD, CAM och CNC Teknik Utbildning med kvalitet (3CTEQ) STOCKHOLM, 9 januari 2014 1 VARFÖR MÖRK ENERGI HAR EN ANMÄRKNINGSVÄRT LITET
VARFÖR MÖRK ENERGI HAR EN ANMÄRKNINGSVÄRT LITET VÄRDE Ahmad Sudirman CAD, CAM och CNC Teknik Utbildning med kvalitet (3CTEQ) STOCKHOLM, 9 januari 2014 1 VARFÖR MÖRK ENERGI HAR EN ANMÄRKNINGSVÄRT LITET
Observationer i Perseus stjärnbild
 Observationer i Perseus stjärnbild Kvällen såg lovande ut och jag bestämde mig för att förbereda mig att ta ut teleskopet. Planen var att observera objekt i Perseus stjärnbild. Det av två anledningar,
Observationer i Perseus stjärnbild Kvällen såg lovande ut och jag bestämde mig för att förbereda mig att ta ut teleskopet. Planen var att observera objekt i Perseus stjärnbild. Det av två anledningar,
Experimentella metoder, FK3001. Datorövning: Finn ett samband
 Experimentella metoder, FK3001 Datorövning: Finn ett samband 1 Inledning Den här övningen går ut på att belysa hur man kan utnyttja dimensionsanalys tillsammans med mätningar för att bestämma fysikaliska
Experimentella metoder, FK3001 Datorövning: Finn ett samband 1 Inledning Den här övningen går ut på att belysa hur man kan utnyttja dimensionsanalys tillsammans med mätningar för att bestämma fysikaliska
Mörk materia och det tidiga universum Joakim Edsjö Stockholms Universitet
 Mörk materia och det tidiga universum Joakim Edsjö edsjo@physto.se Stockholms Universitet Introduktion till kosmologi Mörk materia Den kosmologiska bakgrundsstrålningen Supernovor och universums geometri
Mörk materia och det tidiga universum Joakim Edsjö edsjo@physto.se Stockholms Universitet Introduktion till kosmologi Mörk materia Den kosmologiska bakgrundsstrålningen Supernovor och universums geometri
CO i en spiralgalax. Vintergatans spiralmö. Vintergatans uppbyggnad. Spiralgalaxen M 83. fördelning i Vintergatan. Den neutrala vä.
 Översiktskurs i astronomi Lektion 10: Vintergatan och andra galaxer Upplägg I Vintergatan Vår plats i Vintergatan Vintergatans uppbyggnad rnhopar Population I, II & III Differentiell rotation Mörk materia
Översiktskurs i astronomi Lektion 10: Vintergatan och andra galaxer Upplägg I Vintergatan Vår plats i Vintergatan Vintergatans uppbyggnad rnhopar Population I, II & III Differentiell rotation Mörk materia
1 Den Speciella Relativitetsteorin
 1 Den Speciella Relativitetsteorin Den speciella relativitetsteorin är en fysikalisk teori om lades fram av Albert Einstein år 1905. Denna teori beskriver framför allt hur utfallen (dvs resultaten) från
1 Den Speciella Relativitetsteorin Den speciella relativitetsteorin är en fysikalisk teori om lades fram av Albert Einstein år 1905. Denna teori beskriver framför allt hur utfallen (dvs resultaten) från
Kosmologin söker svar bl.a. på: Hur uppkom universum? Hur gammalt är universum? Hur är materian och energin fördelad?
 7 Kosmologi Kosmologin söker svar bl.a. på: Hur uppkom universum? Hur gammalt är universum? Hur är materian och energin fördelad? Hur uppkom elementarpartiklarna? Hur uppkom grundämnena? Hurdan är universums
7 Kosmologi Kosmologin söker svar bl.a. på: Hur uppkom universum? Hur gammalt är universum? Hur är materian och energin fördelad? Hur uppkom elementarpartiklarna? Hur uppkom grundämnena? Hurdan är universums
Kvasarer och aktiva galaxer
 Kvasarer och aktiva galaxer Radioastronomins födelse: 1931 - Grote Reber (1911 2002) Karl Guthe Jansky (1905 1950) Reber Radio Telescope in Wheaton, Illinois, 1937 Upptäckten av kvasarer Radioemission
Kvasarer och aktiva galaxer Radioastronomins födelse: 1931 - Grote Reber (1911 2002) Karl Guthe Jansky (1905 1950) Reber Radio Telescope in Wheaton, Illinois, 1937 Upptäckten av kvasarer Radioemission
Med sitt märkliga beteende har den mystiska dubbelstjärnan T Pyx förvirrat både forskare och amatörastronomer i decennier. Nu står det klart att det
 Aktuell forskning Stjärndrama i Med sitt märkliga beteende har den mystiska dubbelstjärnan T Pyx förvirrat både forskare och amatörastronomer i decennier. Nu står det klart att det som utspelar sig är
Aktuell forskning Stjärndrama i Med sitt märkliga beteende har den mystiska dubbelstjärnan T Pyx förvirrat både forskare och amatörastronomer i decennier. Nu står det klart att det som utspelar sig är
Universum. Stjärnbilder och Världsbilder
 Universum Stjärnbilder och Världsbilder Stjärnor Stjärngrupp, t.ex. Karlavagnen Stjärnbild, t.ex. Stora Björnen Polstjärnan Stjärnor livscykel -Protostjärna - Huvudseriestjärna - Röd jätte - Vit dvärg
Universum Stjärnbilder och Världsbilder Stjärnor Stjärngrupp, t.ex. Karlavagnen Stjärnbild, t.ex. Stora Björnen Polstjärnan Stjärnor livscykel -Protostjärna - Huvudseriestjärna - Röd jätte - Vit dvärg
Uppdrag för LEGO projektet Hitta en vattensamling på Mars
 LEGO projekt Projektets mål är att ni gruppvis skall öva på att genomföra ett projekt. Vi använder programmet LabVIEW för att ni redan nu skall bli bekant med dess grunder till hjälp i kommande kurser.
LEGO projekt Projektets mål är att ni gruppvis skall öva på att genomföra ett projekt. Vi använder programmet LabVIEW för att ni redan nu skall bli bekant med dess grunder till hjälp i kommande kurser.
Praktisk arbeid i astronomi. Jonas Persson Skolelaboratoriet, PLU, NTNU
 Praktisk arbeid i astronomi Jonas Persson Skolelaboratoriet, PLU, NTNU Astronomi - Læreplanene Etter 4. årstrinn Etter 7. årstrinn Etter 10. årstrinn Fysikk 1 Mål for opplæringen er at eleven skal kunne
Praktisk arbeid i astronomi Jonas Persson Skolelaboratoriet, PLU, NTNU Astronomi - Læreplanene Etter 4. årstrinn Etter 7. årstrinn Etter 10. årstrinn Fysikk 1 Mål for opplæringen er at eleven skal kunne
λ = T 2 g/(2π) 250/6 40 m
 Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
bubblor Spiralen runt R Sculptoris: Våra nya observationer med ALMA bjöd på en rejäl överraskning. För 1 800 år sedan drabbades stjärnan
 Jättarna som blåser bubblor avstjärnstoft av Sofia Ramstedt Möt de röda jättestjärnorna som blåser liv i galaxen. Sofia Ramstedt forskar om AGB-stjärnor, döende solar som skapar himlens vackraste nebulosor
Jättarna som blåser bubblor avstjärnstoft av Sofia Ramstedt Möt de röda jättestjärnorna som blåser liv i galaxen. Sofia Ramstedt forskar om AGB-stjärnor, döende solar som skapar himlens vackraste nebulosor
Solen och andra stjärnor 19 juli 2006. Stefan Larsson. Dagens text: Kap 3 Från Aristoteles till stjärnspektra
 Solen och andra stjärnor 19 juli 2006 Stefan Larsson Dagens text: Kap 3 Från Aristoteles till stjärnspektra Aristotle s Perfect Spheres Epicykler Att beskriva planeternas banor med enkla cirklar fungerar
Solen och andra stjärnor 19 juli 2006 Stefan Larsson Dagens text: Kap 3 Från Aristoteles till stjärnspektra Aristotle s Perfect Spheres Epicykler Att beskriva planeternas banor med enkla cirklar fungerar
Einstein's svårbegripliga teori. Einstein's första relativitetsteori, den Speciella, förklaras så att ALLA kan förstå den
 Einstein's svårbegripliga teori Einstein's första relativitetsteori, den Speciella, förklaras så att ALLA kan förstå den Speciella relativitetsteorin, Allmänt Einsten presenterade teorin 1905 Teorin gäller
Einstein's svårbegripliga teori Einstein's första relativitetsteori, den Speciella, förklaras så att ALLA kan förstå den Speciella relativitetsteorin, Allmänt Einsten presenterade teorin 1905 Teorin gäller
Varifrån kommer grundämnena på jorden och i universum? Tom Lönnroth Institutionen för fysik, Åbo Akademi, Finland
 Varifrån kommer grundämnena på jorden och i universum? Tom Lönnroth Institutionen för fysik, Åbo Akademi, Finland Finlandssvenska fysikdagarna 2009 m/s Silja Symphony, November 13-15 Sammandrag Begynnelsen:
Varifrån kommer grundämnena på jorden och i universum? Tom Lönnroth Institutionen för fysik, Åbo Akademi, Finland Finlandssvenska fysikdagarna 2009 m/s Silja Symphony, November 13-15 Sammandrag Begynnelsen:
Ett expanderande universum Ulf Torkelsson
 Kosmologins postulat Föreläsning 25/5 Ett expanderande universum Ulf Torkelsson När man bygger upp en kosmologisk modell antar man att universum är homogent, det vill säga att det ser likadant ut överallt,
Kosmologins postulat Föreläsning 25/5 Ett expanderande universum Ulf Torkelsson När man bygger upp en kosmologisk modell antar man att universum är homogent, det vill säga att det ser likadant ut överallt,
Sammanfattning av räkneövning 1 i Ingenjörsmetodik för ME1 och IT1. SI-enheter (MKSA)
 Sammanfattning av räkneövning 1 i Ingenjörsmetodik för ME1 och IT1 Torsdagen den 4/9 2008 SI-enheter (MKSA) 7 grundenheter Längd: meter (m), dimensionssymbol L. Massa: kilogram (kg), dimensionssymbol M.
Sammanfattning av räkneövning 1 i Ingenjörsmetodik för ME1 och IT1 Torsdagen den 4/9 2008 SI-enheter (MKSA) 7 grundenheter Längd: meter (m), dimensionssymbol L. Massa: kilogram (kg), dimensionssymbol M.
2060 Chiron - en ovanlig centaur
 2060 Chiron - en ovanlig centaur Claes-Ingvar Lagerkvist 1 Astronomiska Observatoriet, Uppsala Universitet, Box 515, S-75120, Uppsala 2 Claes-Ingvar Lagerkvist 1 Inledning Under 1970-talet sökte Charles
2060 Chiron - en ovanlig centaur Claes-Ingvar Lagerkvist 1 Astronomiska Observatoriet, Uppsala Universitet, Box 515, S-75120, Uppsala 2 Claes-Ingvar Lagerkvist 1 Inledning Under 1970-talet sökte Charles
Inspirationsdag i astronomi. Innehåll. Centret för livslångt lärande vid Åbo Akademi Vasa, 24 mars 2011
 Inspirationsdag i astronomi Centret för livslångt lärande vid Åbo Akademi Vasa, 24 mars 2011 Länkar m.m.: www.astronomi.nu/vasa110324 Magnus Näslund Stockholms observatorium Institutionen för astronomi
Inspirationsdag i astronomi Centret för livslångt lärande vid Åbo Akademi Vasa, 24 mars 2011 Länkar m.m.: www.astronomi.nu/vasa110324 Magnus Näslund Stockholms observatorium Institutionen för astronomi
Översiktskurs i astronomi Hösten 2009
 Översiktskurs i astronomi Hösten 2009 Upplägg Formell information Vår r plats i Universum Grundläggande astronomiska begrepp Formell information I Lärare (idag): Erik Zackrisson Lärare påp resten av kursen:
Översiktskurs i astronomi Hösten 2009 Upplägg Formell information Vår r plats i Universum Grundläggande astronomiska begrepp Formell information I Lärare (idag): Erik Zackrisson Lärare påp resten av kursen:
Gaser: ett av tre aggregationstillstånd hos ämnen. Flytande fas Gasfas
 Kapitel 5 Gaser Kapitel 5 Innehåll 5.1 Tryck 5.2 Gaslagarna från Boyle, Charles och Avogadro 5.3 Den ideala gaslagen 5.4 Stökiometri för gasfasreaktioner 5.5 Daltons lag för partialtryck 5.6 Den kinetiska
Kapitel 5 Gaser Kapitel 5 Innehåll 5.1 Tryck 5.2 Gaslagarna från Boyle, Charles och Avogadro 5.3 Den ideala gaslagen 5.4 Stökiometri för gasfasreaktioner 5.5 Daltons lag för partialtryck 5.6 Den kinetiska
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER
 EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
Lösningar och kommentarer till uppgifter i 2.2
 Lösningar och kommentarer till uppgifter i 2.2 2202 Beräkna Detta ger f(3 + h) f(3) då f(x) x 2 (3 + h) 2 3 2 h 2 + 6h 6 + h 6 h 0 Vi har därmed bestämt riktningskoefficienten (k-värdet) för tangenten
Lösningar och kommentarer till uppgifter i 2.2 2202 Beräkna Detta ger f(3 + h) f(3) då f(x) x 2 (3 + h) 2 3 2 h 2 + 6h 6 + h 6 h 0 Vi har därmed bestämt riktningskoefficienten (k-värdet) för tangenten
Repetitionsuppgifter 1
 Repetitionsuppgifter 1 Beräkna 1 a) 0,5 + 0,7 b) 0,45 + 1,6 c) 2,76 0,8 2 a) 4,5 10 b) 30,5 10 c) 0,45 1 000 3 Vilka av produkterna är a) större än 6 1,09 6 0,87 6 1 6 4,3 6 0,08 6 b) mindre än 6 4 Skriv
Repetitionsuppgifter 1 Beräkna 1 a) 0,5 + 0,7 b) 0,45 + 1,6 c) 2,76 0,8 2 a) 4,5 10 b) 30,5 10 c) 0,45 1 000 3 Vilka av produkterna är a) större än 6 1,09 6 0,87 6 1 6 4,3 6 0,08 6 b) mindre än 6 4 Skriv
Laboration 1 Nedslagskratrar
 Laboration 1 Nedslagskratrar Den här laborationen är uppdelad i två försök, där man i båda försöken ska släppa stålkulor på en sandbädd, vilket kan ses som en mycket enkel simulering av ett meteoritnedslag.
Laboration 1 Nedslagskratrar Den här laborationen är uppdelad i två försök, där man i båda försöken ska släppa stålkulor på en sandbädd, vilket kan ses som en mycket enkel simulering av ett meteoritnedslag.
Upptäckten av gravitationsvågor
 Upptäckten av gravitationsvågor Peter Johansson Institutionen för Fysik Helsingfors Universitet Fysikersamfundet i Finland - Årsmöte Helsingfors, 16.03.2016 Gravitationsvågor som ett fenomen förutspåddes
Upptäckten av gravitationsvågor Peter Johansson Institutionen för Fysik Helsingfors Universitet Fysikersamfundet i Finland - Årsmöte Helsingfors, 16.03.2016 Gravitationsvågor som ett fenomen förutspåddes
Gaser: ett av tre aggregationstillstånd hos ämnen. Fast fas Flytande fas Gasfas
 Kapitel 5 Gaser Kapitel 5 Innehåll 5.1 Tryck 5.2 Gaslagarna från Boyle, Charles och Avogadro 5.3 Den ideala gaslagen 5.4 Stökiometri för gasfasreaktioner 5.5 Daltons lag för partialtryck 5.6 Den kinetiska
Kapitel 5 Gaser Kapitel 5 Innehåll 5.1 Tryck 5.2 Gaslagarna från Boyle, Charles och Avogadro 5.3 Den ideala gaslagen 5.4 Stökiometri för gasfasreaktioner 5.5 Daltons lag för partialtryck 5.6 Den kinetiska
att båda rör sig ett varv runt masscentrum på samma tid. Planet
 Tema: Exoplaneter (Del III, banhastighet och massa) Det vi hittills tittat på är hur man beräknar radien och avståndet till stjärnan för en exoplanet. Omloppstiden kunde vi exempelvis få fram genom att
Tema: Exoplaneter (Del III, banhastighet och massa) Det vi hittills tittat på är hur man beräknar radien och avståndet till stjärnan för en exoplanet. Omloppstiden kunde vi exempelvis få fram genom att
Del 1. Introduktion till ett nytt. Naturvetenskapligt. Paradigm
 ! Åke Hedberg Del 1 Introduktion till ett nytt Naturvetenskapligt Paradigm introduktionen till 2000-talets nya fysikaliska världsbild och kosmologi handlar om hur materien och vårt Universum egentligen
! Åke Hedberg Del 1 Introduktion till ett nytt Naturvetenskapligt Paradigm introduktionen till 2000-talets nya fysikaliska världsbild och kosmologi handlar om hur materien och vårt Universum egentligen
Preliminärt lösningsförslag till Tentamen i Modern Fysik,
 Preliminärt lösningsförslag till Tentamen i Modern Fysik, SH1009, 008 05 19, kl 14:00 19:00 Tentamen har 8 problem som vardera ger 5 poäng. Poäng från inlämningsuppgifter tillkommer. För godkänt krävs
Preliminärt lösningsförslag till Tentamen i Modern Fysik, SH1009, 008 05 19, kl 14:00 19:00 Tentamen har 8 problem som vardera ger 5 poäng. Poäng från inlämningsuppgifter tillkommer. För godkänt krävs
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs B, kapitel 2
 Kapitel.1 101, 10 Exempel som löses i boken. 103 Testa genom att lägga linjalen lodrätt och föra den över grafen. Om den på något ställe skär grafen i mer än en punkt så visar grafen inte en funktion.
Kapitel.1 101, 10 Exempel som löses i boken. 103 Testa genom att lägga linjalen lodrätt och föra den över grafen. Om den på något ställe skär grafen i mer än en punkt så visar grafen inte en funktion.
Solsystemet samt planeter och liv i universum
 Solsystemet samt planeter och liv i universum Kap. 7-8, Solsystemet idag och igår Kap. 9.2, Jordens inre Kap. 10, Månen Kap 17, asteroider, kometer Kap 30, Liv i universum Jordens inre Medeltäthet ca 5500
Solsystemet samt planeter och liv i universum Kap. 7-8, Solsystemet idag och igår Kap. 9.2, Jordens inre Kap. 10, Månen Kap 17, asteroider, kometer Kap 30, Liv i universum Jordens inre Medeltäthet ca 5500
Kosmologi efter elektrosvagt symmetribrott
 Kosmologi efter elektrosvagt symmetribrott Den teoretiska grunden för modern kosmologi Einsteins allmänna relativitetsteori 1907 inser Einstein att man kan lokalt göra sig kvitt med gravitation genom att
Kosmologi efter elektrosvagt symmetribrott Den teoretiska grunden för modern kosmologi Einsteins allmänna relativitetsteori 1907 inser Einstein att man kan lokalt göra sig kvitt med gravitation genom att
Viktig information, aktualiteter! Vi träffas första gång år 2016, på Industrimuséet tisdagen den 12 januari.
 GISLAVEDS ASTRONOMISKA SÄLLSKAP ORION NYHETSBREV Observationer, nyheter från rymden, tips och idéer Nummer 7, december 2015 Viktig information, aktualiteter! Vi träffas första gång år 2016, på Industrimuséet
GISLAVEDS ASTRONOMISKA SÄLLSKAP ORION NYHETSBREV Observationer, nyheter från rymden, tips och idéer Nummer 7, december 2015 Viktig information, aktualiteter! Vi träffas första gång år 2016, på Industrimuséet
Vår galax Vintergatan sedd från sidan. Vår galax Vintergatan sedd uppifrån
 Livet. Detta ord berör hela jorden oavsett religion. I första hand hänvisar jag läsaren till följande länkar: Svarta hålets hemlighet, Vad händer i ett svart hål?, Resan genom det svarta hålet, Livet och
Livet. Detta ord berör hela jorden oavsett religion. I första hand hänvisar jag läsaren till följande länkar: Svarta hålets hemlighet, Vad händer i ett svart hål?, Resan genom det svarta hålet, Livet och
Du är alltså välkommen till tema avstånd, som kommer att (för)-följa Dej under hela denna kurs.
 Tillhör: Inledning. Det finns många intressanta och väsentliga avsnitt inom astronomin. I det här dokumentet skall vi studera och analysera avstånd. Det är ett av de begrepp, som är viktiga att analysera
Tillhör: Inledning. Det finns många intressanta och väsentliga avsnitt inom astronomin. I det här dokumentet skall vi studera och analysera avstånd. Det är ett av de begrepp, som är viktiga att analysera
Kapitel 5. Gaser. är kompressibel, är helt löslig i andra gaser, upptar jämt fördelat volymen av en behållare, och utövar tryck på sin omgivning.
 Kapitel 5 Gaser Kapitel 5 Innehåll 5.1 5. 5.3 Den ideala gaslagen 5.4 5.5 Daltons lag för partialtryck 5.6 5.7 Effusion och Diffusion 5.8 5.9 Egenskaper hos några verkliga gaser 5.10 Atmosfärens kemi Copyright
Kapitel 5 Gaser Kapitel 5 Innehåll 5.1 5. 5.3 Den ideala gaslagen 5.4 5.5 Daltons lag för partialtryck 5.6 5.7 Effusion och Diffusion 5.8 5.9 Egenskaper hos några verkliga gaser 5.10 Atmosfärens kemi Copyright
Till exempel om vi tar den första kol atomen, så har den: 6 protoner, 12 6=6 neutroner, 6 elektroner; atommassan är också 6 men masstalet är 12!
 1) Till exempel om vi tar den första kol atomen, så har den: 6 protoner, 12 6=6 neutroner, 6 elektroner; atommassan är också 6 men masstalet är 12! Om vi tar den tredje kol atomen, så är protonerna 6,
1) Till exempel om vi tar den första kol atomen, så har den: 6 protoner, 12 6=6 neutroner, 6 elektroner; atommassan är också 6 men masstalet är 12! Om vi tar den tredje kol atomen, så är protonerna 6,
CYGNUS. Länktips! Kallelse: Årsmöte 15 mars 2012
 CYGNUS Medlemsblad för Östergötlands Astronomiska Sällskap Nr 2, 2011 Innehåll Länktips! Kallelse till Årsmötet Sammanfattning av Gösta Gahms föredrag under Höstmötet 1 2 Vårens program 3 ÖAS webbplats
CYGNUS Medlemsblad för Östergötlands Astronomiska Sällskap Nr 2, 2011 Innehåll Länktips! Kallelse till Årsmötet Sammanfattning av Gösta Gahms föredrag under Höstmötet 1 2 Vårens program 3 ÖAS webbplats
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 36-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik Kapitel 36-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Science Night Rymden nu och framåt Aktuell forskning om rymden som utgångspunkt för intresseskapande fysik.
 Science Night Rymden nu och framåt Aktuell forskning om rymden som utgångspunkt för intresseskapande fysik. Nobelpriser i fysik 2017 Liv i rymden En app för att hitta på stjärnhimlen Nobelpriset i fysik
Science Night Rymden nu och framåt Aktuell forskning om rymden som utgångspunkt för intresseskapande fysik. Nobelpriser i fysik 2017 Liv i rymden En app för att hitta på stjärnhimlen Nobelpriset i fysik
Final i Wallenbergs Fysikpris
 Final i Wallenbergs Fysikpris 26-27 mars 2010. Teoriprov Lösningsförslag 1. a) Vattens värmekapacitivitet: Isens värmekapacitivitet: Smältvärmet: Kylmaskinen drivs med spänningen och strömmen. Kylmaskinens
Final i Wallenbergs Fysikpris 26-27 mars 2010. Teoriprov Lösningsförslag 1. a) Vattens värmekapacitivitet: Isens värmekapacitivitet: Smältvärmet: Kylmaskinen drivs med spänningen och strömmen. Kylmaskinens
Tentamen Relativitetsteori , 27/7 2019
 KOD: Tentamen Relativitetsteori 9.00 14.00, 27/7 2019 Hjälpmedel: Miniräknare, linjal och bifogad formelsamling. Observera: Samtliga svar ska lämnas på dessa frågepapper. Det framgår ur respektive uppgift
KOD: Tentamen Relativitetsteori 9.00 14.00, 27/7 2019 Hjälpmedel: Miniräknare, linjal och bifogad formelsamling. Observera: Samtliga svar ska lämnas på dessa frågepapper. Det framgår ur respektive uppgift
Kalla Vindar ( och Heta Galaxkärnor) Susanne Aalto Rymd och Geovetenskap Chalmers
 Kalla Vindar ( och Heta Galaxkärnor) Susanne Aalto Rymd och Geovetenskap Chalmers Herschel Space Observatory Massa: ca 3400 kg vid uppskjutning Dimensioner: 7.5m hög, 4m 4m tvärsnitt Våglängder: Infrarött
Kalla Vindar ( och Heta Galaxkärnor) Susanne Aalto Rymd och Geovetenskap Chalmers Herschel Space Observatory Massa: ca 3400 kg vid uppskjutning Dimensioner: 7.5m hög, 4m 4m tvärsnitt Våglängder: Infrarött
Relativitetsteorins grunder, våren 2016 Räkneövning 3 Lösningar
 Relativitetsteorins grunder, våren 2016 Räkneövning 3 Lösningar 1. Den ryska fysikern P.A. Čerenkov upptäckte att om en partikel rör sig snabbare än ljuset i ett medium, ger den ifrån sig ljus. Denna effekt
Relativitetsteorins grunder, våren 2016 Räkneövning 3 Lösningar 1. Den ryska fysikern P.A. Čerenkov upptäckte att om en partikel rör sig snabbare än ljuset i ett medium, ger den ifrån sig ljus. Denna effekt
stjärnor Att mäta en miljard David Hobbs, Lennart Lindegren, Ulrike Heiter och Andreas Korn
 aktuell forskning Att mäta en miljard stjärnor B i ld: ESA Astrometri som forskningsfält fick nytt liv den 8 augusti 1989 då en ny europeisk satellit sändes upp, med det passande namnet hipparcos. Projektet
aktuell forskning Att mäta en miljard stjärnor B i ld: ESA Astrometri som forskningsfält fick nytt liv den 8 augusti 1989 då en ny europeisk satellit sändes upp, med det passande namnet hipparcos. Projektet
