Samband mellan säkerhetslager och orderstorlek
|
|
|
- Erik Gunnarsson
- för 9 år sedan
- Visningar:
Transkript
1 Samband mellan säkerhetslager och orderstorlek Stig-Arne Mattsson Sammanfattning Vid operativ materialstyrning spelar dimensionering av orderstorlekar och säkerhetslager en avgörande roll för hur effektivt materialflöden kan styras med avseende på kapitalbindning, lagerstyrningskostnader och leveransförmåga. Detta gäller oavsett vilken materialstyrningsmetod man använder. Vald orderstorlek påverkar emellertid säkerhetslagrets storlek, alternativt den servicenivå man kan erhålla. Det är därför av intresse att studera vilka konsekvenser som ändrade orderstorlekar får på den totala kapitalbindningen och på leveransförmågan från lager. De resultat som i dessa avseenden erhållits i den här studien kan sammanfattas på följande sätt. Används SERV1 för att dimensionera säkerhetslager ökar bristkvantiteten per period linjärt med avtagande orderstorlek. Ju större efterfrågevariationen är desto fortare ökar bristkvantiteten. För att undvika detta måste servicenivån och därmed säkerhetslagret ökas i takt med att orderstorlekar minskas. Används SERV2 för dimensionering av säkerhetslager anpassar sig säkerhetslagret automatiskt till avtagande orderstorlekar utan att servicenivån behöver anpassas. Säkerhetslagret ökar med avtagande orderstorlek och ökningen blir större ju större efterfrågevariationerna är. Vid stora efterfrågevariationer är säkerhetslagrets ökning så stor att den totala kapitalbindningen i omsättningslager inte eller endast obetydligt minskar trots stora minskningar i orderkvantiteter. Vid dimensionering av orderstorlekar och säkerhetslager med utgångspunkt från en servicenivå definierad som Serv2 tillämpas i allmänhet ett förenklat beräkningssätt som inte tar hänsyn till det samband som finns mellan de båda variablerna. I de flesta fall är det praktiskt sett fullt tillfredsställande att dimensionera orderstorlekar oberoende av säkerhetslager. Endast vid fall med servicenivåer under storleksordningen 95 % och efterfrågevariationer motsvarande variationskoefficienter över storleksordningen 0,5 kan det med avseende på de totala lagerstyrningskostnaderna vara värt att ta hänsyn till säkerhetslagrets storlek vid bestämning av orderstorlek genom att använda ett mer teoretiskt korrekt tillvägagångssätt. Det approximativa förfarande som praktiskt taget alltid används vid dimensionering av säkerhetslager från en fastställd servicenivå ger tillräckligt näroptimala värden då förhållandet mellan orderstorlek och efterfrågevariationernas standardavvikelse under ledtid är mindre än storleksordningen 1. I andra fall blir säkerhetslagret påtagligt för stort och dimensioneringen bör om möjligt göras med hjälp av det teoretiskt korrekta beräkningsförfarandet. Teknisk Logistik stig-arne.mattsson@swipnet.se Lunds Universitet Juni, 2005
2 1 Inledning 1.1 Bakgrund Vid operativ materialstyrning spelar dimensionering av orderstorlekar och säkerhetslager en avgörande roll för hur effektivt materialflöden kan styras med avseende på kapitalbindning, lagerstyrningskostnader och leveransförmåga. Detta gäller oavsett vilken materialstyrningsmetod man använder, dvs vare sig man använder till exempel beställningspunktssystem, täcktidsplanering eller materialbehovsplanering. I dessa materialstyrningsmetoder utnyttjas på samma sätt som i många andra sammanhang olika modeller som stöd för att fatta beslut, bland annat för val av lämpliga orderstorlekar och säkerhetslager. En modell utgör en förenklad bild av verkligheten. Att förenklingar måste göras beror på att verkligheten i allmänhet är alltför komplex för att möjliggöra att alla förekommande påverkande och samverkande faktorer kan beaktas. Genom att förenkla den verklighet som man vill studera får man en mer rationell och hanterbar situation. Är det fråga om en operationsanalytisk modell är förenklingen dessutom i regel nödvändig för att man med tillgängliga matematiska och statistiska metoder över huvud taget skall kunna behandla en problemställning. Eftersom en modell är en förenklad bild av verkligheten och man fattar beslut och drar slutsatser utifrån denna modell i stället för från verkliga förhållanden är det av avgörande betydelse att modellens avbildningsförmåga är acceptabelt hög. Det innebär att de faktorer och sambanden mellan dem som modellen beaktar är de som är mest relevanta av alla de som förekommer i den verkliga problemsituationen. Dessutom måste sambandens utseende och egenskaper på ett acceptabelt sätt överensstämma med verklighetens. Om så inte är fallet kan problemlösningen i bästa fall vara optimal från ett teoretiskt perspektiv men mer eller mindre oanvändbar och vilseledande från ett praktiskt problemlösningsperspektiv. 1.2 Problemställningar och forskningsfrågor De förenklande antaganden som görs i modeller som används för bestämning av ekonomisk orderkvantitet och säkerhetslager och som därigenom påverkar modellernas avbildningsförmåga varierar från modell till modell. Likaså varierar de förutsättningar under vilka modellerna gäller. I kvalificerad facklitteratur redovisas oftast dessa antaganden och förutsättningar så att man utifrån en given problemlösningssituation kan ta ställning till om aktuell modells avbildningsförmåga är tillfredsställande nog för att vara lämplig att använda. Exempelvis finns sådana antaganden redovisade för ett stort antal modeller för bestämning av ekonomiska orderkvantiteter och säkerhetslager beräknade med utgångspunkt från servicenivåer eller bristkostnader i Silver Pyke Peterson (1998). När det gäller i vilken utsträckning modeller för bestämning av ekonomisk orderkvantitet och säkerhetslager på ett rimligt sätt avspeglar verkliga förhållanden måste man också beakta i vilken utsträckning modellerna tar hänsyn till att det finns samband mellan orderstorlek och säkerhetslager. Att ett sådant samband finns framgår tydligt att det faktum att mindre orderstorlekar leder till fler inleveranstillfällen och därmed till fler tillfällen där bristexponering sker. Förekommer det fler bristexponeringstillfällen per peri- 2
3 od måste man ha större säkerhetslager för att inte den totala bristkvantiteten per tidsperiod skall öka i takt med minskande orderstorlekar. Ett i praktisk tillämpning vanligt sätt att dimensionera säkerhetslager är att utgå från en policybestämd servicenivå och från denna servicenivå och data om hur efterfrågan varierar i form av en standardavvikelse beräkna motsvarande säkerhetslager. Två alternativa servicenivådefinitioner brukar användas. Enligt den ena, ofta kallad SERV1, definieras servicenivån som sannolikheten att det inte uppstår brist i lager under en lagercykel. Med en sådan definition kommer inte säkerhetslagrets storlek att påverkas av orderstorleken eftersom servicenivån anges per lagercykel. Antalet bristexponeringstillfällen ökar emellertid som framgick ovan med minskade orderstorlekar och den totala bristkvantiteten per period kommer därför att öka om säkerhetslagret är det samma oavsett orderstorlek. Mot denna bakgrund är det av intresse att besvara följande forskningsfråga. I vilken utsträckning påverkas bristkvantiteten per period av varierande orderstorlekar när säkerhetslagret förblir oförändrat och hur mycket måste servicenivån ökas för att bristkvantiteten per period inte skall öka med minskande orderstorlekar? Enligt det andra vanligt använda alternativt, SERV2, definieras servicenivån som andel av efterfrågan som under en period kan tillfredsställas direkt från lager. Med en sådan definition tas full hänsyn till antalet inleveranser till lager per period och därmed till sambandet mellan orderstorlek och säkerhetslager. Användning av denna servicenivådefinition och den beräkningsmetodik som är kopplad till definitionen kommer följaktligen att leda till att säkerhetslagret blir större ju mindre orderstorlekar det är fråga om. För att klargöra hur sambandet ser ut kan det vara av intresse att studera följande forskningsfråga. Hur förändras kapitalbindningen i omsättningslager och säkerhetslager av minskande orderstorlekar? Eftersom orderstorlek och säkerhetslager är beroende av varandra, innebär det en förenkling att beräkna dem var för sig separat. Så görs emellertid i princip alltid i praktiken. Bland annat beror detta på att det är komplicerat och att det krävs ett iterativt förfarande för att göra någon form samtidig optimering. Endast allmänna riktlinjer för när man kan tillåta sig att optimera storheterna var för sig har hittas i litteraturen. Exempelvis anger Andersson Ljungfeldt Wandel (1970, sid 109) att endast om bristkostnaden är relativt stor eller om mer än en beställning ligger ute, dvs. orderkvantiteten är mindre än beställningspunktskvantiteten, påverkas beställningspunkten (och därmed säkerhetslager) och orderstorleken nämnvärt av varandra. Brown (1967, sid 137) hävdar att skillnaden mellan ekonomisk orderkvantitet beräknad separat och ekonomisk orderkvantitet beräknad med hänsyn tagen till säkerhetslager endast är signifikant om orderstorleken är mindre än tre standardavvikelser (under ledtid). För att få klarare indikationer på om och när man kan tillåta sig att optimera säkerhetslager och orderstorlek separat och vilka konsekvenser det får, kan det vara av intresse att besvara följande forskningsfråga. Under vilka förhållanden skiljer sig orderstorlekar och säkerhetslager signifikant om de beräknas var för sig oberoende av varandra jämfört med om de beräknas samtidigt och vad blir konsekvenserna av att inte beräkna dem samtidigt. 3
4 Vid beräkning av säkerhetslager med hjälp av SERV2 och efterfrågevariationernas standardavvikelse brukar man bortse från en term i den formel som uttrycker bristkvantiteten per period. Detta görs i praktiskt taget alla läroböcker och genomgående i praktisk tillämpning i affärssystem. Enligt Axsäter (1991, sid 74) är denna approximation rimlig om orderstorleken i förhållande till efterfrågans standardavvikelse under ledtid är stor. Någon precisering av vad stor innebär ges inte. För att få en mer preciserad bild av när man kan acceptera att optimera de båda storheterna var för sig kan det vara av värde att följande forskningsfråga besvaras. Under vilka förhållanden kan man tillåta sig att beräkna säkerhetslager baserat på SERV2 med det i praktiken tillämpade approximativa förfarandet. 1.3 Syfte och avgränsningar Syftet med det forskningsprojekt som redovisas i denna rapport är att analysera och värdera effekter av att inte ta hänsyn till att orderstorlekar och säkerhetslager är beroende av varandra genom att besvara de forskningsfrågor som formulerats ovan. Forskningsprojektets inriktning har primärt varit att åstadkomma ökad förståelse för problematiken och utarbeta enkla riktlinjer för hur man skall hantera problemställningen i praktiken. Analyserna har genomförts med i industrin vanligt använda och etablerade modeller för bestämning av orderstorlekar och säkerhetslager. Wilsons formel har använts för bestämning av orderstorlekar och säkerhetslager har beräknats med utgångspunkt från en definierad servicenivå och en standardavvikelse för efterfrågevariationer enligt en normalfördelning. Endast fallet att brist leder till restnotering har analyserats. Eftersom höga servicenivåer använts blir skillnaderna jämfört med fallet att brist leder till förlorad försäljning tämligen försumbara (Axsäter, 1991, sid 72). 2 Säkerhetslagerbestämning med SERV1 Med en lagercykel menas tiden från en lagerpåfyllnad till nästa lagerpåfyllnad. Under en sådan lagercykel uppstår bristrisker strax före påfyllnadstillfället, antingen genom att förbrukningen varit större än beräknat eller genom att leveranstiden för inleverans av ny order varit längre än beräknad. Andel lagercykler utan brist är sålunda förenklat detsamma som sannolikheten för att det finns kvantiteter tillgängliga i lager under en hel lagercykel. Detta motsvarar det ovan definierade servicenivåbegreppet SERV1. Det kan uttryckas på följande sätt. SERV1 = 1 - Antal lagercykler med brist / Antal inleveranstillfällen Utmärkande för denna servicenivådefinition är att bristexponeringen är beroende av antalet inleveranser. För en produkt som endast inlevereras en gång per år uppkommer risk för brist endast en gång per år medan en produkt som inlevereras tolv gånger per år är utsatt för tolv gånger så många bristrisker. Används sålunda samma servicenivå för samtliga produkter oavsett hur många gånger respektive produkt levereras in, kommer produkter som levereras in ofta att råka ut för betydligt fler brister än produkter som levereras in sällan. Alternativt uttryckt kommer artiklar med stora orderstorlekar i förhållande till efterfrågan att få mindre bristkvantiteter än artiklar med små orderstorlekar 4
5 Bristkvantitet per år i förhållande till efterfrågan om allas säkerhetslager dimensioneras med samma SERV1- nivå. För att illustrera och analysera hur bristkvantiteten förändras med avtagande orderstorlekar och hur mycket servicenivån måste ökas för att bristkvantiteten per period inte skall öka vid avtagande orderstorlekar har beräkningar genomförts för ett exempel. I exemplet antas efterfrågan per år vara 1000 st och ledtiden för återanskaffning en månad. Servicenivån har i utgångsläget satts till 94 %. Beräkning av bristkvantitet per period har genomförts genom att först beräkna säkerhetsfaktorn för den aktuella servicenivån från en normalfördelningstabell. Därefter har värdet på servicefunktionen G(k) för denna säkerhetsfaktor bestämts med hjälp normalfördelningstabeller. Se exempelvis Silver Pyke Peterson (1998, sid 724). G(k) kan även bestämmas med hjälp av standardfunktioner i Excel. När värdet på servicefunktionen är känd kan förväntad bristkvantitet per år beräknas med hjälp av följande uttryck. Se exempelvis Silver Pyke Peterson (1998, sid 258). Bk(år) = σ(lt) n G(k) = d(lt) Var(lt) n G(k) där n = antal order per år σ (lt) = efterfrågans standardavvikelse under ledtid d(lt) = efterfrågan under ledtid Var(lt) = variationskoefficienten för efterfrågan under ledtid För exemplet enligt ovan kommer bristkvantiteten att variera med antalet order per år enligt figur 1 för några olika värden på variationskoefficienten. Som framgår av figuren ökar bristkvantiteten linjärt med orderfrekvensen. Detta gäller generellt och är inte specifikt för det genomräknade exemplet. Av formeln kan man också se att bristkvantiteten per period är direkt proportionell mot orderfrekvensen. Med andra ord dubblas bristkvantiteten när orderfrekvensen dubblas. Procentuellt ökar bristkvantiteten lika mycket oberoende av efterfrågevariationen. I absoluta tal ökar den emellertid klart mer ju större efterfrågevariationerna är. 60,0 50,0 40,0 30,0 20,0 10,0 0, Antal order per år Var=0,4 Var=0,7 Var=1,0 Var=1,3 Figur 1 Samband mellan orderfrekvens och bristkvantitet per period för några olika variationskoefficienter vid en servicenivå på 94 % 5
6 Servicenivå En slutsats av de redovisade sambanden mellan bristkvantitet per period och orderfrekvens är att om man inte vill att bristerna i lager skall öka när man ökar orderfrekvensen måste man höja servicenivån. Hur stor denna höjning måste vara kan man beräkna enligt följande. Antag att den bristkvantitet man kan acceptera för en given orderfrekvens n och en given servicenivå är lika med Bk. Servicefunktionen som funktion av n ges då av G(n) = Bk / Var(lt) / d(lt) / n För varje n kan motsvarande säkerhetsfaktor hämtas från normalfördelningstabeller eller beräknas approximativt. Se exempelvis Silver - Pyke - Peterson (1998, sid 736). För varje säkerhetsfaktor kan därefter den servicenivå som krävs för att uppnå den givna bristkvantiteten per period bestämmas med hjälp av normalfördelningstabeller eller med hjälp av den NORMSFÖRD-funktion som finns i Excel. Nödvändig servicenivå för att bristkvantiteten per period vid en inleveransfrekvens på 4 inte skall öka om man ökar inleveransfrekvensen i exemplet ovan visas i figur 2. Som framgår av figuren ökar kraven på höga servicenivåer mycket påtagligt med ökande orderfrekvens. Sambandet är detsamma oberoende av variationskoefficient, dvs oberoende av hur mycket efterfrågan varierar, men ökningen blir större ju jämnare efterfrågan är Antal order per år Var=0,4 Var=0,7 Var=1,0 Figur 2 Samband mellan orderfrekvens och den servicenivå man måste ha för att bristkvantiteten per period inte skall öka med ökande orderfrekvens 3 Säkerhetslagerbestämning med SERV2 SERV2 definieras som den andel av efterfrågan som under en period kan tillfredsställas utan fördröjning direkt från lager. Beräkningsmässigt kan den uttryckas på följande sätt. SERV2 = Kvantitet som kan levereras direkt från lager under en period/totalt efterfrågad kvantitet under samma period 6
7 Säkerhetslager Vid användning av detta servicenivåbegrepp tas hänsyn till storleken på lagerpåfyllnadsorder. Detta framgår tydligt av nedanstående formeln för beräkning av den servicefunktion som används för beräkning av säkerhetsfaktorn och därmed för dimensionering av säkerhetslager (Silver Pyke Peterson,1998, sid 268 ). G(k) = Q (1 SERV2 / 100) / σ(lt) där Q = orderstorleken vid påfyllning av lager σ(lt) = efterfrågans standardavvikelse under ledtid. Som framgår av uttrycket minskar G(k) med minskande orderstorlekar, dvs ökande orderfrekvens. Eftersom säkerhetsfaktorn k ökar med avtagande G(k) blir slutsatsen att säkerhetslagret ökar med ökande orderfrekvens vid given och konstant servicenivå. För att illustrera och analysera hur säkerhetslagret och summan av säkerhetslager och omsättningslager förändras med ökande orderfrekvenser har beräkningar genomförts för ett exempel. Artikeln i exemplet har en årsefterfrågan, d, på st och en återanskaffningstid på en månad. Säkerhetslagret dimensioneras baserat på en servicenivå på 98 %. Servicefunktionen beräknas med hjälp av ovanstående formel och med σ(lt) = Var(lt) d(lt) och Q = d / n. Från det erhållna värdet på G(k) fås motsvarande säkerhetsfaktor från normalfördelningstabeller. Säkerhetslagret erhålls därefter som denna säkerhetsfaktor gånger σ(lt). Det totala lagret erhålls därefter med hjälp av följande uttryck. Totalt lager = d / n / 2 + k σ(lt) Resultaten av beräkningarna för några olika variationskoefficienter visas i figur 3 och 4 visas sambanden för några utvalda variationskoefficienter Antal order per år Serie1 Serie2 Serie3 Serie4 Figur 3 Säkerhetslagret som funktion av orderfrekvens för olika variationskoefficienter vid en servicenivå på 98 % 7
8 Total kapitalbindning Som framgår av figur 3 ökar säkerhetslagret med ökande orderfrekvens. Det framgår också att ökningstakten blir mindre ju högre servicenivå man har. Motsvarande förändringar för den totala kapitalbindningen i säkerhetslager och omsättningslager framgår av figur 4. Vid ökande orderfrekvens minskar den totala kapitalbindningen men betydligt mindre än vad kapitalbindningen i omsättningslager minskar. Inom det frekvensintervall som studerats blir till och med den totala kapitalbindningen praktiskt taget oförändrad vid hög efterfrågevariation trots att orderstorlekarna reducerats kraftigt. Det är i stället så att om orderstorlekarna reduceras ytterligare kommer den totala kapitalbindningen att öka för att uppnå en given servicenivå. Det stämmer väl med följande slutsats av Plossl och Wight (1967, sid 110); The additional inventory required for better service level can be less if the investment is made in cycle stock rather than safety stock Antal order per år Var=0,2 Var=0,5 Var=0,8 Var=1,1 Figur 4 Den totala kapitalbindningen i lager som funktion av orderfrekvens för några olika variationskoefficienter vid en servicenivå på 96 % Motsvarande samband över hur behovet av säkerhetslager ökar med ökande orderfrekvens och bibehållen servicenivå redovisas av Natarajan och Goyal (1994). De påpekar också att endast metoder som dimensionerar säkerhetslager med hänsyn till orderstorlek bör användas. I realiteten innebär detta att SERV2 och inte SERV1 bör användas för säkerhetslagerdimensionering enligt Natarajan och Goyal. 4 Samtidig bestämning av orderstorlek och säkerhetslager I praktisk tillämpning bestäms alltid ekonomisk orderkvantitet och säkerhetslagerstorlek oberoende av varandra eller som ett tvåstegsförfarande. Används SERV1 för att beräkna säkerhetslager är dimensioneringarna av respektive storhet helt oberoende av varandra om inte servicenivån differentieras med avseende på orderfrekvens. Effekter av detta har studerats av Mattsson (2005). Under sådana omständigheter innebär beräkningarna ett tvåstegsförfarande. Först beräknas orderstorlekar och som en konsekvens av detta orderfrekvensen. Därefter beräknas säkerhetslager med hjälp av servicenivåer som fastställt på basis av orderfrekvensklass. 8
9 Om man i stället använder servicenivådefinition SERV2 är det alltid fråga om ett tvåstegsförfarande. Först beräknas ekonomisk orderkvantitet och sedan används den beräknade orderstorleken för att beräkna säkerhetslagret med utgångspunkt från den valda servicenivån. Ekonomisk orderkvantitet påverkas emellertid av de kostnader som uppstår på grund av brist. Ett mer korrekt beräkningsförfarande innebär att ekonomisk orderkvantitet i stället beräknas enligt följande för fallet att brist leder till restorder. Se exempelvis Tersine (1994, sid 269). Q(opt) = 2 d (S + B G(k) σ(lt)) / H där d = efterfrågan per år S = ordersärkostnaden per order B = bristkostnad per styck G(k) = servicefunktionen σ(lt) = standardavvikelsen under ledtid H = lagerhållningskostnaden per år och styck Säkerhetslagret beräknas med hjälp av följande uttryck. SL = σ(lt) k där k bestäms så att P(k) =1 - H Q / B / d P(k) avser den optimala sannolikheten att brist inte uppkommer under en lagercykel. Som framgår av formlerna måste man känna till k för att kunna räkna ut ekonomisk orderkvantitet och känna till ekonomisk orderkvantitet för att bestämma k. Detta dilemma löses som påpekades ovan i praktiken genom att bortse från bristkostnadskomponenten i formeln för ekonomisk orderkvantitet, dvs. man beräknar ekonomisk orderstorlek på traditionellt sätt med Wilsons formel. Därefter beräknar man säkerhetslagrets storlek. Brown (1977, sid 220) anger en någon avvikande praktisk metod. Den innebär att man beräknar ekonomisk orderstorlek med hjälp av den traditionella Wilsons formel men att man inte låter den så beräknade orderstorleken bli mindre än efterfrågans standardavvikelse under ledtid. Brown menar att man med detta tillägg kommer så nära en optimal orderstorlek att det inte är värt besväret att genomföra ett noggrannare beräkningsförfarande. För att få mer optimalt beräknade orderstorlekar och säkerhetslager måste man tillämpa ett iterativt förfarande. Ett sådant har utvecklats av Fetter och Dalleck (1961, sid 17) och innebär att man först beräknar ekonomisk orderkvantitet med Wilsons formel och därefter säkerhetslagret. Den säkerhetsfaktor man får fram vid säkerhetslagerberäkningen används sen för att bestämma bristkostnadstermen i uttrycket för ekonomisk orderkvantitet enligt ovan och en ny mer optimal orderstorlek beräknas. Med hjälp av denna reviderade orderstorlek beräknas ett nytt k och ett nytt säkerhetslager. Detta nya k används för att på nytt beräkna ekonomisk orderkvantitet osv. Iterationen fortsätts tills den senast beräknade orderstorleken skiljer sig acceptabelt lite från den näst senast beräknade. I allmänhet krävs endast ett fåtal iterationer för att nå fram till en enligt modellen ekonomiskt optimal orderkvantitet. För att illustrera och värdera hur mycket det betyder att samtidigt bestämma orderstorlek och säkerhetslager jämfört med att bestämma storheterna delvis oberoende av var- 9
10 andra har det ovan beskrivna iterationsförfarandet tillämpats på ett exempel. Exemplet avser en artikel med efterfrågan på st per år, ett pris på 100 kr, en ordersärkostnad på 250 kr och en lagerhållningskostnad på 20 kr per år och styck. Ledtiden för återfyllning av lagret är en månad. Med dessa datauppgifter blir ekonomisk orderkvantitet enligt Wilsons formel 500 st. Den uppgift om bristkostnad per styck som krävs för att genomföra beräkningarna har bestämts med utgångspunkt från servicenivå och denna orderstorlek. För en variationskoefficient på 0,2 under ledtid har värden enligt tabell 1 erhållits för ett antal olika servicenivåer. I tabellen avser orderstorlek den orderstorlek som erhålls vid samtidig bestämning av orderstorlek och säkerhetslager jämfört med det värde på 500 st som erhålls om orderstorleken beräknas separat. EOK-diff och SL-diff avser den procentuella skillnaden mellan orderstorlek respektive säkerhetslager om de beräknats tillsammans jämfört med om de beräknats var för sig. Kostn.diff avser den procentuella skillnaden mellan summan av ordersärkostnader, lagerhållningskostnader och bristkostnader för fallet att orderstorlek och säkerhetslager beräknats tillsammans jämfört med om de beräknats var för sig. Kap.diff avser motsvarande procentuella skillnad för summa kapitalbindning i omsättningslager och säkerhetslager. Tabell 1 Jämförelse mellan samtidig och separat beräkning av orderstorlekar och säkerhetslager för några olika servicenivåer och en variationskoefficient på 0,2 Servicenivå Orderstorlek EOK-diff SL-diff Kostn.diff Kap.diff 94, ,4-55,9-2,0 8,8 96, ,7-17,4-1,2 7,6 98, ,7-9,3-0,9 6,5 99, ,2-5,2-0,7 5,5 99, ,5-3,5-0,5 4,7 Som framgår av tabellen blir orderstorleken betydligt större om orderstorlek och säkerhetslager beräknas samtidigt. Exempelvis blir orderstorleken 27 % högre vid samtidig beräkning jämfört med att den beräknas separat vid en servicenivå på 94 %. Skillnaderna blir mindre ju högre servicenivåerna är. För säkerhetslagret gäller det motsatta, dvs säkerhetslagret blir mindre om det beräknas samtidigt med orderstorleken jämfört med om det beräknas utan hänsyn till att orderstorleken påverkas av dess värde. Totalt sett får man en lägre lagerstyrningskostnad och en högre kapitalbindning genom att beräkna de båda storheterna tillsammans. För de totala lagerstyrningskostnaderna är emellertid skillnaderna tämligen försumbara, speciellt vid de högre servicenivåerna. Motsvarande beräkningar har gjorts för fallet med 98 % servicenivå och ett antal olika variationskoefficienter. Resultaten från dessa beräkningar visas i tabell 2. Kolumnen längst till höger visar efterfrågevariationernas standardavvikelse under ledtid för motsvarande variationskoefficient. 10
11 Tabell 2 Jämförelse mellan samtidig och separat beräkning av orderstorlekar och säkerhetslager för några olika variationskoefficienter och vid en servicenivå på 98 % Var. Orderstorlek EOK-diff SL-diff Kostn.diff Kap.diff Std. avvik koeff 0, ,0-8,2-0,4 6,0 83 0, ,7-9,3-0,9 6, , ,8-9,6-1,4 5, ,6-10,8-2,0 4, , ,7-12,0-2,5 3, , ,0-13,0-2,9 2, , ,6-14,0-3,4 1, , ,4-14,9-3,8 0,4 666 Av naturliga skäl är resultatmönstret i det här fallet det samma som för resultaten enligt tabell 1. Av tabellen framgår att skillnaderna mellan samtidig och separat bestämning ökar med ökande efterfrågevariation. Resultaten stöder därmed delvis Browns (1967, sid 137) påstående att skillnaden mellan ekonomisk orderkvantitet beräknad separat och ekonomisk orderkvantitet beräknad med hänsyn tagen till säkerhetslager endast är signifikant om orderstorleken är mindre än tre standardavvikelser. Orderstorleken blir mindre än tre standardavvikelser redan när variationskoefficienten är lika med 0,3. För fallen med de högre variationskoefficienterna kan kostnadsskillnaderna inte betraktas som försumbara. Eftersom orderstorlekarna är större än efterfrågans standardavvikelse under ledtid för alla variationskoefficienter under 0,6 skulle orderstorleken sättas till 500 st för variationskoefficienter upp till 0,6 och till 583 och 666 för variationskoefficienter på 0,7respektive 0,8 om Browns (1977, sid 220) förenklade metod enligt ovan används. Minskningen i totalkostnad skulle då bli som mest 2,4 % för variationskoefficienter under 0,6 och 1,8 % och 2,4 % för variationskoefficienter på 0,7 respektive 0,8. 5 Approximationsförfarande vid beräkning av säkerhetslager med SERV2 För att bestämma säkerhetslagret på ett teoretiskt korrekt sätt med utgångspunkt från en fastställd servicenivå kan man använda följande uttryck för att bestämma servicefunktionens värde och därmed säkerhetsfaktorn med hjälp av normalfördelningstabeller. Se exempelvis Silver - Pyke - Peterson (1998, sid 268). Servicenivån är i det här fallet definierad som andel av efterfrågan som kan levereras direkt från lager G(k) G(k + Q / σ(lt)) = Q / σ(lt) (1 SERV2) där G = servicefunktionen Q = orderstorleken σ(lt) = efterfrågans standardavvikelse under ledtid För att förenkla beräkningarna approximeras uttrycket i regel genom att bortse från den andra termen på ekvationens vänstersida. Vid stora värden på Q / σ(lt) är detta uppenbarligen försvarbart eftersom servicefunktionen är en avtagande funktion. För att analy- 11
12 sera och värdera i vilken utsträckning det approximativa förfarandet kan accepteras har beräkningar genomförts för ett exempel. I exemplet antas efterfrågan per år vara 1000 st och ledtiden för återanskaffning en månad. Beräkningarna har dels avsett vilken servicenivå man egentligen dimensionerar säkerhetslagret för och dels hur mycket större säkerhetslagret blir om man använder det approximativa beräkningsförfarandet. Beräkningen av hur servicenivån påverkas utgår från en servicenivå på 98 %. Från denna servicenivå beräknas därefter servicefunktionen och motsvarande säkerhetsfaktor med den approximativa beräkningsmetoden. Denna säkerhetsfaktor ger upphov till ett säkerhetslager som för stora värden på Q / σ(lt) skulle ge en servicenivå på 98 %. Därefter beräknas k + Q / σ(lt). Slutligen beräknas den servicenivå som man egentligen dimensionerat lagret för med hjälp av ovanstående formel. Servicenivåfunktionen har beräknats med hjälp av den approximativa beräkningsfunktion, NORMSFÖRD(k), som finns tillgänglig i Excel. Vidare har säkerhetsfaktorn för en given servicefunktion beräknats med hjälp av ett approximationsförfarande som lämpar sig för Excel och som finns redovisat av Silver - Pyke - Peterson (1998, sid 736). Erhållna resultat för ett antal olika variationskoefficienter och orderfrekvenser redovisas i tabell 3. Tabellelementen visar den servicenivå som man i realiteten använt för att dimensionera säkerhetslagret. Tabell 3 Servicenivå som säkerhetslagret egentligen dimensioneras för om man använder det approximativa beräkningsförfarandet. Variations 10 order/år 20 order/år 30 order/år 40 order/år 50 order/år koefficient 0,2 98,00 98,00 98,00 98,03 98,07 0,4 98,00 98,03 98,12 98,24 98,37 0,6 98,00 98,12 98,31 98,48 98,64 0,8 98,03 98,24 98,48 98,68 98,84 1,0 98,07 98,37 98,64 98,84 98,99 En variationskoefficient på 0,2 och orderfrekvens på 10 order per år motsvarar ett Q / σ(lt)-värde på 5,99 medan en variationskoefficient på 1,0 och en orderfrekvens på 50 gånger per år motsvarar ett Q / σ(lt)-värde på 0,24. För Q / σ(lt)-värden på 0,8 och lägre blir servvicenivån närmre en procentenhet högre än avsett. Även med avseende på hur säkerhetslagret påverkas är utgångsläget en servicenivå på 98 %. Från denna servicenivå beräknas därefter servicefunktionen och motsvarande säkerhetsfaktor med den approximativa beräkningsmetoden. Därefter har med hjälp av ovan beskrivna approximationsförfaranden och med hjälp av interpolation den säkerhetsfaktor som ger samma servicenivå med det exakta beräkningsförfarandet beräknats, dvs. 98 %. Eftersom säkerhetslagret är proportionellt mot säkerhetsfaktorn kan den procentuella påverkan på säkerhetslagret erhållas. Resultaten för ett antal olika variationskoefficienter och orderfrekvenser redovisas i tabell 4. Tabellelementen visar hur mycket för stort det erhållna säkerhetslagret blir procentuellt. 12
13 Tabell 4 Procentuellt för stort säkerhetslager vid 98 % servicenivå och dimensionerat genom det förenklade beräkningsförfarandet Variations 10 order/år 20 order/år 30 order/år 40 order/år 50 order/år koefficient 0,2 0,0 0,0 0,1 0,4 0,9 0,4 0,0 0,4 1,6 3,1 4,5 0,6 0,1 1,6 3,8 5,8 6,7 0,8 0,4 3,0 5,9 8,2 10,1 1,0 0,9 4,5 7,6 10,1 12,1 Som framgår av tabellen är avvikelserna mellan det säkerhetslager man dimensionerat för och det som faktiskt erhålls endast försumbara för låga orderfrekvenser och små efterfrågevariationer. För Q / σ(lt)-värden på 0,8 och lägre blir säkerhetslagret mer än storleksordningen 4 procent för stort om den approximativa formeln används för säkerhetslagerberäkning. 6 Sammanfattning och slutsatser Vid operativ materialstyrning spelar dimensionering av orderstorlekar och säkerhetslager en avgörande roll för hur effektivt materialflöden kan styras med avseende på kapitalbindning, lagerstyrningskostnader och leveransförmåga. Detta gäller oavsett vilken materialstyrningsmetod man använder. Vald orderstorlek påverkar emellertid säkerhetslagrets storlek, alternativt den servicenivå man kan erhålla. Det är därför av intresse att studera vilka konsekvenser som ändrade orderstorlekar får på den totala kapitalbindningen och på leveransförmågan från lager. De resultat som i dessa avseenden erhållits i den här studien kan sammanfattas på följande sätt. Används SERV1 för att dimensionera säkerhetslager ökar bristkvantiteten per period linjärt med avtagande orderstorlek. Ju större efterfrågevariationen är desto fortare ökar bristkvantiteten. För att undvika detta måste servicenivån och därmed säkerhetslagret ökas i takt med att orderstorlekar minskas. Används SERV2 för dimensionering av säkerhetslager anpassar sig säkerhetslagret automatiskt till avtagande orderstorlekar utan att servicenivån behöver anpassas. Säkerhetslagret ökar med avtagande orderstorlek och ökningen blir större ju större efterfrågevariationerna är. Vid stora efterfrågevariationer är säkerhetslagrets ökning så stor att den totala kapitalbindningen i omsättningslager inte eller endast obetydligt minskar trots stora minskningar i orderkvantiteter. Vid dimensionering av orderstorlekar och säkerhetslager tillämpas i allmänhet ett förenklat beräkningssätt som inte tar hänsyn till det samband som finns mellan de båda variablerna. Vilken betydelse dessa förenklingar kan få har analyserats och de erhållna resultaten kan sammanfattas i följande punkter. I båda fallen används SERV2 som servicenivådefinition. Om orderstorlek och säkerhetslager beräknas separat utan hänsyn till det ömsesidiga samband som föreligger blir orderstorlekarna större och säkerhetslagren mindre om variablerna beräknas samtidigt. De totala lagerstyrningskostnaderna blir högre. Ju 13
14 högre servicenivåer man använder och ju mindre efterfrågan varierar, desto mindre blir kostnadsökningen. Om hänsyn till bristkvantitetstermen inte tas vid dimensionering av säkerhetslager kommer säkerhetslagret att bli för stort och följaktligen den erhållna servicenivån större än den avsedda. Speciellt gäller detta vid stor efterfrågevariation och hög orderfrekvens. Eftersom de samband som råder mellan orderstorlekar och säkerhetslager är komplexa och eftersom det finns många faktorer som avgör om man kan tillåta sig att bortse från ett ömsesidigt beroende mellan dem vid dimensionering, är det svårt att redovisa några enkla slutsatser från studien. Följande grova och allmänt hållna användarorienterade riktlinjer för hur man rekommenderas bete sig i konkreta situationer kan emellertid formuleras som ett resultat av studien. När man fattar beslut om att minska orderstorlekar bör man alltid beakta de konsekvenser detta får på säkerhetslagrets storlek så att inte minskande orderstorlekar åstadkoms till priset av ökad total kapitalbindning. Speciellt bör detta uppmärksammas vid stora efterfrågevariationer och låga servicenivåer. På grund av säkerhetslagrets stora beroende av storleken på lagerpåfyllnadsorder bör metoder för dimensionering av säkerhetslager som tar hänsyn till aktuell orderstorlek alltid användas. I de flesta fall är det praktiskt sett fullt tillfredsställande att dimensionera orderstorlekar oberoende av säkerhetslager. Endast vid fall med servicenivåer under storleksordningen 95 % och efterfrågevariationer motsvarande variationskoefficienter över storleksordningen 0,5 kan det med avseende på de totala lagerstyrningskostnaderna vara värt att ta hänsyn till säkerhetslagrets storlek vid bestämning av orderstorlek genom att använda ett mer teoretiskt korrekt tillvägagångssätt. Ett förenklat sätt att ta sådan hänsyn är att aldrig välja en orderstorlek som är mindre än efterfrågevariationernas standardavvikelse under ledtid. Det approximativa förfarande som praktiskt taget alltid används vid dimensionering av säkerhetslager från en fastställd servicenivå ger tillräckligt näroptimala värden då förhållandet mellan orderstorlek och efterfrågevariationernas standardavvikelse under ledtid är större än storleksordningen 1. I andra fall blir säkerhetslagret för stort och dimensioneringen bör om möjligt göras med hjälp av det teoretiskt korrekta beräkningsförfarandet. Ett förenklat alternativ är att vid små orderstorlekar och stora efterfrågevariationer avsiktligt sätta servicenivån från några tiondels till en procentenhet för låg. Referenser Axsäter, S. (1991) Lagerstyrning, Studentlitteratur. Fetter, R. Dalleck,W. (1961) Decision models for inventory management, Richard Irwin. Brown, R, (1967) Decision rules for inventory management, Holt, Rinehart & Winston. 14
15 Brown, R, (1977) Materials management systems, John Wiley & Sons. Mattsson, S-A. (2005) Differentierad styrning av inleveranser till lager, Arbetspapper, Institutionen för Teknisk Ekonomi och Logistik, Lunds Universitet. Natarajan, R. Goyal, S. (1994) Safety stocks in JIT environments, International Jour-nal of Operations and Production Management, Vol.14 No.10. Plossl, G. Wight, O. (1967) Production and inventory control, John Wiley & Sons. Silver, E. Pyke, D. Peterson, R. (1998) Inventory management and production planning and scheduling, John Wiley & Sons. Tersine, R. (1994) Principles of inventory and materials management, Prentice-Hall. 15
Säkerhetslager beräknat från acceptabelt antal bristtillfällen per år
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 28 Säkerhetslager beräknat från acceptabelt antal bristtillfällen per år All materialstyrning är förknippad med osäkerheter av olika slag.
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 28 Säkerhetslager beräknat från acceptabelt antal bristtillfällen per år All materialstyrning är förknippad med osäkerheter av olika slag.
Säkerhetslager beräknat från cykelservice (Serv1)
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 26 Säkerhetslager beräknat från cykelservice (Serv1) All materialstyrning är förknippad med osäkerheter av olika slag. Det kan gälla osäkerheter
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 26 Säkerhetslager beräknat från cykelservice (Serv1) All materialstyrning är förknippad med osäkerheter av olika slag. Det kan gälla osäkerheter
Säkerhetslagrets andel av beställningspunkten som funktion av ledtid
 Säkerhetslagrets andel av beställningspunkten som funktion av ledtid Stig-Arne Mattsson Sammanfattning I den här studien har en analys gjorts av säkerhetslagrets andel av beställningspunkten som funktion
Säkerhetslagrets andel av beställningspunkten som funktion av ledtid Stig-Arne Mattsson Sammanfattning I den här studien har en analys gjorts av säkerhetslagrets andel av beställningspunkten som funktion
Välja servicenivådefinitioner för dimensionering av säkerhetslager
 Handbok i materialstyrning - Del B Parametrar och variabler B 21 Välja servicenivådefinitioner för dimensionering av säkerhetslager Servicenivå är ett mått på leveransförmåga från lager. Det kan allmänt
Handbok i materialstyrning - Del B Parametrar och variabler B 21 Välja servicenivådefinitioner för dimensionering av säkerhetslager Servicenivå är ett mått på leveransförmåga från lager. Det kan allmänt
Säkerhetslager beräknat från en fast bristkostnad per bristtillfälle
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 21 Säkerhetslager beräknat från en fast bristkostnad per bristtillfälle All materialstyrning är förknippad med osäkerheter av olika slag.
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 21 Säkerhetslager beräknat från en fast bristkostnad per bristtillfälle All materialstyrning är förknippad med osäkerheter av olika slag.
Kostnadseffekter av att differentiera fyllnadsgradservice
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 88 Kostnadseffekter av att differentiera fyllnadsgradservice Differentiering av fyllnadsgradsservice på olika klasser av artiklar i en
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 88 Kostnadseffekter av att differentiera fyllnadsgradservice Differentiering av fyllnadsgradsservice på olika klasser av artiklar i en
Välja servicenivådefinitioner för dimensionering av säkerhetslager
 Handbok i materialstyrning - Del B Parametrar och variabler B 21 Välja servicenivådefinitioner för dimensionering av säkerhetslager Servicenivå är ett mått på leveransförmåga från lager. Det kan allmänt
Handbok i materialstyrning - Del B Parametrar och variabler B 21 Välja servicenivådefinitioner för dimensionering av säkerhetslager Servicenivå är ett mått på leveransförmåga från lager. Det kan allmänt
Säkerhetslager beräknat från en fast bristkostnad per bristtillfälle
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 21 Säkerhetslager beräknat från en fast bristkostnad per bristtillfälle All materialstyrning är förknippad med osäkerheter av olika slag.
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 21 Säkerhetslager beräknat från en fast bristkostnad per bristtillfälle All materialstyrning är förknippad med osäkerheter av olika slag.
Beräkna parametern bristkostnader från orderradsservice
 Handbok i materialstyrning - Del B Parametrar och variabler B 31 Beräkna parametern bristkostnader från orderradsservice Med bristkostnader avses alla de kostnader som hänger samman med och som uppstår
Handbok i materialstyrning - Del B Parametrar och variabler B 31 Beräkna parametern bristkostnader från orderradsservice Med bristkostnader avses alla de kostnader som hänger samman med och som uppstår
Säkerhetslager beräknat från antal dagars täcktid
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 13 Säkerhetslager beräknat från antal dagars täcktid All materialstyrning är förknippad med osäkerheter av olika slag. Det kan gälla osäkerheter
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 13 Säkerhetslager beräknat från antal dagars täcktid All materialstyrning är förknippad med osäkerheter av olika slag. Det kan gälla osäkerheter
Alternativa sätt att beräkna standardavvikelser
 Alternativa sätt att beräkna standardavvikelser Stig-Arne Mattsson Sammanfattning I affärssystem är det vanligt att standardavvikelser beräknas per prognosperiod motsvarande en månad eller en fyraveckorsperiod.
Alternativa sätt att beräkna standardavvikelser Stig-Arne Mattsson Sammanfattning I affärssystem är det vanligt att standardavvikelser beräknas per prognosperiod motsvarande en månad eller en fyraveckorsperiod.
Säkerhetslager beräknat från bristkostnad per styck
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 22 Säkerhetslager beräknat från bristkostnad per styck All materialstyrning är förknippad med osäkerheter av olika slag. Det kan gälla
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 22 Säkerhetslager beräknat från bristkostnad per styck All materialstyrning är förknippad med osäkerheter av olika slag. Det kan gälla
Välja cykelservicenivå för dimensionering av säkerhetslager
 Handbok i materialstyrning - Del B Parametrar och variabler B 22 Välja cykelservicenivå för dimensionering av säkerhetslager Leveransförmåga eller servicenivå vid leverans från lager kan allmänt definieras
Handbok i materialstyrning - Del B Parametrar och variabler B 22 Välja cykelservicenivå för dimensionering av säkerhetslager Leveransförmåga eller servicenivå vid leverans från lager kan allmänt definieras
Säkerhetslager beräknat från en fast bristkostnad per restorder
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 23 Säkerhetslager beräknat från en fast bristkostnad per restorder All materialstyrning är förknippad med osäkerheter av olika slag. Det
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 23 Säkerhetslager beräknat från en fast bristkostnad per restorder All materialstyrning är förknippad med osäkerheter av olika slag. Det
Välja servicenivådefinitioner för dimensionering av säkerhetslager
 Handbok i materialstyrning - Del B Parametrar och variabler B 21 Välja servicenivådefinitioner för dimensionering av säkerhetslager Servicenivå är ett mått på leveransförmåga från lager. Det kan allmänt
Handbok i materialstyrning - Del B Parametrar och variabler B 21 Välja servicenivådefinitioner för dimensionering av säkerhetslager Servicenivå är ett mått på leveransförmåga från lager. Det kan allmänt
Kostnadseffekter av att differentiera cykelservice
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 87 Kostnadseffekter av att differentiera cykelservice Differentiering av cykelservice på olika klasser av artiklar i en grupp vid bestämning
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 87 Kostnadseffekter av att differentiera cykelservice Differentiering av cykelservice på olika klasser av artiklar i en grupp vid bestämning
Kostnadseffekter av att differentiera antal dagars täcktid
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 86 Kostnadseffekter av att differentiera antal dagars täcktid Differentiering av antal dagars täcktid för olika klasser av artiklar i en
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 86 Kostnadseffekter av att differentiera antal dagars täcktid Differentiering av antal dagars täcktid för olika klasser av artiklar i en
Brister i använda lagerstyrningsmodeller ger lägre servicenivåer
 Brister i använda lagerstyrningsmodeller ger lägre servicenivåer än önskat 1 Stig-Arne Mattsson, Permatron AB Det finns ett antal lagerstyrningsmetoder som i större eller mindre omfattning används i tillverkande
Brister i använda lagerstyrningsmodeller ger lägre servicenivåer än önskat 1 Stig-Arne Mattsson, Permatron AB Det finns ett antal lagerstyrningsmetoder som i större eller mindre omfattning används i tillverkande
Säkerhetslager beräknat från fyllnadsgrad (Serv2)
 Handok i materialstyrning - Del E Bestämning av säkerhetslager E 7 Säkerhetslager eräknat från fyllnadsgrad (Serv) All materialstyrning är förknippad med osäkerheter av olika slag. Det kan gälla osäkerheter
Handok i materialstyrning - Del E Bestämning av säkerhetslager E 7 Säkerhetslager eräknat från fyllnadsgrad (Serv) All materialstyrning är förknippad med osäkerheter av olika slag. Det kan gälla osäkerheter
Överdrag i materialstyrningssystem
 Handbok i materialstyrning - Del C Materialstyrningsmetoder C 9 Överdrag i materialstyrningssystem De modeller som används i praktisk tillämpning för att styra lager, exempelvis i olika varianter av beställningspunktssystem,
Handbok i materialstyrning - Del C Materialstyrningsmetoder C 9 Överdrag i materialstyrningssystem De modeller som används i praktisk tillämpning för att styra lager, exempelvis i olika varianter av beställningspunktssystem,
Välja nivå på fyllnadsgradsservice för dimensionering
 Handbok i materialstyrning - Del B Parametrar och variabler B 23 Välja nivå på fyllnadsgradsservice för dimensionering av säkerhetslager Leveransförmåga eller servicenivå vid leverans från lager kan allmänt
Handbok i materialstyrning - Del B Parametrar och variabler B 23 Välja nivå på fyllnadsgradsservice för dimensionering av säkerhetslager Leveransförmåga eller servicenivå vid leverans från lager kan allmänt
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter
 Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 12 Ekonomisk orderkvantitet Materialstyrning innebär förenklat att styra materialflöden genom att för varje artikel och vid varje ordertillfälle
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 12 Ekonomisk orderkvantitet Materialstyrning innebär förenklat att styra materialflöden genom att för varje artikel och vid varje ordertillfälle
Handbok i materialstyrning - Del E Bestämning av säkerhetslager
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 13 Säkerhetslager beräknat från antal dagars efterfrågan All materialstyrning är förknippad med osäkerheter av olika slag. Det kan gälla
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 13 Säkerhetslager beräknat från antal dagars efterfrågan All materialstyrning är förknippad med osäkerheter av olika slag. Det kan gälla
Orderkvantitet med hjälp av ekonomiskt beräknad
 Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 32 Orderkvantitet med hjälp av ekonomiskt beräknad täcktid Materialstyrning innebär förenklat att styra materialflöden genom att för
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 32 Orderkvantitet med hjälp av ekonomiskt beräknad täcktid Materialstyrning innebär förenklat att styra materialflöden genom att för
Ekonomisk orderkvantitet med partperiod balansering
 Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 39 Ekonomisk orderkvantitet med partperiod balansering Materialstyrning innebär förenklat att styra materialflöden genom att för varje
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 39 Ekonomisk orderkvantitet med partperiod balansering Materialstyrning innebär förenklat att styra materialflöden genom att för varje
Materialstyrning. Stig-Arne Mattsson
 Logistik Materialstyrning Stig-Arne Mattsson Materialflöden via lager mellan företag Inköpsorder / Kundorder Inköpsorder / Kundorder Leverantörer Företag Kunder/distributörer Informationsbehov för att
Logistik Materialstyrning Stig-Arne Mattsson Materialflöden via lager mellan företag Inköpsorder / Kundorder Inköpsorder / Kundorder Leverantörer Företag Kunder/distributörer Informationsbehov för att
Beräkna standardavvikelser för ledtider
 Handbok i materialstyrning - Del B Parametrar och variabler B 4 Beräkna standardavvikelser för ledtider De formler som traditionellt används för beräkning av standardavvikelser för efterfrågevariationer
Handbok i materialstyrning - Del B Parametrar och variabler B 4 Beräkna standardavvikelser för ledtider De formler som traditionellt används för beräkning av standardavvikelser för efterfrågevariationer
Ekonomisk behovstäckningstid
 Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 32 Ekonomisk behovstäckningstid Materialstyrning innebär förenklat att styra materialflöden genom att för varje artikel och vid varje
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 32 Ekonomisk behovstäckningstid Materialstyrning innebär förenklat att styra materialflöden genom att för varje artikel och vid varje
Ledtidsanpassa standardavvikelser för efterfrågevariationer
 Handbok i materialstyrning - Del B Parametrar och variabler B 43 Ledtidsanpassa standardavvikelser för efterfrågevariationer I affärssystem brukar standardavvikelser för efterfrågevariationer eller prognosfel
Handbok i materialstyrning - Del B Parametrar och variabler B 43 Ledtidsanpassa standardavvikelser för efterfrågevariationer I affärssystem brukar standardavvikelser för efterfrågevariationer eller prognosfel
Säkerhetslager som andel av efterfrågan under ledtid
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 12 Säkerhetslager som andel av efterfrågan under ledtid All materialstyrning är förknippad med osäkerheter av olika slag. Det kan gälla
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 12 Säkerhetslager som andel av efterfrågan under ledtid All materialstyrning är förknippad med osäkerheter av olika slag. Det kan gälla
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter
 Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 12 Ekonomisk orderkvantitet Materialstyrning innebär förenklat att styra materialflöden genom att för varje artikel och vid varje ordertillfälle
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 12 Ekonomisk orderkvantitet Materialstyrning innebär förenklat att styra materialflöden genom att för varje artikel och vid varje ordertillfälle
Beräkning av teoretisk kapitalbindning i lager
 Beräkning av teoretisk kapitalbindning i lager Stig-Arne Mattsson Sammanfattning Vid materialstyrning är det i många sammanhang av intresse att kunna beräkna och analysera hur stort ett lager är eller
Beräkning av teoretisk kapitalbindning i lager Stig-Arne Mattsson Sammanfattning Vid materialstyrning är det i många sammanhang av intresse att kunna beräkna och analysera hur stort ett lager är eller
Lagerstyrningsfrågan Januari 2014 - Fråga och svar
 Lagerstyrningsfrågan Januari 2014 - Fråga och svar När man fastställer kvantiteter att beställa för lagerpåfyllning avrundar man ofta beräknad ekonomiskt orderkvantitet uppåt eller nedåt, exempelvis för
Lagerstyrningsfrågan Januari 2014 - Fråga och svar När man fastställer kvantiteter att beställa för lagerpåfyllning avrundar man ofta beräknad ekonomiskt orderkvantitet uppåt eller nedåt, exempelvis för
Ekonomisk orderkvantitet utan att känna till ordersärkostnader
 Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 13 Ekonomisk orderkvantitet utan att känna till ordersärkostnader Materialstyrning innebär förenklat att styra materialflöden genom att
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 13 Ekonomisk orderkvantitet utan att känna till ordersärkostnader Materialstyrning innebär förenklat att styra materialflöden genom att
Differentiera säkerhetslager med andel efterfrågan under ledtid
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 51 Differentiera säkerhetslager med andel efterfrågan under ledtid Med differentierad materialstyrning menas allmänt att klassificera artiklar
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 51 Differentiera säkerhetslager med andel efterfrågan under ledtid Med differentierad materialstyrning menas allmänt att klassificera artiklar
Vilken servicenivå får man om man dimensionerar säkerhetslager med servicenivå
 Vilken servicenivå får man om man dimensionerar säkerhetslager med servicenivå Stig-Arne Mattsson Sammanfattning En ofta förordad metod för att dimensionera säkerhetslager är att använda en beräkningsmodell
Vilken servicenivå får man om man dimensionerar säkerhetslager med servicenivå Stig-Arne Mattsson Sammanfattning En ofta förordad metod för att dimensionera säkerhetslager är att använda en beräkningsmodell
Välja cykelservicenivå för dimensionering av säkerhetslager
 Handbok i materialstyrning - Del B Parametrar och variabler B 22 Välja cykelservicenivå för dimensionering av säkerhetslager Servicenivå är ett mått på leveransförmåga från lager. Det kan allmänt definieras
Handbok i materialstyrning - Del B Parametrar och variabler B 22 Välja cykelservicenivå för dimensionering av säkerhetslager Servicenivå är ett mått på leveransförmåga från lager. Det kan allmänt definieras
Differentiera säkerhetslager med cykelservice
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 53 Differentiera säkerhetslager med cykelservice Med differentierad materialstyrning menas allmänt att klassificera artiklar och tillämpa
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 53 Differentiera säkerhetslager med cykelservice Med differentierad materialstyrning menas allmänt att klassificera artiklar och tillämpa
Uppskatta bristkostnader i färdigvarulager
 Handbok i materialstyrning - Del B Parametrar och variabler B 14 Uppskatta bristkostnader i färdigvarulager Med bristkostnader i färdigvarulager avses här alla de kostnader som hänger samman med och uppstår
Handbok i materialstyrning - Del B Parametrar och variabler B 14 Uppskatta bristkostnader i färdigvarulager Med bristkostnader i färdigvarulager avses här alla de kostnader som hänger samman med och uppstår
Osäkerhetsgardering genom överdimensionering
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 35 Osäkerhetsgardering genom överdimensionering av produktionsplaner All materialstyrning är förknippad med osäkerheter av olika slag.
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 35 Osäkerhetsgardering genom överdimensionering av produktionsplaner All materialstyrning är förknippad med osäkerheter av olika slag.
En jämförelse av kanbansystem och beställningspunktssystem med avseende på kapitalbindning
 En jämförelse av kanbansystem och beställningspunktssystem med avseende på kapitalbindning Stig-Arne Mattsson Sammanfattning Kanbansystem betraktas av många som effektivare än andra lagerstyrningssystem,
En jämförelse av kanbansystem och beställningspunktssystem med avseende på kapitalbindning Stig-Arne Mattsson Sammanfattning Kanbansystem betraktas av många som effektivare än andra lagerstyrningssystem,
Faktorer som påverkar skillnader i kapitalbindning vid användning av antal dagars behov och fyllnadsgradsservice
 Faktorer som påverkar skillnader i kapitalbindning vid användning av antal dagars behov och fyllnadsgradsservice för säkerhetslagerberäkning Stig-Arne Mattsson Sammanfattning I en tidigare studie har framkommit
Faktorer som påverkar skillnader i kapitalbindning vid användning av antal dagars behov och fyllnadsgradsservice för säkerhetslagerberäkning Stig-Arne Mattsson Sammanfattning I en tidigare studie har framkommit
Den ena är cykelservice och avser andel lagercykler utan brist. Cykelservice kan uttryckt som en procentsats definieras på följande sätt.
 Kapitalbindningsaspekter på val mellan cykelservice och fyllnadsgradsservice Stig-Arne Mattsson Sammanfattning Cykelservice och fyllnadsgradsservice är de två vanligast använda typerna av servicenivå för
Kapitalbindningsaspekter på val mellan cykelservice och fyllnadsgradsservice Stig-Arne Mattsson Sammanfattning Cykelservice och fyllnadsgradsservice är de två vanligast använda typerna av servicenivå för
Bestämning av orderkvantiteter genom differentiering av täcktider från totalt tillåtet antal order
 Bestämning av orderkvantiteter genom differentiering av täcktider från totalt tillåtet antal order Stig-Arne Mattsson Institutionen för ekonomistyrning och logistik Linnéuniversitetet, Växjö Sammanfattning
Bestämning av orderkvantiteter genom differentiering av täcktider från totalt tillåtet antal order Stig-Arne Mattsson Institutionen för ekonomistyrning och logistik Linnéuniversitetet, Växjö Sammanfattning
Orderkvantiteter genom differentiering av antal order per år
 Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 35 Orderkvantiteter genom differentiering av antal order per år Att använda partiformningsmetoden uppskattat antal order per år för bestämning
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 35 Orderkvantiteter genom differentiering av antal order per år Att använda partiformningsmetoden uppskattat antal order per år för bestämning
Normalfördelning och Poissonfördelning för bestämning
 Normalfördelning och Poissonfördelning för bestämning av säkerhetslager Stig-Arne Mattsson Sammanfattning För att kunna dimensionera beställningspunkter och säkerhetslager baserade på en målsatt servicenivå
Normalfördelning och Poissonfördelning för bestämning av säkerhetslager Stig-Arne Mattsson Sammanfattning För att kunna dimensionera beställningspunkter och säkerhetslager baserade på en målsatt servicenivå
Orderkvantiteter vid säsongvariationer
 Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 49 Orderkvantiteter vid säsongvariationer Ett antal alternativa metoder finns tillgängliga för beräkning av ekonomiska orderkvantiteter.
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 49 Orderkvantiteter vid säsongvariationer Ett antal alternativa metoder finns tillgängliga för beräkning av ekonomiska orderkvantiteter.
Handbok i materialstyrning - Del C Materialstyrningsmetoder
 Handbok i materialstyrning - Del C Materialstyrningsmetoder C 31 Täcktidsplanering Materialstyrning innebär förenklat att styra materialflöden genom att för varje artikel och vid varje ordertillfälle fatta
Handbok i materialstyrning - Del C Materialstyrningsmetoder C 31 Täcktidsplanering Materialstyrning innebär förenklat att styra materialflöden genom att för varje artikel och vid varje ordertillfälle fatta
Prognostisering med exponentiell utjämning
 Handbok i materialstyrning - Del F Prognostisering F 23 Prognostisering med exponentiell utjämning Det som karakteriserar lagerstyrda verksamheter är att leveranstiden till kund är kortare än leveranstiden
Handbok i materialstyrning - Del F Prognostisering F 23 Prognostisering med exponentiell utjämning Det som karakteriserar lagerstyrda verksamheter är att leveranstiden till kund är kortare än leveranstiden
Säkerhetslager som andel av efterfrågan
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 12 Säkerhetslager som andel av efterfrågan under ledtid All materialstyrning är förknippad med osäkerheter av olika slag. Det kan gälla
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 12 Säkerhetslager som andel av efterfrågan under ledtid All materialstyrning är förknippad med osäkerheter av olika slag. Det kan gälla
Uppskatta bristkostnader i färdigvarulager
 Handbok i materialstyrning - Del B Parametrar och variabler B 14 Uppskatta bristkostnader i färdigvarulager Med bristkostnader i färdigvarulager, dvs. lager av varor för leverans till kunder, avses alla
Handbok i materialstyrning - Del B Parametrar och variabler B 14 Uppskatta bristkostnader i färdigvarulager Med bristkostnader i färdigvarulager, dvs. lager av varor för leverans till kunder, avses alla
Reservationshantering i beställningspunktssystem
 Handbok i materialstyrning - Del C Materialstyrningsmetoder C 17 Reservationshantering i beställningspunktssystem Vid användning av beställningspunktssystem jämförs beställningspunkten med aktuell lagerposition,
Handbok i materialstyrning - Del C Materialstyrningsmetoder C 17 Reservationshantering i beställningspunktssystem Vid användning av beställningspunktssystem jämförs beställningspunkten med aktuell lagerposition,
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter
 Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 04 Faktorer som påverkar val av orderkvantiteter Materialstyrning innebär förenklat att styra materialflöden genom att för varje artikel
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 04 Faktorer som påverkar val av orderkvantiteter Materialstyrning innebär förenklat att styra materialflöden genom att för varje artikel
Ekonomisk orderkvantitet utan att känna till ordersärkostnader
 Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 13 Ekonomisk orderkvantitet utan att känna till ordersärkostnader Materialstyrning innebär förenklat att styra materialflöden genom att
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 13 Ekonomisk orderkvantitet utan att känna till ordersärkostnader Materialstyrning innebär förenklat att styra materialflöden genom att
Uppskatta ordersärkostnader för inköpsartiklar
 Handbok i materialstyrning - Del B Parametrar och variabler B 11 Uppskatta ordersärkostnader för inköpsartiklar Med ordersärkostnader för inköpsartiklar avses alla de kostnader som är förknippade med att
Handbok i materialstyrning - Del B Parametrar och variabler B 11 Uppskatta ordersärkostnader för inköpsartiklar Med ordersärkostnader för inköpsartiklar avses alla de kostnader som är förknippade med att
Optimal differentiering av servicenivåer för att effektivisera
 Optimal differentiering av servicenivåer för att effektivisera lagerstyrning Stig-Arne Mattsson Sammanfattning Differentiering av servicenivåer innebär att olika artiklar ges olika höga servicenivåer vid
Optimal differentiering av servicenivåer för att effektivisera lagerstyrning Stig-Arne Mattsson Sammanfattning Differentiering av servicenivåer innebär att olika artiklar ges olika höga servicenivåer vid
Kapitalbindningseffekter av uppskattade orderkvantiteter 1
 Kapitalbindningseffekter av uppskattade orderkvantiteter 1 Stig-Arne Mattsson, Permatron AB För att bestämma orderkvantiteter finns det sedan tidigt 1900-tal ett stort antal olika metoder till förfogande,
Kapitalbindningseffekter av uppskattade orderkvantiteter 1 Stig-Arne Mattsson, Permatron AB För att bestämma orderkvantiteter finns det sedan tidigt 1900-tal ett stort antal olika metoder till förfogande,
E 01. Välja metoder för hantering av osäkerheter En översikt. Säkerhetslagerkvantitet. Handbok i materialstyrning - Del E Bestämning av säkerhetslager
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 01 Välja metoder för hantering av osäkerheter En översikt All materialstyrning är förknippad med osäkerheter av olika slag. Det kan gälla
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 01 Välja metoder för hantering av osäkerheter En översikt All materialstyrning är förknippad med osäkerheter av olika slag. Det kan gälla
Materialstyrningsutmaningar i Svensk industri
 CLIP - Högskolan i Gävle den 28 maj 2009 Materialstyrningsutmaningar i Svensk industri Stig-Arne Mattsson Division of Logistics and Transportation Bild 1 Kapitalbindning i svensk tillverkningsindustri
CLIP - Högskolan i Gävle den 28 maj 2009 Materialstyrningsutmaningar i Svensk industri Stig-Arne Mattsson Division of Logistics and Transportation Bild 1 Kapitalbindning i svensk tillverkningsindustri
Kapitalbindningseffekter av att differentiera antal dagars täcktid
 Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 82 Kapitalbindningseffekter av att differentiera antal dagars täcktid Differentiering av antal dagars täcktid på olika klasser av artiklar
Handbok i materialstyrning - Del E Bestämning av säkerhetslager E 82 Kapitalbindningseffekter av att differentiera antal dagars täcktid Differentiering av antal dagars täcktid på olika klasser av artiklar
Uppskatta ledtider för anskaffning
 Handbok i materialstyrning - Del B Parametrar och variabler B 31 Uppskatta ledtider för anskaffning Begreppet ledtid avser generellt den kalendertid som krävs för att genomföra en administrativ process.
Handbok i materialstyrning - Del B Parametrar och variabler B 31 Uppskatta ledtider för anskaffning Begreppet ledtid avser generellt den kalendertid som krävs för att genomföra en administrativ process.
Säkerhetslager som antal dagars medelefterfrågan eller baserat på fyllnadsgradsservice
 Säkerhetslager som antal dagars medelefterfrågan eller baserat på fyllnadsgradsservice Stig-Arne Mattsson Sammanfattning För dimensionering av säkerhetslager finns två i industrin vanligt använda metoder.
Säkerhetslager som antal dagars medelefterfrågan eller baserat på fyllnadsgradsservice Stig-Arne Mattsson Sammanfattning För dimensionering av säkerhetslager finns två i industrin vanligt använda metoder.
Extremvärdens påverkan på beräkning av standardavvikelser
 Extremvärdens påverkan på beräkning av standardavvikelser Stig-Arne Mattsson Sammanfattning Även om efterfrågan under normala omständigheter varierar från period till period, är variationerna i allmänhet
Extremvärdens påverkan på beräkning av standardavvikelser Stig-Arne Mattsson Sammanfattning Även om efterfrågan under normala omständigheter varierar från period till period, är variationerna i allmänhet
Samband mellan några olika beslutsvariabler och lagerstyrningseffektivitet
 Samband mellan några olika beslutsvariabler och lagerstyrningseffektivitet i form av kapitalbindning och erhållna servicenivåer Stig-Arne Mattsson Institutionen för ekonomistyrning och logistik Linnéuniversitetet,
Samband mellan några olika beslutsvariabler och lagerstyrningseffektivitet i form av kapitalbindning och erhållna servicenivåer Stig-Arne Mattsson Institutionen för ekonomistyrning och logistik Linnéuniversitetet,
Konsekvenser av att använda förenklade lagerstyrningsmetoder
 Konsekvenser av att använda förenklade lagerstyrningsmetoder Stig-Arne Mattsson Sammanfattning I svensk industri används i stor utsträckning mycket förenklade modeller och tillvägagångssätt vid lagerstyrning.
Konsekvenser av att använda förenklade lagerstyrningsmetoder Stig-Arne Mattsson Sammanfattning I svensk industri används i stor utsträckning mycket förenklade modeller och tillvägagångssätt vid lagerstyrning.
Effekter av att jämföra beställningspunkter med redovisat eller disponibelt saldo
 Effekter av att jämföra beställningspunkter med redovisat eller disponibelt saldo Stig-Arne Mattsson Institutionen för ekonomistyrning och logistik Linnéuniversitetet, Växjö Sammanfattning Vid användning
Effekter av att jämföra beställningspunkter med redovisat eller disponibelt saldo Stig-Arne Mattsson Institutionen för ekonomistyrning och logistik Linnéuniversitetet, Växjö Sammanfattning Vid användning
Ekonomisk orderkvantitet för artiklar med lågfrekvent efterfrågan
 Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 14 Ekonomisk orderkvantitet för artiklar med lågfrekvent efterfrågan Materialstyrning innebär förenklat att styra materialflöden genom
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 14 Ekonomisk orderkvantitet för artiklar med lågfrekvent efterfrågan Materialstyrning innebär förenklat att styra materialflöden genom
Uppskatta bristkostnader i lager för produktion
 Handbok i materialstyrning - Del B Parametrar och variabler B 15 Uppskatta bristkostnader i lager för produktion Med bristkostnader i lager för produktion, nedan kallat produktionslager, avses här alla
Handbok i materialstyrning - Del B Parametrar och variabler B 15 Uppskatta bristkostnader i lager för produktion Med bristkostnader i lager för produktion, nedan kallat produktionslager, avses här alla
Reservationshantering vid materialbehovsplanering
 Handbok i materialstyrning - Del C Materialstyrningsmetoder C 44 Reservationshantering vid materialbehovsplanering Vid materialstyrning föreligger ofta situationer där man har både prognoser och reservationer
Handbok i materialstyrning - Del C Materialstyrningsmetoder C 44 Reservationshantering vid materialbehovsplanering Vid materialstyrning föreligger ofta situationer där man har både prognoser och reservationer
Lagerstyrning i hög- och lågpresterande företag 1
 Lagerstyrning i hög- och lågpresterande företag 1 Logistik och Transport, Chalmers Tek- Patrik Jonsson Stig-Arne Mattsson niska Högskola Lagerstyrning handlar principiellt om att fastställa kvantiteter
Lagerstyrning i hög- och lågpresterande företag 1 Logistik och Transport, Chalmers Tek- Patrik Jonsson Stig-Arne Mattsson niska Högskola Lagerstyrning handlar principiellt om att fastställa kvantiteter
Differentiering av servicenivåer för effektivare lagerstyrning
 Differentiering av servicenivåer för effektivare lagerstyrning Stig-rne Mattsson Sammanfattning Det är rimligt att förvänta sig att sättet att klassificera artiklar påverkar hur effektiv en servicenivådifferentiering
Differentiering av servicenivåer för effektivare lagerstyrning Stig-rne Mattsson Sammanfattning Det är rimligt att förvänta sig att sättet att klassificera artiklar påverkar hur effektiv en servicenivådifferentiering
C 51. Två-binge system. 1 Metodbeskrivning. Handbok i materialstyrning - Del C Materialstyrningsmetoder
 Handbok i materialstyrning - Del C Materialstyrningsmetoder C 51 Två-binge system Materialstyrning innebär förenklat att styra materialflöden genom att för varje artikel och vid varje ordertillfälle fatta
Handbok i materialstyrning - Del C Materialstyrningsmetoder C 51 Två-binge system Materialstyrning innebär förenklat att styra materialflöden genom att för varje artikel och vid varje ordertillfälle fatta
Försämring av leveransservice från lager vid bristfällig leveransprecision från leverantörer
 Försämring av leveransservice från lager vid bristfällig leveransprecision från leverantörer Stig-Arne Mattsson Sammanfattning Låg leveransprecision i bemärkelsen försenade inleveranser från leverantörer
Försämring av leveransservice från lager vid bristfällig leveransprecision från leverantörer Stig-Arne Mattsson Sammanfattning Låg leveransprecision i bemärkelsen försenade inleveranser från leverantörer
Ledtidens och ledtidsvariationens betydelse för säkerhetslagrets
 Ledtidens och ledtidsvariationens betydelse för säkerhetslagrets storlek Stig-Arne Mattsson Sammanfattning Ett lagerstyrningssystems effektivitet påverkas av ledtidens längd för återpåfyllnad av lager
Ledtidens och ledtidsvariationens betydelse för säkerhetslagrets storlek Stig-Arne Mattsson Sammanfattning Ett lagerstyrningssystems effektivitet påverkas av ledtidens längd för återpåfyllnad av lager
Är det någon skillnad på våra vanligt använda materialplaneringsmetoder?
 Lagerstyrningsakademin.se Är det någon skillnad på våra vanligt använda materialplaneringsmetoder? Stig-Arne Mattsson Det finns nog få frågor inom logistiken där det finns så motsatta uppfattningar som
Lagerstyrningsakademin.se Är det någon skillnad på våra vanligt använda materialplaneringsmetoder? Stig-Arne Mattsson Det finns nog få frågor inom logistiken där det finns så motsatta uppfattningar som
Beräkning av standardavvikelser för efterfrågevariationer vid varierande leveranstider
 Beräkning av standardavvikelser för efterfrågevariationer vid varierande leveranstider Stig-Arne Mattsson Sammanfattning I litteraturen finns en vanligt publicerade formel för beräkning av efterfrågans
Beräkning av standardavvikelser för efterfrågevariationer vid varierande leveranstider Stig-Arne Mattsson Sammanfattning I litteraturen finns en vanligt publicerade formel för beräkning av efterfrågans
Säkerhetslager vid materialbehovsplanering
 Handbok i materialstyrning - Del E Bestämnign av säkerhetslager E 43 Säkerhetslager vid materialbehovsplanering När materialflöden styrs med hjälp av materialbehovsplanering med nedbrytning av produktstrukturer
Handbok i materialstyrning - Del E Bestämnign av säkerhetslager E 43 Säkerhetslager vid materialbehovsplanering När materialflöden styrs med hjälp av materialbehovsplanering med nedbrytning av produktstrukturer
Avvikelser och variationer i erhållna servicenivåer
 Avvikelser och variationer i erhållna servicenivåer Stig-Arne Mattsson Sammanfattning En förutsättning för att kunna bedriva en framgångsrik verksamhet är att kunna prestera en konkurrenskraftig leveransförmåga.
Avvikelser och variationer i erhållna servicenivåer Stig-Arne Mattsson Sammanfattning En förutsättning för att kunna bedriva en framgångsrik verksamhet är att kunna prestera en konkurrenskraftig leveransförmåga.
Välja metod för bestämning av orderkvantiteter
 Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 01 Välja metod för bestämning av orderkvantiteter En översikt Materialstyrning innebär förenklat att styra materialflöden genom att för
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 01 Välja metod för bestämning av orderkvantiteter En översikt Materialstyrning innebär förenklat att styra materialflöden genom att för
Myter om lagerstyrning
 Myter om lagerstyrning Om man dimensionerar ett säkerhetslager för en artikel med en beräkningsmetod som utgår från en önskad servicenivå så får man denna servicenivå - Maj 2013 När man läser om dimensionering
Myter om lagerstyrning Om man dimensionerar ett säkerhetslager för en artikel med en beräkningsmetod som utgår från en önskad servicenivå så får man denna servicenivå - Maj 2013 När man läser om dimensionering
Användning av volymvärdeklassificering vid bestämning
 Användning av volymvärdeklassificering vid bestämning av orderkvantiteter Stig-Arne Mattsson Sammanfattning I företag är det vanligt att man använder täcktider för bestämning av orderkvantiteter vid lagerstyrning,
Användning av volymvärdeklassificering vid bestämning av orderkvantiteter Stig-Arne Mattsson Sammanfattning I företag är det vanligt att man använder täcktider för bestämning av orderkvantiteter vid lagerstyrning,
PLAN s forsknings- och tillämpningskonferens den augusti 2015 i Luleå. Användning av antal dagar som parameter vid lagerstyrning
 PLAN s forsknings- och tillämpningskonferens den 27 28 augusti 2015 i Luleå Användning av antal dagar som parameter vid lagerstyrning Metoder för bestämning av lagerstyrningsparametrar Metoder för bestämning
PLAN s forsknings- och tillämpningskonferens den 27 28 augusti 2015 i Luleå Användning av antal dagar som parameter vid lagerstyrning Metoder för bestämning av lagerstyrningsparametrar Metoder för bestämning
Användning av bristkostnader för att dimensionera säkerhetslager
 Användning av bristkostnader för att dimensionera säkerhetslager Stig-Arne Mattsson Institutionen för ekonomistyrning och logistik Linnéuniversitetet, Växjö Sammanfattning Dimensionering av säkerhetslager
Användning av bristkostnader för att dimensionera säkerhetslager Stig-Arne Mattsson Institutionen för ekonomistyrning och logistik Linnéuniversitetet, Växjö Sammanfattning Dimensionering av säkerhetslager
Orderkvantiteter genom differentiering av antal dagars täcktider
 Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 34 Orderkvantiteter genom differentiering av antal dagars täcktider Att använda partiformningsmetoden uppskattat antal dagars täcktid
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 34 Orderkvantiteter genom differentiering av antal dagars täcktider Att använda partiformningsmetoden uppskattat antal dagars täcktid
Prognostisering med glidande medelvärde
 Handbok i materialstyrning - Del F Prognostisering F 21 Prognostisering med glidande medelvärde Det som karakteriserar lagerstyrda verksamheter är att leveranstiden till kund är kortare än leveranstiden
Handbok i materialstyrning - Del F Prognostisering F 21 Prognostisering med glidande medelvärde Det som karakteriserar lagerstyrda verksamheter är att leveranstiden till kund är kortare än leveranstiden
Beräkning av medelkapitalbindning
 Beräkning av medelkapitalbindning i lager Stig-Arne Mattsson Department of Industrial Management and Logistics Engineering Logistics Lund University Rapport Tlog MS12 Januari 2005 Sammanfattning Vid materialstyrning
Beräkning av medelkapitalbindning i lager Stig-Arne Mattsson Department of Industrial Management and Logistics Engineering Logistics Lund University Rapport Tlog MS12 Januari 2005 Sammanfattning Vid materialstyrning
Uppskatta lagerhållningssärkostnader
 Handbok i materialstyrning - Del B Parametrar och variabler B 13 Uppskatta lagerhållningssärkostnader Med lagerhållningssärkostnader avses alla de kostnader som hänger samman med och uppstår genom att
Handbok i materialstyrning - Del B Parametrar och variabler B 13 Uppskatta lagerhållningssärkostnader Med lagerhållningssärkostnader avses alla de kostnader som hänger samman med och uppstår genom att
Metoder för bestämning av orderkvantiteter
 Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 01 Metoder för bestämning av orderkvantiteter En översikt Materialstyrning innebär förenklat att styra materialflöden genom att för varje
Handbok i materialstyrning - Del D Bestämning av orderkvantiteter D 01 Metoder för bestämning av orderkvantiteter En översikt Materialstyrning innebär förenklat att styra materialflöden genom att för varje
Prognostisera beställningspunkter med verklig efterfrågefördelning
 Handbok i materialstyrning - Del F Prognostisering F 3 Prognostisera beställningspunkter med verklig efterfrågefördelning En av de mest väsentliga materialstyrningsfunktionerna är att avgöra när en ny
Handbok i materialstyrning - Del F Prognostisering F 3 Prognostisera beställningspunkter med verklig efterfrågefördelning En av de mest väsentliga materialstyrningsfunktionerna är att avgöra när en ny
Användning av policybestämd lagerhållningsfaktor för att påverka kapitalbindning i lager
 Användning av policybestämd lagerhållningsfaktor för att påverka kapitalbindning i lager Stig-Arne Mattsson Institutionen för ekonomistyrning och logistik Linnéuniversitetet, Växjö Sammanfattning Många
Användning av policybestämd lagerhållningsfaktor för att påverka kapitalbindning i lager Stig-Arne Mattsson Institutionen för ekonomistyrning och logistik Linnéuniversitetet, Växjö Sammanfattning Många
Känslighetsanalys av prognos- och ledtidskvalitetens påverkan på servicenivå och säkerhetslager
 Känslighetsanalys av prognos- och ledtidskvalitetens påverkan på servicenivå och säkerhetslager Stig-Arne Mattsson Sammanfattning Avgörande för när inleverans bör ske till ett lager är förväntad efterfrågan
Känslighetsanalys av prognos- och ledtidskvalitetens påverkan på servicenivå och säkerhetslager Stig-Arne Mattsson Sammanfattning Avgörande för när inleverans bör ske till ett lager är förväntad efterfrågan
Handbok i materialstyrning - Del A Effektivitetsmått och effektivitetsuppföljning
 Handbok i materialstyrning - Del A Effektivitetsmått och effektivitetsuppföljning A 13 Omsättningshastighet i lager I alla materialflöden binds kapital vare sig det beror på att material ligger i lager
Handbok i materialstyrning - Del A Effektivitetsmått och effektivitetsuppföljning A 13 Omsättningshastighet i lager I alla materialflöden binds kapital vare sig det beror på att material ligger i lager
Optimera totalkostnader eller manipulera kapitalbindning?
 Lagerstyrningsakademin.se Optimera totalkostnader eller manipulera kapitalbindning? Stig-Arne Mattsson Oavsett vilken metod man använder för att beräkna ekonomiska orderkvantiteter är det i grunden fråga
Lagerstyrningsakademin.se Optimera totalkostnader eller manipulera kapitalbindning? Stig-Arne Mattsson Oavsett vilken metod man använder för att beräkna ekonomiska orderkvantiteter är det i grunden fråga
Beställningspunktssystem med saldooberoende orderkvantiteter
 Handbok i materialstyrning - Del C Materialstyrningsmetoder C 11 Beställningspunktssystem med saldooberoende orderkvantiteter Materialstyrning innebär förenklat att styra materialflöden genom att för varje
Handbok i materialstyrning - Del C Materialstyrningsmetoder C 11 Beställningspunktssystem med saldooberoende orderkvantiteter Materialstyrning innebär förenklat att styra materialflöden genom att för varje
tentaplugg.nu av studenter för studenter
 tentaplugg.nu av studenter för studenter Kurskod T0002N Kursnamn Logistik 1 Datum 2012-10-26 Material Fördjupningsuppgift Kursexaminator Betygsgränser Tentamenspoäng Övrig kommentar Försättsblad inlämningsuppgift
tentaplugg.nu av studenter för studenter Kurskod T0002N Kursnamn Logistik 1 Datum 2012-10-26 Material Fördjupningsuppgift Kursexaminator Betygsgränser Tentamenspoäng Övrig kommentar Försättsblad inlämningsuppgift
Konsekvenser av sju vanliga fel vid lagerstyrning
 Konsekvenser av sju vanliga fel vid lagerstyrning Stig-Arne Mattsson Sammanfattning Lagerstyrning är sedan länge ett centralt ämnesområde inom logistiken. Dess rötter kan spåras ända till tidigt nittonhundratal.
Konsekvenser av sju vanliga fel vid lagerstyrning Stig-Arne Mattsson Sammanfattning Lagerstyrning är sedan länge ett centralt ämnesområde inom logistiken. Dess rötter kan spåras ända till tidigt nittonhundratal.
Handbok i materialstyrning - Del F Prognostisering
 Handbok i materialstyrning - Del F Prognostisering F 59 Prognoskonsumtion En föreställning om storleken på framtida efterfrågan är en förutsättning för att effektivt kunna styra materialflöden i försörjningskedjor.
Handbok i materialstyrning - Del F Prognostisering F 59 Prognoskonsumtion En föreställning om storleken på framtida efterfrågan är en förutsättning för att effektivt kunna styra materialflöden i försörjningskedjor.
Planeringsfrekvensens påverkan på leveransförmåga och kapitalbindning
 Planeringsfrekvensens påverkan på leveransförmåga och kapitalbindning Stig-Arne Mattsson Institutionen för ekonomistyrning och logistik Linnéuniversitetet, Växjö Sammanfattning Att planera frisläppning
Planeringsfrekvensens påverkan på leveransförmåga och kapitalbindning Stig-Arne Mattsson Institutionen för ekonomistyrning och logistik Linnéuniversitetet, Växjö Sammanfattning Att planera frisläppning
Vad gör rätt lagerstyrning för sista raden
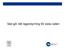 Vad gör rätt lagerstyrning för sista raden Nils Robertsson VD på PromoSoft 100 % fokus på lager och inköp Utvecklar lagerstyrningssystem och säljer WMS och andra moduler för Supply Chain Add-on till affärssystemen
Vad gör rätt lagerstyrning för sista raden Nils Robertsson VD på PromoSoft 100 % fokus på lager och inköp Utvecklar lagerstyrningssystem och säljer WMS och andra moduler för Supply Chain Add-on till affärssystemen
Föreläsning 5. Lagerstyrning
 Föreläsning 5 Lagerstyrning Kursstruktur Innehåll Föreläsning Lek1on Labora1on Introduk*on, produk*onsekonomiska grunder, produk*onssystem, ABC- klassificering Fö 1 Prognos*sering Fö 2 Le 1 La 1 Sälj-
Föreläsning 5 Lagerstyrning Kursstruktur Innehåll Föreläsning Lek1on Labora1on Introduk*on, produk*onsekonomiska grunder, produk*onssystem, ABC- klassificering Fö 1 Prognos*sering Fö 2 Le 1 La 1 Sälj-
