Texturering - förstoring 2(2)
|
|
|
- Per-Olof Öberg
- för 7 år sedan
- Visningar:
Transkript
1 Texturering - förstoring 2(2) De viktigaste ändringarna beror på Texturering i JOGL (Ex. 18) att matriselement i Java inte säkert lagras i sekvens (vilket OpenGL antar) att Java saknar motsvarighet till GLubyte (C:s unsigned char) för tal Vi får därför använda en vanlig vektor respektive datatypen byte för tal -128 till 127. Härvid betyder och (i min version av JOGL verkar det som om -128 också blir 0.0 och -1 blir 1.0, men det är nog en bugg; alla negativa tal borde bli 0.0). Variabler i MyGLEventListener: private const int TexWidth= 4; private const int TexHeight=4; private byte[] Image = new byte[texheight*tex- Width*3]; int[] texname = new int[2]; Initieringarna görs i init. I stället för t ex Image[i,j,1] = (GLubyte)255; får vi skriva Image[i*TexWidth*3+j*3+1] = 127; Slutligen byter vi i anropet av glteximage den parameter beskriver texelns lagring i Image GL_UNSIGNED_BYTE mot GL_BYTE, dvs gl.glteximage2d(gl.gl_texture_2d, 0, GL.GL_RGB, TexWidth, TexHeight, 0, GL.GL_RGB, GL.GL_BYTE, Image); DATORGRAFIK Kanske tycker du att den vänstra bilden (dvs GL_NEAREST) ser bäst ut. Nyttan med GL_LINEAR i förhållande till GL_NEAREST ser vi om linjerna inte är axelparallella I de flesta fall är en utjämning av typen till höger mest tilltalande för ögat, men det finns situationer då man vill bevara de skarpa övergångarna. För krökta ytor är det inte självklart hur matematiken bakom ser ut. Vi nöjer oss med att konstatera att det brukar fungera bra. Texturering - placering av texturen I högra figuren har vi vridit texturen vinkeln v innan den lagts på kvadraten, vilket t ex kan ske med andra texturkoordinater. DATORGRAFIK v Texturering - förstoring 1(2) Problem: Till varje bildpunkt hör texturkoordinatvärden (t ex via mittpunkten). Det verkar då naturligt att som texel välja den som i någon mening ligger närmast dessa värden. Detta är också vad som sker då man har filtreringsegenskapen GL_NEAREST. Men vid uppförstoring, dvs då en texel berör flera bildpunkter (inträffar då betraktaren är nära den texturerade ytan) kan det skapa oönskad taggighet. Det gäller speciellt om texturerna utgörs av bilder med kraftig kontrast. Med GL_LINEAR kommer i stället en linjär interpolation med hjälp av fyra texlar intill den närmsta att äga rum, vilket ger en utjämnad bild. Exempel: Vi har en rutnätstextur där varje linje är en texel bred. Vi lägger den på en yta så att varje texel täcker 4x4 bildpunkter. Till vänster visas resultatet med resultatet GL_NEAREST, till höger med GL_LINEAR. Texturering - förminskning Problem: Vid förminskning kommer flera texlar att höra till samma bildpunkt. Detta inträffar när vi tittar på en texturerad yta på stort avstånd. Vilken texel skall då få bestämma? Vi kan ta den närmsta (GL_NEAREST), men detta blir i verkligheten ett närmast slumpmässigt val och skapar brister, speciellt om användaren rör sig i en scen. GL_LINEAR reducerar problemet bara en aning. Om bildpunkten täcker åtskilliga texlar, så är det enda vettiga att bilda ett medelvärde av alla dessas värden, men det blir kostsamt. I högra delen av figuren, ser vi ett fall utan att några åtgärder vidtagits. Till vänster har man använt s k mipmapping, som ger ett för ögat mycket mera tilltalande resultat. Bilden ritad med en modifierad variant av programmet mipmap.c i GLUT-distributionen. Demo: Från S3 (öppna filen /users/course/tda360/s3/index.htm med någon webbläsare; det sista exemplet visar mipmaps). DATORGRAFIK DATORGRAFIK
2 Tekannan och andra färdiga GLUT-objekt 2(2) Mipmapping Man bildar en hel följd av texturkartor med utgångspunkt från den ursprungliga. Om den första har dimensionen MxM (M=2 N ) så har nästa dimensionen M/2xM/2 osv. Den sista består av en enda texel. Totalt har vi N+1 texturer. Vid halveringen slås fyra texlar ihop till en ny med medelvärdesbildning. En rutnätstextur pålagd en kvadrat, en tekanna och en sfär ritad med den modifierade glutsolidspheremb. Textur N N-1 N förminskning Vid användningen av texturkartorna räknas det fram ett ungefärligt mått på förminskningen och man går in mellan de omgivande texturkartorna och gör (bi)linjär interpolation dels inom dessa, dels mellan dem. Benämningen trilinjär interpolation står för detta. Ordet mip kommer av latinets Multum in parvo, som betyder mycket på ett litet utrymme. Utrymmesmässigt krävs ungefär 33 % mer än utan mipmapping. OpenGL (enklast via GLU) stödjer mipmapping. Och de förändringar som behövs är små. Anropet av glteximage2d ersätts av glubuild2dmipmaps(gl_texture_2d, GL_RGB, TexWidth, TexHeight, GL_RGB, GL_UNSIGNED_BYTE, Image); och filtreringsegenskapen vid förminskning sätts med gltexparameteri(gl_texture_2d, GL_TEXTURE_MIN_FILTER,GL_LINEAR_MIPMAP_LINEAR); Det är allt! (Det finns ett par andra varianter.) I z-led (uppifrån) Enl källkoden till glusphere: If texturing is turned on (with gluquadrictexture), then texture coordinates are generated so that t ranges from 0.0 at z=-radius to 1.0 at z=radius (t increases linearly along longitudinal lines), and s ranges from 0.0 at the +y axis, to 0.25 at the +x axis, to 0.5 at the -y axis, to 0.75 at the -x axis, and back to 1.0 at the +y axis. DATORGRAFIK DATORGRAFIK Tekannan och andra färdiga GLUT-objekt 1(2) Litet inkonsekvent! Dessa kan delas in i plana (glutsolidcube m fl), andragradsytor (glutsolidsphere m fl) och allmänt krökta (glutsolid- Teapot). De senare är baserade på B-splines el dyl, varigenom normaler och texturkoordinater kan genereras (med lämpliga tillstånd). Andragradsytorna är baserade på Quadrics-objekt, som vi inte tagit upp här. glutsolidcube &Co, glutsolidtorus &Co glutsolidsphere &Co Källkoden till glutsolidsphere modifierad så att texturkoordinater genereras void glutsolidspheremb(gldouble radius, GLint slices, GLint stacks) { gluquadricdrawstyle(quadobj, GLU_FILL); gluquadricnormals(quadobj, GLU_SMOOTH); gluquadrictexture(quadobj,gl_true); // default GL_FALSE glusphere(quadobj, radius, slices, stacks); Man måste ha deklarerat static GLUquadric *quadobj; och före användning initierat quadobj = glunewquadric(); DATORGRAFIK glutsolidteapot &Co (FINNS EJ I JOGL nu) Normaler Ja Ja Ja (GL_AUTO_NORMAL satt) Texturkoordinater Nej (man kan med möda ändra i källkoden) Nej (man kan lätt ändra i källkoden) Ja, lämpligt tillstånd är satt i koden Belysning Ja Ja Ja, om vi ändrar på begreppet framsida, dvs om glface- Mode(GL_CW), det normala är GL_CCW. Texturer och ljus I OpenGL ligger ljusberäkningen före texturpåläggningen, vilket är naturligt eftersom beräkningen gäller hörn och inte bildpunkter, men det är inte invändningsfritt. Det finns fyra storheter som påverkar hur ljusvärdena och texturvärdena kombineras. Vi skall bara beskriva dem i huvuddrag. Vi har nämnt att GL_DECAL och GL_REPLACE bara lägger på den aktuella texelns färg och alltså struntar i belysningsvärden. Vårt hopp står då till GL_MODULATE och GL_BLEND. Låt C stå för någon av de tre grundfärgerna R, G och B. Låt C in vara värde enligt belysningsmodellen, C t texelns intensitet och C ut resultatet. Då gäller för (viss skillnad om RGBA) GL_MODULATE: C ut = C in C t GL_BLEND: C ut = C in (1-C t ) (egentligen C ut = C in (1-C t )+C t C c, där C c är förvald till 0, men kan ändras med gltexenv) C ut 1 GL_MODULATE C in Eftersom alla intensiteter ligger mellan 0 och 1, kommer texturen att förmörkas vid användning av GL_MODULATE (om inte C in = 1). Likaledes förmörkas ljusvärdet (om inte C t =1). Men det värdet måste ändå bli vår favorit. Det hade varit önskvärt med fler kombinationsmöjligheter (jämför med andra kommande situationer). DATORGRAFIK GL_BLEND 1 C t
3 Automatisk texturkoordinatgenerering I princip har vi hittills anget texturkoordinater med någon version av gltexcoord. Men det finns också några mer eller mindre väl uttänkta sätt att få texturkoordinaterna automatgenererade. Den första texturkoordinaten kallas i OpenGL s och den andra t (det finns dessutom r och q). Man måste då 1.Tala om hur respektive texturkoordinat skall genereras 2.Aktivera genereringen av respektive texturkoordinat. Eventuellt explicit angivna texturkoordinater ignoreras. Hur respektive texturkoordinat skall genereras gltexgeni(gl_s, GL_TEXTURE_GEN_MODE,GL_OBJECT_LINEAR) GL_T, GL_R DATORGRAFIK GL_EYE_LINEAR GL_SPHERE_MAP GL_NORMAL_MAP_ARB GL_REFLECTION_MAP_ARB De två sista alternativen för tredje parametern är utvidgningar som införts i OpenGL 1.3 och som fungerar på grafikkort med bl a GeForce-processorer och nu även Sun. De tre sista (beskrivs i detalj senare) kräver att man genererar tvådimensionella texturkoordinater (GL_S och GL_T), medan för de två första det räcker med endimensionella (GL_S). I dessa två fall blir texturkoordinaten avståndet från den aktuella punkten till ett plan angivet antingen i modellkoordinater (GL_OBJECT_LINEAR) eller vykoordinater (GL_EYE_LINEAR). Aktivering T ex av s-koordinaten: glenable(gl_texture_gen_s) Dessutom måste vi ha aktiverat texturering med glenable(gl_texture_1d)(bara s) eller glenable(gl_texture_2d)(s och t) Avståndsstyrd texturkoordinatgenerering 2(2) Om vi i stället låter texturkoordinaten genereras som avståndet till planet y = 0 i vykoordinatsystemet, dvs gltexgeni(gl_s, GL_TEXTURE_GEN_MODE,GL_EYE_LINEAR); gltexgenfv(gl_s, GL_EYE_PLANE,plane); med plane som förut, så ligger texturen fast i vykoordinatsystemet och följer inte modellen (vänstra figuren nedan). Man kan naturligtvis lika gärna lägga texturen på ett allmännare objekt, t ex den välkända tekannan (högra figuren). Texturkoordinaterna genereras efter transformationen till vykoordinater. I fallet GL_OBJECT_LINEAR/GL_OBJECT_PLANE transformerar därför OpenGL koefficienterna till vykoordinatsystemet på det sätt som vi beskrivit i Från värld..., avsnitt 8. DATORGRAFIK Avståndsstyrd texturkoordinatgenerering 1(2) Det handlar om GL_OBJECT_LINEAR respektive GL_EYE_LINEAR. Planet beskrivs med ett anrop av formen gltexgenfv(gl_s, GL_OBJECT_PLANE,vektorvariabel) respektive gltexgenfv(gl_s, GL_EYE_PLANE,vektorvariabel) där vektorvariabeln innehåller de fyra koefficienterna i planets ekvation F(x,y,z) = Ax+By+Cz+D = 0. Som vanligt ger F(x,y,z) avståndet från (x,y,z) till planet om normalen (A,B,C) är normerad. Exempel: Vi har en 1D-textur bestående av 32 texlar, där de första fyra är röda och resterande är gröna. Vi lägger den på en fyrkant vinkelrät mot planet y=0. Vi låter texturkoordinaten genereras som avståndet till planet y = 0 i modellkoordinatsystemet, dvs gltexgeni(gl_s, GL_TEXTURE_GEN_MODE,GL_OBJECT_LINEAR); gltexgenfv(gl_s, GL_OBJECT_PLANE,plane); med static GLfloat plane[] = {0.0, 1.0, 0.0, 0.0;. Om vi vrider fyrkanten (högra figuren) följer texturen som väntat modellen. Grönt Rött En sådan är 1D-textur Låt oss för att en aning illustrera den matematiska skillnaden mellan GL_NEAREST och GL_LINEAR anta att svart har värdet 8 och vitt värdet 0 (det riktigare är ju 0 och 255 eller 0.0 och 1.0). Då utgörs texturen av vänstra figuren nedan. Om vi applicerar den på en horisontell linje med 12 bildpunkter så skulle GL_NEAREST ge resultatet överst till höger, medan GL_LINEAR ger ungefär undre figuren nr Matematiken bakom skulle kunna vara som följer. Om antalet texlar i texturen är T och antalet bildpunkter är B, så har vi följande samband mellan texelnummer s och bildpunktsnummer x: s = Tx/B, dvs i figurens fall s = x/3. Om vi betraktar s som ett reellt tal s = i + a, där i är heltalsdelen och a bråkdelen, har vi följande möjliga medelvärdesbildning (t i = intensitet i texel i) intensitet i bildpunkt x = (1-a)t i + at i+1. som ger värdena i figuren. x s i a intensitet /3 16/ /3 8/3 3 DATORGRAFIK DATORGRAFIK
4 Textur från fil 1(4) I allmänhet läser man väl texturkartan från en fil. Om filen bara skall uppfattas som en följd av bytes (vilket gäller t ex textfiler) är det lätt att skriva en läsprocedur. T ex för det byte-baserade formatet PPM P6 ($DG/EXEMPEL_MB/ReadPPM_P6_Texture.c) GLubyte* ReadTexture(char* filename, int* width, int* height) { int i,j, w, h; GLubyte *ptr, *start; // Open file FILE *texfile = fopen(filename,"r"); if (!texfile) { printf("no such file\n"); exit(1) // Ignore first row P6 for (i=1; i<=3; i++) getc(texfile); // Read width and height fscanf(texfile, "%d %d", &w, &h); *width = w; *height = h; ptr = malloc(w*h*3); start = ptr; // Ignore last line for (i=1; i<=5; i++) getc(texfile); // Read the texture for (i=0; i<h; i++){ for (j=0; j<w; j++){ *ptr=(glubyte)getc(texfile); ptr++; *ptr=(glubyte)getc(texfile); ptr++; *ptr=(glubyte)getc(texfile); ptr++; printf("texturen läst\n") fclose(texfile); return start; DATORGRAFIK Textur från fil 3(4) För enkelhets skull antar jag att texturstorleken är känd och att vi har en global variabel Image där texturen skall placeras. void readimage(string filnamn) { try { FileInputStream fin = new FileInputStream(filnamn); int i, p = 0, j, r = 1; byte b; // Assuming size nxn with 10<n<100 // Skips the 13 characters P6\n64 64\n255\n for (j=1; j<=13; j++) { i = fin.read(); b = (byte)i; while ((i = fin.read())!= -1) { b = (byte)(i/2); Image[(TexHeight-r)*TexWidth*3+p]= b; p = p+1; if (p==3*texwidth) { p = 0; r=r+1; //Image[p] = b; p = p+1; catch (FileNotFoundException e) { System.exit(1); catch (IOException e) { System.exit(1); Javas (byte)i omvandlar heltal enligt i (byte)i vilket gör att såväl 255 som 127 ger full intensitet (åtminstone i JOGL enl tidigare), vilket naturligtvis inte är så lyckat. Därför i/2 i koden. DATORGRAFIK Textur från fil 2(4) PPM-formatet (Portable PixMap) utgörs av en följd av bytes, som om texturen är 256x256 inleds med 15 bytes (tecken) (\n är ett tecken, tecknet för nyrad) P6\n \n255\n varpå följer 3 bytes med RGB för översta vänstra punkten och sedan motsvarande för övriga punkter rad för rad. Första 256 avser bildbredden, andra bildhöjden. Avslutande 255 anger maximalt färgvärde. Det kan finnas varianter (t ex lägger xv in en kommentarrad om cirka 60 tecken efter P6-raden. Du kan titta på inledningen av en PPM-fil med ett vanligt redigeringspreogram. Inleds filen med P4 eller P5, så är det fråga om variantformat PBM resp PGM. Funktionen ReadTexture används typiskt så här GLubyte* Image; GLint texwidth, texh; Image = ReadTexture("brick.ppm", &texwidth, &texh); printf("texturen %d x %d\n", texwidth, texh); Texturer lagras nedifrån i OpenGL, dvs en textur som i bildbehandlingsprogram som xpaint eller xv ser ut som till vänster blir med vår funktion upp och nedvänd som till höger. Detta kan vi lätt bota, vilket vi visar i en motsvarande Java-metod. DATORGRAFIK Textur från fil 4(4) Det finns många olika sätt - format - att lagra en bild som t ex en texturkarta på. Vi återkommer till det i slutet av kursen. Bildbehandlingsprogrammet xv (under Linux/UNIX) kan användas för att konvertera mellan de vanligaste. GIMP (för Linux/UNIX eller PC) klarar också det. Formatet.ppm (Portable PixMap) är transportabelt, dvs kan läsas med program skrivet i datoroberoende källkod (t ex med den ovan). I GLUT-distributionen ingår en procedur (finns i filen progs/ advanced/texture.c) för läsning av.rgb- och.bw-format, vilka härrör från Silicon Graphics. Det senare enbart för svartvitt. unsigned * read_texture(char *name, int *width, int *height, int *comps) Koden är utformad så att den fungerar oberoende av dator. Typisk användning int texwidth, texheight, texcomps; GLubyte *image; image=read_texture("brick.rgb", &texwidth,&texheight,&texcomps); Vi får reda på texturens bredd och höjd, liksom antalet bytes per texel (3=GL_RGB, 4=GL_RGBA). Behöver alltså inte införa någon matris! Även ett antal bilder på något av dessa två format medföljer. Innehåller filen heltal eller flyttal på binärform blir det besvärligare åtminstone om man vill ha datoroberoende kod. Förklaringen är att olika datorer/format lagrar bytarna i tal i olika ordning (Sun: Big Endian, PC: Little Endian). Kod på nätet är oftast utformad för PC-miljön. Låg adress Högre adress Little Endian: LSB först Big Endian: MSB först LSB MSB DATORGRAFIK MSB Intel, BMP, GIF,... Sun, Motorola, LSB JPEG,...
5 Belysning i spel 1(3) Säg att vi belyser en tegelvägg med en lampa. Då vill vi ha ett resultat liknande det i översta figuren på nästa OH (hämtad från NVIDIAs promotionsmaterial). Kan vi få det med OpenGL? I första ansatsen räknar man ut ljusvärden i väggens fyra hörn. Även om dessa skulle bli de korrekta, så ger en efterföljande interpolering (Gouraud) ett föga realistiskt resultat. För att få något bättre måste vi dela in väggen i flera mindre fyrkanter och göra ljusberäkning för var och en av dessa. Finns något annat sätt? Inspirerade av framgångarna med texturer införde man i spelet Quake ljuskartor (eng. light map), som är texturkartor med ljusmönster. Längst ned på nästa OH hittar vi en sådan. Ljuskartan byggs upp i förväg (kan vara handtillverkad eller framräknad med stor omsorg). Vid ritningen kombineras ljuskartan med tegeltexturen (texel för texel och därmed pixel för pixel), se andra figuren, innan ritning sker. Med denna teknik kan övertygande effekter åstadkommas. I figurens fall har kartvärdena multiplicerats med varandra, men man kan också tänka sig operationer som + eller någon allmän blandning. Detta har i sin tur lett till ett begrepp som multi-texturering, som innebär att den slutliga texturen bestäms av ett antal olika. För att få snabbhet har de senare grafikkorten allt bättre hårdvara för arbete med sådan texturering. Man har också infört ytterligare möjligheter till automatisk texturgenerering som gör att man med få ljuskartor även kan hantera dynamiska lampor. NVIDIA talar nu om per-pixel-lighting i ställer per-vertex-lighting som är det vanliga i OpenGL. Och nog har man lyckats skapa många imponerande ting. Men det krävs att man har ett grafikkort som stöder dessa utvidgningar av OpenGL. DATORGRAFIK Belysning i spel 3(3) Har man sagt A och B, skall man kanske även säga C även om jag går händelserna i förväg. Här följer det gamla sättet att lägga på ljuskartor. // Först ritar vi kvadraten med tegel utan ljus // Talet 5 ger repetition av texturen glbindtexture(gl_texture_2d, texname[tegelnr]); glcolor3f(1.0, 1.0, 1.0); //Bara om vi använder GL_MODULATE, //lägrevärden skulle förmörka glbegin(gl_quads); gltexcoord2f(0, 0); glvertex2f(-1, -1); gltexcoord2f(5, 0); glvertex2f(1, -1); gltexcoord2f(5, 5); glvertex2f(1, 1); gltexcoordf(0, 5); glvertex2f(-1, 1); glend(); // Sedan är det dags att byta till ljuskartan och se till att // värdena blandas på lämpligt sätt med det redan ritade glenable(gl_blend); glblendfunc(gl_zero, GL_SRC_COLOR); // Ger tegel*ljuskarta gldepthfunc(gl_lequal); // Ser till att det ritas även om // vi redan ritat på just det avståndet; finns // andra sätt glbindtexture(gl_texture_2d, texname[ljusnr]); // Plats för extranummer //Och så ritar vi kvadraten med enbart ljuskartan glcolor3f(1.0, 1.0, 1.0); // Onödig upprepning glbegin(gl_quads); gltexcoord2f(0, 0); glvertex2f(-1, -1); gltexcoord2f(1, 0); glvertex2f(1, -1); gltexcoord2f(1, 1); glvertex2f(1, 1); gltexcoord2f(0, 1); glvertex2f(-1, 1); glend(); Extranummer(låter oss flytta ljustexturen): glmatrixmode(gl_texture);glpushmatrix();gltranslatef(tx, ty, tz);... och efter glend(): glpopmatrix(); glmatrixmode(gl_model_view); DATORGRAFIK Belysning i spel 2(3) Multitexturering 1(2) Detta är ett exempel på en utvidgning som kommit in i specifikationen för OpenGL 1.3 (aug 2001). Från våren 2004 kan vi använda det på våra SUN-ar. Syftet är att kunna använda flera texturer samtidigt utan att som vi tidigare (OH om belysning i spel) gjorde skicka samma geometri flera gånger. Man har infört ett antal texturenheter (minst två) numrerade 0 och uppåt, som har sina egna egenskaper (eget påläggningssätt, egen texturmatris, eget igång-tillstånd etc). Dessa verkar i följd, vilket med modern teknologi och lämpligt matningssätt innebär att de inte kostar något tidsmässigt. Så här fungerar det: En textur En annan c t,0 c t,1 Färgvärde c in Texturenhet 0 Texturenhet 1 c ut,0 =c in *c t,0 (vid GL_MODULATE) Ytterligare texturenheter och till sist ritning Den tidigare koden (se OH 163) förenklas. Vi placerar geometrihanteringen i en separat procedur wall (suffixen ARB och _ARB kan tas bort). void wall() { glbegin(gl_quads); // Första hörnet, ett texturkoordinatpar för // tegelväggen (texturenhet 0), ett annat för // ljuskartan (texturenhet 1) glmultitexcoord2farb(gl_texture0_arb,0, 0); glmultitexcoord2farb(gl_texture1_arb,0, 0); glvertex2f(-1, -1); DATORGRAFIK DATORGRAFIK
6 Multitexturering 2(2) // Övriga hörn, 5 ger upprepning av tegelmönstret glmultitexcoord2farb(gl_texture0_arb,5, 0); glmultitexcoord2farb(gl_texture1_arb,1, 0); glvertex2f(1, -1); glmultitexcoord2farb(gl_texture0_arb,5, 5); glmultitexcoord2farb(gl_texture1_arb,1, 1); glvertex2f(1, 1); glmultitexcoord2farb(gl_texture0_arb,0, 5); glmultitexcoord2farb(gl_texture1_arb,0, 1); glvertex2f(-1, 1); glend(); Och i omritningsproceduren display(): // Med glactivetexture bestämmer vi vilken texturenhet // vars tillstånd skall förändras // Först texturenhet 0 som får ha hand om tegelmönstret glactivetexturearb(gl_texture0_arb); gltexenvi(gl_texture_env, GL_TEXTURE_ENV_MODE, GL_DECAL); glbindtexture(gl_texture_2d, texname[tegelnummer]); glenable(gl_texture_2d); // Sedan texturenhet 1 som hanterar ljuskartan glactivetexturearb(gl_texture1_arb); gltexenvi(gl_texture_env,gl_texture_env_mode,gl_modulate); glbindtexture(gl_texture_2d, texname[ljusnr]); glenable(gl_texture_2d); // Extranumret glmatrixmode(gl_texture); glpushmatrix(); gltranslatef(tx, ty, tz); wall(); glpopmatrix(); // texturmatrisen gldisable(gl_texture_2d); glactivetexturearb(gl_texture0_arb); gldisable(gl_texture_2d); Omgivningsavbildning med sfär 1(3) Det finns flera sätt att plana ut en sfärisk yta. T ex kan man utgå från en vanlig parameterframställning av en sfär. Ett mindre känt sätt är det som beskrivs nedan och har stöd i OpenGL (och av grafikkort). R3 1 Sfären N3 P3 45 o P2 R2 P1 N2 N1 Den sfäriska texturen som är en enhetscirkel i en texturkarta utgörs helt enkelt av den bild vi ser då vi tittar på en högreflekterande enhetssfär ortografiskt. Sfären tänkes placerad med mittpunkten mitt i det reflekterande objektet. Betrakta figuren ovan. Sfären finns till vänster och betraktaren till höger. Allt utspelar sig i vykoordinat/ögon-koordinatsystemet, dvs y-axeln är uppåtriktad och z-axeln är riktad mot betraktaren. En tänkt stråle S1 träffar sfären i punkten P1 och reflekteras tillbaka. Det som syns i P1 placeras alltså mitt i texturkartan (projektionsplanet). Strålen S2 motsvaras av en reflektionsvektor som R2 som går rakt upp. I texturkartan vid S2:s utgångspunkt placeras alltså det som finns rakt ovanför sfären. Strålen S3 går precis förbi sfären och bör alltså motsvaras av det som finns bakom sfären. Mellan utgångspunkterna S3 S2 R1 S1 t t=1(1) 1-1/sqrt(2) 1/sqrt(2) 0.71 t=-1(0) projplan (texturkarta) DATORGRAFIK DATORGRAFIK Environment mapping (omgivningsavbildning) Syfte: Återge omgivningens reflektion i ett reflekterande föremål utan att ta till strålföljning. Metod: Skapa en projicerad platt (2D) bild av omgivningen. Lagra den som en textur. När vi vill rita objektet så låter vi reflektionsvektorn ge upphov till texturkoordinater och applicerar texturen (som vanligt bildpunkt för bildpunkt). Tanken bakom: Om det reflekterande objektet är litet och långt ifrån omgivningen så bestämmer reflektionsvektorn vad som syns i en punkt. Objektet får inte heller reflektera sig självt, dvs det måste vara konvext. Även om förutsättningarna inte är uppfyllda kan resultatet bli sådant att det accepteras. Omgivningsavbildning med sfär 2(3) för strålarna S1 och S2 lagrar vi den delen av världen som finns till höger om sfären. Mellan S2 och S3 det som finns bakom sfären (till vänster om den). De båda delarna får väsentligt olika utrymme. Vi ser att olika reflektionsriktningar motsvarar olika punkter i texturen. Framför Bakom I figuren till vänster visas den sfäriska texturkartan symboliskt. Till höger visas en riktig (kafé Verona i Palo Alto, Calif). Det finns ett antal olika sätt att göra projiceringen. 1. OpenGL (och hårdvaran) ger stöd för omgivningsavbildning med sfär. Några OH beskriver detta sätt, men dessa kan till största delen överhoppas eftersom vi från hösten 2004 kommer åt omgivningsavbildning med kub (se nästa punkt). 2. OpenGL 1.3 (och någorlunda moderna grafikkort) ger stöd för dito med kub, som är en betydligt bättre metod. 3. En 5-6 år gammal metod med paraboloider är lovande och kanske ges hårdvarustöd (finns delvis). Vi tar ej upp den mera här. Man kan ha ett antal invändningar mot såväl metoden i sig som de de enskilda projiceringssätten. Demo: $DG/DEMOS/CUBEMAP/cubemapMB -i eller äldre glut-3.7/progs/ spheremap/glsmap eller glut-3.7/progs/advanced97/usespheremap elleradv97_usespheremapmb2 eller ADV99_spheremapMB+data DATORGRAFIK Hur bildas den sfäriska kartan? Det finns minst tre sätt. 1. Genom fotografering av en sfär placerad i en verklig miljö. 2. Genom strålföljning. 3. Genom att göra lämpliga transformationer av kubavbildning. Vid uppritningen genererar OpenGL texturkoordinater per hörnpunkt (motsv) anpassade för den sfäriska texturen förutsatt att vi gjort följande anrop gltexgeni(gl_s, GL_TEXTURE_GEN_MODE, GL_SPHERE_MAP); gltexgeni(gl_t, GL_TEXTURE_GEN_MODE, GL_SPHERE_MAP); glenable(gl_texture_gen_s); glenable(gl_texture_gen_t); Detta görs dock någorlunda korrekt bara för samma betraktningsrikning som användes då texturen bildades. Perspektiv får gärna vara påslaget. OpenGL har tillräcklig information för att beräkna synstrålen mellan betraktaren och hörnet (ögat är ju givet). Eftersom DATORGRAFIK
7 Omgivningsavbildning med sfär 3(3) hörnet måste vara försett med normal (som automatiskt omräknas till vykoordinater), kan systemet även beräkna en normaliserad reflektionsvektor R = (R x,r y,r z ) i vykoordinatsystemet. Texturkoordinaterna (s,t) beräknas slutligen med 2 2 L = R x + R y + ( R z + 1) 2 s 0.5 R x = L t 0.5 R y = L Omgivningsavbildning med kub 1(2) Sfärtexturen måste förnyas om observatören byter plats (rörelse i synriktningen må passera). Det vore önskvärt att ha ett sätt som är oberoende av var vi finns. Ett sådant sätt är kubavbildning. Man placerar en enhetskub med mittpunkt i det reflekterande objektet. Man projicerar den omgivande världen på vart och en av de sex begränsningsplanen. Det kan ske genom att vi ritar upp scenen med sex olika 90 o -iga synpyramider. Detta görs en gång för alla. Utan additionerna +1 och muliplikationerna med 0.5 hamnar (s,t) på en cirkel med radien 2 2 R x + R y R x + R y + ( R z + 1) 2 1 och mittpunkt i origo. Termen (R z +1) 2 i uttrycket för L gör således att reflektionsvektorer med olika z-komponent får olika texturkoordinater. De nämnda operationerna gör att den i stället hamnar inom det normala texturområdet 0 s,t 1. Topp Vänster Fram Höger Bakom Botten Vid uppritningen gäller det återigen att givet reflektionsvektorn i ett hörn beräkna vilken av de sex texturerna som berörs och koordinater inom den. NVIDIA introducerade hårdvarustöd för detta hösten 1999, vilket gör att sådan avbildning kan göras i realtid. På våra SUN-ar görs det i mjukvara och blir därmed långsamt (går t o m något snabbare med Mesa). I rum 6220 går det från hösten 2004 undan! Man använder alltså moden GL_REFLECTION_MAP för generering av s,t,r-koordinater. Vektorn (s,t,r) är reflektionsvektorn i vykoordinatsystemet. Denna vektor används för val av en av de 6 texturerna och DATORGRAFIK DATORGRAFIK Vektorstyrd texturkoordinatgenerering Det är vad som åstadkommes med parametervärdena (suffixet _ARB behövs inte) GL_SPHERE_MAP GL_NORMAL_MAP_ARB GL_REFLECTION_MAP_ARB Vi har redan avhandlat GL_SPHERE_MAP. Här kommer dock två bilder till. Vi har lagt vårt kvadratiska rutnät på en sfär. Högra bilden är gjord med perspektiv och återger mest korrekt den givna texturen. Den vänstra är med ortografisk projektion och förvränger givetvis på grund av texturkoordinatgenereringen mönstret. Omgivningsavbildning med kub 2(2) sedan indexering i rätt. Låt oss bara antydningsvis belysa detta för 2D-fallet då vektorn är (s,t). Om s och t positiva, väljs höger sida om s>t, etc. Rent praktiskt i OpenGL glenable( Vänster GL_TEXTURE_CUBE_MAP_ARB); och för varje kubsida enligt modellen Topp (s,t) Botten glteximage2d(gl_texture_cube_map_positive_x_arb,... (s,t) Höger Exempel: cubemap.c (i Mesa-distributionen). En reflekterande sfär De två andra fallen styr genereringen av tre texturkoordinater (s,t,r) med hörnets normal respektive reflektionsvektor (samma som med GL_SPHERE_MAP), dvs även glenable(gl_texture_gen_r) och gltex- Geni(GL_R, GL_TEXTURE_GEN_MODE,...)måste vara med. En tillämpning kommer på nästa OH. i ett rum med rutiga väggar. Demo: Bubbles från NVIDIA om jag bara hade kunnat visa det. DATORGRAFIK DATORGRAFIK
8 Bump-mapping 1-2(2) Syfte: Med texturering ökar vi realismen. Men det finns mer att önska sig. Ett äpple är rätt slätt, men det gäller inte en apelsin som har små gropar (eng. bump). Även tegelmurar och gräsmattor är gropiga. Vi vill alltså ge intryck av gropighet eller reliefstruktur utan att detaljmodellera. Metod: Normalerna störs med utgångspunkt från t ex en höjdkarta lagrad som en textur. Man får på det viset en störd normal N för varje bildpunkt och räknar med hjälp av den ut ljusvärdet per bildpunkt i stället för som normalt per hörnpunkt. Förfaringssättet är kostsamt. Men med nyare processorer går det som en dans. På nästa OH finns tre bilder kring bumpmapping som fungerar trycktekniskt (OBS! Ej avsedda som reklam). Överst syns resultatet. Nedtill till höger finns den grundläggande texturen. Till vänster finns den textur, en höjdkarta (vitt=hög höjd, svart = låg), som styr bump-mappingen. Låt oss försöka beskriva idén i en endimensionell variant. Givet höjdkartan (vänstra fig) kan vi beräkna normaler i varje texel. När vi sedan lägger den grundläggande texturen på vår yta (här för enkelhets skull ett plan och 1-1 pixel/texel, högra fig) stör vi vid belysningsberäkningen ytans normaler proportionellt mot den horisontella komponenten av normalen i vänstra fig. Detta gör att ytan illusoriskt upplevs brant (streckad linje i högra fig). intensitet störda normaler 3D-texturer Våra föremål är i allmänhet 3-dimensionella. Ibland är texturerna på angränsande ytor av litet olika typ men ändå måste passa ihop. Ett typiskt exempel är en träkloss, där vi på en sida kan se ringar, men på en annan bara den längsgående ådringen. Lösningen på detta problem är 3D-texturer. Man talar även om solid texturering. Man kan tänka sig två varianter: 1. Ett antal lager av 2D-texturer. Om varje 2D-textur är på 256x256 skulle man kanske ha 256 lager. Utrymmesbehovet växer således krafigt och knappast något grafikkort skulle kunna hålla allt hos sig. Visst kan man minska på texturupplösningen, men då missar man ju detaljer. T ex passar tekniken inte för träklossar. Inte heller eventuell komprimering förbättrar situationen tillräckligt. Men för enklare texturer går det ju bra. OpenGL 1.2 och 1.3 (som finns på våra SUN ar) har stöd för denna teknik. I princip behöver man bara byta ut konstanten GL_TEXTURE_2D mot GL_TEXTURE_3D genomgående och anropa glteximage3d i stället för glteximage2d. Härvid anger man förutom texturbredd och texturhöjd även texturdjup. Dessutom måste man naturligtvis nu ange tre texturkoordinater för varje hörn, vilket sker med gltexcoord3f(...). OpenGL-stödet kan också användas för s k volymvisualisering, dvs visualisering av 3D-mätdata. 2. En annat sätt är att generera erforderlig texturinformationen vid behov. Kort sagt när vi behöver texturen för en texturkoordinat (s,t,u) anropar vi en funktion med punkten som parameter. Funktionen räknar ut aktuellt värde. Detta kan innebära ett omfattande räknearbete och metoden passar inte realtidskrav. Man brukar tala om procedurtexturer (eng procedural textures). OpenGL ger inget som helst stöd. Används av alla avancerade strålföljare. I framtiden kanske den här typen av beräkningar kan utföras av grafikprocessorn (eller någon sidoprocessor till den). Detta sätt kan användas även för 2D-texturer. Ibland kallar man texturer framställda så här för syntetiska texturer texturindex pixelnr DATORGRAFIK DATORGRAFIK Ofta lagras inte höjdkartan utan i stället motsvarande beräknade normalkarta. En komplikation är att om ytan är krökt eller ligger snett, måste texturnormalerna transformeras till ytans tangentplan. Procedurtexturer Ex. 1: Trätextur. Vi tittar mot en kant på en kub. Vänstra figuren. Här liksom i nästa exempel ortografisk projektion. Ex. 2: Blocktextur. Vi tittar mot en sfär. Högra figuren. För trätexturen användes proceduren (funktionen) float wood(int frekvens, float x, float y, float z) { float r; r = sqrt((x-0.5)*(x-0.5)+(y-0.5)*(y-0.5)); return ((int)(frekvens*r))%2; med frekvensen = 32. Den ger 0 eller 1, som får styra vitt/svart. För blocktexturen float block(int frekvens, float x, float y, float z) { int f = frekvens; return ((int)(f*x)+(int)(f*y)+(int)(f*z)) % 2; med frekvensen = 5. Även nu 0 eller 1 som resultat. Vi är inte riktigt nöjda. Vi behöver litet slump för att det skall bli mera verklighetsnära. DATORGRAFIK DATORGRAFIK
OpenGL-översikt. OpenGL. Viktigt att komma ihåg: OpenGL-kommandon. OpenGL är en tillståndsmaskin. Transformationer. Geometrispecifikation
 OpenGL OpenGL-översikt Geometri Operationer på hörn Projective shadows Advanced Rendering Techniques Using OpenGL, SIGGRAPH Courses 997. Gustav Taxén CID gustavt@nada.kth.se Bilddata Operationer på bildelement
OpenGL OpenGL-översikt Geometri Operationer på hörn Projective shadows Advanced Rendering Techniques Using OpenGL, SIGGRAPH Courses 997. Gustav Taxén CID gustavt@nada.kth.se Bilddata Operationer på bildelement
OpenGL AGI HT05. Gustav Taxén
 OpenGL AGI HT05 Gustav Taxén gustavt@nada.kth.se OpenGL-översikt Geometri Operationer på hörn Rastrering Operationer på fragment Bilddata Operationer på bildelement Texturminne Framebuffert (bildbuffert
OpenGL AGI HT05 Gustav Taxén gustavt@nada.kth.se OpenGL-översikt Geometri Operationer på hörn Rastrering Operationer på fragment Bilddata Operationer på bildelement Texturminne Framebuffert (bildbuffert
En introduktion till OpenGL. Gustav Taxén gustavt@csc.kth.se
 En introduktion till OpenGL Gustav Taxén gustavt@csc.kth.se 2D164 Grafik och Interaktionsprogrammering VT 27 Labb 4 görs på PC! Följ det nya labbpeket - eller: Följ stegen i labbpeket för labb 5 för att
En introduktion till OpenGL Gustav Taxén gustavt@csc.kth.se 2D164 Grafik och Interaktionsprogrammering VT 27 Labb 4 görs på PC! Följ det nya labbpeket - eller: Följ stegen i labbpeket för labb 5 för att
OpenGL-översikt. OpenGL. Lokala koordinatsystem. Transformationer. Hierarkiska modeller. Animation. Transformation Byte av koordinatsystem
 OpenGL OpenGL-översikt Geometri Operationer på hörn DOOM 3 id Software, 2004 (?). Gustav Taxén CID gustavt@nada.kth.se Bilddata Operationer på bildelement Rastrering Texturminne Operationer på fragment
OpenGL OpenGL-översikt Geometri Operationer på hörn DOOM 3 id Software, 2004 (?). Gustav Taxén CID gustavt@nada.kth.se Bilddata Operationer på bildelement Rastrering Texturminne Operationer på fragment
OpenGL-översikt. Mer OpenGL. Består-av-hierarki. Hierarkiska modeller. Från hierarki till kod, steg 1. Lokala koordinatsystem
 Mer OpenGL OpenGL-översikt Geometri Operationer på hörn Projective shadows Advanced Rendering Techniques Using OpenGL, SIGGRAPH Courses 997. Gustav Taxén CID gustavt@nada.kth.se Bilddata Operationer på
Mer OpenGL OpenGL-översikt Geometri Operationer på hörn Projective shadows Advanced Rendering Techniques Using OpenGL, SIGGRAPH Courses 997. Gustav Taxén CID gustavt@nada.kth.se Bilddata Operationer på
Laboration 4: Digitala bilder
 Objektorienterad programmering, Z : Digitala bilder Syfte I denna laboration skall vi återigen behandla transformering av data, denna gång avseende digitala bilder. Syftet med laborationen är att få förståelse
Objektorienterad programmering, Z : Digitala bilder Syfte I denna laboration skall vi återigen behandla transformering av data, denna gång avseende digitala bilder. Syftet med laborationen är att få förståelse
Tentamen TNM061, 3D-grafik och animering för MT2. Onsdag 20/ kl SP71. Inga hjälpmedel
 Tentamen TNM061, 3D-grafik och animering för MT2 Onsdag 20/8 2014 kl 14-18 SP71 Inga hjälpmedel Tentamen innehåller 7 uppgifter, vilka tillsammans kan ge maximalt 50 poäng. För betyg G (registreras som
Tentamen TNM061, 3D-grafik och animering för MT2 Onsdag 20/8 2014 kl 14-18 SP71 Inga hjälpmedel Tentamen innehåller 7 uppgifter, vilka tillsammans kan ge maximalt 50 poäng. För betyg G (registreras som
TAIU07 Matematiska beräkningar med Matlab
 TAIU07 Matematiska beräkningar med Matlab Laboration 3. Linjär algebra Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion 2 En Komet Kometer rör sig enligt ellipsformade
TAIU07 Matematiska beräkningar med Matlab Laboration 3. Linjär algebra Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion 2 En Komet Kometer rör sig enligt ellipsformade
TANA17 Matematiska beräkningar med Matlab
 TANA17 Matematiska beräkningar med Matlab Laboration 1. Linjär Algebra och Avbildningar Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion I denna övning skall
TANA17 Matematiska beräkningar med Matlab Laboration 1. Linjär Algebra och Avbildningar Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion I denna övning skall
Kort introduktion till POV-Ray, del 1
 Kort introduktion till POV-Ray, del 1 Kjell Y Svensson, 2004-02-02,2007-03-13 Denna serie av artiklar ger en grundläggande introduktion och förhoppningsvis en förståelse för hur man skapar realistiska
Kort introduktion till POV-Ray, del 1 Kjell Y Svensson, 2004-02-02,2007-03-13 Denna serie av artiklar ger en grundläggande introduktion och förhoppningsvis en förståelse för hur man skapar realistiska
Varför behövs grafikbibliotek? Introduktion till OpenGL. OpenGL är ett grafikbibliotek. Fördelar med OpenGL. Allmänt om OpenGL. Nackdelar med OpenGL
 Introduktion till OpenGL Battlezone Atari corp., 1980. Gustav Taxén CID gustavt@nada.kth.se Varför behövs grafikbibliotek? Grafikhårdvara Skillnader i funktionalitet och möjligheter. Skillnader i styrning.
Introduktion till OpenGL Battlezone Atari corp., 1980. Gustav Taxén CID gustavt@nada.kth.se Varför behövs grafikbibliotek? Grafikhårdvara Skillnader i funktionalitet och möjligheter. Skillnader i styrning.
Avalanche Studios. OpenGL. Vår teknik. Våra spel. Lite inspiration... Stora, öppna spelvärldar. Sandbox-gameplay. Hög audiovisuell standard
 OpenGL Avalanche Studios Sveriges ledande oberoende spelutvecklare Fokus på egenutvecklade IPn Finns på Söder i Stockholm ~6 anställda Just Cause för PS2, PC, XBox, och XBox 36 släpptes 26 Gustav Taxén
OpenGL Avalanche Studios Sveriges ledande oberoende spelutvecklare Fokus på egenutvecklade IPn Finns på Söder i Stockholm ~6 anställda Just Cause för PS2, PC, XBox, och XBox 36 släpptes 26 Gustav Taxén
Tentamen, Programmeringsteknik för BME, F och N
 LUNDS TEKNISKA HÖGSKOLA 1(6) Institutionen för datavetenskap Tentamen, Programmeringsteknik för BME, F och N 2015 06 03, 14.00 19.00 Anvisningar: Preliminärt ger uppgifterna 7 + 11 + 16 + 11 = 45 poäng.
LUNDS TEKNISKA HÖGSKOLA 1(6) Institutionen för datavetenskap Tentamen, Programmeringsteknik för BME, F och N 2015 06 03, 14.00 19.00 Anvisningar: Preliminärt ger uppgifterna 7 + 11 + 16 + 11 = 45 poäng.
Föreläsning 3.1: Datastrukturer, en översikt
 Föreläsning.: Datastrukturer, en översikt Hittills har vi i kursen lagt mycket fokus på algoritmiskt tänkande. Vi har inte egentligen ägna så mycket uppmärksamhet åt det andra som datorprogram också består,
Föreläsning.: Datastrukturer, en översikt Hittills har vi i kursen lagt mycket fokus på algoritmiskt tänkande. Vi har inte egentligen ägna så mycket uppmärksamhet åt det andra som datorprogram också består,
Försättsblad till skriftlig tentamen vid Linköpings Universitet
 Försättsblad till skriftlig tentamen vid Linköpings Universitet (fylls i av ansvarig) Datum för tentamen Sal Tid Kurskod Provkod Kursnamn/benämning Institution Antal uppgifter i tentamen Antal sidor på
Försättsblad till skriftlig tentamen vid Linköpings Universitet (fylls i av ansvarig) Datum för tentamen Sal Tid Kurskod Provkod Kursnamn/benämning Institution Antal uppgifter i tentamen Antal sidor på
Procedurell 3D-eld på grafikkortet
 Procedurell 3D-eld på grafikkortet TNM084 Procedurella metoder för bilder Anders Hedblom, andhe893@student.liu.se 2012-04-04 1. Bakgrund 1.1. Procedurella metoder Procedurella metoder har ett stort användningsområde
Procedurell 3D-eld på grafikkortet TNM084 Procedurella metoder för bilder Anders Hedblom, andhe893@student.liu.se 2012-04-04 1. Bakgrund 1.1. Procedurella metoder Procedurella metoder har ett stort användningsområde
Mätning av fokallängd hos okänd lins
 Mätning av fokallängd hos okänd lins Syfte Labbens syfte är i första hand att lära sig hantera mätfel och uppnå god noggrannhet, även med systematiska fel. I andra hand är syftet att hantera linser och
Mätning av fokallängd hos okänd lins Syfte Labbens syfte är i första hand att lära sig hantera mätfel och uppnå god noggrannhet, även med systematiska fel. I andra hand är syftet att hantera linser och
Tentamen i. Programmering i språket C
 1 of 6 Örebro universitet Akademin för naturvetenskap och teknik Thomas Padron-McCarthy (thomas.padron-mccarthy@oru.se) Tentamen i Programmering i språket C för D1 m fl, även distanskursen lördag 25 februari
1 of 6 Örebro universitet Akademin för naturvetenskap och teknik Thomas Padron-McCarthy (thomas.padron-mccarthy@oru.se) Tentamen i Programmering i språket C för D1 m fl, även distanskursen lördag 25 februari
Tentamen TNM061, 3D-grafik och animering för MT2. Tisdag 3/ kl 8-12 TP51, TP52, TP54, TP56, TP41, TP43. Inga hjälpmedel
 Tentamen TNM061, 3D-grafik och animering för MT2 Tisdag 3/6 2014 kl 8-12 TP51, TP52, TP54, TP56, TP41, TP43 Inga hjälpmedel Tentamen innehåller 8 uppgifter, vilka tillsammans kan ge maximalt 50 poäng.
Tentamen TNM061, 3D-grafik och animering för MT2 Tisdag 3/6 2014 kl 8-12 TP51, TP52, TP54, TP56, TP41, TP43 Inga hjälpmedel Tentamen innehåller 8 uppgifter, vilka tillsammans kan ge maximalt 50 poäng.
Spelutveckling 3d-grafik och modellering. Grunder för 3d-grafik Blender Animering
 Spelutveckling 3d-grafik och modellering Grunder för 3d-grafik Blender Animering Grunderna för 3d-grafik Positionering, transformationer Projektion, kameran Objekt i en 3d-värld Ljusmodeller för 3d-grafik
Spelutveckling 3d-grafik och modellering Grunder för 3d-grafik Blender Animering Grunderna för 3d-grafik Positionering, transformationer Projektion, kameran Objekt i en 3d-värld Ljusmodeller för 3d-grafik
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
RTG-formatet Gustav Taxén,
 RTG-formatet 2004-08-11 Gustav Taxén, gustavt@nada.kth.se Det här texten beskriver kortfattat RTG-filformatet och ett C-bibliotek som kan läsa det. RTG-formatet är ett filformat för geometribeskrivningar
RTG-formatet 2004-08-11 Gustav Taxén, gustavt@nada.kth.se Det här texten beskriver kortfattat RTG-filformatet och ett C-bibliotek som kan läsa det. RTG-formatet är ett filformat för geometribeskrivningar
Exempel på användning av arv: Geometriska figurer
 (9 maj 2014 Klasshierarkier 1 ) Exempel på användning av arv: Geometriska figurer Uppgift: Skriv ett program som kan hantera några olika geometrisk figurer: linjer, cirklar och rektanglar. (9 maj 2014
(9 maj 2014 Klasshierarkier 1 ) Exempel på användning av arv: Geometriska figurer Uppgift: Skriv ett program som kan hantera några olika geometrisk figurer: linjer, cirklar och rektanglar. (9 maj 2014
Geometriska transformationer
 CTH/GU LABORATION 5 TMV6/MMGD - 7/8 Matematiska vetenskaper Inledning Geometriska transformationer Vi skall se på några geometriska transformationer; rotation, skalning, translation, spegling och projektion.
CTH/GU LABORATION 5 TMV6/MMGD - 7/8 Matematiska vetenskaper Inledning Geometriska transformationer Vi skall se på några geometriska transformationer; rotation, skalning, translation, spegling och projektion.
Andragradsekvationer möter elever under sitt första år på gymnasiet.
 Christoph Kirfel Komplettera kvadraten och kuben med bilder Elever som för första gången ställs inför att lösa andragradsekvationer kan få hjälp att förstå kvadratkomplettering med hjälp av väl uttänkta
Christoph Kirfel Komplettera kvadraten och kuben med bilder Elever som för första gången ställs inför att lösa andragradsekvationer kan få hjälp att förstå kvadratkomplettering med hjälp av väl uttänkta
Robotarm och algebra
 Tekniska Högskolan i Linköping Institutionen för Datavetenskap (IDA) Torbjörn Jonsson 2010-12-07 Robotarm och algebra I denna laboration skall du lära dig lite mer om möjlighetera att rita ut mer avancerade
Tekniska Högskolan i Linköping Institutionen för Datavetenskap (IDA) Torbjörn Jonsson 2010-12-07 Robotarm och algebra I denna laboration skall du lära dig lite mer om möjlighetera att rita ut mer avancerade
OpenGL, Maya och specialeffekter
 OpenGL, Maya och specialeffekter Gustav Taxén, gustavt@nada.kth.se Introduktion OpenGL är ett användbart API för att rendera grafik i realtid (om man har det rätta hårdvarustödet). Du har på tidigare kurser
OpenGL, Maya och specialeffekter Gustav Taxén, gustavt@nada.kth.se Introduktion OpenGL är ett användbart API för att rendera grafik i realtid (om man har det rätta hårdvarustödet). Du har på tidigare kurser
.I Minkowskis gitterpunktssats
 1.I Minkowskis gitterpunktssats Minkowskis sats klarar av en mängd problem inom den algebraiska talteorin och teorin för diofantiska ekvationer. en kan ses som en kontinuerlig, eller geometrisk, variant,
1.I Minkowskis gitterpunktssats Minkowskis sats klarar av en mängd problem inom den algebraiska talteorin och teorin för diofantiska ekvationer. en kan ses som en kontinuerlig, eller geometrisk, variant,
Uppgiften är att beskriva en kvadrat i ett Java program. En första version av programmet skulle kunna se ut så här:
 Att skapa en klass kvadrat Uppgiften är att beskriva en kvadrat i ett Java program. En första version av programmet skulle kunna se ut så här: public class Kvadrat { private int sida; Det var väl inte
Att skapa en klass kvadrat Uppgiften är att beskriva en kvadrat i ett Java program. En första version av programmet skulle kunna se ut så här: public class Kvadrat { private int sida; Det var väl inte
. b. x + 2 y 3 z = 1 3 x y + 2 z = a x 5 y + 8 z = 1 lösning?
 Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Omtentamen TNM077, 3D datorgrafik och animering (samt även TNM008, 3D datorgrafik och VR)
 Omtentamen TNM077, 3D datorgrafik och animering (samt även TNM008, 3D datorgrafik och VR) Grupp: MT2 och NO2MT Datum: Fredagen den 23 april 2004 Tid: 14.00-18.00 Hjälpmedel: inga Ansvarig lärare: Stefan
Omtentamen TNM077, 3D datorgrafik och animering (samt även TNM008, 3D datorgrafik och VR) Grupp: MT2 och NO2MT Datum: Fredagen den 23 april 2004 Tid: 14.00-18.00 Hjälpmedel: inga Ansvarig lärare: Stefan
kl Tentaupplägg
 Tentaupplägg TIPS 1: Läs igenom ALLA uppgifterna. Välj den du känner är lättast först. Det kan gärna ta 10-20 minuter. Försök skriva saker som kan vara problem i uppgifterna. Är det något du absolut kommer
Tentaupplägg TIPS 1: Läs igenom ALLA uppgifterna. Välj den du känner är lättast först. Det kan gärna ta 10-20 minuter. Försök skriva saker som kan vara problem i uppgifterna. Är det något du absolut kommer
Johan Karlsson Datavetenskap för teknisk kemi, 10p, moment 1 Datavetenskap Umeå Universitet. Tentamen
 Tentamen för teknisk kemi, 10p, moment 1 29 november 1999 Skrivtid 9-15 Hjälpmedel: av följande böcker. - U. Bilting och J. Skansholm: Vägen till C - A. Kelley & I. Pohl: A Book on C Maxpoäng: Gräns för
Tentamen för teknisk kemi, 10p, moment 1 29 november 1999 Skrivtid 9-15 Hjälpmedel: av följande böcker. - U. Bilting och J. Skansholm: Vägen till C - A. Kelley & I. Pohl: A Book on C Maxpoäng: Gräns för
Karta över Jorden - viktigt exempel. Sfär i (x, y, z) koordinater Funktionen som beskriver detta ser ut till att vara
 Föreläsning 1 Jag hettar Thomas Kragh och detta är kursen: Flervariabelanalys 1MA016/1MA183. E-post: thomas.kragh@math.uu.se Kursplan finns i studentportalens hemsida för denna kurs. Där är två spår: Spår
Föreläsning 1 Jag hettar Thomas Kragh och detta är kursen: Flervariabelanalys 1MA016/1MA183. E-post: thomas.kragh@math.uu.se Kursplan finns i studentportalens hemsida för denna kurs. Där är två spår: Spår
1 som går genom punkten (1, 3) och är parallell med vektorn.
 KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
Det är principer och idéer som är viktiga. Skriv så att du övertygar rättaren om att du har förstått dessa även om detaljer kan vara felaktiga.
 Tentamen Programmeringsteknik II 2014-0-27 Skrivtid: 0800 100 Tänk på följande Skriv läsligt! Använd inte rödpenna! Skriv bara på framsidan av varje papper. Börja alltid ny uppgift på nytt papper. Lägg
Tentamen Programmeringsteknik II 2014-0-27 Skrivtid: 0800 100 Tänk på följande Skriv läsligt! Använd inte rödpenna! Skriv bara på framsidan av varje papper. Börja alltid ny uppgift på nytt papper. Lägg
1 Minkostnadsflödesproblem i nätverk
 Krister Svanberg, april 2012 1 Minkostnadsflödesproblem i nätverk Ett nätverk består av en given mängd noder numrerade från 1 till m (där m är antalet noder) samt en given mängd riktade bågar mellan vissa
Krister Svanberg, april 2012 1 Minkostnadsflödesproblem i nätverk Ett nätverk består av en given mängd noder numrerade från 1 till m (där m är antalet noder) samt en given mängd riktade bågar mellan vissa
Laboration 1: Figurer i hierarki
 Laboration 1: Figurer i hierarki Bakgrund Två grundläggande tekniker i objektorienterad konstruktion är arv och komposition. Mål Laborationen har flera avsikter: 1. Ge kunskaper i hur program kan organiseras
Laboration 1: Figurer i hierarki Bakgrund Två grundläggande tekniker i objektorienterad konstruktion är arv och komposition. Mål Laborationen har flera avsikter: 1. Ge kunskaper i hur program kan organiseras
I rastergrafikens barndom...gjorde man grafik genom att skriva i ett videominne. Operationer på buffert och pixlar. Idag... Varför grafikkort?
 Operationer på buffert och pixlar I rastergrafikens barndom......gjorde man grafik genom att skriva i ett videominne. Lapped textures Emil Praun et al., SIGGRAPH 2000. Gustav Taxén CID gustavt@nada.kth.se
Operationer på buffert och pixlar I rastergrafikens barndom......gjorde man grafik genom att skriva i ett videominne. Lapped textures Emil Praun et al., SIGGRAPH 2000. Gustav Taxén CID gustavt@nada.kth.se
TANA17 Matematiska beräkningar med MATLAB för M, DPU. Fredrik Berntsson, Linköpings Universitet. 9 november 2015 Sida 1 / 28
 TANA17 Matematiska beräkningar med MATLAB för M, DPU Fredrik Berntsson, Linköpings Universitet 9 november 2015 Sida 1 / 28 Föreläsning 3 Linjära ekvationssystem. Invers. Rotationsmatriser. Tillämpning:
TANA17 Matematiska beräkningar med MATLAB för M, DPU Fredrik Berntsson, Linköpings Universitet 9 november 2015 Sida 1 / 28 Föreläsning 3 Linjära ekvationssystem. Invers. Rotationsmatriser. Tillämpning:
Linjära ekvationssystem
 CTH/GU LABORATION MVE0-0/0 Matematiska vetenskaper Inledning Linjära ekvationssystem Redan i första läsperioden löste vi linjära ekvationssystem Ax = b med Matlab. Vi satte ihop koefficentmatrisen A med
CTH/GU LABORATION MVE0-0/0 Matematiska vetenskaper Inledning Linjära ekvationssystem Redan i första läsperioden löste vi linjära ekvationssystem Ax = b med Matlab. Vi satte ihop koefficentmatrisen A med
Mer om geometriska transformationer
 CTH/GU LABORATION 4 TMV141-1/13 Matematiska vetenskaper 1 Inledning Mer om geometriska transformationer Vi fortsätter med geometriska transformationer och ser på ortogonal (vinkelrät) projektion samt spegling.
CTH/GU LABORATION 4 TMV141-1/13 Matematiska vetenskaper 1 Inledning Mer om geometriska transformationer Vi fortsätter med geometriska transformationer och ser på ortogonal (vinkelrät) projektion samt spegling.
Transformationer i R 2 och R 3
 Linjär algebra, I / Matematiska vetenskaper Inledning Transformationer i R och R 3 Vi skall se på några geometriska transformationer; rotation, skalning, translation och projektion. Rotation och skalning
Linjär algebra, I / Matematiska vetenskaper Inledning Transformationer i R och R 3 Vi skall se på några geometriska transformationer; rotation, skalning, translation och projektion. Rotation och skalning
Programmering med Java. Grunderna. Programspråket Java. Programmering med Java. Källkodsexempel. Java API-exempel In- och utmatning.
 Programmering med Java Programmering med Java Programspråket Java Källkodsexempel Källkod Java API-exempel In- och utmatning Grunderna Ann Pan panda@nada.kth.se Rum 1445, plan 4 på Nada 08-7909690 Game.java
Programmering med Java Programmering med Java Programspråket Java Källkodsexempel Källkod Java API-exempel In- och utmatning Grunderna Ann Pan panda@nada.kth.se Rum 1445, plan 4 på Nada 08-7909690 Game.java
EDAA20 Föreläsning Klassen ArrayList. Viktiga operationer på ArrayList. Generisk klass
 EDAA20 Föreläsning 11-12 Klassen ArrayList Klassen ArrayList Skriva program som läser data från en textfil och skriver data till en textfil Repetition inför delmålskontroll 2 är en standardklass (i paketet
EDAA20 Föreläsning 11-12 Klassen ArrayList Klassen ArrayList Skriva program som läser data från en textfil och skriver data till en textfil Repetition inför delmålskontroll 2 är en standardklass (i paketet
Föreläsning 5-6 Innehåll. Exempel på program med objekt. Exempel: kvadratobjekt. Objekt. Skapa och använda objekt Skriva egna klasser
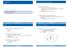 Föreläsning 5-6 Innehåll Exempel på program med objekt Skapa och använda objekt Skriva egna klasser public class DrawSquare { public static void main(string[] args) { SimpleWindow w = new SimpleWindow(600,
Föreläsning 5-6 Innehåll Exempel på program med objekt Skapa och använda objekt Skriva egna klasser public class DrawSquare { public static void main(string[] args) { SimpleWindow w = new SimpleWindow(600,
DGI/SUDOA Den historiska utvecklingen. Globala - lokala belysningsmodeller. Lokala belysningsmodeller. Rendering equation
 DGI/SUDOA - 060329 Rendering equation Belysningsmodeller (lokala och globala) Kort om texturer Den historiska utvecklingen 1. Enkla modeller som utvärderades genom att göra enkla bedömningar 2. Mera sofistikerade
DGI/SUDOA - 060329 Rendering equation Belysningsmodeller (lokala och globala) Kort om texturer Den historiska utvecklingen 1. Enkla modeller som utvärderades genom att göra enkla bedömningar 2. Mera sofistikerade
P Q = ( 2, 1, 1), P R = (0, 1, 0) och QR = (2, 2, 1). arean = 1 2 P Q P R
 1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Programmera i C Varför programmera i C när det finns språk som Simula och Pascal??
 Programmera i C Varför programmera i C när det finns språk som Simula och Pascal?? C är ett språk på relativt låg nivå vilket gör det möjligt att konstruera effektiva kompilatorer, samt att komma nära
Programmera i C Varför programmera i C när det finns språk som Simula och Pascal?? C är ett språk på relativt låg nivå vilket gör det möjligt att konstruera effektiva kompilatorer, samt att komma nära
OpenGL. grafikbibliotek? Nackdelar med OpenGL. Fördelar med OpenGL. En introduktion till OpenGL. OpenGL. rdvara. Grafikhårdvara.
 En introduktion till Gustav Taxén gustavt@nada.kth.se Står för Open Graphics Library. C-bibliotek för 3D-grafik (och( i viss mån 2D). Utvecklat av Silicon Graphics (SGI). Kontrolleras av ett Architectural
En introduktion till Gustav Taxén gustavt@nada.kth.se Står för Open Graphics Library. C-bibliotek för 3D-grafik (och( i viss mån 2D). Utvecklat av Silicon Graphics (SGI). Kontrolleras av ett Architectural
Procedurell grottgenerator och eld i GLSL. Marcus Widegren
 Procedurell grottgenerator och eld i GLSL Marcus Widegren 14 januari 2012 Innehåll 2 Sammanfattning Jag har gjort en enkel procedurell grottgenerator i GLSL och C++. För belysning används en fackla, som
Procedurell grottgenerator och eld i GLSL Marcus Widegren 14 januari 2012 Innehåll 2 Sammanfattning Jag har gjort en enkel procedurell grottgenerator i GLSL och C++. För belysning används en fackla, som
Kvalificeringstävling den 30 september 2008
 SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
Föreläsning 5-6 Innehåll
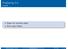 Föreläsning 5-6 Innehåll Skapa och använda objekt Skriva egna klasser Datavetenskap (LTH) Föreläsning 5-6 HT 2017 1 / 32 Exempel på program med objekt public class DrawSquare { public static void main(string[]
Föreläsning 5-6 Innehåll Skapa och använda objekt Skriva egna klasser Datavetenskap (LTH) Föreläsning 5-6 HT 2017 1 / 32 Exempel på program med objekt public class DrawSquare { public static void main(string[]
2D1311 Programmeringsteknik för Bio1 och Bio2, vt 2003 Fiktivt prov På flervalsfrågorna är endast ett svar rätt om inget annat anges i frågan! Det rik
 2D1311 Programmeringsteknik för Bio1 och Bio2, vt 2003 Fiktivt prov På flervalsfrågorna är endast ett svar rätt om inget annat anges i frågan! Det riktiga provet tar 45 minuter (en lektionstimme) och det
2D1311 Programmeringsteknik för Bio1 och Bio2, vt 2003 Fiktivt prov På flervalsfrågorna är endast ett svar rätt om inget annat anges i frågan! Det riktiga provet tar 45 minuter (en lektionstimme) och det
PROCEDUELL TERRÄNG. Proceduella metoder för bilder (TNM084) Jimmy Liikala Institutionen för teknik och naturvetenskap
 PROCEDUELL TERRÄNG Proceduella metoder för bilder (TNM084) Jimmy Liikala (jimli570@student.liu.se) Institutionen för teknik och naturvetenskap Sammanfattning Rapporten beskriver hur en proceduell terräng
PROCEDUELL TERRÄNG Proceduella metoder för bilder (TNM084) Jimmy Liikala (jimli570@student.liu.se) Institutionen för teknik och naturvetenskap Sammanfattning Rapporten beskriver hur en proceduell terräng
LABORATION 1 AVBILDNING OCH FÖRSTORING
 LABORATION 1 AVBILDNING OCH FÖRSTORING Personnummer Namn Laborationen godkänd Datum Labhandledare 1 (6) LABORATION 1: AVBILDNING OCH FÖRSTORING Att läsa före lab: Vad är en bild och hur uppstår den? Se
LABORATION 1 AVBILDNING OCH FÖRSTORING Personnummer Namn Laborationen godkänd Datum Labhandledare 1 (6) LABORATION 1: AVBILDNING OCH FÖRSTORING Att läsa före lab: Vad är en bild och hur uppstår den? Se
Geometrisk optik. Syfte och mål. Innehåll. Utrustning. Institutionen för Fysik 2006-04-25
 Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
732G Linköpings universitet 732G11. Johan Jernlås. Översikt. Repetition. Felsökning. Datatyper. Referenstyper. Metoder / funktioner
 732G11 Linköpings universitet 2011-01-21 1 2 3 4 5 6 Skapa program Kompilera: Källkod Kompilator bytekod Köra: Bytekod Virtuell maskin Ett riktigt program Hej.java class Hej { public static void main (
732G11 Linköpings universitet 2011-01-21 1 2 3 4 5 6 Skapa program Kompilera: Källkod Kompilator bytekod Köra: Bytekod Virtuell maskin Ett riktigt program Hej.java class Hej { public static void main (
Mer om analytisk geometri
 1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
DUGGA Tentaupplägg
 Tentaupplägg TIPS 1: Läs igenom ALLA uppgifterna. Välj den du känner är lättast först. Det kan gärna ta 10-20 minuter. Försök skriva saker som kan vara problem i uppgifterna. Är det något du absolut kommer
Tentaupplägg TIPS 1: Läs igenom ALLA uppgifterna. Välj den du känner är lättast först. Det kan gärna ta 10-20 minuter. Försök skriva saker som kan vara problem i uppgifterna. Är det något du absolut kommer
Programmering i C++ En manual för kursen Datavetenskaplig introduktionskurs 5p
 Programmering i C++ En manual för kursen Datavetenskaplig introduktionskurs 5p Skriven av Michael Andersson Introduktion Programmering I högnivåspråk fokuserar på själv problemet (algoritmen) istället
Programmering i C++ En manual för kursen Datavetenskaplig introduktionskurs 5p Skriven av Michael Andersson Introduktion Programmering I högnivåspråk fokuserar på själv problemet (algoritmen) istället
λ = T 2 g/(2π) 250/6 40 m
 Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Polygoner. Trianglar på tre sätt
 Polygoner Trianglar på tre sätt Man kan skriva in punkter antingen via punktverktyget eller genom att skriva punktens namn och koordinater i inmatningsfältet. Då man ritar månghörningar lönar det sig att
Polygoner Trianglar på tre sätt Man kan skriva in punkter antingen via punktverktyget eller genom att skriva punktens namn och koordinater i inmatningsfältet. Då man ritar månghörningar lönar det sig att
Rumsuppfattning är förmågan att behandla sinnesintryck av former
 Güner Ahmet & Thomas Lingefjärd Tredimensionellt tänkande Tredimensionella matematiska representationer är inte särskilt vanliga i skolans matematikkurser, med undantag för kurs 3 5 i gymnasiet. Varför
Güner Ahmet & Thomas Lingefjärd Tredimensionellt tänkande Tredimensionella matematiska representationer är inte särskilt vanliga i skolans matematikkurser, med undantag för kurs 3 5 i gymnasiet. Varför
Institutionen för matematik och datavetenskap Karlstads universitet. GeoGebra. ett digitalt verktyg för framtidens matematikundervisning
 Karlstads GeoGebrainstitut Institutionen för matematik och datavetenskap Karlstads universitet Mats Brunström Maria Fahlgren GeoGebra ett digitalt verktyg för framtidens matematikundervisning Invigning
Karlstads GeoGebrainstitut Institutionen för matematik och datavetenskap Karlstads universitet Mats Brunström Maria Fahlgren GeoGebra ett digitalt verktyg för framtidens matematikundervisning Invigning
Veckoblad 1, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Att beräkna:: Avstånd
 Att beräkna:: Avstånd Mikael Forsberg :: 27 november 205 Innehåll Punkter, linjer och plan, en sammanställning 2. Punkter i två och tre dimensioner....................... 2.2 Räta linjer i två och tre
Att beräkna:: Avstånd Mikael Forsberg :: 27 november 205 Innehåll Punkter, linjer och plan, en sammanställning 2. Punkter i två och tre dimensioner....................... 2.2 Räta linjer i två och tre
5. En metod som anropar sig själv a) får inte förekomma i Java-program b) kallas destruktiv c) kallas iterativ d) kallas rekursiv 6. Vilka värden har
 Datalogi I, grundkurs med Java 10p, 2D4112, 2002-2003 Exempel på tentafrågor i Java Först följer frågor av flervalstyp. Frågorna är inte ordnade efter svårighetsgrad. 1. Skillnaden mellan typerna int och
Datalogi I, grundkurs med Java 10p, 2D4112, 2002-2003 Exempel på tentafrågor i Java Först följer frågor av flervalstyp. Frågorna är inte ordnade efter svårighetsgrad. 1. Skillnaden mellan typerna int och
Uppgift 1 (vadå sortering?)
 2011-06-08.kl.14-19 Uppgift 1 (vadå sortering?) Du skall skriva ett program som sorterar in en sekvens av tal i en vektor (en array ) enligt en speciell metod. Inledningsvis skall vektorn innehålla endast
2011-06-08.kl.14-19 Uppgift 1 (vadå sortering?) Du skall skriva ett program som sorterar in en sekvens av tal i en vektor (en array ) enligt en speciell metod. Inledningsvis skall vektorn innehålla endast
Elevuppgift: Bågvinkelns storlek i en halvcirkel
 Elevuppgift: Bågvinkelns storlek i en halvcirkel 1. Öppna GeoGebra Classic och välj perspektivet Grafanalys. Dölj koordinataxlarna. 2. Skapa konstruktionen nedan. Det är ingen skillnad var i rutfältet
Elevuppgift: Bågvinkelns storlek i en halvcirkel 1. Öppna GeoGebra Classic och välj perspektivet Grafanalys. Dölj koordinataxlarna. 2. Skapa konstruktionen nedan. Det är ingen skillnad var i rutfältet
Studieanvisning i Optik, Fysik A enligt boken Quanta A
 Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Linköpings Tekniska Högskola Instutitionen för Datavetenskap (IDA) Torbjörn Jonsson, Erik Nilsson Lab 2: Underprogram
 Mål Lab 2: Underprogram Följande laboration introducerar underprogram; procedurer, funktioner och operatorer. I denna laboration kommer du att lära dig: Hur man skriver underprogram och hur dessa anropas.
Mål Lab 2: Underprogram Följande laboration introducerar underprogram; procedurer, funktioner och operatorer. I denna laboration kommer du att lära dig: Hur man skriver underprogram och hur dessa anropas.
Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid , ) Retinoskopet
 Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid 345-353, 358-362) Retinoskopet Utvecklat från oftalmoskopi under slutet av 1800-talet. Objektiv metod för att bestämma patientens
Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid 345-353, 358-362) Retinoskopet Utvecklat från oftalmoskopi under slutet av 1800-talet. Objektiv metod för att bestämma patientens
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
TEM Projekt Transformmetoder
 TEM Projekt Transformmetoder Utförs av: Mikael Bodin 19940414 4314 William Sjöström 19940404 6956 Sammanfattning I denna laboration undersöks hur Fouriertransformering kan användas vid behandling och analysering
TEM Projekt Transformmetoder Utförs av: Mikael Bodin 19940414 4314 William Sjöström 19940404 6956 Sammanfattning I denna laboration undersöks hur Fouriertransformering kan användas vid behandling och analysering
NÄMNARENs. problemavdelning
 NÄMNARENs problemavdelning För problemavdelningen svarar denna gång Bernt Leonardsson och Bo Söderberg från Örebro. Problemen är snarare kluriga än svåra så ge inte upp i tron att du inte kan matematik.
NÄMNARENs problemavdelning För problemavdelningen svarar denna gång Bernt Leonardsson och Bo Söderberg från Örebro. Problemen är snarare kluriga än svåra så ge inte upp i tron att du inte kan matematik.
Matematik. Namn: Datum:
 Matematik Namn: Datum: Multiplikation, tabell 2 och 4. Hur många ben har djuren tillsammans? + = = + + = = + + + + = = + = = + + + = = Skriv färdigt multiplikationen! 3 4 = 4 2 = 2 5 = 4 6 = 4 0 = 4 5
Matematik Namn: Datum: Multiplikation, tabell 2 och 4. Hur många ben har djuren tillsammans? + = = + + = = + + + + = = + = = + + + = = Skriv färdigt multiplikationen! 3 4 = 4 2 = 2 5 = 4 6 = 4 0 = 4 5
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
Att prova på en enkel Applet och att lära sig olika sätt att hämta data från tangentbordet. Du får även prova på att skapa din första riktiga klass.
 Datateknik A, Syfte: Att prova på en enkel Applet och att lära sig olika sätt att hämta data från tangentbordet. Du får även prova på att skapa din första riktiga klass. Att läsa: Lektion 2 Uppgifter:
Datateknik A, Syfte: Att prova på en enkel Applet och att lära sig olika sätt att hämta data från tangentbordet. Du får även prova på att skapa din första riktiga klass. Att läsa: Lektion 2 Uppgifter:
Moment 4.11 Viktiga exempel 4.32, 4.33 Övningsuppgifter Ö4.18-Ö4.22, Ö4.30-Ö4.34. Planet Ett plan i rummet är bestämt då
 Moment 4.11 Viktiga exempel 4.32, 4.33 Övningsuppgifter Ö4.18-Ö4.22, Ö4.30-Ö4.34 Planet Ett plan i rummet är bestämt då två icke parallella riktningar, v 1 och v 2, och en punkt P 1 i planet är givna.
Moment 4.11 Viktiga exempel 4.32, 4.33 Övningsuppgifter Ö4.18-Ö4.22, Ö4.30-Ö4.34 Planet Ett plan i rummet är bestämt då två icke parallella riktningar, v 1 och v 2, och en punkt P 1 i planet är givna.
Agenda. Arrayer deklaration, åtkomst Makron Flerdimensionella arrayer Initiering Strängar Funktioner och arrayer. Övningar nu och då
 Agenda Arrayer deklaration, åtkomst Makron Flerdimensionella arrayer Initiering Strängar Funktioner och arrayer Övningar nu och då 1 Motivering I de flesta problem ingår att hantera multipla data I de
Agenda Arrayer deklaration, åtkomst Makron Flerdimensionella arrayer Initiering Strängar Funktioner och arrayer Övningar nu och då 1 Motivering I de flesta problem ingår att hantera multipla data I de
kl Tentaupplägg
 Tentaupplägg TIPS 1: Läs igenom ALLA uppgifterna. Välj den du känner är lättast först. Det kan gärna ta 10-20 minuter. Försök skriva saker som kan vara problem i uppgifterna. Är det något du absolut kommer
Tentaupplägg TIPS 1: Läs igenom ALLA uppgifterna. Välj den du känner är lättast först. Det kan gärna ta 10-20 minuter. Försök skriva saker som kan vara problem i uppgifterna. Är det något du absolut kommer
Föreläsning 3-4 Innehåll. Diskutera. Metod. Programexempel med metod
 Föreläsning 3-4 Innehåll Diskutera Vad gör programmet programmet? Föreslå vilka satser vi kan bryta ut till en egen metod. Skriva egna metoder Logiska uttryck Algoritm för att beräkna min och max Vektorer
Föreläsning 3-4 Innehåll Diskutera Vad gör programmet programmet? Föreslå vilka satser vi kan bryta ut till en egen metod. Skriva egna metoder Logiska uttryck Algoritm för att beräkna min och max Vektorer
Det finns en referensbok (Java) hos tentavakten som du får gå fram och läsa men inte ta tillbaka till bänken.
 Tentamen Programmeringsteknik I 2012-06-04 Skrivtid: 1400-1700 Hjälpmedel: Java-bok Tänk på följande Det finns en referensbok (Java) hos tentavakten som du får gå fram och läsa men inte ta tillbaka till
Tentamen Programmeringsteknik I 2012-06-04 Skrivtid: 1400-1700 Hjälpmedel: Java-bok Tänk på följande Det finns en referensbok (Java) hos tentavakten som du får gå fram och läsa men inte ta tillbaka till
kl Tentaupplägg
 Tentaupplägg TIPS 1: Läs igenom ALLA uppgifterna. Välj den du känner är lättast först. Det kan gärna ta 10-20 minuter. Försök skriva saker som kan vara problem i uppgifterna. Är det något du absolut kommer
Tentaupplägg TIPS 1: Läs igenom ALLA uppgifterna. Välj den du känner är lättast först. Det kan gärna ta 10-20 minuter. Försök skriva saker som kan vara problem i uppgifterna. Är det något du absolut kommer
Laboration 3 HI1024, Programmering, grundkurs, 8.0 hp
 Laboration 3 HI1024, Programmering, grundkurs, 8.0 hp Dataingenjörsprogrammet, elektroingenjörsprogrammet och medicinsk teknik KTH Skolan för Teknik och Hälsa Redovisning: Se Kurs-PM om hur redovisningen
Laboration 3 HI1024, Programmering, grundkurs, 8.0 hp Dataingenjörsprogrammet, elektroingenjörsprogrammet och medicinsk teknik KTH Skolan för Teknik och Hälsa Redovisning: Se Kurs-PM om hur redovisningen
2D1339 Programkonstruktion för F1, ht 2003
 2D1339 Programkonstruktion för F1, ht 2003 Kontrollskrivning 1 Onsdag 19/11 2003 kl 9.15 10.00 Endast ett svar är rätt på varje fråga! Om mer än ett svar givits blir det noll poäng på frågan. Alla skriftliga
2D1339 Programkonstruktion för F1, ht 2003 Kontrollskrivning 1 Onsdag 19/11 2003 kl 9.15 10.00 Endast ett svar är rätt på varje fråga! Om mer än ett svar givits blir det noll poäng på frågan. Alla skriftliga
Bildbehandling i frekvensdomänen
 Uppsala Tekniska Högskola Signaler och system Handledare: Mathias Johansson Uppsala 2002-11-27 Bildbehandling i frekvensdomänen Erika Lundberg 800417-1602 Johan Peterson 790807-1611 Terese Persson 800613-0267
Uppsala Tekniska Högskola Signaler och system Handledare: Mathias Johansson Uppsala 2002-11-27 Bildbehandling i frekvensdomänen Erika Lundberg 800417-1602 Johan Peterson 790807-1611 Terese Persson 800613-0267
Homogena koordinater och datorgrafik
 Linjär algebra, AT3 2011/2012 Matematiska vetenskaper Inledning Homogena koordinater och datorgrafik Vi såg tidigare på några geometriska transformationer; rotation, skalning, translation och projektion.
Linjär algebra, AT3 2011/2012 Matematiska vetenskaper Inledning Homogena koordinater och datorgrafik Vi såg tidigare på några geometriska transformationer; rotation, skalning, translation och projektion.
Föreläsning 3-4 Innehåll
 Föreläsning 3-4 Innehåll Skriva egna metoder Logiska uttryck Algoritm för att beräkna min och max Vektorer Datavetenskap (LTH) Föreläsning 3-4 HT 2017 1 / 36 Diskutera Vad gör programmet programmet? Föreslå
Föreläsning 3-4 Innehåll Skriva egna metoder Logiska uttryck Algoritm för att beräkna min och max Vektorer Datavetenskap (LTH) Föreläsning 3-4 HT 2017 1 / 36 Diskutera Vad gör programmet programmet? Föreslå
TENTAMEN PROGRAMMERING I JAVA, 5P SOMMARUNIVERSITETET
 UMEÅ UNIVERSITET Datavetenskap 010824 TENTAMEN PROGRAMMERING I JAVA, 5P SOMMARUNIVERSITETET Datum : 010824 Tid : 9-15 Hjälpmedel : Inga Antal uppgifter : 7 Totalpoäng : 40 (halva poängtalet krävs normalt
UMEÅ UNIVERSITET Datavetenskap 010824 TENTAMEN PROGRAMMERING I JAVA, 5P SOMMARUNIVERSITETET Datum : 010824 Tid : 9-15 Hjälpmedel : Inga Antal uppgifter : 7 Totalpoäng : 40 (halva poängtalet krävs normalt
1. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft.
 Problem. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft. (p) Det finns många förklaringar, till exempel Hewitt med insekten
Problem. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft. (p) Det finns många förklaringar, till exempel Hewitt med insekten
ANDREAS REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se. Coulombs lag och Maxwells första ekvation
 ANDREA REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se oulombs lag och Maxwells första ekvation oulombs lag och Maxwells första ekvation Inledning Två punktladdningar q 1 samt q 2 i rymden
ANDREA REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se oulombs lag och Maxwells första ekvation oulombs lag och Maxwells första ekvation Inledning Två punktladdningar q 1 samt q 2 i rymden
Enkla datatyper minne
 Enkla datatyper minne 143.56 sant Sonja A falskt 18 1999-10-29 Bertil Gralvik, KTH Ingenjörsskolan 1 Addera två tal Algoritmen Summera tal Mata in två tal Beräkna Skriv ut resultat Mata in tal 1 Mata in
Enkla datatyper minne 143.56 sant Sonja A falskt 18 1999-10-29 Bertil Gralvik, KTH Ingenjörsskolan 1 Addera två tal Algoritmen Summera tal Mata in två tal Beräkna Skriv ut resultat Mata in tal 1 Mata in
Vilken version av Dreamweaver använder du?
 Sida 1 av 7 Lektion 1: sida 1 av 4 Till kursens framsida Sida 2 av 4» Lektion 1 Då ska vi sätta igång med den här kursens första lektion! Här kommer du att få lära dig hur man skapar och förbereder webbplatser
Sida 1 av 7 Lektion 1: sida 1 av 4 Till kursens framsida Sida 2 av 4» Lektion 1 Då ska vi sätta igång med den här kursens första lektion! Här kommer du att få lära dig hur man skapar och förbereder webbplatser
Uppgifter till praktiska tentan, del A. (7 / 27)
 Uppgifter till praktiska tentan, del A. (7 / 27) I. Sortering/Sökning: III II. Representation/Omvandling/format/protokoll: II III. Strukturering: II I alla problem, där bokstäver förekommer, antar vi att
Uppgifter till praktiska tentan, del A. (7 / 27) I. Sortering/Sökning: III II. Representation/Omvandling/format/protokoll: II III. Strukturering: II I alla problem, där bokstäver förekommer, antar vi att
Föreläsning 5: Kardinalitet. Funktioners tillväxt
 Föreläsning 5: Kardinalitet. Funktioners tillväxt A = B om det finns en bijektion från A till B. Om A har samma kardinalitet som en delmängd av naturliga talen, N, så är A uppräknelig. Om A = N så är A
Föreläsning 5: Kardinalitet. Funktioners tillväxt A = B om det finns en bijektion från A till B. Om A har samma kardinalitet som en delmängd av naturliga talen, N, så är A uppräknelig. Om A = N så är A
