RNDr. Tom Havl t, CSc. Organizace dat Z pisky z p edn ky zpracoval: Ji Dobe 20. dubna 1995 Obsah 1 Vyhled v n Z kladn pojmy : : : : : : : : : :

Transkript

1 RNDr. Tom Havl t, CSc. Organizace dat Z pisky z p edn ky zpracoval: Ji Dobe 20. dubna 1995 Obsah 1 Vyhled v n Z kladn pojmy : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 2 2 Implementace slovn ku Adresov vyhled v n : : : : : : : : : : : : : : : : : : : : : : : : : : Slovn k pomoc charakteristick ho vektoru : : : : : : : : : : : Ha ov n : : : : : : : : : : : : : : : : : : : : : : : : : : : : : Asociativn vyhled v n : : : : : : : : : : : : : : : : : : : : : : : : : Line rn : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : Set d n pole : : : : : : : : : : : : : : : : : : : : : : : : : : : Blokov set d n pole : : : : : : : : : : : : : : : : : : : : : : S ov (m ov ) set d n pole : : : : : : : : : : : : : : : : : Rotovan seznam : : : : : : : : : : : : : : : : : : : : : : : : : Set d n seznam rotovan ch seznam : : : : : : : : : : : : : Bin rn vyhled vac stromy : : : : : : : : : : : : : : : : : : : Vyv en stromy : : : : : : : : : : : : : : : : : : : : : : : : : stromy : : : : : : : : : : : : : : : : : : : : : : : : : : : : 5 3 V cerozm rn vyhled v n Dotaz na plnou shodu : : : : : : : : : : : : : : : : : : : : : : : : : Neset d n prostor : : : : : : : : : : : : : : : : : : : : : : : Lexikogracky uspo dan prostor : : : : : : : : : : : : : : : k-rozm rn lexikograck vyhled vac strom : : : : : : : : : Dotaz na ste nou shodu : : : : : : : : : : : : : : : : : : : : : : : : Dotaz na intervalovou shodu : : : : : : : : : : : : : : : : : : : : : : Metoda hrub s ly : : : : : : : : : : : : : : : : : : : : : : : : Metoda projekc : : : : : : : : : : : : : : : : : : : : : : : : : Metoda p ihr dek : : : : : : : : : : : : : : : : : : : : : : : : k-dimenzion ln BVS : : : : : : : : : : : : : : : : : : : : : : : Dotaz na nejbli ho souseda : : : : : : : : : : : : : : : : : : : : : : Metoda projekc : : : : : : : : : : : : : : : : : : : : : : : : : Voron ho diagramy : : : : : : : : : : : : : : : : : : : : : : : : 7 4 Vyhled v n v extern ch pam tech 7 1

2 OBSAH 2 5 Statick organizace soubor Sekven n SOS : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : Indexsekven n SOS : : : : : : : : : : : : : : : : : : : : : : : : : : : Indexov SOS : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : SOS s p m m p stupem : : : : : : : : : : : : : : : : : : : : : : : : Cormackovo ha ov n : : : : : : : : : : : : : : : : : : : : : : Ha ov n Laroon, Kolja : : : : : : : : : : : : : : : : : : : : : 10 6 Dynamick organizace soubor Roz i iteln ha ov n : : : : : : : : : : : : : : : : : : : : : : : : : : : Dynamick ha ov n : : : : : : : : : : : : : : : : : : : : : : : : : : : Line rn ha ov n : : : : : : : : : : : : : : : : : : : : : : : : : : : : : Skupinov t pen str nek : : : : : : : : : : : : : : : : : : : : : : : : Stromov SOS: : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : SOS s v cerozm rnou m kou : : : : : : : : : : : : : : : : : : : : : : 14

3 1 VYHLED V N 3 1 Vyhled v n dat 1.1 Z kladn pojmy Vyhled vac probl m je funkce Q : A 2 U! B, kde U je vyhled vac prostor (univerzum) A mno ina dotaz B mno ina odpov d. Statick vyhled vac probl m je funkce Q : A S! B, kdes je statick slovn k, S U. Dynamick vyhled vac probl m jako v e, ale slovn k je mo no m nit(operace INSERT,DELETE). Vyhled vac algoritmy (realizuj c Q) jsou v z sad dvoj ho druhu: Algoritmy asociativn ho vyhled v n vyu vaj um st n prvk U v S na z klad relativn ch hodnot. Algoritmy adresov ho vyhled v n vyu vaj vztah mezi hodnotami a jejich absolutn m um st n m ve slovn ku. 2 Implementace slovn ku 2.1 Adresov vyhled v n Slovn k pomoc charakteristick ho vektoru P edpokl d me, e U je kone n a uspo dan, S 2 2 U implementov no pomoc array[1..ju j] of boolean. Nev hoda : asto se st v, e jsj juj tedy nepou iteln Ha ov n Ha ovac tabulka array[1..m ; 1] of element plus ha ovac funkce h : U!f0 ::: m; 1g. h nen prost, z eho vypl vaj kolize. Ty se e tzv. kolizn funkc k : U!f0 ::: m; 1g, tasevol v p pad ne sp chu, zkou se (h(x) + k(x)) mod m, obvykle k(x) =x mod m, kde m je prvo slo. function member(x:element,s:slovn k,m:d lka-slovn ku):bool j:=h(x) while (x 6= A[j]andA[j] =!) do j := (j ; k(x)) mod m /* pozn mka:! nen prvkem U if (x = A[j]) then member :=true else member :=false Slo itost z vis na napln n tabulky = jsj m. sp n vyhled v n : 1 2 ( ; ). Ne sp n vyhled v n : 1 2 (1+1 (1;) 2 ).

4 2 IMPLEMENTACE SLOVN KU 4 Set d n ha ovac tabulka Motiv: sn en po tu pokus p i ne sp n m vyhled v n. V tabulce plat : pro 8 prvky na prohled van ch pozic ch mezi pozic h(x) v etn a skute nou pozic prvku x jsou v t ne x. 2.2 Asociativn vyhled v n Line rn prvky v poli jeden po druh m, p padn pou it n razn ku Set d n pole A[1] <A[2] <:::<A[N ] bin rn vyhled v n Blokov set d n pole obsahuje bloky d lky i[log 2 n(i +1)]pro i =1 2 ::: B. Pro n po et prvk pole plat : B;1 X i=1 i[log 2 (i + 1)] BX i=1 Pro po et blok B: O( p n log 2 n) A pro d lku nejv t ho bloku: O(p n log2 n) S ov (m ov ) set d n pole i[log 2 (i + 1)] Je to struktura, kter organizuje prvky pole do orientovan s t. Tato s je implementovan jako set d n pole rozd len na bloky o velikostech 1,2,...,n. a A[i] je prvek b-t ho bloku v poli. Vyhled v n prvku X v poli: A[i + b] A[i] A[i + b +1] function member(x:prvek):bool i:=1 b:=1 while i n and X 6= A[i] do if X<A[i] then i := i + b /* jde se vlevo */ if X>A[i] then i := i + b +1/* jde se vpravo */ b := b +1 member:=(i n) Rotovan seznam nebo tak cyklick seznam je b n pou van datov struktura. D le itou operac je zde nalezen maxim ln ho prvku podle n m eme organizovat bin rn vyhled v n. Operace vyhled v n prvku v seznamu: 1. Ur me pozici maxim ln ho prvku co je v podstat bin rn vyhled v n. 2. Bin rn prohled v me jednu polovinu seznamu.

5 2 IMPLEMENTACE SLOVN KU Set d n seznam rotovan ch seznam je zalo en na my lence lehk v m ny. pole je rozd leno na bloky d lky 1,2,3,... blok je O( p n), d lka nejdel ho O( p n) ka d blok je rotovan m seznamem prvky bloku B jsou men ne prvky bloku B +1. Vyhled v n : 1. Bin rn m vyhled v n m nad 1. prvky blok ur me 2 sousedn bloky, v nich by m l b t hledan prvek. 2. Podez el bloky prohled v me algoritmem pro rotovan seznamy. Slo itost vyhled v n je logaritmick, samotn vyhled v n prob h nejprve p es prvn prvky blok, potom uvnit podez el ch blok. Operace INSERT a DELETE maj slo itost O( p n log 2n) a je v nich pou ito principu lehk v m ny: Odebran minim ln (analogicky pro vkl d n maxim ln ) prvek bloku nahrad me minim ln m (maxim ln m) prvkem bloku n sleduj c ho, toto opakujeme a posledn blok dot d me Bin rn vyhled vac stromy Slovn k S je uspo dan mno ina S U, kde U je univerzum. Slovn k je reprezentov n bin rn m vyhled vac m stromem (BVS), v jeho vrcholech jsou prvky S tak, e pro ka d vrchol V plat, e hodnoty ulo en v jeho lev m podstromu jsou men ne hodnota ulo en ve V. Naopak hodnoty v prav m podstromu jsouv t. Slo itost vyhled v n je logaritmick (v p pad vyv en ch strom ) a, v nejhor m p pad, line rn. Stejnou slo itost maj operace INSERT a DELETE Vyv en stromy nebo tak AVL-stromy (Adelson,Velsk,Landes), jsou BVS, kter spl uj : pro 8 uzel se v ky lev ho a prav ho podstromu li maxim ln o 1. V ka AVL-stromu on uzlech jemen neborovna 2 log 2 n. Vyv en uzel je uzel, jeho lev i prav podstrom maj stejnou v ku. Vlevo t uzel je uzel, jeho lev podstrom je o 1 del. Vpravo t analogicky. P i implementaci mus uzel obsahovat p znak vyv enosti. Operace INSERT provede v prvn m kroku vlo en do stromu jako by to byl oby ejn BVS, potom v ak mohou nastat tyto varianty: vyv en uzelsem e st t vlevo (vpravo) t. uzel vlevo (vpravo) t se stane vyv en m. uzel vlevo (vpravo) t se stane nevyv en m. Nevyv en ch uzl m e b t cel ada, ten nejd l od ko ene se naz v kritick uzel. Je to ten prvn nalezen sm rem od vkl dan ho uzlu ke ko eni.

6 2 IMPLEMENTACE SLOVN KU 6 Principy obnoven rovnov hy jednoduch LL rotace kritick uzel m lev ho syna vlevo t. jednoduch RR rotace kritick uzel m prav ho syna vpravo t. LR (dvojit ) rotace kritick uzel se stal nevyv en m vlevo, ale jeho lev syn je vpravo t. RL (dvojit ) rotace kritick uzel se stal vpravo nevyv en m a jeho prav syn je vlevo t. Celou operaci INSERT lze prov st v logaritmick m ase. Operace DELETE je analogick. Provede se DELETE jako na BVS a pot, je-li to nutn (existuje-li n jak kritick uzel) obnoven rovnov hy AVL-stromu. Tak zde je logaritmick asov slo itost stromy Tern rn strom je 2-3 stromem, kdy ka d vnit n uzel T m 2 nebo 3 syny, v echny listy stromu T le ve stejn vzd lenosti od ko ene. 2-3 strom v ky h m alespo 2 h list a nejv e 3 h list. Analogicky pro v ku stromu h plat : dlog 3 ne dlog 2 ne Prvky S jsou ulo eny v listech zleva doprava v rostouc m po ad. Ka d mu vnit n mu uzlu v jsou p i azeny hodnoty L(v) a M (v) takto: L(v) je nejv t hodnotou v listech lev ho podstromu uzlu v. Zde je tak ulo ena hodnota uzlu v p pad, e je uzel listem. M (v) je nejv t hodnotou v listech prost edn ho podstromu uzlu v. Dohoda: uzel s 2 syny m syna lev ho a prost edn ho. Operace INSERT m dv varianty: uzel m dva listy: tedy p id me t et. v p pad p id n ke t em list m rozd l me listy nadv dvojice a vytvo me pro jednu dvojici nov ho otce. Nelze-li, rekurzivn zkou me o rove v e. Operace DELETE bude vypadat obdobn : m -li uzel t i listy, tedy jeden odebereme. uzel m dva listya? n kter str c m pouze dva syny, pak m e zbyl list adoptovat.? oba str cov maj t i syny tedy otec mus prov st adopci n kter ho listu ze sousedn ch trojic (snad bratr nka?).

7 3 V CEROZM RN VYHLED V N 7 3 V cerozm rn vyhled v n V t to kapitole budeme za vyhled vac prostor pova ovat mno inu U = U 1 U 2 ::: U k, kde U i je uspo dan mno ina. Prvky U jsou potom vektory ~v = (c 1 (v) ::: c k (v)), kde c i (v) 2 U i.slovn k je mno ina V U. Rozezn v me tyto typy dotaz : dotaz na plnou shodu: m me w 2 U,chceme zjistit, zda je w 2 V. dotaz na ste nou shodu: je d no 1 t k a 1 i 1 ::: i t k,tedy m me vybr no t rozm r vyhled vac ho prostoru. Pro dan dotaz na w 2 U jsou odpov d 8v 2 V takov, e c ij (w) =c ij (v) pro 8j. dotaz na intervalovou shodu: dotaz vypad takto: r s 2 U takov, e c i (r) c i (s) pro 8i.Odpov m tuto podobu: 8v 2 V takov, e c i (r) c i (v) c i (s) pro 8i. dotaz na nejbli ho souseda: dotaz je w 2 U a zadan metrika.pak odpov d jsou 8v 2 V takov, e pro 8z 2 V je (z w) (w v). 3.1 Dotaz na plnou shodu Neset d n prostor Vyhled vac prostor mohutnosti n je tvaru matice n k. Pou iteln je zde pouze sekven n vyhled v n se slo itost n:k Lexikogracky uspo dan prostor Prvky vyhled vac ho prostoru jsou uspo d ny podle zvolen ho uspo d n. Je mo no zvolit bin rn vyhled v n s logaritmickou slo itost O(k: log 2 n) k-rozm rn lexikograck vyhled vac strom Struktura je tern rn vyhled vac strom, ve vnit n ch uzlech jsou ulo eny komponenty prvk z V, v listech k-tice z V. Je budov n tak, aby ka d porovn n komponent s v sledkem < nebo > d lilo prostor o n prvc ch na2 stinev t ne dn=2e prvk a porovn n s v sledkem = sn ilo dimenzi vyhled v n o1. Nen vhodnou strukturou pro operace INSERT a DELETE. as na vybudov n je O(n: log 2 (n + k)) asov slo itost vyhled v n je O(dlog(n +1)e + k ; 1) 3.2 Dotaz na ste nou shodu Jako strukturu pro ulo en slovn ku zvol me k-rozm rn BVS. V ka d m uzlu je cel k-tice z V a uzlu je nav c p i azen tzv. diskrimin tor j, 0 j k ;1, Diskrimin tor uzlu na rovni p je ur en j = p (mod k). Konstrukce k-bvs pro dan V = fv 1 v 2 ::: v n g: v 1 je ko enem stromu v i, i>1 je p id n jako nov list na m sto ur en vyhled v n m. M -li b t v i synem vrcholu v s diskrimin torem j pak, je-li c j+1 (v i ) >c j+1 (v) (c j je j-t komponenta) stane se v i prav m synem, je-li <, pak bude lev m synem, je-li = rozhoduje se na dal ch komponent ch. Vyhled v n prob h analogicky jako v 1-BVS, s t m, e v dy porovn v me jen j +1: komponenty. V p pad ste n shody prohled v me oba podstromy.

8 3 V CEROZM RN VYHLED V N Dotaz na intervalovou shodu Metoda hrub s ly M me na mysli sekven n prohled v n. Tento zp sob m ur it v hody: jednoduch implementace nez vislost na typu pam ti (mo n je i p ska) v p pad d vkov ho zad v n dotaz za p edpokladu, e mno ina odpov d bude rozs hl v p pad mal ho po tu prvk slovn ku a velk dimenze Metoda projekc Pro v echny komponenty nebo jen pro vybran udr ujeme index: invertovan seznam set d n dle dan komponenty. Obsahuje pro ka dou k-tici hodnotu komponenty a ukazatel na k-tici. Prohled v n : zjistit pomoc index kandid ty aty prohledat sekven n. p i v ce indexech vz t ten interval, kter zab r nejm n prvk ty pak prohled vat Metoda p ihr dek Rozd len roviny na p sy ve sm ru obou os. Zasa en p ihr dky pak prohled v me. Zde odkazuji na p edm t Geometrick algoritmy I.(4.ro n k), kapitola Vyhled v n v rovinn ch rozd len ch k-dimenzion ln BVS Prohled v n prob h podle t to z sady: je-li hodnota v uzlu v t ne cel dotazovan interval, pokra ujeme lev m podstromem ve stromu, je-li to naopak, potom pokra ujeme vpravo a je-li hodnota uzlu v intervalu, pak pokra ujeme v obou v tv ch. 3.4 Dotaz na nejbli ho souseda Metoda projekc V rovin jsou denov ny body. m me zavedeny sou adn osy x,y. Jde o nalezen nejbli ho prvku ze zn m mno iny bod kn jak mu boduroviny. Pou it metrika je denovan takto: vzd lenost dvou bod je (u v) = max jc i (u) ; c i (v)j p es v echna i. Mus b t denov ny indexy pro jednotliv komponenty. Hledaj se nejd ve v jedn dimenzi postupn nejbli body. Z nich se vyb r ten, kter je nejbl e pro celou metriku Voron ho diagramy Zde odkazuji na p edm t Geometrick algoritmy I.(4.ro n k), kde je dan problematika probr na podrobn ji.

9 4 VYHLED V N V EXTERN CH PAM TECH 9 4 Vyhled v n v extern ch pam tech Z kladn m pojmem je zde soubor, intuitivn denovan jako kolekce z znam obecn r zn ch typ. Tak z znamy mohou b t ch p ny obecn r zn : v echny atributy zastoupeny v pevn m po ad, ka d atribut m d nu pevnou (maxim ln ) d lku. v echny atributy zastoupeny v pevn m po ad, hodnoty atribut prom nn d lky. vz znamu jsou hodnoty jen n kter ch atribut. Data se mezi extern a intern pam t p esunuj po bloc ch, str nk ch pevn d lky p es vyrovn vac pam ti. Z p edpokladu pevn d lky bloku budeme d le vych zet. R zn zp soby organizace z znam v souboru naz v me sch mata organizace soubor (SOS) apr v ty te budeme postupn prob rat. 5 Statick organizace soubor Charakterizuje je p edem ur en prostor pro ukl d n. Po ur it m po tu operac INSERT se sni uje efektivita vyhled v n. Nutn je operace REORGANIZACE, kter o iv celou strukturu ulo en ch polo ek. 5.1 Sekven n SOS Hromada, r zn z znamy r zn ch d lek Neuspo dan sekven n soubor, homogenn z znamy Uspo dan sekven n soubor, tak homogenn Pou van operace jsou FETCH nalezen z znamu, v neuspo dan m p pad mus me p e st pr m rn polovinuz znam (blok souboru). V p pad set d n ho prostoru za p edpokladu, e m me mo nost p m adresace, m eme m t slo itost logaritmickou. Pro asovou slo itost je rozhoduj c veli ina pr v po et p enesen ch blok mezi extern a intern pam t. Operace INSERT se provede jako p id n nakonec (app) s t m, e po ase je nutno prov d t REORGANIZACI. Operace DELETE se prov d tak, e odstra- ovan z znam se pouze ozna jako zru en. Fyzick zru en se provede p i n sleduj c REORGANIZACI. Posledn uvedenou operac je UPDATE, kter se m e slo it z operac DELETE a INSERT nebo, nem n -li se d lka, lze ji prov st p mo p eps n m bloku. 5.2 Indexsekven n SOS Skl d se z t chto komponent: 1. prim rn soubor, obsahuje sekven n ulo en v ty set d n dle hodnot prim rn ho kl e 2. index(y), soubor index obsahuje z znam pro ka d blok prim rn ho souboru, tento z znam m 2 polo ky: adresu bloku a hodnotu kl e 1. v ty bloku. Indexy jsou set d ny podle hodnot kl, na kter aplikuji bin rn vyhled v n. Nevejde-li se soubor index do opera n pam ti, vznikne sekund rn index index index. rove indexace ur uje slo itost vyhled v n.

10 5 STATICK ORGANIZACE SOUBOR oblast p ete en, co je m sto, kam se ukl daj nov v ty (INSERT). P i vyhled v n se mus prohled vat i tato oblast, co p i v t m zapln n sni uje efektivitu. Proto je nutn operace REORGANIZACE. Oblast p ete en m e b t denov na jedin pro cel prim rn soubor, jedna pro ka dou str nku nebo jedna pro ka d index. 5.3 Indexov SOS Obsahuje tyto sti: 1. prim rn soubor, nemus b t set d n. 2. index(y), soubor index obsahuje polo ku pro ka dou v tu prim rn ho souboru: (kl v ty, adresa). Tento soubor index je nejl pe organizovat jako indexsekven n soubor, mus me se ov em vyhnout situaci, kdy doch z k p ete en. To zajist me tak, e nech v me bloky indexov ho souboru napln n jen z poloviny, pozd ji pak pln bloky d l me na 2 nov. Do prim rn ho souboru pak m eme p id vat zcela libovoln, indexy je nutno aktualizovat podle druhu jejich organizace. 5.4 SOS s p m m p stupem P m p stup zde znamen n co jin ho ne ve vnit n pam ti. Pou vaj se perfektn ha ov n, co jsou ha ovac techniky, kter zaru konstantn po et p stup na disk bez ohledu na velikost souboru Cormackovo ha ov n Jde o perfektn ha ov n s K = 2 (na 2 p stupy na disk najdu nebo zjist m, e tam nen ). Cenou, kterou je nutno zaplatit, je existence p davn pam ti a re ie p i operac ch INSERT a DELETE. Skl d se z t chto st : 1. posloupnost ha ovac ch funkc fh i (K r)g i, kde K je kl a r velikost ha ovan ho prostoru. Funkce jsou denov ny takto: h i : K! f0 ::: r ; 1g, tedy z mno iny kl do adresov ho prostoru. 2. hlava souboru H, obsahuje s z znam, s = n=2 tohoto typu: (p:adresa,i: slo ha ovac funkce,r:velikost bloku nebo po et v t p es tento dek ulo en ch). Polo ky hlavy jsou odkazov ny p es ha ovac funkci h : K!f0 ::: s; 1g 3. prim rn soubor, m z znamy tohoto typu: (kl,data). Vyhled v n v ty s kl em K: j:=h(k) /* z sk m adresu v hlav souboru */ t:=h[j].i /* index ha ovac funkce */ if H[j].r =0 then na el:=false else adr:= H[j]:p + h t (K H[j]:r) if P[adr].k =K then na el:=true else na el:=false. Operace INSERT v ty s kl em K by prob hala takto: zjist m v e uveden m algoritmem, zda tam v ta ji nen.

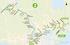
11 5 STATICK ORGANIZACE SOUBOR 11 0 adr i r prim rn soubor h(k)=j 20 t ; -? h t(k r) s-1 Obr zek 1: Vyhled v n v ty podle kl e pri Cormackov ha ov n p i vkl d n inkrementuji slo r v hlav o 1. Najdu na disku m sto, kam se vejdu s blokem v t m o jednu polo ku, p id m polo ku a p esunu blok na nov m sto. T m se zm n tak adresa v hlav. Ha ovac funkce h i mus b t zaru en prost. Strukturu po ur it m po tu vkl d n a ru en prvk mus m zotavit pomoc operace REORGANIZACE Ha ov n Laroon, Kolja Jde o dal perfektn ha ov n, tentokr t je nutno p id vat pam mk bit, kde m je po et blok prim rn ho souboru a k je konstanta, velikost separ toru 4 k 32. Komponenty SOS jsou: 1. prohled vac posloupnost adres pro ka d kl K: h 0 (K) =K mod m = adr 0 h i (K) =(adr i;1 + krok) modm = adr i pro i =1 ::: m; 1. Jde o analogii kolizn funkce. 2. Pro ka d kl K posloupnost signatur sig i (K), i =1 ::: m; 1. Signatura je k-bitov et zec. 3. Tabulka separ tor sep[0::m ; 1] of signatura loha a vztah separ tor a signatur Signatury jsou spojeny s kl em a separ tory p slu bloku. Nech blok j m kapacitu l z znam. Nech je do n j ha ov no rz znam, r l. V bloku j z stanou jen v ty s ni mi signaturami, ostatn jdou do jin ch str nek podle sv ch posloupnost prohled vac ch adres. Nejni ze signatur takto p ete en ch v t se st v separ torem bloku. Vyhled v n v ty skl emk: for i:=0 to m-1 do adr:= h i (K) sign := sig i (K) if sign sep[adr] then

12 6 DYNAMICK ORGANIZACE SOUBOR 12 getpage(adr,page) /* na te str nku s adresou adr do vnit n pam ti bueru pg */ search(pg,k,found) return found return false. Sta jedin p stup na disk! Samoz ejm za p edpokladu, e separ tory jsou ve vnit n pam ti po ta e. Cenou za jedin p stup je tak re ie p i operaci INSERT. 6 Dynamick organizace soubor Reorganizace struktury je sou st re ie operac INSERT a DELETE. Je to v podstat vyva ov n za elem optimalizace vyhled vac ch struktur. 6.1 Roz i iteln ha ov n Komponenty SOS: 1. pomocn dynamick pam ov struktura, tzv. adres (obsahuj c adresy str nek prim rn ho souboru) 2. ha ovac funkce h vracej c adresy str nek. Hodnoty h(k) jsou rovnom rn distribuov ny do intervalu h0 2 r+1 ; 1i, kde r +1 je d lka h(k) v bitech. P stup do adres e: v t s kl em K p slu z znam adres e na adrese ur en prvn mi d bity ha ovac ho kl e h(k), 0 <d r. d ozna ujeme jako hloubku adres e. Pro ka dou str nku je zavedeno slo d 0, d 0 d.jetolok ln hloubka, ud v, e p slu n str nka obsahuje polo ky s prvn mi d 0 bity shodn mi. 3. prim rn soubor P i napln n str nky se str nka rozd l na 2 nov a do okam iku, kdy nastane d 0 = d. V tom p pad je nutn zv t it hloubku adres e d o1. Vyhled v n v ty skl emk:. b := h(k) /* ha ovac kl */ pt := adres[b r b r;1 :::b r;d+1 ] /* adresa str nky prim rn ho souboru*/ getpage(pt,pg) search(pg,k,found) 6.2 Dynamick ha ov n Ha ovac funkce zde p edstavuje gener tor pseudon hodn ch bitov ch et zc neomezen d lky (vyu v se jenom tolik bit, kolik je t eba). B(K) =b K1 b K2 b K3 ::: et zce se vyu vaj knavigaci v indexu, kter je organizov n jako bin rn strom (0 vlevo, 1 vpravo). V listech jsou ukazatele na datov str nky. Aby nevzr stala p li hloubka, u v se cel les bin rn ch strom (index ). Volba stromu pro danou v tu je provedena ha ovac funkc H 0 (K)!f0 ::: n; 1g. Vlo en v ty s kl em K:

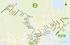
13 6 DYNAMICK ORGANIZACE SOUBOR 13 adres d= : XXXXXXXz H HHHH 110 XXXXXXXz Hj : d'=2 d'=3 d'=1 prim rn soubor Obr zek 2: Princip roz i iteln ho ha ov n procedure INSERT(K:key) s:= H 0 (K) b n uzel:=ko en s-t ho stromu k:=0 while b n uzel nen list do pou ij k-t ho bitu B(K) k nastaven nov ho uzlu k := k +1 if list nem datovou str nku then vezmi novou str nku (ukazatelnanidolistu) ulo v tu do str nky return if datov str nka nen pln then vlo v tu return while p epln n str nky do p em jej list ve vnit n uzel a p idej 2 nov listy rozh zej v ty z p epln n str nky (v etn nov ) do dvou nov ch str nek (lev a prav ) dle bitu b k+1 et zce B(K) if jedna ze str nek je pr zdn then odpoj ji od jej ho listu a z druh st le p epln n str nky u i b nou str nku k := k Line rn ha ov n Vych z z dynamick ho ha ov n, sna se vy e it jeho pam ov n roky. Ha ovac funkce zobrazuje kl do adresov ho prostoru et zc str nek (prim rn str nka + str nky p epln n ). V ka d m okam iku jsou aktivn dv ha ovac funkce. Jedna pro aktu ln rove t pen et zc u, druh pro n sleduj c rove u +1. h rove (kl) =kl mod (N 2 rove ) kde N je po te n po et et zc (adresov prostor 0 1 :::N ; 1), inici ln rove t pen je u =0.Vedle ha ovac funkce h u, rovn t pen u, jeudr ov n ukazatel

14 6 DYNAMICK ORGANIZACE SOUBOR 14 NEXT na p t et zec, kter bude t pen (po te n NEXT =0) a faktor vyu it pam ti,, co je pom r po tu vlo en ch v t k celkov kapacit souboru. Vlo en v ty s kl em K: procedure INSERT(K:key) m := h u (K) if m<next then m := h u+1 (K) za a v tu do et zce m /* v dy se povede */ while >do vytvo nov et zec s adresou NEXT + N 2 u for v echny v ty z et zce NEXT do if h u+1 (K) 6= NEXT then p esu v tu do nov ho et zce for NEXT := NEXT +1 if NEXT >N 2 u then NEXT := 0 u := u +1 /* while */ 6.4 Skupinov t pen str nek Soubor obsahuje prim rn str nky ulo en fyzicky za sebou a str nky p ete en. Prim rn str nky jsou rozd leny dos skupin po g str nk ch. Adresov prosto prim rn ch str nek je tedy f0 1 ::: s g ; 1g. j-t skupina (pro j = f0 1 ::: s; 1g) je tvo ena str nkami o adres ch j j + s j +2s ::: j +(g ; 1)s. Po et skupin s je parametr, kter se dynamicky m n na po tku p i vytvo en souboru o n z znamech m hodnotus 0 (n s 0 :g:l, kde L je douc po et v t na str nku, nap klad L =80%). V dy po vlo en L z znam dojde k p id n prim rn str nky ke skupin j, na n ukazuje ukazatel t pen sp. V ty ulo en ve str nk ch j-t skupiny (j j + s j + 2s ::: j+(g;1)s) plus p padn v tyve str nk ch p ete en se p erozd l do str nek j j + s j +2s ::: j +(g ; 1)s j + gs aukazatel t pen sp se p esune o skupinu d l. Po roz t pen v ech skupin se soubor rozroste z p vodn ch gs str nek na (g +1)s str nek. Po expanzi je nutn prov st nov rozd len do skupin po g str nk ch, jejich nov po et je s i = bs i;1 (g +1)=gc. t pen prob h nez visle na tom, do kter ch str nek se ukl d. V po et adresy v ty s kl em K:. Je d na inici ln ha ovac funkce H : K!f0 1 ::: gs 0 ; 1g a posloupnost nez visl ch ha ovac ch funkc fh i g i=0 : K!f0 1 ::: g; 1g. Po et proveden ch expanz ozna me jako d, inici ln d =0. h := H(K) s := s 0 for j:=0 to d-1 do h := (h mod s) +h j (K) s s := bs (g +1)=gc if (h mod s) <spthen h := (h mod s) +h d (K) s

15 6 DYNAMICK ORGANIZACE SOUBOR 15 g=4 s=3 sp? t skupina - - str nky p ete en NZI na nult skupin sp t skupina p idan prim.str nka Obr zek 3: Skupinov t pen str nek V pr b hu algoritmu seproch z cel historie, kde kdy byla v ta ulo ena v pr b hu cel existence souboru. Cenou je n r st p stup na disk p i del m et zci str nek p epln n. 6.5 Stromov SOS Vyu vaj k organizaci p stupu k polo k m soubor B-strom. Denice 6.1 B-strom du m, m>2 je strom spl uj c tyto po adavky: 1. Ko en m nejm n dva syny, pokud nen listem. 2. Ka d uzel mimo ko ene a list m nejm n dm=2e syn. 3. V echny cestyzko ene do list jsou stejn dlouh. 4. Je-li n +1po et syn uzlu,pak uzel obsahuje n kl k 1 k 2 ::: k n k 1 < k 2 <:::<k n a n +1ukazatel na syny p 0 p 1 ::: p n. 5. Nech ukazateli p i odpov d podstrom K(p i ) i =0 1 ::: n.pak plat (a) pro 8 hodnotu kl e k v K(p i ; 1) je k k i (b) pro 8 hodnotu kl e k v K(p i ) je k>k i i =1 ::: n. i =1 ::: n 6. Listy strom obsahuj plnou mno inu kl souboru a ukazatele na v ty st mito kl i. Plat dm=2e;1 PKL m ; 1, kde PKL je po et kl list. d m vol me tak aby byla optim ln zapln na str nka, na kterou ukl d me jeden uzel. P i zm n stromu jsou m n ny uzly na cel cest od ko ene. Vyhled v n v ty skl emk: type page = record m: int leaf: bool body: array(1..m) of r type r=record p: pageadr K: key type branch =record h:int /* v ka stromu */

16 6 DYNAMICK ORGANIZACE SOUBOR 16 ptr:array(1..hmax) of pageadr ind: array(1..hmax) of int procedure FIND(root: pageadr, k: key, var s: branch, var found: bool) var pt: pageadr pg:page i:int s.h:=0 pt:=root if pt = nil then found :=false return repeat /* cesta stromem */ s.h:=s.h+1 s.ptr(s.h):=pt getpage(pt,pg) /*str nka do vnit n pam ti */ search(pg,k,found,i,pt) s.ind(s.h):=i /* cesta */ until pg.leaf /* jsme v listu */ 6.6 SOS s v cerozm rnou m kou Tuto organizaci soubor m eme ch pat jako analogii s metodou p ihr dek. Z kladem je v cerozm rn vyhled vac prostor. M sto bod v prostoru uva ujeme v cerozm rn kostky. Body pat c do t e kostky ulo me do t e str nky. P ete e-li str nkajenutn kostku rozp lit nadrovinou rovnob nou s jednou z os vyhled vac ho prostoru. P ete e-li n jak str nka op t, provedeme p l c ez podle dal z os. M ka d l c pole na p slu n kostky m e b t denov na jako n-rozm rn pole ukazatel na str nky. Jako pomocnou strukturu je v hodn m t k ly pro ka dou dimenzi, co jsou meze interval ( ez mezi kostkami).