Maskinorienterad Programmering /2011. Maskinorienterad Programmering 2010/11. Maskinnära programmering C och assemblerspråk
|
|
|
- Martin Ström
- för 9 år sedan
- Visningar:
Transkript
1 Maskinorienterad Programmering 2010/11 Maskinnära programmering C och assemblerspråk Ur innehållet: 32-bitars aritmetik med 16-bitars processor IEEE754 flyttal Maskinnära programmering - C 1 CPU12, ordlängder och datatyper byte long word char c; /* 8-bitars datatyp, storlek byte */ short s; /* 16-bitars datatyp, storlek word */ long l; /* 32-bitars datatyp, storlek long */ int i; /* storlek implementationsberoende */ Lämpliga arbetsregister för short och char är D respektive B 32 bitars datatyper ryms ej i något CPU12-register. Maskinnära programmering - C 2
2 Aritmetiska operatorer (+,-,,/,%) Addition Subtraktion Multiplikation Heltalsdivision Restdivision I den bästa av världar kan alla operatorer användas på godtyckliga sifferkombinationer. Dagens programspråk lever dessvärre inte i den bästa världen Operator OCH datatyp avgör val av maskininstruktion, eller sekvens av instruktioner Maskinnära programmering - C 3 Addition Pseudo språk: char ca,cb,cc; ca = cb + cc; 8bitar LDAB cb ; operand 1 ADDB cc ; adderas STAB ca ; skriv i minnet Pseudo språk: short sa,sb,sc; sa = sb + sc; 16 bitar LDD sb ; operand 1 ADDD sc ; adderas STD sa ; skriv i minnet Pseudo språk: long la,lb,lc; la = lb + lc; 32 bitar LDD lb+2 ; minst signifikanta word av b ADDD lc+2 ; adderas till minst signifikanta word av c STD la+2 ; tilldela, minst signifikanta word LDD lb ; mest signifikanta word av b ADCB lc+1 ; adderas till låg byte av mest signifikanta ; word av c ADCA lc ; adderas till hög byte av mest signifikanta ; word av c STD la ; tilldela, mest signifikanta word Maskinnära programmering - C 4
3 Subtraktion Pseudo språk: char ca,cb,cc; ca = cb - cc; 8bitar LDAB cb ; operand 1 SUBB cc ; subtraheras STAB ca ; skriv i minnet Pseudo språk: short sa,sb,sc; sa = sb - sc; 16 bitar LDD sb ; operand 1 SUBD sc ; subtraheras STD sa ; skriv i minnet Pseudo språk: long la,lb,lc; la = lb - lc; 32 bitar LDD lb+2 ; minst signifikanta word av b SUBD lc+2 ; subtraheras från minst signifikanta word av c STD la+2 ; tilldela, minst signifikanta word LDD lb ; mest signifikanta word av b SBCB lc+1 ; subtrahera låg byte av mest signifikanta ; word av c SBCA lc ; subtrahera hög byte av mest signifikanta ; word av c STD la ; tilldela, mest signifikanta word Maskinnära programmering - C 5 Multiplikation (P=X Y) tal utan tecken, med addition/skift, X>0, Y>0. X=6= Y=5=y 3 y 2 y 1 y 0 =0110 (multiplikand) =0101 (multiplikator) PP(0) 0000 y 0 =1 ADD X skifta PP(1) y 1 =0 ADD skifta PP(2) y 2 =1 ADD X skifta PP(3) y 3 =0 ADD skifta P=PP(4)= = = 30 Maskinnära programmering - C 6
4 Multiplikation (P=X Y) tal med tecken, med addition/aritmetiskt skift, X<0, Y<0. X=-6= =1010 (multiplikand)-x = 0110 Y=-5=y 3 y 2 y 1 y 0 =1011 (multiplikator) Observera hur vi här använder en extra teckenbit, (5-bitars tal i operationen) PP(0) y 0 =1 ADD X skifta aritmetiskt PP(1) y 1 =1 ADD X skifta aritmetiskt PP(2) y 2 =0 ADD skifta aritmetiskt PP(3) y 3 =1 ADD -X skifta aritmetiskt P=PP(4)= = 30 Maskinnära programmering - C 7 Slutsatser: Multiplikation utförs enkelt med grundläggande operationer addition och skift. Vi kan inte använda exakt samma algoritm på tal med respektive utan tecken. Resultatet av en unsigned multiplikation av 2 st. n-bitars tal kräver 2 n bitars register. Resultatet av en signed multiplikation av 2 st n-bitars tal kräver (2 n)-1 bitars register. Maskinnära programmering - C 8
5 Implementering papper och penna-metod long mul32 ( long a, long b) /* Multiplikation med "skift/add" */ long result, mask; int i; mask = 1; result = 0; for( i = 0; i<32; i++ ) if ( mask & a ) result = result + b ; b = b << 1; mask = mask << 1; return result; Fungerande men långsam metod Maskinnära programmering - C 9 HCS12, 8-bitars multiplikation Pseudo språk: unsigned char ca = cb * cc; ca,cb,cc; Assemblerspråk: LDAB cb ; operand 1 LDAA cc ; adderas MUL ; multiplicera STAB ca ; skriv i minnet Endast unsigned Maskinnära programmering - C 10
6 HCS12, 16-bitars multiplikation (unsigned) Pseudo språk: unsigned short ua,ub,uc; ua = ub * uc; Assemblerspråk: LDD ub ; operand 1 LDY uc ; operand 2 EMUL ; multiplicera STD ua ; skriv i minnet Resultat (2n bitar) Y D b 31 b 16 b 15 b 0 Spill om Y!=0 ua Maskinnära programmering - C 11 HCS12, 16-bitars multiplikation (signed) Pseudo språk: short ua,ub,uc; ua = ub * uc; Assemblerspråk: LDD ub ; operand 1 LDY uc ; operand 2 EMULS ; multiplicera STD ua ; skriv i minnet Resultat (2n bitar) Y D b 31 b 16 b 15 b 0 Spill om Y!= b 15 ua Maskinnära programmering - C 12
7 HCS12, 32-bitars multiplikation, med EMUL Antag a, b 32-bitars tal, skriv: a = ah al, b = bh bl, Det gäller då att: a b =(ah al ) (bh bl )= 2 32 ( ah bh )+2 16 ( ah bl + al bh )+(al bl ) Detta är samma sak som: ( ah bh )<<32+(ah bl + al bh )<<16+(al bl ) vi kan därför skriva: a b = ( ah bl + al bh ) < < 16 + ( al bl ) Endast unsigned Maskinnära programmering - C 13 Implementering unsigned long mulu32 ( unsigned long a, unsigned long b) unsigned long result; unsigned short ah,al,bh,bl; ah = (unsigned short )( a >> 16 ); al = (unsigned short ) a ; bh = (unsigned short )( b >> 16 ); bl = (unsigned short ) b ; result = (((unsigned long)( ah*bl + al*bh ))<< 16 ) + ( al*bl ); return result; long muls32 (long a, long b) long r; r = mulu32 ( ((a < 0)? -a : a),((b < 0)? -b : b) ); if ( (a < 0) ^ (b < 0)) return -r; else return r; Maskinnära programmering - C 14
8 Division En division kan skrivas som: X R = Q + Y Y Där: X är dividend Y är divisor Q är kvot, resultatet av heltalsdivisionen X/Y. R är resten, resultatet av modulusdivisionen X mod Y. Av sambandet framgår att resten kan uttryckas: R = X - Q Y Maskinnära programmering - C 15 Exempel: Decimal division, återställning av resten, 3967/15 X = 3967 Y = 15 R = X - Q Y 0264, ,0 3967= Utgångsläge ,0 3967=3967-( ) 15 steg ,0 967=3967-( *10 2 ) 15 steg ,0 67=3967-( ) 15 steg 3-60,0 7,0 7=3967-( ) 15 steg 4-6,0 1,0 1=3967-( ) 15 steg 5 DVS. 3967/15 = 264,4 + 10/ Maskinnära programmering - C 16
9 En divisionsalgoritm Algoritm: Division med återställning R=X-Q Y Q=q 0 q 1 q 2 q n-1 n=antal kvotbitar att beräkna R 0 =X R 1 =R 0 -q 0 Y q 0 =1 om R 1 0, q 0 = 0 annars för i =2..n R i =2 R i -1 -q i Y q i =1 om R i 0, q i = 0 annars Anm: För binära tal reduceras operationen q i Y till ADD Y. Maskinnära programmering - C 17 Implementering: 32-bitars unsigned heltalsdivision unsigned long divu32 (unsigned long a, unsigned long b) unsigned long rest = 0L; unsigned char count = 31; unsigned char c; do if( a & 0x ) c = 1; else c = 0; a = a << 1; rest = rest << 1; if(c) rest = rest 1L; if(rest >= b) rest = rest - b; a = a 1L; while(count--); return a; Maskinnära programmering - C 18
10 Implementering: 32-bitars signed heltalsdivision long divs32 (long a, long b) long r; r = divu32((a < 0? -a : a),(b < 0? -b : b)); if ( (a < 0) ^ (b < 0)) return -r; else return r; Maskinnära programmering - C 19 Implementering: 32-bitars unsigned restdivision unsigned long modu32 (unsigned long a,unsigned long b) unsigned long c = a/b; /* heltalsdivision */ return ( a - b * c ); Resultatet vid signed restdivision är implementationsberoende. Maskinnära programmering - C 20
11 Normaliserat flyttalsformat Ett flyttal uttrycks allmänt som: (-1) S M 2 E där: S (sign) är teckenbiten för flyttalet S=0 anger ett positivt flyttal ty (-1) 0 =1 S=1 anger ett negativt flyttal ty (-1) 1 =-1 M utgör talets mantissa E utgör talets exponent. Exponenten väljs från någon representation med inbyggt tecken. Det är värt att notera att för ett normaliserat flyttal på binär form gäller att: (M) 2 = 1.xxxxx dvs. mantissans första siffra är alltid är 1. Maskinnära programmering - C 21 IEEE-754 flyttal standard specificerar: flyttalsformat noggrannhet i resultat från aritmetiska operationer omvandling mellan heltal och flyttal omvandling till/från andra flyttalsformat avrundning undantagshantering vid operationer på flyttal, exempelvis division med 0 och resultat som ej kan representeras av flyttalsformatet. Standarden definierar fyra olika flyttalsformat: Single format, totalt 32 bitar Double format, totalt 64 bitar Single extended format, antalet bitar är implementationsberoende Double extended format, totalt 80 bitar Maskinnära programmering - C 22
12 IEEE-754 flyttalsformat: MSB S E' F LSB där: F(fractional part) kallas också signifikand, är den normaliserade mantissan 2, dvs. den första (implicita) ettan i mantissan utelämnas i representationen och mantissan skiftas ett steg till vänster. På så sätt uppnår vi ytterligare noggrannhet eftersom vi får ytterligare en siffra i det lagrade talet. E'(karakteristika) är exponenten uttryckt på excess(n) format, n beror på vilket av de fyra formaten som avses. S(sign) är teckenbit för F. Följande tabell anger hur de olika formaten disponeras enligt standarden: Format S E F Single 1 bit 8 bitar excess(127) 23 bitar Double 1 bit 11 bitar excess(1023) 52 bitar Extended 1 bit 15 bitar excess(2047) 64 bitar Maskinnära programmering - C 23 Speciella kodningar Första ordningens singulariteter ±0 MSB LSB S ± MSB LSB S Andra ordningens singulariteter Denormaliserat MSB S F (Not 0) LSB MSB Not a Number S F (Not 0) LSB Maskinnära programmering - C 24
13 Typomvandlingar unsigned long ui; float f; f = ui; /* Heltal till flyttal */ ui = f; /* Flyttal till heltal */ Vissa processorer har en speciell enhet för hantering av flyttal (floating-point coprocessor). Sådana enheter har maskininstruktioner för såväl typomvandlingar som aritmetiska flyttalsoperationer. Maskinnära programmering - C 25 Typomvandlingar Då vi inte har hårdvarustöd för flyttal, dvs. speciella maskininstruktioner, måste vi tillhandahålla programbibliotek för alla operationer på flyttal unsigned long ui; float f; f = ui; /* Heltal till flyttal */ ui = f; /* Flyttal till heltal */ float signed long int (ftol, float to long ) unsigned long int float (ultof, unsigned long to float ) Maskinnära programmering - C 26
14 Typomvandlingar Då vi inte har hårdvarustöd för flyttal, dvs. speciella maskininstruktioner, måste vi tillhandahålla programbibliotek för alla operationer på flyttal unsigned long ui; float f; f = ui; /* Heltal till flyttal */ ui = f; /* Flyttal till heltal */ float signed long int (ftol, float to long ) unsigned long int float (ultof, unsigned long to float ) Maskinnära programmering - C 27 Exempel: Skriv talet (2,52) som ett IEEE754-single format flyttal Omvandling till binär, normaliserad form ger: (2,52) = ( ) Mantissan ska ha totalt 24 bitar (varav 23 lagras) M = ( ) 2 Signifikanden F dvs. den del av mantissan som ska lagras fås om vi stryker den mest signifikanta ettan, vi har då: F = ( ) 2 Exponenten uttrycks av karakteristikan E, excess(127) kod, dvs. E' = E+127, där E betecknar exponenten i talet vi utgår från (2 14 ) dvs. E=14 varför E' = = 141 = ( ) 2 eftersom talet är positivt får vi S = 0. Vi får slutligen: (2,52) =( ) SFP Maskinnära programmering - C 28
15 Algoritm: Omvandling av 32 bitars tal x, utan tecken, till flyttal sfp, sfp x 1. sfp(s)=0; x' x; 2: Bestäm signifikand, bitar x 32.. x 24, ryms ej i mantissan, dividera därför successivt x' med 2, justera exponenten: while( x' > (2 24-1) ) begin sfp(e') sfp(e') + 1; x' ( x' >> 1 ); end 4: Normalisera mantissa, för en normaliserad mantissa ska bit 23 vara 1, om inte så är fallet vänsterskiftar vi x tills detta är sant. Observera att algoritmen här förutsätter att x är skild från 0. while( x' < 2 23 ) begin x' ( x' << 1 ); end Mantissan är nu normaliserad, eftersom den inledande ettan (bit x 23 ) inte lagras) nollställer vi den x 23 0 sfp(m) x 5: Sätt samman flyttalet: sfp ( sfp(s) << 31 ) ( sfp(e ) << 23 ) sfp(m) Maskinnära programmering - C 29 Algoritm: Omvandling av flyttal sfp till 32 bitars tal x, med tecken, x sfp 1. Extrahera tecken sign = sfp(0); 2. Extrahera exponenten ( Karakteristika med subtraherad förskjutning ) exp = sfp(e ) ; Om denna exponent är större än 8 är talet för stort för att kunna representeras if ( exp > 8 ) x LONG_MAX; Om denna exponent är mindre än -25 är talet för litet för att kunna representeras if ( exp < -24 ) x LONG_MIN; 3. Extrahera mantissa ( signifikand med inledande etta ) mant = sfp(m) b Skifta mantissan tills exponenten blir 0 if ( exp >0) (mant << exp ); if ( exp <0) (mant >> exp ); 5. Returnera heltal med rätt tecken if( sign ) x -(mant); else x mant; Maskinnära programmering - C 30
16 Implementering Då alla tre IEEE-formaten finns tillgängliga motsvaras dessa vanligtvis av datatyper enligt : float Single precision (32 bitar) double Double precision (64 bitar) long double Extended precision (80 bitar) Observera dock att detta är implementationsberoende, dvs. det kan skilja mellan olika kompilatorer. Maskinnära programmering - C 31 Implementering: heltal till flyttal union float_long float f; long l; ; float ultof ( unsigned long a ) /* unsigned long till float */ union float_long fl; int exp = ; if ( a==0 ) /* Specialfall, måste testas först */ return 0.0; /* Normalisera */ while (a & 0xFF000000) a = a >> 1; exp = exp + 1; while ( a < 0x ) a = a << 1; exp = exp - 1; a = a & ~0x ; /* nollställ implicit inledande etta */ /* tilldelning till union medlem typ long */ fl.l = (unsigned long) exp<<23 a; return (fl.f); /* returnera som flyttal, teckenbit är 0 */ Maskinnära programmering - C 32
17 Implementering: flyttal till heltal long ftol (float a1) union float_long fl; int exp; char sign=0; long l; fl.f = a1; if (!fl.l) return (0); if( fl.l & 0x ) sign++; exp = (((unsigned long)( fl.l ) >> 23) & (unsigned int) 0x00FF) ; l = ((( fl.l ) & (unsigned long)0x007fffff) 0x ); if (exp > 8) return LONG_MAX; /* största möjliga long int */ if (exp < -25) return LONG_MIN; /* minsta möjliga long int */ /* exponenten ska vara noll */ if( exp > 0 ) /* skifta mantissan till vänster */ l = l << exp; if (exp < 0 ) /* skifta mantissan till höger */ l = l >> -exp; if( sign ) return -l; return l; Maskinnära programmering - C 33 Addition/subtraktion av flyttal 1. Bestäm talens mantissor ur F (dvs. lägg till en etta framför den mest signifikanta biten i respektive F). 2. Bestäm talens exponenter på tvåkomplementsform. 3. Beräkna exponentskillnaden 4. Skifta mantissan för talet med minst exponent höger det antal gånger som exponentskillnaden anger (minns att exponenten anger binärpunkten i flyttalet). 5. Utför addition (subtraktion) av mantissorna efter tecken-överläggning. 6. Normalisera resultatet genom att skifta resultatmantissan samtidigt som resultatexponenten korrigeras. Maskinnära programmering - C 34
18 Exempel: Additionen av 2, , , IEEE-single format flyttal Omvandla talen till binärformat: A=(2,52) =( ) SFP B=(2,52) =( ) SFP 1. och 2. Dela upp talen i tecken, exponent och mantissa: A = (-1) S A M A E A och B = (-1) S B M B E B S A = 0 M A = (1.F) A = ( ) E A = E A = ( ) (dvs = 14) S B = 0 M B = (1.F) B = ( ) E B = E B = ( ) (dvs = 11) 3. Exponentskillnaden (14-11 ) är Skifta talet med minst exponent (M B ) tre steg höger M B = observera att vi tillåter större upplösning hos mantissan under utförande av operationen. Maskinnära programmering - C 35 Exempel: fortsättning 5. Utför additionen, båda talen positiva: M A M B = Normalisera resultatet, i detta fall är resultatet redan i normaliserad form: S R = 0 M R = E R = 14 Vilket nu ger oss representationen: F R = ( ) E R = = ( ) 2 Vi kan slutligen sätta samman resultatet: R = ( ) SFP Maskinnära programmering - C 36
19 Multiplikation/division av flyttal En flyttalsmultiplikation/division utförs betydligt enklare än addition och subtraktion. Vid flyttalsmultiplikation multipliceras mantissorna medan exponenterna adderas. Vid flyttalsdivision divideras mantissorna medan dividendens exponent subtraheras från divisorns exponent, detta kan kortare skrivas som: A B = 2 (E A +E B ) * M A M B respektive A/B = 2 (E A -E B ) * M A / M B Maskinnära programmering - C 37 Implementering: multiplikation 1(3) float mulf (float f1, float f2) union float_long fl1, fl2; unsigned long result; int exp; unsigned long sign; union float_long float f; long l; ; fl1.f = f1; fl2.f = f2; if (!fl1.l!fl2.l) return ( 0.0 ); Maskinnära programmering - C 38
20 Implementering: multiplikation 2(3) /* Bestäm tecken hos resultatet */ sign = (0x & fl1.l) ^ (0x & fl2.l); /* Addition av exponenter, endast en förskjutning i resultatet */ exp = (((unsigned long)(fl1.l >> 23)) & 0xFF) 126; exp = exp + (((unsigned long)( fl2.l >> 23)) & 0xFF); /* Extrahera mantissor, maska in implicit bit */ fl1.l = (((fl1.l) & (unsigned long)0x007fffff) 0x800000); fl2.l = (((fl2.l) & (unsigned long)0x007fffff) 0x800000); /* Multiplicera mantissor */ result = fl1.l * fl2.l; Maskinnära programmering - C 39 Implementering: multiplikation 3(3) /* skifta 32 bitars resultat till 24 bitar och avrunda (uppåt) */ if (result & (unsigned long)0x ) result += 0x80; result >>= 8; result &= ~0x800000; /* nollställ implicit inledande etta */ else /* Vi sparar ytterligare en bits precision här */ result += 0x40; result >>= 7; exp--; /* packa ihop flyttalet */ fl1.l = (unsigned long) exp<<23 result sign ; return (fl1.f); Maskinnära programmering - C 40
21 Testoperationer på flyttal En test av ett IEEE-flyttal kan ge följande resultat: normaliserat denormaliserat plus noll minus noll negativt plus oändligheten minus oändligheten plus Not A Number minus Not A Number Detta kan jämföras med de testresultat vi kan få då ett vanligt heltal testas (Zero eller Negative). En enhet för flyttalsaritmetik har därför ytterligare en uppsättning flaggbitar som är avsedda att återspegla de speciella resultat som fås vid en flyttalstest. Maskinnära programmering - C 41 Jämförelseoperationer på flyttal En flyttalsjämförelse ska, enligt standarden, kunna testa vilkoren: Equal To Greater Than Less Than Unordered Tack vare kodningen blir dessa jämförelseoperationer enkla att implementera. Equal To, indikerar att operanderna är identiska Greater Than/Less Than, indikerar att operand A är större/mindre än operand B, detta inbegriper en teckenöverläggning och om talen har samma tecken kan resterande del av operanderna jämföras på samma sätt som vid heltalsjämförelse. Detta är en av fördelarna med att koda exponenten på excess-form i stället för tvåkomplementsform. Unordered innebär att minst ett av talen är Not A Number. Maskinnära programmering - C 42
Kodningskonventioner (XCC12) Specifikation av strncpy: Övningsexempel: Maskinorienterad Programmering 2011/2012
 Maskinorienterad Programmering 2011/2012 Kodningskonventioner och programbibliotek Ur innehållet: Kodningskonventioner maskinnära programmering i C och assemblerspråk Programbibliotek 32-bitars operationer
Maskinorienterad Programmering 2011/2012 Kodningskonventioner och programbibliotek Ur innehållet: Kodningskonventioner maskinnära programmering i C och assemblerspråk Programbibliotek 32-bitars operationer
Maskinorienterad programmering. Kompendium: Aritmetik för HC12 Roger Johansson, 2013
 Maskinorienterad programmering Kompendium: Aritmetik för HC12 Roger Johansson, 2013 0 Aritmetik för HC12 1 Aritmetik 32 bitars multiplikation/division med 16-bitars processor. IEEE-754, flyttalsrepresentation
Maskinorienterad programmering Kompendium: Aritmetik för HC12 Roger Johansson, 2013 0 Aritmetik för HC12 1 Aritmetik 32 bitars multiplikation/division med 16-bitars processor. IEEE-754, flyttalsrepresentation
Programmering av inbyggda system 2012/2013. Kodningskonventioner och programbibliotek. maskinnära programmering i C och assemblerspråk
 2012/2013 Kodningskonventioner och programbibliotek Ur innehållet: Kodningskonventioner maskinnära programmering i C och assemblerspråk Programbibliotek 32-bitars operationer med 16 bitars processor Kodningskonventioner
2012/2013 Kodningskonventioner och programbibliotek Ur innehållet: Kodningskonventioner maskinnära programmering i C och assemblerspråk Programbibliotek 32-bitars operationer med 16 bitars processor Kodningskonventioner
Föreläsning 8: Aritmetik och stora heltal
 2D1458, Problemlösning och programmering under press Föreläsning 8: Aritmetik och stora heltal Datum: 2006-11-06 Skribent(er): Elias Freider och Ulf Lundström Föreläsare: Per Austrin Den här föreläsningen
2D1458, Problemlösning och programmering under press Föreläsning 8: Aritmetik och stora heltal Datum: 2006-11-06 Skribent(er): Elias Freider och Ulf Lundström Föreläsare: Per Austrin Den här föreläsningen
Datorsystemteknik DVG A03 Föreläsning 3
 Datorsystemteknik DVG A03 Föreläsning 3 Datoraritmetik Större delen av materialet framtaget av :Jan Eric Larsson, Mats Brorsson och Mirec Novak IT-inst LTH Hur stora tal kan vi få med N bitar? Största
Datorsystemteknik DVG A03 Föreläsning 3 Datoraritmetik Större delen av materialet framtaget av :Jan Eric Larsson, Mats Brorsson och Mirec Novak IT-inst LTH Hur stora tal kan vi få med N bitar? Största
Digital- och datorteknik
 Digital- och datorteknik Föreläsning #24 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Allmänt Behovet av processorinstruktioner för multiplikation
Digital- och datorteknik Föreläsning #24 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Allmänt Behovet av processorinstruktioner för multiplikation
Maskinorienterad Programmering 2010/11
 Maskinorienterad Programmering 2010/11 Maskinnära programmering en introduktion Ur innehållet: Assemblatorn, assemblerspråk Datatyper Tilldelningar, l i unära och binära operationer Permanenta/tillfälliga
Maskinorienterad Programmering 2010/11 Maskinnära programmering en introduktion Ur innehållet: Assemblatorn, assemblerspråk Datatyper Tilldelningar, l i unära och binära operationer Permanenta/tillfälliga
Assemblerprogrammets struktur; exempel
 Maskinorienterad Programmering 2010/11 Maskinnära programmering en introduktion Ur innehållet: Assemblatorn, assemblerspråk Datatyper Tilldelningar, l i unära och binära operationer Permanenta/tillfälliga
Maskinorienterad Programmering 2010/11 Maskinnära programmering en introduktion Ur innehållet: Assemblatorn, assemblerspråk Datatyper Tilldelningar, l i unära och binära operationer Permanenta/tillfälliga
Dagens föreläsning. Repetition. Repetition - Programmering i C. Repetition - Vad C består av. Repetition Ett första C-program
 Dagens föreläsning Programmeringsteknik för Ingenjörer VT05 Föreläsning 3-4 Repetition Datatyper Uttryck Operatorer Satser Algoritmer Programmeringsteknik VT05 2 Repetition Repetition - Programmering i
Dagens föreläsning Programmeringsteknik för Ingenjörer VT05 Föreläsning 3-4 Repetition Datatyper Uttryck Operatorer Satser Algoritmer Programmeringsteknik VT05 2 Repetition Repetition - Programmering i
IE1205 Digital Design: F6 : Digital aritmetik 2
 IE1205 Digital Design: F6 : Digital aritmetik 2 Talrepresentationer Ett tal kan representeras binärt på många sätt. De vanligaste taltyperna som skall representeras är: Heltal, positiva heltal (eng. integers)
IE1205 Digital Design: F6 : Digital aritmetik 2 Talrepresentationer Ett tal kan representeras binärt på många sätt. De vanligaste taltyperna som skall representeras är: Heltal, positiva heltal (eng. integers)
Datoraritmetik. Binär addition papper och penna metod. Binär subtraktion papper och penna metod. Binär multiplikation papper och penna metod
 inär addition papper och penna metod Dagens föreläsning: Lärobok, kapitel rbetsbok, kapitel Ur innehållet: hur man adderar och subtraherar tal i det binära talsystemet hur man kan koda om negativa binära
inär addition papper och penna metod Dagens föreläsning: Lärobok, kapitel rbetsbok, kapitel Ur innehållet: hur man adderar och subtraherar tal i det binära talsystemet hur man kan koda om negativa binära
I denna laboration undersöker vi hur aritmetiska beräkningar utförs. Vi tittar på olika variabeltyper: 8-bitars, 16-bitars, 32-bitars och flyttal.
 Laboration:. Jämförelser mellan assembler och C. I denna laboration undersöker vi hur aritmetiska beräkningar utförs. Vi tittar på olika variabeltyper: 8-bitars, 16-bitars, 32-bitars och flyttal. Förberedelser:
Laboration:. Jämförelser mellan assembler och C. I denna laboration undersöker vi hur aritmetiska beräkningar utförs. Vi tittar på olika variabeltyper: 8-bitars, 16-bitars, 32-bitars och flyttal. Förberedelser:
Dagens föreläsning. Repetition. Repetition - Programmering i C. Repetition - Vad C består av. Repetition Ett första C-program
 Dagens föreläsning Programmeringsteknik för Ingenjörer VT05 Föreläsning 3-4 Repetition Datatyper Uttryck Operatorer Satser Algoritmer Programmeringsteknik för ingenjörer, VT06 2 Repetition Repetition -
Dagens föreläsning Programmeringsteknik för Ingenjörer VT05 Föreläsning 3-4 Repetition Datatyper Uttryck Operatorer Satser Algoritmer Programmeringsteknik för ingenjörer, VT06 2 Repetition Repetition -
Föreläsning 8: Aritmetik och stora heltal
 DD2458, Problemlösning och programmering under press Föreläsning 8: Aritmetik och stora heltal Datum: 2007-11-06 Skribent(er): Martin Tittenberger, Patrik Lilja Föreläsare: Per Austrin Denna föreläsning
DD2458, Problemlösning och programmering under press Föreläsning 8: Aritmetik och stora heltal Datum: 2007-11-06 Skribent(er): Martin Tittenberger, Patrik Lilja Föreläsare: Per Austrin Denna föreläsning
F2 Datarepresentation talbaser, dataformat och teckenkodning EDAA05 Datorer i system! Roger Henriksson!
 F2 Datarepresentation talbaser, dataformat och teckenkodning EDAA05 Roger Henriksson Von Neumann-arkitekturen Gemensamt minne för programinstruktioner och data. Sekventiell exekvering av instruktionerna.
F2 Datarepresentation talbaser, dataformat och teckenkodning EDAA05 Roger Henriksson Von Neumann-arkitekturen Gemensamt minne för programinstruktioner och data. Sekventiell exekvering av instruktionerna.
Enkla datatyper minne
 Enkla datatyper minne 143.56 sant Sonja A falskt 18 1999-10-29 Bertil Gralvik, KTH Ingenjörsskolan 1 Addera två tal Algoritmen Summera tal Mata in två tal Beräkna Skriv ut resultat Mata in tal 1 Mata in
Enkla datatyper minne 143.56 sant Sonja A falskt 18 1999-10-29 Bertil Gralvik, KTH Ingenjörsskolan 1 Addera två tal Algoritmen Summera tal Mata in två tal Beräkna Skriv ut resultat Mata in tal 1 Mata in
Flyttal kan också hantera vanliga tal som både 16- och 32-bitars dataregister hanterar.
 FLYTTAL REAL Flyttal används i datorsystem för s k flytande beräkning vilket innebär att decimalkommat inte har någon fix (fast) position. Flyttal består av 2 delar (mantissa och exponent). När ett datorsystem
FLYTTAL REAL Flyttal används i datorsystem för s k flytande beräkning vilket innebär att decimalkommat inte har någon fix (fast) position. Flyttal består av 2 delar (mantissa och exponent). När ett datorsystem
Binär addition papper och penna metod
 EDA4 - Digital och Datorteknik 9/ EDA 4 - Digital och Datorteknik 8/9 Dagens föreläsning: Aritmetik, lärobok kapitel 6 Ur innehållet: hur man adderar och subtraherar tal i det binära talsystemet hur man
EDA4 - Digital och Datorteknik 9/ EDA 4 - Digital och Datorteknik 8/9 Dagens föreläsning: Aritmetik, lärobok kapitel 6 Ur innehållet: hur man adderar och subtraherar tal i det binära talsystemet hur man
ÖH kod. ( en variant av koden används i dag till butikernas streck-kod ) William Sandqvist
 ÖH 8.4 7-4-2-1 kod Kodomvandlare 7-4-2-1-kod till BCD-kod. Vid kodning av siffrorna 0 9 användes förr ibland en kod med vikterna 7-4-2-1 i stället för den binära kodens vikter 8-4-2-1. I de fall då en
ÖH 8.4 7-4-2-1 kod Kodomvandlare 7-4-2-1-kod till BCD-kod. Vid kodning av siffrorna 0 9 användes förr ibland en kod med vikterna 7-4-2-1 i stället för den binära kodens vikter 8-4-2-1. I de fall då en
Det finns en hemsida. Adressen är http://www.idt.mdh.se/kurser/ct3760/
 CT3760 Mikrodatorteknik Föreläsning 1 Torsdag 2005-08-25 Upprop. Det finns en hemsida. Adressen är http://www.idt.mdh.se/kurser/ct3760/ Kurslitteratur är Per Foyer Mikroprocessorteknik. Finns på bokhandeln.
CT3760 Mikrodatorteknik Föreläsning 1 Torsdag 2005-08-25 Upprop. Det finns en hemsida. Adressen är http://www.idt.mdh.se/kurser/ct3760/ Kurslitteratur är Per Foyer Mikroprocessorteknik. Finns på bokhandeln.
Föreläsning 8: Aritmetik I
 DD2458, Problemlösning och programmering under press Föreläsning 8: Aritmetik I Datum: 2009-11-03 Skribent(er): Andreas Sehr, Carl Bring, Per Almquist Föreläsare: Fredrik Niemelä 1 Flyttal Att representera
DD2458, Problemlösning och programmering under press Föreläsning 8: Aritmetik I Datum: 2009-11-03 Skribent(er): Andreas Sehr, Carl Bring, Per Almquist Föreläsare: Fredrik Niemelä 1 Flyttal Att representera
Grunderna i stegkodsprogrammering
 Kapitel 1 Grunderna i stegkodsprogrammering Följande bilaga innehåller grunderna i stegkodsprogrammering i den form som används under kursen. Vi kommer att kort diskutera olika datatyper, villkor, operationer
Kapitel 1 Grunderna i stegkodsprogrammering Följande bilaga innehåller grunderna i stegkodsprogrammering i den form som används under kursen. Vi kommer att kort diskutera olika datatyper, villkor, operationer
Assemblerprogrammering för ARM del 1
 Assemblerprogrammering för ARM del 1 Ur innehållet: Ordlängder och heltalstyper i C Variabeldeklarationer Programkonstruktioner Tilldelningar Uttrycksevaluering Ovillkorliga programflöden Funktion med
Assemblerprogrammering för ARM del 1 Ur innehållet: Ordlängder och heltalstyper i C Variabeldeklarationer Programkonstruktioner Tilldelningar Uttrycksevaluering Ovillkorliga programflöden Funktion med
Språket Python - Del 1 Grundkurs i programmering med Python
 Hösten 2009 Dagens lektion Ett programmeringsspråks byggstenar Några inbyggda datatyper Styra instruktionsflödet Modulen sys 2 Ett programmeringsspråks byggstenar 3 ETT PROGRAMMERINGSSPRÅKS BYGGSTENAR
Hösten 2009 Dagens lektion Ett programmeringsspråks byggstenar Några inbyggda datatyper Styra instruktionsflödet Modulen sys 2 Ett programmeringsspråks byggstenar 3 ETT PROGRAMMERINGSSPRÅKS BYGGSTENAR
IE1204 Digital Design
 IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska kretsar F7 F8 Ö4 F9 Ö5 Multiplexor KK2 LAB2 Låskretsar, vippor, FSM
IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska kretsar F7 F8 Ö4 F9 Ö5 Multiplexor KK2 LAB2 Låskretsar, vippor, FSM
Assemblerprogrammering för ARM del 1
 Assemblerprogrammering för ARM del 1 Ur innehållet: Assemblerspråk Ordlängder och heltalstyper i C Variabeldeklarationer Programkonstruktioner Tilldelningar Uttrycksevaluering Ovillkorliga programflöden
Assemblerprogrammering för ARM del 1 Ur innehållet: Assemblerspråk Ordlängder och heltalstyper i C Variabeldeklarationer Programkonstruktioner Tilldelningar Uttrycksevaluering Ovillkorliga programflöden
Assemblerprogrammering för HCS12
 Assemblerprogrammering för HCS12 Ur innehållet: Assemblatorn, assemblerspråk Ordlängder och datatyper Tilldelningar, binära operationer Registerspill, permanenta och tillfälliga variabler Programkonstruktioner
Assemblerprogrammering för HCS12 Ur innehållet: Assemblatorn, assemblerspråk Ordlängder och datatyper Tilldelningar, binära operationer Registerspill, permanenta och tillfälliga variabler Programkonstruktioner
Programmera i C Varför programmera i C när det finns språk som Simula och Pascal??
 Programmera i C Varför programmera i C när det finns språk som Simula och Pascal?? C är ett språk på relativt låg nivå vilket gör det möjligt att konstruera effektiva kompilatorer, samt att komma nära
Programmera i C Varför programmera i C när det finns språk som Simula och Pascal?? C är ett språk på relativt låg nivå vilket gör det möjligt att konstruera effektiva kompilatorer, samt att komma nära
Övning1 Datorteknik, HH vt12 - Talsystem, logik, minne, instruktioner, assembler
 Övning1 Datorteknik, HH vt12 - Talsystem, logik, minne, instruktioner, assembler Talsystem Talsystem - binära tal F1.1) 2 n stycken tal från 0 till 2 n 1 F1.2) 9 bitar (512 kombinationer) Talsystem - 2-
Övning1 Datorteknik, HH vt12 - Talsystem, logik, minne, instruktioner, assembler Talsystem Talsystem - binära tal F1.1) 2 n stycken tal från 0 till 2 n 1 F1.2) 9 bitar (512 kombinationer) Talsystem - 2-
Moment 2 - Digital elektronik. Föreläsning 1 Binära tal och logiska grindar
 Moment 2 - Digital elektronik Föreläsning 1 Binära tal och logiska grindar Jan Thim 1 F1: Binära tal och logiska grindar Innehåll: Introduktion Talsystem och koder Räkna binärt Logiska grindar Boolesk
Moment 2 - Digital elektronik Föreläsning 1 Binära tal och logiska grindar Jan Thim 1 F1: Binära tal och logiska grindar Innehåll: Introduktion Talsystem och koder Räkna binärt Logiska grindar Boolesk
Datatyper och kontrollstrukturer. Skansholm: Kapitel 2) De åtta primitiva typerna. Typ Innehåll Defaultvärde Storlek
 De åtta primitiva typerna Java, datatyper, kontrollstrukturer Skansholm: Kapitel 2) Uppsala Universitet 11 mars 2005 Typ Innehåll Defaultvärde Storlek boolean true, false false 1 bit char Tecken \u000
De åtta primitiva typerna Java, datatyper, kontrollstrukturer Skansholm: Kapitel 2) Uppsala Universitet 11 mars 2005 Typ Innehåll Defaultvärde Storlek boolean true, false false 1 bit char Tecken \u000
SMD 134 Objektorienterad programmering
 SMD 134 Objektorienterad programmering Dagens agenda: Typer i Java: primitiva datatyperna, referenstyper Variabler och variabeltilldelningar med primitiva typer Konstanter av de olika typerna. Heltalsräkning
SMD 134 Objektorienterad programmering Dagens agenda: Typer i Java: primitiva datatyperna, referenstyper Variabler och variabeltilldelningar med primitiva typer Konstanter av de olika typerna. Heltalsräkning
F2 Datarepresentation talbaser, dataformat och teckenkodning
 F2 Datarepresentation talbaser, dataformat och teckenkodning EDAA05 Roger Henriksson Jonas Wisbrant Datarepresentation I en dator lagras och behandlas all information i form av binära tal ettor och nollor.
F2 Datarepresentation talbaser, dataformat och teckenkodning EDAA05 Roger Henriksson Jonas Wisbrant Datarepresentation I en dator lagras och behandlas all information i form av binära tal ettor och nollor.
Assemblerprogrammets. struktur; exempel
 Assemblerprogrammering för HCS12 Absolut assemblering Ur innehållet: Assemblatorn, assemblerspråk Ordlängder och datatyper Tilldelningar, binära operationer Registerspill, permanenta och tillfälliga variabler
Assemblerprogrammering för HCS12 Absolut assemblering Ur innehållet: Assemblatorn, assemblerspråk Ordlängder och datatyper Tilldelningar, binära operationer Registerspill, permanenta och tillfälliga variabler
Programmeringsteknik med C och Matlab
 Programmeringsteknik med C och Matlab Kapitel 2: C-programmeringens grunder Henrik Björklund Umeå universitet Björklund (UmU) Programmeringsteknik 1 / 32 Mer organisatoriskt Imorgon: Datorintro i lab Logga
Programmeringsteknik med C och Matlab Kapitel 2: C-programmeringens grunder Henrik Björklund Umeå universitet Björklund (UmU) Programmeringsteknik 1 / 32 Mer organisatoriskt Imorgon: Datorintro i lab Logga
0.1. INTRODUKTION 1. 2. Instruktionens opcode decodas till en språknivå som är förstålig för ALUn.
 0.1. INTRODUKTION 1 0.1 Introduktion Datorns klockfrekvens mäts i cykler per sekund, eller hertz. En miljon klockcykler är en megahertz, MHz. L1 cache (level 1) är den snabbaste formen av cache och sitter
0.1. INTRODUKTION 1 0.1 Introduktion Datorns klockfrekvens mäts i cykler per sekund, eller hertz. En miljon klockcykler är en megahertz, MHz. L1 cache (level 1) är den snabbaste formen av cache och sitter
Talrepresentation. Ett tal kan representeras binärt på många sätt. De vanligaste taltyperna som skall representeras är:
 Talrepresentation Ett tal kan representeras inärt på många sätt. De vanligaste taltyperna som skall representeras är: Heltal, positiva heltal (eng. integers ett-komplementet, två-komplementet, sign-magnitude
Talrepresentation Ett tal kan representeras inärt på många sätt. De vanligaste taltyperna som skall representeras är: Heltal, positiva heltal (eng. integers ett-komplementet, två-komplementet, sign-magnitude
Programmering A. Johan Eliasson johane@cs.umu.se
 Programmering A Johan Eliasson johane@cs.umu.se 1 Jag Undervisar mest grundläggande programmering på Institutionen för datavetensakap Applikationsutveckling för iphone Applikationsutveckling i Java Datastrukturer
Programmering A Johan Eliasson johane@cs.umu.se 1 Jag Undervisar mest grundläggande programmering på Institutionen för datavetensakap Applikationsutveckling för iphone Applikationsutveckling i Java Datastrukturer
Datorsystem. Övningshäfte. Senast uppdaterad: 22 oktober 2012 Version 1.0d
 Datorsystem Övningshäfte Senast uppdaterad: 22 oktober 2012 Version 1.0d Innehåll Innehåll i 1 Introduktion 1 1.1 Errata............................................... 1 2 Datorns grunder 2 2.1 Övningsuppgifter.........................................
Datorsystem Övningshäfte Senast uppdaterad: 22 oktober 2012 Version 1.0d Innehåll Innehåll i 1 Introduktion 1 1.1 Errata............................................... 1 2 Datorns grunder 2 2.1 Övningsuppgifter.........................................
Data, typ, selektion, iteration
 Data, typ, selektion, iteration En programmeringkurs på halvfart IDT, MDH ttp://www.negative-g.com/nolimits/no%20limits%20defunct%20coasters.htm 1 Dagens agenda Talrepresentation Typkonvertering Sekvens
Data, typ, selektion, iteration En programmeringkurs på halvfart IDT, MDH ttp://www.negative-g.com/nolimits/no%20limits%20defunct%20coasters.htm 1 Dagens agenda Talrepresentation Typkonvertering Sekvens
Datoraritmetik. Från labben. Från labben. Några exempel
 Datoraritmetik Beräkningsvetenskap I Från labben Två huvudtyper av fel: diskretiseringsfel och avrundningsfel Olika sätt att mäta fel: relativt fel, absolut fel Begreppen ε M, Inf, NaN, overflow, underflow,
Datoraritmetik Beräkningsvetenskap I Från labben Två huvudtyper av fel: diskretiseringsfel och avrundningsfel Olika sätt att mäta fel: relativt fel, absolut fel Begreppen ε M, Inf, NaN, overflow, underflow,
Inledande programmering med C# (1DV402) 27+15=42 1 (22)
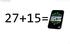 27+15=42 1 (22) Variabler Upphovsrätt för detta verk Detta verk är framtaget i anslutning till kursen Inledande programmering med C# vid Linnéuniversitetet. Du får använda detta verk så här: Allt innehåll
27+15=42 1 (22) Variabler Upphovsrätt för detta verk Detta verk är framtaget i anslutning till kursen Inledande programmering med C# vid Linnéuniversitetet. Du får använda detta verk så här: Allt innehåll
1 Datorn som miniräknare. 1.1 Räkneoperationer. 1.2 Variabler
 1 Datorn som miniräknare I detta avsnitt tas upp hur man kan skriva program som utför enkla räkneoperationer och skriver resultat på skärmen. Syftet är i huvudsak att se hur flera satser kan bygga upp
1 Datorn som miniräknare I detta avsnitt tas upp hur man kan skriva program som utför enkla räkneoperationer och skriver resultat på skärmen. Syftet är i huvudsak att se hur flera satser kan bygga upp
Objektorienterad programmering Föreläsning 4
 Objektorienterad programmering Föreläsning 4 Copyright Mahmud Al Hakim mahmud@dynamicos.se www.webbacademy.se Agenda Introduktion till objektorientering Klasser och Objekt Instansvariabler Metoder Introduktion
Objektorienterad programmering Föreläsning 4 Copyright Mahmud Al Hakim mahmud@dynamicos.se www.webbacademy.se Agenda Introduktion till objektorientering Klasser och Objekt Instansvariabler Metoder Introduktion
Exempelsamling Assemblerprogrammering
 Exempelsamling Assemblerprogrammering I uppgifterna nedan utgå från följande programskelett: #include.data var1:.word 12 var2:.word 19 sum: prod:.float 0.set noreorder.text.globl start.ent start
Exempelsamling Assemblerprogrammering I uppgifterna nedan utgå från följande programskelett: #include.data var1:.word 12 var2:.word 19 sum: prod:.float 0.set noreorder.text.globl start.ent start
F2 Binära tal EDA070 Datorer och datoranvändning
 Datarepresentation F2 Binära tal EDA070 Roger Henriksson I en dator lagras och behandlas all information i form av binära tal ettor och nollor. En binär siffra kallas för en bit BInary digit. Ett antal
Datarepresentation F2 Binära tal EDA070 Roger Henriksson I en dator lagras och behandlas all information i form av binära tal ettor och nollor. En binär siffra kallas för en bit BInary digit. Ett antal
F2 Datatyper och variabler. ID1004 Objektorienterad programmering Fredrik Kilander
 F2 Datatyper och variabler ID1004 Objektorienterad programmering Fredrik Kilander fki@kth.se Datatyper Java är ett starkt typat språk Varje slags data har en datatyp Datatyp Javasyntax Exempel Teckensträng
F2 Datatyper och variabler ID1004 Objektorienterad programmering Fredrik Kilander fki@kth.se Datatyper Java är ett starkt typat språk Varje slags data har en datatyp Datatyp Javasyntax Exempel Teckensträng
Per Holm Lågnivåprogrammering 2014/15 24 / 177. int och double = = 2, 147, 483, 647
 Lågnivåprogrammering Föreläsning 2 Lågnivåprogrammering Förberedelse inför laboration 2. Maskinspråk, assemblerspråk Talrepresentation En enkel dator, komponenter Instruktionsformat, instruktionscykel
Lågnivåprogrammering Föreläsning 2 Lågnivåprogrammering Förberedelse inför laboration 2. Maskinspråk, assemblerspråk Talrepresentation En enkel dator, komponenter Instruktionsformat, instruktionscykel
Institutionen för elektro- och informationsteknologi, LTH
 Datorteknik Föreläsning 1 Kursinformation, introduktion, aritmetik Innehåll Hur kan en dator se ut? Vilka är kursens mål? Hur är denna kurs upplagd? Hur ser ett datorsystem ut från applikation till hårdvara?
Datorteknik Föreläsning 1 Kursinformation, introduktion, aritmetik Innehåll Hur kan en dator se ut? Vilka är kursens mål? Hur är denna kurs upplagd? Hur ser ett datorsystem ut från applikation till hårdvara?
Innehåll. Datorteknik. Abstraktionsnivå 1. Spelkonsol - blockschema. Spelkonsol abstraktionsnivå 2. Abstraktionsnivå 2
 Innehåll Datorteknik Föreläsning 1 Hur kan en dator se ut? Vilka är kursens mål? Hur är denna kurs upplagd? Hur ser ett datorsystem ut från applikation till hårdvara? Vilken är relationen mellan programvara
Innehåll Datorteknik Föreläsning 1 Hur kan en dator se ut? Vilka är kursens mål? Hur är denna kurs upplagd? Hur ser ett datorsystem ut från applikation till hårdvara? Vilken är relationen mellan programvara
Tentamen i. för D1 m fl, även distanskursen. fredag 13 januari 2012
 1 of 6 Örebro universitet Akademin för naturvetenskap och teknik Thomas Padron-McCarthy (thomas.padron-mccarthy@oru.se) Tentamen i Programmering grundkurs och Programmering C för D1 m fl, även distanskursen
1 of 6 Örebro universitet Akademin för naturvetenskap och teknik Thomas Padron-McCarthy (thomas.padron-mccarthy@oru.se) Tentamen i Programmering grundkurs och Programmering C för D1 m fl, även distanskursen
Digital- och datorteknik
 Digital- och datorteknik Föreläsning #7 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Aritmetik i digitala system Speciella egenskaper: Systemet
Digital- och datorteknik Föreläsning #7 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Aritmetik i digitala system Speciella egenskaper: Systemet
Övning1 Datorteknik, HH vt12 - Talsystem, logik, minne, instruktioner, assembler
 Övning1 Datorteknik, HH vt12 - Talsystem, logik, minne, instruktioner, assembler Talsystem Talsystem - binära tal F1.1. Hur många unsigned integers kan man göra med n bitar? Vilket talområde får dessa
Övning1 Datorteknik, HH vt12 - Talsystem, logik, minne, instruktioner, assembler Talsystem Talsystem - binära tal F1.1. Hur många unsigned integers kan man göra med n bitar? Vilket talområde får dessa
Digital- och datorteknik
 Digital- och datorteknik Föreläsning #7 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Speciella egenskaper: Systemet arbetar med kodord (s k
Digital- och datorteknik Föreläsning #7 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Speciella egenskaper: Systemet arbetar med kodord (s k
DE FYRA RÄKNESÄTTEN (SID. 11) MA1C: AVRUNDNING
 DE FYRA RÄKNESÄTTEN (SID. 11) 1. Benämn med korrekt terminologi talen som: adderas. subtraheras. multipliceras. divideras.. Addera 10 och. Dividera sedan med. Subtrahera 10 och. Multiplicera sedan med..
DE FYRA RÄKNESÄTTEN (SID. 11) 1. Benämn med korrekt terminologi talen som: adderas. subtraheras. multipliceras. divideras.. Addera 10 och. Dividera sedan med. Subtrahera 10 och. Multiplicera sedan med..
TDIU01 - Programmering i C++, grundkurs
 TDIU01 - Programmering i C++, grundkurs Sammanfattning period 1 Eric Elfving Institutionen för datavetenskap 1 oktober 2013 Översikt Ett C++-programs uppbyggnad Variabler Datatyper Satser Uttryck Funktioner
TDIU01 - Programmering i C++, grundkurs Sammanfattning period 1 Eric Elfving Institutionen för datavetenskap 1 oktober 2013 Översikt Ett C++-programs uppbyggnad Variabler Datatyper Satser Uttryck Funktioner
Grunderna i SQL del 1
 Grunderna i SQL del 1 1. SELECT-frågor 2. SELECT 3. WHERE 4. ORDER BY 5. Inre join 6. Yttre join 7. Andra typer av join 8. Union 9. Aggregatfunktioner 10. Gruppera och summera Kap. 3 Kap. 4 Kap. 5 utom
Grunderna i SQL del 1 1. SELECT-frågor 2. SELECT 3. WHERE 4. ORDER BY 5. Inre join 6. Yttre join 7. Andra typer av join 8. Union 9. Aggregatfunktioner 10. Gruppera och summera Kap. 3 Kap. 4 Kap. 5 utom
Klassdeklaration. Metoddeklaration. Parameteröverföring
 Syntax: Class Declaration Modifier Class Body Basic Class Member Klassdeklaration class Class Member Field Declaration Constructor Declaration Method Declaration Identifier Class Associations Motsvarar
Syntax: Class Declaration Modifier Class Body Basic Class Member Klassdeklaration class Class Member Field Declaration Constructor Declaration Method Declaration Identifier Class Associations Motsvarar
Objektorienterad programmering D2
 Objektorienterad programmering D2 Laboration nr 2. Syfte Att få förståelse för de grundläggande objektorienterade begreppen. Redovisning Källkoden för uppgifterna skall skickas in via Fire. För senaste
Objektorienterad programmering D2 Laboration nr 2. Syfte Att få förståelse för de grundläggande objektorienterade begreppen. Redovisning Källkoden för uppgifterna skall skickas in via Fire. För senaste
Assemblerprogrammering för ARM del 2
 Assemblerprogrammering för ARM del 2 Ur innehållet Programflöde Subrutiner, parametrar och returvärden Tillfälliga (lokala) variabler Läsanvisningar: Arbetsbok kap 2 Quick-guide, instruktionslistan Assemblerprogrammering
Assemblerprogrammering för ARM del 2 Ur innehållet Programflöde Subrutiner, parametrar och returvärden Tillfälliga (lokala) variabler Läsanvisningar: Arbetsbok kap 2 Quick-guide, instruktionslistan Assemblerprogrammering
Assemblerprogrammering för ARM del 1
 Assemblerprogrammering för ARM del 1 Ur innehållet: Assemblerspråk Ordlängder och datatyper Variabeldeklarationer Programkonstruktioner Tilldelningar Uttrycksevaluering Ovillkorliga programflöden Läsanvisningar:
Assemblerprogrammering för ARM del 1 Ur innehållet: Assemblerspråk Ordlängder och datatyper Variabeldeklarationer Programkonstruktioner Tilldelningar Uttrycksevaluering Ovillkorliga programflöden Läsanvisningar:
Institutionen för datavetenskap 2014/15
 LUNDS TEKNISKA HÖGSKOLA Datorer och datoranvändning Institutionen för datavetenskap 2014/15 ME en dator 1 Inledning ME är en påhittad dator, men den har likheter med riktiga datorer: det finns ett maskinspråk
LUNDS TEKNISKA HÖGSKOLA Datorer och datoranvändning Institutionen för datavetenskap 2014/15 ME en dator 1 Inledning ME är en påhittad dator, men den har likheter med riktiga datorer: det finns ett maskinspråk
Datorsystemteknik D. Lösningar till tentamen i kursen EDA330 14/1 2000
 1(6) Lösningar till tentamen i kursen EDA330 Datorsystemteknik D 14/1 2000 Följande är skisser till lösningar av uppgifterna. Full poäng på en uppgift kräver i de flesta fall en något fylligare motivering.
1(6) Lösningar till tentamen i kursen EDA330 Datorsystemteknik D 14/1 2000 Följande är skisser till lösningar av uppgifterna. Full poäng på en uppgift kräver i de flesta fall en något fylligare motivering.
Tentamen. Datorteknik Y, TSEA28
 Tentamen Datorteknik Y, TSEA28 Datum 2015-08-18 Lokal TERE, TER4 Tid 14-18 Kurskod TSEA28 Provkod TEN1 Kursnamn Provnamn Datorteknik Y Skriftlig tentamen Institution ISY Antal frågor 7 Antal sidor (inklusive
Tentamen Datorteknik Y, TSEA28 Datum 2015-08-18 Lokal TERE, TER4 Tid 14-18 Kurskod TSEA28 Provkod TEN1 Kursnamn Provnamn Datorteknik Y Skriftlig tentamen Institution ISY Antal frågor 7 Antal sidor (inklusive
Elektroteknik MF1016 föreläsning 9 MF1017 föreläsning 7 Mikrodatorteknik
 Elektroteknik MF1016 föreläsning 9 MF1017 föreläsning 7 - Inbyggda system - Analog till digital signal - Utvecklingssystem, målsystem - Labutrustningen - Uppbyggnad av mikrokontroller - Masinkod, assemblerkod
Elektroteknik MF1016 föreläsning 9 MF1017 föreläsning 7 - Inbyggda system - Analog till digital signal - Utvecklingssystem, målsystem - Labutrustningen - Uppbyggnad av mikrokontroller - Masinkod, assemblerkod
Introduktion till Datalogi DD1339. Föreläsning 2 22 sept 2014
 Introduktion till Datalogi DD1339 Föreläsning 2 22 sept 2014 Namn Fält1 Fält2 Fält3 Metod1 Metod2 Metod3 Metod4 public class { public class { Åtkomst, public betyder fullt tillgänglig utifrån public
Introduktion till Datalogi DD1339 Föreläsning 2 22 sept 2014 Namn Fält1 Fält2 Fält3 Metod1 Metod2 Metod3 Metod4 public class { public class { Åtkomst, public betyder fullt tillgänglig utifrån public
GRUNDER I VHDL. Innehåll. Komponentmodell Kodmodell Entity Architecture Identifierare och objekt Operationer för jämförelse
 GRUNDER I VHDL Innehåll Komponentmodell Kodmodell Entity Architecture Identifierare och objekt Operationer för jämförelse KOMPONENTMODELL Modell för att beskriva komponenter Externt interface Intern funktion
GRUNDER I VHDL Innehåll Komponentmodell Kodmodell Entity Architecture Identifierare och objekt Operationer för jämförelse KOMPONENTMODELL Modell för att beskriva komponenter Externt interface Intern funktion
Lösningar till tentauppgifterna sätts ut på kurssidan på nätet idag kl 19. Omtentamen i Programmering C, 5p, fristående, kväll, 040110.
 1(8) ÖREBRO UNIVERSITET INSTITUTIONEN FÖR TEKNIK Lösningar till tentauppgifterna sätts ut på kurssidan på nätet idag kl 19. Denna tenta kommer att vara färdigrättad On 14/1-04 och kan då hämtas på mitt
1(8) ÖREBRO UNIVERSITET INSTITUTIONEN FÖR TEKNIK Lösningar till tentauppgifterna sätts ut på kurssidan på nätet idag kl 19. Denna tenta kommer att vara färdigrättad On 14/1-04 och kan då hämtas på mitt
Digital Aritmetik Unsigned Integers Signed Integers"
 Digital Aritmetik Unsigned Integers Signed Integers" Slides! Per Lindgren! EISLAB! Per.Lindgren@ltu.se! Original Slides! Ingo Sander! KTH/ICT/ES! ingo@kth.se! Talrepresentationer" Ett tal kan representeras
Digital Aritmetik Unsigned Integers Signed Integers" Slides! Per Lindgren! EISLAB! Per.Lindgren@ltu.se! Original Slides! Ingo Sander! KTH/ICT/ES! ingo@kth.se! Talrepresentationer" Ett tal kan representeras
F5: Högnivåprogrammering
 F5: Högnivåprogrammering Parameteröverföring Koppling mellan låg- och högnivåprogrammering Lokala variabler Heapen Datatyper 1 Subrutin, parameteröverföring: 1(3) Via register genom värde Skicka data via
F5: Högnivåprogrammering Parameteröverföring Koppling mellan låg- och högnivåprogrammering Lokala variabler Heapen Datatyper 1 Subrutin, parameteröverföring: 1(3) Via register genom värde Skicka data via
F5: Högnivåprogrammering
 1 F5: Högnivåprogrammering Parameteröverföring Koppling mellan låg- och högnivåprogrammering Lokala variabler Heapen Datatyper 1 Subrutin, parameteröverföring: 1(3) Via register genom värde Skicka data
1 F5: Högnivåprogrammering Parameteröverföring Koppling mellan låg- och högnivåprogrammering Lokala variabler Heapen Datatyper 1 Subrutin, parameteröverföring: 1(3) Via register genom värde Skicka data
6. Ge korta beskrivningar av följande begrepp a) texteditor b) kompilator c) länkare d) interpretator e) korskompilator f) formatterare ( pretty-print
 Datalogi I, grundkurs med Java 10p, 2D4112, 2002-2003 Exempel på tentafrågor på boken Lunell: Datalogi-begreppen och tekniken Obs! Andra frågor än dessa kan komma på tentan! 1. Konvertera talet 186 till
Datalogi I, grundkurs med Java 10p, 2D4112, 2002-2003 Exempel på tentafrågor på boken Lunell: Datalogi-begreppen och tekniken Obs! Andra frågor än dessa kan komma på tentan! 1. Konvertera talet 186 till
ANDRA BASER ÄN TIO EXTRAMATERIAL TILL. Matematikens grunder. för lärare. Anders Månsson
 ANDRA BASER ÄN TIO EXTRAMATERIAL TILL Matematikens grunder för lärare Anders Månsson Extramaterial till boken Matematikens grunder för lärare (art.nr. 38994), Anders Månsson. Till Tallära-kapitlet: Andra
ANDRA BASER ÄN TIO EXTRAMATERIAL TILL Matematikens grunder för lärare Anders Månsson Extramaterial till boken Matematikens grunder för lärare (art.nr. 38994), Anders Månsson. Till Tallära-kapitlet: Andra
Föreläsning 3: Typomvandling, villkor och val, samt textsträngar
 Föreläsning 3: Typomvandling, villkor och val, samt textsträngar Camilla Kirkegaard camilla.kirkegaard@liu.se Linköpings universitet Sweden October 14, 2013 1 Innehåll n n n n n Repetition Typomvandlingar
Föreläsning 3: Typomvandling, villkor och val, samt textsträngar Camilla Kirkegaard camilla.kirkegaard@liu.se Linköpings universitet Sweden October 14, 2013 1 Innehåll n n n n n Repetition Typomvandlingar
Tentamen Datorteknik Y, TSEA28 Datum 2012-08-14
 Tentamen Datorteknik Y, TSEA28 Datum 2012-08-14 Lokal TER2 Tid 8-12 Kurskod TSEA28 Provkod TEN1 Kursnamn Datorteknik Y Institution ISY Antal frågor 6 Antal sidor (inklusive denna sida) 7 Kursansvarig Andreas
Tentamen Datorteknik Y, TSEA28 Datum 2012-08-14 Lokal TER2 Tid 8-12 Kurskod TSEA28 Provkod TEN1 Kursnamn Datorteknik Y Institution ISY Antal frågor 6 Antal sidor (inklusive denna sida) 7 Kursansvarig Andreas
Grundläggande programmering med C# 7,5 högskolepoäng
 Grundläggande programmering med C# 7,5 högskolepoäng Provmoment: TEN1 Ladokkod: NGC011 Tentamen ges för: Omtentamen DE13, IMIT13 och SYST13 samt öppen för alla (Ifylles av student) (Ifylles av student)
Grundläggande programmering med C# 7,5 högskolepoäng Provmoment: TEN1 Ladokkod: NGC011 Tentamen ges för: Omtentamen DE13, IMIT13 och SYST13 samt öppen för alla (Ifylles av student) (Ifylles av student)
Struktur: Elektroteknik A. Digitalteknik 3p, vt 01. F1: Introduktion. Motivation och målsättning för kurserna i digital elektronik
 Digitalteknik 3p, vt 01 Struktur: Elektroteknik A Kurslitteratur: "A First Course in Digital Systems Design - An Integrated Approach" Antal föreläsningar: 11 (2h) Antal laborationer: 4 (4h) Examinationsform:
Digitalteknik 3p, vt 01 Struktur: Elektroteknik A Kurslitteratur: "A First Course in Digital Systems Design - An Integrated Approach" Antal föreläsningar: 11 (2h) Antal laborationer: 4 (4h) Examinationsform:
DIGITALA TAL OCH BOOLESK ALGEBRA
 DIGITALA TAL OCH BOOLESK ALGEBRA Innehåll Talsystem och koder Aritmetik för inära tal Grundläggande logiska operationer Logiska grindar Definitioner i Boolesk algera Räknelagar BINÄRA TALSYSTEMET Binärt
DIGITALA TAL OCH BOOLESK ALGEBRA Innehåll Talsystem och koder Aritmetik för inära tal Grundläggande logiska operationer Logiska grindar Definitioner i Boolesk algera Räknelagar BINÄRA TALSYSTEMET Binärt
Tentamen. Datorteknik Y, TSEA28
 Tentamen Datorteknik Y, TSEA28 Datum 2017-10-26 Lokal TER1, TER3 Tid 8-12 Kurskod TSEA28 Provkod TEN1 Kursnamn Provnamn Datorteknik Y Skriftlig tentamen Institution ISY Antal frågor 6 Antal sidor (inklusive
Tentamen Datorteknik Y, TSEA28 Datum 2017-10-26 Lokal TER1, TER3 Tid 8-12 Kurskod TSEA28 Provkod TEN1 Kursnamn Provnamn Datorteknik Y Skriftlig tentamen Institution ISY Antal frågor 6 Antal sidor (inklusive
CE_O1. Nios II. Enkla assembler-instruktioner.
 IS1500 ösningsförslag till övning CE_O1 2014 CE_O1. Nios II. Enkla assembler-instruktioner. 1.1. Datorarkitektur för Nios II a) Tabell 3 1 i Nios II Processor Reference Handbook visar processorns register:
IS1500 ösningsförslag till övning CE_O1 2014 CE_O1. Nios II. Enkla assembler-instruktioner. 1.1. Datorarkitektur för Nios II a) Tabell 3 1 i Nios II Processor Reference Handbook visar processorns register:
Twincat: PLC Control
 Dokument Förklaring Dat. Revision KI-221-003-003 Kom igång med trukturerad Text 080402 1.0 Twincat: PLC Control Kom igång med Strukturerad Text (ST) programmering 1. Kod exempel. a. Exemplen som demonstreras
Dokument Förklaring Dat. Revision KI-221-003-003 Kom igång med trukturerad Text 080402 1.0 Twincat: PLC Control Kom igång med Strukturerad Text (ST) programmering 1. Kod exempel. a. Exemplen som demonstreras
översiktskurs (5DV031)
 Programmeringsteknisk översiktskurs (5DV031) Föreläsning 10 kallin@cs.umu.se Innehåll Ändlig aritmetik Fler exempel på funktioner med arrayer som parametrar Läsanvisningar: Dessa bilder, kapitel 11 kallin@cs.umu.se
Programmeringsteknisk översiktskurs (5DV031) Föreläsning 10 kallin@cs.umu.se Innehåll Ändlig aritmetik Fler exempel på funktioner med arrayer som parametrar Läsanvisningar: Dessa bilder, kapitel 11 kallin@cs.umu.se
A-del motsvarande KS1
 MÄLARDALENS HÖGSKOLA Institutionen för elektroteknik Tentamen Mikrodatorteknik CT3760 Datum 2005-10-28 Tid 08.30 12.30 Svar till A- och B-del A-del motsvarande KS1 Uppgift A1. Vad blir resultatet då instruktionen
MÄLARDALENS HÖGSKOLA Institutionen för elektroteknik Tentamen Mikrodatorteknik CT3760 Datum 2005-10-28 Tid 08.30 12.30 Svar till A- och B-del A-del motsvarande KS1 Uppgift A1. Vad blir resultatet då instruktionen
Repetitionsuppgifter i Matematik inför Basår. Matematiska institutionen Linköpings universitet 2014
 Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Teknisk Beräkningsvetenskap I Tema 1: Avrundning och populationsmodellering
 Teknisk Beräkningsvetenskap I Tema 1: Avrundning och populationsmodellering Eddie Wadbro 5 november 2014 Eddie Wadbro, Tema 1: Avrundning och populationsmodellering, 5 november 2014 (1 : 21) Innehåll Datoraritmetik
Teknisk Beräkningsvetenskap I Tema 1: Avrundning och populationsmodellering Eddie Wadbro 5 november 2014 Eddie Wadbro, Tema 1: Avrundning och populationsmodellering, 5 november 2014 (1 : 21) Innehåll Datoraritmetik
Sidor i boken 110-113, 68-69 2, 3, 5, 7, 11,13,17 19, 23. Ett andragradspolynom Ett tiogradspolynom Ett tredjegradspolynom
 Sidor i boken 110-113, 68-69 Räkning med polynom Faktorisering av heltal. Att primtalsfaktorisera ett heltal innebär att uppdela heltalet i faktorer, där varje faktor är ett primtal. Ett primtal är ett
Sidor i boken 110-113, 68-69 Räkning med polynom Faktorisering av heltal. Att primtalsfaktorisera ett heltal innebär att uppdela heltalet i faktorer, där varje faktor är ett primtal. Ett primtal är ett
Föreläsning 9: Talteori
 DD2458, Problemlösning och programmering under press Föreläsning 9: Talteori Datum: 2007-11-13 Skribent(er): Niklas Lindbom och Daniel Walldin Föreläsare: Per Austrin Den här föreläsningen behandlar modulär
DD2458, Problemlösning och programmering under press Föreläsning 9: Talteori Datum: 2007-11-13 Skribent(er): Niklas Lindbom och Daniel Walldin Föreläsare: Per Austrin Den här föreläsningen behandlar modulär
C konstruerades i början på sjuttiotalet av Dennis Ritchie vid Bell Laboratories.
 C C konstruerades i början på sjuttiotalet av Dennis Ritchie vid Bell Laboratories. För att användas vid implementering av UNIX. Bygger på de tidigare språken BCPL och B. Målsättning: Att få ett högnivåspråks
C C konstruerades i början på sjuttiotalet av Dennis Ritchie vid Bell Laboratories. För att användas vid implementering av UNIX. Bygger på de tidigare språken BCPL och B. Målsättning: Att få ett högnivåspråks
Lågnivåprogrammering. Föreläsning 2 Lågnivåprogrammering. Binära tal. En enkel modell av datorns inre
 Lågnivåprogrammering Föreläsning 2 Lågnivåprogrammering Förberedelse inför laboration 2. Maskinspråk, assemblerspråk Talrepresentation En enkel dator, komponenter Instruktionsformat, instruktionscykel
Lågnivåprogrammering Föreläsning 2 Lågnivåprogrammering Förberedelse inför laboration 2. Maskinspråk, assemblerspråk Talrepresentation En enkel dator, komponenter Instruktionsformat, instruktionscykel
Tentamen. Datorteknik Y, TSEA28
 Tentamen Datorteknik Y, TSEA28 Datum 2016-08-16 Lokal TER2, TER4 Tid 14-18 Kurskod TSEA28 Provkod TEN1 Kursnamn Provnamn Datorteknik Y Skriftlig tentamen Institution ISY Antal frågor 6 Antal sidor (inklusive
Tentamen Datorteknik Y, TSEA28 Datum 2016-08-16 Lokal TER2, TER4 Tid 14-18 Kurskod TSEA28 Provkod TEN1 Kursnamn Provnamn Datorteknik Y Skriftlig tentamen Institution ISY Antal frågor 6 Antal sidor (inklusive
Programmeringsteknik I
 Programmeringsteknik I Föreläsning 2: Grundläggande Java Johan Öfverstedt Java Grundläggande begrepp Datatyper Selektion if Räckvidd (scope) Iteration while Klasser Objekt Metoder Metodhuvudet Kodstandarden
Programmeringsteknik I Föreläsning 2: Grundläggande Java Johan Öfverstedt Java Grundläggande begrepp Datatyper Selektion if Räckvidd (scope) Iteration while Klasser Objekt Metoder Metodhuvudet Kodstandarden
Vem är vem på kursen. Objektorienterad programvaruutveckling GU (DIT011) Kursbok Cay Horstmann: Big Java 3rd edition.
 Institutionen för Datavetenskap Göteborgs universitet HT2009 DIT011 Vem är vem på kursen Objektorienterad programvaruutveckling GU (DIT011) Kursansvarig : Katarina Blom, tel 772 10 60 Rum: 6126 (E-huset)
Institutionen för Datavetenskap Göteborgs universitet HT2009 DIT011 Vem är vem på kursen Objektorienterad programvaruutveckling GU (DIT011) Kursansvarig : Katarina Blom, tel 772 10 60 Rum: 6126 (E-huset)
Microprocessor / Microcontroller. Industrial Electrical Engineering and Automation
 Microprocessor / Microcontroller Varför? Billiga Innehåller bara det nödvändigaste Kräver få kringkomponenter Enkla att programmera PIC16F887 PIC16F887 In- och utgångar Pinnar på PIC16F887 Exempel: pinne
Microprocessor / Microcontroller Varför? Billiga Innehåller bara det nödvändigaste Kräver få kringkomponenter Enkla att programmera PIC16F887 PIC16F887 In- och utgångar Pinnar på PIC16F887 Exempel: pinne
n Kap 4.1, 4.2, (4.3), 4.4, 4.5 n Numerisk beräkning av derivata med n Felen kan t ex vara avrundningsfel eller mätfel n Felet kan mätas
 Datoraritmetik Beräkningsvetenskap I/KF Kursboken n Kap 4., 4., (4.3), 4.4, 4. n I kap 4.3 används Taylorutvecklingar. Om du ännu inte gått igenom detta i matematiken, kan du oppa över de delar som beandlar
Datoraritmetik Beräkningsvetenskap I/KF Kursboken n Kap 4., 4., (4.3), 4.4, 4. n I kap 4.3 används Taylorutvecklingar. Om du ännu inte gått igenom detta i matematiken, kan du oppa över de delar som beandlar
Översikt Introduktion DST 1. Nicholas Wickström. IDE, Högskolan i Halmstad. N. Wickström
 DST 1 Nicholas Wickström IDE, Högskolan i Halmstad 2009 1 Outline 1 Vad är Hårdvara? (Datorsystemmodell; processor m. periferi, IO, Minne) Typiskt för hårdvarunära programmering (datablad, register, datastrukturer,...)
DST 1 Nicholas Wickström IDE, Högskolan i Halmstad 2009 1 Outline 1 Vad är Hårdvara? (Datorsystemmodell; processor m. periferi, IO, Minne) Typiskt för hårdvarunära programmering (datablad, register, datastrukturer,...)
SVAR TILL TENTAMEN I DATORSYSTEM, HT2013
 Rahim Rahmani (rahim@dsv.su.se) Division of SAS Department of Computer and Systems Sciences Stockholm University SVAR TILL TENTAMEN I DATORSYSTEM, HT2013 Tentamensdatum: 2013-10-30 Tentamen består av totalt
Rahim Rahmani (rahim@dsv.su.se) Division of SAS Department of Computer and Systems Sciences Stockholm University SVAR TILL TENTAMEN I DATORSYSTEM, HT2013 Tentamensdatum: 2013-10-30 Tentamen består av totalt
Lösningar till uppgifterna sätts ut på kurssidan på nätet idag kl 13.00. Omtentamen i Programmering C, 5p, A1, D1, E1, Fri, Pr1, Te/Ek1, 040607.
 1(8) ÖREBRO UNIVERSITET INSTITUTIONEN FÖR TEKNIK Lösningar till uppgifterna sätts ut på kurssidan på nätet idag kl 13.00. Denna tenta kommer att vara färdigrättad On 9/6 och kan då hämtas på mitt tjänsterum,
1(8) ÖREBRO UNIVERSITET INSTITUTIONEN FÖR TEKNIK Lösningar till uppgifterna sätts ut på kurssidan på nätet idag kl 13.00. Denna tenta kommer att vara färdigrättad On 9/6 och kan då hämtas på mitt tjänsterum,
Föreläsning 1 & 2 INTRODUKTION
 Föreläsning 1 & 2 INTRODUKTION Denna föreläsning Vad händer under kursen? praktisk information Kursens mål vad är programmering? Skriva små program i programspråket Java Skriva program som använder färdiga
Föreläsning 1 & 2 INTRODUKTION Denna föreläsning Vad händer under kursen? praktisk information Kursens mål vad är programmering? Skriva små program i programspråket Java Skriva program som använder färdiga
Introduktion till programmering SMD180. Föreläsning 2: Variabler, uttryck och satser
 Introduktion till programmering Föreläsning 2: Variabler, uttryck och satser 1 1 Värden De grundläggande saker som en dator manipulerar resultaten av beräkningar kallas värden Värden vi stött på: 2 och
Introduktion till programmering Föreläsning 2: Variabler, uttryck och satser 1 1 Värden De grundläggande saker som en dator manipulerar resultaten av beräkningar kallas värden Värden vi stött på: 2 och
Assemblerprogrammering, ARM-Cortex M4 del 1
 Assemblerprogrammering, ARM-Cortex M4 del 1 Ur innehållet: Assemblatorn, assemblerspråk Ordlängder och datatyper Variabeldeklarationer Programkonstruktioner Tilldelningar Uttrycksevaluering Ovillkorliga
Assemblerprogrammering, ARM-Cortex M4 del 1 Ur innehållet: Assemblatorn, assemblerspråk Ordlängder och datatyper Variabeldeklarationer Programkonstruktioner Tilldelningar Uttrycksevaluering Ovillkorliga
