Föreläsning 8: Aritmetik och stora heltal
|
|
|
- Lisa Öberg
- för 6 år sedan
- Visningar:
Transkript
1 2D1458, Problemlösning och programmering under press Föreläsning 8: Aritmetik och stora heltal Datum: Skribent(er): Elias Freider och Ulf Lundström Föreläsare: Per Austrin Den här föreläsningen handlar om beräkningar med flyttal och behandling av heltal som inte ryms i grundläggande datatyper. 1 Flyttalsaritmetik Flyttal beter sig inte alltid som man tror. Exempel 1 - Avrundning double x = 0.29; int y = (int)(100*x); print(y); //Skriver ut 28 Exempel 2 - Jämförelse for(double x = 0.0; x!=1.0; x+=0.1) print("hello"); //fortsätter i all oändlighet 1.1 Flyttalsrepresentation Anledningen till beteendena vi stötte på ovan är att alla reella tal inte kan representeras exakt med grundläggande datatyper. Detta beror på hur flyttalen representeras i minnet. I C/C++/Java representeras ett flyttal x enligt följande: x = S M 2 E S teckenbit {1, 1} M mantissan (heltal) E exponenten (heltal) Storleken på mantissan och exponenten varierar med datatypen enligt tabell 1. flyttalstyp storlek S E M float double long double Tabell 1: Antal bitar för S, E, M och totalt för olika flyttalstyper. Siffrorna för long double gäller sun-datorerna på Nada och kan variera mellan plattformar. 1
2 2 2D1458 Popup HT 2006 Som man ser i tabell 1 så är summan av antal bitar för de olika delarna ett mer än totala antalet bitar. Detta beror på att man använder normaliserad representation där den mest signifikanta biten i mantissan alltid är satt. Detta fungerar eftersom man alltid kan justera exponenten för att kompensera för en större mantissa. Om den mest signifikanta biten inte skulle vara satt kan man i stället representera talet med S(2M)2 E 1. Därför behöver inte den högsta biten lagras En närmare titt på double En double x representeras alltså på följande sätt: x =( 1) s (1 + M 2 52 ) 2 E 1023 där 0 M<2 52, 0 E<2 11. Vissa värden på E är reserverade för speciella tal som inte kan representeras enligt denna formel. En double med E =0representerar i stället x =( 1) s (M 2 52 ) där ettan från föregående formel tagits bort för att kunna representera ±0. E = 2047,M =0betyder ± beroende på s. I C++ ger med många kompilatorer en varning om man skriver t.ex. 1.0/0.0 för att få doublevärdet för. För att slippa varningen kan man istället skriva std::numeric_limits<double>::infinity() E = 2047,M 0representerar Not a number, NaN. Detta är t.ex. resultatet av 0.0/0.0 och /. NaN har den speciella egenskapen att NaN == NaN är falskt. NaN kan man få utan kompileringsfel genom std::numeric_limits<double>::quiet_nan() 1.2 float vs. double I de allra flesta fall där man behöver flyttal bör man använda double. Det ger en betydligt högre precision är float, men går ändå nästan lika fort att räkna med. Float kan dock vara bra om man har ont om minne, eller om avrundningsfel inte har någon betydelse, som t.ex. i datorgrafiksammanhang. 1.3 Varför blir det fel? Exemplen i början har enkla förklaringar om man känner till datorns flyttalsrepresentation. Exempel kan inte representeras exakt med en double. Datorn lagrar då istället det doublevärde som ligger närmast 0.29 vilket råkar vara ungefär = När detta multipliceras med 100 och trunkeras till ett heltal får vi då 28.
3 Aritmetik och stora heltal 3 Exempel kan inte heller representeras exakt med en double. Det kan däremot 1. När vi har adderat 0.1 tio gånger kommer vi därför få ett tal som inte är exakt 1 och loopens slutkriterium kommer därför inte att uppfyllas. 1.4 Hur löser vi problemen? Det finns ett antal lösningar på problemen i båda exemplen i början. Exempel 1 Lösning 1: Avrunda till närmsta istället för nedåt vid omvandling till heltal. Detta görs enklast genom y=(int)(x* ). Detta funkar om x inte är ohyggligt stort. Lösning 2: Skriv ut talet som en double med 0 decimaler. Lösning 3: Problemet uppstår normalt vid inläsning av flyttal. Då kan man istället läsa in talet som heltal, punkt, heltal. Tänk dock på att =5.10. Exempel 2 Lösning: Använd ej a == b för att kontrollera likhet mellan a och b. Använd istället a b < ɛ för något litet ɛ (absolut jämförelse) eller a b < ɛ( a + b ) (relativ jämförelse). Absolut jämförelse fungerar dåligt för mycket stora tal a och b eftersom differensen mellan talen då kan vara stor trots att den är relativt obetydlig. Relativ jämförelse fungerar dåligt för mycket små tal a och b eftersom. Vill man vara helt säker kan man använda båda. Då ska man anse det som likhet om någon av relativ eller absolut jämförelse ger likhet. Välj lämpligen ɛ 10 7.,<,,>kan i vissa fall behöva implementeras på motsvarande sätt. 1.5 Flyttal vs. heltal I de flesta fall där man kan välja bör man använda heltal istället för flyttal, eftersom man då slipper avrundningsfel. Det finns dock vissa fall då flyttal har sina fördelar Exempel: Finn 4 x givet att detta är ett heltal. Lösning: Läs in x som en double, låt y = pow(x, 0.25) och skriv ut y avrundat till 0 decimaler. Motivering: Låt X x (1 ± ɛ) vara vår approximation av (d.v.s. det doublevärde som ligger närmast) x. Låt Y = pow(x, 0.25) = (1± ɛ) X 1/4 = (1± ɛ) e ln(x)/4 (1 ± ɛ) e ln(x) 4 (1±ɛ) = (1± ɛ) ye ɛ ln(y) (1 ± ɛ)(1 ± ɛ ln(y))y y ± y ɛ ln(y).
4 4 2D1458 Popup HT 2006 I näst sista steget används att e w =1+w + w och w 0 ew 1+w. Vi får då ett fel i vår beräkning som är Y y y ɛ ln(y) 0.5 vilket är vad som krävs för att få korrekt svar efter avrundning. 1.6 Mer information Mer utförlig information om flyttalshantering i datorer finns i följande artikel: 2 Floor och Ceil Givet x R defineras x = floor(x) som x avrundat till närmsta heltal nedåt samt x = ceil(x) som x avrundat till närmsta helatal uppåt. Tabell 2: Exempel på ceil och floor x x x Operationer x = n n x<n+1 x = n n 1 <x n 2.2 Identiteter x = x x = x x ± n = x ±n x ± n = x ±n n n + m +1 = för m>0 m m 2.3 Beräkning av n m och n m Om m, n inte är för stora är det enklast att konvertera talen till doubles och använda floor()- eller ceil()-funktionerna. Genom att använda identiteterna ovan kan man skriva mer robusta funktioner förfloorochceil:
5 Aritmetik och stora heltal 5 floor(int n, int m) 1: if m<0 then 2: return floor(-n, -m) 3: else if n<0 then 4: return -ceil(-n, m) 5: else 6: return n/m 7: end if ceil(int n, int m) 1: if m>0 then 2: return floor(n+m-1, m) 3: else 4: return floor(-n-m-1,-m) 5: end if 2.4 Rare easy problem Kattisproblemet rare easy problem ( har en enkel explicit lösning som kan härledas med ceil och floor. Problemet går ut på att finna N givet K = M N där M är N med sista siffran borttagen. Vi börjar med att observera M = N/10. Vi vill alltså lösa N N/10 = K N N/10 = K K = N + N/10 K = 9N/10 K 1 < 9N/10 K 10K 9 9N 10K 10K/9 1 N 10K/9 (10K/9 1) N 10K/9 Om K är delbart med 9 är lösningarna 10K/9 och 10K/9 1 annars 10K/9. 3 Stora heltal Stora heltal är heltal som inte får plats i standard-datatyper som long i Java och long long i C/C++. I Java finns BigInteger för att hantera dessa och i C/C++ finns GMP (GNU Multiprecision Library), men den senare finns oftast ej tillgänglig på Kattis. 3.1 Representation Ett stort heltal x kan representeras i basen b som x = x n 1 b n x 1 b + x 0 där 0 x i <b.talenx =(x i ) kan lagras som en vektor av tal. Olika val av b kan vara fördelaktiga i olika sammanhang.
6 6 2D1458 Popup HT 2006 Potens av 2 t.ex. 2 32, 2 64 eller Detta är mest effektivt eftersom man utnyttjar minnesutrymmet väl och det då blir få x i. Dessutom kan division- och modulo-operationerna som krävs i nedanstående algoritmer utföras effektivare med dessa baser eftersom det är den interna representationen i datorn. En nackdel är att det blir jobbigt med inläsning och utskrift i basen 10. b =10 Detta är enkelt men ineffektivt då det kräver många x i och därmed mycket minnesutrymme och fler beräkningar än med större b. b =10 d Bra kompromiss för enkel kod då det lätt går att skriva ut och mata in tal i basen 10 samtidigt som minnet utnyttjas ganska väl. T.ex. d = 9 och vi har 2 64 long long. Vill ha att 10 2d = b 2 får plats i datatypen för att slippa overflow vid t.ex. multiplikation. 3.2 Operationer Variablerna x, y och z är stora positiva tal representerade i basen b som ovan. Vi tänker oss att x i =0om i>ndär n är antalet tal i vektorn x. Samma sak gäller för y och z. Endast små logiska tillägg krävs för att kunna hantera även negativa tal. Algoritmerna är samma eller snarlika de som man använder vid beräkning på papper Addition z x + y 1: carry 0 2: n maximala storleken av x och y 3: for i =0to n 1 do 4: tmp x i + y i + carry 5: z i tmp mod b 6: carry [tmp b] 8: z n carry Subtraktion z x y där x antas vara större än y. 1: borrow 0 2: n maximala storleken av x och y 3: for i =0to n 1 do 4: tmp x i y i borrow 5: z i tmp mod b 6: borrow [tmp < 0]
7 Aritmetik och stora heltal Multiplikation z x y 1: z 0 2: m storleken av x 3: n storleken av y 4: for i =0to m 1 do 5: for j =0to n 1 do 6: z i+j z i+j + x i y j 8: propagera minnessiffror iz 9: end for Algoritmen kräver att den primitiva datatypen rymmer b 2 1. Det finns betydligt snabbare algoritmer för multiplikation av stora tal Division z x/y och r x mod y där y<b 1: r 0 2: n storleken av x 3: for i = n 1 to 0 do 4: tmp b r + x i 5: z i tmp/y 6: r tmp mod y För att kunna hantera division med stora heltal krävs en betydligt krångligare algoritm.
Föreläsning 8: Aritmetik och stora heltal
 DD2458, Problemlösning och programmering under press Föreläsning 8: Aritmetik och stora heltal Datum: 2007-11-06 Skribent(er): Martin Tittenberger, Patrik Lilja Föreläsare: Per Austrin Denna föreläsning
DD2458, Problemlösning och programmering under press Föreläsning 8: Aritmetik och stora heltal Datum: 2007-11-06 Skribent(er): Martin Tittenberger, Patrik Lilja Föreläsare: Per Austrin Denna föreläsning
Föreläsning 8: Aritmetik I
 DD2458, Problemlösning och programmering under press Föreläsning 8: Aritmetik I Datum: 2009-11-03 Skribent(er): Andreas Sehr, Carl Bring, Per Almquist Föreläsare: Fredrik Niemelä 1 Flyttal Att representera
DD2458, Problemlösning och programmering under press Föreläsning 8: Aritmetik I Datum: 2009-11-03 Skribent(er): Andreas Sehr, Carl Bring, Per Almquist Föreläsare: Fredrik Niemelä 1 Flyttal Att representera
Datoraritmetik. Från labben. Från labben. Några exempel
 Datoraritmetik Beräkningsvetenskap I Från labben Två huvudtyper av fel: diskretiseringsfel och avrundningsfel Olika sätt att mäta fel: relativt fel, absolut fel Begreppen ε M, Inf, NaN, overflow, underflow,
Datoraritmetik Beräkningsvetenskap I Från labben Två huvudtyper av fel: diskretiseringsfel och avrundningsfel Olika sätt att mäta fel: relativt fel, absolut fel Begreppen ε M, Inf, NaN, overflow, underflow,
n Kap 4.1, 4.2, (4.3), 4.4, 4.5 n Numerisk beräkning av derivata med n Felen kan t ex vara avrundningsfel eller mätfel n Felet kan mätas
 Datoraritmetik Beräkningsvetenskap I/KF Kursboken n Kap 4., 4., (4.3), 4.4, 4. n I kap 4.3 används Taylorutvecklingar. Om du ännu inte gått igenom detta i matematiken, kan du oppa över de delar som beandlar
Datoraritmetik Beräkningsvetenskap I/KF Kursboken n Kap 4., 4., (4.3), 4.4, 4. n I kap 4.3 används Taylorutvecklingar. Om du ännu inte gått igenom detta i matematiken, kan du oppa över de delar som beandlar
Teknisk Beräkningsvetenskap I Tema 1: Avrundning och populationsmodellering
 Teknisk Beräkningsvetenskap I Tema 1: Avrundning och populationsmodellering Eddie Wadbro 5 november 2014 Eddie Wadbro, Tema 1: Avrundning och populationsmodellering, 5 november 2014 (1 : 21) Innehåll Datoraritmetik
Teknisk Beräkningsvetenskap I Tema 1: Avrundning och populationsmodellering Eddie Wadbro 5 november 2014 Eddie Wadbro, Tema 1: Avrundning och populationsmodellering, 5 november 2014 (1 : 21) Innehåll Datoraritmetik
F2 Datarepresentation talbaser, dataformat och teckenkodning EDAA05 Datorer i system! Roger Henriksson!
 F2 Datarepresentation talbaser, dataformat och teckenkodning EDAA05 Roger Henriksson Von Neumann-arkitekturen Gemensamt minne för programinstruktioner och data. Sekventiell exekvering av instruktionerna.
F2 Datarepresentation talbaser, dataformat och teckenkodning EDAA05 Roger Henriksson Von Neumann-arkitekturen Gemensamt minne för programinstruktioner och data. Sekventiell exekvering av instruktionerna.
Maskinorienterad Programmering - 2010/2011. Maskinorienterad Programmering 2010/11. Maskinnära programmering C och assemblerspråk
 Maskinorienterad Programmering 2010/11 Maskinnära programmering C och assemblerspråk Ur innehållet: 32-bitars aritmetik med 16-bitars processor IEEE754 flyttal Maskinnära programmering - C 1 CPU12, ordlängder
Maskinorienterad Programmering 2010/11 Maskinnära programmering C och assemblerspråk Ur innehållet: 32-bitars aritmetik med 16-bitars processor IEEE754 flyttal Maskinnära programmering - C 1 CPU12, ordlängder
IE1205 Digital Design: F6 : Digital aritmetik 2
 IE1205 Digital Design: F6 : Digital aritmetik 2 Talrepresentationer Ett tal kan representeras binärt på många sätt. De vanligaste taltyperna som skall representeras är: Heltal, positiva heltal (eng. integers)
IE1205 Digital Design: F6 : Digital aritmetik 2 Talrepresentationer Ett tal kan representeras binärt på många sätt. De vanligaste taltyperna som skall representeras är: Heltal, positiva heltal (eng. integers)
F2 Datarepresentation talbaser, dataformat och teckenkodning
 F2 Datarepresentation talbaser, dataformat och teckenkodning EDAA05 Roger Henriksson Jonas Wisbrant Datarepresentation I en dator lagras och behandlas all information i form av binära tal ettor och nollor.
F2 Datarepresentation talbaser, dataformat och teckenkodning EDAA05 Roger Henriksson Jonas Wisbrant Datarepresentation I en dator lagras och behandlas all information i form av binära tal ettor och nollor.
Föreläsning 9: Talteori
 DD2458, Problemlösning och programmering under press Föreläsning 9: Talteori Datum: 2007-11-13 Skribent(er): Niklas Lindbom och Daniel Walldin Föreläsare: Per Austrin Den här föreläsningen behandlar modulär
DD2458, Problemlösning och programmering under press Föreläsning 9: Talteori Datum: 2007-11-13 Skribent(er): Niklas Lindbom och Daniel Walldin Föreläsare: Per Austrin Den här föreläsningen behandlar modulär
Digital- och datorteknik
 Digital- och datorteknik Föreläsning #24 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Allmänt Behovet av processorinstruktioner för multiplikation
Digital- och datorteknik Föreläsning #24 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Allmänt Behovet av processorinstruktioner för multiplikation
7 november 2014 Sida 1 / 21
 TANA09 Föreläsning 2 Talrepresentation i datorer. Flyttalssystem. Datoraritmetik och Beräkningsfel. Beräkningsfelsanalys och Kancellation. Serier och Resttermsuppskattningar. Tillämpning - Beräkning av
TANA09 Föreläsning 2 Talrepresentation i datorer. Flyttalssystem. Datoraritmetik och Beräkningsfel. Beräkningsfelsanalys och Kancellation. Serier och Resttermsuppskattningar. Tillämpning - Beräkning av
Enkla datatyper minne
 Enkla datatyper minne 143.56 sant Sonja A falskt 18 1999-10-29 Bertil Gralvik, KTH Ingenjörsskolan 1 Addera två tal Algoritmen Summera tal Mata in två tal Beräkna Skriv ut resultat Mata in tal 1 Mata in
Enkla datatyper minne 143.56 sant Sonja A falskt 18 1999-10-29 Bertil Gralvik, KTH Ingenjörsskolan 1 Addera två tal Algoritmen Summera tal Mata in två tal Beräkna Skriv ut resultat Mata in tal 1 Mata in
Dagens föreläsning. Repetition. Repetition - Programmering i C. Repetition - Vad C består av. Repetition Ett första C-program
 Dagens föreläsning Programmeringsteknik för Ingenjörer VT05 Föreläsning 3-4 Repetition Datatyper Uttryck Operatorer Satser Algoritmer Programmeringsteknik VT05 2 Repetition Repetition - Programmering i
Dagens föreläsning Programmeringsteknik för Ingenjörer VT05 Föreläsning 3-4 Repetition Datatyper Uttryck Operatorer Satser Algoritmer Programmeringsteknik VT05 2 Repetition Repetition - Programmering i
Datorsystemteknik DVG A03 Föreläsning 3
 Datorsystemteknik DVG A03 Föreläsning 3 Datoraritmetik Större delen av materialet framtaget av :Jan Eric Larsson, Mats Brorsson och Mirec Novak IT-inst LTH Hur stora tal kan vi få med N bitar? Största
Datorsystemteknik DVG A03 Föreläsning 3 Datoraritmetik Större delen av materialet framtaget av :Jan Eric Larsson, Mats Brorsson och Mirec Novak IT-inst LTH Hur stora tal kan vi få med N bitar? Största
Lösningsanvisningar till de icke obligatoriska workoutuppgifterna
 Lösningsanvisningar till de icke obligatoriska workoutuppgifterna Linjära system 7. (a) Falskt. Kondition är en egenskap hos problemet oberoende av precisionen i beräkningarna. (b) Falskt. Pivotering påverkar
Lösningsanvisningar till de icke obligatoriska workoutuppgifterna Linjära system 7. (a) Falskt. Kondition är en egenskap hos problemet oberoende av precisionen i beräkningarna. (b) Falskt. Pivotering påverkar
Föreläsning 9: Talteori
 DD2458, Problemlösning och programmering under press Föreläsning 9: Talteori Datum: 2009-11-11 Skribent(er): Ting-Hey Chau, Gustav Larsson, Åke Rosén Föreläsare: Fredrik Niemelä Den här föreläsningen handlar
DD2458, Problemlösning och programmering under press Föreläsning 9: Talteori Datum: 2009-11-11 Skribent(er): Ting-Hey Chau, Gustav Larsson, Åke Rosén Föreläsare: Fredrik Niemelä Den här föreläsningen handlar
översiktskurs (5DV031)
 Programmeringsteknisk översiktskurs (5DV031) Föreläsning 10 kallin@cs.umu.se Innehåll Ändlig aritmetik Fler exempel på funktioner med arrayer som parametrar Läsanvisningar: Dessa bilder, kapitel 11 kallin@cs.umu.se
Programmeringsteknisk översiktskurs (5DV031) Föreläsning 10 kallin@cs.umu.se Innehåll Ändlig aritmetik Fler exempel på funktioner med arrayer som parametrar Läsanvisningar: Dessa bilder, kapitel 11 kallin@cs.umu.se
Binär addition papper och penna metod
 EDA4 - Digital och Datorteknik 9/ EDA 4 - Digital och Datorteknik 8/9 Dagens föreläsning: Aritmetik, lärobok kapitel 6 Ur innehållet: hur man adderar och subtraherar tal i det binära talsystemet hur man
EDA4 - Digital och Datorteknik 9/ EDA 4 - Digital och Datorteknik 8/9 Dagens föreläsning: Aritmetik, lärobok kapitel 6 Ur innehållet: hur man adderar och subtraherar tal i det binära talsystemet hur man
I Skapa Hej.java och skriv programmet. I Kompilera med javac Hej.java. I Rätta fel och repetera tills du lyckas kompilera ditt program
 Kompilera och köra programmet Objektorienterad Programmering (TDDC77) Föreläsning II: utmatning, variabler, typer Ahmed Rezine IDA, Linköpings Universitet Hösttermin 2016 under terminal 2: I Skapa Hej.java
Kompilera och köra programmet Objektorienterad Programmering (TDDC77) Föreläsning II: utmatning, variabler, typer Ahmed Rezine IDA, Linköpings Universitet Hösttermin 2016 under terminal 2: I Skapa Hej.java
Objektorienterad Programmering (TDDC77)
 Objektorienterad Programmering (TDDC77) Föreläsning II: utmatning, variabler, typer Ahmed Rezine IDA, Linköpings Universitet Hösttermin 2016 Kompilera och köra programmet under terminal 2: I Skapa Hej.java
Objektorienterad Programmering (TDDC77) Föreläsning II: utmatning, variabler, typer Ahmed Rezine IDA, Linköpings Universitet Hösttermin 2016 Kompilera och köra programmet under terminal 2: I Skapa Hej.java
Språket Python - Del 1 Grundkurs i programmering med Python
 Hösten 2009 Dagens lektion Ett programmeringsspråks byggstenar Några inbyggda datatyper Styra instruktionsflödet Modulen sys 2 Ett programmeringsspråks byggstenar 3 ETT PROGRAMMERINGSSPRÅKS BYGGSTENAR
Hösten 2009 Dagens lektion Ett programmeringsspråks byggstenar Några inbyggda datatyper Styra instruktionsflödet Modulen sys 2 Ett programmeringsspråks byggstenar 3 ETT PROGRAMMERINGSSPRÅKS BYGGSTENAR
Variabler, värden och typer
 Variabler, värden och typer Viktigt att förstå på djupet: För programmering i många språk, t.ex. Java För kommande objektorientering! TDDD78, TDDE30, 729A85 jonas.kvarnstrom@liu.se 2018 Fråga kommentera
Variabler, värden och typer Viktigt att förstå på djupet: För programmering i många språk, t.ex. Java För kommande objektorientering! TDDD78, TDDE30, 729A85 jonas.kvarnstrom@liu.se 2018 Fråga kommentera
Variabler, värden och typer
 Variabler, värden och typer Viktigt att förstå på djupet: För programmering i många språk, t.ex. Java För kommande objektorientering! jonas.kvarnstrom@liu.se 2017 Fråga kommentera avbryt! Intro till variabler
Variabler, värden och typer Viktigt att förstå på djupet: För programmering i många språk, t.ex. Java För kommande objektorientering! jonas.kvarnstrom@liu.se 2017 Fråga kommentera avbryt! Intro till variabler
Digital- och datorteknik
 Digital- och datorteknik Föreläsning #7 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Aritmetik i digitala system Speciella egenskaper: Systemet
Digital- och datorteknik Föreläsning #7 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Aritmetik i digitala system Speciella egenskaper: Systemet
Digital- och datorteknik
 Digital- och datorteknik Föreläsning #7 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Speciella egenskaper: Systemet arbetar med kodord (s k
Digital- och datorteknik Föreläsning #7 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Speciella egenskaper: Systemet arbetar med kodord (s k
Datastrukturer. Erik Forslin. Rum 1445, plan 4 på Nada
 Datastrukturer Vad är en datastruktur? Vad är en datatyp? Primitiva datatyper i Java Icke-primitiva datatyper i Java Minnesexempel med datastrukturer Vektorer i Java Erik Forslin efo@nada.kth.se Rum 1445,
Datastrukturer Vad är en datastruktur? Vad är en datatyp? Primitiva datatyper i Java Icke-primitiva datatyper i Java Minnesexempel med datastrukturer Vektorer i Java Erik Forslin efo@nada.kth.se Rum 1445,
Digitalitet. Kontinuerlig. Direkt proportionerlig mot källan. Ex. sprittermometer. Elektrisk signal som representerar ljud.
 Analog Digitalitet Kontinuerlig Direkt proportionerlig mot källan Ex. sprittermometer Elektrisk signal som representerar ljud Diskret Digital Representation som siffror/symboler Ex. CD-skiva Varje siffra
Analog Digitalitet Kontinuerlig Direkt proportionerlig mot källan Ex. sprittermometer Elektrisk signal som representerar ljud Diskret Digital Representation som siffror/symboler Ex. CD-skiva Varje siffra
Datoraritmetik. Binär addition papper och penna metod. Binär subtraktion papper och penna metod. Binär multiplikation papper och penna metod
 inär addition papper och penna metod Dagens föreläsning: Lärobok, kapitel rbetsbok, kapitel Ur innehållet: hur man adderar och subtraherar tal i det binära talsystemet hur man kan koda om negativa binära
inär addition papper och penna metod Dagens föreläsning: Lärobok, kapitel rbetsbok, kapitel Ur innehållet: hur man adderar och subtraherar tal i det binära talsystemet hur man kan koda om negativa binära
Datorsystem. Övningshäfte. Senast uppdaterad: 22 oktober 2012 Version 1.0d
 Datorsystem Övningshäfte Senast uppdaterad: 22 oktober 2012 Version 1.0d Innehåll Innehåll i 1 Introduktion 1 1.1 Errata............................................... 1 2 Datorns grunder 2 2.1 Övningsuppgifter.........................................
Datorsystem Övningshäfte Senast uppdaterad: 22 oktober 2012 Version 1.0d Innehåll Innehåll i 1 Introduktion 1 1.1 Errata............................................... 1 2 Datorns grunder 2 2.1 Övningsuppgifter.........................................
F2 Binära tal EDA070 Datorer och datoranvändning
 Datarepresentation F2 Binära tal EDA070 Roger Henriksson I en dator lagras och behandlas all information i form av binära tal ettor och nollor. En binär siffra kallas för en bit BInary digit. Ett antal
Datarepresentation F2 Binära tal EDA070 Roger Henriksson I en dator lagras och behandlas all information i form av binära tal ettor och nollor. En binär siffra kallas för en bit BInary digit. Ett antal
Dagens föreläsning. Repetition. Repetition - Programmering i C. Repetition - Vad C består av. Repetition Ett första C-program
 Dagens föreläsning Programmeringsteknik för Ingenjörer VT05 Föreläsning 3-4 Repetition Datatyper Uttryck Operatorer Satser Algoritmer Programmeringsteknik för ingenjörer, VT06 2 Repetition Repetition -
Dagens föreläsning Programmeringsteknik för Ingenjörer VT05 Föreläsning 3-4 Repetition Datatyper Uttryck Operatorer Satser Algoritmer Programmeringsteknik för ingenjörer, VT06 2 Repetition Repetition -
Programmering i C++ En manual för kursen Datavetenskaplig introduktionskurs 5p
 Programmering i C++ En manual för kursen Datavetenskaplig introduktionskurs 5p Skriven av Michael Andersson Introduktion Programmering I högnivåspråk fokuserar på själv problemet (algoritmen) istället
Programmering i C++ En manual för kursen Datavetenskaplig introduktionskurs 5p Skriven av Michael Andersson Introduktion Programmering I högnivåspråk fokuserar på själv problemet (algoritmen) istället
Programmera i C Varför programmera i C när det finns språk som Simula och Pascal??
 Programmera i C Varför programmera i C när det finns språk som Simula och Pascal?? C är ett språk på relativt låg nivå vilket gör det möjligt att konstruera effektiva kompilatorer, samt att komma nära
Programmera i C Varför programmera i C när det finns språk som Simula och Pascal?? C är ett språk på relativt låg nivå vilket gör det möjligt att konstruera effektiva kompilatorer, samt att komma nära
Datatyper och kontrollstrukturer. Skansholm: Kapitel 2) De åtta primitiva typerna. Typ Innehåll Defaultvärde Storlek
 De åtta primitiva typerna Java, datatyper, kontrollstrukturer Skansholm: Kapitel 2) Uppsala Universitet 11 mars 2005 Typ Innehåll Defaultvärde Storlek boolean true, false false 1 bit char Tecken \u000
De åtta primitiva typerna Java, datatyper, kontrollstrukturer Skansholm: Kapitel 2) Uppsala Universitet 11 mars 2005 Typ Innehåll Defaultvärde Storlek boolean true, false false 1 bit char Tecken \u000
DD1314 Programmeringsteknik
 Skolan för Datavetenskap och kommunikation DD1314 Programmeringsteknik Föreläsning 1 o print o variabler o reserverade ord o input o kommentarer o beräkningar o datatyper o if-satser Kursinformation Programmering:
Skolan för Datavetenskap och kommunikation DD1314 Programmeringsteknik Föreläsning 1 o print o variabler o reserverade ord o input o kommentarer o beräkningar o datatyper o if-satser Kursinformation Programmering:
Per Holm Lågnivåprogrammering 2014/15 24 / 177. int och double = = 2, 147, 483, 647
 Lågnivåprogrammering Föreläsning 2 Lågnivåprogrammering Förberedelse inför laboration 2. Maskinspråk, assemblerspråk Talrepresentation En enkel dator, komponenter Instruktionsformat, instruktionscykel
Lågnivåprogrammering Föreläsning 2 Lågnivåprogrammering Förberedelse inför laboration 2. Maskinspråk, assemblerspråk Talrepresentation En enkel dator, komponenter Instruktionsformat, instruktionscykel
1/15/2013. DD1310/DD1314/DA3009 Programmeringsteknik. Lärandemål... Vilka läser kursen? ...fler lärandemål VARFÖR? Föreläsning 1
 Skolan för Datavetenskap och kommunikation DD1310/DD1314/DA3009 Programmeringsteknik Föreläsning 1 Kursinfo Diagnostiskt prov Python-intro: print variabler reserverade ord input kommentarer beräkningar
Skolan för Datavetenskap och kommunikation DD1310/DD1314/DA3009 Programmeringsteknik Föreläsning 1 Kursinfo Diagnostiskt prov Python-intro: print variabler reserverade ord input kommentarer beräkningar
a = a a a a a a ± ± ± ±500
 4.1 Felanalys Vill man hårddra det hela, kan man påstå att det inte finns några tal i den tillämpade matematiken, bara intervall. Man anger till exempel inte ett uppmätt värde till 134.78 meter utan att
4.1 Felanalys Vill man hårddra det hela, kan man påstå att det inte finns några tal i den tillämpade matematiken, bara intervall. Man anger till exempel inte ett uppmätt värde till 134.78 meter utan att
Övning2. Variabler. Data typer
 Vahid 28 okt 2002 prgk02 Övning2 -Repetition -Variabler -Primitiva typer (+ boolean) -Operatörer +, ++, --, -Typ konvertering -Wrapper klasser -Jämförelse operatörer,(==, =, ,!=,!) -String hur man
Vahid 28 okt 2002 prgk02 Övning2 -Repetition -Variabler -Primitiva typer (+ boolean) -Operatörer +, ++, --, -Typ konvertering -Wrapper klasser -Jämförelse operatörer,(==, =, ,!=,!) -String hur man
Fel- och störningsanalys
 Fel- och störningsanalys Terminologi Antag att x är ett exakt värde och x är en approximation av x. Vi kallar då absoluta felet i x = x x, relativa felet i x = x x x. Ofta känner vi inte felet precis utan
Fel- och störningsanalys Terminologi Antag att x är ett exakt värde och x är en approximation av x. Vi kallar då absoluta felet i x = x x, relativa felet i x = x x x. Ofta känner vi inte felet precis utan
Grundläggande programmering med C# 7,5 högskolepoäng
 Grundläggande programmering med C# 7,5 högskolepoäng Provmoment: TEN1 Ladokkod: NGC011 Tentamen ges för: Omtentamen DE13, IMIT13 och SYST13 samt öppen för alla (Ifylles av student) (Ifylles av student)
Grundläggande programmering med C# 7,5 högskolepoäng Provmoment: TEN1 Ladokkod: NGC011 Tentamen ges för: Omtentamen DE13, IMIT13 och SYST13 samt öppen för alla (Ifylles av student) (Ifylles av student)
Maskinorienterad programmering. Kompendium: Aritmetik för HC12 Roger Johansson, 2013
 Maskinorienterad programmering Kompendium: Aritmetik för HC12 Roger Johansson, 2013 0 Aritmetik för HC12 1 Aritmetik 32 bitars multiplikation/division med 16-bitars processor. IEEE-754, flyttalsrepresentation
Maskinorienterad programmering Kompendium: Aritmetik för HC12 Roger Johansson, 2013 0 Aritmetik för HC12 1 Aritmetik 32 bitars multiplikation/division med 16-bitars processor. IEEE-754, flyttalsrepresentation
6. Ge korta beskrivningar av följande begrepp a) texteditor b) kompilator c) länkare d) interpretator e) korskompilator f) formatterare ( pretty-print
 Datalogi I, grundkurs med Java 10p, 2D4112, 2002-2003 Exempel på tentafrågor på boken Lunell: Datalogi-begreppen och tekniken Obs! Andra frågor än dessa kan komma på tentan! 1. Konvertera talet 186 till
Datalogi I, grundkurs med Java 10p, 2D4112, 2002-2003 Exempel på tentafrågor på boken Lunell: Datalogi-begreppen och tekniken Obs! Andra frågor än dessa kan komma på tentan! 1. Konvertera talet 186 till
Inledande programmering med C# (1DV402) 27+15=42 1 (22)
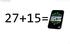 27+15=42 1 (22) Variabler Upphovsrätt för detta verk Detta verk är framtaget i anslutning till kursen Inledande programmering med C# vid Linnéuniversitetet. Du får använda detta verk så här: Allt innehåll
27+15=42 1 (22) Variabler Upphovsrätt för detta verk Detta verk är framtaget i anslutning till kursen Inledande programmering med C# vid Linnéuniversitetet. Du får använda detta verk så här: Allt innehåll
Klassdeklaration. Metoddeklaration. Parameteröverföring
 Syntax: Class Declaration Modifier Class Body Basic Class Member Klassdeklaration class Class Member Field Declaration Constructor Declaration Method Declaration Identifier Class Associations Motsvarar
Syntax: Class Declaration Modifier Class Body Basic Class Member Klassdeklaration class Class Member Field Declaration Constructor Declaration Method Declaration Identifier Class Associations Motsvarar
Fel- och störningsanalys
 Fel- och störningsanalys 1 Terminologi Antag att x är ett exakt värde och x är en approximation av x. Vi kallar då absoluta felet i x = x x, relativa felet i x = x x x. Ofta känner vi inte felet precis
Fel- och störningsanalys 1 Terminologi Antag att x är ett exakt värde och x är en approximation av x. Vi kallar då absoluta felet i x = x x, relativa felet i x = x x x. Ofta känner vi inte felet precis
Förenklad förklaring i anslutning till kompedieavsnitten 6.3 och 6.4
 Ext-6 (Ver 2010-08-09) 1(5) Förenklad förklaring i anslutning till kompedieavsnitten 6.3 och 6.4 Tecken-beloppsrepresentation av heltal Hur skall man kunna räkna med negativa tal i ett digitalt system,
Ext-6 (Ver 2010-08-09) 1(5) Förenklad förklaring i anslutning till kompedieavsnitten 6.3 och 6.4 Tecken-beloppsrepresentation av heltal Hur skall man kunna räkna med negativa tal i ett digitalt system,
DD1310/DD1314/DA3009 Programmeringsteknik LÄRANDEMÅL... Vilka läser kursen? ...FLER LÄRANDEMÅL. Föreläsning 1
 Skolan för Datavetenskap och kommunikation DD1310/DD1314/DA3009 Programmeringsteknik Föreläsning 1 Kursinfo Python-intro: print variabler reserverade ord input kommentarer beräkningar datatyper if-satser
Skolan för Datavetenskap och kommunikation DD1310/DD1314/DA3009 Programmeringsteknik Föreläsning 1 Kursinfo Python-intro: print variabler reserverade ord input kommentarer beräkningar datatyper if-satser
Översikt Introduktion DST 1. Nicholas Wickström. IDE, Högskolan i Halmstad. N. Wickström
 DST 1 Nicholas Wickström IDE, Högskolan i Halmstad 2009 1 Outline 1 Vad är Hårdvara? (Datorsystemmodell; processor m. periferi, IO, Minne) Typiskt för hårdvarunära programmering (datablad, register, datastrukturer,...)
DST 1 Nicholas Wickström IDE, Högskolan i Halmstad 2009 1 Outline 1 Vad är Hårdvara? (Datorsystemmodell; processor m. periferi, IO, Minne) Typiskt för hårdvarunära programmering (datablad, register, datastrukturer,...)
Programmeringsteknik I
 Programmeringsteknik I Föreläsning 2: Grundläggande Java Johan Öfverstedt Java Grundläggande begrepp Datatyper Selektion if Räckvidd (scope) Iteration while Klasser Objekt Metoder Metodhuvudet Kodstandarden
Programmeringsteknik I Föreläsning 2: Grundläggande Java Johan Öfverstedt Java Grundläggande begrepp Datatyper Selektion if Räckvidd (scope) Iteration while Klasser Objekt Metoder Metodhuvudet Kodstandarden
Loopar och datatyper. Föreläsning 3
 Loopar och datatyper Föreläsning 3 Dagens kluringar int x; printf("ange x:"); scanf("%d",&x); if(/*fyll i kod*/) printf("du angav x mellan 7 och 14"); int i=0; if(i++) i++; printf("%d",i++); //vad skrivs
Loopar och datatyper Föreläsning 3 Dagens kluringar int x; printf("ange x:"); scanf("%d",&x); if(/*fyll i kod*/) printf("du angav x mellan 7 och 14"); int i=0; if(i++) i++; printf("%d",i++); //vad skrivs
Loopar och datatyper. Föreläsning 3
 Loopar och datatyper Föreläsning 3 Dagens kluringar int x; printf("ange x:"); scanf("%d",&x); if(/*fyll i kod*/) printf("du angav x mellan 7 och 14"); int i=0; if(i++) i++; printf("%d",i++); //vad skrivs
Loopar och datatyper Föreläsning 3 Dagens kluringar int x; printf("ange x:"); scanf("%d",&x); if(/*fyll i kod*/) printf("du angav x mellan 7 och 14"); int i=0; if(i++) i++; printf("%d",i++); //vad skrivs
Objektorienterad programmering Föreläsning 4
 Objektorienterad programmering Föreläsning 4 Copyright Mahmud Al Hakim mahmud@dynamicos.se www.webbacademy.se Agenda Introduktion till objektorientering Klasser och Objekt Instansvariabler Metoder Introduktion
Objektorienterad programmering Föreläsning 4 Copyright Mahmud Al Hakim mahmud@dynamicos.se www.webbacademy.se Agenda Introduktion till objektorientering Klasser och Objekt Instansvariabler Metoder Introduktion
732G Linköpings universitet 732G11. Johan Jernlås. Översikt. Repetition. Felsökning. Datatyper. Referenstyper. Metoder / funktioner
 732G11 Linköpings universitet 2011-01-21 1 2 3 4 5 6 Skapa program Kompilera: Källkod Kompilator bytekod Köra: Bytekod Virtuell maskin Ett riktigt program Hej.java class Hej { public static void main (
732G11 Linköpings universitet 2011-01-21 1 2 3 4 5 6 Skapa program Kompilera: Källkod Kompilator bytekod Köra: Bytekod Virtuell maskin Ett riktigt program Hej.java class Hej { public static void main (
Extramaterial till Matematik Y
 LIBER PROGRAMMERING OCH DIGITAL KOMPETENS Extramaterial till Matematik Y NIVÅ TVÅ Taluppfattning och tals användning ELEV Det finns många olika programmeringsspråk. I den här uppgiften ska du få bekanta
LIBER PROGRAMMERING OCH DIGITAL KOMPETENS Extramaterial till Matematik Y NIVÅ TVÅ Taluppfattning och tals användning ELEV Det finns många olika programmeringsspråk. I den här uppgiften ska du få bekanta
Föreläsning 3: Typomvandling, villkor och val, samt textsträngar
 Föreläsning 3: Typomvandling, villkor och val, samt textsträngar Camilla Kirkegaard camilla.kirkegaard@liu.se Linköpings universitet Sweden October 14, 2013 1 Innehåll n n n n n Repetition Typomvandlingar
Föreläsning 3: Typomvandling, villkor och val, samt textsträngar Camilla Kirkegaard camilla.kirkegaard@liu.se Linköpings universitet Sweden October 14, 2013 1 Innehåll n n n n n Repetition Typomvandlingar
Data, typ, selektion, iteration
 Data, typ, selektion, iteration En programmeringkurs på halvfart IDT, MDH ttp://www.negative-g.com/nolimits/no%20limits%20defunct%20coasters.htm 1 Dagens agenda Talrepresentation Typkonvertering Sekvens
Data, typ, selektion, iteration En programmeringkurs på halvfart IDT, MDH ttp://www.negative-g.com/nolimits/no%20limits%20defunct%20coasters.htm 1 Dagens agenda Talrepresentation Typkonvertering Sekvens
F2 Datatyper och variabler. ID1004 Objektorienterad programmering Fredrik Kilander
 F2 Datatyper och variabler ID1004 Objektorienterad programmering Fredrik Kilander fki@kth.se Datatyper Java är ett starkt typat språk Varje slags data har en datatyp Datatyp Javasyntax Exempel Teckensträng
F2 Datatyper och variabler ID1004 Objektorienterad programmering Fredrik Kilander fki@kth.se Datatyper Java är ett starkt typat språk Varje slags data har en datatyp Datatyp Javasyntax Exempel Teckensträng
Objektorienterad Programmering (TDDC77)
 Objektorienterad Programmering (TDDC77) Föreläsning II: utmatning, variabler, typer Ahmed Rezine IDA, Linköpings Universitet Hösttermin 2017 Outline Java Språket Utmatning av Sträng litteraler Variabler
Objektorienterad Programmering (TDDC77) Föreläsning II: utmatning, variabler, typer Ahmed Rezine IDA, Linköpings Universitet Hösttermin 2017 Outline Java Språket Utmatning av Sträng litteraler Variabler
Algoritmer, datastrukturer och komplexitet
 Algoritmer, datastrukturer och komplexitet Övning 6 Anton Grensjö grensjo@csc.kth.se 4 oktober 2017 1 Idag Algoritmkonstruktion (lite blandat) Redovisning och inlämning av labbteori 3 2 Uppgifter Uppgift
Algoritmer, datastrukturer och komplexitet Övning 6 Anton Grensjö grensjo@csc.kth.se 4 oktober 2017 1 Idag Algoritmkonstruktion (lite blandat) Redovisning och inlämning av labbteori 3 2 Uppgifter Uppgift
Föreläsning 2. Variabler, tilldelning och kodblock{} if-satsen Logiska operatorer Andra operatorer Att programmera
 Föreläsning 2 Variabler, tilldelning och kodblock if-satsen Logiska operatorer Andra operatorer Att programmera Variabler Det är i variabler som all data (information) lagras. Genom att ändra värde på
Föreläsning 2 Variabler, tilldelning och kodblock if-satsen Logiska operatorer Andra operatorer Att programmera Variabler Det är i variabler som all data (information) lagras. Genom att ändra värde på
a) A = 3 B = 4 C = 9 D = b) A = 250 B = 500 C = a) Tvåhundrasjuttiotre b) Ettusenfemhundranittio
 Övningsblad 2.1 A Heltal 1 Skriv det tal som motsvaras av bokstaven på tallinjen. A B C D E F 0 10 0 50 A = B = C = D = E = F = G H I J K L 10 20 50 100 G = H = I = J = K = L = 2 Placera ut talen från
Övningsblad 2.1 A Heltal 1 Skriv det tal som motsvaras av bokstaven på tallinjen. A B C D E F 0 10 0 50 A = B = C = D = E = F = G H I J K L 10 20 50 100 G = H = I = J = K = L = 2 Placera ut talen från
Alla datorprogram har en sak gemensam; alla processerar indata för att producera något slags resultat, utdata.
 Att förstå variabler Alla datorprogram har en sak gemensam; alla processerar indata för att producera något slags resultat, utdata. Vad är en variabel? En variabel är en plats att lagra information. Precis
Att förstå variabler Alla datorprogram har en sak gemensam; alla processerar indata för att producera något slags resultat, utdata. Vad är en variabel? En variabel är en plats att lagra information. Precis
TAL OCH RÄKNING HELTAL
 1 TAL OCH RÄKNING HELTAL Avsnitt Heltal... 6 Beräkningar med heltal...16 Test Kan du?... 1, 27 Kapiteltest... 28 Begrepp addition avrundning bas differens division exponent faktor kvadratroten ur kvot
1 TAL OCH RÄKNING HELTAL Avsnitt Heltal... 6 Beräkningar med heltal...16 Test Kan du?... 1, 27 Kapiteltest... 28 Begrepp addition avrundning bas differens division exponent faktor kvadratroten ur kvot
Kompilering och exekvering. Föreläsning 1 Objektorienterad programmering DD1332. En kompilerbar och körbar java-kod. Kompilering och exekvering
 Föreläsning 1 Objektorienterad programmering DD1332 Introduktion till Java Kompilering, exekvering, variabler, styrstrukturer Kompilering och exekvering Ett program måste översättas till datorns språk
Föreläsning 1 Objektorienterad programmering DD1332 Introduktion till Java Kompilering, exekvering, variabler, styrstrukturer Kompilering och exekvering Ett program måste översättas till datorns språk
Flyttal kan också hantera vanliga tal som både 16- och 32-bitars dataregister hanterar.
 FLYTTAL REAL Flyttal används i datorsystem för s k flytande beräkning vilket innebär att decimalkommat inte har någon fix (fast) position. Flyttal består av 2 delar (mantissa och exponent). När ett datorsystem
FLYTTAL REAL Flyttal används i datorsystem för s k flytande beräkning vilket innebär att decimalkommat inte har någon fix (fast) position. Flyttal består av 2 delar (mantissa och exponent). När ett datorsystem
Algoritmer, datastrukturer och komplexitet
 Algoritmer, datastrukturer och komplexitet Övning 6 Anton Grensjö grensjo@csc.kth.se 9 oktober 2015 Anton Grensjö ADK Övning 6 9 oktober 2015 1 / 23 Översikt Kursplanering Ö5: Grafalgoritmer och undre
Algoritmer, datastrukturer och komplexitet Övning 6 Anton Grensjö grensjo@csc.kth.se 9 oktober 2015 Anton Grensjö ADK Övning 6 9 oktober 2015 1 / 23 Översikt Kursplanering Ö5: Grafalgoritmer och undre
ÖH kod. ( en variant av koden används i dag till butikernas streck-kod ) William Sandqvist
 ÖH 8.4 7-4-2-1 kod Kodomvandlare 7-4-2-1-kod till BCD-kod. Vid kodning av siffrorna 0 9 användes förr ibland en kod med vikterna 7-4-2-1 i stället för den binära kodens vikter 8-4-2-1. I de fall då en
ÖH 8.4 7-4-2-1 kod Kodomvandlare 7-4-2-1-kod till BCD-kod. Vid kodning av siffrorna 0 9 användes förr ibland en kod med vikterna 7-4-2-1 i stället för den binära kodens vikter 8-4-2-1. I de fall då en
IE1204 Digital Design
 IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska kretsar F7 F8 Ö4 F9 Ö5 Multiplexor KK2 LAB2 Låskretsar, vippor, FSM
IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska kretsar F7 F8 Ö4 F9 Ö5 Multiplexor KK2 LAB2 Låskretsar, vippor, FSM
Blandade uppgifter om tal
 Blandade uppgifter om tal Uppgift nr A/ Beräkna värdet av (-3) 2 B/ Beräkna värdet av - 3 2 Uppgift nr 2 Skriv (3x) 2 utan parentes Uppgift nr 3 Multiplicera de de två talen 2 0 4 och 4 0 med varandra.
Blandade uppgifter om tal Uppgift nr A/ Beräkna värdet av (-3) 2 B/ Beräkna värdet av - 3 2 Uppgift nr 2 Skriv (3x) 2 utan parentes Uppgift nr 3 Multiplicera de de två talen 2 0 4 och 4 0 med varandra.
Objektorienterad programmering i Java I. Uppgifter: 2 Beräknad tid: 5-8 timmar (OBS! Endast ett labbtillfälle) Att läsa: kapitel 5 6
 Laboration 2 Objektorienterad programmering i Java I Uppgifter: 2 Beräknad tid: 5-8 timmar (OBS! Endast ett labbtillfälle) Att läsa: kapitel 5 6 Syfte: Att kunna använda sig av olika villkors- och kontrollflödeskonstruktioner
Laboration 2 Objektorienterad programmering i Java I Uppgifter: 2 Beräknad tid: 5-8 timmar (OBS! Endast ett labbtillfälle) Att läsa: kapitel 5 6 Syfte: Att kunna använda sig av olika villkors- och kontrollflödeskonstruktioner
Feluppskattning och räknenoggrannhet
 Vetenskapliga beräkningar III 10 Kapitel 2. Feluppskattning och räknenoggrannhet Sedan datorerna togs i bruk på 1950 talet, har det blivit möjligt att utföra beräkningar i långt större skala än tidigare.
Vetenskapliga beräkningar III 10 Kapitel 2. Feluppskattning och räknenoggrannhet Sedan datorerna togs i bruk på 1950 talet, har det blivit möjligt att utföra beräkningar i långt större skala än tidigare.
F4. programmeringsteknik och Matlab
 Programmeringsspråk Föreläsning 4 programmeringsteknik och Matlab 2D1312/ 2D1305 Introduktion till Java Kompilering, exekvering, variabler, styrstrukturer 1 Ett program är en eller flera instruktioner
Programmeringsspråk Föreläsning 4 programmeringsteknik och Matlab 2D1312/ 2D1305 Introduktion till Java Kompilering, exekvering, variabler, styrstrukturer 1 Ett program är en eller flera instruktioner
Exempelsamling Assemblerprogrammering
 Exempelsamling Assemblerprogrammering I uppgifterna nedan utgå från följande programskelett: #include.data var1:.word 12 var2:.word 19 sum: prod:.float 0.set noreorder.text.globl start.ent start
Exempelsamling Assemblerprogrammering I uppgifterna nedan utgå från följande programskelett: #include.data var1:.word 12 var2:.word 19 sum: prod:.float 0.set noreorder.text.globl start.ent start
Arbetsblad 1:1. Tiondelar på tallinjen 0,1 0,5 0,9 0,2 0,8 0,3 0,8 1,1 1,5 1,6 2,1 2,4 1,1 1,4 2,6 3,2 3,8
 Arbetsblad 1:1 Tiondelar på tallinjen 1 Skriv rätt tal på pilarna. 0,1 0,5 0,9 1,2 0 1 2 0,3 0,8 1,1 1,5 0 1 3 1,1 1,6 2,1 2,4 1 2 4 5 0,2 0,8 1,4 2,6 0 1 2 3 1,4 2,6 3,2 3,8 1 2 3 4 6 Sätt ut pilar som
Arbetsblad 1:1 Tiondelar på tallinjen 1 Skriv rätt tal på pilarna. 0,1 0,5 0,9 1,2 0 1 2 0,3 0,8 1,1 1,5 0 1 3 1,1 1,6 2,1 2,4 1 2 4 5 0,2 0,8 1,4 2,6 0 1 2 3 1,4 2,6 3,2 3,8 1 2 3 4 6 Sätt ut pilar som
Arbetsblad 1:1. Tiondelar på tallinjen 0,9 1,1 0,8. 6 Sätt ut pilar som pekar på talen: A = 0,3 B = 0,8 C = 1,4
 Arbetsblad 1:1 Tiondelar på tallinjen 1 Skriv rätt tal på pilarna. 0,9 0 1 2 0 1 3 1,1 1 2 4 0,8 0 1 2 3 5 1 2 3 4 6 Sätt ut pilar som pekar på talen: A = 0,3 B = 0,8 C = 1,4 0 1 7 Sätt ut pilar som pekar
Arbetsblad 1:1 Tiondelar på tallinjen 1 Skriv rätt tal på pilarna. 0,9 0 1 2 0 1 3 1,1 1 2 4 0,8 0 1 2 3 5 1 2 3 4 6 Sätt ut pilar som pekar på talen: A = 0,3 B = 0,8 C = 1,4 0 1 7 Sätt ut pilar som pekar
Arbetsblad 1:1. Tiondelar på tallinjen. 6 Sätt ut pilar som pekar på talen: A = 0,3 B = 0,8 C = 1,4
 Arbetsblad 1:1 Tiondelar på tallinjen 1 Skriv rätt tal på pilarna. 0 1 2 0 1 3 1 2 4 0 1 2 3 5 1 2 3 4 6 Sätt ut pilar som pekar på talen: A = 0,3 B = 0,8 C = 1,4 0 1 7 Sätt ut pilar som pekar på talen:
Arbetsblad 1:1 Tiondelar på tallinjen 1 Skriv rätt tal på pilarna. 0 1 2 0 1 3 1 2 4 0 1 2 3 5 1 2 3 4 6 Sätt ut pilar som pekar på talen: A = 0,3 B = 0,8 C = 1,4 0 1 7 Sätt ut pilar som pekar på talen:
Föreläsning 4. Val, boolska värden, läsbarhet, osv
 Föreläsning 4 Val, boolska värden, läsbarhet, osv Exempel /* Programmeringsteknik med C och Matlab Programmering i C HT13 Exempel Fil: plus_one.c Författare: Jonny Pettersson Användare: jonny Datum: 7
Föreläsning 4 Val, boolska värden, läsbarhet, osv Exempel /* Programmeringsteknik med C och Matlab Programmering i C HT13 Exempel Fil: plus_one.c Författare: Jonny Pettersson Användare: jonny Datum: 7
Kapitel 2. Feluppskattning och räknenoggrannhet
 Kapitel 2. Feluppskattning och räknenoggrannhet Sedan datorerna togs i bruk på 1950 talet, har det blivit möjligt att utföra beräkningar i långt större skala än tidigare. Liksom vid beräkningar för hand
Kapitel 2. Feluppskattning och räknenoggrannhet Sedan datorerna togs i bruk på 1950 talet, har det blivit möjligt att utföra beräkningar i långt större skala än tidigare. Liksom vid beräkningar för hand
Talrepresentation. Ett tal kan representeras binärt på många sätt. De vanligaste taltyperna som skall representeras är:
 Talrepresentation Ett tal kan representeras inärt på många sätt. De vanligaste taltyperna som skall representeras är: Heltal, positiva heltal (eng. integers ett-komplementet, två-komplementet, sign-magnitude
Talrepresentation Ett tal kan representeras inärt på många sätt. De vanligaste taltyperna som skall representeras är: Heltal, positiva heltal (eng. integers ett-komplementet, två-komplementet, sign-magnitude
Föreläsning 3. Iteration while-satsen
 Föreläsning 3 Iteration while-satsen Datatypen double I en dator kan man inte lagra hur stora eller hur små tal som helst. De enkla datatyperna, som används för att lagra tal (t.ex. int och double), har
Föreläsning 3 Iteration while-satsen Datatypen double I en dator kan man inte lagra hur stora eller hur små tal som helst. De enkla datatyperna, som används för att lagra tal (t.ex. int och double), har
Vem är vem på kursen. Objektorienterad programvaruutveckling GU (DIT011) Kursbok Cay Horstmann: Big Java 3rd edition.
 Institutionen för Datavetenskap Göteborgs universitet HT2009 DIT011 Vem är vem på kursen Objektorienterad programvaruutveckling GU (DIT011) Kursansvarig : Katarina Blom, tel 772 10 60 Rum: 6126 (E-huset)
Institutionen för Datavetenskap Göteborgs universitet HT2009 DIT011 Vem är vem på kursen Objektorienterad programvaruutveckling GU (DIT011) Kursansvarig : Katarina Blom, tel 772 10 60 Rum: 6126 (E-huset)
DIGITALA TAL OCH BOOLESK ALGEBRA
 DIGITALA TAL OCH BOOLESK ALGEBRA Innehåll Talsystem och koder Aritmetik för inära tal Grundläggande logiska operationer Logiska grindar Definitioner i Boolesk algera Räknelagar BINÄRA TALSYSTEMET Binärt
DIGITALA TAL OCH BOOLESK ALGEBRA Innehåll Talsystem och koder Aritmetik för inära tal Grundläggande logiska operationer Logiska grindar Definitioner i Boolesk algera Räknelagar BINÄRA TALSYSTEMET Binärt
Uppgift: Algoritm för att beräkna kontrollsiffran i ett personnummer givet de 9 första siffrorna. Torrsimning av algoritm för personnummer
 F6 Observera att när man utvecklar program så är inte alla lösningar på vägen korrekta. Speciellt den här gången så finns många OH med program som inte fungerar eftersom det är just det vi skall se på
F6 Observera att när man utvecklar program så är inte alla lösningar på vägen korrekta. Speciellt den här gången så finns många OH med program som inte fungerar eftersom det är just det vi skall se på
Digital Aritmetik Unsigned Integers Signed Integers"
 Digital Aritmetik Unsigned Integers Signed Integers" Slides! Per Lindgren! EISLAB! Per.Lindgren@ltu.se! Original Slides! Ingo Sander! KTH/ICT/ES! ingo@kth.se! Talrepresentationer" Ett tal kan representeras
Digital Aritmetik Unsigned Integers Signed Integers" Slides! Per Lindgren! EISLAB! Per.Lindgren@ltu.se! Original Slides! Ingo Sander! KTH/ICT/ES! ingo@kth.se! Talrepresentationer" Ett tal kan representeras
Iteration while-satsen
 Datatypen double TDA143 I1 Programmerade system Föreläsning 3 (OH-bilder 3) Iteration while-satsen Christer Carlsson I en dator kan man inte lagra hur stora eller hur små tal som helst. De enkla datatyperna,
Datatypen double TDA143 I1 Programmerade system Föreläsning 3 (OH-bilder 3) Iteration while-satsen Christer Carlsson I en dator kan man inte lagra hur stora eller hur små tal som helst. De enkla datatyperna,
Sammanfattninga av kursens block inför tentan
 FÖRELÄSNING 14 Sammanfattninga av kursens block inför tentan BILD Vi har jobbat med numerisk metoder, datorprogram och tolkning av lösning. Numeriska metoder BILD olika områden: Linjära ekvationssytem,
FÖRELÄSNING 14 Sammanfattninga av kursens block inför tentan BILD Vi har jobbat med numerisk metoder, datorprogram och tolkning av lösning. Numeriska metoder BILD olika områden: Linjära ekvationssytem,
Föreläsning 2 Programmeringsteknik och Matlab DD1312. Programspråk. Utskrift på skärmen
 Föreläsning 2 Programmeringsteknik och Matlab DD1312 Introduktion till python Variabler,datatyper, omvandling av typer sfunktioner Två olika typer av program omvandlar högnivå till lågnivå program: Interpreterande
Föreläsning 2 Programmeringsteknik och Matlab DD1312 Introduktion till python Variabler,datatyper, omvandling av typer sfunktioner Två olika typer av program omvandlar högnivå till lågnivå program: Interpreterande
i LabVIEW. Några programmeringstekniska grundbegrepp
 Institutionen för elektroteknik Några programmeringstekniska grundbegrepp 1999-02-16 Inledning Inom datorprogrammering förekommer ett antal grundbegrepp som är i stort sett likadana oberoende om vi talar
Institutionen för elektroteknik Några programmeringstekniska grundbegrepp 1999-02-16 Inledning Inom datorprogrammering förekommer ett antal grundbegrepp som är i stort sett likadana oberoende om vi talar
Grunderna i C++ T A. Skapad av Matz Johansson BergströmLIMY
 Grunderna i C++ ARK 385: Virtuella Verktyg i en Materiell värld AT Arkitektur & Teknik Chalmers Tekniska Högskola 2009 - Kursen skapades (3 förel.) 2010-6 förel. + 2 projekt 2011-8 förel. Helt omarbetade
Grunderna i C++ ARK 385: Virtuella Verktyg i en Materiell värld AT Arkitektur & Teknik Chalmers Tekniska Högskola 2009 - Kursen skapades (3 förel.) 2010-6 förel. + 2 projekt 2011-8 förel. Helt omarbetade
Övningshäfte 2: Induktion och rekursion
 GÖTEBORGS UNIVERSITET MATEMATIK 1, MMG200, HT2017 INLEDANDE ALGEBRA Övningshäfte 2: Induktion och rekursion Övning D Syftet är att öva förmågan att utgående från enkla samband, aritmetiska och geometriska,
GÖTEBORGS UNIVERSITET MATEMATIK 1, MMG200, HT2017 INLEDANDE ALGEBRA Övningshäfte 2: Induktion och rekursion Övning D Syftet är att öva förmågan att utgående från enkla samband, aritmetiska och geometriska,
Föreläsning 2 - Intro till Java
 Föreläsning 2 - Intro till Java Sammanfattning av Lektion 1 (kap 2): Vad behövs för att kunna programmera? DrJava (t ex) Java (installera först!) Reserverade ord (t ex if, while...) Primitiva variabler
Föreläsning 2 - Intro till Java Sammanfattning av Lektion 1 (kap 2): Vad behövs för att kunna programmera? DrJava (t ex) Java (installera först!) Reserverade ord (t ex if, while...) Primitiva variabler
Föreläsning 2 Programmeringsteknik och Matlab DD1312. Programspråk. Utskrift på skärmen
 Föreläsning 2 Programmeringsteknik och Matlab DD1312 Introduktion till python Variabler, datatyper, omvandling av typer sfunktioner Två olika typer av program omvandlar högnivå till lågnivå program: Interpreterande
Föreläsning 2 Programmeringsteknik och Matlab DD1312 Introduktion till python Variabler, datatyper, omvandling av typer sfunktioner Två olika typer av program omvandlar högnivå till lågnivå program: Interpreterande
Programmering, grundkurs, 8.0 hp HI1024, HI1900 etc., Tentamen TEN1. Måndagen den 10 januari 2011,
 Programmering, grundkurs, 8.0 hp HI1024, HI1900 etc., Tentamen TEN1 Måndagen den 10 januari 2011, 8.15 12.15 Tentamen består av två delar, del A och del B. Del A innehåller 10 kryssfrågor på olika teman
Programmering, grundkurs, 8.0 hp HI1024, HI1900 etc., Tentamen TEN1 Måndagen den 10 januari 2011, 8.15 12.15 Tentamen består av två delar, del A och del B. Del A innehåller 10 kryssfrågor på olika teman
Lösningsanvisningar till de icke obligatoriska workoutuppgifterna
 Lösningsanvisningar till de icke obligatoriska workoutuppgifterna Linjära system 7. (a) Falskt. Kondition är en egenskap hos problemet oberoende av precisionen i beräkningarna. (b) Falskt. Pivotering påverkar
Lösningsanvisningar till de icke obligatoriska workoutuppgifterna Linjära system 7. (a) Falskt. Kondition är en egenskap hos problemet oberoende av precisionen i beräkningarna. (b) Falskt. Pivotering påverkar
Föreläsning 2 Programmeringsteknik och C DD1316. Mikael Djurfeldt
 Föreläsning 2 Programmeringsteknik och C DD1316 Mikael Djurfeldt Föreläsning 2 Programmeringsteknik och C Python introduktion Utskrift Inläsning Variabler Datatyp Aritmetiska operatorer Omvandling
Föreläsning 2 Programmeringsteknik och C DD1316 Mikael Djurfeldt Föreläsning 2 Programmeringsteknik och C Python introduktion Utskrift Inläsning Variabler Datatyp Aritmetiska operatorer Omvandling
LAB 1. FELANALYS. 1 Inledning. 2 Flyttal. 1.1 Innehåll. 2.1 Avrundningsenheten, µ, och maskinepsilon, ε M
 TANA21+22/ 5 juli 2016 LAB 1. FELANALYS 1 Inledning I laborationerna används matrishanteringsprogrammet MATLAB. som genomgående använder dubbel precision vid beräkningarna. 1.1 Innehåll Du ska 1. bestämma
TANA21+22/ 5 juli 2016 LAB 1. FELANALYS 1 Inledning I laborationerna används matrishanteringsprogrammet MATLAB. som genomgående använder dubbel precision vid beräkningarna. 1.1 Innehåll Du ska 1. bestämma
PASS 2. POTENSRÄKNING. 2.1 Definition av en potens
 PASS. POTENSRÄKNING.1 Definition av en potens Typiskt för matematik är ett kort, lätt och vackert framställningssätt. Den upprepade additionen går att skriva kortare i formen där anger antalet upprepade
PASS. POTENSRÄKNING.1 Definition av en potens Typiskt för matematik är ett kort, lätt och vackert framställningssätt. Den upprepade additionen går att skriva kortare i formen där anger antalet upprepade
Lösningar till tentauppgifterna sätts ut på kurssidan på nätet idag kl 19. Omtentamen i Programmering C, 5p, fristående, kväll, 040110.
 1(8) ÖREBRO UNIVERSITET INSTITUTIONEN FÖR TEKNIK Lösningar till tentauppgifterna sätts ut på kurssidan på nätet idag kl 19. Denna tenta kommer att vara färdigrättad On 14/1-04 och kan då hämtas på mitt
1(8) ÖREBRO UNIVERSITET INSTITUTIONEN FÖR TEKNIK Lösningar till tentauppgifterna sätts ut på kurssidan på nätet idag kl 19. Denna tenta kommer att vara färdigrättad On 14/1-04 och kan då hämtas på mitt
