Grundläggande digitalteknik
|
|
|
- Dan Lund
- för 9 år sedan
- Visningar:
Transkript
1 Grundläggande digitalteknik Jan Carlsson Inledning I den verkliga världen vet vi att vi kan få vilka värden som helst när vi mäter på något. En varm sommardag visar termometern kanske 6, 7 C. Men när det gäller digitaltekniken så gäller inte detta. Här kan man bara arbeta med vissa distinkta värden som man vanligen benämner och. Dessa är digitalteknikens grundläggande byggstenar. Skulle vi bara ha dessa två tal att spela med skulle vi inte komma så långt. Vi kommer därför att se på hur man kan representera vanliga tal så att de passar för digitaltekniken i ett avsnitt om talrepresentation. Sedan ska vi börja titta lite närmare på den egentliga digitaltekniken och se vad vi kan använda den till. Digitaltekniken brukar indelas i kombinatoriska nät och sekvensnät. Dessa kan sedan realiseras på en mängd olika sätt. Detta kan vara till exempel med hjälp av pneumatik, hydraulik, PLC, vanligen menar man dock, när man talar om digitalteknik, elektroniska realiseringar och det är det enda som vi nu kommer att beröra 3. Det finns dock många sätt att göra digitaltekniska realiseringar med hjälp av elektronik. Kombinatoriska nät är nät som inte har något minne. Det som man lägger in som indata kommer direkt ut på andra sidan. Vad som kommer ut avgörs av något logiskt vilkor. Låt oss ta ett exempel: Det är vanligt att maskiner i verkstadsindustrin har en säkerhetsutrustning som gör att man måste använda båda händerna. Skälet är givetvis att operatören inte ska skadas. Detta kan vi uppfatta som att vi har ett logiskt vilkor som måste vara uppfyllt för att maskinen ska göra sitt jobb. Kallar vi vänstra handen för V, högra handen för H och maskinen för M får vi det logiska sambandet M = V och H. Detta är ett exempel på en logisk funktion. Sekvensnät är digitala nät som, i någon mening, minns sin förhistoria. Utsignalerna är med andra ord beroende av vad som har hänt tidigare. Låt oss ta ett exempel: Vi ska räkna,, 3, 4,,, 3, 4,,... och så vidare. Här kommer Generellt hänvisas till Alciatore[] kap 6 för denna del i kursen. I en sådan här kurs kommer vi, naturligtvis, bara kunna pressentera de mest grundläggande delarna. Den som är intresserad av att lära sig mera hänvisas till någon lämplig lärobok i ämnet, till exempel Hemert[]. 3 Den första fungerande datorn var mekanisk och bygdes av svensken Georg Scheutz, tillsammans med sin son Edvard Scheutz. Vanligen anförs Charles Babbage som den förste som konstruerade en dator, men hans konstruktion blev inte färdig under Babbages livstid.
2 tvåan alltid efter ettan, trean alltid efter tvåan och så vidare. I industriella sammanhang är det inte ovanligt att man har denna typ av styrsystem. Det är vanligt att man realiserar dessa med hjälp av PLC-styrning. Ett sekvensnät kan, emellertid, vara mycket komplext. Som exempel på detta kan man tänka på styrenheten i en dator. Ett program består av instruktioner, dessa skall hämtas, avkodas, utföras och sedan kan man behöva skriva tillbaka information till minnet. Kallar vi hämta för H, avkoda för A, utföra för U och tillbakaskrivningen för T får vi ett sekvensnät H, A, U, T, H, A, U, T, H,... Detta fortgår, i princip, tills dess att programmet är klart. Realiseringen av ett digitalt nät bör man, principiellt sett, skilja från det digitala nätets logiska konstruktion. Vi kommer här främst att se hur man kan använda sig av olika standardkretsar, men ni bör vara medveterna om att det blir vanligare och vanligare med andra lösningar, till exempel olika former av programmerbar logik. Det finns flera olika halvledarteknologier som används, vi kommer att, kortfattat, behandla TTL och CMOS, främst i samband med laborationen. Talrepresentation Det vanliga talsystemet går från 9, vi använder oss således av tio olika symboler. Detta talsystem kallas därför det decimala talsystemet. 4 Det binära talsystemet använder bara symbolerna och. Sambandet mellan de decimala talen och de binära framgår av nedanstående tabell. Det binära talsystemet är bra för datorer, men det passar inte särskilt bra för människor. Därför buntar man ofta samman fyra binära tal i ett paket om fyra bitar. Då får man det hexadecimala talsystemet. Ibland använder man även ett talsystem som går från till 7, detta kallas för det oktala talsystemet 5. 4 Decem är latin för talet tio. Det är inte självklart att vi har detta system. Babylonerna och Yuki-indianerna i Californien använde det oktala talsystemet. Mayaindianerna använde ett talsystem med basen. 5 För datorer behöver man även kunna representera flyttal, tillexemel , För att veta hur detta görs hänvisar jag till någon bok om datorarkitektur, till exempel Stallings[3].
3 Decimalt Binärt Hexadecimalt A B C 3 D 4 E 5 F 3 Kombinatoriska nät 3. Grundläggande funktioner Vi har redan sett hur man kan realisera en logisk grundfunktion, nämligen ochfunktionen. Det finns emellertid flera sådana funktioner. Vi ska gå igenom de vanligaste med hjälp av sanningstabeller som kan användas för att definniera dessa funktioner. Det första som man ska göra klart för sig är att står för sann, det vill säga att ett vist vilkor är uppfyllt och att står för falsk, det vill säga att ett vist vilkor inte är uppfyllt. Om A och B står för insignalerna så får C vara deras utsignaler. Vi kan då få följande tabeller: A C Inverterare C = A A B C Och-funktion C = A B A B C Inklusivt Eller-funktion C = A + B 3
4 A B C Exklusivt Eller-funktion C = A B Här kan vi göra några anmärkningar, notera att vi har sambandet + =. Det är här inte fråga om aritmetik utan om logik! Antingen är något sant eller falskt, det finns inget jättesant. Sen kan vi se att Eller förekommer i två varianter. Detta beror på att det vardagliga språket är mångtydigt, medan de logiska uttrycken måste var entydiga. Antag att jag säger: I morgon regnar det eller går jag på bio. Denna sats kommer att vara uppfyld om det regnar eller om jag går på bio, men man kan ju faktiskt inte utesluta att jag går på bio trots att det regnar. Detta är ett exempel på Inklusivt Eller. Säger jag i stället: I morgon, klockan, kommer jag att vara i Kalmar eller Oskarshamn. Satsen kommer att vara uppfyld om jag är i Kalmar eller Oskarshamn vid den aktuella tidpunkten, däremot kan jag knappast vara på två ställen samtidigt. Detta är ett exempel på Exklusivt Eller. Det är vanligt att man kopplar en inverterare efter Och-kretsar samt Ellerkretsar. Dessa har fått egna namn. A B C NAND-funktion C = A B A B C NOR-funktion C = A + B A B C Inverterad Exklusivt Eller-funktion C = A B 3. Boolesk algebra I Alciatore[] pp ges ett antal samband som gäller för Boolesk algebra 6. Till exempel kan man finna att A = A. Jag hänvisar till dessa sidor utan att 6 George Boole,
5 återge dem här. Man kan emellertid notera att dessa samband gäller parvis. De Morgans 7 lagar kan till exempel skrivas som: { A + B + C +... = A B C... A B C... = A + B + C +... De Booleska räknereglerna kan användas till att förenkla logiska funktioner så att de inte blir onödigt komplicerade. Vi ska nu ta upp frågan om hur man går tillväga för att bestämma en Boolesk funktion. Det första man ska göra är, naturligtvis, att tänka efter vilket problem som man egentligen skall lösa, så att själva problemställningen är relevant. Därefter bör man försöka ställa upp en sanningstabell som beskriver den logiska funktionen. Man har därvid nytta av att kunna sätta upp funktionens mintermer. Vi kan se hur detta fungerar för det fall med tre variabler. Variabelnummer A B C Minterm A B C A B C A B C 3 A B C 4 A B C 5 A B C 6 A B C 7 A B C Vi kan nu ställa upp en sanningstabell för den funktion som vi önskar realisera. Därefter kan vi erhålla det Booleska uttrycket genom att bilda summan av de mintermer för vilken funktionen antar värdet ett. Exempel Variabelnummer A B C Minterm Funktion f A B C A B C A B C 3 A B C 4 A B C 5 A B C 6 A B C 7 A B C Vi kan direkt konstatera att det är ganska utrymmeskrävande att skriva funkrionen på detta sätt. Ofta använder man sig därför ofta av ett kortare skrivsätt genom helt enkelt skriva summan av de variabelnummer där funktionen antar värdet ett. Funktionen kan då skrivas som: 7 Augustus De Morgan, f(a, B, C) = (,, 4, 6) 5
6 Nu kan vi bilda den Boolska funktionen som summan av mintermerna har värdet ett. Den blir då följande: f(a, B, C) = A B C + A B C + A B C + A B C Nu kan vi få användning för de Booleska räknereglerna för att förenkla det. f(a, B, C) = A B (C + C) + A C(B + B) Eftersom det gäller att C + C = och B + B = får vi: 3.3 Karnaugh-diagram f(a, B, C) = A B + A C Det kan ibland vara besvärligt att förenkla ett uttryck genom algebraiska räkningar. Det kan ofta vara praktiskt att, istället för att räkna, lösa minimeringsuppgiften grafiskt med hjälp av Karnaugh 8 -diagram. När man använder sig av Karnaugh-diagram utnyttjar man räkneregeln X+X = på ett systematiskt sätt genom att göra inringningar i ett diagram. På diagrammets axlar sätter man in de ingående variablerna ordnade på ett sådant sätt att mellan två näraliggande rader eller kollumner är ett. Sedan ringar man in ettorna i Karnaudiagrammet. Man får bara ringa in vertikalt eller horisontellt. Inga diagonaler, med andra ord. Antalet ettor får bara vara en potens av två, det vill säga n =,,, 4, 8,... då n =,,, 3,... Man ska eftersträva att göra inringningarna så stora som möjligt och de får gärna överlappa varandra. Flera inringningar förbinds med ett logiskt eller. Sedan tittar man på inringningen för att se vad som är konstant under inringningen. Variabler som ändrar på sig i en inringning försvinner på grund av räkneregeln X + X =. Exempel Vi kan se hur man kan använda denna teknik genom att se på ett exempel. Vi tittar på funktionen f(a, B) = (, ). Variabelnummer A B f(a, B) 3 A 3 B Vi ser att B vaierar över ingingningen, således försvinner B. A är däremot konstant under inringningen och har värdet. Vi får därför att: 8 Maurice Karnaugh f(a, B) = A 6
7 Vi återvänder nu till Exempel. Karnaugh-diagrammet för funktionen f(a, B, C) = (,, 4, 6) blir då: A C 5 4 B Här har vi två stycken inringningar. För den vänstra ser vi att C, medan både A och B är konstanta med värdet noll. Denna inriningen motsvars av A B För den högra inringningen gäller det att A är konstant med värdet ett och att C är konstant med värdet noll. Däremot ser vi att B varierar varför B försvinner. Denna inringning motsvaras av A C. Eftersom inringningarna förbinds met ett logiskt Eller får vi att funktionen blir: f(a, B, C) = A B + A C Ibland är det så att vissa värden i en sanningstabell inte är specificerade. Detta kallar man för ett don t care värde och man markerat det med ett i Karnaughdiagrammet. Detta utnyttjar man genom att själv välja om man skall ringa in det eller låta bli. 4 Sekvensnät Sekvensnät består av ett kombinatoriskt nät som man, på något sätt, har för sett med ett minneselement. I praktiken innebär det för det mesta att man använder sig av en vippa. Vi kan ta en D-vippa som exempel. En D-vippa har en dataingång D, en klocksignalsingång clk, samt q och dess invers q som utgångar. En D-vippa fungerar så att man lägger indata på D-ingången. Värdet på D- ingången kommer att läggas ut på q-utgången, vid nästa klockning. Klocksignalen clk kommer således att fungera som en form av spärrvakt som inte släpper ut något innan det är dags för detta. Sekvensnät som har en gemensam klockning kallas för synkrona sekvensnät. Sekvensnät son inte är synkrona kallas för asynkrona. Ska man generallisera så kan man konstatera att det är betydligt svårare att konstruera asynkrona nät på ett tillförlitligt sätt än vad det är att konstruera synkrona nät. Sekvensnät har vanligen flera ingångar än bara klocksignalen clk. Antag att ett sekvensnät har en insignal x, beror då utsignalen u direkt av insignalen x, det vill säga att u(x) så kallar man sekvensnätet för ett Mealy-nät. Annars är sekvensnätet ett Moore-nät. För ett Mealy-nät kan utsignalen således ändras mellan två klockpulser, vilket kan vara problematiskt. 7
8 4. Konstruktion av synkrona sekvensnät När man ska konstruera ett synkront sekvensnät bör mna först tänka efter vad nätet ska göra. Detta kan låta självklart, men att verkligen ta reda på hur nätet skall bete sig i alla situationer kan vara nog så besvärligt. Man har då ofta stor nytta av att rita en tillsåndsgraf, som beskriver nätets beteende 9. Ett alternativ är att använda sig av en tillståndstabell. Lämpligen ger man tillstånden namn som är relevanta för nätets funktion i detta tillstånd. Emellertid måste man, då man skall realisera nätet, döpa om tillstånden till ett binärt tal. Detta kallas för tillståndskodning. Därefter sätter man upp en ny tillståndstabell, där man har ersatt tillståndens nämn med dess koder. En sådan tabell kallas för en kodad tillståndstabell. Använder vi andra vippor än D-vippor, till exempel JK-vippor, måste man modifiera den kodade tillståndstabellen efter vippans övergångstabell. Sedan skall man bestämma vilka värden som ska in på vippornas ingångar. För D-vippor gäller det att D = q +. Detta gör man oftast lämpligen med hjälp av Karnaugh-diagram. Man kan, på detta sätt, få fram minimerade uttryck för vippornas ingångar, samt för utsignalsfunktionen. Arbetsgången torde framgå av följande exempel. Exempel 3 Antag att vi vill konstruera en räknare som räknar,, 3,,, 3,,... Vi kan nu sätta upp en tillståndstabell som beskriver detta. S S S står för det nuvarande tillståndet och S + för nästa tillstånd. Nästa steg är att välja en tillståndskod, detta gör vi med hjälp av följande tabell. S q q 3 q och q är sekvensnätets tillståndsvariabler. Därefter ska vi översätta tillståndstabellen med hjälp av tillståndstabellen så att vi får en kodad tillståndstabell. 9 Det kan givetvis vara så att man då tar med onödigt många tillstånd. Det finns metoder att minimera antalet tillstånd för ett sekvensnät, men dessa metoder ingår inte i denna kurs. Nätets komplexitet kommer att bero på vilken kod som man har valt. Vi kommer inte att gå in på några metoder om hur man kan välja tillståndskoder på bästa sätt i denna kurs. 8
9 q q q + q+ q + och q+ kallas nätets nästa-tillståndsfunktioner. Vi sätter nu upp Karnaugh-diagram för nätets nästa-tillståndsfunktioner. Vi börjar med nästa-tillståndsfunktionen för q. -, 3 På Karnaugh-dagrammets axlar står för q och för q. Då det för en D-vippa gäller att D = q + får vi således att: D = q + q Vi fortsätter med nästa-tillståndsfunktionen för q. - 3 På Karnaugh-dagrammets axlar står för q och för q. Då det för en D-vippa gäller att D = q + får vi således att: D = q Nätets utsignaler kommer att utgöras av tillståndsvariablerna q och q. Nätet är således ett Moore-nät. Exempel 4 Vi ska nu modifiera exempel 3 på så sätt att vi ska göra den styrbar. Vi tänker oss att om en insignal bestämmer om vi ska räkna eller stanna kvar i det tillstånd vi befinner oss i. Om vi väljer att låta fallet x = innebära att vi ligger kvar i det gamla tillståndet och fallet att x = betyda att sekvensnätet går vidare till nästa tillstånd. Vi kan då sätta upp följande tillståndstabell: S x = x = Vi använder samma tillståndskod som i föregående fall, det vill säga: 9
10 S q q 3 Då erhåller vi följande kodade tillståndstabell: q q x = x = Vi kan nu sätta upp Karnaugh-diagram för nätets nästa-tillståndsfunktioner. Vi börjar med q x står för q och står för q. Då det, för en D-vippa, gäller att D = q + får vi följaktligen: D = q + q x + q x = q + q x För q + får vi följande Karnaugh-diagram: x står för q och står för q. Då det, för en D-vippa, gäller att D = q + får vi följaktligen: D = q x + q x Nätets utsignaler kommer att utgöras av tillståndsvariablerna q och q. Nätets utsignalsfunktion är oberoende av insignalen x, det är således ett Moore-nät.
11 Referenser [] Alciatore, David G. & Histand, Michael B. Introduction to Mechatronics and Measurement Systems, ed. McGraw-Hill, ISBN [] Hemert, Lars-Hugo Digitala kretsar, 3 ed. Studentlitteratur, ISBN [3] Stallings, William Computer Organization & Architecture Designing for Performance, 6 ed. Prentic-Hall, ISBN
F5 Introduktion till digitalteknik
 George Boole och paraplyet F5 Introduktion till digitalteknik EDAA05 Roger Henriksson Jonas Wisbrant p = b! (s " r) George Boole (1815-1864) Professor i Matematik, Queens College, Cork, Irland 2 Exklusiv
George Boole och paraplyet F5 Introduktion till digitalteknik EDAA05 Roger Henriksson Jonas Wisbrant p = b! (s " r) George Boole (1815-1864) Professor i Matematik, Queens College, Cork, Irland 2 Exklusiv
IE1204 Digital Design
 IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska kretsar F7 F8 Ö4 F9 Ö5 Multiplexor KK2 LAB2 Låskretsar, vippor, FSM
IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska kretsar F7 F8 Ö4 F9 Ö5 Multiplexor KK2 LAB2 Låskretsar, vippor, FSM
T1-modulen Lektionerna 10-12. Radioamatörkurs OH6AG - 2011 OH6AG. Bearbetning och översättning: Thomas Anderssén, OH6NT Heikki Lahtivirta, OH2LH
 T1-modulen Lektionerna 10-12 Radioamatörkurs OH6AG - 2011 Bearbetning och översättning: Thomas Anderssén, OH6NT Original: Heikki Lahtivirta, OH2LH 1 Logikkretsar Logikkretsarna är digitala mikrokretsar.
T1-modulen Lektionerna 10-12 Radioamatörkurs OH6AG - 2011 Bearbetning och översättning: Thomas Anderssén, OH6NT Original: Heikki Lahtivirta, OH2LH 1 Logikkretsar Logikkretsarna är digitala mikrokretsar.
F5 Introduktion till digitalteknik
 Exklusiv eller XOR F5 Introduktion till digitalteknik EDAA05 Roger Henriksson Jonas Wisbrant På övning 2 stötte ni på uttrycket x = (a b) ( a b) som kan utläsas antingen a eller b, men inte både a och
Exklusiv eller XOR F5 Introduktion till digitalteknik EDAA05 Roger Henriksson Jonas Wisbrant På övning 2 stötte ni på uttrycket x = (a b) ( a b) som kan utläsas antingen a eller b, men inte både a och
Maurice Karnaugh. Karnaugh-diagrammet gör det enkelt att minimera Boolska uttryck! William Sandqvist
 Maurice Karnaugh Karnaugh-diagrammet gör det enkelt att minimera Boolska uttryck! En funktion av fyra variabler a b c d Sanningstabellen till höger innehåller 11 st 1:or och 5 st 0:or. Funktionen kan uttryckas
Maurice Karnaugh Karnaugh-diagrammet gör det enkelt att minimera Boolska uttryck! En funktion av fyra variabler a b c d Sanningstabellen till höger innehåller 11 st 1:or och 5 st 0:or. Funktionen kan uttryckas
Digital Design IE1204
 Digital Design IE24 F4 Karnaugh-diagrammet, två- och fler-nivå minimering william@kth.se IE24 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB
Digital Design IE24 F4 Karnaugh-diagrammet, två- och fler-nivå minimering william@kth.se IE24 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB
Digitala system EDI610 Elektro- och informationsteknik
 Digitala system EDI610 Elektro- och informationsteknik Digitala System EDI610 Aktiv under hela första året, höst- och vår-termin Poäng 15.0 Godkännande; U,3,4,5 Under hösten i huvudsak Digitalteknik Under
Digitala system EDI610 Elektro- och informationsteknik Digitala System EDI610 Aktiv under hela första året, höst- och vår-termin Poäng 15.0 Godkännande; U,3,4,5 Under hösten i huvudsak Digitalteknik Under
Laboration Kombinatoriska kretsar
 Laboration Kombinatoriska kretsar Digital Design IE1204/5 Observera! För att få laborera måste Du ha: bokat en laborationstid i bokningssystemet (Daisy). löst ditt personliga web-häfte med förkunskapsuppgifter
Laboration Kombinatoriska kretsar Digital Design IE1204/5 Observera! För att få laborera måste Du ha: bokat en laborationstid i bokningssystemet (Daisy). löst ditt personliga web-häfte med förkunskapsuppgifter
Moment 2 - Digital elektronik. Föreläsning 1 Binära tal och logiska grindar
 Moment 2 - Digital elektronik Föreläsning 1 Binära tal och logiska grindar Jan Thim 1 F1: Binära tal och logiska grindar Innehåll: Introduktion Talsystem och koder Räkna binärt Logiska grindar Boolesk
Moment 2 - Digital elektronik Föreläsning 1 Binära tal och logiska grindar Jan Thim 1 F1: Binära tal och logiska grindar Innehåll: Introduktion Talsystem och koder Räkna binärt Logiska grindar Boolesk
DIGITALTEKNIK. Laboration D173. Grundläggande digital logik
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Håkan Joëlson 2007-11-19 v 1.1 DIGITALTEKNIK Laboration D173 Grundläggande digital logik Innehåll Mål. Material.... Uppgift 1...Sanningstabell
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Håkan Joëlson 2007-11-19 v 1.1 DIGITALTEKNIK Laboration D173 Grundläggande digital logik Innehåll Mål. Material.... Uppgift 1...Sanningstabell
Definition av kombinatorisk logik Olika sätt att representera kombinatorisk logik Minimering av logiska uttryck
 KOMBINATORISK LOGIK Innehåll Definition av kombinatorisk logik Olika sätt att representera kombinatorisk logik Minimering av logiska uttryck Boolesk algebra Karnaugh-diagram Realisering av logiska funktioner
KOMBINATORISK LOGIK Innehåll Definition av kombinatorisk logik Olika sätt att representera kombinatorisk logik Minimering av logiska uttryck Boolesk algebra Karnaugh-diagram Realisering av logiska funktioner
Laboration D184. ELEKTRONIK Digitalteknik. Sekvensnät beskrivna med VHDL och realiserade med PLD
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Lars Wållberg/Dan Weinehall/ Håkan Joëlson 2010-05-06 v 1.7 ELEKTRONIK Digitalteknik Laboration D184 Sekvensnät beskrivna med VHDL och realiserade
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Lars Wållberg/Dan Weinehall/ Håkan Joëlson 2010-05-06 v 1.7 ELEKTRONIK Digitalteknik Laboration D184 Sekvensnät beskrivna med VHDL och realiserade
IE1205 Digital Design: F4 : Karnaugh-diagrammet, två- och fler-nivå minimering
 IE25 Digital Design: F4 : Karnaugh-diagrammet, två- och fler-nivå minimering Mintermer 2 3 OR f En minterm är en produktterm som innehåller alla variabler och som anger den kombination av :or och :or som
IE25 Digital Design: F4 : Karnaugh-diagrammet, två- och fler-nivå minimering Mintermer 2 3 OR f En minterm är en produktterm som innehåller alla variabler och som anger den kombination av :or och :or som
Tentamen i IE1204/5 Digital Design onsdagen den 5/
 Tentamen i IE1204/5 Digital Design onsdagen den 5/6 2013 9.00-13.00 Tentamensfrågor med lösningsförslag Allmän information Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista
Tentamen i IE1204/5 Digital Design onsdagen den 5/6 2013 9.00-13.00 Tentamensfrågor med lösningsförslag Allmän information Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista
LABORATIONSINSTRUKTION
 Högskolan Dalarna Institutionen för Elektroteknik LABORATION LABORATIONSINSTRUKTION LOG/iC, PLD, kombinatorik, sekvensnät KURS Digitalteknik LAB NR 6 INNEHÅLL. Inledning 2. Prioritetskodare 3. Elektronisk
Högskolan Dalarna Institutionen för Elektroteknik LABORATION LABORATIONSINSTRUKTION LOG/iC, PLD, kombinatorik, sekvensnät KURS Digitalteknik LAB NR 6 INNEHÅLL. Inledning 2. Prioritetskodare 3. Elektronisk
Laboration Kombinatoriska kretsar
 Laboration Kombinatoriska kretsar Digital Design IE1204/5 Observera! För att få laborera måste Du ha: en bokad laborationstid i bokningssystemet (Daisy). löst ditt personliga web-häfte med förkunskapsuppgifter
Laboration Kombinatoriska kretsar Digital Design IE1204/5 Observera! För att få laborera måste Du ha: en bokad laborationstid i bokningssystemet (Daisy). löst ditt personliga web-häfte med förkunskapsuppgifter
Mintermer. SP-form med tre mintermer. William Sandqvist
 Mintermer OR f 2 3 En minterm är en produktterm som innehåller alla variabler och som anger den kombination av :or och :or som tillsammans gör att termen antar värdet. SP-form med tre mintermer. f = m
Mintermer OR f 2 3 En minterm är en produktterm som innehåller alla variabler och som anger den kombination av :or och :or som tillsammans gör att termen antar värdet. SP-form med tre mintermer. f = m
Det finns en hemsida. Adressen är http://www.idt.mdh.se/kurser/ct3760/
 CT3760 Mikrodatorteknik Föreläsning 1 Torsdag 2005-08-25 Upprop. Det finns en hemsida. Adressen är http://www.idt.mdh.se/kurser/ct3760/ Kurslitteratur är Per Foyer Mikroprocessorteknik. Finns på bokhandeln.
CT3760 Mikrodatorteknik Föreläsning 1 Torsdag 2005-08-25 Upprop. Det finns en hemsida. Adressen är http://www.idt.mdh.se/kurser/ct3760/ Kurslitteratur är Per Foyer Mikroprocessorteknik. Finns på bokhandeln.
Försättsblad till skriftlig tentamen vid Linköpings Universitet
 Försättsblad till skriftlig tentamen vid Linköpings Universitet Datum för tentamen 03-05-3 Salar U, KÅRA, U3 Tid -8 Kurskod TSEA Provkod TEN Kursnamn Digitalteknik Institution ISY Antal uppgifter som ingår
Försättsblad till skriftlig tentamen vid Linköpings Universitet Datum för tentamen 03-05-3 Salar U, KÅRA, U3 Tid -8 Kurskod TSEA Provkod TEN Kursnamn Digitalteknik Institution ISY Antal uppgifter som ingår
Digitalteknik 7.5 hp distans: 5.1 Generella sekvenskretsar 5.1.1
 Digitalteknik 7.5 hp distans: 5.1 Generella sekvenskretsar 5.1.1 Från Wikipedia: Sekvensnät Ett sekvensnäts utgångsvärde beror inte bara på indata, utan även i vilken ordning datan kommer (dess sekvens).
Digitalteknik 7.5 hp distans: 5.1 Generella sekvenskretsar 5.1.1 Från Wikipedia: Sekvensnät Ett sekvensnäts utgångsvärde beror inte bara på indata, utan även i vilken ordning datan kommer (dess sekvens).
A/D- och D/A- omvandlare
 A/D- och D/A- omvandlare Jan Carlsson 1 Inledning Om vi tänker oss att vi skall reglera en process så ställer vi in ett börvärde, det är det värde som man vill processen skall åstadkomma. Sedan har vi
A/D- och D/A- omvandlare Jan Carlsson 1 Inledning Om vi tänker oss att vi skall reglera en process så ställer vi in ett börvärde, det är det värde som man vill processen skall åstadkomma. Sedan har vi
Sekvensnät i VHDL del 2
 Laboration 6 i digitala system ht-16 Sekvensnät i VHDL del 2 Realisering av Mealy och Moore i VHDL............................. Namn............................. Godkänd (datum/sign.) 2 Laborationens syfte
Laboration 6 i digitala system ht-16 Sekvensnät i VHDL del 2 Realisering av Mealy och Moore i VHDL............................. Namn............................. Godkänd (datum/sign.) 2 Laborationens syfte
Digital elektronik CL0090
 Digital elektronik CL0090 Föreläsning 2 2007-0-25 08.5 2.00 Naos De logiska unktionerna implementeras i grindar. Här visas de vanligaste. Svenska IEC standard SS IEC 87-2 Amerikanska ANSI/IEEE Std.9.984
Digital elektronik CL0090 Föreläsning 2 2007-0-25 08.5 2.00 Naos De logiska unktionerna implementeras i grindar. Här visas de vanligaste. Svenska IEC standard SS IEC 87-2 Amerikanska ANSI/IEEE Std.9.984
EDA451 - Digital och Datorteknik 2010/2011. EDA Digital och Datorteknik 2010/2011
 EDA 451 - Digital och Datorteknik 2010/2011 Ur innehållet: Vi repeterar kursens lärandemål Diskussion i kring övningstentor t Övriga frågor 1 Lärandemål Det övergripande målet är att den studerande ska
EDA 451 - Digital och Datorteknik 2010/2011 Ur innehållet: Vi repeterar kursens lärandemål Diskussion i kring övningstentor t Övriga frågor 1 Lärandemål Det övergripande målet är att den studerande ska
Föreläsning 3.1: Datastrukturer, en översikt
 Föreläsning.: Datastrukturer, en översikt Hittills har vi i kursen lagt mycket fokus på algoritmiskt tänkande. Vi har inte egentligen ägna så mycket uppmärksamhet åt det andra som datorprogram också består,
Föreläsning.: Datastrukturer, en översikt Hittills har vi i kursen lagt mycket fokus på algoritmiskt tänkande. Vi har inte egentligen ägna så mycket uppmärksamhet åt det andra som datorprogram också består,
Laboration D181. ELEKTRONIK Digitalteknik. Kombinatoriska kretsar, HCMOS. 2008-01-24 v 2.1
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Christer Ardlin/Lars Wållberg/ Dan Weinehall/Håkan Joëlson 2008-01-24 v 2.1 ELEKTRONIK Digitalteknik Laboration D181 Kombinatoriska kretsar,
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Christer Ardlin/Lars Wållberg/ Dan Weinehall/Håkan Joëlson 2008-01-24 v 2.1 ELEKTRONIK Digitalteknik Laboration D181 Kombinatoriska kretsar,
Digital- och datorteknik
 Digital- och datorteknik Föreläsning #5 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Vad är ett bra grindnät? De egenskaper som betraktas som
Digital- och datorteknik Föreläsning #5 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Vad är ett bra grindnät? De egenskaper som betraktas som
Tentamen i TTIT07 Diskreta Strukturer
 Tentamen i TTIT07 Diskreta Strukturer 2004-10-28, kl 8 13, TER1 och TERC Inga hjälpmedel är tillåtna Kom ihåg att svaren på samtliga uppgifter måste MOTIVERAS, och att motiveringarna skall vara uppställda
Tentamen i TTIT07 Diskreta Strukturer 2004-10-28, kl 8 13, TER1 och TERC Inga hjälpmedel är tillåtna Kom ihåg att svaren på samtliga uppgifter måste MOTIVERAS, och att motiveringarna skall vara uppställda
HF0010. Introduktionskurs i datateknik 1,5 hp
 HF0010 Introduktionskurs i datateknik 1,5 hp Välkommna - till KTH, Haninge, Datateknik, kursen och till första steget mot att bli programmerare! Er lärare och kursansvarig: Nicklas Brandefelt, bfelt@kth.se
HF0010 Introduktionskurs i datateknik 1,5 hp Välkommna - till KTH, Haninge, Datateknik, kursen och till första steget mot att bli programmerare! Er lärare och kursansvarig: Nicklas Brandefelt, bfelt@kth.se
Tentamen i IE1204/5 Digital Design måndagen den 15/
 Tentamen i IE1204/5 Digital Design måndagen den 15/10 2012 9.00-13.00 Allmän information Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista IE1204), Tentamensuppgifterna
Tentamen i IE1204/5 Digital Design måndagen den 15/10 2012 9.00-13.00 Allmän information Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista IE1204), Tentamensuppgifterna
Grundläggande Datorteknik Digital- och datorteknik
 Grundläggande Datorteknik Digital- och datorteknik Kursens mål: Fatta hur en dator är uppbggd (HDW) Fatta hur du du programmerar den (SW) Fatta hur HDW o SW samverkar Digital teknik Dator teknik Grundläggande
Grundläggande Datorteknik Digital- och datorteknik Kursens mål: Fatta hur en dator är uppbggd (HDW) Fatta hur du du programmerar den (SW) Fatta hur HDW o SW samverkar Digital teknik Dator teknik Grundläggande
Tentamen i IE1204/5 Digital Design onsdagen den 5/
 Tentamen i IE1204/5 Digital Design onsdagen den 5/6 2013 9.00-13.00 Allmän information Exaator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista IE1204) Tentamensuppgifterna behöver
Tentamen i IE1204/5 Digital Design onsdagen den 5/6 2013 9.00-13.00 Allmän information Exaator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista IE1204) Tentamensuppgifterna behöver
Laboration Sekvenskretsar
 Laboration Sekvenskretsar Digital Design IE1204/5 Observera! För att få laborera måste Du ha: bokat en laborationstid i bokningssystemet (Daisy). löst ditt personliga web-häfte med förkunskapsuppgifter
Laboration Sekvenskretsar Digital Design IE1204/5 Observera! För att få laborera måste Du ha: bokat en laborationstid i bokningssystemet (Daisy). löst ditt personliga web-häfte med förkunskapsuppgifter
Exempeluppgift i Logikstyrning. 1 Inledning. 2 Insignaler och utsignaler
 Exempeluppgift i Logikstyrning Inledning Idén med detta papper är att ge en allmän beskrivning av labbutrustningen och tips för hur man kan lösa olika praktiska problem i samband med laborationen. Läs
Exempeluppgift i Logikstyrning Inledning Idén med detta papper är att ge en allmän beskrivning av labbutrustningen och tips för hur man kan lösa olika praktiska problem i samband med laborationen. Läs
Exempel på tentamensfrågor Digitalteknik
 Exempel på tentamensfrågor Digitalteknik Till dessa frågor (som kommer från lite olika tidgare tentor) gällde förutsättningen: Hjälpmedel: Kurslitteratur, föreläsningsantecknigar lab. med mätresultat,
Exempel på tentamensfrågor Digitalteknik Till dessa frågor (som kommer från lite olika tidgare tentor) gällde förutsättningen: Hjälpmedel: Kurslitteratur, föreläsningsantecknigar lab. med mätresultat,
Digital elektronik CL0090
 Digital elektronik CL9 Föreläsning 5 27-2-2 8.5 2. Naxos Demonstration av uartus programvara. Genomgång av uartus flödesschema. Detta dokument finns på kurshemsidan. http://www.idt.mdh.se/kurser/cl9/ VHDL-kod
Digital elektronik CL9 Föreläsning 5 27-2-2 8.5 2. Naxos Demonstration av uartus programvara. Genomgång av uartus flödesschema. Detta dokument finns på kurshemsidan. http://www.idt.mdh.se/kurser/cl9/ VHDL-kod
MA 1202 Matematik B Mål som deltagarna skall ha uppnått efter avslutad kurs.
 MA 202 Matematik B Mål som deltagarna skall ha uppnått efter avslutad kurs. Deltagaren skall kunna formulera, analysera och lösa matematiska problem av betydelse för tillämpningar och vald studieinriktning
MA 202 Matematik B Mål som deltagarna skall ha uppnått efter avslutad kurs. Deltagaren skall kunna formulera, analysera och lösa matematiska problem av betydelse för tillämpningar och vald studieinriktning
Grunderna i stegkodsprogrammering
 Kapitel 1 Grunderna i stegkodsprogrammering Följande bilaga innehåller grunderna i stegkodsprogrammering i den form som används under kursen. Vi kommer att kort diskutera olika datatyper, villkor, operationer
Kapitel 1 Grunderna i stegkodsprogrammering Följande bilaga innehåller grunderna i stegkodsprogrammering i den form som används under kursen. Vi kommer att kort diskutera olika datatyper, villkor, operationer
VHDL och laborationer i digitalteknik
 V:1.1 VHDL och laborationer i digitalteknik Vid laborationskursen i digitalteknik används VHDL till alla laborationerna utom den första. VHDL är ett stort språk och enbart en liten del av språket behövs
V:1.1 VHDL och laborationer i digitalteknik Vid laborationskursen i digitalteknik används VHDL till alla laborationerna utom den första. VHDL är ett stort språk och enbart en liten del av språket behövs
Laboration i digitalteknik Introduktion till digitalteknik
 Linköpings universitet Institutionen för systemteknik Laborationer i digitalteknik Datorteknik 6 Laboration i digitalteknik Introduktion till digitalteknik TSEA Digitalteknik D TSEA5 Digitalteknik Y TDDC75
Linköpings universitet Institutionen för systemteknik Laborationer i digitalteknik Datorteknik 6 Laboration i digitalteknik Introduktion till digitalteknik TSEA Digitalteknik D TSEA5 Digitalteknik Y TDDC75
Programmerbar logik. Kapitel 4
 Kapitel 4 Programmerbar logik Programmerbar logik (PLC: Programmable Logic Controller; fi. ohjelmoitava logiikka) är en sorts mikrodatorliknande instrument som är speciellt avsedda för logik- och sekvensstyrningsproblem.
Kapitel 4 Programmerbar logik Programmerbar logik (PLC: Programmable Logic Controller; fi. ohjelmoitava logiikka) är en sorts mikrodatorliknande instrument som är speciellt avsedda för logik- och sekvensstyrningsproblem.
Uppgift 12: Konstruera en elektronisk tärning. Resultatet av ett tärningskast ska visas på en 7- segmentindikator.
 Uppgift 12: Konstruera en elektronisk tärning. Resultatet av ett tärningskast ska visas på en 7- segmentindikator. Tärningen ska ha två utfallsrum: U 1 = {1, 2, 3, 4, 5, 6, 6, 6} U 2 = {1, 2, 3, 4, 5,
Uppgift 12: Konstruera en elektronisk tärning. Resultatet av ett tärningskast ska visas på en 7- segmentindikator. Tärningen ska ha två utfallsrum: U 1 = {1, 2, 3, 4, 5, 6, 6, 6} U 2 = {1, 2, 3, 4, 5,
Tenta i Digitalteknik
 Tenta i Digitalteknik Kurskod D0011E Tentamensdatum 2010-06-01 Skrivtid 9.00-14.00 (5 timmar) Maximalt resultat 50 poäng Godkänt resultat 25 poäng inkl bonus Jourhavande lärare Per Lindgren Tel 070 376
Tenta i Digitalteknik Kurskod D0011E Tentamensdatum 2010-06-01 Skrivtid 9.00-14.00 (5 timmar) Maximalt resultat 50 poäng Godkänt resultat 25 poäng inkl bonus Jourhavande lärare Per Lindgren Tel 070 376
DIGITALTEKNIK I. Laboration DE2. Sekvensnät och sekvenskretsar
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Håkan Joëlson, John Berge 203 DIGITALTEKNIK I Laboration DE2 Sekvensnät och sekvenskretsar Namn... Personnummer... Epost-adress... Datum för
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Håkan Joëlson, John Berge 203 DIGITALTEKNIK I Laboration DE2 Sekvensnät och sekvenskretsar Namn... Personnummer... Epost-adress... Datum för
DIGITALTEKNIK I. Laboration DE1. Kombinatoriska nät och kretsar
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Björne Lindberg/Håkan Joëlson John Berge 2013 DIGITALTEKNIK I Laboration DE1 Kombinatoriska nät och kretsar Namn... Personnummer... Epost-adress...
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Björne Lindberg/Håkan Joëlson John Berge 2013 DIGITALTEKNIK I Laboration DE1 Kombinatoriska nät och kretsar Namn... Personnummer... Epost-adress...
Digital Design IE1204
 Digital Design IE24 F2 : Logiska Grindar och Kretsar, Boolesk Algebra william@kth.se IE24 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska
Digital Design IE24 F2 : Logiska Grindar och Kretsar, Boolesk Algebra william@kth.se IE24 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska
RödGrön-spelet Av: Jonas Hall. Högstadiet. Tid: 40-120 minuter beroende på variant Material: TI-82/83/84 samt tärningar
 Aktivitetsbeskrivning Denna aktivitet är utformat som ett spel som spelas av en grupp elever. En elev i taget agerar Gömmare och de andra är Gissare. Den som är gömmare lagrar (gömmer) tal i några av räknarens
Aktivitetsbeskrivning Denna aktivitet är utformat som ett spel som spelas av en grupp elever. En elev i taget agerar Gömmare och de andra är Gissare. Den som är gömmare lagrar (gömmer) tal i några av räknarens
Programmeringsteknik med C och Matlab
 Programmeringsteknik med C och Matlab Kapitel 2: C-programmeringens grunder Henrik Björklund Umeå universitet Björklund (UmU) Programmeringsteknik 1 / 32 Mer organisatoriskt Imorgon: Datorintro i lab Logga
Programmeringsteknik med C och Matlab Kapitel 2: C-programmeringens grunder Henrik Björklund Umeå universitet Björklund (UmU) Programmeringsteknik 1 / 32 Mer organisatoriskt Imorgon: Datorintro i lab Logga
EDA Digital och Datorteknik 2009/2010
 EDA45 - Digital och Datorteknik 29/2 EDA 45 - Digital och Datorteknik 29/2, lärobokens kapitel 3 Ur innehållet: Satslogik och Boolesk algebra Grindar Funktionstabell Binär evaluering Normal orm/förenklad
EDA45 - Digital och Datorteknik 29/2 EDA 45 - Digital och Datorteknik 29/2, lärobokens kapitel 3 Ur innehållet: Satslogik och Boolesk algebra Grindar Funktionstabell Binär evaluering Normal orm/förenklad
SMD033 Digitalteknik. Digitalteknik F1 bild 1
 SMD033 Digitalteknik Digitalteknik F1 bild 1 Vi som undervisar Anders Hansson A3209 91 230 aha@sm.luth.se Digitalteknik F1 bild 2 Registrering Registrering via email till diglabs@luth.se Digitalteknik
SMD033 Digitalteknik Digitalteknik F1 bild 1 Vi som undervisar Anders Hansson A3209 91 230 aha@sm.luth.se Digitalteknik F1 bild 2 Registrering Registrering via email till diglabs@luth.se Digitalteknik
Tentamen. TSEA22 Digitalteknik 5 juni, 2015, kl
 Tentamen TSEA22 Digitalteknik 5 juni, 2015, kl. 08.00-12.00 Tillåtna hjälpmedel: Inga. Ansvarig lärare: Mattias Krysander Visning av skrivningen sker mellan 10.00-10.30 den 22 juni på Datorteknik. Totalt
Tentamen TSEA22 Digitalteknik 5 juni, 2015, kl. 08.00-12.00 Tillåtna hjälpmedel: Inga. Ansvarig lärare: Mattias Krysander Visning av skrivningen sker mellan 10.00-10.30 den 22 juni på Datorteknik. Totalt
Omtentamen IE Digital Design Måndag 14/
 Omtentamen IE204-5 Digital Design Måndag 4/3 206 4.00-8.00 Allmän information ( TCOMK, Ask for an english version of this exam if needed ) Examinator: Ingo Sander. Ansvarig lärare: Kista, William Sandqvist
Omtentamen IE204-5 Digital Design Måndag 4/3 206 4.00-8.00 Allmän information ( TCOMK, Ask for an english version of this exam if needed ) Examinator: Ingo Sander. Ansvarig lärare: Kista, William Sandqvist
IE1204 Digital Design
 IE204 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska kretsar F7 F8 Ö4 F9 Ö5 Multiplexor KK2 LAB2 Låskretsar, vippor, FSM F0 F
IE204 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska kretsar F7 F8 Ö4 F9 Ö5 Multiplexor KK2 LAB2 Låskretsar, vippor, FSM F0 F
Laboration D159. Sekvensnät beskrivna med VHDL och realiserade med PLD. Namn: Datum: Epostadr: Kurs:
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Lars Wållberg/Håkan Joëlson 2001-03-01 v 1.5 ELEKTRONIK Digitalteknik Laboration D159 Sekvensnät beskrivna med VHDL och realiserade med PLD
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Lars Wållberg/Håkan Joëlson 2001-03-01 v 1.5 ELEKTRONIK Digitalteknik Laboration D159 Sekvensnät beskrivna med VHDL och realiserade med PLD
Digital- och datorteknik
 Digital- och datorteknik Föreläsning #3 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Logikgrindar Från data till digitala byggblock: Kursens
Digital- och datorteknik Föreläsning #3 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Logikgrindar Från data till digitala byggblock: Kursens
Försättsblad till skriftlig tentamen vid Linköpings universitet
 Försättsblad till skriftlig tentamen vid Linköpings universitet Datum för tentamen 08-03-3 Sal (5) Tid 8- Kurskod TSEA Provkod TEN Kursnamn/benämning Provnamn/benämning Institution Antal uppgifter som
Försättsblad till skriftlig tentamen vid Linköpings universitet Datum för tentamen 08-03-3 Sal (5) Tid 8- Kurskod TSEA Provkod TEN Kursnamn/benämning Provnamn/benämning Institution Antal uppgifter som
IE1205 Digital Design: F9: Synkrona tillståndsautomater
 IE25 Digital Design: F9: Synkrona tillståndsautomater Moore och Mealy automater F8 introducerade vippor och vi konstruerade räknare, skift-register etc. F9-F skall vi titta på hur generella tillståndsmaskiner
IE25 Digital Design: F9: Synkrona tillståndsautomater Moore och Mealy automater F8 introducerade vippor och vi konstruerade räknare, skift-register etc. F9-F skall vi titta på hur generella tillståndsmaskiner
5:2 Digitalteknik Boolesk algebra. Inledning OCH-funktionen
 5:2 Digitalteknik Boolesk algebra. Inledning I en dator representeras det binära talsystemet med signaler i form av elektriska spänningar. 0 = 0 V (låg spänning), 1 = 5 V(hög spänning). Datorn kombinerar
5:2 Digitalteknik Boolesk algebra. Inledning I en dator representeras det binära talsystemet med signaler i form av elektriska spänningar. 0 = 0 V (låg spänning), 1 = 5 V(hög spänning). Datorn kombinerar
EDA Digital och Datorteknik 2010/2011
 EDA45 - Digital och Datorteknik 2/2 EDA 45 - Digital och Datorteknik 2/2, lärobokens kapitel 3 Ur innehållet: Satslogik och Boolesk algebra Grindar Funktionstabell Binär evaluering Normal orm/förenklad
EDA45 - Digital och Datorteknik 2/2 EDA 45 - Digital och Datorteknik 2/2, lärobokens kapitel 3 Ur innehållet: Satslogik och Boolesk algebra Grindar Funktionstabell Binär evaluering Normal orm/förenklad
Tentamen i Digital Design
 Kungliga Tekniska Högskolan Tentamen i Digital Design Kursnummer : Kursansvarig: 2B56 :e fo ingenjör Lars Hellberg tel 79 7795 Datum: 27-5-25 Tid: Kl 4. - 9. Tentamen rättad 27-6-5 Klagotiden utgår: 27-6-29
Kungliga Tekniska Högskolan Tentamen i Digital Design Kursnummer : Kursansvarig: 2B56 :e fo ingenjör Lars Hellberg tel 79 7795 Datum: 27-5-25 Tid: Kl 4. - 9. Tentamen rättad 27-6-5 Klagotiden utgår: 27-6-29
Laboration D151. Kombinatoriska kretsar, HCMOS. Namn: Datum: Epostadr: Kurs:
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Christer Ardlin/Lars Wållberg/ Håkan Joëlson 2000-01-28 v 2.3 ELEKTRONIK Digitalteknik Laboration D151 Kombinatoriska kretsar, HCMOS Namn:
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Christer Ardlin/Lars Wållberg/ Håkan Joëlson 2000-01-28 v 2.3 ELEKTRONIK Digitalteknik Laboration D151 Kombinatoriska kretsar, HCMOS Namn:
DIGITALA TAL OCH BOOLESK ALGEBRA
 DIGITALA TAL OCH BOOLESK ALGEBRA Innehåll Talsystem och koder Aritmetik för inära tal Grundläggande logiska operationer Logiska grindar Definitioner i Boolesk algera Räknelagar BINÄRA TALSYSTEMET Binärt
DIGITALA TAL OCH BOOLESK ALGEBRA Innehåll Talsystem och koder Aritmetik för inära tal Grundläggande logiska operationer Logiska grindar Definitioner i Boolesk algera Räknelagar BINÄRA TALSYSTEMET Binärt
Tentamen EDAA05 Datorer i system
 LUNDS TEKNISKA HÖGSKOLA 1(5) Institutionen för datavetenskap Tentamen EDAA05 Datorer i system 2011 10 17, 8.00 13.00 Tillåtna hjälpmedel: bifogad formel- och symbolsamling. För godkänt betyg på tentamen
LUNDS TEKNISKA HÖGSKOLA 1(5) Institutionen för datavetenskap Tentamen EDAA05 Datorer i system 2011 10 17, 8.00 13.00 Tillåtna hjälpmedel: bifogad formel- och symbolsamling. För godkänt betyg på tentamen
Digital Design IE1204
 Digital Design IE1204 F10 Tillståndsautomater del II william@kth.se IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska
Digital Design IE1204 F10 Tillståndsautomater del II william@kth.se IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska
Tentamen i Digitalteknik, EITF65
 Elektro- och informationsteknik Tentamen i Digitalteknik, EITF65 3 januari 2018, kl. 14-19 Skriv anonymkod och identifierare, eller personnummer, på alla papper. Börja en ny uppgift på ett nytt papper.
Elektro- och informationsteknik Tentamen i Digitalteknik, EITF65 3 januari 2018, kl. 14-19 Skriv anonymkod och identifierare, eller personnummer, på alla papper. Börja en ny uppgift på ett nytt papper.
Logik. Boolesk algebra. Logik. Operationer. Boolesk algebra
 Logik F4 Logik Boolesk algebra EDAA05 Roger Henriksson Jonas Wisbrant Konsten att, och vetenskapen om, att resonera och dra slutsatser. Vad behövs för att man ska kunna dra en slutsats? Hur kan man dra
Logik F4 Logik Boolesk algebra EDAA05 Roger Henriksson Jonas Wisbrant Konsten att, och vetenskapen om, att resonera och dra slutsatser. Vad behövs för att man ska kunna dra en slutsats? Hur kan man dra
TSIU05 Digitalteknik. LAB1 Kombinatorik LAB2 Sekvensnät LAB3 System
 1 TSIU05 Digitalteknik LAB1 Kombinatorik LAB2 Sekvensnät LAB3 System Sammanställning september 2013 Läs detta först Läs igenom hela laborationen så du vet vad du skall göra på laborationspasset. Hela
1 TSIU05 Digitalteknik LAB1 Kombinatorik LAB2 Sekvensnät LAB3 System Sammanställning september 2013 Läs detta först Läs igenom hela laborationen så du vet vad du skall göra på laborationspasset. Hela
Repetition TSIU05 Digitalteknik Di/EL. Michael Josefsson
 Repetition TSIU05 Digitalteknik Di/EL Michael Josefsson Här kommer några frågeställningar och uppgifter du kan använda för att använda som egenkontroll på om du förstått huvudinnehållet i respektive föreläsning.
Repetition TSIU05 Digitalteknik Di/EL Michael Josefsson Här kommer några frågeställningar och uppgifter du kan använda för att använda som egenkontroll på om du förstått huvudinnehållet i respektive föreläsning.
Elektroteknik MF1016 föreläsning 9 MF1017 föreläsning 7 Mikrodatorteknik
 Elektroteknik MF1016 föreläsning 9 MF1017 föreläsning 7 - Inbyggda system - Analog till digital signal - Utvecklingssystem, målsystem - Labutrustningen - Uppbyggnad av mikrokontroller - Masinkod, assemblerkod
Elektroteknik MF1016 föreläsning 9 MF1017 föreläsning 7 - Inbyggda system - Analog till digital signal - Utvecklingssystem, målsystem - Labutrustningen - Uppbyggnad av mikrokontroller - Masinkod, assemblerkod
Institutionen för systemteknik, ISY, LiTH. Tentamen i. Tid: kl
 Institutionen för systemteknik, ISY, LiTH Tentamen i Digitalteknik TSIU05/TEN1 Tid: 2016 10 26 kl. 14 18 Lokal : TER3 TER4 Ansvarig lärare: Michael Josefsson. Besöker lokalen kl 16. Tel.: 013-28 12 64
Institutionen för systemteknik, ISY, LiTH Tentamen i Digitalteknik TSIU05/TEN1 Tid: 2016 10 26 kl. 14 18 Lokal : TER3 TER4 Ansvarig lärare: Michael Josefsson. Besöker lokalen kl 16. Tel.: 013-28 12 64
K3 Om andra ordningens predikatlogik
 KTH Matematik Bengt Ek Maj 2005 Kompletteringsmaterial till kursen 5B1928 Logik för D1: K3 Om andra ordningens predikatlogik Vi presenterar på dessa sidor kortfattat andra ordningens predikatlogik, vilket
KTH Matematik Bengt Ek Maj 2005 Kompletteringsmaterial till kursen 5B1928 Logik för D1: K3 Om andra ordningens predikatlogik Vi presenterar på dessa sidor kortfattat andra ordningens predikatlogik, vilket
Digital- och datorteknik
 Digital- och datorteknik 7,5 högskolepoäng läsperiod 1+2 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Kursens organisation Föreläsningar (29
Digital- och datorteknik 7,5 högskolepoäng läsperiod 1+2 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Kursens organisation Föreläsningar (29
IE1204/IE1205 Digital Design
 TENTAMEN IE1204/IE1205 Digital Design 2012-12-13, 09.00-13.00 Inga hjälpmedel är tillåtna! Hjälpmedel Tentamen består av tre delar med sammanlagd tolv uppgifter, och totalt 30 poäng. Del A1 (Analys) innehåller
TENTAMEN IE1204/IE1205 Digital Design 2012-12-13, 09.00-13.00 Inga hjälpmedel är tillåtna! Hjälpmedel Tentamen består av tre delar med sammanlagd tolv uppgifter, och totalt 30 poäng. Del A1 (Analys) innehåller
Digital Design IE1204
 Digital Design IE204 Kursomgång för Högskoleingenjörsinriktningarna: Datateknik, Elektronik och Datorteknik. Kandidatinriktningen: Informations- och Kommunikationsteknik F3 Asynkrona sekvensnät del 2 william@kth.se
Digital Design IE204 Kursomgång för Högskoleingenjörsinriktningarna: Datateknik, Elektronik och Datorteknik. Kandidatinriktningen: Informations- och Kommunikationsteknik F3 Asynkrona sekvensnät del 2 william@kth.se
Bokens innehåll 1. MEKATRONIK en del av vår vardag 2. Styrning med LOGISKA FUNKTIONER
 1. MEKATRONIK en del av vår vardag Mekatronik i hemmet Mekatronik i fabriken Elektromekaniska styrsystem Pneumatiska styrsystem Hydrauliska styrsystem Elektriska styrsystem 2. Styrning med LOGISKA FUNKTIONER
1. MEKATRONIK en del av vår vardag Mekatronik i hemmet Mekatronik i fabriken Elektromekaniska styrsystem Pneumatiska styrsystem Hydrauliska styrsystem Elektriska styrsystem 2. Styrning med LOGISKA FUNKTIONER
Lilla lyckohjulet Lina
 Lilla lyckohjulet Lina Lyckohjulet snurrar och du kan spela precis som på tivoli! Se en film på produkten: http://youtu.be/mlh6rpuhqmm Vilket material behöver man? Trälist 15 x 33 mm Plywood 8 mm Träskruv
Lilla lyckohjulet Lina Lyckohjulet snurrar och du kan spela precis som på tivoli! Se en film på produkten: http://youtu.be/mlh6rpuhqmm Vilket material behöver man? Trälist 15 x 33 mm Plywood 8 mm Träskruv
Introduktion till digitalteknik
 Inledning Introduktion till digitalteknik Stefan Gustavson 997, lätt uppdaterat 2004-09-06 Digitalteknik är grunden till alla moderna datorer. I datorernas barndom förekom visserligen så kallade analogimaskiner,
Inledning Introduktion till digitalteknik Stefan Gustavson 997, lätt uppdaterat 2004-09-06 Digitalteknik är grunden till alla moderna datorer. I datorernas barndom förekom visserligen så kallade analogimaskiner,
En ideal op-förstärkare har oändlig inimedans, noll utimpedans och oändlig förstärkning.
 F5 LE1460 Analog elektronik 2005-11-23 kl 08.15 12.00 Alfa En ideal op-förstärkare har oändlig inimedans, noll utimpedans och oändlig förstärkning. ( Impedans är inte samma sak som resistans. Impedans
F5 LE1460 Analog elektronik 2005-11-23 kl 08.15 12.00 Alfa En ideal op-förstärkare har oändlig inimedans, noll utimpedans och oändlig förstärkning. ( Impedans är inte samma sak som resistans. Impedans
7, Diskreta strukturer
 Objektorienterad modellering och diskreta strukturer 7, Diskreta strukturer Sven Gestegård Robertz Datavetenskap, LTH 2015 Modeller Matematiska modeller Kontinuerliga modeller Kontinuerliga funktioner
Objektorienterad modellering och diskreta strukturer 7, Diskreta strukturer Sven Gestegård Robertz Datavetenskap, LTH 2015 Modeller Matematiska modeller Kontinuerliga modeller Kontinuerliga funktioner
D/A- och A/D-omvandlarmodul MOD687-31
 D/A- och A/D-omvandlarmodul MOD687-31 Allmänt Modulen är helt självförsörjande, det enda du behöver för att komma igång är en 9VAC väggtransformator som du kopplar till jacket J2. När du så småningom vill
D/A- och A/D-omvandlarmodul MOD687-31 Allmänt Modulen är helt självförsörjande, det enda du behöver för att komma igång är en 9VAC väggtransformator som du kopplar till jacket J2. När du så småningom vill
Manual för deltagare kursen Bakgavellyft 1010-03-31 1. Så går du kursen Bakgavellyft
 Manual för deltagare kursen Bakgavellyft 1010-03-31 1 Så går du kursen Bakgavellyft Manual för deltagare kursen Bakgavellyft 1010-03-31 2 Starta kursen 1. Öppna ett Internetfönster och fyll i adressen
Manual för deltagare kursen Bakgavellyft 1010-03-31 1 Så går du kursen Bakgavellyft Manual för deltagare kursen Bakgavellyft 1010-03-31 2 Starta kursen 1. Öppna ett Internetfönster och fyll i adressen
Struktur: Elektroteknik A. Digitalteknik 3p, vt 01. F1: Introduktion. Motivation och målsättning för kurserna i digital elektronik
 Digitalteknik 3p, vt 01 Struktur: Elektroteknik A Kurslitteratur: "A First Course in Digital Systems Design - An Integrated Approach" Antal föreläsningar: 11 (2h) Antal laborationer: 4 (4h) Examinationsform:
Digitalteknik 3p, vt 01 Struktur: Elektroteknik A Kurslitteratur: "A First Course in Digital Systems Design - An Integrated Approach" Antal föreläsningar: 11 (2h) Antal laborationer: 4 (4h) Examinationsform:
Bedöma elevers förmågor i muntlig uppgift
 BEDÖMNINGSSTÖD I MATEMATIK Bedöma elevers förmågor i muntlig uppgift Innehåll Syftet med materialet sid. 2 Bedömning av muntliga prestationer i matematik sid. 2 Olika typer av bedömningssituationer sid.
BEDÖMNINGSSTÖD I MATEMATIK Bedöma elevers förmågor i muntlig uppgift Innehåll Syftet med materialet sid. 2 Bedömning av muntliga prestationer i matematik sid. 2 Olika typer av bedömningssituationer sid.
Tentamen i Grundläggande ellära och digitalteknik ETA 013 för D
 Lars-Erik ederlöf Per Liljas Tentamen i Grundläggande ellära och digitalteknik ET 03 för D 200-08-20 Tentamen omfattar 40 poäng, 2 poäng för varje uppgift. 20 poäng ger godkänd tentamen. Tillåtet hjälpmedel
Lars-Erik ederlöf Per Liljas Tentamen i Grundläggande ellära och digitalteknik ET 03 för D 200-08-20 Tentamen omfattar 40 poäng, 2 poäng för varje uppgift. 20 poäng ger godkänd tentamen. Tillåtet hjälpmedel
Introduktion till logik
 Introduktion till logik Av Johan Johansson Johan.johansson@guldstadsgymnasiet.se Logik sägs som många andra saker komma från de grekiska filosoferna, och ordet kommer också därifrån. Grekerna kallade det
Introduktion till logik Av Johan Johansson Johan.johansson@guldstadsgymnasiet.se Logik sägs som många andra saker komma från de grekiska filosoferna, och ordet kommer också därifrån. Grekerna kallade det
Översikt, kursinnehåll
 Översikt, kursinnehåll Specifikation av digitala funktioner och system Digitala byggelement Kombinatoriska system Digital Aritmetik Synkrona system och tillståndsmaskiner Asynkrona system och tillståndsmaskiner
Översikt, kursinnehåll Specifikation av digitala funktioner och system Digitala byggelement Kombinatoriska system Digital Aritmetik Synkrona system och tillståndsmaskiner Asynkrona system och tillståndsmaskiner
Tentamen i Grundläggande ellära och digitalteknik ETA 013 för D
 Lars-Erik Cederlöf Per Liljas Tentamen i Grundläggande ellära och digitalteknik ETA 013 för D1 2001-05-28 Tentamen omfattar 40 poäng, 2 poäng för varje uppgift. 20 poäng ger godkänd tentamen. Tillåtet
Lars-Erik Cederlöf Per Liljas Tentamen i Grundläggande ellära och digitalteknik ETA 013 för D1 2001-05-28 Tentamen omfattar 40 poäng, 2 poäng för varje uppgift. 20 poäng ger godkänd tentamen. Tillåtet
Tentamen med lösningar för IE1204/5 Digital Design Torsdag 15/
 Tentamen med lösningar för IE4/5 Digital Design Torsdag 5/ 5 9.-. Allmän information Eaminator: Ingo Sander. Ansvarig lärare: Kista, William Sandqvist, tel 8-79 44 87. KTH Valhallavägen, Fredrik Jonsson,
Tentamen med lösningar för IE4/5 Digital Design Torsdag 5/ 5 9.-. Allmän information Eaminator: Ingo Sander. Ansvarig lärare: Kista, William Sandqvist, tel 8-79 44 87. KTH Valhallavägen, Fredrik Jonsson,
Tenta i Digitalteknik
 Tenta i Digitalteknik Kurskod D0011E Tentamensdatum 2010-08-27 Skrivtid 9.00-14.00 Maximalt resultat 50 poäng Godkänt resultat 25 poäng inkl bonus Jourhavande lärare Per Lindgren Tel 070 376 8150 Tillåtna
Tenta i Digitalteknik Kurskod D0011E Tentamensdatum 2010-08-27 Skrivtid 9.00-14.00 Maximalt resultat 50 poäng Godkänt resultat 25 poäng inkl bonus Jourhavande lärare Per Lindgren Tel 070 376 8150 Tillåtna
Laboration: Att inhägna ett rektangulärt område
 Laboration: Att inhägna ett rektangulärt område Du har tillgång till ett hoprullat staket som är 30 m långt. Med detta vill du inhägna ett område och använda allt staket. Du vill göra inhägnaden rektangelformad.
Laboration: Att inhägna ett rektangulärt område Du har tillgång till ett hoprullat staket som är 30 m långt. Med detta vill du inhägna ett område och använda allt staket. Du vill göra inhägnaden rektangelformad.
IE1205 Digital Design: F8: Minneselement: Latchar och Vippor. Räknare
 IE1205 Digital Design: F8: Minneselement: Latchar och Vippor. Räknare IE1205 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska
IE1205 Digital Design: F8: Minneselement: Latchar och Vippor. Räknare IE1205 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska
Digital Design IE1204
 Digital Design IE1204 F9 Tillståndsautomater del1 william@kth.se IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska kretsar
Digital Design IE1204 F9 Tillståndsautomater del1 william@kth.se IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska kretsar
Digitalteknik F9. Automater Minneselement. Digitalteknik F9 bild 1
 Digitalteknik F9 Automater Minneselement Digitalteknik F9 bild Automater Från F minns vi följande om en automat (sekvenskrets): Utsignalerna beror av insignal och gammalt tillstånd: Insignaler Utsignaler
Digitalteknik F9 Automater Minneselement Digitalteknik F9 bild Automater Från F minns vi följande om en automat (sekvenskrets): Utsignalerna beror av insignal och gammalt tillstånd: Insignaler Utsignaler
Digital elektronik CL0090
 Digital elektronik CL9 Föreläsning 3 27--29 8.5 2. My Talsystem Binära tal har basen 2 Exempel Det decimala talet 9 motsvarar 2 Den första ettan är MSB, Most Significant Bit, den andra ettan är LSB Least
Digital elektronik CL9 Föreläsning 3 27--29 8.5 2. My Talsystem Binära tal har basen 2 Exempel Det decimala talet 9 motsvarar 2 Den första ettan är MSB, Most Significant Bit, den andra ettan är LSB Least
Digitalt lärande och programmering i klassrummet
 Digitalt lärande och programmering i klassrummet Innehåll Programmering Vad är programmering och varför behövs det? Argument för (och emot) programmering Kort introduktion om programmering Några grundbegrepp
Digitalt lärande och programmering i klassrummet Innehåll Programmering Vad är programmering och varför behövs det? Argument för (och emot) programmering Kort introduktion om programmering Några grundbegrepp
Tentamen i IE1204/5 Digital Design Torsdag 29/
 Tentamen i IE1204/5 Digital Design Torsdag 29/10 2015 9.00-13.00 Allmän information ( TCOMK, Ask for an english version of this exam if needed ) Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist
Tentamen i IE1204/5 Digital Design Torsdag 29/10 2015 9.00-13.00 Allmän information ( TCOMK, Ask for an english version of this exam if needed ) Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist
Lära känna skrivbordet
 Är det första gången du använder Windows 7? Den här versionen har mycket gemensamt med tidigare versioner av Windows, men du kan behöva hjälp med att få upp farten. Den här guiden innehåller praktisk information
Är det första gången du använder Windows 7? Den här versionen har mycket gemensamt med tidigare versioner av Windows, men du kan behöva hjälp med att få upp farten. Den här guiden innehåller praktisk information
Så här fungerar datorer Baserad på T-J Hallbergs minimalmaskin. 2008-08-26 Högskolan i Jönköping/JTH Ragnar Nohre
 Baserad på T-J Hallbergs minimalmaskin 2008-08-26 Högskolan i Jönköping/JTH Ragnar Nohre Innehåll 1 Översikt... 3 2 Binära tal och koder... 3 2.1 Positionssystemet... 3 2.2 De binära talen... 4 2.3 Kilo
Baserad på T-J Hallbergs minimalmaskin 2008-08-26 Högskolan i Jönköping/JTH Ragnar Nohre Innehåll 1 Översikt... 3 2 Binära tal och koder... 3 2.1 Positionssystemet... 3 2.2 De binära talen... 4 2.3 Kilo
MATEMATIKENS SPRÅK. Syftet med denna övning är att med hjälp av logik lära oss att uttrycka matematik mer exakt,
 Explorativ övning 1 MATEMATIKENS SPRÅK Syftet med denna övning är att med hjälp av logik lära oss att uttrycka matematik mer exakt, lära oss förstå språket. Vi skall försöka utveckla vårt matematiska språk,
Explorativ övning 1 MATEMATIKENS SPRÅK Syftet med denna övning är att med hjälp av logik lära oss att uttrycka matematik mer exakt, lära oss förstå språket. Vi skall försöka utveckla vårt matematiska språk,
Följddiagram för händelsestyrda rörelser
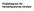 Följddiagram för händelsestyrda rörelser 2 STYROBJEKT UNIKA FASER Två arbetscylindrar ska röra sig i följande ordning. När man ger startkommando ska kolvstången i cylinder gå ut. När den har nått sitt
Följddiagram för händelsestyrda rörelser 2 STYROBJEKT UNIKA FASER Två arbetscylindrar ska röra sig i följande ordning. När man ger startkommando ska kolvstången i cylinder gå ut. När den har nått sitt
