Programkonstruktion och datastrukturer. Moment 5 Om generella datastrukturer och träd. PKD 2011/12 moment 5 Sida 1 Uppdaterad
|
|
|
- Göran Andersson
- för 8 år sedan
- Visningar:
Transkript
1 Programkonstruktion och datastrukturer Moment 5 Om generella datastrukturer och träd PKD 2011/12 moment 5 Sida 1 Uppdaterad
2 Sammanblandning av representerade data I en tillämpning behöver man använda koder för veckodagar, t.ex. 1 måndag, 2 tisdag, etc. För att göra programmet mera lättläst och oberoende av de specifika koderna namnger man dem (definitionsabstraktion): val Mon = 1; (* Monday *) val Tue = 2; (* Tuesday *) val Wed = 3; (* Wednesday *) etc Koderna är nu tal och de går att räkna med (Wed*2), men de representerar egentligen veckodagar, som inte skall gå att räkna med. ML blir i praktiken otypat vad beträffar tal och veckodagar. PKD 2011/12 moment 5 Sida 2 Uppdaterad
3 Vad definitionsabstraktion inte kan göra Felaktiga mönster: Hopblandning av data: (* weekend d (* overtimepay(d,x) TYPE: int->bool TYPE: int*int->int PRE: d är en korrekt dag PRE: d är en korrekt dag. POST: true om d är en POST: Timlönen veckodagen veckoslutsdag (lö/sö), d med hänsyn false annars *) till övertid om grundtimlönen är x. *) fun weekend Sat = true ajaj... weekend Sun = true ajaj... fun overtimepay(d,x) = weekend _ = false; ujuj... if weekend d then d * 2 ujuj... Felaktigt värde: weekend(8) ojoj... else x; Sat, Sun är identifierare vilka som helst de binds i mönster. PKD 2011/12 moment 5 Sida 3 Uppdaterad
4 Uppräkningstyper datatype weekday = Mon Tue Wed Thu Fri Sat Sun; weekday blir en helt ny datatyp med de angivna värdena. (* weekend d (* overtimepay(d,x) TYPE: weekday->bool TYPE: weekday*int->int PRE: (inget) Obs! PRE: (inget) Obs! POST: true om d är en POST: Timlönen veckodagen veckoslutsdag (lö/sö), d med hänsyn false annars *) till övertid om grundtimlönen är x. *) fun weekend Sat = true Ok! weekend Sun = true Ok! fun overtimepay(d,x) = weekend _ = false; if weekend d then Felaktigt värde: d * 2 else Typfel! weekend(8) Typfel! x; Sat, Sun är värden som true, false de binds inte i mönster. PKD 2011/12 moment 5 Sida 4 Uppdaterad
5 Konvertering av uppräkningstyper datatype weekday = Mon Tue Wed Thu Fri Sat Sun; ML definierar ingen speciell ordning av värdena i weekday. Inte heller finns något inbyggt sätt att omvandla dem till/från heltal som man t.ex. kan med tecken (ord, chr). Sådant får man göra själv... (* daynumber d (* numberday n TYPE: weekday->int TYPE: int->weekday PRE: (inget) PRE: 1 <= n <= 7 POST: ordningstalet POST: veckodagen med för veckodagen d *) ordningstal n *) fun daynumber Mon = 1 fun numberday 1 = Mon daynumber Tue = 2 numberday 2 = Tue daynumber Wed = 3 numberday 3 = Wed daynumber Thu = 4 numberday 4 = Thu daynumber Fri = 5 numberday 5 = Fri daynumber Sat = 6 numberday 6 = Sat daynumber Sun = 7; numberday 7 = Sun numberday _ = raise Domain; PKD 2011/12 moment 5 Sida 5 Uppdaterad
6 Vissa inbyggda typer kan definieras datatype bool = true false; datatype unit = (); Dessa datatyper är fördefinierade i ML och kan inte definieras igen, men de fungerar som om de definierats på detta sätt. PKD 2011/12 moment 5 Sida 6 Uppdaterad
7 Sammanblandning av representerade data Rationella tal (se exempel tidigare i kursen) har speciella egenskaper och borde ha en egen typ. Ex.vis. heltalsvektorer (punkter i rutnät eller matriser) representeras också naturligt som int*int-tupler likadant som rationella tal. Fastän datastrukturen är samma är egenskaperna helt annorlunda.t.ex. utförs addition av vektorer komponentvis (1,2) + (1,3) = (2,5) ML-program blir i praktiken otypade beträffande dessa sorters data. Risk för sammanblanding: addition av vektorer med qadd eller blandning av rationella tal och vektorer. PKD 2011/12 moment 5 Sida 7 Uppdaterad
8 Konstruerade (taggade) typer Med deklarationen datatype kan man skapa nya typer som skiljer sig från alla andra: datatype intvec = Intvec of int*int; datatype rational = Q of int*int; intvec och rational är nu helt nya datatyper som båda innehåller en int*int-tupel men som har en etikett (tag) som skiljer dem åt. Värden av typen intvec skrivs föregångna av konstruktorn Intvec, t.ex. Intvec(1,2). Samma med rationella tal, t.ex. Q(1,2). Jämför konstruktorn :: som skapar en listcell. PKD 2011/12 moment 5 Sida 8 Uppdaterad
9 Användning av konstruerade typer Man kan betrakta en värde av en konstruerad datatyp som ett kuvert med konstruktorn påskriven, i vilken man har stoppat ned de data som ingår i värdet. Q (1,2) Försök att blanda ihop en heltalsvektor och ett rationellt tal ger typfel eftersom ML kan se på konstruktorerna att de hör till olika typer. Intvec och Q har funktionstyper: Intvec:int*int->intvec Q:int*int->rational och ser ut och kan användas som funktioner men är inte funktioner i vanlig mening eftersom de inte utför någon beräkning. De skapar ett nytt värde på samma sätt som den infixa konstruktorn ::. PKD 2011/12 moment 5 Sida 9 Uppdaterad
10 Användning av konstruerade typer För att komma åt delarna i ett värde av en konstruerad typ måste de tas ut ur kuvertet. För detta använder man matchning på liknande sätt som man matchar på listceller med ::. Nya värden av konstruerad typ kan skapas genom att ge uttryck som beräknas som argument till konstruktorn. (* qadd(x,y) TYPE: rational*rational->rational PRE: x och y skall vara korrekta rationella tal (dvs nämnaren skall vara 0). POST: Summan av x och y EX: qadd(q(1,2),q(1,3)) = Q(5,6) *) fun qadd(q(p1,q1),q(p2,q2)) = Q(p1*q2+p2*q1,q1*q2); PKD 2011/12 moment 5 Sida 10 Uppdaterad
11 Typsystemet förhindrar sammanblandning > qadd(q(1,2),q(1,3)); val it = Q (5,6) : rational - qadd(intvec(1,2),intvec(1,3)); Error-Type error in function application. Function: qadd : rational * rational -> rational Argument: (Intvec(1,2),Intvec(1,3)):intvec*intvec Reason: Can't unify rational with intvec (Different type constructors) Found near qadd (Intvec (1, 2), Intvec (1,...)) PKD 2011/12 moment 5 Sida 11 Uppdaterad
12 Alternativa former för konstruerade typer Formerna hos datatype-deklarationen för uppräkningstyper och konstruerade typen kan kombineras! datatype number = Int of int Real of real; Ett värde i number är antingen ett heltal med etiketten Int eller ett flyttal med etiketten Real. Tack vare att etiketten skiljer kan man alltid veta om det handlar om ett heltal eller ett flyttal. Användning: Om man vill ha värden med olika form (utseende). Om man vill ha funktioner som kan ha olika typer som argument eller värde. (Namnet Int ovan är valt av mig för att vara likt int, men det finns ingen koppling mellan dem i ML. Samma gäller Real och real.) PKD 2011/12 moment 5 Sida 12 Uppdaterad
13 Kombinerade typer Typen number kan innehålla ett heltal eller ett flyttal. Vid addition av number konverteras termerna automatiskt till flyttal om det behövs. (* toreal n TYPE: number -> number POST: Talet n konverterat till flyttal EX: toreal (Int 30) = Real 30.0 *) fun toreal (Real r) = Real r toreal (Int i) = Real (real i); (* addnumbers(x,y) TYPE: number*number->number POST: summan av x och y, heltal konverteras till flyttal om det behövs. EX: addnumbers(int 30, Real 2.0) = Real 32.0 *) fun addnumbers(int x, Int y) = Int (x+y) addnumbers(x,y) = let val Real xr = toreal x; val Real yr = toreal y in Real (xr+yr) end; PKD 2011/12 moment 5 Sida 13 Uppdaterad
14 Exempel: Representation av fordon Vi definierar en datatyp för att beskriva olika fordon. Vi anger för: bilar: reg.beteckning, färg och motorstyrka cyklar: färg och hjuldiameter skateboard: färg datatype vehicle = Car of string*string*int Bicycle of string*int Skateboard of string; Olika värden av typen vehicle: Car("XYZ123","green",100) Bicycle("red",26) Skateboard "silver" PKD 2011/12 moment 5 Sida 14 Uppdaterad
15 Exempel: räkna fordon av viss färg (* vehiclecolour vehicle TYPE: vehicle->string POST: Färgen hos vehicle. EX: vehiclecolour(bicycle("green",24)) = "green" *) fun vehiclecolour (Car(_,colour,_)) = colour vehiclecolour (Bicycle(colour,_)) = colour vehiclecolour (Skateboard colour) = colour; (* countcolourvehicles(colour,vehicles) TYPE: string*vehicle list->int POST: antal fordon i vehicles med färgen colour. EX: countcolourvehicles("green", [Car("XYZ123","green",100),Skateboard "silver", Bicycle("green",24)]) = 2 *) (* VARIANT: length vehicles *) fun countcolourvehicles(_,[]) = 0 countcolourvehicles(colour,vehicle::rest) = (if vehiclecolour vehicle = colour then 1 else 0)+ countcolourvehicles(colour,rest); PKD 2011/12 moment 5 Sida 15 Uppdaterad
16 Intern dokumentation av datatyper Inte bara funktioner utan också konstruerade datatyper behöver dokumenteras. Varje datatype skall förses med en kommentar liknande en funktionsspecifikation som har två delar: En beskrivning av hur data är representerat Datastrukturinvarianten datatype rational = Q of int*int; (* REPRESENTATION CONVENTION: Ett rationellt tal representeras som Q(t,n) där t är täljaren och n är nämnaren. REPRESENTATION INVARIANT: Nämnaren får inte vara 0. *) PKD 2011/12 moment 5 Sida 16 Uppdaterad
17 Polymorfa datatyper En eller flera komponentdatatyper i en konstruerad datatyp kan vara en typvariabel: datatype 'a option = NONE SOME of 'a option blir här en typkonstruktor precis som list och vector. Instansen int option är en typ med två slags värden: Konstanten NONE. Ett heltal taggat med konstruktorn SOME. Exempel på värden av typen int option: NONE, SOME 4, SOME ~2, SOME 0 Exempel på värden av typen string option: NONE, SOME "Hej", SOME "", SOME "ABC" PKD 2011/12 moment 5 Sida 17 Uppdaterad
18 Användning av option option är en inbyggd typkonstruktor i ML. Den används t.ex. när man vill ha ett bättre sätt att hantera felsituationer i programmet än att avbryta körningen eller göra något odefinierat. (* sumuptoopt n Type: int->int option Post: SOME s, där s är summan av talen 0...n om n>=0. NONE annars. Ex: sumuptoopt 4 = SOME 10, sumuptoopt ~2 = NONE *) (* Variant: n *) fun sumuptoopt n = if n < 0 then NONE else if n = 0 then SOME 0 else SOME(n+valOf(sumUpToOpt(n-1))); Förvillkor saknas jämför med defensiva sumupto i kursmoment 4! (valof är en inbyggd funktion i ML: fun valof(some x) = x) PKD 2011/12 moment 5 Sida 18 Uppdaterad
19 Rekursiva typer Komponenterna i en konstruerad datatyps värde får höra till datatypen själv! (En rekursiv typ.) En listcell head tail cons-cell kan definieras som en konstruerad datatyp som innehåller en tupel med två komponenter för head resp. tail: datatype 'a list = [] :: of 'a*'a list; Listor i ML fungerar exakt som om de var definierade med denna deklaration. (Man kan inte göra om deklarationen för att prova ML tillåter inte att man gör en ny deklaration av listor.) PKD 2011/12 moment 5 Sida 19 Uppdaterad
20 Träd Listor kan representera data med linjär struktur t.ex. förteckningar och sekvenser. Ofta har dock data trädstruktur, t.ex. i ett släktträd: delträd rot gren noder Mattias Annika Lars-Henrik Yvonne Karl-Gustaf Birgit Sverker Detta är ett binärt träd varje nod har maximalt två grenar. Löv är noder som saknar grenar. Roten är trädets början. Djupet hos en nod är avståndet till roten. löv Martin PKD 2011/12 moment 5 Sida 20 Uppdaterad
21 Hur representera ett träd? (Dålig lösning) Varje nod läggs i en lista tillsammans med delträdens rotnoder: [("Mattias","Annika","Lars-Henrik"), ("Annika", "Yvonne", "Karl-Gustaf"), ("Yvonne", "", ""), ("Karl-Gustaf", "", ""), ("Lars-Henrik", "Birgit", "Sverker"), ("Sverker", "", "Martin"), ("Birgit", "", ""), ("Martin", "", "")] : (string*string*string) list + Enkel representation Navigering i trädet kräver sökning i listan. Hur hitta farfar? Vilken nod är rotnoden? Uppdatering av trädet kräver också sökning. Denna representation är inte bra i praktiken! PKD 2011/12 moment 5 Sida 21 Uppdaterad
22 Träddatatyper Binära träd kan representeras direkt i ML som en rekursiv datatyp! datatype familytree = Empty Person of string*familytree*familytree; Mattias Annika Lars-Henrik Yvonne Karl-Gustaf Birgit Sverker Martin Person("Mattias", Person("Annika",Person("Yvonne",Empty,Empty), Person("Karl-Gustaf",Empty,Empty)), Person("Lars-Henrik",Person("Birgit",Empty,Empty), Person("Sverker",Empty, Person("Martin", Empty,Empty)))) PKD 2011/12 moment 5 Sida 22 Uppdaterad
23 Enkel navigering (* farfar t TYPE: familytree -> familytree PRE: Det finns en farfader till rotnoden i t. POST: Delträdet till t där farfadern är rotnod. EX: farfar (Person("Mattias",..., Person("Lars-Henrik",..., Person("Sverker",...,...)))) = Person("Sverker",...,...) *) fun farfar(person(_,_,person(_,_,ff))) = ff; PKD 2011/12 moment 5 Sida 23 Uppdaterad
24 Rekursion över träd Rekursion över träd är normalt dubbel rekursion man måste göra rekursion över båda grenarna från en given nod. (* countpersons t TYPE: familytree -> int PRE: (inget) POST: Antal personer i trädet t EX: countpersons( Person("Ronja",Person("Lovis",Empty,Empty), Person("Mattis",Empty,Empty))) = 3 *) (* VARIANT: Antal noder i trädet t *) fun countpersons Empty = 0 countpersons(person(_,left,right)) = 1 + countpersons Left + countpersons Right; PKD 2011/12 moment 5 Sida 24 Uppdaterad
25 Rekursion över träd (forts.) fun countpersons Empty = 0 countpersons(person(_,left,right)) = 1 + countpersons Left + countpersons Right; countpersons(person("ronja",person("lovis",empty,e mpty), Person("Mattis",Empty,Empty))) > 1+countPersons(Person("Lovis",Empty,Empty)+ countpersons(person("mattis",empty,empty)) > 1+(1+countPersons Empty+countPersons Empty)+ countpersons(person("mattis",empty,empty)) > 1+(1+0+countPersons Empty)+ countpersons(person("mattis",empty,empty)) > 1+(1+countPersons Empty)+ countpersons(person("mattis",empty,empty)) > 1+(1+0)+countPersons > 2+countPersons(Person("Mattis",Empty,Empty)) > 2+(1+countPersons Empty+countPersons Empty) > 3 PKD 2011/12 moment 5 Sida 25 Uppdaterad
26 Syntaxträd Strukturen hos en formel kan beskrivas med ett syntaxträd. 3+2*x-1 : + 1 datatype expr = Const of int Var of string Plus of expr*expr Minus of expr*expr Times of expr*expr Div of expr*expr; Minus(Plus(Const 3,Times(Const 2,Var "x")), Const 1) PKD 2011/12 moment 5 Sida 26 Uppdaterad * x
27 Beräkning av uttryck (utan variabler) (* eval(expr) TYPE: expr->int PRE: expr innehåller inga variabler. POST: Värdet av expr. Ex: eval(minus(plus(const 3, Times(Const 2,Const 4)), Const 1)) = 10 *) (* VARIANT: Storleken hos expr. *) fun eval(const c) = c eval(plus(e1,e2)) = eval e1 + eval e2 eval(minus(e1,e2)) = eval e1 - eval e2 eval(times(e1,e2)) = eval e1 * eval e2 eval(div(e1,e2)) = eval e1 div eval e2; Vi återkommer till variabler i syntaxträdet senare PKD 2011/12 moment 5 Sida 27 Uppdaterad
28 Beräkning av uttryck (forts.) fun eval(const c) = c eval(plus(e1,e2)) = eval e1 + eval e2 eval(minus(e1,e2)) = eval e1 - eval e2 eval(times(e1,e2)) = eval e1 * eval e2 eval(div(e1,e2)) = eval e1 div eval e2; eval(minus(plus(const 3,Times(Const 2,Const 4)),Const 1)) > eval(plus(const 3,Times(Const 2,Const 4))) - eval(const 1) > (eval(const 3)+eval(Times(Const 2,Const 4))))- eval(const 1) > (3+eval(Times(Const 2,Const 4))))-eval(Const 1) > (3+(eval(Const 2)*eval(Const 4)))-eval(Const 1) > (3+(2*eval(Const 4)))-eval(Const 1) > (3+(2*4))-eval(Const 1) > (3+8)-eval(Const 1) > 11-eval(Const 1) > 11-1 > 10 PKD 2011/12 moment 5 Sida 28 Uppdaterad
29 Teologiska fakulteten Hum.-Sam. vetenskapsområdet Juridiska fakulteten Allmänna träd Uppsala universitet... Språkvet. fakulteten Inst. för IT... Tek.-Nat. vetenskapsområdet Tek.-Nat. fakulteten Inst. för matematik... Inst. för teknikvet. datatype 'a tree = Tree of 'a*('a tree) list; 'a är typen för informationen i varje nod. PKD 2011/12 moment 5 Sida 29 Uppdaterad
30 Exempel på träd datatype 'a tree = Tree of 'a*('a tree) list; Tree("Uppsala universitet", [Tree("Hum.-Sam. vetenskapsområdet", [Tree("Teologiska fakulteten",[]), Tree("Juridiska fakulteten",[]), Tree("Språkvet. fakulteten",[]),...]), Tree("Tek.-Nat. vetenskapsområdet", [Tree("Tek.-Nat. fakulteten"), [Tree("Inst. för IT",[]), Tree("Inst. för matematik",[]), Tree("Inst. för teknikvet.",[]),...])]),...]) : string tree PKD 2011/12 moment 5 Sida 30 Uppdaterad
31 Minns ni analysen av summeringsproblemet? För att summera talen från 0 till n kan jag lösa det enklare problemet att summera från 0 till n-1 och sedan lägga till n! Om n=0 kan jag direkt säga att summan är 0. fun sumupto 0 = 0 sumupto n = sumupto(n-1) + n sumupto 3 > sumupto(3-1)+3 > sumupto 2+3 >(sumupto(2-1)+2)+3 > (sumupto 1+2)+3 > ((sumupto(1-1)+1)+2)+3 > ((sumupto 0+1)+2)+3 > ((0+1)+2)+3 > (1+2)+3 > 3+3 > 6 PKD 2011/12 moment 5 Sida 31 Uppdaterad
32 En annan analys av summeringsproblemet Start. Låt summan vara 0. Är n=0? Ja. Stopp. Nej. Addera n till summan. Subtrahera 1 från n. Konstruktionen kallas för en loop. Här adderar vi det största talet först (n+...+0) och inte det minsta (0+...+n), men det ger samma resultat. (I detta fall!!) PKD 2011/12 moment 5 Sida 32 Uppdaterad
33 Iteration i ML Basfall fun sumupto n = sumuptoaux(n,0) Rekursivt anrop fun sumuptoaux(0,sum) = sum sumuptoaux(n,sum) = sumuptoaux(n-1,sum+n) En hjälpfunktion sumuptoaux implementerar loopen. Tekniken kallas iteration (svansrekursion) och är ett specialfall av rekursion. Argumentet sum kallas för ackumulator. Obs att nya värden för n och sum beräknas samtidigt. sumupto 2 > sumuptoaux(2,0) > sumuptoaux(2-1,0+2) > sumuptoaux(1,2) > sumuptoaux(1-1,2+1) > sumuptoaux(0,3) > 3 PKD 2011/12 moment 5 Sida 33 Uppdaterad
34 Bindningar i iteration fun sumuptoaux(0,sum) = sum sumuptoaux(n,sum) = sumuptoaux(n-1,sum+n) sumuptoaux(2,0) > sumuptoaux(n-1,sum+n)[n >2,sum >0] > sumuptoaux(2-1,sum+n)[n >2,sum >0] > sumuptoaux(1,sum+n) [n >2,sum >0] > sumuptoaux(1,0+n) [n >2,sum >0] > sumuptoaux(1,0+2) [n >2,sum >0] > sumuptoaux(1,2) [n >2,sum >0] > sumuptoaux(n-1,sum+n)[n >1,sum >2] [n >2,sum >0] skuggas bort helt > sumuptoaux(1-1,sum+n)[n >1,sum >2] > sumuptoaux(0,sum+n) [n >1,sum >2] > sumuptoaux(0,2+n) [n >1,sum >2] > sumuptoaux(0,2+1) [n >1,sum >2] > sumuptoaux(0,3) [n >1,sum >2] > 3 PKD 2011/12 moment 5 Sida 34 Uppdaterad
35 Funktionsspecifikationen för sumuptoaux sumuptoaux(n,sum) Type: int*int->int För att rekursionen skall terminera krävs att n inte är mindre än 0: Pre: n>=0 Man kan inte kräva sum=0. Det gäller inte för de rekursiva anropen! Eftervillkoret är inte att sumuptoaux summerar talen 0 till n. Så är den avsedd att användas men det är inte vad den faktiskt gör. Post: Summan av sum och talen från 0 till n. Exempel behövs också... Ex.: sumuptoaux(3,0) = 6 sumuptoaux(4,5) = 15 sumuptoaux(0,2) = 2 Rekursionsvarianten anges som del av programdokumentationen. Variant: n PKD 2011/12 moment 5 Sida 35 Uppdaterad
36 Minnesbehov Rekursion i allmänhet behöver minne i proportion till antalet rekursiva anrop eftersom en del av beräkningen väntar. sumupto 3 > sumupto(3-1)+3 > sumupto 2+3 >(sumupto(2-1)+2)+3 > (sumupto 1+2)+3 > ((sumupto(1-1)+1)+2)+3 > ((sumupto 0+1)+2)+3 > ((0+1)+2)+3 > (1+2)+3 > 3+3 > 6 Uttrycket blir hela tiden större... Programmet kan få slut på minne om de rekursiva anropen är många och/eller kräver mycket minne. PKD 2011/12 moment 5 Sida 36 Uppdaterad
37 Minnesbehov vid iteration Iteration har konstant minnesåtgång. fun sumupto n = sumuptoaux(n,0); fun sumuptoaux(0,sum) = sum sumuptoaux(n,sum) = sumuptoaux(n-1,sum+n) sumupto 3 > sumuptoaux(3,0) > sumuptoaux(3-1,0+3) > sumuptoaux(2,0) > sumuptoaux(2-1,3+2) > sumuptoaux(1,2) > sumuptoaux(1-1,5+1) > sumuptoaux(0,6) > 6 Minnet kan aldrig ta slut (inte pga rekursionen i alla fall). PKD 2011/12 moment 5 Sida 37 Uppdaterad
38 Beräkningsordning i rekursion fun foo [] = [] foo(first::rest) = first::foo rest; foo plockar isär en lista men sätter genast ihop den igen! foo [1,2,3,4] = [1,2,3,4] Vad händer om man gör samma sak iterativt? fun revaux([],ack) = ack revaux(first::rest,ack) = revaux(rest,first::ack); fun rev l = revaux(l,[]); Låt oss se rev [1,2,3,4] = [4,3,2,1] revaux gör beräkningen i omvänd ordning jämfört med foo! PKD 2011/12 moment 5 Sida 38 Uppdaterad
39 Vänd på en lista (körexempel) fun revaux([],ack) = ack revaux(first::rest,ack) = revaux(rest,first::ack) fun rev l = revaux(l,[]) rev [1,2,3,4] > revaux([1,2,3,4],[]) > revaux([2,3,4],[1]) > revaux([3,4],[2,1]) > revaux([4],[3,2,1]) > revaux([],[4,3,2,1]) > [4,3,2,1] (rev är en inbyggd funktion i ML för att vända på listor.) PKD 2011/12 moment 5 Sida 39 Uppdaterad
40 Kodningsmönster för iteration Flödesschema för funktionen foo: Kod för funktionen foo: Start. A. Ja. T? C. Stopp. Nej. B. fun foo x = fooaux A fun fooaux x = if T then C else fooaux B Iterativa program är i vissa fall de bästa, men i allmänhet blir programmen lättare att skriva och förstå med vanlig rekursion! PKD 2011/12 moment 5 Sida 40 Uppdaterad
41 Ett mindre snyggt program (* notwins l TYPE: ''a list -> ''a list POST: l med alla följder av samma element ersatta av en enda förekomst. EX: notwins [1,2,2,3,4,4,4] = [1,2,3,4] *) (* VARIANT: length l *) fun notwins [] = [] notwins [x] = [x] notwins (first::rest) = if first = hd rest then notwins rest else first::notwins rest; Här skulle man vilja ha ett mönster som delar upp svansen av argumentet ytterligare så att man inte behöver använda hd. PKD 2011/12 moment 5 Sida 41 Uppdaterad
42 Ett till mindre snyggt program för samma sak (Samma funktionsspecifikation.) fun notwins [] = [] notwins [x] = [x] notwins (first::second::rest) = if first = second then notwins(second::rest) else first::notwins(second::rest); Svansen av argumentet är nu uppdelad i second och rest, men då måste man sätta ihop dem igen i de rekursiva anropen! PKD 2011/12 moment 5 Sida 42 Uppdaterad
43 Mönstret as Med konstruktionen as kan man både binda en datastruktur och matcha den mot ytterligare mönster. fun notwins [] = [] notwins [x] = [x] notwins (first::(rest as second::_)) = if first = second then notwins rest else first::notwins rest; I tredje klausulen kommer svansen på argumentet dels bindas till rest. dels matchas vidare mot mönstret second::_ Då behöver man varken använda hd eller sätta ihop det man redan tagit isär. PKD 2011/12 moment 5 Sida 43 Uppdaterad
Programkonstruktion och datastrukturer. Moment 6 Om generella datastrukturer och träd. PKD 2012/13 moment 6 Sida 1 Uppdaterad
 Programkonstruktion och datastrukturer Moment 6 Om generella datastrukturer och träd PKD 2012/13 moment 6 Sida 1 Uppdaterad 2012-12-05 Tabeller En viktig tillämpning är tabellen att ifrån en nyckel kunna
Programkonstruktion och datastrukturer Moment 6 Om generella datastrukturer och träd PKD 2012/13 moment 6 Sida 1 Uppdaterad 2012-12-05 Tabeller En viktig tillämpning är tabellen att ifrån en nyckel kunna
Programmeringsmetodik DV1 Programkonstruktion 1. Moment 4 Om rekursion. PK1&PM1 HT-06 moment 4 Sida 1 Uppdaterad
 Programmeringsmetodik DV1 Programkonstruktion 1 Moment 4 Om rekursion PK1&PM1 HT-06 moment 4 Sida 1 Uppdaterad 2006-10-17 Summera godtyckligt antal tal (* sumupto n Type: int->int Pre: n >= 0, n
Programmeringsmetodik DV1 Programkonstruktion 1 Moment 4 Om rekursion PK1&PM1 HT-06 moment 4 Sida 1 Uppdaterad 2006-10-17 Summera godtyckligt antal tal (* sumupto n Type: int->int Pre: n >= 0, n
Summera godtyckligt antal tal. Programkonstruktion. Moment 4 Om rekursion. Fullständigt resonemang för summeringen. Analys av summeringsproblemet
 Summera godtyckligt antal tal Programkonstruktion Moment 4 Om rekursion Pre: n >=, n
Summera godtyckligt antal tal Programkonstruktion Moment 4 Om rekursion Pre: n >=, n
Programmeringsmetodik DV1 Programkonstruktion 1. Moment 8 Om abstrakta datatyper och binära sökträd
 Programmeringsmetodik DV1 Programkonstruktion 1 Moment 8 Om abstrakta datatyper och binära sökträd PK1&PM1 HT-06 moment 8 Sida 1 Uppdaterad 2005-09-22 Tabeller En viktig tillämpning är tabellen att ifrån
Programmeringsmetodik DV1 Programkonstruktion 1 Moment 8 Om abstrakta datatyper och binära sökträd PK1&PM1 HT-06 moment 8 Sida 1 Uppdaterad 2005-09-22 Tabeller En viktig tillämpning är tabellen att ifrån
Tabeller. Programkonstruktion. Moment 8 Om abstrakta datatyper och binära sökträd. Implementering av tabellen. Operationer på tabellen
 Programkonstruktion Moment 8 Om abstrakta datatyper och binära sökträd Tabeller En viktig tillämpning är tabellen att ifrån en nyckel kunna ta fram ett tabellvärde. Ett typiskt exempel är en telefonkatalog:
Programkonstruktion Moment 8 Om abstrakta datatyper och binära sökträd Tabeller En viktig tillämpning är tabellen att ifrån en nyckel kunna ta fram ett tabellvärde. Ett typiskt exempel är en telefonkatalog:
Programkonstruktion och datastrukturer. Moment 9 Om högre ordningens funktioner. PKD 2010/11 moment 9 Sida 1 Uppdaterad
 Programkonstruktion och datastrukturer Moment 9 Om högre ordningens funktioner PKD 2010/11 moment 9 Sida 1 Uppdaterad 2010-12-02 Anonyma funktioner igen En funktion som inte är namngiven kallas för en
Programkonstruktion och datastrukturer Moment 9 Om högre ordningens funktioner PKD 2010/11 moment 9 Sida 1 Uppdaterad 2010-12-02 Anonyma funktioner igen En funktion som inte är namngiven kallas för en
Programmeringsmetodik DV1 Programkonstruktion 1. Moment 9 Om högre ordningens funktioner. PK1&PM1 HT-06 moment 9 Sida 1 Uppdaterad
 Programmeringsmetodik DV1 Programkonstruktion 1 Moment 9 Om högre ordningens funktioner PK1&PM1 HT-06 moment 9 Sida 1 Uppdaterad 2006-09-06 Anonyma funktioner igen En funktion som inte är namngiven kallas
Programmeringsmetodik DV1 Programkonstruktion 1 Moment 9 Om högre ordningens funktioner PK1&PM1 HT-06 moment 9 Sida 1 Uppdaterad 2006-09-06 Anonyma funktioner igen En funktion som inte är namngiven kallas
Tabeller. Programkonstruktion. Moment 8 Om abstrakta datatyper och binära sökträd. Specifikationer för tabellfunktionerna. Operationer på tabellen
 Programkonstruktion Moment 8 Om abstrakta datatyper och binära sökträd Tabeller En viktig tillämpning är tabeller att ifrån en nyckel kunna ta fram ett tabellvärde. Ett typiskt exempel är en telefonkatalog:
Programkonstruktion Moment 8 Om abstrakta datatyper och binära sökträd Tabeller En viktig tillämpning är tabeller att ifrån en nyckel kunna ta fram ett tabellvärde. Ett typiskt exempel är en telefonkatalog:
Omtentamen (del 1, 6 högskolepoäng) i Programkonstruktion och datastrukturer (1DL201)
 Omtentamen (del 1, 6 högskolepoäng) i Programkonstruktion och datastrukturer (1DL201) Lars-Henrik Eriksson Fredag 5 april 2013, kl 14:00 17:00, i Polacksbackens skrivsal Hjälpmedel: Inga. Inte heller elektronisk
Omtentamen (del 1, 6 högskolepoäng) i Programkonstruktion och datastrukturer (1DL201) Lars-Henrik Eriksson Fredag 5 april 2013, kl 14:00 17:00, i Polacksbackens skrivsal Hjälpmedel: Inga. Inte heller elektronisk
Programkonstruktion och datastrukturer. Moment 9 Om högre ordningens funktioner. PKD 2011/12 moment 9 Sida 1 Uppdaterad
 Programkonstruktion och datastrukturer Moment 9 Om högre ordningens funktioner PKD 2011/12 moment 9 Sida 1 Uppdaterad 2012-01-15 Anonyma funktioner igen En funktion som inte är namngiven kallas för en
Programkonstruktion och datastrukturer Moment 9 Om högre ordningens funktioner PKD 2011/12 moment 9 Sida 1 Uppdaterad 2012-01-15 Anonyma funktioner igen En funktion som inte är namngiven kallas för en
Programkonstruktion. Tentamen,
 Programkonstruktion (Programmeringsmetodik DV1) Tentamen, 2009-08-24 Lars-Henrik Eriksson Institutionen för informationsteknologi Uppsala Universitet Tid: 14:00-19:00. Börja med att läsa igenom alla frågorna
Programkonstruktion (Programmeringsmetodik DV1) Tentamen, 2009-08-24 Lars-Henrik Eriksson Institutionen för informationsteknologi Uppsala Universitet Tid: 14:00-19:00. Börja med att läsa igenom alla frågorna
TDDC74 Programmering: Abstraktion och modellering Datortenta , kl 14-18
 TDDC74 Programmering: Abstraktion och modellering Datortenta - 017-10-7, kl 14-18 Läs alla frågorna först och bestäm dig för i vilken ordning du vill lösa uppgifterna. Uppgifterna är inte nödvändigtvis
TDDC74 Programmering: Abstraktion och modellering Datortenta - 017-10-7, kl 14-18 Läs alla frågorna först och bestäm dig för i vilken ordning du vill lösa uppgifterna. Uppgifterna är inte nödvändigtvis
Programkonstruktion. Tentamen,
 Programkonstruktion (Programmeringsmetodik DV1) Tentamen, 2008-03-10 Lars-Henrik Eriksson Institutionen för informationsteknologi Uppsala Universitet Tid: 0900-14:00. Börja med att läsa igenom alla frågorna
Programkonstruktion (Programmeringsmetodik DV1) Tentamen, 2008-03-10 Lars-Henrik Eriksson Institutionen för informationsteknologi Uppsala Universitet Tid: 0900-14:00. Börja med att läsa igenom alla frågorna
Programmeringsmetodik DV1, Programkonstruktion del 1 Tentamen,
 Programmeringsmetodik DV1, Programkonstruktion del 1 Tentamen, 2007-08-21 Lars-Henrik Eriksson Institutionen för informationsteknologi Uppsala Universitet Tid: 0900-14:00. Börja med att läsa igenom alla
Programmeringsmetodik DV1, Programkonstruktion del 1 Tentamen, 2007-08-21 Lars-Henrik Eriksson Institutionen för informationsteknologi Uppsala Universitet Tid: 0900-14:00. Börja med att läsa igenom alla
Två fall: q Tom sekvens: () q Sekvens av element: (a b c) ; (sum-rec '(2 4 6)) = 12. q Första elementet uppfyller vissa villkor: (2 a b c)
 Programmönster: # Listan som sekvens, Rekursiv process Enkel genomgång av sekvens (element på toppnivån i en lista)) TDDC60 Programmering: abstraktion och modellering Föreläsning 5 Rekursiva och iterativa
Programmönster: # Listan som sekvens, Rekursiv process Enkel genomgång av sekvens (element på toppnivån i en lista)) TDDC60 Programmering: abstraktion och modellering Föreläsning 5 Rekursiva och iterativa
Programkonstruktion. Tentamen,
 Programkonstruktion (Programmeringsmetodik DV1) Tentamen, 2008-06-12 Lars-Henrik Eriksson Institutionen för informationsteknologi Uppsala Universitet Tid: 0900-14:00. Börja med att läsa igenom alla frågorna
Programkonstruktion (Programmeringsmetodik DV1) Tentamen, 2008-06-12 Lars-Henrik Eriksson Institutionen för informationsteknologi Uppsala Universitet Tid: 0900-14:00. Börja med att läsa igenom alla frågorna
Funktionell programmering DD1361
 Funktionell programmering DD1361 Tupler Två eller fler (men ändligt) antal element. Elementen kan vara av olika typer. Ex: (1,2) :: (Integer, Integer) (( 2, hejsan ), True) ::? Tupel med två element ->
Funktionell programmering DD1361 Tupler Två eller fler (men ändligt) antal element. Elementen kan vara av olika typer. Ex: (1,2) :: (Integer, Integer) (( 2, hejsan ), True) ::? Tupel med två element ->
Programkonstruktion och datastrukturer. Formell verifiering eller hur man bevisar att program gör rätt utan att testa dem
 Programkonstruktion och datastrukturer Formell verifiering eller hur man bevisar att program gör rätt utan att testa dem PKD 2012/13 Formell verifiering Sida 1 Uppdaterad 2008-11-28 Formell verifiering:
Programkonstruktion och datastrukturer Formell verifiering eller hur man bevisar att program gör rätt utan att testa dem PKD 2012/13 Formell verifiering Sida 1 Uppdaterad 2008-11-28 Formell verifiering:
Tentamen (del 2) (4 högskolepoäng) i Programkonstruktion och datastrukturer (1DL201)
 Tentamen (del 2) (4 högskolepoäng) i Programkonstruktion och datastrukturer (1DL201) Lars-Henrik Eriksson Onsdag 20 mars 2013, kl. 08:00 11:00, i Bergsbrunnagatans skrivsal 1 Hjälpmedel: Inga. Inte heller
Tentamen (del 2) (4 högskolepoäng) i Programkonstruktion och datastrukturer (1DL201) Lars-Henrik Eriksson Onsdag 20 mars 2013, kl. 08:00 11:00, i Bergsbrunnagatans skrivsal 1 Hjälpmedel: Inga. Inte heller
Tentamen 1 (6 högskolepoäng) i Programkonstruktion och datastrukturer (1DL201)
 Tentamen 1 (6 högskolepoäng) i Programkonstruktion och datastrukturer (1DL201) Lars-Henrik Eriksson och Pierre Flener Fredag 17 december 2010, kl 14:00 17:00, i Gimogatan 4, sal 1 Hjälpmedel: Inga. Inte
Tentamen 1 (6 högskolepoäng) i Programkonstruktion och datastrukturer (1DL201) Lars-Henrik Eriksson och Pierre Flener Fredag 17 december 2010, kl 14:00 17:00, i Gimogatan 4, sal 1 Hjälpmedel: Inga. Inte
Programkonstruktion. Moment 11 Om sidoeffekter In/utmatning och imperativ programmering. PKD 2011/12 moment 11 Sida 1 Uppdaterad
 Programkonstruktion Moment 11 Om sidoeffekter In/utmatning och imperativ programmering PKD 2011/12 moment 11 Sida 1 Uppdaterad 2012-01-30 Referentiell transparens I ren funktionell programmering kan man
Programkonstruktion Moment 11 Om sidoeffekter In/utmatning och imperativ programmering PKD 2011/12 moment 11 Sida 1 Uppdaterad 2012-01-30 Referentiell transparens I ren funktionell programmering kan man
Programkonstruktion och Datastrukturer
 Programkonstruktion och Datastrukturer VT 2012 Tidskomplexitet Elias Castegren elias.castegren.7381@student.uu.se Problem och algoritmer Ett problem är en uppgift som ska lösas. Beräkna n! givet n>0 Räkna
Programkonstruktion och Datastrukturer VT 2012 Tidskomplexitet Elias Castegren elias.castegren.7381@student.uu.se Problem och algoritmer Ett problem är en uppgift som ska lösas. Beräkna n! givet n>0 Räkna
Rekursiva algoritmer sortering sökning mönstermatchning
 Anders Haraldsson 1 Anders Haraldsson 2 Dagens föreläsning Programmering i Lisp Fö 6-7 Rekursiva strukturer rekursiva definitioner rekursiva funktioner rekursiva bevis: induktion - rekursion strukturell
Anders Haraldsson 1 Anders Haraldsson 2 Dagens föreläsning Programmering i Lisp Fö 6-7 Rekursiva strukturer rekursiva definitioner rekursiva funktioner rekursiva bevis: induktion - rekursion strukturell
Universitetet i Linköping Institutionen för datavetenskap Anders Haraldsson 2
 Anders Haraldsson 1 Anders Haraldsson 2 Dagens föreläsning Programmering i Lisp Fö 5 - Funktioner - lambda-uttryck (avs 7.1) - funcall och function (avs 7.2) - Högre ordningens funktioner (avs 7.) - Iteratorer
Anders Haraldsson 1 Anders Haraldsson 2 Dagens föreläsning Programmering i Lisp Fö 5 - Funktioner - lambda-uttryck (avs 7.1) - funcall och function (avs 7.2) - Högre ordningens funktioner (avs 7.) - Iteratorer
Tentamen, Algoritmer och datastrukturer
 UNDS TEKNISKA ÖGSKOA (6) Institutionen för datavetenskap Tentamen, Algoritmer och datastrukturer 23 8 29, 8. 3. Anvisningar: Denna tentamen består av fem uppgifter. Totalt är skrivningen på 36 poäng och
UNDS TEKNISKA ÖGSKOA (6) Institutionen för datavetenskap Tentamen, Algoritmer och datastrukturer 23 8 29, 8. 3. Anvisningar: Denna tentamen består av fem uppgifter. Totalt är skrivningen på 36 poäng och
Dagens föreläsning Programmering i Lisp Fö 5
 Anders Haraldsson 1 Dagens föreläsning Programmering i Lisp Fö 5 - Funktioner - lambda-uttryck (avs 7.1) - funcall och function (avs 7.2) - Högre ordningens funktioner (avs 7.3) - Iteratorer - Egenskaper
Anders Haraldsson 1 Dagens föreläsning Programmering i Lisp Fö 5 - Funktioner - lambda-uttryck (avs 7.1) - funcall och function (avs 7.2) - Högre ordningens funktioner (avs 7.3) - Iteratorer - Egenskaper
Instruktioner - Datortentamen TDDD73 Funktionell och imperativ programmering i Python
 Instruktioner - Datortentamen TDDD73 Funktionell och imperativ programmering i Python Hjälpmedel Följande hjälpmedel är tillåtna: Exakt en valfri bok, t.ex. den rekommenderade kursboken. Boken får ha anteckningar,
Instruktioner - Datortentamen TDDD73 Funktionell och imperativ programmering i Python Hjälpmedel Följande hjälpmedel är tillåtna: Exakt en valfri bok, t.ex. den rekommenderade kursboken. Boken får ha anteckningar,
Programmering II (ID1019) :00-17:00
 ID1019 Johan Montelius Programmering II (ID1019) 2014-03-10 14:00-17:00 Förnamn: Efternamn: Instruktioner Du får inte ha något materiel med dig förutom skrivmateriel. Mobiler etc, skall lämnas till tentamensvakten.
ID1019 Johan Montelius Programmering II (ID1019) 2014-03-10 14:00-17:00 Förnamn: Efternamn: Instruktioner Du får inte ha något materiel med dig förutom skrivmateriel. Mobiler etc, skall lämnas till tentamensvakten.
Språket Python - Del 1 Grundkurs i programmering med Python
 Hösten 2009 Dagens lektion Ett programmeringsspråks byggstenar Några inbyggda datatyper Styra instruktionsflödet Modulen sys 2 Ett programmeringsspråks byggstenar 3 ETT PROGRAMMERINGSSPRÅKS BYGGSTENAR
Hösten 2009 Dagens lektion Ett programmeringsspråks byggstenar Några inbyggda datatyper Styra instruktionsflödet Modulen sys 2 Ett programmeringsspråks byggstenar 3 ETT PROGRAMMERINGSSPRÅKS BYGGSTENAR
Programmeringsmetodik DV1 Programkonstruktion 1. Moment 2 Introduktion till funktioner och programutveckling
 Programmeringsmetodik DV1 Programkonstruktion 1 Moment 2 Introduktion till funktioner och programutveckling PK1&PM1 HT-06 moment 2 Sida 1 Uppdaterad 2005-09-20 Återanvändning av kod? String.substring("Hägg",size
Programmeringsmetodik DV1 Programkonstruktion 1 Moment 2 Introduktion till funktioner och programutveckling PK1&PM1 HT-06 moment 2 Sida 1 Uppdaterad 2005-09-20 Återanvändning av kod? String.substring("Hägg",size
Datastrukturer, algoritmer och programkonstruktion (DVA104, VT 2015) Föreläsning 6
 Datastrukturer, algoritmer och programkonstruktion (DVA104, VT 2015) Föreläsning 6? DAGENS AGENDA Komplexitet Ordobegreppet Komplexitetsklasser Loopar Datastrukturer Några nyttiga regler OBS! Idag jobbar
Datastrukturer, algoritmer och programkonstruktion (DVA104, VT 2015) Föreläsning 6? DAGENS AGENDA Komplexitet Ordobegreppet Komplexitetsklasser Loopar Datastrukturer Några nyttiga regler OBS! Idag jobbar
Former av rekursion. Programkonstruktion. Moment 5 Mera om rekursion. Fakultetsfunktionen. Största gemensamma delare (repris!
 Programkonstruktion Moment 5 Mera om rekursion Former av rekursion enkel rekursion ett rekursivt anrop. fullständig rekursion argumenten (varianten) kan mska olika många steg i det rekursiva anropet. multipel
Programkonstruktion Moment 5 Mera om rekursion Former av rekursion enkel rekursion ett rekursivt anrop. fullständig rekursion argumenten (varianten) kan mska olika många steg i det rekursiva anropet. multipel
TDDC74 Programmering: Abstraktion och modellering Tentamen, lördag 27 augusti 2016, kl 8 12
 TDDC74 Programmering: Abstraktion och modellering Tentamen, lördag 27 augusti 2016, kl 8 12 Läs alla frågorna först, och bestäm dig för i vilken ordning du vill lösa uppgifterna. Skriv tydligt och läsligt.
TDDC74 Programmering: Abstraktion och modellering Tentamen, lördag 27 augusti 2016, kl 8 12 Läs alla frågorna först, och bestäm dig för i vilken ordning du vill lösa uppgifterna. Skriv tydligt och läsligt.
Imperativ programmering. Imperativ programmering konstruktioner i Lisp. Datastrukturer (kap ) arraystruktur poststruktur
 Imperativ programmering konstruktioner i Lisp Imperativ programmering I den imperativa programmeringen skriver vi program satsvist. Datastrukturer (kap.-.) aystruktur poststruktur Iterativa uttryck (avs.)
Imperativ programmering konstruktioner i Lisp Imperativ programmering I den imperativa programmeringen skriver vi program satsvist. Datastrukturer (kap.-.) aystruktur poststruktur Iterativa uttryck (avs.)
TDDC74 Programmering: Abstraktion och modellering Tentamen, onsdag 9 juni 2016, kl 14 18
 TDDC74 Programmering: Abstraktion och modellering Tentamen, onsdag 9 juni 2016, kl 14 18 Läs alla frågorna först, och bestäm dig för i vilken ordning du vill lösa uppgifterna. Skriv tydligt och läsligt.
TDDC74 Programmering: Abstraktion och modellering Tentamen, onsdag 9 juni 2016, kl 14 18 Läs alla frågorna först, och bestäm dig för i vilken ordning du vill lösa uppgifterna. Skriv tydligt och läsligt.
Programmering II (ID1019)
 ID1019 Johan Montelius Instruktioner Betyg Programmering II (ID1019) 2019-03-08 Svaren skall lämnas på dessa sidor, använd det utrymme som nns under varje uppgift för att skriva ner ditt svar (inte på
ID1019 Johan Montelius Instruktioner Betyg Programmering II (ID1019) 2019-03-08 Svaren skall lämnas på dessa sidor, använd det utrymme som nns under varje uppgift för att skriva ner ditt svar (inte på
Föreläsning Datastrukturer (DAT037)
 Föreläsning Datastrukturer (DAT037) Nils Anders Danielsson 2015-11-23 Idag Mer om grafer: Minsta uppspännande träd (för oriktade grafer). Djupet först-sökning. Minsta uppspännande träd Träd (utan rot)
Föreläsning Datastrukturer (DAT037) Nils Anders Danielsson 2015-11-23 Idag Mer om grafer: Minsta uppspännande träd (för oriktade grafer). Djupet först-sökning. Minsta uppspännande träd Träd (utan rot)
Tentamen i. TDDC67 Funktionell programmering och Lisp
 1 Linköpings tekniska högskola Institutionen för datavetenskap Anders Haraldsson Tentamen i TDDC67 Funktionell programmering och Lisp och äldre kurser TDDC57 Programmering, Lisp och funktionell programmering
1 Linköpings tekniska högskola Institutionen för datavetenskap Anders Haraldsson Tentamen i TDDC67 Funktionell programmering och Lisp och äldre kurser TDDC57 Programmering, Lisp och funktionell programmering
DD1361 Programmeringsparadigm. Carina Edlund
 DD1361 Programmeringsparadigm Carina Edlund carina@nada.kth.se Funktionell programmering Grundidéen med funktionell programmering är att härma matematiken och dess funktionsbegrepp. Matematiskt funktionsbegrepp
DD1361 Programmeringsparadigm Carina Edlund carina@nada.kth.se Funktionell programmering Grundidéen med funktionell programmering är att härma matematiken och dess funktionsbegrepp. Matematiskt funktionsbegrepp
Träd, binära träd och sökträd. Koffman & Wolfgang kapitel 6, avsnitt 1 4
 Träd, binära träd och sökträd Koffman & Wolfgang kapitel 6, avsnitt 1 4 1 Träd Träd är ickelinjära och hierarkiska: i motsats till listor och fält en trädnod kan ha flera efterföljare ( barn ) men bara
Träd, binära träd och sökträd Koffman & Wolfgang kapitel 6, avsnitt 1 4 1 Träd Träd är ickelinjära och hierarkiska: i motsats till listor och fält en trädnod kan ha flera efterföljare ( barn ) men bara
Programmering II (ID1019) :00-11:00
 ID1019 Johan Montelius Programmering II (ID1019) 2015-06-11 08:00-11:00 Instruktioner Du får inte ha något materiel med dig förutom skrivmateriel. Mobiler etc, skall lämnas till tentamensvakten. Svaren
ID1019 Johan Montelius Programmering II (ID1019) 2015-06-11 08:00-11:00 Instruktioner Du får inte ha något materiel med dig förutom skrivmateriel. Mobiler etc, skall lämnas till tentamensvakten. Svaren
Tillämpad Programmering (ID1218) :00-13:00
 ID1218 Johan Montelius Tillämpad Programmering (ID1218) 2014-03-13 09:00-13:00 Förnamn: Efternamn: Regler Du får inte ha något materiel med dig förutom skrivmateriel. Mobiler etc, skall lämnas till tentamensvakten.
ID1218 Johan Montelius Tillämpad Programmering (ID1218) 2014-03-13 09:00-13:00 Förnamn: Efternamn: Regler Du får inte ha något materiel med dig förutom skrivmateriel. Mobiler etc, skall lämnas till tentamensvakten.
GRUNDER I VHDL. Innehåll. Komponentmodell Kodmodell Entity Architecture Identifierare och objekt Operationer för jämförelse
 GRUNDER I VHDL Innehåll Komponentmodell Kodmodell Entity Architecture Identifierare och objekt Operationer för jämförelse KOMPONENTMODELL Modell för att beskriva komponenter Externt interface Intern funktion
GRUNDER I VHDL Innehåll Komponentmodell Kodmodell Entity Architecture Identifierare och objekt Operationer för jämförelse KOMPONENTMODELL Modell för att beskriva komponenter Externt interface Intern funktion
Föreläsning 6: Introduktion av listor
 Föreläsning 6: Introduktion av listor Med hjälp av pekare kan man bygga upp datastrukturer på olika sätt. Bland annat kan man bygga upp listor bestående av någon typ av data. Begreppet lista bör förklaras.
Föreläsning 6: Introduktion av listor Med hjälp av pekare kan man bygga upp datastrukturer på olika sätt. Bland annat kan man bygga upp listor bestående av någon typ av data. Begreppet lista bör förklaras.
Återanvändning av kod? Programkonstruktion. Moment 2 Introduktion till funktioner och programutveckling. Funktionsdefinitioner. Egna funktioner i ML
 Programkonstruktion Moment 2 Introduktion till funktioner och programutveckling Återanvändning av kod? String.substring("Hägg",size "Hägg"-3,3) > "ägg" Detta uttryck plockar ut ett visst antal tecken (3)
Programkonstruktion Moment 2 Introduktion till funktioner och programutveckling Återanvändning av kod? String.substring("Hägg",size "Hägg"-3,3) > "ägg" Detta uttryck plockar ut ett visst antal tecken (3)
Föreläsning Datastrukturer (DAT036)
 Föreläsning Datastrukturer (DAT036) Nils Anders Danielsson 2013-11-18 Idag Mer om grafer: Minsta uppspännande träd (för oriktade grafer). Prims algoritm. Kruskals algoritm. Djupet först-sökning. Cykel
Föreläsning Datastrukturer (DAT036) Nils Anders Danielsson 2013-11-18 Idag Mer om grafer: Minsta uppspännande träd (för oriktade grafer). Prims algoritm. Kruskals algoritm. Djupet först-sökning. Cykel
Innehåll. Föreläsning 12. Binärt sökträd. Binära sökträd. Flervägs sökträd. Balanserade binära sökträd. Sökträd Sökning. Sökning och Sökträd
 Innehåll Föreläsning 12 Sökträd Sökning Sökning och Sökträd 383 384 Binärt sökträd Används för sökning i linjära samlingar av dataobjekt, specifikt för att konstruera tabeller och lexikon. Organisation:
Innehåll Föreläsning 12 Sökträd Sökning Sökning och Sökträd 383 384 Binärt sökträd Används för sökning i linjära samlingar av dataobjekt, specifikt för att konstruera tabeller och lexikon. Organisation:
GOTO och lägen. Några saker till och lite om snabbare sortering. GOTO och lägen (3) GOTO och lägen (2)
 Några saker till och lite om snabbare sortering GOTO och lägen GOTO hemskt eller ett måste? CASE enkla val över diskreta värdemängder Snabb sortering principer Snabb sortering i Scheme och Pascal QuickSort
Några saker till och lite om snabbare sortering GOTO och lägen GOTO hemskt eller ett måste? CASE enkla val över diskreta värdemängder Snabb sortering principer Snabb sortering i Scheme och Pascal QuickSort
Några saker till och lite om snabbare sortering
 Några saker till och lite om snabbare sortering GOTO hemskt eller ett måste? CASE enkla val över diskreta värdemängder Snabb sortering principer Snabb sortering i Scheme och Pascal QuickSort (dela städat
Några saker till och lite om snabbare sortering GOTO hemskt eller ett måste? CASE enkla val över diskreta värdemängder Snabb sortering principer Snabb sortering i Scheme och Pascal QuickSort (dela städat
TDIU01 - Programmering i C++, grundkurs
 TDIU01 - Programmering i C++, grundkurs Sammanfattning period 1 Eric Elfving Institutionen för datavetenskap 1 oktober 2013 Översikt Ett C++-programs uppbyggnad Variabler Datatyper Satser Uttryck Funktioner
TDIU01 - Programmering i C++, grundkurs Sammanfattning period 1 Eric Elfving Institutionen för datavetenskap 1 oktober 2013 Översikt Ett C++-programs uppbyggnad Variabler Datatyper Satser Uttryck Funktioner
6 Rekursion. 6.1 Rekursionens fyra principer. 6.2 Några vanliga användningsområden för rekursion. Problem löses genom:
 6 Rekursion 6.1 Rekursionens fyra principer Problem löses genom: 1. förenkling med hjälp av "sig själv". 2. att varje rekursionssteg löser ett identiskt men mindre problem. 3. att det finns ett speciellt
6 Rekursion 6.1 Rekursionens fyra principer Problem löses genom: 1. förenkling med hjälp av "sig själv". 2. att varje rekursionssteg löser ett identiskt men mindre problem. 3. att det finns ett speciellt
Programkonstruktion och datastrukturer. Moment 3 Rekursion och listor. PKD 2012/13 moment 3 Sida 1 Uppdaterad
 Programkonstruktion och datastrukturer Moment 3 Rekursion och listor PKD 2012/13 moment 3 Sida 1 Uppdaterad 2012-11-04 Summera godtyckligt antal tal sumupto n skall beräkna summan av talen från 0 till
Programkonstruktion och datastrukturer Moment 3 Rekursion och listor PKD 2012/13 moment 3 Sida 1 Uppdaterad 2012-11-04 Summera godtyckligt antal tal sumupto n skall beräkna summan av talen från 0 till
SCB :-0. Uno Holmer, Chalmers, höger 2 Ex. Induktiv definition av lista. // Basfall
 Rekursiva funktioner Föreläsning 10 (Weiss kap. 7) Induktion och rekursion Rekursiva funktioner och processer Weiss 7.1-3 (7.4, 7.5.3 utgår) Fibonaccital (7.3.4) Exempel: Balansering av mobil (kod se lab
Rekursiva funktioner Föreläsning 10 (Weiss kap. 7) Induktion och rekursion Rekursiva funktioner och processer Weiss 7.1-3 (7.4, 7.5.3 utgår) Fibonaccital (7.3.4) Exempel: Balansering av mobil (kod se lab
Instruktioner - Datortentamen TDDD73 Funktionell och imperativ programmering i Python TDDE24 Funktionell och imperativ programmering del 2
 Instruktioner - Datortentamen TDDD73 Funktionell och imperativ programmering i Python TDDE24 Funktionell och imperativ programmering del 2 Hjälpmedel Följande hjälpmedel är tillåtna: Exakt en valfri bok,
Instruktioner - Datortentamen TDDD73 Funktionell och imperativ programmering i Python TDDE24 Funktionell och imperativ programmering del 2 Hjälpmedel Följande hjälpmedel är tillåtna: Exakt en valfri bok,
Programkonstruktion och. Datastrukturer
 Programkonstruktion och Datastrukturer Repetitionskurs, sommaren 2011 Datastrukturer (Listor, Träd, Sökträd och AVL-träd) Elias Castegren elias.castegren.7381@student.uu.se Datastrukturer Vad är en datastruktur?
Programkonstruktion och Datastrukturer Repetitionskurs, sommaren 2011 Datastrukturer (Listor, Träd, Sökträd och AVL-träd) Elias Castegren elias.castegren.7381@student.uu.se Datastrukturer Vad är en datastruktur?
Repetition i Python 3. Exemplen fac. Exemplen fac motivering. Exemplen fac i Python
 Repetition i Python 3 Exemplen fac Orginalet I Scheme använde vi rekursion för all slags repetition. Efterom Scheme är ett funktionellt språk återsänder alla språkkonstruktioner ett värde men i Python
Repetition i Python 3 Exemplen fac Orginalet I Scheme använde vi rekursion för all slags repetition. Efterom Scheme är ett funktionellt språk återsänder alla språkkonstruktioner ett värde men i Python
Föreläsningsanteckningar, Introduktion till datavetenskap HT S4 Datastrukturer. Tobias Wrigstad
 1 Datatyper Tobias Wrigstad Det finns flera olika typer av (slags) data Olika datatyper har olika egenskaper. T.ex. är ett personnummer inte ett tal. (Den sista siffran skall stämma enligt den s.k. Luhnalgoritmen
1 Datatyper Tobias Wrigstad Det finns flera olika typer av (slags) data Olika datatyper har olika egenskaper. T.ex. är ett personnummer inte ett tal. (Den sista siffran skall stämma enligt den s.k. Luhnalgoritmen
FÖRELÄSNING 2, TDDC74, VT2018 BEGREPP PROBLEMLÖSNING MED HJÄLP AV FALLANALYS PROBLEMLÖSNING MED HJÄLP AV REKURSION
 FÖRELÄSNING 2, TDDC74, VT2018 Begrepp och definitioner (delvis från föreläsning 1) Fallanalys som problemlösningsmetod Rekursivt fallanalys Rekursiva beskrivningar och processer de kan skapa Rekursiva
FÖRELÄSNING 2, TDDC74, VT2018 Begrepp och definitioner (delvis från föreläsning 1) Fallanalys som problemlösningsmetod Rekursivt fallanalys Rekursiva beskrivningar och processer de kan skapa Rekursiva
Instruktioner - Datortentamen TDDD73 Funktionell och imperativ programmering i Python
 Instruktioner - Datortentamen TDDD73 Funktionell och imperativ programmering i Python Hjälpmedel Följande hjälpmedel är tillåtna: Exakt en valfri bok, t.ex. den rekommenderade kursboken. Boken får ha anteckningar,
Instruktioner - Datortentamen TDDD73 Funktionell och imperativ programmering i Python Hjälpmedel Följande hjälpmedel är tillåtna: Exakt en valfri bok, t.ex. den rekommenderade kursboken. Boken får ha anteckningar,
Idag: Dataabstraktion
 Idag: Dataabstraktion Hur använder vi det vi hittills kan om Scheme för att realisera (implementera) sammansatta data? DA2001 (Föreläsning 7) Datalogi 1 Hösten 2013 1 / 16 Idag: Dataabstraktion Hur använder
Idag: Dataabstraktion Hur använder vi det vi hittills kan om Scheme för att realisera (implementera) sammansatta data? DA2001 (Föreläsning 7) Datalogi 1 Hösten 2013 1 / 16 Idag: Dataabstraktion Hur använder
Lösningar Datastrukturer TDA
 Lösningar Datastrukturer TDA416 2016 12 21 roblem 1. roblem 2. a) Falskt. Urvalssortering gör alltid samma mängd av jobb. b) Sant. Genom att ha en referens till sista och första elementet, kan man nå både
Lösningar Datastrukturer TDA416 2016 12 21 roblem 1. roblem 2. a) Falskt. Urvalssortering gör alltid samma mängd av jobb. b) Sant. Genom att ha en referens till sista och första elementet, kan man nå både
Inom datalogin brukar man använda träd för att beskriva vissa typer av problem. Om man begränsar sig till träd där varje nod förgrenar sig högst två
 Binära träd Inom datalogin brukar man använda träd för att beskriva vissa typer av problem. Om man begränsar sig till träd där varje nod förgrenar sig högst två gånger, talar man om binära träd. Sådana
Binära träd Inom datalogin brukar man använda träd för att beskriva vissa typer av problem. Om man begränsar sig till träd där varje nod förgrenar sig högst två gånger, talar man om binära träd. Sådana
F11 - Rekursion. ID1004 Objektorienterad programmering Fredrik Kilander
 F11 - Rekursion ID1004 Objektorienterad programmering Fredrik Kilander fki@kth.se Rekursion Rekursion är en programmeringsteknik En metod anropar sig själv public String reverse (String s) { if (s.length()
F11 - Rekursion ID1004 Objektorienterad programmering Fredrik Kilander fki@kth.se Rekursion Rekursion är en programmeringsteknik En metod anropar sig själv public String reverse (String s) { if (s.length()
Textsträngar från/till skärm eller fil
 Textsträngar från/till skärm eller fil Textsträngar [Kapitel 8.1] In- och utmatning till skärm [Kapitel 8.2] Rekursion Gränssnitt Felhantering In- och utmatning till fil Histogram 2010-10-25 Datorlära,
Textsträngar från/till skärm eller fil Textsträngar [Kapitel 8.1] In- och utmatning till skärm [Kapitel 8.2] Rekursion Gränssnitt Felhantering In- och utmatning till fil Histogram 2010-10-25 Datorlära,
BINÄRA TRÄD. (X = pekarvärdet NULL): struct int_bt_node *pivot, *ny; X X X 12 X X 12 X X -3 X X
 Algoritmer och Datastrukturer Kary FRÄMLING/Göran PULKKIS (v23) Kap. 7, Sid 1 BINÄRA TRÄD Träd används för att representera olika slags hierarkier som ordnats på något sätt. Den mest använda trädstrukturen
Algoritmer och Datastrukturer Kary FRÄMLING/Göran PULKKIS (v23) Kap. 7, Sid 1 BINÄRA TRÄD Träd används för att representera olika slags hierarkier som ordnats på något sätt. Den mest använda trädstrukturen
Omgivningar. Omgivningar är viktiga eftersom de avgör vilka namn som är synliga och därmed dessas innebörd och de värden som är förknippade med dem.
 Omgivningar Omgivningar är viktiga eftersom de avgör vilka namn som är synliga och därmed dessas innebörd och de värden som är förknippade med dem. (define (sqrroot c) (define (fixpoint guess c eps) (define
Omgivningar Omgivningar är viktiga eftersom de avgör vilka namn som är synliga och därmed dessas innebörd och de värden som är förknippade med dem. (define (sqrroot c) (define (fixpoint guess c eps) (define
Programmering II (ID1019) :00-11:00
 ID1019 Johan Montelius Programmering II (ID1019) 2015-06-11 08:00-11:00 Instruktioner Du får inte ha något materiel med dig förutom skrivmateriel. Mobiler etc, skall lämnas till tentamensvakten. Svaren
ID1019 Johan Montelius Programmering II (ID1019) 2015-06-11 08:00-11:00 Instruktioner Du får inte ha något materiel med dig förutom skrivmateriel. Mobiler etc, skall lämnas till tentamensvakten. Svaren
Abstrakta datatyper. Primitiva vektorer. Deklarera en vektor
 Abstrakta datatyper 1 Primitiva vektorer Vektorer kan skapas av primitiva datatyper, objektreferenser eller andra vektorer. Vektorer indexeras liksom i C från 0. För att referera en vektor används hakparenteser.
Abstrakta datatyper 1 Primitiva vektorer Vektorer kan skapas av primitiva datatyper, objektreferenser eller andra vektorer. Vektorer indexeras liksom i C från 0. För att referera en vektor används hakparenteser.
TDDC74 Programmering, abstraktion och modellering. Tentamen
 AID-nummer: Datum: 2011-01-11 1 Tekniska högskolan vid Linköpings universitet Institutionen för datavetenskap Anders Haraldsson TDDC74 Programmering, abstraktion och modellering Tentamen Tisdag 11 januari
AID-nummer: Datum: 2011-01-11 1 Tekniska högskolan vid Linköpings universitet Institutionen för datavetenskap Anders Haraldsson TDDC74 Programmering, abstraktion och modellering Tentamen Tisdag 11 januari
Att förstå hur man konstruerar modulära program Att kunna skapa nya funktioner Att förstå hur data skickas mellan funktioner
 Lektion 4, del 1, kapitel 10 Funktioner i JavaScript Inlärningsmål Att förstå hur man konstruerar modulära program Att kunna skapa nya funktioner Att förstå hur data skickas mellan funktioner Introduktion
Lektion 4, del 1, kapitel 10 Funktioner i JavaScript Inlärningsmål Att förstå hur man konstruerar modulära program Att kunna skapa nya funktioner Att förstå hur data skickas mellan funktioner Introduktion
Metodanrop - primitiva typer. Föreläsning 4. Metodanrop - referenstyper. Metodanrop - primitiva typer
 Föreläsning 4 Metodanrop switch-slingor Rekursiva metoder Repetition av de första föreläsningarna Inför seminariet Nästa föreläsning Metodanrop - primitiva typer Vid metodanrop kopieras värdet av en variabel
Föreläsning 4 Metodanrop switch-slingor Rekursiva metoder Repetition av de första föreläsningarna Inför seminariet Nästa föreläsning Metodanrop - primitiva typer Vid metodanrop kopieras värdet av en variabel
Linjärt minne. Sammanhängande minne är ej flexibelt. Effektivt
 Binära träd (forts) Ett binärt träd kan lagras i ett enda sammanhängande minne Roten har index 1 Vänster barn till nod i har index 2*i Höger barn till nod i har index 2*i + 1 Föräldern till nod i har index
Binära träd (forts) Ett binärt träd kan lagras i ett enda sammanhängande minne Roten har index 1 Vänster barn till nod i har index 2*i Höger barn till nod i har index 2*i + 1 Föräldern till nod i har index
Föreläsning 8 Datastrukturer (DAT037)
 Föreläsning 8 Datastrukturer (DAT037) Fredrik Lindblad 1 2016-11-23 1 Slides skapade av Nils Anders Danielsson har använts som utgångspunkt. Se http://www.cse.chalmers.se/edu/year/2015/course/dat037 Förra
Föreläsning 8 Datastrukturer (DAT037) Fredrik Lindblad 1 2016-11-23 1 Slides skapade av Nils Anders Danielsson har använts som utgångspunkt. Se http://www.cse.chalmers.se/edu/year/2015/course/dat037 Förra
TDIU01 - Programmering i C++, grundkurs
 TDIU01 - Programmering i C++, grundkurs Pekare och Listor Eric Elfving Institutionen för datavetenskap 31 oktober 2014 Översikt 2/41 Internminne Pekare Dynamiska datastrukturer (Enkellänkade) listor Arbeta
TDIU01 - Programmering i C++, grundkurs Pekare och Listor Eric Elfving Institutionen för datavetenskap 31 oktober 2014 Översikt 2/41 Internminne Pekare Dynamiska datastrukturer (Enkellänkade) listor Arbeta
Python. Python är, som Scheme, ett interpreterat språk men det finns kompilatorer för Python.
 är, som Scheme, ett interpreterat språk men det finns kompilatorer för. När man interpreterar ett språk tillhandahåller man en interpretator som läser sats för sats och försöker tolka den. När man kompilerar
är, som Scheme, ett interpreterat språk men det finns kompilatorer för. När man interpreterar ett språk tillhandahåller man en interpretator som läser sats för sats och försöker tolka den. När man kompilerar
Övningsuppgifter #11, Programkonstruktion och datastrukturer
 Övningsuppgifter #11, Programkonstruktion och datastrukturer Lösningsförslag Elias Castegren elias.castegren@it.uu.se Övningar 1. 1 2. 2 3. Ett binomialträd med rang n har 2 n noder. En binomial heap innehåller
Övningsuppgifter #11, Programkonstruktion och datastrukturer Lösningsförslag Elias Castegren elias.castegren@it.uu.se Övningar 1. 1 2. 2 3. Ett binomialträd med rang n har 2 n noder. En binomial heap innehåller
Föreläsning 7 Innehåll. Rekursion. Rekursiv problemlösning. Rekursiv problemlösning Mönster för rekursiv algoritm. Rekursion. Rekursivt tänkande:
 Föreläsning 7 Innehåll Rekursion Rekursivt tänkande: Hur många år fyller du? Ett år mer än förra året! Rekursion Rekursiv problemlösning Binärsökning Generiska metoder Rekursiv problemlösning: Dela upp
Föreläsning 7 Innehåll Rekursion Rekursivt tänkande: Hur många år fyller du? Ett år mer än förra året! Rekursion Rekursiv problemlösning Binärsökning Generiska metoder Rekursiv problemlösning: Dela upp
Pythons standardbibliotek
 Pythons standardbibliotek Python 3 skall, enligt standarddokumenten http://docs.python.org/py3k/library/index.html ha stöd för vissa funktioner, typer och datastrukturer Så länge man håller sig till detta
Pythons standardbibliotek Python 3 skall, enligt standarddokumenten http://docs.python.org/py3k/library/index.html ha stöd för vissa funktioner, typer och datastrukturer Så länge man håller sig till detta
Python. Python är, som Scheme, ett interpreterat språk men det finns kompilatorer för Python.
 är, som Scheme, ett interpreterat språk men det finns kompilatorer för. När man interpreterar ett språk tillhandahåller man en interpretator som läser sats för sats och försöker tolka den. När man kompilerar
är, som Scheme, ett interpreterat språk men det finns kompilatorer för. När man interpreterar ett språk tillhandahåller man en interpretator som läser sats för sats och försöker tolka den. När man kompilerar
Föreläsning 9 Datastrukturer (DAT037)
 Föreläsning Datastrukturer (DAT07) Fredrik Lindblad 27 november 207 Slides skapade av Nils Anders Danielsson har använts som utgångspunkt Se http://wwwcsechalmersse/edu/year/20/course/dat07 Innehåll 2
Föreläsning Datastrukturer (DAT07) Fredrik Lindblad 27 november 207 Slides skapade av Nils Anders Danielsson har använts som utgångspunkt Se http://wwwcsechalmersse/edu/year/20/course/dat07 Innehåll 2
Sätt att skriva ut binärträd
 Tilpro Övning 3 På programmet idag: Genomgång av Hemtalet samt rättning Begreppet Stabil sortering Hur man kodar olika sorteringsvilkor Inkapsling av data Länkade listor Användning av stackar och köer
Tilpro Övning 3 På programmet idag: Genomgång av Hemtalet samt rättning Begreppet Stabil sortering Hur man kodar olika sorteringsvilkor Inkapsling av data Länkade listor Användning av stackar och köer
Procedurer och villkor
 Procedurer och villkor (define lessorequal (lambda (x y) (or (< x y) (= x y)))) (define between (lambda (x y z) (and (lessorequal x y) (lessorequal y z)))) > (between 3 4 5) #t > (between 3 2 5) #f DA2001
Procedurer och villkor (define lessorequal (lambda (x y) (or (< x y) (= x y)))) (define between (lambda (x y z) (and (lessorequal x y) (lessorequal y z)))) > (between 3 4 5) #t > (between 3 2 5) #f DA2001
TDDC74 Programmering: Abstraktion och modellering Datortenta , kl 14-18
 TDDC74 Programmering: Abstraktion och modellering Datortenta - 2018-06-07, kl 14-18 Läs alla frågorna först och bestäm dig för i vilken ordning du vill lösa uppgifterna. Uppgifterna är inte nödvändigtvis
TDDC74 Programmering: Abstraktion och modellering Datortenta - 2018-06-07, kl 14-18 Läs alla frågorna först och bestäm dig för i vilken ordning du vill lösa uppgifterna. Uppgifterna är inte nödvändigtvis
Dugga Datastrukturer (DAT036)
 Dugga Datastrukturer (DAT036) Duggans datum: 2012-11-21. Författare: Nils Anders Danielsson. För att en uppgift ska räknas som löst så måste en i princip helt korrekt lösning lämnas in. Enstaka mindre
Dugga Datastrukturer (DAT036) Duggans datum: 2012-11-21. Författare: Nils Anders Danielsson. För att en uppgift ska räknas som löst så måste en i princip helt korrekt lösning lämnas in. Enstaka mindre
Inledande programmering med C# (1DV402) 27+15=42 1 (22)
 27+15=42 1 (22) Variabler Upphovsrätt för detta verk Detta verk är framtaget i anslutning till kursen Inledande programmering med C# vid Linnéuniversitetet. Du får använda detta verk så här: Allt innehåll
27+15=42 1 (22) Variabler Upphovsrätt för detta verk Detta verk är framtaget i anslutning till kursen Inledande programmering med C# vid Linnéuniversitetet. Du får använda detta verk så här: Allt innehåll
Procedurer och villkor. Rekursiva procedurer. Exempel: n-fakultet
 Procedurer och villkor Rekursiva procedurer (define lessorequal (lambda (x y) (or (< x y) (= x y)))) (define between (lambda (x y z) (and (lessorequal x y) (lessorequal y z)))) > (between 3 4 5) #t > (between
Procedurer och villkor Rekursiva procedurer (define lessorequal (lambda (x y) (or (< x y) (= x y)))) (define between (lambda (x y z) (and (lessorequal x y) (lessorequal y z)))) > (between 3 4 5) #t > (between
Föreläsning 5. Rekursion
 Föreläsning 5 Rekursion Föreläsning 5 Algoritm Rekursion Rekursionsträd Funktionsanrop på stacken Binär sökning Problemlösning (möjliga vägar) Algoritm En algoritm är ett begränsat antal instruktioner/steg
Föreläsning 5 Rekursion Föreläsning 5 Algoritm Rekursion Rekursionsträd Funktionsanrop på stacken Binär sökning Problemlösning (möjliga vägar) Algoritm En algoritm är ett begränsat antal instruktioner/steg
Programmering II (ID1019) :00-12:00
 ID1019 Johan Montelius Programmering II (ID1019) 2018-03-13 08:00-12:00 Instruktioner Betyg Svaren skall lämnas på dessa sidor, använd det utrymme som nns under varje uppgift för att skriva ner ditt svar.
ID1019 Johan Montelius Programmering II (ID1019) 2018-03-13 08:00-12:00 Instruktioner Betyg Svaren skall lämnas på dessa sidor, använd det utrymme som nns under varje uppgift för att skriva ner ditt svar.
Föreläsning 7: Syntaxanalys
 DD2458, Problemlösning och programmering under press Föreläsning 7: Syntaxanalys Datum: 2007-10-30 Skribent(er): Erik Hammar, Jesper Särnesjö Föreläsare: Mikael Goldmann Denna föreläsning behandlade syntaxanalys.
DD2458, Problemlösning och programmering under press Föreläsning 7: Syntaxanalys Datum: 2007-10-30 Skribent(er): Erik Hammar, Jesper Särnesjö Föreläsare: Mikael Goldmann Denna föreläsning behandlade syntaxanalys.
Datastrukturer i kursen. Föreläsning 8 Innehåll. Träd rekursiv definition. Träd
 Föreläsning 8 Innehåll Datastrukturer i kursen Träd, speciellt binära träd egenskaper användningsområden implementering Undervisningsmoment: föreläsning 8, övningsuppgifter 8, lab 4 Avsnitt i läroboken:
Föreläsning 8 Innehåll Datastrukturer i kursen Träd, speciellt binära träd egenskaper användningsområden implementering Undervisningsmoment: föreläsning 8, övningsuppgifter 8, lab 4 Avsnitt i läroboken:
TDDC74 Lab 04 Muterbara strukturer, omgivningar
 TDDC74 Lab 04 Muterbara strukturer, omgivningar 1 Översikt I den här laborationen kommer ni att lära er mer om: Tillstånd, och skillnader mellan ren funktionell programmering och imperativ. Skillnaden
TDDC74 Lab 04 Muterbara strukturer, omgivningar 1 Översikt I den här laborationen kommer ni att lära er mer om: Tillstånd, och skillnader mellan ren funktionell programmering och imperativ. Skillnaden
Introduktion till programmering SMD180. Föreläsning 4: Villkor och rekursion
 Introduktion till programmering Föreläsning 4: Villkor och rekursion 1 1 Några inbyggda funktioner (med resultat!) Konverterar mellan de grundläggande typerna: >>> int("32") 32 >>> int(3.999) 3 >>> float(32)
Introduktion till programmering Föreläsning 4: Villkor och rekursion 1 1 Några inbyggda funktioner (med resultat!) Konverterar mellan de grundläggande typerna: >>> int("32") 32 >>> int(3.999) 3 >>> float(32)
TDDI16 Datastrukturer och algoritmer. Algoritmanalys
 TDDI16 Datastrukturer och algoritmer Algoritmanalys 2017-08-28 2 Översikt Skäl för att analysera algoritmer Olika fall att tänka på Medelfall Bästa Värsta Metoder för analys 2017-08-28 3 Skäl till att
TDDI16 Datastrukturer och algoritmer Algoritmanalys 2017-08-28 2 Översikt Skäl för att analysera algoritmer Olika fall att tänka på Medelfall Bästa Värsta Metoder för analys 2017-08-28 3 Skäl till att
Datastrukturer, algoritmer och programkonstruktion (DVA104, HT 2014) Föreläsning 5
 Datastrukturer, algoritmer och programkonstruktion (DVA104, HT 2014) Föreläsning 5? FORTSÄTTNING TRÄD RECAP (förra föreläsningen) RECAP (förra föreläsningen) Träd är icke-linjära datastrukturer som ofta
Datastrukturer, algoritmer och programkonstruktion (DVA104, HT 2014) Föreläsning 5? FORTSÄTTNING TRÄD RECAP (förra föreläsningen) RECAP (förra föreläsningen) Träd är icke-linjära datastrukturer som ofta
Programmering II (ID1019) :00-12:00
 ID1019 Johan Montelius Programmering II (ID1019) 2015-03-13 09:00-12:00 Instruktioner Du får inte ha något materiel med dig förutom skrivmateriel. Mobiler etc, skall lämnas till tentamensvakten. Svaren
ID1019 Johan Montelius Programmering II (ID1019) 2015-03-13 09:00-12:00 Instruktioner Du får inte ha något materiel med dig förutom skrivmateriel. Mobiler etc, skall lämnas till tentamensvakten. Svaren
DD1320 Tillämpad datalogi. Lösning (skiss) till tenta 20 okt 2011
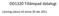 DD1320 Tillämpad datalogi Lösning (skiss) till tenta 20 okt 2011 1 KMP P I P P I N i 1 2 3 4 5 6 Next[i] 0 1 0 2 1 3 2 Huffmankodning: Algoritmen 1. Sortera tecknen som ska kodas i stigande förekomstordning.
DD1320 Tillämpad datalogi Lösning (skiss) till tenta 20 okt 2011 1 KMP P I P P I N i 1 2 3 4 5 6 Next[i] 0 1 0 2 1 3 2 Huffmankodning: Algoritmen 1. Sortera tecknen som ska kodas i stigande förekomstordning.
TDDC74 Programmering, abstraktion och modellering DUGGA 2
 AID-nummer: Datum: 2011-02-18 1 Tekniska högskolan vid Linköpings universitet Institutionen för datavetenskap Anders Haraldsson TDDC74 Programmering, abstraktion och modellering DUGGA 2 Fredag 18 feb 2011
AID-nummer: Datum: 2011-02-18 1 Tekniska högskolan vid Linköpings universitet Institutionen för datavetenskap Anders Haraldsson TDDC74 Programmering, abstraktion och modellering DUGGA 2 Fredag 18 feb 2011
TDIU01 Programmering i C++
 TDIU01 Programmering i C++ Föreläsning 6 - Klasser Eric Elfving, eric.elfving@liu.se Institutionen för datavetenskap (IDA) Avdelningen för Programvara och system (SaS) Klasser När vi skapade vår lista
TDIU01 Programmering i C++ Föreläsning 6 - Klasser Eric Elfving, eric.elfving@liu.se Institutionen för datavetenskap (IDA) Avdelningen för Programvara och system (SaS) Klasser När vi skapade vår lista
Obligatorisk uppgift 5
 (5 oktober 2018 Symbolisk kalkylator 1 ) Obligatorisk uppgift 5 En kalkylator som hanterar uttryck symboliskt dvs värden är uttryck inte bara tal. Uppgiften exemplifierar: objektorientering återanvändning
(5 oktober 2018 Symbolisk kalkylator 1 ) Obligatorisk uppgift 5 En kalkylator som hanterar uttryck symboliskt dvs värden är uttryck inte bara tal. Uppgiften exemplifierar: objektorientering återanvändning
MMA132: Laboration 2 Matriser i MATLAB
 MMA132: Laboration 2 Matriser i MATLAB Introduktion I den här labben skall vi lära oss hur man använder matriser och vektorer i MATLAB. Det är rekommerad att du ser till att ha laborationshandledningen
MMA132: Laboration 2 Matriser i MATLAB Introduktion I den här labben skall vi lära oss hur man använder matriser och vektorer i MATLAB. Det är rekommerad att du ser till att ha laborationshandledningen
