1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 4 C: kvadrat Exempel på hur formerna kan konstrueras:
|
|
|
- Bo Danielsson
- för 8 år sedan
- Visningar:
Transkript
1 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b + 2b + b = 4b. Omkretsen blir 2(3a + 4b) 4 C: kvadrat Exempel på hur formerna kan konstrueras: 5 B: 3 Man skjuter den vänstra nedåt och de två översta åt vänster och får plats för en till bredvid den stående längst till höger. 6 B: 6 Alla vita eller alla grå ger 2 sätt. Tre grå och en vit eller tre vita och en grå ger 2 sätt. Två vita och två grå, samma färg diagonalt eller samma färg intill varandra ger 2 sätt. 7 E: 45 Det mittersta av de tre minsta talen måste vara 33/3 = 11. De tre minsta talen är 10, 11 och 12. Då är de övriga talen 13, 14, 1 5 och 16. Summan av de tre största är = 45. Algebraisk lösning: Låt x vara det mittersta talet. Då är de tre minsta talen: x 3 + x 2 + x 1 = 33, x 6 = 33, x = 13 och summan av de tre största är = C: 100 Differensen av två på varandra följande heltal är alltid 1 och det finns 100 sådana differenser. 9 E: 30 Den minsta gemensamma multipeln till 3, 5 och 6 är A: 1 Arean av rektangel ABCD är 6 10 = 60 och arean av kvadraten PQRS är 6 6 = 36. Det skuggade området XYRS har arean 60/2 = 30. Arean av rektangel PQRS är då = 6. Eftersom PQ = 6 blir PX = D: 45 För att sätta samman tre kedjor behövs två sammanfogningar. En sammanfogning tar då 18/2 = 9 minuter. För att sätta samman sex kedjor behövs fem sammanfogningar som då tar 5 9 = 45 minuter. Kungl Vetenskapsakademien & NCM/Nämnaren 2
2 12 D: 25 Den största summan av tre olika ensiffriga tal är = = , 15 = , 23 = C: 19 Vi kan först konstatera att antal blå (b) brickor kan vara 1, 2, 3 eller 4. Om b = 1 så är de vita (v) 11 och de röda (r) 38, motsäger förutsättningarna. Om b = 2 så är v = 22 och r = 26, motsäger också förutsättningarna. Om b = 3 så är v = 33 och r = 14, det ger v r = 1 9. Om b = 4 så är v = 44 och r = 2, motsäger förutsättningarna. Alternativ lösning: Givet: v = 11b (1), v + b + r = 50 (2) och b < r < v (3). (1) och (2) ger att r = 50 12b (4). Alltså kan b vara 1, 2, 3, 4. (1) (4) ger v - r = 23b 50. Det ger att b bara kan vara 3 eller 4. b = 4 ger v = 44 och r = 2 och (3) är inte uppfyllt. Alltså b = 3, v = 33 och r = 14, (3) är uppfyllt och v r = B: 55 I triangeln ACD får vi vinkeln ADC = 180 ( ) = 65. Triangeln är alltså likbent och det blir även triangeln ABC. Vinkeln ABC = ( ) / 2 = 55. B A C D 15 C: 19 För varje snitt ökar vi antal vedträn med 1. Har vi bara en stock kan vi med 53 snitt få 54 vedträn. Det behövs alltså ytterligare = 18 stockar, dvs totalt 19 för att få 72 vedträn. Algebraisk lösning: Låt n vara antal stockar. För varje gång vi sågar i en stock ökar antal vedträn med 1. Låt s i vara antal snitt i stock i, då ger stock i, s i + 1 vedträn. Vi får då s s s n + 1 = s 1 + s s n + n vedträn, 53 + n = 72, n = B: 4 En linje delar planet i två områden. Drar vi en linje parallell med den första ökas antal områden med ett (3 områden) medan en linje som skär ökar antal områden med två (4 delar). Vi får minst antal delar om linjerna är parallella och fyra parallella linjer ger exakt 5 delar. 17 B: 6 Vi ser att 8 och 9 måste stå i de yttersta ringarna eftersom 9 bara kan kombineras med talet 2, och att 8 därmed måste kombineras med talet 3. Återstår talen 1, 4, 5, 6 och 7. Sen resonerar vi vidare och ser vilka tal som kan kombineras med 2 respektive 3 och tillsammans med ytterligare ett tal bli 11. Resonemanget ger att det endast finns en lösning, samt dess spegling. (forts) Kungl Vetenskapsakademien & NCM/Nämnaren 3
3 Alternativt resonemang: = 45, men de fem cirklarna ska innehålla tal med sammanlagd summa 5 11 = 55, dvs 10 mer. Det är möjligt eftersom talen i snittområdena räknas två gånger. Alltså ska summan av de fyra talen i snittområdena vara 10. De tal som ska stå där är då 1, 2, 3 och 4. Summan av talen i de tre övre cirklarna i figuren ska vara 3 11 = 33 och summan i de två nedre områdena blir därför = 12. Inget av dessa två områden kan innehålla talet 6, eftersom talen ska vara olika. Talet 6 ska alltså stå i ett av de tre områdena överst men kan inte stå i något av de yttre eftersom 6 + (högst 4) < 11. Alltså står talet 6 i den mittersta cirkeln. 18 B: 1 4 Den skuggade arean motsvarar arean för en halvcirkel med radien 4. Hela figurens area motsvarar arean för en halvcirkel med radien 8. Förhållandet mellan deras inbördes radier är 1:2 och eftersom areaskalan är längdskalan i kvadrat är förhållandet mellan deras areor 1:4. 19 C: 16 Ur tabellen kan vi se att man behöver 4 höns för att få 1 gås. Då behöver man 6 höns för att få 3 tuppar, dvs 2 höns för att få 1 tupp. För att få 1 kalkon behövs det 5 2 höns = 10 höns. Det ger ( ) = 16 höns för att få en gås, en kalkon och en tupp. Han växlar 12 höns till 3 gäss, sen 2 gäss + 4 höns till 6 tuppar och sen 5 tuppar till en kalkon. Algebraisk lösning: Med beteckningarna k (kalkon), t (tupp), g (gås) och h (höns) kan följande tre samband ställas upp: k = 5t (1), g + 2h = 3t (2), 4h = g (3). (2) och (3) ger 6h = 3t t = 2h som insatt i (1) ger k = 10h. k + g + t = 16h. 20 B: 5 Om det på alla 18 kort står 4 så blir summan 72, om det på alla 18 kort står 5 blir summan 90. Det enda talet mellan 72 och 90 som är delbar med 17 är 85. Om vi utgår från 90 så måste fem av korten ersättas med ett kort med 4. Algebraisk lösning: Låt x vara antal kort där det står 4, 0 < x < 18. Antalet kort där det står 5 är då 18 x. Då gäller att 4x + 5 (18 x) = 17k där k är något heltal. 90 x = 17k ger den enda positiva heltalslösningen x = B: 8 En 2 x 2 x 2 kub är byggd av 8 små kuber som möts i mitten i ett gemensamt hörn, alltså behövs det åtta olika färger för att bygga den enligt Josefs regel. En 3 x 3 x 3 kub innehåller (flera) 2 x 2 x 2 kuber, så Josef kan inte göra sin kub av småkuber med färre än 8 färger. Men med 8 färger kan han klara det så här: I en 3 x 3 x 3 kub finns det 4 sorters småkuber: 8 hörnkuber, 1 mittenkub mitt i den stora kuben, 6 sidokuber (en mitt på varje sida) och 12 kantkuber (en mitt på varje kant). De 6 sidokuberna delar vi i 3 par av motstående kuber (de som ligger vid motstående sidor). Kungl Vetenskapsakademien & NCM/Nämnaren 4
4 De 12 kantkuberna delar vi i 3 kvartetter av parallellkuber (de som ligger vid parallella kanter). Om Josef låter samtliga hörnkuber ha en färg (1), mittenkuben en annan färg (2), varje par av motstående kuber nya färger (3, 4 och 5) och varje kvartett av kantkuber ytterligare nya färger (6, 7 och 8) så har han lyckats. Dvs, totalt 8 färger. Lösning 2: Dela kuben i tre lager. Börja färglägga det mittersta lagret. Mittkuben i detta lager har färg 1. I lagret kan alla fyra hörnkuberna ha samma färg 2, de återstående kantkuberna måste ha två nya färger (färg 3 och färg 4). Det övre och det undre lagret kan vara identiska då de saknar angränsande hörn. Vi betraktar nu det övre lagret. Mittkuben måste ha en ny färg 5, då den gränsar till mittlagrets samtliga färger. Hörnkuberna i det övre lagret måste också ha en ny färg 6. Kantkuberna behöver också ha två nya färger, 7 och 8. Dvs totalt 8 olika färger. V 22 A: 11 Med hjälp av punkten P kan vi skapa parallello grammerna RCPA, CQBP och APBS. Varje parallellogram är till häften R C skuggad. Den skuggade delen är Q 12/2 + 4/2 + 6/2 = 11 P Alternativ lösning: A Triangeln ABT har 4 gånger så stor T S B U area som triangeln AST, dvs en enhetstriangel, eftersom den har lika stor höjd men 4 gånger så lång bas. Motsvarande gäller för triangeln CUB, som har tre gånger så stor höjd och två gånger så lång bas. Triangeln AVC har på motsvarande sätt 5 gånger så stor höjd och 3 gånger så lång bas. Då får vi arean av triangeln ABC som 36 ( ) = D: 13 Trianglarna ABC, BCD, osv är alla likbenta. Om de lika stora vinklarna i den första triangeln är v grader, så kommer de lika stora vinklarna i de följande trianglarna att vara 2v, 3v, 4v,... För varje triangel ökar alltså de lika vinklarna med v grader. Vi kan fortsätta att konstruera trianglar på detta sätt så länge kv < 90, där k är antal trianglar. Eftersom v = 7 ger olikheten att k = 12 och antal sträckor blir 13. E C A B D F 24 C: Det var 4 personer i rummet, 2 av dem var lögnare De tre personernas första påståenden motsäger varandra, alltså kan högst en av dem som uttalar sig vara riddare. Den första personens andra påstående skulle aldrig uttalas av en riddare, alltså är han en lögnare. Då är person 2 en riddare eftersom han påstår motsatsen. Vi vet då att person tre är lögnare, eftersom han påstår att de är fem. Det finns alltså 4 personer i rummet, varav 2 är lögnare. Vi vet att den tredje ljuger, så det kan inte vara tre. Kungl Vetenskapsakademien & NCM/Nämnaren 5
5 Arbeta vidare med Cadet för gymnasiet 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. Eleverna har vid själva tävlingstillfället med olika metoder och i olika grad klarat problemen. Problemen är kanske inte av samma karaktär som eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper. Det är därför viktigt att låta problemen leva vidare och inte se tävlingstillfället som något som avbryter den ordinarie undervisningen. I samband med genomgång kan det passa bra att först låta eleverna resonera sig fram till lösningarna i grupp. Diskutera gruppernas lösningar i klassen och jämför idéer och angreppssätt. Låt också eleverna få bedöma kamraternas lösningar: Har de tagit hänsyn till alla förutsättningar? Är de tydliga? Är resonemanget korrekt? Fungerar lösningsmetoden på andra, liknande problem? Diskutera vilken information i problemet som är nödvändig och vad som kan ändras utan att problemet förändras. Att analysera och diskutera varandras lösningar är bra, men det kräver förstås att man arbetar långsiktigt så att eleverna vänjer sig vid att både ge kritik på ett konstruktivt sätt och att bli granskad. Om de redan från början får uppleva att det är en del av undervisningen kan det bli en naturlig och uppskattad form av arbete med problem. I samband med diskussion av problemen kommer ett antal matematiska termer att aktualiseras. Gå igenom dem. För definitioner hänvisar vi till Matematiktermer för skolan (Kiselman & Mouwitz, 2008). Några frågor att återkomma till när problemet är löst: Kontrollera att lösningen verkligen svarar mot frågan. Är det ett rimligt svar? Hur vet vi det? Påminner problemet om något annat problem vi löst tidigare? Vilka kunskaper hade vi nytta av när vi löste problemet? Vilka nya frågor kan problemet väcka? Lärde vi oss något nytt av problemet? Gå igenom de felaktiga svarsalternativen och resonera om varför dessa inte är riktiga. Låt eleverna göra förändringar i uppgiften så att de andra alternativen blir riktiga. Utmaningen kan vara att göra så små förändringar som möjligt. Avsluta med att låta eleverna konstruera egna liknande problem. Det är ett sätt att se om de har förstått det som varit centralt i problemet. Att arbeta vidare med problemen kan innebära att man noggrant går igenom lösningsstrategier och repeterar eller tar upp teori kring använda begrepp. Här finns många tillfällen att utveckla olika matematiska förmågor. I efterarbetet är det lämpligt att hämta in snarlika problem från de andra tävlingsnivåerna detta år och från tidigare års Kängurutävlingar. Kungl Vetenskapsakademien & NCM/Nämnaren 1
6 Tal Många problem som förkommer i Kängurun och i andra matematiktävlingar bygger på heltalsmatematik. Det naturliga räknandet börjar med de positiva heltalen, som sedan utvidgas till negativa heltal. Egenskaper hos heltal, såsom faktor, multipel av, delbarhet, primtal, primtalsfaktorisering är därför viktiga att arbeta med. De här kunskaperna ligger till grund för arbete med tal i bråkform. Heltalsumma Uppgift 8, 12 och 17. Vilket är det minsta tal som man kan skriva som en summa av tre olika ensiffriga tal, fyra olika ensiffriga tal osv? Vilket är det största? Att se tal som summor av ensiffriga tal är något som man har användning av i Kakuro. Vi kan även fortsätta att betrakta summor av de positiva heltalen och inte bara nöja oss med de ensiffriga. De tal som vi får om vi beräknar summorna 1, 1+2, 1+2+3,, n kallas triangeltal. Låt eleverna resonera om den beteckningen. n(n + 1) Låt dem även försöka bevisa att n =, både geometriskt och algebraiskt. 2 Undersök summor av de udda positiva heltalen, dvs 1, 1 + 3, ,, (2k+1). På Benjamin 12, Junior 7 och Student 1 finns problem som behandlar denna summa i ett fall. Gör även motsvarande undersökning av summor av de jämna positiva heltalen. Låt eleverna resonera, göra påståenden och bevisa dem. I GyCadet 8 är strategin att inte beräkna summorna utan att se mönstret. Det här problemet kan användas till att öka förståelsen för vad som händer när man tar bort parenteser och det står ett minustecken framför. Ett aritmetiskt uttryck för texten är: ( ) ( ) (1) Vi skriver summan av de jämna talen på en rad, och summan av de udda talen nedanför: Subtraktion term för term ger (2) Vi skriver alla positiva termer först och därefter alla negativa (3) Vi har tre olika sätt att uttrycka denna summa. Resonera med eleverna varför (2) är att föredra om man snabbt vill beräkna denna summa. I det fortsatta arbetet kan man fråga efter respektive summa. Här följer exempel på andra frågeställningar som handlar om på varandra följande tal, sk konsekutiva tal, och som kan användas i det fortsatta arbetet: Vad blir summan av fem på varandra följande tal om det i mitten är 15? Vad blir summan av fem på varandra följande udda tal om det i mitten är 15? Vad blir summan av fem på varandra följande tal delbara med tre om det i mitten är 15? Vad blir summan av 25 på varandra följande tal delbara med 6 om det i mitten är 3210? Andra varianter med summor är Ecolier 12, Junior 3, Junior 5. I uppgift 17 ska talen 1 9 placeras in i cirklarna så att summan av talen i varje cirkel är 11. Resonera om olika sätt att lösa problemet. Gör samma problem men låt först summan i varje cirkel vara 13 och låt sedan summan anta andra värden. Kungl Vetenskapsakademien & NCM/Nämnaren 2
7 Problem 15 handlar egentligen om uppdelning av heltal. 1.a) Rita ett antal raka sträckor, lika eller olika långa. Dela av sträckorna med små streck. En del av sträckan mellan två streck eller mellan ett streck och en av sträckans ändpunkter kallar vi en bit. En sträcka utan streck räknas också som en bit. b) Rita en tabell och fyll i det du ser i exemplet. Antal sträckor Antal streck Antal bitar c) Upprepa a och b för olika antal sträckor, streck och bitar. Glöm inte att fylla i resultatet i tabellen. d) Försök hitta ett samband med hjälp av det du skrivit i tabellen. Kan du förklara varför det samband du funnit alltid gäller, oavsett vilket antalet sträckor, streck och bitar är? 2. Låt antalet sträckor, antalet streck och antalet bitar vara som i exemplet i tabellen. Kan sträckorna ha delats in på något annat sätt än det som visas i exemplet? Försök i så fall komma på alla möjligheter. 3. Tänk nu att man bara vet att det blev 6 bitar. Vilket kan antalet sträckor och antalet streck ha varit då? Försök komma på alla möjligheter! 4. När du gjort uppgift 3 vet du hur många möjligheter det finns om det blev 6 bitar. Gör en systematisk undersökning! Hur många olika möjligheter finns det om det blev 1 bit, 2 bitar, 3 bitar, och så vidare. Det problem du jobbat med i uppgifterna 3 och 4 handlar om att se varje positivt heltal som en summa av positiva termer på så många olika sätt som möjligt. Delbar och multipel Delbar och multipel är två begrepp som många elever har svårt med. I problem 9 ska morfar dela en kaka, så att varje barnbarn får lika mycket kaka. Hur många bitar får varje barn, hur stor del av kakan om det kommer 3, 5 eller 6 barnbarn. Ändra antal barnbarn. I problem 20 ska en summa vara delbar med 17. Undersök vilka summor som skulle kunna förekomma och vilka tal de är delbara med. Kungl Vetenskapsakademien & NCM/Nämnaren 3
8 Geometri Som vanligt handlar flera problem om geometri. Det är naturligtvis allra lättast att lösa dem konkret, men syftet med problemen är inte att hitta det korrekta svaret i första hand. Det konkreta arbetet ska hjälpa eleverna att få förståelse. Därför är det också viktigt att samtala om det konkreta arbetet och lyfta fram de samband som ska illustreras. Under tävlingen har eleverna löst problemen utan hjälpmedel. I efterarbetet kan eleverna jämföra hur de tänkt, dvs deras föreställning, med en konkret representation. Att tolka en tredimensionell bild exempelvis är inte lätt och många måste få många möjligheter att jämföra bild och verklighet för att utveckla den förmågan. Symmetri behandlas i problem 1. Resonera om varför det bara finns två symmetrilinjer. Låt eleverna ersätta kängururna med andra figurer så att det bildas fler symmetrilinjer. Undersök symmetrier i verkligheten, i naturen och på byggnader och i olika geometriska figurer. I problem 4 förekommer också symmetri. Hur många symmetrilinjer finns det i en sexhörning? Vad kännetecknar en regelbunden sexhörning? Diskutera generella egenskaper såsom antal diagonaler och vinkelsumma hos regelbundna månghörningar. Låt eleverna rita in alla möjliga lägen för de olika figurerna. Låt eleverna även pröva på Junior 6. I problem 22 kan man också ta upp begreppet symmetriaxlar. Hur många finns det i en liksidig triangel? Vilken sida och höjd har den stora liksidiga triangeln och de små liksidiga trianglarna? Vad händer med det skuggade områdets area om punkten B får glida utefter triangelsidan? Problem 3 kan användas i två syften, för att resonera om omkrets och area men även för att bygga upp förståelse för algebran. Det kan vara lämpligt att först låta a och b representeras av tal. Hur lång blir då sidan 2b? Hur ser ett aritmetiskt uttryck för omkretsen ut? Går det att konstruera andra områden med samma omkrets men med större area? Mindre area? I nästa steg kan eleverna låta b representeras av ett tal och bestämma vilket värde a får för en given omkrets. Skriv upp den erhållna ekvationen och lös den. Slutför med att skriva upp algebraiska uttryck för omkrets och area. Problem 10 handlar om två fyrhörningar med speciella egenskaper. Be eleverna definiera rektangel respektive kvadrat. Ändra förutsättningarna, t ex att det skuggade området har en tredjedel eller en fjärdedel så stor area. Vilket förhållande gäller mellan det skuggade områdets omkrets och omkretsen av rektangel ABCD? I problem 9 ska morfar baka en kaka. Vilken form kan kakan ha och hur ska den delas om alla ska få lika stor bit? I samband med problem 18 kan det vara lämpligt att repetera cirkelns omkrets och area. Vilken area respektive omkrets har hela området? Låt eleverna även pröva på Junior 13, Student 12. Problem 14 och 23 handlar om likbenta trianglar och vinklar. Be eleverna beskriva en likbent triangel. Låt eleverna med hjälp av passare konstruera sträckorna AB, BC, CD osv i problem 23. Vad händer med antal sträckor om man ändrar vinkeln vid A, t ex om A = 8. Hur stor är vinkeln vid A om man kan rita 6 sträckor? Låt eleverna även pröva på Junior 9, 11 och Student 6. GyCadet 16 handlar om att dela ett plan i ett antal områden med räta linjer. Låt eleverna undersöka i hur många områden ett plan delas av 1, 2, 3, räta linjer. Största antal områden, minsta antal områden. Kungl Vetenskapsakademien & NCM/Nämnaren 4
9 Problemlösningsstrategier I några problem är det främst en generell problemlösningsförmåga som efterfrågas. Att tolka problemet, plocka ut väsentlig information, finna en passande metod och bedöma resultatet. I problem 6 handlar det om att finna alla sätt och också att veta att alla sätt är funna. Här gäller det att vara systematisk. Ändra antal kvadrater, t ex 3 3 och undersök antal sätt. Ändra villkoret så att de fyra kvadraterna i problemexemplet betraktas som olika? I Benjamin 5 finns ett liknande problem, färgläggning av en blomma med 5 blomblad. Utveckla frågeställningen till kvadrater som gränsar till varandra ska ha olika färg. Gränsar innebär att de har minst ett hörn gemensamt. Hur många olika färger behövs? Undersök 2 x 2, 3 3, 4 4,, n n kvadrater. Diskutera fyrfärgsproblemet. Ta även upp problem 21. I problem 24 gäller det att systematiskt gå igenom påståendena och avgöra om de är sanna eller falska. Ett liknande problem är Junior 21. Problem av den här typen tycker många är svåra. Det blir mycket information att hålla reda på och man behöver gå tillbaka och kontrollera mot förutsättningarna flera gånger. Problemet är komplext. Vi har haft en hel del liknande problem tidigare i alla tävlingsklasser. De är inte beroende av vilka matematikkurser eleverna läst utan handlar mer om förmågan att resonera logiskt. Pröva därför liknande problem från andra klasser och andra år. T ex: Ecolier 17, 2010; Cadet 13, 2009; Benjamin 19 och Cadet 17, 2008; Benjamin 13, Junior , Ecoier 17, 2006; Benjamin 21, Att läsa Hagland, K., Hedrén, R. & Taflin, E. (2005). Rika matematiska problem inspiration till variation. Stockholm: Liber. Kiselman, C. & Mouwitz, L. (2008). Matematiktermer för skolan. NCM, Göteborgs universitet. McIntosh, A. (2008). Förstå och använda tal. NCM, Göteborgs universitet. NämnarenTema (1997) Algebra för alla. NCM, Göteborgs universitet. Rystedt, E. &Trygg, L. (2010). Laborativ matematikundervisning vad vet vi? NCM, Göteborgs universitet. Nämnaren. I varje nummer finns Problemavdelningen och Kängurusidan. Läs också tidigare artiklar kring problemlösning. Nämnarenartiklar publicerade finns fritt tillgängliga som pdf dokument på Nämnaren på nätet, ncm.gu.se/namnaren. Du finner dem via artikeldatabasen. Under ArkivN finns alla publicerade Uppslag och Problemavdelningar samlade. Nämnaren på nätet presenterar varje månad nya problem under rubriken Månadens problem. Strävorna finns på ncm.gu.se/stravorna. Där finns aktiviteter, problem och artiklar samlade och ordnade efter kursplanens mål. Kungl Vetenskapsakademien & NCM/Nämnaren 5
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt.
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Avdelning 1, trepoängsproblem
 vdelning 1, trepoängsproblem 1. Hur många symmetrilinjer har figuren? : 0 : 1 : 2 D: 4 E: oändligt många 2. Robert arbetar på leksaksfabriken. Han ska packa kängurur som ska fraktas till affärerna. Varje
vdelning 1, trepoängsproblem 1. Hur många symmetrilinjer har figuren? : 0 : 1 : 2 D: 4 E: oändligt många 2. Robert arbetar på leksaksfabriken. Han ska packa kängurur som ska fraktas till affärerna. Varje
Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Arbeta vidare med Junior 2010
 Arbeta vidare med Junior 010 Känguruproblemen är kanske inte av samma karaktär som de problem eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper.
Arbeta vidare med Junior 010 Känguruproblemen är kanske inte av samma karaktär som de problem eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper.
Avdelning 1, trepoängsproblem
 vdelning 1, trepoängsproblem 1. Hur många symmetrilinjer har figuren? : 0 : 1 : 2 : 4 E: oändligt många 2. Robert arbetar på leksaksfabriken. Han ska packa kängurur som ska fraktas till affärerna. Varje
vdelning 1, trepoängsproblem 1. Hur många symmetrilinjer har figuren? : 0 : 1 : 2 : 4 E: oändligt många 2. Robert arbetar på leksaksfabriken. Han ska packa kängurur som ska fraktas till affärerna. Varje
Arbeta vidare med Ecolier 2010
 Arbeta vidare med Ecolier 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att
Arbeta vidare med Ecolier 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte.
 Svar och lösningar 1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte. 3 C: 1 och 3 4 C: David 5 B: 2 Flytta myntet på toppen och myntet som ligger i mitten
Svar och lösningar 1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte. 3 C: 1 och 3 4 C: David 5 B: 2 Flytta myntet på toppen och myntet som ligger i mitten
4. A. 4, 6, 11 Viker man ihop till en kub, så kommer talet 1 mitt emot 3, 2 mitt emot 4 och 5 mitt emot 6. Det ger summorna 4, 6, 11.
 N G A RA Kängurutävlingen 2015 Cadet svar och korta lösningar 1. B Betrakta de fem alternativen och jämför med paraplyet. (A) N är upp- och ner. (C) R är felvänd. (D) G är felvänd. (E) R ska inte stå mellan
N G A RA Kängurutävlingen 2015 Cadet svar och korta lösningar 1. B Betrakta de fem alternativen och jämför med paraplyet. (A) N är upp- och ner. (C) R är felvänd. (D) G är felvänd. (E) R ska inte stå mellan
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Junior 011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Lösningsförslag Cadet 2014
 Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
Kortfattade lösningar med svar till Cadet 2006
 3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
Känguru 2010 Cadet (klass 8 och 9) sida 1 / 6
 Känguru 2010 Cadet (klass 8 och 9) sida 1 / 6 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara
Känguru 2010 Cadet (klass 8 och 9) sida 1 / 6 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt
Kängurutävlingen Matematikens hopp Junior 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2013 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Cadet 2013 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Arbeta vidare med Benjamin
 Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Kängurutävlingen 2017 NCM 1
 Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Student 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Student 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kortfattade lösningar med svar till Gymnasiets Cadet 2006
 Kängurun Matematikens hopp Gymnasiets Cadet 2006 Kortfattade lösningar med svar till Gymnasiets Cadet 2006 3 poäng 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D
Kängurun Matematikens hopp Gymnasiets Cadet 2006 Kortfattade lösningar med svar till Gymnasiets Cadet 2006 3 poäng 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Svar och lösningar. Kängurutävlingen 2009 Cadet för gymnasiet
 Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder till svaret 6.
 Kängurutävlingen 2015 Ecolier, svar och lösningar Facit Ecolier 1 E 15 2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder
Kängurutävlingen 2015 Ecolier, svar och lösningar Facit Ecolier 1 E 15 2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Student 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Student 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Svar och arbeta vidare med Student 2008
 Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
1 B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3.
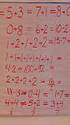 Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Svar och korta lösningar Benjamin 2006
 3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
Välkommen till Kängurutävlingen Matematikens hopp 17 mars Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Svar och lösningar Benjamin
 Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
Lösningsförslag Junior 2014
 Kängurutävlingen 014 Junior, svar och lösningar Lösningsförslag Junior 014 1 E: c < b < a Längden av linje a är 16 l.e., linje b (8 + ) l.e. och linje c (8+4 p ) l.e. Alternativ lösning: Grundfiguren har
Kängurutävlingen 014 Junior, svar och lösningar Lösningsförslag Junior 014 1 E: c < b < a Längden av linje a är 16 l.e., linje b (8 + ) l.e. och linje c (8+4 p ) l.e. Alternativ lösning: Grundfiguren har
Svar och arbeta vidare med Cadet 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Svar och arbeta vidare med Benjamin 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Student 016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till
Kängurutävlingen Matematikens hopp Student 016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Cadet 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp Cadet 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Avdelning 1, trepoängsproblem
 Avdelning 1, trepoängsproblem 1. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Var är kängurun? A: I cirkeln och i triangeln, men inte i kvadraten. B: I cirkeln
Avdelning 1, trepoängsproblem 1. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Var är kängurun? A: I cirkeln och i triangeln, men inte i kvadraten. B: I cirkeln
Svar och lösningar Benjamin
 Kängurutävlingen 2014 Svar och lösningar Benjamin 1: A 0 Summerar vi entalen ger de 9, hundratalen ger 3 så det är inga minnessiffror att beakta. Summan av tiotalen är 0. 2: A 1 9999 + 1= 10 000. Talet
Kängurutävlingen 2014 Svar och lösningar Benjamin 1: A 0 Summerar vi entalen ger de 9, hundratalen ger 3 så det är inga minnessiffror att beakta. Summan av tiotalen är 0. 2: A 1 9999 + 1= 10 000. Talet
2. 1 L ä n g d, o m k r e t s o c h a r e a
 2. 1 L ä n g d, o m k r e t s o c h a r e a Ett plan är en yta som inte är buktig och som är obegränsad åt alla håll. På ett plan kan man rita en linje som är rak (rät). En linje är obegränsad åt båda
2. 1 L ä n g d, o m k r e t s o c h a r e a Ett plan är en yta som inte är buktig och som är obegränsad åt alla håll. På ett plan kan man rita en linje som är rak (rät). En linje är obegränsad åt båda
Högstadiets matematiktävling 2018/19 Finaltävling 19 januari 2019 Lösningsförslag
 Högstadiets matematiktävling 2018/19 Finaltävling 19 januari 2019 Lösningsförslag 1. Lösningsförslag: Vi börjar med att notera att delbarhet med 6 betyder att N är delbart med 2 och 3. Om N är delbart
Högstadiets matematiktävling 2018/19 Finaltävling 19 januari 2019 Lösningsförslag 1. Lösningsförslag: Vi börjar med att notera att delbarhet med 6 betyder att N är delbart med 2 och 3. Om N är delbart
Cadet. a: 1001 b: 11 c: 223 d: 191 e: 123 (Sverige) 2 Boris är född 1 januari 2002 och han är 1 år och 1 dag äldre än Irina. Vilken dag föddes Irina?
 Cadet Avdelning. Trepoängsproblem 2007 2 + 0 + 0 + 7 = a: 00 b: c: 223 d: 9 e: 23 (Sverige) 2 Boris är född januari 2002 och han är år och dag äldre än Irina. Vilken dag föddes Irina? a: 2 januari 2003
Cadet Avdelning. Trepoängsproblem 2007 2 + 0 + 0 + 7 = a: 00 b: c: 223 d: 9 e: 23 (Sverige) 2 Boris är född januari 2002 och han är år och dag äldre än Irina. Vilken dag föddes Irina? a: 2 januari 2003
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Junior 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Student 2009 Här följer svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag till lösningsmetod. Bland eleverna i klassen finns säkert andra lösningsmetoder
Kängurun Matematikens Hopp Student 2009 Här följer svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag till lösningsmetod. Bland eleverna i klassen finns säkert andra lösningsmetoder
Cadet för gymnasiet. a: 1001 b: 11 c: 223 d: 191 e: 123 (Sverige)
 Avdelning. Trepoängsproblem 007 + 0 + 0 + 7 = Cadet för gymnasiet a: 00 b: c: 3 d: 9 e: 3 (Sverige) Boris är född januari 00 och han är år och dag äldre än Irina. Vilken dag föddes Irina? a: januari 003
Avdelning. Trepoängsproblem 007 + 0 + 0 + 7 = Cadet för gymnasiet a: 00 b: c: 3 d: 9 e: 3 (Sverige) Boris är född januari 00 och han är år och dag äldre än Irina. Vilken dag föddes Irina? a: januari 003
3: A I den vita asken. Kolan ligger i den röda asken så chokladbiten måste ligga i den vita. Problemet kan lösas konkret och med en enkel bild.
 Svar och lösningar 1: D 200 9 Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett
Svar och lösningar 1: D 200 9 Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
Planering Geometri år 7
 Planering Geometri år 7 Innehåll Övergripande planering... 2 Bedömning... 2 Begreppslista... 3 Metodlista... 6 Arbetsblad... 6 Facit Diagnos + Arbeta vidare... 10 Repetitionsuppgifter... 11 Övergripande
Planering Geometri år 7 Innehåll Övergripande planering... 2 Bedömning... 2 Begreppslista... 3 Metodlista... 6 Arbetsblad... 6 Facit Diagnos + Arbeta vidare... 10 Repetitionsuppgifter... 11 Övergripande
Svar och lösningar Ecolier
 Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
NAMN KLASS/GRUPP. Poängsumma: Känguruskutt: UPPGIFT 1 2 3 4 5 6 7 8 9 10 SVAR UPPGIFT 11 12 13 14 15 16 17 18 19 20 SVAR
 Känguru 2010 Junior (gymnasiet åk 1) sida 1 / 6 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara
Känguru 2010 Junior (gymnasiet åk 1) sida 1 / 6 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Känguru Student (gymnasiet åk 2 och 3) sida 1 / 6
 Känguru Student (gymnasiet åk 2 och 3) sida 1 / 6 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara
Känguru Student (gymnasiet åk 2 och 3) sida 1 / 6 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara
Facit åk 6 Prima Formula
 Facit åk 6 Prima Formula Kapitel 1 Omkrets och area Sidan 7 1 A och C 2 D och E 3 a G, H och J b I och J c J Sidan 8 4 a 1 b 1 c 1 d 4 5 A = 0 B = 2 C = 4 D = 2 6 a 8 0 8 b 1 0 1 c 3 8 3 d 1 3 8 F7 A B
Facit åk 6 Prima Formula Kapitel 1 Omkrets och area Sidan 7 1 A och C 2 D och E 3 a G, H och J b I och J c J Sidan 8 4 a 1 b 1 c 1 d 4 5 A = 0 B = 2 C = 4 D = 2 6 a 8 0 8 b 1 0 1 c 3 8 3 d 1 3 8 F7 A B
Avdelning 1. Trepoängsproblem
 vdelning 1. Trepoängsproblem Kängurutävlingen Matematikens hopp 1. Hur många tärningsögon finns det sammanlagt på de sidor som du inte kan se på bilden? ) 15 B) 1 C) 7 D) 7 E) Inget av dessa svar (Bulgarien).
vdelning 1. Trepoängsproblem Kängurutävlingen Matematikens hopp 1. Hur många tärningsögon finns det sammanlagt på de sidor som du inte kan se på bilden? ) 15 B) 1 C) 7 D) 7 E) Inget av dessa svar (Bulgarien).
Undersökande arbetssätt i matematik 1 och 2
 Matematik Gymnasieskola Modul: Matematikundervisning med digitala verktyg Del 6: Undersökande arbetssätt med matematisk programvara Undersökande arbetssätt i matematik 1 och 2 I texten Undersökande arbetssätt
Matematik Gymnasieskola Modul: Matematikundervisning med digitala verktyg Del 6: Undersökande arbetssätt med matematisk programvara Undersökande arbetssätt i matematik 1 och 2 I texten Undersökande arbetssätt
Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Kängurutävlingen genomförs i år den 16 mars. Om den dagen inte
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Kängurutävlingen genomförs i år den 16 mars. Om den dagen inte
Kängurun Matematikens hopp
 Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna
Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna
Ma7-Per: Geometri. Det tredje arbetsområdet handlar om geometri.
 Ma7-Per: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda
Ma7-Per: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda
7F Ma Planering v2-7: Geometri
 7F Ma Planering v2-7: Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
7F Ma Planering v2-7: Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
Matematikbokens Prio kapitel Kap 3,.,Digilär, NOMP
 Geometri Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, - använda och analysera begrepp
Geometri Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, - använda och analysera begrepp
9 Geometriska begrepp
 9 Geometriska begrepp Rita figurer som visar vad vi menar med... 261 a) 4 cm och 4 cm 2 b) 5 cm och 5 cm 2 262 Rita två olika figurer som båda har arean 8 cm 2 263 Rita tre olika figurer som alla har arean
9 Geometriska begrepp Rita figurer som visar vad vi menar med... 261 a) 4 cm och 4 cm 2 b) 5 cm och 5 cm 2 262 Rita två olika figurer som båda har arean 8 cm 2 263 Rita tre olika figurer som alla har arean
Känguru 2016 Student gymnasieserien
 sid 1 / 10 NAMN GRUPP Poäng: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Felaktigt svar ger minus 1/4 poäng av uppgiftens totala poängantal! Så om du t.ex. svarar
sid 1 / 10 NAMN GRUPP Poäng: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Felaktigt svar ger minus 1/4 poäng av uppgiftens totala poängantal! Så om du t.ex. svarar
Arbeta vidare med Milou 2008
 Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom
Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom
Avdelning 1, trepoängsproblem
 vdelning, trepoängsproblem. Med hjälp av bilden bredvid kan vi se att + 3 + 5 + 7 = 4 4. Vad är + 3 + 5 + 7 + 9 +... + 7 + 9 + 2? : 0 0 : C: 2 2 D: 3 3 E: 4 4 2. Summan av talen i båda raderna är den samma.
vdelning, trepoängsproblem. Med hjälp av bilden bredvid kan vi se att + 3 + 5 + 7 = 4 4. Vad är + 3 + 5 + 7 + 9 +... + 7 + 9 + 2? : 0 0 : C: 2 2 D: 3 3 E: 4 4 2. Summan av talen i båda raderna är den samma.
Avdelning 1, trepoängsproblem
 Avdelning 1, trepoängsproblem 1. I ett akvarium finns det 00 fiskar varav 1 % är blå medan övriga är gula. Hur många gula fiskar måste avlägsnas från akvariet för att de blå fiskarna ska utgöra % av alla
Avdelning 1, trepoängsproblem 1. I ett akvarium finns det 00 fiskar varav 1 % är blå medan övriga är gula. Hur många gula fiskar måste avlägsnas från akvariet för att de blå fiskarna ska utgöra % av alla
8F Ma Planering v2-7 - Geometri
 8F Ma Planering v2-7 - Geometri Arbetsform under en vecka: Tisdagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
8F Ma Planering v2-7 - Geometri Arbetsform under en vecka: Tisdagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
1. Det står KANGAROO på mitt paraply. Du kan se det på bilden. Vilken av följande bilder visar också mitt paraply? A: B: C: D: E:
 N G A RA Kängurutävlingen 2015 Cadet Trepoängsproblem 1. Det står KANGAROO på mitt paraply. Du kan se det på bilden. Vilken av följande bilder visar också mitt paraply? A: B: C: D: E: O O K 2. Rektangeln
N G A RA Kängurutävlingen 2015 Cadet Trepoängsproblem 1. Det står KANGAROO på mitt paraply. Du kan se det på bilden. Vilken av följande bilder visar också mitt paraply? A: B: C: D: E: O O K 2. Rektangeln
Kängurutävlingen Matematikens Hopp Cadet 2003 Lösningar, Arbeta vidare
 Kängurutävlingen Matematikens Hopp Lösningar, Arbeta vidare Arrangeras av Många problem kan lösas på flera sätt. Följande förslag ger inte någon heltäckande beskrivning. Diskutera olika lösningsförslag
Kängurutävlingen Matematikens Hopp Lösningar, Arbeta vidare Arrangeras av Många problem kan lösas på flera sätt. Följande förslag ger inte någon heltäckande beskrivning. Diskutera olika lösningsförslag
Gymnasiets Cadet. a: 2 b: 4 c: 5 d: 6 e: 11
 Gymnasiets Cadet Avdelning 1. Trepoängsproblem 1. I en klass finns 1 flickor och 9 pojkar. Hälften av eleverna i klassen är förkylda. Vilket är det minsta antalet flickor som är förkylda? a: 2 b: 4 c:
Gymnasiets Cadet Avdelning 1. Trepoängsproblem 1. I en klass finns 1 flickor och 9 pojkar. Hälften av eleverna i klassen är förkylda. Vilket är det minsta antalet flickor som är förkylda? a: 2 b: 4 c:
Explorativ övning euklidisk geometri
 Explorativ övning euklidisk geometri De viktigaste begreppen och satser i detta avsnitt är: Kongruens och likhet mellan sträckor, vinklar och trianglar. Kongruensfallen för trianglar. Parallella linjer
Explorativ övning euklidisk geometri De viktigaste begreppen och satser i detta avsnitt är: Kongruens och likhet mellan sträckor, vinklar och trianglar. Kongruensfallen för trianglar. Parallella linjer
Delprov A Muntligt delprov
 Delprov A Muntligt delprov Äp6Ma15 Delprov A 15 Beskrivning av delprov A, muntligt delprov Det muntliga delprovet kan genomföras fr.o.m. vecka 11 och resten av vårterminen. Det muntliga delprovet handlar
Delprov A Muntligt delprov Äp6Ma15 Delprov A 15 Beskrivning av delprov A, muntligt delprov Det muntliga delprovet kan genomföras fr.o.m. vecka 11 och resten av vårterminen. Det muntliga delprovet handlar
9E Ma Planering v2-7 - Geometri
 9E Ma Planering v2-7 - Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (45 min): Läsa på anteckningar
9E Ma Planering v2-7 - Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (45 min): Läsa på anteckningar
En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant?
 En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant? P har större omkrets än Q. P har mindre omkrets än Q. P har mindre area än Q Q och P har
En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant? P har större omkrets än Q. P har mindre omkrets än Q. P har mindre area än Q Q och P har
Problem Svar
 Känguru Benjamin, svarsblankett Namn Klass/Grupp Poängsumman Känguruskuttet Ta lös svarsblanketten. Skriv ditt svarsalternativ under numret. Lämna rutan tom om du inte vet svaret. Gissa inte, felaktigt
Känguru Benjamin, svarsblankett Namn Klass/Grupp Poängsumman Känguruskuttet Ta lös svarsblanketten. Skriv ditt svarsalternativ under numret. Lämna rutan tom om du inte vet svaret. Gissa inte, felaktigt
Välkommen till. Kängurutävlingen Matematikens hopp 2009 Student för elever på kurs D och E. Kängurutävlingen 2009 Student.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 009 Student för elever på kurs D och E. Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 0 7 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 009 Student för elever på kurs D och E. Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 0 7 mars användas, däremot
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2012 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Junior 2012 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
= A: 0 B: 1 C: 2013 D: 2014 E: 4028
 Trepoängsproblem 1. 2014 2014 2014 2014 = A: 0 B: 1 C: 2013 D: 2014 E: 4028 2. Kängurutävlingen hålls den tredje torsdagen i mars varje år. Vilket datum är det senaste som tävlingen kan hållas? A: 14 mars
Trepoängsproblem 1. 2014 2014 2014 2014 = A: 0 B: 1 C: 2013 D: 2014 E: 4028 2. Kängurutävlingen hålls den tredje torsdagen i mars varje år. Vilket datum är det senaste som tävlingen kan hållas? A: 14 mars
Trepoängsproblem. Kängurutävlingen 2011 Junior
 Trepoängsproblem 1 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen börjar och slutar med ett vitt streck. På Storgatan har ett övergångsställe totalt åtta vita
Trepoängsproblem 1 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen börjar och slutar med ett vitt streck. På Storgatan har ett övergångsställe totalt åtta vita
Kvalificeringstävling den 30 september 2008
 SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
Känguru 2012 Student sid 1 / 8 (gymnasiet åk 2 och 3) i samarbete med Jan-Anders Salenius vid Brändö gymnasiet
 Känguru 2012 Student sid 1 / 8 NAMN GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara den frågan. Felaktigt
Känguru 2012 Student sid 1 / 8 NAMN GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara den frågan. Felaktigt
Lathund geometri, åk 7, matte direkt (nya upplagan)
 Lathund geometri, åk 7, matte direkt (nya upplagan) Det som står i den här lathunden ska du kunna till provet. Du ska kunna ställa upp och räkna ut liknande tal som de nedan: a) 39,8 + 2,62 b) 16,42 5,8
Lathund geometri, åk 7, matte direkt (nya upplagan) Det som står i den här lathunden ska du kunna till provet. Du ska kunna ställa upp och räkna ut liknande tal som de nedan: a) 39,8 + 2,62 b) 16,42 5,8
5: D 3 23 kan bara fås på ett sätt: Här har man nytta av att känna igen 24 som ett tal i sexans tabell.
 Svar och lösningar 1: D 200 9 = 1800 Om eleverna inte redan kan multiplicera med 200 kan lösningen förklaras via 100 9 = 9 100 = 900. 200 9 är alltså dubbelt så mycket, 1800. Vi kan också utesluta de andra
Svar och lösningar 1: D 200 9 = 1800 Om eleverna inte redan kan multiplicera med 200 kan lösningen förklaras via 100 9 = 9 100 = 900. 200 9 är alltså dubbelt så mycket, 1800. Vi kan också utesluta de andra
Känguru 2012 Junior sivu 1 / 8 (gymnasiet åk 1) i samarbete med Jan-Anders Salenius vid Brändö gymnasiet
 Känguru 2012 Junior sivu 1 / 8 NAMN GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara den frågan. Felaktigt
Känguru 2012 Junior sivu 1 / 8 NAMN GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara den frågan. Felaktigt
Explorativ övning euklidisk geometri
 Explorativ övning euklidisk geometri De viktigaste begreppen och satser i detta avsnitt är: Kongruens och likhet mellan sträckor, vinklar och trianglar. Kongruensfallen för trianglar. Parallella linjer
Explorativ övning euklidisk geometri De viktigaste begreppen och satser i detta avsnitt är: Kongruens och likhet mellan sträckor, vinklar och trianglar. Kongruensfallen för trianglar. Parallella linjer
Sidor i boken Figur 1:
 Sidor i boken 5-6 Mer trigonometri Detta bör du kunna utantill Figur 1: Triangeln till vänster är en halv liksidig triangel. Varje triangel med vinklarna 0,60,90 är en halv liksidig triangel. Hypotenusan
Sidor i boken 5-6 Mer trigonometri Detta bör du kunna utantill Figur 1: Triangeln till vänster är en halv liksidig triangel. Varje triangel med vinklarna 0,60,90 är en halv liksidig triangel. Hypotenusan
Lösningar till udda övningsuppgifter
 Lösningar till udda övningsuppgifter Övning 1.1. (i) {, } (ii) {0, 1,, 3, 4} (iii) {0,, 4, 6, 8} Övning 1.3. Påståendena är (i), (iii) och (v), varav (iii) och (v) är sanna. Övning 1.5. andra. (i) Nej.
Lösningar till udda övningsuppgifter Övning 1.1. (i) {, } (ii) {0, 1,, 3, 4} (iii) {0,, 4, 6, 8} Övning 1.3. Påståendena är (i), (iii) och (v), varav (iii) och (v) är sanna. Övning 1.5. andra. (i) Nej.
Bedömning för lärande i matematik
 HANDLEDNING TILL Bedömning för lärande i matematik FÖR ÅRSKURS 1 9 1 Handledning I denna handledning ges förslag på hur du kan komma igång med materialet Bedömning för lärande i matematik åk 1 9. Du börjar
HANDLEDNING TILL Bedömning för lärande i matematik FÖR ÅRSKURS 1 9 1 Handledning I denna handledning ges förslag på hur du kan komma igång med materialet Bedömning för lärande i matematik åk 1 9. Du börjar
Matematik 92MA41 (15hp) Vladimir Tkatjev
 Matematik 92MA41 (15hp) Vladimir Tkatjev Med anledning av de nya kursplanerna har Strävorna reviderats. Formen, en matris med rutor, är densamma men istället för att som tidigare anknyta till mål att sträva
Matematik 92MA41 (15hp) Vladimir Tkatjev Med anledning av de nya kursplanerna har Strävorna reviderats. Formen, en matris med rutor, är densamma men istället för att som tidigare anknyta till mål att sträva
Trepoängsproblem. Kängurutävlingen 2014 Junior. 1 Bilden visar tre kurvor med längderna a, b respektive c. Vilket av följande påståenden är korrekt?
 Trepoängsproblem 1 Bilden visar tre kurvor med längderna a, b respektive c. Vilket av följande påståenden är korrekt? A: a < b < c B: a < c < b C: b < a < c D: b < c < a E: c < b < a 2 Sidolängderna i
Trepoängsproblem 1 Bilden visar tre kurvor med längderna a, b respektive c. Vilket av följande påståenden är korrekt? A: a < b < c B: a < c < b C: b < a < c D: b < c < a E: c < b < a 2 Sidolängderna i
Trepoängsproblem. Kängurutävlingen 2011 Cadet. 1 Vilket av följande uttryck har störst värde? 1 A: B: C: D: E: 2011
 Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Matematik CD för TB = 5 +
 Föreläsning 4 70 a) Vi delar figuren i två delar, en triangel (på toppen) och en rektangel. Summan av dessa två figurers area ger den eftersökta. Vi behöver följande formler: A R = b h A T = b h Svar:
Föreläsning 4 70 a) Vi delar figuren i två delar, en triangel (på toppen) och en rektangel. Summan av dessa två figurers area ger den eftersökta. Vi behöver följande formler: A R = b h A T = b h Svar:
Avdelning 1, trepoängsproblem
 Avdelning, trepoängsproblem. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Stjärnan i figuren har bildats av 2 identiska, liksidiga trianglar. Stjärnans omkrets
Avdelning, trepoängsproblem. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Stjärnan i figuren har bildats av 2 identiska, liksidiga trianglar. Stjärnans omkrets
Arbeta vidare med aritmetik 2018
 Arbeta vidare med aritmetik 2018 I det här materialet har vi samlat problem inom aritmetik från flera olika tävlingsklasser, från Ecolier till Student. Årtal Varje år förekommer det problem som utgår från
Arbeta vidare med aritmetik 2018 I det här materialet har vi samlat problem inom aritmetik från flera olika tävlingsklasser, från Ecolier till Student. Årtal Varje år förekommer det problem som utgår från
Detta prov består av del 1 och 2. Här finns också facit och förslag till poängsättning
 Allmänt om proven Detta prov består av del 1 och. Här finns också facit och förslag till poängsättning och bedömning. Provet finns på lärarwebben, dels som pdf-fil och dels som redigerbar Word-fil. Del
Allmänt om proven Detta prov består av del 1 och. Här finns också facit och förslag till poängsättning och bedömning. Provet finns på lärarwebben, dels som pdf-fil och dels som redigerbar Word-fil. Del
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 0, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av klassens
Kängurun Matematikens hopp Ecolier 0, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av klassens
Student. a: 5 b: 6 c: 7 d: 8 e: 3
 Student Avdelning. Trepoängsproblem. Talen 3 och 4 samt två okända tal skrivs in i de fyra rutorna. Summan av talen i raderna blir 5 och 0 och summan av talen i den ena kolumnen blir 9. Vilket är det största
Student Avdelning. Trepoängsproblem. Talen 3 och 4 samt två okända tal skrivs in i de fyra rutorna. Summan av talen i raderna blir 5 och 0 och summan av talen i den ena kolumnen blir 9. Vilket är det största
