Kängurun Matematikens hopp
|
|
|
- Julia Bergqvist
- för 6 år sedan
- Visningar:
Transkript
1 Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna i detta dokument följer förslag till hur ni kan arbeta vidare med problemen. Där finns också ytterligare kommentarer till lösningarna i vissa fall. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på nätet. Rätta elevernas lösningar och redovisa resultaten på webbadressen ncm.gu.se/kanguru/ Om du får problem med att redovisa via nätet, hör av dig till oss på kanguru@ncm.gu.se eller på telefon Vi ber er redovisa era resultat senast 29 april. Uppmärksamma gärna goda prestationer i klassen och i skolan. Namnen på de elever som fått bäst resultat, i varje årskurs, kommer att publiceras på webben. Där publiceras också lösningsfrekvenser på alla uppgifter liksom en sammanställning av hur elevernas resultat fördelar sig på olika poängintervall. Du kan sedan jämföra dina elevers resultat med övriga elever i samma åldersgrupp och du kan se om de problem som dina elever hade svårt för också var svåra för andra. Vi är medvetna om att redovisningen tar tid, men vi ber er ändå att redovisa resultaten. De är värdefulla för oss och många lärare frågar efter sammanställningen med lösningsfrekvenser. Förhoppningsvis ger en översikt av klassens resultat även ett bra underlag för ert vidare arbete. Låt eleverna få en ny chans att lösa de problem de inte hann med Endast några enstaka elever hinner att lösa alla problem under tävlingstillfället. Ordna därför gärna ett extra tillfälle utom tävlan, där klassen kan lösa problemen utan tidsbegränsning. Många skulle säkert utmanas av de svårare problemen om de fick tid att arbeta med dem. Nominera till Mikael Passares stipendium Mikael Passare ( ) var professor i matematik vid Stockholms universitet. Han hade ett stort intresse för matematikundervisning på alla nivåer och var den som tog initiativ till Kängurutävlingen i Sverige. Mikel Passares minnesfond har instiftat ett stipendium för att uppmärksamma elevers matematik prestationer. I samband med Kängurutävlingen kommer därför en elev från vardera tävlingsklass Ecolier, Benjamin och Cadet och en gymnasieelev (Cadet, Junior eller Student) att belönas med 500 kr. För att kunna nomineras måste eleven ha genomfört tävlingen på korrekt sätt och klassens resultat måste vara inrapporterade (åtminstone redovisning A). Nomineringen ska innehålla elevens namn, skola och årskurs, tävlingsklass, resultat på årets tävling samt uppgift om vilken dag tävlingen genomfördes och namn och e-post till den nominerande läraren. Dessutom ska det finnas en motivering till varför just denna elev är värd att speciellt uppmärksammas. Det kan tex vara en ovanligt god prestation i tävlingen, oväntat bra resultat i relation till tidigare prestationer eller annat hos eleven som är värt att speciellt uppmärksammas i relation till arbetet med Kängurun. Förutom detta premieras att eleven är hjälpsam och visar gott kamratskap. Ett underlag att använda för nomineringen finns att hämta på ncm.gu.se/kanguru. Nomineringen skickas senast 29 april till: Kängurutävlingen NCM, Göteborgs universitet Box GÖTEBORG NCM & Kungl Vetenskapsakademien 1
2 Kängurutävlingen 2016 Ecolier, svar och lösningar Facit Ecolier 1: E Ernst = 9. De andra har slagit 7, 6, 5 och 8. 2: A = 24 3: D Fel i de andra alternativen: A: Endast två prickar på rosetten, rosetten är inte speglad. B: Trianglar på rosetten, huvudet är inte speglat. C: Blomman är inte speglad E: Blomman saknas och Pipo är inte alls speglad. 4: B 3 Sex barn delar på äpplena. 6 1/2 = 3 5: A triangel Figuren måste ha ett av rektangelns hörn plus två som bildas där gardinkanten skär figuren. 6: C cirklarna är dubbelt så många som trianglarna Det finns 4 cirklar och 2 trianglar. De andra alternativen stämmer inte. 7: B 16 kg 4 4 kg = 16 kg. Till varje kg torkad svamp går det åt 4 kg färsk. 8: C 30 cm Omkretsen påverkas inte, den sammanlagda längden av sidorna är fortfarande 30 cm. 9: B = 9. Årtalet börjar med 20 så de två andra siffrorna ska ge summan 7. De kan vara 0 + 7, 1 + 6, 2 + 5, 3 + 4, 4 + 3, 5 + 2, och har redan varit, 2016 är det nu så nästa år blir : B 4 Musen har i första rummet två möjliga vägar, i nästa oberoende av vilken han väljer en möjlig väg, i det följande två vägar ut, därefter en och från sista rummet finns endast en väg ut: = 4. 11: D 3 Kvadraten ligger under triangeln i den första, fjärde och femte högen. 12: A 1, 3 och : C 4 I rutan överst i mitten måste det stå 3 och därför 2 i övre högra rutan. Summan av de skuggade rutorna är därför ( ) 2 = 4. 14: C 11 och 4 Varje kort har summan 16, vilket ger 16 5 = 11 och = = är det enda alternativ som är : C 18 En kyckling, ett får och en get har tillsammans 10 ben. Det finns alltså 18 grupper med djur, = 180 NCM & Kungl Vetenskapsakademien 2
3 Kängurutävlingen 2016 Ecolier, svar och lösningar 16: D 5 Om Fariba lägger mynt med början i ena kanten blir tre rutor i andra kanten tomma. De sex yttersta rutorna, tre i vardera sidan, kan vi alltså inte vara säkra på att hon använder. Däremot måste Fariba alltid använda de mittersta fem rutorna. Det finns flera sätt att placera mynten, men dessa fem rutor måste användas. Om någon av de fem mittersta rutorna ska vara tom finns det inte 8 rutor i rad att lägga mynt i. 17: C 6 En hund har 3 fler ben än nosar. Sex hundar har 6 3 = 18 fler ben än nosar. 18: D Alternati D är den enda bild som är identisk med bilden på kortet. De andra är spegelbilder. 19: C 1234Luuap4321 Endast C uppfyller alla villkor: siffror på de tre sista platserna; alla bokstäver i Paul finns med, Luap; och högst tre versaler, ett L. De andra alternativen uppfyller inte villkoren: Alternativ A har fyra versaler, alternativ B, D och E har inte siffror på alla de tre sista positionerna. 20: B 27 Om vi drar bort 3, som är det antal år som Leo är äldre, ska den sammanlagda åldern gå att dela med 4. Endast med alternativet 27 uppfylls detta: 27 3 = /4 = 6, så Tim, Tom och Jim fyller 6 år och Leo fyller 9 år. 21: B mellan skål Q och skål R Cirkeln är tyngre än triangeln, alltså är en cirkel och en triangel tyngre än två trianglar men lättare än två cirklar. I alla skålar finns en kvadrat som vi kan bortse från. 22: C 1917 Det tal som ändras minskar med 99: = 99. Summan måste alltså minska med : E 10 Malte får bitar av längden 18 och 9 i första delningen, därefter 12 och 6 eller 6 och 3 och slutligen 8 och 4, 4 och 2 eller 2 och 1. De olika längder som staplarna kan få är alltså 12, 8, 6, 4, 3, 2 och 1. 24: D 50 Eftersom båda träden har samma förhållande mellan äpplen och päron, det är dubbelt så många päron som äpplen, måste det vara 50 päron. Det kan vi få med exempelvis 7 träd av ena sorten och 1 av den andra: 7 6 päron äpplen + 8 päron + 4 äpplen = 50 päron + 25 äpplen. NCM & Kungl Vetenskapsakademien 3
4 Kängurutävlingen 2016 Ecolier, svar och lösningar Rättningsmall Uppgift A B C D E Poäng 1 E 3 2 A 3 3 D 3 4 B 3 5 A 3 6 C 3 7 B 3 8 C 3 9 B 4 10 B 4 11 D 4 12 A 4 13 C 4 14 C 4 15 C 4 16 D 4 17 C 5 18 D 5 19 C 5 20 B 5 21 B 5 22 C 5 23 E 5 24 D 5 SUMMA 96 NCM & Kungl Vetenskapsakademien 4
5 Kängurutävlingen 2016 Ecolier, svar och lösningar Redovisningsblankett A Redovisning av resultat sker på webbadress ncm.gu.se/kanguru. Om du får problem med att redovisa via nätet, hör av dig till oss på kanguru@ncm.gu.se eller på telefon Redovisa senast den 29 april. Namn och poäng för de 2 bästa eleverna i varje årskurs: Åk Namn Poäng 3 4 Om du har fler elever med mycket bra resultat, mer än 77 poäng, kan du redovisa deras namn i ett e-brev till kanguru@ncm.gu.se Antal elever med åk 3 åk poäng poäng poäng poäng poäng 0 12 poäng Totalt antal deltagare NCM & Kungl Vetenskapsakademien 5
6 Kängurutävlingen 2016 Ecolier, svar och lösningar Redovisningsblankett B För uppföljning av resultaten är vi intresserade av lösningsfrekvensen per uppgift. Uppgift nr Antal elever med rätt svar på uppgiften åk 3 åk 4 NCM & Kungl Vetenskapsakademien 6
7 Arbeta vidare med Ecolier Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta eleverna arbeta med lösningarna i grupp. Låt alla först få möjlighet att lösa problemen på egen hand om de inte hann det i samband med tävlingen. Diskutera gruppernas lösningar i klassen och jämför idéer och angreppssätt. Låt också eleverna få granska kamraternas lösningar: Har de tagit hänsyn till alla förutsättningar? Är lösningarna tydliga? Är resonemanget korrekt? Fungerar lösningsmetoden på andra, liknande problem? Att analysera och diskutera varandras lösningar är bra, men det kräver förstås att man arbetar långsiktigt så att eleverna vänjer sig vid att både ge kritik på ett konstruktivt sätt och att ta emot kritik. Om de redan från början får uppleva att det är en del av undervisningen kan det bli en naturlig och uppskattad form av arbete med problem. Att presentera en lösning som andra kan följa och som är korrekt uppbyggd är något som eleverna måste få tid och möjlighet att utveckla med hjälp av lärare. Välj några av årets problem, arbeta igenom lösningarna noga och gör en riktigt genomarbetad redovisning. Alla problem kan naturligtvis diskuteras utifrån valda lösningsmetoder. De flesta problem kan lösas på olika sätt och det är alltid bra att jämföra dessa och se på likheter och skillnader. Det är också bra att beskriva lösningarna med hjälp av olika uttrycksformer, konkret material, bilder, muntligt eller skriftligt tal och med symboler. Jämför de olika formerna och se hur den konkreta representationen uttrycks i ord och med symboler. Några frågor att återkomma till när problemet är löst: Kontrollera att lösningen verkligen svarar mot frågan. Är det ett rimligt svar? Hur vet vi det? Påminner problemet om något annat problem vi löst tidigare? Vilka kunskaper hade vi nytta av när vi löste problemet? Vilka nya frågor kan problemet väcka? Lärde vi oss något nytt av problemet? Gå också igenom de felaktiga svarsalternativen och resonera om varför dessa inte är riktiga. Låt eleverna göra förändringar i uppgiften så att de andra alternativen blir riktiga. Utmaningen kan vara att göra så små förändringar som möjligt. De felaktiga svarsalternativen kan också användas som utgångspunkt för diskussion om vad som skulle kunna leda fram till dessa svar: Hur tror ni att den som har fått alternativ a som svar har tänkt? Elever behöver få diskutera både matematik innehållet och strategier för att utveckla sin matematiska kompetens. Låt dem också få argumentera för sina lösningar och sina val av metoder. I arbetet med alla problem bör förmågorna att resonera och argumentera vara centrala. I samband med problemen kommer ett antal termer att aktualiseras. Gå igenom dem. Låt eleverna använda och själva få definiera olika begrepp och återkom till dem i olika sammanhang. För definitioner hänvisar vi till Matematiktermer för skolan (Kiselman & Mouwitz, 2008). Här har vi sorterat förslag under några rubriker Tal, Geometri och Problemlösning och logiska resonemang. Naturligtvis kan flera av problemen passa under flera rubriker. Många problemtyper återkommer år från år, i olika skepnader och i olika varianter. Vi hänvisar här till några tidigare liknande problem och problem som som kan användas i samband med arbetet med årets. Det finns många fler att hämta på Kängurusidan på nätet, ncm.gu.se/kanguru, där alla tidigare omgångar är samlade. Tidigare problem inom området geometri finns dessutom samlade i boken Geometri och rumsuppfattning med känguru problem. Läs mer om den på ncm.gu.se/node/4742. NCM & Kungl Vetenskapsakademien 1
8 Tal Med utgångspunkt i problem kan vi diskutera egenskaper hos tal. Några grundläggande aspekter som barn i denna ålder möter är positionssytemet, udda och jämna tal, räknesättens innebörd, tals uppdelning och enklare faktorisering. Dessutom brukar det ofta i Kängurun finnas problem som handlar om grundläggande bråk och siffersummor. Problemen utmanar också barnen strategiska tänkande och förhoppningsvis väcker de frågor om tal. Uppmuntra därför eleverna att ställa fördjupande frågor. Hjälp dem också att se samband både inom matematiken och mellan matematiken och omvärlden. 1: I den här åldern känner nog alla elever igen tärningsmönstren och kan använda dem utan att räkna prickarna. Enkel addition eller parvisa jämförelser ger svaret. Vilken metod använder eleverna? Uppgiften kan användas för att eleverna ska få diskutera tal utan att ha en exakt beräkning att utgå från. Låt eleverna försöka motivera rätt svar utan att använda den beräknade summan i argumenten, endast jämförelser. Ersätt prickarna med tal, och gör motsvarande. Diskutera smarta strategier för jämförelser. Undersök summor på tärningar: Vilka olika summor är möjliga att få? Vilken är den högsta och lägsta? Vad är det högst sannolikhet att få, om man slår en tärning? Vilken summa är det högst sannolikhet att få, om man slår två tärningar? Att läsa: Per Berggren och Maria Lindroth: Uppslaget En sannolik hästkapplöpning. Nämnaren 1998:4. Per Nilsson: Summaspelet ett spel för lärande i sannolikhet. Nämnaren 2009:3. Tidigare problem: Ecolier 2009:5; Ecolier 2011:14. En mer utmanande uppgift: Benjamin2010:14 2: En enkel beräkning ger svaret. Vad händer om vi lyfter upp plustecknet: Byt plats på och Byt tecken i de första uttrycken: 17 3, Låt eleverna beskriva beräkningarna med hjälp av konkret material och med en situation. Varför kan vi byta plats på och men inte byta plats på tecknen? Uppgiften leder in på räknelagar och prioriteringsregler: Exemplifiera den kommutativa lagen för addition: a + b = b + a och för multiplikation a b = b a, med exempel och låt eleverna inse och uttrycka dem generellt med egna ord. Visa sedan hur vi uttrycker det symboliskt. Gör på liknande sätt med den associativa lagen: (a + b) + c = a + (b + c), a (b c) = (a b) c Undersök t ex Spelar det någon roll i vilken ordning vi utför beräkningen? Låt eleverna även här beskriva med konkret material och med en situation. Vilken skillnad är det mellan (12 + 4) 4 och 12 + (4 4)? Berätta varför vi använder parenteser om prioriteringsregeln. Låt eleverna konstruera olika situationer som kamraterna får beskriva med symboler. Tidigare problem: E 2003:5; E2007:8; E2013:1; E2014:6; E2015:1; B2002:4; B2005:15; B2013:1;. 4: Uppgiften passar bra för arbete med matematisk text och för undervisning om hur vi översätter skriven text, eller muntliga berättelser, till matematiskt symbolspråk. Hur många barn är det som delar på äpplena? Hur vet vi det? Hur många barn hade äpplena i de andra alternativen räckt till? Hur skriver vi 2 och ett halvt med bara siffror? Hur skriver vi att 6 (barn) delar på 3 äpplen? 3 6 Hur skriver vi 3 äpplen är hur många halvor? NCM & Kungl Vetenskapsakademien 2
9 Gå igenom alla alternativ på samma sätt och jämför med det eleverna tidigare kommit fram till. Här är ett konkret exempel på delnings- och innehållsdivision, dessutom med divisionen med bråk. I det här sammanhanget har det en konkret innebörd, vilket gör det möjligt att hantera redan i dessa åldrar. Gör flera liknande exempel och låt eleverna både berätta och uttrycka sig med symboler. Tidigare problem: E2004:17; E2009:3; E2012:4. 7: Proportionalitet kan vara utmanande för eleverna. Beskriv förhållande mellan torkad och färsk svamp med ord, bild och symboler. Låt också eleverna beskriva förhållandet. Gå igenom hur mycket torkad svamp Petrus får av den färska svampen i de andra svarsalternativen. Vänd på frågan och utgå från att det är mängden torkad svamp hur mycket färsk svamp behöver han? Konstruera egna liknande problem. Undersök också andra förhållanden: 1:2, 1:3, 1:5, 1:10. Jämför med erfarenheter från vardagen och med skalan på kartor. Tidigare problem: E2001:3; B2007:4; B2012:13. 9: Diskutera begreppet siffersumma. En del elever har säkert kunnat lösa uppgiften utan att tidigare ha stött på termen siffersumma. Vilken siffersumma har de andra alternativen, årtalet då eleverna föddes, andra årtal. Ordet är egentligen inte så bra, då summan beräknas av tal om vi ska vara noggranna, men siffersumma är en vedertagen term. Gå igenom skillnaden mellan siffra och tal. Låt eleverna ange se största och minsta ensiffriga, tvåsiffriga, tresiffriga etc talet. Se efter mönstret. I en tidigare tävling var en uppgift: Vilken är skillnaden mellan det minsta femsiffriga talet och det största fyrsiffriga talet? Gör flera sådana exempel och låt eleverna resonera sig fram till en generell lösning. Låt dem se kopplingen mellan positionssystemet och en trippmätare (eller annat räkneverk i verkligheten). Diskutera strategier i uppgiften. Vilka årtal kan komma ifråga. Gör en systematiskt ordnad lista över årtal med siffersumman 9. Med hjälp av siffersumman kan vi avgöra om ett tal är delbart med 3. Undersök många tal för att göra det troligt att om siffersumman är delbar med 3 är också talet delbart med 3. Andra delbarhetsregler som elever i den här åldern kan förstå och förklara är delbarhet med 2, 5 och 10. Tidigare problem: E2001:17; E2007:6; E2015:6; B2003:12. 14: Ytterligare ett problem där texten kan behöva analyseras. Vilken information är uttryckt i texten och vad kan vi sluta oss till av det? Vilka slutsatser kan vi dra om de dolda talen? Uttryck olika sätt att resonemangen både muntligt och symboliskt, t ex: 32 (5 + 12) = = x + 5 = 16, y + 12 = x = 12 + y x + y = Låt eleverna konstruera likadana problem med andra tal och eventuellt med andra räknesätt. Tidigare problem: E2008:17. NCM & Kungl Vetenskapsakademien 3
10 17: Jämför detta problem med nr 15. Vilka likheter finns? Skillnader? Vilka olika tal är möjliga i frågan? Varför? Jämför med nr 7 och diskutera likheter. Även här handlar det alltså om ett proportionellt samband. Tidigare problem: E2003:16; B2009:10. 20: Gör en tabell över deras åldrar, från det att trillingarna föds: Kan eleverna se något mönster? (2 + 3) = 11 Ställ frågor i anslutning till tabellen:... Vad betyder (2 + 3)? Varför ökar den sammanlagda ålder med 4? Jämför med talen i svarsalternativen vilka kan dyka upp i tabellen? Om vi tar bort 3, dvs de år som Leo är äldre, vilka tal får vi då? Hur kan vi uttrycka brödernas sammanlagda ålder generellt? Låt eleverna beskriva sina resonemang och hjälps åt att formulera dessa med symboler. Låt eleverna konstruera liknande problem. Variera antalet syskon och åldersskillnaden. Tidigare problem: E2004:2; E2010:15; B2001:7; B2013:4; B2016:15. 22: Vilken information i uppgiften är överflödig? Varför? Ser eleverna att skillnaden mellan 201 och 102 är 99, och kan de utnyttja detta på ett effektivt sätt? Låt eleverna upptäcka hur enkelt uppgiften kan lösas, när man ser hur den är konstruerad. Gör fler exempel på sådana enkla subtraktioner och låt eleverna utnyttja dessa för snabba beräkningar. Tidigare problem: E2004:16; 2012:13. 23: Att ena stapeln ska vara dubbelt så lång som den andra innebär att vi måste dela med 3. Visa och diskutera detta samband. Be eleverna att med ord förklara. Undersök ev problemet konkret och uppmana eleverna att pröva alla möjligheter. Gör en tabell som håller ordning på uppdelningarna. Vilka olika längder på stavar kan Sara få? Hur skulle stapeln ha sett ut för att det skulle vara möjligt att få 10 klossar? Tidigare problem: E2009:17. Geometri Geometri är ett område som lämpar sig väl för problemlösning. Att resonera sig fram till lösningen och att sedan kunna argumentera för den är väsentliga delar av problemlösningsförmågan. 3: Förutom att kunna vända bilden i huvudet kräver uppgiften att man är uppmärksam på detaljer. Gå igenom bilderna och uteslut de felaktiga alternativen. Diskutera hur en spegelbild skiljer sig från ett fotografi. Arbeta med spegelsymmetrier, spegling i en linje. Spegla längs en lodrät linje och längs en vågrät. Låt eleverna också spegla i ett koordinatsystem, så att de får tre spegelbilder. Låt dem också beskriva speglingen med ord. Tidigare problem: E2001:1 och 9; E2014:4; B2010: (0 + 3) = (1 + 3) = 7 NCM & Kungl Vetenskapsakademien 4
11 5: Uppgiften går att lösa genom att man ritar den del som döljs bakom gardinen. Man kan också resonera om antalet hörn. Vi ser tre av rektangelns hörn, så ett måste vara dolt. Där gardinens linje korsar rektangeln bildas två nya hörn. Samtal om formerna ger rika möjligheter att utveckla språket och att bygga upp förståelse för de geometriska objektens egenskaper. Vilken form har gardinen? Vad vet vi om rektangelns dolda hörn? Hur vet vi det? Vad vet vi om den triangel som bildas? Hur kan vi veta att det inte är en liksidig triangel? Gör fler exempel som stimulerar lösningar utifrån geometriska resonemang. Tidigare problem: E2008:10; E2009:6; E2013:3 och 11; B2011:5. 6: Uppgiften passar för grundligt arbete med texten och ordens exakta betydelse. Här finns grundläggande geometriska begrepp men också andra centrala begrepp: lika många, fler, färre, dubbelt. Byt plats på figurerna i alternativen och jämför. Formulera alternativen omvända och justera så att innebörden i meningen blir densamma. Låt eleverna konstruera liknande uppgifter till varandra. Tidigare problem: E2004:2; E2009:2; E2011:5; E2014:2. 8: För att utmana elevernas föreställning (många tror nog att omkretsen har blivit mindre) kan man formulera om frågan och säga att omkretsen på de tre bortklippta rektanglarna är 30 cm. Då bör det bli uppenbart att det inte handlar om att subtrahera omkretsen. Resonera gemensamt om varför omkretsen är oförändrad. Varför behöver vi inte markera i bilden att vinklarna i den inre figuren är räta? Hur kan vi klippa bort delar från rektangeln och få en större omkrets? Hur förhåller sig arean i den ursprungliga rektangeln till arean i den inre figuren? Eleverna behöver få upprepade möjligheter att undersöka area och omkrets och resonera om hur de förändras av olika operationer. Att omkretsen i två figurer är densamma betyder inte att arean också är densamma. Tidigare problem: E201:11, E2002:6; E2004:3; E2006:9; E2008:16; E2009:13; B2013:14; B2015:16; B2016:19. 11: Även här handlar det om att känna igen geometriska former. Man behöver också kunna tolka bilden i tre dimensioner. Diskutera med eleverna hur de ser vilka figurer som ligger över och under varandra. I vilken ordning har de fem barnen lagt sina figurer? Låt eleverna konstruera liknande bilder efter muntliga och skriftliga instruktioner. Hur kan man tolka ordet under i det här sammanhanget? Om bilden hade sett ut så här hade det inte varit helt klart. Då måste vi bestämma om vi ska betrakta verkligheten eller bilden av verkligheten. Att kunna föreställa sig hur något ser ut från ett annat perspektiv är nödvändigt för att förstå kartor och ritningar, tex. Ett förslag: Ta ett fotografi eller en bild från en tidning som visar ett antal personer eller föremål. Låt eleverna fundera över och sedan rita hur motivet skulle se ut om det var fångat bakifrån eller från sidan. Denna uppgift kan göras mer eller mindre komplicerad och kan därför anpassas efter barnen. Att läsa: Karin Wallby: Matematiken i bilden eller bilden i matematiken. Nämnaren1996:2. Tidigare problem: E2004:7; E2009:2; B2008:4. NCM & Kungl Vetenskapsakademien 5
12 12: Vad kallar vi de former som är illustrerade i problemet? Många barn uppfattar kanske att figur 3 saknar namn. Det är en fyrhörning och en parallelltrapets. Undersök fyrhörningarna i bilden och diskutera vilka egenskaper de har: Vad är gemensamt för alla? (Fyra sidor och minst ett par parallella sidor.) Vad är gemensamt för 2 och 4? (Två par parallella lika långa sidor och räta vinklar.) Gå igenom definitioner på parallelltrapets, rektangel och kvadrat. Se vilka av figurerna som uppfyller kraven. Komplettera med en parallellogram (som inte är en rektangel) och jämför med de andra figurerna. Vilka egenskaper har de gemensamt (fyra hörn och minst ett par parallella sidor) och vilka egenskaper saknar parallellogrammen? Dessa fyra former kan nu ordnas: alla motsvarar definition på en parallelltrapets, tre av dem är också en parallellogram, två en rektangel och en är kvadrat. Konstruera en fyrhörning som inte passar in på någon av definitionerna den kallar vi fyrhörning. Undersök en snedställd romb. Vilka egenskaper har den? Var hör den hemma i ordningen? Varför är kvadraten en romb? Att ofta gå tillbaka till definitionerna på de geometriska formerna hjälper eleverna att se på egenskaperna och inte bara på helheten. Undersök vilka olika former man kan få genom att dela en kvadrat med ett snitt. Att kunna dela upp och sätta samman figurer, först konkret men sedan också i huvudet, är nödvändigt för att utveckla förståelse för areabegreppet. Den grundläggande idén att arean inte ändras om figuren delas upp och bitarna byggs samman till en ny figur ligger till grund för att kunna gå vidare från att beräkna area av en rektangel. Intressant är att också jämföra omkretsen. Blir den också oförändrad om figuren delas och flyttas? Pussel illustrerar tydligt att uppdelning av en form i mindre bitar inte förändrar arean, men den sammanlagda omkretsen. Med lösa pusselbitar kan vi bygga sammanhängande figurer med väsentligt större omkrets än det lagda pusslet. Tidigare problem: E2005:7; E20012:6; E2014:7. 18: Att vrida och vända i huvudet är en utmaning för vissa. Undersök konkret och låt eleverna beskriva med ord, som stöd för att uppmärksamma var olika delar av bilden hamnar. Låt eleverna med ord beskriva hur bilden i figur 1 ser ut om vi tänker oss att kortet ligger på ett glasbord och vi ser underifrån. Undersök hur alternativen förhåller sig till varandra. A, B, C och E är alla vridningar av en och samma bild. Jämför alternativ A och D, de är speglingar liksom C och D. Jämför alternativen med bilden på kortet i uppgiften. Vilket alternativ visar samma bild? Tidigare problem: E2003:12; E2005:3; E2009:15; E2015:18; B2007:8; B2010:2; Cadet2003:10. NCM & Kungl Vetenskapsakademien 6
13 Problemlösning och logiska resonemang Många uppfattar textproblem som svåra, speciellt om det är mycket information att hantera. Eleverna behöver få undervisning om hur de ska angripa den typen av uppgifter. Arbeta därför gemensamt med texterna. Gå igenom tillsammans och uppmuntra eleverna att sätta sig in i problemet, exempelvis med hjälp av stödjande frågor. Hjälp eleverna att strukturera informationen i texten. Att förstå vad problemet handlar om är en förutsättning för att kunna lösa det. Men att förstå vad det handlar om och vad som efterfrågas är inte detsamma som att veta vad man ska göra. I problemlösning ingår att komma från att förstå situationen till att komma på hur man ska komma fram till svaret på den formulerade frågan. Problemlösningsprocessen består av flera steg, ofta med både misslyckade och lyckade insatser. Att lära sig hantera motgångar och misslyckade försök är viktigt för att utveckla problemlösningsförmågan. 10: Rita in de olika vägarna i labyrinten så att lösningen blir tydlig och konkret för eleverna. Lösningen av problemet kan illustreras av ett träddiagram, där antalet möjliga val i varje rum blir en gren på trädet. Jämför den konkreta lösningen med träddiagrammet. Undersök motsvarande problem med ytterligare ett rum med två dörrar. Gör fler enkla exempel, där möjligheterna går att illustrera konkret och överblicka, och försök resonera er fram till hur man kan beräkna antalet möjligheter. Tidigare problem: E2006:4; E2007:3; E2010:2; E2011:10; E2012:15; B2011:8. 13: Diskutera olika strategier att lösa uppgiften. Måste vi fylla i alla rutor för att kunna svara? Genomför olika resonemang gemensamt. Låt eleverna konstruera egna 3 x 3-sudokun. Hur många olika möjligheter finns det? Vad är lika i dem? Gör ett 4 x 4-sudoku. Resonera gemensamt och hjälp eleverna att motivera sina förslag. För att kunna utveckla förmågan att föra resonemang är det bra att få följa ett väl underbyggt resonemang. Delta gärna själv och visa eleverna hur man kan resonera. Tidigare problem: E2004:5; E2005:6; E2007:7; E2011:16; E2012:5.; E2014:17; E2015:19; B2008:3; B2009:12; B2009:17, B2001:19. 15: Detta är ett klassiskt problem som förekommit i olika skepnader flera gånger tidigare. Diskutera olika lösningsmetoder och lös flera problem så att eleverna får använda sig av olika metoder. Låt eleverna konstruera liknande problem och diskutera i samband med det vad som är centralt, vilka möjligheter som finns. Varför kan man inte välja antalet ben slumpvis? Tidigare problem: E2009:14; E2012:8; B2010:5. 16: Gå igenom texten noga. Diskutera betydelsen av ordet säkra. Vilka olika möjligheter har Fariba? Rita upp alla eller lägg på papper så att alla möjligheter kan jämföras. Då blir lösningen förhoppningsvis tydlig. Pröva att lägga ut mynten om någon av de fem rutorna i mitten är tom. Hur många rutor skulle det vara på planen för att vi inte alls skulle kunna vara säkra? Tidigare problem: E2012:9. NCM & Kungl Vetenskapsakademien 7
14 19: Man kan kanske hävda att detta i första hand är en läsförståelseuppgift, inte ett matematikproblem. Det stämmer att textförståelsen är avgörande. I denna text måste man observera och tolka uttrycket högst tre korrekt. Man måste också tolka innebörden av att Paul har använt alla bokstäver i sitt namn. Det betyder att bokstäverna P, A, U och L ingår. Däremot säger det inget om antalet bokstäver och inte heller något om huruvida det finns andra bokstäver också. Det är heller inte utsagt om det är versaler eller gemener.cdet är viktigt att eleverna får arbeta med den här typen av läsning, att tolka innebörden i formuleringar, för att kunna klara av matematiska texter. I matematikproblem har uttryck en exakt betydelse, och små detaljer i formuleringar kan vara avgörande. Gå igenom texten noga. Diskutera vad varje mening ger för information, och vilka möjligheter de ger i relation till alternativen. Gå sen igenom texten utan att relatera till alternativen. Vilka tänkbara lösenord finns det då? Låt eleverna konstruera liknande problem. Lista gärna ett antal grundläggande formuleringar som de kan använda sig av, t ex det finns högst, det finns åtminstone, exakt en. Tidigare problem: E2009:8; B2009:3. 21: Gå igenom förutsättningarna noga. Jämför skålarna två och två och dra de slutsatser som går att dra. Några förslag på frågor: Vilken är tyngst, triangeln eller cirkeln? Hur vet vi det? Vilken är tyngst, triangeln eller kvadraten? Hur vet vi det? Varför kan vi bortse från en kvadrat i alla skålar? Tidigare problem: E2003:20; E2004:8; E2012:10; E2013:13; B2013:11; B2015:9. 24: Vilket samband finns mellan äpplen och päron i varje träd? Varför kommer det alltid att vara dubbelt så många päron som äpplen i trädgården? Vilka olika möjligheter att få 25 äpplen finns det? Hur många äpplen skulle det finna för att de andra alternativen skulle vara riktiga? Är alla alternativ möjliga? Vilka olika antal päron kan det finnas? Äpplen. Låt eleverna konstruera egna frågor som utgår från denna trädgård. Tidigare problem: E2010:14. NCM & Kungl Vetenskapsakademien 8
15 Att läsa Bergius, B. & Emanuelsson, L. (2008). Hur många prickar har en gepard? NCM, Göteborgs universitet. Gennow, S. & Wallby, K. (2010). Geometri och rumsuppfattning med Känguruproblem. NCM, Göteborgs universitet. Hagland, K., Hedrén, R. & Taflin, E. (2005). Rika matematiska problem inspiration till variation. Stockholm: Liber. Kiselman, C. & Mouwitz, L. (2008). Matematiktermer för skolan. NCM, Göteborgs universitet. McIntosh, A. (2008). Förstå och använda tal. NCM, Göteborgs universitet. Rystedt, E. & Trygg, L. (2010). Laborativ matematikundervisning vad vet vi? NCM, Göteborgs universitet. Wallby, K m fl (red) (2014). Matematikundervisning i praktiken. NämnarenTema 10. NCM, Göteborgs universitet. Nämnaren. I varje nummer finns Problemavdelningen och Kängurusidan. Läs också tidigare artiklar kring problemlösning. Nämnarenartiklar publicerade finns fritt tillgängliga som pdfdokument på Nämnaren på nätet, namnaren.ncm.gu.se. Du finner dem via artikeldatabasen. Under ArkivN finns alla publicerade Uppslag och Problemavdelningar samlade. Nämnaren på nätet presenterar varje månad nya problem under rubriken Månadens problem. Strävorna finns på ncm.gu.se/stravorna. Där finns aktiviteter, problem och artiklar samlade och ordnade efter kursplanens beskrivning av matematikämnets syfte och mål. Matematiklyftets lärportal matematiklyftet.skolverket.se. På lärportalen finns moduler om problemlösning för alla stadier. Dessa ingår i Matematiklyftet men finns fritt tillgängliga för alla. Modulerna innehåller teoritexter, underlag för lärares gemensamma fortbildning samt problem för eleverna. Om ni inte har och inte planerar att läsa problemlösningsmodulen inom Matematiklyftet, finns den alltså ändå tillgänglig. På lärportalen finns också andra moduler där problemlösning ingår. NCM & Kungl Vetenskapsakademien 9
Ecolier för elever i åk 3 och 4
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Ecolier för elever i åk 3 och 4 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Ecolier för elever i åk 3 och 4 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 017, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på
Kängurun Matematikens hopp Ecolier 017, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder till svaret 6.
 Kängurutävlingen 2015 Ecolier, svar och lösningar Facit Ecolier 1 E 15 2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder
Kängurutävlingen 2015 Ecolier, svar och lösningar Facit Ecolier 1 E 15 2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Junior 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Svar och lösningar Benjamin
 Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
Kängurutävlingen 2017 NCM 1
 Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
Svar och lösningar Ecolier
 Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Arbeta vidare med Milou 2008
 Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom
Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Svar och lösningar Benjamin
 Kängurutävlingen 2014 Svar och lösningar Benjamin 1: A 0 Summerar vi entalen ger de 9, hundratalen ger 3 så det är inga minnessiffror att beakta. Summan av tiotalen är 0. 2: A 1 9999 + 1= 10 000. Talet
Kängurutävlingen 2014 Svar och lösningar Benjamin 1: A 0 Summerar vi entalen ger de 9, hundratalen ger 3 så det är inga minnessiffror att beakta. Summan av tiotalen är 0. 2: A 1 9999 + 1= 10 000. Talet
Arbeta vidare med Ecolier 2010
 Arbeta vidare med Ecolier 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att
Arbeta vidare med Ecolier 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att
Svar och arbeta vidare med Benjamin 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till
Kängurutävlingen Matematikens hopp Junior 2016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
4. A. 4, 6, 11 Viker man ihop till en kub, så kommer talet 1 mitt emot 3, 2 mitt emot 4 och 5 mitt emot 6. Det ger summorna 4, 6, 11.
 N G A RA Kängurutävlingen 2015 Cadet svar och korta lösningar 1. B Betrakta de fem alternativen och jämför med paraplyet. (A) N är upp- och ner. (C) R är felvänd. (D) G är felvänd. (E) R ska inte stå mellan
N G A RA Kängurutävlingen 2015 Cadet svar och korta lösningar 1. B Betrakta de fem alternativen och jämför med paraplyet. (A) N är upp- och ner. (C) R är felvänd. (D) G är felvänd. (E) R ska inte stå mellan
Lösningsförslag Cadet 2014
 Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte.
 Svar och lösningar 1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte. 3 C: 1 och 3 4 C: David 5 B: 2 Flytta myntet på toppen och myntet som ligger i mitten
Svar och lösningar 1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte. 3 C: 1 och 3 4 C: David 5 B: 2 Flytta myntet på toppen och myntet som ligger i mitten
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. De flesta problem kan lösas på flera sätt och med olika representationsformer.
Kängurun Matematikens hopp Ecolier 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. De flesta problem kan lösas på flera sätt och med olika representationsformer.
Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 0, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av klassens
Kängurun Matematikens hopp Ecolier 0, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av klassens
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Student 016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till
Kängurutävlingen Matematikens hopp Student 016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till
Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Kängurutävlingen genomförs i år den 16 mars. Om den dagen inte
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Kängurutävlingen genomförs i år den 16 mars. Om den dagen inte
Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Välkommen till Kängurutävlingen Matematikens hopp 17 mars Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Kortfattade lösningar med svar till Cadet 2006
 3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Milou 2018, svar och korta kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Kängurun Matematikens hopp Milou 2018, svar och korta kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Svar och lösningar Benjamin
 Kängurutävlingen 208 Benjamin, facit och kommentarer Svar och lösningar Benjamin : D: 3 2: E 3: B 8 Pilarna i den första omgången ger 7 poäng vardera. I den andra omgången ger den bästa pilen 2 poäng mer,
Kängurutävlingen 208 Benjamin, facit och kommentarer Svar och lösningar Benjamin : D: 3 2: E 3: B 8 Pilarna i den första omgången ger 7 poäng vardera. I den andra omgången ger den bästa pilen 2 poäng mer,
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt.
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Arbeta vidare med Benjamin
 Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Junior för elever på kurs Ma 2 och Ma 3
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Junior för elever på kurs Ma 2 och Ma 3 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Junior för elever på kurs Ma 2 och Ma 3 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
3: A I den vita asken. Kolan ligger i den röda asken så chokladbiten måste ligga i den vita. Problemet kan lösas konkret och med en enkel bild.
 Svar och lösningar 1: D 200 9 Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett
Svar och lösningar 1: D 200 9 Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett
5: D 3 23 kan bara fås på ett sätt: Här har man nytta av att känna igen 24 som ett tal i sexans tabell.
 Svar och lösningar 1: D 200 9 = 1800 Om eleverna inte redan kan multiplicera med 200 kan lösningen förklaras via 100 9 = 9 100 = 900. 200 9 är alltså dubbelt så mycket, 1800. Vi kan också utesluta de andra
Svar och lösningar 1: D 200 9 = 1800 Om eleverna inte redan kan multiplicera med 200 kan lösningen förklaras via 100 9 = 9 100 = 900. 200 9 är alltså dubbelt så mycket, 1800. Vi kan också utesluta de andra
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Milou 2019, facit och kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Kängurun Matematikens hopp Milou 2019, facit och kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Delprov A Muntligt delprov
 Delprov A Muntligt delprov Äp6Ma15 Delprov A 15 Beskrivning av delprov A, muntligt delprov Det muntliga delprovet kan genomföras fr.o.m. vecka 11 och resten av vårterminen. Det muntliga delprovet handlar
Delprov A Muntligt delprov Äp6Ma15 Delprov A 15 Beskrivning av delprov A, muntligt delprov Det muntliga delprovet kan genomföras fr.o.m. vecka 11 och resten av vårterminen. Det muntliga delprovet handlar
Kängurutävlingen Matematikens hopp 2016 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 4 C: kvadrat Exempel på hur formerna kan konstrueras:
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2013 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Cadet 2013 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Välkommen till Kängurutävlingen Matematikens hopp 2019 Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2019 Benjamin för elever i åk 5, 6 och 7 Tävlingen genomförs under perioden 21 mars 29 mars. Uppgifterna får inte användas tidigare. Sista
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2019 Benjamin för elever i åk 5, 6 och 7 Tävlingen genomförs under perioden 21 mars 29 mars. Uppgifterna får inte användas tidigare. Sista
Facit och kommentarer Ecolier 2019
 Facit och kommentarer Ecolier 2019 1 E 2 C 5+5+1+1 3 A tisdag Om det var söndag igår är det måndag idag. 4 D,, Det kvadratiska hålet kommer att hamna tre rutor från mittvikningen och då syns motorcykeln.
Facit och kommentarer Ecolier 2019 1 E 2 C 5+5+1+1 3 A tisdag Om det var söndag igår är det måndag idag. 4 D,, Det kvadratiska hålet kommer att hamna tre rutor från mittvikningen och då syns motorcykeln.
Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas, däremot
Kortfattade lösningar med svar till Gymnasiets Cadet 2006
 Kängurun Matematikens hopp Gymnasiets Cadet 2006 Kortfattade lösningar med svar till Gymnasiets Cadet 2006 3 poäng 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D
Kängurun Matematikens hopp Gymnasiets Cadet 2006 Kortfattade lösningar med svar till Gymnasiets Cadet 2006 3 poäng 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D
Arbeta vidare med Junior 2010
 Arbeta vidare med Junior 010 Känguruproblemen är kanske inte av samma karaktär som de problem eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper.
Arbeta vidare med Junior 010 Känguruproblemen är kanske inte av samma karaktär som de problem eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper.
Kängurutävlingen 2017
 Kängurutävlingen 2017 Arbeta vidare med Ecolier 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. Låt alla först få
Kängurutävlingen 2017 Arbeta vidare med Ecolier 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. Låt alla först få
Svar och arbeta vidare med Student 2008
 Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
1 B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3.
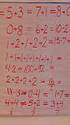 Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
5: B grön Någon har den gröna ryggsäcken och det är inte Anna (och inte Maja), så det måste vara Tom.
 Kängurutävlingen 2018 Ecolier, svar och kommentarer Facit Ecolier 1: E 6 2: B 6 Liam behöver 0, 1, 2, 3, 5 och 8. 3: C 18 Syskonen är 5 år, 6 år och 7 år, 5 + 6 + 7 = 18 4: E 5 Om skruv 5 hade varit lika
Kängurutävlingen 2018 Ecolier, svar och kommentarer Facit Ecolier 1: E 6 2: B 6 Liam behöver 0, 1, 2, 3, 5 och 8. 3: C 18 Syskonen är 5 år, 6 år och 7 år, 5 + 6 + 7 = 18 4: E 5 Om skruv 5 hade varit lika
En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant?
 En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant? P har större omkrets än Q. P har mindre omkrets än Q. P har mindre area än Q Q och P har
En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant? P har större omkrets än Q. P har mindre omkrets än Q. P har mindre area än Q Q och P har
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Svar och korta lösningar Benjamin 2006
 3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
Ecolier. Avdelning 1. Trepoängsproblem. 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6.
 Ecolier Avdelning 1. Trepoängsproblem 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6 (Ryssland) 2 Gilda har 50 kr. Hon tänker köpa fem skrivböcker som
Ecolier Avdelning 1. Trepoängsproblem 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6 (Ryssland) 2 Gilda har 50 kr. Hon tänker köpa fem skrivböcker som
Arbeta vidare med aritmetik 2018
 Arbeta vidare med aritmetik 2018 I det här materialet har vi samlat problem inom aritmetik från flera olika tävlingsklasser, från Ecolier till Student. Årtal Varje år förekommer det problem som utgår från
Arbeta vidare med aritmetik 2018 I det här materialet har vi samlat problem inom aritmetik från flera olika tävlingsklasser, från Ecolier till Student. Årtal Varje år förekommer det problem som utgår från
Matematik. Ämnesprov, läsår 2013/2014. Bedömningsanvisningar Delprov B, C, D, E. Årskurs
 Ämnesprov, läsår 2013/2014 Matematik Bedömningsanvisningar Delprov B, C, D, E Årskurs 6 Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Ämnesprov, läsår 2013/2014 Matematik Bedömningsanvisningar Delprov B, C, D, E Årskurs 6 Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Ecolier för elever i åk 3 och 4
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Ecolier för elever i åk 3 och 4 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Ecolier för elever i åk 3 och 4 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Facit och kommentarer Benjamin 2019
 Facit och kommentarer Benjamin 2019 1 B 2 C 3 D 419 380 + 39 = 419 eller 380 + 20 + 19 = 419 4 C 5 E 1 Hälften av 26 barn är 13 barn. Eftersom det finns 12 pojkar i gruppen måste det som minst vara en
Facit och kommentarer Benjamin 2019 1 B 2 C 3 D 419 380 + 39 = 419 eller 380 + 20 + 19 = 419 4 C 5 E 1 Hälften av 26 barn är 13 barn. Eftersom det finns 12 pojkar i gruppen måste det som minst vara en
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Matematik. Mål att sträva mot. Mål att uppnå. År 1 Mål Kriterier Eleven ska kunna. Taluppfattning koppla ihop antal och siffra kan lägga rätt antal
 Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Junior 011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Matematik Steg: Bas. Mål att sträva mot Mål Målkriterier Omdöme Åtgärder/Kommentarer
 Matematik Steg: Bas ha en grundläggande taluppfattning som omfattar naturliga tal och enkla tal i talområdet 0-10 bråk- och decimalform ordningstal upp till 5 ha en grundläggande rumsuppfattning och kunna
Matematik Steg: Bas ha en grundläggande taluppfattning som omfattar naturliga tal och enkla tal i talområdet 0-10 bråk- och decimalform ordningstal upp till 5 ha en grundläggande rumsuppfattning och kunna
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt
Kängurutävlingen Matematikens hopp Junior 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt
Arbeta vidare med Milou
 Kängurutävlingen 2009 Arbeta vidare med Milou Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. När ni nu diskuterar lösningarna kan ni också kontrollera
Kängurutävlingen 2009 Arbeta vidare med Milou Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. När ni nu diskuterar lösningarna kan ni också kontrollera
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2016, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2016, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurutävlingen Matematikens hopp 2010 Benjamin för elever i åk 5, 6 och 7.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 200 Benjamin för elever i åk 5, 6 och 7. Kängurutävlingen genomförs den 8 mars. Om den dagen inte passar kan hela veckan 9 26 mars användas,
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 200 Benjamin för elever i åk 5, 6 och 7. Kängurutävlingen genomförs den 8 mars. Om den dagen inte passar kan hela veckan 9 26 mars användas,
Bedömning för lärande i matematik
 HANDLEDNING TILL Bedömning för lärande i matematik FÖR ÅRSKURS 1 9 1 Handledning I denna handledning ges förslag på hur du kan komma igång med materialet Bedömning för lärande i matematik åk 1 9. Du börjar
HANDLEDNING TILL Bedömning för lärande i matematik FÖR ÅRSKURS 1 9 1 Handledning I denna handledning ges förslag på hur du kan komma igång med materialet Bedömning för lärande i matematik åk 1 9. Du börjar
Kängurutävlingen Matematikens Hopp Cadet 2003 Lösningar, Arbeta vidare
 Kängurutävlingen Matematikens Hopp Lösningar, Arbeta vidare Arrangeras av Många problem kan lösas på flera sätt. Följande förslag ger inte någon heltäckande beskrivning. Diskutera olika lösningsförslag
Kängurutävlingen Matematikens Hopp Lösningar, Arbeta vidare Arrangeras av Många problem kan lösas på flera sätt. Följande förslag ger inte någon heltäckande beskrivning. Diskutera olika lösningsförslag
Välkommen till Kängurun Matematikens hopp 2008 Benjamin
 Till läraren Välkommen till Kängurun Matematikens hopp 2008 enjamin Kängurutävlingen genomförs april. Om den dagen inte passar går det bra 4 april eller veckan därpå, däremot inte tidigare. Se till att
Till läraren Välkommen till Kängurun Matematikens hopp 2008 enjamin Kängurutävlingen genomförs april. Om den dagen inte passar går det bra 4 april eller veckan därpå, däremot inte tidigare. Se till att
Lösningsförslag Junior 2014
 Kängurutävlingen 014 Junior, svar och lösningar Lösningsförslag Junior 014 1 E: c < b < a Längden av linje a är 16 l.e., linje b (8 + ) l.e. och linje c (8+4 p ) l.e. Alternativ lösning: Grundfiguren har
Kängurutävlingen 014 Junior, svar och lösningar Lösningsförslag Junior 014 1 E: c < b < a Längden av linje a är 16 l.e., linje b (8 + ) l.e. och linje c (8+4 p ) l.e. Alternativ lösning: Grundfiguren har
Svar och lösningar. Kängurutävlingen 2009 Cadet för gymnasiet
 Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Bagarmossens skolas kravnivåer beträffande tal och talens beteckningar som eleven ska ha uppnått efter:
 Matematik 1-5 Skolan skall i sin undervisning i matematik sträva efter att eleven utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik och
Matematik 1-5 Skolan skall i sin undervisning i matematik sträva efter att eleven utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik och
Välkommen till Kängurutävlingen Matematikens hopp 17 mars Junior för elever på kurs Ma 2 och Ma 3
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Junior för elever på kurs Ma 2 och Ma 3 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Junior för elever på kurs Ma 2 och Ma 3 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Student 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Student 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurutävlingen Matematikens hopp
 Kängrtävlingen Matematikens hopp Cadet 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förtom svar ger vi också några olika lösningsförslag. Under vecka 12 pbliceras
Kängrtävlingen Matematikens hopp Cadet 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förtom svar ger vi också några olika lösningsförslag. Under vecka 12 pbliceras
Om Lgr 11 och Favorit matematik 4 6
 Om Lgr 11 och Favorit matematik 4 6 TYDLIG OCH MEDVETEN MATEMATIKUNDERVISNING En stark koppling mellan läroplan/kunskaps mål, innehåll och bedömning finns för att medvetande göra eleverna om syftet med
Om Lgr 11 och Favorit matematik 4 6 TYDLIG OCH MEDVETEN MATEMATIKUNDERVISNING En stark koppling mellan läroplan/kunskaps mål, innehåll och bedömning finns för att medvetande göra eleverna om syftet med
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Cadet 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp Cadet 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
kan använda sig av matematiskt tänkande för vidare studier och i vardagslivet kan lösa problem och omsätta idéer i handling på ett kreativt sätt
 Lokal pedagogisk planering Matematik år 2 Syfte Undervisningen i matematikämnet ska syfta till att eleverna ska utveckla kunskaper om matematik och visa intresse och tilltro till sin förmåga att använda
Lokal pedagogisk planering Matematik år 2 Syfte Undervisningen i matematikämnet ska syfta till att eleverna ska utveckla kunskaper om matematik och visa intresse och tilltro till sin förmåga att använda
Välkommen till. Kängurutävlingen Matematikens hopp 2016 Milou, för elever i förskoleklass åk 2. Till läraren. Lycka till med årets Känguru!
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Milou, för elever i förskoleklass åk 2 Syftet med Kängurun är att skapa intresse för matematik med hjälp av intressanta problem. Vår
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Milou, för elever i förskoleklass åk 2 Syftet med Kängurun är att skapa intresse för matematik med hjälp av intressanta problem. Vår
Matematik. Ämnesprov, läsår 2014/2015. Bedömningsanvisningar Delprov B, C, D, E. Årskurs
 Ämnesprov, läsår 2014/2015 Matematik Bedömningsanvisningar Delprov B, C, D, E Årskurs 6 Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Ämnesprov, läsår 2014/2015 Matematik Bedömningsanvisningar Delprov B, C, D, E Årskurs 6 Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Lokal studieplan matematik åk 1-3
 Lokal studieplan matematik åk 1-3 Kunskaps område Taluppfat tning och tals användni ng Centralt Innehåll Kunskapskrav Moment Åk1 Moment Åk2 Moment Åk3 Naturliga tal och deras egenskaper samt hur talen
Lokal studieplan matematik åk 1-3 Kunskaps område Taluppfat tning och tals användni ng Centralt Innehåll Kunskapskrav Moment Åk1 Moment Åk2 Moment Åk3 Naturliga tal och deras egenskaper samt hur talen
Här är två korta exempel på situationer då vi tillämpar den distributiva lagen:
 Modul: Algebra Del 8: Avslutande reflektion och utvärdering Distributiva lagen Cecilia Kilhamn, Göteborgs Universitet Distributiva lagen a (b + c) = a b + a c Den distributiva lagen kallas den räknelag
Modul: Algebra Del 8: Avslutande reflektion och utvärdering Distributiva lagen Cecilia Kilhamn, Göteborgs Universitet Distributiva lagen a (b + c) = a b + a c Den distributiva lagen kallas den räknelag
Trepoängsproblem. Kängurutävlingen 2011 Cadet. 1 Vilket av följande uttryck har störst värde? 1 A: B: C: D: E: 2011
 Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Välkommen till Kängurutävlingen Matematikens hopp Ecolier för elever i åk 3 och 4
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp Ecolier för elever i åk 3 och 4 Tävlingen genomförs under perioden 21 mars 29 mars. Uppgifterna får inte användas tidigare. Sista dag för
Till läraren Välkommen till Kängurutävlingen Matematikens hopp Ecolier för elever i åk 3 och 4 Tävlingen genomförs under perioden 21 mars 29 mars. Uppgifterna får inte användas tidigare. Sista dag för
4-4 Parallellogrammer Namn:..
 4-4 Parallellogrammer Namn:.. Inledning Hittills har du arbetat bl.a. med linjer och vinklar. En linje är ju någonting som bara har en dimension, längd. Men när två linjer skär varandra och det bildas
4-4 Parallellogrammer Namn:.. Inledning Hittills har du arbetat bl.a. med linjer och vinklar. En linje är ju någonting som bara har en dimension, längd. Men när två linjer skär varandra och det bildas
Detta prov består av del 1 och 2. Här finns också facit och förslag till poängsättning
 Allmänt om proven Detta prov består av del 1 och. Här finns också facit och förslag till poängsättning och bedömning. Provet finns på lärarwebben, dels som pdf-fil och dels som redigerbar Word-fil. Del
Allmänt om proven Detta prov består av del 1 och. Här finns också facit och förslag till poängsättning och bedömning. Provet finns på lärarwebben, dels som pdf-fil och dels som redigerbar Word-fil. Del
Svar och arbeta vidare med Cadet 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Student 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Student 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Matematik. Mål som eleverna skall ha uppnått i slutet av det fjärde skolåret. Mål som eleverna skall ha uppnått i slutet av det femte skolåret
 Balderskolan, Uppsala musikklasser 2009 Matematik Mål som eleverna skall ha uppnått i slutet av det fjärde skolåret läsa och skriva tal inom talområdet 0 10 000 räkna de fyra räknesätten med olika metoder
Balderskolan, Uppsala musikklasser 2009 Matematik Mål som eleverna skall ha uppnått i slutet av det fjärde skolåret läsa och skriva tal inom talområdet 0 10 000 räkna de fyra räknesätten med olika metoder
