Arbeta vidare med Milou 2008
|
|
|
- Jan Nyberg
- för 9 år sedan
- Visningar:
Transkript
1 Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom att ändra i förutsättningarna, t ex ändra de ingående talen. Pröva också att undersöka hur problemet skulle ha varit formulerade för att andra alternativ skulle vara riktiga. Här ger vi några kommentarer till problemen och förslag på hur ni kan arbeta vidare med dem. Det finns naturligtvis mycket mer att göra och en del av nedanstående förslag passar kanske inte för dina elever i år. Säkert har du också en hel del egna idéer. Dela gärna med dig av dem, skriv till [email protected]. Om du inte redan har tillgång till årets Ecolier kan du hämta dem på ncm.gu.se/node/1778. Där finns ytterligare problem som ni kan arbeta med i par, i grupp och tillsammans. På Kängurusidan, ncm.gu.se/kanguru/ finns alla tidigare problem. Där finner du många problem som går att använda även med yngre elever. Vi ger här några förslag på tidigare använda problem inom de områden som behandlas här. De är alla hämtade från tidigare Ecolier, E. Vi ger också några läsförslag. Mer om var du finner det finns i slutet under rubriken Litteratur. Övningsproblemet: I den stora triangeln ser vi fyra mindre trianglar, dvs totalt finns där 5 trianglar. Sök efter trianglar av olika storlek och med olika form i klassrummet och på skolgården. Undersök trianglar med olika form och diskutera vad som är gemensamt för alla trianglar. Sortera trianglar av olika slag (t ex rätvinkliga, liksidiga, likbenta). Gör tesselleringar med trianglar och undersök vilka andra former kan man få genom att pussla ihop olika antal trianglar. Motsvarande uppgift som i övningsexemplet kan också göras med kvadrater. Ett exempel på utvecklat problem fanns i Nämnaren 1994:4 Kvadrater i kvadrat. Problem 10 i årets Ecolier rör trianglar och problem 3 mönster med kvadrater. Se också E 14, : Pusselbiten Det enklaste sättet att kontrollera lösningen här är att klippa ur bitarna och prova. Om man färglägger figurerna blir det också något lättare att se vilken av bitarna som fattas. Genom att beskriva bilden kan man se att halsen ska ligga i övre vänstra kanten på bilden, som på pusselbit nr 2. Låt eleverna beskriva bitarna med ord och med hjälp av höger och vänster komma fram till vilka bitar som säkert inte passar. 2: Kulorna på bordet Det här handlar både om att bestämma antal och om att inse att antalet inte är beroende av formen på högarna. Många har säkert räknat efter att det är 9 kulor på vänstra bordet och 7 på det högra och så kommit fram till att det saknas 2. Man kan också se det som = 7 +? Här behöver vi inte utföra additionen för att se svaret. Utgå från ovanstående relativt enkla likhet och gör motsvarande med mer komplicerade likheter, t ex = 343 +?. Jämför subtraktion: 7 2= 8? och = 775? Se också E 16, 2004, E 2, 2005 Kungl. Vetenskapsakademien & NCM/Nämnaren 1
2 3: Veckodagar Här handlar det om att tänka sig in i att vara någon annanstans i tiden, och begreppen idag, imorgon och igår. I morgon är i dag igår och igår var idag i morgon. Att kunna hantera räkning med tid är en väsentlig vardagskunskap, t ex vi har tre dagars ledigt med början på tisdag, du får låna boken i 14 dagar, ät din medicin i 10 dagar. Arbeta med liknande uttryck som avanstående och avgör start och slutdag. I vilka sammanhang ska man räkna med idag? Resonera kring varför vi alltid kommer till samma veckodag om vi rör oss med 7, 14, 21 etc dagar. Det finns i tidigare Kängurutävlingar flera problem som rör tid. År och almanackan: E 12, 2002, E 13, 2007 Veckodagar: E 3, 2006, E 14, 2004 Klockan: E 7, 2003, E 14, 2002, E 9, 2004, E 12, : Tärningsprickarna Här saknas 1, 3 och 5 vilket ger totalt 9. Hur många prickar finns det totalt på en tärning? Så ett alternativt sätt att lösa problemet vore En normal tärning har summan 7 på motstående sidor. Hur många prickar är det på sidan som ligger mot bordet i exemplet? Utveckla problemet genom att göra tärningsstaplar och diskutera hur många prickar som kan finnas på de dolda sidorna. En aktivitet för att stärka barns förmåga att dela upp tal beskrivs i Hur arbetar duktiga lärare? i NämnarenTema 7, s 58. Barnen slår 3 tärningar och får en summa, t ex 10. Hur visade tärningarna det? Variera antalet tärningar och utveckla övningen så at televerna ska finna alla tänkbara kombinationer. Att läsa: Rika tärningar i Nämnaren nr 4, : Hälften av kakorna Begreppen hälften och dubbelt är centrala. Här handlar det om hälften av antalet. Hälften är hjärtan, hälften något annat. Om det vore dubbelt så många hjärtan, hur stor andel vore då något annat? Vilken andel är hjärtan på de andra plåtarna? Gör flera exempel hämtade från närmiljön är det mer eller mindre än hälften av gruppen som är flickor? Ett liknande problem om fjärdedelar var E 6, Mer komplexa problem är E 16, 2003 och E 10 och E 17, Låt dina elever pröva att lösa dem med hjälp av konkret material. 6. Kvadraten och trianglarna Här är ytterligare ett rumsligt problem. Nu måste man också tänka sig att figurerna vrids. Att först göra problemet i tanken är viktigt. Det är inte svaret som är väsentligt utan hur man bearbetar informationen i huvudet. För att kontrollera kan man sen börja med att färglägga bitarna för att se hur de ska byggas, sedan klippa ut och se att det stämmer. Vilka egenskaper har trianglarna som gör att de kan läggas samman till en kvadrat? Tidigare problem är E 3, 2002, E 9, 2003, E 7, 2005, E 11, 2006 och E 5, Problem E 12, 2003 är ett problem i tre dimensioner, Vikhuset. Gör det med eleverna, men låt dem först få pröva i tanken, dvs utan att klippa. Sen kan de klippa och vika. Pröva också E 13, Kungl. Vetenskapsakademien & NCM/Nämnaren
3 7: Cirkeln Detta till synes enkla problem berör definitionen av en cirkel, dvs att avståndet från cirkeln till mittpunkten är lika stort längs hela cirkeln. Anna står närmast Bob, eftersom hon är innanför. Här behöver vi alltså inte mäta. Tillverka cirklar med hjälp av rep eller snören som bestämmer radiens längd. Klipp ur cirkelskivor, vik och undersök mittpunkten. Att läsa: Undersökning med snöre och rep, Nämnaren 3, Skogstrollen i uterummet, Nämnaren nr 3, 2005 handlar om arbete på en förskola. Upptäckter i och med cirklar i Hur många prickar har en gepard? s 44. 8: Talet i molnet Här tar + 2 och -2 ut varandra, så vi kan gå direkt till + 1, de andra beräkningarna behöver inte utföras. Illustrera både med föremål och på en tallinje. Lägg ett antal kulor i en påse och låt eleverna kontrollera hur många det är. Låt någon lägga ner ytterligare valfritt antal kulor, visa hur många kulor som läggs ner, men räkna inte efter hur många det finns sammanlagt i påsen. Tag bort lika många kulor och låt eleverna avgöra hur många som finns kvar i påsen, utan att räkna efter. Diskutera varför vi inte behöver kontrollera. Arbeta med andra liknande stegvisa beräkningar där operationer tar ut varandra och variera svårigheten. När eleverna är säkra på addition och subtraktion kan du pröva med exempel med multiplikation också, där ordningen spelar roll. Det är viktigt att eleverna uppmärksammas på att regler som gäller för ett räknesätt inte nödvändigtvis gäller för alla räknesätt. Att förenkla beräkningar genom att se efter möjliga genvägar är en användbar strategi. Gör ofta sådana gemensamma övningar då eleverna får diskutera.ex: = = = 9: Klossbygget Här gäller det att föreställa sig de klossar som inte syns, men som måste finnas om inte några klossar ska sväva i luften. Det finns kanske två korrekta svar. Om dina elever svarat 12 kan du be att de berättar hur de tänkt, kanske har de tänkt att det sticker ut klossar som trappsteg på baksidan, i så fall är det också möjligt. Låt eleverna bygga tornet och sen rita av det. Bygg flera olika figurer och se på dem från olika håll. Prata om hur det ser ut och vad man ser. Att rita tredimensionellt är inte lätt och behöver tränas. Eleverna kan bygga figurer och rita av och låta ritningen vara underlag för kamrater att bygga efter. Låt eleverna rita av varandra ur olika perspektiv: framifrån, bakifrån och ovanifrån. En kan ligga raklång på golvet med armar och ben utsträckta och kamrater kan rita av, gärna från olika håll. Se på bilder i tidningar hur skulle bilden se ut från ett annat håll. Se Matematiken i bilden, eller bilden i matematiken i Nämnaren 2, Liknande uppgifter, med klossbyggen från olika håll har funnits med i Kängurutävlingen så gott som alla år. Se på tidigare omgångar och också på de andra klasser, för äldre elever. Detta är en typ av problem där vi inte tydlig ser att äldre elever presterar bättre än yngre. Kanske beror det på att vi inte arbetar speciellt mycket med dem så att det som eleverna kan har de lärt sig utanför skolan, och att det vi gör i skolan inte påverkar detta särskilt mycket? Att läsa: Villa Villekulla och andra hus i den Nordiska boken Matematikk och undervisning, Norden Kungl. Vetenskapsakademien & NCM/Nämnaren 3
4 10: Talet i tornet Här handlar det i första hand om att identifiera mönstret. Talet i rutan är summan av talen i rutorna under, så högst upp kommer det att stå 11 (5 + 6). Variera problemet genom att ändra tal och bygga högre eller bredare torn. Att arbeta med talmönster är tacksamt och lätt att anpassa, så att det blir tillräckligt svårt för att vara utmanande. Pröva också detta, där du kanske måste ändra de ingående talen.? ? Vilka tal ska stå i rutorna med frågetecken? Detta problem var med på klass Benjamin för ganska många år sen. Det visade sig vara tämligen svårt. Varför, tror du? Liknande problem E 4, : Tändsticksmönster Ytterligare ett problem kring mönster. Nu mönster som växer enligt en speciell regel, i det här fallet lägger vi till 3 stickor för varje ny ruta, så att den tredje figuren har 10 och den fjärde 13 stickor. Hur ser figur 10 ut? Diskutera med eleverna och låt dem beskriva med ord. Skriv upp det de säger på tavlan, med ord, och skriv sedan gemensamt detsamma med blandning av ord och symboler. Gör andra mönster och arbeta med dem på samma sätt. Den här typen av uppgifter är viktiga som förberedelse för algebra. Att läsa: Variabler och mönster och Mönster med stickor i Nämnaren nr 1, Mönster i Nämnaren nr 2, Ett motsvarande problem var E 12, Se också E 18, Spegelsiffror Detta problem behandlar symmetri. Hur ser 5 ut i samma spegling som de övriga siffrorna, dvs med den korrekta siffran till höger och speglingen till vänster? Pröva att titta på siffrorna i en spegel, eventuellt får ni göra dem större. Undersök symmetrier i våra bokstäver. Vilka har en symmetriaxel? Vilka har flera? Vilka saknar? Gör speglingar till de bokstäver som inte är symmetriska. Undersök symmetrier i omvärlden i klassrummet, på skolgården och i tidningar. Rita en figur och spegla den i olika linjer och jämför resultaten. Läs om grundläggande arbete med symmetri i Former och mönster, Symmetrier i Små barns matematik, s 125. Läs också Vi utforskar symmetrier i Hur många prickar har en gepard? s 80. E 9,2001 behandlar också spegling. 4 Kungl. Vetenskapsakademien & NCM/Nämnaren
5 Litteratur Alla tidigare Känguruproblem finns på Kängurusidan: ncm.gu.se/kanguru Nämnarenartiklar publicerade finns tillgängliga som pdf-dokument och är fritt tillgängliga. Du finner dem via artikeldatabasen på namnaren.ncm.gu.se. Bergius, B. & Emanuelsson, L. (2008). Hur många pricakr har en gepard. Göteborg: NCM. Doverborg, E. & Emanuelsson, G. (red) (2007). Små barns matematik. Göteborg: NCM. Emanuelsson, G. & Doverborg, E. (red) (2006). Matematik i förskolan. NämnarenTema 7. Göteborg: NCM. Matematikk & undervisning. Norden Tillgänglig på: ncm.gu.se under rubriken Publikationer Böcker Kungl. Vetenskapsakademien & NCM/Nämnaren 5
Arbeta vidare med Milou
 Kängurutävlingen 2009 Arbeta vidare med Milou Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. När ni nu diskuterar lösningarna kan ni också kontrollera
Kängurutävlingen 2009 Arbeta vidare med Milou Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. När ni nu diskuterar lösningarna kan ni också kontrollera
Svar och arbeta vidare med Benjamin 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
3: A I den vita asken. Kolan ligger i den röda asken så chokladbiten måste ligga i den vita. Problemet kan lösas konkret och med en enkel bild.
 Svar och lösningar 1: D 200 9 Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett
Svar och lösningar 1: D 200 9 Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett
Välkommen till. Kängurutävlingen Matematikens hopp 2016 Milou, för elever i förskoleklass åk 2. Till läraren. Lycka till med årets Känguru!
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Milou, för elever i förskoleklass åk 2 Syftet med Kängurun är att skapa intresse för matematik med hjälp av intressanta problem. Vår
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Milou, för elever i förskoleklass åk 2 Syftet med Kängurun är att skapa intresse för matematik med hjälp av intressanta problem. Vår
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
Ecolier för elever i åk 3 och 4
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Ecolier för elever i åk 3 och 4 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Ecolier för elever i åk 3 och 4 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Kängurutävlingen Matematikens hopp 2010 Benjamin för elever i åk 5, 6 och 7.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 200 Benjamin för elever i åk 5, 6 och 7. Kängurutävlingen genomförs den 8 mars. Om den dagen inte passar kan hela veckan 9 26 mars användas,
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 200 Benjamin för elever i åk 5, 6 och 7. Kängurutävlingen genomförs den 8 mars. Om den dagen inte passar kan hela veckan 9 26 mars användas,
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Milou 2018, svar och korta kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Kängurun Matematikens hopp Milou 2018, svar och korta kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Tränarguide del 2. Mattelek. www.flexprogram.se
 Tränarguide del 2 Mattelek www.flexprogram.se 1 ANTALSUPPFATTNING - MINST/STÖRST ANTAL Övningarna inom detta område tränar elevernas uppfattning av antal. Ett antal objekt presenteras i två separata rutor.
Tränarguide del 2 Mattelek www.flexprogram.se 1 ANTALSUPPFATTNING - MINST/STÖRST ANTAL Övningarna inom detta område tränar elevernas uppfattning av antal. Ett antal objekt presenteras i två separata rutor.
Arbeta vidare med Benjamin
 Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Välkommen till. Kängurutävlingen Matematikens hopp 2011 Milou, för elever i förskoleklass åk 2. Till läraren. Lycka till med årets Känguru!
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2011 Milou, för elever i förskoleklass åk 2 Kängurutävlingen genomförs i år den 17 mars. Syftet med Kängurun är att skapa intresse för matematik
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2011 Milou, för elever i förskoleklass åk 2 Kängurutävlingen genomförs i år den 17 mars. Syftet med Kängurun är att skapa intresse för matematik
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Junior 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 017, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på
Kängurun Matematikens hopp Ecolier 017, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på
Svar och arbeta vidare med Cadet 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Kängurutävlingen genomförs i år den 16 mars. Om den dagen inte
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Kängurutävlingen genomförs i år den 16 mars. Om den dagen inte
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. De flesta problem kan lösas på flera sätt och med olika representationsformer.
Kängurun Matematikens hopp Ecolier 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. De flesta problem kan lösas på flera sätt och med olika representationsformer.
A: måndag B: tisdag C: onsdag D: torsdag E: fredag. Vilken av följande bitar behöver vi för att det ska bli ett rätblock?
 Trepoängsproblem 1 Doris gör en skylt till djurparken. På skylten ska det stå ordet KÄNGURUR. Hon målar en bokstav varje dag. Hon målar den första på en onsdag. Vilken dag kommer hon att måla den sista
Trepoängsproblem 1 Doris gör en skylt till djurparken. På skylten ska det stå ordet KÄNGURUR. Hon målar en bokstav varje dag. Hon målar den första på en onsdag. Vilken dag kommer hon att måla den sista
Junior för elever på kurs Ma 2 och Ma 3
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Junior för elever på kurs Ma 2 och Ma 3 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Junior för elever på kurs Ma 2 och Ma 3 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Avdelning 1, trepoängsproblem
 Avdelning 1, trepoängsproblem 1. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Var är kängurun? A: I cirkeln och i triangeln, men inte i kvadraten. B: I cirkeln
Avdelning 1, trepoängsproblem 1. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Var är kängurun? A: I cirkeln och i triangeln, men inte i kvadraten. B: I cirkeln
Milou 2016 lösningar och arbeta vidare
 Kängurutävlingen 2016 Milou 2016 lösningar och arbeta vidare Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Kängurutävlingen 2016 Milou 2016 lösningar och arbeta vidare Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Välkommen till Kängurutävlingen Matematikens hopp 2019 Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2019 Benjamin för elever i åk 5, 6 och 7 Tävlingen genomförs under perioden 21 mars 29 mars. Uppgifterna får inte användas tidigare. Sista
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2019 Benjamin för elever i åk 5, 6 och 7 Tävlingen genomförs under perioden 21 mars 29 mars. Uppgifterna får inte användas tidigare. Sista
Kängurutävlingen 2017 NCM 1
 Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Välkommen till. Kängurutävlingen Matematikens hopp 2017 Milou, för elever i förskoleklass åk 2. Till läraren. Lycka till med årets Känguru!
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Milou, för elever i förskoleklass åk 2 Syftet med Kängurun är att skapa intresse för matematik med hjälp av intressanta problem. Vår
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Milou, för elever i förskoleklass åk 2 Syftet med Kängurun är att skapa intresse för matematik med hjälp av intressanta problem. Vår
Välkommen till Kängurutävlingen Matematikens hopp 17 mars Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
1 B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3.
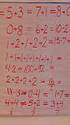 Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Trepoängsproblem. Kängurutävlingen 2012 Junior
 Trepoängsproblem 1. M och N är mittpunkterna på de lika långa sidorna i en likbent triangel. Hur stor är arean av fyrhörningen markerad med X? : 3 : 4 C: 5 D: 6 E: 7 M? X 3 3 6 N 2. När lice skickar ett
Trepoängsproblem 1. M och N är mittpunkterna på de lika långa sidorna i en likbent triangel. Hur stor är arean av fyrhörningen markerad med X? : 3 : 4 C: 5 D: 6 E: 7 M? X 3 3 6 N 2. När lice skickar ett
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
Svar och lösningar Ecolier
 Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Om undervisningen. Att förstå tal. Förstå och använda tal en handbok
 Om undervisningen Inledningsvis kan man nöja sig med att uttrycka bråk muntligt. Vi bör uppmuntra eleverna att använda de språkliga uttrycken halv och fjärdedel när de delar i två eller fyra lika delar.
Om undervisningen Inledningsvis kan man nöja sig med att uttrycka bråk muntligt. Vi bör uppmuntra eleverna att använda de språkliga uttrycken halv och fjärdedel när de delar i två eller fyra lika delar.
Kängurun Matematikens hopp
 Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna
Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna
Här är två korta exempel på situationer då vi tillämpar den distributiva lagen:
 Modul: Algebra Del 8: Avslutande reflektion och utvärdering Distributiva lagen Cecilia Kilhamn, Göteborgs Universitet Distributiva lagen a (b + c) = a b + a c Den distributiva lagen kallas den räknelag
Modul: Algebra Del 8: Avslutande reflektion och utvärdering Distributiva lagen Cecilia Kilhamn, Göteborgs Universitet Distributiva lagen a (b + c) = a b + a c Den distributiva lagen kallas den räknelag
Avdelning 1, trepoängsproblem
 Avdelning, trepoängsproblem. Vi vet att + + 6 = + + +. motsvarar samma tal överallt. Vilket är talet? A: 2 B: 3 C: 4 D: 5 E: 6 2. Siffran fyra speglas två gånger så som på bilden. Vi gör samma sak med
Avdelning, trepoängsproblem. Vi vet att + + 6 = + + +. motsvarar samma tal överallt. Vilket är talet? A: 2 B: 3 C: 4 D: 5 E: 6 2. Siffran fyra speglas två gånger så som på bilden. Vi gör samma sak med
Arbeta vidare med Milou 2013, med lösningar
 Kängurutävlingen 2012 Arbeta vidare med Milou 2013, med lösningar Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Kängurutävlingen 2012 Arbeta vidare med Milou 2013, med lösningar Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Matematik. Mål att sträva mot. Mål att uppnå. År 1 Mål Kriterier Eleven ska kunna. Taluppfattning koppla ihop antal och siffra kan lägga rätt antal
 Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Bo skola 1 Matematikmål år F-3 Skriftligt omdöme/kunskapsinformation
 Bo skola Matematikmål år - Namn: Strävansmål: Vi strävar efter att varje elev ska Utveckla goda baskunskaper i de fyra räknesätten Utvecklar en god förståelse för matematik och matematiska begrepp att
Bo skola Matematikmål år - Namn: Strävansmål: Vi strävar efter att varje elev ska Utveckla goda baskunskaper i de fyra räknesätten Utvecklar en god förståelse för matematik och matematiska begrepp att
Lokal studieplan matematik åk 1-3
 Lokal studieplan matematik åk 1-3 Kunskaps område Taluppfat tning och tals användni ng Centralt Innehåll Kunskapskrav Moment Åk1 Moment Åk2 Moment Åk3 Naturliga tal och deras egenskaper samt hur talen
Lokal studieplan matematik åk 1-3 Kunskaps område Taluppfat tning och tals användni ng Centralt Innehåll Kunskapskrav Moment Åk1 Moment Åk2 Moment Åk3 Naturliga tal och deras egenskaper samt hur talen
Matematiken i Lpfö 98 och Lpo 94
 Matematiken i Lpfö 98 och Lpo 94 Rumsuppfattning lära sig hitta och lokalisera sig i rummet, utveckla inre rumsuppfattning, förstå lägen och placeringar och att föremål kan se olika ut om de avbildas från
Matematiken i Lpfö 98 och Lpo 94 Rumsuppfattning lära sig hitta och lokalisera sig i rummet, utveckla inre rumsuppfattning, förstå lägen och placeringar och att föremål kan se olika ut om de avbildas från
Ecolier för elever i åk 3 och 4
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Ecolier för elever i åk 3 och 4 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Ecolier för elever i åk 3 och 4 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Ecolier. Avdelning 1. Trepoängsproblem. 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6.
 Ecolier Avdelning 1. Trepoängsproblem 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6 (Ryssland) 2 Gilda har 50 kr. Hon tänker köpa fem skrivböcker som
Ecolier Avdelning 1. Trepoängsproblem 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6 (Ryssland) 2 Gilda har 50 kr. Hon tänker köpa fem skrivböcker som
Vad är geometri? För dig? I förskolan?
 Vad är geometri? För dig? I förskolan? Vad är geometri? Betyder jordmätning En del i matematiken som handlar om rum i olika dimensioner, storlek, figurer och kroppar och deras egenskaper. Viktiga didaktiska
Vad är geometri? För dig? I förskolan? Vad är geometri? Betyder jordmätning En del i matematiken som handlar om rum i olika dimensioner, storlek, figurer och kroppar och deras egenskaper. Viktiga didaktiska
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Milou 2019, facit och kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Kängurun Matematikens hopp Milou 2019, facit och kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Kängurutävlingen Matematikens Hopp Benjamin 2003 Uppgifter
 Kängurutävlingen Matematikens Hopp Uppgifter Arrangeras av Kungl. Vetenskapsakademien & NCM/Nämnaren 3-poängsuppgifter 1. Tomas har 9 hundrakronors-sedlar, 9 tiokronor och 10 enkronor. Hur mycket pengar
Kängurutävlingen Matematikens Hopp Uppgifter Arrangeras av Kungl. Vetenskapsakademien & NCM/Nämnaren 3-poängsuppgifter 1. Tomas har 9 hundrakronors-sedlar, 9 tiokronor och 10 enkronor. Hur mycket pengar
kan använda sig av matematiskt tänkande för vidare studier och i vardagslivet kan lösa problem och omsätta idéer i handling på ett kreativt sätt
 Lokal pedagogisk planering Matematik år 2 Syfte Undervisningen i matematikämnet ska syfta till att eleverna ska utveckla kunskaper om matematik och visa intresse och tilltro till sin förmåga att använda
Lokal pedagogisk planering Matematik år 2 Syfte Undervisningen i matematikämnet ska syfta till att eleverna ska utveckla kunskaper om matematik och visa intresse och tilltro till sin förmåga att använda
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Kortfattade lösningar med svar till Cadet 2006
 3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt.
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Svar och lösningar. Kängurutävlingen 2009 Cadet för gymnasiet
 Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 0, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av klassens
Kängurun Matematikens hopp Ecolier 0, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av klassens
Kängurutävlingen Matematikens hopp 2016 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurutävlingen Matematikens hopp 2019 Benjamin
 Kängurutävlingen Matematikens hopp 2019 Benjamin Trepoängsproblem 1 Carrie har börjat att rita en katt. Hur kan hennes färdiga teckning se ut? (Norge) 2 Mayafolket skrev tal på ett annat sätt än vi gör.
Kängurutävlingen Matematikens hopp 2019 Benjamin Trepoängsproblem 1 Carrie har börjat att rita en katt. Hur kan hennes färdiga teckning se ut? (Norge) 2 Mayafolket skrev tal på ett annat sätt än vi gör.
Tal i bråkform. Kapitlet behandlar. Att förstå tal
 Att förstå tal Tal i bråkform Kapitlet behandlar Test Användning av hälften och fjärdedel 2 Representation i bråkform av del av antal och av del av helhet 3, 4 Bråkform i vardagssituationer 4 Stambråk,
Att förstå tal Tal i bråkform Kapitlet behandlar Test Användning av hälften och fjärdedel 2 Representation i bråkform av del av antal och av del av helhet 3, 4 Bråkform i vardagssituationer 4 Stambråk,
Provkapitel Mitt i Prick matematik FK
 FK innehåll 1 2 Antal 1 5................................ 4 Begreppet lika många................ 5 Antal 1 8.............................. 22 Siffra antal, talraden............. 23 Tal och antal 1 och
FK innehåll 1 2 Antal 1 5................................ 4 Begreppet lika många................ 5 Antal 1 8.............................. 22 Siffra antal, talraden............. 23 Tal och antal 1 och
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 4 C: kvadrat Exempel på hur formerna kan konstrueras:
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas, däremot
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Mönster statiska och dynamiska
 Modul: Didaktiska perspektiv på matematikundervisningen 1 Del 3: Fantasi, mönster och sannolikhet Mönster statiska och dynamiska Berit Bergius & Lena Trygg, NCM I många matematiska aktiviteter ska deltagarna
Modul: Didaktiska perspektiv på matematikundervisningen 1 Del 3: Fantasi, mönster och sannolikhet Mönster statiska och dynamiska Berit Bergius & Lena Trygg, NCM I många matematiska aktiviteter ska deltagarna
Svar och lösningar Benjamin
 Kängurutävlingen 208 Benjamin, facit och kommentarer Svar och lösningar Benjamin : D: 3 2: E 3: B 8 Pilarna i den första omgången ger 7 poäng vardera. I den andra omgången ger den bästa pilen 2 poäng mer,
Kängurutävlingen 208 Benjamin, facit och kommentarer Svar och lösningar Benjamin : D: 3 2: E 3: B 8 Pilarna i den första omgången ger 7 poäng vardera. I den andra omgången ger den bästa pilen 2 poäng mer,
Kängurutävlingen Matematikens hopp 2018 Ecolier
 Kängurutävlingen Matematikens hopp 2018 Ecolier Trepoängsproblem 1 På bilden ser du 3 pilar som rör sig och 9 ballonger som sitter fast. När en pil träffar en ballong spricker ballongen. Pilen fortsätter
Kängurutävlingen Matematikens hopp 2018 Ecolier Trepoängsproblem 1 På bilden ser du 3 pilar som rör sig och 9 ballonger som sitter fast. När en pil träffar en ballong spricker ballongen. Pilen fortsätter
Välkommen till Kängurutävlingen Matematikens hopp Ecolier för elever i åk 3 och 4
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp Ecolier för elever i åk 3 och 4 Tävlingen genomförs under perioden 21 mars 29 mars. Uppgifterna får inte användas tidigare. Sista dag för
Till läraren Välkommen till Kängurutävlingen Matematikens hopp Ecolier för elever i åk 3 och 4 Tävlingen genomförs under perioden 21 mars 29 mars. Uppgifterna får inte användas tidigare. Sista dag för
Svar och lösningar Benjamin
 Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Välkommen till Kängurutävlingen Matematikens hopp 2019 Milou, för elever i förskoleklass åk 2
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2019 Milou, för elever i förskoleklass åk 2 Kängurutävlingen genomförs i år den 21 mars. Om den 21 mars inte passar går det bra att genomföra
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2019 Milou, för elever i förskoleklass åk 2 Kängurutävlingen genomförs i år den 21 mars. Om den 21 mars inte passar går det bra att genomföra
Gymnasiets Cadet. a: 2 b: 4 c: 5 d: 6 e: 11
 Gymnasiets Cadet Avdelning 1. Trepoängsproblem 1. I en klass finns 1 flickor och 9 pojkar. Hälften av eleverna i klassen är förkylda. Vilket är det minsta antalet flickor som är förkylda? a: 2 b: 4 c:
Gymnasiets Cadet Avdelning 1. Trepoängsproblem 1. I en klass finns 1 flickor och 9 pojkar. Hälften av eleverna i klassen är förkylda. Vilket är det minsta antalet flickor som är förkylda? a: 2 b: 4 c:
Milou 2015 lösningar och arbeta vidare
 Kängurutävlingen 2015 Milou 2015 lösningar och arbeta vidare Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Kängurutävlingen 2015 Milou 2015 lösningar och arbeta vidare Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Avdelning 1, trepoängsproblem
 Avdelning, trepoängsproblem. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Stjärnan i figuren har bildats av 2 identiska, liksidiga trianglar. Stjärnans omkrets
Avdelning, trepoängsproblem. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Stjärnan i figuren har bildats av 2 identiska, liksidiga trianglar. Stjärnans omkrets
Arbeta vidare med Milou
 Kängurutävlingen 2010 Arbeta vidare med Milou Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni kontrollera lösningarna genom att pröva laborativt.
Kängurutävlingen 2010 Arbeta vidare med Milou Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni kontrollera lösningarna genom att pröva laborativt.
Tillsammans med barn i åldrarna 5 6
 Monica Kable Den är rund runt hela konstruera och förklara med Pinneman Tillsammans med barn i åldrarna 5 6 år på avdelningen Guldgruvan har jag arbetat med sagan Herr Pinnemans äventyr (Donaldsson, 2008)
Monica Kable Den är rund runt hela konstruera och förklara med Pinneman Tillsammans med barn i åldrarna 5 6 år på avdelningen Guldgruvan har jag arbetat med sagan Herr Pinnemans äventyr (Donaldsson, 2008)
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Fundera tillsammans. Victor är 5 år och Åsa är 8 år. Hur gammal kommer Victor att vara när Åsa är dubbelt så gammal som hon är nu?
 STARTAKTIVITET 5 Fundera tillsammans Victor är 5 år och Åsa är 8 år. Hur gammal kommer Victor att vara när Åsa är dubbelt så gammal som hon är nu? 13 år Nils är född den 20 mars. Linus är född samma år
STARTAKTIVITET 5 Fundera tillsammans Victor är 5 år och Åsa är 8 år. Hur gammal kommer Victor att vara när Åsa är dubbelt så gammal som hon är nu? 13 år Nils är född den 20 mars. Linus är född samma år
Svar och arbeta vidare med Student 2008
 Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Tema: Pythagoras sats. Linnéa Utterström & Malin Öberg
 Tema: Pythagoras sats Linnéa Utterström & Malin Öberg Innehåll: Introduktion till Pythagoras sats! 3 Pythagoras sats! 4 Variabler! 5 Potenser! 5 Att komma tillbaka till ursprunget! 7 Vi bevisar Pythagoras
Tema: Pythagoras sats Linnéa Utterström & Malin Öberg Innehåll: Introduktion till Pythagoras sats! 3 Pythagoras sats! 4 Variabler! 5 Potenser! 5 Att komma tillbaka till ursprunget! 7 Vi bevisar Pythagoras
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Likhetstecknets innebörd
 Likhetstecknets innebörd Följande av Görel Sterner översatta och bearbetade text bygger på boken: arithmetic & algebra in elementary school. Portsmouth: Heinemann Elever i åk 1 6 fick följande uppgift:
Likhetstecknets innebörd Följande av Görel Sterner översatta och bearbetade text bygger på boken: arithmetic & algebra in elementary school. Portsmouth: Heinemann Elever i åk 1 6 fick följande uppgift:
A: 111 B: 900 C: 909 D: 990 E: 999
 3-poängsproblem 1. 1000 100 + 10 1 =? A: 111 B: 900 C: 909 D: 990 E: 999 2. Miriam har 16 kort, fyra av varje färg: 4 spader, 4 klöver, 4 ruter och 4 hjärter. Hon vill lägga dem på rutnätet här bredvid
3-poängsproblem 1. 1000 100 + 10 1 =? A: 111 B: 900 C: 909 D: 990 E: 999 2. Miriam har 16 kort, fyra av varje färg: 4 spader, 4 klöver, 4 ruter och 4 hjärter. Hon vill lägga dem på rutnätet här bredvid
Trepoängsproblem. Kängurutävlingen 2011 Cadet. 1 Vilket av följande uttryck har störst värde? 1 A: B: C: D: E: 2011
 Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Svar och korta lösningar Benjamin 2006
 3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
Under en forskningscirkel, som vi matematikutvecklare i Göteborg har
 Britt Holmberg Analysera mera i geometri Inom undervisningen i geometri behöver vi utmana elevernas nyfikenhet med frågeställningar och ge dem tid att undersöka geometriska objekt. Praktiskt arbete där
Britt Holmberg Analysera mera i geometri Inom undervisningen i geometri behöver vi utmana elevernas nyfikenhet med frågeställningar och ge dem tid att undersöka geometriska objekt. Praktiskt arbete där
Per Berggren och Maria Lindroth 2014-11-19
 Varierad matematikundervisning Per Berggren och Maria Lindroth 2014-11-19 Luffarschack Med en utmaning! Sfinxen En rik laborativ matematikuppgift som tar sin början i de första skolåren och fortsätter
Varierad matematikundervisning Per Berggren och Maria Lindroth 2014-11-19 Luffarschack Med en utmaning! Sfinxen En rik laborativ matematikuppgift som tar sin början i de första skolåren och fortsätter
Kängurutävlingen Matematikens Hopp Cadet 2003 Uppgifter
 Kängurutävlingen Matematikens Hopp Uppgifter Arrangeras av Kungl. Vetenskapsakademien & NCM/Nämnaren 3-poängsuppgifter. Ett papper viks två gånger. Därefter klipper man hack i det. Hur ser pappret ut när
Kängurutävlingen Matematikens Hopp Uppgifter Arrangeras av Kungl. Vetenskapsakademien & NCM/Nämnaren 3-poängsuppgifter. Ett papper viks två gånger. Därefter klipper man hack i det. Hur ser pappret ut när
Vad kommer det att stå i rutan som är märkt med ett X? A: 2 B: 3 C: 4 D: 5 E: 6 A: 5 B: 6 C: 7 D: 8 E: 9 A: 40 B: 37 C: 35 D: 34 E: 32
 Trepoängsproblem Vad kommer det att stå i rutan som är märkt med ett X? 2 Elsas kub Natalies kub Natalie ville bygga en likadan kub som Elsa hade byggt, men hennes klossar tog slut. Hur många klossar till
Trepoängsproblem Vad kommer det att stå i rutan som är märkt med ett X? 2 Elsas kub Natalies kub Natalie ville bygga en likadan kub som Elsa hade byggt, men hennes klossar tog slut. Hur många klossar till
1 Fortsätt talmönstret. (2) 46, 47, 48, 49, 50, Fortsätt talmönstret. (2) 64, 63, 62, 61, 60, 59
 Instruktion Instruktioner och kommentarer är desamma som för testet i den ursprungliga versionen. I denna version är små förändringar av ingående tal gjorda och någon uppgift är formulerad på annat sätt.
Instruktion Instruktioner och kommentarer är desamma som för testet i den ursprungliga versionen. I denna version är små förändringar av ingående tal gjorda och någon uppgift är formulerad på annat sätt.
Aktivitetsbank. Matematikundervisning med digitala verktyg II, åk 1-3. Maria Johansson, Ulrica Dahlberg
 Aktivitetsbank Matematikundervisning med digitala, åk 1-3 Maria Johansson, Ulrica Dahlberg Matematik: Grundskola åk 1-3 Modul: Matematikundervisning med digitala Aktivitetsbank till modulen Matematikundervisning
Aktivitetsbank Matematikundervisning med digitala, åk 1-3 Maria Johansson, Ulrica Dahlberg Matematik: Grundskola åk 1-3 Modul: Matematikundervisning med digitala Aktivitetsbank till modulen Matematikundervisning
