fördjupning inom induktion och elektromagnetism
|
|
|
- Emil Hermansson
- för 8 år sedan
- Visningar:
Transkript
1 9 fördjupning inom induktion och elektromagnetism Innehåll 12 Matematiska samband i RL-kretsen 9:2 13 Magnetisk energi 9:3 14 Elektrisk svängningskrets 9:5 15 Kvantitativ behandling av svängningskretsen 9:6 16 Elektromagnetisk vågrörelse 9:9 Svar till kontrolluppgifter 9:13 induktion 9:1
2 12 Matematiska samband i RL-kretsen Inkopplingsförlopp Fig 27. I figurerna är ström och spänningar i RL-kretsen markerade omedelbart efter inkoppling resp kortslutning av spänningen U. All resistans i kretsen förutsätts samlad i resistorn. Små bokstäver används för att markera tidsberoende värden. (a) Inkopplingsförloppet (b) Kortslutningsförloppet Den seriekopplade kretsen i fig 27 består av en resistor med resistansen R, en spole med induktansen L och med försumbar resistans samt en spänningskälla med polspänning U som kan kortslutas. Vi gör en potentialvandring medurs i den s k RL-kretsen vid en tidpunkt då strömmen ökar (fig 27a): U Ri L = 0 eller U = Ri + L Summan Ri + L är tydligen konstant. Det ger oss en kvalitativ förklaring till strömkurvans utseende i fig 16 efter inkopplingen av spänningen. Kurvans lutning,, är stor i början så länge strömmen och därmed termen Ri är liten, men lutningen avtar efter hand som i ökar. Slutligen blir lutningen noll, och induktionen upphör. Då har strömmen vuxit till sitt fulla värde, I = U/R. Vilken funktion i av tiden t är det som satisfierar den ekvation vi nyss ställt upp, och som samtigt ger i = 0 för t = 0 och i = U/R för t =? Följande exponentialfunktion uppfyller alla tre kraven och är följaktligen den funktion vi söker. U R t i = (1 e L R ) Man kan enkelt visa att funktionen är en lösning genom att derivera den och sätta in i ekvationen U Ri L = 0 9:2 induktion
3 Kortslutningsförlopp Potentialvandring medurs i den krets som bildas då spänningskällan kortsluts så att U blir noll ger (fig 27 b): Ri + e = 0 I ekvationen ska e ha ett positivt värde. Strömmen avtar emellertid under detta skede, och derivatan är därför negativ. För att kompensera för detta måste vi skriva e = L. Alltså: Ri L = 0 eller Ri + L = 0 De slutsatser vi kan dra av detta samband stämmer med utseendet hos strömkurvan i fig 16 efter att spänningen växlat från U till noll. I växlingsögonblicket har strömmen och därmed termen Ri sitt största värde. Kurvans lutning, /, måste då ha sitt största negativa värde. Vi söker en strömfunktion som dels satisfierar den ekvation vi ställt upp, dels ger i = U/R för t = 0 och i = 0 för t =. Lösningen är: i = U R e R t L Graferna till de två strömfunktionerna återges i i-t-agrammet i fig Magnetisk energi När spänningskällan i fig 27 kortsluts, upphör omedelbart all tillförsel av energi från spänningskällan till kretsen. I stället tar den inducerade spänningen över och fortsätter att under en stund driva ström genom kretsen. Även den strömmen innebär naturligtvis värmeutveckling i resistorn. Varifrån kommer den energi som omsätts i kretsen sedan energileveransen från spänningskällan slutat? Svaret är att den kommer från spolens magnetfält. Vi möter här en ny form av energi magnetisk energi i ett magnetfält. Under strömmens uppbyggnadsskede övergår en del av den elektriska energi som skapas i spänningskällan till magnetisk energi i spolens magnetfält. Det är denna lagrade magnetiska energi som efter spänningskällans urkoppling omvandlas till elenergi genom induktionen. induktion 9:3
4 Vi ska härleda ett uttryck för den energimängd som finns lagrad i en strömförande spoles magnetfält. Vi börjar med en potentialvandring runt RL-kretsen i fig 17a i en tidpunkt under strömmens uppbyggnadsskede: i U Ri L = 0 t eller i U = Ri + L t Multiplikation med strömmen i och det korta tidsintervallet t ger termerna energimension: Ui t = Ri 2 i t + Li t t Termen Ui t är den energi spänningskällan levererar till kretsen under tiden t. Den energin omsätts i kretsen på två sätt. Ri 2 t är värmeutvecklingen i resistorn, och Li t måste vara den energi som matas in i t i magnetfältet. Uttrycket för den magnetiska energin kan förenklas: i Li t = Li i t Detta är ökningen av den magnetiska energin i spolen vid en liten strömökning i. Den totala magnetiska energin E m vid en ström I är summan av alla sådana bidrag under det att strömmen ändras från 0 till I. Den summan innebär matematiskt en integral: I Li E m = Li = [ 2 ] I LI = Den magnetiska energi som finns lagrad i en spole med induktansen L och strömmen I är alltså: E m = LI 2 2 KONTROLL 1 En ström på 2,0 A går igenom en 1200-varvs spole med induktansen 22 mh. Hur stor magnetisk energi finns lagrad i spolens magnetfält? 9:4 induktion
5 14 Elektrisk svängningskrets Fig 28. När strömställaren i kretsen sluts, omvandlas kondensatorns elektriska lägesenergi till värme i lampans glöråd. En laddad kondensator innehåller elektrisk lägesenergi. Ansluter vi den till en lampa (fig 28), börjar en ström, begränsad av lampans resistans, flyta genom kretsen. Kondensatorns energi omsätts till värme i lampan. När kondensatorn urladdats, har all elektrisk energi omvandlats till värme, och strömmen har upphört. Helt annorlunda blir det, om vi ansluter en laddad kondensator till en spole (fig 29a). Även om spolens resistans är praktiskt taget noll kan urladdningsströmmen inte plötsligt rusa i höjden, eftersom den bromsas av en inducerad spänning u L (fig 29 b). I stället växer den efter hand och bygger under tiden upp ett magnetfält i spolen. Förloppet innebär att elektrisk energi i kondensatorn överförs till magnetisk energi i spolen. Den magnetiska energin, och därmed strömmen, slutar att växa först när kondensatorn urladdats och förlorat all sin energi (fig 29 c). (a) (b) (c) (d) (e) Fig 29. Då kretsen i (a) sluts, börjar spänningen mellan plattorna driva en ström genom spolen, och kondensatorn urladdas (b). När strömmen vuxit till sitt största värde, har kondensatorns energi omvandlats till magnetisk energi (c). När magnetfältet sedan avtar, börjar självinduktionen att mata ström i samma riktning som tigare, och kondensatorn laddas igen (d och e). Vad händer nu när kondensatorspänningen är noll och kondensatorn inte längre kan fungera som spänningskälla? Strömmen och det magnetiska fältet kan inte försvinna plötsligt. Så fort de tenderar att avta, växlar den inducerade spänningen u L polaritet och driver strömmen vidare i samma riktning som förut (fig 29 d). Det betyder att kondensatorn laddas på nytt, och att spolens magnetiska energi återgår till elektrisk energi hos kondensatorn. När all magnetisk energi blivit elektrisk energi igen, är strömmen noll och situationen likadan som vid starten, bortsett från att plattorna har bytt laddning (fig 29 e). Det betyder att förloppet startar om och upprepas med motsatta riktningar hos ström och magnetfält. När kondensatorn omladdats på nytt är kretsen tillbaka i det ursprungliga tillståndet (fig 29 a). En hel svängning är fullbordad. Vi får alltså en växelström i kretsen och en stäng växling mellan elektrisk och magne- induktion 9:5
6 En spole och en kondensator bildar tillsammans en elektrisk svängningskrets. tisk energi. Kondensatorn och spolen utgör tillsammans en elektrisk svängningskrets. En krets som svänger odämpat, dvs utan energiförluster, kan jämföras med en mekanisk pendel, som svänger fram och tillbaka utan att amplituden minskar. Även här är det en kontinuerlig växling mellan två energiformer. I vändlägena uppträder all svängningsenergi som lägesenergi, i jämviktsläget som rörelseenergi. Pendelns lägesenergi motsvaras alltså av den elektriska lägesenergin hos kondensatorn, medan pendelns rörelseenergi kan jämföras med den magnetiska energi ledningselektronernas rörelse i spolvarven ger upphov till. Innan det här avsnittet studeras, är det lämpligt att repetera avsnitten 9 i kap 7 och 7 i kap 9 om kondensator och självinduktion. + q C q u C = q C Fig 30. Ström och spänningar i en odämpad svängningskrets vid en tidpunkt, då kondensatorn håller på att laddas upp. i L + e 15 Kvantitativ behandling av svängningskretsen Svängningstid vid odämpade svängningar Tiden för en hel svängning betecknas T. Vilka faktorer inverkar på den? Byter vi till en spole med större induktans L, får självinduktionen en större inverkan än förut. Eftersom den inducerade spänningen hela tiden bromsar strömändringarna i spolen, bör det nu ta längre tid för strömmen att nå sitt toppvärde och att återgå till noll. Svängningstiden bör öka, om spolens induktans ökar. Även kondensatorns kapacitans C bör inverka. Ju större kapacitansen är, desto mera laddning rymmer kondensatorn vid en viss spänning, och desto längre tid bör omladdningarna ta. Det verkar sannolikt att svängningstiden ökar med kondensatorns kapacitans. Kan vi komma åt sambandet mellan T, L och C? Fig 30 visar ström och spänningar i en svängningskrets med försumbar resistans i ett skede när kondensatorn laddas upp och strömmen avtar. Jfr fig 29 d. En inducerad spänning över spolen med beloppet e = L driver uppladdningen. Potentialvandring ett varv moturs ger: e u C = 0 eller q e = 0 C Vid potentialvandringen räknade vi den inducerade spänningen e positiv. När vi nu sätter in uttrycket för e måste vi skriva L, eftersom strömmen avtar under det aktuella skedet och derivatan därför är negativ. Alltså: 9:6 induktion
7 q 1 L = 0 eller + q = 0 C LC jämviktsläge Fig 31. Vid harmonisk svängning är den återförande resulterande kraften proportionell mot elongationen och riktad mot jämviktsläget. Den odämpade elektriska svängningen är sinusformad och har svängningstiden T = 2π ÖLØØ C. ØØØØ dq dq d Men i =. (q växer och är positiv.) Derivering ger = 2 q, 2 och vi kan skriva: d 2 q 1 + q = 0 2 LC eller 1 q + q = 0 (1) LC En ekvation av denna typ har vi träffat på tigare när vi behandlade harmoniska svängningar. Ett föremål med massan m, som utför harmoniska svängningar i en fjäder med fjäderkonstanten k (fig 31), påverkas av en resulterande kraft F = ky vid utslaget y från jämviktsläget. (Minustecknet visar att kraften har motsatt riktning mot elongationen y.) Kraftekvationen F = ma ger då, eftersom accelerationen a = v (t) = = y (t): ky = my eller k y + y = 0 (2) m Likheterna mellan ekvationerna (1) och (2) är påfallande. Den tidsberoende lägefunktionen y och konstanten i den ena motsvaras av ladd- k m 1 ningsfunktionen q och konstanten i den andra. LC I avsnitt 4, kap 6, fann vi följande uttryck för svängningstiden hos den harmoniska svängningen: m T = 2π Ö k Av symmetrin mellan ekvationerna kan vi dra slutsatsen att uttrycket för svängningstiden hos den odämpade elektriska svängningen måste ha följande utseende: T = 2π ÖØ LC Kondensatorladdningen vid en odämpad elektrisk svängning är, liksom läget vid en harmonisk svängning, en sinusfunktion av tiden. Därmed har också kondensatorspänningen u C = q/c, strömmen i = dq/ och spolens spänning u L = L / ett sinusformat tidsberoende. Se fig 32a. induktion 9:7
8 Dämpade svängningar En pendel slutar så småningom svänga. Svängningsenergin övergår till värme genom oundviklig friktion. Inte heller de elektriska svängningarna i en svängningskrets kan fortsätta hur länge som helst. Det finns alltid någon resistans i kretsen, varför en viss värmeutveckling blir ofrånkomlig då elektronerna rör sig fram och tillbaka. Vid varje omladdning av kondensatorn förbrukas därför en del av energin, och den maximala laddningen på plattorna blir mindre än förut. Svängningarna dämpas och dör så småningom ut. För att demonstrera dämpade elektriska svängningar ansluter vi ett s k minnesoscilloskop till en svängningskrets (fig 32 b). Genom att välja en lämplig svephastighet kan vi studera spänningen över kondensatorn under hela den tid svängningarna varar. Ett foto av oscilloskopskärmen efter ett sådant experiment visas i fig 32 c. Vi ser hur svängningarna tämligen snabbt dämpas, men att svängningstiden inte märkbart beror av amplituden utan hela tiden upptar en och en halv ruta i sidled. (b) (a) (c) Fig 32. Genom att ansluta ett oscilloskop till en svängningskrets kan man studera svängningar. Fotona av oscilloskopskärmen visar, hur kondensatorspänningen u eller kondensatorladdningen q = Cu varierar med tiden. (a) Odämpad svängning. (b) Med denna anslutning kan man studera en dämpad svängning. (c) Dämpad svängning. 9:8 induktion
9 Om vi varierar induktansen L resp kapacitansen C i svängningskretsen i fig 32, finner vi att svängningstiden inom mätnoggrannheten ges av sambandet T = 2π ÖLC, trots att svängningen här är dämpad. Dämpningen ökar med resistansen hos kretsen. Inom tekniken har man stor användning av elektriska svängningskretsar eller oscillatorer, där ny energi stängt matas in för att förhindra att svängningarna dämpas. Sådana kretsar ingår exempelvis i raosändare och raomottagare. KONTROLL 2 Vilken är svängningstiden resp frekvensen hos en odämpad svängningskrets, där induktansen är 35 mh och kapacitansen 0,12 µf? 16 Elektromagnetisk vågrörelse I fig 33 ser vi en svängningskrets som är induktivt kopplad till en oscillator. Kopplingen innebär att svängningskretsens spole placeras så att den känner det magnetfält som oscillatorströmmen alstrar i en annan spole. I svängningskretsen uppstår då tvungna svängningar med samma frekvens som i oscillatorkretsen. Resonans uppkommer om oscillatorfrekvensen sammanfaller med LC-kretsens egenfrekvens, och strömmen i svängningskretsen får då maximal amplitud. oscillator Fig 33. Med en oscillator kan man åstadkomma tvungna svängningar i en svängningskrets. Hittills har vi studerat en sluten svängningskrets, där det magnetiska fältet i huvudsak varit koncentrerat till spolen och det elektriska till mellanrummet mellan kondensatorplattorna. Vi antar nu att vi ändrar en svängningskrets genom att successivt minska spolens varvtal och kondensatorplattornas storlek, samtigt som vi ökar plattavståndet (fig 34). Kretsen förvandlas slutligen till en enda rak ledare, en öppen svängningskrets eller en antenn. induktion 9:9
10 Fig 34. Omvandling av en sluten svängningskrets till en öppen. Fig 35. Tvungna svängningar i en öppen svängningskrets. På grund av förändringarna avtar både induktansen L och kapacitansen C kraftigt, och den öppna kretsens egenfrekvens 1 f= = T 1 2π ÖLC är därför hög, kanske av storleksordningen GHz. En oscillator som, på samma sätt som i fig 33, ska driva svängningarna i den öppna kretsen, måste därför vara högfrekvent för att resonansvillkoret ska vara uppfyllt. I den öppna svängningskretsen i fig 35 pendlar laddningar fram och tillbaka precis som i den slutna kretsen. Under ena halvperioden är antennens övre ände positiv och den nedre negativ. En halvperiod senare har laddningarna bytt plats. Mellan antennens ändpunkter uppträder en växelspänning, och i antennen flyter en växelström. När spänningen har sitt största värde, är den elektriska fältstyrkan intill antennen maximal (fig 36 a). I det ögonblicket är strömmen noll. En fjärdedels period senare är spänningen noll, men i stället har strömmen vuxit till maximum, och det elektriska fältet har bytts ut mot ett magnetiskt, (fig 36 b). Under nästa kvartsperiod byggs ett elektriskt fält upp på nytt, motriktat det ursprungliga, och det magnetiska fältet försvinner. Intill antennen sker en stäng växling mellan elektriska och magnetiska fält som är vinkelräta mot varandra. (a) (b) e Fig 36. Kring den öppna svängningskretsen utbildas omväxlande elektriska fält (a) och magnetiska fält (b). 9:10 induktion
11 Elektromagnetisk strålning Vad händer med de fält som kontinuerligt ska ersättas med andra? De innehåller energi och kan därför inte utan vidare försvinna. En del av energin återgår till antennen, men delar av fälten utbreder sig bort från den (fig 37). Ju högre frekvensen är, desto större del av energin sänds på detta sätt ut från antennen. Elektromagnetiska vågor eller elektromagnetisk strålning rör sig bort ifrån antennen. Strålningen uppför sig som en transversell vågrörelse, där vågorna utgörs av mot varandra vinkelräta elektriska och magnetiska fält. Inga partikelsvängningar behövs för att fortplanta de elektromagnetiska vågorna, och därför utbreder de sig obehindrat i vakuum. Fig 37. Förändringar hos det elektriska fältet under svängningarna i antennen. (a) (b) Fig 38. Ögonblicksbilder av det elektriska fältet i papperets plan och av det magnetiska fältet i ett plan vinkelrätt mot papperet (b). e Fig 39. Fältstyrkan E och flödestätheten B i en punkt ett stycke ut från antennen, som funktion av tiden. Från och med några våglängders avstånd är E och B i fas, trots att de intill antennen är fasförskjutna i förhållande till varandra. induktion 9:11
12 I vågen som utsänds från en vertikal antenn är det elektriska fältet vertikalt och det magnetiska horisontellt (fig 38 och 39). Den elektriska fältstyrkan är omväxlande riktad uppåt och nedåt, och den magnetiska fältvektorn pekar ömsom åt höger och ömsom åt vänster, sett i vågens rörelseriktning. När de båda fälten får verka på ledningselektronerna i en metall, t ex i en mottagarantenn, tvingas dessa utföra en vertikal svängningsrörelse. (De båda fälten samarbetar i detta fall. I fortsättningen behöver vi bara tala om det elektriska fältet.) Svängningen blir kraftigast om mottagarantennen är parallell med sändarantennen, men obetydlig om antennerna står i rät vinkel mot varandra. I det senare fallet är ju ledningselektronernas rörelseutrymme starkt begränsat. När det sägs om en rao- eller TV-sändning att den har vertikal polarisation, innebär detta att det elektriska fältet från sändarantennen är vertikalt, vilket har betydelse då man monterar upp sin mottagande antenn. Vi har tigare sett att ljus kan polariseras (avsnitt 6, kap 3). Med hjälp av en experimentutrustning för mikrovågor kan vi få en inblick i hur detta går till när man använder de polaroider som nämndes i avsnittet. Utrustningen består av en sändare och en mottagare för elektromagnetiska vågor med några få cm våglängd. Mellan en mikrovågssändare S och en mikrovågmottagare M, med inbördes parallella antenner, placeras ett trådgaller vinkelrätt mot linjen SM (fig 40). När gallrets trådar är parallella med antennerna (fig 40 a) hejdas mikrovågorna praktiskt taget helt. Vrids nu gallret kring axeln SM, inkerar M en våg, vars styrka växer till ett maximum då gallrets trådar står i rät vinkel mot antennerna (fig 40 b). (a) (b) Fig 40. 9:12 induktion
13 Fig 40 c. I det senare fallet har vågens fält mycket liten möjlighet att framkalla elektronsvängningar i gallret. Vågen går igenom gallret med i stort sett oförminskad energi. När trådarna i gallret är parallella med det elektriska fältet, omsätts emellertid vågens energi till strömvärme i gallertrådarna, och vågens energi reduceras kraftigt. Fig 40 c visar vad som händer om gallret har samma orientering som i (b), men sändarantennen vrids från sitt ursprungliga läge. En svagare våg når mottagaren, eftersom den elektriska fältstyrkan nu har en komposant parallell med gallrets trådar. Det måste medföra att vågens energi minskar. Oberoende av sändarantennens orientering är den våg som kommer igenom gallret planpolariserad, vinkelrätt mot gallertrådarna. Gallret verkar som en polarisator. Vi kan nu få en uppfattning om hur en polaroid kan polarisera ljuset från en glödlampa. I glödlampsljuset förekommer svängningar av alla riktningar ljuset är opolariserat. Polaroidens parallella kedjor av långsträckta kristaller innehåller lättrörliga elektroner. Dessa kedjor spelar samma roll som trådarna i gallret som påverkade mikrovågorna. När opolariserat ljus passerar en polaroid, släcks alla elektriska svängningskomposanter som är parallella med molekylkedjorna ut, och alla svängningar i det genomgående ljuset är parallella dvs ljuset är planpolariserat. Svar till kontrolluppgifter K 1 K 2 44 mj T = 0,41 ms, f = 2,5 khz induktion 9:13
4. Elektromagnetisk svängningskrets
 4. Elektromagnetisk svängningskrets L 15 4.1 Resonans, resonansfrekvens En RLC krets kan betraktas som en harmonisk oscillator; den har en egenfrekvens. Då energi tillförs kretsen med denna egenfrekvens
4. Elektromagnetisk svängningskrets L 15 4.1 Resonans, resonansfrekvens En RLC krets kan betraktas som en harmonisk oscillator; den har en egenfrekvens. Då energi tillförs kretsen med denna egenfrekvens
Sammanfattning av likströmsläran
 Innehåll Sammanfattning av likströmsläran... Testa-dig-själv-likströmsläran...9 Felsökning.11 Mätinstrument...13 Varför har vi växelström..17 Växelspännings- och växelströmsbegrepp..18 Vektorräknig..0
Innehåll Sammanfattning av likströmsläran... Testa-dig-själv-likströmsläran...9 Felsökning.11 Mätinstrument...13 Varför har vi växelström..17 Växelspännings- och växelströmsbegrepp..18 Vektorräknig..0
2.7 Virvelströmmar. Om ledaren är i rörelse kommer den att bromsas in, eftersom det inducerade magnetfältet och det yttre fältet är motsatt riktade.
 2.7 Virvelströmmar L8 Induktionsfenomenet uppträder för alla metaller. Ett föränderligt magnetfält inducerar en spänning, som i sin tur åstadkommer en ström. Detta kan leda till problem,men det kan också
2.7 Virvelströmmar L8 Induktionsfenomenet uppträder för alla metaller. Ett föränderligt magnetfält inducerar en spänning, som i sin tur åstadkommer en ström. Detta kan leda till problem,men det kan också
Prov 3 2014-10-13. (b) Hur stor är kraften som verkar på en elektron mellan plattorna? [1/0/0]
![Prov 3 2014-10-13. (b) Hur stor är kraften som verkar på en elektron mellan plattorna? [1/0/0] Prov 3 2014-10-13. (b) Hur stor är kraften som verkar på en elektron mellan plattorna? [1/0/0]](/thumbs/25/5742088.jpg) Namn: Område: Elektromagnetism Datum: 13 Oktober 2014 Tid: 100 minuter Hjälpmedel: Räknare och formelsamling. Betyg: E: 25. C: 35, 10 på A/C-nivå. A: 45, 14 på C-nivå, 2 på A-nivå. Tot: 60 (34/21/5). Instruktioner:
Namn: Område: Elektromagnetism Datum: 13 Oktober 2014 Tid: 100 minuter Hjälpmedel: Räknare och formelsamling. Betyg: E: 25. C: 35, 10 på A/C-nivå. A: 45, 14 på C-nivå, 2 på A-nivå. Tot: 60 (34/21/5). Instruktioner:
Sammanfattning av kursen ETIA01 Elektronik för D, Del 1 (föreläsning 1-10)
 Sammanfattning av kursen ETIA0 Elektronik för D, Del (föreläsning -0) Kapitel : sid 37 Definitioner om vad laddning, spänning, ström, effekt och energi är och vad dess enheterna är: Laddningsmängd q mäts
Sammanfattning av kursen ETIA0 Elektronik för D, Del (föreläsning -0) Kapitel : sid 37 Definitioner om vad laddning, spänning, ström, effekt och energi är och vad dess enheterna är: Laddningsmängd q mäts
isolerande skikt positiv laddning Q=CV negativ laddning -Q V V
 1 Föreläsning 5 Hambley avsnitt 3.1 3.6 Kondensatorn och spolen [3.1 3.6] Kondensatorn och spolen är två mycket viktiga kretskomponenter. Kondensatorn kan lagra elektrisk energi och spolen magnetisk energi.
1 Föreläsning 5 Hambley avsnitt 3.1 3.6 Kondensatorn och spolen [3.1 3.6] Kondensatorn och spolen är två mycket viktiga kretskomponenter. Kondensatorn kan lagra elektrisk energi och spolen magnetisk energi.
Fysik 1 kapitel 6 och framåt, olika begrepp.
 Fysik 1 kapitel 6 och framåt, olika begrepp. Pronpimol Pompom Khumkhong TE12C Laddningar som repellerar varandra Samma sorters laddningar stöter bort varandra detta innebär att de repellerar varandra.
Fysik 1 kapitel 6 och framåt, olika begrepp. Pronpimol Pompom Khumkhong TE12C Laddningar som repellerar varandra Samma sorters laddningar stöter bort varandra detta innebär att de repellerar varandra.
4. Allmänt Elektromagnetiska vågor
 Det är ett välkänt faktum att det runt en ledare som det flyter en viss ström i bildas ett magnetiskt fält, där styrkan hos det magnetiska fältet beror på hur mycket ström som flyter i ledaren. Om strömmen
Det är ett välkänt faktum att det runt en ledare som det flyter en viss ström i bildas ett magnetiskt fält, där styrkan hos det magnetiska fältet beror på hur mycket ström som flyter i ledaren. Om strömmen
1. Mekanisk svängningsrörelse
 1. Mekanisk svängningsrörelse Olika typer av mekaniska svängningar och vågrörelser möter oss överallt i vardagen allt från svajande höghus till telefoner med vibrationen påslagen hör till denna kategori.
1. Mekanisk svängningsrörelse Olika typer av mekaniska svängningar och vågrörelser möter oss överallt i vardagen allt från svajande höghus till telefoner med vibrationen påslagen hör till denna kategori.
3.4 RLC kretsen. 3.4.1 Impedans, Z
 3.4 RLC kretsen L 11 Växelströmskretsar kan ha olika utsende, men en av de mest använda är RLC kretsen. Den heter så eftersom den har ett motstånd, en spole och en kondensator i serie. De tre komponenterna
3.4 RLC kretsen L 11 Växelströmskretsar kan ha olika utsende, men en av de mest använda är RLC kretsen. Den heter så eftersom den har ett motstånd, en spole och en kondensator i serie. De tre komponenterna
Svar och anvisningar
 15030 BFL10 1 Tenta 15030 Fysik : BFL10 Svar och anvisningar Uppgift 1 a) Enligt superpositionsprincipen ska vi addera elongationerna: y/cm 1 1 x/cm b) Reflektionslagen säger att reflektionsvinkeln är
15030 BFL10 1 Tenta 15030 Fysik : BFL10 Svar och anvisningar Uppgift 1 a) Enligt superpositionsprincipen ska vi addera elongationerna: y/cm 1 1 x/cm b) Reflektionslagen säger att reflektionsvinkeln är
1( ), 2( ), 3( ), 4( ), 5( ), 6( ), 7( ), 8( ), 9( )
 Inst. för Fysik och materialvetenskap Ola Hartmann Tentamen i ELEKTROMAGNETISM I 2008-10-08 Skrivtid: 5 tim. för Kand_Fy 2 och STS 3. Hjälpmedel: Physics Handbook, formelblad i Elektricitetslära, räknedosa
Inst. för Fysik och materialvetenskap Ola Hartmann Tentamen i ELEKTROMAGNETISM I 2008-10-08 Skrivtid: 5 tim. för Kand_Fy 2 och STS 3. Hjälpmedel: Physics Handbook, formelblad i Elektricitetslära, räknedosa
Vecka 4 INDUKTION OCH INDUKTANS (HRW 30-31) EM-OSCILLATIONER OCH VÄXELSTRÖMSKRETSAR
 Vecka 4 INDUKTION OCH INDUKTANS (HRW 30-31) EM-OSCILLATIONER OCH VÄXELSTRÖMSKRETSAR Inlärningsmål Induktion och induktans Faradays lag och inducerad källspänning Lentz lag Energiomvandling vid induktion
Vecka 4 INDUKTION OCH INDUKTANS (HRW 30-31) EM-OSCILLATIONER OCH VÄXELSTRÖMSKRETSAR Inlärningsmål Induktion och induktans Faradays lag och inducerad källspänning Lentz lag Energiomvandling vid induktion
4:3 Passiva komponenter. Inledning
 4:3 Passiva komponenter. Inledning I det här kapitlet skall du gå igenom de tre viktigaste passiva komponenterna, nämligen motståndet, kondensatorn och spolen. Du frågar dig säkert varför de kallas passiva
4:3 Passiva komponenter. Inledning I det här kapitlet skall du gå igenom de tre viktigaste passiva komponenterna, nämligen motståndet, kondensatorn och spolen. Du frågar dig säkert varför de kallas passiva
~ växelström. växelström 1. Heureka B Natur och Kultur 91-27-56722-2
 ~ växelström Det flyter växelström och inte likström i de flesta elnät världen över! Skälen är många. Hittills har det varit enklare att bygga generatorer som levererar växelspänning. Transport av elenergi
~ växelström Det flyter växelström och inte likström i de flesta elnät världen över! Skälen är många. Hittills har det varit enklare att bygga generatorer som levererar växelspänning. Transport av elenergi
Bra tabell i ert formelblad
 Bra tabell i ert formelblad Vi har gått igenom hur magnetfält alstrar krafter, kap. 7. Vi har gått igenom hur strömmar alstrar magnetfält, kap. 8. Återstår att lära sig hur strömmarna alstras. Tidigare
Bra tabell i ert formelblad Vi har gått igenom hur magnetfält alstrar krafter, kap. 7. Vi har gått igenom hur strömmar alstrar magnetfält, kap. 8. Återstår att lära sig hur strömmarna alstras. Tidigare
Tentamen i El- och vågrörelselära,
 Tentamen i El- och vågrörelselära, 204 08 28. Beräkna den totala kraft på laddningen q = 7.5 nc i origo som orsakas av laddningarna q 2 = 6 nc i punkten x,y) = 5,0) cm och q 3 = 0 nc i x,y) = 3,4) cm.
Tentamen i El- och vågrörelselära, 204 08 28. Beräkna den totala kraft på laddningen q = 7.5 nc i origo som orsakas av laddningarna q 2 = 6 nc i punkten x,y) = 5,0) cm och q 3 = 0 nc i x,y) = 3,4) cm.
Lösningar till Tentamen i fysik B del 1 vid förutbildningar vid Malmö högskola
 Lösningar till Tentamen i fysik B del 1 vid förutbildningar vid Malmö högskola Tid: Måndagen 5/3-2012 kl: 8.15-12.15. Hjälpmedel: Räknedosa. Bifogad formelsamling. Lösningar: Lösningarna skall vara väl
Lösningar till Tentamen i fysik B del 1 vid förutbildningar vid Malmö högskola Tid: Måndagen 5/3-2012 kl: 8.15-12.15. Hjälpmedel: Räknedosa. Bifogad formelsamling. Lösningar: Lösningarna skall vara väl
Sensorer, effektorer och fysik. Grundläggande fysikaliska begrepp som är viktiga inom mättekniken
 Sensorer, effektorer och fysik Grundläggande fysikaliska begrepp som är viktiga inom mättekniken Innehåll Grundläggande begrepp inom mekanik. Elektriskt fält och elektrisk potential. Gauss lag Dielektrika
Sensorer, effektorer och fysik Grundläggande fysikaliska begrepp som är viktiga inom mättekniken Innehåll Grundläggande begrepp inom mekanik. Elektriskt fält och elektrisk potential. Gauss lag Dielektrika
FK Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (1:a omtentan), tisdag 17 juni 2014, kl 9:00-14:00
 FK4010 - Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (1:a omtentan), tisdag 17 juni 2014, kl 9:00-14:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror
FK4010 - Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (1:a omtentan), tisdag 17 juni 2014, kl 9:00-14:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror
Införa begreppen ström, strömtäthet och resistans Ohms lag Tillämpningar på enkla kretsar Energi och effekt i kretsar
 Kapitel: 25 Ström, motstånd och emf (Nu lämnar vi elektrostatiken) Visa under vilka villkor det kan finnas E-fält i ledare Införa begreppet emf (electromotoric force) Beskriva laddningars rörelse i ledare
Kapitel: 25 Ström, motstånd och emf (Nu lämnar vi elektrostatiken) Visa under vilka villkor det kan finnas E-fält i ledare Införa begreppet emf (electromotoric force) Beskriva laddningars rörelse i ledare
Lösningar Heureka 2 Kapitel 7 Harmonisk svängningsrörelse
 Lösningar Heureka Kapitel 7 Harmonisk svängningsrörelse Andreas Josefsson Tullängsskolan Örebro Lo sningar Fysik Heureka Kapitel 7 7.1 a) Av figuren framgår att amplituden är 0,30 m. b) Skuggan utför en
Lösningar Heureka Kapitel 7 Harmonisk svängningsrörelse Andreas Josefsson Tullängsskolan Örebro Lo sningar Fysik Heureka Kapitel 7 7.1 a) Av figuren framgår att amplituden är 0,30 m. b) Skuggan utför en
Svängningar. Innehåll. Inledning. Litteraturhänvisning. Förberedelseuppgifter. Svängningar
 Svängningar Innehåll Inledning Inledning... 1 Litteraturhänvisning... 1 Förberedelseuppgifter... 1 Utförande... 3 Det dämpade men odrivna systemet... 3 Det drivna systemet... 4 Några praktiska tips...
Svängningar Innehåll Inledning Inledning... 1 Litteraturhänvisning... 1 Förberedelseuppgifter... 1 Utförande... 3 Det dämpade men odrivna systemet... 3 Det drivna systemet... 4 Några praktiska tips...
Steget vidare. (By JaunJimenez at English Wikipedia, CC BY 3.0, https://commons.wikimedia.org/w/index.php? curid= )
 Steget vidare I en växelström hoppar elektronerna fram och tillbaka 50 gånger per sekund i Sverige. I andra länder har man andra system. I USA hoppar elektronerna med 60Hz. Man kan även ha andra spänningar.
Steget vidare I en växelström hoppar elektronerna fram och tillbaka 50 gånger per sekund i Sverige. I andra länder har man andra system. I USA hoppar elektronerna med 60Hz. Man kan även ha andra spänningar.
Elektroakustik Något lite om analogier
 Elektroakustik 2003-09-02 10.13 Något lite om analogier Svante Granqvist 2002 Något lite om analogier När man räknar på mekaniska system behöver man ofta lösa differentialekvationer och dessutom tänka
Elektroakustik 2003-09-02 10.13 Något lite om analogier Svante Granqvist 2002 Något lite om analogier När man räknar på mekaniska system behöver man ofta lösa differentialekvationer och dessutom tänka
för gymnasiet Polarisation
 Chalmers tekniska högskola och November 2006 Göteborgs universitet 9 sidor + bilaga Rikard Bergman 1992 Christian Karlsson, Jan Lagerwall 2002 Emma Eriksson 2006 O4 för gymnasiet Polarisation Foton taget
Chalmers tekniska högskola och November 2006 Göteborgs universitet 9 sidor + bilaga Rikard Bergman 1992 Christian Karlsson, Jan Lagerwall 2002 Emma Eriksson 2006 O4 för gymnasiet Polarisation Foton taget
Svar och anvisningar
 160322 BFL102 1 Tenta 160322 Fysik 2: BFL102 Svar och anvisningar Uppgift 1 a) Centripetalkraften ligger i horisontalplanet, riktad in mot cirkelbanans mitt vid B. A B b) En centripetalkraft kan tecknas:
160322 BFL102 1 Tenta 160322 Fysik 2: BFL102 Svar och anvisningar Uppgift 1 a) Centripetalkraften ligger i horisontalplanet, riktad in mot cirkelbanans mitt vid B. A B b) En centripetalkraft kan tecknas:
Motorprincipen. William Sandqvist
 Motorprincipen En strömförande ledare befinner sig i ett magnetfält B (längden l är den del av ledaren som befinner sig i fältet). De magnetiska kraftlinjerna får inte korsa varandra. Fältet förstärks
Motorprincipen En strömförande ledare befinner sig i ett magnetfält B (längden l är den del av ledaren som befinner sig i fältet). De magnetiska kraftlinjerna får inte korsa varandra. Fältet förstärks
IF1330 Ellära KK1 LAB1 KK2 LAB2 KK4 LAB4. tentamen
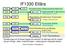 F330 Ellära F/Ö F/Ö4 F/Ö F/Ö5 F/Ö3 Strömkretslära Mätinstrument Batterier Likströmsnät Tvåpolsatsen KK LAB Mätning av och F/Ö6 F/Ö7 Magnetkrets Kondensator Transienter KK LAB Tvåpol mät och sim F/Ö8 F/Ö9
F330 Ellära F/Ö F/Ö4 F/Ö F/Ö5 F/Ö3 Strömkretslära Mätinstrument Batterier Likströmsnät Tvåpolsatsen KK LAB Mätning av och F/Ö6 F/Ö7 Magnetkrets Kondensator Transienter KK LAB Tvåpol mät och sim F/Ö8 F/Ö9
Lösningar Kap 7 Elektrisk energi, spänning och ström. Andreas Josefsson. Tullängsskolan Örebro
 Lösningar Kap 7 Elektrisk energi, spänning och ström Andreas Josefsson Tullängsskolan Örebro Lösningar Fysik 1 Heureka: kap 7 7.1) Om kulan kan "falla" från A till B minskar dess potentiella elektriska
Lösningar Kap 7 Elektrisk energi, spänning och ström Andreas Josefsson Tullängsskolan Örebro Lösningar Fysik 1 Heureka: kap 7 7.1) Om kulan kan "falla" från A till B minskar dess potentiella elektriska
Förslag: En laddad partikel i ett magnetfält påverkas av kraften F = qvb, dvs B = F qv = 0.31 T.
 1. En elektron rör sig med v = 100 000 m/s i ett magnetfält. Den påverkas av en kraft F = 5 10 15 N vinkelrätt mot rörelseriktningen. Rita figur och beräkna den magnetiska flödestätheten. Förslag: En laddad
1. En elektron rör sig med v = 100 000 m/s i ett magnetfält. Den påverkas av en kraft F = 5 10 15 N vinkelrätt mot rörelseriktningen. Rita figur och beräkna den magnetiska flödestätheten. Förslag: En laddad
Tentamen: Baskurs B i Fysik, del1, 4p 2007-03-23 kl. 08.00-13.00
 Institutionen för teknik, fysik och matematik Nils Olander och Herje Westman Tentamen: Baskurs B i Fysik, del1, 4p 2007-03-23 kl. 08.00-13.00 Max: 30 p A-uppgifterna 1-8 besvaras genom att ange det korrekta
Institutionen för teknik, fysik och matematik Nils Olander och Herje Westman Tentamen: Baskurs B i Fysik, del1, 4p 2007-03-23 kl. 08.00-13.00 Max: 30 p A-uppgifterna 1-8 besvaras genom att ange det korrekta
Tentamen i Fysik för M, TFYA72
 Tentamen i Fysik för M, TFYA72 Onsdag 2015-06-10 kl. 8:00-12:00 Tillåtna hjälpmedel: Bifogat formelblad Avprogrammerad räknedosa enlig IFM:s regler. Christopher Tholander kommer att besöka tentamenslokalen
Tentamen i Fysik för M, TFYA72 Onsdag 2015-06-10 kl. 8:00-12:00 Tillåtna hjälpmedel: Bifogat formelblad Avprogrammerad räknedosa enlig IFM:s regler. Christopher Tholander kommer att besöka tentamenslokalen
9. Magnetisk energi Magnetisk energi för en isolerad krets
 9. Magnetisk energi [RM] Elektrodynamik, vt 013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets anod
9. Magnetisk energi [RM] Elektrodynamik, vt 013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets anod
9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1
![9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1](/thumbs/61/46243221.jpg) 9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
Tentamen i El- och vågrörelselära,
 Tentamen i El- och vågrörelselära, 23 2 8 Hjälpmedel: Physics Handbook, räknare. Ensfäriskkopparkulamedradie = 5mmharladdningenQ = 2.5 0 3 C. Beräkna det elektriska fältet som funktion av avståndet från
Tentamen i El- och vågrörelselära, 23 2 8 Hjälpmedel: Physics Handbook, räknare. Ensfäriskkopparkulamedradie = 5mmharladdningenQ = 2.5 0 3 C. Beräkna det elektriska fältet som funktion av avståndet från
Lösningsförslag Inlämningsuppgift 3 Kapacitans, ström, resistans
 Inst. för fysik och astronomi 2017-11-26 1 Lösningsförslag Inlämningsuppgift 3 Kapacitans, ström, resistans Elektromagnetism I, 5 hp, för ES och W (1FA514) höstterminen 2017 (3.1) En plattkondensator har
Inst. för fysik och astronomi 2017-11-26 1 Lösningsförslag Inlämningsuppgift 3 Kapacitans, ström, resistans Elektromagnetism I, 5 hp, för ES och W (1FA514) höstterminen 2017 (3.1) En plattkondensator har
LABKOMPENDIUM Fysik del B1
 LABKOMPENDIUM Fysik del B1 BFL111: Fysik för bastermin BFL122: Fysik B för tekniskt/naturvetenskapligt basår Innehåll Laboration 1: Kretsar och kondensatorer Förberedelseuppgifter 3 Del 1: Plattkondensator
LABKOMPENDIUM Fysik del B1 BFL111: Fysik för bastermin BFL122: Fysik B för tekniskt/naturvetenskapligt basår Innehåll Laboration 1: Kretsar och kondensatorer Förberedelseuppgifter 3 Del 1: Plattkondensator
T1-modulen Lektionerna Radioamatörkurs OH6AG Bearbetning och översättning: Thomas Anderssén, OH6NT Heikki Lahtivirta, OH2LH
 T1-modulen Lektionerna 13-15 Radioamatörkurs - 2011 Bearbetning och översättning: Thomas Anderssén, OH6NT Original: Heikki Lahtivirta, OH2LH 1 Spolar gör större motstånd ju högre strömmens frekvens är,
T1-modulen Lektionerna 13-15 Radioamatörkurs - 2011 Bearbetning och översättning: Thomas Anderssén, OH6NT Original: Heikki Lahtivirta, OH2LH 1 Spolar gör större motstånd ju högre strömmens frekvens är,
9. Magnetisk energi Magnetisk energi för en isolerad krets
 9. Magnetisk energi [RMC] Elektrodynamik, ht 005, Krister Henriksson 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
9. Magnetisk energi [RMC] Elektrodynamik, ht 005, Krister Henriksson 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
IE1206 Inbyggd Elektronik
 IE1206 Inbyggd Elektronik F1 F3 F4 F2 Ö1 Ö2 PIC-block Dokumentation, Seriecom Pulsgivare I, U, R, P, serie och parallell KK1 LAB1 Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchoffs
IE1206 Inbyggd Elektronik F1 F3 F4 F2 Ö1 Ö2 PIC-block Dokumentation, Seriecom Pulsgivare I, U, R, P, serie och parallell KK1 LAB1 Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchoffs
Tentamen ellära 92FY21 och 27
 Tentamen ellära 92FY21 och 27 2014-06-04 kl. 8 13 Svaren anges på separat papper. Fullständiga lösningar med alla steg motiverade och beteckningar utsatta ska redovisas för att få full poäng. Poängen för
Tentamen ellära 92FY21 och 27 2014-06-04 kl. 8 13 Svaren anges på separat papper. Fullständiga lösningar med alla steg motiverade och beteckningar utsatta ska redovisas för att få full poäng. Poängen för
4:2 Ellära: ström, spänning och energi. Inledning
 4:2 Ellära: ström, spänning och energi. Inledning Det samhälle vi lever i hade inte utvecklats till den höga standard som vi ser nu om inte vi hade lärt oss att utnyttja elektricitet. Därför är det viktigt
4:2 Ellära: ström, spänning och energi. Inledning Det samhälle vi lever i hade inte utvecklats till den höga standard som vi ser nu om inte vi hade lärt oss att utnyttja elektricitet. Därför är det viktigt
Elektriska och elektroniska fordonskomponenter. Föreläsning 4 & 5
 Elektriska och elektroniska fordonskomponenter Föreläsning 4 & 5 Kondensatorn För att lagra elektrisk laddning Användning Att skydda brytarspetsarna (laddas upp istället för att gnistan bildas) I datorminnen
Elektriska och elektroniska fordonskomponenter Föreläsning 4 & 5 Kondensatorn För att lagra elektrisk laddning Användning Att skydda brytarspetsarna (laddas upp istället för att gnistan bildas) I datorminnen
BFL102/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik mars :00 12:00. Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
 Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm BFL102/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik 2 17 mars 2017 8:00 12:00 Tentamen består av 6 uppgifter som vardera kan ge upp till 4
Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm BFL102/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik 2 17 mars 2017 8:00 12:00 Tentamen består av 6 uppgifter som vardera kan ge upp till 4
Chalmers Tekniska Högskola Tillämpad Fysik Igor Zoric
 Chalmers Tekniska Högskola 2002 05 28 Tillämpad Fysik Igor Zoric Tentamen i Fysik för Ingenjörer 2 Elektricitet, Magnetism och Optik Tid och plats: Tisdagen den 28/5 2002 kl 8.45-12.45 i V-huset Examinator:
Chalmers Tekniska Högskola 2002 05 28 Tillämpad Fysik Igor Zoric Tentamen i Fysik för Ingenjörer 2 Elektricitet, Magnetism och Optik Tid och plats: Tisdagen den 28/5 2002 kl 8.45-12.45 i V-huset Examinator:
FK Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (1:a omtentan), tisdag 16 juni 2015, kl 9:00-14:00
 FK4010 - Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (1:a omtentan), tisdag 16 juni 2015, kl 9:00-14:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror
FK4010 - Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (1:a omtentan), tisdag 16 juni 2015, kl 9:00-14:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror
IE1206 Inbyggd Elektronik
 IE1206 Inbyggd Elektronik F1 F3 F4 F2 Ö1 Ö2 PIC-block Dokumentation, Seriecom Pulsgivare I, U, R, P, serie och parallell KK1 LAB1 Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchhoffs
IE1206 Inbyggd Elektronik F1 F3 F4 F2 Ö1 Ö2 PIC-block Dokumentation, Seriecom Pulsgivare I, U, R, P, serie och parallell KK1 LAB1 Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchhoffs
Prov Fysik B Lösningsförslag
 Prov Fysik B Lösningsförslag DEL I 1. Högerhandsregeln ger ett cirkulärt magnetfält med riktning medurs. Kompass D är därför korrekt. 2. Orsaken till den i spolen inducerade strömmen kan ses som stavmagnetens
Prov Fysik B Lösningsförslag DEL I 1. Högerhandsregeln ger ett cirkulärt magnetfält med riktning medurs. Kompass D är därför korrekt. 2. Orsaken till den i spolen inducerade strömmen kan ses som stavmagnetens
Elektro och Informationsteknik LTH. Laboration 3 RC- och RL-nät i tidsplanet. Elektronik för D ETIA01
 Elektro och Informationsteknik LTH Laboration 3 R- och RL-nät i tidsplanet Elektronik för D ETIA01??? Telmo Santos Anders J Johansson Lund Februari 2008 Laboration 3 Mål Efter laborationen vill vi att
Elektro och Informationsteknik LTH Laboration 3 R- och RL-nät i tidsplanet Elektronik för D ETIA01??? Telmo Santos Anders J Johansson Lund Februari 2008 Laboration 3 Mål Efter laborationen vill vi att
Föreläsning 17: Jämviktsläge för flexibla system
 1 KOMIHÅG 16: --------------------------------- Ellipsbanans storaxel och mekaniska energin E = " mgm 2a ------------------------------------------------------ Föreläsning 17: Jämviktsläge för flexibla
1 KOMIHÅG 16: --------------------------------- Ellipsbanans storaxel och mekaniska energin E = " mgm 2a ------------------------------------------------------ Föreläsning 17: Jämviktsläge för flexibla
Koppla spänningsproben till spolen.
 LÄRARHANDLEDNING Induktion Materiel: Utförande: Dator med programmet LoggerPro Mätinterfacet LabQuest eller LabPro spänningsprobe spolar (300, 600 och 1200 varv), stavmagnet plaströr och kopparrör (ca
LÄRARHANDLEDNING Induktion Materiel: Utförande: Dator med programmet LoggerPro Mätinterfacet LabQuest eller LabPro spänningsprobe spolar (300, 600 och 1200 varv), stavmagnet plaströr och kopparrör (ca
Elektricitetslära och magnetism - 1FY808. Lab 3 och Lab 4
 Linnéuniversitetet Institutionen för fysik och elektroteknik Elektricitetslära och magnetism - 1FY808 Lab 3 och Lab 4 Ditt namn:... eftersom labhäften far runt i labsalen. 1 Laboration 3: Likström och
Linnéuniversitetet Institutionen för fysik och elektroteknik Elektricitetslära och magnetism - 1FY808 Lab 3 och Lab 4 Ditt namn:... eftersom labhäften far runt i labsalen. 1 Laboration 3: Likström och
Q I t. Ellära 2 Elektrisk ström, kap 23. Eleonora Lorek. Ström. Ström är flöde av laddade partiklar.
 Ellära 2 Elektrisk ström, kap 23 Eleonora Lorek Ström Ström är flöde av laddade partiklar. Om vi har en potentialskillnad, U, mellan två punkter och det finns en lämplig väg rör sig laddade partiklar i
Ellära 2 Elektrisk ström, kap 23 Eleonora Lorek Ström Ström är flöde av laddade partiklar. Om vi har en potentialskillnad, U, mellan två punkter och det finns en lämplig väg rör sig laddade partiklar i
Svar och anvisningar
 170317 BFL10 1 Tenta 170317 Fysik : BFL10 Svar och anvisningar Uppgift 1 a) Den enda kraft som verkar på stenen är tyngdkraften, och den är riktad nedåt. Alltså är accelerationen riktad nedåt. b) Vid kaströrelse
170317 BFL10 1 Tenta 170317 Fysik : BFL10 Svar och anvisningar Uppgift 1 a) Den enda kraft som verkar på stenen är tyngdkraften, och den är riktad nedåt. Alltså är accelerationen riktad nedåt. b) Vid kaströrelse
LÄRARHANDLEDNING Harmonisk svängningsrörelse
 LÄRARHANDLEDNING Harmonisk svängningsrörelse Utrustning: Dator med programmet LoggerPro LabQuest eller LabPro Avståndsmätare Kraftgivare Spiralfjäder En vikt Stativmateriel Kraftgivare Koppla mätvärdesinsamlaren
LÄRARHANDLEDNING Harmonisk svängningsrörelse Utrustning: Dator med programmet LoggerPro LabQuest eller LabPro Avståndsmätare Kraftgivare Spiralfjäder En vikt Stativmateriel Kraftgivare Koppla mätvärdesinsamlaren
Andra ordningens kretsar
 Andra ordningens kretsar Svängningskretsar LCR-seriekrets U L (t) U s U c (t) U R (t) L di(t) dt + Ri(t) + 1 C R t0 i(t)dt + u c (0) = U s LCR-seriekrets För att undvika integralen i ekvationen, så deriverar
Andra ordningens kretsar Svängningskretsar LCR-seriekrets U L (t) U s U c (t) U R (t) L di(t) dt + Ri(t) + 1 C R t0 i(t)dt + u c (0) = U s LCR-seriekrets För att undvika integralen i ekvationen, så deriverar
10. Kretsar med långsamt varierande ström
 1. Kretsar med långsamt varierande ström [RMC] Elektrodynamik, ht 25, Krister Henriksson 1.1 1.1. Villkor för långsamt varierande I detta kapitel behandlas den teori som kan användas för att analysera
1. Kretsar med långsamt varierande ström [RMC] Elektrodynamik, ht 25, Krister Henriksson 1.1 1.1. Villkor för långsamt varierande I detta kapitel behandlas den teori som kan användas för att analysera
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER
 EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
Hjälpmedel: Grafritande miniräknare, gymnasieformelsamling, linjal och gradskiva
 Fysik Bas 2 Provmoment: Ladokkod: Tentamen ges för: KBAST17h KBASX17h 9 högskolepoäng Tentamensdatum: 2018-05-28 Tid: 09:00-13:00 Hjälpmedel: Grafritande miniräknare, gymnasieformelsamling, linjal och
Fysik Bas 2 Provmoment: Ladokkod: Tentamen ges för: KBAST17h KBASX17h 9 högskolepoäng Tentamensdatum: 2018-05-28 Tid: 09:00-13:00 Hjälpmedel: Grafritande miniräknare, gymnasieformelsamling, linjal och
Övningsuppgifter/repetition inom elektromagnetism + ljus (OBS: ej fullständig)
 Övningsuppgifter/repetition inom elektromagnetism + ljus (OBS: ej fullständig) Elektrostatik 1. Ange Faradays lag i elektrostatiken. 2. Vad är kravet för att ett vektorfält F är konservativt? 3. En låda
Övningsuppgifter/repetition inom elektromagnetism + ljus (OBS: ej fullständig) Elektrostatik 1. Ange Faradays lag i elektrostatiken. 2. Vad är kravet för att ett vektorfält F är konservativt? 3. En låda
1.3 Uppkomsten av mekanisk vågrörelse
 1.3 Uppkomsten av mekanisk vågrörelse För att en mekanisk vågrörelse skall kunna uppstå, behövs ett medium, något som rörelsen kan framskrida i. Det kan vara vatten, luft, ett bord, jordskorpan, i princip
1.3 Uppkomsten av mekanisk vågrörelse För att en mekanisk vågrörelse skall kunna uppstå, behövs ett medium, något som rörelsen kan framskrida i. Det kan vara vatten, luft, ett bord, jordskorpan, i princip
Spänning, ström och energi!
 Spänning, ström och energi! Vi lever i ett samhälle som inte hade haft den höga standard som vi har nu om inte vi hade lärt oss att utnyttja elektricitet. Därför är det viktigt att lära sig förstå några
Spänning, ström och energi! Vi lever i ett samhälle som inte hade haft den höga standard som vi har nu om inte vi hade lärt oss att utnyttja elektricitet. Därför är det viktigt att lära sig förstå några
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 14 Harmonisk oscillator 1 Vågrörelselära och optik 2 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator:
Vågrörelselära och optik Kapitel 14 Harmonisk oscillator 1 Vågrörelselära och optik 2 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator:
Elektriska komponenter och kretsar. Emma Björk
 Elektriska komponenter och kretsar Emma Björk Elektromotorisk kraft Den mekanism som alstrar det E-fält som driver runt laddningarna i en sluten krets kallas emf(electro Motoric Force trots att det ej
Elektriska komponenter och kretsar Emma Björk Elektromotorisk kraft Den mekanism som alstrar det E-fält som driver runt laddningarna i en sluten krets kallas emf(electro Motoric Force trots att det ej
Växelström K O M P E N D I U M 2 ELEKTRO
 MEÅ NIVERSITET Tillämpad fysik och elektronik Sverker Johansson Johan Pålsson 999-09- Rev.0 Växelström K O M P E N D I M ELEKTRO INNEHÅLL. ALLMÄNT OM LIK- OCH VÄXELSPÄNNINGAR.... SAMBANDET MELLAN STRÖM
MEÅ NIVERSITET Tillämpad fysik och elektronik Sverker Johansson Johan Pålsson 999-09- Rev.0 Växelström K O M P E N D I M ELEKTRO INNEHÅLL. ALLMÄNT OM LIK- OCH VÄXELSPÄNNINGAR.... SAMBANDET MELLAN STRÖM
Vågor. En våg är en störning som utbreder sig En våg överför energi från en plats till en annan. Det sker ingen masstransport
 Vågor En våg är en störning som utbreder sig En våg överför energi från en plats till en annan. Det sker ingen masstransport Vågtyper Transversella Mediets partiklar rör sig vinkelrätt mot vågens riktning.
Vågor En våg är en störning som utbreder sig En våg överför energi från en plats till en annan. Det sker ingen masstransport Vågtyper Transversella Mediets partiklar rör sig vinkelrätt mot vågens riktning.
 IN Inst. för Fysik och materialvetenskap ---------------------------------------------------------------------------------------------- INSTRUKTION TILL LABORATIONEN INDUKTION ---------------------------------------------------------------------------------------------
IN Inst. för Fysik och materialvetenskap ---------------------------------------------------------------------------------------------- INSTRUKTION TILL LABORATIONEN INDUKTION ---------------------------------------------------------------------------------------------
Sensorer och elektronik. Grundläggande ellära
 Sensorer och elektronik Grundläggande ellära Innehåll Grundläggande begrepp inom mekanik Elektriskt fält och elektrisk potential Dielektrika och kapacitans Ström och strömtäthet Ohms lag och resistans
Sensorer och elektronik Grundläggande ellära Innehåll Grundläggande begrepp inom mekanik Elektriskt fält och elektrisk potential Dielektrika och kapacitans Ström och strömtäthet Ohms lag och resistans
Elektricitetslära och magnetism - 1FY808
 Linnéuniversitetet Institutionen för datavetenskap, fysik och matematik Laborationshäfte för kursen Elektricitetslära och magnetism - 1FY808 Ditt namn:... eftersom labhäften far runt i labsalen. 1 1. Instrumentjämförelse
Linnéuniversitetet Institutionen för datavetenskap, fysik och matematik Laborationshäfte för kursen Elektricitetslära och magnetism - 1FY808 Ditt namn:... eftersom labhäften far runt i labsalen. 1 1. Instrumentjämförelse
Räkneuppgifter på avsnittet Fält Tommy Andersson
 Räkneuppgifter på avsnittet Fält Tommy Andersson 1. En negativt laddad pappersbit befinner sig nära en oladdad metallplåt. Får man attraktion, repulsion eller ingen kraftpåverkan? Motivera! 2. På ett mönsterkort
Räkneuppgifter på avsnittet Fält Tommy Andersson 1. En negativt laddad pappersbit befinner sig nära en oladdad metallplåt. Får man attraktion, repulsion eller ingen kraftpåverkan? Motivera! 2. På ett mönsterkort
Fysik. Laboration 3. Ljusets vågnatur
 Fysik Laboration 3 Ljusets vågnatur Laborationens syfte: att hjälpa dig att förstå ljusfenomen diffraktion och interferens och att förstå hur olika typer av spektra uppstår Utförande: laborationen skall
Fysik Laboration 3 Ljusets vågnatur Laborationens syfte: att hjälpa dig att förstå ljusfenomen diffraktion och interferens och att förstå hur olika typer av spektra uppstår Utförande: laborationen skall
IE1206 Inbyggd Elektronik
 E6 nbyggd Elektronik F F3 F4 F Ö Ö P-block Dokumentation, Seriecom Pulsgivare,,, P, serie och parallell KK AB Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchhoffs lagar Nodanalys Tvåpolsatsen
E6 nbyggd Elektronik F F3 F4 F Ö Ö P-block Dokumentation, Seriecom Pulsgivare,,, P, serie och parallell KK AB Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchhoffs lagar Nodanalys Tvåpolsatsen
Föreläsning 8. Ohms lag (Kap. 7.1) 7.1 i Griffiths
 1 Föreläsning 8 7.1 i Griffiths Ohms lag (Kap. 7.1) i är bekanta med Ohms lag i kretsteori som = RI. En mer generell framställning är vårt mål här. Sambandet mellan strömtätheten J och den elektriska fältstyrkan
1 Föreläsning 8 7.1 i Griffiths Ohms lag (Kap. 7.1) i är bekanta med Ohms lag i kretsteori som = RI. En mer generell framställning är vårt mål här. Sambandet mellan strömtätheten J och den elektriska fältstyrkan
1 Grundläggande Ellära
 1 Grundläggande Ellära 1.1 Elektriska begrepp 1.1.1 Ange för nedanstående figur om de markerade delarna av kretsen är en nod, gren, maska eller slinga. 1.2 Kretslagar 1.2.1 Beräknar spänningarna U 1 och
1 Grundläggande Ellära 1.1 Elektriska begrepp 1.1.1 Ange för nedanstående figur om de markerade delarna av kretsen är en nod, gren, maska eller slinga. 1.2 Kretslagar 1.2.1 Beräknar spänningarna U 1 och
IDE-sektionen. Laboration 5 Växelströmsmätningar
 9428 IDEsektionen Laboration 5 Växelströmsmätningar 1 Förberedelseuppgifter laboration 4 1. Antag att vi mäter spänningen över en okänd komponent resultatet blir u(t)= 3sin(ωt) [V]. Motsvarande ström är
9428 IDEsektionen Laboration 5 Växelströmsmätningar 1 Förberedelseuppgifter laboration 4 1. Antag att vi mäter spänningen över en okänd komponent resultatet blir u(t)= 3sin(ωt) [V]. Motsvarande ström är
RC-kretsar, transienta förlopp
 13 maj 2013 Labinstruktion: RC-kretsar, magnetiska fält och induktion Ellära, 92FY21/27 1(5) RC-kretsar, transienta förlopp I den här laborationen kommer du att titta på urladdning av en RC-krets och hur
13 maj 2013 Labinstruktion: RC-kretsar, magnetiska fält och induktion Ellära, 92FY21/27 1(5) RC-kretsar, transienta förlopp I den här laborationen kommer du att titta på urladdning av en RC-krets och hur
r 2 Arbetet är alltså endast beroende av start- och slutpunkt. Det följer av att det elektriska fältet är konservativt ( E = 0).
 1 Föreläsning 2 Motsvarar avsnitten 2.4 2.5 i Griffiths. Arbete och potentiell energi (Kap. 2.4) r 1 r 2 C Låt W vara det arbete som måste utföras mot ett givet elektriskt fält E, då en laddning Q flyttas
1 Föreläsning 2 Motsvarar avsnitten 2.4 2.5 i Griffiths. Arbete och potentiell energi (Kap. 2.4) r 1 r 2 C Låt W vara det arbete som måste utföras mot ett givet elektriskt fält E, då en laddning Q flyttas
Uppgift 1: När går en glödlampa sönder?
 Uppgift 1: När går en glödlampa sönder? Materiel: Glödlampa, strömkälla, motstånd samt dator försedd med analog/digital omvandlare och tillhörande programvara för datainsamling. Beskrivning: Kanske tycker
Uppgift 1: När går en glödlampa sönder? Materiel: Glödlampa, strömkälla, motstånd samt dator försedd med analog/digital omvandlare och tillhörande programvara för datainsamling. Beskrivning: Kanske tycker
Tenta svar. E(r) = E(r)ˆr. Vi tillämpar Gauss sats på de tre områdena och väljer integrationsytan S till en sfär med radie r:
 Tenta 56 svar Uppgift a) På grund av sfäriskt symmetri ansätter vi att: E(r) = E(r)ˆr Vi tillämpar Gauss sats på de tre områdena och väljer integrationsytan S till en sfär med radie r: 2π π Q innesluten
Tenta 56 svar Uppgift a) På grund av sfäriskt symmetri ansätter vi att: E(r) = E(r)ˆr Vi tillämpar Gauss sats på de tre områdena och väljer integrationsytan S till en sfär med radie r: 2π π Q innesluten
IE1206 Inbyggd Elektronik
 E06 nbyggd Elektronik F F3 F4 F Ö Ö P-block Dokumentation, Seriecom Pulsgivare,,, P, serie och parallell KK AB Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchhoffs lagar Nodanalys Tvåpolsatsen
E06 nbyggd Elektronik F F3 F4 F Ö Ö P-block Dokumentation, Seriecom Pulsgivare,,, P, serie och parallell KK AB Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchhoffs lagar Nodanalys Tvåpolsatsen
Kaströrelse. 3,3 m. 1,1 m
 Kaströrelse 1. En liten kula, som vi kallar kula 1, släpps ifrån en höjd över marken. Exakt samtidigt skjuts kula 2 parallellt med marken ifrån samma höjd som kula 1. Luftmotståndet som verkar på kulorna
Kaströrelse 1. En liten kula, som vi kallar kula 1, släpps ifrån en höjd över marken. Exakt samtidigt skjuts kula 2 parallellt med marken ifrån samma höjd som kula 1. Luftmotståndet som verkar på kulorna
Tentamen Modellering och simulering inom fältteori, 21 oktober, 2006
 Institutionen för elektrovetenskap Tentamen Modellering och simulering inom fältteori, oktober, 006 Tillåtna hjälpmedel: Formelsamling i Elektromagnetisk fältteori Varje uppgift ger 0 poäng. Delbetyget
Institutionen för elektrovetenskap Tentamen Modellering och simulering inom fältteori, oktober, 006 Tillåtna hjälpmedel: Formelsamling i Elektromagnetisk fältteori Varje uppgift ger 0 poäng. Delbetyget
Vi börjar med en vanlig ledare av koppar.
 Vi börjar med en vanlig ledare av koppar. [Från Wikipedia] Skineffekt är tendensen hos en växelström (AC) att omfördela sig inom en elektrisk ledare så att strömtätheten är störst nära ledarens yta, och
Vi börjar med en vanlig ledare av koppar. [Från Wikipedia] Skineffekt är tendensen hos en växelström (AC) att omfördela sig inom en elektrisk ledare så att strömtätheten är störst nära ledarens yta, och
Hur funkar 3D bio? Laborationsrapporter Se efter om ni har fått tillbaka dem och om de är godkända!
 Hur funkar 3D bio? Laborationsrapporter Se efter om ni har fått tillbaka dem och om de är godkända! Sista dag för godkännande av laborationer är torsdagen den 10/6 2015 Räknestuga Förra veckan kapitel
Hur funkar 3D bio? Laborationsrapporter Se efter om ni har fått tillbaka dem och om de är godkända! Sista dag för godkännande av laborationer är torsdagen den 10/6 2015 Räknestuga Förra veckan kapitel
Ellära och Elektronik Moment AC-nät Föreläsning 4
 Ellära och Elektronik Moment AC-nät Föreläsning 4 Kapacitans och Indktans Uppladdning av en kondensator Medelvärde och Effektivvärde Sinsvåg över kondensator och spole Copyright 8 Börje Norlin Kondensatorer
Ellära och Elektronik Moment AC-nät Föreläsning 4 Kapacitans och Indktans Uppladdning av en kondensator Medelvärde och Effektivvärde Sinsvåg över kondensator och spole Copyright 8 Börje Norlin Kondensatorer
ETEF15 Krets- och mätteknik, fk Fältteori och EMC föreläsning 3
 ETEF15 Krets- och mätteknik, fk Fältteori och EMC föreläsning 3 Daniel Sjöberg daniel.sjoberg@eit.lth.se Institutionen for Elektro- och informationsteknik Lunds universitet Oktober 2013 Outline 1 Introduktion
ETEF15 Krets- och mätteknik, fk Fältteori och EMC föreläsning 3 Daniel Sjöberg daniel.sjoberg@eit.lth.se Institutionen for Elektro- och informationsteknik Lunds universitet Oktober 2013 Outline 1 Introduktion
2. Mekaniska vågrörelser i en dimension
 2. Mekaniska vågrörelser i en dimension Reflexion Även om alla vågrörelser kan beskrivas med begreppen och, för de flesta naturligt förekommande vågorna, de matematiska uttrycken introducerade i kapitel
2. Mekaniska vågrörelser i en dimension Reflexion Även om alla vågrörelser kan beskrivas med begreppen och, för de flesta naturligt förekommande vågorna, de matematiska uttrycken introducerade i kapitel
Upp gifter I=2,3 A. B=37 mt. I=1,9 A B=37 mt. B=14 mt I=4,7 A
 Upp gifter 1. Beskriv den magnetiska kraften som verkar på ledaren, både till storlek och till riktning. Den del av ledaren som är inne i magnetfältet kan antas vara 45 cm i samtliga fall. a. b. I=1,9
Upp gifter 1. Beskriv den magnetiska kraften som verkar på ledaren, både till storlek och till riktning. Den del av ledaren som är inne i magnetfältet kan antas vara 45 cm i samtliga fall. a. b. I=1,9
Fysikum Kandidatprogrammet FK VT16 DEMONSTRATIONER MAGNETISM II. Helmholtzspolen Elektronstråle i magnetfält Bestämning av e/m
 DEMONSTRATIONER MAGNETISM II Helmholtzspolen Elektronstråle i magnetfält Bestämning av e/m Uppdaterad den 10 november 015 Introduktion I litteraturen och framför allt på webben kan du enkelt hitta ett
DEMONSTRATIONER MAGNETISM II Helmholtzspolen Elektronstråle i magnetfält Bestämning av e/m Uppdaterad den 10 november 015 Introduktion I litteraturen och framför allt på webben kan du enkelt hitta ett
Laboration Photovoltic Effect Diode IV -Characteristics Solide State Physics. 16 maj 2005
 Laboration Photovoltic Effect Diode I -Characteristics Solide State Physics Farid Bonawiede Michael Litton Johan Mörtberg fabo2@kth.se litton@kth.se jmor2@kth.se 16 maj 25 1 I denna laboration ska vi förklara
Laboration Photovoltic Effect Diode I -Characteristics Solide State Physics Farid Bonawiede Michael Litton Johan Mörtberg fabo2@kth.se litton@kth.se jmor2@kth.se 16 maj 25 1 I denna laboration ska vi förklara
FK Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (2:a omtentan), fredag 30 augusti 2013, kl 9:00-14:00
 FK4010 - Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (2:a omtentan), fredag 30 augusti 2013, kl 9:00-14:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror
FK4010 - Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (2:a omtentan), fredag 30 augusti 2013, kl 9:00-14:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror
Tentamen eem076 Elektriska Kretsar och Fält, D1
 Tentamen eem076 Elektriska Kretsar och Fält, D1 Examinator: Ants R. Silberberg 21 maj 2012 kl. 08.30-12.30, sal: M Förfrågningar: Ants Silberberg, tel. 1808 Lösningar: Anslås tisdagen den 22 maj på institutionens
Tentamen eem076 Elektriska Kretsar och Fält, D1 Examinator: Ants R. Silberberg 21 maj 2012 kl. 08.30-12.30, sal: M Förfrågningar: Ants Silberberg, tel. 1808 Lösningar: Anslås tisdagen den 22 maj på institutionens
Föreläsning 3/12. Transienter. Hambley avsnitt
 1 Föreläsning 3/1 Hambley avsnitt 4.1 4.4 Transienter Inom elektroniken betecknar transienter signaler som har kort varaktighet. Transienterna avtar ofta exponentiellt med tiden. I detta avsnitt studerar
1 Föreläsning 3/1 Hambley avsnitt 4.1 4.4 Transienter Inom elektroniken betecknar transienter signaler som har kort varaktighet. Transienterna avtar ofta exponentiellt med tiden. I detta avsnitt studerar
LABORATION 3. Växelström
 Chalmers Tekniska Högskola november 01 Fysik 14 sidor Kurs: Elektrisk mätteknik och vågfysik. FFY616 LABORATION 3 Växelström Växelströmskretsar (seriekoppling), Serieresonans. Förberedelse: i) Läs noggrant
Chalmers Tekniska Högskola november 01 Fysik 14 sidor Kurs: Elektrisk mätteknik och vågfysik. FFY616 LABORATION 3 Växelström Växelströmskretsar (seriekoppling), Serieresonans. Förberedelse: i) Läs noggrant
