interferens och diffraktion
|
|
|
- Ingegerd Jonasson
- för 8 år sedan
- Visningar:
Transkript
1 Kapitel 1. Vågrörelselära: interferens och diffraktion [Understanding physics: , , 12.15] Som en inledning till den moderna fysiken skall vi studera hur två vågrörelser påverkar varandra. Detta sker med hjälp av den s.k. superpositionsprincipen, som säger att om ett medium störs av två växelverkande vågrörelser, så är den totala störningen som åstadkoms lika med den algebraiska summan av de störningar, som vågrörelserna åstadkommer var för sig. Då två vågrörelser y 1 (x, t) och y 2 (x, t) superponeras, blir alltså den totala störningen y(x, t) = y 1 (x, t) + y 2 (x, t). Den moderna fysikens grunder, Tom Sundius
2 1.1. Interferens mellan vågor Om vi låter två identiska sinusformiga vågor som är i fas interferera, så kommer summeringen av vågorna att ge upphov till en ny sinusvåg med samma frekvens, men dubbelt så stor amplitud. Detta kallas för konstruktiv interferens. Om de två sinusvågorna är identiska, men har fasskillnaden π (=180 ), så kommer de att ta ut varandra, och ger då inte upphov till någon störning. Detta fenomen kallar vi destruktiv interferens. Observera att destruktiv interferens kan inträffa, om vågrörelsernas källor S 1 och S 2 oscillerar i fas (dvs de har samma värde av fasvinkeln φ då t = 0), men är förskjutna en halv våglängd i förhållande till varandra. En våg som utsänds från S 2 är då ur fas med beloppet π då den når fram till S 1. Typen av interferens är därför beroende av fasskillnaden mellan vågorna i den punkt där de superponeras. De båda källorna S 1 och S 2 och punkten P där deras växelverkan observeras behöver inte befinna sig på samma räta linje. Vår beskrivning av interferensfenomenet kan alltså lätt utsträckas till två dimensioner. Typen av interferens bestäms av den extra vägsträcka x 2 x 1 som vågorna måste färdas från S 2 innan de når P. Den moderna fysikens grunder, Tom Sundius
3 Låt oss nu för enkelhetens skull anta att de båda källorna S 1 och S 2 har samma amplitud, frekvens och fas (synkrona källor). Störningarna, som vågorna från S 1 och S 2 alstrar i punkten P kan då beskrivas med två gående vågor: y 1 = A sin(kx 1 ωt + φ) Av superpositionsprincipen följer då y 2 = A sin(kx 2 ωt + φ). y = y 1 + y 2 = A[sin(kx 1 ωt + φ) + sin(kx 2 ωt + φ)], som med hjälp av den trigonometriska identiteten sin α + sin β = 2 sin[(α + β)/2] cos[(α β)/2] kan skrivas y = 2A sin k(x1 + x 2 ) 2 Vi skall nu behandla två specialfall: ωt + φ cos k(x1 x 2 ). 2 a) Vägskillnaden är ett heltaligt antal våglängder, dvs (x 2 x 1 ) = nλ = 2πn/k, n = 0, 1, 2,.... Då är x 2 = x 1 + 2πn/k (x 1 + x 2 ) = 2x 1 + 2πn/k k[(x 1 + x 2 )/2] = kx 1 + nπ. Ekvationens sinuskomponent är alltså sin(kx 1 ωt + φ + nπ) = ± sin(kx 1 ωt + φ), där plustecknet gäller om n är jämnt, och minustecknet i motsatt fall. Den moderna fysikens grunder, Tom Sundius
4 Cosinuskomponenten av den totala störningen kan i sin tur uttryckas som cos[k(x 1 x 2 )/2] = cos( nπ). Om n är udda, så blir uttrycket +1, och då n är jämnt, så blir det 1. Ekvationen för den totala störningen blir alltså y = 2A sin(kx 1 ωt + φ) = 2y 1, som beskriver en gående våg med dubbelt så stor amplitud som en av de ursprungliga vågorna. I a) fallet får vi alltså konstruktiv interferens. b) Vägskillnaden är ett halvtaligt antal våglängder. I detta fall gäller (x 2 x 1 ) = (2n+1)λ/2 = (2n+ 1)π/k, n = 0, 1, 2,..., som leder till cos[k(x 1 x 2 )/2] = cos{ [(k/2)(2n + 1)π/k]} = cos{ [(2n + 1)π/2]} = 0. Således gäller alltid y = 0, och vi får destruktiv interferens i b) fallet. Ekvationen för den totala störningen y kan också skrivas y = A sin[k(x 1 + x 2 )/2 ωt + φ], som är en gående våg med variabel amplitud: A = 2A cos[k(x 1 x 2 )/2]. Eftersom vågens intensitet är proportionell mot kvadraten på amplituden, kommer den att variera som en cos 2 funktion av vägskillnaden (x 1 x 2 ). Man kommer därför att se alternerande intensitetsmaxima och minima (ett interferensmönster), som är typiskt för interferens mellan vågor. Den moderna fysikens grunder, Tom Sundius
5 Ljus, liksom elektromagnetisk strålning i allmänhet, har typiska vågegenskaper, såsom frekvens, våglängd, amplitud och fas. Man skulle därför vänta sig att se ett interferensmönster på en skärm som belyses av två ljuskällor. Detta sker dock endast om man kan kontrollera ljuskällans fas, som t.ex. i en laser, som alltid ger koherent ljus. Men man kan också konstruera två källor som oscillerar i fas utgående från en enda ljuskälla, om man låter ljuset gå genom två spalter på samma avstånd från källan, innan det träffar skärmen. Dessa sekundära ljuskällor är i fas (koherenta) och kan producera interferens. Fasskillnaden mellan vågorna bestäms av vägskillnaden mellan de sekundära källorna, och fasskillnaden i en given punkt är därför bestämd. Med hjälp av två spalter kan man alltså producera koherenta vågor och observera interferens, ett fenomen som upptäcktes av engelsmannen Thomas Young i början av 1800 talet. Den moderna fysikens grunder, Tom Sundius
6 1.2. Diffraktion och upplösningsförmåga Interferens kan också uppstå mellan vågor som kommer från olika punkter på samma vågfront. Detta fenomen kallas för diffraktion. Även om vi vanligen behandlar ljusvågor, är det skäl att minnas att diffraktion kan uppträda vid alla typer av vågrörelse. Vi ska betrakta en plan våg som infaller vinkelrätt mot en avlång spalt med bredden a. För att studera diffraktionen i spalten tänker oss vågfronten uppdelad på N delar, var och en med bredden a/n. Enligt Huygens princip kommer varje del att fungera som en självständig källa. Vi skall betrakta superposition av vågor från två närliggande delar S 1 och S 2, som betraktas under vinkeln θ i förhållande till den infallande vågens riktning. Den moderna fysikens grunder, Tom Sundius
7 Vägskillnaden mellan vågkammarna från S 1 och S 2 är (a/n) sin θ som synes av figuren. I föregående avsnitt såg vi att en vägskillnad av en våglängd (λ) mellan två vågkammar svarar mot fasdifferensen 2π. Vägskillnaden (a/n) sin θ svarar därför mot fasdifferensen N φ = 2πa sin θ λ Vi skall nu försöka superponera N vågor med lika stora amplituder A men med fasvinklar som växer med beloppet φ från den ena vågen till den andra. Metoden som används kallas addition av fasvektorer (en fasvektor är ett komplext tal som representerar både amplitud och fas av en sinuskurva). Den moderna fysikens grunder, Tom Sundius
8 Med hjälp av denna metod kan vi beräkna resultatet av att superponera två vågor med amplituderna A 1 och A 2, som skiljer sig i fas med beloppet φ. Man kan representera vågamplituderna med två vektorer A 1 och A 2 med den mellanliggande vinkeln φ. Resultatet av superpositionen ges av resultantvektorn A 1 + A 2. På samma sätt fås resultatet av att superponera N vågor med lika stor amplitud A men med fasvinklar som växer med beloppet φ genom att konstruera en vektorbåge. Om N får växa mot oändligheten övergår vektorbågen till en cirkelbåge, där resultantvektorn är en korda. Fasdifferensen 2α mellan den första och N:te spaltdelen ges av vinkeln mellan tangenterna till cirkelbågen i dess ändpunkter. Den totala fasdifferensen är Nφ, varav följer 2α = Nφ (se bild i boken). Ur längden av kordan RQ kan vi beräkna A θ, som är den resulterande vågamplituden i riktningen θ. Observera, att då θ = 0, och således även φ = 0 enligt uttrycket ovan (då vågen fortskrider utan att ändra riktning), så är den maximala amplituden A 0 en rät linje med längden NA, eftersom alla delamplituderna har samma längd. Längden av denna linje är lika med längden av bågen RQ. Den moderna fysikens grunder, Tom Sundius
9 Som vi ser av figuren nedan är A θ /A 0 = kordan RQ/bågen RQ. Om C är cirkelns medelpunkt och CD är medelnormalen till RQ, så är sin α = RD/RC. Således är RD = RC sin α och RQ = 2RC sin α. På grund av radianens definition är båglängden RQ = 2RCα, och vi får alltså A θ A 0 = kordan RQ bågen RQ = 2RC sin α 2RCα = sin α α. Eftersom intensiteten av en våg är proportionell mot kvadraten på amplituden, så blir intensitetsförhållandet Den moderna fysikens grunder, Tom Sundius
10 I θ I 0 = A2 θ A 2 0 = sin2 α α 2 Av sambandet mellan φ och θ följer att även vinkeln α kan uttryckas med θ: α = Nφ 2 = N a 2 2π N sin θ = πa λ λ sin θ. Då α 0 och sin α 0 och således sin α/α 1 blir intensiteten maximal (I 0 ). Då α växer, kommer I θ att oscillera med minskande amplitud. Då θ växer, kommer också α att växa, så att I θ som funktion av α uppvisar både maximer och minimer. Minimerna uppstår då sin α = 0, dvs då α = nπ. Sidomaximernas lägen på ömse sidor om det centrala maximet I 0 kan bestämmas grafiskt ur en figur. De uppträder för α ±1.430π,±2.459π, ±3.471π,... (lösningar till den transcendentala ekvationen α = tan α), eller approximativt α = (2n + 1)π/2. De motsvarande värdena av sin θ blir då sin θ = αλ 2n + 1 πa = 2 Den moderna fysikens grunder, Tom Sundius λ a
11 De maximala intensiteterna blir då approximativt I θ = sin2 α = I 0 α 2 4 (2n + 1) 2 π 2. Intensiteterna för de två första sidomaxima (n = 1, 2) blir alltså approximativt I 1 = 0.045I 0 och I 2 = 0.016I 0. Fastän de är små, kan sidomaximerna ändå påverka diffraktionsmönstret. Det första sidomaximet (för n = 1) inträffar då sin θ 3λ 2a. Om a < λ så finns det inte något värde av θ som satisfierar denna ekvation, och inga sidomaximer observeras. Men om a λ så kommer sidomaximerna att inträffa vid så små vinklar θ, att det blir svårt att observera diffraktionseffekterna. Våglängden för synligt ljus varierar mellan 400 och 750 nm, och öppningarna i optiska instrument (t.ex. Den moderna fysikens grunder, Tom Sundius
12 linsens diameter) är mycket större än så. Därför kan man vanligen försumma diffraktionseffekterna för ljusvågor, och som en första approximation kan man anse att ljuset rör sig rätlinjigt. Men detta gäller inte för ljudvågor, där våglängden kan vara flera meter, så att diffraktionseffekterna kan vara betydliga. I ett optiskt instrument sprider diffraktionen ljusets intensitet utanför det område som täcks av ljusstrålen och suddar ut bilden. Det innebär att den noggrannhet varmed bilden kan lokaliseras beror på våglängden av det använda ljuset. Betrakta ljuset som kommer från två närliggande källor och passerar genom en öppning med bredden a. Källorna kan t.ex. vara stjärnor som observeras genom ett teleskop där objektivets diameter är a. Två (överlappande) diffraktionsmönster kommer då att ses på en skärm som placeras bakom öppningen. Bilderna av de två källorna på skärmen kan upplösas (dvs separeras) ifall de centrala maximerna i de båda diffraktionsmönstren kan åtskiljas i mönstret. En praktisk, men något godtycklig metod som kallas Rayleighs kriterium (efter John Strutt, Lord Rayleigh, ) är att anse de båda källorna vara upplösta ifall det centrala maximet i diffraktionsmönstret för den ena källan sammanfaller med det första minimet i den andra källans diffraktionsmönster. Som vi tidigare har visat, kommer det första minimet att inträffa då α = π, dvs då πa λ sin θ = π och således sin θ = λ a. Detta betyder, att kriteriet för att källorna skall kunna upplösas, då de betraktas genom en spalt, svarar mot en minimal vinkelresolution (eftersom θ är liten) Den moderna fysikens grunder, Tom Sundius
13 θ λ a Man kan visa, att Rayleighs kriterium för den minimala vinkelresolutionen för en cirkulär öppning med diametern d kan uttryckas θ = 1.22 λ d. För att få en hög resolution (dvs litet θ) borde man därför använda ljus av kort våglängd och en stor öppning. Detta är orsaken till att man strävar efter att använda stora objektiv i astronomiska instrument (förutom att de samlar mera ljus). Upplösningsförmågan för ett teleskop växer, då objektivdiametern ökar. Teoretiskt borde man med ett 5- meters teleskop kunna nå en vinkelupplösning av 0.11, men i praktiken är det inte möjligt. Detta beror på turbulens i atmosfären, som åstadkommer slumpmässiga fasvariationer hos de elektromagnetiska vågorna. Bilden av en stjärna kan då uppdelas på flere bilder, som undergår ständiga förändringar. Den verkliga resolutionen kan därför vara sämre än 0.5, beroende på seeingen. Det finns flere sätt att kringgå detta problem. Ett sätt är att skicka upp teleskopet i en bana runt jorden, utanför jordatmosfärens störande inverkan. En annan lösning, som på sista tiden mycket diskuterats, går ut på att försöka kompensera effekterna av rörelserna i jordatmosfären (adaptiv optik). Den moderna fysikens grunder, Tom Sundius
14 1.3. Interferens och diffraktion från två spalter Thomas Young gjorde år 1801 ett experiment, där han lät ljus, som passerat genom en smal spalt träffa en skärm, som hade två små hål, som var mycket nära varandra. Bakom skärmen placerade han en annan skärm, där han uppfångade strålarna från de två hålen. Istället för en jämnt upplyst skärm, kunde han då observera en serie med färgade band, som småningom försvann, när han ökade avståndet mellan hålen. Vi ska tänka oss två rektangulära spalter med bredden a på avståndet b ifrån varandra, och uppdela varje spalt i identiska remsor. Bidragen från varje spalt adderas vektoriellt (liksom vid behandlingen av diffraktion). Om vi först behandlar spalten AB, så ser vi att diagrammet är likadant som vi fick för diffraktion i en spalt, där α = πa λ sin θ. Den moderna fysikens grunder, Tom Sundius
15 Om vi adderar bidragen från båda spalterna, AB och CD, så får vi ett diagram, som visas i fig. (i) på nästa sida. Mellan bidragen från spalterna finns en ogenomskinlig komponent BC. Vägskillnaden mellan vågor som utsänds från punkten A och punkten C är (a + b) sin θ, och fasskillnaden mellan dessa vågor blir då 2π π(a+b) λ (a + b) sin θ = 2γ, varav följer γ = λ sin θ. Vinkeln mellan tangenterna till cirkelbågen i A och C är således 2γ. Eftersom b a, så är γ α. Den moderna fysikens grunder, Tom Sundius
16 Den resulterande intensiteten för vågor från två spalter som betraktas under vinkeln θ kan beräknas genom addition av amplituderna, som beskrivs av kordorna AB och CD. Eftersom båda amplituderna har storleken A 1 fås amplituden A (se fig. (ii) ovan) ur cosinusteoremet A 2 = A A A2 1 cos 2γ = 2A2 1 (1 + cos 2γ). Med hjälp av den trigonometriska formeln cos 2γ = 2 cos 2 γ 1 kan ekvationen skrivas i formen A 2 = 4A 2 1 cos2 γ, eller alltså A = 2A 1 cos γ. För en enkel spalt fann vi i föregående avsnitt att A θ A 0 = kordan RQ bågen RQ = sin α α. Den moderna fysikens grunder, Tom Sundius
17 Då detta resultat tillämpas på den ena av spalterna fås A 1 α. Amplituden för en våg som går rakt igenom (θ = 0) är 2A 0. Den totala amplituden för vinkeln θ blir då A 0 = sin α 0 sin α A = 2A 1 cos γ = 2A cos γ, α och intensiteten för denna vinkel blir alltså I θ I0 spalterna, då vågen går rakt igenom (θ = 0). = A2 4A 2 0 = sin2 α α 2 cos 2 γ, där I 0 är intensiteten för båda Den första faktorn i ekvationen (dvs sin2 α α 2 " ) uttrycker diffraktionsmönstret för en spalt, som kan skrivas med hjälp av spaltbredden a som θ #2 sin πa λ sin πa λ sin θ Den andra faktorn i ekvationen (alltså cos 2 γ) anger interferensmönstret för två källor. Denna faktor kan skrivas i formen cos 2hπ(a+b) λ sin θi. Intensitetsmaxima uppstår då γ = nπ, dvs om π(a+b) λ sin θ = nπ, som kan skrivas som (a + b) sin θ = nλ eller d sin θ = nλ där d = a + b anger avståndet mellan två ekvivalenta punkter, A och C, eller B och D, på spalterna. Den moderna fysikens grunder, Tom Sundius
18 Om b a, som vanligen gäller, så varierar den andra faktorn (interferensfaktorn) snabbare än den första. Vi får då ett mönster som består av ett snabbt föränderligt interferensmönster från de två spalterna, som har formen cos 2 γ, och moduleras av enveloppfunktion av formen sin 2 α/α 2 som anger diffraktion i en spalt (se bilden ovan). Detta innebär, att interferensmönstret vanligen försvinner för vissa värden av θ. Youngs interferensmönster från två spalter kan iakttas på en skärm som placeras bakom spalterna. Om d är känt, så kan våglängden λ beräknas ur den inramade ekvationen, om man mäter skillnaden i vinkel mellan på varandra följande maxima eller minima. På grund av att maxima och minima inte är så tydliga, är det svårt att bestämma vinkelseparationen noggrannt, och därur våglängden. För detta ändamål används diffraktionsgitter, som består av ett stort antal smala spalter. Också för ett sådant gitter gäller samma villkor för intensitetsmaxima som för två spalter. Den moderna fysikens grunder, Tom Sundius
19 Observera, att interferens och diffraktion egentligen är två sätt att betrakta samma fenomen. Diffraktion betecknar vanligen spridningen i vågmönstret, som beror på interferens mellan närliggande punkter på samma vågfront, medan interferens betecknar interferensen mellan vågor från olika källor, eller från olika partier av samma vågfront som har blivit åtskilda och sedan förenade på nytt. Den moderna fysikens grunder, Tom Sundius
20 1.4. Röntgendiffraktion (Braggspridning) Röntgenstrålarna är i likhet med ljusstrålarna elektromagnetiska vågor, men deras våglängd är av storleksordningen 0.1 nm, dvs ca 1/1000 av ljusets. Då röntgenstrålar faller på ett diffraktionsgitter med mycket smala spalter, t.ex. d = 1µm, följer av gitterekvationen att diffraktionsvinkeln av första ordningen (n = 1) kan beräknas ur formeln θ = arcsin λ d = arcsin En så liten vinkel är det mycket svårt att mäta noggrannt. Därför måste vi använda ett gitter med ett spaltavstånd av storleksordningen 0.1 nm för att kunna mäta våglängder i röntgenområdet. Det kan vara mycket svårt att konstruera ett sådant gitter, men i naturen finns ett sådant färdigt, nämligen atomstrukturen i ett kristallgitter. För att fullt förstå vad som händer då en röntgenstråle träffar en kristall borde man beakta dess tredimensionella struktur. Dessutom är det fråga om spridning av elektromagnetiska vågor från atomer eller molekyler och inte vågrörelse genom spalter. Men det grundläggande interferensvillkoret kan man ändå finna genom att studera interferens mellan vågor som sprids från närliggande plan bildade av kristallens atomer. Principiellt kan alltså problemet studeras i två dimensioner. Antag att röntgenstrålarna sprids så, att vinkeln θ mellan de spridda strålarna och kristallplanet är lika stor som vinkeln mellan de infallande röntgenstrålarna och kristallplanet. Man kan då anse att röntgenstrålarna Den moderna fysikens grunder, Tom Sundius
21 reflekteras i planet. Konstruktiv interferens mellan två vågor som infaller under samma vinkel mot närliggande plan inträffar, ifall de reflekterade strålarnas vägskillnad är en heltalig multipel av våglängden (se figuren), dvs 2d sin θ = nλ, där n är ett heltal och d avståndet mellan närliggande plan. Ekvationen kallas Braggvillkoret efter William Henry Bragg och William Lawrence Bragg (far och son), som fann det år Villkoret leder också till konstruktiv interferens för röntgenstrålar, som reflekterats från andra och tredje kristallplanet, osv. Det påminner om motsvarande ekvation för diffraktionsgittret, men man bör minnas, att d och θ tolkas på annat sätt. Den moderna fysikens grunder, Tom Sundius
22 Fenomenet, som kallas Braggspridning, kan utnyttjas på följande sätt: a) Om vi känner d, θ och n så kan λ beräknas. Denna metod används i röntgenspektrometrar för att bestämma våglängder. b) Om vi känner θ, n och λ, så kan vi bestämma d, avståndet mellan planen i en kristall. Denna metod kallas för kristalldiffraktion och är ett viktigt hjälpmedel vid strukturbestämningar av molekyler och kristaller. Strukturen av DNA-molekylen t.ex. har bestämts på detta sätt. Interferens kan också observeras mellan andra plan i samma kristall. Om avståndet mellan kristallplanen är d blir Braggvillkoret i detta fall 2d sin θ = nλ. Braggvillkoret är alltså mera komplicerat än villkoret för det endimensionella gittret. Den moderna fysikens grunder, Tom Sundius
23 1.5. Stående vågor Om vågor infaller mot en fixerad punkt i ett medium (en sträng, t.ex.), så kommer de att reflekteras. Den infallande vågen kan beskrivas med gående våg i x riktningen y 1 = A sin(kx + ωt + φ). Den reflekterade vågen, som har samma amplitud och frekvens men rör sig i +x riktningen kommer då att beskrivas då av ekvationen y 2 = A sin(kx ωt + φ). I praktiken ändras vanligen fasen vid reflektion, men detta har oftast inte någon större inverkan på resultatet. Med hjälp av superpositionsprincipen kan vi beräkna den resulterande störningen genom att addera vågorna: y = y 1 + y 2 = A sin(kx + ωt + φ) + A sin(kx ωt + φ). Med hjälp av identiteten följer härav y = 2A sin(kx + φ) cos ωt. sin α + sin β = 2 sin[ 1 2 (α + β)] cos[1 2 (α β)] För att förenkla behandlingen skall vi välja x = 0 som den punkt där strängen är fixerad. För x = 0 gäller då alltid y = 0 varav följer att φ = 0 och ekvationen kan skrivas y = 2A sin kx cos ωt Den moderna fysikens grunder, Tom Sundius
24 Observera, att oscillationerna i x och t sker nu oberoende av varandra. Vågrörelsen fortskrider inte genom mediet, det finns ingen gående våg. Vågorna som alstras kallas därför stående (eller stationära) vågor. Ekvationen ovan kan tolkas som enkel harmonisk rörelse y = A cos ωt, där amplituden A = 2A sin kx är en funktion av positionen längs strängen. I en bestämd punkt oscillerar störningen med en konstant amplitud A (se figuren). Observera, att i vissa punkter (där kx = nπ) är amplituden A alltid noll. Sådana punkter kallas noder. Villkoret för en nod kan alltså uttryckas 2πx λ = nπ, och de inträffar alltså då x = 1 2nλ, dvs med ett mellanrum av en halv våglängd längs strängen. I vissa andra punkter (för vilka kx = 1 2 (2n + 1)π, dvs x = 2n+1 4 λ) är amplituden 2A. De kallas antinoder och befinner sig mittemellan noderna. Om strängen fixeras i båda ändarna, så måste de fungera som noder i alla stående vågrörelser. På grund av valet av origo befinner sig den ena noden i x = 0. Om längden av strängen är l, så kan vi tillämpa nodvillkoret kx = nπ på den andra änden där x = l, och får då kx = kl = nπ och 2πl λ = nπ, dvs Den moderna fysikens grunder, Tom Sundius
25 λ = 2l n För ett bestämt värde av l så får man stående vågor endast för vissa våglängder och således endast bestämda frekvenser f = v λ = nv 2l där n är ett heltal. Dessa frekvenser, som kallas resonansfrekvenser, bestäms av strängens längd l, och den gående vågens hastighet v. I boken visas också, att vågens hastighet längs strängen, och således resonansfrekvensen när den är fastspänd i vardera ändan, beror av spänningen i strängen och massan per enhetslängd. Denna princip används i musikinstrument. För att ändra resonansfrekvensen för en sträng, ändrar man spänningen eller längden. Blåsinstrument använder stående ljudvågor för att alstra toner. Värdet av resonansfrekvensen beror då på längden av luftpelarens höjd i instrumentet. Om instrumentet är stängt i båda ändarna, uppstår där noder, men om det är stängt i den ena änden, uppstår där en nod, och i den andra änden en antinod. Tonerna som alstras i ett musikinstrument, ger sällan upphov till enkla sinusvågor, utan vanligen förekommer andra frekvenser (övertoner, som svarar mot större värde av n) jämte grundfrekvensen, som har n = 1. Den moderna fysikens grunder, Tom Sundius
26 1.6. Vågekvationen Som vi tidigare sett, kan en gående våg längs x axeln uttryckas genom ekvationen y(x, t) = A sin(ωt kx + φ) Vi ska derivera denna ekvation partiellt två gånger, både med avseende på x och t: y x = ka cos(ωt kx + φ) 2 y x = 2 k2 A sin(ωt kx + φ) y = ωa cos(ωt kx + φ) t 2 y t 2 = ω2 A sin(ωt kx + φ) Den moderna fysikens grunder, Tom Sundius
27 Genom att dividera 2 y/ 2 x med 2 y/ 2 t får vi (jfr ekv. 12.5) 2 y x 2 2 y t 2 = k 2 ω 2 = 1 v 2. Man kan visa, att detta resultat gäller för en godtycklig funktion av formen f(kx ± ωt ± a), där a är en konstant. Således gäller följande ekvation (som kallas vågekvationen) Detta resultat kan generaliseras till tre dimensioner: där symbolen ξ använts för att beteckna störningen. 2 y x = 1 2 y 2 v 2 t 2 2 ξ x + 2 ξ 2 y + 2 ξ 2 z = 1 2 ξ 2 v 2 t, 2 Den inramade ekvationen säger, att vi kan uttrycka den andra rumsderivatan av en störning i ett godtyckligt medium som en konstant C multiplicerad med den andra tidsderivatan av störningen. Konstantens värde är 1/v 2, dvs om 2 y/ 2 x = C 2 y/ 2 t, så är v = p 1/C. Den moderna fysikens grunder, Tom Sundius
Fysik (TFYA14) Fö 5 1. Fö 5
 Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
Vinkelupplösning, exempel hålkameran. Vinkelupplösning När är två punkter upplösta? FAF260. Lars Rippe, Atomfysik/LTH 1. Böjning i en spalt
 Kursavsnitt Böjning och interferens Böjning i en spalt bsin m m 1,... 8 9 Böjning i en spalt Böjning i cirkulär öppning med diameter D Böjningsminimum då =m Första min: Dsin 1. 10 11 Vinkelupplösning,
Kursavsnitt Böjning och interferens Böjning i en spalt bsin m m 1,... 8 9 Böjning i en spalt Böjning i cirkulär öppning med diameter D Böjningsminimum då =m Första min: Dsin 1. 10 11 Vinkelupplösning,
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 36-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik Kapitel 36-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Diffraktion... Diffraktion (Kap. 36) Diffraktion... Enkel spalt. Parallellt monokromatiskt ljus gör att skuggan av rakbladet uppvisar en bandstruktur.
 Diffraktion (Kap. 36) Diffraktion... Fjärilens (Blå Morpho) vingar har en ytstruktur som gör att endast vissa färger (blå) blir synligt under vissa vinklar genom diffraktionseffekter: idag försöker forskare
Diffraktion (Kap. 36) Diffraktion... Fjärilens (Blå Morpho) vingar har en ytstruktur som gör att endast vissa färger (blå) blir synligt under vissa vinklar genom diffraktionseffekter: idag försöker forskare
Kapitel 36, diffraktion
 Kapitel 36, diffraktion Diffraktionsbegreppet, en variant av interferens Hitta min värden för enkelspalt med vidden a Intensitet för enkelspalt med vidden a Två spalter med vidd a och separation d Många
Kapitel 36, diffraktion Diffraktionsbegreppet, en variant av interferens Hitta min värden för enkelspalt med vidden a Intensitet för enkelspalt med vidden a Två spalter med vidd a och separation d Många
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi
 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Vinkelupplösning, exempel hålkameran. Vinkelupplösning När är två punkter upplösta? FAF260. Lars Rippe, Atomfysik/LTH 1. Böjning i en spalt
 Kursavsnitt Böjning och interferens Böjning i en spalt bsin m m 1,... 8 9 Böjning i en spalt Böjning i cirkulär öppning med diameter D Böjningsminimum då =m Första min: Dsin 1. 10 11 Vinkelupplösning,
Kursavsnitt Böjning och interferens Böjning i en spalt bsin m m 1,... 8 9 Böjning i en spalt Böjning i cirkulär öppning med diameter D Böjningsminimum då =m Första min: Dsin 1. 10 11 Vinkelupplösning,
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 35-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik Kapitel 35-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Gauss Linsformel (härledning)
 α α β β S S h h f f ' ' S h S h f S h f h ' ' S S h h ' ' f f S h h ' ' 1 ' ' ' f S f f S S S ' 1 1 1 S f S f S S 1 ' 1 1 Gauss Linsformel (härledning) Avbilding med lins a f f b Gauss linsformel: 1 a
α α β β S S h h f f ' ' S h S h f S h f h ' ' S S h h ' ' f f S h h ' ' 1 ' ' ' f S f f S S S ' 1 1 1 S f S f S S 1 ' 1 1 Gauss Linsformel (härledning) Avbilding med lins a f f b Gauss linsformel: 1 a
Böjning. Tillämpad vågrörelselära. Föreläsningar. Vad är optik? Huygens princip. Böjning vs. interferens FAF260. Lars Rippe, Atomfysik/LTH 1
 Tillämpad vågrörelselära 2 Föreläsningar Vad är optik? F10 och upplösning (kap 16) F11 Interferens och böjning (kap 17) F12 Multipelinterferens (kap 18) F13 Polariserat ljus (kap 20) F14 Reserv / Repetition
Tillämpad vågrörelselära 2 Föreläsningar Vad är optik? F10 och upplösning (kap 16) F11 Interferens och böjning (kap 17) F12 Multipelinterferens (kap 18) F13 Polariserat ljus (kap 20) F14 Reserv / Repetition
Fysik. Laboration 3. Ljusets vågnatur
 Fysik Laboration 3 Ljusets vågnatur Laborationens syfte: att hjälpa dig att förstå ljusfenomen diffraktion och interferens och att förstå hur olika typer av spektra uppstår Utförande: laborationen skall
Fysik Laboration 3 Ljusets vågnatur Laborationens syfte: att hjälpa dig att förstå ljusfenomen diffraktion och interferens och att förstå hur olika typer av spektra uppstår Utförande: laborationen skall
Diffraktion och interferens
 Institutionen för Fysik 005-10-17 Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det
Institutionen för Fysik 005-10-17 Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det
(ii) Beräkna sidoförskjutningen d mellan in- och utgående strålar, uttryckt i vinklarna θ i och tjocklekar t i. (2p)
 Tentamen i Vågrörelselära(FK49) Datum: Onsdag, 4 Augusti,, Tid: 9: - 4: Tillåten Hjälp: Physics handbook eller dylikt och miniräknare Förklara resonemang och uträkningar klart och tydligt. Tentamensskrivningen
Tentamen i Vågrörelselära(FK49) Datum: Onsdag, 4 Augusti,, Tid: 9: - 4: Tillåten Hjälp: Physics handbook eller dylikt och miniräknare Förklara resonemang och uträkningar klart och tydligt. Tentamensskrivningen
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 15 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 : Kapitel 15.1 15.8 Ljud och
Vågrörelselära och optik Kapitel 15 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 : Kapitel 15.1 15.8 Ljud och
λ = T 2 g/(2π) 250/6 40 m
 Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Kapitel 35, interferens
 Kapitel 35, interferens Interferens hos ljusvågor, koherensbegreppet Samband för max och min för ideal dubbelspalt Samband för intensitetsvariation för ideal dubbelspalt Interferens i tunna filmer Michelson
Kapitel 35, interferens Interferens hos ljusvågor, koherensbegreppet Samband för max och min för ideal dubbelspalt Samband för intensitetsvariation för ideal dubbelspalt Interferens i tunna filmer Michelson
Laboration 1 Fysik
 Laboration 1 Fysik 2 2015 : Fysik 2 för tekniskt/naturvetenskapligt basår Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen på
Laboration 1 Fysik 2 2015 : Fysik 2 för tekniskt/naturvetenskapligt basår Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen på
Luft. film n. I 2 Luft
 Tentamen i Vågrörelselära(FK49) Datum: Måndag, 14 Juni, 21, Tid: 9: - 15: Tillåten Hjälp: Physics handbook eller dylikt och miniräknare Förklara resonemang och uträkningar klart och tydligt. Tentamensskrivningen
Tentamen i Vågrörelselära(FK49) Datum: Måndag, 14 Juni, 21, Tid: 9: - 15: Tillåten Hjälp: Physics handbook eller dylikt och miniräknare Förklara resonemang och uträkningar klart och tydligt. Tentamensskrivningen
Diffraktion och interferens
 Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det är just detta fenomen som gör att
Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det är just detta fenomen som gör att
FAFF Johan Mauritsson 1. Föreläsningar. Våglära och optik. Världens minsta film. Projekten
 Våglära och optik FAFF30 JOHAN MAURITSSON Föreläsningar F10 Fraunhoferdiffraktion F11 Diffraktionsgitter F12 Fresneldiffraktion F13 Matrisrepresentation av polariserat ljus F14 Polariserat ljus F15 Repetition
Våglära och optik FAFF30 JOHAN MAURITSSON Föreläsningar F10 Fraunhoferdiffraktion F11 Diffraktionsgitter F12 Fresneldiffraktion F13 Matrisrepresentation av polariserat ljus F14 Polariserat ljus F15 Repetition
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 14 Harmonisk oscillator 1 Vågrörelselära och optik 2 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator:
Vågrörelselära och optik Kapitel 14 Harmonisk oscillator 1 Vågrörelselära och optik 2 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator:
Vågor. En våg är en störning som utbreder sig En våg överför energi från en plats till en annan. Det sker ingen masstransport
 Vågor En våg är en störning som utbreder sig En våg överför energi från en plats till en annan. Det sker ingen masstransport Vågtyper Transversella Mediets partiklar rör sig vinkelrätt mot vågens riktning.
Vågor En våg är en störning som utbreder sig En våg överför energi från en plats till en annan. Det sker ingen masstransport Vågtyper Transversella Mediets partiklar rör sig vinkelrätt mot vågens riktning.
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER
 EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
Diffraktion och interferens Kapitel 35-36
 Diffraktion och interferens Kapitel 35-36 1.3.2016 Natalie Segercrantz Centrala begrepp Huygens princip: Tidsskillnaden mellan korresponderande punkter på två olika vågfronter är lika för alla par av korresponderande
Diffraktion och interferens Kapitel 35-36 1.3.2016 Natalie Segercrantz Centrala begrepp Huygens princip: Tidsskillnaden mellan korresponderande punkter på två olika vågfronter är lika för alla par av korresponderande
3. Mekaniska vågor i 2 (eller 3) dimensioner
 3. Mekaniska vågor i 2 (eller 3) dimensioner Brytning av vågor som passerar gränsen mellan två material Eftersom utbredningshastigheten för en mekanisk våg med största sannolikhet ändras då den passerar
3. Mekaniska vågor i 2 (eller 3) dimensioner Brytning av vågor som passerar gränsen mellan två material Eftersom utbredningshastigheten för en mekanisk våg med största sannolikhet ändras då den passerar
Vågfysik. Superpositionsprincipen
 Vågfysik Superposition Knight, Kap 21 Superpositionsprincipen Superposition = kombination av två eller fler vågor. Vågor partiklar Elongation = D 1 +D 2 D net = Σ D i Superpositionsprincipen 1 2 vågor
Vågfysik Superposition Knight, Kap 21 Superpositionsprincipen Superposition = kombination av två eller fler vågor. Vågor partiklar Elongation = D 1 +D 2 D net = Σ D i Superpositionsprincipen 1 2 vågor
ett uttryck för en våg som beskrivs av Jonesvektorn: 2
 Tentamen i Vågrörelselära(FK49) Datum: Tisdag, 6 Juni, 29, Tid: 9: - 5: Tillåten Hjälp: Physics handbook eller dylikt Förklara resonemang och uträkningar klart och tydligt. Tentamensskrivningen består
Tentamen i Vågrörelselära(FK49) Datum: Tisdag, 6 Juni, 29, Tid: 9: - 5: Tillåten Hjälp: Physics handbook eller dylikt Förklara resonemang och uträkningar klart och tydligt. Tentamensskrivningen består
Institutionen för Fysik 2013-10-17. Polarisation
 Polarisation Syfte Syftet med denna laboration är att lära sig om ljusets polarisation. Du kommer att se exempel på opolariserat, linjär- och cirkulärpolariserat ljus. Exempel på komponenter som kan ändra
Polarisation Syfte Syftet med denna laboration är att lära sig om ljusets polarisation. Du kommer att se exempel på opolariserat, linjär- och cirkulärpolariserat ljus. Exempel på komponenter som kan ändra
Handledning laboration 1
 : Fysik 2 för tekniskt/naturvetenskapligt basår Handledning laboration 1 VT 2017 Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen
: Fysik 2 för tekniskt/naturvetenskapligt basår Handledning laboration 1 VT 2017 Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen
Strålningsfält och fotoner. Kapitel 25: Vågor och partiklar
 Strålningsfält och fotoner Kapitel 25: Vågor och partiklar Ljus: vågor eller partiklar? Modellen av ljus som partiklar, fotoner, gör det möjligt att förklara fenomen som absorption och emission av ljus
Strålningsfält och fotoner Kapitel 25: Vågor och partiklar Ljus: vågor eller partiklar? Modellen av ljus som partiklar, fotoner, gör det möjligt att förklara fenomen som absorption och emission av ljus
1. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (1p)
 Problem Energi. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (p) b) Ge en tydlig förklaring av hur frekvens, period, våglängd och våghastighet hänger
Problem Energi. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (p) b) Ge en tydlig förklaring av hur frekvens, period, våglängd och våghastighet hänger
Vågrörelselära & Kvantfysik, FK2002 1 december 2011
 Räkneövning 6 Vågrörelselära & Kvantfysik, FK2002 december 20 Problem 36.23 Avståndet mellan två konvexa linser i ett mikroskop, l = 7.5 cm. Fokallängden för objektivet f o = 0.8 cm och för okularet f
Räkneövning 6 Vågrörelselära & Kvantfysik, FK2002 december 20 Problem 36.23 Avståndet mellan två konvexa linser i ett mikroskop, l = 7.5 cm. Fokallängden för objektivet f o = 0.8 cm och för okularet f
1. Betrakta en plan harmonisk elektromagnetisk våg i vakuum där det elektriska fältet E uttrycks på följande sätt (i SI-enheter):
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Måndagen den 5 maj 2008 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare.
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Måndagen den 5 maj 2008 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare.
Ljudhastighet (vätska & gas) RT v M Intensitet från en punktkälla P I medel 2 4 r Ljudintensitetsnivå I 12 2 LI 10lg med Io 1,0 10 W/m Io Dopplereffek
 Ljudhastighet (vätska & gas) RT v M Intensitet från en punktkälla P I medel 4 r Ljudintensitetsnivå I 1 LI 10lg med Io 1,0 10 W/m Io Dopplereffekt, ljud v v f m m fs v v s Relativistisk Dopplereffekt,
Ljudhastighet (vätska & gas) RT v M Intensitet från en punktkälla P I medel 4 r Ljudintensitetsnivå I 1 LI 10lg med Io 1,0 10 W/m Io Dopplereffekt, ljud v v f m m fs v v s Relativistisk Dopplereffekt,
BFL122/BFL111 Fysik för Tekniskt/ Naturvetenskapligt Basår/ Bastermin Föreläsning 7 Kvantfysik, Atom-, Molekyl- och Fasta Tillståndets Fysik
 Föreläsning 7 Kvantfysik 2 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det
Föreläsning 7 Kvantfysik 2 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det
1 Figuren nedan visar en transversell våg som rör sig åt höger. I figuren är en del i vågens medium markerat med en blå ring prick.
 10 Vågrörelse Vågor 1 Figuren nedan visar en transversell våg som rör sig åt höger. I figuren är en del i vågens medium markerat med en blå ring prick. y (m) 0,15 0,1 0,05 0-0,05 0 0,5 1 1,5 2 x (m) -0,1-0,15
10 Vågrörelse Vågor 1 Figuren nedan visar en transversell våg som rör sig åt höger. I figuren är en del i vågens medium markerat med en blå ring prick. y (m) 0,15 0,1 0,05 0-0,05 0 0,5 1 1,5 2 x (m) -0,1-0,15
Lösningsförslag - tentamen. Fysik del B2 för tekniskt / naturvetenskapligt basår / bastermin BFL 122 / BFL 111
 Linköpings Universitet Institutionen för Fysik, Kemi, och Biologi Avdelningen för Tillämpad Fysik Mike Andersson Lösningsförslag - tentamen Torsdagen den 27:e maj 2010, kl 08:00 12:00 Fysik del B2 för
Linköpings Universitet Institutionen för Fysik, Kemi, och Biologi Avdelningen för Tillämpad Fysik Mike Andersson Lösningsförslag - tentamen Torsdagen den 27:e maj 2010, kl 08:00 12:00 Fysik del B2 för
5. Elektromagnetiska vågor - interferens
 Interferens i dubbelspalt A λ/2 λ/2 Dal för ena vågen möter topp för den andra och vice versa => mörkt (amplitud = 0). Dal möter dal och topp möter topp => ljust (stor amplitud). B λ/2 Fig. 5.1 För ljusvågor
Interferens i dubbelspalt A λ/2 λ/2 Dal för ena vågen möter topp för den andra och vice versa => mörkt (amplitud = 0). Dal möter dal och topp möter topp => ljust (stor amplitud). B λ/2 Fig. 5.1 För ljusvågor
Kapitel 33 The nature and propagation of light. Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion)
 Kapitel 33 The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Kapitel 33 The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Interferens (Kap. 35) Interferens (Kap. 35) Interferens mellan vågor från två punktformiga källor. Skillnad mellan interferens och diffraktion
 Interferens (Kap. 35) Interferens (Kap. 35) Varför syns regnbågs färger särskilt bra ifall lite olja är spilld i en vattenpöl på asfalt? Hur tunn måste en oljefim vara för att visa upp sådana regnbågs
Interferens (Kap. 35) Interferens (Kap. 35) Varför syns regnbågs färger särskilt bra ifall lite olja är spilld i en vattenpöl på asfalt? Hur tunn måste en oljefim vara för att visa upp sådana regnbågs
Ljusets interferens. Sammanfattning
 HERMODS DISTANSGYMNASIUM Naturvetenskapsprogrammet Emilia Dunfelt Fysik 2 2017-05-06 Ljusets interferens Sammanfattning I försöket undersöks ljusets vågegenskaper med hjälp av gitterekvationen. Två olika
HERMODS DISTANSGYMNASIUM Naturvetenskapsprogrammet Emilia Dunfelt Fysik 2 2017-05-06 Ljusets interferens Sammanfattning I försöket undersöks ljusets vågegenskaper med hjälp av gitterekvationen. Två olika
Diffraktion och interferens
 Diffraktion och interferens Laboration i kursen Syfte Laborationen ska ge förståelse för begreppen interferens och diffraktion och hur de karaktäriseras genom experiment. Vidare visar laborationen exempel
Diffraktion och interferens Laboration i kursen Syfte Laborationen ska ge förståelse för begreppen interferens och diffraktion och hur de karaktäriseras genom experiment. Vidare visar laborationen exempel
Presentationsmaterial Ljus som vågrörelse - Fysik B. Interferens i dubbelspalt gitter tunna skikt
 Presentationsmaterial Ljus som vågrörelse - Fysik B Interferens i ubbelspalt gitter tunna skikt Syfte och omfattning Detta material behanlar på intet sätt fullstänigt såant som kan ingå i avsnitt me innebören
Presentationsmaterial Ljus som vågrörelse - Fysik B Interferens i ubbelspalt gitter tunna skikt Syfte och omfattning Detta material behanlar på intet sätt fullstänigt såant som kan ingå i avsnitt me innebören
1. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft.
 Problem. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft. (p) Det finns många förklaringar, till exempel Hewitt med insekten
Problem. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft. (p) Det finns många förklaringar, till exempel Hewitt med insekten
Institutionen för Fysik Polarisation
 Polarisation Syfte Syftet med denna laboration är att lära sig om ljusets polarisation. Du kommer att se exempel på opolariserat-, linjärt- och cirkulär polariserat ljus. Exempel på komponenter som kan
Polarisation Syfte Syftet med denna laboration är att lära sig om ljusets polarisation. Du kommer att se exempel på opolariserat-, linjärt- och cirkulär polariserat ljus. Exempel på komponenter som kan
FAFA55 HT2016 Laboration 1: Interferens av ljus Nicklas Anttu och August Bjälemark, 2012, Malin Nilsson och David Göransson, 2015, 2016
 Inför Laborationen Laborationen sker i två lokaler: K204 (datorsal) och H226. I början av laborationen samlas ni i H212. Laborationen börjar 15 minuter efter heltimmen som är utsatt på schemat. Ta med
Inför Laborationen Laborationen sker i två lokaler: K204 (datorsal) och H226. I början av laborationen samlas ni i H212. Laborationen börjar 15 minuter efter heltimmen som är utsatt på schemat. Ta med
4. Allmänt Elektromagnetiska vågor
 Det är ett välkänt faktum att det runt en ledare som det flyter en viss ström i bildas ett magnetiskt fält, där styrkan hos det magnetiska fältet beror på hur mycket ström som flyter i ledaren. Om strömmen
Det är ett välkänt faktum att det runt en ledare som det flyter en viss ström i bildas ett magnetiskt fält, där styrkan hos det magnetiska fältet beror på hur mycket ström som flyter i ledaren. Om strömmen
Elektromagnetiska vågor (Ljus)
 Föreläsning 4-5 Elektromagnetiska vågor (Ljus) Ljus kan beskrivas som bestående av elektromagnetiska vågrörelser, d.v.s. ett tids- och rumsvarierande elektriskt och magnetiskt fält. Dessa ljusvågor följer
Föreläsning 4-5 Elektromagnetiska vågor (Ljus) Ljus kan beskrivas som bestående av elektromagnetiska vågrörelser, d.v.s. ett tids- och rumsvarierande elektriskt och magnetiskt fält. Dessa ljusvågor följer
Tentamen i Vågor och Optik 5hp F, Q, kandfys, gylärfys-programm, den 11. juni 2010
 Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 8-13 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 8-13 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
Diffraktion och interferens
 Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det är just detta fenomen som gör att
Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det är just detta fenomen som gör att
3. Ljus. 3.1 Det elektromagnetiska spektret
 3. Ljus 3.1 Det elektromagnetiska spektret Synligt ljus är elektromagnetisk vågrörelse. Det följer samma regler som vi tidigare gått igenom för mekanisk vågrörelse; reflexion, brytning, totalreflexion
3. Ljus 3.1 Det elektromagnetiska spektret Synligt ljus är elektromagnetisk vågrörelse. Det följer samma regler som vi tidigare gått igenom för mekanisk vågrörelse; reflexion, brytning, totalreflexion
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 21 augusti 2008 kl 9-15
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 1 augusti 008 kl 9-15 Hjälpmedel: handbok och räknare. Varje uppgift ger maximalt 4 poäng. Var
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 1 augusti 008 kl 9-15 Hjälpmedel: handbok och räknare. Varje uppgift ger maximalt 4 poäng. Var
The nature and propagation of light
 Ljus Emma Björk The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Ljus Emma Björk The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Hjälpmedel: Typgodkänd räknare, Physics Handbook, Mathematics Handbook.
 CHALMERS TEKNISKA HÖGSKOLA 2009-01-13 Teknisk Fysik 14.00-18.00 Sal: V Tentamen i Optik för F2 (FFY091) Lärare: Bengt-Erik Mellander, tel. 772 3340 Hjälpmedel: Typgodkänd räknare, Physics Handbook, Mathematics
CHALMERS TEKNISKA HÖGSKOLA 2009-01-13 Teknisk Fysik 14.00-18.00 Sal: V Tentamen i Optik för F2 (FFY091) Lärare: Bengt-Erik Mellander, tel. 772 3340 Hjälpmedel: Typgodkänd räknare, Physics Handbook, Mathematics
TFEI02: Vågfysik. Tentamen : Lösningsförslag
 160530: TFEI0 1 Uppgift 1 TFEI0: Vågfysik Tentamen 016-05-30: Lösningsförslag a) Ljudintensiteten, I, är ett mått på hur stor effekt, P eff, som transporteras per area. Om vi vet amplituden på vågen kan
160530: TFEI0 1 Uppgift 1 TFEI0: Vågfysik Tentamen 016-05-30: Lösningsförslag a) Ljudintensiteten, I, är ett mått på hur stor effekt, P eff, som transporteras per area. Om vi vet amplituden på vågen kan
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 33 - Ljus 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Vågrörelselära och optik Kapitel 33 - Ljus 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 32 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik Kapitel 32 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Polarisation Laboration 2 för 2010v
 Polarisation Laboration 2 för 2010v Stockholms Universitet 2007 Innehåll 1 Vad är polariserat ljus? 2 Teoretisk beskrivning av polariserat ljus 2.1 Linjärpolariserat ljus 2.2 Cirkulärpolariserat ljus
Polarisation Laboration 2 för 2010v Stockholms Universitet 2007 Innehåll 1 Vad är polariserat ljus? 2 Teoretisk beskrivning av polariserat ljus 2.1 Linjärpolariserat ljus 2.2 Cirkulärpolariserat ljus
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi
 1 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus kan ses so elektroagnetiska vågor so rör sig fraåt. När vi ritar strålar
1 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus kan ses so elektroagnetiska vågor so rör sig fraåt. När vi ritar strålar
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
Förklara dessa begrepp: Ackommodera Avbildning, Brytning Brytningslagen Brytningsindex Brytningsvinkel Brännvidd Diffus och regelbunden reflektion
 Förklara dessa begrepp: Ackommodera, ögats närinställning, är förmågan att förändra brytkraften i ögats lins. Ljus från en enda punkt på ett avlägset objekt och ljus från en punkt på ett närliggande objekt
Förklara dessa begrepp: Ackommodera, ögats närinställning, är förmågan att förändra brytkraften i ögats lins. Ljus från en enda punkt på ett avlägset objekt och ljus från en punkt på ett närliggande objekt
Lösningar till repetitionsuppgifter
 Lösningar till repetitionsuppgifter 1. Vågen antas röra sig i positiva x-axelns riktning dvs s = a sin(ω t k x +δ). Elongationen = +0,5 a för x = 0 vid t = 0 0,5 a = a sin(δ) sin(δ) = 0,5 δ 1 = π/6 och
Lösningar till repetitionsuppgifter 1. Vågen antas röra sig i positiva x-axelns riktning dvs s = a sin(ω t k x +δ). Elongationen = +0,5 a för x = 0 vid t = 0 0,5 a = a sin(δ) sin(δ) = 0,5 δ 1 = π/6 och
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Tisdagen den 17 juni 2008 kl 9-15
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 1,5 högskolepoäng, FK49 Tisdagen den 17 juni 28 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 1,5 högskolepoäng, FK49 Tisdagen den 17 juni 28 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare
7. Atomfysik väteatomen
 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det nödvändigt att betrakta
Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det nödvändigt att betrakta
Kapitel 4. Materievågor
 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Kapitel 4. Materievågor 1 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Överblick Överblick Kring 1925 började många viktiga kvantkoncept ha sett
Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Kapitel 4. Materievågor 1 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Överblick Överblick Kring 1925 började många viktiga kvantkoncept ha sett
Vågor och Optik. Mekaniska vågor (Kap. 15) Mekaniska vågor (Kap. 15)
 Mekaniska vågor (Kap. 15) Vågor och Optik Mekaniska vågor (Kap. 15) D Alemberts allmäna lösning i 1D En mekanisk våg är en störning i ett medium som fortplantar sig. 1 $ 1 '$ 1 ' =& )& + ) = 0 x v t %
Mekaniska vågor (Kap. 15) Vågor och Optik Mekaniska vågor (Kap. 15) D Alemberts allmäna lösning i 1D En mekanisk våg är en störning i ett medium som fortplantar sig. 1 $ 1 '$ 1 ' =& )& + ) = 0 x v t %
Vågfysik. Ljus: våg- och partikelbeteende
 Vågfysik Modern fysik & Materievågor Kap 25 (24 1:st ed.) Ljus: våg- och partikelbeteende Partiklar Lokaliserade Bestämd position & hastighet Kollision Vågor Icke-lokaliserade Korsar varandra Interferens
Vågfysik Modern fysik & Materievågor Kap 25 (24 1:st ed.) Ljus: våg- och partikelbeteende Partiklar Lokaliserade Bestämd position & hastighet Kollision Vågor Icke-lokaliserade Korsar varandra Interferens
v = v = c = 2 = E m E2 cµ 0 rms = 1 2 cε 0E 2 rms (33-26) I =
 Kap. 33 Elektromagnetiska vågor Den klassiska beskrivningen av EM-vågorna, går tillbaka till mitten av 1800-talet, då Maxwell formulerade samband mellan elektriska och magnetiska fält (Maxwells ekvationer).
Kap. 33 Elektromagnetiska vågor Den klassiska beskrivningen av EM-vågorna, går tillbaka till mitten av 1800-talet, då Maxwell formulerade samband mellan elektriska och magnetiska fält (Maxwells ekvationer).
Ljusets böjning & interferens
 ... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Ljusets böjning & interferens Ljusets vågegenskaper Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen ska
... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Ljusets böjning & interferens Ljusets vågegenskaper Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen ska
Om ellipsen och hyperbelns optiska egenskaper
 Om ellipsen och hyperbelns optiska egenskaper Anders Källén MatematikCentrum LTH anderskallen@gmail.com Sammanfattning Ellipser och hyperbler är, liksom parabeln, s.k. kägelsnitt, dvs kurvor som uppkommer
Om ellipsen och hyperbelns optiska egenskaper Anders Källén MatematikCentrum LTH anderskallen@gmail.com Sammanfattning Ellipser och hyperbler är, liksom parabeln, s.k. kägelsnitt, dvs kurvor som uppkommer
Kikaren. Synvinkel. Kepler och Galileikikare. Vinkelförstoring. Keplerkikaren. Keplerkikaren FAF260. Lars Rippe, Atomfysik/LTH 1
 Kikaren Synvinkel Ökar synvinkeln os avlägsna objekt 1 2 Vinkelörstoring Deinition: med optiskt instrument G utan optiskt instrument Kepler oc Galileikikare Avlägsna objekt (t. ex. med kikare): synvinkeln
Kikaren Synvinkel Ökar synvinkeln os avlägsna objekt 1 2 Vinkelörstoring Deinition: med optiskt instrument G utan optiskt instrument Kepler oc Galileikikare Avlägsna objekt (t. ex. med kikare): synvinkeln
Tentamen i Vågor och Optik 5hp F, Q, kandfys, gylärfys-programm, den 15. mars 2010
 Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 14-19 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 14-19 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
Ljusets böjning & interferens
 Ljusets böjning & interferens Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter 3 Appendix Ljusets vågegenskaper Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen
Ljusets böjning & interferens Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter 3 Appendix Ljusets vågegenskaper Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen
Laborationer i OPTIK och AKUSTIK (NMK10) Augusti 2003
 TEKNISKA HÖGSKOLAN I LINKÖPING Institutionen för teknik och naturvetenskap Campus Norrköping Igor Zozoulenko Laborationer i OPTIK och AKUSTIK (NMK10) Augusti 2003 Laboration 1: Ljudhastigheten i luft;
TEKNISKA HÖGSKOLAN I LINKÖPING Institutionen för teknik och naturvetenskap Campus Norrköping Igor Zozoulenko Laborationer i OPTIK och AKUSTIK (NMK10) Augusti 2003 Laboration 1: Ljudhastigheten i luft;
Optik, F2 FFY091 TENTAKIT
 Optik, F2 FFY091 TENTAKIT Datum Tenta Lösning Svar 2005-01-11 X X 2004-08-27 X X 2004-03-11 X X 2004-01-13 X 2003-08-29 X 2003-03-14 X 2003-01-14 X X 2002-08-30 X X 2002-03-15 X X 2002-01-15 X X 2001-08-31
Optik, F2 FFY091 TENTAKIT Datum Tenta Lösning Svar 2005-01-11 X X 2004-08-27 X X 2004-03-11 X X 2004-01-13 X 2003-08-29 X 2003-03-14 X 2003-01-14 X X 2002-08-30 X X 2002-03-15 X X 2002-01-15 X X 2001-08-31
Läs i vågläraboken om holografi (sid ) och sid 5 17 i detta kompendium.
 1 Förberedelser Läs i vågläraboken om holografi (sid 370-372) och sid 5 17 i detta kompendium. Gör följande uppgifter: Lösningarna inlämnas renskrivna vid laborationens början till handledaren för kontroll.
1 Förberedelser Läs i vågläraboken om holografi (sid 370-372) och sid 5 17 i detta kompendium. Gör följande uppgifter: Lösningarna inlämnas renskrivna vid laborationens början till handledaren för kontroll.
TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t s(x,t) =s 0 sin 2π T x. v = fλ =3 5 m/s = 15 m/s
 140528: TFEI02 1 TFEI02: Vågfysik Tentamen 140528: Svar och anvisningar Uppgift 1 a) En fortskridande våg kan skrivas på formen: t s(x,t) =s 0 sin 2π T x λ Vi ser att periodtiden är T =1/3 s, vilket ger
140528: TFEI02 1 TFEI02: Vågfysik Tentamen 140528: Svar och anvisningar Uppgift 1 a) En fortskridande våg kan skrivas på formen: t s(x,t) =s 0 sin 2π T x λ Vi ser att periodtiden är T =1/3 s, vilket ger
Vågrörelselära. Christian Karlsson Uppdaterad: Har jag använt någon bild som jag inte får använda så låt mig veta så tar jag bort den.
 Vågrörelselära Christian Karlsson Uppdaterad: 161003 Har jag använt någon bild som jag inte får använda så låt mig veta så tar jag bort den. christian.karlsson@ckfysik.se [14] 1 Elasticitet (bl.a. fjädrar)
Vågrörelselära Christian Karlsson Uppdaterad: 161003 Har jag använt någon bild som jag inte får använda så låt mig veta så tar jag bort den. christian.karlsson@ckfysik.se [14] 1 Elasticitet (bl.a. fjädrar)
1 AKUSTIK Håkan Wennlöf, I = P A m 2 P effekt, A arean effekten är spridd över (ofta en sfär, ljud utbreds sfärsiskt).
 AKUSTIK Håkan Wennlöf, hwennlof@kth.se Övning : Akustik. Intensitet är effekt per area I = P A [ ] W m 2 P effekt, A arean effekten är spridd över (ofta en sfär, ljud utbreds sfärsiskt). För ljudvåg gäller
AKUSTIK Håkan Wennlöf, hwennlof@kth.se Övning : Akustik. Intensitet är effekt per area I = P A [ ] W m 2 P effekt, A arean effekten är spridd över (ofta en sfär, ljud utbreds sfärsiskt). För ljudvåg gäller
Interferens och diffraktion
 Laborationsinstruktion Vågrörelselära Interferens och diffraktion VT11 Stockholms Universitet Innehåll Uppgift 1 Diffraktionsförsök med laserljus Uppgift Mäta våglängden med linjal Uppgift 3 Luftens brytningsindex
Laborationsinstruktion Vågrörelselära Interferens och diffraktion VT11 Stockholms Universitet Innehåll Uppgift 1 Diffraktionsförsök med laserljus Uppgift Mäta våglängden med linjal Uppgift 3 Luftens brytningsindex
Dispersionsrelation för fononer hos en diatomär atomkedja
 Dispersionsrelation för fononer hos en diatomär atomkedja Betrakta en endimensionell kedja av atomer med alternerande atomslag (massor M 1 respektive M ), dvs. kedjan består av ett endimensionellt gitter
Dispersionsrelation för fononer hos en diatomär atomkedja Betrakta en endimensionell kedja av atomer med alternerande atomslag (massor M 1 respektive M ), dvs. kedjan består av ett endimensionellt gitter
TFYA58, Fysik, 8 hp, 3 delar
 1. Vågrörelselära (mekaniska vågor, optik, diffraktion ) 7x2 tim föreläsning 6x2tim lektion 2. Experimentell problemlösning TFYA58, Fysik, 8 hp, 3 delar Ht 1 Ht 2 2x1 tim föreläsning 2 st Richardslabbar
1. Vågrörelselära (mekaniska vågor, optik, diffraktion ) 7x2 tim föreläsning 6x2tim lektion 2. Experimentell problemlösning TFYA58, Fysik, 8 hp, 3 delar Ht 1 Ht 2 2x1 tim föreläsning 2 st Richardslabbar
Geometrisk optik. Syfte och mål. Innehåll. Utrustning. Institutionen för Fysik 2006-04-25
 Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
för gymnasiet Polarisation
 Chalmers tekniska högskola och November 2006 Göteborgs universitet 9 sidor + bilaga Rikard Bergman 1992 Christian Karlsson, Jan Lagerwall 2002 Emma Eriksson 2006 O4 för gymnasiet Polarisation Foton taget
Chalmers tekniska högskola och November 2006 Göteborgs universitet 9 sidor + bilaga Rikard Bergman 1992 Christian Karlsson, Jan Lagerwall 2002 Emma Eriksson 2006 O4 för gymnasiet Polarisation Foton taget
E-strängen rör sig fyra gånger så långsamt vid samma transversella kraft, accelerationen. c) Hur stor är A-strängens våglängd?
 Problem. Betrakta en elgitarr. Strängarna är 660 mm långa. Stämningen är E-A-d-g-b-e, det vill säga att strängen som ger tonen e-prim (330 Hz) ligger två oktav högre i frekvens än E-strängen. Alla strängar
Problem. Betrakta en elgitarr. Strängarna är 660 mm långa. Stämningen är E-A-d-g-b-e, det vill säga att strängen som ger tonen e-prim (330 Hz) ligger två oktav högre i frekvens än E-strängen. Alla strängar
Vågrörelselära och Optik VT14 Lab 3 - Polarisation
 Vågrörelselära och Optik VT14 Lab 3 - Polarisation Stockholms Universitet 2014 Kontakt: olga.bylund@fysik.su.se Instruktioner för redogörelse för Laboration 3 Denna laboration består utav fyra experiment
Vågrörelselära och Optik VT14 Lab 3 - Polarisation Stockholms Universitet 2014 Kontakt: olga.bylund@fysik.su.se Instruktioner för redogörelse för Laboration 3 Denna laboration består utav fyra experiment
Kvantmekanik. Kapitel Natalie Segercrantz
 Kvantmekanik Kapitel 38-39 Natalie Segercrantz Centrala begrepp Schrödinger ekvationen i en dimension Fotoelektriska effekten De Broglie: partikel-våg dualismen W 0 beror av materialet i katoden minimifrekvens!
Kvantmekanik Kapitel 38-39 Natalie Segercrantz Centrala begrepp Schrödinger ekvationen i en dimension Fotoelektriska effekten De Broglie: partikel-våg dualismen W 0 beror av materialet i katoden minimifrekvens!
Kvalificeringstävling den 30 september 2008
 SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
Vågrörelselära, akustik och optik. Lösningsförslag till räkneuppgifter
 Vågrörelselära, akustik och optik. Lösningsförslag till räkneuppgifter Jonas Persson 5 juli 2007 Förord Som författare försöker man att anpassa sig till läsarna och presentera materialet på ett så lättläst
Vågrörelselära, akustik och optik. Lösningsförslag till räkneuppgifter Jonas Persson 5 juli 2007 Förord Som författare försöker man att anpassa sig till läsarna och presentera materialet på ett så lättläst
Repetitionsuppgifter i vågrörelselära
 Repetitionsuppgifter i vågrörelselära 1. En harmonisk vågrörelse med frekvensen 6, Hz och utbredningshastigheten 1 m/s har amplituden a. I en viss punkt och vid en viss tid är elongationen +,5a. Hur stor
Repetitionsuppgifter i vågrörelselära 1. En harmonisk vågrörelse med frekvensen 6, Hz och utbredningshastigheten 1 m/s har amplituden a. I en viss punkt och vid en viss tid är elongationen +,5a. Hur stor
Tillämpad vågrörelselära FAF260. Svängningar genererar vågor - Om en svängande partikel är kopplad till andra partiklar uppkommer vågor
 FF60 Tillämpad vågrörelselära FF60 Karaktäristiskt för periodiska svängningar är att det finns en återförande kraft riktad mot jämviktsläget y 0 F F F k y F m a 4 Svängningar genererar vågor - Om en svängande
FF60 Tillämpad vågrörelselära FF60 Karaktäristiskt för periodiska svängningar är att det finns en återförande kraft riktad mot jämviktsläget y 0 F F F k y F m a 4 Svängningar genererar vågor - Om en svängande
Hur elektromagnetiska vågor uppstår. Elektromagnetiska vågor (Kap. 32) Det elektromagnetiska spektrumet
 Elektromagnetiska vågor (Kap. 32) Hur elektromagnetiska vågor uppstår Laddning i vila:symmetriskt radiellt fält, Konstant hastighet: osymmetriskt radiellt fält samt ett magnetfält. Konstant acceleration:
Elektromagnetiska vågor (Kap. 32) Hur elektromagnetiska vågor uppstår Laddning i vila:symmetriskt radiellt fält, Konstant hastighet: osymmetriskt radiellt fält samt ett magnetfält. Konstant acceleration:
Föreläsning 3: Radiometri och fotometri
 Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
Holografi. Förberedelser. Referensvåg. Konstruktiv interferens. Läs i vågläraboken om holografi (sid ) och hela laborationsinstruktionen.
 Holografi Förberedelser Läs i vågläraboken om holografi (sid 370 372) och hela laborationsinstruktionen. Referensvåg 50 Objektvåg Gör följande uppgifter: Lösningarna inlämnas renskrivan vid laborationens
Holografi Förberedelser Läs i vågläraboken om holografi (sid 370 372) och hela laborationsinstruktionen. Referensvåg 50 Objektvåg Gör följande uppgifter: Lösningarna inlämnas renskrivan vid laborationens
för M Skrivtid i hela (1,0 p) 3 cm man bryningsindex i glaset på ett 2. två spalter (3,0 p)
 Tentamen i tillämpad Våglära FAF260, 2016 06 01 för M Skrivtid 08.00 13.00 Hjälpmedel: Formelblad och miniräknare Uppgifterna är inte sorteradee i svårighetsgrad Börja varje ny uppgift på ett nytt blad
Tentamen i tillämpad Våglära FAF260, 2016 06 01 för M Skrivtid 08.00 13.00 Hjälpmedel: Formelblad och miniräknare Uppgifterna är inte sorteradee i svårighetsgrad Börja varje ny uppgift på ett nytt blad
Fysik TFYA86. Föreläsning 9/11
 Fysik TFYA86 Föreläsning 9/11 1 Elektromagnetiska vågor (ljus) University Physics: Kapitel 32, 33, 35, 36 (delar, översiktligt!) Översikt och breddning! FÖ: 9 (ljus) examineras främst genom ljuslabben
Fysik TFYA86 Föreläsning 9/11 1 Elektromagnetiska vågor (ljus) University Physics: Kapitel 32, 33, 35, 36 (delar, översiktligt!) Översikt och breddning! FÖ: 9 (ljus) examineras främst genom ljuslabben
I 1 I 2 I 3. Tentamen i Fotonik , kl Här kommer först några inledande frågor.
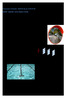 FAFF25-2014-03-14 Tentamen i Fotonik - 2014-03-14, kl. 14.00-19.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2014-03-14 Tentamen i Fotonik - 2014-03-14, kl. 14.00-19.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Tenta Elektrisk mätteknik och vågfysik (FFY616) 2013-12-19
 Tenta Elektrisk mätteknik och vågfysik (FFY616) 013-1-19 Tid och lokal: Torsdag 19 december kl. 14:00-18:00 i byggnad V. Examinator: Elsebeth Schröder (tel 031 77 844). Hjälpmedel: Chalmers-godkänd räknare,
Tenta Elektrisk mätteknik och vågfysik (FFY616) 013-1-19 Tid och lokal: Torsdag 19 december kl. 14:00-18:00 i byggnad V. Examinator: Elsebeth Schröder (tel 031 77 844). Hjälpmedel: Chalmers-godkänd räknare,
Parbildning. Om fotonens energi är mer än dubbelt så stor som elektronens vileoenergi (m e. c 2 ):
 Parbildning Vi ar studerat två sätt med vilket elektromagnetisk strålning kan växelverka med materia. För ögre energier ar vi även en tredje: Parbildning E mc Innebär att omvandling mellan energi oc massa
Parbildning Vi ar studerat två sätt med vilket elektromagnetisk strålning kan växelverka med materia. För ögre energier ar vi även en tredje: Parbildning E mc Innebär att omvandling mellan energi oc massa
