Syntes av digitala filter
|
|
|
- Per-Erik Engström
- för 6 år sedan
- Visningar:
Transkript
1 Kapitel 8 Syntes av digitala filter 8. Digitala filter I kapitel 7 hade vi sambandet (7.8) för ett linjärt system, enligt vilket utsignalens z-transform är insignalens transform multiplicerad med systemets överföringsfunktion Ŷ (z) = H(z) ˆX(z) (8.) Här är z-transformerna nära besläktade med signalernas spektra eller Fouriertransformer. Enligt (7.6) har vi sambanden X(ω) = ˆX(z) och Y (ω) = Ŷ (z) z=e (8.2) z=e jω jω Vi får således Y (ω) = H(e jω )X(ω) (8.3) Om vi uttrycker de komplexa funktionerna ovan med hjälp av magnitud och fas, X(ω) = X(ω) e j arg(x(ω)) (8.4) H(e jω ) = H(e jω ) e j arg(h(ejω )), (8.5) så ges magnituden och fasen hos utsignalens spektrum av där Y (ω) = Y (ω) e j arg(y (ω)) (8.6) Y (ω) = H(e jω ) X(ω) (8.7) arg(y (ω)) = arg(x(ω)) + arg(h(e jω )) (8.8) Sambandet (8.3) eller (8.6) visar hur ett linjärt system H påverkar de olika frekvenskomponenterna i insignalen. Systemet H fungerar som ett filter, som förstärker eller dämpar olika frekvenskomponenter hos insignalen x beroende på beloppet av H(e jω ). Funktionen H(e jω ) visar hur magnituden av olika frekvenskomponenter påverkas av 2
2 systemet H. Förutom att inverka på magnituden hos de olika frekvenskomponenterna, inför systemet även en fasförskjutning av storleken arg(h(e jω )). Den komplexa funktionen H(e jω ) kallas filtrets frekvenssvar. Ett filters frekvenssvar H(e jω ) kan åskådliggöras grafiskt i ett s.k. Bode-diagram, som anger magnituden H(e jω ) och fasförskjutningen arg(h(e jω )) som funktioner av frekvensen ω (jämför kurserna i reglerteknik). Det är värt att notera det enkla sambandet (8.3) mellan in- och utsignalernas spektra. Detta enkla samband, som kan karakteriseras med hjälp av en komplex multiplikation, utgör en av orsakerna till den stora betydelse som frekvensalysen har fått inom flera tillämpningar. En följd av (8.3) är att utsignalen från ett linjärt tidsinvariant system ej kan innehålla frekvenser som ej finns i insignalen. Endast tidsvarianta system eller olinjära system kan generera sådana frekvenskomponenter i utsignalen som ej finns i insignalen. Det är skäl att notera några egenskaper hos frekvenssvaret H(e jω ). Från definitionen av H(z) har vi H(e jω ) = h(n)e jωn (8.9) n= Frekvenssvaret är alltså Fouriertransformen av impulssvaret {h(n)} = {h(), h(), h(2),...}. Då koefficienterna h(n) är reella följer H(e jω ) = H (e jω ) (8.) Från den komplexa exponentialfunktionens periodicitet följer dessutom att H(e jω ) = H(e j(2π ω) ). Frekvenssvaret satisfierar således symmetriegenskapen H(e j(2π ω) ) = H (e jω ) (8.) dvs frekvenssvaret i intervallet [π, 2π] är komplexa konjugatet av frekvessvaret i intervallet [, π]. Det räcker därför med att specificera frekvenssvaret i intervallet [, π] för att entydigt definiera det för alla frekvenser. Följande exempel visar, hur ett filter som uppdelar en signal i sina frekvenskomponenter kan tillämpas för signalrekonstruktion. Exempel 8.. I exempel 2. betraktades problemet att rekonstruera en signal x från en observerad signal y = F x + e. Om signalerna är diskreta ges spektret hos y av Y (ω) = F (e jω )X(ω) + E(ω) Antag att x har ett spektrum som är koncentrerat till ett lågfrekvensband ω ω, medan bruset e består av höga frekvenser ω ω 2 > ω. Signalen x kunde då rekonstrueras genom att konstruera ett lågpassfilter H(z) som satisfierar H(e jω ), ω ω och H(e jω ), ω ω 2. Då fås H(e jω )Y (e jω ) = H(e jω )F (e jω )X(e jω ) + H(e jω )E(e jω ) F (e jω )X(e jω ) 3
3 och signalen x kan approximativt rekonstrueras genom att välja x r = F Hy, vilket ger X r (e jω ) = F (e jω )H(e jω )Y (e jω ) X(e jω ) som är ekvivalent med x r x. Anmärkning 8.. Frekvenssvaret hos ett linjärt system för en periodisk signal {x(n)} = {e jωn } bestående av en enda frekvens ω kan enkelt härledas i tidsplanet direkt utgående från ekvationen (7.2). Vi får y(n) = h()x(n) + h()x(n ) + h(2)x(n 2) + = h()e jωn + h()e jω(n ) + h(2)e jω(n 2) + = [h() + h()e jω + h(2)e 2jω + ]e jωn = H(e jω )e jωn (8.2) vilket är ekvivalent med (8.3) begränsad till en frekvenskomponent. Vi skall ännu verifiera att systemet har den förväntade effekten på signaler av formen {sin(ωn)} och {cos(ωn)}. Insignalsekvensen i (8.2) kan skrivas i en reell och imaginär komponent enligt e jωn = cos(ωn) + j sin(ωn), n =, ±, ±2,... Det följer att den reella komponenten av utsignalen y(n) är systemets svar på insignalen {cos(ωn)}, och den imaginära komponenten av utsignalen är systemets svar för insignalen {sin(ωn)}. De reella och imaginära komponenterna hos utsignalen (8.2) kan bestämmas genom att introducera magnituden och fasen hos överföringsoperatorn, H(e jω ) = H(e jω ) e j arg(h(ejω )), varvid (8.2) kan skrivas Här har vi y(n) = H(e jω ) e j arg(h(ejω )) e jωn = H(e jω ) e j(ωn+arg(h(ejω ))) e j(ωn+arg(h(ejω ))) = cos[ωn + arg(h(e jω ))] + j sin[ωn + arg(h(e jω ))] Det följer att systemets transformerar sekvensen {cos(ωn)} enligt (8.3) y(n) = H(e jω ) cos[ωn + arg(h(e jω ))] (8.4) och på samma sätt fås att systemets svar för insignalsekvensen {sin(ωn)} är y(n) = H(e jω ) sin[ωn + arg(h(e jω ))] (8.5) Systemet förstärkning och fasförskjutning av frekvensenkomponenten ω är således i enlighet med det tidigare erhållna resultatet. Problem 8.. Betrakta ett diskret system av första ordningen, y(n) ay(n ) = x(n) (8.6) Bestäm systemets frekvenssvar (förstärkning och fasförskjutning) för de numeriska värdena a =.6 och a =.6. Åskådliggör sambanden i form av ett Bode-diagram. 4
4 8.. Klassificering av digitala filter Filtren klassificeras enligt sitt impulssvar i filter med ändligt impulssvar och filter med oändligt impulssvar. Ett filter med ett ändligt impulssvar ges av y(n) = N k= h(k)x(n k) = h()x(n) + h()x(n ) + + h(n )x(n N + ) (8.7) En standard förkortning för sådana filter är FIR filter (från Finite Impulse Response ). Ett filter med ett oändligt impulssvar har formen y(n) = h(k)x(n k) (8.8) k= Standardförkortningen för sådana filter är IIR filter (från Infinite Impulse Response ). I praktiken har IIR filter en ändlig ordning, och de kan därför skrivas i formen (jämför ekvation (7.28)) y(n) + b y(n ) + + b N y(n N) = a x(n) + a x(n ) + + a M x(n M), n =...,,,,... (8.9) 8.2 Filterspecifikationer Filtersyntes går ut på att konstruera ett filter vars frekvenssvar uppfyller givna specifikationer. Typiska specifikationer är att filtret effektivt skall spärra vissa oönskade frekvenskomponenter i insignalen, medan de intressanta frekvenskomponenternas storlek och (relativa) fasförskjutning skall vara opåverkad. Vid filtersyntesen bör olika begränsningar beaktas som filtret i praktiken skall uppfylla. En viktig begränsning i flera tillämpningar är att filtret bör vara kausalt. En annan begränsning är att filtret skall ha ändlig ordning (som i praktiken dock kan vara mycket högt). Såsom vi skall se begränsar dessa krav de frekvenssvar som i praktiken kan realiseras Ideala filter För att belysa några av de begränsningar som uppstår vid filtersyntes skall vi undersöka impulssvaret hos ideala filter. Ett idealt lågpassfilter H D med bandbredden ω c < π har frekvenssvaret {, ω H D (e jω ωc ) = (8.2), ω > ω c Frekvensbandet ω ω c kallas filtrets passband och frekvensbandet ω > ω c är filtrets spärrband (eng. stopband). Ett idealt bandpassfilter och ett idealt högpassfilter definieras på analogt sätt. Observera att filtrets frekvenssvar p.g.a. symmetriegenskapen (8.) härvid betraktas i intervallet ω π. Passbandet hos ett digitalt högpassfilter är därför koncentrerat till frekvenser kring π. 5
5 Eftersom överföringsoperatorn är impulssvarets Fouriertransform, ges impulssvaret {h D (n)} hos det ideala lågpassfiltret genom att beräkna inversa Fouriertransformen av H D (e jω ). Enligt ekvation (4.24) fås vilket ger h D (n) = 2π π π h D () = ω c π h D (n) = ω c π H D (e jω )e jωn dω = 2π ωc ω c e jωn dω (8.2) (8.22) sin(nω c ) nω c, n = ±, ±2,... (8.23) Det ideala filtret kan ej representeras i form av en rationell överföringsfunktion av ändlig ordning. En annan viktig observation är, att impulssvaret hos det ideala filtret ej försvinner för negativa n. Det ideala filtret är icke-kausalt. I de flesta tillämpningar krävs att filtret skall vara kausalt. Det visar sig att kravet på kausalitet begränsar de filtersvar som kan erhållas. Det finns ett kvantitativt matematiskt resultat, det s.k. Paley-Wiener villkoret, enligt vilket det finns ett kausalt filter H(z) som har en given filterförstärkning H(e jω ) = g(ω), om och endast om π π log g(ω) dω <. Från detta villkor följer att förstärkningen hos ett kausalt filter ej kan försvinna i ett intervall. Det ideala filtret ovan uppfyller inte Paley-Wiener villkoret. Kravet på kausalitet begränsar även formen hos filtrets fasförskjutning. Från Fouriertransformens egenskaper i kapitel 4 följer att H(e jω ) är reellt om och endast om impulssvaret är symmetriskt; h( n) = h(n), och imaginärt om och endast om impulssvaret är antisymmetriskt; h( n) = h(n). För kausala system med h(n) =, n <, är impulssvarets symmetriska och antisymmetriska komponenter ekvivalenta, vilket introducerar ett samband mellan de reella och imaginära komponenterna hos frekvenssvaret H(e jω ). Från detta samband följer att fasförskjutningen hos ett kausalt filter ej kan specificeras oberoende av magnituden. Av reella filter som kan implementeras i praktiken krävs, att de har ändlig ordning och (vanligen) att de är kausala. Vid syntes av filter försöker man så väl som möjligt satisfiera specifikationerna med hjälp av reella filter Krav på linjär fasförskjutning Förutom filterförstärkningen påverkar även filtrets fasförskjutning utsignalen. Om fasförskjutningen i ett filters passband varierar så, att olika frekvenskomponenters faser förändras i förhållande till varandra, kommer signalen att förvrängas trots att förstärkningen i passbandet vore konstant. Detta är givetvis oacceptabelt i flera tillämpningar, bl.a. vid behandling av audiosignaler. För att se hurudana fasförskjutningar som kan tolereras, betrakta inverkan av ett linjärt diskret system H(z) på sinusformade signaler av formen x(t) = sin(ωt) (8.24) 6
6 Från avsnitt 8. har vi att systemet H(z) transformerar den periodiska signalen x(t) till en annan periodisk signal x f (t) med samma frekvens men med en annan amplitud och fas, x f (t) = A(ω) sin(ωt + θ(ω)) (8.25) där A(ω) = H(e jω ) och θ(ω) = arg(h(e jω )) (8.26) Det visar sig att för att ett filter ej skall införa fasförvrängning bör fasförskjutningen θ(ω) ges av det linjära sambandet eller θ(ω) = αω (8.27) θ(ω) = αω + π (8.28) där α är konstant. Ett filter vars fasförskjutning satisfierar (8.27) eller (8.28) säges vara faslinjärt. För sambnadet (8.27) ges den filtrerade signalen av x f (t) = A(ω) sin(ω(t α)) (8.29) Detta innebär att alla frekvenskomponenter tidsfördröjs med tiden α, och fasförskjutningen försorsakar därför ingen förvrängning av en signal med flera frekvenskomponenter. För sambandet (8.28) blir den filtrerade signalen x f (t) = A(ω) sin(ω(t α) + π) = A(ω) sin(ω(t α)) (8.3) Förutom tidsfördröjningen tillkommer i detta fall ett teckenbyte p.g.a. fasförskjutningen π. Det är lätt att inse att ett filter bör vara faslinjärt för att det ej skall införa fasförvrängning p.g.a. att olika frekvenskomponenters faser påverkas på olika sätt I vissa tillämpningar används s.k. generaliserat faslinjära filter. Fasförskjutningen hos generaliserat faslinjära filter satisfierar där α och β är konstanter. Den filtrerade signalen ges då av θ(ω) = β αω (8.3) x f (t) = A(ω) sin(ω(t α) + β) (8.32) dvs alla frekvenskomponenter tidsfördröjs med tiden α och fasförskjuts med vinkeln β. Faslinjära filter är en delmängd av generaliserat faslinjära filter. Ett generaliserat faslinjärt filter förorsakar fasförvrängning om β eller π. Vid studiet av ett filters fasförskjutning brukar man införa den s.k. faslöptiden eller fasfördröjningen T p (eng. phase delay) och den s.k. grupplöptiden eller gruppfördröjningen T g (eng. group delay): T p = θ(ω)/ω (8.33) T g = dθ(ω)/dω (8.34) 7
7 Faslöptiden T p är den tidsfördröjning som frekvenskomponenten ω får p.g.a. fasförskjutningen i filtret, ty sin(ωt + θ(ω)) = sin(ω(t T p )). Grupplöptiden T g är en vanligt använd storhet vid karakterisering av linjära filter, som uppstår vid analysen av ett filters inverkan på en amplitudmodulerad signal. Vi ser att ett filter är faslinjärt om det har en konstant fasfördröjning och generaliserat faslinjärt om och endast om det har en konstant grupplöptid. Följande exempel demonstrerar betydelsen av linjär fasförskjutning vid filtrering..5 s.5.5 s s 2 Figur 8.: Signalkomponenterna s och s 2 samt signalen s i exempel 8.2. Exempel 8.2. Betrakta en signal s som består av två komponenter enligt s(n) = s (n) + s 2 (n) där s och s 2 är lågfrekventa sinusformade komponenter, s (n) = sin(ω n) s 2 (n) = sin(ω 2 n) Komponenterna s och s 2 samt signalen s visas i figur 8.. Låt signalen s påverkas av en störning e så att vi får signalen x(n) = s(n) + e(n) 8
8 2 s 2.5 e.5 2 x 2 Figur 8.2: Den störningsfria signalen s, störningen e, samt signalen x i exempel 8.2. där e(n) är en högfrekvent sinusformad signal, e(n) = sin(ω e n) med ω e > ω och ω e > ω 2. Signalerna s, e och x visas i figur 8.2. Den lågfrekventa störningsfria signalen s kan bestämmas ur x genom lågpassfiltrering med ett filter H(z) som har frekvenskomponenterna ω och ω 2 i passbandet och som spärrar frekvensen ω e, dvs H(e jω ) och H(e jω 2 ), samt H(e jω e ). Den filtrerade signalen y ges då av y(n) y (n) + y 2 (n) där y (n) = sin ( ω n + arg(h(e jω )) ) y 2 (n) = sin ( ω 2 n + arg(h(e jω 2 )) ) Figur 8.3 visar signalkomponenterna s, s 2 och y, s 2 samt den filtrerade signalen y(n) för två olika lågpassfilter. Till vänster i figuren visas resultatet med ett filter som fasförskjuter de lågfrekventa komponenterna på olika sätt, varför den filtrerade signalen y blir förvrängd och signalen s rekonstrueras ej korrekt. Till höger visas resultatet med ett faslinjärt filter. I detta fall är fasförskjutningen sådan att den motsvarar samma 9
9 tidsförskjutning för alla frekvenskomponenter i passbandet, och den filtrerade signalen y är därför endast en tidsförskuten version av signalen s..5 s,y.5.5 s,y.5.5 s,y s,y s,y 2 2 s,y 2 Figur 8.3: Signaler i exempel 8.2. Överst: signalkomponenten s (heldragen) och motsvarande filtrerade signal y (streckad). I mitten: signalkomponenten s 2 (heldragen) och motsvarande filtrerade signal y 2 (streckad). Nederst: den störningsfria signalen s (heldragen) och den lågpassfiltrerade signalen y (streckad). Till vänster visas resultatet som fås med ett lågpassfilter med olinjär fasförskjutning, och till höger resultatet som fås med ett faslinjärt lågpassfilter Reella lågpass, bandpass- och högpassfilter Reella filter, som är kausala och har en ändlig ordning, kan endast approximativt uppfylla specifikationerna hos ideala lågpass-, bandpass- och högpassfilter. För reella filter anges specifikationerna därför med hjälp av toleranser, jämför figur 8.4. För ett lågpassfilter är specifikationerna av formen δ p H(e jω ) + δ p, ω ω p (8.35) H(e jω ) δ s, ω ω s (8.36) 2
10 Här är - ω ω p passbandet, - ω ω s spärrbandet, och - ω (ω p, ω s ) övergångsbandet. Talet δ p anger toleransen i passbandet, dvs den största tillåtna avvikelsen från det konstanta värdet ett hos filtrets förstärkning i passbandet. Talet δ s är toleransen i spärrbandet, dvs den maximala tillåtna förstärkningen i spärrbandet. Eftersom förstärkningen hos reella filter inte kan förändras diskontinuerligt som funktion av frekvensen, finns mellan passband och spärrband ett övergångsband. Ju snävare toleranser och smalare övergångsbandet är, desto högre filterordning fordras för att satisfiera specifikationerna. I stället för vinkelfrekvenser anges frekvensspecifikationerna ofta i form av frekvenser f p (= ω p /(2π)) respektive f s (= ω s /(2π)) och uppfattas som normerade i förhållande till samplingsfrekvensen. Om frekvenserna anges i Hz eller khz bör man observera att beakta samplingsfrekvensen f s vid filtersyntesen, så att frekvensen f motsvarar filtersvaret H(e jω ) vid ω = 2πf/f s. Vanligt är också att toleranserna anges i den logaritmiska enheten decibel. Den största avvikelsen A p i passbandet och den minsta dämpningen A s i spärrbandet angivna i decibel är således A p = 2 log( + δ p ) (8.37) A s = 2 log(δ s ) (8.38) Observera att för små δ p gäller med god noggrannhet approximationen A p = 2 log( + δ p ) = 2 ln( + δ p )/ ln 8.7δ p Bandpassfilter och högpassfilter definieras på analogt sätt. För bandpassfilter består passbandet av ett frekvensband [ω, ω 2 ]. För högpassfilter med bandbredden ω p är passbandet beläget i ett högfrekvent band [π ω p, π + ω p ] Frekvenstransformationer Ett bandpass- och högpassfilter skiljer sig från ett lågpassfilter endast i avseende å passbandets och spärrbandets lägen. Det är därför möjligt att ur ett lågpassfilter konstruera motsvarande bandpass- eller högpassfilter genom en frekvenstransformation som förskjuter passbandet till det önskade frekvensbandet. Denna metod är mycket användbar, eftersom man då kan utnyttja standardmetoder för syntes av lågpassfilter även för beräkning av andra filtertyper. Vid frekvenstransformation av ett filter substitueras variabeln z i överföringsfunktionen med en rationell funktion g(z ), så att det frekvenstransformerade filtret definieras av H f (z) = H(z) (8.39) z =g(z ) För att filtret H f (z) skall vara väldefinierat krävs att avbildningen z g(z ) bevarar filtrets stabilitet, samt att punkter på enhetscirkeln e jω, som ju definierar 2
11 Figur 8.4: Specifikationer för förstärkningen hos ett lågpassfilter, samt förstärkningen H(e jω ) hos ett reellt filter som funktion av normerad frekvens ω/π. frekvenssvaret, avbildas till andra punkter på enhetscirkel i enlighet med den önskade frekvenstransformationen. Dylika frekvenstransformationer finns utvecklade, se t.ex. tabell 8.3 i Proakis och Manolakis (996). En speciellt enkel formel fås för tranformationen av ett lågpassfilter H LP (z) till ett högpassfilter H HP (z) med samma bandbredd. Transformationen består då helt enkelt av en förskjutning av frekvenserna enligt ω ω + π, så att lågpassbandet lokaliserat runt frekvensen noll förskjuts till ett högpassband lokaliserat runt frekvensen π. Högpassfiltrets frekvenssvar definieras då av och dess överföringsfunktion är således Eftersom H HP (e jω ) = H LP (e j(ω+π) ) = H LP ( e jω ) (8.4) följer att högpassfiltrets impulssvar h HP (k) ges av H HP (z) = H LP ( z) (8.4) H LP ( z) = ( ) k h LP (k)z k (8.42) k= h HP (k) = ( ) k h LP (k) (8.43) Problem 8.2. Betrakta de två filtren som studerades i problem 8. (a =.6 och a =.6). Visa att de är relaterade enligt (8.4) och (8.43), och att deras frekvenssvar är förskjutna i förhållnade till varandra med π. 22
12 8.3 Syntes av filter med ändligt impulssvar I detta avsnitt diskuteras syntes av filter med ändligt impulssvar (FIR filter). Sådana filter beskrivs av y(n) = h()x(n) + h()x(n ) + + h(n )x(n N + ) (8.44) och deras överföringsfunktion har formen H(z) = h() + h()z + + h(n )z N+ (8.45) Filter av denna typ har en del fördelar som har gjort dem mycket populära inom signalbehandlingstillämpningar. Syntesen av FIR filter är i flera avseenden enklare än syntesen av IIR filter. Deras stabilitet är i motsats till IIR filter garanterad, ty kriteriet (7.37) är automatiskt uppfyllt. Eventuell instabilitet behöver därför inte kontrolleras eller beaktas i samband med syntesen. Dessutom har de den trevliga egenskapen att det är enkelt att konstruera FIR filter med exakt linjär fasförskjutning, vilket är viktigt i flera tillämpningar (jämför avsnitt 8.2.2). Däremot finns det ej IIR filter som beskrivs av en rationell överföringsfunktion som skulle ha en exakt linjär fasförskjutning. Vid syntesen av FIR filter bestäms filterparametrarna så att det önskade frekvenssvaret approximeras möjligast väl. De viktigaste metoderna för syntes av FIR filter baserar sig dels på de ideala filterformlerna i kombination med s.k. fönsterfunktioner eller s.k. frekvenssampling, dels på direkt optimering av filterparametrarna. Vi kommer att behandla dessa metoder nedan Faslinjära FIR filter Såsom tidigare diskuterats är det i flera tillämpningar viktigt att filtrets fasförskjutning är linjär i passbandet, dvs θ(ω) = arg(h(e jω )) = β αω. En trevlig egenskap hos filter med ändligt impulssvar är att de enkelt kan konstrueras så att fasförskjutningen är linjär. För att se hur detta kan åstadkommas, betrakta FIR filtret i ekvation (8.45). Filtrets frekvenssvar är H(e jω ) = N k= h(k)e jωk = h() + h()e jω + h(2)e j2ω + + h(n )e j(n )ω (8.46) Låt N vara udda, och antag att impulssvaret väljs så att h(k) = h(n k), k =,,..., (N )/2 (8.47) Ett sådant impulssvar säges vara symmetriskt. Betrakta för enkelhetens skull fallet N = 5. Då implicerar symmetrin h() = h(4) och h() = h(3). Frekvenssvaret ges av H(e jω ) = h() + h()e jω + h(2)e j2ω + h()e j3ω + h()e j4ω 23
13 Här är = e j2ω[ ) ) h() (e j2ω + e j2ω + h() (e jω + e jω + h(2) ] = e j2ω[ 2h() cos(2ω) + 2h() cos(ω) + h(2) ] (8.48) = e j2ω H r (ω) (8.49) H r (ω) = 2h() cos(2ω) + 2h() cos(ω) + h(2) (8.5) reell. Vi kan skriva sambandet ovan i formen och, eftersom e jπ =, H(e jω ) = H r (ω) e j2ω, om H r (ω) > (8.5) H(e jω ) = H r (ω) e j2ω = H r (ω) e j(2ω π), om H r (ω) < (8.52) Det följer att filtrets fasförskjutning är linjär, om H r (ω) ej byter tecken. Det är fallet endast om H(z) har nollställen på enhetscirkeln z = e jω. För jämna N fås ett analogt resultat. Betrakta t.ex. fallet N = 4. Då har vi h() = h(3) och h() = h(2), och impulssvaret blir H(e jω ) = h() + h()e jω + h()e j2ω + h()e j3ω = e j3ω/2[ ) ) ] h() (e j3ω/2 + e j3ω/2 + h() (e jω/2 + e jω/2 = e j3ω/2[ 2h() cos(3ω/2) + 2h() cos(ω/2)] (8.53) = e j3ω/2 H r (ω) (8.54) och fasförskjutningens linjäritet följer på samma sätt som ovan. Resultatet kan generaliseras till det allmänna fallet, och kan sammanfattas enligt följande. Frekvenssvaret hos symmetriska FIR filter. Betrakta ett symmetriskt FIR filter av längden N, för vilket impulssvaret satisfierar h(k) = h(n k). Dess frekvenssvar är där H(e jω ) = e j(n )ω/2 H r (ω) (8.55) H r (ω) = h( N (N 3)/2 ) + 2 h(k) cos [ ( N ], ω k) N udda (8.56) 2 2 k= (N/2) H r (ω) = 2 h(k) cos [ ω k= ( N ], k) N jämn (8.57) 2 24
14 Faslinjära FIR filter kan också åstadkommas genom att välja impulssvaret antisymmetriskt, varvid h(k) = h(n k), k =,,..., (N )/2 (8.58) För k = (N )/2 implicerar villkoret h( N ) =. Frekvenssvaret för detta fall 2 kan bestämmas i analogi med ovan. På grund av den antisymmetiska egenskapen kombineras de komplexa exponentialfunktionerna i frekvenssvaret i detta fall till sinusfunktioner. Vi kan sammanfatta resultatet enligt följande. Frekvenssvaret hos antisymmetriska FIR filter. Betrakta ett antisymmetriskt FIR filter av längden N, för vilket impulssvaret satisfierar h(k) = h(n k). Dess frekvenssvar är där H(e jω ) = e j[(n )ω/2 π/2] H r (ω) (8.59) (N 3)/2 H r (ω) = 2 h(k) sin [ ( N ], ω k) N udda (8.6) 2 k= (N/2) H r (ω) = 2 h(k) sin [ ( N ], ω k) N jämn (8.6) 2 k= Anmärkning 8.2. Vi har ovan specificerat FIR filtrets längd N, som antalet impulssvarskoefficienter h(), h(),..., h(n ). Denna konvention används bl.a. i böckerna av Ifeachor och Jervis (993) och Proakis och Manolakis (996). En annan vanlig konvention är att specificera filtrets ordning M, som den högsta potens z M i överföringsfunktionen. Ett filter vars längd är N har således ordningen M = N. Vid diskussion av symmetriska och antisymmetriska FIR filter bör man observera att filter med ett jämnt antal koefficienter N har en udda ordning M och vice versa. Anmärkning 8.3. De ovan beskrivna faslinjära FIR filtren är av fyra typer beroende på om N är udda eller jämnt och om filtret är symmetriskt eller antisymmetriskt. Enligt en standardklassificering uppdelas de faslinjära FIR filtren i typerna I IV enligt följande schema: Typ I: Symmetriskt med N udda (M jämnt) Typ II: Symmetriskt med N jämnt (M udda) Typ III: Antisymmetriskt med N udda (M jämnt) Typ IV: Antisymmetriskt med N jämnt (M udda) 25
15 Vid syntes av FIR filter bestäms filterkoefficienterna h(k), k =,,..., N, så att frekvenssvaret uppfyller specifikationerna. Villkoren för faslinjäritet är härvid enkla att beakta. Vid val av filtertyp bör man observera att de olika filtertyperna har olika egenskaper. Speciellt gäller att de symmetriska och antisymmetriska filtren har olikheter som gör dem lämpade för olika sorters tillämpningar. Vi har t.ex. att för de antisymmetriska filtren gäller H r () =, vilket gör dem olämpliga vid syntes av lågpassfilter. För det antisymmetriska filtret med udda N (filtertyp III) gäller dessutom H r (π) =, varur följer att denna filtertyp är ett bandpassfilter och är ej lämpad för syntes av lågpass- eller högpassfilter. Exempel 8.3. En enkel lågpassfiltreringsmetod består av att bilda det aritmetiska medelvärdet av ett antal signalvärden, y(n) = N N k= x(n k) (8.62) Filtret är tydligen ett faslinjärt FIR filter av typ I eller II, beroende på om N är udda eller jämn. Filtrets överföringsfunktion är H(z) = N N k= z k = N z N z (8.63) Överföringsfunktionen nollställen består av lösningarna till z N = med undantag av z =, som förkortas av nämnaren, dvs punkterna z k = e j2πk/n, k =, 2,..., N Alla nollställen befinner sig således på enhetscirkeln. Problem 8.3. Bestäm förstärkningen och fasförskjutningen som funktion av frekvensen för filtret (8.62) för fallet N = Syntes baserad på fönsterfunktioner I detta avsnitt diskuteras en standardmetod för syntes av faslinjära FIR filter, som baserar sig på trunkering av impulssvaret hos ett idealt filter. För att undvika en försämring av filtrets frekvenssvar som en direkt trunkeringen av det optimala impulssvaret medför, utnyttjas speciella viktfunktioner. Impulssvaret hos ett idealt lågpassfilter med bandbredden f c = ω c /(2π) ges av (8.22), h D () = ω c π = 2f c (8.64) h D (n) = ω c sin(nω c ) sin(nω c ) = 2f c, n π nω c nω c (8.65) 26
16 På samma sätt kan man bestämma impulssvaret hos ideala högpass, bandpass- och bandspärrfilter, se tabell 6.2 i Ifeachor och Jervis (993) för en sammanfattning. Som vi tidigare såg kan de ideala filtren ej realiseras med system av ändlig ordning. Ett sätt att approximera det ideala filtret är att trunkera dess Fourierserieutveckling. Enligt tidigare har vi att det ideala filtrets frekvenssvar är impulssvarets Fouriertransform, H D (e jω ) = h D (n)e jωn (8.66) n= Genom att trunkera summan fås en approximation enligt H M (e jω ) = som motsvaras av överföringsfunktionen M n= M h D (n)e jωn (8.67) H M (z) = h D ( M)z M + h D ( M + )z M + + h D (M)z M (8.68) Detta filter är fortfarande icke-kausalt, men genom att introducera en extra tidsfördröjning på M tidsenheter, fås det kausala filtret H M,kausal (z) = z M H M (z) = h D ( M) + h D ( M + )z + + h D (M)z 2M (8.69) Det ideala filtrets frekvenssvar är en pulsfunktion. Trunkeringen enligt (8.67) är därför jämförbar med approximationen i ekvation (3.48) av en pulsfunktion med en trunkerad Fourierserieutveckling. Vi såg i kapitel 3 att en dylik trunkerad summautveckling av en pulsfunktion ger överskjutningar vid diskontinuitetspunkterna, jämför anmärkning 3.3 och Gibbs fenomen. Detta illustreras i figur 8.5, som visar förstärkningen hos filtret (8.68) (eller (8.69)) för olika M. För att få en bättre approximation av det ideala filtret bör det trunkerade filtret i (8.69) därför i praktiken modifieras. En praktisk procedur för att förbättra den trunkerade utvecklingen är att införa en funktion w(n) och ersätta approximationen (8.67) med H(e jω ) = M n= M w(n)h D (n)e jωn (8.7) Funktionen w(n) kallas fönsterfunktion (eng. window function). Observera att den trunkerade summan (8.67) är ett specialfall av (8.7) med den rektangulära fönsterfunktionen w(n) = {, n M, n > M (8.7) För att se hur fönsterfunktionen påverkar frekvenssvaret H(e jω ) betraktar vi operationen i högra ledet av (8.7) i frekvensplanet. Vi introducerar Fouriertransformen 27
17 Figur 8.5: Förstärkningen H M (e jω ) hos trunkerade filter av formen (8.68) (eller (8.69)) för M = 6, 2 och 25. Det ideala lågpassfiltrets bandbredd är 2.4π. Frekvensen är angiven som en normerad frekvens ω/π. av fönsterfunktionen w(n), W (ω) = M n= M w(n)e jωn (8.72) Enligt (8.7) är H(e jω ) Fouriertransformen av sekvensen w(n)h D (n). Precis som diskret faltning i tidsplanet motsvarades av multiplikation i frekvensplanet, så kan man visa att multiplikationen w(n)h D (n) i tidsplanet motsvaras av en kontinuerlig faltningsintegral i frekvensplanet. Fouriertransformen av produkten w(n)h D (n) kan således uttryckas som faltningen av Fouriertransformerna H D (e jω ) och W (ω) av sekvenserna {h D (n)} 28
18 respektive {w(n)}, och det följer att H(e jω ) ges av H(e jω ) = π π H D (e jθ )W (ω θ)dθ (8.73) Hur väl (8.73) approximerar det ideala frekvenssvaret H D (e jω ) beror av formen hos fönsterfunktionen W (ω). Ur (8.73) följer, att ju bättre W (ω) är koncentrerad till frekvensen ω =, desto bättre approximerar (8.73) det ideala frekvenssvaret. Exakt likhet kan emellertid endast fås om fönsterfunktionen väljs oändligt bred (M ). Problemet är därför att välja en fönsterfunktion av given längd M, så att möjligast god approximation fås. För att undersöka formen hos fönsterfunktioner av ändlig längd, betrakta den rektangulära fönsterfunktionen i ekvation (8.7). Dess Fouriertransform är Dess absoluta belopp, W (ω) = W (ω) = M n= M e jωn = sin(ω(2m + )/2) sin(ω/2) (8.74) sin(ω(2m + )/2), ω π (8.75) sin(ω/2) har en karakteristisk form bestående av en s.k. huvudlob (eng. main lobe) vid ω = omgiven av ett antal sidlober (eng. side lobes), se figur 8.6. Det visar sig att andra fönsterfunktioner har en liknande form, och genom lämpligt val av fönsterfunktion kan man påverka huvudlobens bredd och sidlobernas amplitud. Dessa påverkar filterapproximationen, och för god approximation skall huvudloben vara möjligast smal och sidlobernas amplitud möjligast liten. För en fönsterfunktion av given längd kan dessa storheter ej minimeras oberoende av varandra. Vi har följande generella egenskaper: Då fönstrets längd N = 2M + ökas, minskar huvudlobens bredd, vilket resulterar i ett smalare övergångsband mellan passband och spärrband. Övergångsbandets bredd f ges approximativt av en formel av typen f = c/n (8.76) där c är en konstant som beror av fönsterfunktionens form. Den dominerande sidlobens amplitud beror främst av fönsterfunktionens form, och är ej starkt beroende av fönsterlängden. En fönsterfunktion som reducerar sidlobens amplitud resulterar i allmänhet i en bredare huvudlob. De vanligaste fönsterfunktionerna är Hanningfönstret, med fönsterfunktionen w(n) = cos(2πn/n), n (N )/2 (8.77) 29
19 Figur 8.6: Förstärkningen W (ω) hos en rektangulär fönsterfunktion (M = 5) som funktion av normerad frekvens ω/π. Hammingfönstret, med fönsterfunktionen w(n) = cos(2πn/n), n (N )/2 (8.78) Blackmanfönstret, med fönsterfunktionen och w(n) = cos[2πn/(n )] +.8 cos[4πn/(n )], n (N )/2 (8.79) Kaiserfönstret, med fönsterfunktionen ( β( [2n/(N )] 2 ) /2) w(n) = I I (β), n (N )/2 (8.8) där β är en positiv parameter och funktionen I (x) är en modifierad Besselfunktion av nollte ordning, som ges av serieutvecklingen I (x) = + [ ] (x/2) k 2 (8.8) De olika fönsterfunktionernas viktigaste egenskaper kan sammanfattas i övergångsbandets bredd f, den maximala avvikelsen i passbandet, förhållandet mellan huvudlobens och den dominerande sidlobens amplituder, samt dämpningen i spärrbandet. Se tabell 8.. k= k! 3
20 Fönster- Övergångsbandets Maximal avvikelse Förhållande Dämpning i Fönsterfunktionens bredd (Hz) i passbandet mellan huvudlob spärrbandet funktion namm (normerad) (db) och sidlob (db) (db) w(n) Rektangulär.9/N (8.7) Hanning 3./N (8.77) Hamming 3.3/N (8.78) Blackman 5.5/N (8.79) Kaiser 2.93/N (β = 4.54) (8.8) 4.32/N (β = 6.76) /N (β = 8.96) Tabell 8.: Några viktiga egenskaper hos ett antal vanliga fönsterfunktioner. I tabellen ges Kaiserfönster som ger dämpningen 5, 7 och 9dB i spärrbandet. Hanning-, Hamming- och Blackmanfönstren har fixerade egenskaper som beror enbart av N och som ej kan påverkas. Kaiserfönstret har däremot en parameter β, med vilken filtrets egenskaper kan påverkas för att uppnå önskad kompromiss mellan huvudlobens bredd och sidlobens amplitud. För β = reduceras Kaiserfönstret till ett rektangulärt fönster, medan t.ex. värdet β = 5.44 ger ett fönster som är mycket likt Hammingfönstret. Kaiserfönstret är även nära optimal i den meningen att för en given amplitud hos sidloben har ett Kaiserfönster den mesta energin koncentrerad i huvudloben. Filtersyntes med hjälp av fönsterfunktioner består av följande faser: Specificering av det ideala frekvanssvaret H D (e jω ) och dess impulssvar h D (n). Val av en lämplig fönsterfunktion och fönsterlängd N så att förstärkningen i passband och spärrband, samt övergångsbandets bredd f uppfyller givna specifikationer. Bestämning av filterapproximationen (8.7), där M H(z) = h(n)z n (8.82) n= M h(n) = w(n)h D (n), n = M, M +,..., M = (N )/2 (8.83) Bestämning av det sökta kausala FIR filtret genom introduktion av en tidsfördröjning motsvarande faktorn z M, H kausal (z) = z M H(z) (8.84) 3
21 Observera att alla de ovan beskrivna fönsterfunktionerna uppfyller symmetriegenskapen w( n) = w(n). Då det ideala filtrets impulssvar h D (n) normalt har en motsvarande symmetriegenskap, följer att h(n) i (8.83) satisfierar h( n) = h(n), n =,,..., M (8.85) Det följer att det kausala FIR filtret (8.84) är symmetriskt, och således ett faslinjärt filter, jämför avsnitt Syntes av FIR filter som baserar sig på det ideala frekvenssvaret och fönsterfunktioner är en enkel och i praktiken mycket användbar metod. En begränsning hos metoden är att det kräver beräkning av det ideala filtrets impulssvar, vilket kan vara besvärligt i vissa tillämpningar där det ideala frekvenssvaret H D (e jω ) är sådant att impulssvaret h D (n) ej kan erhållas analytiskt. Exempel 8.4. Betrakta problemet att konstruera ett lågpass FIR filter som satisfierar följande specifikationer: - passbandets bredd:.5khz - övergångsbandets bredd:.5 khz - dämpning i spärrbandet: > 5 db, då samplingsfrekvensen är 8 khz. Det ideala lågpassfiltret har impulssvaret (8.22), h D () = 2f c h D (n) = 2f c sin(nω c ) nω c, n Enligt tabell 6.3 i Ifeachor och Jervis (993) uppfyller Hamming-, Blackman- och Kaiserfönstren (men inte det rektangulära fönstret eller Hanningfönstret) kravet på dämpning i spärrbandet. Vi väljer i detta exempel ett Hammingfönster. Med samplingsfrekvensen f s = 8 khz motsvarar den specificerade bredden.5 khz för övergångsbandet (normerad till samplingsperioden T s = ) f =.5/8 =.625. Övergångsbandets bredd som en funktion av filterlängden ges av (8.76). Enligt tabellen är för ett Hammingfönster c = 3.3, och det följer att filtrets längd bör vara minst N = 3.3/ f c = 3.3/.625 = Vi väljer därför N = 53. Då är M = (N )/2 = 26 och filterkoefficienterna ges av (8.83), h(n) = w(n)h D (n), n 26 där h D (n) är givet ovan och w(n) är Hammingfönsterfunktionen w(n) = cos(2πn/n), n 26 För att få god approximation i det specificerade passbandet är det vanlig praxis att välja det ideala lågpassfiltrets bandbredd f c mitt i övergångsbandet, dvs f c = (.5 +.5/2)kHz =.75kHz 32
22 vilket med samplingsfrekvensen f s = 8 khz motsvarar den normerade bandbredden f c =.75/8 = Filterkoefficienterna kan nu bestämmas enligt ovan. Tack vare symmetrin behöver endast h(), h(),..., h(26) beräknas, ty h( n) = h(n). För n = fås På samma sätt fås för n =, h D () = =.4375 w() = cos() = h() = w()h D () =.4375 sin(2π.2875) h D () = =.329 2π.2875 w() = cos(2π/53) =.9873 h() = h( ) = w()h D () =.39 De övriga koefficienterna fås på analogt sätt. Ett kausalt filter bestäms till slut enligt ekvation (8.84). Det kausala filtrets koefficienter ges i tabell 6.4 i Ifeachor och Jervis (993). Filtrets förstärkning och fasförskjutning visas i figur 8.7. Man kan verifiera att filtret satisfierar specifikationerna. 2 Magnitude (db) Frequency (Hz) Phase (degrees) Frequency (Hz) Figur 8.7: Förstärkning och fasförskjutning hos filtret i exempel Frekvenssampling Ett alternativt sätt att approximera ett idealt filter med ett kausalt FIR filter är genom s.k. frekvenssampling. Om det ideala filtret har frekvenssvaret H D (e jω ) ges impulssvaret av (jämför ekvation (8.2)) h D (n) = 2π π π H D (e jω )e jωn dω = 2π 33 2π H D (e jω )e jωn dω (8.86)
23 Frekvenssampling går ut på att approximera det ideala frekvenssvaret med en sekvens diskreta värden vid N ekvidistanta frekvenspunkter ω k = 2πk/N, k =,,..., N, så att vi har sekvensen H(k) = H D (e j(2π/n)k ), k =,,..., N (8.87) bestående av sampel av frekvenssvaret. Den diskreta sekvensen {H(k)} utgör en diskret Fouriertransform (DFT) av sekvensen {h(n)}, som kan bestämmas med hjälp av invers DFT (jämför avsnitt 4.3), h(n) = N N k= H(k)e j2πkn/n, n =,,..., N (8.88) Denna sekvens kan tas som koefficienterna hos ett FIR filter av längden N som approximerar det ideala filtret, H N (z) = h() + h()z + + h(n )z N+ (8.89) Från konstruktionen följer att frekvenssvaret överensstämmer exakt vid frekvenserna 2πk/N, H N (e j(2π/n)k ) = H D (e j(2π/n)k ), k =,,..., N (8.9) men tyvärr finns det inga garantier för att överensstämmelsen är god också mellan de diskreta frekvenspunkterna. För att förbättra approximationens egenskaper brukar man införa frekvenssampel i ett övergångsband mellan det ideala filtrets passband och spärrband. Sampelvärdena i övergångsbandet kan optimeras så att variationerna i passbandet och förstärkningen i passbandet minimeras. Se Ifeachor och Jervis (993) för detaljer Syntes baserad på optimering av filterkoefficienter De ovan beskrivna syntesmetoderna är inte optimala i den meningen att de skulle ge den bästa approximationen av det ideala frekvenssvaret för en given filterlängd. Ett optimalt filter kan beräknas genom att direkt optimera filtrets koefficienter h(n) så att avvikelsen från det ideala svaret minimeras. Låt H D (e jω ) vara det ideala frekvenssvaret som skall approximeras av ett FIR filter av längden N, vars frekvenssvar är H(e jω ) = N n= Vi introducerar ett frekvensviktat fel mellan frekvenssvaren, h(n)e jωn (8.9) E(e jω ) = W (e jω )[H D (e jω ) H(e jω )] (8.92) där W (e jω ) är en viktfunktion som reflekterar det faktum att att de tillåtna felen i t.ex. passbandet och spärrbandet kan vara olika stora. I den optimeringsbaserade 34
24 metoden minimeras det maximala värdet av det absoluta felet E(e jω ) med avseende å filterkoefficienterna {h(n)}, dvs man bestämmer filterkoefficienterna genom att lösa optimeringsproblemet [ min max h(),...,h(n ) ω π E(ejω ) ] (8.93) I allmänhet kräver man dessutom att filterkoefficienterna satisfierar symmetriegenskapen h(n) = h(n n) (8.94) eftersom man då kan garantera att det konstruerade filtret är faslinjärt. Då ett faslinjärt filter ej ger upphov till fasförvrängning räcker det i detta fall med att den ideala filterförstärkningen approximeras, medan fasförskjutningen kan ignoreras vid optimeringen. Felfunktionen (8.92) förenklas då till E(e jω ) = W (e jω )[ H D (e jω ) H(e jω ) ] (8.95) Då filtret är symmetriskt ges H(e jω ) som funktion av filterkoefficienterna av (8.56) eller (8.57). Optimeringsproblemet (8.93) är ett s.k. minimax optimeringsproblem, och filter som konstrueras genom lösning av (8.93) kallas därför även minimax filter. Minimax optimeringsproblem är i allmänhet numeriskt mycket krävande. Optimeringsproblemet (8.93) har emellertid en speciell struktur som gör det möjligt att konstruera effektiva algoritmer för dess lösning. Speciellt gäller att de optimala koefficienterna h(n) som minimerar (8.93) är sådana att det existerar L frekvenser ω l, l =,..., L, för vilka E(e jω ) antar sitt maximala värde, E(e jω l ) = max ω π E(ejω ), l =,..., L (8.96) Här beror L av filterlängden och de antagna symmetriegenskaperna hos impulssvaret. Ur egenskapen (8.96) följer, att felet hos det optimala filtret i passbandet och spärrbandet kommer att variera mellan maxima och minima vars absoluta belopp är lika stora (s.k. equiripple filter). För givna frekvenser ω l definierar (8.96) ett linjärt ekvationssystem från vilket koefficienterna h(),..., h(n ) kan beräknas. I praktiken är frekvenserna ω l emellertid ej kända, utan måste sökas fram iterativt. Detta kan göras med hjälp av en s.k. utbytesalgoritm, i vilken frekvenserna ω l iterativt byts ut mot nya frekvenser enligt en algoritm som ger konvergens till lösningen. Sådana utbytesalgoritmer är standardmetoder inom funktionsapproximering. En effektiv implementering av utbytesalgoritmen för optimering av filterkoefficienterna är Parks-McClellan algoritmen, som baserar sig på Remez utbytesalgoritm. Parks-McClellan metoden för syntes av FIR filter med optimerade koefficienter tillhör en av de mest populära filtersyntesmetoderna. Effektiv programvara som implementerar algoritmen finns tillgänglig. Den filterlängd N som fordras för att uppnå givna specifikationer kan i princip bestämmas iterativt genom att lösa minimax optimeringsproblemet för att antal filterlängder tills specifikationerna uppfylls. Då N i praktiken kan vara rätt stort är denna 35
25 metod emellertid inte speciellt effektiv. Därför har det utvecklats empiriska formler med vilka den fordrade filterlängden kan uppskattas. För ett faslinjärt lågpassfilter med toleransen δ p i passbandet och toleransen δ s i spärrbandet (jämför avsnitt 8.2.3), och med ett övergångsband av bredden f har vi skattningen N log(δ pδ s ) f + (8.97) Se även Ifeachor och Jervis (993) för ytterligare formler för skattning av filterordning. Exempel 8.5. Ett faslinjärt lågpassfilter skall ha passbandet ω ω p =.3π och spärrbandet skall börja vid ω s =.35π. Toleransen i passbandet är δ p =. och toleransen i spärrbandet är δ s =. (motsvarande 6 db dämpning). Filtrets ordning kan uppskattas med (8.97), vilket ger N log( 5 ) 3 4.6(.35.3)/2 + 3 Eftersom toleransen i spärrbandet är ggr strängare än toleransen i passbandet skall felet i (8.95) viktas i motsvarande förhållande. Därför väljs viktfunktionen W (e jω ) = {, ω.3π,.35π ω π Optimering av filtret med hjälp av Parks-McClellan algoritmen kan utföras med hjälp av programmet remez i MATLABs Signal Procesing Toolbox. Optimeringen ger ett faslinjärt FIR filter som uppfyller specifikationerna. Filtrets förstärkning och fasförskjutning visas i figur Syntes av filter med oändligt impulssvar I detta avsnitt behandlas några standardmetoder för syntes av filter med oändligt impulssvar (IIR filter). Ett IIR filter av ordningen N beskrivs av differensekvationen y(n) + b y(n ) + + b N y(n N) = a x(n) + a x(n ) + + a M y(n M) (8.98) och dess överföringsfunktion är H(z) = a z N + a z N + + a M z N M z N + b z N + + b N (8.99) En styrka hos filter med oändligt impulssvar är den extra flexibilitet som nämnarpolynomet hos H(z) erbjuder. Ett IIR filter kräver därför i allmänhet ett färre 36
26 2 Magnitude (db) Normalized Angular Frequency ( π rads/sample) 5 Phase (degrees) Normalized Angular Frequency ( π rads/sample) Figur 8.8: Förstärkning och fasförskjutning hos filtret i exempel 8.5. antal koefficienter än ett FIR filter för att uppnå givna specifikationer. De är därför lämpade för tillämpningar där höga krav ställs på prestanda och beräkningshastighet. En nackdel hos IIR filter är att de kan vara känsligare för t.ex. kvantiseringsfel. Detta beror på den återkopplingsmekanism som uppstår p.g.a. att filtrets utsignal y(n) är en funktion av tidigare utsignaler y(n k). Om man vid syntesen inte tar hänsyn till filtrets känslighet kan avrundningsfel ha en betydande effekt på prestandan eller till och med göra filtret instabilt. Det är också i allmänhet svårare att beräkna koefficienterna hos ett IIR filter än det är för ett FIR filter. Det finns t.ex. inte lika effektiva algoritmer för beräkning av optimala koefficienter hos IIR filter som de som utvecklats för FIR filter (avsnitt 8.3.4). Vi skall i detta avsnitt diskutera tre standardmetoder för syntes av IIR filter: direkt placering av poler och nollställen, diskretisering av analoga standardfilter, samt en optimeringsbaserad syntesmetod Placering av poler och nollställen En enkel metod för syntes av filter baserar sig på direkt placering av filtrets poler och nollställen utgående från filterspecifikationerna. Låt överföringsfunktionen (8.99) ha nollställena z, z 2,..., z M och polerna p, p 2,..., p N. Genom faktorisering av täljaroch nämnarpolynomen kan överföringsfunktionen kan då skrivas i formen H(z) = K(z z )(z z 2 ) (z z M ) (z p )(z p 2 ) (z p N ) (8.) Filtersyntes kan utföras genom direkt placering av poler och nollställen genom att utnyttja följande observationer. Fullständig eliminering av en frekvens ω s fås genom att placera ett nollställe i z = e jω s, vilket implicerar H(e jω s ) =. Om e jω s ej är reell, dvs ω s är olikt eller 37
27 π, bör ett komplexkonjugerat nollställe placeras i z 2 = e jω s för att koefficienterna hos H(z) skall vara reella. Ett smalt passband vid frekvensen ω p kan åstadkommas genom att placera en pol vid p = re jωp, där den positiva radien r bör satisfiera r < för att ge ett stabilt filter. Om e jω p ej är reell, bör en komplexkonjugerad pol placeras i p 2 = re jω p. Valet av r påverkar passbandets bredd. Ett lämpligt värde för r kan bestämmas ur det approximativa sambandet r Bπ (8.) där B (Hz) anger den önskade bandbredden, definierad som frekvensbandet mellan de frekvenser där förstärkningen är 2 /2 3dB. Det approximativa sambandet mellan B och r kan användas om B <.3. Ett filter med ett smalt spärrband vid frekvensen ω s, och som helt eliminerar denna frekvens (ett s.k. notch-filter), kan konstrueras genom att placera ett nollställe vid z = e jω s och en pol vid p = re jω s (jämte motsvarande komplexkonjugerade nollställen och poler vid behov). Polerna introduceras för att påverka filterförstärkningens form kring notch-frekvensen, och för att göra spärrbandet smalare. Spärrbandets bredd beror av r, och även för det gäller det approximativa sambandet (8.). Vid behov kan filtrets förstärkning i passbandet justeras med den konstanta faktorn K i filteruttrycket (8.). Följande exempel visar hur metoden kan användas för att konstruera ett notchfilter. Exempel 8.6. Ett digitalt notch-filter skall konstrueras för att eliminera 5 Hz komponenten från nätet. Spärrbandets 3 db bredd skall vara 5 ± 5 Hz. Samplingsfrekvensen är 5 Hz. Med samplingsfrekvensen 5 Hz motsvaras notch-frekvensen 5 Hz av den normerade frekvensen 5/5 =., och den normerade bredden hos spärrbandet är B = /5 =.2. För eliminering av 5 Hz komponenten bör vi ha nollställen vid z = e j2π. och z 2 = e j2π.. För att få den specificerade bandbredden placeras poler i p = re j2π. och p 2 = re j2π.. Radien r bestäms enligt (8.), Filtrets överföringsfunktion blir således r =.2π =.937 (z e j2π. )(z e j2π. ) H(z) = (z.937e j2π. )(z.937e j2π. ) z 2 2 cos(2π.) z + = z cos(2π.) z = z2.68z + z 2.56z
28 Filtret beskrivs i tidsplanet av differensekvationen y(n).56y(n ) +.878y(n 2) = x(n).68x(n ) + x(n 2) och dess förstärkning visas i figur Figur 8.9: Förstärkningen hos filtret i exempel Metoder baserade på diskretisering av analoga filterprototyper I motsats till FIR filter, som saknar en direkt analog motsvarighet, är IIR filter den diskreta motsvarigheten till standard analoga filter som beskrivs av differentialekvationer. Differensekvationbeskrivningen för ett IIR filter kan uppfattas som en diskret approximation av en differentialekvation. Ett IIR filter av ändlig ordning kan därför betraktas som en diskret approximation av ett analogt filter. En viktig metod för syntes av digitala filter med oändligt impulssvar baserar sig på analoga filterprototyper, som sedan diskretiseras så, att filterspecifikationerna bibehålls hos det digitala filtret. Denna syntesmetod består således av två faser enligt följande. Syntes baserad på diskretisering av analoga filter: Steg. Konstruera ett analogt filter med överföringoperatorn H a (s) enligt de givna filterspecifikationerna. Steg 2. Diskretisera det i steg beräknade filtret för att ge ett digitalt IIR filter H(z) som satisfierar filterspecifikationerna. Denna metod kan verka som en onödig omväg. Varför gå omvägen att först konstruera ett analogt filter som sedan diskretiseras, om målsättningen är att beräkna ett digitalt filter? Det naturliga vore väl att beräkna det digitala filtret direkt utgående från specifikationerna. Trots detta är proceduren en av de vanligaste metoderna för 39
29 syntes av digitala IIR filter, så man väntar sig att det finns någon rationell orsak till detta. En orsak till att först beräkna ett analogt filter kan vara den, att de signaler som manipuleras vanligen är analoga. Det kan då vara naturligt att först beräkna det bästa analoga filtret för ifrågavarande signalbehandlingsuppgift, och sedan diskretisera filtret. Syntesmetoden reflekterar således direkt implementeringsprocessen, i vilket ett analogt signalbehandlingsproblem implementeras digitalt. På detta sätt får man också en direkt uppfattning om vad som kan utföras i kontinuerlig tid, och hur stor försämring i prestanda som den diskreta implementeringen medför. Detta resonemang beaktar emellertid inte det faktum att de digitala filtren inte har samma begränsningar som analoga filter. Det är därför möjligt att med digitala filter lösa signalbehandlingsuppgifter som inte kan utföras med analoga filter. Det är t.ex. inte möjligt att konstruera exakt faslinjära analoga filter av ändlig ordning, vilket som vi ovan sett utan svårighet kan åstadkommas med ett symmetriskt FIR filter. I detta ljus utgör det en onödig inskränkning att begränsa sig till filtertyper som fås genom diskretisering av analoga standardfilter. En viktig orsak till metodens popularitet torde helt enkelt vara den att metoder för analog filtersyntes har utvecklats tidigare än syntesmetoderna för digitala filter. Då digitaltekniken först infördes i olika tillämpningar var det mest ändamålsenligt att helt enkelt diskretisera de tidigare använda analoga filtren, med vilka man redan hade en lång erfarenhet och vars funktionssätt man kände till. Det finns ockå en mängd effektiva klassiska syntesmetoder utvecklade för analoga filter, medan motsvarande digitala syntesmetoder tenderar att vara mera komplicerade. I praktiken är en diskretisering av de analoga filtren en enkel och effektiv, och helt acceptabel syntesmetod för beräkning av digitala filter. Proceduren har däför kvarlevt som en standardmetod för digital filtersyntes, och den finns implementerad i de flesta programbibliotek för syntes av digitala filter. Vi skall i det följande beskriva en effektiv diskretiseringsmetod samt några av de viktigaste analoga filterprototyperna. Den viktigaste metoden för diskretisering av analoga filter baserar sig på den s.k. bilinjära transformationen. I denna metod bildas det diskreta filtret H(z) från det analoga filtret H a (s) enligt H(z) = H a (s) s= 2 z T +z ( 2 z ) = H a T + z (8.2) där T >. Avbildningen s = 2 z, T > (8.3) T + z kallas bilinjär transformation. Den har inversen z = + (T/2)s (T/2)s 4 (8.4)
GRUNDKURS I SIGNALBEHANDLING (454300), 5sp Tentamen
 GRUNDKURS I SIGNALBEHANDLING (454300), 5sp Tentamen 26.02013 kursens övningsuppgifter eller gamla tentamensuppgifter, eller Matlab-, Scilab- eller Octave- programmerbara kalkylatorer eller datorer. 1.
GRUNDKURS I SIGNALBEHANDLING (454300), 5sp Tentamen 26.02013 kursens övningsuppgifter eller gamla tentamensuppgifter, eller Matlab-, Scilab- eller Octave- programmerbara kalkylatorer eller datorer. 1.
DIGITALA FILTER. Tillämpad Fysik Och Elektronik 1. Frekvensfunktioner FREKVENSSVAR FÖR ETT TIDSDISKRET SYSTEM. x(n)= Asin(Ωn)
 DIGITALA FILTER TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 1 Frekvensfunktioner x(n)= Asin(Ωn) y(n) H(z) TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 2 FREKVENSSVAR FÖR ETT TIDSDISKRET SYSTEM
DIGITALA FILTER TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 1 Frekvensfunktioner x(n)= Asin(Ωn) y(n) H(z) TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 2 FREKVENSSVAR FÖR ETT TIDSDISKRET SYSTEM
Implementering av digitala filter
 Kapitel 9 Implementering av digitala filter Som vi sett i kapitel 8 kan det behövas ett mycket stort antal koefficienter för att representera ett digitalt filter. Detta gäller i synnerhet FIR filter. Det
Kapitel 9 Implementering av digitala filter Som vi sett i kapitel 8 kan det behövas ett mycket stort antal koefficienter för att representera ett digitalt filter. Detta gäller i synnerhet FIR filter. Det
TIDSDISKRETA SYSTEM SYSTEMEGENSKAPER. Minne Kausalitet Tidsinvarians. Linjäritet Inverterbarhet Stabilitet. System. Tillämpad Fysik och Elektronik 1
 TIDSDISKRETA SYSTEM TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 1 SYSTEMEGENSKAPER x[n] System y[n] Minne Kausalitet Tidsinvarians Linjäritet Inverterbarhet Stabilitet TILLÄMPAD FYSIK OCH ELEKTRONIK,
TIDSDISKRETA SYSTEM TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 1 SYSTEMEGENSKAPER x[n] System y[n] Minne Kausalitet Tidsinvarians Linjäritet Inverterbarhet Stabilitet TILLÄMPAD FYSIK OCH ELEKTRONIK,
Signaler några grundbegrepp
 Kapitel 2 Signaler några grundbegrepp I detta avsnitt skall vi behandla några grundbegrepp vid analysen av signaler. För att illustrera de problemställningar som kan uppstå skall vi först betrakta ett
Kapitel 2 Signaler några grundbegrepp I detta avsnitt skall vi behandla några grundbegrepp vid analysen av signaler. För att illustrera de problemställningar som kan uppstå skall vi först betrakta ett
Spektrala Transformer
 Spektrala Transformer Kurssammanfattning Fyra kärnkoncept Sampling Faltning Poler och nollställen Fouriertransform Koncept #1: Sampling En korrekt samplad signal kan rekonstrueras exakt, dvs ingen information
Spektrala Transformer Kurssammanfattning Fyra kärnkoncept Sampling Faltning Poler och nollställen Fouriertransform Koncept #1: Sampling En korrekt samplad signal kan rekonstrueras exakt, dvs ingen information
Resttentamen i Signaler och System Måndagen den 11.januari 2010, kl 14-19
 Resttentamen i Signaler och System Måndagen den 11.januari 2010, kl 14-19 Tillåtna hjälpmedel: Valfri miniräknare (utan möjlighet till trådlös kommunkation). Valfri litteratur, inkl. kursböcker, formelsamlingar.
Resttentamen i Signaler och System Måndagen den 11.januari 2010, kl 14-19 Tillåtna hjälpmedel: Valfri miniräknare (utan möjlighet till trådlös kommunkation). Valfri litteratur, inkl. kursböcker, formelsamlingar.
DT1130 Spektrala transformer Tentamen
 DT Spektrala transformer Tentamen 72 Tentamen består av fem uppgifter där varje uppgift maximalt ger 4 p. Normalt gäller följande betygsgränser: E: 9 p, D:.5 p, C: 4 p, B: 6 p, A: 8 p Tillåtna hjälpmedel:
DT Spektrala transformer Tentamen 72 Tentamen består av fem uppgifter där varje uppgift maximalt ger 4 p. Normalt gäller följande betygsgränser: E: 9 p, D:.5 p, C: 4 p, B: 6 p, A: 8 p Tillåtna hjälpmedel:
i(t) C i(t) = dq(t) dt = C dy(t) dt y(t) + (4)
 2 Andra lektionen 2. Impulssvar 2.. En liten krets Beräkna impulssvaret för kretsen i figur genom att beräkna hur y(t) beror av x(t). R x(t) i(t) C y(t) Figur : Första ordningens lågpassfilter. Utsignalen
2 Andra lektionen 2. Impulssvar 2.. En liten krets Beräkna impulssvaret för kretsen i figur genom att beräkna hur y(t) beror av x(t). R x(t) i(t) C y(t) Figur : Första ordningens lågpassfilter. Utsignalen
Diskreta signaler och system
 Kapitel 7 Diskreta signaler och system I detta kapitel diskuteras grundläggande teori för diskreta signaler och system. För diskreta signaler introduceras z-transformen, som ligger som grund för representationen
Kapitel 7 Diskreta signaler och system I detta kapitel diskuteras grundläggande teori för diskreta signaler och system. För diskreta signaler introduceras z-transformen, som ligger som grund för representationen
Laplace, Fourier och resten varför alla dessa transformer?
 Laplace, Fourier och resten varför alla dessa transformer? 1 Bakgrund till transformer i kontinuerlig tid Idé 1: Representera in- och utsignaler till LTI-system i samma basfunktion Förenklad analys! Idé
Laplace, Fourier och resten varför alla dessa transformer? 1 Bakgrund till transformer i kontinuerlig tid Idé 1: Representera in- och utsignaler till LTI-system i samma basfunktion Förenklad analys! Idé
Exempelsamling Grundläggande systemmodeller. Klas Nordberg Computer Vision Laboratory Department of Electrical Engineering Linköping University
 Exempelsamling Grundläggande systemmodeller Klas Nordberg Computer Vision Laboratory Department of Electrical Engineering Linköping University Version: 0.11 September 14, 2015 Uppgifter markerade med (A)
Exempelsamling Grundläggande systemmodeller Klas Nordberg Computer Vision Laboratory Department of Electrical Engineering Linköping University Version: 0.11 September 14, 2015 Uppgifter markerade med (A)
FÖRELÄSNING 13: Analoga o p. 1 Digitala filter. Kausalitet. Stabilitet. Ex) på användning av analoga p. 2 filter = tidskontinuerliga filter
 FÖRELÄSNING 3: Analoga o p. Digitala filter. Kausalitet. Stabilitet. Analoga filter Ideala filter Butterworthfilter (kursivt här, kommer inte på tentan, men ganska bra för förståelsen) Kausalitet t oh
FÖRELÄSNING 3: Analoga o p. Digitala filter. Kausalitet. Stabilitet. Analoga filter Ideala filter Butterworthfilter (kursivt här, kommer inte på tentan, men ganska bra för förståelsen) Kausalitet t oh
DT1130 Spektrala transformer Tentamen
 DT3 Spektrala transformer Tentamen 3 Tentamen består av fem uppgifter där varje uppgift maximalt ger 4 p. Normalt gäller följande betygsgränser: E: 9 p, D:.5 p, C: 4 p, B: 6 p, A: 8 p Tillåtna hjälpmedel:
DT3 Spektrala transformer Tentamen 3 Tentamen består av fem uppgifter där varje uppgift maximalt ger 4 p. Normalt gäller följande betygsgränser: E: 9 p, D:.5 p, C: 4 p, B: 6 p, A: 8 p Tillåtna hjälpmedel:
Exempelsamling Grundläggande systemmodeller. Klas Nordberg Computer Vision Laboratory Department of Electrical Engineering Linköping University
 Exempelsamling Grundläggande systemmodeller Klas Nordberg Computer Vision Laboratory Department of Electrical Engineering Linköping University Version: 0.1 August 25, 2015 Uppgifter markerade med (A) är
Exempelsamling Grundläggande systemmodeller Klas Nordberg Computer Vision Laboratory Department of Electrical Engineering Linköping University Version: 0.1 August 25, 2015 Uppgifter markerade med (A) är
Tentamen i TMA 982 Linjära System och Transformer VV-salar, 27 aug 2013, kl
 Tentamen i TMA 982 Linjära System och Transformer VV-salar, 27 aug 2013, kl 8.30-12.30 Examinatorer: Lars Hammarstrand och Thomas Wernstål Tentamen består av två delar (Del I och Del II) på sammanlagt
Tentamen i TMA 982 Linjära System och Transformer VV-salar, 27 aug 2013, kl 8.30-12.30 Examinatorer: Lars Hammarstrand och Thomas Wernstål Tentamen består av två delar (Del I och Del II) på sammanlagt
Tentamen i ESS 010 Signaler och System E3 V-sektionen, 16 augusti 2005, kl 8.30 12.30
 Tentamen i ESS 00 Signaler och System E3 V-sektionen, 6 augusti 2005, kl 8.30 2.30 Examinator: Mats Viberg Tentamen består av 5 uppgifter som vardera ger maximalt 0 p. För godkänd tentamen fordras ca 20
Tentamen i ESS 00 Signaler och System E3 V-sektionen, 6 augusti 2005, kl 8.30 2.30 Examinator: Mats Viberg Tentamen består av 5 uppgifter som vardera ger maximalt 0 p. För godkänd tentamen fordras ca 20
RÄKNEEXEMPEL FÖRELÄSNINGAR Signaler&System del 2
 t 1) En tidskontinuerlig signal x( t) = e 106 u( t) samplas med sampelperioden 1 µs, varefter signalen trunkeras till 5 sampel. Den så erhållna signalen får utgöra insignal till ett tidsdiskret LTI-system
t 1) En tidskontinuerlig signal x( t) = e 106 u( t) samplas med sampelperioden 1 µs, varefter signalen trunkeras till 5 sampel. Den så erhållna signalen får utgöra insignal till ett tidsdiskret LTI-system
DIGITALA FILTER DIGITALA FILTER. Tillämpad Fysik Och Elektronik 1
 DIGITALA FILTER TILLÄMPAD FYIK OCH ELEKTRONIK, UMEÅ UNIVERITET 1 DIGITALA FILTER Digitala filter förekommer t.ex.: I Photoshop och andra PC-programvaror som filtrerar. I apparater med signalprocessorer,
DIGITALA FILTER TILLÄMPAD FYIK OCH ELEKTRONIK, UMEÅ UNIVERITET 1 DIGITALA FILTER Digitala filter förekommer t.ex.: I Photoshop och andra PC-programvaror som filtrerar. I apparater med signalprocessorer,
Lösningar till Övningsuppgifter
 Lösningar till Övningsuppgifter Digital Signal Processing Övningar med svar och lösningar Mikael Swartling Nedelko Grbic Bengt Mandersson rev. 07 Department of Electrical and Information Technology Lund
Lösningar till Övningsuppgifter Digital Signal Processing Övningar med svar och lösningar Mikael Swartling Nedelko Grbic Bengt Mandersson rev. 07 Department of Electrical and Information Technology Lund
1. Vi har givet två impulssvar enligt nedan (pilen under sekvenserna indikerar den position där n=0) h 1 (n) = [ ]
![1. Vi har givet två impulssvar enligt nedan (pilen under sekvenserna indikerar den position där n=0) h 1 (n) = [ ] 1. Vi har givet två impulssvar enligt nedan (pilen under sekvenserna indikerar den position där n=0) h 1 (n) = [ ]](/thumbs/55/36091918.jpg) TEKNISKA HÖGSKOLAN I LUND Institutionen för elektro- och informationsteknik Kurskod: ESS00 Tentamen i Digital Signalbehanding Datum: 0 5 Time period: 08.00 3.00 Bedömning: Sex uppgifter. Varje uppgift
TEKNISKA HÖGSKOLAN I LUND Institutionen för elektro- och informationsteknik Kurskod: ESS00 Tentamen i Digital Signalbehanding Datum: 0 5 Time period: 08.00 3.00 Bedömning: Sex uppgifter. Varje uppgift
Digitala filter. FIR Finit Impulse Response. Digitala filter. Digitala filter. Digitala filter
 Digitala filter Digitala filter FIR Finit Impulse Response Digitala filter förekommer t.ex.: I Matlab, Photoshop oh andra PCprogramvaror som filtrerar. I apparater med signalproessorer, t.ex. mobiltelefoner,
Digitala filter Digitala filter FIR Finit Impulse Response Digitala filter förekommer t.ex.: I Matlab, Photoshop oh andra PCprogramvaror som filtrerar. I apparater med signalproessorer, t.ex. mobiltelefoner,
DT1120/DT1130 Spektrala transformer Tentamen
 DT/DT3 Spektrala transformer Tentamen 86 Tentamen består av fem uppgifter där varje uppgift maximalt ger 4 p. Normalt gäller följande betygsgränser: E: 9 p, D:.5 p, C: 4 p, B: 6 p, A: 8 p Tillåtna hjälpmedel:
DT/DT3 Spektrala transformer Tentamen 86 Tentamen består av fem uppgifter där varje uppgift maximalt ger 4 p. Normalt gäller följande betygsgränser: E: 9 p, D:.5 p, C: 4 p, B: 6 p, A: 8 p Tillåtna hjälpmedel:
Innehåll. Innehåll. sida i
 1 Introduktion... 1.1 1.1 Kompendiestruktur... 1.1 1.2 Inledning... 1.1 1.3 Analogt/digitalt eller tidskontinuerligt/tidsdiskret... 1.2 1.4 Konventioner... 1.3 1.5 Varför digital signalbehandling?... 1.4
1 Introduktion... 1.1 1.1 Kompendiestruktur... 1.1 1.2 Inledning... 1.1 1.3 Analogt/digitalt eller tidskontinuerligt/tidsdiskret... 1.2 1.4 Konventioner... 1.3 1.5 Varför digital signalbehandling?... 1.4
DT1130 Spektrala transformer Tentamen
 DT3 Spektrala transformer Tentamen 5 Tentamen består av fem uppgifter där varje uppgift maximalt ger p. Normalt gäller följande betygsgränser: E: 9 p, D:.5 p, C: p, B: 6 p, A: 8 p Tillåtna hjälpmedel:
DT3 Spektrala transformer Tentamen 5 Tentamen består av fem uppgifter där varje uppgift maximalt ger p. Normalt gäller följande betygsgränser: E: 9 p, D:.5 p, C: p, B: 6 p, A: 8 p Tillåtna hjälpmedel:
Impulssvaret Betecknas h(t) respektive h(n). Impulssvaret beskriver hur ett system reagerar
 6 Sjätte lektionen 6.1 Transformvärlden 6.1.1 Repetera Rita upp en tankekarta över följande begrepp där du anger hur de hänger ihop och hur de betecknas. Vad beskriver de? Impulssvaret Amplitudsvaret (frekvensgången)
6 Sjätte lektionen 6.1 Transformvärlden 6.1.1 Repetera Rita upp en tankekarta över följande begrepp där du anger hur de hänger ihop och hur de betecknas. Vad beskriver de? Impulssvaret Amplitudsvaret (frekvensgången)
Laplace, Fourier och resten varför alla dessa transformer?
 Laplace, Fourier och resten varför alla dessa transformer? 1 Vi har sett hur ett LTI-system kan ges en komplett beskrivning av dess impulssvar. Genom att falta insignalen med impulssvaret erhålls systemets
Laplace, Fourier och resten varför alla dessa transformer? 1 Vi har sett hur ett LTI-system kan ges en komplett beskrivning av dess impulssvar. Genom att falta insignalen med impulssvaret erhålls systemets
Tentamen ssy080 Transformer, Signaler och System, D3
 Tentamen ssy080 Transformer, Signaler och System, D3 Examinator: Ants R. Silberberg oktober 009 kl. 4.00-8.00 lokal: Johanneberg Förfrågningar: Ants Silberberg, tel. 808 Lösningar: Anslås torsdag okt.
Tentamen ssy080 Transformer, Signaler och System, D3 Examinator: Ants R. Silberberg oktober 009 kl. 4.00-8.00 lokal: Johanneberg Förfrågningar: Ants Silberberg, tel. 808 Lösningar: Anslås torsdag okt.
Introduktion Digitala filter. Filter. Staffan Grundberg. 12 maj 2016
 12 maj 216 Innehåll Introduktion Första ordningens system Andra ordningens system Fördröjning Allmänt om filter Butterworthfilter Första ordningens system Andra ordningens system Fördröjning Allmänt om
12 maj 216 Innehåll Introduktion Första ordningens system Andra ordningens system Fördröjning Allmänt om filter Butterworthfilter Första ordningens system Andra ordningens system Fördröjning Allmänt om
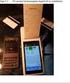
Diskret representation av kontinuerliga signaler
 Kapitel 6 Diskret representation av kontinuerliga signaler I digital signalbehandling är det vanligt att en kontinuerlig signal representeras i form av en diskret sekvens, t.ex. för att överföras eller
Kapitel 6 Diskret representation av kontinuerliga signaler I digital signalbehandling är det vanligt att en kontinuerlig signal representeras i form av en diskret sekvens, t.ex. för att överföras eller
Vad gör vi när vi bara har en mätserie och ingen elegant matematisk funktion? Spektrum av en samplad signal. Trunkering i tiden
 Vad gör vi när vi bara har en mätserie och ingen elegant matematisk funktion? 1 Spektrum av en samplad signal Samplingsprocessen kan skrivas som Fouriertranformen kan enligt linjäritetsoch tidsskiftsatsen
Vad gör vi när vi bara har en mätserie och ingen elegant matematisk funktion? 1 Spektrum av en samplad signal Samplingsprocessen kan skrivas som Fouriertranformen kan enligt linjäritetsoch tidsskiftsatsen
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna 15-18, 30/11-12/
 Uppsala Universitet Matematiska Institutionen Bo Styf Transformmetoder, 5 hp ES, gyl, Q, W 0-0-9 Sammanfattning av föreläsningarna 5-8, 30/ - / 0. Z-transformen ska avslutas och sedan blir det tentaförberedelser.
Uppsala Universitet Matematiska Institutionen Bo Styf Transformmetoder, 5 hp ES, gyl, Q, W 0-0-9 Sammanfattning av föreläsningarna 5-8, 30/ - / 0. Z-transformen ska avslutas och sedan blir det tentaförberedelser.
TSDT15 Signaler och System
 TSDT5 Signaler och System DATORUPPGIFTER VÅREN 03 OMGÅNG Mikael Olofsson, mikael@isy.liu.se Efter en förlaga av Lasse Alfredsson February, 03 Denna uppgiftsomgång behandlar faltning samt system- & signalanalys
TSDT5 Signaler och System DATORUPPGIFTER VÅREN 03 OMGÅNG Mikael Olofsson, mikael@isy.liu.se Efter en förlaga av Lasse Alfredsson February, 03 Denna uppgiftsomgång behandlar faltning samt system- & signalanalys
Elektronik 2018 EITA35
 Elektronik 218 EITA35 Föreläsning 1 Filter Lågpassfilter Högpassfilter (Allpassfilter) Bodediagram Hambley 296-32 218-1-2 Föreläsning 1, Elektronik 218 1 Laboration 2 Förberedelseuppgifter! (Ingen anmälan
Elektronik 218 EITA35 Föreläsning 1 Filter Lågpassfilter Högpassfilter (Allpassfilter) Bodediagram Hambley 296-32 218-1-2 Föreläsning 1, Elektronik 218 1 Laboration 2 Förberedelseuppgifter! (Ingen anmälan
DT1130 Spektrala transformer Tentamen
 DT3 Spektrala transformer Tentamen 6 Tentamen består av fem uppgifter där varje uppgift maximalt ger 4 p. Normalt gäller följande betygsgränser: E: 9 p, D:.5 p, C: 4 p, B: 6 p, A: 8 p Tillåtna hjälpmedel:
DT3 Spektrala transformer Tentamen 6 Tentamen består av fem uppgifter där varje uppgift maximalt ger 4 p. Normalt gäller följande betygsgränser: E: 9 p, D:.5 p, C: 4 p, B: 6 p, A: 8 p Tillåtna hjälpmedel:
Bildbehandling i frekvensdomänen
 Uppsala Tekniska Högskola Signaler och system Handledare: Mathias Johansson Uppsala 2002-11-27 Bildbehandling i frekvensdomänen Erika Lundberg 800417-1602 Johan Peterson 790807-1611 Terese Persson 800613-0267
Uppsala Tekniska Högskola Signaler och system Handledare: Mathias Johansson Uppsala 2002-11-27 Bildbehandling i frekvensdomänen Erika Lundberg 800417-1602 Johan Peterson 790807-1611 Terese Persson 800613-0267
Föreläsning 10, Egenskaper hos tidsdiskreta system
 Föreläsning 10, Egenskaper hos tidsdiskreta system Reglerteknik, IE1304 1 / 26 Innehåll Kapitel 18.1. Skillnad mellan analog och digital reglering 1 Kapitel 18.1. Skillnad mellan analog och digital reglering
Föreläsning 10, Egenskaper hos tidsdiskreta system Reglerteknik, IE1304 1 / 26 Innehåll Kapitel 18.1. Skillnad mellan analog och digital reglering 1 Kapitel 18.1. Skillnad mellan analog och digital reglering
Övningsuppgifter. Digital Signal Processing. Övningar med svar och lösningar. Mikael Swartling Nedelko Grbic Bengt Mandersson. rev.
 Övningsuppgifter Digital Signal Processing Övningar med svar och lösningar Mikael Swartling Nedelko Grbic Bengt Mandersson rev. 17 Department of Electrical and Information Technology Lund University Introduktion
Övningsuppgifter Digital Signal Processing Övningar med svar och lösningar Mikael Swartling Nedelko Grbic Bengt Mandersson rev. 17 Department of Electrical and Information Technology Lund University Introduktion
Kan vi beskriva ett system utan någon fysikalisk kännedom om systemet?
 Kan vi beskriva ett system utan någon fysikalisk kännedom om systemet? 1 Om svaret på frågan är ja så öppnar sig möjligheten att skapa en generell verktygslåda som fungerar för analys och manipulering
Kan vi beskriva ett system utan någon fysikalisk kännedom om systemet? 1 Om svaret på frågan är ja så öppnar sig möjligheten att skapa en generell verktygslåda som fungerar för analys och manipulering
Signal- och bildbehandling TSBB03
 Tentamen i Signal- och bildbehandling TSBB03 Tid: 2004-06-0 kl. 8-2 Lokaler: Garnisonen Ansvarig lärare: Maria Magnusson Seger besöker lokalen kl. 9.00 och 0.45. tel 073-804 38 67 Hjälpmedel: Räknedosa,
Tentamen i Signal- och bildbehandling TSBB03 Tid: 2004-06-0 kl. 8-2 Lokaler: Garnisonen Ansvarig lärare: Maria Magnusson Seger besöker lokalen kl. 9.00 och 0.45. tel 073-804 38 67 Hjälpmedel: Räknedosa,
Miniräknare, formelsamling i signalbehandling.
 LUNDS TEKNISKA HÖGSKOLA Inst. för Elektro- och Informationsteknik Tentamen 05-0-4 DIGITAL SIGNALBEHANDLING, ESS040 Tid: 4.00 9.00 Sal: Sparta B, D Hjälpmedel: Miniräknare, formelsamling i signalbehandling.
LUNDS TEKNISKA HÖGSKOLA Inst. för Elektro- och Informationsteknik Tentamen 05-0-4 DIGITAL SIGNALBEHANDLING, ESS040 Tid: 4.00 9.00 Sal: Sparta B, D Hjälpmedel: Miniräknare, formelsamling i signalbehandling.
TSDT18/84 SigSys Kap 4 Laplacetransformanalys av tidskontinuerliga system. De flesta begränsade insignaler ger upphov till begränsade utsignaler
 9 Stabilitet för energifria LTI-system Marginellt stabilt system: De flesta begränsade insignaler ger upphov till begränsade utsignaler Kap 2, bild 4 h t h( t) dt /< < t gäller för marginellt stabila LTI-system
9 Stabilitet för energifria LTI-system Marginellt stabilt system: De flesta begränsade insignaler ger upphov till begränsade utsignaler Kap 2, bild 4 h t h( t) dt /< < t gäller för marginellt stabila LTI-system
TSRT91 Reglerteknik: Föreläsning 5
 TSRT9 Reglerteknik: Föreläsning 5 Martin Enqvist Reglerteknik Institutionen för systemteknik Linköpings universitet Föreläsningar / 23 Inledning, grundläggande begrepp. 2 Matematiska modeller. Stabilitet.
TSRT9 Reglerteknik: Föreläsning 5 Martin Enqvist Reglerteknik Institutionen för systemteknik Linköpings universitet Föreläsningar / 23 Inledning, grundläggande begrepp. 2 Matematiska modeller. Stabilitet.
( ), så kan du lika gärna skriva H ( ω )! ( ) eftersom boken går igenom laplacetransformen före
 Några allmänna kommentarer gällande flera av lösningarna: Genomgående används kausala signaler och kausala system, vilket innebär att det är den enkelsidiga laplacetransformen som används. Bokens författare
Några allmänna kommentarer gällande flera av lösningarna: Genomgående används kausala signaler och kausala system, vilket innebär att det är den enkelsidiga laplacetransformen som används. Bokens författare
Signal- och bildbehandling TSEA70
 Tentamen i Signal- och bildbehandling TSEA70 Tid: 2003-08-22 kl. 4-8 Lokaler: G36 Ansvarig lärare: Maria Magnusson Seger besöker lokalen kl. 6.00. tel 0702/33 79 48 Hjälpmedel: Räknedosa, OH-film, medskickad
Tentamen i Signal- och bildbehandling TSEA70 Tid: 2003-08-22 kl. 4-8 Lokaler: G36 Ansvarig lärare: Maria Magnusson Seger besöker lokalen kl. 6.00. tel 0702/33 79 48 Hjälpmedel: Räknedosa, OH-film, medskickad
Föreläsning 1: Inledning till Digital signalbehandling i audio & video. Leif Sörnmo 11 mars 2009
 Föreläsning 1: Inledning till Digital signalbehandling i audio & video Leif Sörnmo 11 mars 2009 1 Schema Föreläsningar: Måndag 10.15 12.00 i sal E:2311 Fredag 08.15 10.00 i sal E:2311 Övningar: Tisdag
Föreläsning 1: Inledning till Digital signalbehandling i audio & video Leif Sörnmo 11 mars 2009 1 Schema Föreläsningar: Måndag 10.15 12.00 i sal E:2311 Fredag 08.15 10.00 i sal E:2311 Övningar: Tisdag
Kompletterande räkneuppgifter i Spektrala Transformer Komplex analys, sampling, kvantisering, serier och filter Laura Enflo & Giampiero Salvi
 Kompletterande räkneuppgifter i Spektrala Transformer Komplex analys, sampling, kvantisering, serier och filter & Giampiero Salvi Komplex analys Om man endast använder den reella tallinjen är det inte
Kompletterande räkneuppgifter i Spektrala Transformer Komplex analys, sampling, kvantisering, serier och filter & Giampiero Salvi Komplex analys Om man endast använder den reella tallinjen är det inte
Signal- och bildbehandling TSBB03
 Tentamen i Signal- och bildbehandling TSBB3 Tid: 28-5-29 kl. 8-2 Lokal: TER2 Ansvarig lärare: Maria Magnusson besöker lokalen kl. 9. och.4 tel 73-84 38 67 Hjälpmedel: Räknedosa, medskickad formelsamling,
Tentamen i Signal- och bildbehandling TSBB3 Tid: 28-5-29 kl. 8-2 Lokal: TER2 Ansvarig lärare: Maria Magnusson besöker lokalen kl. 9. och.4 tel 73-84 38 67 Hjälpmedel: Räknedosa, medskickad formelsamling,
Signal- och bildbehandling TSBB14
 Tentamen i Signal- och bildbehandling TSBB4 Tid: -5-8 Lokaler: TER3 Ansvarig lärare: Maria Magnusson besöker lokalen kl. 8.45 och.45 tel 8336, 73-84 38 67 Hjälpmedel: Räknedosa, medskickad formelsamling,
Tentamen i Signal- och bildbehandling TSBB4 Tid: -5-8 Lokaler: TER3 Ansvarig lärare: Maria Magnusson besöker lokalen kl. 8.45 och.45 tel 8336, 73-84 38 67 Hjälpmedel: Räknedosa, medskickad formelsamling,
Föreläsning 6: Spektralskattning: icke parametriska metoder. Leif Sörnmo 4 oktober 2009
 Föreläsning 6: Spektralskattning: icke parametriska metoder Leif Sörnmo 4 oktober 2009 1 Metoder för spektralskattning icke-parametriska korrelogram, periodogram fönstring, medelvärdesbildning minimum-varians
Föreläsning 6: Spektralskattning: icke parametriska metoder Leif Sörnmo 4 oktober 2009 1 Metoder för spektralskattning icke-parametriska korrelogram, periodogram fönstring, medelvärdesbildning minimum-varians
Fouriertransformen av diskreta signaler
 Kapitel 4 Fouriertransformen av diskreta signaler I detta kapitel beskrivs Fouriertransformer av diskreta signaler. I analogi med det kontinuerliga fallet har periodiska diskreta signaler ett diskret spektrum,
Kapitel 4 Fouriertransformen av diskreta signaler I detta kapitel beskrivs Fouriertransformer av diskreta signaler. I analogi med det kontinuerliga fallet har periodiska diskreta signaler ett diskret spektrum,
62n 105n) c) cos(3πn) d) sin(3n) e) sin(π. 1.8 Ett analogt elektrokardiogram (EKG) innehåller frekvenser upp till 100 Hz.
 Kapitel Övningsuppgifter. Bestäm vilka av följande signaler som är periodiska och bestäm periodtiden. a) cos(.πn) b) cos(π 3 6n 5n) c) cos(3πn) d) sin(3n) e) sin(π )..5 Den analoga signalen x a (t) är
Kapitel Övningsuppgifter. Bestäm vilka av följande signaler som är periodiska och bestäm periodtiden. a) cos(.πn) b) cos(π 3 6n 5n) c) cos(3πn) d) sin(3n) e) sin(π )..5 Den analoga signalen x a (t) är
Digital Signalbehandling
 Digital Signalbehandling Institutionen för Elektro- och informationsteknik Övningar och lösningar Proakis bok (upplaga 4) Nedelko Grbić Lund 4 Innehåll Övningsuppgifter 5 Lösningar till övningsuppgifter
Digital Signalbehandling Institutionen för Elektro- och informationsteknik Övningar och lösningar Proakis bok (upplaga 4) Nedelko Grbić Lund 4 Innehåll Övningsuppgifter 5 Lösningar till övningsuppgifter
System. Z-transformen. Staffan Grundberg. 8 februari 2016
 Z-transformen 8 februari 2016 Innehåll Z-transformen Tidsdiskreta LTI-system Överföringsfunktioner Frekvensegenskaper Z-transformen Z-transformen av en tidsdiskret signal y[n] ges av Y (z) = Z[y] = y[n]z
Z-transformen 8 februari 2016 Innehåll Z-transformen Tidsdiskreta LTI-system Överföringsfunktioner Frekvensegenskaper Z-transformen Z-transformen av en tidsdiskret signal y[n] ges av Y (z) = Z[y] = y[n]z
Signal- och bildbehandling TSBB14
 Tentamen i Signal- och bildbehandling TSBB Tid: 3-5-3 Lokaler: TER Ansvarig lärare: Maria Magnusson besöker lokalen kl. 8.5 och.3 tel 73-8 38 67 Hjälpmedel: Räknedosa, medskickad formelsamling, OH-film,
Tentamen i Signal- och bildbehandling TSBB Tid: 3-5-3 Lokaler: TER Ansvarig lärare: Maria Magnusson besöker lokalen kl. 8.5 och.3 tel 73-8 38 67 Hjälpmedel: Räknedosa, medskickad formelsamling, OH-film,
2F1120 Spektrala transformer för Media Tentamen
 F Spektrala transformer för Media Tentamen 68 Tentamen består av fem uppgifter där varje uppgift maximalt ger p. Normalt gäller följande betygsgränser: :9 p, : p, 5: 7 p Tillåtna hjälpmedel: räknare, formelblad
F Spektrala transformer för Media Tentamen 68 Tentamen består av fem uppgifter där varje uppgift maximalt ger p. Normalt gäller följande betygsgränser: :9 p, : p, 5: 7 p Tillåtna hjälpmedel: räknare, formelblad
Spektrala Transformer
 Spektrala Transformer Tidsdiskreta signaler, kvantisering & sampling Tidsdiskreta signaler Tidskontinuerlig signal Ex: x(t) = sin(ωt) t är ett reellt tal ω har enheten rad/s Tidsdiskret signal Ex: x(n)
Spektrala Transformer Tidsdiskreta signaler, kvantisering & sampling Tidsdiskreta signaler Tidskontinuerlig signal Ex: x(t) = sin(ωt) t är ett reellt tal ω har enheten rad/s Tidsdiskret signal Ex: x(n)
Tillämpning av komplext kommunikationssystem i MATLAB
 (Eller: Vilken koppling har Henrik Larsson och Carl Bildt?) 1(5) - Joel Nilsson joelni at kth.se Martin Axelsson maxels at kth.se Sammanfattning Kommunikationssystem används för att överföra information,
(Eller: Vilken koppling har Henrik Larsson och Carl Bildt?) 1(5) - Joel Nilsson joelni at kth.se Martin Axelsson maxels at kth.se Sammanfattning Kommunikationssystem används för att överföra information,
Föreläsning 9, Bestämning av tidsdiksreta överföringsfunktioner
 Föreläsning 9, Bestämning av tidsdiksreta överföringsfunktioner Reglerteknik, IE1304 1 / 20 Innehåll Kapitel 17.1. Inledning 1 Kapitel 17.1. Inledning 2 3 2 / 20 Innehåll Kapitel 17.1. Inledning 1 Kapitel
Föreläsning 9, Bestämning av tidsdiksreta överföringsfunktioner Reglerteknik, IE1304 1 / 20 Innehåll Kapitel 17.1. Inledning 1 Kapitel 17.1. Inledning 2 3 2 / 20 Innehåll Kapitel 17.1. Inledning 1 Kapitel
Hambley avsnitt
 Föreläsning Hambley avsnitt 6.6.8 Filter [6.2, 6.5 6.8] Nästan all trådlös och trådbunden kommunikation är baserad på tidsharmoniska signaler. Signalerna utnyttjar ett frekvensband centrerad kring en bärfrekvens.
Föreläsning Hambley avsnitt 6.6.8 Filter [6.2, 6.5 6.8] Nästan all trådlös och trådbunden kommunikation är baserad på tidsharmoniska signaler. Signalerna utnyttjar ett frekvensband centrerad kring en bärfrekvens.
Signal- och bildbehandling TSBB03, TSBB14
 Tentamen i Signal- och bildbehandling TSBB03, TSBB4 Tid: 00-0- Lokaler: G33 Ansvarig lärare: Maria Magnusson besöker lokalen kl. 4.50 och 6.50 tel 073-804 38 67 Hjälpmedel: Räknedosa, medskickad formelsamling,
Tentamen i Signal- och bildbehandling TSBB03, TSBB4 Tid: 00-0- Lokaler: G33 Ansvarig lärare: Maria Magnusson besöker lokalen kl. 4.50 och 6.50 tel 073-804 38 67 Hjälpmedel: Räknedosa, medskickad formelsamling,
6. Stabilitet. 6. Stabilitet
 6. Stabilitet 6. Stabilitet Såsom framgått i de två inledande kapitlen förutsätter en lyckad regulatordesign kompromisser mellan prestanda ( snabbhet ) och stabilitet. Ett system som oreglerat är stabilt
6. Stabilitet 6. Stabilitet Såsom framgått i de två inledande kapitlen förutsätter en lyckad regulatordesign kompromisser mellan prestanda ( snabbhet ) och stabilitet. Ett system som oreglerat är stabilt
7. Sampling och rekonstruktion av signaler
 Arbetsmaterial 5, Signaler&System I, VT04/E.P. 7. Sampling och rekonstruktion av signaler (Se också Hj 8.1 3, OW 7.1 2) 7.1 Sampling och fouriertransformering Man säger att man samplar en signal x(t) vid
Arbetsmaterial 5, Signaler&System I, VT04/E.P. 7. Sampling och rekonstruktion av signaler (Se också Hj 8.1 3, OW 7.1 2) 7.1 Sampling och fouriertransformering Man säger att man samplar en signal x(t) vid
Tentamen ssy080 Transformer, Signaler och System, D3
 Tentamen ssy080 Transformer, Signaler och System, D3 Examinator: Ants R. Silberberg 19 oktober 2011 kl. 08.30-12.30 sal: Hörsalsvägen Förfrågningar: Ants Silberberg, tel. 1808 Lösningar: Anslås torsdag
Tentamen ssy080 Transformer, Signaler och System, D3 Examinator: Ants R. Silberberg 19 oktober 2011 kl. 08.30-12.30 sal: Hörsalsvägen Förfrågningar: Ants Silberberg, tel. 1808 Lösningar: Anslås torsdag
Digital Signalbehandling i Audio/Video
 Digital Signalbehandling i Audio/Video Institutionen för Elektrovetenskap Laboration 1 (del 2) Stefan Dinges Lund 25 2 Kapitel 1 Digitala audioeffekter Den här delen av laborationen handlar om olika digitala
Digital Signalbehandling i Audio/Video Institutionen för Elektrovetenskap Laboration 1 (del 2) Stefan Dinges Lund 25 2 Kapitel 1 Digitala audioeffekter Den här delen av laborationen handlar om olika digitala
Frekvensplanet och Bode-diagram. Frekvensanalys
 Frekvensplanet och Bode-diagram Frekvensanalys Signaler Allt inom elektronik går ut på att manipulera signaler genom signalbehandling (Signal Processing). Analog signalbehandling Kretsteori: Nod-analys,
Frekvensplanet och Bode-diagram Frekvensanalys Signaler Allt inom elektronik går ut på att manipulera signaler genom signalbehandling (Signal Processing). Analog signalbehandling Kretsteori: Nod-analys,
Spektrala Transformer
 Spektrala Transformer Tidsdiskreta signaler, kvantisering & sampling Tidsdiskreta signaler Tidskontinuerlig signal Ex: x(t) = sin(ωt) t är ett reellt tal ω har enheten rad/s Tidsdiskret signal Ex: x(n)
Spektrala Transformer Tidsdiskreta signaler, kvantisering & sampling Tidsdiskreta signaler Tidskontinuerlig signal Ex: x(t) = sin(ωt) t är ett reellt tal ω har enheten rad/s Tidsdiskret signal Ex: x(n)
Ulrik Söderström 20 Jan Signaler & Signalanalys
 Ulrik Söderström ulrik.soderstrom@tfe.umu.se 20 Jan 2009 Signaler & Signalanalys Sinusspänning Sinus och cosinus samma form men fasförskjutna Fasförskjutning tidsfördröjning Sinus och cosinus är väldigt
Ulrik Söderström ulrik.soderstrom@tfe.umu.se 20 Jan 2009 Signaler & Signalanalys Sinusspänning Sinus och cosinus samma form men fasförskjutna Fasförskjutning tidsfördröjning Sinus och cosinus är väldigt
Miniräknare och en valfri formelsamling i signalbehandling eller matematik. Allowed items: calculator, DSP and mathematical tables of formulas
 LUNDS TEKNISKA HÖGSKOLA Institutionen för Elektro- och Informationsteknik Tentamen 08-05-3 SIGNALBEHANDLING i MULTIMEDIA, EITA50 Tid: 08.00-3.00 Sal: Vic A Hjälpmedel: Viktigt: Miniräknare och en valfri
LUNDS TEKNISKA HÖGSKOLA Institutionen för Elektro- och Informationsteknik Tentamen 08-05-3 SIGNALBEHANDLING i MULTIMEDIA, EITA50 Tid: 08.00-3.00 Sal: Vic A Hjälpmedel: Viktigt: Miniräknare och en valfri
Tillämpad Fysik Och Elektronik 1
 FREKVENSSPEKTRUM (FORTS) TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 1 ICKE-PERIODISKA FUNKTIONER Icke- periodiska funktioner kan betraktas som periodiska, med oändlig periodtid P. TILLÄMPAD FYSIK
FREKVENSSPEKTRUM (FORTS) TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 1 ICKE-PERIODISKA FUNKTIONER Icke- periodiska funktioner kan betraktas som periodiska, med oändlig periodtid P. TILLÄMPAD FYSIK
Laboration i tidsdiskreta system
 Laboration i tidsdiskreta system A. Tips Användbara MATLAB-funktioner: conv Faltning square Skapa en fyrkantvåg wavread Läs in en ljudfil soundsc Spela upp ett ljud ones Skapa en vektor med godtyckligt
Laboration i tidsdiskreta system A. Tips Användbara MATLAB-funktioner: conv Faltning square Skapa en fyrkantvåg wavread Läs in en ljudfil soundsc Spela upp ett ljud ones Skapa en vektor med godtyckligt
DigSig AV. Repetition. Leif Sörnmo 10 maj 2007
 DigSig AV Repetition Leif Sörnmo 10 maj 2007 1 Syftet med digital filterdesign Att bestämma en realiserbar överföringsfunktion G(z) så att den approximerar en given specifikation på frekvensfunktion. För
DigSig AV Repetition Leif Sörnmo 10 maj 2007 1 Syftet med digital filterdesign Att bestämma en realiserbar överföringsfunktion G(z) så att den approximerar en given specifikation på frekvensfunktion. För
Flerdimensionella signaler och system
 Luleå tekniska universitet Avd för signalbehandling Magnus Sandell (reviderad av Frank Sjöberg) Flerdimensionell signalbehandling SMS033 Laboration 1 Flerdimensionella signaler och system Syfte: Den här
Luleå tekniska universitet Avd för signalbehandling Magnus Sandell (reviderad av Frank Sjöberg) Flerdimensionell signalbehandling SMS033 Laboration 1 Flerdimensionella signaler och system Syfte: Den här
Tentamen i Elektronik, ESS010, del 1 den 21 oktober 2008 klockan 8:00 13:00
 Tentamen i Elektronik, ESS00, del den oktober 008 klockan 8:00 :00 Tekniska Högskolan i Lund Institutionen för Elektrovetenskap Tentamen i Elektronik, ESS00, del den oktober 008 klockan 8:00 :00 Uppgifterna
Tentamen i Elektronik, ESS00, del den oktober 008 klockan 8:00 :00 Tekniska Högskolan i Lund Institutionen för Elektrovetenskap Tentamen i Elektronik, ESS00, del den oktober 008 klockan 8:00 :00 Uppgifterna
Bestäm uttrycken för följande spänningar/strömmar i kretsen, i termer av ( ) in a) Utspänningen vut b) Den totala strömmen i ( ) c) Strömmen () 2
 7 Elektriska kretsar Av: Lasse Alfredsson och Klas Nordberg 7- Nedan finns en krets med resistanser. Då kretsen ansluts till en annan elektrisk krets uppkommer spänningen vin ( t ) och strömmen ( ) Bestäm
7 Elektriska kretsar Av: Lasse Alfredsson och Klas Nordberg 7- Nedan finns en krets med resistanser. Då kretsen ansluts till en annan elektrisk krets uppkommer spänningen vin ( t ) och strömmen ( ) Bestäm
6. Stabilitet. 6. Stabilitet. 6. Stabilitet. 6.1 Stabilitetsdefinitioner. 6. Stabilitet. 6.2 Poler och stabilitet. 6.1 Stabilitetsdefinitioner
 Såsom framgått i de två inledande kapitlen förutsätter en lyckad regulatordesign kompromisser mellan prestanda ( snabbhet ) och stabilitet. Ett system som oreglerat är stabilt kan bli instabilt genom för
Såsom framgått i de två inledande kapitlen förutsätter en lyckad regulatordesign kompromisser mellan prestanda ( snabbhet ) och stabilitet. Ett system som oreglerat är stabilt kan bli instabilt genom för
Välkomna till TSRT19 Reglerteknik Föreläsning 5. Sammanfattning av föreläsning 4 Frekvensanalys Bodediagram
 Välkomna till TSRT19 Reglerteknik Föreläsning 5 Sammanfattning av föreläsning 4 Frekvensanalys Bodediagram Sammanfattning av förra föreläsningen 2 Givet ett polpolynom med en varierande parameter, och
Välkomna till TSRT19 Reglerteknik Föreläsning 5 Sammanfattning av föreläsning 4 Frekvensanalys Bodediagram Sammanfattning av förra föreläsningen 2 Givet ett polpolynom med en varierande parameter, och
REGLERTEKNIK Laboration 5
 6 SAMPLADE SYSTEM 6. Sampling av signaler När man använder en dator som regulator, kan man endast behandla signaler i diskreta tidpunkter. T.ex. mäts systemets utsignal i tidpunkter med visst mellanrum,
6 SAMPLADE SYSTEM 6. Sampling av signaler När man använder en dator som regulator, kan man endast behandla signaler i diskreta tidpunkter. T.ex. mäts systemets utsignal i tidpunkter med visst mellanrum,
Hambley avsnitt
 Föreläsning 0 Hambley avsnitt 6.6.8 Filter [6.2, 6.5 6.8] Vid kommunikation används tidsharmoniska signaler. Dessa har ett visst frekvensband centrerad kring en bärfrekvens. Som exempel kan en sändare
Föreläsning 0 Hambley avsnitt 6.6.8 Filter [6.2, 6.5 6.8] Vid kommunikation används tidsharmoniska signaler. Dessa har ett visst frekvensband centrerad kring en bärfrekvens. Som exempel kan en sändare
Ulrik Söderström 19 Jan Signalanalys
 Ulrik Söderström ulrik.soderstrom@tfe.umu.se 9 Jan 200 Signaler & Signalanalys l Sinusspänning Sinus och cosinus samma form men fasförskjutna Fasförskjutning tidsfördröjning Sinus och cosinus är väldigt
Ulrik Söderström ulrik.soderstrom@tfe.umu.se 9 Jan 200 Signaler & Signalanalys l Sinusspänning Sinus och cosinus samma form men fasförskjutna Fasförskjutning tidsfördröjning Sinus och cosinus är väldigt
Övningar med Digitala Filter med exempel på konstruktion och analys i MatLab
 Övningar med Digitala Filter med exempel på konstruktion och analys i MatLab Eddie Alestedt Vt-2002 Digitala filter Digitala filter appliceras på samplade signaler och uppvisar helt andra egenskaper än
Övningar med Digitala Filter med exempel på konstruktion och analys i MatLab Eddie Alestedt Vt-2002 Digitala filter Digitala filter appliceras på samplade signaler och uppvisar helt andra egenskaper än
2 Ortogonala signaler. Fourierserier. Enkla filter.
 Ortogonala signaler. Fourierserier. Enkla filter. ktuella ekvationer: Se formelsamlingen och förberedelsehäftet. För effektivvärdet av en summa av N ortogonala signaler gäller: ν rms = ν rms1 + ν rms +...
Ortogonala signaler. Fourierserier. Enkla filter. ktuella ekvationer: Se formelsamlingen och förberedelsehäftet. För effektivvärdet av en summa av N ortogonala signaler gäller: ν rms = ν rms1 + ν rms +...
Försättsblad till skriftlig tentamen vid Linköpings universitet G33(1) TER4(63)
 Försättsblad till skriftlig tentamen vid Linköpings universitet Datum för tentamen 2017-01-07 Sal (2) G33(1) TER4(63) Tid 8-12 Kurskod TSBB16 Provkod TEN2 Kursnamn/benämning Provnamn/benämning Institution
Försättsblad till skriftlig tentamen vid Linköpings universitet Datum för tentamen 2017-01-07 Sal (2) G33(1) TER4(63) Tid 8-12 Kurskod TSBB16 Provkod TEN2 Kursnamn/benämning Provnamn/benämning Institution
1. Rita följande tidssekvenser. 2. Givet tidssekvensen x n i nedanstående figur. Rita följande tidssekvenser.
 Lasse Björkma 999 . Rita följade tidssekveser. a) δ e) u b) δ f) u u c) δ + δ g) u d) u h) u. Givet tidssekvese x i edaståede figur. Rita följade tidssekveser. a) x c) x b) x + 3 d) x 3. Givet tidssekvesera
Lasse Björkma 999 . Rita följade tidssekveser. a) δ e) u b) δ f) u u c) δ + δ g) u d) u h) u. Givet tidssekvese x i edaståede figur. Rita följade tidssekveser. a) x c) x b) x + 3 d) x 3. Givet tidssekvesera
DT1120 Spektrala transformer för Media Tentamen
 DT Spektrala transformer för Media Tentamen 77 Tentamen består av fem uppgifter där varje uppgift maximalt ger 4 p. Normalt gäller följande betygsgränser: 3:9 p, 4: 3 p, 5: 7 p Tillåtna hjälpmedel: räknare,
DT Spektrala transformer för Media Tentamen 77 Tentamen består av fem uppgifter där varje uppgift maximalt ger 4 p. Normalt gäller följande betygsgränser: 3:9 p, 4: 3 p, 5: 7 p Tillåtna hjälpmedel: räknare,
Signal- och Bildbehandling FÖRELÄSNING 4. Multiplikationsteoremet. Derivatateoremet
 Signal- och Bildbehandling FÖRELÄSNING 4 Fouriertransformen, forts Mer egenskaper av fouriertransformen Enkel tillämpning: Filtrera bort oönskat buller från vacker visselton Fouriertransformen, slutsats
Signal- och Bildbehandling FÖRELÄSNING 4 Fouriertransformen, forts Mer egenskaper av fouriertransformen Enkel tillämpning: Filtrera bort oönskat buller från vacker visselton Fouriertransformen, slutsats
Teori... SME118 - Mätteknik & Signalbehandling SME118. Johan Carlson 2. Teori... Dagens meny
 Tidigare har vi gått igenom Fourierserierepresentation av periodiska signaler och Fouriertransform av icke-periodiska signaler. Fourierserierepresentationen av x(t) ges av: där a k = 1 T + T a k e jkω
Tidigare har vi gått igenom Fourierserierepresentation av periodiska signaler och Fouriertransform av icke-periodiska signaler. Fourierserierepresentationen av x(t) ges av: där a k = 1 T + T a k e jkω
LUNDS TEKNISKA HÖGSKOLA Inst. för Elektro- och Informationsteknik
 LUNDS TEKNISKA HÖGSKOLA Inst. för Elektro- och Informationsteknik Tentamen 04-05-7 SIGNALBEHANDLING I MULTIMEDIA, ETI65 Tid: 4.00 9.00 Sal: MA:0 Hjälpmedel: Miniräknare, formelsamling i signalbehandling
LUNDS TEKNISKA HÖGSKOLA Inst. för Elektro- och Informationsteknik Tentamen 04-05-7 SIGNALBEHANDLING I MULTIMEDIA, ETI65 Tid: 4.00 9.00 Sal: MA:0 Hjälpmedel: Miniräknare, formelsamling i signalbehandling
Lösningsförslag, Tentamen, Differentialekvationer och transformer II, del 2, för CTFYS2 och CMEDT3, SF1629, den 9 juni 2011, kl.
 Lösningsförslag, Tentamen, Differentialekvationer och transformer II, del 2, för CTFYS2 och CMEDT3, SF629, den 9 juni 2, kl. 8: 3: Uppgift (av 8 (5 poäng. i. sant, ii. falskt, iii. falskt, iv. sant, v.
Lösningsförslag, Tentamen, Differentialekvationer och transformer II, del 2, för CTFYS2 och CMEDT3, SF629, den 9 juni 2, kl. 8: 3: Uppgift (av 8 (5 poäng. i. sant, ii. falskt, iii. falskt, iv. sant, v.
Laboration i Fourieranalys för F2, TM2, Kf2 2011/12 Signalanalys med snabb Fouriertransform (FFT)
 Laboration i Fourieranalys för F2, TM2, Kf2 2011/12 Signalanalys med snabb Fouriertransform (FFT) Den här laborationen har två syften: dels att visa hur den snabba Fouriertransformen fungerar och vad man
Laboration i Fourieranalys för F2, TM2, Kf2 2011/12 Signalanalys med snabb Fouriertransform (FFT) Den här laborationen har två syften: dels att visa hur den snabba Fouriertransformen fungerar och vad man
Adaptiva Filter. Johan Haarala Signaler och System
 Adaptiva Filter Johan Haarala 2002-12-11 Signaler och System Abstract Målet med den här rapporten är att ge en introduktion samt översikt till adaptiva filter. I den beskrivs några av de algoritmer som
Adaptiva Filter Johan Haarala 2002-12-11 Signaler och System Abstract Målet med den här rapporten är att ge en introduktion samt översikt till adaptiva filter. I den beskrivs några av de algoritmer som
Vad gör vi när vi bara har en mätserie och ingen elegant matematisk funktion?
 Vad gör vi när vi bara har en mätserie och ingen elegant matematisk funktion? 1 Ett problem med Fourier- och Laplacetransformen är att de kräver att signalen som skall transformeras kan skrivas som en
Vad gör vi när vi bara har en mätserie och ingen elegant matematisk funktion? 1 Ett problem med Fourier- och Laplacetransformen är att de kräver att signalen som skall transformeras kan skrivas som en
Försättsblad till skriftlig tentamen vid Linköpings universitet KÅRA T1 T2 U2 U4
 Försättsblad till skriftlig tentamen vid Linköpings universitet Datum för tentamen 2016-10-28 Sal (5) KÅRA T1 T2 U2 U4 Tid 8-12 Kurskod TSBB16 Provkod TEN2 Kursnamn/benämning Provnamn/benämning Grundläggande
Försättsblad till skriftlig tentamen vid Linköpings universitet Datum för tentamen 2016-10-28 Sal (5) KÅRA T1 T2 U2 U4 Tid 8-12 Kurskod TSBB16 Provkod TEN2 Kursnamn/benämning Provnamn/benämning Grundläggande
Tentamen i Signaler och kommunikation, ETT080
 Inst. för informationsteknologi Tentamen i Signaler och kommunikation, ETT080 2 juni 2006, kl 14 19 Skriv namn och årskurs på alla papper. Börja en ny lösning på ett nytt papper. Använd bara en sida av
Inst. för informationsteknologi Tentamen i Signaler och kommunikation, ETT080 2 juni 2006, kl 14 19 Skriv namn och årskurs på alla papper. Börja en ny lösning på ett nytt papper. Använd bara en sida av
Signal- och bildbehandling TSEA70
 Tentamen i Signal- och bildbehandling TSEA70 Tid: 2003-0-0 kl. 4-8 Lokaler: Examinator: U Maria Magnusson Seger Ansvarig lärare: Olle Seger besöker lokalen kl. 5 och 7. tel 259, 0702/337948 Hjälpmedel:
Tentamen i Signal- och bildbehandling TSEA70 Tid: 2003-0-0 kl. 4-8 Lokaler: Examinator: U Maria Magnusson Seger Ansvarig lärare: Olle Seger besöker lokalen kl. 5 och 7. tel 259, 0702/337948 Hjälpmedel:
Kompletterande material till föreläsning 5 TSDT08 Signaler och System I. Erik G. Larsson LiU/ISY/Kommunikationssystem
 ompletterande material till föreläsning 5 TSDT8 Signaler och System I Erik G. Larsson LiU/ISY/ommunikationssystem erik.larsson@isy.liu.se November 8 5.1. Första och andra ordningens tidskontinuerliga LTI
ompletterande material till föreläsning 5 TSDT8 Signaler och System I Erik G. Larsson LiU/ISY/ommunikationssystem erik.larsson@isy.liu.se November 8 5.1. Första och andra ordningens tidskontinuerliga LTI
Frekvenssvaret är utsignalen då insginalen är en sinusvåg med frekvens ω och amplitud A,
 Övning 8 Introduktion Varmt välkomna till åttonde övningen i Reglerteknik AK! Håkan Terelius hakante@kth.se Repetition Frekvenssvar Frekvenssvaret är utsignalen då insginalen är en sinusvåg med frekvens
Övning 8 Introduktion Varmt välkomna till åttonde övningen i Reglerteknik AK! Håkan Terelius hakante@kth.se Repetition Frekvenssvar Frekvenssvaret är utsignalen då insginalen är en sinusvåg med frekvens
Transformer och differentialekvationer M3, 2010/2011 Ett par tillämpningar av Fourieranalys.
 Chalmers tekniska högskola och Göteborgs universitet Matematik februari 0 Transformer och differentialekvationer M3, 00/0 Ett par tillämpningar av Fourieranalys. Design av system, filter Som en intressant
Chalmers tekniska högskola och Göteborgs universitet Matematik februari 0 Transformer och differentialekvationer M3, 00/0 Ett par tillämpningar av Fourieranalys. Design av system, filter Som en intressant
Lösningar Reglerteknik AK Tentamen
 Lösningar Reglerteknik AK Tentamen 060 Uppgift a G c (s G(sF (s + G(sF (s s + 3, Y (s s + 3 s ( 3 s s + 3 Svar: y(t 3 ( e 3t Uppgift b Svar: (i insignal u levererad insulinmängd från pumpen, mha tex spänningen
Lösningar Reglerteknik AK Tentamen 060 Uppgift a G c (s G(sF (s + G(sF (s s + 3, Y (s s + 3 s ( 3 s s + 3 Svar: y(t 3 ( e 3t Uppgift b Svar: (i insignal u levererad insulinmängd från pumpen, mha tex spänningen
