Ellära 2, Tema 3. Ville Jalkanen Tillämpad fysik och elektronik, UmU. 1
|
|
|
- Oliver Bergman
- för 7 år sedan
- Visningar:
Transkript
1 Ellära 2, ema 3 Ville Jalkanen illämpad fysik och elektronik, UmU ville.jalkanen@umu.se 1
2 Innehåll Periodiska signaler Storlek, frekvens,... Filter Överföringsfunktion, belopp och fas, gränsfrekvens 2
3 Ellära 2 PERIODISKA SIGNALER ville.jalkanen@umu.se 3
4 Signal Fysikalisk storhet id (eller avstånd/läge) Informationsbärare Signaler i naturen omvandlas av en sensor till en elektrisk storhet Elektrisk signal: Spänning/ström som funktion av tiden ville.jalkanen@umu.se 4
5 Periodisk signal Spänningen u(t) har ett värde vid varje tidpunkt och det värdet är återkommande i tiden på ett regelbundet sätt upprepas med periodtiden, Exempel: sinusformad växelspänning (AC) u(t) har ett värde vid varje tidpunkt, dvs ett momentanvärde. Detta värde upprepas efter multiplar av periodtiden. u t = u t + n n heltal u(t) En period Växelspänningen antar både positiva och negativa värden 0 tid re perioder ville.jalkanen@umu.se 5
6 DC-nivå Vanliga periodiska signaler Sinusformad spänning med likspänningskomponent AC+DC (sinus förkjuten vertikalt) DC-nivå Pulserande likspänning Växelspänning med fyrkantform (fyrkantvåg) Växelspänning med triangelform (triangelvåg) Pulsbreddmodulerad växelspänning (serie av pulser) t.ex. För effektivare styrning av motor 6
7 Frekvens Oscillationshastighet, dvs antalet svängningar per tidsenhet Frekvens (f) = Antal perioder per sekund enheten Hertz (Hz) Exempel: Sinus-våg Svarta signalen har en period på 1 s, f = 1/1 = 1Hz Blåa signalen har två perioder på 1 s, f = 2/1 = 2Hz (eller en period på 0.5 s, f = 1/0.5 = 2 Hz) 1 sekund Röda signalen har tio perioder på 1 s, f = 10/1 = 10Hz (eller en period på 0.1 s, f = 1/0.1 = 10 Hz) Frekvens = en period per periodtid (i sekunder) Ovan: = 1/f = 1/1 = 1 s = 1/f = 1/2 = 0.5 s = 1/f = 1/10 = 0.1 s f = 1 ville.jalkanen@umu.se 7
8 Amplitud, topp-värde, topp-till-topp (peak-to-peak) Symmetrisk sinus-signal (kring noll-linjen) (ren växelspänning (AC) dvs ingen DC-del) Amplitud (max-avstånd från noll-linjen) opp-värde (maxvärdet) = amplitud opp-till-topp (avståndet mellan topparna) = 2*amplitud (max - min) Osymmetrisk sinus-signal (AC+DC-del): opp-värde är signalens maxvärde opp-till-topp (avståndet mellan topparna) (rena AC-delen har fortfarande en amplitud relativt symmetrilinjen (signalens noll-linje)) ville.jalkanen@umu.se 8
9 Sinus-signalens matematiska form Matematiska (tids-)formen för sinus-signalen, dvs sinus-växelspänningen (AC) A u(t) u t u t = A sin ωt = A sin ωt + θ A är amplituden θ är fasvinkeln i radianer, rad ω är vinkelfrekvensen i rad/s t (s) ω = 2πf t = θ ω Sinus-spänning (AC) med en likspännings-komponent (DC) u(t) u t = U DC + A sin ωt + θ U DC t (s) ville.jalkanen@umu.se 9
10 Fyrkantvågens frekvens f = 1 är fyrkantvågens grundfrekvens (grundton), men inte dess hela frekvensinnehåll! f och 3f f, 3f, 5f f, 3f, 5f, 7f f, 3f, 5f, 7f, 9f Fyrkantvågen består av en summa av sinus-vågor med grundfrekvensen (f) och udda multiplar av grundfrekvensen, dvs övertoner 3f, 5f, 7f,... Amplituden hos övertonerna minskar med ökad frekvens. Denna serie av sinus-vågor kallas fyrkantvågens Fourier-serie. Summerar man oändligt många av sådana sinus-vågor får man en fyrkantvåg f, 3f, 5f, 7f, 9f, 11f ville.jalkanen@umu.se 10
11 Fyrkantvågens amplitud, topp-till-topp Symmetrisk fyrkantvåg (kring nollan) (ren växelspänning (AC) dvs ingen DC-del) Amplitud (max-avstånd från noll-linjen) opp-till-topp (avståndet mellan topparna) = 2*amplitud Osymmetrisk signal (AC+DC-del): opp-värde är signalens maxvärde opp-till-topp (avståndet mellan topparna) (rena AC-delen har fortfarande en amplitud relativt symmetrilinjen (signalens noll-linje)) DC ville.jalkanen@umu.se 11
12 Fyrkantvågens matematiska form u(t) Fyrkantvågen betraktas som en styckvis funktion (piecewise function) A -A 2 t (s) u t = A 0 t 2 A 2 t Enkelt att räkna med integraler! Fyrkantvåg med en likspännings-komponent, U DC u(t) A U DC t (s) u t = A + U DC 0 t 2 A + U DC 2 t -A 2 ville.jalkanen@umu.se 12
13 Olika mått på signalens storlek Amplitud, topp-till-topp (peak to peak) Medelvärde = medelamplitud under en period Effektivvärde, rms-värde Likriktat medelvärde (Beloppsmedelvärde/absolutbelopp) ville.jalkanen@umu.se 13
14 Medelvärde Medelamplitud under en period och definieras som: u = 1 u t dt 0 Summerar momentanvärden under en period och delar med periodtiden ville.jalkanen@umu.se 14
15 Exempel: beräkning av medelvärde Sinus-signal: u t = U DC + A sin ωt U DC A u = 1 0 U DC + A sin ωt dt = = U DC Fyrkant-signal: u t = A + U DC 0 t 2 A + U DC 2 t U DC A t (s) u = A + U DC dt + A + U DC dt 2 = = U DC Slutsats: Medelvärdet är likspänningskomponenten, dvs den anger noll-linjen för växelspänning (AC). En ren AC-signal (dvs DC = 0 V) har medelvärdet = 0V, dvs symmetrisk kring noll-linjen. ville.jalkanen@umu.se 15
16 Effektivvärde (rms-värde) Vanligt sätt att ange storleken på växelspänning/ström (AC). Kallas kvadratiskt medelvärde. Effektivvärdet är samma värde som likspänning (DC) ska ha för att ge samma effekt i en resistor R. U eff = U rms = 1 u t 2 dt 0 rms = root-mean-square ville.jalkanen@umu.se 16
17 Exempel: effektivvärde för sinus För ren sinus-spänning (utan DC-komponent, dvs medelvärde = 0V): u t = A sin ωt U rms = 1 0 A sin ωt 2 dt = A cos 2ωt dt = = A 2 Effektivvärde = amplituden/roten ur 2 ville.jalkanen@umu.se 17
18 Exempel: effektivvärde för en fyrkantvåg För en ren fyrkant-spänning (utan DC): u t = A 0 t 2 A 2 t A t (s) U rms = A 2 dt + 2 A 2 dt = 1 A A2 A 2 2 = A 2 = A Fyrkantvåg med en DC-komponent, U DC U DC A t (s) u t = A + U DC 0 t 2 A + U DC 2 t U rms = A + U 2 DC dt + A + U DC 2 dt 2 = 1 A + U DC A + U DC 2 A + U DC 2 2 = = U DC 2 + A 2 Rms för rena fyrkantvågen ville.jalkanen@umu.se 18
19 Mer om effektivvärde Enligt definitionen gäller att en signals U rms är lika med den likspänning som ger samma effektutveckling över en resistans som signalen ger. Därför måste även en eventuell DC-komponent i växelspänningen bidra till det totala effektivvärdet, U true rms. Generellt: U total rms = U DC 2 + U rms(ac) 2 För AC-spänning med DC-komponent, utnyttja detta! Enklare beräkningar av effektivvärde. ville.jalkanen@umu.se 19
20 Mätning av effektivvärde Medelvärdesvisande-instrument: Effektivvärde = (likriktad medelvärde)*(formfaktor för sinus) Effektivvärdesvisande-instrument: rue rms (sant effektivvärde)-instrument: kan mäta andra vågformer än sinus. Mäter även DC-komponentens bidrag. (Obs! Inte alltid) AC-effektivvärde: mäter endast för AC-signaler (AC-kopplat dvs relativt signalens noll-linje) DC-komponentens bidrag får mätas separat. Bestäm det totala effektivvärdet genom att mäta både: 1. DC-komponentens medelvärde (i läge DC dvs DC-kopplat) och 2. AC-komponentens effektivvärde (i läge AC dvs AC-kopplat) U total rms = U DC 2 + U rms(ac) 2 ville.jalkanen@umu.se 20
21 Likriktat medelvärde Kallas beloppsmedelvärde eller absolutbelopp (eng. Rectified mean value). u = 1 0 u t dt Belopps-tecknet betyder att man likriktar signalen, Alla negativa värden blir positiva. För AC-kopplad mätning räknar man relativt signalens noll-linje. För en ren sinus-formad signal (utan DC dvs medelvärde = 0) blir: u = 2 amplitud π ville.jalkanen@umu.se 21
22 Formfaktor Formfaktor Kvoten mellan effektivvärdet och likriktade medelvärdet ξ = U rms u Formfaktorn använd främst vid mätningar med instrument som bara kan mäta likriktat medelvärde. Multiplicera uppmätt värde med formfaktorn, så får man effektivvärdet. Formfaktorn varierar med vilken form signalen har. För ren sinus (utan DC dvs medelvärde = 0): ξ = π ville.jalkanen@umu.se 22
23 Crestfaktor Crestfaktor (toppfaktor) Kvoten mellan toppvärde (maxvärde) och effektivvärdet. Anger hur extrema toppar (maxvärden) signalen har. Ett mått på voltmeterns prestanda (mäta signaler som skiljer sig från ren sinus (true rms)) λ = U topp U rms För ren likspänning blir λ = 1 För ren sinus (utan DC, dvs medel = 0): λ = ville.jalkanen@umu.se 23
24 Ellära 2 FILER ÖVERFÖRINGSFUNKION ville.jalkanen@umu.se 24
25 Sinus-signalen matematiskt ids-representation u 1 t = A sin ωt A u(t) u 2 t = A sin ωt + θ 0 t (s) tidsaxel θ ω id och fas (fasförkjutning = tidsförskjutning) A α = ωt 1 0 ωt (rad) α = ωt 1 fasaxel (Motsvarar en tidsförflyttning) Varje punkt i signalen kan representeras med en vektor med längden A och en fasvinkel ωt. vektor-representationen / visardiagram ville.jalkanen@umu.se 25
26 Vid t = 0 s u 1 t = A sin ωt u 2 t = A sin ωt + θ A θ 0 ωt (rad) θ Vid t = t 1 A θ ωt 1 ω θ ωt 1 ωt (rad) Signalen u 2 t ligger vinkeln θ före u 1 t..ex. u 2 t når värdet A före u 1 t. Vektorerna roterar med vinkelfrekvensen ω. Vektor-representationen för signalerna innehåller Amplitud och Fas (relativt 0) vid en specifik frekvens. ville.jalkanen@umu.se 26
27 Vektorer och komplexa tal Komplexa tal används för att representera vektorerna i visardiagrammet. Betrakta det komplexa talplanet: b Im r θ a z Re Rektangulär form z kan representeras av dess realdel a och dess imaginärdel b: z = a + jb Polär form z kan också representeras av en vektor med längden r och vinkeln θ (relativt Re-axeln): z = r θ j = 1 Samband: r = a 2 + b 2 θ = tan 1 b a a = r cos θ b = r sin θ z = a + jb = r cos θ + j sin θ e jθ ville.jalkanen@umu.se 27
28 Spänning, ström, impedans på vektorform Sinus-formad växelspänning/ström kan representeras som vektorer i det komplexa talplanet. Om u t = U sin ωt + α U = U α Om i t = I sin ωt + β I = I β (polär form) De har storlek och riktning och kan skrivas på polär form eller rektangulär form. R, C, L i växelströmskretsar kan betraktas som komplexa impedanser (enhet Ω ) dvs de ger en fasvridning. ω 0 ω Resistorn R: R R R R Kondensatorn C: Z C = 1 jωc = j 1 ωc Spolen L: Z L = jωl j 1 ωc (avbrott) jωl 0 (kortslutning) 0 (kortslutning) (avbrott) Ohms lag gäller: U = Z I Frekvensberoende! ville.jalkanen@umu.se 28
29 Exempel: RC-krets R = 1kΩ u in C = 0.16μF u ut u in t = 1 sin ωt U in = 1 0 Spänningsdelning ger U ut U ut = Z C R + Z C U in = 1 jωc R + 1 U in = jωc jωrc U in Sätt in R, C och ω = 2πf f = 100 Hz U ut = j = f = 1000 Hz U ut = j = f = Hz U ut = j = Frekvensen påverkas inte! Amplituden och fasen påverkas! ville.jalkanen@umu.se 29
30 Slutsatser av exemplet * ill kretsen skickar vi en signal med en amplitud, fas, och frekvens * Ut från kretsen får vi en signal med samma frekvens men med förändrad amplitud och fas * Förändringen i amplitud och fas beror på vald frekvens hos insignalen. Filter! * Vilken typ av filter? En signal med relativt låg frekvens släpps igenom relativt oförändrad. En signal med relativt hög frekvens förändras kraftigt. Dämpas och fasvrids. (dvs amplituden minskar vid ökad frekvens) Detta är ett lågpass (LP)-filter eftersom lågfrekventa signaler släpps igenom filtret. ville.jalkanen@umu.se 30
31 Byt plats på R och C C = 0.16μF u in R = 1kΩ u ut u in t = 1 sin ωt U in = 1 0 Spänningsdelning ger U ut U ut = R R + Z C U in = R R + 1 jωc U in = jωrc 1 + jωrc U in Sätt in R, C och ω = 2πf f = 100 Hz U ut = j = f = 1000 Hz U ut = j = f = Hz U ut = j = Positivt fasvridning värtom Högpass (HP)-filter ville.jalkanen@umu.se 31
32 Filter En krets med uppgift att släppa igenom signaler med önskad frekvens och stoppa (dämpa) signaler med övriga frekvenser. Vilka frekvenser ska dämpas/släppas igenom? hur kan vi kontrollera detta? Överföringsfunktion, gränsfrekvens 32
33 Överföringsfunktion Ett matematiskt samband som beskriver ett systems frekvensberoende egenskaper.ex. Filter, förstärkare Sambandet beskriver hur amplituden och fasvinkeln förändras då en sinusformad insignal (med viss frekvens) passerar systemet Insignal X ω H ω utsignal Y ω H ω = Y ω X ω Ett samband mellan sinus-formad insignal och utsignal (spänning) för variabeln frekvens, dvs H = Uut/Uin (förstärkning, dämpning) ville.jalkanen@umu.se 33
34 Exempel: överföringsfunktionen för LP- och HP-filter Lågpass-filter R u in C u ut U ut = Z C R + Z C U in = 1 jωc R + 1 U in = jωc jωrc U in H = U ut 1 = U in 1 + jωrc Högpass-filter C u in R u ut U ut = R R + Z C U in = R R + 1 jωc U in = jωrc 1 + jωrc U in H = U ut = jωrc U in 1 + jωrc ville.jalkanen@umu.se 34
35 Överföringsfunktion: amplitud och fas Överföringsfunktionen (H(ω)) beskriver hur amplituden och fasvinkeln förändras då en sinus-formad signal passerar systemet H är ett komplext tal. För varje frekvens, betrakta den som en vektor med storlek och riktning. Beloppet av H: H ω = Re H 2 + Im H 2 beskriver amplitudförhållandet mellan in- och utsignal. Fasvinkeln (dvs argumentet) för H: (förstärkningen/dämpningen) φ ω = arg H ω = tan 1 Im H ω Re H ω beskriver fasförskjutningen mellan in- och utsignal. H ω = H ω φ ω ville.jalkanen@umu.se 35
36 Gränsfrekvens Definition: Den frekvens där en sinusformad spänning minskat till 1 2 av dess ursprungliga storlek efter passage genom den frekvensberoende kretsen (t.ex. filter). Fås ur överföringsfunktionens amplitudinformation, dvs ur belopps-funktionen. H ω g = ω g = 2πf g är gräns(vinkel)frekvensen Kallas också brytfrekvens. På engelska cutoff frequency ville.jalkanen@umu.se 36
37 Gränsfrekvensen för LP-filtret Lågpass-filter R H = U ut 1 = U in 1 + jωrc u in C u ut H ω g = U ut U in = jω g RC = ω g RC 2 = ω g RC 2 = 2 ω g = 1 RC f g = 1 2πRC Gränsfrekvensen bestäms av komponenterna R och C som vi kan välja! Den sätter gränsen då en signals frekvens betraktas som relativt låg eller relativt hög. t.ex. 10f g är en hög frekvens medan 0.1f g är en låg frekvens från filtrets perspektiv ville.jalkanen@umu.se 37
38 Exempel: LP-filtret och dess gränsfrekvens u in R = 1kΩ C = 0.16μF u ut H = U ut 1 = U in 1 + jωrc H ω = H ω φ ω u in t = 1 sin ωt f = 100 Hz U ut U in = j0.10 = f = 1000 Hz U ut U in = j0.50 = Notera! H ω g = gränsfrekvens f g = 1 = 1000 Hz 2πRC f = Hz U ut U in = j0.10 = ville.jalkanen@umu.se 38
39 Gränsfrekvensen för HP-filtret Högpass-filter u in C R u ut H ω g H = U ut = jωrc U in 1 + jωrc = U ut = jω ω grc g RC U in 1 + jω g RC = = ω g RC ω g RC 2 = 2 ω g RC 2 ω g = 1 RC f g = 1 2πRC Gränsfrekvensen bestäms på samma sätt som för LP-filtret! ville.jalkanen@umu.se 39
40 Exempel: HP-filtret och dess gränsfrekvens C = 0.16μF u in t = 1 sin ωt u in R = 1kΩ u ut H = U ut = jωrc U in 1 + jωrc f = 100 Hz U ut U in = j0.10 = f = 1000 Hz U ut U in = j0.50 = H ω g = Gränsfrekvensen! f g = 1 = 1000 Hz 2πRC f = Hz U ut U in = j0.10 = ville.jalkanen@umu.se 40
41 Rita överföringsfunktionen Eftersom H(ω) är frekvensberoende så är det praktiskt att rita H mot ω. Men H är komplex. Bode-diagram H ω = H ω φ ω Ger snabb överblick över systemets (filtrets) frekvensegenskaper ville.jalkanen@umu.se 41
42 Bode diagram Den frekvensberende överföringsfunktionen med beloppet H ω och fasvinkeln φ ω kan presenteras med Bode-diagram. Beloppet graderas ofta i decibel (logaritmisk). Fasen graderas i grader. Båda mot en logaritmisk frekvensskala. H db = 20 log 10 H Överföringsfunktionen H = Uut/Uin förstärkningen H ω φ ω ville.jalkanen@umu.se 42
43 R = 1kΩ Bodediagram: exempel LP-filtret Belopp & fas mot frekvens H ω = H ω φ ω u in C = 0.16μF u ut Obs! Logaritmisk skala på belopp (ej db) och frekvens f = 100 Hz U ut U in = f = Hz U ut U in = Gränsfrekvensen i exemplet f = 1000 Hz U ut U in = Inte snyggt! Vi kan bättre! ville.jalkanen@umu.se 43
44 För några fler frekvenser får vi bättre översikt över LP-filtrets egenskaper Obs! Log-skala Lutningen ( roll off ) passband stoppband 100, 1000, Hz från tidigare f g = 1000 Hz i exemplet ville.jalkanen@umu.se 44
45 Linjär-, log-, db-skala Jämförelse mellan linjär-, log-, och decibel-skala för beloppet för LP-filter exemplet. linjär Omvandla till decibel H db = 20 log 10 H 10 H db 20 = H 20 log 10 1 = 0 db 20 log db 20 log db 20 log = 20 db 20 log db 20 log = 40 db 20 log = 60 db Log/dB-skala visar samma avstånd mellan varje dekad skalstreck log 10 -skala decibel-skala Lutningen -20 db/dekad ville.jalkanen@umu.se 45
46 Bodediagram: exemplet HP-filtret C = 0.16μF u in R = 1kΩ u ut f = 100 Hz U ut U in = f = 1000 Hz U ut U in = f = Hz U ut U in = ville.jalkanen@umu.se 46
47 Skissa Bode-diagram Hur får vi fram Bode-diagrammet ur H(ω)? Simulera med programvara Skissa för hand genom att titta på beloppet då ω 0 och då ω. Skissa för hand om överföringsfunktionen är på Bode s normalform, dvs uttnyttja kurvor för deluttryck. I senare kurs. ville.jalkanen@umu.se 47
48 Ellära 2 FREKVENSANALYS ville.jalkanen@umu.se 48
49 Frekvensanalys Sinus Om signalen istället är: vå sinus med olika frekvenser (sammansatt) Fyrkantvåg Sinus med brus annat Finns det metoder att ta reda på en signals frekvensinnehåll? Ja! Matematiskt (men utanför kursen) Fouriertransform, DF, FF tid frekvens 49
Periodiska signaler, frekvens, filter, överföringsfunktion
 Periodiska signaler, frekvens, filter, överföringsfunktion Ville Jalkanen illämpad fysik och elektronik, UmU ville.jalkanen@umu.se 1 Informationsbärare Signal Fysikalisk storhet som varierar pga annan
Periodiska signaler, frekvens, filter, överföringsfunktion Ville Jalkanen illämpad fysik och elektronik, UmU ville.jalkanen@umu.se 1 Informationsbärare Signal Fysikalisk storhet som varierar pga annan
Filter. Mätteknik. Ville Jalkanen, TFE, UmU. 1
 Filter Mätteknik Ville Jalkanen, TFE, UmU ville.jalkanen@umu.se 1 Decibel (db) Förstärkningen anges ofta i decibel (db) A V(dB) = 20 log 10 A V Exempel: En A V = 10 ggr motsvaras av 20 log 10 10 = 20 db
Filter Mätteknik Ville Jalkanen, TFE, UmU ville.jalkanen@umu.se 1 Decibel (db) Förstärkningen anges ofta i decibel (db) A V(dB) = 20 log 10 A V Exempel: En A V = 10 ggr motsvaras av 20 log 10 10 = 20 db
Växelström K O M P E N D I U M 2 ELEKTRO
 MEÅ NIVERSITET Tillämpad fysik och elektronik Sverker Johansson Johan Pålsson 999-09- Rev.0 Växelström K O M P E N D I M ELEKTRO INNEHÅLL. ALLMÄNT OM LIK- OCH VÄXELSPÄNNINGAR.... SAMBANDET MELLAN STRÖM
MEÅ NIVERSITET Tillämpad fysik och elektronik Sverker Johansson Johan Pålsson 999-09- Rev.0 Växelström K O M P E N D I M ELEKTRO INNEHÅLL. ALLMÄNT OM LIK- OCH VÄXELSPÄNNINGAR.... SAMBANDET MELLAN STRÖM
Spolen och Kondensatorn motverkar förändringar
 Spolen och Kondensatorn motverkar förändringar Spolen och kondensatorn motverkar förändringar, tex vid inkoppling eller urkoppling av en källa till en krets. Hur går det då om källan avger en sinusformad
Spolen och Kondensatorn motverkar förändringar Spolen och kondensatorn motverkar förändringar, tex vid inkoppling eller urkoppling av en källa till en krets. Hur går det då om källan avger en sinusformad
Laboration - Va xelstro mskretsar
 Laboration - Va xelstro mskretsar 1 Introduktion och redovisning I denna laboration simuleras spänning och ström i enkla växelströmskretsar bestående av komponenter som motstånd, kondensator, och spole.
Laboration - Va xelstro mskretsar 1 Introduktion och redovisning I denna laboration simuleras spänning och ström i enkla växelströmskretsar bestående av komponenter som motstånd, kondensator, och spole.
Frekvensplanet och Bode-diagram. Frekvensanalys
 Frekvensplanet och Bode-diagram Frekvensanalys Signaler Allt inom elektronik går ut på att manipulera signaler genom signalbehandling (Signal Processing). Analog signalbehandling Kretsteori: Nod-analys,
Frekvensplanet och Bode-diagram Frekvensanalys Signaler Allt inom elektronik går ut på att manipulera signaler genom signalbehandling (Signal Processing). Analog signalbehandling Kretsteori: Nod-analys,
IE1206 Inbyggd Elektronik
 E1206 nbyggd Elektronik F1 F3 F4 F2 Ö1 Ö2 PC-block Dokumentation, Seriecom Pulsgivare,, R, P, serie och parallell KK1 LAB1 Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchoffs lagar Nodanalys
E1206 nbyggd Elektronik F1 F3 F4 F2 Ö1 Ö2 PC-block Dokumentation, Seriecom Pulsgivare,, R, P, serie och parallell KK1 LAB1 Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchoffs lagar Nodanalys
Elektroteknikens grunder Laboration 1
 Elektroteknikens grunder Laboration 1 Grundläggande ellära Elektrisk mätteknik Elektroteknikens grunder Laboration 1 1 Mål Du skall i denna laboration få träning i att koppla elektriska kretsar och att
Elektroteknikens grunder Laboration 1 Grundläggande ellära Elektrisk mätteknik Elektroteknikens grunder Laboration 1 1 Mål Du skall i denna laboration få träning i att koppla elektriska kretsar och att
Spä nningsmä tning äv periodiskä signäler
 UMEÅ UNIVERSITET v, 6-- Tillämpad fysik och elektronik Sverker Johansson Bo Tannfors Nils Lundgren Ville Jalkanen Spä nningsmä tning äv periodiskä signäler Introduktion Laborationen går ut på att med mätinstrument
UMEÅ UNIVERSITET v, 6-- Tillämpad fysik och elektronik Sverker Johansson Bo Tannfors Nils Lundgren Ville Jalkanen Spä nningsmä tning äv periodiskä signäler Introduktion Laborationen går ut på att med mätinstrument
DET ÄR INGEN KONST ATT MÄTA SPÄNNING OCH STRÖM
 DE ÄR INGEN KONS A MÄA SPÄNNING OCH SRÖM OM MAN VE HR DE FNGERAR! lite grundläggande el-mätteknik 010 INNEHÅLL Inledning 3 Grunder 3 Växelspänning 4 Effektivvärde 5 Likriktat medelvärde 6 Överlagrad spänning
DE ÄR INGEN KONS A MÄA SPÄNNING OCH SRÖM OM MAN VE HR DE FNGERAR! lite grundläggande el-mätteknik 010 INNEHÅLL Inledning 3 Grunder 3 Växelspänning 4 Effektivvärde 5 Likriktat medelvärde 6 Överlagrad spänning
Elektronik 2018 EITA35
 Elektronik 218 EITA35 Föreläsning 1 Filter Lågpassfilter Högpassfilter (Allpassfilter) Bodediagram Hambley 296-32 218-1-2 Föreläsning 1, Elektronik 218 1 Laboration 2 Förberedelseuppgifter! (Ingen anmälan
Elektronik 218 EITA35 Föreläsning 1 Filter Lågpassfilter Högpassfilter (Allpassfilter) Bodediagram Hambley 296-32 218-1-2 Föreläsning 1, Elektronik 218 1 Laboration 2 Förberedelseuppgifter! (Ingen anmälan
AC-kretsar. Växelströmsteori. Lund University / Faculty / Department / Unit / Document / Date
 AC-kretsar Växelströmsteori Signaler Konstant signal: Likström och likspänning (DC) Transienta strömmar/spänningar Växelström och växelspänning (AC) Växelström/spänning Växelström alternating current (AC)
AC-kretsar Växelströmsteori Signaler Konstant signal: Likström och likspänning (DC) Transienta strömmar/spänningar Växelström och växelspänning (AC) Växelström/spänning Växelström alternating current (AC)
Tentamen i Elektronik, ESS010, del1 4,5hp den 19 oktober 2007 klockan 8:00 13:00 För de som är inskrivna hösten 2007, E07
 Tentamen i Elektronik, ESS00, del 4,5hp den 9 oktober 007 klockan 8:00 :00 För de som är inskrivna hösten 007, E07 Tekniska Högskolan i Lund Institutionen för Elektrovetenskap Tentamen i Elektronik, ESS00,
Tentamen i Elektronik, ESS00, del 4,5hp den 9 oktober 007 klockan 8:00 :00 För de som är inskrivna hösten 007, E07 Tekniska Högskolan i Lund Institutionen för Elektrovetenskap Tentamen i Elektronik, ESS00,
Spolen och Kondensatorn motverkar förändringar
 Spolen och Kondensatorn motverkar förändringar Spolen och kondensatorn motverkar förändringar, tex vid inkoppling eller urkoppling av en källa till en krets. Hur går det då om källan avger en sinusformad
Spolen och Kondensatorn motverkar förändringar Spolen och kondensatorn motverkar förändringar, tex vid inkoppling eller urkoppling av en källa till en krets. Hur går det då om källan avger en sinusformad
Introduktion till fordonselektronik ET054G. Föreläsning 3
 Introduktion till fordonselektronik ET054G Föreläsning 3 1 Elektriska och elektroniska fordonskomponenter Att använda el I Sverige Fas: svart Nolla: blå Jord: gröngul Varför en jordkabel? 2 Jordning och
Introduktion till fordonselektronik ET054G Föreläsning 3 1 Elektriska och elektroniska fordonskomponenter Att använda el I Sverige Fas: svart Nolla: blå Jord: gröngul Varför en jordkabel? 2 Jordning och
Ellära. Laboration 4 Mätning och simulering. Växelströmsnät.
 Ellära. Laboration 4 Mätning och simulering. Växelströmsnät. Labhäftet underskrivet av läraren gäller som kvitto för labben. Varje laborant måste ha ett eget labhäfte med ifyllda förberedelseuppgifter
Ellära. Laboration 4 Mätning och simulering. Växelströmsnät. Labhäftet underskrivet av läraren gäller som kvitto för labben. Varje laborant måste ha ett eget labhäfte med ifyllda förberedelseuppgifter
Lab 3. Några slides att repetera inför Lab 3. William Sandqvist
 Lab 3 Några slides att repetera inför Lab 3 Medelvärde och effektivvärde Alla rena växelspänningar har medelvärdet 0. Intressantare är effektivvärdet det kvadratiska medelvärdet. U med T 0 = 1 T u( t)dt
Lab 3 Några slides att repetera inför Lab 3 Medelvärde och effektivvärde Alla rena växelspänningar har medelvärdet 0. Intressantare är effektivvärdet det kvadratiska medelvärdet. U med T 0 = 1 T u( t)dt
IF1330 Ellära KK1 LAB1 KK2 LAB2. tentamen
 F1330 Ellära F/Ö1 F/Ö4 F/Ö F/Ö5 F/Ö3 Strömkretslära Mätinstrument Batterier Likströmsnät Tvåpolsatsen KK1 LAB1 Mätning av och F/Ö6 F/Ö7 Magnetkrets Kondensator Transienter KK LAB Tvåpol mät och sim F/Ö8
F1330 Ellära F/Ö1 F/Ö4 F/Ö F/Ö5 F/Ö3 Strömkretslära Mätinstrument Batterier Likströmsnät Tvåpolsatsen KK1 LAB1 Mätning av och F/Ö6 F/Ö7 Magnetkrets Kondensator Transienter KK LAB Tvåpol mät och sim F/Ö8
IF1330 Ellära KK1 LAB1 KK2 LAB2. tentamen
 IF330 Ellära F/Ö F/Ö4 F/Ö F/Ö5 F/Ö3 Strömkretslära Mätinstrument Batterier Likströmsnät Tvåpolsatsen KK LAB Mätning av U och I F/Ö6 F/Ö7 Magnetkrets Kondensator Transienter KK LAB Tvåpol mät och sim F/Ö8
IF330 Ellära F/Ö F/Ö4 F/Ö F/Ö5 F/Ö3 Strömkretslära Mätinstrument Batterier Likströmsnät Tvåpolsatsen KK LAB Mätning av U och I F/Ö6 F/Ö7 Magnetkrets Kondensator Transienter KK LAB Tvåpol mät och sim F/Ö8
IDE-sektionen. Laboration 5 Växelströmsmätningar
 9428 IDEsektionen Laboration 5 Växelströmsmätningar 1 Förberedelseuppgifter laboration 4 1. Antag att vi mäter spänningen över en okänd komponent resultatet blir u(t)= 3sin(ωt) [V]. Motsvarande ström är
9428 IDEsektionen Laboration 5 Växelströmsmätningar 1 Förberedelseuppgifter laboration 4 1. Antag att vi mäter spänningen över en okänd komponent resultatet blir u(t)= 3sin(ωt) [V]. Motsvarande ström är
DEL-LINJÄRA DIAGRAM I
 Institutionen för Tillämpad fysik och elektronik Ulf Holmgren 95124 DEL-LINJÄRA DIAGRAM I Laboration E15 ELEKTRO Personalia: Namn: Kurs: Datum: Återlämnad (ej godkänd): Rättningsdatum Kommentarer Godkänd:
Institutionen för Tillämpad fysik och elektronik Ulf Holmgren 95124 DEL-LINJÄRA DIAGRAM I Laboration E15 ELEKTRO Personalia: Namn: Kurs: Datum: Återlämnad (ej godkänd): Rättningsdatum Kommentarer Godkänd:
Ulrik Söderström 20 Jan Signaler & Signalanalys
 Ulrik Söderström ulrik.soderstrom@tfe.umu.se 20 Jan 2009 Signaler & Signalanalys Sinusspänning Sinus och cosinus samma form men fasförskjutna Fasförskjutning tidsfördröjning Sinus och cosinus är väldigt
Ulrik Söderström ulrik.soderstrom@tfe.umu.se 20 Jan 2009 Signaler & Signalanalys Sinusspänning Sinus och cosinus samma form men fasförskjutna Fasförskjutning tidsfördröjning Sinus och cosinus är väldigt
Ulrik Söderström 19 Jan Signalanalys
 Ulrik Söderström ulrik.soderstrom@tfe.umu.se 9 Jan 200 Signaler & Signalanalys l Sinusspänning Sinus och cosinus samma form men fasförskjutna Fasförskjutning tidsfördröjning Sinus och cosinus är väldigt
Ulrik Söderström ulrik.soderstrom@tfe.umu.se 9 Jan 200 Signaler & Signalanalys l Sinusspänning Sinus och cosinus samma form men fasförskjutna Fasförskjutning tidsfördröjning Sinus och cosinus är väldigt
Samtidig visning av alla storheter på 3-fas elnät
 Samtidig visning av alla storheter på 3-fas elnät Med nätanalysatorerna från Qualistar+ serien visas samtliga parametrar på tre-fas elnätet på en färgskärm. idsbaserad visning Qualistar+ visar insignalerna
Samtidig visning av alla storheter på 3-fas elnät Med nätanalysatorerna från Qualistar+ serien visas samtliga parametrar på tre-fas elnätet på en färgskärm. idsbaserad visning Qualistar+ visar insignalerna
Lab 4. Några slides att repetera inför Lab 4. William Sandqvist
 Lab 4 Några slides att repetera inför Lab 4 Oscilloskopets Wave-generator Waveform Sine Square Ramp Pulse DC Noise BNC-kontakt Frequency Amplitude Offset Man kan använda oscilloskopets inbyggda Wave-generator!
Lab 4 Några slides att repetera inför Lab 4 Oscilloskopets Wave-generator Waveform Sine Square Ramp Pulse DC Noise BNC-kontakt Frequency Amplitude Offset Man kan använda oscilloskopets inbyggda Wave-generator!
IE1206 Inbyggd Elektronik
 IE06 Inbyggd Elektronik F F3 F4 F Ö Ö PI-block Dokumentation, Seriecom Pulsgivare I,, R, P, serie och parallell KK LAB Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchhoffs lagar Nodanalys
IE06 Inbyggd Elektronik F F3 F4 F Ö Ö PI-block Dokumentation, Seriecom Pulsgivare I,, R, P, serie och parallell KK LAB Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchhoffs lagar Nodanalys
VÄXELSTRÖM SPÄNNINGSDELNING
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Agneta Bränberg Patrik Eriksson (uppdatering) 1996-06-12 uppdaterad 2005-04-13 VÄXELSTRÖM SPÄNNINGSDELNING Laboration E10 ELEKTRO Personalia: Namn: Kurs:
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Agneta Bränberg Patrik Eriksson (uppdatering) 1996-06-12 uppdaterad 2005-04-13 VÄXELSTRÖM SPÄNNINGSDELNING Laboration E10 ELEKTRO Personalia: Namn: Kurs:
Instruktioner för laboration 2, Elektromagnetism och elektriska nät 1TE025 Elektriska system 1TE014
 Instruktioner för laboration 2, Elektromagnetism och elektriska nät 1TE025 Elektriska system 1TE014 Mattias Wallin Datum: 15 februari 2010 16 februari 2010 1 Inledning I denna laboration ingår förberedande
Instruktioner för laboration 2, Elektromagnetism och elektriska nät 1TE025 Elektriska system 1TE014 Mattias Wallin Datum: 15 februari 2010 16 februari 2010 1 Inledning I denna laboration ingår förberedande
Tentamen i Elektronik, ESS010, del 1 den 21 oktober 2008 klockan 8:00 13:00
 Tentamen i Elektronik, ESS00, del den oktober 008 klockan 8:00 :00 Tekniska Högskolan i Lund Institutionen för Elektrovetenskap Tentamen i Elektronik, ESS00, del den oktober 008 klockan 8:00 :00 Uppgifterna
Tentamen i Elektronik, ESS00, del den oktober 008 klockan 8:00 :00 Tekniska Högskolan i Lund Institutionen för Elektrovetenskap Tentamen i Elektronik, ESS00, del den oktober 008 klockan 8:00 :00 Uppgifterna
Mät kondensatorns reaktans
 Ellab012A Mät kondensatorns reaktans Namn Datum Handledarens sign Varför denna laboration? Avsikten med den här laborationen är att träna grundläggande analys- och mätteknik vid mätning på växelströmkretsar
Ellab012A Mät kondensatorns reaktans Namn Datum Handledarens sign Varför denna laboration? Avsikten med den här laborationen är att träna grundläggande analys- och mätteknik vid mätning på växelströmkretsar
Fö 1 - TMEI01 Elkraftteknik Trefassystemet
 Fö 1 - TMEI01 Elkraftteknik Trefassystemet Per Öberg 16 januari 2015 Outline 1 Introduktion till Kursen Outline 1 Introduktion till Kursen 2 Repetition växelströmslära Outline 1 Introduktion till Kursen
Fö 1 - TMEI01 Elkraftteknik Trefassystemet Per Öberg 16 januari 2015 Outline 1 Introduktion till Kursen Outline 1 Introduktion till Kursen 2 Repetition växelströmslära Outline 1 Introduktion till Kursen
Tentamen i Elektronik, ESS010, del 2 den 17 dec 2007 klockan 8:00 13:00 för inskrivna på elektroteknik Ht 2007.
 Tekniska Högskolan i Lund Institutionen för Elektrovetenskap Tentamen i Elektronik, ESS010, del 2 den 17 dec 2007 klockan 8:00 13:00 för inskrivna på elektroteknik Ht 2007. Uppgifterna i tentamen ger totalt
Tekniska Högskolan i Lund Institutionen för Elektrovetenskap Tentamen i Elektronik, ESS010, del 2 den 17 dec 2007 klockan 8:00 13:00 för inskrivna på elektroteknik Ht 2007. Uppgifterna i tentamen ger totalt
Ellära och Elektronik Moment AC-nät Föreläsning 5
 Ellära och Elektronik Moment A-nät Föreläsning 5 Visardiagram Impendans jω-metoden Komplex effekt, effekttriangeln Visardiagram Om man tar projektionen på y- axeln av en roterande visare får man en sinusformad
Ellära och Elektronik Moment A-nät Föreläsning 5 Visardiagram Impendans jω-metoden Komplex effekt, effekttriangeln Visardiagram Om man tar projektionen på y- axeln av en roterande visare får man en sinusformad
2 Ortogonala signaler. Fourierserier. Enkla filter.
 Ortogonala signaler. Fourierserier. Enkla filter. ktuella ekvationer: Se formelsamlingen och förberedelsehäftet. För effektivvärdet av en summa av N ortogonala signaler gäller: ν rms = ν rms1 + ν rms +...
Ortogonala signaler. Fourierserier. Enkla filter. ktuella ekvationer: Se formelsamlingen och förberedelsehäftet. För effektivvärdet av en summa av N ortogonala signaler gäller: ν rms = ν rms1 + ν rms +...
Spänningsmätning av periodiska signaler
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Sverker Johansson Bo Tannfors 1996-05-15 Spänningsmätning av periodiska signaler Laboration E8 ELEKTRO Laboration E8 Spänningsmätning av periodiska signaler
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Sverker Johansson Bo Tannfors 1996-05-15 Spänningsmätning av periodiska signaler Laboration E8 ELEKTRO Laboration E8 Spänningsmätning av periodiska signaler
Växelspänning och effekt. S=P+jQ. Olof Samuelsson Industriell Elektroteknik och Automation
 Växelspänning och effekt S=P+jQ VA W var Olof Samuelsson Industriell Elektroteknik och Automation Översikt Synkronmaskinens uppbyggnad Växelspänning Komplexräkning Komplex, aktiv och reaktiv effekt Ögonblicksvärde
Växelspänning och effekt S=P+jQ VA W var Olof Samuelsson Industriell Elektroteknik och Automation Översikt Synkronmaskinens uppbyggnad Växelspänning Komplexräkning Komplex, aktiv och reaktiv effekt Ögonblicksvärde
Växelspänning och effekt. S=P+jQ. Ingmar Leisse Industriell Elektroteknik och Automation
 Växelspänning och effekt S=P+jQ VA W var Ingmar Leisse Industriell Elektroteknik och Automation Översikt Synkronmaskinens uppbyggnad Växelspänning Komplexräkning Komplex, aktiv och reaktiv effekt Ögonblicksvärde
Växelspänning och effekt S=P+jQ VA W var Ingmar Leisse Industriell Elektroteknik och Automation Översikt Synkronmaskinens uppbyggnad Växelspänning Komplexräkning Komplex, aktiv och reaktiv effekt Ögonblicksvärde
Passiva filter. Laboration i Elektronik E151. Tillämpad fysik och elektronik UMEÅ UNIVERSITET Ulf Holmgren. Ej godkänd. Godkänd
 Tillämpad fysik och elektronik UMEÅ UNIVESITET Ulf Holmgren LABOATION Analog elektronik 961219 Passiva filter Laboration i Elektronik E151 Namn Namn Ej godkänd Datum Datum Godkänd Datum PASSIVA FILTE -
Tillämpad fysik och elektronik UMEÅ UNIVESITET Ulf Holmgren LABOATION Analog elektronik 961219 Passiva filter Laboration i Elektronik E151 Namn Namn Ej godkänd Datum Datum Godkänd Datum PASSIVA FILTE -
Komplexa tal. j 2 = 1
 1 Komplexa tal De komplexa talen används när man behandlar växelström inom elektroniken. Imaginära enheten betecknas i elektroniken med j (i, som används i matematiken, är ju upptaget av strömmen). Den
1 Komplexa tal De komplexa talen används när man behandlar växelström inom elektroniken. Imaginära enheten betecknas i elektroniken med j (i, som används i matematiken, är ju upptaget av strömmen). Den
Växelström i frekvensdomän [5.2]
![Växelström i frekvensdomän [5.2] Växelström i frekvensdomän [5.2]](/thumbs/101/150871096.jpg) Föreläsning 7 Hambley avsnitt 5.-4 Tidsharmoniska (sinusformade) signaler är oerhört betydelsefulla inom de flesta typer av kommunikationssystem. adio, T, mobiltelefoner, kabel-t, bredband till datorer
Föreläsning 7 Hambley avsnitt 5.-4 Tidsharmoniska (sinusformade) signaler är oerhört betydelsefulla inom de flesta typer av kommunikationssystem. adio, T, mobiltelefoner, kabel-t, bredband till datorer
VÄXELSTRÖM SPÄNNINGSDELNING
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Agneta Bränberg 1996-06-12 VÄXELSTRÖM SPÄNNINGSDELNING Laboration E10 ELEKTRO Personalia: Namn: Kurs: Datum: Återlämnad (ej godkänd): Rättningsdatum Kommentarer
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Agneta Bränberg 1996-06-12 VÄXELSTRÖM SPÄNNINGSDELNING Laboration E10 ELEKTRO Personalia: Namn: Kurs: Datum: Återlämnad (ej godkänd): Rättningsdatum Kommentarer
Tentamen i Elektronik, ESS010, den 15 december 2005 klockan 8:00 13:00
 Tekniska Högskolan i Lund Institutionen för Elektrovetenskap Tentamen i Elektronik, ESS00, den 5 december 005 klockan 8:00 3:00 Uppgifterna i tentamen ger totalt 60p. Uppgifterna är inte ordnade på något
Tekniska Högskolan i Lund Institutionen för Elektrovetenskap Tentamen i Elektronik, ESS00, den 5 december 005 klockan 8:00 3:00 Uppgifterna i tentamen ger totalt 60p. Uppgifterna är inte ordnade på något
Fö 1 - TMEI01 Elkraftteknik Trefassystemet
 Fö 1 - TMEI01 Elkraftteknik Trefassystemet Christofer Sundström 20 januari 2019 Outline 1 Introduktion till Kursen 2 Repetition växelströmslära 3 Huvudspänning och fasspänning 4 Y- och D-koppling 5 Symmetrisk
Fö 1 - TMEI01 Elkraftteknik Trefassystemet Christofer Sundström 20 januari 2019 Outline 1 Introduktion till Kursen 2 Repetition växelströmslära 3 Huvudspänning och fasspänning 4 Y- och D-koppling 5 Symmetrisk
Bestäm uttrycken för följande spänningar/strömmar i kretsen, i termer av ( ) in a) Utspänningen vut b) Den totala strömmen i ( ) c) Strömmen () 2
 7 Elektriska kretsar Av: Lasse Alfredsson och Klas Nordberg 7- Nedan finns en krets med resistanser. Då kretsen ansluts till en annan elektrisk krets uppkommer spänningen vin ( t ) och strömmen ( ) Bestäm
7 Elektriska kretsar Av: Lasse Alfredsson och Klas Nordberg 7- Nedan finns en krets med resistanser. Då kretsen ansluts till en annan elektrisk krets uppkommer spänningen vin ( t ) och strömmen ( ) Bestäm
Hambley avsnitt
 Föreläsning Hambley avsnitt 6.6.8 Filter [6.2, 6.5 6.8] Nästan all trådlös och trådbunden kommunikation är baserad på tidsharmoniska signaler. Signalerna utnyttjar ett frekvensband centrerad kring en bärfrekvens.
Föreläsning Hambley avsnitt 6.6.8 Filter [6.2, 6.5 6.8] Nästan all trådlös och trådbunden kommunikation är baserad på tidsharmoniska signaler. Signalerna utnyttjar ett frekvensband centrerad kring en bärfrekvens.
Strömmätning på riktigt
 Strömmätning på riktigt RMS TRMS Kategorier Strömmätning på riktigt Strömmätning på riktigt Kan vi använda vilket instrument som helst för att få ett korrekt värde vid strömmätning? När visar instrumentet
Strömmätning på riktigt RMS TRMS Kategorier Strömmätning på riktigt Strömmätning på riktigt Kan vi använda vilket instrument som helst för att få ett korrekt värde vid strömmätning? När visar instrumentet
Ellära och Elektronik Moment Filter och OP Föreläsning 8
 Ellära och Elektronik Moment Filter och OP Föreläsning 8 Mer om bandpassfilter och bandspärrfilter esonanskretsar Copyright 008 Börje Norlin Bandpassfilter För att konstruera denna typ av filter krävs
Ellära och Elektronik Moment Filter och OP Föreläsning 8 Mer om bandpassfilter och bandspärrfilter esonanskretsar Copyright 008 Börje Norlin Bandpassfilter För att konstruera denna typ av filter krävs
Grundläggande signalbehandling
 Beskrivning av en enkel signal Sinussignal (Alla andra typer av signaler och ljud kan skapas genom att sätta samman sinussignaler med olika frekvens, Amplitud och fasvridning) Periodtid T y t U Amplitud
Beskrivning av en enkel signal Sinussignal (Alla andra typer av signaler och ljud kan skapas genom att sätta samman sinussignaler med olika frekvens, Amplitud och fasvridning) Periodtid T y t U Amplitud
Laboration 4: Tidsplan, frekvensplan och impedanser. Lunds universitet / Fakultet / Institution / Enhet / Dokument / Datum
 Laboration 4: Tidsplan, frekvensplan och impedanser Decibel Ett relativt mått på effekt, med enheten [db]: Man kan också mäta absoluta värden genom att relatera till en referens: Impedans på ingång och
Laboration 4: Tidsplan, frekvensplan och impedanser Decibel Ett relativt mått på effekt, med enheten [db]: Man kan också mäta absoluta värden genom att relatera till en referens: Impedans på ingång och
Laborationsrapport. Kurs Elinstallation, begränsad behörighet. Lab nr 2. Laborationens namn Växelströmskretsar. Kommentarer. Utförd den.
 Laborationsrapport Kurs Elinstallation, begränsad behörighet Lab nr 2 version 3.1 Laborationens namn Växelströmskretsar Namn Kommentarer Utförd den Godkänd den Sign 1 Inledning I denna laboration skall
Laborationsrapport Kurs Elinstallation, begränsad behörighet Lab nr 2 version 3.1 Laborationens namn Växelströmskretsar Namn Kommentarer Utförd den Godkänd den Sign 1 Inledning I denna laboration skall
Umeå universitet Tillämpad fysik och elektronik Ville Jalkanen mfl Laboration Tema OP. Analog elektronik för Elkraft 7.
 Laboration Tema OP Analog elektronik för Elkraft 7.5 hp 1 Applikationer med operationsförstärkare Operationsförstärkaren är ett byggblock för analoga konstruktörer. Den går att använda för att förstärka
Laboration Tema OP Analog elektronik för Elkraft 7.5 hp 1 Applikationer med operationsförstärkare Operationsförstärkaren är ett byggblock för analoga konstruktörer. Den går att använda för att förstärka
Växelström i frekvensdomän [5.2]
![Växelström i frekvensdomän [5.2] Växelström i frekvensdomän [5.2]](/thumbs/62/47119214.jpg) Föreläsning 7 Hambley avsnitt 5.-4 Tidsharmoniska (sinusformade) signaler är oerhört betydelsefulla inom de flesta typer av kommunikationssystem. adio, T, mobiltelefoner, kabel-t, bredband till datorer
Föreläsning 7 Hambley avsnitt 5.-4 Tidsharmoniska (sinusformade) signaler är oerhört betydelsefulla inom de flesta typer av kommunikationssystem. adio, T, mobiltelefoner, kabel-t, bredband till datorer
10. Kretsar med långsamt varierande ström
 1. Kretsar med långsamt varierande ström [RMC] Elektrodynamik, ht 25, Krister Henriksson 1.1 1.1. Villkor för långsamt varierande I detta kapitel behandlas den teori som kan användas för att analysera
1. Kretsar med långsamt varierande ström [RMC] Elektrodynamik, ht 25, Krister Henriksson 1.1 1.1. Villkor för långsamt varierande I detta kapitel behandlas den teori som kan användas för att analysera
Spolens reaktans och resonanskretsar
 Ellab013A Spolens reaktans och resonanskretsar Namn Datum Handledarens sign Laboration Varför denna laboration? Avsikten med den här laborationen är att träna grundläggande analys- och mätteknik vid mätning
Ellab013A Spolens reaktans och resonanskretsar Namn Datum Handledarens sign Laboration Varför denna laboration? Avsikten med den här laborationen är att träna grundläggande analys- och mätteknik vid mätning
Fö 3 - TSFS11 Energitekniska system Trefassystemet
 Fö 3 - TSFS11 Energitekniska system Trefassystemet Christofer Sundström 23 mars 2018 Kursöversikt Fö 11 Fö 5,13 Fö 4 Fö 2 Fö 6 Fö 3 Fö 7,9,10 Fö 13 Fö 12 Fö 8 Outline 1 Repetition växelströmslära 2 Huvudspänning
Fö 3 - TSFS11 Energitekniska system Trefassystemet Christofer Sundström 23 mars 2018 Kursöversikt Fö 11 Fö 5,13 Fö 4 Fö 2 Fö 6 Fö 3 Fö 7,9,10 Fö 13 Fö 12 Fö 8 Outline 1 Repetition växelströmslära 2 Huvudspänning
Spänningsmätning K O M P E N D I U M 1 ELEKTRO
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Sverker Johansson Johan Pålsson 1999-09-17 Rev 1.0 Spänningsmätning K O M P E N D I U M 1 ELEKTRO INNEHÅLL 1. ALLMÄNT OM VÄXELSPÄNNINGAR...2 2. NÅGRA DEFINITIONER...3
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Sverker Johansson Johan Pålsson 1999-09-17 Rev 1.0 Spänningsmätning K O M P E N D I U M 1 ELEKTRO INNEHÅLL 1. ALLMÄNT OM VÄXELSPÄNNINGAR...2 2. NÅGRA DEFINITIONER...3
i(t) C i(t) = dq(t) dt = C dy(t) dt y(t) + (4)
 2 Andra lektionen 2. Impulssvar 2.. En liten krets Beräkna impulssvaret för kretsen i figur genom att beräkna hur y(t) beror av x(t). R x(t) i(t) C y(t) Figur : Första ordningens lågpassfilter. Utsignalen
2 Andra lektionen 2. Impulssvar 2.. En liten krets Beräkna impulssvaret för kretsen i figur genom att beräkna hur y(t) beror av x(t). R x(t) i(t) C y(t) Figur : Första ordningens lågpassfilter. Utsignalen
Grundläggande ellära - - 1. Induktiv och kapacitiv krets. Förberedelseuppgifter. Labuppgifter U 1 U R I 1 I 2 U C U L + + IEA Lab 1:1 - ETG 1
 IEA Lab 1:1 - ETG 1 Grundläggande ellära Motivering för laborationen: Labmomenten ger träning i att koppla elektriska kretsar och att mäta med oscilloskop och multimetrar. Den ger också en koppling till
IEA Lab 1:1 - ETG 1 Grundläggande ellära Motivering för laborationen: Labmomenten ger träning i att koppla elektriska kretsar och att mäta med oscilloskop och multimetrar. Den ger också en koppling till
Välkomna till TSRT19 Reglerteknik Föreläsning 5. Sammanfattning av föreläsning 4 Frekvensanalys Bodediagram
 Välkomna till TSRT19 Reglerteknik Föreläsning 5 Sammanfattning av föreläsning 4 Frekvensanalys Bodediagram Sammanfattning av förra föreläsningen 2 Givet ett polpolynom med en varierande parameter, och
Välkomna till TSRT19 Reglerteknik Föreläsning 5 Sammanfattning av föreläsning 4 Frekvensanalys Bodediagram Sammanfattning av förra föreläsningen 2 Givet ett polpolynom med en varierande parameter, och
( ), så kan du lika gärna skriva H ( ω )! ( ) eftersom boken går igenom laplacetransformen före
 Några allmänna kommentarer gällande flera av lösningarna: Genomgående används kausala signaler och kausala system, vilket innebär att det är den enkelsidiga laplacetransformen som används. Bokens författare
Några allmänna kommentarer gällande flera av lösningarna: Genomgående används kausala signaler och kausala system, vilket innebär att det är den enkelsidiga laplacetransformen som används. Bokens författare
Ellära och Elektronik Moment AC-nät Föreläsning 4
 Ellära och Elektronik Moment AC-nät Föreläsning 4 Kapacitans och Indktans Uppladdning av en kondensator Medelvärde och Effektivvärde Sinsvåg över kondensator och spole Copyright 8 Börje Norlin Kondensatorer
Ellära och Elektronik Moment AC-nät Föreläsning 4 Kapacitans och Indktans Uppladdning av en kondensator Medelvärde och Effektivvärde Sinsvåg över kondensator och spole Copyright 8 Börje Norlin Kondensatorer
Laboration ACT Växelström och transienta förlopp.
 Laboration ACT Växelström och transienta förlopp. Laborationen består av två delar. Målet med den första delen av laborationen är att öka förståelsen för kopplingen mellan teoretiska samband och praktiska
Laboration ACT Växelström och transienta förlopp. Laborationen består av två delar. Målet med den första delen av laborationen är att öka förståelsen för kopplingen mellan teoretiska samband och praktiska
Sammanfattning av likströmsläran
 Innehåll Sammanfattning av likströmsläran... Testa-dig-själv-likströmsläran...9 Felsökning.11 Mätinstrument...13 Varför har vi växelström..17 Växelspännings- och växelströmsbegrepp..18 Vektorräknig..0
Innehåll Sammanfattning av likströmsläran... Testa-dig-själv-likströmsläran...9 Felsökning.11 Mätinstrument...13 Varför har vi växelström..17 Växelspännings- och växelströmsbegrepp..18 Vektorräknig..0
Tentamen i Elektronik, ESS010, del 1 den 18 oktober, 2010, kl
 Institutionen för Elektro och informationsteknik, LTH Tentamen i Elektronik, ESS00, del den 8 oktober, 00, kl. 08.00.00 Ansvariga lärare: Anders Karlsson, tel. 40 89, 07 98 (kursexp. 90 0). arje uppgift
Institutionen för Elektro och informationsteknik, LTH Tentamen i Elektronik, ESS00, del den 8 oktober, 00, kl. 08.00.00 Ansvariga lärare: Anders Karlsson, tel. 40 89, 07 98 (kursexp. 90 0). arje uppgift
Svar till Hambley edition 6
 Svar till Hambley edition 6 Carl Gustafson, Bertil Larsson 2011-01-20, mod 2012-11-07, mod 13-11-19 1 Svar Kapitel 1 P1.21P a = 60 W P b = 60 W P c = 210 W Positiv: absorbed (=upptagen, förbrukad) och
Svar till Hambley edition 6 Carl Gustafson, Bertil Larsson 2011-01-20, mod 2012-11-07, mod 13-11-19 1 Svar Kapitel 1 P1.21P a = 60 W P b = 60 W P c = 210 W Positiv: absorbed (=upptagen, förbrukad) och
IDE-sektionen. Laboration 5 Växelströmsmätningar
 080501 IDE-sektionen Laboration 5 Växelströmsmätningar 1 1. Bestämning av effektivvärde hos olika kurvformer Uppgift: Att mäta och bestämma effektivvärdet på tre olika kurvformer. Dels en fyrkantssignal,
080501 IDE-sektionen Laboration 5 Växelströmsmätningar 1 1. Bestämning av effektivvärde hos olika kurvformer Uppgift: Att mäta och bestämma effektivvärdet på tre olika kurvformer. Dels en fyrkantssignal,
Tentamen i Elektronik för F, 13 januari 2006
 Tentamen i Elektronik för F, 3 januari 006 Tillåtna hjälpmedel: Formelsamling i kretsteori, miniräknare Du har fått tag på 6 st glödlampor från USA. Tre av dem visar 60 W och tre 40 W. Du skall nu koppla
Tentamen i Elektronik för F, 3 januari 006 Tillåtna hjälpmedel: Formelsamling i kretsteori, miniräknare Du har fått tag på 6 st glödlampor från USA. Tre av dem visar 60 W och tre 40 W. Du skall nu koppla
1 Grundläggande Ellära
 1 Grundläggande Ellära 1.1 Elektriska begrepp 1.1.1 Ange för nedanstående figur om de markerade delarna av kretsen är en nod, gren, maska eller slinga. 1.2 Kretslagar 1.2.1 Beräknar spänningarna U 1 och
1 Grundläggande Ellära 1.1 Elektriska begrepp 1.1.1 Ange för nedanstående figur om de markerade delarna av kretsen är en nod, gren, maska eller slinga. 1.2 Kretslagar 1.2.1 Beräknar spänningarna U 1 och
IDE-sektionen. Laboration 6 Växelströmsmätningar
 090508 IDE-sektionen Laboration 6 Växelströmsmätningar 1 Förberedelseuppgifter laboration 5 1. Antag att L=250 mh och resistansen i spolen är ca: 150 Ω i figur 3. Skissa på spänningen över resistansen
090508 IDE-sektionen Laboration 6 Växelströmsmätningar 1 Förberedelseuppgifter laboration 5 1. Antag att L=250 mh och resistansen i spolen är ca: 150 Ω i figur 3. Skissa på spänningen över resistansen
Tentamen i Elektronik för E, ESS010, 12 april 2010
 Tentamen i Elektronik för E, ESS00, april 00 Tillåtna hjälpmedel: Formelsamling i kretsteori v i v in i Spänningen v in och är kända. a) Bestäm i och i. b) Bestäm v. W lampa spänningsaggregat W lampa 0
Tentamen i Elektronik för E, ESS00, april 00 Tillåtna hjälpmedel: Formelsamling i kretsteori v i v in i Spänningen v in och är kända. a) Bestäm i och i. b) Bestäm v. W lampa spänningsaggregat W lampa 0
Förstärkarens högfrekvensegenskaper. Återkoppling och stabilitet. Återkoppling och förstärkning/bandbredd. Operationsförstärkare.
 FÖRELÄSNING 5 Förstärkarens högfrekvensegenskaper Återkoppling och stabilitet Återkoppling och förstärkning/bandbredd Operationsförstärkare Kaskadkoppling Per Larsson-Edefors, Chalmers tekniska högskola
FÖRELÄSNING 5 Förstärkarens högfrekvensegenskaper Återkoppling och stabilitet Återkoppling och förstärkning/bandbredd Operationsförstärkare Kaskadkoppling Per Larsson-Edefors, Chalmers tekniska högskola
ELLÄRA Laboration 4. Växelströmslära. Seriekrets med resistor, spole och kondensator
 ELLÄA Laboration 4 Växelströmslära Moment 1: Moment 2: Moment 3: Moment 4: Moment 5: Moment 6: eriekrets med resistor och kondensator eriekrets med resistor och spole Parallellkrets med resistor och spole
ELLÄA Laboration 4 Växelströmslära Moment 1: Moment 2: Moment 3: Moment 4: Moment 5: Moment 6: eriekrets med resistor och kondensator eriekrets med resistor och spole Parallellkrets med resistor och spole
Komplexa tal. j 2 = 1
 Komplexa tal De komplexa talen används när man behandlar växelström inom elektroniken. Imaginära enheten betecknas i elektroniken med j (i, som används i matematiken, är ju upptaget av strömmen). Den definieras
Komplexa tal De komplexa talen används när man behandlar växelström inom elektroniken. Imaginära enheten betecknas i elektroniken med j (i, som används i matematiken, är ju upptaget av strömmen). Den definieras
Hambley avsnitt
 Föreläsning 0 Hambley avsnitt 6.6.8 Filter [6.2, 6.5 6.8] Vid kommunikation används tidsharmoniska signaler. Dessa har ett visst frekvensband centrerad kring en bärfrekvens. Som exempel kan en sändare
Föreläsning 0 Hambley avsnitt 6.6.8 Filter [6.2, 6.5 6.8] Vid kommunikation används tidsharmoniska signaler. Dessa har ett visst frekvensband centrerad kring en bärfrekvens. Som exempel kan en sändare
Kapitel: 31 Växelström Beskrivning av växelström och växelspänning Phasor-diagram metoden Likriktning av växelström
 Kapitel: 31 Växelström Beskrivning av växelström och växelspänning Phasor-diagram metoden Likriktning av växelström Relation mellan ström och spänning i R, L och C. RLC-krets Elektrisk oscillator, RLC-krets
Kapitel: 31 Växelström Beskrivning av växelström och växelspänning Phasor-diagram metoden Likriktning av växelström Relation mellan ström och spänning i R, L och C. RLC-krets Elektrisk oscillator, RLC-krets
Cirkelkriteriet (12.3)
 Föreläsning 3-4 Cirkelkriteriet (12.3) En situation där global stabilitetsanalys kan utföras. r + u G(s) y f( ) där f( ) är en statisk olinjäritet, t ex f(y) = 1 y 0 1 y < 0 eller Antag att: f(y) = y 2
Föreläsning 3-4 Cirkelkriteriet (12.3) En situation där global stabilitetsanalys kan utföras. r + u G(s) y f( ) där f( ) är en statisk olinjäritet, t ex f(y) = 1 y 0 1 y < 0 eller Antag att: f(y) = y 2
Tentamen i Elektronik för F, 2 juni 2005
 Tentamen i Elektronik för F, juni 005 Tid: 83 Tillåtna hjälpmedel: Formelsamling i kretsteori, miniräknare CEQ: Fyll i enkäten efter det att du lämnat in tentan. Det går bra att stanna kvar efter 3.00
Tentamen i Elektronik för F, juni 005 Tid: 83 Tillåtna hjälpmedel: Formelsamling i kretsteori, miniräknare CEQ: Fyll i enkäten efter det att du lämnat in tentan. Det går bra att stanna kvar efter 3.00
Tentamen i Grundläggande ellära och digitalteknik ETA 013 för D
 Lars-Erik Cederlöf Tentamen i Grundläggande ellära och digitalteknik ET 013 för D1 1999-04-28 Tentamen omfattar 40 poäng, 2 poäng för varje uppgift. 20 poäng ger godkänd tentamen. Tillåtet hjälpmedel är
Lars-Erik Cederlöf Tentamen i Grundläggande ellära och digitalteknik ET 013 för D1 1999-04-28 Tentamen omfattar 40 poäng, 2 poäng för varje uppgift. 20 poäng ger godkänd tentamen. Tillåtet hjälpmedel är
LABORATION 3. Växelström
 Chalmers Tekniska Högskola november 01 Fysik 14 sidor Kurs: Elektrisk mätteknik och vågfysik. FFY616 LABORATION 3 Växelström Växelströmskretsar (seriekoppling), Serieresonans. Förberedelse: i) Läs noggrant
Chalmers Tekniska Högskola november 01 Fysik 14 sidor Kurs: Elektrisk mätteknik och vågfysik. FFY616 LABORATION 3 Växelström Växelströmskretsar (seriekoppling), Serieresonans. Förberedelse: i) Läs noggrant
Tentamen i Elektronik, ESS010, och Elektronik för D, ETI190 den 10 jan 2006 klockan 14:00 19:00
 Tentamen i Elektronik, ESS00, och Elektronik för D, ETI90 den 0 jan 006 klockan 4:00 9:00 Tekniska Högskolan i Lund Institutionen för Elektrovetenskap Tentamen i Elektronik, ESS00, och Elektronik för D,
Tentamen i Elektronik, ESS00, och Elektronik för D, ETI90 den 0 jan 006 klockan 4:00 9:00 Tekniska Högskolan i Lund Institutionen för Elektrovetenskap Tentamen i Elektronik, ESS00, och Elektronik för D,
Växelspänning och effekt. S=P+jQ. Industriell Elektroteknik och Automation
 Växelspänning och effekt S=P+jQ VA W var Industriell Elektroteknik och Automation Översikt Synkronmaskinens uppbyggnad Stationär växelström Komplexräkning Komplex, aktiv och reaktiv effekt Ögonblicksvärde
Växelspänning och effekt S=P+jQ VA W var Industriell Elektroteknik och Automation Översikt Synkronmaskinens uppbyggnad Stationär växelström Komplexräkning Komplex, aktiv och reaktiv effekt Ögonblicksvärde
Institutionen för Fysik
 Institutionen för Fysik KURS-PM KURS: Elektronik 1: Ellära FYD101 LÄSÅR: 16/17 HT16 FÖR: Datorstödd Fysikalisk Mätteknik (samt fristående kurs) EXAMINATOR: Vitali Zhaunerchyk 031-786 9150 KURSANSVARIG:
Institutionen för Fysik KURS-PM KURS: Elektronik 1: Ellära FYD101 LÄSÅR: 16/17 HT16 FÖR: Datorstödd Fysikalisk Mätteknik (samt fristående kurs) EXAMINATOR: Vitali Zhaunerchyk 031-786 9150 KURSANSVARIG:
DIGITALA FILTER. Tillämpad Fysik Och Elektronik 1. Frekvensfunktioner FREKVENSSVAR FÖR ETT TIDSDISKRET SYSTEM. x(n)= Asin(Ωn)
 DIGITALA FILTER TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 1 Frekvensfunktioner x(n)= Asin(Ωn) y(n) H(z) TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 2 FREKVENSSVAR FÖR ETT TIDSDISKRET SYSTEM
DIGITALA FILTER TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 1 Frekvensfunktioner x(n)= Asin(Ωn) y(n) H(z) TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 2 FREKVENSSVAR FÖR ETT TIDSDISKRET SYSTEM
TENTAMEN Elektronik för elkraft
 Umeå Universitet Tillämpad Fysik och Elektronik JH TENTAMEN Elektronik för elkraft HT 2012 Omtentamen 9/1 2013 Tillåtna hjälpmedel: Räknedosa. Lärobok (Analog elektronik, Bengt Molin) Labbar Tentamen består
Umeå Universitet Tillämpad Fysik och Elektronik JH TENTAMEN Elektronik för elkraft HT 2012 Omtentamen 9/1 2013 Tillåtna hjälpmedel: Räknedosa. Lärobok (Analog elektronik, Bengt Molin) Labbar Tentamen består
Tentamen i Elektronik, ESS010, del 2 den 6 mars 2006 SVAR
 Tekniska Högskolan i Lund Institutionen för Elektrovetenskap Tentamen i Elektronik, ESS010, del 2 den 6 mars 2006 SVAR 1 Bandbredd anger maximal frekvens som oscilloskopet kan visa. Signaler nära denna
Tekniska Högskolan i Lund Institutionen för Elektrovetenskap Tentamen i Elektronik, ESS010, del 2 den 6 mars 2006 SVAR 1 Bandbredd anger maximal frekvens som oscilloskopet kan visa. Signaler nära denna
Laboration ACT Växelström och transienta förlopp.
 Laboration ACT Växelström och transienta förlopp. Laborationen består av två delar. Målet med den första delen av laborationen är att öka förståelsen för kopplingen mellan teoretiska samband och praktiska
Laboration ACT Växelström och transienta förlopp. Laborationen består av två delar. Målet med den första delen av laborationen är att öka förståelsen för kopplingen mellan teoretiska samband och praktiska
Elektroteknikens grunder Laboration 3. OP-förstärkare
 Elektroteknikens grunder Laboration 3 OPförstärkare Elektroteknikens grunder Laboration 3 Mål Du ska i denna laboration studera tre olika användningsområden för OPförstärkare. Den ska användas som komparator,
Elektroteknikens grunder Laboration 3 OPförstärkare Elektroteknikens grunder Laboration 3 Mål Du ska i denna laboration studera tre olika användningsområden för OPförstärkare. Den ska användas som komparator,
Fö 8 - TMEI01 Elkraftteknik Kraftelektronik
 Fö 8 - TMEI1 Elkraftteknik Kraftelektronik Christofer Sundström 14 februari 218 Outline 1 Kraftelektronik Översikt 2 Likriktning Grunder Ostyrda kopplingar Enfas Flerfas Styrda kopplingar 3 Växelriktning
Fö 8 - TMEI1 Elkraftteknik Kraftelektronik Christofer Sundström 14 februari 218 Outline 1 Kraftelektronik Översikt 2 Likriktning Grunder Ostyrda kopplingar Enfas Flerfas Styrda kopplingar 3 Växelriktning
Sven-Bertil Kronkvist. Elteknik. Komplexa metoden j -metoden. Revma utbildning
 Sven-Bertil Kronkvist Elteknik Komplexa metoden j -metoden evma utbildning KOMPEXA METODEN Avsnittet handlar om hur växelströmsproblem kan lösas med komplexa metoden, jω - eller symboliska metoden som
Sven-Bertil Kronkvist Elteknik Komplexa metoden j -metoden evma utbildning KOMPEXA METODEN Avsnittet handlar om hur växelströmsproblem kan lösas med komplexa metoden, jω - eller symboliska metoden som
IE1206 Inbyggd Elektronik
 IE06 Inbyggd Elektronik F F3 F4 F Ö Ö PIC-block Dokumentation, Seriecom Pulsgivare I,, R, P, serie och parallell KK LAB Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchoffs lagar Nodanalys
IE06 Inbyggd Elektronik F F3 F4 F Ö Ö PIC-block Dokumentation, Seriecom Pulsgivare I,, R, P, serie och parallell KK LAB Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchoffs lagar Nodanalys
Tentamen ssy080 Transformer, Signaler och System, D3
 Tentamen ssy080 Transformer, Signaler och System, D3 Examinator: Ants R. Silberberg oktober 009 kl. 4.00-8.00 lokal: Johanneberg Förfrågningar: Ants Silberberg, tel. 808 Lösningar: Anslås torsdag okt.
Tentamen ssy080 Transformer, Signaler och System, D3 Examinator: Ants R. Silberberg oktober 009 kl. 4.00-8.00 lokal: Johanneberg Förfrågningar: Ants Silberberg, tel. 808 Lösningar: Anslås torsdag okt.
IF1330 Ellära KK1 LAB1 KK2 LAB2 KK4 LAB4. tentamen
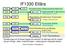 F330 Ellära F/Ö F/Ö4 F/Ö F/Ö5 F/Ö3 Strömkretslära Mätinstrument Batterier Likströmsnät Tvåpolsatsen KK LAB Mätning av och F/Ö6 F/Ö7 Magnetkrets Kondensator Transienter KK LAB Tvåpol mät och sim F/Ö8 F/Ö9
F330 Ellära F/Ö F/Ö4 F/Ö F/Ö5 F/Ö3 Strömkretslära Mätinstrument Batterier Likströmsnät Tvåpolsatsen KK LAB Mätning av och F/Ö6 F/Ö7 Magnetkrets Kondensator Transienter KK LAB Tvåpol mät och sim F/Ö8 F/Ö9
insignal H = V ut V in
 1 Föreläsning 8 och 9 Hambley avsnitt 5.56.1 Tvåport En tvåport är en krets som har en ingångsport och en gångsport. Den brukar ritas som en låda med ingångsporten till vänster och gångsporten till höger.
1 Föreläsning 8 och 9 Hambley avsnitt 5.56.1 Tvåport En tvåport är en krets som har en ingångsport och en gångsport. Den brukar ritas som en låda med ingångsporten till vänster och gångsporten till höger.
Laborationshandledning för mätteknik
 Laborationshandledning för mätteknik - digitalteknik och konstruktion TNE094 LABORATION 1 Laborant: E-post: Kommentarer från lärare: Institutionen för Teknik och Naturvetenskap Campus Norrköping, augusti
Laborationshandledning för mätteknik - digitalteknik och konstruktion TNE094 LABORATION 1 Laborant: E-post: Kommentarer från lärare: Institutionen för Teknik och Naturvetenskap Campus Norrköping, augusti
Tentamen i TMA 982 Linjära System och Transformer VV-salar, 27 aug 2013, kl
 Tentamen i TMA 982 Linjära System och Transformer VV-salar, 27 aug 2013, kl 8.30-12.30 Examinatorer: Lars Hammarstrand och Thomas Wernstål Tentamen består av två delar (Del I och Del II) på sammanlagt
Tentamen i TMA 982 Linjära System och Transformer VV-salar, 27 aug 2013, kl 8.30-12.30 Examinatorer: Lars Hammarstrand och Thomas Wernstål Tentamen består av två delar (Del I och Del II) på sammanlagt
IE1206 Inbyggd Elektronik
 IE06 Inbyggd Elektronik F F3 F4 F Ö Ö PI-block Dokumentation, Seriecom Pulsgivare I,,, P, serie och parallell KK LAB Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchhoffs lagar Nodanalys
IE06 Inbyggd Elektronik F F3 F4 F Ö Ö PI-block Dokumentation, Seriecom Pulsgivare I,,, P, serie och parallell KK LAB Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchhoffs lagar Nodanalys
Kap 3 - Tidskontinuerliga LTI-system. Användning av Laplacetransformen för att beskriva LTI-system: Samband poler - respons i tidsplanet
 Kap 3 - Tidskontinuerliga LTI-system Användning av Laplacetransformen för att beskriva LTI-system: Överföringsfunktion Poler, nollställen, stabilitet Samband poler - respons i tidsplanet Slut- och begynnelsevärdesteoremen
Kap 3 - Tidskontinuerliga LTI-system Användning av Laplacetransformen för att beskriva LTI-system: Överföringsfunktion Poler, nollställen, stabilitet Samband poler - respons i tidsplanet Slut- och begynnelsevärdesteoremen
Laborationsrapport. Kurs El- och styrteknik för tekniker ET1015. Lab nr. Laborationens namn Lik- och växelström. Kommentarer. Utförd den.
 Laborationsrapport Kurs El- och styrteknik för tekniker ET1015 Lab nr 1 version 1.2 Laborationens namn Lik- och växelström Namn Kommentarer Utförd den Godkänd den Sign 1 Inledning I denna laboration skall
Laborationsrapport Kurs El- och styrteknik för tekniker ET1015 Lab nr 1 version 1.2 Laborationens namn Lik- och växelström Namn Kommentarer Utförd den Godkänd den Sign 1 Inledning I denna laboration skall
Kompletterande material till föreläsning 5 TSDT08 Signaler och System I. Erik G. Larsson LiU/ISY/Kommunikationssystem
 ompletterande material till föreläsning 5 TSDT8 Signaler och System I Erik G. Larsson LiU/ISY/ommunikationssystem erik.larsson@isy.liu.se November 8 5.1. Första och andra ordningens tidskontinuerliga LTI
ompletterande material till föreläsning 5 TSDT8 Signaler och System I Erik G. Larsson LiU/ISY/ommunikationssystem erik.larsson@isy.liu.se November 8 5.1. Första och andra ordningens tidskontinuerliga LTI
IF1330 Ellära KK1 LAB1 KK2 LAB2 KK4 LAB4. tentamen
 IF330 Ellära F/Ö F/Ö4 F/Ö F/Ö5 F/Ö3 Strömkretslära Mätinstrument Batterier Likströmsnät Tvåpolsatsen KK LAB Mätning av och I F/Ö6 F/Ö7 Magnetkrets Kondensator Transienter KK LAB Tvåpol mät och sim F/Ö8
IF330 Ellära F/Ö F/Ö4 F/Ö F/Ö5 F/Ö3 Strömkretslära Mätinstrument Batterier Likströmsnät Tvåpolsatsen KK LAB Mätning av och I F/Ö6 F/Ö7 Magnetkrets Kondensator Transienter KK LAB Tvåpol mät och sim F/Ö8
