mer om kvantmekanik relativitetsteori
|
|
|
- Britta Hansson
- för 8 år sedan
- Visningar:
Transkript
1 18 mer om kvantmekanik och relativitetsteori Detta kapitel ingår inte i grundkursen. Det lämpar sig för självstudier för den som valt kvantmekanik eller relativitetseori som fördjupningsuppgift. mer om kvantmekanik och relativitetsteori 18 : 1
2 1 En partikel i en låda Idén att partiklar motsvaras av vågor kommer från de Broglie (se avsnitt 7, kap 10) och utvecklades av Erwin Schrödinger på 1920-talet. Samtidigt utarbetades en teori för atomer av Werner Heisenberg, och denna teori visade sig vara helt i överensstämmelse med Schrödingers. Teorin kallas vågmekanik eller kvantmekanik och har visat sig vara nödvändig vid utforskandet av materiens inre. Teorin används inte bara vid studiet av atomens elektroner utan även av atomkärnans inre. Vi ska ge en vågmekanisk beskrivning av en partikel som bara kan röra sig i ett begränsat område. Först antar vi att partikeln är instängd mellan två parallella väggar, som den studsar elastiskt emot (fig 2 a). Inga krafter verkar på partikeln i området mellan väggarna. Dess lägesenergi är därför konstant, och vi sätter den lika med noll. Vi tänker oss att partikeln studsar vinkelrätt mot väggarna och låter den representeras av en plan våg som går fram och tillbaka. Interferensen ger en stående våg, som påminner om den stående vågen i en svängande sträng (se fig 1). En innestängd partikel kan alltså beskrivas på ett liknande sätt som en spänd sträng. Fig 1. Några svängningstillstånd hos en spänd sträng. Strängens amplitud motsvarar vågfunktionen Ψ hos partikeln. Det enklaste fallet motsvarar grundsvängningen hos strängen. Vågfunktionen Ψ framgår av fig 2 (b). Grafen i fig 2 (c) visar vågfunktionens kvadrat, som ger en bild av hur sannolikheten att påträffa partikeln beror av x. Avståndet a mellan väggarna är ett nodavstånd eller partikelns halva våglängd i grundtillståndet: a = λ 2 18 : 2 mer om kvantmekanik och relativitetsteori
3 massa m Fig 2. En partikel instängd mellan två väggar enligt (a) får i grundtillståndet en vågfunktion enligt (b), vars kvadrat (c) representerar sannolikheten att påträffa partikeln i olika lägen x. Vågfunktion och sannolikhetsfördelning för det första exciterade tillståndet visas i fig (d) resp (e). Men som vi ser i fig 1 finns det flera stående vågor som passar in mellan väggarna. Allmänt får vi följande samband, där n = 1, 2, 3,... λ a = n ; λ = 2 p = h λ 2a n p = n h 2a 1 E = mv 2 = p 2 2 2m E = n 2 h 2 8ma 2 mer om kvantmekanik och relativitetsteori 18 : 3
4 Av energiuttrycket E framgår att rörelseenergin endast kan ha vissa bestämda värden energin är kvantiserad. Redan i detta enkla exempel framträder ett av atomens mest typiska drag, nämligen energinivåerna. Vi kan säga att partikeln i exemplet har ett grundtillstånd (n = 1) med energin E 1 : h E 1 = 2 8ma 2 Dessutom har den en rad exciterade tillstånd med energierna E 2 = E = 4 E 1 Partikelns rörelseenergi kan inte vara noll och partikeln kan inte stå stilla. Ju mindre rörelseutrymme partikeln har, desto högre rörelseenergi får den. E 3 = E = 9 E 1 osv. Heltalet n = 1, 2, 3,... kallas kvanttal. Grundtillståndets energi och rörelsemängd är de minsta som kan förekomma. En mindre rörelsemängd än h/2a skulle ge en våglängd λ = h/p, som är större än 2a och alltså för stor för att passa in mellan väggarna. Rörelseenergin hos partikeln kan därför inte vara noll, och partikeln kan inte stå stilla! Lägg märke till att minimienergin är omvänt proportionell mot a 2. Ju mer vi begränsar partikelns rörelseutrymme, desto högre rörelseenergi får den. Schrödinger-ekvationen Vågfunktionen i fig 2 (b) kan beskrivas med en cosinusfunktion: Ψ (x) = A cos ( π x ) a a Vi ser att funktionen har nollställen då x = ±. 2 λ h h Av sambanden a = och λ = får vi p = och 2 p 2a Ψ (x) = A cos ( 2πp x h ) A är en konstant som väljs så att sannolikheten att finna partikeln någonstans mellan väggarna blir ett. Integralen av Ψ 2 (x) från a till a 2 2 ska alltså ha värdet ett. Deriverar vi funktionen Ψ två gånger får vi 4π Ψ (x) = 2 p 2 A cos ( 2πp x ) Ψ (x) = h 2 4π 2 p 2 h 2 Ψ (x) h 18 : 4 mer om kvantmekanik och relativitetsteori
5 h 2 Ψ (x) = Ψ (x) 4π 2 p 2 mv eller eftersom E k = 2 p = 2 och alltså p 2 = 2 me 2 2m k Ψ (x) = Ψ (x) 8π 2 m E k h 2 h 2 Ψ (x) = E k Ψ (x) 8π 2 m Schrödinger-ekvationen är en av fysikens mest berömda ekvationer. För vår cosinusfunktion Ψ(x) gäller tydligen denna differentialekvation, som innehåller E k, partikelns energi. Det har visat sig att ekvationen gäller för alla partiklar med lägesenergin noll. Ekvationen är Schrödinger-ekvationen för partiklar med lägesenergin noll. Differentialekvationen har inte endast lösningen Ψ = A cos ( 2πp x ) h utan även alla de andra lösningarna som uppfyller villkoret att funktionen ska vara noll i ändpunkterna av intervallet. Ψ n (x) = A n cos ( 2πp n x ) nh där p n = (n = 1, 2, 3,...) h 2a Vi ser av ekvationen att vi kan erhålla rörelseenergin E k hos en partikel då vi multiplicerar vågfunktionens andraderivata med h 2 8π 2 m I den klassiska fysiken gäller att summan av rörelseenergin och den potentiella energin är lika med den totala energin, E k + E p = E. Om partikeln rör sig i ett område där lägesenergin E p inte är noll utan kanske också beror på läget, E p = E p (x), bör vi lägga till det bidraget för att få totala energin E. Vi kan förmoda att då bör gälla: Kvadraten på värdet av en partikels vågfunktion Ψ (x) i ett litet område är ett mått på sannolikheten att påträffa partikeln inom området. h 2 Ψ (x) + E p (x) Ψ (x) = E Ψ (x) 8π 2 m Detta är en av fysikens mest berömda ekvationer; Schrödingers differentialekvation för en partikel med konstant total energi. Vågfunktionen Ψ (x) tolkas så att kvadraten på dess värde i ett litet område är ett mått på sannolikheten att partikeln ska påträffas i detta område. mer om kvantmekanik och relativitetsteori 18 : 5
6 2 Tunneleffekten Genom Schrödinger-ekvationen blir uppgiften att hitta en fullständig, kvantmekanisk beskrivning av partiklarna reducerad till det matematiska problemet att lösa en differentialekvation. Vågfunktionerna i fig 2 är lösningar till Schrödinger-ekvationen med potentiella energin 0 mellan a/2 och +a/2 och oändlig utanför. Vad händer om vi mer realistiskt antar att potentiella energin inte är oändlig utanför intervallet, utan att den har ett ändligt värde? Vi ska inte genomföra en matematisk lösning av problemet, men i princip är det klart hur man ska gå tillväga. Vi sätter in potentialen E p (x) = 0 i Schrödinger-ekvationen och får lösningar, som passar mellan värdena x = a/2 och x = a/2. Vi sätter också in E p (x) = b och får lösningar som passar utanför intervallet ( a/2; a/2). Vi får sedan försöka jämka ihop lösningarna så att vi får en mjukt krökt, sammanhängande kurva. En lösning som motsvarar grundtillståndet, dvs tillståndet med lägst total energi visas i fig 3. Fig 3. Vågfunktionen för grundtillståndet hos en partikel som är instängd mellan två väggar, utanför vilka den potentiella energin är lika med E(x) = b. 18 : 6 mer om kvantmekanik och relativitetsteori Vi ser att sannolikheten för att hitta partikeln i väggarna utanför intervallet blir mycket liten långt in i barriärerna. Det verkar ju rimligt eftersom partikeln enligt klassisk fysik inte har tillräckligt stor kinetisk energi för att kunna klättra upp till den högre potentiella energin. Vad som däremot är slående är att det trots allt finns en liten sannolikhet för att partikeln ska befinna sig i det klassiskt förbjudna området. Om området med den högre potentiella energin har ändlig bredd finns det alltså en viss sannolikhet för att partikeln ska läcka ut genom väggen (se fig 4). Den möjligheten för partiklar att passera energibarriärer, som de i den klassiska mekaniken inte har tillräcklig energi för att kunna ta sig igenom, kallas tunneleffekten. Sannolikheten för denna tunnling beror mycket starkt på barriärens höjd och bredd. Tunneleffekten har fått många viktiga tekniska tillämpningar, bl a i form av elektroniska tunneldioder och det extremt känsliga svep-tunnelelektronmikroskopet (STM). I ett STM använder man sig av det faktum att elektroner vid en yta genom tunneleffekten kan förflytta sig till en mycket skarp, elektriskt laddad spets på mikroskopet. Då uppstår en
7 Fig 4. Om energibarriären är av ändlig bredd, l, kan partikeln ta sig igenom väggen. Den oscillerande delen av vågfunktionen (till höger) representerar de Broglie-vågen för en fri partikel. ström som varierar med avståndet mellan spets och yta. Man låter nålen svepa över ytan och styr den så att strömmen är konstant. Nålen kommer då att röra sig på konstant höjd över ytan. Metoden är så känslig att enskilda atomer i ytan kan lokaliseras i mikroskopet (se fig 5). (a) (b) Fig 5. (a) Tunnelmikroskop. De tre reglerstavarna x, y och z, som manövreras elektriskt, styr en nål så att tunnelströmmen genom nålen blir konstant. Rörelserna hos z-staven anger då den undersökta ytans utseende. (b) Avbildning av en kiselyta med tunnelmikroskop. I djupled kan man få en noggrannhet av 0,01 nm. mer om kvantmekanik och relativitetsteori 18 : 7
8 3 Rörelse i tre dimensioner Vi kan tänka oss att partikeln i vårt första exempel rör sig i y- och z-led samtidigt som den studsar mot väggarna. Rörelsens projektion i x-led är densamma som vi beskrev i avsnitt 1. Det betyder att den del av rörelseenergin som rörelsen i x-led bidrar med, alltså E x = p x2 /2m, kan skrivas h 2 2 E x = n 8ma 2 x Index x markerar att energikvantiseringen gäller i rörelsen i x-led. Resultatet är oberoende av hur partikeln rör sig i y- och z-led. Slutligen antar vi att partikeln är instängd i en kub med sidan a. En enkel generalisering av vårt tidigare resonemang ger följande uttryck för partikelns rörelseenergi E: h 2 E = E x + E y + E z = (n x2 + n y2 + n z2 ) 8ma 2 Vi har fått tre olika kvanttal, som var för sig kan anta olika positiva heltalsvärden. Fig 6. Vågfunktioner och sannolikhetsfördelningar för de två lägsta energitillstånden hos en partikel innesluten i ett klot med radien R. De nedersta figurerna visar sannolikhetsfördelningen i klotet. Ju tätare skuggningen är i ett område, desto sannolikare är det att partikeln befinner sig där. 18 : 8 mer om kvantmekanik och relativitetsteori
9 Återigen kan vi konstatera att en partikels minimienergi blir större, ju mindre utrymme den har till sitt förfogande. Denna slutsats och energins kvantisering har inte med inneslutningens form att göra. Om man i stället för en kub har ett klot med ogenomträngliga väggar, bestäms partikelns rörelseenergi på liknande sätt av radien och värdet på tre olika kvanttal. I fig 6 visas vågfunktioner och sannolikhetsfördelningar för en sådan partikel i grundtillståndet och i ett exciterat tillstånd med sfärisk symmetri. 4 Väteatomen Väteatomen kan vi enklast beskriva som en stillastående, positivt laddad atomkärna och en elektron som befinner sig i kärnans närhet. Förutom rörelseenergi har elektronen också en potentiell elektrisk energi, som är större ju längre bort från kärnan som elektronen befinner sig. Med hjälp av de Broglies formel kan vi teckna elektronens totala energi: E = E k + E p E k = p = h λ p 2 2m E k = h 2 E= + E p 2mλ 2 2mλ 2 Ur det energiuttryck vi fått löser vi ut elektronens våglängd λ: h λ = 2m( E E p) För en given total energi E beror λ av E p och därmed av elektronens läge i förhållande till kärnan. Vi ska alltså åstadkomma en stående våg med en våglängd som varierar med avståndet till kärnan. Situationen påminner om stående vågor i en hängande kedja (fig 7). Dessutom ska vågen passas in i ett utrymme utan skarpa gränser. h 2 Fig 7. Tre olika svängningstillstånd hos en hängande kedja. Kedjan är hårdare spänd i sin övre del än i sin nedre på grund av sin egen tyngd. Det medför att våghastigheten är större upptill än nedtill. Man kan då säga att våglängden varierar längs kedjan. mer om kvantmekanik och relativitetsteori 18 : 9
10 Problemet kan lösas med Schrödinger-ekvationen. Vågfunktionerna karakteriseras även nu av tre kvanttal, vanligen betecknade n, m l och l. De antar heltalsvärden, som det finns särskilda regler för. För lösningar med sfärisk symmetri har de två senare värdet noll. Mot varje vågfunktion svarar en sannolikhetsfördelning. Den kan åskådliggöras som ett elektronmoln, där tätheten i ett område är ett mått på sannolikheten för att elektronen ska påträffas där. Vågfunktionen för en bunden elektron innehåller tre kvanttal, n, l och m l, som bara kan anta vissa heltalsvärden. Vågfunktioner och sannolikhetsfördelningar för de två lägsta energitillstånden återges i fig 8. Observera att vågfunktionen klingar av mot värdet noll, när avståndet r från kärnan växer. Det är ju rimligt, eftersom sannolikheten att påträffa elektronen på stort avstånd måste vara liten. Fig 8. Vågfunktioner, sannolikhetsfördelningar och elektronmoln för väteatomens två lägsta energitillstånd. 18 : 10 mer om kvantmekanik och relativitetsteori
11 I fig 8 lägger vi också märke till att sannolikhetsfunktionen Ψ 2 har sitt högsta värde i centrum, alltså inuti atomkärnan. Kan det vara sannolikare att hitta elektronen där än t ex på avståndet 0,05 nm? För att få klarhet i detta kan vi resonera på följande sätt. Vågfunktionens kvadrat anger sannolikhetstätheten, vilket innebär att vågfunktionens kvadrat gånger en viss volym anger sannolikheten att partikeln ska finnas inom denna volym. En hög sannolikhetstäthet gånger en liten volym kan ge mindre sannolikhet än en låg sannolikhetstäthet gånger en stor volym. Så är t ex sannolikheten att återfinna elektronen inom ett 0,001 nm tjockt skal på avståndet 0,05 nm från centrum mer än 100 gånger så stor som att finna den i ett klot med diametern 0,001 nm i centrum. Skalet har nämligen en mer än 1000 gånger så stor volym som klotet. Diagrammet med Ψ 2 som funktion av r ger därför ingen direkt upplysning om sannolikheten att finna elektronen på olika avstånd från kärnan. Bättre är den funktion som visas i fig 9. Fig 9. Den radiella sannolikhetsfunktionen för elektronen i väteatomens grundtillstånd. Sannolikheten att elektronen finns i området mellan r 1 och r 2 anges av den markerade arean i grafen. Huvudkvanttalet n kan anta värdena 1, 2, 3, I väteatomen bestämmer värdet på n atomens energi. Liksom hos partikeln i lådan innebär varje vågfunktion ett bestämt energitillstånd hos väteatomen. De uttryck man får för energinivåerna hos en väteatom är precis desamma som Bohr härledde i sin atommodell och som stämmer med de experimentella värdena från kap 12: E R n 2 E = (n = 1, 2, 3,...) där E R är joniseringsenergin. Kvanttalet n kallas huvudkvanttalet och bestämmer tydligen ensamt energin hos väteatomen. Värdet på de andra kvanttalen inverkar bara på vågfunktionens och sannolikhetsfördelningens utseende, inte på energin. I fig 10 visas två olika icke sfäriska elektronmoln med samma energi. mer om kvantmekanik och relativitetsteori 18 : 11
12 Fig 10. Sannolikhetsfördelning eller elektronmoln i två tillstånd med n = 2 och l = 1 men med olika värden på m l. Båda molnen har rotationssymmetri kring respektive axel. En vanlig bild av en atom är den som visas i fig 11, där elektronerna går i distinkta banor kring kärnan. Den bilden har inte mycket gemensamt med den kvantmekaniska modellen, där inga bestämda elektronbanor är möjliga. Varför inte? Förklaringen är följande: Vågor, exempelvis ett ljusknippe, breder ut sig rätlinjigt som en ström av partiklar, så länge knippets diameter a är mycket större än våglängden λ. Men ju mindre a blir i jämförelse med λ, desto mer framträder vågegenskaperna. Diffraktion sker, och knippets konturer och utbredningsriktning blir allt diffusare. Anta att elektronen rör sig inom en volym formad som en rund ring, ungefär som en cykelslang. För att det ska vara möjligt måste ringens tjocklek a vara mycket större än λ. Men det är ju otänkbart i atomens grundtillstånd, där λ som vi vet har en storlek som är jämförbar med hela atomens utsträckning, dvs hela ringens diameter. Det är därför vi får nöja oss med att ge en sannolikhetsfördelning för möjligheterna att träffa på elektronen. Med hjälp av vågfunktionen kan man beräkna ett medelvärde på elektronens avstånd från kärnan i ett visst tillstånd. Resultaten stämmer ganska väl med de värden på elektronbanornas radier som beräknades med Rutherford-modellen i avsnitt 4, kap 12. Fig 11. Detta kan passera som symbol för atomer och atomåldern, men man ska inte förledas att tro att en atom är ett välordnat planetsystem. 18 : 12 mer om kvantmekanik och relativitetsteori
13 5 Vidareutveckling av atommodellen Den modell av väteatomen som just beskrivits utgår från att det bara finns en elektrostatisk växelverkan mellan elektronen och kärnan. Vid sidan om denna dominerande kraftverkan finns en annan, som ger sig tillkänna som en s k finstruktur i spektrum. Med en tillräckligt noggrann spektrometer kan man konstatera att fotoner med två olika våglängder sänds ut då väteatomer övergår från energinivån n = 2 till grundtillståndet. Skillnaden är mycket liten. Orsaken är att den exciterade nivån i själva verket är två tätt liggande nivåer. Modellen kan förfinas, så att denna nivåuppdelning framträder. Det sker genom att man tar hänsyn till att elektronen har s k spinn, som gör att den uppträder som en liten magnet. Därigenom får den en svag magnetisk växelverkan med kärnladdningen, som ur elektronens synpunkt är i rörelse och känns som en ström med ett magnetfält. I det magnetfältet kan elektronspinnet ställa in sig på två sätt. Det anges med ett fjärde kvanttal, det s k spinnkvanttalet m s, som kan anta värdena +1/2 och 1/2. Elektronens energi är något olika för de två inställningarna på spinnet. Det fjärde kvanttalet, spinnkvanttalet m s, kan anta värdena ±1/2. 6 Den kvantmekaniska paradoxen När kvantmekaniken slog igenom på 1920-talet innebar det en revolution inom fysiken. Borta var den klassiska fysikens mekaniska och bestämda beskrivning av utvecklingen av de olika fenomenen i naturvetenskaperna. Denna föreställning, att allting är förutsägbart i princip om bara begynnelsevillkoren är givna, kallas determinism. Kvantmekaniken, å andra sidan, är till sin natur icke-deterministisk. Som vi har sett kan vi enligt kvantmekaniken aldrig med bestämdhet förutsäga hur exempelvis en partikel som passerar genom en spalt rör sig. Kvantmekaniken ger endast sannolikheten för att vi påträffar partikeln i ett visst område vid en given tidpunkt. Denna osäkerhet (kvantifierad i Heisenbergs obestämdhetsrelationer) är inneboende hos materien och har ingenting att göra med rent tekniska svårigheter att mäta en partikels läge eller hastighet. Den är en konsekvens av materiens vågnatur. Även med helt perfekta mätinstrument kan vi aldrig komma ifrån den kvantmekaniskt betingade osäkerheten. mer om kvantmekanik och relativitetsteori 18 : 13
14 För de fysiker som var skolade i klassisk mekanik och elektromagnetism var denna slumpmässighet hos kvantmekaniken mycket svår att smälta. Till och med en framstående fysiker som Einstein (som ju faktiskt spelade en avgörande roll för kvantmekanikens genombrott) vägrade att acceptera att det inte skulle gå att ge en fullständig, deterministisk beskrivning av hur materiens minsta beståndsdelar rör sig och växelverkar med varandra. Kunde det inte vara så att anledningen till att kvantmekaniken bara ger sannolikheter är att den inte ger en fullständig beskrivning av tillståndet för en uppsättning partiklar? Kanske finns det några andra, för oss okända, dolda variabler som måste finnas med i beskrivningen om en klassisk, deterministisk mekanik ska fungera? Dialogen mellan Einstein och Bohr (som accepterade och utvecklade kvantmekanikens beskrivning) har blivit legendarisk. Einstein försökte gång på gång hitta på finurliga paradoxer som han hoppades skulle bevisa att kvantmekaniken är en ofullständig teori, men varje gång lyckades Bohr visa att paradoxen bara berodde på ofullständiga antaganden. I ett känt citat angående sannolikhetsegenskaperna hos kvantmekaniken sade Einstein Gud spelar inte tärning!. Successivt fick Bohrs ståndpunkt allt fler anhängare, och fysikerna accepterade att materien fungerar på ett annorlunda sätt på mikronivå än på de nivåer vi kommer i kontakt med i vår vardag. Bells olikhet Det mest svårsmälta i kvantmekanikens beskrivning av verkligheten kan åskådliggöras på följande sätt. Anta att en elektron eller en foton passerar genom en dubbelspalt och därefter träffar en fotografisk plåt. Man kan då inte förutsäga var på plåten partikeln träffar, men man kan med stor säkerhet uttala sig om sannolikheten för en träff inom ett visst område. Omedelbart innan partikeln registrerats på plåten finns det fortfarande chans att partikeln hamnar på ett helt annat ställe. Den våg som är förknippad med partikeln har kanske brett ut sig över ett stort område. Men i och med att partikeln träffat plåten är sannolikheten noll för träffar inom andra områden. Hela vågen måste alltså upphöra att existera i och med att partikeln träffar plåten. Man kallar detta att vågfunktionen kollapsar. Men hur kan vågfunktionen långt från träffpunkten veta att den ska försvinna? Denna mystiska avståndsverkan brukar kallas EPR-paradoxen (Einstein-Podolsky-Rosen-paradoxen). Kunde det inte i stället vara så att partikeln redan vid passagen av dubbelspalten bestämmer sig för en viss riktning mot den fotografiska plåten? Det skulle vara lättare för vårt sunda förnuft att acceptera. Fanns det någon möjlighet att med experiment avgöra hur det förhåller sig? År 1964 beskrev den nordirländske teoretiska fysikern John Bell hur ett sådant test kunde utföras. Vid vissa processer bildas par av partiklar, som beskrivs av samma vågfunktion. Om t ex kalciumatomer 18 : 14 mer om kvantmekanik och relativitetsteori
15 exciteras till en viss energinivå, så avger de samtidigt två stycken fotoner åt motsatta håll men med samma polarisationsplan. Om man nu med en mätning med t ex polarisationsfilter och detektor kan konstatera att den ena fotonen har t ex vertikal polarisation, så måste alltså även den andra ha det. Frågan är nu: När bestämmer sig fotonerna för ett visst polarisationsplan? Är det vid utsändandet från kalciumatomen eller är det vid mätningen? Enligt kvantmekaniken borde avgörandet ske vid mätningen, medan enligt vårt sunda förnuft det borde ske vid utsändandet. Bell lyckades visa att resultaten av ett stort antal mätningar på sådana fotonpar skulle bli olika i de två fallen. Han uppställde en olikhet (Bells olikhet) som måste gälla om fotonerna bestämmer sig redan vid utsändandet, men som inte skulle gälla om polarisationsplanet bestämdes först vid mätningen. Först år 1982 lyckades man slutgiltigt avgöra hur det förhåller sig. Det var fransmannen Alain Aspect som använde en apparat enligt fig 12. I en vakuumkammare utsätts kalciumatomer för laserljus. Atomerna exciteras då och utsänder par av fotoner, vilka fått passera polarisationsfilter och detektorer. Fig 12. Principskiss som visar Alain Aspects apparatuppställning. Kalciumatomerna exciteras med laserljus, varvid de utsänder fotonpar med samma polarisationsplan. Resultatet var fullständigt entydigt. Fotonernas polarisationsplan avgörs först vid mätningen. Vågfunktionen innehåller information om hur de båda fotonernas polarisationer är korrelerade. Mätningen av den ena polarisationen bestämmer därför automatiskt den andra. Det verkar som om vi måste försöka vänja oss och anpassa vårt tänkande efter de experimentella resultaten. Som så många gånger förr har det sunda förnuftet fått ge vika för fysikaliska mätresultat. Mänskligheten har fått vänja sig vid att jorden är rund, att den rör sig, att tiden går olika fort i olika rörelsesystem. Vi får nu ta ytterligare ett steg, även om detta verkar vara större än de tidigare: Vi kan med stor precision förutsäga sannolikheten för olika resultat av en mätning, men vi har svårt att föreställa oss vad som styr förloppen i atomernas värld och orsakar det ena eller det andra resultatet. Dessa kvantmekaniska korrelationer har på en del håll tagits till intäkt för att den moderna fysiken skulle kunna förklara parapsykologiska fenomen, österländska religioner och allehanda föreställningar om att allmer om kvantmekanik och relativitetsteori 18 : 15
16 ting i universum hänger ihop etc. Detta är att missuppfatta de fysikaliska resultaten. Den avståndsverkan vi talar om här kan aldrig användas för att sända signaler från ett ställe till ett annat. Det är sant att mätningar på ett ställe kan påverka utfallet av en mätning på ett annat ställe, men resultaten är slumpmässiga och kan inte användas för att överföra information. Kvantmekaniken ger alltså en fullständig beskrivning av verkligheten på mikronivå, och några dolda variabler tycks inte existera. 7 Den moderna synen på relativitetsteorin När Einstein publicerade sitt arbete om relativitetsteorin år 1905, var många av hans kollegor i början skeptiska till den. Att invanda begrepp som längd och tid inte är konstanta utan beror på observatörens hastighet är något som strider mot vår intuition, som ju bygger på vardagens låga hastigheter där Newtons lagar är giltiga med stor noggrannhet. Lika underligt är det att ingenting tycks kunna färdas snabbare än ljuset. Det är kanske inte att undra på att den svenska nobelpriskommittén inte ens 15 år efter publiceringen vågade ge Einstein nobelpriset för relativitetsteorin (han fick det i stället för sin förklaring av den fotoelektriska effekten). I dag, nästan ett sekel senare, fascineras vi fortfarande av effekter som tidsdilatation och längdkontraktion. De många noggranna experimentella bekräftelserna av relativitetsteorins förutsägelser gör det omöjligt att längre tvivla på att den är korrekt. Under åren som gått har fysikerna också hittat eleganta formuleringar av teorin, som gör att den kan ges en geometrisk tolkning. Vi ska här ge en förenklad beskrivning av hur relativitetsteorin kan uppfattas med det nya synsättet. 8 Newtons och Galileis mekanik Vi börjar med något välbekant, Newtonsk och Galileisk mekanik. Det enklaste mekaniska system vi kan tänka oss är en partikel som rör sig i rummet. För att beskriva rörelsen måste vi kunna ange partikelns läge vid olika tidpunkter. Vi kan använda oss av ett tredimensionellt koordinatsystem och en lägesvektor som börjar i origo och med sin spets pekar ut partikelns läge. Se fig 13. I fortsättningen betecknar vi vektorer med fet stil. Vi anger alltså lägesvektorn med r och dess belopp med r. 18 : 16 mer om kvantmekanik och relativitetsteori
17 Fig 13. Lägesvektorn r har komponenterna (x, y, z). Vi kan även ange en vektor som ändras i tiden med komponenterna r (t) = (x(t), y(t), z(t)). I vektorläran låter man kvadraten på en vektor vara lika med kvadraten på vektorns belopp. Av fig 14 framgår att r 2 = x 2 + y 2 + z 2 och vi kan skriva r 2 = x 2 + y 2 + z 2 Fig 14. r 2 = x 2 + y 2 + z 2 eftersom sträckan OR är x 2 + y 2 och (OR)2 + z 2 = r 2. Om vi ser hur läget har förändrats under en kort tid t, kan vi beräkna hastigheten som v = r/ t. Om vi vet partikelns massa m, beräknar vi rörelsemängden ur p = mv, och rörelseenergin ur E k = mv 2 /2. Om en kraft F verkar på partikeln, ändras rörelsemängden enligt Newtons rörelseekvation: F = p/ t (eller F = ma eftersom p = mv och a = v/ t). Om inga yttre krafter verkar på ett system av partiklar bevaras som vi har sett den totala rörelsemängden. Det koordinatsystem vi infört förutsätts varken rotera eller accelerera. Det är bekvämt att införa en klass av sådana s k inertialsystem som bara får röra sig med konstant fart relativt varandra. I sådana system rör sig en partikel rätlinjigt och med konstant hastighet, om den inte påverkas av en yttre kraft. mer om kvantmekanik och relativitetsteori 18 : 17
18 Men det koordinatsystem vi infört är ju bara ett hjälpmedel och ingenting som existerar i verkligheten. Vad hade hänt om vi valt ett helt annat koordinatsystem för att beskriva rörelsen? Låt oss se efter. Den enklaste förändringen av koordinatsystemet är att låta z-axeln vara oförändrad, men vrida x- och y-axlarna en vinkel θ (se fig 15). Fig 15. Vridning av ett koordinatsystem vinkeln θ kring positiva z-axeln lämnar z-koordinaten för en given punkt oförändrad, men ger nya x- och y-koordinater x och y. Dessa är linjärkombinationer av de gamla koordinaterna x och y. Ur enkel geometri kan vi då bestämma de nya x-, y- och z-koordinaterna (fig 15). För en godtycklig punkt kallar vi dem x, y och z : x = x cos θ + y sin θ y = x sin θ + y cos θ (A) z = z Eftersom tiden är ett absolut begrepp i Newtons mekanik, t = t, får rörelselagarna samma form i det nya koordinatsystemet, dvs F = ma, förutsatt att även komponenterna i F transformeras på exakt samma sätt som komponenterna i lägesvektorn r när vi vrider koordinatsystemet. Vi kan föra samma resonemang vid en vridning av koordinatsystemet som även ändrar z-axelns riktning, och vi kan låta det nya koordinatsystemet röra sig med konstant hastighet u i förhållande till det gamla systemet. Då får vår partikel hastigheten v u i det nya systemet, men det förändrar inte rörelseekvationen, eftersom a = v/ t är oförändrad om u är konstant (vilket ju betyder att u/ t = 0). I det enklaste fallet med likformig rörelse kan vi låta det nya koordinatsystemet sammanfalla med det gamla vid tiden t = 0 och sedan röra sig i x-axelns riktning med konstant fart u (se fig 16). 18 : 18 mer om kvantmekanik och relativitetsteori
19 Fig 16. Två inertialsystem, där det högra rör sig med hastigheten u i x-riktningen i förhållande till det vänstra. Om systemens origo sammanföll vid tiden t = t = 0, gäller enligt Galilei-transformationen att x = x ut, medan övriga koordinater samt tiden är desamma i de båda systemen. Då gäller x = x ut y = y z = z t = t (B) Naturligtvis kan vi också kombinera en godtycklig vridning med likformig rörelse i godtycklig riktning. Vid en sådan Galilei-transformation blir ekvationssystemet visserligen krångligare, men fortfarande gäller F = ma med de nya koordinaterna. Gemensam både för vridningen av koordinatsystemet och rörelsen med konstant hastighet är att längden vid en viss tidpunkt t 1 av en liten förflyttningsvektor r inte ändras: r = Ö x 2 + y 2 + z 2 = r. Exempel Kontrollera detta påstående för vridningen i ekvationssystem (A) och den likformiga rörelsen i ekvationssystem (B). Lösning x = cos θ x + sin θ y y = sin θ x + cos θ y och z = z ger genom insättning r = Ö x 2 + y 2 + z 2 = = Ö(cos 2 θ + sin 2 θ) x 2 + (cos 2 θ + sin 2 θ) y 2 + z 2 = r mer om kvantmekanik och relativitetsteori 18 : 19
20 I det andra fallet gäller y = y, z = z och x = x (ut 1 ) = = x, eftersom både u och t 1 är konstanter. Alltså är även i det fallet r = r. Vi har nu sett hur den klassiska mekanikens rörelseekvationer som F = ma eller energins bevarande bevarar sin form vid övergång till ett koordinatsystem som är vridet eller satt i likformig rörelse i förhållande till det givna systemet. Galilei-transformationerna har egenskapen att de inte förändrar längden på skillnadsvektorn till två vektorer. Speciellt är längden i kvadrat r 2 = x 2 + y 2 + z 2 oförändrad, invariant. Vidare har vi antagit att tiden inte förändras, t = t. Vi kan nu vända på resonemanget och postulera A. Den klassiska mekanikens lagar har samma form i alla inertialsystem som är relaterade till varandra med Galilei-transformationer. B. Tiden är densamma i alla sådana inertialsystem. Det visar sig att dessa postulat spelar en viktig roll när man härleder lagarna i mekaniken, t ex rörelsemängdens och energins bevarande. 9 Relativistisk mekanik När Maxwell ställde upp sina berömda ekvationer i mitten av talet, stod det efter hand klart att dessa lagar för elektrodynamiken inte behåller samma form vid Galilei-transformationer. Einstein funderade mycket över orsaken till detta, och genom att göra tankeexperiment (bl a försökte han föreställa sig vad som skulle hända om man åkte ifatt en ljusvåg) insåg han att om Maxwells ekvationer är korrekta måste ljuset ha samma hastighet c = m/s i alla inertialsystem. (Detta resultat hade Michelson och Morley erhållit experimentellt på 1880-talet, men det är oklart om Einstein kände till det.) Om vi tittar på hur en vågfront utbreder sig under tiden t, så ändras läget r med beloppet c t, dvs om vi kvadrerar och subtraherar så gäller r 2 (c t) 2 = x 2 + y 2 + z 2 (c t) 2 = 0. Om vi för enkelhets skull betraktar vågutbredning i x-axelns riktning, gäller c t = x eller c = x/ t. I ett inertialsystem som rör sig med farten u i x-axelns riktning (fig 15) gäller enligt Galilei-transformationerna t = t och x x x c = = = u = c u. t t t 18 : 20 mer om kvantmekanik och relativitetsteori
21 Det är den vanliga hastighetslagen som vi är så vana vid i vår vardag. Men enligt Maxwell samt Michelson-Morleys experiment ska ljushastigheten vara densamma i alla inertialsystem, dvs c = c. Ställd inför detta mysterium drog Einstein den geniala slutsatsen att det måste vara något fel på Galilei-transformationerna. Han ersatte därför den klassiska mekanikens postulat ovan med följande: A. Fysikens lagar har samma form i alla inertialsystem. B. Ljushastigheten är en konstant som har samma värde i alla inertialsystem oavsett ljuskällans och observatörens rörelse. Fyravektorer Vi ser att Einstein i det första postulatet har övergivit kravet på att det är Galilei-transformationerna som relaterar olika inertialsystem, och i det andra postulatet har kravet på att tiden är absolut (dvs t = t i alla inertialsystem) fått ge vika för kravet att i stället ljushastigheten ska vara konstant (c = c i alla inertialsystem). Det är faktiskt så att alla de överraskande resultaten från relativitetsteorin (tidsdilatation, längdkontraktion, rörelsemängdens och energins kraftiga hastighetsberoende nära ljushastigheten) stämmer överens med dessa två postulat! Ett intressant sätt att uppfatta skillnaden mellan de två systemen av postulat är att observera att Galilei-transformationerna som vi såg lämnar både tiden t och längden av en liten vektor r oförändrade, medan enligt Einsteins andra postulat bara kombinationen r 2 (c t) 2 ska vara oförändrad (och ha värdet noll om man i vilket inertialsystem som helst låter r vara den sträcka en ljusfront rört sig under tiden t). Det betyder att r kan ändras om bara t ändras i motsvarande mån. Men vi har stött på något liknande tidigare. I exemplet i avsnitt 8 såg vi att x och y ändrades var och en för sig till x och y, men summan av kvadraterna r 2 var ändå oförändrad. Tydligen uppträder c t på samma sätt som en fjärde koordinat, och i stället för den tredimensionella lägesvektorn r = (x, y, z) är det naturligt i relativitetsteorin att införa fyravektorn s = (x, y, z, ct) som kortare kan skrivas s = (r, ct). Om Galilei-transformationerna var de transformationer som lämnar r 2 invariant, får vi i stället relativitetsteorins motsvarighet (de s k Lorentztransformationerna) som de transformationer som lämnar uttrycket s 2 = r 2 (c t) 2 invariant. mer om kvantmekanik och relativitetsteori 18 : 21
22 Precis som vridningar blandar x-, y- och z-komponenterna, måste vi kunna ha transformationer som blandar tids- och rumskomponenter. Redan Galilei-transformationen i fig 15 blandade ju x och t, eftersom x = x ut. Låt oss försöka att behålla den transformationen när vi betraktar en ljusfront i de båda inertialsystemen. Då gäller x 2 (c t) 2 = 0 (1) och x = x u t. (2) Enligt Einsteins postulat ska då också gälla: x 2 (c t ) 2 = 0 Vi provar: Ekvation (2) ger x 2 = x 2 2u x t + u 2 t 2 eller x 2 x 2 = u 2 t 2 + 2u x t som med hjälp av ekvation (1) kan skrivas x 2 (c t) 2 = u 2 t 2 2u x t Om t = t får vi x 2 (c t ) 2 = u 2 t 2 2u x t 0! Men om vi tillåter att t får en inblandning av x kan vi få bort korstermen 2u x t genom att sätta u c t = c t x c Vi har då fått x 2 (c t ) 2 = = x 2 (c t) 2 2u x t + u 2 t 2 u 2 x u x t = = (1 ) ( x 2 (c t) 2 ) Vi har hittat den transformation mellan de två systemen i fig 16 som lämnar x 2 (c t) 2 invariant, så när som på att vi fått den extra faktorn (1 2 ). Men den är lätt att få bort genom att från början baka u c 2 in faktorn u 2 c u 2 c 2 i transformationerna. Detta uttryck uppträder så ofta i relativitetsteorin att det är praktiskt att införa beteckningen γ : 1 γ (u) = 1 u 2 c 2 18 : 22 mer om kvantmekanik och relativitetsteori Om vi definierar systemen så att deras origo sammanfaller vid tiderna t = t = 0, kan vi skriva Lorentz-transformationerna: c 2
23 x = γ (x ut) y = y z = z ux t = γ (t ) Ur dessa formler kan längdkontraktion och tidsdilatation härledas. Exempel c 2 Härled formeln för längdkontraktion. Lösning Låt vilolängden för t ex en måttstock vara x = L. I ett rörligt system där den rör sig mäter vi längden genom att beräkna x för t = 0 (för att mäta längden på något som rör sig måste vi förstås mäta läget på fram- respektive bakända vid samma tid t ). t = 0 ger u t = x. c 2 Insättning i första formeln ger L = x = L 1 u 2 c 2 vilket är formeln för Lorentz-kontraktionen. Vi ser att längden L < L, dvs måttstocken är kortare i ett system där den rör sig. mer om kvantmekanik och relativitetsteori 18 : 23
24 10 Rum och tid bildar rumtid Vi har sett att rum och tid kopplas ihop i relativitetsteorin till något som brukar kallas rumtiden. Tiden (multiplicerad med ljushastigheten c, så att den får dimensionen längd precis som x-, y- och z-koordinaterna) fungerar som en fjärde dimension. En punkt i den fyrdimensionella rumtiden svarar mot ett läge i rummet vid en viss tid, dvs en händelse (t ex att en ljusblixt avfyras). Tiden skiljer sig dock från rumsdimensionerna eftersom dess bidrag till längden i kvadrat på läges-fyravektorn har negativt tecken. I den klassiska mekaniken har vi behandlat många vektorstorheter: läge, hastighet, acceleration, rörelsemängd osv. Alla dessa borde kunna generaliseras till fyravektorer i relativitetsteorin. Einsteins första postulat säger att naturlagarna ska ha samma form i alla inertialsystem. Om vi t ex skriver en naturlag på formen (fyravektor 1) = (fyravektor 2), och kräver att alla fyravektorer transformeras på samma sätt (dvs i enlighet med Lorentz-transformationerna) vid byte av inertialsystem, så blir det kravet automatiskt uppfyllt. Den enda fyravektor vi från början har tillgång till när vi beskriver en partikels rörelse är dess lägesfyravektor s. Hur ska vi bilda nya fyravektorer? Vi kan förstås addera och subtrahera fyravektorer. Om vi vill multiplicera eller dividera givna fyravektorer med något, måste vi använda storheter som observatörer i alla inertialsystem är överens om (s k skalärer), om vi inte vill förstöra invariansen. Betrakta en partikel som rör sig. Bilda rumtidsavståndet i kvadrat mellan två näraliggande punkter på partikelns bana, s 2 = r 2 (c t) 2. Till skillnad från fallet med ljus är värdet på denna längd inte noll. Det är dock lätt att visa att den är invariant, dvs har samma värde i alla inertialsystem. Detta värde är lätt att räkna ut. Vi kan ju sätta oss i ett system som följer med partikeln. Då är r 2 = 0 och s 2 = (c τ) 2, där τ är den tid som mäts upp av en klocka som följer med partikeln, partikelns egentid. Egentiden är alltså en skalär storhet som vi kan använda för att bilda nya fyravektorer. Precis som derivatan av ortsvektorn r med avseende på tiden t ger hastigheten i klassisk mekanik, kan vi bilda derivatan med avseende på egentiden τ av lägesfyravektorn s och får på så sätt fyrahastigheten v = lim s. Eftersom tidsdilatationen innebär att egentiden τ är kortare än t med faktorn 1/γ, går det att skriva: τ 0 τ v r c t = γ (, ) = γ (u, c) t t där u är den vanliga trehastigheten. Vi kan bilda fyr-kvadraten v 2 = γ 2 (u 2 c 2 ) = c 2 18 : 24 mer om kvantmekanik och relativitetsteori
25 Detta visar för övrigt att till skillnad från längder i tre dimensioner behöver kvadraten på en fyravektor inte vara positiv utan kan vara både större än 0, mindre än 0 och lika med 0. Fyra-accelerationen a ges förstås av a = v/ τ osv. Precis som egentiden är invariant är även partikelns vilomassa m invariant (observatörer i alla inertialsystem är överens om vad partikelns massa är, uppmätt i dess eget vilosystem). Vi kan då på analogt sätt bilda fyra-rörelsemängden som p = mv = m s. τ Dess kvadrat är p 2 = m 2 v 2 = m 2 γ 2 (u 2 c 2 ) = m 2 c 2 Om vi sätter in uttrycket för v ser vi att p = (γ mv, γ mc). De tre första komponenterna känner vi igen som den relativistiska rörelsemängden, och den fjärde komponenten kan vi koppla ihop med energin. Vi definierar den totala relativistiska energin som γ mc 2 (se kap 11) och den fjärde komponenten blir då E/c. Det kan i början kännas ovant att hantera dessa fyravektorer, men efter ett tag inser man vilken förenkling de medför. Om man en gång har lärt sig att hantera vanliga tredimensionella vektorer betyder övergången till relativitetsteori i stort sett bara att man till varje trevektor fogar en fjärde komponent så att man får en fyravektor. Den transformeras i enlighet med Lorentz-transformationerna när man byter inertialsystem. Som ett exempel kan vi nämna att i elektrodynamiken bildar strömtäthetsvektorn i och laddningstätheten ρ tillsammans en sådan fyravektor. Alla Maxwells ekvationer kan sammanfattas i en enkel formel med fyravektorer: úf = J 11 Den allmänna relativitetsteorin Hittills har vi använt inertialsystem för att beskriva partiklars rörelse både i den klassiska och den relativistiska mekaniken. Även Einstein gjorde detta när han ställde upp sin speciella relativitetsteori, men han var egentligen missnöjd med den inskränkningen. Han gick vidare och lyckades till slut formulera en teori, den allmänna relativitetsteorin, som gäller även om vi har accelererade referenssystem eller befinner oss i tyngdkraftfält. mer om kvantmekanik och relativitetsteori 18 : 25
26 Som vanligt gjorde Einstein sina teoretiska framsteg genom att göra tankeexperiment. För att komma fram till den allmänna relativitetsteorin funderade Einstein på ett märkligt faktum som rör gravitationen. Enligt Newtons gravitationslag är gravitationskraften t ex från jorden på en massa m proportionell mot m, F = GmM/R 2 = mg. Samtidigt säger Newtons rörelseekvation att F = ma, dvs a = g helt oberoende av massan m. Detta är ju helt enkelt den upptäckt Galilei sägs ha gjort vid experiment i lutande tornet i Pisa: Om vi bortser från luftmotståndet faller alla kroppar lika snabbt i tyngdkraftfältet. (Med moderna metoder har det bekräftats med en noggrannhet av ett på några miljarder!) Gravitationen fungerar alltså ungefär som om vi skulle befinna oss i en rymdfarkost som accelererar med den konstanta accelerationen g (se fig 17). Fig 17. En vikt släpps mot den accelererande raketens golv. Det finns ingen skillnad mellan ett homogent tyngdkraftfält och ett likformigt accelererat system. Alla fysikaliska processer sker på exakt samma sätt i båda fallen. Einsteins genidrag var nu att upphöja detta faktum, som ju är rimligt för fallande kroppar, till ett postulat som gäller för alla naturlagar, den s k ekvivalensprincipen: Det finns ingen skillnad mellan ett homogent tyngdkraftfält och ett likformigt accelererat system. Alla fysikaliska processer sker på exakt samma sätt i båda fallen. Detta till synes mycket enkla (och dessutom rimliga) postulat leder till minst lika häpnadsväckande konsekvenser som Einsteins postulat för den speciella relativitetsteorin. Exempelvis innebär det att massiva kroppar kröker rumtiden. Dessutom leder det till att tiden går långsammare i källaren av ett hus än i översta våningen men skillnaden är inte större än någon nanosekund per sekel! I starka tyngdkraftfält, t ex nära ytan på mycket kompakta stjärnor, är sådana effekter mycket viktiga. Låt oss se hur postulatet medför att massa kröker rumtiden. Vi betraktar hur en ljusstråle rör sig genom ett rymdskepp som vid tiden t = 0 börjar accelerera med konstant acceleration (fig 18). Strålen kommer in i rymdskeppet vid A och rör sig vågrätt enligt en observatör i det inertialsystem där rymdskeppet var i vila från början. Enligt en observatör som följer med rymdskeppet börjar strålen vågrätt, men sedan accelererar ju den bortre väggen uppåt, så att strålen kommer att träffa nedanför mitten. Ljusstrålen kommer att tyckas följa en parabelbana för observatören i rymdskeppet. 18 : 26 mer om kvantmekanik och relativitetsteori
27 Fig 18. Hur beter sig ljuset i ett tyngdkraftfält? Enligt ekvivalenspricipen beter det sig på exakt samma sätt som i ett system med konstant acceleration. Alltså följer ljus en parabelbana även i ett konstant tyngdkraftfält. Men enligt optikens lagar följer ljuset alltid den kortaste vägen (det kallas ibland Fermats princip). Hur kan vi få detta att gå ihop? Ljuset följer den kortaste vägen genom rymden, men om rymden är uppfylld av ett tyngdkraftfält är den vägen inte en rät linje! Den enda möjligheten är att rymden är krökt. Jämför med situationen på jordytan: Om vi ska resa t ex mellan Stockholm och New York, får vi den kortaste vägen om vi följer en del av den storcirkelbåge som passerar båda städerna. Denna kortaste väg är inte en rät linje, och det beror ju på att jordytan är krökt. Matematiskt fungerar det på likartat sätt när massa kröker rumtiden, men vi har ju svårt att få någon intuitiv bild av den fyrdimensionella rumtiden. Einstein gjorde mer än detta när han ställde upp sin allmänna relativitetsteori. Han gav också ett system av ekvationer som talar om exakt hur mycket en viss mängd materia påverkar rumtidens krökning. Precis som Maxwells ekvationer har våglösningar (ljus och annan elektromagnetisk strålning) har även Einsteins ekvationer sådana lösningar: gravitationsstrålning. För närvarande konstrueras detektorer som bör kunna påvisa sådan gravitationsstrålning från våldsamma förlopp ute i världsrymden, t ex när två neutronstjärnor kolliderar. mer om kvantmekanik och relativitetsteori 18 : 27
28 Fig 19. Principen för LIGO-detektorn (Laser Interferometer Gravitational-Wave Observatory) som är under uppbyggnad i USA. Ljuset från lasern delas upp i två strålar. Var och en av dessa reflekteras upprepade gånger mellan två speglar, vilkas inbördes avstånd är L 1 respektive L 2. När de två strålarna förs ihop igen och detekteras av den ljuskänsliga fotodioden, kan även mycket små skillnader i väglängd upptäckas, genom att det interferensmönster som bildas ändras om vägskillnaden ändras. En gravitationsvåg kröker rummet så att längdskillnaden L 1 L 2 påverkas. Förskjutningar så små som m tros kunna detekteras när detektorn står klar. Andra delar av Einsteins allmänna relativitetsteori har redan testats experimentellt och befunnits vara korrekta med stor precision. Teorin utgör dessutom grunden för den moderna kosmologin, beskrivningen av hur hela universum har utvecklats från Big Bang fram till idag. En intressant följd av Einsteins allmänna relativitetsteori är att eftersom närvaron av massa kröker rumtiden, kan ljusstrålar brytas när de passerar nära en himlakropp. Stjärnor, planeter och galaxer fungerar alltså som gravitationslinser. Det var för övrigt den engelske astronomen Eddingtons observationer av avböjningen av ljuset från en stjärna nära solen vid en total solförmörkelse utanför Afrikas kust år 1919 som blev genombrottet för Einstein som vetenskaplig megastjärna. Även med Newtons gravitationsteori kan man nämligen göra troligt att ljus avböjs nära massiva kroppar (åtminstone om ljus också är partiklar, som attraheras av gravitationen). Newtons resultat är emellertid en faktor 2 mindre än Einsteins, eftersom Einsteins beräkning också tar hänsyn till rumtidens krökning. När Eddingtons resultat blev kända orsakade detta nästan krigsrubriker i engelska tidningar Newton hade fel! Nutida astronomer använder sig av gravitationslinser för att uppskatta mängden massa hos galaxer och galaxhopar. Avlägsna, mycket ljusstarka objekt (s k kvasarer) kan ge upphov till flera bilder, se fig : 28 mer om kvantmekanik och relativitetsteori
29 Fig 20. En gravitationslins. Ljuset från en avlägsen kvasar avböjs i det starka tyngdkraftfältet från galaxen i mitten och ger fyra bilder. mer om kvantmekanik och relativitetsteori 18 : 29
1 Den Speciella Relativitetsteorin
 1 Den Speciella Relativitetsteorin Den speciella relativitetsteorin är en fysikalisk teori om lades fram av Albert Einstein år 1905. Denna teori beskriver framför allt hur utfallen (dvs resultaten) från
1 Den Speciella Relativitetsteorin Den speciella relativitetsteorin är en fysikalisk teori om lades fram av Albert Einstein år 1905. Denna teori beskriver framför allt hur utfallen (dvs resultaten) från
Andra föreläsningen kapitel 7. Patrik Lundström
 Andra föreläsningen kapitel 7 Patrik Lundström Kvantisering i klassisk fysik: Uppkomst av heltalskvanttal För att en stående våg i en ring inte ska släcka ut sig själv krävs att den är tillbaka som den
Andra föreläsningen kapitel 7 Patrik Lundström Kvantisering i klassisk fysik: Uppkomst av heltalskvanttal För att en stående våg i en ring inte ska släcka ut sig själv krävs att den är tillbaka som den
Den Speciella Relativitetsteorin DEL I
 Den Speciella Relativitetsteorin DEL I Elektronens Tvilling Den unge patentverksarbetaren År 1905 publicerar en ung patentverksarbetare tre artiklar som revolutionerar fysiken. En av dessa artiklar är
Den Speciella Relativitetsteorin DEL I Elektronens Tvilling Den unge patentverksarbetaren År 1905 publicerar en ung patentverksarbetare tre artiklar som revolutionerar fysiken. En av dessa artiklar är
1 Den Speciella Relativitetsteorin
 1 Den Speciella Relativitetsteorin På tidigare lektioner har vi studerat rotationer i två dimensioner samt hur vi kan beskriva föremål som roterar rent fysikaliskt. Att från detta gå över till den speciella
1 Den Speciella Relativitetsteorin På tidigare lektioner har vi studerat rotationer i två dimensioner samt hur vi kan beskriva föremål som roterar rent fysikaliskt. Att från detta gå över till den speciella
BFL122/BFL111 Fysik för Tekniskt/ Naturvetenskapligt Basår/ Bastermin Föreläsning 7 Kvantfysik, Atom-, Molekyl- och Fasta Tillståndets Fysik
 Föreläsning 7 Kvantfysik 2 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det
Föreläsning 7 Kvantfysik 2 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det
1.5 Våg partikeldualism
 1.5 Våg partikeldualism 1.5.1 Elektromagnetisk strålning Ljus uppvisar vågegenskaper. Det är bland annat möjligt att åstadkomma interferensmönster med ljus det visades av Young redan 1803. Interferens
1.5 Våg partikeldualism 1.5.1 Elektromagnetisk strålning Ljus uppvisar vågegenskaper. Det är bland annat möjligt att åstadkomma interferensmönster med ljus det visades av Young redan 1803. Interferens
Utveckling mot vågbeskrivning av elektroner. En orientering
 Utveckling mot vågbeskrivning av elektroner En orientering Nikodemus Karlsson Februari 00 . Bohrs Postulat Niels Bohr (885-96) ställde utifrån iakttagelser upp fyra postulat gällande väteatomen ¹:. Elektronen
Utveckling mot vågbeskrivning av elektroner En orientering Nikodemus Karlsson Februari 00 . Bohrs Postulat Niels Bohr (885-96) ställde utifrån iakttagelser upp fyra postulat gällande väteatomen ¹:. Elektronen
Kommer sig osäkerheten av att vår beskrivning av naturen är ofullständig, eller av att den fysiska verkligheten är genuint obestämd?
 Inte mycket verkar säkert här...? Våg-partikeldualitet Ett system kan ha både vågoch partikelegenskaper i samma experiment. Vågfunktionen har en sannolikhetstolkning. Heisenbergs osäkerhetsrelation begränsar
Inte mycket verkar säkert här...? Våg-partikeldualitet Ett system kan ha både vågoch partikelegenskaper i samma experiment. Vågfunktionen har en sannolikhetstolkning. Heisenbergs osäkerhetsrelation begränsar
Relativitetsteori, introduktion
 Relativitetsteori, introduktion En av bristerna med den klassiska fysiken är att alla observatörer antas ha samma tidsuppfattning, oavsett sin egen rörelse. Einstein kunde visa att så inte kunde vara fallet.
Relativitetsteori, introduktion En av bristerna med den klassiska fysiken är att alla observatörer antas ha samma tidsuppfattning, oavsett sin egen rörelse. Einstein kunde visa att så inte kunde vara fallet.
Tentamen Relativitetsteori , 29/7 2017
 KOD: Tentamen Relativitetsteori 9.00 14.00, 29/7 2017 Hjälpmedel: Miniräknare, linjal och bifogad formelsamling. Observera: Samtliga svar ska lämnas på dessa frågepapper. Det framgår ur respektive uppgift
KOD: Tentamen Relativitetsteori 9.00 14.00, 29/7 2017 Hjälpmedel: Miniräknare, linjal och bifogad formelsamling. Observera: Samtliga svar ska lämnas på dessa frågepapper. Det framgår ur respektive uppgift
BFL122/BFL111 Fysik för Tekniskt/ Naturvetenskapligt Basår/ Bastermin Föreläsning 10 Relativitetsteori den 26 april 2012.
 Föreläsning 10 Relativa mätningar Allting är relativt är ett välbekant begrepp. I synnerhet gäller detta när vi gör mätningar av olika slag. Många mätningar består ju i att man jämför med någonting. Temperatur
Föreläsning 10 Relativa mätningar Allting är relativt är ett välbekant begrepp. I synnerhet gäller detta när vi gör mätningar av olika slag. Många mätningar består ju i att man jämför med någonting. Temperatur
4-1 Hur lyder Schrödingerekvationen för en partikel som rör sig i det tredimensionella
 KVANTMEKANIKFRÅGOR Griffiths, Kapitel 4-6 Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths.
KVANTMEKANIKFRÅGOR Griffiths, Kapitel 4-6 Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths.
Kvantmekanik. Kapitel Natalie Segercrantz
 Kvantmekanik Kapitel 38-39 Natalie Segercrantz Centrala begrepp Schrödinger ekvationen i en dimension Fotoelektriska effekten De Broglie: partikel-våg dualismen W 0 beror av materialet i katoden minimifrekvens!
Kvantmekanik Kapitel 38-39 Natalie Segercrantz Centrala begrepp Schrödinger ekvationen i en dimension Fotoelektriska effekten De Broglie: partikel-våg dualismen W 0 beror av materialet i katoden minimifrekvens!
Rörelsemängd och energi
 Föreläsning 3: Rörelsemängd och energi Naturlagarna skall gälla i alla interial system. Bl.a. gäller att: Energi och rörelsemängd bevaras i all växelverkan mu p = Relativistisk rörelsemängd: 1 ( u c )
Föreläsning 3: Rörelsemängd och energi Naturlagarna skall gälla i alla interial system. Bl.a. gäller att: Energi och rörelsemängd bevaras i all växelverkan mu p = Relativistisk rörelsemängd: 1 ( u c )
7. Atomfysik väteatomen
 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det nödvändigt att betrakta
Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det nödvändigt att betrakta
Instuderingsfrågor, Griffiths kapitel 4 7
 Joakim Edsjö 15 oktober 2007 Fysikum, Stockholms Universitet Tel.: 08-55 37 87 26 E-post: edsjo@physto.se Instuderingsfrågor, Griffiths kapitel 4 7 Teoretisk Kvantmekanik II HT 2007 Tanken med dessa frågor
Joakim Edsjö 15 oktober 2007 Fysikum, Stockholms Universitet Tel.: 08-55 37 87 26 E-post: edsjo@physto.se Instuderingsfrågor, Griffiths kapitel 4 7 Teoretisk Kvantmekanik II HT 2007 Tanken med dessa frågor
Kvantmekanik. Kvantmekaniken: De naturlagar som styr förlopp i den mikroskopiska världen (och i den makroskopiska!) Kvantmekanik.
 Kap. 7. Kvantmekanik: introduktion 7A.1- I begynnelsen Kvantmekanik Kvantmekaniken: De naturlagar som styr förlopp i den mikroskopiska världen och i den makroskopiska! Kvantmekanik Klassisk fysik Specialfall!
Kap. 7. Kvantmekanik: introduktion 7A.1- I begynnelsen Kvantmekanik Kvantmekaniken: De naturlagar som styr förlopp i den mikroskopiska världen och i den makroskopiska! Kvantmekanik Klassisk fysik Specialfall!
I once saw Einstein on a train which whistled past our station. - Your clock ticks much too slow, I yelled. - Ach, nein. That's time dilation
 I once saw Einstein on a train which whistled past our station. - Your clock ticks much too slow, I yelled. - Ach, nein. That's time dilation - Gordon Judge Om man åker fortare än ljuset, svartnar det
I once saw Einstein on a train which whistled past our station. - Your clock ticks much too slow, I yelled. - Ach, nein. That's time dilation - Gordon Judge Om man åker fortare än ljuset, svartnar det
Kapitel 4. Materievågor
 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Kapitel 4. Materievågor 1 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Överblick Överblick Kring 1925 började många viktiga kvantkoncept ha sett
Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Kapitel 4. Materievågor 1 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Överblick Överblick Kring 1925 började många viktiga kvantkoncept ha sett
Speciell relativitetsteori inlämningsuppgift 2
 Speciell relativitetsteori inlämningsuppgift 2 Christian von Schultz 2006 11 29 1 Tre satser Vi definierar en rumslik vektor A som en vektor som har A 2 < 0; en tidslik vektor har A 2 > 0 och en ljuslik
Speciell relativitetsteori inlämningsuppgift 2 Christian von Schultz 2006 11 29 1 Tre satser Vi definierar en rumslik vektor A som en vektor som har A 2 < 0; en tidslik vektor har A 2 > 0 och en ljuslik
101-åringen som klev ut ur teorin Om gravitationsvågor (2016) och Einsteins allmänna relativitetsteori (1915)
 101-åringen som klev ut ur teorin Om gravitationsvågor (2016) och Einsteins allmänna relativitetsteori (1915) Filosoficirkeln, Lund, 7 mars 2017 Bengt EY Svensson https://www.ligo.caltech.edu/video/ligo20160211v2
101-åringen som klev ut ur teorin Om gravitationsvågor (2016) och Einsteins allmänna relativitetsteori (1915) Filosoficirkeln, Lund, 7 mars 2017 Bengt EY Svensson https://www.ligo.caltech.edu/video/ligo20160211v2
4 rörelsemängd. en modell för gaser. Innehåll
 4 rörelsemängd. en modell för gaser. Innehåll 8 Allmänna gaslagen 4: 9 Trycket i en ideal gas 4:3 10 Gaskinetisk tolkning av temperaturen 4:6 Svar till kontrolluppgift 4:7 rörelsemängd 4:1 8 Allmänna gaslagen
4 rörelsemängd. en modell för gaser. Innehåll 8 Allmänna gaslagen 4: 9 Trycket i en ideal gas 4:3 10 Gaskinetisk tolkning av temperaturen 4:6 Svar till kontrolluppgift 4:7 rörelsemängd 4:1 8 Allmänna gaslagen
Innehåll. Fysik Relativitetsteori. fy8_modernfysik.notebook. December 19, Relativitetsteorin Ljusets dualism Materiens struktur Kärnfysik
 Fysik 8 Modern fysik Innehåll Relativitetsteorin Ljusets dualism Materiens struktur Kärnfysik 1. Relativitetsteori Speciella relativitetsteorin Allmänna relativitetsteorin Two Postulates Special Relativity
Fysik 8 Modern fysik Innehåll Relativitetsteorin Ljusets dualism Materiens struktur Kärnfysik 1. Relativitetsteori Speciella relativitetsteorin Allmänna relativitetsteorin Two Postulates Special Relativity
Lösningar - Rätt val anges med fet stil i förekommande fall (obs att svaren på essäfrågorna inte är uttömmande).
 STOCKHOLMS UNIVERSITET FYSIKUM Tentamensskrivning i Materiens Minsta Byggstenar, 5p. Lördag den 15 juli, kl. 9.00 14.00 Lösningar - Rätt val anges med fet stil i förekommande fall (obs att svaren på essäfrågorna
STOCKHOLMS UNIVERSITET FYSIKUM Tentamensskrivning i Materiens Minsta Byggstenar, 5p. Lördag den 15 juli, kl. 9.00 14.00 Lösningar - Rätt val anges med fet stil i förekommande fall (obs att svaren på essäfrågorna
10. Relativitetsteori Tid och Längd
 Relativa mätningar Allting är relativt är ett välbekant begrepp. I synnerhet gäller detta när vi gör mätningar av olika slag. Många mätningar består ju i att man jämför med någonting. Temperatur är en
Relativa mätningar Allting är relativt är ett välbekant begrepp. I synnerhet gäller detta när vi gör mätningar av olika slag. Många mätningar består ju i att man jämför med någonting. Temperatur är en
1 Hur förklarar du att det blev ett interferensmönster i interferensexperimentet med elektroner?
 Session: okt28 Class Points Avg: 65.38 out of 100.00 (65.38%) 1 Hur förklarar du att det blev ett interferensmönster i interferensexperimentet med elektroner? A 0% Vi måste ha haft "koincidens", dvs. flera
Session: okt28 Class Points Avg: 65.38 out of 100.00 (65.38%) 1 Hur förklarar du att det blev ett interferensmönster i interferensexperimentet med elektroner? A 0% Vi måste ha haft "koincidens", dvs. flera
Tentamen Relativitetsteori , 27/7 2019
 KOD: Tentamen Relativitetsteori 9.00 14.00, 27/7 2019 Hjälpmedel: Miniräknare, linjal och bifogad formelsamling. Observera: Samtliga svar ska lämnas på dessa frågepapper. Det framgår ur respektive uppgift
KOD: Tentamen Relativitetsteori 9.00 14.00, 27/7 2019 Hjälpmedel: Miniräknare, linjal och bifogad formelsamling. Observera: Samtliga svar ska lämnas på dessa frågepapper. Det framgår ur respektive uppgift
1-1 Hur lyder den tidsberoende Schrödingerekvationen för en partikel som rör sig längs x-axeln? Definiera ingående storheter!
 KVANTMEKANIKFRÅGOR, GRIFFITHS Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths. 1 Kapitel
KVANTMEKANIKFRÅGOR, GRIFFITHS Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths. 1 Kapitel
Tentamen Relativitetsteori
 KOD: Tentamen Relativitetsteori 9.00 14.00, 16/7 2011 Hjälpmedel: Miniräknare, linjal och bifogad formelsamling. Observera samtliga svar ska lämnas på dessa frågepapper. Det framgår ur respektive uppgift
KOD: Tentamen Relativitetsteori 9.00 14.00, 16/7 2011 Hjälpmedel: Miniräknare, linjal och bifogad formelsamling. Observera samtliga svar ska lämnas på dessa frågepapper. Det framgår ur respektive uppgift
KEMA00. Magnus Ullner. Föreläsningsanteckningar och säkerhetskompendium kan laddas ner från
 KEMA00 Magnus Ullner Föreläsningsanteckningar och säkerhetskompendium kan laddas ner från http://www.kemi.lu.se/utbildning/grund/kema00/dold Användarnamn: Kema00 Lösenord: DeltaH0 F2 Periodiska systemet
KEMA00 Magnus Ullner Föreläsningsanteckningar och säkerhetskompendium kan laddas ner från http://www.kemi.lu.se/utbildning/grund/kema00/dold Användarnamn: Kema00 Lösenord: DeltaH0 F2 Periodiska systemet
Dopplereffekt och lite historia
 Dopplereffekt och lite historia Outline 1 Lite om relativitetsteorins historia 2 Dopplereffekt och satelliter 3 Dopplereffekt och tidsdilatation L. H. Kristinsdóttir (LU/LTH) Dopplereffekt och lite historia
Dopplereffekt och lite historia Outline 1 Lite om relativitetsteorins historia 2 Dopplereffekt och satelliter 3 Dopplereffekt och tidsdilatation L. H. Kristinsdóttir (LU/LTH) Dopplereffekt och lite historia
Mer om E = mc 2. Version 0.4
 1 (6) Mer om E = mc Version 0.4 Varifrån kommer formeln? För en partikel med massan m som rör sig med farten v har vi lärt oss att rörelseenergin är E k = mv. Denna formel är dock inte korrekt, även om
1 (6) Mer om E = mc Version 0.4 Varifrån kommer formeln? För en partikel med massan m som rör sig med farten v har vi lärt oss att rörelseenergin är E k = mv. Denna formel är dock inte korrekt, även om
Relativistisk energi. Relativistisk energi (forts) Ekin. I bevarad energi ingår summan av kinetisk energi och massenergi. udu.
 Föreläsning 3: Relativistisk energi Om vi betraktar tillskott till kinetisk energi som utfört arbete för att aelerera från till u kan dp vi integrera F dx, dvs dx från x 1 där u = till x där u = u, mha
Föreläsning 3: Relativistisk energi Om vi betraktar tillskott till kinetisk energi som utfört arbete för att aelerera från till u kan dp vi integrera F dx, dvs dx från x 1 där u = till x där u = u, mha
Innehåll. Förord...11. Del 1 Inledning och Bakgrund. Del 2 Teorin om Allt en Ny modell: GET. GrundEnergiTeorin
 Innehåll Förord...11 Del 1 Inledning och Bakgrund 1.01 Vem var Martinus?... 17 1.02 Martinus och naturvetenskapen...18 1.03 Martinus världsbild skulle inte kunna förstås utan naturvetenskapen och tvärtom.......................
Innehåll Förord...11 Del 1 Inledning och Bakgrund 1.01 Vem var Martinus?... 17 1.02 Martinus och naturvetenskapen...18 1.03 Martinus världsbild skulle inte kunna förstås utan naturvetenskapen och tvärtom.......................
Kapitel 33 The nature and propagation of light. Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion)
 Kapitel 33 The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Kapitel 33 The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Fysikaliska krumsprång i spexet eller Kemister och matematik!
 Fysikaliska krumsprång i spexet eller Kemister och matematik! Mats Linder 10 maj 2009 Ingen sammanfattning. Sammanfattning För den hugade har vi knåpat ihop en liten snabbguide till den fysik och kvantmekanik
Fysikaliska krumsprång i spexet eller Kemister och matematik! Mats Linder 10 maj 2009 Ingen sammanfattning. Sammanfattning För den hugade har vi knåpat ihop en liten snabbguide till den fysik och kvantmekanik
Svarta håls existens är en förutsägelse av Einsteins allmänna relativitetsteori (Einsteinsk mekanik med gravitation), som generaliserar Newtonsk
 Svarta hål Svarta håls existens är en förutsägelse av Einsteins allmänna relativitetsteori (Einsteinsk mekanik med gravitation), som generaliserar Newtonsk mekanik (med gravitation). För att förstå svarta
Svarta hål Svarta håls existens är en förutsägelse av Einsteins allmänna relativitetsteori (Einsteinsk mekanik med gravitation), som generaliserar Newtonsk mekanik (med gravitation). För att förstå svarta
Parbildning. Om fotonens energi är mer än dubbelt så stor som elektronens vileoenergi (m e. c 2 ):
 Parbildning Vi ar studerat två sätt med vilket elektromagnetisk strålning kan växelverka med materia. För ögre energier ar vi även en tredje: Parbildning E mc Innebär att omvandling mellan energi oc massa
Parbildning Vi ar studerat två sätt med vilket elektromagnetisk strålning kan växelverka med materia. För ögre energier ar vi även en tredje: Parbildning E mc Innebär att omvandling mellan energi oc massa
Vad vi ska prata om idag:
 Vad vi ska prata om idag: Om det omöjliga i att färdas snabbare än ljuset...... och om gravitation enligt Newton och enligt Einstein. Äpplen, hissar, rökelse, krökta rum......och stjärnor som används som
Vad vi ska prata om idag: Om det omöjliga i att färdas snabbare än ljuset...... och om gravitation enligt Newton och enligt Einstein. Äpplen, hissar, rökelse, krökta rum......och stjärnor som används som
Preliminärt lösningsförslag till Tentamen i Modern Fysik,
 Preliminärt lösningsförslag till Tentamen i Modern Fysik, SH1009, 008 05 19, kl 14:00 19:00 Tentamen har 8 problem som vardera ger 5 poäng. Poäng från inlämningsuppgifter tillkommer. För godkänt krävs
Preliminärt lösningsförslag till Tentamen i Modern Fysik, SH1009, 008 05 19, kl 14:00 19:00 Tentamen har 8 problem som vardera ger 5 poäng. Poäng från inlämningsuppgifter tillkommer. För godkänt krävs
Fysikaliska modeller
 Fysikaliska modeller Olika syften med fysiken Grundforskarens syn Finna förklaringar på skeenden i naturen Ställa upp lagar för fysikaliska skeenden Kritiskt granska uppställda lagar Kontrollera uppställda
Fysikaliska modeller Olika syften med fysiken Grundforskarens syn Finna förklaringar på skeenden i naturen Ställa upp lagar för fysikaliska skeenden Kritiskt granska uppställda lagar Kontrollera uppställda
Kvantmekanik - Gillis Carlsson
 Kvantmekanik - Föreläsning 1 Gillis Carlsson gillis.carlsson@matfys.lth.se LP2 Föreläsningarna i kvantmekanik LP1 V1): Repetition av kvant-nano kursen. Sid 5-84 V2 : V3 : Formalism (I). Sid 109-124, 128-131,
Kvantmekanik - Föreläsning 1 Gillis Carlsson gillis.carlsson@matfys.lth.se LP2 Föreläsningarna i kvantmekanik LP1 V1): Repetition av kvant-nano kursen. Sid 5-84 V2 : V3 : Formalism (I). Sid 109-124, 128-131,
Fysik TFYA68. Föreläsning 11/14
 Fysik TFYA68 Föreläsning 11/14 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 38-39* (*) 38.1, 38.4, 39.1-3, 6 koncept enklare uppgifter Översikt och breddningskurs! 2 Introduktion Kvantmekanik
Fysik TFYA68 Föreläsning 11/14 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 38-39* (*) 38.1, 38.4, 39.1-3, 6 koncept enklare uppgifter Översikt och breddningskurs! 2 Introduktion Kvantmekanik
BFL102/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik mars :00 12:00. Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
 Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm BFL12/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik 2 22 mars 216 8: 12: Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm BFL12/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik 2 22 mars 216 8: 12: Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
Newtons 3:e lag: De par av krafter som uppstår tillsammans är av samma typ, men verkar på olika föremål.
 1 KOMIHÅG 8: --------------------------------- Hastighet: Cylinderkomponenter v = r e r + r" e " + z e z Naturliga komponenter v = ve t Acceleration: Cylinderkomponenter a = ( r " r# 2 )e r + ( r # + 2
1 KOMIHÅG 8: --------------------------------- Hastighet: Cylinderkomponenter v = r e r + r" e " + z e z Naturliga komponenter v = ve t Acceleration: Cylinderkomponenter a = ( r " r# 2 )e r + ( r # + 2
Tentamen Relativitetsteori , 22/8 2015
 KOD: Tentamen Relativitetsteori 9.00 14.00, 22/8 2015 Hjälpmedel: Miniräknare, linjal och bifogad formelsamling. Observera: Samtliga svar ska lämnas på dessa frågepapper. Det framgår ur respektive uppgift
KOD: Tentamen Relativitetsteori 9.00 14.00, 22/8 2015 Hjälpmedel: Miniräknare, linjal och bifogad formelsamling. Observera: Samtliga svar ska lämnas på dessa frågepapper. Det framgår ur respektive uppgift
ANDREAS REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se. Coulombs lag och Maxwells första ekvation
 ANDREA REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se oulombs lag och Maxwells första ekvation oulombs lag och Maxwells första ekvation Inledning Två punktladdningar q 1 samt q 2 i rymden
ANDREA REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se oulombs lag och Maxwells första ekvation oulombs lag och Maxwells första ekvation Inledning Två punktladdningar q 1 samt q 2 i rymden
BFL102/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik mars :00 12:00. Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
 Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm BFL102/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik 2 17 mars 2017 8:00 12:00 Tentamen består av 6 uppgifter som vardera kan ge upp till 4
Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm BFL102/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik 2 17 mars 2017 8:00 12:00 Tentamen består av 6 uppgifter som vardera kan ge upp till 4
Solen i dag.
 Solen i dag http://www.spaceweather.com/ The Regimes of Stellar Death for core remnants of different masses Core mass < 1.4 solar masses, Star core shrinks down to a white dwarf the size of the Earth.
Solen i dag http://www.spaceweather.com/ The Regimes of Stellar Death for core remnants of different masses Core mass < 1.4 solar masses, Star core shrinks down to a white dwarf the size of the Earth.
Relativitetsteorins grunder, våren 2016 Räkneövning 3 Lösningar
 Relativitetsteorins grunder, våren 2016 Räkneövning 3 Lösningar 1. Den ryska fysikern P.A. Čerenkov upptäckte att om en partikel rör sig snabbare än ljuset i ett medium, ger den ifrån sig ljus. Denna effekt
Relativitetsteorins grunder, våren 2016 Räkneövning 3 Lösningar 1. Den ryska fysikern P.A. Čerenkov upptäckte att om en partikel rör sig snabbare än ljuset i ett medium, ger den ifrån sig ljus. Denna effekt
Kapitel 7. Atomstruktur och periodicitet. Kvantmekanik Aufbau Periodiska systemet
 Avsnitt 7.1 Elektromagnetisk strålning Kapitel 7 Fyrverkeri i olika färger Atomstruktur och periodicitet Copyright Cengage Learning. All rights reserved 2 Illuminerad saltgurka Kapitel 7 Innehåll Kvantmekanik
Avsnitt 7.1 Elektromagnetisk strålning Kapitel 7 Fyrverkeri i olika färger Atomstruktur och periodicitet Copyright Cengage Learning. All rights reserved 2 Illuminerad saltgurka Kapitel 7 Innehåll Kvantmekanik
Tentamen Relativitetsteori , 27/7 2013
 KOD: Tentamen Relativitetsteori 9.00 14.00, 27/7 2013 Hjälpmedel: Miniräknare, linjal och bifogad formelsamling. Observera: Samtliga svar ska lämnas på dessa frågepapper. Det framgår ur respektive uppgift
KOD: Tentamen Relativitetsteori 9.00 14.00, 27/7 2013 Hjälpmedel: Miniräknare, linjal och bifogad formelsamling. Observera: Samtliga svar ska lämnas på dessa frågepapper. Det framgår ur respektive uppgift
Fysik TFYA86. Föreläsning 10/11
 Fysik TFYA86 Föreläsning 10/11 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 38-41* (*) 38.1, 38.4, 39.1-3, 6 40.1-4 (översikt) koncept enklare uppgifter Översikt och breddningskurs!
Fysik TFYA86 Föreläsning 10/11 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 38-41* (*) 38.1, 38.4, 39.1-3, 6 40.1-4 (översikt) koncept enklare uppgifter Översikt och breddningskurs!
Väteatomen. Matti Hotokka
 Väteatomen Matti Hotokka Väteatomen Atom nummer 1 i det periodiska systemet Därför har den En proton En elektron Isotoper är möjliga Protium har en proton i atomkärnan Deuterium har en proton och en neutron
Väteatomen Matti Hotokka Väteatomen Atom nummer 1 i det periodiska systemet Därför har den En proton En elektron Isotoper är möjliga Protium har en proton i atomkärnan Deuterium har en proton och en neutron
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 32 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik Kapitel 32 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Om den lagen (N2) är sann så är det också sant att: r " p = r " F (1)
 1 KOMIHÅG 12: --------------------------------- Den mekaniska energin, arbetet ---------------------------------- Föreläsning 13: FLER LAGAR-härledning ur N2 Momentlag Hur påverkas rörelsen av ett kraftmoment??
1 KOMIHÅG 12: --------------------------------- Den mekaniska energin, arbetet ---------------------------------- Föreläsning 13: FLER LAGAR-härledning ur N2 Momentlag Hur påverkas rörelsen av ett kraftmoment??
Einstein's Allmänna relativitetsteori. Einstein's komplexa Allmänna relativitetsteori förklaras så att ALLA kan förstå den
 Einstein's Allmänna relativitetsteori Einstein's komplexa Allmänna relativitetsteori förklaras så att ALLA kan förstå den Allmänna relativitetsteorin - Fakta Einsten presenterade teorin 10 år efter den
Einstein's Allmänna relativitetsteori Einstein's komplexa Allmänna relativitetsteori förklaras så att ALLA kan förstå den Allmänna relativitetsteorin - Fakta Einsten presenterade teorin 10 år efter den
Lösningar Heureka 2 Kapitel 14 Atomen
 Lösningar Heureka Kapitel 14 Atomen Andreas Josefsson Tullängsskolan Örebro Lo sningar Fysik Heureka Kapitel 14 14.1) a) Kulorna från A kan ramla på B, C, D, eller G (4 möjligheter). Från B kan de ramla
Lösningar Heureka Kapitel 14 Atomen Andreas Josefsson Tullängsskolan Örebro Lo sningar Fysik Heureka Kapitel 14 14.1) a) Kulorna från A kan ramla på B, C, D, eller G (4 möjligheter). Från B kan de ramla
The nature and propagation of light
 Ljus Emma Björk The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Ljus Emma Björk The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Kapitel 7. Atomstruktur och periodicitet
 Kapitel 7 Atomstruktur och periodicitet Avsnitt 7.1 Elektromagnetisk strålning Fyrverkeri i olika färger Copyright Cengage Learning. All rights reserved 2 Avsnitt 7.2 Materians karaktär Illuminerad saltgurka
Kapitel 7 Atomstruktur och periodicitet Avsnitt 7.1 Elektromagnetisk strålning Fyrverkeri i olika färger Copyright Cengage Learning. All rights reserved 2 Avsnitt 7.2 Materians karaktär Illuminerad saltgurka
Relativistisk kinematik Ulf Torkelsson. 1 Relativistisk rörelsemängd, kraft och energi
 Föreläsning 13/5 Relativistisk kinematik Ulf Torkelsson 1 Relativistisk rörelsemängd, kraft och energi Antag att en observatör O följer med en kropp i rörelse. Enligt observatören O så har O hastigheten
Föreläsning 13/5 Relativistisk kinematik Ulf Torkelsson 1 Relativistisk rörelsemängd, kraft och energi Antag att en observatör O följer med en kropp i rörelse. Enligt observatören O så har O hastigheten
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Fysik. Laboration 3. Ljusets vågnatur
 Fysik Laboration 3 Ljusets vågnatur Laborationens syfte: att hjälpa dig att förstå ljusfenomen diffraktion och interferens och att förstå hur olika typer av spektra uppstår Utförande: laborationen skall
Fysik Laboration 3 Ljusets vågnatur Laborationens syfte: att hjälpa dig att förstå ljusfenomen diffraktion och interferens och att förstå hur olika typer av spektra uppstår Utförande: laborationen skall
Alla bilder finns på kursens hemsida http://www.physto.se/~lbe/poeter.html
 Alla bilder finns på kursens hemsida http://www.physto.se/~lbe/poeter.html Fysik för poeter 2010 Professor Lars Bergström Fysikum, Stockholms universitet Vi ska börja med lite klassisk fysik. Galileo Galilei
Alla bilder finns på kursens hemsida http://www.physto.se/~lbe/poeter.html Fysik för poeter 2010 Professor Lars Bergström Fysikum, Stockholms universitet Vi ska börja med lite klassisk fysik. Galileo Galilei
Kapitel: 32 Elektromagnetiska vågor Maxwells ekvationer Hur accelererande laddningar kan ge EM-vågor
 Kapitel: 3 lektromagnetiska vågor Maxwells ekvationer Hur accelererande laddningar kan ge M-vågor genskaper hos M-vågor nergitransport i M-vågor Det elektromagnetiska spektrat Maxwell s ekvationer Kan
Kapitel: 3 lektromagnetiska vågor Maxwells ekvationer Hur accelererande laddningar kan ge M-vågor genskaper hos M-vågor nergitransport i M-vågor Det elektromagnetiska spektrat Maxwell s ekvationer Kan
= v! p + r! p = r! p, ty v och p är dt parallella. Definiera som en ny storhet: Rörelsemängdsmoment: H O
 1 KOMIHÅG 15: --------------------------------- Definitioner: Den potentiella energin, mekaniska energin Formulera: Energiprincipen ---------------------------------- Föreläsning 16: FLER LAGAR-härledning
1 KOMIHÅG 15: --------------------------------- Definitioner: Den potentiella energin, mekaniska energin Formulera: Energiprincipen ---------------------------------- Föreläsning 16: FLER LAGAR-härledning
MATEMATIK GU. LLMA60 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 2014. Block 5, översikt
 MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
Stephen Hawking. f. 1942
 Stephen Hawking Stephen Hawking har i sin forskning använt kvantmekanik och allmän relativitetsteori för att beskriva svarta hål och hela universum. Innehåll som anknyter till det finns i alla tre gymnasiekurser
Stephen Hawking Stephen Hawking har i sin forskning använt kvantmekanik och allmän relativitetsteori för att beskriva svarta hål och hela universum. Innehåll som anknyter till det finns i alla tre gymnasiekurser
Tentamen: Baskurs B i Fysik, del1, 4p 2007-03-23 kl. 08.00-13.00
 Institutionen för teknik, fysik och matematik Nils Olander och Herje Westman Tentamen: Baskurs B i Fysik, del1, 4p 2007-03-23 kl. 08.00-13.00 Max: 30 p A-uppgifterna 1-8 besvaras genom att ange det korrekta
Institutionen för teknik, fysik och matematik Nils Olander och Herje Westman Tentamen: Baskurs B i Fysik, del1, 4p 2007-03-23 kl. 08.00-13.00 Max: 30 p A-uppgifterna 1-8 besvaras genom att ange det korrekta
e 3 e 2 e 1 Kapitel 3 Vektorer i planet och i rummet precis ett sätt skrivas v = x 1 e 1 + x 2 e 2
 Kapitel 3 Vektorer i planet och i rummet B e 3 e 2 A e 1 C Figur 3.16 Vi har ritat de riktade sträckor som representerar e 1, e 2, e 3 och v och som har utgångspunkten A. Vidare har vi skuggat planet Π
Kapitel 3 Vektorer i planet och i rummet B e 3 e 2 A e 1 C Figur 3.16 Vi har ritat de riktade sträckor som representerar e 1, e 2, e 3 och v och som har utgångspunkten A. Vidare har vi skuggat planet Π
Fysiska institutionen april 1983 Hans Linusson, Carl-Axel Sjöblom, Örjan Skeppstedt januari 1993 FY 2400 april 1998 Distanskurs LEKTION 25.
 GÖTEBORGS UNIVERSITET Fysiska institutionen april 1983 Hans Linusson, Carl-Axel Sjöblom, Örjan Skeppstedt januari 1993 FY 2400 april 1998 Distanskurs LEKTION 25 Delkurs 4 KVANTMEKANIK: GRUNDER, TILLÄMPNINGAR
GÖTEBORGS UNIVERSITET Fysiska institutionen april 1983 Hans Linusson, Carl-Axel Sjöblom, Örjan Skeppstedt januari 1993 FY 2400 april 1998 Distanskurs LEKTION 25 Delkurs 4 KVANTMEKANIK: GRUNDER, TILLÄMPNINGAR
Tentamen, Kvantfysikens principer FK2003, 7,5 hp
 Tentamen, Kvantfysikens principer FK2003, 7,5 hp Tid: 17:00-22:00, tisdag 3/3 2015 Hjälpmedel: utdelad formelsamling, utdelad miniräknare Var noga med att förklara införda beteckningar och att motivera
Tentamen, Kvantfysikens principer FK2003, 7,5 hp Tid: 17:00-22:00, tisdag 3/3 2015 Hjälpmedel: utdelad formelsamling, utdelad miniräknare Var noga med att förklara införda beteckningar och att motivera
Lösningsförslag Inlämningsuppgift 1 elstatikens grunder
 Inst. för fysik och astronomi 017-11-08 1 Lösningsförslag Inlämningsuppgift 1 elstatikens grunder Elektromagnetism I, 5 hp, för ES och W (1FA514) höstterminen 017 (1.1) Laddningen q 1 7,0 10 6 C placeras
Inst. för fysik och astronomi 017-11-08 1 Lösningsförslag Inlämningsuppgift 1 elstatikens grunder Elektromagnetism I, 5 hp, för ES och W (1FA514) höstterminen 017 (1.1) Laddningen q 1 7,0 10 6 C placeras
Fysik (TFYA14) Fö 5 1. Fö 5
 Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
Mekanik Föreläsning 8
 Mekanik Föreläsning 8 CBGA02, FYGA03, FYGA07 Jens Fjelstad 2010 02 19 1 / 16 Repetition Polära koordinater (r, θ): ange punkter i R 2 m h a r: avståndet från origo (0, 0) θ: vinkeln mot positiva x axeln
Mekanik Föreläsning 8 CBGA02, FYGA03, FYGA07 Jens Fjelstad 2010 02 19 1 / 16 Repetition Polära koordinater (r, θ): ange punkter i R 2 m h a r: avståndet från origo (0, 0) θ: vinkeln mot positiva x axeln
GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin 2
 GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin Tid: Plats: Ansvarig: Hjälpmedel: Tisdag juni 009, kl 8 30 13 30 V-huset Lennart Sjögren,
GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin Tid: Plats: Ansvarig: Hjälpmedel: Tisdag juni 009, kl 8 30 13 30 V-huset Lennart Sjögren,
Innehåll. Fysik Relativitetsteori. fy8_modernfysik.notebook. December 12, Relativitetsteorin Ljusets dualism Materiens struktur Kärnfysik
 Fysik 8 Modern fysik Innehåll Relativitetsteorin Ljusets dualism Materiens struktur Kärnfysik 1. Relativitetsteori Speciella relativitetsteorin Allmänna relativitetsteorin Two Postulates Special Relativity
Fysik 8 Modern fysik Innehåll Relativitetsteorin Ljusets dualism Materiens struktur Kärnfysik 1. Relativitetsteori Speciella relativitetsteorin Allmänna relativitetsteorin Two Postulates Special Relativity
Fotoelektriska effekten
 Fotoelektriska effekten Bakgrund År 1887 upptäckte den tyska fysikern Heinrich Hertz att då man belyser ytan på en metallkropp med ultraviolett ljus avges elektriska laddningar från ytan. Noggrannare undersökningar
Fotoelektriska effekten Bakgrund År 1887 upptäckte den tyska fysikern Heinrich Hertz att då man belyser ytan på en metallkropp med ultraviolett ljus avges elektriska laddningar från ytan. Noggrannare undersökningar
FK Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 21 december 2016, kl 17:00-22:00
 FK2003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 21 december 2016, kl 17:00-22:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du
FK2003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 21 december 2016, kl 17:00-22:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du
BFL102/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik 2. 5 juni :00 12:00. Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
 Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm BFL02/TEN: Fysik 2 för basår (8 hp) Tentamen Fysik 2 5 juni 205 8:00 2:00 Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm BFL02/TEN: Fysik 2 för basår (8 hp) Tentamen Fysik 2 5 juni 205 8:00 2:00 Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
Vågfysik. Ljus: våg- och partikelbeteende
 Vågfysik Modern fysik & Materievågor Kap 25 (24 1:st ed.) Ljus: våg- och partikelbeteende Partiklar Lokaliserade Bestämd position & hastighet Kollision Vågor Icke-lokaliserade Korsar varandra Interferens
Vågfysik Modern fysik & Materievågor Kap 25 (24 1:st ed.) Ljus: våg- och partikelbeteende Partiklar Lokaliserade Bestämd position & hastighet Kollision Vågor Icke-lokaliserade Korsar varandra Interferens
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 14 Harmonisk oscillator 1 Vågrörelselära och optik 2 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator:
Vågrörelselära och optik Kapitel 14 Harmonisk oscillator 1 Vågrörelselära och optik 2 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator:
Rydbergs formel. Bohrs teori för väteliknande system
 Chalmers Tekniska Högskola och Göteborgs Universitet Sektionen för Fysik och Teknisk Fysik Arne Rosén, Halina Roth Uppdaterad av Erik Reimhult, januari A4 Enelektronspektrum Namn... Utförd den... Godkänd
Chalmers Tekniska Högskola och Göteborgs Universitet Sektionen för Fysik och Teknisk Fysik Arne Rosén, Halina Roth Uppdaterad av Erik Reimhult, januari A4 Enelektronspektrum Namn... Utförd den... Godkänd
Kaströrelse. 3,3 m. 1,1 m
 Kaströrelse 1. En liten kula, som vi kallar kula 1, släpps ifrån en höjd över marken. Exakt samtidigt skjuts kula 2 parallellt med marken ifrån samma höjd som kula 1. Luftmotståndet som verkar på kulorna
Kaströrelse 1. En liten kula, som vi kallar kula 1, släpps ifrån en höjd över marken. Exakt samtidigt skjuts kula 2 parallellt med marken ifrån samma höjd som kula 1. Luftmotståndet som verkar på kulorna
s 1 och s 2 är icke kvantmekaniska partiklar? e. (1p) Vad blir sannolikheterna i uppgifterna b, c och d om vinkeln = /2?
 FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 7e mars 018, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 7e mars 018, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
Einstein's svårbegripliga teori. Einstein's första relativitetsteori, den Speciella, förklaras så att ALLA kan förstå den
 Einstein's svårbegripliga teori Einstein's första relativitetsteori, den Speciella, förklaras så att ALLA kan förstå den Speciella relativitetsteorin, Allmänt Einsten presenterade teorin 1905 Teorin gäller
Einstein's svårbegripliga teori Einstein's första relativitetsteori, den Speciella, förklaras så att ALLA kan förstå den Speciella relativitetsteorin, Allmänt Einsten presenterade teorin 1905 Teorin gäller
Kosmologi. Ulf Torkelsson Teoretisk fysik CTH/GU
 Kosmologi Ulf Torkelsson Teoretisk fysik CTH/GU Program Universums expansion, observationer Universums expansion, teori Universums geometri Universums expansion och sammansättning Exotisk materia Andromedagalaxen
Kosmologi Ulf Torkelsson Teoretisk fysik CTH/GU Program Universums expansion, observationer Universums expansion, teori Universums geometri Universums expansion och sammansättning Exotisk materia Andromedagalaxen
Vågrörelselära & Kvantfysik, FK januari 2012
 Räkneövning 9 Vågrörelselära & Kvantfysik, FK00 9 januari 0 Problem 4.3 En elektron i vila accelereras av en potentialskillnad U = 0 V. Vad blir dess de Broglie-våglängd? Elektronen tillförs den kinetiska
Räkneövning 9 Vågrörelselära & Kvantfysik, FK00 9 januari 0 Problem 4.3 En elektron i vila accelereras av en potentialskillnad U = 0 V. Vad blir dess de Broglie-våglängd? Elektronen tillförs den kinetiska
4. Allmänt Elektromagnetiska vågor
 Det är ett välkänt faktum att det runt en ledare som det flyter en viss ström i bildas ett magnetiskt fält, där styrkan hos det magnetiska fältet beror på hur mycket ström som flyter i ledaren. Om strömmen
Det är ett välkänt faktum att det runt en ledare som det flyter en viss ström i bildas ett magnetiskt fält, där styrkan hos det magnetiska fältet beror på hur mycket ström som flyter i ledaren. Om strömmen
Einsteins relativitetsteori, enkelt förklarad. Einsteins första relativitetsteori, den Speciella, förklaras enkelt så att ALLA kan förstå den
 Einsteins relativitetsteori, enkelt förklarad Einsteins första relativitetsteori, den Speciella, förklaras enkelt så att ALLA kan förstå den Speciella relativitetsteorin, Allmänt Einstein presenterade
Einsteins relativitetsteori, enkelt förklarad Einsteins första relativitetsteori, den Speciella, förklaras enkelt så att ALLA kan förstå den Speciella relativitetsteorin, Allmänt Einstein presenterade
Svar och anvisningar
 170317 BFL10 1 Tenta 170317 Fysik : BFL10 Svar och anvisningar Uppgift 1 a) Den enda kraft som verkar på stenen är tyngdkraften, och den är riktad nedåt. Alltså är accelerationen riktad nedåt. b) Vid kaströrelse
170317 BFL10 1 Tenta 170317 Fysik : BFL10 Svar och anvisningar Uppgift 1 a) Den enda kraft som verkar på stenen är tyngdkraften, och den är riktad nedåt. Alltså är accelerationen riktad nedåt. b) Vid kaströrelse
Svarta håls existens är en förutsägelse av Einsteins allmänna relativitetsteori (Einsteinsk mekanik med gravitation), som generaliserar Newtonsk
 Svarta hål Svarta håls existens är en förutsägelse av Einsteins allmänna relativitetsteori (Einsteinsk mekanik med gravitation), som generaliserar Newtonsk mekanik (med gravitation). För att förstå svarta
Svarta hål Svarta håls existens är en förutsägelse av Einsteins allmänna relativitetsteori (Einsteinsk mekanik med gravitation), som generaliserar Newtonsk mekanik (med gravitation). För att förstå svarta
FAFA Föreläsning 7, läsvecka 3 13 november 2017
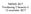 FAFA55 2017 Föreläsning 7, läsvecka 3 13 november 2017 Schrödingers ekvation kan tolkas som en ekvation som har sin utgångspunkt i A) konservering av rörelsemängd B) energikonservering C) Newtons andra
FAFA55 2017 Föreläsning 7, läsvecka 3 13 november 2017 Schrödingers ekvation kan tolkas som en ekvation som har sin utgångspunkt i A) konservering av rörelsemängd B) energikonservering C) Newtons andra
Strålningsfält och fotoner. Våren 2016
 Strålningsfält och fotoner Våren 2016 1. Fält i rymden Vi har lärt oss att beräkna elektriska fält utgående från laddningarna som orsakar dem Kan vi härleda nånting åt andra hållet? 2 1.1 Gauss lag Låt
Strålningsfält och fotoner Våren 2016 1. Fält i rymden Vi har lärt oss att beräkna elektriska fält utgående från laddningarna som orsakar dem Kan vi härleda nånting åt andra hållet? 2 1.1 Gauss lag Låt
F3: Schrödingers ekvationer
 F3: Schrödingers ekvationer Backgrund Vi behöver en ny matematik för att beskriva elektroner, atomer och molekyler! Den nya fysiken skall klara av att beskriva: Experiment visar att för bundna system så
F3: Schrödingers ekvationer Backgrund Vi behöver en ny matematik för att beskriva elektroner, atomer och molekyler! Den nya fysiken skall klara av att beskriva: Experiment visar att för bundna system så
Dugga i FUF040 Kvantfysik för F3/Kf3
 Dugga i FUF040 Kvantfysik för F3/Kf3 fredagen den 23 oktober 2015 kl 14.00-16.00 i V Examinator: Måns Henningson, ankn 3245. Inga hjälpmedel. Ringa in bokstaven svarande mot det unika rätta svaret på svarsblanketten!
Dugga i FUF040 Kvantfysik för F3/Kf3 fredagen den 23 oktober 2015 kl 14.00-16.00 i V Examinator: Måns Henningson, ankn 3245. Inga hjälpmedel. Ringa in bokstaven svarande mot det unika rätta svaret på svarsblanketten!
Förslag: En laddad partikel i ett magnetfält påverkas av kraften F = qvb, dvs B = F qv = 0.31 T.
 1. En elektron rör sig med v = 100 000 m/s i ett magnetfält. Den påverkas av en kraft F = 5 10 15 N vinkelrätt mot rörelseriktningen. Rita figur och beräkna den magnetiska flödestätheten. Förslag: En laddad
1. En elektron rör sig med v = 100 000 m/s i ett magnetfält. Den påverkas av en kraft F = 5 10 15 N vinkelrätt mot rörelseriktningen. Rita figur och beräkna den magnetiska flödestätheten. Förslag: En laddad
Strängar och extra dimensioner
 Strängar och extra dimensioner Världens vackraste ekvation? Rummet, rymden, är arenan där allt i universum utspelar sig. Tiden ger rörelse och dynamik. Av materia är vi alla uppbyggda. Men hur hänger allt
Strängar och extra dimensioner Världens vackraste ekvation? Rummet, rymden, är arenan där allt i universum utspelar sig. Tiden ger rörelse och dynamik. Av materia är vi alla uppbyggda. Men hur hänger allt
