Linjer och plan Låt ABCD vara en fyrhörning i planet. Om A väljs till origo och
|
|
|
- Isak Andreasson
- för 7 år sedan
- Visningar:
Transkript
1 Linjer oh plan Läs Sparr, avsn. 3. Många läroböker likställer koordinatsystem med rätvinkligt koordinatsystem, närmare bestämt: med ett ortonormerat system (ON-system). O:et står för ortogonal = rätvinklig, N:et för normerat, d.v.s.att enhet på axlarna svarar mot längdenhet i "verkligheten". Sparr visar att vissa saker 306. Låt ABCD vara en fyrhörning i planet. Om A väljs till origo oh AB oh AD till basvektorer, får C koordinaterna (2, 3). Vilka koordinater får A, om man till origo väljer C oh till basvektorer väljer CB oh CD? 307. Markera oh beskriv mängden av punkter vars koordinater (x, y) uppfyller y ange punkters lägen beskriva räta linjer oh plan bestämma skärningspunkter mellan linjer/plan beräkna förhållanden mellan längder går alldeles utmärkt att göra även med ett ike-on-system. Koordinatangivelserna nedan antas hänföra sig till givna parallellkoordinatsystem Oe x e y alt. Oe x e y e z. (Alltså ej nödvändigtvis rätvinkliga, såvida det inte sägs uttrykligen!) 30. Ange koordinaterna för mittpunkten på sträkan mellan (a) (, 0, 2) oh (, 2, 2) (b) (x,y,z ) oh (x 2,y 2,z 2 ) 302. Ange tyngdpunktens läge för en triangel med hörn i (x,y,z ), (x 2,y 2,z 2 ), (x 3,y 3,z 3 ) Låt O vara origo, A :(,, ), B :(6, 4, 4), oh låt P vara den punkt som delar sträkan AB i förhållandet 2:3, d.v.s. P ligger på sträkan AB oh AP PB = 2 3 Bestäm koordinaterna för den punkt Q som är sådan att OQ = OP En parallellogram har tre av sina hörn i (, 0), (, ) oh (2, 3). Var finns det fjärde hörnet? 30. En partikel startar i (, 2, 3) oh rör sig med konstant hastighet (alltså rätlinjigt oh med samma fart). Enminutefterstartbefinner den sig i (2, 0, 2). Var finns den 0 minuter efter start? 3 0 (a) x 2, y=3 (b) x 2 () 0 x, 0 y (d) x + y =,x,yheltal (e) x + y = (f) x 0, y 0, x+ y 308. Punkterna A :(a,a 2 ), B :(b,b 2 ) oh O :(0, 0) bildar en triangel i planet. Beskriv geometriskt punktmängderna s (a,a 2 )+t (b,b 2 ) som fås då man låter de reella talen s oh t genomlöpa mängden (a) s 2, t=3 (b) s 2 () 0 s, 0 t (d) s + t =,s,theltal (e) s + t = (f) s 0, t 0, s+ t x 27
2 Läs Sparr, avsn Ange en riktningsvektor för en linje med riktningskoeffiienten k relativt ett vanligt rätvinkligt koordinatsystem. 30. En rät linje med riktningsvektor v oh som går genom punkten med ortsvektor r 0 har parameterframställningen r = r 0 + tv, <t< (Tolkning: En punkt ligger på linjen omm 6 dess ortsvektor r kan skrivas på ovanstående sätt.) Ange analoga parameterframställningar för en (a) sträka AB, dels med vektorerna OA oh AB, dels med OA oh OB; (b) triangel ABC, inkl. dess inre, dels med vektorerna OA, AB, oh AC, dels med vektorerna OA, OB, oh OC; () parallellogram ABCD, inkl. dess inre (AC oh BD diagonaler), dels med vektorerna OA, AB, oh AD dels med vektorerna OA, OB, OB oh OD. (d) parallellepiped ABCDEF GH (övn. 203), med vektorerna OA, AB, oh AD oh AE; (e) tetraeder ABCD (inkl. dess inre), med vektorerna OA, OB, OC oh OD. 3. Visa att tre punkter P,P 2 oh P 3 ligger på rät linje då oh endast då det finns tre tal λ,λ 2 oh λ 3, ej alla =0, men med summan λ + λ 2 + λ 3 =0, sådana att λ OP + λ 2OP2 + λ 3OP3 = 0 för alla punkter O. 32. Bestäm skärningen mellan planet 2x + y z =oh linjen x = t y = 3t z = 2 + t 33. Bestäm en ekvation för skärningslinjen mellan planen 3x 2y +2z =2oh 2x +2y z =. 34. Linjen ½ x + y + z = : 2x +3y +2z =0 projieras på planet 3x y +2z =4genom parallellprojektion med riktningen (,, ). Ange en ekvation för bildlinjen. 6 omm =omohendastom dåå = då oh endast då (är synonymer) 3. Ett flygplan kör rätlinjigt från (, 2, 3) till (, 6, 9). Dess koordinater som funktioner av tiden t är x =+2t y =2+2t z =3+3t, 0 t 2 Ett annat flygplan färdas enligt x =+t y =8 2t, 0 t 3 z = 3t Visa att (3, 4, 6) ligger på båda rutterna. Kolliderar planen? 36. Linjen går genom punkten (3,, ) oh skär de två linjerna ½ ½ x = x = : oh y = 2 : z = Bestäm en ekvation för linjen. 37. Undersök om det finns en rät linje som går genom punkten (,, 2) oh skär de båda linjerna. x = 2 + t y = 2t z = 2 + t oh x = + t y = 3 + t z = 4 + t Om ja: ange en ekvation för linjen på parameterform samt skärningspunkterna. 38. Bestäm ekvationen för en rät linje som går genom punkten (p, q, r) oh skär de räta linjerna y = z =0oh x = z =0. I vilket fall är den sökta linjen entydigt bestämd? 39. Två linjer har ekvationerna : (x, y, z) =(+t, +2t, +3t) 2 : (x, y, z) =(t, 2+t, b 2t) (a) Bestäm talet b så att linjerna skär varandra. (b) Ange för detta värde på b ekvationen på parameterform för det plan som innehåller de båda linjerna. 28
3 320. I ett plan har man lagt ett koordinatsystem Oe e 2, vars basvektorer har längden, men vinkeln mellan dem är 60. Bestäm en ekvation för linjen genom origo som är vinkelrät mot e Låt ABCDEF GH vara en godtyklig parallellepiped H 32. I ett plan med koordinatsystem Oe e 2 införsettnyttkoordinatsystemobe be 2 genom ½ be =3e +2e 2 be 2 = e +6e 2 (a) Punkten P har koordinaterna (2, ) relativt Oe e 2. Ange dess koordinater relativt Obe be 2 A E D F C G (b) Linjen har ekvationen bx + bx 2 = 0 relativt Obe be 2. Ange dess ekvation i Oe e 2 -systemet. B 322. I ett visst (ej nödvändigtvis ortonormerat) koordinatsystem Oe e 2 iplanetär punkterna P :(, 0) oh Q :(0, 2), samt den räta linjen :2x + y +4=0givna. EttnyttkoordinatsystemO 0 e 0 e 0 2 väljs genom O 0 = P, e 0 = OP oh e 0 2 = PQ. Ange en ekvation för i koord.systemet O 0 e 0 e Låt P :(0,, 2),P 2 :(,, ),P 3 :(a, 2, ) (a) Visa att för varje a bestämmer punkterna P,P 2,P 3 ett plan π a oh ange detta plans ekvation på affin form. (b) Bestäm a så att linjen Vi tänker oss ett plan genom mittpunkten på AE, mittpunkten på BC samt D. Detta plan skär rymddiagonalen AG i punkten P. Beräkna längdförhållandet AP : PG. 32. Fyra personer simmar i en stor vik, var oh en i sin egen jämna takt, var oh en längs sin egen räta linje. Inga två av de räta linjerna är parallella oh inga tre skär varandra. Nu råkar det bli så att simmare stöter på vägen med såväl simmare 2, 3 som 4, oh likaså simmare 2 stöter ihop med, förutom, även 3 oh4.visaattäven3oh4träffas! (x, y, z) =(7, 3, ) + t (, 2, 3) blir parallell med π a. Affin geometri metrisk geometri Geometrin i Sparr, kap.2 & 3 har, om du tänker efter, inte berört längder oh vinklar (s.k. metrisk geometri), utan har handlat om parallellitet, inidens (skärningar) oh delningsförhållanden affina problem / affin geometri, säger man ibland. Först i Sparr, kap.4 går vi in på huvudverktyget för metriska problem skalärprodukt. 29
4 ON oh ike-on-system. Alternativ med normal oh vektorprodukt Följande sidor handlar om hur vissa problem om linjer oh plan, som Sparr tar upp i kap.3, p.g.a. att deras lösning inte beror på om koordinatsystemet är ON eller inte, kan lösas m. h.a. skalärprodukt oh vektorprodukt, som gås igenom i kap.4&. Följaktigen kan dessa sidor med fördel sparas till efter att du gått igenom skalär- oh vektorprodukt. Nedan följer dok en sammanfattning av de resultat man behöver. Det anmärkningsvärda är att, fastän resonemang oh formler förutsätter ett ON-koord.system (för vektorprodukt till oh med litet mer än så), fås korrekta resultat även för snedvinkliga koord.system! Planets ekvation: rekapitulation Sparr, kap.3 härleder ekvationer för plan oh räta linjer relativt ett godtykligt koordinatsystem vinklarna mellan koord.axlarna behöver inte vara räta! Man kommer fram till att varje plan kan beskrivas som mängden av punkter vars koordinater (x, y, z) satisfierar ett samband av typ Ax + By + Cz = D, där A, B, C, D fixa konstanter A, B, C ej alla 0 Oh omvänt: varje sådan ekvation definierar ett plan. (Oavsett hur snett koordinataxlarna ligger.) Normal till ett plan Sparr, kap.4 visar att, i ett ON-koordinatsystem, pekar vektorn (A, B, C) vinkelrätt mot planet i fråga: (A, B, C) ger planets normalriktning Anm. Med riktning avses i detta sammanhang egentligen en oriktad linje/axel: t.ex. (, 0) oh (, 0) sägs definiera samma riktning! Alla vektorer 6= 0, som är sinsemellan parallella, d.v.s. som skiljer sig på en skalär faktor (som får vara negativ) sägs ge en oh samma riktning! (Man säger ofta planets normalvektor, fast det inte är fråga om någon entydigt bestämd vektor!) Skalärprodukt oh ortogonalitet Två vektorer, vars koordinater relativt ett ON-system är(a, b, ) resp. (x, y, z), är vinkelräta (=ortogonala) om oh endast om den s.k. skalärprodukten (a, b, ) (x, y, z) =ax + by + z =0 Vektorprodukt I Sparr, kap. introdueras vektorprodukten, som till två givna vektorer ordnar en tredje som är vinkelrät mot båda de givna. Om koordinatsystemet är ortonormerat oh dessutom högerorienterat, s.k.hon-system (du behöver inte bekymra dig nu om vad det är det förklaras tydligt av Sparr, avsn..) fås vektorproduktens koordinater på följande sätt a b x y = z bz y x az ay bx Hur vektorprodukt beräknas är nu inte det intressanta det är lätt att programmera en maskin att utföra det studera i lösningarna nedan hur dess ovannämnda egenskap kan användas! Minnesregel för beräkning av vektorprodukt (För den som ändå är nyfiken.) Varje komponent fås som en determinant (jfr. sid.9): bz y = b y z x az = z a x ay bx = a x b y För att få första komponentens determinant, stryk faktorernas första komponenter: a b x µ µ y b y z b z För att få andra komponentens determinant, skifta faktorernas komponenter ykliskt ett steg oh gör sedan på samma sätt : a b x y z b a y z x a För den tredje komponenten, skifta en gång till. Sparr, kap. ställer upp vektorerna radvis 7 : (a, b, ) (x, y, z) = b µ y z, z a x, a x y z z x b y 7 Härärdetkolonnerinteminstavdatortekniskaskäl:-) 30
5 Från parameterform till affin form Vektorprodukten kan användas t.ex. för att gå över från parameterform-ekvationen för ett plan x = x 0 + sa + tα y = y 0 + sb + tβ z = z 0 + s + tγ till den parameterfria (affina) formen Ax + By + Cz = D, s,t R på följande sätt: Planet spänns upp av vektorerna (a, b, ) oh (α, β, γ). Dess normalriktning är den entydigt bestämda riktning som är vinkelrät mot båda dessa, oh vektorprodukten ger just den riktningen. Så A B C = a b α β γ oh sedan återstår att bestämma D, så att (x 0,y 0,z 0 ) uppfyller ekvationen: D = Ax 0 + By 0 + Cz 0 =... Om koordinatsystemet inte är ortonormerat? Då är (A, B, C) från Ax + By + Cz = D i allmänhet inte normalvektor till planet oh vektorprodukt kan inte heller beräknas med determinantformeln". Men ovanstående metod att gå över från parameterform till affin form fungerar ändå! (Illustreras av 326 nedan.) Hur kan det komma sig? Linjära ekvationssystem har samma lösning, oavsett om variablerna står för koordinater relativt ett ON-system eller ett snedvinkligt system. Första lösningen till 326 nedan visar att problemet kan redueras till en fråga om ett linjärt ekvationssystem. Svaret på denna fråga måste bli detsamma, oavsett om de inblandade talen är koordinater relativt ett ON- eller ett snedvinkligt system. Den metod som löser frågan för ett ON-system måste fungera även för alla andra system! Uppgifterna med lösningar på de följande sidorna är alla exempel på fall, där räkning som ytligt betraktat förutsätter ON-system, ändå ger korrekt resultat för alla koordinatsystem! 326. Vilket samband skall råda mellan x, y oh z för att punkten (x, y, z) skall ligga i planet x =+s t y =2+s + t z =3 s +2t Lösning m.h.a. ekvationssystem (Sparr, kap.3) : Frågan är: För vilka x, y, z finns s oh t sådana att de tre likheterna blir sanna? Med andra ord: Om ovanstående betraktas som ett ekvationssystem, där x, y, z är givna, medan s oh t söks, så för vilka x, y, z.har då detta system lösningar? Det kan vi undersöka med suessiv elimination: Skriv om systemet på standardform: s t = x s + t = y 2 s +2t = z 3 x y 2 2 z 3 x 0 2 (y 2) (x ) 0 (z 3) + (x ) Byt rader 2 oh 3, så slipper vi division med 2 x 0 (z 3) + (x ) 0 2 (y 2) (x ) x 0 (z 3) + (x ) 0 0 (y 2) 3(x ) 2(z 3) Härav syns att lösningar finns om oh endast om (y 2) 3(x ) 2(z 3) = 0 y 3x 2z +7 = 0 3x y +2z = 7 Lösning m.h.a. vektorprodukt: Planet spänns upp av (,, ) oh (,, 2). Taltrippeln (A, B, C) i Ax + By + Cz = D kan vi få med vektorprodukt: = 3 2 2? En punkt i planet ser vi direkt: (, 2, 3). Alltså är planets ekvation 3x y +2z =
6 327. Skriv på formen ax + by + z = d ekv. för planet (a) (b) () (d) x = + s + t y = s + 2t z = s t x = + s t y = 2s t z = + s + 2t x = + s t y = 2 s z = + 2s + t x = + s y = z = 3 + t Lösning med vektorprodukt som i föregående: (Gausseliminationvarianten är väl omständligare.) a) 2 = Planets ekv.: x 2y 3z = b) 2 = 2 Planets ekv.: x 3y + z = ) 2 0 = Planets ekv.: 2y + z =2 2 d) = Planets ekv.: y = I övning 32 fik vi att linjen oh planet inte hade någon skärningspunkt. Hur kan man se detta m.h.a. skalärprodukt? ingen skärningspunkt linjen är parallell med planet oh innehåller en punkt utanför planet (För en linje som är parallell med ett plan finns två alternativ: alla eller ingen av linjens punkter tillhör planet!) Vidare ( står för "är vinkelrät mot") : linjen är parallell med planet linjens riktning planets normal Nu tänker vi oss att koord.systemet är ON: normalvektor till planet är (2,, ) u v u v =0 (, 3, ) (2,, ) = 2+3 =0 Att linjen innehåller en punkt utanför planet syns lätt: (, 0, 2) är den punkt på linjen som t = 0 ger, = 6= Ange ekvationen på parameterform för den linje som går genom punkten (2, 2, ), skär linjen (x, y, z) =(, 2, 0) + t (, 3, ) oh är parallell med planet x + y +7z =2. Lösning: Betekna den sökta linjen med, dengivnamedm. Återstår att hitta en riktningsvektor för. Låt s vara det värde på t i ekv. för m, som svarar mot skärningspunkten mellan linjerna. En riktningsvektor är då v = (, 2, 0) + s (, 3, ) (2, 2, ) = = (s 3, 3s, s ) Att är parallell med ett visst plan är ekvivalent med att v är vinkelrät mot planets normal: (s 3, 3s, s ) (,, 7) = 0 s 0 = 0 s = 2 Svar: (x, y, z) =(2, 2, ) + t (, 6, ) 32
7 330. Avgör vilka av vektorerna (, 2, 0), (,, ), (2,, 3) oh (2,, 3) som är parallella med planet 2x y + z +3=0. Lösning med skalärprodukt: Kontrollera vilka vektorer som är ortogonala mot planets normal. Ifall av ON-system kan detta göras så här: (, 2, 0) (2,, ) = 0 ja (,, ) (2,, ) = 2 nej (2,, 3) (2,, ) = 6 nej (2,, 3) (2,, ) = 0 ja Men varför skulle detta ge korrekt resultat även ifall av ike-on-system? Jo, problemet kan redueras till en fråga om ett linjärt ekvationssystem: Om en given vektor kan skrivas som en linjärkombination av två andra givna vektorer (två som spänner upp planet i fråga). Svaret på en sådan fråga är oberoende av om vektorernas koordinater hänför sig till ett ON- eller ett snedvinkligt koordinatsystem! En konkretare förklaring är okså möjlig: Lösning utan skalärprodukt: En vektor (u, v, w) är parallell med planet om oh endast om (förkortas omm) den kan skrivas som differensen mellan ortsvektorerna för två punkter i planet, d.v.s. omm u v = w där x y z x 2 y 2 z 2 ½ 2x y + z +3=0 2x 2 y 2 + z 2 +3=0 Subtraherar vi andra ekv. från första, så får vi 2(x x 2 ) (y y 2 )+(z z 2 )=0 33. Två linjer har ekvationerna (x, y, z) = (+t, +2t, +3t), t R resp. (x, y, z) = (t, 2+t, b 2t), t R (a) Bestäm b så att linjerna skär varandra. (b) Bestäm för detta b en ekvation för det plan som innehåller båda linjerna. Lösning: a) +t = s +2t =2+s +3t = b 2s +t = s +2t =2++t +3t = b 2(+t) +t = s t =2 3 = b Svar: b =3 b) Planets normalriktning bestäms av att den skall vara ortogonal mot båda linjerna : 2 = Från a) hämtar vi skärningspunkten mellan linjerna: +t +2t med t =2 +3t Planets ekvation blir 7x +y z = x y + z = 3 oh vänsterledet är identiskt med skalärprodukten av normalen (2,, ) oh (u, v, w). 33
8 332. För planen 3x 2y + z =6oh x + y 2z =8 samt linjen (x, y, z) =(,, ) + t (,, ) (a) visa att de har en punkt gemensam oh beräkna denna punkts koordinater, (b) ange, på formen ax+by +z = d, ekvationen för det plan som innehåller skärningslinjen mellan de givna planen samt den givna linjen. Lösning a) Skärningspunkten mellan linjen oh (t.ex.) det andra planet fås ur lösningen till x + y 2z =8 x =+t y =+t z = t ( + t)+(+t) 2( t) =8 x =+t y =+t z = t t = 2,x= 7 2, y = 3 2,z= 3 2 Punkten 7 2, 3 2, 3 2 ligger även i det första planet, ty µ 3 =6 2 Lösning b), variant omständlig: Skärn. linjen mellan planen: ½ x + y 2z =8 3x 2y + z =6 ½ x + y 2z =8 y +7z = 8 x =22/+3t y =8/+7t z = t, t R Omvandling till parameterfri form : z +3/2 7 y 3/2 3 x 7/2 z +3/2 0 2 (y 3/2) + (z +3/2) 0 28 (x 7/2) + (z +3/2) z +3/2 0 2 y + z 0 0 (x +z +4) 28 2 (y + z) Ekv.systemet för s oh t har alltså lösning dåå (x +z +4) 7 (y + z) 3 = 0 3x +z +2 7y 7z = 0 3x 7y +8z = 2 Alternativlösning till b) m.h.a. vektorprodukt: När vi redan har en punkt på planet (från a) behöver vi endast planets normalvektor. Skärningslinjen mellan planen har riktningen (måste vara ortogonal mot båda planens normaler) 3 2 = Det sökta planet skall som normal ha en vektor som är vinkelrät mot såväl (3, 7, ) som (,, ), alltså en vektor parallell med 3 7 = 2 28 k Därmed planets ekvation : 3x 7y +8z = µ x 7y +8z = 2 (z =t iställetförz = t, för färre bråk) Det sökta planet spänns alltså upp av oh 3 7 oh går genom (7/2, 3/2, 3/2). Dess ekv. på parameterform x =7/2+s +3t y =3/2+s +7t z = 3/2 s +t 34
9 333. Ange ekvationen för den räta linje som är parallell med planet x 2y z =, skär skärningslinjen s mellan planen x + y + z =2oh x + y +3z =, samt går genom punkten (0,, ). Lösning m.h.a. skalärprodukt: Om (a, b, ) beteknar :s skärningspunkt med s, så är problemet att lösa ekvationssystemet a + b + =2 a b a + b +3 = 0 2 (Det tredje villkoret kommer sig av att en linje är parallell med ett plan linjens riktn.vektor planets normal.) a + b + =2 a + b +3 = a 2b = a =/2 b =0 =3/2 Alltså, linjens riktning: a b 0 oh linjens ekvation: x y = 0 z = + t /2 /2 2 = Alternativ lösning till 34 m.h.a. vektorprodukt: Linjen tillsammans med projektionsstrålarna bildar ett plan, kalla det Π. Bildlinjen är skärningen mellan Π oh planet 3x y +2z =4. Linjen har riktningsvektor 2 3 = 0 2 Normal till Π är 0 = 2 En riktningsvektor till bildlinjen är 2 3 = 3 2 Återstår att hitta en punkt på bildlinjen. En sådan är :s skärning med planet vi projierar på: y = 2 z =7 x = 4 Bildlinjens ekvation: x y = 4 2 z 7 + t 3 Detta är ekvivalent med svaret till 34, eftersom 2 4 =
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer III Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer III Innehåll
Linjer och plan (lösningar)
 Linjer och plan (lösningar) 0. Enligt mittpunktsformeln (med O i just origo) OM = ³ OA + OB a) b) ((, 0, ) + (,, )) = (0,, ) µ +, +, z + z 0. Enligt tngdpunktsformeln (med O i just origo) ³ OA + OB + OC
Linjer och plan (lösningar) 0. Enligt mittpunktsformeln (med O i just origo) OM = ³ OA + OB a) b) ((, 0, ) + (,, )) = (0,, ) µ +, +, z + z 0. Enligt tngdpunktsformeln (med O i just origo) ³ OA + OB + OC
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer I Innehåll
Lösningar till utvalda uppgifter i kapitel 1
 Lösningar till utvalda uppgifter i kapitel. Vi utnyttjar definitionen av skalärprodukt som ger att u v u v, där α är (minsta) vinkeln mellan u v. I vårt fall så får vi 7 =. Alltså är den sökta vinkeln
Lösningar till utvalda uppgifter i kapitel. Vi utnyttjar definitionen av skalärprodukt som ger att u v u v, där α är (minsta) vinkeln mellan u v. I vårt fall så får vi 7 =. Alltså är den sökta vinkeln
Vektorer. Vektoriella storheter skiljer sig på ett fundamentalt sätt från skalära genom att de förutom storlek också har riktning.
 Vektorer. 3 / 18 Vektorer är ett mycket viktigt och användbart verktyg för att kunna beskriva sammanhang som innehåller riktade storheter, t.ex. kraft och hastighet. Vektoriella storheter skiljer sig på
Vektorer. 3 / 18 Vektorer är ett mycket viktigt och användbart verktyg för att kunna beskriva sammanhang som innehåller riktade storheter, t.ex. kraft och hastighet. Vektoriella storheter skiljer sig på
Vektorgeometri. En vektor v kan representeras genom pilar från en fotpunkt A till en spets B.
 Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
===================================================
 AVSTÅNDSBERÄKNING ( I ETT TREDIMENSIONELLT ORTONORMERAT KOORDINATSYSTEM ) Avståndet mellan två punkter Låt A ( x1, och B ( x, y, z) vara två punkter i rummet Avståndet d mellan A och B är d AB ( x z x1)
AVSTÅNDSBERÄKNING ( I ETT TREDIMENSIONELLT ORTONORMERAT KOORDINATSYSTEM ) Avståndet mellan två punkter Låt A ( x1, och B ( x, y, z) vara två punkter i rummet Avståndet d mellan A och B är d AB ( x z x1)
Räta linjer i 3D-rummet: Låt L vara den räta linjen genom som är parallell med
 RÄTA LINJER OCH PLAN Räta linjer i 3D-rummet: Låt L vara den räta linjen genom punkten P = ( x, y, som är parallell med vektorn v = v, v, v ) 0. ( 3 P Räta linjens ekvation på parameterform kan man ange
RÄTA LINJER OCH PLAN Räta linjer i 3D-rummet: Låt L vara den räta linjen genom punkten P = ( x, y, som är parallell med vektorn v = v, v, v ) 0. ( 3 P Räta linjens ekvation på parameterform kan man ange
Eftersom ON-koordinatsystem förutsätts så ges vektorernas volymprodukt av:
 MATA15 Algebra, delprov, 6 hp Lördagen den 8:e december 01 Skrivtid: 800 100 Matematikcentrum Matematik NF Lösningsförslag 1 Ligger punkterna P 1 = (0, 1, 1), P = (1,, 0), P = (, 1, 1) och P 4 = (, 6,
MATA15 Algebra, delprov, 6 hp Lördagen den 8:e december 01 Skrivtid: 800 100 Matematikcentrum Matematik NF Lösningsförslag 1 Ligger punkterna P 1 = (0, 1, 1), P = (1,, 0), P = (, 1, 1) och P 4 = (, 6,
Explorativ övning Vektorer
 Eplorativ övning Vektorer Syftet med denna övning är att ge grundläggande kunskaper om vektorräkning och dess användning i geometrin Liksom många matematiska begrepp kommer vektorbegreppet från fysiken
Eplorativ övning Vektorer Syftet med denna övning är att ge grundläggande kunskaper om vektorräkning och dess användning i geometrin Liksom många matematiska begrepp kommer vektorbegreppet från fysiken
Linjen P Q tangerar cirkeln i P och enligt en sats i geometrin är OP vinkelrät. tan u = OP. tan(180 v) = RS. cos v = sin v = tan v, tan v = RS.
 Lösningar till några övningar i Kap 1 i Vektorgeometri 17. I figuren är u en spetsig vinkel som vi har markerat i enhetscirkeln. Linjen P Q tangerar cirkeln i P och enligt en sats i geometrin är OP vinkelrät
Lösningar till några övningar i Kap 1 i Vektorgeometri 17. I figuren är u en spetsig vinkel som vi har markerat i enhetscirkeln. Linjen P Q tangerar cirkeln i P och enligt en sats i geometrin är OP vinkelrät
1 Vektorer i koordinatsystem
 1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
. b. x + 2 y 3 z = 1 3 x y + 2 z = a x 5 y + 8 z = 1 lösning?
 Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Vektorgeometri. En inledning Hasse Carlsson
 Vektorgeometri En inledning Hasse Carlsson Matematiska institutionen Göteborgs universitet och Chalmers tekniska högskola Version 01 Innehåll 1 Inledning Geometriska vektorer.1 Definition av vektorer........................
Vektorgeometri En inledning Hasse Carlsson Matematiska institutionen Göteborgs universitet och Chalmers tekniska högskola Version 01 Innehåll 1 Inledning Geometriska vektorer.1 Definition av vektorer........................
Tentamen 1 i Matematik 1, HF okt 2018, Skrivtid: 14:00-18:00 Examinator: Armin Halilovic
 Tentamen i Matematik, HF9 4 okt 8, Skrivtid: 4:-8: Examinator: Armin Halilovic För godkänt betyg krävs av max 4 poäng Betygsgränser: För betyg A, B, C, D, E krävs, 9, 6, respektive poäng Komplettering:
Tentamen i Matematik, HF9 4 okt 8, Skrivtid: 4:-8: Examinator: Armin Halilovic För godkänt betyg krävs av max 4 poäng Betygsgränser: För betyg A, B, C, D, E krävs, 9, 6, respektive poäng Komplettering:
Veckoblad 1, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Studiehandledning till. MAA123 Grundläggande vektoralgebra
 Studiehandledning till MAA13 Grundläggande vektoralgebra vid kurstillfället i period 4 läsåret 013/14 Version 014-05- Information om kursen MAA13 Avsikt Avsikten med kursen MAA13 Grundläggande vektoralgebra
Studiehandledning till MAA13 Grundläggande vektoralgebra vid kurstillfället i period 4 läsåret 013/14 Version 014-05- Information om kursen MAA13 Avsikt Avsikten med kursen MAA13 Grundläggande vektoralgebra
kan vi uttrycka med a, b och c. Avsnitt 2, Vektorer SA + AB = SB AB = SB SA = b a, Vi ritar först en figur av hur pyramiden måste se ut.
 vsnitt 2, Vektorer kan vi uttrycka med a, b och c. W109 är basytan (en kvadrat) i en regelbunden fyrsidig pyramid med spetsen. Låt = a, = b och = c. eräkna. Vi ritar först en figur av hur pyramiden måste
vsnitt 2, Vektorer kan vi uttrycka med a, b och c. W109 är basytan (en kvadrat) i en regelbunden fyrsidig pyramid med spetsen. Låt = a, = b och = c. eräkna. Vi ritar först en figur av hur pyramiden måste
= ( 1) ( 1) = 4 0.
 MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
October 9, Innehållsregister
 October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
Där a = (1, 2,0), b = (1, 1,2) och c = (0,3, 1) Problem 10. Vilket är det enda värdet hos x för vilket det finns a och b så att
 Här följer 3 problem att lösa. Längre bak i dokumentet finns utförliga penna-papper lösningar. Filen Föreläsning08.zip finns motsvarande lösningar utförda med Mathematica. Problem 1. Bestäm a så att avståndet
Här följer 3 problem att lösa. Längre bak i dokumentet finns utförliga penna-papper lösningar. Filen Föreläsning08.zip finns motsvarande lösningar utförda med Mathematica. Problem 1. Bestäm a så att avståndet
{ 1, om i = j, e i e j = 0, om i j.
 34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
Moment 4.11 Viktiga exempel 4.32, 4.33 Övningsuppgifter Ö4.18-Ö4.22, Ö4.30-Ö4.34. Planet Ett plan i rummet är bestämt då
 Moment 4.11 Viktiga exempel 4.32, 4.33 Övningsuppgifter Ö4.18-Ö4.22, Ö4.30-Ö4.34 Planet Ett plan i rummet är bestämt då två icke parallella riktningar, v 1 och v 2, och en punkt P 1 i planet är givna.
Moment 4.11 Viktiga exempel 4.32, 4.33 Övningsuppgifter Ö4.18-Ö4.22, Ö4.30-Ö4.34 Planet Ett plan i rummet är bestämt då två icke parallella riktningar, v 1 och v 2, och en punkt P 1 i planet är givna.
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
2+t = 4+s t = 2+s 2 t = s
 Extra 1. Ta fram räta linjens ekvation på parameterform då linjen går genom punkterna (1, 1,0) och (2,0,1) (3, 1,4) och ( 1,1,6) (4,3, 1) och (7, 2,5) (11,3, 6) och (9, 1,3) Lösning: (x,y,z) = (1+t, 1+t,t)
Extra 1. Ta fram räta linjens ekvation på parameterform då linjen går genom punkterna (1, 1,0) och (2,0,1) (3, 1,4) och ( 1,1,6) (4,3, 1) och (7, 2,5) (11,3, 6) och (9, 1,3) Lösning: (x,y,z) = (1+t, 1+t,t)
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. t 2
 SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
Vektorgeometri och funktionslära
 Vektorgeometri och funktionslära Xantcha 009 Del A: Beräkningsdel Räkningar behöver inte redovisas. Samtliga uppgifter måste vara korrekta om tentamen skall godkännas (möjligen kan något slarvfel tolereras),
Vektorgeometri och funktionslära Xantcha 009 Del A: Beräkningsdel Räkningar behöver inte redovisas. Samtliga uppgifter måste vara korrekta om tentamen skall godkännas (möjligen kan något slarvfel tolereras),
Moment 4.2.1, 4.2.2, 4.2.3, Viktiga exempel 4.1, 4.3, 4.4, 4.5, 4.6, 4.13, 4.14 Övningsuppgifter 4.1 a-h, 4.2, 4.3, 4.4, 4.5, 4.
 Moment 4.2.1, 4.2.2, 4.2., 4.2.4 Viktiga exempel 4.1, 4., 4.4, 4.5, 4.6, 4.1, 4.14 Övningsuppgifter 4.1 a-h, 4.2, 4., 4.4, 4.5, 4.7 Många av de objekt man arbetar med i matematiken och naturvetenskapen
Moment 4.2.1, 4.2.2, 4.2., 4.2.4 Viktiga exempel 4.1, 4., 4.4, 4.5, 4.6, 4.1, 4.14 Övningsuppgifter 4.1 a-h, 4.2, 4., 4.4, 4.5, 4.7 Många av de objekt man arbetar med i matematiken och naturvetenskapen
1.1 Skriv följande vektorsummor som en vektor (a) AB + BC (b) BC + CD + DA.
 Övningsuppgifter i anslutning till Kapitel. Skriv följande vektorsummor som en vektor a AB + BC b BC + CD + DA..2 Sök i nedanstående figur de vektorer som har samma längd och samma riktning som vektorn
Övningsuppgifter i anslutning till Kapitel. Skriv följande vektorsummor som en vektor a AB + BC b BC + CD + DA..2 Sök i nedanstående figur de vektorer som har samma längd och samma riktning som vektorn
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2016-05-10 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 2016-05-10 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
z = 4 + 3t P R = (5 + 2t, 4 + 2t, 4 + 3t) (1, 1, 3) = (4 + 2t, 3 + 2t, 1 + 3t)
 Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
Datum: 24 okt Betygsgränser: För. finns på. Skriv endast på en. omslaget) Denna. Uppgift. Uppgift Beräkna. Uppgift Låt z. Var god. vänd.
 Tentamen i Linjär algebra, HF94 Datum: 4 okt 8 Skrivtid: 4:-8: Lärare: Marina Arakelyan, Elias Said Examinator: Armin Halilovic För godkänt betyg krävs av max 4 poäng Betygsgränser: För betyg A, B, C,
Tentamen i Linjär algebra, HF94 Datum: 4 okt 8 Skrivtid: 4:-8: Lärare: Marina Arakelyan, Elias Said Examinator: Armin Halilovic För godkänt betyg krävs av max 4 poäng Betygsgränser: För betyg A, B, C,
VEKTORGEOMETRI. Christian Gottlieb
 VEKTORGEOMETRI Christian Gottlieb Matematiska institutionen Stockholms universitet 2:a upplagan 2001 2014 Förord Detta kompendium har sedan några år använts i utbildningen av grundskolelärare i matematik
VEKTORGEOMETRI Christian Gottlieb Matematiska institutionen Stockholms universitet 2:a upplagan 2001 2014 Förord Detta kompendium har sedan några år använts i utbildningen av grundskolelärare i matematik
1. Beräkna determinanten
 MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Examinator: Lars-Göran Larsson TENTAMEN I MATEMATIK MAA3 Grundläggande vektoralgebra, TEN6 alt.
MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Examinator: Lars-Göran Larsson TENTAMEN I MATEMATIK MAA3 Grundläggande vektoralgebra, TEN6 alt.
KOKBOKEN 1. Håkan Strömberg KTH STH
 KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
P Q = ( 2, 1, 1), P R = (0, 1, 0) och QR = (2, 2, 1). arean = 1 2 P Q P R
 1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
Skalärprodukt (lösningar)
 Skalärprodukt (lösningar) 404. Nej : 40. Utnyttja definitionen u v u v cos θ u v 4 6 u och distributiviteten (u v) (u + v) u u 6v u + u v v v 4 5 6 0 (Ritar man noggrant, ser man att u v och u + v mycket
Skalärprodukt (lösningar) 404. Nej : 40. Utnyttja definitionen u v u v cos θ u v 4 6 u och distributiviteten (u v) (u + v) u u 6v u + u v v v 4 5 6 0 (Ritar man noggrant, ser man att u v och u + v mycket
ax + y + 2z = 3 ay = b 3 (b 3) z = 0 har (a) entydig lösning, (b) oändligt många lösningar och (c) ingen lösning.
 UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Prov i matematik ES, Frist, KandMa LINJÄR ALGEBRA och GEOMETRI I 2010 10 21 Skrivtid: 8.00 13.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Prov i matematik ES, Frist, KandMa LINJÄR ALGEBRA och GEOMETRI I 2010 10 21 Skrivtid: 8.00 13.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
M0043M Integralkalkyl och Linjär Algebra, H14,
 M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 1 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 31 Lärare Ove Edlund Föreläsningar
M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 1 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 31 Lärare Ove Edlund Föreläsningar
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
Vektorer för naturvetare. Kjell Elfström
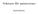 Vektorer för naturvetare Kjell Elfström Copyright c Kjell Elfström 2015 Första upplagan, mars 2015 Innehållsförteckning 1 Vektorer 5 1.1 Vektorbegreppet......................... 5 1.2 Operationer på vektorer.....................
Vektorer för naturvetare Kjell Elfström Copyright c Kjell Elfström 2015 Första upplagan, mars 2015 Innehållsförteckning 1 Vektorer 5 1.1 Vektorbegreppet......................... 5 1.2 Operationer på vektorer.....................
2x+y z 5 = 0. e x e y e z = 4 e y +4 e z +8 e x + e z = (8,4,5) n 3 = n 1 n 2 =
 Problem 1. Nedan presenteras ekvationen för en rät linje och ett plan i rummet. Du ska avgöra om linjen är vinkelrät mot planet. x = 2 4t y = 3 2t z = 1+2t 2x+y z 5 = 0 Lösning: Linjen har riktningsvektorn
Problem 1. Nedan presenteras ekvationen för en rät linje och ett plan i rummet. Du ska avgöra om linjen är vinkelrät mot planet. x = 2 4t y = 3 2t z = 1+2t 2x+y z 5 = 0 Lösning: Linjen har riktningsvektorn
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
3i)z 2013(1 ) och ge i det komplexa talplanet en illustration av lösningsmängden.
 MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Examinator: Lars-Göran Larsson TENTAMEN I MATEMATIK MAA Grundläggande vektoralgebra, TEN6 alt.
MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Examinator: Lars-Göran Larsson TENTAMEN I MATEMATIK MAA Grundläggande vektoralgebra, TEN6 alt.
Att beräkna:: Avstånd
 Att beräkna:: Avstånd Mikael Forsberg :: 27 november 205 Innehåll Punkter, linjer och plan, en sammanställning 2. Punkter i två och tre dimensioner....................... 2.2 Räta linjer i två och tre
Att beräkna:: Avstånd Mikael Forsberg :: 27 november 205 Innehåll Punkter, linjer och plan, en sammanställning 2. Punkter i två och tre dimensioner....................... 2.2 Räta linjer i två och tre
SF1624 Algebra och geometri
 SF1624 Algebra och geometri Föreläsning 2 David Rydh Institutionen för matematik KTH 28 augusti 2018 Detta gjorde vi igår Punkter Vektorer och skalärer, multiplikation med skalär Linjärkombinationer, spannet
SF1624 Algebra och geometri Föreläsning 2 David Rydh Institutionen för matematik KTH 28 augusti 2018 Detta gjorde vi igår Punkter Vektorer och skalärer, multiplikation med skalär Linjärkombinationer, spannet
Föreläsning 13 Linjär Algebra och Geometri I
 Föreläsning 13 Linjär Algebra och Geometri I Se slide 1: det är i rymden oftast lättast att jobba med parametrar för linjer och ekvationer för plan. Exempel: Låt l : (x, y, z) = (1 t, 3 + t, 4t), t R och
Föreläsning 13 Linjär Algebra och Geometri I Se slide 1: det är i rymden oftast lättast att jobba med parametrar för linjer och ekvationer för plan. Exempel: Låt l : (x, y, z) = (1 t, 3 + t, 4t), t R och
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
Inför tentamen i Linjär algebra TNA002.
 Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 1 Måndagen den 29 november, 2010
 SF624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning Måndagen den 29 november, 200 UPPGIFT () Betrakta det linjära ekvationssystemet x + x 2 + x 3 = 7, x x 3 + x 4
SF624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning Måndagen den 29 november, 200 UPPGIFT () Betrakta det linjära ekvationssystemet x + x 2 + x 3 = 7, x x 3 + x 4
x+2y 3z = 7 x+ay+11z = 17 2x y+z = 2
 Problem 1. Avgör för vilka värden på a som ekvationssystemet nedan har oändligt antal lösningar. Ange lösningarna i dessa fall! Lösning: Genom x+2y 3z = 7 x+ay+11z = 17 2x y+z = 2 1 2 3 1 a 11 2 1 1 =
Problem 1. Avgör för vilka värden på a som ekvationssystemet nedan har oändligt antal lösningar. Ange lösningarna i dessa fall! Lösning: Genom x+2y 3z = 7 x+ay+11z = 17 2x y+z = 2 1 2 3 1 a 11 2 1 1 =
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
LYCKA TILL! kl 8 13
 LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
e 3 e 2 e 1 Kapitel 3 Vektorer i planet och i rummet precis ett sätt skrivas v = x 1 e 1 + x 2 e 2
 Kapitel 3 Vektorer i planet och i rummet B e 3 e 2 A e 1 C Figur 3.16 Vi har ritat de riktade sträckor som representerar e 1, e 2, e 3 och v och som har utgångspunkten A. Vidare har vi skuggat planet Π
Kapitel 3 Vektorer i planet och i rummet B e 3 e 2 A e 1 C Figur 3.16 Vi har ritat de riktade sträckor som representerar e 1, e 2, e 3 och v och som har utgångspunkten A. Vidare har vi skuggat planet Π
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
ax + y + 4z = a x + y + (a 1)z = 1. 2x + 2y + az = 2 Ange dessutom samtliga lösningar då det finns oändligt många.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
Vektoralgebra. En inledning Hasse Carlsson
 Vektoralgebra En inledning Hasse Carlsson Matematiska institutionen Göteborgs universitet och Chalmers tekniska högskola Version 2005 Innehåll 1 Inledning 2 2 Geometriska vektorer 2 2.1 Definition av vektorer.......................
Vektoralgebra En inledning Hasse Carlsson Matematiska institutionen Göteborgs universitet och Chalmers tekniska högskola Version 2005 Innehåll 1 Inledning 2 2 Geometriska vektorer 2 2.1 Definition av vektorer.......................
Dagens ämnen. Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer
 Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
Moment Viktiga exempel 4.37, 4.38, 4.39 Övningsuppgifter 4.52, P 0 P = t v OP och OP 0 är ortsvektorer för punkterna P och P 0, så
 Tisdagen september kl 10:15, Sal 093, Moment 4.3.1 Viktiga exempel 4.37, 4.38, 4.39 Övningsuppgifter 4.5, 4.55 Räta linjen i rummet En rät linje l i rummet är bestämd då en punkt P 0 på linjen och en riktningsvektor
Tisdagen september kl 10:15, Sal 093, Moment 4.3.1 Viktiga exempel 4.37, 4.38, 4.39 Övningsuppgifter 4.5, 4.55 Räta linjen i rummet En rät linje l i rummet är bestämd då en punkt P 0 på linjen och en riktningsvektor
September 13, Vektorer En riktad sträcka P Q, där P Q, är en pil med foten i P och med spetsen i Q. Denna har. (i) en riktning, och
 Fö : September 3, 205 Vektorer En riktad sträcka P Q, där P Q, är en pil med foten i P och med spetsen i Q. Denna har i en riktning, och ii en nollskild längd betecknad P Q. Man använder riktade sträckor
Fö : September 3, 205 Vektorer En riktad sträcka P Q, där P Q, är en pil med foten i P och med spetsen i Q. Denna har i en riktning, och ii en nollskild längd betecknad P Q. Man använder riktade sträckor
SF1624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 2010 DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
Linjär algebra och geometri I
 UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Jörgen Östensson Vårterminen 2010 Kurslitteratur Linjär algebra och geometri I för X, geo, frist, lärare H. Anton, C. Rorres, Elementary Linear Algebra (Application
UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Jörgen Östensson Vårterminen 2010 Kurslitteratur Linjär algebra och geometri I för X, geo, frist, lärare H. Anton, C. Rorres, Elementary Linear Algebra (Application
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Determinant Vi förekommer bokens avsnitt, som handlar om determinanter eftersom de kommer att användas i detta avsnitt. a 11 a 12 a 21 a 22
 Moment 5.3, 4.2.9 Viktiga exempel 5.13, 5.14, 5.15, 5.17, 4.24, 4.25, 4.26 Handräkning 5.35, 5.44a, 4.31a, 4.34 Datorräkning Determinant Vi förekommer bokens avsnitt, som handlar om determinanter eftersom
Moment 5.3, 4.2.9 Viktiga exempel 5.13, 5.14, 5.15, 5.17, 4.24, 4.25, 4.26 Handräkning 5.35, 5.44a, 4.31a, 4.34 Datorräkning Determinant Vi förekommer bokens avsnitt, som handlar om determinanter eftersom
(a) Bestäm för vilka värden på den reella konstanten c som ekvationssystemet är lösbart. (b) Lös ekvationssystemet för dessa värden på c.
 UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
Moment 4.2.1, 4.2.2, 4.2.3, Viktiga exempel 4.4, 4.5, 4.6, 4.7, 4.13 Handräkning 4.1, 4.2, 4.3, 4.4, 4.5, 4.7 Datorräkning 1-9 i detta dokument
 Moment 4.2.1, 4.2.2, 4.2.3, 4.2.4 Viktiga exempel 4.4, 4.5, 4.6, 4.7, 4.13 Handräkning 4.1, 4.2, 4.3, 4.4, 4.5, 4.7 Datorräkning 1-9 i detta dokument Många av de objekt man arbetar med i matematiken och
Moment 4.2.1, 4.2.2, 4.2.3, 4.2.4 Viktiga exempel 4.4, 4.5, 4.6, 4.7, 4.13 Handräkning 4.1, 4.2, 4.3, 4.4, 4.5, 4.7 Datorräkning 1-9 i detta dokument Många av de objekt man arbetar med i matematiken och
TENTAMEN. Matematik 1 Kurskod HF1903 Skrivtid 13:15-17:15 Onsdagen 25 september 2013 Tentamen består av 3 sidor
 TENTAMEN Matematik Kurskod HF903 Skrivtid 3:5-7:5 Onsdagen 5 september 03 Tentamen består av 3 sidor Hjälpmedel: Utdelat formelblad. Räknedosa ej tillåten. Tentamen består av 3 uppgifter som totalt kan
TENTAMEN Matematik Kurskod HF903 Skrivtid 3:5-7:5 Onsdagen 5 september 03 Tentamen består av 3 sidor Hjälpmedel: Utdelat formelblad. Räknedosa ej tillåten. Tentamen består av 3 uppgifter som totalt kan
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
Uppsala Universitet Matematiska Institutionen Bo Styf. Svar till tentan. Del A. Prov i matematik Linj. alg. o geom
 Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
Linjär algebra och geometri 1
 UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Ryszard Rubinsztein Oswald Fogelklou Linjär algebra och geometri 1 för K1, W1, KandKe1 Höstterminen 2009 Kurslitteratur H.Anton, C.Rorres, Elementary Linear
UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Ryszard Rubinsztein Oswald Fogelklou Linjär algebra och geometri 1 för K1, W1, KandKe1 Höstterminen 2009 Kurslitteratur H.Anton, C.Rorres, Elementary Linear
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
LÖSNINGAR LINJÄR ALGEBRA LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
Analys o Linjär algebra. Lektion 7.. p.1/65
 Analys o Lektion 7 p1/65 Har redan (i matlab bla) stött på tal-listor eller vektorer av typen etc Vad kan sådana tänkas representera/modellera? Hur kan man räkna med sådana? Skall närmast fokusera på ordnade
Analys o Lektion 7 p1/65 Har redan (i matlab bla) stött på tal-listor eller vektorer av typen etc Vad kan sådana tänkas representera/modellera? Hur kan man räkna med sådana? Skall närmast fokusera på ordnade
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
4x az = 0 2ax + y = 0 ax + y + z = 0
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
Betygsgränser: För betyg. Vem som har. Hjälpmedel: av papperet. Uppgift. 1. (4p) 0. (2p) 3 (2p) Uppgift. 2. (4p) B-2C om. vektor A (1p) b) Bestäm k så
 Kurs: HF90 Matematik, Moment TEN (Linjär Algebra) ) Datum: 4 augusti 08 Skrivtid 08:00 :000 Examinator: Armin Halilovic För godkänt betyg krävss 0 av maxx 4 poäng. Betygsgränser: För betyg A, B, C, D,
Kurs: HF90 Matematik, Moment TEN (Linjär Algebra) ) Datum: 4 augusti 08 Skrivtid 08:00 :000 Examinator: Armin Halilovic För godkänt betyg krävss 0 av maxx 4 poäng. Betygsgränser: För betyg A, B, C, D,
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorer. Kapitel 1. Vektorbegreppet. 1.1 Låt u=(4,0, 1,3) och v=(2,1,4, 2). Beräkna vektorn 2u 3v.
 Kapitel 1 Vektorer Vektorbegreppet 1.1 Låt u=(4,0, 1,3) och v=(2,1,4, 2). Beräkna vektorn 2u 3v. 1.2 Rita ut vektorerna u=(3,1) och v=( 2,2) i samma koordinatsystem. Illustrera additionerna/subtraktionerna
Kapitel 1 Vektorer Vektorbegreppet 1.1 Låt u=(4,0, 1,3) och v=(2,1,4, 2). Beräkna vektorn 2u 3v. 1.2 Rita ut vektorerna u=(3,1) och v=( 2,2) i samma koordinatsystem. Illustrera additionerna/subtraktionerna
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4.
![Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4. Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4.](/thumbs/93/112939298.jpg) LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 8-- kl 4-9 a) Triangelns area är en halv av parallellograms area som spänns upp av tex P P (,, ) och P P (,, ), således area av P P P (,, ) (,,
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 8-- kl 4-9 a) Triangelns area är en halv av parallellograms area som spänns upp av tex P P (,, ) och P P (,, ), således area av P P P (,, ) (,,
1 Grundläggande kalkyler med vektorer och matriser
 Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Kontrollskrivning i Linjär algebra ,
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk Kurskod: TATA Provkod: KTR Kontrollskrivning i Linjär algebra 7 8, 8. Inga hjälpmedel. Ej räknedosa. På uppgift skall endast svar ges. Varje
LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk Kurskod: TATA Provkod: KTR Kontrollskrivning i Linjär algebra 7 8, 8. Inga hjälpmedel. Ej räknedosa. På uppgift skall endast svar ges. Varje
Linjär algebra kurs TNA002
 Linjär algebra kurs TNA002 Lektionsanteckningar klass ED1 I detta dokument finns ett utdrag av de tavelanteckningar som uppkommit under lektionstid under kursen TNA002. Alltså kan detta dokument långt
Linjär algebra kurs TNA002 Lektionsanteckningar klass ED1 I detta dokument finns ett utdrag av de tavelanteckningar som uppkommit under lektionstid under kursen TNA002. Alltså kan detta dokument långt
Tentamen 1 i Matematik 1, HF1903, för BD10 onsdag 22 september 2010, kl
 entamen i Matematik, HF9, för D onsdag september, kl 8.. Hjälpmedel: Endast formelblad (miniräknare är inte tillåten) För godkänt krävs poäng av möjliga poäng (betygsskala är,,,d,e,fx,f). Den som uppnått
entamen i Matematik, HF9, för D onsdag september, kl 8.. Hjälpmedel: Endast formelblad (miniräknare är inte tillåten) För godkänt krävs poäng av möjliga poäng (betygsskala är,,,d,e,fx,f). Den som uppnått
Bestäm den matris B som löser ekvationen = 1 2
 MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Examinator: Lars-Göran Larsson TENTAMEN I MATEMATIK MAA Grundläggande vektoralgebra, TEN5 alt.
MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Examinator: Lars-Göran Larsson TENTAMEN I MATEMATIK MAA Grundläggande vektoralgebra, TEN5 alt.
Tentamen 1 i Matematik 1, HF1903 Torsdag 22 augusti Skrivtid: 14:00-18:00 Examinator: Armin Halilovic
 Tentamen i Matematik, HF90 Torsdag augusti Skrivtid: 4:00-8:00 Examinator: Armin Halilovic För godkänt betyg krävs 0 av max 4 poäng Betygsgränser: För betyg A, B, C, D, E krävs, 9, 6, respektive 0 poäng
Tentamen i Matematik, HF90 Torsdag augusti Skrivtid: 4:00-8:00 Examinator: Armin Halilovic För godkänt betyg krävs 0 av max 4 poäng Betygsgränser: För betyg A, B, C, D, E krävs, 9, 6, respektive 0 poäng
