Geometri, talteori och kombinatorik
|
|
|
- Birgitta Andersson
- för 7 år sedan
- Visningar:
Transkript
1 Geometri, talteori och kombinatorik Föreläsning 2: Primtal Eric Järpe C 2015 Eric Järpe MPE-lab ITE-akademin Högskolan i Halmstad January 14, 2015 Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
2 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
3 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
4 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
5 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
6 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
7 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
8 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
9 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
10 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
11 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
12 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
13 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
14 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
15 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
16 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
17 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
18 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
19 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
20 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
21 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
22 Primtal Tal som inte kan delas jämnt med något annat heltal utom sig självt och 1 kallas primtal. De första primtalen är 2, 3, 5, 7, 11, 13, 17, 19,... Exempel 7 är ett primtal för det det delas endast av sig självt och 1: 7 ger rest 1 vid div med 6, 7 ger rest 2 vid div med 5, 7 ger rest 3 vid div med 4, 7 ger rest 1 vid div med 3, 7 ger rest 1 vid div med 2. Exempel 8 är inte ett primtal eftersom 8 delas av 2 och 4. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
23 Primtal Sats 5 Det finns oändligt många primtal. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
24 Primtalsbestämning Snabbast: AKS-algoritmen (2002). Fortfarande aktuell: Eratosthenes såll (200 f Kr). Eratosthenes såll Antag att vi vill avgöra om N är ett primtal. 1. Beräkna det största heltalet n N. 2. Lista alla heltal 2, 3, 4,..., n. 3. Om alla tal i listan så är strukna är N ett primtal. Gå till Låt k vara det minsta ostrukna talet ur listan och kolla om k delar N. 5. Om ja: då är N inte ett primtal. Gå till 6. Om nej: stryk alla multipler av k ur listan och gå till Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
25 Primtalsbestämning Snabbast: AKS-algoritmen (2002). Fortfarande aktuell: Eratosthenes såll (200 f Kr). Eratosthenes såll Antag att vi vill avgöra om N är ett primtal. 1. Beräkna det största heltalet n N. 2. Lista alla heltal 2, 3, 4,..., n. 3. Om alla tal i listan så är strukna är N ett primtal. Gå till Låt k vara det minsta ostrukna talet ur listan och kolla om k delar N. 5. Om ja: då är N inte ett primtal. Gå till 6. Om nej: stryk alla multipler av k ur listan och gå till Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
26 Primtalsbestämning Snabbast: AKS-algoritmen (2002). Fortfarande aktuell: Eratosthenes såll (200 f Kr). Eratosthenes såll Antag att vi vill avgöra om N är ett primtal. 1. Beräkna det största heltalet n N. 2. Lista alla heltal 2, 3, 4,..., n. 3. Om alla tal i listan så är strukna är N ett primtal. Gå till Låt k vara det minsta ostrukna talet ur listan och kolla om k delar N. 5. Om ja: då är N inte ett primtal. Gå till 6. Om nej: stryk alla multipler av k ur listan och gå till Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
27 Primtalsbestämning Snabbast: AKS-algoritmen (2002). Fortfarande aktuell: Eratosthenes såll (200 f Kr). Eratosthenes såll Antag att vi vill avgöra om N är ett primtal. 1. Beräkna det största heltalet n N. 2. Lista alla heltal 2, 3, 4,..., n. 3. Om alla tal i listan så är strukna är N ett primtal. Gå till Låt k vara det minsta ostrukna talet ur listan och kolla om k delar N. 5. Om ja: då är N inte ett primtal. Gå till 6. Om nej: stryk alla multipler av k ur listan och gå till Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
28 Primtalsbestämning Snabbast: AKS-algoritmen (2002). Fortfarande aktuell: Eratosthenes såll (200 f Kr). Eratosthenes såll Antag att vi vill avgöra om N är ett primtal. 1. Beräkna det största heltalet n N. 2. Lista alla heltal 2, 3, 4,..., n. 3. Om alla tal i listan så är strukna är N ett primtal. Gå till Låt k vara det minsta ostrukna talet ur listan och kolla om k delar N. 5. Om ja: då är N inte ett primtal. Gå till 6. Om nej: stryk alla multipler av k ur listan och gå till Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
29 Primtalsbestämning Snabbast: AKS-algoritmen (2002). Fortfarande aktuell: Eratosthenes såll (200 f Kr). Eratosthenes såll Antag att vi vill avgöra om N är ett primtal. 1. Beräkna det största heltalet n N. 2. Lista alla heltal 2, 3, 4,..., n. 3. Om alla tal i listan så är strukna är N ett primtal. Gå till Låt k vara det minsta ostrukna talet ur listan och kolla om k delar N. 5. Om ja: då är N inte ett primtal. Gå till 6. Om nej: stryk alla multipler av k ur listan och gå till Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
30 Primtalsbestämning Snabbast: AKS-algoritmen (2002). Fortfarande aktuell: Eratosthenes såll (200 f Kr). Eratosthenes såll Antag att vi vill avgöra om N är ett primtal. 1. Beräkna det största heltalet n N. 2. Lista alla heltal 2, 3, 4,..., n. 3. Om alla tal i listan så är strukna är N ett primtal. Gå till Låt k vara det minsta ostrukna talet ur listan och kolla om k delar N. 5. Om ja: då är N inte ett primtal. Gå till 6. Om nej: stryk alla multipler av k ur listan och gå till Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
31 Primtalsbestämning Snabbast: AKS-algoritmen (2002). Fortfarande aktuell: Eratosthenes såll (200 f Kr). Eratosthenes såll Antag att vi vill avgöra om N är ett primtal. 1. Beräkna det största heltalet n N. 2. Lista alla heltal 2, 3, 4,..., n. 3. Om alla tal i listan så är strukna är N ett primtal. Gå till Låt k vara det minsta ostrukna talet ur listan och kolla om k delar N. 5. Om ja: då är N inte ett primtal. Gå till 6. Om nej: stryk alla multipler av k ur listan och gå till Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
32 Primtalsbestämning Snabbast: AKS-algoritmen (2002). Fortfarande aktuell: Eratosthenes såll (200 f Kr). Eratosthenes såll Antag att vi vill avgöra om N är ett primtal. 1. Beräkna det största heltalet n N. 2. Lista alla heltal 2, 3, 4,..., n. 3. Om alla tal i listan så är strukna är N ett primtal. Gå till Låt k vara det minsta ostrukna talet ur listan och kolla om k delar N. 5. Om ja: då är N inte ett primtal. Gå till 6. Om nej: stryk alla multipler av k ur listan och gå till Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
33 Primtalsbestämning Snabbast: AKS-algoritmen (2002). Fortfarande aktuell: Eratosthenes såll (200 f Kr). Eratosthenes såll Antag att vi vill avgöra om N är ett primtal. 1. Beräkna det största heltalet n N. 2. Lista alla heltal 2, 3, 4,..., n. 3. Om alla tal i listan så är strukna är N ett primtal. Gå till Låt k vara det minsta ostrukna talet ur listan och kolla om k delar N. 5. Om ja: då är N inte ett primtal. Gå till 6. Om nej: stryk alla multipler av k ur listan och gå till Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
34 Primtalsbestämning Snabbast: AKS-algoritmen (2002). Fortfarande aktuell: Eratosthenes såll (200 f Kr). Eratosthenes såll Antag att vi vill avgöra om N är ett primtal. 1. Beräkna det största heltalet n N. 2. Lista alla heltal 2, 3, 4,..., n. 3. Om alla tal i listan så är strukna är N ett primtal. Gå till Låt k vara det minsta ostrukna talet ur listan och kolla om k delar N. 5. Om ja: då är N inte ett primtal. Gå till 6. Om nej: stryk alla multipler av k ur listan och gå till Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
35 Primtalsbestämning Snabbast: AKS-algoritmen (2002). Fortfarande aktuell: Eratosthenes såll (200 f Kr). Eratosthenes såll Antag att vi vill avgöra om N är ett primtal. 1. Beräkna det största heltalet n N. 2. Lista alla heltal 2, 3, 4,..., n. 3. Om alla tal i listan så är strukna är N ett primtal. Gå till Låt k vara det minsta ostrukna talet ur listan och kolla om k delar N. 5. Om ja: då är N inte ett primtal. Gå till 6. Om nej: stryk alla multipler av k ur listan och gå till Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
36 Primtalsbestämning Snabbast: AKS-algoritmen (2002). Fortfarande aktuell: Eratosthenes såll (200 f Kr). Eratosthenes såll Antag att vi vill avgöra om N är ett primtal. 1. Beräkna det största heltalet n N. 2. Lista alla heltal 2, 3, 4,..., n. 3. Om alla tal i listan så är strukna är N ett primtal. Gå till Låt k vara det minsta ostrukna talet ur listan och kolla om k delar N. 5. Om ja: då är N inte ett primtal. Gå till 6. Om nej: stryk alla multipler av k ur listan och gå till Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
37 Primtalsbestämning Snabbast: AKS-algoritmen (2002). Fortfarande aktuell: Eratosthenes såll (200 f Kr). Eratosthenes såll Antag att vi vill avgöra om N är ett primtal. 1. Beräkna det största heltalet n N. 2. Lista alla heltal 2, 3, 4,..., n. 3. Om alla tal i listan så är strukna är N ett primtal. Gå till Låt k vara det minsta ostrukna talet ur listan och kolla om k delar N. 5. Om ja: då är N inte ett primtal. Gå till 6. Om nej: stryk alla multipler av k ur listan och gå till Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
38 Primtalsbestämning Snabbast: AKS-algoritmen (2002). Fortfarande aktuell: Eratosthenes såll (200 f Kr). Eratosthenes såll Antag att vi vill avgöra om N är ett primtal. 1. Beräkna det största heltalet n N. 2. Lista alla heltal 2, 3, 4,..., n. 3. Om alla tal i listan så är strukna är N ett primtal. Gå till Låt k vara det minsta ostrukna talet ur listan och kolla om k delar N. 5. Om ja: då är N inte ett primtal. Gå till 6. Om nej: stryk alla multipler av k ur listan och gå till Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
39 Primtalsbestämning Snabbast: AKS-algoritmen (2002). Fortfarande aktuell: Eratosthenes såll (200 f Kr). Eratosthenes såll Antag att vi vill avgöra om N är ett primtal. 1. Beräkna det största heltalet n N. 2. Lista alla heltal 2, 3, 4,..., n. 3. Om alla tal i listan så är strukna är N ett primtal. Gå till Låt k vara det minsta ostrukna talet ur listan och kolla om k delar N. 5. Om ja: då är N inte ett primtal. Gå till 6. Om nej: stryk alla multipler av k ur listan och gå till Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
40 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
41 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
42 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
43 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
44 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
45 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
46 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
47 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
48 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
49 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
50 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
51 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
52 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
53 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
54 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
55 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
56 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
57 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
58 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
59 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
60 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
61 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
62 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
63 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
64 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
65 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
66 Exempel Avgör om talet 199 är ett primtal. Lösning 1. Först n = [ 199] = Lista talen 2, 3,..., Alla tal ej strukna ännu. 4. Eftersom 2 är det lägsta ostrukna är k = Eftersom 199 är udda så delas 199 ej av 2 stryk alla multipler av 2. Gå till Fortfarande alla ej strukna. 7. k = 3 lägsta ostrukna ej delare till 199 så stryk multipler av 3. osv med k = 5, 7, 11, Alla strukna Ja, 199 är ett primtal! 12. Terminera. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
67 Sammansatta tal Om ett tal inte är ett primtal kallas det sammansatt. Om a = bc kan a skrivas som produkten av b och c vilket innebär att a delas jämnt av b och c, varmed b och c kallas delare av a. Att b och c är delare till a kan skrivas b a och c a. Om b a och 1<b <a så kallas b äkta delare av a. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
68 Sammansatta tal Om ett tal inte är ett primtal kallas det sammansatt. Om a = bc kan a skrivas som produkten av b och c vilket innebär att a delas jämnt av b och c, varmed b och c kallas delare av a. Att b och c är delare till a kan skrivas b a och c a. Om b a och 1<b <a så kallas b äkta delare av a. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
69 Sammansatta tal Om ett tal inte är ett primtal kallas det sammansatt. Om a = bc kan a skrivas som produkten av b och c vilket innebär att a delas jämnt av b och c, varmed b och c kallas delare av a. Att b och c är delare till a kan skrivas b a och c a. Om b a och 1<b <a så kallas b äkta delare av a. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
70 Sammansatta tal Om ett tal inte är ett primtal kallas det sammansatt. Om a = bc kan a skrivas som produkten av b och c vilket innebär att a delas jämnt av b och c, varmed b och c kallas delare av a. Att b och c är delare till a kan skrivas b a och c a. Om b a och 1<b <a så kallas b äkta delare av a. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
71 Sammansatta tal Om ett tal inte är ett primtal kallas det sammansatt. Om a = bc kan a skrivas som produkten av b och c vilket innebär att a delas jämnt av b och c, varmed b och c kallas delare av a. Att b och c är delare till a kan skrivas b a och c a. Om b a och 1<b <a så kallas b äkta delare av a. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
72 Sammansatta tal Om ett tal inte är ett primtal kallas det sammansatt. Om a = bc kan a skrivas som produkten av b och c vilket innebär att a delas jämnt av b och c, varmed b och c kallas delare av a. Att b och c är delare till a kan skrivas b a och c a. Om b a och 1<b <a så kallas b äkta delare av a. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
73 Sammansatta tal Om ett tal inte är ett primtal kallas det sammansatt. Om a = bc kan a skrivas som produkten av b och c vilket innebär att a delas jämnt av b och c, varmed b och c kallas delare av a. Att b och c är delare till a kan skrivas b a och c a. Om b a och 1<b <a så kallas b äkta delare av a. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
74 Sammansatta tal Sats 2 Om a b och a c så a (b+c). Sats 3 Minsta äkta delaren av ett tal är ett primtal. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
75 Sammansatta tal Sats 2 Om a b och a c så a (b+c). Sats 3 Minsta äkta delaren av ett tal är ett primtal. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
76 Sammansatta tal Sats 2 Om a b och a c så a (b+c). Sats 3 Minsta äkta delaren av ett tal är ett primtal. Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
77 Centralt vid modern kryptering är faktorisering. Den fullständiga faktoriseringen är entydig: primtalsfaktoriseringen Allmänna faktoriseringsmetoder är: Snabbast: General number field sieve, 2007, fritt tillgänglig Näst snabbast: Quadratic sieve, 1981 Dixon s faktoriseringsmetod, 1981 Continued fraction factorization method, 1975 (1931) Fermat s faktoriseringsmetod... och dess utvecklingar. År 2002 lyckades Prof. Agrawal och ett par av hans studenter vid Indian Institute of Technology, Kanpur konstruera algoritmen AKS för primtalsbestämning. Snabb algoritm. Också relativt enkel! Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
78 Centralt vid modern kryptering är faktorisering. Den fullständiga faktoriseringen är entydig: primtalsfaktoriseringen Allmänna faktoriseringsmetoder är: Snabbast: General number field sieve, 2007, fritt tillgänglig Näst snabbast: Quadratic sieve, 1981 Dixon s faktoriseringsmetod, 1981 Continued fraction factorization method, 1975 (1931) Fermat s faktoriseringsmetod... och dess utvecklingar. År 2002 lyckades Prof. Agrawal och ett par av hans studenter vid Indian Institute of Technology, Kanpur konstruera algoritmen AKS för primtalsbestämning. Snabb algoritm. Också relativt enkel! Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
79 Centralt vid modern kryptering är faktorisering. Den fullständiga faktoriseringen är entydig: primtalsfaktoriseringen Allmänna faktoriseringsmetoder är: Snabbast: General number field sieve, 2007, fritt tillgänglig Näst snabbast: Quadratic sieve, 1981 Dixon s faktoriseringsmetod, 1981 Continued fraction factorization method, 1975 (1931) Fermat s faktoriseringsmetod... och dess utvecklingar. År 2002 lyckades Prof. Agrawal och ett par av hans studenter vid Indian Institute of Technology, Kanpur konstruera algoritmen AKS för primtalsbestämning. Snabb algoritm. Också relativt enkel! Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
80 Centralt vid modern kryptering är faktorisering. Den fullständiga faktoriseringen är entydig: primtalsfaktoriseringen Allmänna faktoriseringsmetoder är: Snabbast: General number field sieve, 2007, fritt tillgänglig Näst snabbast: Quadratic sieve, 1981 Dixon s faktoriseringsmetod, 1981 Continued fraction factorization method, 1975 (1931) Fermat s faktoriseringsmetod... och dess utvecklingar. År 2002 lyckades Prof. Agrawal och ett par av hans studenter vid Indian Institute of Technology, Kanpur konstruera algoritmen AKS för primtalsbestämning. Snabb algoritm. Också relativt enkel! Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
81 Centralt vid modern kryptering är faktorisering. Den fullständiga faktoriseringen är entydig: primtalsfaktoriseringen Allmänna faktoriseringsmetoder är: Snabbast: General number field sieve, 2007, fritt tillgänglig Näst snabbast: Quadratic sieve, 1981 Dixon s faktoriseringsmetod, 1981 Continued fraction factorization method, 1975 (1931) Fermat s faktoriseringsmetod... och dess utvecklingar. År 2002 lyckades Prof. Agrawal och ett par av hans studenter vid Indian Institute of Technology, Kanpur konstruera algoritmen AKS för primtalsbestämning. Snabb algoritm. Också relativt enkel! Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
82 Centralt vid modern kryptering är faktorisering. Den fullständiga faktoriseringen är entydig: primtalsfaktoriseringen Allmänna faktoriseringsmetoder är: Snabbast: General number field sieve, 2007, fritt tillgänglig Näst snabbast: Quadratic sieve, 1981 Dixon s faktoriseringsmetod, 1981 Continued fraction factorization method, 1975 (1931) Fermat s faktoriseringsmetod... och dess utvecklingar. År 2002 lyckades Prof. Agrawal och ett par av hans studenter vid Indian Institute of Technology, Kanpur konstruera algoritmen AKS för primtalsbestämning. Snabb algoritm. Också relativt enkel! Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
83 Centralt vid modern kryptering är faktorisering. Den fullständiga faktoriseringen är entydig: primtalsfaktoriseringen Allmänna faktoriseringsmetoder är: Snabbast: General number field sieve, 2007, fritt tillgänglig Näst snabbast: Quadratic sieve, 1981 Dixon s faktoriseringsmetod, 1981 Continued fraction factorization method, 1975 (1931) Fermat s faktoriseringsmetod... och dess utvecklingar. År 2002 lyckades Prof. Agrawal och ett par av hans studenter vid Indian Institute of Technology, Kanpur konstruera algoritmen AKS för primtalsbestämning. Snabb algoritm. Också relativt enkel! Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
84 Centralt vid modern kryptering är faktorisering. Den fullständiga faktoriseringen är entydig: primtalsfaktoriseringen Allmänna faktoriseringsmetoder är: Snabbast: General number field sieve, 2007, fritt tillgänglig Näst snabbast: Quadratic sieve, 1981 Dixon s faktoriseringsmetod, 1981 Continued fraction factorization method, 1975 (1931) Fermat s faktoriseringsmetod... och dess utvecklingar. År 2002 lyckades Prof. Agrawal och ett par av hans studenter vid Indian Institute of Technology, Kanpur konstruera algoritmen AKS för primtalsbestämning. Snabb algoritm. Också relativt enkel! Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
85 Centralt vid modern kryptering är faktorisering. Den fullständiga faktoriseringen är entydig: primtalsfaktoriseringen Allmänna faktoriseringsmetoder är: Snabbast: General number field sieve, 2007, fritt tillgänglig Näst snabbast: Quadratic sieve, 1981 Dixon s faktoriseringsmetod, 1981 Continued fraction factorization method, 1975 (1931) Fermat s faktoriseringsmetod... och dess utvecklingar. År 2002 lyckades Prof. Agrawal och ett par av hans studenter vid Indian Institute of Technology, Kanpur konstruera algoritmen AKS för primtalsbestämning. Snabb algoritm. Också relativt enkel! Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
86 Centralt vid modern kryptering är faktorisering. Den fullständiga faktoriseringen är entydig: primtalsfaktoriseringen Allmänna faktoriseringsmetoder är: Snabbast: General number field sieve, 2007, fritt tillgänglig Näst snabbast: Quadratic sieve, 1981 Dixon s faktoriseringsmetod, 1981 Continued fraction factorization method, 1975 (1931) Fermat s faktoriseringsmetod... och dess utvecklingar. År 2002 lyckades Prof. Agrawal och ett par av hans studenter vid Indian Institute of Technology, Kanpur konstruera algoritmen AKS för primtalsbestämning. Snabb algoritm. Också relativt enkel! Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
87 Centralt vid modern kryptering är faktorisering. Den fullständiga faktoriseringen är entydig: primtalsfaktoriseringen Allmänna faktoriseringsmetoder är: Snabbast: General number field sieve, 2007, fritt tillgänglig Näst snabbast: Quadratic sieve, 1981 Dixon s faktoriseringsmetod, 1981 Continued fraction factorization method, 1975 (1931) Fermat s faktoriseringsmetod... och dess utvecklingar. År 2002 lyckades Prof. Agrawal och ett par av hans studenter vid Indian Institute of Technology, Kanpur konstruera algoritmen AKS för primtalsbestämning. Snabb algoritm. Också relativt enkel! Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
88 Centralt vid modern kryptering är faktorisering. Den fullständiga faktoriseringen är entydig: primtalsfaktoriseringen Allmänna faktoriseringsmetoder är: Snabbast: General number field sieve, 2007, fritt tillgänglig Näst snabbast: Quadratic sieve, 1981 Dixon s faktoriseringsmetod, 1981 Continued fraction factorization method, 1975 (1931) Fermat s faktoriseringsmetod... och dess utvecklingar. År 2002 lyckades Prof. Agrawal och ett par av hans studenter vid Indian Institute of Technology, Kanpur konstruera algoritmen AKS för primtalsbestämning. Snabb algoritm. Också relativt enkel! Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
89 Centralt vid modern kryptering är faktorisering. Den fullständiga faktoriseringen är entydig: primtalsfaktoriseringen Allmänna faktoriseringsmetoder är: Snabbast: General number field sieve, 2007, fritt tillgänglig Näst snabbast: Quadratic sieve, 1981 Dixon s faktoriseringsmetod, 1981 Continued fraction factorization method, 1975 (1931) Fermat s faktoriseringsmetod... och dess utvecklingar. År 2002 lyckades Prof. Agrawal och ett par av hans studenter vid Indian Institute of Technology, Kanpur konstruera algoritmen AKS för primtalsbestämning. Snabb algoritm. Också relativt enkel! Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
90 Centralt vid modern kryptering är faktorisering. Den fullständiga faktoriseringen är entydig: primtalsfaktoriseringen Allmänna faktoriseringsmetoder är: Snabbast: General number field sieve, 2007, fritt tillgänglig Näst snabbast: Quadratic sieve, 1981 Dixon s faktoriseringsmetod, 1981 Continued fraction factorization method, 1975 (1931) Fermat s faktoriseringsmetod... och dess utvecklingar. År 2002 lyckades Prof. Agrawal och ett par av hans studenter vid Indian Institute of Technology, Kanpur konstruera algoritmen AKS för primtalsbestämning. Snabb algoritm. Också relativt enkel! Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
91 Algoritmen vid Fermats faktoriseringsmetod 1. Vi får ett heltal n och vill hitta heltal a, b så att ab = n. 2. Låt x = [ n] + 1 ( heltalsdelen av roten ur n plus 1 ) 3. Beräkna x 2 n. 4. Blir det en jämn kvadrat? 5. Om ja: Låt a = x + x 2 n b = x x 2 n Om nej: x++(ticka upp 1 steg) Gå tillbaks till steg Då är ab = = (x + x 2 n)(x x 2 n) = x 2 (x 2 n) = n Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
92 Algoritmen vid Fermats faktoriseringsmetod 1. Vi får ett heltal n och vill hitta heltal a, b så att ab = n. 2. Låt x = [ n] + 1 ( heltalsdelen av roten ur n plus 1 ) 3. Beräkna x 2 n. 4. Blir det en jämn kvadrat? 5. Om ja: Låt a = x + x 2 n b = x x 2 n Om nej: x++(ticka upp 1 steg) Gå tillbaks till steg Då är ab = = (x + x 2 n)(x x 2 n) = x 2 (x 2 n) = n Eric Järpe (Högskolan i Halmstad) Geometri, talteori och kombinatorik January 14, / 13
Kapitel 2: De hela talen
Kapitel 2: De hela talen Divisionsalgoritmen ( a a Z, d Z\{0} q, r Z : d = q + r ) d, 0 r d c 2005 Eric Järpe Högskolan i Halmstad där q kallas kvoten och r kallas principala resten vid heltalsdivision.
Talteori (OBS en del frågor gäller diofantiska ekvationer och de tas inte upp från och med hösten 2012)
Talteori (OBS en del frågor gäller diofantiska ekvationer och de tas inte upp från och med hösten 2012) T4.4-T4.7, 4.3, 4.7,T4.13-T4.14 S: Jag har svårt för visa-uppgifter. i kapitel 4 Talteori. Kan du
Lösningar till utvalda uppgifter i kapitel 5
Lösningar till utvalda uppgifter i kapitel 5 5.3. Vi använder Euklides algoritm och får 4485 = 1 3042 + 1443 3042 = 2 1443 + 156 1443 = 9 156 + 39 156 = 4 39. Alltså är sgd(3042, 4485) = 39. Om vi startar
4. Bestäm alla trippler n 2, n, n + 2 av heltal som samtliga är primtal. 5. Skriv upp additions- och multiplikationstabellen för räkning modulo 4.
Uppvärmningsproblem. Hur kan man se på ett heltal om det är delbart med, 2, 3, 4, 5, 6, 7, 8, 9, 0 respektive? Varför? 2. (a) Tänk på ett tresiffrigt tal abc, a 0. Bilda abcabc genom att skriva talet två
(A B) C = A C B C och (A B) C = A C B C. Bevis: (A B) C = A C B C : (A B) C = A C B C : B C (A B) C A C B C
Sats 1.3 De Morgans lagar för mängder För alla mängder A och B gäller att (A B) C = A C B C och (A B) C = A C B C. (A B) C = A C B C : A B A C (A B) C B C A C B C (A B) C = A C B C : A B A C (A B) C B
Gaussiska heltal. Maja Wallén. U.U.D.M. Project Report 2014:38. Department of Mathematics Uppsala University
U.U.D.M. Project Report 014:38 Gaussiska heltal Maja Wallén Examensarbete i matematik, 15 hp Handledare och examinator: Gunnar Berg Juni 014 Department of Mathematics Uppsala University Innehållsförteckning
Quadratic Sieve. Avancerade algoritmer (2D1440) 8/ Joel Brynielsson, TCS/Nada (f.d. D95)
Quadratic Sieve Avancerade algoritmer (2D1440) 8/11-2000 Joel Brynielsson, TCS/Nada (f.d. D95) http://www.nada.kth.se/~joel/qs.pdf Huvudidé Vill hitta x och y så att x 2 y 2 mod n x ±y mod n Då vet vi
Kryptering och primtalsfaktorisering
Institutionen för Numerisk analys och datalogi Kryptering och primtalsfaktorisering Johan Håstad Nada, KTH johanh@nada.kth.se Ett Exempel N = 9324894190123791048152332319394135 4114125392348254384792348320134094
Primtalen och aritmetikens fundamentalsats
Primtalen och aritmetikens fundamentalsats Tomas Malm Bokförlaget Bärarna c 2015 Tomas Malm & Bokförlaget Bärarna Version av texten: 15 november 2016 Redigering/bearbetning av text & bild: Tomas Malm Detta
Några satser ur talteorin
Några satser ur talteorin LCB 997/2000 Fermats, Eulers och Wilsons satser Vi skall studera några klassiska satser i talteori, vilka är av betydelse bland annat i kodningsteknik och kryptoteknik. De kan
Pythagoreiska taltripplar
Pythagoreiska taltripplar Mellan sidlängderna a, b, c i en rätvinklig triangel råder som bekant sambandet a + b = c och det finns heltal som uppfyller detta: 3 +4 = 5 5 +1 = 13 6 +8 = 10 8 +15 = 17 9 +1
MA 11. Hur starkt de binder. 2 Reella tal 3 Slutledning 4 Logik 5 Mängdlära 6-7 Talteori 8 Diofantiska ekvationer 9 Fördjupning och kryptografi
MA 11 Talteori och logik 2 Reella tal 3 Slutledning 4 Logik 5 Mängdlära 6-7 Talteori 8 Diofantiska ekvationer 9 Fördjupning och kryptografi propositionssymboler: bokstäver konnektiv Paranteser konnektiv
10! = =
Algebra II: Gamla tentor Algebra II: Lösningar till tentan den 28. maj 2012 Hjälpmedel: Papper skrivdon samt miniräknare. 1. Låt ϕ : N N vara Eulers ϕ-funktion. (a) Primfaktorisera ϕ(10!). Lösning: Faktoriseringen
Lennart Rolandsson, Uppsala universitet, Ulrica Dahlberg och Ola Helenius, NCM
Matematik Gymnasieskola Modul: Matematikundervisning med digitala verktyg II Del 1: Om programmering Aktiviteter Del 1 Lennart Rolandsson, Uppsala universitet, Ulrica Dahlberg och Ola Helenius, NCM Ni
Delbarhet och primtal
Talet 35 är delbart med 7 eftersom 35 = 5 7 Delbarhet och primtal 7 är en faktor i 35 kan skrivas 7 35 7 är en delare (divisor) till 35 35 är en multipel av 7 De hela talen kan delas in i jämna och udda
Föreläsning 9: Talteori
DD2458, Problemlösning och programmering under press Föreläsning 9: Talteori Datum: 2007-11-13 Skribent(er): Niklas Lindbom och Daniel Walldin Föreläsare: Per Austrin Den här föreläsningen behandlar modulär
A B A B A B S S S S S F F S F S F S F F F F
Uppsala Universitet Matematiska institutionen Isac Hedén isac distans@math.uu.se Algebra I, 5 hp Vecka 17. Logik När man utför matematiska resonemang så har man alltid vissa logiska spelregler att förhålla
PRIMTALEN, MULTIPLIKATION OCH DIOFANTISKA EKVATIONER
Explorativ övning 4 PRIMTALEN, MULTIPLIKATION OCH DIOFANTISKA EKVATIONER Syftet med detta avsnitt är att bekanta sig med delbarhetsegenskaper hos heltalen. De viktigaste begreppen är Aritmetikens fundamentalsats
Primtal, faktorisering och RSA
17 november, 2007 Ett Exempel N = 93248941901237910481523319394135 4114125392348254384792348320134094 3019134151166139518510341256153023 2324525239230624210960123234120156 809104109501303498614012865123
Sats 2.1 (Kinesiska restsatsen) Låt n och m vara relativt prima heltal samt a och b två godtyckliga heltal. Då har ekvationssystemet
Avsnitt 2 Tillägg om kongruensräkning Detta avsnitt handlar om två klassiska satser som används för att förenkla kongruensräkning: Kinesiska restsatsen och Fermats lilla sats. Den första satsen används
Föreläsning 9: Talteori
DD2458, Problemlösning och programmering under press Föreläsning 9: Talteori Datum: 2009-11-11 Skribent(er): Ting-Hey Chau, Gustav Larsson, Åke Rosén Föreläsare: Fredrik Niemelä Den här föreläsningen handlar
SJÄLVSTÄNDIGA ARBETEN I MATEMATIK
SJÄLVSTÄNDIGA ARBETEN I MATEMATIK MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET Asymmetriska krypteringssystem: hur de är konstruerade och vilka matematiska problem de bygger på av Sara Leufstadius
Offentlig kryptering
127 Offentlig kryptering Johan Håstad KTH 1. Inledning. Denna uppgift går ut på att studera ett offentligt kryptosystem. Med detta menas ett kryptosystem där det är offentligt hur man krypterar, men trots
RSA-kryptografi för gymnasiet. Jonas Gustafsson & Isac Olofsson
RSA-kryptografi för gymnasiet Jonas Gustafsson & Isac Olofsson HT 2010 Innehåll 1 Grundläggande beräkningsmetoder och begrepp 5 1.1 Mängder.............................. 5 1.2 Kvot och rest...........................
Algebra och talteori MMGL31
Algebra oh talteori MMGL3 Lärarprogrammet, Göteborgsuniversitet VT 008 Samuel Bengmar Lite om mig Dotorerat i Algebrais geometri Letor vid Matematisa vetensaper, Chalmers oh Göteborgs universitet Anställd
Matematisk kommunikation för Π Problemsamling
Problemsamling Charlotte Soneson & Niels Chr. Overgaard september 200 Problem. Betrakta formeln n k = k= n(n + ). 2 Troliggör den först genom att exempelvis i summan +2+3+4+5+6 para ihop termer två och
Matematisk kommunikation för Π Problemsamling
Problemsamling Niels Chr. Overgaard & Johan Fredriksson 3 september 205 Problem 0. Skriv följande summor mha summationstecken. ( Dvs på formen q k=p a k där k är en räknare som löper med heltalssteg mellan
Diskret matematik: Övningstentamen 1
Diskret matematik: Övningstentamen 1 1. Bevisa att de reella talen är en icke-uppräknelig mängd.. För två mängder av positiva heltal A och B skriver vi A C B, om det är så att A innehåller ett heltal som
LMA033/LMA515. Fredrik Lindgren. 4 september 2013
LMA033/LMA515 Fredrik Lindgren Matematiska vetenskaper Chalmers tekniska högskola och Göteborgs universitet 4 september 2013 F. Lindgren (Chalmers&GU) Matematik 4 september 2013 1 / 25 Outline 1 Föreläsning
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Examinator: Daniel Bergh. Lösningsförslag Algebra och kombinatorik
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Examinator: Daniel Bergh Lösningsförslag Algebra och kombinatorik 015-01-16 Uppgift 1 Vi noterar att 31 är ett primtal, så Z 31 är en kropp.
RSA-kryptering och primalitetstest
Matematik, KTH Bengt Ek augusti 2016 Material till kurserna SF1630 och SF1679, Diskret matematik: RSA-kryptering och primalitetstest Hemliga koder (dvs koder som används för att göra meddelanden oläsbara
TALTEORI FÖR ALLA 1 Juliusz Brzezinski
TALTEORI FÖR ALLA 1 Juliusz Brzezinski För exakt 10 år sedan publicerade Andrew Wiles sitt bevis av Fermats Stora Sats. Nyheten om hans resultat väckte enorm uppmärksamhet i hela världen. Vägen till lösningen
A4-papper där det på varje papper står en siffra, på ett papper står det ett decimaltecken. Det kan också finnas papper med de olika räknesättens
Aktivitet 1:1 LÄRARVERSION Göra tal av siffror Eleverna ska träna på positionssystemet. A4-papper där det på varje papper står en siffra, på ett papper står det ett decimaltecken. Det kan också finnas
Pythagoreiska trianglar
173 Pythagoreiska trianglar Sten Kaijser Uppsala Universitet Kort beskrivning av specialarbetet. Pythagoreiska trianglar har varit kända i minst 4000 år och kanske ännu längre. De utgör därmed ett av de
NÅGOT OM KRYPTERING. Kapitel 1
Kapitel 1 NÅGOT OM KRYPTERING Behovet av att skydda information har funnits mycket länge, men först i samband med utvecklingen av datatekniken har det blivit ett allmänt problem för alla moderna samhällen.
Gaussiska primtal. Christer Kiselman. Institut Mittag-Leffler & Uppsala universitet
195 Gaussiska primtal Christer Kiselman Institut Mittag-Leffler & Uppsala universitet 1. Beskrivning av uppgiften. De förslag som presenteras här kan behandlas på flera olika sätt. Ett första syfte är
Entydig faktorisering och Fermats stora sats i fallet n = 3
AKADEMIN FÖR TEKNIK OCH MILJÖ Avdelningen för elektronik, matematik och naturvetenskap Entydig faktorisering och Fermats stora sats i fallet n = 3 Leroy Kermanshahani 2018 Examensarbete, Grundnivå (kandidatexamen),
Övningshäfte 3: Polynom och polynomekvationer
LMA100 VT2005 ARITMETIK OCH ALGEBRA DEL 2 Övningshäfte 3: Polynom och polynomekvationer Syftet med denna övning är att repetera gymnasiekunskaper om polynom och polynomekvationer samt att bekanta sig med
Hela tal LCB 1999/2000
Hela tal LCB 1999/2000 Ersätter Grimaldi 4.3 4.5 1 Delbarhet Alla förekommande tal i fortsättningen är heltal. DEFINITION 1. Man säger att b delar a om det finns ett heltal n så att a Man skriver b a när
TALSYSTEM, DELBARHET OCH PRIMTAL
Explorativ övning 3 TALSYSTEM, DELBARHET OCH PRIMTAL Syftet med detta avsnitt är att titta närmare på positionssystemet och på heltalens multiplikativa struktur. De viktigaste begreppen är presentation
Läsanvisning till Discrete matematics av Norman Biggs - 5B1118 Diskret matematik
Läsanvisning till Discrete matematics av Norman Biggs - 5B1118 Diskret matematik Mats Boij 28 oktober 2001 1 Heltalen Det första kapitlet handlar om heltalen och deras aritmetik, dvs deras egenskaper som
KTHs Matematiska Cirkel. Talteori. Andreas Enblom Alan Sola
KTHs Matematiska Cirkel Talteori Andreas Enblom Alan Sola Institutionen för matematik, 2008 Finansierat av Marianne och Marcus Wallenbergs Stiftelse Innehåll 0 Mängdlära 1 0.1 Mängder...............................
1 Talteori. Det här kapitlet inleder vi med att ta
1 Talteori DELKAPITEL 1.1 Kongruensräkning 1. Talföljder och induktionsbevis FÖRKUNSKAPER Faktorisering av tal Algebraiska förenklingar Formler Direkta och indirekta bevis CENTRALT INNEHÅLL Begreppet kongruens
Anteckningar propp SMT2
Anteckningar propp SMT2 Lars Åström 11 december 2015 Under proppen ska följande gås igenom: Induktion - dominoeffekten Falluppdelning Extremprincipen Invarians Andra knep som används Induktion Vi använder
Binära kvadratiska former
U.U.D.M. Project Report 2016:14 Binära kvadratiska former Vasam Mazraeh Examensarbete i matematik, 15 hp Handledare: Andreas Strömbergsson Examinator: Veronica Crispin Quinonez Juni 2016 Department of
Algebra och talteori MMGL31. Repetition. Idag. Föreläsning 9 VT FLS och primtalstestning. Carmichaeltal. Rabin-Miller test.
Algebra och talteori MMGL Föreläsning 9 VT 008 Samuel Bengmark Repetition FLS och primtalstestning Carmichaeltal Rabin-Miller test F-funktionen Idag Ordning av ett element i Z m Primitiv rot Index (diskret
DEL I. Matematiska Institutionen KTH
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Diskret Matematik, moment A, för D2 och F, SF1631 och SF1630, den 25 mars 2008. DEL I 1. (3p Bestäm antalet binära ord av längd
MA2047 Algebra och diskret matematik
MA2047 Algebra och diskret matematik Något om restklassaritmetik Mikael Hindgren 19 september 2018 Exempel 1 Klockan är nu 8.00 Vad är klockan om 78 timmar? Vad var klockan för 53 timmar sedan? 8 + 78
Algoritmer, datastrukturer och komplexitet
Algoritmer, datastrukturer och komplexitet Övning 12 Anton Grensjö grensjo@csc.kth.se 10 december 2015 Anton Grensjö ADK Övning 12 10 december 2015 1 / 19 Idag Idag Komplexitetsklasser Blandade uppgifter
SJÄLVSTÄNDIGA ARBETEN I MATEMATIK
SJÄLVSTÄNDIGA ARBETEN I MATEMATIK MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET Gaussiska primtal och andra prima faktorer av Jenny Arthur 2016 - No 13 MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET,
Läsanvisning till Discrete matematics av Norman Biggs - 5B1118 Diskret matematik
Läsanvisning till Discrete matematics av Norman Biggs - 5B1118 Diskret matematik Mats Boij 18 november 2001 15 Ringar, kroppar och polynom Det fjortonde kapitlet behandlar ringar. En ring har till skillnad
2 (6) k 0 2 (7) n 1 F k F n. k F k F n F k F n F n 1 2 (8)
De naturliga talen. Vi skall till att börja med stanna kvar i världen av naturliga tal, N 3. Vi har redan använt (i beviset av Euklides primtalssats) att de naturliga talen är uppbyggda (genom multiplikation)
Lars-Daniel Öhman Lördag 2 maj 2015 Skrivtid: 9:00 15:00 Hjälpmedel: Miniräknare, lock till miniräknare
Umeå universitet Tentamen i matematik Institutionen för matematik Introduktion till och matematisk statistik diskret matematik Lars-Daniel Öhman Lördag 2 maj 2015 Skrivtid: 9:00 15:00 Hjälpmedel: Miniräknare,
KUNSKAP OCH KOMMUNIKATION
KUNSKAP OCH KOMMUNIKATION SIFFERDJÄVULENS PERSPEKTIV JULIUSZ BRZEZINSKI MATEMATISKA VETENSKAPER CHALMERS TEKNISKA HÖGSKOLA OCH GÖTEBORGS UNIVERSITET KOMMUNIKATION FORMELL : YRKESROLL, LÄRARROLL, MED- VERKAN
Grupper och RSA-kryptering
UPPSALA UNIVERSITET Matematiska institutionen Erik Melin Specialkursen HT07 26 oktober 2007 Grupper och RSA-kryptering Dessa blad utgör skissartade föreläsningsanteckningar kombinerat med övningar. Framställningen
EXAMENSARBETEN I MATEMATIK
EXAMENSARBETEN I MATEMATIK MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET AKS-algoritmen för att bestämma om ett tal är ett primtal eller inte av Per Westerlund 2005 - No 14 MATEMATISKA INSTITUTIONEN,
UPPSALA UNIVERSITET Institutionen för informationsteknologi NUMERISK TALTEORI. Eva-Lotta Högberg Daniel Norin Linn Stengård Joakim Widén
UPPSALA UNIVERSITET Institutionen för informationsteknologi NUMERISK TALTEORI Eva-Lotta Högberg Daniel Norin Linn Stengård Joakim Widén INLEDNING Vi skall i detta arbete belysa den numeriska talteorins
Material till kursen SF1679, Diskret matematik: Lite om kedjebråk. 0. Inledning
Matematik, KTH Bengt Ek november 207 Material till kursen SF679, Diskret matematik: Lite om kedjebråk 0 Inledning Talet π (kvoten mellan en cirkels omkrets och dess diameter) är inte ett rationellt tal
Lösningsförslag till Tentamen i 5B1118 Diskret matematik 5p 14 augusti, 2002
Institutionen för matematik, KTH Mats Boij och Niklas Eriksen Lösningsförslag till Tentamen i 5B1118 Diskret matematik 5p 14 augusti, 2002 1. Använd induktion för att visa att 8 delar (2n + 1 2 1 för alla
Algebra och kryptografi Facit till udda uppgifter
VK Algebra och kryptografi Facit till udda uppgifter Tomas Ekholm Niklas Eriksen Magnus Rosenlund Matematiska institutionen, 2002 48 Grupper. Lösning 1.1. Vi väljer att studera varje element i G H för
INDUKTION OCH DEDUKTION
Explorativ övning 3 INDUKTION OCH DEDUKTION Syftet med övningen är att öka Din problemlösningsförmåga och bekanta Dig med olika bevismetoder. Vårt syfte är också att öva skriftlig framställning av matematisk
Euklides algoritm för polynom
Uppsala Universitet Matematiska institutionen Isac Hedén isac distans@math.uu.se Algebra I, 5 hp Vecka 22. Euklides algoritm för polynom Ibland kan det vara intressant att bestämma den största gemensamma
forts. Kapitel A: Komplexa tal
forts. Kapitel A: Komplexa tal c 005 Eric Järpe Högskolan i Halmstad Andragradsekvationer Obs! i är antingen 1 1 + i) eller 1 1 + i), dvs i = 1 1 + i). Obs! Se upp med roten ur negativa tal: regeln ab
Sommarmatte. Matematiska Vetenskaper. 12 mars 2012
Sommarmatte Matematiska Vetenskaper 1 mars 01 Innehåll 1 Aritmetik och algebra 5 1.1 Räkning med naturliga tal och heltal.................. 5 1.1.1 Naturliga tal.......................... 5 1.1. Negativa
, S(6, 2). = = = =
1 Matematiska Institutionen KTH Lösningar till tentamensskrivning på kursen Diskret Matematik, moment A, för D2 och F, SF161 och SF160, den 17 april 2010 kl 09.00-14.00. Examinator: Olof Heden. DEL I 1.
Tal och polynom. Johan Wild
Tal och polynom Johan Wild 14 augusti 2008 Innehåll 1 Inledning 3 2 Att gå mellan olika typer av tal 3 3 De hela talen och polynom 4 3.1 Polynom........................... 4 3.2 Räkning med polynom...................
Faktoriseringsalgoritmer och Kryptografi
Faktoriseringsalgoritmer och Kryptografi Examensarbete för kandidatexamen i matematik vid Göteborgs universitet Kandidatarbete inom civilingenjörsutbildningen vid Chalmers David Elinder Eric Lindström
Algebra II. Isac Hedén och Johan Björklund
Algebra II Isac Hedén och Johan Björklund 1 2 Innehåll 0 Introduktion 4 1 Talteori 4 1.1 Rationella tal och decimalrepresentationer............. 4 1.2 Delbarhet................................ 8 1.3 Primtal.................................
Kängurun Matematikens Hopp
Kängurun Matematikens Hopp Student 2009 Här följer svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag till lösningsmetod. Bland eleverna i klassen finns säkert andra lösningsmetoder
Pythagoreiska taltripplar
Pythagoreiska taltripplar In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle. Euclid s Elements, Book I, Proposition
Tentamen består av 26 uppgifter fördelade på fem olika ämnesområden. Del 2 5 ger maximalt 11 poäng/del.
Skolmatematiktenta LPGG05 Kreativ Matematik 23 augusti 2016 8.15 13.15 Hjälpmedel: - Ansvarig lärare: Maria Lindström 054-7002146 eller 070-5699283 På omslagsbladet står att ni måste använda ett blad per
DELBARHET OCH PRIMTAL. Syftet med detta avsnitt är att bekanta sig med delbarhetsegenskaper hos heltalen.
Explorativ övning 3 DELBARHET OCH PRIMTAL Syftet med detta avsnitt är att bekanta sig med delbarhetsegenskaper hos heltalen. De viktigaste begreppen är delbarhet och divisionsalgoritmen största gemensamma
Exempel. Komplexkonjugerade rotpar
TATM79: Föreläsning 4 Polynomekvationer och funktioner Johan Thim 2 augusti 2016 1 Polynomekvationer Vi börjar med att upprepa definitionen av ett polynom. Polynom Definition. Ett polynom p(z) är ett uttryck
D. x 2 + y 2 ; E. Stockholm ligger i Sverige; F. Månen är en gul ost; G. 3 2 = 6; H. x 2 + y 2 = r 2.
Logik Vid alla matematiskt resonemang måste man vara säker på att man verkligen menar det man skriver ner på sitt papper. Därför måste man besinna hur man egentligen tänker. Den vetenskap, som sysslar
SP:PROG3 HT12 Tenta 2013-01-19
DSV SU/KTH sid 1 (5) SP:PROG3 SP:PROG3 HT12 Tenta 2013-01-19 Tentan består av tre uppgifter. Max poäng är 30. För betyget E (godkänd) krävs minst 18 poäng och minst en poäng på varje uppgift. Betygskriteria
DD1350 Logik för dataloger. Fö 7 Predikatlogikens semantik
DD1350 Logik för dataloger Fö 7 Predikatlogikens semantik 1 Kryssprodukt av mängder Om A och B är två mängder så är deras kryssprodukt A B mängden av alla par (a,b), där a A och b B. Ex: A={1,2}, B={3,4},
Algebra och talteori MMGL31. Lite om mig. Lite om er. Lärarprogrammet, Göteborgsuniversitet VT 2008
Algebra och talteori MMGL3 Lärarprogrammet, Göteborgsniersitet VT 008 Samel Bengmar Lite om mig Dotorerat i Algebrais geometri Letor id Matematisa etensaper, Chalmers och Göteborgs niersitet Anställd på
Datorprogram, algoritmer och Turing-maskiner
Datorprogram, algoritmer och Turing-maskiner Uppsala universitet Turing-året 2012 Inledning Det är bekvämt om en maskin, till exempel en dator, kan utföra en uppgift, särskilt om den kan göra det avsevärt
MA2047 Algebra och diskret matematik
MA2047 Algebra och diskret matematik Något om heltal Mikael Hindgren 17 september 2018 Delbarhet Exempel 1 42 = 6 7 Vi säger: 7 är en faktor i 42 eller 7 delar 42 Vi skriver: 7 42 Definition 1 Om a, b
LABBA MED PRIMTAL OCH DELBARHET. Andreas Wannebo
LABBA MED PRIMTAL OCH DELBARHET Andreas Wannebo Vi ska studera egenskaper för heltalen. Det finns heltal såsom 1,2,3,4,... De är de positiva heltalen och det är dem vi vill studera. Först kan man ställa
C/D-UPPSATS. Talteori
C/D-UPPSATS 2008:03 Talteori Från kvadratisk reciprocitet till Riemanns zeta-funktion via primtalssatsen Joakim Larsson Luleå tekniska universitet C/D-uppsats Matematik Institutionen för Matematik 2008:03
Svar och lösningar. Kängurutävlingen 2009 Cadet för gymnasiet
Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Repetition i Python 3. Exemplen fac. Exemplen fac motivering. Exemplen fac i Python
Repetition i Python 3 Exemplen fac Orginalet I Scheme använde vi rekursion för all slags repetition. Efterom Scheme är ett funktionellt språk återsänder alla språkkonstruktioner ett värde men i Python
Hur man skriver matematik
Hur man skriver matematik Niels Chr. Overgaard 2018-10-01 N. Chr. Overgaard Skriva matematik 2018-10-01 1 / 12 Information: Opposition och kompisgranskning En del av inlämningsuppgift går ut på att man
Lösningsförslag till Tentamen i 5B1118 Diskret matematik 5p 22 augusti, 2001
Institutionen för matematik, KTH Mats Boij Lösningsförslag till Tentamen i 5B1118 Diskret matematik 5p 22 augusti, 2001 1. Ange kvot och rest vid division av 5BE med 1F där båda talen är angivna i hexadecimal
Lösning till tentamensskrivning i Diskret Matematik för CINTE och CMETE, m fl, SF1610, tisdagen den 2 juni 2015, kl
1 Matematiska Institutionen KTH Lösning till tentamensskrivning i Diskret Matematik för CINTE och CMETE, m fl, SF1610, tisdagen den juni 015, kl 1.00-19.00. Examinator: Olof Heden Hjälpmedel: Inga hjälpmedel
Induktion, mängder och bevis för Introduktionskursen på I
Induktion, mängder och bevis för Introduktionskursen på I J A S, ht 04 1 Induktion Detta avsnitt handlar om en speciell teknik för att försöka bevisa riktigheten av påståenden eller formler, för alla heltalsvärden
SAMMANFATTNING TATA82 Diskret matematik
SAMMANFATTNING TATA82 Diskret matematik LÄST SOM EN DEL AV CIVILINGENJÖRSPROGRAMMET I INDUSTRIELL EKONOMI VID LITH, VT 2016 Senast reviderad: 2018-05-27 Författare: Viktor Cheng och Erik Frank Innehållsförteckning
Elementär talteori. Lars-Åke Lindahl
Elementär talteori Lars-Åke Lindahl 2012 Förord Detta kompendium innehåller material för en fempoängskurs i elementär talteori och har sammanställts av föreläsningsanteckningarna till en kurs i ämnet
Algoritmer, datastrukturer och komplexitet
Algoritmer, datastrukturer och komplexitet Övning 6 Anton Grensjö grensjo@csc.kth.se 4 oktober 2017 1 Idag Algoritmkonstruktion (lite blandat) Redovisning och inlämning av labbteori 3 2 Uppgifter Uppgift
29 Det enda heltalet n som satisfierar båda dessa villkor är n = 55. För detta värde på n får vi x = 5, y = 5.
Tentamenskrivning MATA15 Algebra: delprov 1, 6hp Lördagen den 3 november 01 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1 a) Lös den diofantiska ekvationen 9x + 11y 00 b) Ange alla lösningar x, y) sådana
Signalflödesmodellen. Två (gamla) exempel: Kvadratera alla jämna löv.
Strömmar (streams) De sista dagarna objekt med tillstånd modellerades som beräkningsobjekt med tillstånd. Isådana modeller är tiden modelerad (implicit) som en sekvens av tillstånd. För att kunna modellera
ÄNDLIGT OCH OÄNDLIGT AVSNITT 4
VSNITT ÄNDLIGT OCH OÄNDLIGT Är det möjligt att jämföra storleken av olika talmängder? Har det någon mening om man säger att det finns fler irrationella tal än rationella? Är det överhuvudtaget möjligt
Pythagoreiska taltripplar
Pythagoreiska taltripplar In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle. Euclid s Elements, Book I, Proposition
Låt n vara ett heltal som är 2 eller större. Om a och b är två heltal så säger vi att. a b (mod n)
Uppsala Universitet Matematiska institutionen Isac Hedén Algebra I, 5 hp Sammanfattning av föreläsning 9. Kongruenser Låt n vara ett heltal som är 2 eller större. Om a och b är två heltal så säger vi att
SJÄLVSTÄNDIGA ARBETEN I MATEMATIK
SJÄLVSTÄNDIGA ARBETEN I MATEMATIK MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET Kedjebråk av Joel Carlgren 206 - No 7 MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET, 06 9 STOCKHOLM Kedjebråk Joel
Kompendium i Algebra, del 3 för fysikinriktade kandidatprogram. Rikard Bøgvad och Paul Vaderlind
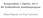Kompendium i Algebra, del 3 för fysikinriktade kandidatprogram Rikard Bøgvad och Paul Vaderlind Innehåll Kapitel 1. Absolutbelopp. 1 1. Absolutbelopp. 1 2. Räkneregler. 5 2.1. Att beskriva intervall med
Mattestegens matematik
höst Decimaltal pengar kr 0 öre,0 kr Rita 0,0 kr på olika sätt. räkna,0,0 storleksordna decimaltal Sub för lite av två talsorter 7 00 0 tallinjer heltal 0 0 Add med tiotalsövergångar 0 7 00 0 Sub för lite
Algoritmer, datastrukturer och komplexitet
Algoritmer, datastrukturer och komplexitet Övning 6 Anton Grensjö grensjo@csc.kth.se 9 oktober 2015 Anton Grensjö ADK Övning 6 9 oktober 2015 1 / 23 Översikt Kursplanering Ö5: Grafalgoritmer och undre
Kängurutävlingen Matematikens hopp
Kängurutävlingen Matematikens hopp Student 016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till