TVE Examensarbete 15 hp September Chord King. Guitar Hero for acoustic guitars. Mattias Johansson Peter Nordström Sebastian Ärleryd
|
|
|
- Ingvar Ulf Bergqvist
- för 8 år sedan
- Visningar:
Transkript
1 TVE Examensarbete 15 hp September 2011 Chord King Guitar Hero for acoustic guitars Mattias Johansson Peter Nordström Sebastian Ärleryd
2 Abstract Chord King Mattias Johansson, Peter Nordström, Sebastian Ärleryd Teknisk- naturvetenskaplig fakultet UTH-enheten Besöksadress: Ångströmlaboratoriet Lägerhyddsvägen 1 Hus 4, Plan 0 Postadress: Box Uppsala A game for acoustic guitars has been written in the Python programming language. The game has a graphical user interface and there are several song to choose from. The game shows to the user what chords and string plucks should be played and when to play them. Points are awarded if the correct chord or string pluck is played. The game works well in a moderately quiet environment if the guitar is played somewhat clean. There are a lot of room for improvement. Telefon: Telefax: Hemsida: Handledare: Lars-Johan Brännmark Ämnesgranskare: Tomas Olofsson Examinator: Urban Lundin ISSN: , TVE
3 Table of Contents 1 Inledning Målsättning Teori Musikteori Ljudalstring på gitarr Ljudanalys Metod Harmonic Product Spectrum metoden Strängplock Ackord Ljudanalys i realtid Resultat Språket Färdig kod Ljudinläsning Grafik och användargränssnitt Låtfiler och låtinläsning Att spela Diskussion Metoddiskussion Resultatdiskussion Programförbättringar Slutsatser Referenser
4 1 Inledning Många är vi som har en akustisk gitarr hemma någonstans. Det skulle vara roligt att lära sig spela men det är svårt att komma igång med själva övandet. Än fler är vi som tycker det är roligt att spela musikspel såsom Activisions Guitar Hero. [1] Detta spel har blivit populärt och många har spelat det i timmar. Nackdelen med det är att hur mycket man än spelar så blir man inte bättre på att spela gitarr. Plastgitarren som medföljer musikspelet har endast sex knappar och liknar en riktig gitarr endast till formen. För att spelaren ska bli bättre på att spela gitarr måste musikspelet vara mer verklighetstroget. Det allra bästa vore om en riktig gitarr användes för att styra musikspelet. På detta sätt får spelaren träna på riktigt samtidigt som den blir motiverad av och får saker att öva på från musikspelet. Vi har tagit fram just ett sådant musikspel. För att spela vårt spel behöver man bara en vanlig persondator med mikrofon och en akustisk gitarr. I spelet visas vilka ackord och strängplock som ska spelas och när man ska spela dem. Om spelaren spelar rätt delas poäng ut. 2 Målsättning Målsättningen med detta projekt är att utveckla ett verklighetstroget musikspel för gitarrer till persondatorer. Spelet ska fungera både som underhållning och som en sätt att lära sig spela gitarr på riktigt. Det ska kunna spelas på de allra flesta persondatorer utrustade med en mikrofon bara spelaren har en egen akustisk gitarr. Spelet ska använda sig av datorns mikrofon för att läsa in ljud och analysera detta i realtid. Under ljudanalysen ska spelet kunna hitta ackord och enskilda strängplock, en sträng anslagen på ett band. De ackord vi vill att spelet ska kunna hitta är treklang-ackorden C, D, E, F, G, A och B i dur och moll spelade på vanligt sätt. Spelet ska kunna avgöra om spelaren spelat rätt eller fel genom att jämföra inlästa ackord och plock med en fördefinierad sång. Om spelaren spelar rätt ska spelet dela ut poäng.vi kräver inte att programmet hittar när man spelat rätt 100% av gångerna, men det ska vara tillräckligt ofta för att det ska vara spelbart utan större störningsmoment. För att visa spelaren vad den ska spela ska spelet ha ett grafiskt användargränssnitt. Spelet ska visa grafiska element som representerar sången som spelas. Det ska synas tydligt vilket ackord eller vilken sträng och vilket band spelaren ska spela. Det ska också vara tydligt när spelaren ska spela dessa. För att störningar på ljudsignalen inte ska göra analysen för svår begränsar vi oss till att spelet ska fungera i en relativt tyst miljö där ljudnivån inte överstiger normal talnivå. Vi begränsar oss även genom att kräva att den akustiska gitarren som används är välstämd samt att den är nylonsträngad då övertonernas styrkor skiljer sig mycket mellan nylon- och stålsträngade gitarrer. Våra huvudmål utgörs alltså av följande. Spelet ska: kunna spelas på en vanlig dator med mikrofon, kunna användas med en vanlig, välstämd nylonsträngad akustisk gitarr, känna igen de vanliga treklang-ackorden C, D, E, F, G, A och B i dur och moll, ha få störningsmoment och ha ett grafiskt användargränssnitt. 3
5 3 Teori Teorikapitlet går igenom den grundläggande teori som krävs för att utföra ljudanalysen i vårt program. Kapitlet inleds med en beskrivning av den grundläggande musikteorin. Med denna som grund beskrivs hur gitarren fungerar som musikinstrument. Kapitlet avslutas med teori för själva ljudanalysen. 3.1 Musikteori Avsnittet tar upp hur vi människor klassificerat de frekvenser som finns i musiken i det vanliga tonsystemet i västvärlden. Det går även igenom hur toner harmonierar i ett ackord. Musik är uppbyggt av så kallade toner. En ton är en ljudvåg av hörbar frekvens. I det västerländska musiksystemet har toner namngivits enligt bokstäver i tolv steg från A till G och placerats i så kallade oktaver. Varje oktav har sin egen uppsättning toner från A till G. Oktaver ligger i frekvensspektrumet på så sätt att det frekvensmässigt alltid finns en oktav ovanför och en oktav under. En oktavs toner har dubbla frekvensen jämfört med tonerna i oktaven under och halva frekvensen jämfört med tonerna i oktaven ovanför. För att fixera detta system definieras ofta en A ton till 440 Hz. Detta A kallas ofta A4, A tonen i den fjärde oktaven. Nästa A, A5, som tillhör oktaven ovanför har frekvens 880 Hz. Det A som tillhör oktaven under har frekvens 220 Hz och kallas A3. Varje oktav har också halvtoner. En halvton är tonen man får om man går ett halvt steg från en ton mot en annan. Dessa är också döpta enligt bokstäver och namnges efter den ton man utgår från och om man går ett halvt steg upp eller ner från denna ton. Till exempel kallas tonen halvvägs mellan C och D både för C#, vilket uttalas ciss, eller D, vilket uttalas des, beroende på om man utgår från C eller D. Eftersom det bara är tolv steg av toner i en oktav är tonerna upplagda på så sätt att det inte finns halvtoner mellan varje ton. De toner som finns är C, C#/D, D, D#/E, E, F, F#/G, G, G#/A, A, A#/B och B. När man går från en av dessa toner till nästa kallas det att man gått upp en halvton. Frekvensen har då ökat med en faktor 2 1/12. Förutom de motsvarande tonerna i andra oktaver har också varje ton sina egna övertoner. En given tons övertoner är alla toner vars frekvens är en heltalsmultipel av tonens frekvens. Till exempel har A4 på 440 Hz övertonerna 880 Hz, 1320 Hz, 1760 Hz, 2200 Hz och så vidare. Spelar man en ton kommer de allra flesta instrument också att ge ifrån sig många övertoner av betydande intensitet. Denna samling övertoner spelar stor roll i hur instrumentets ljud upplevs. På många instrument kan man spela flera toner på samma gång. Det kallas då att man spelar ett ackord. Då ger instrumentet ifrån sig både flera toner och övertoner till dessa toner. Det finns många olika typer av ackord. Den typ av ackord vi koncentrerar oss på kallas treklang-ackord och består av tre toner. Den första tonen kallas grundtonen och är den tonen som de två andra utgår från. Nästa ton ligger en stor eller liten ters ovanför grundtonen. En stor ters är 5/4 av grundtonens frekvens och en liten ters är 6/5 av grundtonens frekvens. Den sista tonen kallas kvinten, och den är 3/2 av grundtonens frekvens. 4
6 3.2 Ljudalstring på gitarr Detta avsnitt beskriver vad som händer i en gitarrsträng efter anslag. Det tar upp hur strängen svänger, hur dessa svängningar bildar ljud och hur detta kan skapa musikaliska toner. De flesta gitarrer har sex strängar och är stämda på samma sätt. I denna stämning är den lägsta strängen stämd i E2 med de resterande strängarna är stämda i A2, D3, G3, B3 och den högsta i E4. Det är denna stämning vi använder och när vi skriver om välstämda gitarrer är det denna stämning vi syftar på. När en gitarrsträng anslås bildas stående vågor av flera olika frekvenser i strängen. Dessa vågor svänger i strängens grundfrekvens samt heltalsmultiplar av denna. [2] Den lägsta av dessa frekvenser är grundtonens frekvens och heltalsmultiplarna är övertonernas frekvenser. Tillsammans bildar dessa toner en ljudsignal. Figur visar en strängs grundton och tre övertoner. Figur 3.2-1: Överst syns en gitarrsträng som svänger i sin grundton. Under syns samma sträng som svänger i sin första, andra och tredje överton. Stående vågor är indelade i segment som svänger och punkter där strängen inte svänger. Punkterna som inte svänger kallas noder och de punkter som svänger som mest kallas bukar. Grundtonens och dess övertoners amplituder kommer att vara beroende av hur strängen slogs an. Detta har att göra med var övertonernas noder och bukar ligger. På grund av att grundtonens buk ligger mitt på strängen kommer dess amplitud bli så stor som möjligt om man slår an mitt på strängen. Slår man an någon annanstans på strängen kommer man få en annan kombination av amplituder på grundtonen och övertonerna i ljudsignalen. På grund av detta är det i princip omöjligt att få samma kombination två gånger trots att man slår an på (nästan) samma ställe. Det kommer dock låta tillräckligt lika för att det mänskliga örat inte ska kunna skilja på ljudsignalerna. För att kunna spela fler grundtoner än de sex grundtoner som strängarna är stämda i kan man trycka ned en gitarrs strängar på de band som finns längs dess hals. Den del av strängen som kommer att svänga då den anslås blir då kortare vilket resulterar i att tonen blir högre, den svänger i en högre frekvens. Banden är separerade på så sätt att tonen höjs eller sänks med en halvton om man trycker ned strängen vid ett band längre ned eller upp då man anslår den. Som resultat av hur banden är upplagda och den vanliga stämningen kommer tonerna från lägre strängarna att komma igen på de högre strängarna. Spelas till exempel det femte bandet på den lägsta strängen fås samma ton som om den näst lägsta strängen spelats utan att hålla ner något band. På grund av detta kan till exempel en gitarr med 18 band på den högst stämda strängen spela 42 olika halvtoner. 5
7 3.3 Ljudanalys Detta avsnitt förklarar teori bakom grundläggande ljudanalys. Vanliga toner spelade på instrument så som en gitarr beter sig som periodiska signaler. Dessa kan beskrivas som summan av ett oändligt antal sinussignaler av olika amplituder och frekvenser. För en enskild sträng består dessa frekvenser och amplituder av grundtonen och övertonernas frekvenser och amplituder. En sådan signal som består av en amplitud som förändras över tid sägs ligga i tidsdomänen. Med hjälp av Fouriertransformen kan man överföra en sådan signal till frekvensdomänen och på så sätt få reda på amplituderna hos de frekvenser som bygger upp signalen. [3] Ljudsignaler som vi hör är kontinuerliga signaler med ett oändligt antal amplitudnivåer för ett givet tidsintervall. När en sådan signal spelas in till en dator med en mikrofon fås, på grund av hur datorer fungerar, en representation av signalen som en samling amplitudvärden av diskret storlek. Varje amplitudvärde kallas då sampel och tiden mellan varje sampel är oftast konstant. I de fall tiden mellan samplen är konstant beskrivs den lättast av den så kallade samplingsfrekvensen. För att Fouriertransformera en tidsdiskret signal används den diskreta Fouriertransformen, eller med fördel den snabbare ekvivalenta varianten av denna som kallas Fast Fourier Transform. Figur 2 visar en signal samt dess Fast Fourier Transform. Figur 3.3-1: Övre grafen visar signalen y(t) = 20sin(5*2pi*t) + 12sin(10*2pi*t) + 15sin(15*2pi*t). Det syns hur de olika sinussignalerna samverkar för att skapa en signal som varierar periodiskt över tiden.undre grafen visar Fast Fourier transformen av signalen i den övre grafen. Denna visar de relativa amplituderna på de sinussignaler som ingår i signalen. För att kunna rekonstruera en signal från tidsdiskreta samplingar behövs två samplingar per period hos den högsta frekvens som ingår i signalen man vill kunna återskapa. På grund av detta kommer en tidsdiskret inspelning av en ljudsignal bara kunna rekonstruera de delar av ljudsignalen vars frekvenser är under halva samplingsfrekvensen. Denna gräns ges a Nyquist/Shannons samplingsteorem och kallas Nyquistfrekvensen. Frekvenser i signalen som befinner sig ovanför Nyquistfrekvensen kan uppfattas som låga frekvenser när man samplar dem varför filtrering av höga frekvenser innan analys kan vara nödvändigt. Vi har dock inte filtrerat de signaler vi Fouriertransformerar. Längden på den signal man samplar bestämmer hur stor noggrannhet man får när man försöker urskilja frekvenser ur den. Upplösningen är direkt omvänt proportionell mot inspelningstiden. Samplas till exempel en signal under två sekunder kommer Fast Fourier transformen ha en 6
8 upplösning på en halv Hertz. [4] 4 Metod Detta kapitel beskriver hur de metoder som används i programmet fungerar och hur problem som uppstår vid ljudanalys har lösts. För att kunna skapa ett spel enligt målsättningen behövs metoder för att hitta vilket ackord eller strängplock som spelats. För att kunna ta fram dessa metoder behöver man först få en bild av hur ljudet från en gitarr ser ut. Detta gjordes genom att studera gitarrens frekvensspektrum i olika situationer. Till detta användes det matrisbaserade beräkningsprogrammet MATLAB. [5] Detta program har mycket inbyggd funktionalitet som är användbar vid ljudanalys. Med MATLAB kan ljud spelas in via inbyggda funktioner och analyseras med Fast Fourier transformen och vektormanipulationer. När ljudet från en gitarr analyseras upptäcks snabbt att amplituderna på ett strängplocks grundton och övertoner är väldigt oförutsägbara. I regel är grundtonen och de första övertonerna starkast men det går inte att förutse vilken av dessa toner som kommer vara allra starkast. Detta ställer till med problem när ett program ska ta ut grundtonen från ett spektrum. Figur 4-1 visar ett spektrum när A- strängen spelats. Figur 4-1: Spektrum för en spelad A-sträng. Grundtonen är 110 Hz och de två första övertonerna syns vid 220 Hz respektive 330 Hz. 7
9 4.1 Harmonic Product Spectrum metoden Detta avsnitt går igenom en metod som löser problemet med att grundtonen och dess övertoner till gitarrsträngar har oförutsägbar styrka. Denna metod kallas Harmonic Product Spectrum metoden och utnyttjar att en tons övertoner ligger på heltalsmultiplar av tonens frekvens. [6] Idéen är att efter denna metod utförts ska bara frekvenstoppar som har ett visst antal övertoner inom spektrumet finnas kvar. Vi utför denna metod genom att kopiera vektorn med spektrumet för det inspelade ljudet ett flertal gånger. Antalet gånger spektrumet kopieras motsvarar hur många övertoner som ska användas. I den första kopian behålls var annat element, i den andra behålls var tredje element och så vidare. Detta kallas att man nedsamplar spektrumsvektorn. Efter att kopiorna fyllts ut med nollor tills de är lika långa som spektrumsvektorn multipliceras alla vektorer elementvis med varandra. Resultatet har endast toppar på de ställen alla vektorerna hade toppar. Det sätt som spektrumsvektorn nedsamplades kommer resultera i att alla kopior har toppar där det i spektrumsvektorn fanns en grundton. I Figur visas ett exempel på detta, där den nedersta grafen visar resultatet efter multiplicering av vektorerna. Figur 4.1-1: Harmonic Product Spectrum metoden. Ett spektrum och två stycken nedsamplingar samt resultatet vid elementvis multiplikation av dessa. Här syns hur det, efter elementvis multiplikation mellan spektrumet och dess nedsamplingar, endast återstår en topp vid grundtonen. 4.2 Strängplock För att hitta strängplock bland inspelat ljud används den ovan nämnda Harmonic Product Spectrum metoden. Vi använde fem övertoner för att få ett bra resultat. Denna metod fungerar även då det finns bakgrundsbrus i det inspelade ljudet. Eftersom bruset vid vanliga inspelningar kan antas komma från slumpmässiga ljud, dålig mikrofon och andra ickemusikaliska källor utan övertoner försvinner detta brus då metoden används. Därav fungerar metoden mycket bra då strängplock från en gitarr ska hittas i ett spektrum där en mängd andra ljud också spelats in. 8
10 4.3 Ackord För att hitta ett ackord bland inspelat ljud letar vi i spektrumet efter frekvenser som ingår i ackordet. Medelvärdet av dessa frekvensers amplituder i spektrumet ses som ett mått på ackordets styrka. På detta sätt jämförs styrkorna på de fördefinierade treklang-ackorden C, D, E, F, G, A och B i dur och moll. Det ackord med högst sådant medelvärde anses då vara det som sannolikt har spelats. De frekvenser vi letar efter för treklang-ackorden är grundfrekvensen, kvinten och tersen. Att leta efter dessa frekvenser har vi upptäckt ger bättre resultat än att leta efter grundtonen för de strängplock som ingår i varje ackord. Anledningen till att detta fungerar bättre är att grundtonerna för de låga strängplocken i ett ackord ofta har övertoner som överlappar grundtonerna hos de höga strängplocken i ackordet. Om en metod då letar efter varje enskild grundton hos ett ackords strängplock kommer den då även att mäta bidrag från låga strängars övertoner. Detta resulterar i ett oväntat högt amplitudmedelvärde och kan resultera i att fel ackord hittas, till synes av en slump. 4.4 Ljudanalys i realtid Ett spel som styrs av en gitarr måste analysera ljud i realtid. På grund av detta räcker det inte med att göra en lång inspelning som sedan analyseras. Spelet måste dela upp ljudinspelningen i mindre tidsintervall och analysera dessa inspelningar under spelets gång. Desto kortare inspelningstiden är desto kortare tid tar det innan spelet kan reagera på vad som spelats. Problemet här är, enligt slutet på teoriavsnittet 3.3, att möjligheten att skilja mellan frekvenser som ligger nära varandra blir sämre med kortare inspelningstid. Här måste en avvägning göras mellan noggrannheten i när ett ackord eller strängplock spelats och noggrannheten i avläsningen av vilka frekvenser det innehöll. Det viktigaste här är att spelet kan se skillnad på grundtonen hos de strängplock som kan spelas på en gitarr. Som nämns i teoriavsnittet 3.2 är skillnaden i ton mellan två efterföljande strängplock en halvton. Detta steg är i sin tur, enligt teoriavsnittet 3.1, proportionellt mot tonen man tar steget från. Alltså är inte skillnaden mellan två efterföljande strängplock fix, den beror istället på deras grundtoner och ökar med högre frekvens. Den minsta skillnaden som fås på en gitarr är mellan den öppna låga E strängen och när samma sträng anslås då första bandet är nedtryckt. Den öppna låga E strängen har en frekvens på 82.4 Hz och när det första bandet hålls ned ökar tonen med en halvton och frekvensen 87.3 Hz fås. Skillnaden här är 4.9 Hz. Således måste punkterna i spektrumet efter att Fast Fourier Transformen utförts ligga 4.9 Hz ifrån varandra eller närmare för att dessa två frekvenser ska hamna på varsin punkt i spektrumet. Om detta uppnås kommer varje strängplock på gitarren att hamna minst en punkt i spektrumet ifrån sin närmsta granne. Den inspelningstid som detta motsvarar kan lätt räknas ut. Som nämns i slutet på teoriavsnittet 3.3 är inspelningstiden direkt omvänt proportionell mot frekvensupplösningen. Ett punktavstånd i spektrumet på 4.9 Hz motsvarar en inspelningstid på 1 / 4.9 s = 204 ms. För att kunna urskilja den minsta skillnaden i grundton mellan strängplocken på en gitarr behöver alltså inspelningens längd vara mer än 204 ms. Med detta kan spelet skilja på alla gitarrens strängplock. Dock kan det inte avgöra om två toppar precis bredvid varandra i spektrumet kommer från två närliggande frekvenser eller om det är en enda frekvenstopp mitt emellan frekvenserna för punkterna som runnit över på dessa. Detta händer dock endast då två låga strängplock spelas snabbt i följd och hamnar i samma inspelning. En enkel lösning skulle vara att bara förlänga inspelningstiden. Dock skulle detta också föra med sig en ökad osäkerhet i när ackord och strängplock spelats. Vi har inte tagit fram någon lösning på detta och det blir istället en felkälla för oss vid inspelning av ackord och strängplock. 9
11 5 Resultat I detta kapitel beskrivs programmet. Här står vilket programmeringsspråk som använts, vilken färdig kod programmet bygger på, programmets olika delar beskrivs och hur spelet fungerar för användaren förklaras samt bilder på programmet visas. Programmet är i form av ett spel. Spelet består av menyer och spelskärmen. När spelet startas visas huvudmenyn varifrån det går att klicka vidare till ackordhjälpmenyn som visar hur de ackord spelet använder sig av spelas och en meny med en låtlista. Väljs en låt i låtlistan visas spelskärmen och spelet börjar. När låten är slut visas poängmenyn där de uppnådda poängen skrivs ut och hur många noter som träffats och så vidare. Figur 5-1: Spelets huvudmeny. I mitten av bilden ses tre knappar. Via knapparna kan spelaren klicka sig till låtlistan, ackordhjälpmenyn samt stänga spelet. 5.1 Språket Programmet är skrivet i programmeringsspråket Python. [7] Python är ett så kallat skriptspråk och har ett simpelt syntax. Språkuppbyggnaden liknar Java och C++ då det har de vanliga byggstenarna så som if-satser, for-loopar, while-loopar, funktioner och klasser. Fördelarna med Python som gjorde att vi valde språket är att det är enkelt, plattformsoberoende och att det finns mycket färdig kod att använda. En av nackdelarna med Python är att processorintensiva program många gånger inte blir lika snabba som program skrivna i t.ex. C++ eller Java. Trots att vi skulle göra ett spel, som generellt sett är väldigt krävande program, tyckte vi att fördelarna med Python övervägde nackdelarna. Språkets enkelhet gör att det går snabbt och lätt att skriva kod i det. Detta var viktigt för oss då vi ville koncentrera oss på ljudanalysen och att hinna få fram ett fungerande spel. Plattformsoberoendet var också viktigt för oss eftersom två av oss kör Windows medan en kör Mac. Det var avgörande att mycket färdig kod finns att tillgå gratis. Utan färdig kod skulle vi inte haft möjlighet att slutföra projektet på given tid. Den färdiga koden vi använder presenteras i avsnitt
12 5.2 Färdig kod Förutom den grundläggande funktionaliteten som finns inbyggd i Python använde vi oss av fem samlingar av färdig kod, kallade kodbibliotek. För inläsning av ljud använde vi oss av PyAudio, för grafik och fönster använde vi Pygame, för vektorberäkningar använde vi NumPy, för den diskreta Fouriertransformen använde vi SciPy och för att läsa in våra låtfiler använde vi PyYAML. [8-12] PyAudio är ett kodbibliotek som använder sig av PortAudio, ett kodbibliotek för programmeringsspråket C. Detta kodbibliotek klarar av att läsa in och spela upp ljud på flera olika plattformar, inklusive Windows, Linux och Mac. Man kan bland annat välja samplingsfrekvens, bufferstorlek och samplestorlek. [8] Pygame är ett kodbibliotek som använder sig av SDL, Simple DirectMedia Layer, ett kodbibliotek för programmeringsspråket C. Med detta kodbibliotek kan man öppna grafiska fönster, rita tvådimensionell grafik och hantera mus och tangentbord. Vi har använt detta kodbibliotek för att rita all grafik som syns i spelet samt för att ta emot musrörelser och klick och tangentbordstryck. [9] NumPy är ett kodbibliotek som har funktionalitet för att hantera stora vektorer och matriser. Kodbiblioteket innehåller också många väldigt optimerade matematiska operationer man kan utföra på dessa vektorer och matriser. Använder man dessa vektorer och matriser och de medföljande operationerna på dessa kan man skriva kod som går nästan lika snabbt som samma kod skriven snabbare språk så som C. Tack vare NumPy kan vårt spel utföra ganska många operationer på stora vektorer utan att det går sakta. [10] SciPy är ett kodbibliotek som har funktionalitet för signalanalys, diskret Fouriertransform, bildanalys, optimering etc. SciPy använder sig av NumPys vektorer och matriser. Vi använde SciPy för att utföra den diskreta Fouriertransformen på ljudet vi läst in med PyAudio. [11] PyYAML är ett kodbibliotek som kan läsa och skriva dataserialiseringsspråket YAML. Detta språk liknar andra dataserialiseringsspråk så som XML och JSON men är till för att vara lättare att läsa för människor. Det går snabbt och lätt att strukturera upp ett filformat med YAML som sedan lätt kan läsas in i ett program. Vi använde PyYAML för att läsa in våra låtfiler skrivna i YAML. [12] Förutom dessa fem kodbibliotek använde vi en färdig metod för att hitta amplitudtoppar i vektorer. Metoden hittades på internet och används i programmet för att avgöra vilka frekvenser som är starkast i en inspelad ljudsignal. [13] 5.3 Ljudinläsning Ljudet läses in via mikrofon med hjälp av PyAudio. Detta görs genom att en separat exekveringstråd startas vars enda uppgift är att läsa ljuddata med PyAudio och skicka vidare denna data till spelets huvudtråd. I huvudtråden körs huvudloopen som sköter ljudanalys, mus och tangentbord, jämföring av funna ackord och strängplock med sången och uppritning av grafik. Under ljudanalysen används den diskreta Fouriertransformen i form av Fast Fourier transformen från kodbiblioteket SciPy. Efter detta används olika metoder vi tagit fram och läst om, beskrivna under rubriken metoder. Typiska värden vi använt på samplingsfrekvensen är 8192 Hz med en bufferstorlek på 2048 sampel, dvs. ett fönster på 250 ms. Vi använder en sampelstorlek på 16 bitar som ger oss en amplitud för varje sampel på mellan och
13 5.4 Grafik och användargränssnitt För att öppna fönster, rita grafik och hantera mus och tangentbord använde vi kodbiblioteket Pygame. Ovanpå Pygame utvecklades ett grafiksystem uppbyggt av skärmar som i sig fylls med grafikelement. För varje meny i spelet finns en speciell fördefinerad skärm fylld med de grafikelement som ska synas. Ett grafikelement kan vara till exempel en knapp, en text eller en färgad ruta. Spelets grafik drivs med mus och tangentbord via händelser. Varje mustryck, musförflyttning och tangentbordstryck översätts av Pygame till en händelse som sedan hanteras av spelet. Händelser från musen skickas till det grafikelement som befinner sig under musen då händelsen skedde. Ett grafikelement väljer sedan själv om den ska hantera händelsen. På detta sätt kan en knapp tryckas in genom att föra musen över den och klicka medan en text inte påverkas av musen. De skärmar som finns i spelet hanteras i grafiksystemet av en så kallad skärmhållare. Den skärm som är synlig kan signalera till skärmhållaren att en annan skärm ska öppnas. Skärmhållaren byter då till denna samtidigt som den sparar en historik över vilka skärmar som varit öppna. På det sättet kan en skärm signalera till skärmhållaren att den ska gå tillbaka till föregående skärm utan att den signalerande skärmen själv vet vilken skärm som var dess föregångare. 5.5 Låtfiler och låtinläsning Varje låt som kan väljas från låtlistan är sparad i en egen låtfil. Låtfilerna följer ett format som vi själva skapat med hjälp av YAML. I varje låtfil står låtnamn, författare, svårighetsgrad, längd, fördröjning innan start och slag per minut. Förutom denna information innehåller varje låt också en lista med noter. Varje not har en typ, plock eller ackord, och ett värde på hur många taktslag som ska passera från förra noten innan noten ska spelas. Noter av typen plock innehåller vilken sträng och vilket band som ska spelas och noter av typen ackord innehåller vilket av de fördefinerade ackorden som ska spelas. När en låt startas läses den först in i spelet med hjälp av PyYAML och översätts sedan till spelets interna sätt att representera låtar. 5.6 Att spela Väl inne i spelet visas vilka noter som ska spelas och när de ska spelas. Det som visas på skärmen under spelets gång är noterna, strängarna, träffzonen, poängtavlan, tidsmätaren, ljudintensitetsmätaren, paustexten samt en tillbakaknapp. Noterna rör sig från höger till vänster. Varje not representerar antingen ett ackord eller ett strängplock och är placerade på strängarna beroende på vilken eller vilka strängar som ska spelas för noten. Noter som representerar ackord sträcker sig över de strängar som ingår i ackordet. Noter som representerar strängplock ligger på den sträng som de ska spelas på. Noterna för strängplock visar också en siffra för att indikera vilket band som ska spelas. När en not spelas då den befinner sig i träffzonen färgas dess kant grön för att indikera detta. Om en not hinner röra sig igenom träffzonen utan att den spelas färgas dess kant röd för att visa att den missades. Noter som inte kommit in i träffzonen har svart kantfärg. Träffzonen ligger till vänster om mitten och utgörs av ett stort grönt fält. Från högra kanten på träffzonen sträcker sig strängarna hela vägen till högra kanten på skärmen. Poängtavlan visar hur många poäng spelaren uppnåt samt hur hög multiplicerare spelaren har. Multipliceraren går från 1 upp till max 4 och ökar med ett varje gång en not spelas inom träffzonen. Poängen spelaren får när den spelar en not inom träffzonen multipliceras med multipliceraren. Det lönar sig därför extra mycket att spela rätt flera gånger i rad. 12
14 Längs skärmens undre kant visas tidsmätaren, paustexten och tillbakaknappen. Tidsmätaren fylls från låtens början till dess slut för att visa hur långt som gått och hur långt som är kvar på låten. Paustexten talarom för användaren hur spelet pausas. Klickar spelaren på tillbakaknappen tas den från spelet till låtlistan. Vid skärmens vänstra kant visas en ljudintensitetsmätare. Denna kan användas för att få en uppfattning av om datorns mikrofon tar emot ljud som den ska. Spelas något på en gitarr bör ett tydligt utslag synas på mätaren. Figur 5-1: Skärmdump som visar spelskärmen. Till vänster om mitten syns den gröna träffzonen. Från dess högra kant och åt höger är gitarrsträngarna representerade. Till vänster inom träffzonen syns en ackord-not. Dess gröna kant indikerar att den spelades inom träffzonen. Noten till vänster om denna har röd kant för att indikera att den aldrig spelades inom träffzonen. Noterna till höger om båda dessa har alla svart kant, de har inte kommit in i träffzonen än. Uppe i vänster syns poängtavlan, till vänster intensitetsmätaren och nere längs skärmens underkant syns tidsmätaren, paustexten och tillbakaknappen. 13
15 6 Diskussion I detta kapitel tar vi upp våra tankar kring varför vi valt de metoder vi valt och tankar kring resultatet. Det diskuteras även kring vilka programförbättringar man kan tänka sig och vilka begränsningar just vårt program har. 6.1 Metoddiskussion Under arbetets gång har problem dykt upp och dessa har lösts med olika metoder. Detta avsnitt tar upp tankar kring de metoder vi valt och varför vi valt dem. När frekvensspektrumen från olika anslag av samma sträng jämfördes visade det sig att frekvenskomponenternas amplituder varierar kraftigt. Ibland blir grundtonen starkare än övertonerna, ibland blev vissa övertoner starkare än grundtonen. Brus kan också ställa till med problem och ibland se ut som toner som inte borde finnas där. Situationen blir än mer komplicerad då flera strängar anslås samtidigt. Här kan vibrationer från en anslagen sträng få en icke anslagen sträng i svängning på grund av att till exempel övertoner matchar. På så vis kan oförutsedda frekvenser hittas. Dessa vibrationer håller sig dock oftast tillräckligt små för att de inte ska ställa till med problem. Figurerna 6.1-1och visar frekvensspektrumet för två olika anslag av ackordet D-dur. Figur 6.1-1: Effektspektrum av ett spelat D-dur. De frekvenskomponenter som ingår är 146, 220, 293 samt 370 Hz. Noter att amplituden vid D-dur ackordets frekvens 370 Hz är osynligt låg samt att amplituderna på övertonerna är väldigt låga. Figur 6.1-2: Effektspektrum av D-dur. De frekvenskomponenter som ingår är 146, 220, 293 samt 370 Hz. Noter att amplituden vid D-dur ackordets frekvens 370 Hz är osynligt låg samt hur amplituderna på övertonerna varierar väldigt mycket. 14
16 Oregelbundheterna i effektspektrumen skapade problem då vi till en början funderade på att använda ett matchat filter för att avgöra vilken/vilka sträng/strängar som slagits. Det gick inte att använda då vi inte riktigt kan förutse hur frekvensspektrumet kommer se ut. Tanken att digitalt skapa ett idealt plock/ackord och sedan göra ett matchat filter utifrån detta fanns. Detta tror vi dock hade varit svårt att göra i praktiken. Dels måste ett filter skapas för alla ackord/plock vi vill ha med i programmet. Dels hade vi troligtvis varit tvungna att skicka signalen genom var och ett av de matchade filter vi skapat. Med denna metod måste också fasen hos inspelningen relativt filtrena tas i beaktning. Metoden vi använder där vi hittar ackord genom att leta efter det ackord vars frekvenser har det största medelvärdet bland de fördefinerade ackorden har sina problem. Det kan vara svårt att skilja på två ackord som har många frekvenser gemensamma. Med oregelbundenheterna i amplituder som uppvisas och andra strängar som klingar kvar sedan tidigare, kan då ett närliggande ackord hittas om det medelvärdet råkar bli större. En möjlighet att hitta strängplock som övervägdes är att titta efter största topparna i frekvensspektrumet. En nackdel med denna metod är att man snabbt märker att grundtonen hos ett strängplock sällan är den största toppen i frekvensspektrumet. Denna metod hade, om den implementerades i ett spel, oftast resulterat i att spelet tror att spelaren spelar en av övertonerna i strängplocket och inte själva grundtonen. Om denna metod används men spelet istället letar i spektrumet och ger rätt direkt om den hittar frekvensen den letar efter skulle det istället bli väldigt lätt att fuska. Spelaren skulle ofta kunna slå på måfå och träffa rätt frekvens med något strängplock eller överton. Vår lösning på detta problem var att använda Harmonic Product Spectrum metoden, vilken beskrivs i avsnitt 4.1. Under våra tester hittar denna metod oftast rätt grundton bland topparna i ett frekvensspektrum vid ett spelat strängplock. Denna metod skulle dock kunna kompletteras med andra metoder som räknar före, efter eller på sidan om för att förbättra resultatet. Vi har dock funnit att metoden räcker för våra ändamål. 15
17 6.2 Resultatdiskussion Som beskrivs mer ingående i avsnitt 2 ställde vi upp följande huvudmål inför projektet. Spelet som slutprodukt skulle: kunna spelas på en vanlig dator med mikrofon, kunna användas med en vanlig, välstämd nylonsträngad akustisk gitarr, känna igen de vanliga treklang-ackorden A-G i dur och moll, ha få störningsmoment och ha ett grafiskt användargränssnitt. Slutprodukten uppfyller denna målsättning. Spelet fungerar på de allra flesta datorer som är utrustade med en mikrofon. Under utvecklingen användes nylonsträngade gitarrer och spelet kan då hitta treklang-ackorden A-G i dur och moll. Under spelets gång störs inte användaren av att spelet beter sig oväntat eller att det inte hittar tillräckligt många av de spelade ackorden och strängplocken. Hela spelet inklusive menyer och gränssnitt då man spelar visas grafiskt. Potentiella störningsmoment är till exempel fördröjning från anslag av ackord eller strängplock tills dess att spelet reagerar och att spelet inte hittar de ackord och strängplock som spelas. Fördröjningen påverkas av hur lång tid ljud spelas in innan det analyseras och hur lång denna analys tar. Vi fann under utvecklingen att en inspelningstid per block på 250 ms täcker alla krav vi ställde på noggrannhet vid urskiljning av frekvenser. Här blir beräkningstiden obetydlig då den ofta hamnar runt ms. Vi märkte att denna fördröjning inte upplevs störande då spelet spelas. Under våra tester av spelet har vi också märkt att det hittar rätt ackord och strängplock oftare än 9 av 10 gånger. Detta upplevs enligt oss under spelets gång inte som störande. Spelet kräver att en välstämd nylonsträngad gitarr används. Detta kommer av att frekvensspektrumet förvrängs om gitarren är felstämd samt att frekvensspektrumet skiljer sig mellan olika strängtyper. Båda begränsningarna ansågs vara vettiga för detta projekt eftersom det är lätt att stämma en gitarr tillräckligt bra med en vanlig stämapparat och nylonsträngning är väldigt vanlig på akustiska gitarrer. Utöver detta krävs också att vissa parametrar i spelet ställs in för varje dator och gitarrkombination. Detta beror på att varje mikrofon hör varje frekvens olika starkt och att varje gitarr ger ifrån sig olika starka övertoner. Ackord som har många frekvenser gemensamt är svårare att skilja från varandra. Någon enstaka gång kan man kan få rätt för andra ackord än det man ska spela om dess frekvenskomponenter är snarlika. Detta händer oftast för dur och moll ackord för samma ton men också, mer sällan, för ackord för olika toner. En bieffekt av att inspelningstiden för varje block är 250 ms blir att det är svårt att skilja på ackord som spelas kortare än 500 ms ifrån varandra. Detta måste tas i hänsyn när en låt skapas för spelet. Eftersom 500 ms ofta är en ganska kort tidsperiod i jämförelse med hur lång tid det tar att spela ett ackord så orsakar denna begränsning sällan problem. 16
18 6.3 Programförbättringar Spelet klarar nu av de vanligaste ackorden. Detta går naturligtvis att utöka så fler ackord ingår. Man kan även tänka sig att det går att hitta en algoritm som kan urskilja olika gitarrtekniker såsom slide, då en sträng anslås på ett band varefter det finger som håller ned strängen hålls nedtryckt och dras till ett annat band, och hammer on, då strängen hålls ned på ett nytt lägre band då den redan svänger. Det förutsätter dock att det finns något regelbundet mönster i spektrumet som man kan identifiera på ett tillförlitligt sätt. Det skulle också vara möjligt att lägga till fler lägen i spelet så att det kan användas med fler instrument än nylonsträngad akustisk gitarr. Om man studerar spektrumet från instrumentet och ser vad som är karaktäristiskt för dess olika toner skulle detta inte vara ett allt för stort projekt. Spelet skulle då kunna ha en till meny där man väljer instrument och sedan låt man vill spela. Eftersom listan av ackord och plockade strängar är lång finns möjligheter att göra väldigt många låtar. Problemet med att inspelningstiden per block är 250 ms, att ackord inte kan komma för tätt i spelets låtar, skulle kunna lösas genom att spelet spelar in under kortare tidsintervall. Dessa kortare inspelningar skulle sedan analyseras flera åt gånger samtidigt som de block som analyseras byts ut en åt gången. På detta sätt skulle upplösningen i frekvens kunna behållas samtidigt som en ökad uppfattning om när ett ackord spelats skulle fås. Som spelet är nu måste en ny textfil skapas manuellt för varje låt som läggs till i spelet. För att göra denna process enklare skulle en låteditor kunna konstrueras. Här skulle användaren kunna grafiskt lägga in de ackord och strängplock som ska spelas och bestämma när de ska spelas. Editorn skulle också kunna utnyttja spelets förmåga att läsa av vad som spelas på en gitarr för att föra in ackord och strängplock i låteditorn, vilka sedan skulle kunna justeras grafiskt i editorn. Denna inspelning från gitarr skulle få begränsningen att det inte går att avgöra med större noggrannhet än 250 ms när ett ackord eller plock spelades då inspelningstiden är 250 ms per block innan ljud analyseras. Det skulle också kunna bli omständigt eftersom spelet ofta hittar fler ackord och strängplock än de som faktiskt spelats. En annan möjlighet är att låteditorn skulle kunna läsa in redan etablerade format så som MIDI [14] eller GuitarPro-filer [15]. Som spelet fungerar nu behöver några värden ställas om för varje kombination av dator och gitarr. Detta skulle kunna åtgärdas genom att man lägga till en kalibreringsfunktion i spelet. Denna funktion skulle låta spelaren spela på sin gitarr och analysera amplitudnivåerna på de frekvenser som spelet hör. Denna information skulle kunna sparas för att normalisera amplituden mellan olika frekvenser och på så sätt komma runt problemet med att olika mikrofoner hör olika frekvenser olika bra. Detta skulle kunna sparas som en profil för varje mikrofon och gitarr som spelaren har. Det skulle också kunna finnas fördefinierade profiler för olika sorters gitarrer för att hantera att olika gitarrer ger ifrån sig olika starka övertoner. 7 Slutsatser Med tanke på framgången som Guitar Hero haft kan man fundera på varför spel för riktiga gitarrer inte växt och blivit stora. Vi har i och med detta projekt visat att det går att skapa ett spel till vanliga PC datorer som går att styras med en vanlig gitarr via datorns mikrofon. Det resulterande spelet uppfyller vår målsättning och dess spelbarhet är mycket god. Den tid vi lagt ned på detta spel motsvarar inte alls den tid som läggs ner på kommersiella spel vilket borde tyda på att de problem och förbättringsmöjligheter vi sett bör kunna lösas ifall någon skulle ta denna ide och realisera den på marknaden. 17
19 8 Referenser [1] Musikspelet Guitar Hero [2] Spänd strängs svängningsfrekvenser [3] Fouriertransformen [4] Frekvensupplösning vid diskret Fouriertransformering G. Heinzel, A. Rudiger och R. Schilling, : Spectrum and spectral density estimation by the Discrete Fourier transform (DFT), including a comprehensive list of window functions and some new at-top windows. Teilinstitut Hannover. [5] MATLAB [6] Harmonic Product Spectrum metoden M. R. Schroeder : Period Histogram and Product Spectrum: New Methods for Fundamental-Frequency Measurement. Bell Telephone Laboratories, Murray Hill, New Jersey. [7] Python [8] PyAudio [9] Pygame [10] NumPy [11] SciPy [12] PyYAML [13] Metod för att hitta toppar i vektorer, Eli Billauer [14] Ljudfilformatet MIDI [15] Gitarrprogrammet GuitarPro 18
Signalbehandling Röstigenkänning
 L A B O R A T I O N S R A P P O R T Kurs: Klass: Datum: I ämnet Signalbehandling ISI019 Enk3 011211 Signalbehandling Röstigenkänning Jonas Lindström Martin Bergström INSTITUTIONEN I SKELLEFTEÅ Sida: 1
L A B O R A T I O N S R A P P O R T Kurs: Klass: Datum: I ämnet Signalbehandling ISI019 Enk3 011211 Signalbehandling Röstigenkänning Jonas Lindström Martin Bergström INSTITUTIONEN I SKELLEFTEÅ Sida: 1
Tema - Matematik och musik
 Tema - Matematik och musik Författarna och Bokförlaget Borken, 2011 Allt vi uppfattar som ljud, från den nästan smärtsamma upplevelsen på en rockkonsert till insekternas surr en sommardag, består av mer
Tema - Matematik och musik Författarna och Bokförlaget Borken, 2011 Allt vi uppfattar som ljud, från den nästan smärtsamma upplevelsen på en rockkonsert till insekternas surr en sommardag, består av mer
Ulrik Söderström 20 Jan Signaler & Signalanalys
 Ulrik Söderström ulrik.soderstrom@tfe.umu.se 20 Jan 2009 Signaler & Signalanalys Sinusspänning Sinus och cosinus samma form men fasförskjutna Fasförskjutning tidsfördröjning Sinus och cosinus är väldigt
Ulrik Söderström ulrik.soderstrom@tfe.umu.se 20 Jan 2009 Signaler & Signalanalys Sinusspänning Sinus och cosinus samma form men fasförskjutna Fasförskjutning tidsfördröjning Sinus och cosinus är väldigt
DIGITALA FILTER. Tillämpad Fysik Och Elektronik 1. Frekvensfunktioner FREKVENSSVAR FÖR ETT TIDSDISKRET SYSTEM. x(n)= Asin(Ωn)
 DIGITALA FILTER TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 1 Frekvensfunktioner x(n)= Asin(Ωn) y(n) H(z) TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 2 FREKVENSSVAR FÖR ETT TIDSDISKRET SYSTEM
DIGITALA FILTER TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 1 Frekvensfunktioner x(n)= Asin(Ωn) y(n) H(z) TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 2 FREKVENSSVAR FÖR ETT TIDSDISKRET SYSTEM
Ulrik Söderström 19 Jan Signalanalys
 Ulrik Söderström ulrik.soderstrom@tfe.umu.se 9 Jan 200 Signaler & Signalanalys l Sinusspänning Sinus och cosinus samma form men fasförskjutna Fasförskjutning tidsfördröjning Sinus och cosinus är väldigt
Ulrik Söderström ulrik.soderstrom@tfe.umu.se 9 Jan 200 Signaler & Signalanalys l Sinusspänning Sinus och cosinus samma form men fasförskjutna Fasförskjutning tidsfördröjning Sinus och cosinus är väldigt
TEM Projekt Transformmetoder
 TEM Projekt Transformmetoder Utförs av: Mikael Bodin 19940414 4314 William Sjöström 19940404 6956 Sammanfattning I denna laboration undersöks hur Fouriertransformering kan användas vid behandling och analysering
TEM Projekt Transformmetoder Utförs av: Mikael Bodin 19940414 4314 William Sjöström 19940404 6956 Sammanfattning I denna laboration undersöks hur Fouriertransformering kan användas vid behandling och analysering
Prov i vågrörelselära vt06 Lösningsförslag
 Prov i vågrörelselära vt06 Lösningsförslag Hjälpmedel: Formelsamling, fysikbok, miniräknare, linjal, sunt förnuft. 7 uppgifter vilka inlämnas på separat papper snyggt och välstrukturerat! Låt oss spela
Prov i vågrörelselära vt06 Lösningsförslag Hjälpmedel: Formelsamling, fysikbok, miniräknare, linjal, sunt förnuft. 7 uppgifter vilka inlämnas på separat papper snyggt och välstrukturerat! Låt oss spela
Tentamen i TMA 982 Linjära System och Transformer VV-salar, 27 aug 2013, kl
 Tentamen i TMA 982 Linjära System och Transformer VV-salar, 27 aug 2013, kl 8.30-12.30 Examinatorer: Lars Hammarstrand och Thomas Wernstål Tentamen består av två delar (Del I och Del II) på sammanlagt
Tentamen i TMA 982 Linjära System och Transformer VV-salar, 27 aug 2013, kl 8.30-12.30 Examinatorer: Lars Hammarstrand och Thomas Wernstål Tentamen består av två delar (Del I och Del II) på sammanlagt
Bildbehandling i frekvensdomänen
 Uppsala Tekniska Högskola Signaler och system Handledare: Mathias Johansson Uppsala 2002-11-27 Bildbehandling i frekvensdomänen Erika Lundberg 800417-1602 Johan Peterson 790807-1611 Terese Persson 800613-0267
Uppsala Tekniska Högskola Signaler och system Handledare: Mathias Johansson Uppsala 2002-11-27 Bildbehandling i frekvensdomänen Erika Lundberg 800417-1602 Johan Peterson 790807-1611 Terese Persson 800613-0267
Upp gifter. c. Hjälp Bengt att förklara varför det uppstår en stående våg.
 1. Bengt ska just demonstrera stående vågor för sin bror genom att skaka en slinkyfjäder. Han lägger fjädern på golvet och ber sin bror hålla i andra änden. Sen spänner han fjädern genom att backa lite
1. Bengt ska just demonstrera stående vågor för sin bror genom att skaka en slinkyfjäder. Han lägger fjädern på golvet och ber sin bror hålla i andra änden. Sen spänner han fjädern genom att backa lite
Grundläggande ljud- och musikteori
 Grundläggande ljud- och musikteori Jan Thim Magnus Eriksson Lektionens syfte Syftet med denna lektion är är att att ge ge förståelse för för decibelbegreppet, spektrum, digitalisering och och olika olika
Grundläggande ljud- och musikteori Jan Thim Magnus Eriksson Lektionens syfte Syftet med denna lektion är är att att ge ge förståelse för för decibelbegreppet, spektrum, digitalisering och och olika olika
Projekt 3: Diskret fouriertransform
 Projekt 3: Diskret fouriertransform Diskreta fouriertransformer har stor praktisk användning inom en mängd olika områden, från analys av mätdata till behandling av digital information som ljud och bildfiler.
Projekt 3: Diskret fouriertransform Diskreta fouriertransformer har stor praktisk användning inom en mängd olika områden, från analys av mätdata till behandling av digital information som ljud och bildfiler.
Att fånga den akustiska energin
 Att fånga den akustiska energin När vi nu har en viss förståelse av vad ljud egentligen är kan vi börja sätta oss in i hur det kan fångas upp och efterhand lagras. När en ljudvåg sprider sig är det inte
Att fånga den akustiska energin När vi nu har en viss förståelse av vad ljud egentligen är kan vi börja sätta oss in i hur det kan fångas upp och efterhand lagras. När en ljudvåg sprider sig är det inte
Spektrala Transformer
 Spektrala Transformer Tidsdiskreta signaler, kvantisering & sampling Tidsdiskreta signaler Tidskontinuerlig signal Ex: x(t) = sin(ωt) t är ett reellt tal ω har enheten rad/s Tidsdiskret signal Ex: x(n)
Spektrala Transformer Tidsdiskreta signaler, kvantisering & sampling Tidsdiskreta signaler Tidskontinuerlig signal Ex: x(t) = sin(ωt) t är ett reellt tal ω har enheten rad/s Tidsdiskret signal Ex: x(n)
DIGITALA FILTER DIGITALA FILTER. Tillämpad Fysik Och Elektronik 1
 DIGITALA FILTER TILLÄMPAD FYIK OCH ELEKTRONIK, UMEÅ UNIVERITET 1 DIGITALA FILTER Digitala filter förekommer t.ex.: I Photoshop och andra PC-programvaror som filtrerar. I apparater med signalprocessorer,
DIGITALA FILTER TILLÄMPAD FYIK OCH ELEKTRONIK, UMEÅ UNIVERITET 1 DIGITALA FILTER Digitala filter förekommer t.ex.: I Photoshop och andra PC-programvaror som filtrerar. I apparater med signalprocessorer,
Mål med temat vad är ljud?
 Vad är ljud? När vi hör är det luftens molekyler som har satts i rörelse. När en mygga surrar och låter är det för att den med sina vingar puttar på luften. När en högtalare låter är det för att den knuffar
Vad är ljud? När vi hör är det luftens molekyler som har satts i rörelse. När en mygga surrar och låter är det för att den med sina vingar puttar på luften. När en högtalare låter är det för att den knuffar
Grundläggande signalbehandling
 Beskrivning av en enkel signal Sinussignal (Alla andra typer av signaler och ljud kan skapas genom att sätta samman sinussignaler med olika frekvens, Amplitud och fasvridning) Periodtid T y t U Amplitud
Beskrivning av en enkel signal Sinussignal (Alla andra typer av signaler och ljud kan skapas genom att sätta samman sinussignaler med olika frekvens, Amplitud och fasvridning) Periodtid T y t U Amplitud
Läslandet 2 Ord och meningar
 Läslandet 2 Ord och meningar Av LäraMera Program AB och Leripa AB Grafik Musik Röst Kristina Grundström Erik truedsson Gerda Nilsson 1 Innehållsförteckning LÄSLANDET 2 ORD OCH MENINGAR 3 Styrsätt 4 Menyn
Läslandet 2 Ord och meningar Av LäraMera Program AB och Leripa AB Grafik Musik Röst Kristina Grundström Erik truedsson Gerda Nilsson 1 Innehållsförteckning LÄSLANDET 2 ORD OCH MENINGAR 3 Styrsätt 4 Menyn
Spektralanalys - konsten att hitta frekvensinnehållet i en signal
 Spektralanalys - konsten att hitta frekvensinnehållet i en signal Bengt Carlsson, Erik Gudmundson och Marcus Björk Systems and Control Dept. of Information Technology, Uppsala University 7 november 013
Spektralanalys - konsten att hitta frekvensinnehållet i en signal Bengt Carlsson, Erik Gudmundson och Marcus Björk Systems and Control Dept. of Information Technology, Uppsala University 7 november 013
Mätningar med avancerade metoder
 Svante Granqvist 2008-11-12 13:41 Laboration i DT2420/DT242V Högtalarkonstruktion Mätningar på högtalare med avancerade metoder Med datorerna och signalprocessningens intåg har det utvecklats nya effektivare
Svante Granqvist 2008-11-12 13:41 Laboration i DT2420/DT242V Högtalarkonstruktion Mätningar på högtalare med avancerade metoder Med datorerna och signalprocessningens intåg har det utvecklats nya effektivare
Spektrala Transformer
 Spektrala Transformer Tidsdiskreta signaler, kvantisering & sampling Tidsdiskreta signaler Tidskontinuerlig signal Ex: x(t) = sin(ωt) t är ett reellt tal ω har enheten rad/s Tidsdiskret signal Ex: x(n)
Spektrala Transformer Tidsdiskreta signaler, kvantisering & sampling Tidsdiskreta signaler Tidskontinuerlig signal Ex: x(t) = sin(ωt) t är ett reellt tal ω har enheten rad/s Tidsdiskret signal Ex: x(n)
Laboration i Fourieranalys, TMA132 Signalanalys med snabb Fouriertransform
 Laboration i Fourieranalys, TMA132 Signalanalys med snabb Fouriertransform Den laborationen har syften: dels att visa lite hur den snabba Fouriertransformen fungerar, och lite om vad man den an dels att
Laboration i Fourieranalys, TMA132 Signalanalys med snabb Fouriertransform Den laborationen har syften: dels att visa lite hur den snabba Fouriertransformen fungerar, och lite om vad man den an dels att
Ljudnivåmätare med frekvensanalysator Art.nr: 61508
 Förrådsgatan 33A 542 35 Mariestad Tel: 0501 163 44 Fax: 0501 787 80 Ljudnivåmätare med frekvensanalysator Art.nr: 61508 Grundläggande inställningar och mätning På/Av Man startar ljudnivåmätaren genom att
Förrådsgatan 33A 542 35 Mariestad Tel: 0501 163 44 Fax: 0501 787 80 Ljudnivåmätare med frekvensanalysator Art.nr: 61508 Grundläggande inställningar och mätning På/Av Man startar ljudnivåmätaren genom att
Digital signalbehandling Digitalt Ljud
 Signalbehandling Digital signalbehandling Digitalt Ljud Bengt Mandersson Hur låter signalbehandling Institutionen för elektro- och informationsteknik 2008-10-06 Elektronik - digital signalbehandling 1
Signalbehandling Digital signalbehandling Digitalt Ljud Bengt Mandersson Hur låter signalbehandling Institutionen för elektro- och informationsteknik 2008-10-06 Elektronik - digital signalbehandling 1
Signalanalys med snabb Fouriertransform
 Laboration i Fourieranalys, MVE030 Signalanalys med snabb Fouriertransform Den här laborationen har två syften: dels att visa lite på hur den snabba Fouriertransformen fungerar, och lite om vad man bör
Laboration i Fourieranalys, MVE030 Signalanalys med snabb Fouriertransform Den här laborationen har två syften: dels att visa lite på hur den snabba Fouriertransformen fungerar, och lite om vad man bör
Faltningsreverb i realtidsimplementering
 Faltningsreverb i realtidsimplementering SMS45 Lp1 26 DSP-system i praktiken Jörgen Anderton - jorand-3@student.ltu.se Henrik Wikner - henwik-1@student.ltu.se Introduktion Digitala reverb kan delas upp
Faltningsreverb i realtidsimplementering SMS45 Lp1 26 DSP-system i praktiken Jörgen Anderton - jorand-3@student.ltu.se Henrik Wikner - henwik-1@student.ltu.se Introduktion Digitala reverb kan delas upp
Ämnesområde Hörselvetenskap A Kurs Akustik och ljudmiljö, 7 hp Kurskod: HÖ1015 Tentamenstillfälle 4
 IHM Kod: Ämnesområde Hörselvetenskap A Kurs Akustik och ljudmiljö, 7 hp Kurskod: HÖ115 Tentamenstillfälle 4 Datum 213-11-7 Tid 4 timmar Kursansvarig Susanne Köbler Tillåtna hjälpmedel Miniräknare Linjal
IHM Kod: Ämnesområde Hörselvetenskap A Kurs Akustik och ljudmiljö, 7 hp Kurskod: HÖ115 Tentamenstillfälle 4 Datum 213-11-7 Tid 4 timmar Kursansvarig Susanne Köbler Tillåtna hjälpmedel Miniräknare Linjal
Samtidig visning av alla storheter på 3-fas elnät
 Samtidig visning av alla storheter på 3-fas elnät Med nätanalysatorerna från Qualistar+ serien visas samtliga parametrar på tre-fas elnätet på en färgskärm. idsbaserad visning Qualistar+ visar insignalerna
Samtidig visning av alla storheter på 3-fas elnät Med nätanalysatorerna från Qualistar+ serien visas samtliga parametrar på tre-fas elnätet på en färgskärm. idsbaserad visning Qualistar+ visar insignalerna
Laboration i Fourieroptik
 Laboration i Fourieroptik David Winge Uppdaterad 30 januari 2015 1 Introduktion I detta experiment ska vi titta på en verklig avbildning av Fouriertransformen. Detta ska ske med hjälp av en bild som projiceras
Laboration i Fourieroptik David Winge Uppdaterad 30 januari 2015 1 Introduktion I detta experiment ska vi titta på en verklig avbildning av Fouriertransformen. Detta ska ske med hjälp av en bild som projiceras
Hörselkontroll Bullerskydd med öronproppar
 Laborationer i miljöfysik Hörselkontroll Bullerskydd med öronproppar Målet med övningen är att ta upp ett audiogram för en person, samt att undersöka hur mycket ljudet dämpas i olika frekvensområden med
Laborationer i miljöfysik Hörselkontroll Bullerskydd med öronproppar Målet med övningen är att ta upp ett audiogram för en person, samt att undersöka hur mycket ljudet dämpas i olika frekvensområden med
1 Kravspecifikation Snake App
 Kravspecifikation Snake App - Kravspecifikation Snake App Utskriven/PDF Export: 2011-09-07 Copyright 2011 Sidan 1 av 7 1 Kravspecifikation Snake App 1.1 Vad är Snake App? Vi skall gör ett Snake Spel för
Kravspecifikation Snake App - Kravspecifikation Snake App Utskriven/PDF Export: 2011-09-07 Copyright 2011 Sidan 1 av 7 1 Kravspecifikation Snake App 1.1 Vad är Snake App? Vi skall gör ett Snake Spel för
Tentamen ssy080 Transformer, Signaler och System, D3
 Tentamen ssy080 Transformer, Signaler och System, D3 Examinator: Ants R. Silberberg 19 oktober 2011 kl. 08.30-12.30 sal: Hörsalsvägen Förfrågningar: Ants Silberberg, tel. 1808 Lösningar: Anslås torsdag
Tentamen ssy080 Transformer, Signaler och System, D3 Examinator: Ants R. Silberberg 19 oktober 2011 kl. 08.30-12.30 sal: Hörsalsvägen Förfrågningar: Ants Silberberg, tel. 1808 Lösningar: Anslås torsdag
Words and Sentences Träna engelska!
 Words and Sentences Träna engelska! Av LäraMera Program AB och Leripa AB Grafik Musik Röst Kristina Grundström Erik truedsson Helen Melhuish 1 Innehållsförteckning WORDS AND SENTENCES 1 Words and Sentences
Words and Sentences Träna engelska! Av LäraMera Program AB och Leripa AB Grafik Musik Röst Kristina Grundström Erik truedsson Helen Melhuish 1 Innehållsförteckning WORDS AND SENTENCES 1 Words and Sentences
Guide till att använda Audacity för uttalsövningar
 Guide till att använda Audacity för uttalsövningar Victoria Johansson Humlabbet, SOL-center, Lund IT-pedagog@sol.lu.se 28 mars 2006 1 Inledning Audacity är ett program som kan användas för att spela in
Guide till att använda Audacity för uttalsövningar Victoria Johansson Humlabbet, SOL-center, Lund IT-pedagog@sol.lu.se 28 mars 2006 1 Inledning Audacity är ett program som kan användas för att spela in
Spektrala Transformer
 Spektrala Transformer Kurssammanfattning Fyra kärnkoncept Sampling Faltning Poler och nollställen Fouriertransform Koncept #1: Sampling En korrekt samplad signal kan rekonstrueras exakt, dvs ingen information
Spektrala Transformer Kurssammanfattning Fyra kärnkoncept Sampling Faltning Poler och nollställen Fouriertransform Koncept #1: Sampling En korrekt samplad signal kan rekonstrueras exakt, dvs ingen information
Programmeringsuppgift Game of Life
 CTH/GU STUDIO TMV06a - 0/0 Matematiska vetenskaper Programmeringsuppgift Game of Life Analys och Linär Algebra, del A, K/Kf/Bt Inledning En cellulär automat är en dynamisk metod som beskriver hur komplicerade
CTH/GU STUDIO TMV06a - 0/0 Matematiska vetenskaper Programmeringsuppgift Game of Life Analys och Linär Algebra, del A, K/Kf/Bt Inledning En cellulär automat är en dynamisk metod som beskriver hur komplicerade
DT1130 Spektrala transformer Tentamen
 DT3 Spektrala transformer Tentamen 6 Tentamen består av fem uppgifter där varje uppgift maximalt ger 4 p. Normalt gäller följande betygsgränser: E: 9 p, D:.5 p, C: 4 p, B: 6 p, A: 8 p Tillåtna hjälpmedel:
DT3 Spektrala transformer Tentamen 6 Tentamen består av fem uppgifter där varje uppgift maximalt ger 4 p. Normalt gäller följande betygsgränser: E: 9 p, D:.5 p, C: 4 p, B: 6 p, A: 8 p Tillåtna hjälpmedel:
Ett enkelt OCR-system
 P r o j e k t i B i l d a n a l y s Ett enkelt OCR-system av Anders Fredriksson F98 Fredrik Rosqvist F98 Handledare: Magnus Oskarsson Lunds Tekniska Högskola 2001-11-29 - Sida 1 - 1.Inledning Många människor
P r o j e k t i B i l d a n a l y s Ett enkelt OCR-system av Anders Fredriksson F98 Fredrik Rosqvist F98 Handledare: Magnus Oskarsson Lunds Tekniska Högskola 2001-11-29 - Sida 1 - 1.Inledning Många människor
ANVÄNDARGUIDE VITAL & TALANDE TANGENTBORD
 ANVÄNDARGUIDE VITAL & TALANDE TANGENTBORD INNEHÅLL 1. KOM IGÅNG MED VITAL 1.1. Vad är ViTal? 1.2. Vem behöver ViTal? 1.3. Hur kan ViTal användas i skolan? 1.4. Hur får jag eleverna att börja använda ViTal?
ANVÄNDARGUIDE VITAL & TALANDE TANGENTBORD INNEHÅLL 1. KOM IGÅNG MED VITAL 1.1. Vad är ViTal? 1.2. Vem behöver ViTal? 1.3. Hur kan ViTal användas i skolan? 1.4. Hur får jag eleverna att börja använda ViTal?
Skärminspelningsprogram Screencast-o-matic (med stimulated recall)
 Skärminspelningsprogram Screencast-o-matic (med stimulated recall) Victoria Johansson Humanistlaboratoriet, Lunds universitet it-pedagog@humlab.lu.se 1 Skärminspelningsprogram Det finns fler skärminspelningsprogram
Skärminspelningsprogram Screencast-o-matic (med stimulated recall) Victoria Johansson Humanistlaboratoriet, Lunds universitet it-pedagog@humlab.lu.se 1 Skärminspelningsprogram Det finns fler skärminspelningsprogram
EXEMPEL 1: ARTVARIATION FÖRELÄSNING 1. EEG frekvensanalys EXEMPEL 2: EEG
 FÖRELÄSNING EXEMPEL : ARTVARIATION Kurs- och transform-översikt. Kursintroduktion med typiska signalbehandlingsproblem och kapitelöversikt. Rep av transformer 3. Rep av aliaseffekten Givet: data med antal
FÖRELÄSNING EXEMPEL : ARTVARIATION Kurs- och transform-översikt. Kursintroduktion med typiska signalbehandlingsproblem och kapitelöversikt. Rep av transformer 3. Rep av aliaseffekten Givet: data med antal
Guide till rockgruppens instrument
 Guide till rockgruppens instrument Gitarr, elgitarr, bas, keyboard och trummor Detta häfte är tänkt för att du som elev ska kunna jobba självständigt med att lära dig en del om gitarr, bas, keyboard och
Guide till rockgruppens instrument Gitarr, elgitarr, bas, keyboard och trummor Detta häfte är tänkt för att du som elev ska kunna jobba självständigt med att lära dig en del om gitarr, bas, keyboard och
Datorövning: Fouriertransform med Python
 Datorövning i Elektromagnetism och vågor (FK5019) Övningsledare: bart.pelssers@fysik.su.se & ashraf@fysik.su.se Datorövning: Fouriertransform med Python Skicka in individuellt skrivna rapporter på engelska
Datorövning i Elektromagnetism och vågor (FK5019) Övningsledare: bart.pelssers@fysik.su.se & ashraf@fysik.su.se Datorövning: Fouriertransform med Python Skicka in individuellt skrivna rapporter på engelska
3. Välj den sprajt (bild) ni vill ha som fallande objekt, t ex en tårta, Cake. Klicka därefter på OK.
 Moment 2: Klonspel Instruktioner för deltagare Idag ska du få lära dig om: Kloner - kopior av samma figur (sprajt) Variabler - ett värde, exempelvis antal poäng Slumptal - slå en tärning för att välja
Moment 2: Klonspel Instruktioner för deltagare Idag ska du få lära dig om: Kloner - kopior av samma figur (sprajt) Variabler - ett värde, exempelvis antal poäng Slumptal - slå en tärning för att välja
Laboration 3 Sampling, samplingsteoremet och frekvensanalys
 Laboration 3 Sampling, samplingsteoremet och frekvensanalys 1 1 Introduktion Syftet med laborationen är att ge kunskaper i att tolka de effekter (speglingar, svävningar) som uppkommer vid sampling av en
Laboration 3 Sampling, samplingsteoremet och frekvensanalys 1 1 Introduktion Syftet med laborationen är att ge kunskaper i att tolka de effekter (speglingar, svävningar) som uppkommer vid sampling av en
Harry Peronius. ilife
 Harry Peronius ilife Del 4 GARAGEBAND 21. Skapa ett GarageBand-projekt... 75 22. Spela in via mikrofon... 83 23. Redigera regioner... 88 24. Tillämpa effekter... 92 25. Exportera till itunes... 94 26.
Harry Peronius ilife Del 4 GARAGEBAND 21. Skapa ett GarageBand-projekt... 75 22. Spela in via mikrofon... 83 23. Redigera regioner... 88 24. Tillämpa effekter... 92 25. Exportera till itunes... 94 26.
Gränssnitt för FakeGranska. Lars Mattsson
 Gränssnitt för FakeGranska av Lars Mattsson (larsmatt@kth.se) Innehållsförteckning 1 Introduktion...3 2 Genomförande:...3 3 Användning...5 4 Kända buggar:...6 5 Källförteckning...6 2 1 Introduktion Taken
Gränssnitt för FakeGranska av Lars Mattsson (larsmatt@kth.se) Innehållsförteckning 1 Introduktion...3 2 Genomförande:...3 3 Användning...5 4 Kända buggar:...6 5 Källförteckning...6 2 1 Introduktion Taken
bergerdata hb www.bergerdata.se/guidemaster info@bergerdata.se 0708-72 23 00 1.10 2015-05-19 Sid 1 (11)
 bergerdata hb www.bergerdata.se/guidemaster info@bergerdata.se 0708-72 23 00 1.10 2015-05-19 Sid 1 (11) Vad, varför och hur?...2 Vad är?...2 Varför?...3 Hur fungerar?...3 Några tips om användningen...3
bergerdata hb www.bergerdata.se/guidemaster info@bergerdata.se 0708-72 23 00 1.10 2015-05-19 Sid 1 (11) Vad, varför och hur?...2 Vad är?...2 Varför?...3 Hur fungerar?...3 Några tips om användningen...3
TSBB16 Datorövning A Samplade signaler Faltning
 Name: ID number: Passed: LiU-ID: Date: TSBB16 Datorövning A Samplade signaler Faltning Utvecklad av Klas Nordberg Computer Vision Laboratory, Linköping University, Sweden 24 augusti 2015 Introduktion Denna
Name: ID number: Passed: LiU-ID: Date: TSBB16 Datorövning A Samplade signaler Faltning Utvecklad av Klas Nordberg Computer Vision Laboratory, Linköping University, Sweden 24 augusti 2015 Introduktion Denna
1. Starta programmet 2. Välja projekt antingen redan skapat eller nytt
 1. Starta programmet Först öppnar vi programmet. Antingen finns det i rullningslisten, som jag har längst ner på skärmen. Klicka och programmet startas.1 Om det inte finns där välj program, hitta garageband
1. Starta programmet Först öppnar vi programmet. Antingen finns det i rullningslisten, som jag har längst ner på skärmen. Klicka och programmet startas.1 Om det inte finns där välj program, hitta garageband
2 Laborationsutrustning
 Institutionen för data- och elektroteknik 2002-02-11 1 Inledning Denna laboration syftar till att illustrera ett antal grundbegrepp inom digital signalbehandling samt att närmare studera frekvensanalys
Institutionen för data- och elektroteknik 2002-02-11 1 Inledning Denna laboration syftar till att illustrera ett antal grundbegrepp inom digital signalbehandling samt att närmare studera frekvensanalys
Generering av ljud utifrån fysikalisk simulering
 UMEÅ UNIVERSITET Projektrapport Enheten för professionskurser 2010-05-18 Generering av ljud utifrån fysikalisk simulering Introduktion till ingenjörsarbete Namn Anders Berglund Viktor Johansson Sara Leonardsson
UMEÅ UNIVERSITET Projektrapport Enheten för professionskurser 2010-05-18 Generering av ljud utifrån fysikalisk simulering Introduktion till ingenjörsarbete Namn Anders Berglund Viktor Johansson Sara Leonardsson
Laboration 3: Musikbibliotek
 Laboration 3: Musikbibliotek Objektorienterad programmering, Z1 Syfte I denna laboration ska ni definiera ett litet bibliotek för att generera musik som kan avlyssnas med vanliga musikprogram. Tiden medger
Laboration 3: Musikbibliotek Objektorienterad programmering, Z1 Syfte I denna laboration ska ni definiera ett litet bibliotek för att generera musik som kan avlyssnas med vanliga musikprogram. Tiden medger
Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker. GeoGebraexempel
 matematik Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker 4 GeoGebraexempel Till läsaren I elevböckerna i serien Matematik Origo finns uppgifter där vi rekommenderar användning
matematik Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker 4 GeoGebraexempel Till läsaren I elevböckerna i serien Matematik Origo finns uppgifter där vi rekommenderar användning
RemoteBud. Inlämnas: Patrik Johnsson, e01pjo Viktor Karlsson, e01vk
 RemoteBud Inlämnas: 2005-02-01 Patrik Johnsson, e01pjo Viktor Karlsson, e01vk Abstract Skulle du också vilja styra dina lampor och rulla ner dina persienner med hjälp av din TV-fjärrkontroll? Remotebud
RemoteBud Inlämnas: 2005-02-01 Patrik Johnsson, e01pjo Viktor Karlsson, e01vk Abstract Skulle du också vilja styra dina lampor och rulla ner dina persienner med hjälp av din TV-fjärrkontroll? Remotebud
Introduktion till programmering och Python Grundkurs i programmering med Python
 Introduktion till programmering och Python Hösten 2009 Dagens lektion Vad är programmering? Vad är en dator? Filer Att tala med datorer En första titt på Python 2 Vad är programmering? 3 VAD ÄR PROGRAMMERING?
Introduktion till programmering och Python Hösten 2009 Dagens lektion Vad är programmering? Vad är en dator? Filer Att tala med datorer En första titt på Python 2 Vad är programmering? 3 VAD ÄR PROGRAMMERING?
Resttentamen i Signaler och System Måndagen den 11.januari 2010, kl 14-19
 Resttentamen i Signaler och System Måndagen den 11.januari 2010, kl 14-19 Tillåtna hjälpmedel: Valfri miniräknare (utan möjlighet till trådlös kommunkation). Valfri litteratur, inkl. kursböcker, formelsamlingar.
Resttentamen i Signaler och System Måndagen den 11.januari 2010, kl 14-19 Tillåtna hjälpmedel: Valfri miniräknare (utan möjlighet till trådlös kommunkation). Valfri litteratur, inkl. kursböcker, formelsamlingar.
Introduktion till Matlab
 Introduktion till Matlab Inledande matematik, I1, ht10 1 Inledning Detta är en koncis beskrivning av de viktigaste delarna av Matlab. Till en början är det enkla beräkningar och grafik som intresserar
Introduktion till Matlab Inledande matematik, I1, ht10 1 Inledning Detta är en koncis beskrivning av de viktigaste delarna av Matlab. Till en början är det enkla beräkningar och grafik som intresserar
Följande program utvecklades av BITTECH. De flesta såldes via Elevdata, Frölunda Data och VetaMer. De finns inte längre till försäljning.
 Programvaror utvecklade av BITTECH under åren 1990 till 2004 Följande program utvecklades av BITTECH. De flesta såldes via Elevdata, Frölunda Data och VetaMer. De finns inte längre till försäljning. Meteor
Programvaror utvecklade av BITTECH under åren 1990 till 2004 Följande program utvecklades av BITTECH. De flesta såldes via Elevdata, Frölunda Data och VetaMer. De finns inte längre till försäljning. Meteor
Ljudmaskiner. Dra med en fuktig pappersbit längs tråden som sitter fast i plastburken. Till påsken kan du göra en påsktupp av en likadan burk.
 Ljud åk 3-4; station a) Ljudmaskiner 1. Kacklande burk. Beskrivning: Se länk på sidan 'Bygga'. Dra med en fuktig pappersbit längs tråden som sitter fast i plastburken. Till påsken kan du göra en påsktupp
Ljud åk 3-4; station a) Ljudmaskiner 1. Kacklande burk. Beskrivning: Se länk på sidan 'Bygga'. Dra med en fuktig pappersbit längs tråden som sitter fast i plastburken. Till påsken kan du göra en påsktupp
TETRIS. LTH, Campus Helsingborg EITA15 Digitala System
 TETRIS LTH, Campus Helsingborg EITA15 Digitala System Handledare: Bertil Lindvall Författare: Isak Shamun, Viktor Kulle, Mark Slipac och Dennis Järnåsen Datum: 2019-05-09 Abstract This report concerns
TETRIS LTH, Campus Helsingborg EITA15 Digitala System Handledare: Bertil Lindvall Författare: Isak Shamun, Viktor Kulle, Mark Slipac och Dennis Järnåsen Datum: 2019-05-09 Abstract This report concerns
web: www.injektor.com 2003-09-12 e-mail: info@injektor.com fax: 0709 66 78 96 tel: kontor 08-753 00 04, Toby Edmundsson mobil: 0704 38 01 99, Jan
 Quick-Start Manual TempRecord Temprecord är ett välbeprövat system för att ta in mätdata och möjliggöra senare analys av dessa. Företaget har funnits en längre tid på marknaden och borgar för god kvalitet.
Quick-Start Manual TempRecord Temprecord är ett välbeprövat system för att ta in mätdata och möjliggöra senare analys av dessa. Företaget har funnits en längre tid på marknaden och borgar för god kvalitet.
Laboration i Fourieroptik
 Laboration i Fourieroptik David Winge Uppdaterad 4 januari 2016 1 Introduktion I detta experiment ska vi titta på en verklig avbildning av Fouriertransformen. Detta ska ske med hjälp av en bild som projiceras
Laboration i Fourieroptik David Winge Uppdaterad 4 januari 2016 1 Introduktion I detta experiment ska vi titta på en verklig avbildning av Fouriertransformen. Detta ska ske med hjälp av en bild som projiceras
Garageband. Garageband är ett program för att skapa och spela in musik på roliga och enkla sätt. Och så här ser appen ut.
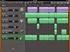 Garageband Garageband är ett program för att skapa och spela in musik på roliga och enkla sätt. Och så här ser appen ut. Startsidan När man klickar på appen så kommer man till startsidan. Här ifrån når
Garageband Garageband är ett program för att skapa och spela in musik på roliga och enkla sätt. Och så här ser appen ut. Startsidan När man klickar på appen så kommer man till startsidan. Här ifrån når
TSKS21 Signaler, Information och Bilder Lab 2: Digitalisering
 TSKS21 Signaler, Information och Bilder Lab 2: Digitalisering Mikael Olofsson 8 februari 2017 Fyll i detta med bläckpenna Laborant Personnummer Datum Godkänd 1 1 Allmänt Denna laboration syftar till att
TSKS21 Signaler, Information och Bilder Lab 2: Digitalisering Mikael Olofsson 8 februari 2017 Fyll i detta med bläckpenna Laborant Personnummer Datum Godkänd 1 1 Allmänt Denna laboration syftar till att
Manual Skogsappen - Hemkomstkontroll
 Manual Skogsappen - Hemkomstkontroll Detta dokument utgör användarhandledningen till funktionen hemkomstkontroll i mobilappen Skogsappen som tillhör tjänsten epiforest. E p i s c o p e M o n i t o r i
Manual Skogsappen - Hemkomstkontroll Detta dokument utgör användarhandledningen till funktionen hemkomstkontroll i mobilappen Skogsappen som tillhör tjänsten epiforest. E p i s c o p e M o n i t o r i
Ljudlära. Ljud är Periodicitet. Introduktion. Ljudlära viktigt ur två aspekter:
 Introduktion Ljudlära Ljudlära viktigt ur två aspekter: 1. Ljudets fysikaliska egenskaper 2. Vad vi uppfattar med hörseln Syfte: att lära sig göra relevanta kopplingar mellan faktisk vetenskap och sinnlig
Introduktion Ljudlära Ljudlära viktigt ur två aspekter: 1. Ljudets fysikaliska egenskaper 2. Vad vi uppfattar med hörseln Syfte: att lära sig göra relevanta kopplingar mellan faktisk vetenskap och sinnlig
Word Grunderna 1. Om du kan det allra enklaste i Word, hoppa över uppgifterna A-E.
 Word Grunderna 1 Om du kan det allra enklaste i Word, hoppa över uppgifterna A-E. A Starta programmet Word. Titta på skärmen efter en bild som det finns ett W på. Tryck med musknappen snabbt två gånger
Word Grunderna 1 Om du kan det allra enklaste i Word, hoppa över uppgifterna A-E. A Starta programmet Word. Titta på skärmen efter en bild som det finns ett W på. Tryck med musknappen snabbt två gånger
1 Försnack och ordlista
 1 9 Välkommen till denna guide in i Cubase underbara värld - en värld full av musik, menyer, ångest, glädje, kortkommandon och kreativitet. Cubase historia går långt bak i tiden grunden lades redan 1984
1 9 Välkommen till denna guide in i Cubase underbara värld - en värld full av musik, menyer, ångest, glädje, kortkommandon och kreativitet. Cubase historia går långt bak i tiden grunden lades redan 1984
Csound. Csound exempel
 Csound Lång historia, föregångare (Music 4), tidigt 60-tal programstyrda oscillatorer som sammankopplas till instrument i en orkester -fil (.orc) en notfil ( score.sco) anger när och hur instrumenten skall
Csound Lång historia, föregångare (Music 4), tidigt 60-tal programstyrda oscillatorer som sammankopplas till instrument i en orkester -fil (.orc) en notfil ( score.sco) anger när och hur instrumenten skall
Mäta rakhet Scanning med M7005
 Matematikföretaget jz M7005.metem.se 141121/150411/150704/SJn Mäta rakhet Scanning med M7005 Mätgivare Detalj Mäta rakhet - Scanning 1 (12) Innehåll 1 Ett exempel... 3 2 Beskrivning... 6 2.1 Scanna in
Matematikföretaget jz M7005.metem.se 141121/150411/150704/SJn Mäta rakhet Scanning med M7005 Mätgivare Detalj Mäta rakhet - Scanning 1 (12) Innehåll 1 Ett exempel... 3 2 Beskrivning... 6 2.1 Scanna in
Teori... SME118 - Mätteknik & Signalbehandling SME118. Johan Carlson 2. Teori... Dagens meny
 Tidigare har vi gått igenom Fourierserierepresentation av periodiska signaler och Fouriertransform av icke-periodiska signaler. Fourierserierepresentationen av x(t) ges av: där a k = 1 T + T a k e jkω
Tidigare har vi gått igenom Fourierserierepresentation av periodiska signaler och Fouriertransform av icke-periodiska signaler. Fourierserierepresentationen av x(t) ges av: där a k = 1 T + T a k e jkω
Laborationsprojekt i digital ljudsyntes
 Laborationsprojekt i digital ljudsyntes A. Målsättning Att studenten skall få fördjupade kunskaper i digital signalbehandling genom att lära sig de grundläggande principerna för digital ljudsyntes av stränginstrumentliknande
Laborationsprojekt i digital ljudsyntes A. Målsättning Att studenten skall få fördjupade kunskaper i digital signalbehandling genom att lära sig de grundläggande principerna för digital ljudsyntes av stränginstrumentliknande
DT1130 Spektrala transformer Tentamen
 DT3 Spektrala transformer Tentamen 5 Tentamen består av fem uppgifter där varje uppgift maximalt ger p. Normalt gäller följande betygsgränser: E: 9 p, D:.5 p, C: p, B: 6 p, A: 8 p Tillåtna hjälpmedel:
DT3 Spektrala transformer Tentamen 5 Tentamen består av fem uppgifter där varje uppgift maximalt ger p. Normalt gäller följande betygsgränser: E: 9 p, D:.5 p, C: p, B: 6 p, A: 8 p Tillåtna hjälpmedel:
Grunder. Grafiktyper. Vektorgrafik
 2 Grunder All vår början bliver svår eller hur det nu brukar heta, och detta är något som gäller även Flash. För den som är ovan vid Flash gäller det säkert extra mycket, då det kan vara knepigt att förstå
2 Grunder All vår början bliver svår eller hur det nu brukar heta, och detta är något som gäller även Flash. För den som är ovan vid Flash gäller det säkert extra mycket, då det kan vara knepigt att förstå
Kapitel 2 o 3 Information och bitar Att skicka signaler på en länk. Att sända information mellan datorer. Information och binärdata
 Kapitel 2 o 3 Information och bitar Att skicka signaler på en länk Jens A Andersson (Maria Kihl) Att sända information mellan datorer värd 11001000101 värd Två datorer som skall kommunicera. Datorer förstår
Kapitel 2 o 3 Information och bitar Att skicka signaler på en länk Jens A Andersson (Maria Kihl) Att sända information mellan datorer värd 11001000101 värd Två datorer som skall kommunicera. Datorer förstår
Föreläsning 2. Operativsystem och programmering
 Föreläsning 2 Operativsystem och programmering Behov av operativsystem En dator så som beskriven i förra föreläsningen är nästan oanvändbar. Processorn kan bara ges enkla instruktioner såsom hämta data
Föreläsning 2 Operativsystem och programmering Behov av operativsystem En dator så som beskriven i förra föreläsningen är nästan oanvändbar. Processorn kan bara ges enkla instruktioner såsom hämta data
Laboration: Grunderna i MATLAB
 Laboration: Grunderna i MATLAB 25 augusti 2005 Grunderna i MATLAB Vad är MATLAB? MATLAB är ett interaktivt program för vetenskapliga beräkningar. Som användare ger du enkla kommandon och MATLAB levererar
Laboration: Grunderna i MATLAB 25 augusti 2005 Grunderna i MATLAB Vad är MATLAB? MATLAB är ett interaktivt program för vetenskapliga beräkningar. Som användare ger du enkla kommandon och MATLAB levererar
DT1120/DT1130 Spektrala transformer Tentamen
 DT/DT3 Spektrala transformer Tentamen 86 Tentamen består av fem uppgifter där varje uppgift maximalt ger 4 p. Normalt gäller följande betygsgränser: E: 9 p, D:.5 p, C: 4 p, B: 6 p, A: 8 p Tillåtna hjälpmedel:
DT/DT3 Spektrala transformer Tentamen 86 Tentamen består av fem uppgifter där varje uppgift maximalt ger 4 p. Normalt gäller följande betygsgränser: E: 9 p, D:.5 p, C: 4 p, B: 6 p, A: 8 p Tillåtna hjälpmedel:
Musik finns överallt omkring
 Johan Thorssell Musikens matematik Går det att lyssna på funktioner? Artikelförfattaren har använt akustiska instrument och syntar i gymnasiets matematik för att introducera Fourieranalys. Vi får här smakprov
Johan Thorssell Musikens matematik Går det att lyssna på funktioner? Artikelförfattaren har använt akustiska instrument och syntar i gymnasiets matematik för att introducera Fourieranalys. Vi får här smakprov
GRUNDLÄGGANDE MUSIKTEORI
 GRUNDLÄGGANDE MUSIKTEORI Puls All musik utgår från en grundpuls. När man spelar tillsammans måste alla känna samma puls om det ska funka. Puls är en serie slag som återkommer med jämna mellanrum. Det är
GRUNDLÄGGANDE MUSIKTEORI Puls All musik utgår från en grundpuls. När man spelar tillsammans måste alla känna samma puls om det ska funka. Puls är en serie slag som återkommer med jämna mellanrum. Det är
Matriser och Inbyggda funktioner i Matlab
 Matematiska vetenskaper 2010/2011 Matriser och Inbyggda funktioner i Matlab 1 Inledning Vi skall denna vecka se på matriser och funktioner som är inbyggda i Matlab, dels (elementära) matematiska funktioner
Matematiska vetenskaper 2010/2011 Matriser och Inbyggda funktioner i Matlab 1 Inledning Vi skall denna vecka se på matriser och funktioner som är inbyggda i Matlab, dels (elementära) matematiska funktioner
Inledning till Wavesurfer av Christine Ericsdotter (Lingvistik, Stockholms universitet)
 Inledning till Wavesurfer av Christine Ericsdotter (Lingvistik, Stockholms universitet) WaveSurfer är ett program för analys av tal utvecklat vid Centrum för talteknologi, Institutionen för tal, musik
Inledning till Wavesurfer av Christine Ericsdotter (Lingvistik, Stockholms universitet) WaveSurfer är ett program för analys av tal utvecklat vid Centrum för talteknologi, Institutionen för tal, musik
Signaler & Signalanalys
 Ulrik Söderström ulrik.soderstrom@tfe.umu.se Jan 8 Signaler & Signalanals Sinusspänning Sinus och cosinus samma form men fasförskjutna Fasförskjutning tidsfördröjning Sinus och cosinus är väldigt enkla
Ulrik Söderström ulrik.soderstrom@tfe.umu.se Jan 8 Signaler & Signalanals Sinusspänning Sinus och cosinus samma form men fasförskjutna Fasförskjutning tidsfördröjning Sinus och cosinus är väldigt enkla
Fyra i rad Javaprojekt inom TDDC32
 Fyra i rad Javaprojekt inom TDDC32 Analys och design-dokument Version 2.0 Datum 2008-05-19 Dokumentnummer 20080303 Sammanfattning Detta är analys och design-dokumentet för programmet Fyra i rad. Fyra i
Fyra i rad Javaprojekt inom TDDC32 Analys och design-dokument Version 2.0 Datum 2008-05-19 Dokumentnummer 20080303 Sammanfattning Detta är analys och design-dokumentet för programmet Fyra i rad. Fyra i
E-strängen rör sig fyra gånger så långsamt vid samma transversella kraft, accelerationen. c) Hur stor är A-strängens våglängd?
 Problem. Betrakta en elgitarr. Strängarna är 660 mm långa. Stämningen är E-A-d-g-b-e, det vill säga att strängen som ger tonen e-prim (330 Hz) ligger två oktav högre i frekvens än E-strängen. Alla strängar
Problem. Betrakta en elgitarr. Strängarna är 660 mm långa. Stämningen är E-A-d-g-b-e, det vill säga att strängen som ger tonen e-prim (330 Hz) ligger två oktav högre i frekvens än E-strängen. Alla strängar
Audio & Videoteknik 2D2021, 2D1518
 TENTAMEN Kurs: Kursnummer: Moment: Program: Åk: Examinator: Rättande lärare: Datum: Tid: Hjälpmedel: Audio & Videoteknik 2D2021, 2D1518 Tentamen Medieteknik 2 Trille Fellstenius Trille Fellstenius, Svante
TENTAMEN Kurs: Kursnummer: Moment: Program: Åk: Examinator: Rättande lärare: Datum: Tid: Hjälpmedel: Audio & Videoteknik 2D2021, 2D1518 Tentamen Medieteknik 2 Trille Fellstenius Trille Fellstenius, Svante
Space Invaders - Slutrapport
 Projekt inda14 Sida 1 av 6 Space Invaders - Slutrapport A. Projektplanen Programbeskrivning Vi tänker göra en version av det gamla arkadspelet Space Invaders i java. Spelet går ut på att spelaren styr
Projekt inda14 Sida 1 av 6 Space Invaders - Slutrapport A. Projektplanen Programbeskrivning Vi tänker göra en version av det gamla arkadspelet Space Invaders i java. Spelet går ut på att spelaren styr
Introduktion till MySQL
 Introduktion till MySQL Vad är MySQL? MySQL är ett programmerings- och frågespråk för databaser. Med programmeringsspråk menas att du kan skapa och administrera databaser med hjälp av MySQL, och med frågespråk
Introduktion till MySQL Vad är MySQL? MySQL är ett programmerings- och frågespråk för databaser. Med programmeringsspråk menas att du kan skapa och administrera databaser med hjälp av MySQL, och med frågespråk
Matriser och Inbyggda funktioner i Matlab
 CTH/GU STUDIO 1 TMV036a - 2012/2013 Matematiska vetenskaper Matriser och Inbyggda funktioner i Matlab Analys och Linjär Algebra, del A, K1/Kf1/Bt1 Moore: 2.3, 3.1-3.4, 3..1-3.., 4.1, 7.4 1 Inledning Nu
CTH/GU STUDIO 1 TMV036a - 2012/2013 Matematiska vetenskaper Matriser och Inbyggda funktioner i Matlab Analys och Linjär Algebra, del A, K1/Kf1/Bt1 Moore: 2.3, 3.1-3.4, 3..1-3.., 4.1, 7.4 1 Inledning Nu
CD-ORD 9.0. Snabbhjälp
 CD-ORD 9.0 Snabbhjälp CD-ORD Denna manual innehåller information för att komma igång med CD-ORD 9.0. I CD-ORDs verktygslist finner du en mer detaljerad manual för programmet. Hjälp i verktygslisten Snabbhjälp
CD-ORD 9.0 Snabbhjälp CD-ORD Denna manual innehåller information för att komma igång med CD-ORD 9.0. I CD-ORDs verktygslist finner du en mer detaljerad manual för programmet. Hjälp i verktygslisten Snabbhjälp
Digitalitet. Kontinuerlig. Direkt proportionerlig mot källan. Ex. sprittermometer. Elektrisk signal som representerar ljud.
 Analog Digitalitet Kontinuerlig Direkt proportionerlig mot källan Ex. sprittermometer Elektrisk signal som representerar ljud Diskret Digital Representation som siffror/symboler Ex. CD-skiva Varje siffra
Analog Digitalitet Kontinuerlig Direkt proportionerlig mot källan Ex. sprittermometer Elektrisk signal som representerar ljud Diskret Digital Representation som siffror/symboler Ex. CD-skiva Varje siffra
1. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (1p)
 Problem Energi. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (p) b) Ge en tydlig förklaring av hur frekvens, period, våglängd och våghastighet hänger
Problem Energi. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (p) b) Ge en tydlig förklaring av hur frekvens, period, våglängd och våghastighet hänger
Bilaga A, Akustiska begrepp
 (5), Akustiska begrepp Beskrivning av ljud Ljud som vi hör med örat är tryckvariationer i luften. Ljudet beskrivs av dess styrka (ljudtrycksnivå), dess frekvenssammansättning och dess varaktighet. Ljudtrycksnivå
(5), Akustiska begrepp Beskrivning av ljud Ljud som vi hör med örat är tryckvariationer i luften. Ljudet beskrivs av dess styrka (ljudtrycksnivå), dess frekvenssammansättning och dess varaktighet. Ljudtrycksnivå
Enkla inspelningsverktyg PowerPoint
 Enkla inspelningsverktyg PowerPoint Att snabbt och enkelt kunna spela in röst och bild kan vara mycket användbart i undervisningen. Att publicera inspelningar på nätet kan däremot vara lite knepigt eftersom
Enkla inspelningsverktyg PowerPoint Att snabbt och enkelt kunna spela in röst och bild kan vara mycket användbart i undervisningen. Att publicera inspelningar på nätet kan däremot vara lite knepigt eftersom
Analys/syntes-kodning
 Analys/syntes-kodning Många talkodare bygger på en princip som kallas analys/syntes-kodning. Istället för att koda en vågform, som man normalt gör i generella ljudkodare och i bildkodare, så har man parametrisk
Analys/syntes-kodning Många talkodare bygger på en princip som kallas analys/syntes-kodning. Istället för att koda en vågform, som man normalt gör i generella ljudkodare och i bildkodare, så har man parametrisk
MEMORERINGSARK Ackord-typer och Beteckningar
 MEMORERINGSARK Ackord-typer och Beteckningar En ackord-typ talar om vilka intervall (sett från ackordets grundton) ackordet ska innehålla. Eftersom den inte säger någonting om vilken variant dessa intervall
MEMORERINGSARK Ackord-typer och Beteckningar En ackord-typ talar om vilka intervall (sett från ackordets grundton) ackordet ska innehålla. Eftersom den inte säger någonting om vilken variant dessa intervall
DD1311 Programmeringsteknik för S1 Laborationer läsåret 2007-2008
 DD1311 meringsteknik för S1 Laborationer läsåret 2007-2008 Fyll i ditt namn och personnummer med bläck eller motsvarande. Kursledare är Linda Kann, linda@nada.kth.se. Namn... Personnr... Laborationer Labb
DD1311 meringsteknik för S1 Laborationer läsåret 2007-2008 Fyll i ditt namn och personnummer med bläck eller motsvarande. Kursledare är Linda Kann, linda@nada.kth.se. Namn... Personnr... Laborationer Labb
TeamViewer Installation och användning
 TeamViewer Installation och användning Funktioner i TeamViewer TeamViewer möjliggör för lärare och faddrar att hjälpa elever och användare på distans. Det finns 2 huvudsakliga användningsområden: Fjärrstyrning
TeamViewer Installation och användning Funktioner i TeamViewer TeamViewer möjliggör för lärare och faddrar att hjälpa elever och användare på distans. Det finns 2 huvudsakliga användningsområden: Fjärrstyrning
