Kontroll 13. Uppgift 1. Uppgift 2. Uppgift 3. Uppgift 4. Uppgift 5. Uppgift 6. Uppgift 7
|
|
|
- Jakob Månsson
- för 7 år sedan
- Visningar:
Transkript
1 Kontroll 13 Uppgift 1 Avståndet, r parsec, till en stjärna kan bestämmas med formeln M = m lgr där M =stjärnans absoluta ljusstyrka och m =stjärnans skenbara ljusstyrka. (1 parsec= 3.26 ljusår= km). Beräkna avståndet i km till Sirius, då M = 1.4 och m = Uppgift 2 En vara kostade 123 kr när dess pris plötsligt höjdes med 18%. Med hur många procent ska det nya priset sänkas, för att varan ska återfå sitt ursprungliga pris? Uppgift 3 Sedan 1979 har oljetillförseln minskat med i genomsnitt 5% per år. Efter hur många år var oljetillförseln halverad? Uppgift 4 Kalle började ett nytt jobb och fick en månadslön på 18000, med löfte om 4% löneförhöjning varje halvår. Pelle skrattade åt detta, eftersom han själv just börjat ett jobb där han får i månadslön och med löfte om 5% påökt, visserligen per år, men ändå. När kan Kalle börja skratta åt Pelle? Det vill säga efter hur lång tid kommer Kalle att ha en högre månadslön än Pelle? Eller kommer han aldrig att få det? Uppgift hade jorden cirka 2.98 miljarder invånare. Folkmängden har sedan dess vuxit exponentiellt med 2%/år, ett uttalande som gällde hade jorden cirka 6.52 miljarder invånare. Hur väl tycker du att modellen gäller? Uppgift 6 Hur mycket pengar ska jag sätta in på banken idag om jag om 6 år ska har ett sparkapital på kr till 10.5% ränta? Uppgift 7 En kärnreaktor är omgiven av ett strålskydd av järnmalmsbetong. Strålningens intensitet avtar exponentiellt med den väg strålningen går genom skyddet. Efter 6 cm har intensiteten gått ned till hälften Håkan Strömberg 1 KTH Syd Haninge
2 av den ursprungliga. Efter hur lång passage genom skyddet har intensiteten gått ned till 0.1 promille av det ursprungliga värdet? Uppgift 8 Här en annan prognos för antalet människor på jorden var antalet invånare på jorden cirka miljarder. Den tillväxte då på ett sätt som innebar en fördubbling på år. Vid vilket år skulle, med denna modell, antalet invånare vara 6.52 miljarder? Uppgift 9 Herr Svenssons månadslön har en exponentiell utveckling. För 10 år sedan tjänade han 000 kr/månad. Idag tjänar han kr/månad. Vilken månadslön kommer han att ha när han går i pension om 7 år? Uppgift 10 Bestäm den exponentialfunktion vi söker, på vars kurva två punkter är kända: P1(4, ) och P2(6, ). The hard way. Håkan Strömberg 2 KTH Syd Haninge
3 Lösningar till Kontroll 13 Uppgift 1 Antag: Avståndet är r parsec 1.4 = lgr = 5 lgr 5 lgr = 2.15 lgr = lg r = 0.43 r = r 2.69 Avståndet blir då km Svar: km Uppgift 2 Priset p 2 efter höjning är p 2 = För att priset p 1 = 123 ska återfås måste tillväxtfaktorn vara a. Vi får 123 = ( )a ger a = = Svaret får man genom att invertera den första tillväxtfaktorn. Priset har förstås inget med saken att göra. Uppgift 3 a 2 = a 0.95 x 0.95 x = 1 2 ln0.95 x = ln 1 2 x ln0.95 = ln 1 2 x = ln 1 2 ln Håkan Strömberg 3 KTH Syd Haninge
4 Uppgift 4 Kalles lön stiger efter L K (x) = x och Pelles efter L P (x) = x. Genom ekvationen nedan får vi reda på vid vilken tidpunkt de har samma månadslön x = x x 1.05 x = ( ) x = ( ) x ln = ln ( ) x ln = ln x = ln x 3.55 / ln ( ) 1.05 Redan efter fyra år har Kalle en högre månadslön än Pelle. Efter har fortfarande Pelle lite högre lön. Så här kan man lösa problemet med ett C-program 1 #include <stdio.h> 2 int main(void){ 3 float kalle=18000,pelle=20000; 4 int halvar=1; 5 while (pelle>kalle){ 6 kalle=kalle 1.04; 7 if(halvar%2==0) 8 pelle=pelle 1.05; 9 halvar++; 10 } 11 printf("efter %d halvår\n",halvar); 12 } Programmet svarar att det behövs 8 halvår. Uppgift 5 Med hjälp av uttrycket kan vi se vad den prognosen hade förväntat sig Nästan en miljard färre och det är kanske skönt. Håkan Strömberg 4 KTH Syd Haninge
5 Uppgift 6 Hur mycket pengar ska jag sätta in på banken idag om jag om 6 år ska har ett sparkapital på kr till 10.5% ränta? Antag att det startkapitalet är x kr och vi får följande ekvation = x x = x Uppgift 7 Antag att det har skett efter x cm. Vi får ekvationen = 0.5 x 6 lg10 4 = lg0.5 x 6 4lg10 = x 6 lg = x lg0.5 x = x lg0.5 Svar: Efter 80 cm Uppgift 8 Antag att det kommer att dröja x år efter Vi får då ekvationen 6.52 = 2 x 6.52 lg 6.52 lg 6.52 lg 6.52 lg2 = 2 x = lg2 x = x lg2 = x x 21 Håkan Strömberg 5 KTH Syd Haninge
6 = Det skulle alltså ha inträffat för 9 år sedan. Uppgift 9 Vi ska använda oss av exponentialfunktionen f(t) = C 10 k t C och k är konstanter och t är tiden. Först måste vi då bestämma C och k. Detta kan vi göra genom de två givna punkterna P1(0,000) och P2(10,30000). När vi har bestämt funktionens konstanter ska vi ta reda på f(17) Nu över till att bestämma k Vi får Funktionen får till sist följande utseende f(0) = C 10 k 0 f(0) = C men också f(0) = 000 C = 000 f(10) = k Vi ska lösa ekvationen k = k = k = lg10 10k = lg 30 10k lg 10 = lg 30 10k = lg 30 k = lg k f(t) = t Vi kan nu använda den för att bestämma f(17) och med det får man väl nöja sig. En enklare lösning Uppgiften kan lösas på ett mycket enklare sätt. Vi antar att tillväxtfaktorn är x och skriver ekvationen = 000 x 10 ( x = 000 x ) 1 10 Vi använder oss nu av faktorn för att få svaret = kr Håkan Strömberg 6 KTH Syd Haninge
7 Uppgift 10 Vi ansätter f(x) = C a x och ska alltså bestämma C och a med hjälp av f(4) = och f(6) = Vi får ett ekvationssystem: { C a 4 = C a 6 = Från första ekvationen får vi C a 4 = C = a 4 Vi substituerar C i den andra ekvationen och får a 4 a 6 = a 2 = a 2 = a = ± Vi vet nu att a = 1.10 och kan använda det för att bestämma C. Vi tecknar till sist funktionen f(x) = x C = Håkan Strömberg 7 KTH Syd Haninge
Lösningar och kommentarer till Övningstenta 1
 Lösningar och kommentarer till Övningstenta 1 1 a b b a a b + b a + 2 (a + b) + b a 2 b2 a 2 + b2 + 2 (a + b) + b a 2 b 2 a 2 + b 2 (a + b) + b + 2 a 2 b 2 a 2 + b 2 (a + b) + b + 2 (a b)(a + b)(a + b)
Lösningar och kommentarer till Övningstenta 1 1 a b b a a b + b a + 2 (a + b) + b a 2 b2 a 2 + b2 + 2 (a + b) + b a 2 b 2 a 2 + b 2 (a + b) + b + 2 a 2 b 2 a 2 + b 2 (a + b) + b + 2 (a b)(a + b)(a + b)
52 = 1041. 1040 1.00096 Vi kan nu teckna hur mycket pengar han har, just när han har satt in sina 280 kr den tredje måndagen + 280 1040
 Tillämpningar på främst geometriska, men även aritmetiska summor och talföljder. Att röka är ett fördärv. Förutom att man kan förlora hälsan går en mängd pengar upp i rök. Vi träffar Cigge, som röker 20
Tillämpningar på främst geometriska, men även aritmetiska summor och talföljder. Att röka är ett fördärv. Förutom att man kan förlora hälsan går en mängd pengar upp i rök. Vi träffar Cigge, som röker 20
f(t 2 ) f(t 1 ) = y 2 y 1 Figur 1:
 Som en inledning till begreppet derivata, ska vi här diskutera genomsnittlig förändingshastighet. Utan att veta vad som hänt mellan två givna tider t 1 och t 2 kan vi läsa av temperaturen, beloppet, hastigheten,
Som en inledning till begreppet derivata, ska vi här diskutera genomsnittlig förändingshastighet. Utan att veta vad som hänt mellan två givna tider t 1 och t 2 kan vi läsa av temperaturen, beloppet, hastigheten,
KOKBOKEN. Håkan Strömberg KTH STH
 KOKBOKEN Håkan Strömberg KTH STH Hösten 2007 Håkan Strömberg 2 KTH Syd Innehåll Genomsnittlig förändringshastighet...................... 5 Uppgift 1................................. 5 Uppgift 2.................................
KOKBOKEN Håkan Strömberg KTH STH Hösten 2007 Håkan Strömberg 2 KTH Syd Innehåll Genomsnittlig förändringshastighet...................... 5 Uppgift 1................................. 5 Uppgift 2.................................
Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = 1 x.
 Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = x 8 6 4 2-3 -2-2 3-2 -4-6 -8 Figur : Vi konstaterar följande: Då
Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = x 8 6 4 2-3 -2-2 3-2 -4-6 -8 Figur : Vi konstaterar följande: Då
Lösningar och kommentarer till uppgifter i 2.3
 Lösningar och kommentarer till uppgifter i 2.3 2303 d) TB: Jaha, nu gäller det att kunna sina deriveringsregler. Polynom kommer man alltid ihåg hur de ska deriveras. f(x) = 4x 2 + 5x 3 ger derivatan f
Lösningar och kommentarer till uppgifter i 2.3 2303 d) TB: Jaha, nu gäller det att kunna sina deriveringsregler. Polynom kommer man alltid ihåg hur de ska deriveras. f(x) = 4x 2 + 5x 3 ger derivatan f
5 Blandade problem. b(t) = t. b t ln b(t) = e
 5 Blandade problem 5.1 Dagens Teori Ett person sätter in 10000 kr på banken vid nyår 2000 till 4% ränta. Teckna en funktion, b(t) för beloppets utveckling. b(t) = 10000 1.04 t Skriv om funktionen med basen
5 Blandade problem 5.1 Dagens Teori Ett person sätter in 10000 kr på banken vid nyår 2000 till 4% ränta. Teckna en funktion, b(t) för beloppets utveckling. b(t) = 10000 1.04 t Skriv om funktionen med basen
Lösningar och kommentarer till uppgifter i 2.2
 Lösningar och kommentarer till uppgifter i 2.2 2202 Beräkna Detta ger f(3 + h) f(3) då f(x) x 2 (3 + h) 2 3 2 h 2 + 6h 6 + h 6 h 0 Vi har därmed bestämt riktningskoefficienten (k-värdet) för tangenten
Lösningar och kommentarer till uppgifter i 2.2 2202 Beräkna Detta ger f(3 + h) f(3) då f(x) x 2 (3 + h) 2 3 2 h 2 + 6h 6 + h 6 h 0 Vi har därmed bestämt riktningskoefficienten (k-värdet) för tangenten
y y 1 = k(x x 1 ) f(x) = 3 x
 Räta linjen på olika former Här ska vi bara påpeka att förutom k-form, den som vi är mest vana vid y = k y + m finns också allmän form: ax + by + c = 0 där a och b är konstanter, som inte någon står för
Räta linjen på olika former Här ska vi bara påpeka att förutom k-form, den som vi är mest vana vid y = k y + m finns också allmän form: ax + by + c = 0 där a och b är konstanter, som inte någon står för
Lästal från förr i tiden
 Lästal från förr i tiden Nedan presenteras ett antal problem som normalt leder till ekvationer av första graden. Inled din lösning med ett antagande. Teckna sedan ekvationen. Då ekvationen är korrekt uppställt
Lästal från förr i tiden Nedan presenteras ett antal problem som normalt leder till ekvationer av första graden. Inled din lösning med ett antagande. Teckna sedan ekvationen. Då ekvationen är korrekt uppställt
20 Gamla tentamensuppgifter
 20 Gamla tentamensuppgifter 20.1 Lätta avdelningen Övning 20.1 Beräkna f 0 ( 3) för f(x) = 3x2 2x + 1 med jälp av derivatans definition. Lösning: Här är det allmänna uttrycket för derivatans definition
20 Gamla tentamensuppgifter 20.1 Lätta avdelningen Övning 20.1 Beräkna f 0 ( 3) för f(x) = 3x2 2x + 1 med jälp av derivatans definition. Lösning: Här är det allmänna uttrycket för derivatans definition
Ingen ny teori denna dag. Istället koncentrerar vi oss på att lösa två tränings-ks:ar.
 Ingen ny teori denna dag. Istället koncentrerar vi oss på att lösa två tränings-ks:ar. 1 Bestäm med jälp av derivatans definition f () då f(x) = x + x + Funktionen f(x) = x 4x + 8 ar en minpunkt. Bestäm
Ingen ny teori denna dag. Istället koncentrerar vi oss på att lösa två tränings-ks:ar. 1 Bestäm med jälp av derivatans definition f () då f(x) = x + x + Funktionen f(x) = x 4x + 8 ar en minpunkt. Bestäm
Matematik CD för TB. x + 2y 6 = 0. Figur 1:
 Kontroll 8 1 Bestäm ekvationen för den linje som går genom punkterna P 1 (,4) och P 2 (9, 2). 2 Bestäm riktningskoefficienten för linjen x + 4y 6 = 0 Bestäm ekvationen för en linje som går genom punkten
Kontroll 8 1 Bestäm ekvationen för den linje som går genom punkterna P 1 (,4) och P 2 (9, 2). 2 Bestäm riktningskoefficienten för linjen x + 4y 6 = 0 Bestäm ekvationen för en linje som går genom punkten
Dagens tema är exponentialfunktioner. Egentligen inga nyheter, snarare repetition. Vi vet att alla exponentialfunktioner.
 Dagens tema är exponentialfunktioner. Egentligen inga nyheter, snarare repetition. Vi vet att alla exponentialfunktioner f(x) = C a x kan, om man så vill, skrivas om, med basen e, till Vi vet också att
Dagens tema är exponentialfunktioner. Egentligen inga nyheter, snarare repetition. Vi vet att alla exponentialfunktioner f(x) = C a x kan, om man så vill, skrivas om, med basen e, till Vi vet också att
Fler uppgifter på andragradsfunktioner
 Fler uppgifter på andragradsfunktioner 1 I grafen nedan visas tre andragradsfunktioner. Bestäm a,b och c för p(x) = ax 2 + bx + c genom att läsa av lämpliga punkter i grafen. 10 5 1 3 5 Figur 1: 2 Vi har
Fler uppgifter på andragradsfunktioner 1 I grafen nedan visas tre andragradsfunktioner. Bestäm a,b och c för p(x) = ax 2 + bx + c genom att läsa av lämpliga punkter i grafen. 10 5 1 3 5 Figur 1: 2 Vi har
Vi tolkar det som att beloppet just vid denna tidpunkt stiger med 459 kr/år, alltså en sorts hastighet. Vi granskar graferna till b(x) och b (x)
 Ett person sätter in 0000 kr på banken vid nyår 000 till 4% ränta. Teckna en funktion för beloppets utveckling. b(t) = 0000.04 t Skriv om funktionen med basen e istället för.04. Derivera denna funktion
Ett person sätter in 0000 kr på banken vid nyår 000 till 4% ränta. Teckna en funktion för beloppets utveckling. b(t) = 0000.04 t Skriv om funktionen med basen e istället för.04. Derivera denna funktion
13 Potensfunktioner. Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till
 3 Potensfunktioner 3. Dagens teori Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = x 8 6 4 2-3 -2-2 3-2 -4-6 -8
3 Potensfunktioner 3. Dagens teori Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = x 8 6 4 2-3 -2-2 3-2 -4-6 -8
Sekantens riktningskoefficient (lutning) kan vi enkelt bestämma genom. k = Men hur ska vi kunna bestämma tangentens riktningskoefficient (lutning)?
 I figuren ser vi grafen till funktionen f(x) x + Inritad finns dels en sekant, som skär kurvan i punkterna ( 1, 7) oc (4, ). Dessutom finns en tangent som tangerar kurvan i (, 10) Sekantens riktningskoefficient
I figuren ser vi grafen till funktionen f(x) x + Inritad finns dels en sekant, som skär kurvan i punkterna ( 1, 7) oc (4, ). Dessutom finns en tangent som tangerar kurvan i (, 10) Sekantens riktningskoefficient
Allt du behöver veta om exponentialfunktioner
 Allt du behöver veta om exponentialfunktioner Problem 1. Funktionerna a) a(x) = e x b) b(x) = e x c) c(x) = 4 x e x ln4 d) d(x) = 3 10 x 3 e x ln10 e) e(x) = ex 3 avbildas i figuren. Vilken är vilken?
Allt du behöver veta om exponentialfunktioner Problem 1. Funktionerna a) a(x) = e x b) b(x) = e x c) c(x) = 4 x e x ln4 d) d(x) = 3 10 x 3 e x ln10 e) e(x) = ex 3 avbildas i figuren. Vilken är vilken?
Belopp Belopp > procent
 Dagens problem Försäljarprovision Lönen för en försäljare är helt grundad på provision, direkt kopplad till den omsättning han lyckas skapa under en månad. Tabellen nedan anger procentsatser för olika
Dagens problem Försäljarprovision Lönen för en försäljare är helt grundad på provision, direkt kopplad till den omsättning han lyckas skapa under en månad. Tabellen nedan anger procentsatser för olika
Linjära ekvationssystem
 Sidor i boken KB 7-15 Linjära ekvationssystem Exempel 1. Kalle och Pelle har tillsammans 00 kulor. Pelle har dubbelt så många som Kalle. Hur många kulor har var och en? Lösning: Antag att Kalle har x kulor.
Sidor i boken KB 7-15 Linjära ekvationssystem Exempel 1. Kalle och Pelle har tillsammans 00 kulor. Pelle har dubbelt så många som Kalle. Hur många kulor har var och en? Lösning: Antag att Kalle har x kulor.
Gamla tentemensuppgifter
 Inte heller idag någon ny teori! Gamla tentemensuppgifter 1 Bestäm det andragradspolynom vars kurva skär x-axeln i x = 3 och x = 1 och y-axeln i y = 3 f(x) = (x 3)(x + 1) = x x 3 är en bra start, men vi
Inte heller idag någon ny teori! Gamla tentemensuppgifter 1 Bestäm det andragradspolynom vars kurva skär x-axeln i x = 3 och x = 1 och y-axeln i y = 3 f(x) = (x 3)(x + 1) = x x 3 är en bra start, men vi
x+2y 3z = 7 x+ay+11z = 17 2x y+z = 2
 Problem 1. Avgör för vilka värden på a som ekvationssystemet nedan har oändligt antal lösningar. Ange lösningarna i dessa fall! Lösning: Genom x+2y 3z = 7 x+ay+11z = 17 2x y+z = 2 1 2 3 1 a 11 2 1 1 =
Problem 1. Avgör för vilka värden på a som ekvationssystemet nedan har oändligt antal lösningar. Ange lösningarna i dessa fall! Lösning: Genom x+2y 3z = 7 x+ay+11z = 17 2x y+z = 2 1 2 3 1 a 11 2 1 1 =
kvoten mellan två på varandra följande tal i en talföljd är konstant alltid lika stor.
 Turen har kommit till geometriska talföljder och summan av en geometrisk talföljd. Talföljden 1,, 4, 8, 16, 3,... är ett exempel på en geometrisk talföljd. Utmärkande för en geometrisk talföljd är att
Turen har kommit till geometriska talföljder och summan av en geometrisk talföljd. Talföljden 1,, 4, 8, 16, 3,... är ett exempel på en geometrisk talföljd. Utmärkande för en geometrisk talföljd är att
Lösningar och kommentarer till uppgifter i 1.1
 Lösningar och kommentarer till uppgifter i 1.1 1106 d) 1107 d) 5t(t t 1) t (t 3) + t 3 5t 3 10t 5t (t 3 3t ) + t 3 5t 3 10t 5t t 3 + 3t + t 3 6t 3 7t 5t Kommentarer: Starta med att multiplicera in faktorerna
Lösningar och kommentarer till uppgifter i 1.1 1106 d) 1107 d) 5t(t t 1) t (t 3) + t 3 5t 3 10t 5t (t 3 3t ) + t 3 5t 3 10t 5t t 3 + 3t + t 3 6t 3 7t 5t Kommentarer: Starta med att multiplicera in faktorerna
4 Fler deriveringsregler
 4 Fler deriveringsregler 4. Dagens Teori Derivatan av potensfunktioner. Potensfunktioner med heltalsexponenter, som du redan kan derivera, kallas polynomfunktioner, som till exempel: f(x) = 2x4 x3 + 2x
4 Fler deriveringsregler 4. Dagens Teori Derivatan av potensfunktioner. Potensfunktioner med heltalsexponenter, som du redan kan derivera, kallas polynomfunktioner, som till exempel: f(x) = 2x4 x3 + 2x
10.1 Linjära första ordningens differentialekvationer
 10.1 Linjära första ordningens differentialekvationer Här ska vi studera linjära första ordningens differentialekvationer som kan skrivas y (x) + g(x)y(x) = h(x) Om g(x) har en primitiv funktion G(x) så
10.1 Linjära första ordningens differentialekvationer Här ska vi studera linjära första ordningens differentialekvationer som kan skrivas y (x) + g(x)y(x) = h(x) Om g(x) har en primitiv funktion G(x) så
Lite extramaterial i anslutning till boken
 Lite extramaterial i anslutning till boken Kapitel 1 Elementär algebra Prioritetsregler för räknesätten Det är av avgörande betydelse i vilken ordning räkneoperationer utförs. För att på ett otvetydigt
Lite extramaterial i anslutning till boken Kapitel 1 Elementär algebra Prioritetsregler för räknesätten Det är av avgörande betydelse i vilken ordning räkneoperationer utförs. För att på ett otvetydigt
Moment 4.11 Viktiga exempel 4.32, 4.33 Övningsuppgifter Ö4.18-Ö4.22, Ö4.30-Ö4.34. Planet Ett plan i rummet är bestämt då
 Moment 4.11 Viktiga exempel 4.32, 4.33 Övningsuppgifter Ö4.18-Ö4.22, Ö4.30-Ö4.34 Planet Ett plan i rummet är bestämt då två icke parallella riktningar, v 1 och v 2, och en punkt P 1 i planet är givna.
Moment 4.11 Viktiga exempel 4.32, 4.33 Övningsuppgifter Ö4.18-Ö4.22, Ö4.30-Ö4.34 Planet Ett plan i rummet är bestämt då två icke parallella riktningar, v 1 och v 2, och en punkt P 1 i planet är givna.
Matematik CD för TB = 5 +
 Föreläsning 4 70 a) Vi delar figuren i två delar, en triangel (på toppen) och en rektangel. Summan av dessa två figurers area ger den eftersökta. Vi behöver följande formler: A R = b h A T = b h Svar:
Föreläsning 4 70 a) Vi delar figuren i två delar, en triangel (på toppen) och en rektangel. Summan av dessa två figurers area ger den eftersökta. Vi behöver följande formler: A R = b h A T = b h Svar:
Moment Viktiga exempel Övningsuppgifter I
 Moment Viktiga eempel Övningsuppgifter I Inga Inga Inga Grafritning Vi använder en sjustegsprocess Funktionens definitionsmängd 2 Funktionens skärningspunkter med alarna Asymptoter 4 Stationära punkter
Moment Viktiga eempel Övningsuppgifter I Inga Inga Inga Grafritning Vi använder en sjustegsprocess Funktionens definitionsmängd 2 Funktionens skärningspunkter med alarna Asymptoter 4 Stationära punkter
Repetition inför tentamen
 Sidor i boken Repetition inför tentamen Läxa 1. Givet en rätvinklig triangel ACD, där AD = 10 cm, AB = 40 cm och BC = 180 cm. Beräkna vinkeln BDC. Läxa. Beräkna omkretsen av ABC, där BE = 4 cm, EA = 8
Sidor i boken Repetition inför tentamen Läxa 1. Givet en rätvinklig triangel ACD, där AD = 10 cm, AB = 40 cm och BC = 180 cm. Beräkna vinkeln BDC. Läxa. Beräkna omkretsen av ABC, där BE = 4 cm, EA = 8
Sidor i boken f(x) = a x 2 +b x+c
 Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
1 Förändingshastigheter och derivator
 Förändingsastigeter oc derivator. Dagens Teori Som en inledning till begreppet derivata, ska vi är diskutera genomsnittlig förändingsastiget. Utan att veta vad som änt mellan två givna tider t oc t 2 kan
Förändingsastigeter oc derivator. Dagens Teori Som en inledning till begreppet derivata, ska vi är diskutera genomsnittlig förändingsastiget. Utan att veta vad som änt mellan två givna tider t oc t 2 kan
2 Derivator. 2.1 Dagens Teori. Figur 2.1: I figuren ser vi grafen till funktionen. f(x) = x
 Derivator.1 Dagens Teori Figur.1: I figuren ser vi grafen till funktionen f(x) = x 3 + Inritad finns dels en sekant, som skär kurvan i punkterna ( 1, 7 3 finns en tangent som tangerar kurvan i (, 10 3
Derivator.1 Dagens Teori Figur.1: I figuren ser vi grafen till funktionen f(x) = x 3 + Inritad finns dels en sekant, som skär kurvan i punkterna ( 1, 7 3 finns en tangent som tangerar kurvan i (, 10 3
1, 2, 3, 4, 5, 6,...
 Dagens nyhet handlar om talföljder, ändliga och oändliga. Talföljden 1,, 3, 4, 5, 6,... är det första vi, som barn, lär oss om matematik över huvud taget. Så småningom lär vi oss att denna talföljd inte
Dagens nyhet handlar om talföljder, ändliga och oändliga. Talföljden 1,, 3, 4, 5, 6,... är det första vi, som barn, lär oss om matematik över huvud taget. Så småningom lär vi oss att denna talföljd inte
3, 6, 9, 12, 15, 18. 1, 2, 4, 8, 16, 32 Nu är stunden inne, då vill vill summera talen i en talföljd
 I föreläsning 18 bekantade vi oss med talföljder, till exempel eller 3, 6, 9, 1, 15, 18 1,, 4, 8, 16, 3 Nu är stunden inne, då vill vill summera talen i en talföljd och 3 + 6 + 9 + 1 + 15 + 18 1 + + 4
I föreläsning 18 bekantade vi oss med talföljder, till exempel eller 3, 6, 9, 1, 15, 18 1,, 4, 8, 16, 3 Nu är stunden inne, då vill vill summera talen i en talföljd och 3 + 6 + 9 + 1 + 15 + 18 1 + + 4
Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen.
 Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
Moment Viktiga exempel Övningsuppgifter I Ö5.1b, Ö5.2b, Ö5.3b, Ö5.6, Ö5.7, Ö5.11a
 Moment 5.1-5.5 Viktiga exempel 5.1-5.10 Övningsuppgifter I Ö5.1b, Ö5.2b, Ö5.3b, Ö5.6, Ö5.7, Ö5.11a Kvadratiska linjära ekvationssystem Vi startar vår utredning med det vi känner bäst till, ekvationssystem
Moment 5.1-5.5 Viktiga exempel 5.1-5.10 Övningsuppgifter I Ö5.1b, Ö5.2b, Ö5.3b, Ö5.6, Ö5.7, Ö5.11a Kvadratiska linjära ekvationssystem Vi startar vår utredning med det vi känner bäst till, ekvationssystem
NpMa2c vt Provet består av tre skriftliga delprov (Delprov B, C och D). Tillsammans kan de ge 57 poäng varav 20 E-, 20 C- och 17 A-poäng.
 NpMac vt 015 Delprov B Delprov C Provtid Hjälpmedel Uppgift 1-9. Endast svar krävs. Uppgift 10-17. Fullständiga lösningar krävs. 10 minuter för Delprov B och Delprov C tillsammans. Formelblad och linjal.
NpMac vt 015 Delprov B Delprov C Provtid Hjälpmedel Uppgift 1-9. Endast svar krävs. Uppgift 10-17. Fullständiga lösningar krävs. 10 minuter för Delprov B och Delprov C tillsammans. Formelblad och linjal.
f(t 2 ) f(t 1 ) = y 2 y 1 Figur 1:
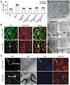 Som en inledning till begreppet derivata, ska vi här diskutera genomsnittlig förändingshastighet. Utan att veta vad som hänt mellan två givna tider t 1 och t kan vi läsa av temperaturen, beloppet, hastigheten,
Som en inledning till begreppet derivata, ska vi här diskutera genomsnittlig förändingshastighet. Utan att veta vad som hänt mellan två givna tider t 1 och t kan vi läsa av temperaturen, beloppet, hastigheten,
Exponentialfunktioner och logaritmer
 Eponentialfunktioner och logaritmer Tidigare i kurserna har du gått igenom potenslagarna, hur man räknar med potenser och potensfunktioner av typen y. En potens- funktion är en funktion som innefattar
Eponentialfunktioner och logaritmer Tidigare i kurserna har du gått igenom potenslagarna, hur man räknar med potenser och potensfunktioner av typen y. En potens- funktion är en funktion som innefattar
Den räta linjens ekvation
 Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Teori och teori idag, som igår är det praktik som gäller! 1 (Bokens nr 3216) Figur 1:
 Teori och teori idag, som igår är det praktik som gäller! 1 (Bokens nr 316) Figur 1: a) Bestäm y som funktion av x genom att utnyttja likformiga trianglar. Se figur 1. b) Ange funktionens definitionsmängd
Teori och teori idag, som igår är det praktik som gäller! 1 (Bokens nr 316) Figur 1: a) Bestäm y som funktion av x genom att utnyttja likformiga trianglar. Se figur 1. b) Ange funktionens definitionsmängd
Kan du det här? o o. o o o o. Derivera potensfunktioner, exponentialfunktioner och summor av funktioner. Använda dig av derivatan i problemlösning.
 Kan du det här? o o o o o o Vad innebär det att x går mot noll? Vad händer då x går mot oändligheten? Vad betyder sekant, tangent och ändringskvot och vad har dessa begrepp med derivatan att göra? Derivera
Kan du det här? o o o o o o Vad innebär det att x går mot noll? Vad händer då x går mot oändligheten? Vad betyder sekant, tangent och ändringskvot och vad har dessa begrepp med derivatan att göra? Derivera
Den räta linjens ekvation
 Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
a = a a a a a a ± ± ± ±500
 4.1 Felanalys Vill man hårddra det hela, kan man påstå att det inte finns några tal i den tillämpade matematiken, bara intervall. Man anger till exempel inte ett uppmätt värde till 134.78 meter utan att
4.1 Felanalys Vill man hårddra det hela, kan man påstå att det inte finns några tal i den tillämpade matematiken, bara intervall. Man anger till exempel inte ett uppmätt värde till 134.78 meter utan att
KOKBOKEN 1. Håkan Strömberg KTH STH
 KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
Logaritmer. Joakim Östlund Patrik Lindegrén Andreas Lillqvist Carlos
 Logaritmer Joakim Östlund Patrik Lindegrén Andreas Lillqvist Carlos 24 september 2003 Innehåll 1 Introduktion 2 2 Naturliga logaritmer 3 2.1 Talet e................................. 3 2.2 Den naturliga
Logaritmer Joakim Östlund Patrik Lindegrén Andreas Lillqvist Carlos 24 september 2003 Innehåll 1 Introduktion 2 2 Naturliga logaritmer 3 2.1 Talet e................................. 3 2.2 Den naturliga
Övningstenta 6. d b = 389. c d a b = 1319 b a
 Övningstenta 6 Problem 1. Vilket är det största antalet olika element en symmetrisk matris A(n n kan ha? Problem. Bestäm de reella talen a,b,c och d då man vet att a b d c = 109 a c d b = 389 c d a b =
Övningstenta 6 Problem 1. Vilket är det största antalet olika element en symmetrisk matris A(n n kan ha? Problem. Bestäm de reella talen a,b,c och d då man vet att a b d c = 109 a c d b = 389 c d a b =
f (x) = 8x 3 3x Men hur är det när exponenterna inte är heltal eller är negativ, som till exempel g(x) = x h (x) = n x n 1
 Derivatan av potensfunktioner. Potensfunktioner med heltalsexponenter, som du redan kan derivera, kallas polynomfunktioner, som till exempel: Derivatan blir: f(x) = x 4 x + x + 8 f (x) = 8x x + Men hur
Derivatan av potensfunktioner. Potensfunktioner med heltalsexponenter, som du redan kan derivera, kallas polynomfunktioner, som till exempel: Derivatan blir: f(x) = x 4 x + x + 8 f (x) = 8x x + Men hur
f (a) sin
 Hur kan datorn eller räknedosan känna till värdet hos till exempel sin0.23 eller e 2.4? Denna fråga är berättigad samtidigt som ingen tror att apparaterna innehåller en gigantisk tabell. Svaret på frågan
Hur kan datorn eller räknedosan känna till värdet hos till exempel sin0.23 eller e 2.4? Denna fråga är berättigad samtidigt som ingen tror att apparaterna innehåller en gigantisk tabell. Svaret på frågan
Tal Repetitionsuppgifter
 epetitionsuppgifter Till varje kapitel finns repetitionsuppgifter i form av Arbetsblad. Uppgifterna är relaterade till innehållet i respektive kapitel och täcker hela kapitlet. De uppgifter som kräver
epetitionsuppgifter Till varje kapitel finns repetitionsuppgifter i form av Arbetsblad. Uppgifterna är relaterade till innehållet i respektive kapitel och täcker hela kapitlet. De uppgifter som kräver
DOP-matematik Copyright Tord Persson. Logövningar. Slumpad ordning. Uppgift nr 10 Lös ekvationen 10 y = 0,001. Uppgift nr 13 Lös ekvationen lg x = 4
 Logövningar Uppgift nr 1 lg y -2 Uppgift nr 2 Huvudräkna lg200 + lg5 Uppgift nr 3 71 z 70 Uppgift nr 4 Ange derivatan till y e x Uppgift nr 5 Skriv 3 lg5 som en logaritm utan faktor framför. Uppgift nr
Logövningar Uppgift nr 1 lg y -2 Uppgift nr 2 Huvudräkna lg200 + lg5 Uppgift nr 3 71 z 70 Uppgift nr 4 Ange derivatan till y e x Uppgift nr 5 Skriv 3 lg5 som en logaritm utan faktor framför. Uppgift nr
Lösningar och kommentarer till uppgifter i 3.1
 Lösningar och kommentarer till uppgifter i.1 102 b) TB: Kör de med dessa uppgifter i det här kapitlet också? Det gör inget, jag börjar bli ganska bra på det. Vi har funktionen fx) = x x 2 24x + 1 och man
Lösningar och kommentarer till uppgifter i.1 102 b) TB: Kör de med dessa uppgifter i det här kapitlet också? Det gör inget, jag börjar bli ganska bra på det. Vi har funktionen fx) = x x 2 24x + 1 och man
Lösningar och kommentarer till uppgifter i 1.1
 Lösigar och kommetarer till uppgifter i. 407 d) 408 d) 40 a) 3 /5 5) 5 3 0 ) 0) 3 5 5 4 0 6 5 x 5 x) 5 x + 5 x 5 x 5 x 5 x + 5 x 40 Om det u är eklare så här a x a 3x + a x) a 4x + 43 a) 43 45 5 3 5 )
Lösigar och kommetarer till uppgifter i. 407 d) 408 d) 40 a) 3 /5 5) 5 3 0 ) 0) 3 5 5 4 0 6 5 x 5 x) 5 x + 5 x 5 x 5 x 5 x + 5 x 40 Om det u är eklare så här a x a 3x + a x) a 4x + 43 a) 43 45 5 3 5 )
När vi blickar tillbaka på föregående del av kursen påminns vi av en del moment som man aldrig får tappa bort. x 2 x 1 +2 = 1. x 1
 Lathund inför tentan När vi blickar tillbaka på föregående del av kursen påminns vi av en del moment som man aldrig får tappa bort Ekvationer Ekvationer av första och andra graden kommer alltid att kunna
Lathund inför tentan När vi blickar tillbaka på föregående del av kursen påminns vi av en del moment som man aldrig får tappa bort Ekvationer Ekvationer av första och andra graden kommer alltid att kunna
Ekvationslösning genom substitution, rotekvationer
 Sidor i boken -3, 70-73 Ekvationslösning genom substitution, rotekvationer Rotekvationer Med en rotekvation menas en ekvation, i vilken den obekanta förekommer under ett rotmärke. Observera att betecknar
Sidor i boken -3, 70-73 Ekvationslösning genom substitution, rotekvationer Rotekvationer Med en rotekvation menas en ekvation, i vilken den obekanta förekommer under ett rotmärke. Observera att betecknar
polynomfunktioner potensfunktioner exponentialfunktioner
 Vi ar lärt oss derivera en funktion, främst polynom, med jälp av derivatans definition. Vi ar funnit denna teknik ganska krävande. Desto trevligare blir det då att konstatera att det finns enkla deriveringsregler,
Vi ar lärt oss derivera en funktion, främst polynom, med jälp av derivatans definition. Vi ar funnit denna teknik ganska krävande. Desto trevligare blir det då att konstatera att det finns enkla deriveringsregler,
2+t = 4+s t = 2+s 2 t = s
 Extra 1. Ta fram räta linjens ekvation på parameterform då linjen går genom punkterna (1, 1,0) och (2,0,1) (3, 1,4) och ( 1,1,6) (4,3, 1) och (7, 2,5) (11,3, 6) och (9, 1,3) Lösning: (x,y,z) = (1+t, 1+t,t)
Extra 1. Ta fram räta linjens ekvation på parameterform då linjen går genom punkterna (1, 1,0) och (2,0,1) (3, 1,4) och ( 1,1,6) (4,3, 1) och (7, 2,5) (11,3, 6) och (9, 1,3) Lösning: (x,y,z) = (1+t, 1+t,t)
Moment Viktiga exempel Övningsuppgifter
 Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Fler exempel på optimering Exempel 1. Utifrån en rektangulär pappskiva med bredden 7 dm och längden 11 dm, vill man åstadkomma en kartong utan lock,
Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Fler exempel på optimering Exempel 1. Utifrån en rektangulär pappskiva med bredden 7 dm och längden 11 dm, vill man åstadkomma en kartong utan lock,
Ma2bc. Komvux, Lund. Prov
 Ma2bc. Komvux, Lund. Prov 1. 151013. (Lärare: Ingemar Carlsson) Anvisningar Provtid Hjälpmedel Del A Del B Del C Kravgränser 120 minuter för Del B, C och Del D. Du får påbörja del D (och börja använda
Ma2bc. Komvux, Lund. Prov 1. 151013. (Lärare: Ingemar Carlsson) Anvisningar Provtid Hjälpmedel Del A Del B Del C Kravgränser 120 minuter för Del B, C och Del D. Du får påbörja del D (och börja använda
Moment Viktiga exempel Övningsuppgifter Ö , Ö1.25, Ö1.55, Ö1.59
 Moment.0-. Viktiga exempel Övningsuppgifter Ö.9-., Ö.5, Ö.55, Ö.59 Funktioner Definition. En funktion y = f(x) är ett samband mellan variablerna x och y, sådant att ett x-värde motsvaras av högst ett värde
Moment.0-. Viktiga exempel Övningsuppgifter Ö.9-., Ö.5, Ö.55, Ö.59 Funktioner Definition. En funktion y = f(x) är ett samband mellan variablerna x och y, sådant att ett x-värde motsvaras av högst ett värde
Egentligen har vi ingen ny teori att presentera idag. Målet för den närmaste framtiden är att nöta in undersökandet av polynomfunktioner.
 Egentligen har vi ingen ny teori att presentera idag. Målet för den närmaste framtiden är att nöta in undersökandet av polynomfunktioner. 1 (Bokens nr 3204) Ett straffkast i basket följer ekvationen h(x)
Egentligen har vi ingen ny teori att presentera idag. Målet för den närmaste framtiden är att nöta in undersökandet av polynomfunktioner. 1 (Bokens nr 3204) Ett straffkast i basket följer ekvationen h(x)
Repetitionsuppgifter 1
 Repetitionsuppgifter 1 1 Är talet a) 5 ett heltal b) 9 ett naturligt tal c) π ett rationellt tal d) 5 ett reellt tal 6 2 Rita av figuren och placera in talen rätt talmängd. naturliga tal hela tal rationella
Repetitionsuppgifter 1 1 Är talet a) 5 ett heltal b) 9 ett naturligt tal c) π ett rationellt tal d) 5 ett reellt tal 6 2 Rita av figuren och placera in talen rätt talmängd. naturliga tal hela tal rationella
Moment 1.15, 2.1, 2.4 Viktiga exempel 2.2, 2.3, 2.4 Övningsuppgifter Ö2.2ab, Ö2.3. Polynomekvationer. p 2 (x) = x 7 +1.
 Moment.5, 2., 2.4 Viktiga exempel 2.2, 2.3, 2.4 Övningsuppgifter Ö2.2ab, Ö2.3 Ett polynom vilket som helst kan skrivas Polynomekvationer p(x) = a 0 +a x+a 2 x 2 +...+a n x n +a n x n Talen a 0,a,...a n
Moment.5, 2., 2.4 Viktiga exempel 2.2, 2.3, 2.4 Övningsuppgifter Ö2.2ab, Ö2.3 Ett polynom vilket som helst kan skrivas Polynomekvationer p(x) = a 0 +a x+a 2 x 2 +...+a n x n +a n x n Talen a 0,a,...a n
Karolina Klü ft (4/2/0)
 Karolina Klü ft (4/2/0) Klüft tävlade i sjukamp och var en av Sveriges främsta medaljkandidater i VM i friidrott 2005. I sjukamp tävlar deltagarna i olika grenar. För att kunna summera resultaten från
Karolina Klü ft (4/2/0) Klüft tävlade i sjukamp och var en av Sveriges främsta medaljkandidater i VM i friidrott 2005. I sjukamp tävlar deltagarna i olika grenar. För att kunna summera resultaten från
1. Amanda tänker på ett femsiffrigt heltal. Talet börjar med 1 och slutar med 8. Vilket är talet?
 2 1. Amanda tänker på ett femsiffrigt heltal. Talet börjar med 1 och slutar med 8. Vilket är talet? (1) Tiotalssiffran är dubbelt så stor som tusentalssiffran. (2) Hundratalssiffran är hälften så stor
2 1. Amanda tänker på ett femsiffrigt heltal. Talet börjar med 1 och slutar med 8. Vilket är talet? (1) Tiotalssiffran är dubbelt så stor som tusentalssiffran. (2) Hundratalssiffran är hälften så stor
x+2y+3z = 14 x 3y+z = 2 3x+2y 4z = 5
 Uppgifter med linjära ekvationssystem Tips för att lösa linjära ekvationssystem Då systemet saknar parametrar ställer man direkt upp totalmatrisen. Detta är endast av administrativa skäl, blir mer lättöverskådligt.
Uppgifter med linjära ekvationssystem Tips för att lösa linjära ekvationssystem Då systemet saknar parametrar ställer man direkt upp totalmatrisen. Detta är endast av administrativa skäl, blir mer lättöverskådligt.
Moment Viktiga exempel 4.37, 4.38, 4.39 Övningsuppgifter 4.52, P 0 P = t v OP och OP 0 är ortsvektorer för punkterna P och P 0, så
 Tisdagen september kl 10:15, Sal 093, Moment 4.3.1 Viktiga exempel 4.37, 4.38, 4.39 Övningsuppgifter 4.5, 4.55 Räta linjen i rummet En rät linje l i rummet är bestämd då en punkt P 0 på linjen och en riktningsvektor
Tisdagen september kl 10:15, Sal 093, Moment 4.3.1 Viktiga exempel 4.37, 4.38, 4.39 Övningsuppgifter 4.5, 4.55 Räta linjen i rummet En rät linje l i rummet är bestämd då en punkt P 0 på linjen och en riktningsvektor
8 + h. lim 8 + h = 8
 Nu ar vi kretsat kring oc förberett oss på begreppet derivata i två föreläsningar. Nu är tiden inne! Men innan dess ska vi diskutera gränsvärde, ett annat begrepp. Om vi ar uttrycket 8 + oc låter gå mot
Nu ar vi kretsat kring oc förberett oss på begreppet derivata i två föreläsningar. Nu är tiden inne! Men innan dess ska vi diskutera gränsvärde, ett annat begrepp. Om vi ar uttrycket 8 + oc låter gå mot
Sammanfattningar Matematikboken Y
 Sammanfattningar Matematikboken Y KAPitel 1 TAL OCH RÄKNING Numeriska uttryck När man beräknar ett numeriskt uttryck utförs multiplikation och division före addition och subtraktion. Om uttrycket innehåller
Sammanfattningar Matematikboken Y KAPitel 1 TAL OCH RÄKNING Numeriska uttryck När man beräknar ett numeriskt uttryck utförs multiplikation och division före addition och subtraktion. Om uttrycket innehåller
Talmängder. Målet med första föreläsningen:
 Moment 1..1, 1.., 1..4, 1..5, 1.. 1..5, 1..6 Viktiga exempel 1.7, 1.8, 1.8,1.19,1. Handräkning 1.7, 1.9, 1.19, 1.4, 1.9 b,e 1.0 a,b Datorräkning 1.6-1.1 Målet med första föreläsningen: 1 En första kontakt
Moment 1..1, 1.., 1..4, 1..5, 1.. 1..5, 1..6 Viktiga exempel 1.7, 1.8, 1.8,1.19,1. Handräkning 1.7, 1.9, 1.19, 1.4, 1.9 b,e 1.0 a,b Datorräkning 1.6-1.1 Målet med första föreläsningen: 1 En första kontakt
Funktioner. Räta linjen
 Sidor i boken 14-143, 145-147 Funktioner. Räta linjen Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter
Sidor i boken 14-143, 145-147 Funktioner. Räta linjen Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter
Planering för kurs A i Matematik
 Planering för kurs A i Matematik Läromedel: Holmström/Smedhamre, Matematik från A till E, kurs A Antal timmar: 90 (80 + 10) I nedanstående planeringsförslag tänker vi oss att A-kursen studeras på 90 klocktimmar.
Planering för kurs A i Matematik Läromedel: Holmström/Smedhamre, Matematik från A till E, kurs A Antal timmar: 90 (80 + 10) I nedanstående planeringsförslag tänker vi oss att A-kursen studeras på 90 klocktimmar.
Repetitionsuppgifter i Matematik inför Basår. Matematiska institutionen Linköpings universitet 2014
 Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
6 cm. 106 Beräkna a) 3 ( 4) b) ( 2) 5 c) 4 ( 2,5) d) ( 8) 1,5. T.ex. print(3 * -4) 13 Beräkna cirkelns a) diameter b) omkrets
 1 Print 1 Tal Multiplikation och division med negativa tal 106 Beräkna a) 3 ( 4) b) ( 2) 5 c) 4 ( 2,5) d) ( 8) 1,5 print(3 * -4) 2 Geometri Cirkelns omkrets 13 Beräkna cirkelns a) diameter b) omkrets 6
1 Print 1 Tal Multiplikation och division med negativa tal 106 Beräkna a) 3 ( 4) b) ( 2) 5 c) 4 ( 2,5) d) ( 8) 1,5 print(3 * -4) 2 Geometri Cirkelns omkrets 13 Beräkna cirkelns a) diameter b) omkrets 6
Del I Denna del består av 8 uppgifter och är avsedd att genomföras utan miniräknare.
 Del I Denna del består av 8 uppgifter och är avsedd att genomföras utan miniräknare. Dina lösningar på denna del görs på separat papper som ska lämnas in innan du får tillgång till din miniräknare. Observera
Del I Denna del består av 8 uppgifter och är avsedd att genomföras utan miniräknare. Dina lösningar på denna del görs på separat papper som ska lämnas in innan du får tillgång till din miniräknare. Observera
Högskoleverket. Delprov NOG
 Högskoleverket Delprov NOG 2002-04-06 1. Ett tusen kronor sattes in på ett konto. Pengarna var insatta på kontot i två år och efter halva tiden ändrades räntan. Vilken var räntesatsen under det första
Högskoleverket Delprov NOG 2002-04-06 1. Ett tusen kronor sattes in på ett konto. Pengarna var insatta på kontot i två år och efter halva tiden ändrades räntan. Vilken var räntesatsen under det första
Algebra, exponentialekvationer och logaritmer
 Höstlov Uppgift nr 1 Ge en lösning till ekvationen 0 434,2-13x 3 Ange både exakt svar och avrundat till två decimalers noggrannhet. Uppgift nr 2 Huvudräkna lg20 + lg50 Uppgift nr 3 Ge en lösning till ekvationen
Höstlov Uppgift nr 1 Ge en lösning till ekvationen 0 434,2-13x 3 Ange både exakt svar och avrundat till två decimalers noggrannhet. Uppgift nr 2 Huvudräkna lg20 + lg50 Uppgift nr 3 Ge en lösning till ekvationen
5 Om f (r) = 0 kan andraderivatan inte avgöra vilken typ av extrempunkt det handlar om. Återstår att avgöra punktens typ med teckenstudium.
 Så här hittar man extrempunkter, max-, min eller terrasspunkter, till en kurva y = f(x) med hjälp av i första hand f (x) 1 Bestäm f (x) och f (x) 2 Lös ekvationen f (x) = 0. Om ekvationen saknar rötter
Så här hittar man extrempunkter, max-, min eller terrasspunkter, till en kurva y = f(x) med hjälp av i första hand f (x) 1 Bestäm f (x) och f (x) 2 Lös ekvationen f (x) = 0. Om ekvationen saknar rötter
Ylioppilastutkintolautakunta S tudentexamensnämnden
 Ylioppilastutkintolautakunta S tudentexamensnämnden PROVET I MATEMATIK, KORT LÄROKURS.9.013 BESKRIVNING AV GODA SVAR De beskrivningar av svarens innehåll som ges här är inte bindande för studentexamensnämndens
Ylioppilastutkintolautakunta S tudentexamensnämnden PROVET I MATEMATIK, KORT LÄROKURS.9.013 BESKRIVNING AV GODA SVAR De beskrivningar av svarens innehåll som ges här är inte bindande för studentexamensnämndens
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 4. b) = 3 1 = 2
 Kapitel.1 101, 102 Exempel som löses i boken 10 a) x= 1 11+ x= 11+ 1 = 2 c) x= 11 7 x= 7 11 = 77 b) x= 5 x 29 = 5 29 = 6 d) x= 2 26 x= 26 2= 1 10 a) x= 6 5+ 9 x= 5+ 9 6= 5+ 5= 59 b) a = 8a 6= 8 6= 2 6=
Kapitel.1 101, 102 Exempel som löses i boken 10 a) x= 1 11+ x= 11+ 1 = 2 c) x= 11 7 x= 7 11 = 77 b) x= 5 x 29 = 5 29 = 6 d) x= 2 26 x= 26 2= 1 10 a) x= 6 5+ 9 x= 5+ 9 6= 5+ 5= 59 b) a = 8a 6= 8 6= 2 6=
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs B, kapitel 2
 Kapitel.1 101, 10 Exempel som löses i boken. 103 Testa genom att lägga linjalen lodrätt och föra den över grafen. Om den på något ställe skär grafen i mer än en punkt så visar grafen inte en funktion.
Kapitel.1 101, 10 Exempel som löses i boken. 103 Testa genom att lägga linjalen lodrätt och föra den över grafen. Om den på något ställe skär grafen i mer än en punkt så visar grafen inte en funktion.
M0038M Differentialkalkyl, Lekt 7, H15
 M0038M Differentialkalkyl, Lekt 7, H15 Staffan Lundberg Luleå Tekniska Universitet Staffan Lundberg M0038M H15 1/ 21 Tentamen M0038M Tentamensdatum 2015-10-28 Sista anmälningsdag 2015-10-08 Tentamensanmälan
M0038M Differentialkalkyl, Lekt 7, H15 Staffan Lundberg Luleå Tekniska Universitet Staffan Lundberg M0038M H15 1/ 21 Tentamen M0038M Tentamensdatum 2015-10-28 Sista anmälningsdag 2015-10-08 Tentamensanmälan
TENTAMEN. Linjär algebra och analys Kurskod HF1006. Skrivtid 8:15-13:00. Tisdagen 31 maj Tentamen består av 3 sidor
 TENTAMEN Linjär algebra och analys Kurskod HF1006 Skrivtid 8:15-13:00 Tisdagen 31 maj 2011 Tentamen består av 3 sidor Hjälpmedel: Mathematica samt allt tryckt material Tentamen består av 12 uppgifter,
TENTAMEN Linjär algebra och analys Kurskod HF1006 Skrivtid 8:15-13:00 Tisdagen 31 maj 2011 Tentamen består av 3 sidor Hjälpmedel: Mathematica samt allt tryckt material Tentamen består av 12 uppgifter,
Problemlösning Lösningar
 Problemlösning Lösningar Lösning Problemlösning. Julpromenaden (2) Vi antar först att sträckan på slät mark är km och att backen är y km lång. Från det kända sambandet får vi t = s/v och kan nu teckna
Problemlösning Lösningar Lösning Problemlösning. Julpromenaden (2) Vi antar först att sträckan på slät mark är km och att backen är y km lång. Från det kända sambandet får vi t = s/v och kan nu teckna
Kontrollskrivning KS1T
 Kontrollskrivning KS1T Matematik 2 Kurskod HF100 Skrivtid 8:15-11:15 måndagen 9 februari 2009 Tentamen består av 4 sidor Hjälpmedel: Utdelat formelblad. Räknedosa. Formelsamling Korrekt löst uppgift ger
Kontrollskrivning KS1T Matematik 2 Kurskod HF100 Skrivtid 8:15-11:15 måndagen 9 februari 2009 Tentamen består av 4 sidor Hjälpmedel: Utdelat formelblad. Räknedosa. Formelsamling Korrekt löst uppgift ger
2x+y z 5 = 0. e x e y e z = 4 e y +4 e z +8 e x + e z = (8,4,5) n 3 = n 1 n 2 =
 Problem 1. Nedan presenteras ekvationen för en rät linje och ett plan i rummet. Du ska avgöra om linjen är vinkelrät mot planet. x = 2 4t y = 3 2t z = 1+2t 2x+y z 5 = 0 Lösning: Linjen har riktningsvektorn
Problem 1. Nedan presenteras ekvationen för en rät linje och ett plan i rummet. Du ska avgöra om linjen är vinkelrät mot planet. x = 2 4t y = 3 2t z = 1+2t 2x+y z 5 = 0 Lösning: Linjen har riktningsvektorn
Provet består av tre skriftliga delprov (Delprov B, C och D). Tillsammans kan de ge 53 poäng varav 22 E-, 18 C- och 13 A-poäng.
 NpMaa ht 013 Delprov D Provtid Hjälpmedel Uppgift 15-3. Fullständiga lösningar krävs. 10 minuter. Digitala verktyg, formelblad och linjal. Kravgränser Provet består av tre skriftliga delprov (Delprov B,
NpMaa ht 013 Delprov D Provtid Hjälpmedel Uppgift 15-3. Fullständiga lösningar krävs. 10 minuter. Digitala verktyg, formelblad och linjal. Kravgränser Provet består av tre skriftliga delprov (Delprov B,
a) Ange ekvationen för den räta linjen L. (1/0/0)
 Delprov B: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet. 1. Ange det uttryck som ska stå i parentesen för att likheten ska gälla. ( ) ( x 5) = x 5 (1/0/0).
Delprov B: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet. 1. Ange det uttryck som ska stå i parentesen för att likheten ska gälla. ( ) ( x 5) = x 5 (1/0/0).
Uppgift 1-9. Endast svar krävs. Uppgift 10-14. Fullständiga lösningar krävs. 120 minuter för Delprov B och Delprov C tillsammans.
 Delprov B Delprov C Provtid Hjälpmedel Uppgift 1-9. Endast svar krävs. Uppgift 10-14. Fullständiga lösningar krävs. 10 minuter för Delprov B och Delprov C tillsammans. Formelblad och linjal. Kravgränser
Delprov B Delprov C Provtid Hjälpmedel Uppgift 1-9. Endast svar krävs. Uppgift 10-14. Fullständiga lösningar krävs. 10 minuter för Delprov B och Delprov C tillsammans. Formelblad och linjal. Kravgränser
vux GeoGebraexempel 2b/2c Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker
 matematik Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker vux 2b/2c GeoGebraexempel Till läsaren i elevböckerna i serien matematik origo finns uppgifter där vi rekommenderar användning
matematik Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker vux 2b/2c GeoGebraexempel Till läsaren i elevböckerna i serien matematik origo finns uppgifter där vi rekommenderar användning
Del A: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt på provpappret.
 NAN: KLASS: Del A: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt på provpappret. 1) a) estäm ekvationen för den räta linjen i figuren. b) ita i koordinatsystemet en rät linje
NAN: KLASS: Del A: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt på provpappret. 1) a) estäm ekvationen för den räta linjen i figuren. b) ita i koordinatsystemet en rät linje
NpMa2b vt Kravgränser
 Kravgränser Provet består av ett muntligt delprov (Del A) och tre skriftliga delprov (Del B, Del C och Del D). Tillsammans kan de ge 67 poäng varav 26 E-, 24 C- och 17 A-poäng. Observera att kravgränserna
Kravgränser Provet består av ett muntligt delprov (Del A) och tre skriftliga delprov (Del B, Del C och Del D). Tillsammans kan de ge 67 poäng varav 26 E-, 24 C- och 17 A-poäng. Observera att kravgränserna
Problemlösning Lösningar
 Problemlösning Lösningar Lösning Problemlösning 1. Dela bröd och pengar (0) Luffarna åt 8/3 bröd var. Luffare A gav bort 3 8/3 = 1/3 bröd till C och luffare B gav bort 5 8/3 = 7/3 bröd till C. Alltså ska
Problemlösning Lösningar Lösning Problemlösning 1. Dela bröd och pengar (0) Luffarna åt 8/3 bröd var. Luffare A gav bort 3 8/3 = 1/3 bröd till C och luffare B gav bort 5 8/3 = 7/3 bröd till C. Alltså ska
19.1 Funktioner av stokastiska variabler
 9. Funktioner av stokastiska variabler 9.. Oberoende stokastiska variabler Som vi minns innebär P(A B) = P(A) P(B) att händelserna A och B är oberoende. Låt A vara händelsen att X < x och B vara händelsen
9. Funktioner av stokastiska variabler 9.. Oberoende stokastiska variabler Som vi minns innebär P(A B) = P(A) P(B) att händelserna A och B är oberoende. Låt A vara händelsen att X < x och B vara händelsen
STOCKHOLMS UNIVERSITET FYSIKUM
 STOCKHOLMS UNIVERSITET FYSIKUM Tentamensskrivning i Fysikexperiment, 7,5 hp, för FK2002 Onsdagen den 15 december 2010 kl. 9-14. Skrivningen består av två delar A och B. Del A innehåller enkla frågor och
STOCKHOLMS UNIVERSITET FYSIKUM Tentamensskrivning i Fysikexperiment, 7,5 hp, för FK2002 Onsdagen den 15 december 2010 kl. 9-14. Skrivningen består av två delar A och B. Del A innehåller enkla frågor och
9 Skissa grafer. 9.1 Dagens Teori
 9 Skissa grafer 9.1 Dagens Teori Så här hittar man etrempunkter, ma-, min eller terrasspunkter, till en kurva y = f() med hjälp av i första hand f () 1 Bestäm f () och f () 2 Lös ekvationen f () = 0. Om
9 Skissa grafer 9.1 Dagens Teori Så här hittar man etrempunkter, ma-, min eller terrasspunkter, till en kurva y = f() med hjälp av i första hand f () 1 Bestäm f () och f () 2 Lös ekvationen f () = 0. Om
Trigonometri. Sidor i boken 26-34
 Sidor i boken 6-34 Trigonometri Definition: Gren av matematiken som studerar samband mellan vinklar och sträckor i planet (och rymden). Det grundläggande trigonometriska problemet är att beräkna alla sidor
Sidor i boken 6-34 Trigonometri Definition: Gren av matematiken som studerar samband mellan vinklar och sträckor i planet (och rymden). Det grundläggande trigonometriska problemet är att beräkna alla sidor
