Lösningar och kommentarer till uppgifter i 3.2
|
|
|
- Carina Arvidsson
- för 7 år sedan
- Visningar:
Transkript
1 Lösningar och kommentarer till uppgifter i 3.2 Så har vi då nått fram till sista avsnittet före tentamen. Uppgifterna i detta avsnitt är ganska trevliga, därför att de ofta har en, åtminstone påhittad, historia som stöd. KTH: Jaha, då sätter vi väl igång då. Är du pigg idag? 3202 TB: Så där. Det börjar bli lite mycket nu, men jag ska försöka samla mig och göra mitt bästa. En funktion är given. Jag väljer lite andra beteckningar än de som föreslås i boken. h(t) = 4.8t t Genom den här funktionen kan jag ta reda på hur högt över vattnet raketen befinner sig. Efter till exempel t = 10 blir h(10) = = Oj då raketen är på väg mot botten om det nu överhuvudtaget är så djupt där. Men nu var det inte det vi skulle ta reda på. Vid vilken tid som raketen når sin högsta punkt får jag reda på genom att derivera h(t) och lösa h (t) = 0 h(t) = 4.8t t h (t) = 9.6t h (t) = 0 då 9.6t = 0 t = 1 Snälla värden eller hur. Redan efter 1 sekund vänder raketen och börjar falla igen. Hur högt den då befinner sig över vattenytan får jag reda på genom att beräkna h(1) = = 43 meter. Det var inte högt. KTH: Kan du se hur högt över havet själva startrampen ligger? TB: Då t = 0, innan uppskjutningen, befinner sig raketen h(0) = 38.2 meter över havet. Så själva skuttet är inte högre än knappa 5 meter! KTH: Om du fick i uppgift att bestämma när raketen slår i vattnet, hur skulle du göra då? TB: Nu frågas det faktiskt inte om det, men antagligen skulle jag lösa ekvationen h(t) = 0. KTH: h(t) = 0 är en andragradsekvation och en sådan har ju som bekant två rötter. Betyder det att raketen landar två gånger? TB: Nu går vi till nästa uppgift föreslår jag. KTH: Jag vill bara berätta att rötterna är t 1 = och t 2 = och att funktionen inte är definierad för t < 0. Detta förklarar min fråga. TB: Vi kommer aldrig att bli klara om du ska hålla på och utvidga uppgifterna på det här sättet TB: Finns det sådana här funktioner i verkligheten? Funktioner med vars hjälp man kan bestämma vilken vinst man får för olika priser. KTH: Jo man försöker nog bestämma sådana inom ekonomin, men de bygger förstås på psykologi och blir därför ganska osäkra. TB: Hur som helst har vi funktionen v(p) = 1000p 5p 2. Vinsten v, som funktion av priset p. Jag är på jakt efter ett maximum. Jag vet sedan tidigare andragradspolynom med en negativ koefficient till x 2 har just ett maximum. För vilket pris p som maximal vinst uppkommer, får jag genom att Håkan Strömberg 1 KTH Syd Haninge
2 3207 bestämma v (p) = 0 v(p) = 1000p 5p 2 v (p) = p v (p) = 0 då p = 0 p = 100 Svaret är att den maximala vinsten får jag om biljettpriset sätts till 100 kr. Jag behöver inte beräkna v(100) som skulle ge mig den maximala vinsten. Tack för det. TB: Det är förunderligt att det finns funktioner för en sådan här sak. KTH: Egentligen så finns det ju inte det. Den här funktionen är på sin höjd en modell av verkligheten. Kanske tillräckligt bra för att kunna användas i någon situation. TB: Funktionen T(t) = 0.5t 2 5t + 10 har ett minimum, det vet jag säkert. Om detta minimum ligger i intervallet 0 t 12 kan jag inte omedelbart säga. Om inte så är det värdet vid något av intervallets ändpunkter som ger det sökta värdet T(t) = 0.5t 2 5t + 10 T (t) = t 5 T (t) = 0 då t 5 = 0 t = 5 Minimat ligger i intervallet. 5 timmar efter midnatt, alltså kl 5 : 00 är temperaturen som lägst T(5) = 2.5 C TB: Jag ritar inte om figuren som finns i boken. Det finns ingen funktion given den här gången, men allt är ganska väl tillrättalagt. Jag kan skriva A(x), x som funktion av arean som 3209 A(x) = x(28 x) A(x) = 28x x 2 A (x) = 28 2x A (x) = 0 då 28 2x = 0 x = 14 Det är inte speciellt överraskande att x = 14 m, det vill säga att båda sidorna av staket är lika långa så att hagen blir en kvadrat. A(14) = 196 m 2 TB: Återigen en inhägnad, men nu vill man ha skilda hagar får (förlåt för) tackor och baggar! Figuren säger allt och jag får följande funktion A(x) = x(420 3x) A(x) = 420x 3x 2 A (x) = 420 6x A (x) = 0 då 420 6x = 0 x = 70 Långsidan skrivs 420 3x eftersom det behövs tre kortsidor, var och en med längden x m. Då x = 70 m får vi den maximala arean A(70) = 70( ) = m 2. Var den här uppgiften svårare än den förra eller? Håkan Strömberg 2 KTH Syd Haninge
3 KTH: Nej, men eftersom upprepning är pedagogikens moder så gör vi detta endast för att det ska sitta TB: Konstigt villkor: Summan av höjden h och radien r ska vara r + h = 12. Men jag bryr mig inte. Men nu blir jag lite osäker vi ska beräkna volymen för en cylinder. Hur gjorde man det nu igen? KTH: Här har du formeln Den kan du hitta i formelsamlingen. V c = π r 2 h TB: Tack. Ja, här finns två storheter h och r!? Nu vet jag. Jag ska använda r + h = 12. Skriva om det som h = 12 r och substituera h med detta uttryck i den formel du gav mig. Lite småklurigt faktiskt. Är det rätt tänkt? KTH: Javisst, bra TB: Jag kommer nu in på samma spår som i tidigare uppgifter. Jag får V c (r) = π r 2 (12 r) V c (r) = 12πr 2 πr 3 V c (r) = 24πr 3πr2 V c(r) = 0 då 24πr 3πr 2 = 0 r 1 = 0,r 2 = 8 Funktionen kan bara fungera för 0 < r < 12. Här kommer två grafer. Först V c (r) och sedan V c (r). V c (r) är ett polynom av tredje graden, som verkar ha ett maximum vid r = 8 vilket stämmer med mina beräkningar Figur 1: Det finns två extrempunkter i det aktuella intervallet, allt enligt teorin, att V c (r) = 0, som är en andragradsekvation, ska ha två rötter. Den första är ett minimum då r = 0, som är ointressant här. TB: De efterlyser för vilka värden på r och h som burken har maximal volym under gällande villkor. Svaret är r = 8 som ger h = 4 och volymen V c (8) (för den som har lust att räkna ut den) TB: Normalt räknar man ut arean hos en triangel med formeln A T = b h/2, men här finns vare sig höjd eller bas given till den skuggade triangeln. Hur gör man då? KTH: Tänk en liten stund så kommer du säkert på det. TB: Arean för hela rektangeln kan man räkna ut A R = = 192. Sedan finns det tre rätvinkliga trianglar där höjd och bas alla är givna, eller åtminstone uttryckta med hjälp av x. Jag tror att jag får rita en ny figur. Håkan Strömberg 3 KTH Syd Haninge
4 Figur 2: Figur 3: Nu kan jag skriva arean A(x) för den grå triangeln: ( 16(12 x) A(x) = x 2 A(x) = 192 (96 8x + 12x + 8x x 2 ) A(x) = 96 12x + x 2 + ) x(16 2x) 2 Vad ska jag nu med denna funktion till? Jo jag vill veta för vilket x som A(x) blir så liten som möjligt. Derivera mera... A(x) = 96 12x + x 2 A (x) = 2x 12 A (x) = 0 då x = 6 A(6) = 60 är den minsta arean. En ny figur visar när detta inträffar. KTH: För vilket x har triangeln så stor area som möjligt? TB: Nu kommer du med egna frågor igen. Vad vill du jag ska svara? Det handlar om ett polynom av andra graden med positiv koefficient till x 2. Det finns bara en extrempunkt och det är ett minimum. Alltså finns det ingen största triangel. KTH: Du behöver väl inte brusa upp! Mellan vilka värden kan x ligga? TB: 0 x 6 eller hur. KTH: Ja, då plottar vi funktionen så kommer du att få en aha-upplevelse. Minimum får vi mycket riktigt för x = 6 och maximum i en av intervallens ändpunkter, för x = 0, då triangeln utgör halva rektangeln A(0) = 96 Håkan Strömberg 4 KTH Syd Haninge
5 Figur 4: Figur 5: 3218 TB: Problemen har blivit lite svårare plötsligt. Här handlar det om en kartong. Jag måste rita den med mina egna beteckningar insatta. Figur 6: Är du med på mina beteckningar? Jag har bestämt att de kvadrater, som ska skäras ut och som alla är lika stora har sidan x. Nu kan jag sätta upp en funktion V(x), volymen som funktion av x 160 3x V(x) = x(100 2x) 2 Det är den här funktionen jag ska derivera och finna eventuella extrempunkter för. Jag ser att det rör sig om ett polynom av tredje graden. Men innan jag kan derivera måste jag förenkla Håkan Strömberg 5 KTH Syd Haninge
6 funktionen multiplicera samman parenteserna. Jag tar inte med alla stegen här: V(x) = 8000x 310x 2 + 3x 3 V (x) = x + 9x 2 x 1 = ,x 2 = Två rötter men x 2 fungerar inte, så stora kvadrater kan man inte skära ut. Maximal volym blir då V[ ] = Taskiga siffror den här gången. Nej, det stämmer inte med facit! KTH: Jaså. Nu förstår jag inte... Nu ser jag. Jämför din figur med den i boken. TB: Åh, nej jag orkar inte. KTH: Bit ihop och kom igen. Vad jag kan se har du funnit korrekt lösning till fel problem. TB: Hur skulle du ha bedömt detta på en tentamen? KTH: Fullt rätt kan du aldrig få även om du beräkningarna blivit svårare. En tröstpoäng möjligen får du nöja dig med. Figur 7: TB: OK, här är min nya figur. Vad tycker du om den? Funktionen blir nu istället: V(x) = x(80 x)(100 2x) V(x) = 8000x 260x 2 + 2x 3 V (x) = x + 6x 2 x 1 = 20,x 2 = 200/3 x 2 är på tok för stort, ligger utanför intervallet 0 < x < 50. Så svaret är alltså x = 20 och V(20) = Du, en sak som jag kom att tänka på. Då vi maximerade areor, så handlade det alltid om andragradare och nu när det är volymer så är det tredjegradare som gäller. Så är det väl? KTH: Ja, det är en korrekt upptäckt TB: Det här är faktiskt en ganska rolig uppgift. Ja, jag tycker det. Med hjälp av Pythagoras sats kan vi bestämma den tredje och just nu obekanta sidan y, i triangeln behövs det? y = 58 2 y = y = 42 Håkan Strömberg 6 KTH Syd Haninge
7 Figur 8: y = 42, det blev ett heltal, vilken tur vi hade. Nu blir det lite geometri här. Topptriangeln är likformig med hela triangeln och vi kan sätta upp följande samband som bygger på likformighet: Löser jag ut x ur denna funktion får jag x 42 = 40 z 40 Nu kan jag teckna rektangelns area x = 21(40 z) 20 A(z) = 21(40 z)z 20 A(z) = 42z 21z2 20 A (z) = 42 21z 10 A (z) = 0 då 42 21z 10 = 0 z = 20 Jag har en andragradspolynom med ett maximum. Jag vet att 0 z 40. Alltså ger z = 20 maximalt värde. Jag får x = 21 och att den maximala tomten är 420 m TB: En uppgift utan tillhörande historia. Jag börjar med att derivera: Det finns två värden på a sådana att f (a) = 2. f(x) = x 3 + 2x 2 + 3x + 4 f (x) = 3x 2 + 4x + 3 f (a) = 2 då 3a 2 + 4a + 3 = 2 a 1 = 1 3,a 2 = 1 Håkan Strömberg 7 KTH Syd Haninge
8 3223 TB: Funktionen har en positiv derivata fram till x = a då ett maximum inträffar. Sedan har kurvan en negativ lutning fram till x = b då den åter blir 0. Vi har nått fram till ett minimum. Nu är lutningen positiv tills den åter blir 0 i x = c. Eftersom lutningen fortsätter att vara positiv så finns det en terrasspunkt i x = c TB: Jag ska alltså bestämma a,b,c och d i funktionen f(x) = ax 3 + bx 2 + cx + d. De tre rötterna till ekvationen f(x) = 0 är kända. Jag vet inte riktigt, men jag chansar f(x) = (x + 6)(x 1/2)(x 4). Är det riktigt? KTH: Testa med f(2) = 5 och dessutom har du inte bestämt a,b,c och d, som du sa att du skulle göra. TB: Kan du inte säga om det är rätt istället? Jag testar väl då f(2) = (2+6)(2 1/2)(2 4) = 8 3/2 ( 2). Jag ser redan nu att det inte kan fungera eftersom detta värde blir negativt och därmed inte = 5. Nu får du hjälpa mig KTH: Först ska vi ta det omständliga sättet: f( 6) ger ( 6) 3 a + ( 6) 2 b + ( 6)c + d = 0 f(1/2) ger (1/2) 3 a + (1/2) 2 b + (1/2)c + d = 0 f(4) ger 4 3 a b + 4c + d = 0 f(2) ger 2 3 a b + 2c + d = 5 Vi har ett ekvationssystem med fyra obekanta och fyra ekvationer. Normalt har detta system en lösning. Man brukar skriva det så här. Vi passar på att snygga till det lite: Ekvationssystemet har lösningen a = a + 36b 6c + d = 0 a/8 + b/4 + c/2 + d = 0 64a + 16b + 4c + d = 0 8a + 4b + 2c + d = 5 b = 5 16 c = d = 5 2 Det är ganska jobbigt att komma fram till detta men med en dator eller en avancerad räknedosa går det lättare. Det viktiga är att du förstår hur systemet är konstruerat. Nu över till en enklare metod, som börjar på samma sätt som du föreslog. Men först ska vi titta på en sak som förklarar varför din metod inte fungerar direkt. Här har vi tre ekvationer x 3 + 2x 2 5x 6 = 0 4x 3 + 8x 2 20x 24 = 0 3x 3 + 6x 2 15x 18 = 0 Det är lätt att se att de egentligen är fråga om samma ekvation i alla tre fallen. Om man dividerar båda sidor i den andra med 4 så uppstår den första. I den tredje ekvationen dividerar vi båda sidor med 3, så kommer vi också fram till den översta ekvationen. Rötterna är förresten x 1 = 3, x 2 = 2 och x 2 = 1. Dessa kan vi i denna kurs bara komma fram till genom att gissa. Nu tittar vi på följande tre funktioner f 1 (x) = x 3 + 2x 2 5x 6 f 2 (x) = 4x 3 + 8x 2 20x 24 f 3 (x) = 3x 3 + 6x 2 15x 18 Håkan Strömberg 8 KTH Syd Haninge
9 Figur 9: 3231 Dessa är inte identiska, vilket vi ser när vi tar fram deras graf: Visserligen har de alla samma nollställen, men däremellan beter de sig på olika sätt, eller hur. För att kunna bestämma en polynom av tredje graden behöver man 4 punkter på kurvan. Du använde bara 3 i ditt försök. Nu går vi tillbaka till din ansats: f(x) = (x + 6)(x 1/2)(x 4) f(x) = x 3 + 3x2 2 25x + 12 Som du ser har x 3 koefficienten 1, bara en av alla funktioner med de tre nollställena. Alltså ska vi finna ett m, så att f(2) = m( ) = m = 5 m = 5/24 Om vi multiplicerar ditt resultat med m = 5/24, så får vi just det resultat som jag fick från ekvationssystemet. f(x) = 5 24 x x x 5 2 TB: Punkten (1,0) ligger verkligen på kurvan eftersom f(1) = = 0. Funktionen f(x) = x x 2 har derivatan f (x) = 1 2x. Speciellt är då f (1) = 1 Tangenten till kurvan i den aktuella punkten har lutningen k t = 1. Normalen har då k n = 1 eftersom vi vet att k t k n = 1. Vet man k-värdet och en punkt kan man bestämma linjens funktion f(x) = kx + m ger oss 0 = m. m = 1 och vi kan skriva funktionen f(x) = x 1 eller y = x 1 som vi gjorde förr. Sen då? KTH: Det blir en ekvation. Kan du ställa upp den. TB: Vi är på jakt efter en punkt som finns på både kurvan och normalen. Borde bli: x x 2 = x 1 x 2 = 1 x 1 = 1,x 2 = 1 ger punkterna (1,0)) och ( 1, 2). Den första hade vi ju redan från början, den andra är alltså svaret. Håkan Strömberg 9 KTH Syd Haninge
10 3232 TB: En punkt och en funktion är given, Q(1.5,0) respektive f(x) = x. Jag förstår att det finns många punkter på kurvan och att avståndet från Q till dessa punkter varierar och att det bör finnas ett minsta. Men jag har ingen aning om hur jag ska lösa problemet. KTH: Accepterar du detta skrivsätt P(x, x)? Det beskriver samtliga punkter på kurvan, eller hur? Hur bestämmer man avståndet mellan två punkter i koordinatsystemet? TB: Ingen aning. KTH: Jag förstår det. Vi har inte berört detta tidigare i den här kursen, men troligtvis kommer du att känna igen det jag kommer att berätta nu. Först över till en figur: Figur 10: Vi ska beräkna avståndet mellan punkterna (2,2) och (4,5). y = 5 2 = 3 och x = 4 2 = 2. x och y är katetrar i en rätvinklig triangel. Med hjälp av Pythagoras sats, c 2 = a 2 + b 2, kan vi räkna ut hypotenusan, som samtidigt är det sökta avståndet = 13 Mer generellt kan vi nu skriva formeln för avståndet mellan punkterna (x 1,y 1 ) och (x 2,y 2 ) som (x1 x 2 ) 2 + (y 1 y 2 ) 2. Kan du nu använda detta för att lösa vårt problem. TB: Jag börjar så här. Avståndet a mellan en punkt vilken som helst på kurvan och Q kan skrivas a(x) = (1.5 x) 2 + (0 x) 2. Jag plottar funktionen för att se vad jag håller på med Det är helt klart så att det finns ett minimum att det finns kring x = 1. Ett minimum finner man genom att derivera funktionen och ta reda på var derivatan är 0. Men det känns inte lätt att derivera den här funktionen. KTH: Det har du rätt i. Vi har ännu inte nått fram till de deriveringsregler som behövs för det. Derivatan blir så komplicerad som a 2x 2 (x) = 9 8x + 4x 2 Man ska nu inse att om man kvadrerar funktionen a(x) så kommer man fortfarande att få ett minimum i samma x-koordinat. Grafen av båda kurvorna visar detta: Så om du accepterar detta kan du nu gå vidare Håkan Strömberg 10 KTH Syd Haninge
11 Figur 11: TB: Jag ska nu istället derivera denna funktion 3236 a 2 (x) = ( 3 2 x)2 + ( x ) 2 a 2 (x) = x2 3x + x a 2 (x) = 2x 2 a 2 (x) = 0 då 2x 2 = 0 x = 1 Jag lästa av grafen ganska bra eller hur? Punkten på kurvan vi är på jakt efter är (1,1). Avståndet mellan punkterna får vi genom a(1) = ( 3 2 1)2 + (0 1) 2 = 5/2 En ganska jobbig uppgift. TB: Den här kommer jag att klara. Vi har funktionen f(x) = ax 2 + bx + c. Derivatan som vi kommer att behöva är f (x) = 2ax + b. a,b och c är alla obekanta och ska bestämmas. Följande är givet f(1) = 4, f(0) = 0 och f (0) = 1. Man får ut två ledtrådar ur tangerar linjen y = x i origo. Linjen y = x har ju som bekant lutningen k = 1. Nu får vi ett ekvationssystem: KTH: Bra 3238 Huvudräkning ger funktionen f(x) = 3x 2 + x f(1) = 4 a + b + c = 4 f(0) = 0 c = 0 f (0) = 1 b = 1 TB: En sådan där jobbig uppgift igen. Jag fattar ingenting. KTH: Vad krävs för att en funktion ska ha två extrempunkter? TB: Att derivatan har två nollställen, eller åtminstone två nollställen. Det kan ju dessutom finnas terrasspunkter. KTH: Räcker det inte för att du ska kunna komma på något. TB: Jag deriverar f(x) = x 3 +ax 2 +bx och får f (x) = 3x 2 +2ax+b. Det är alltså ekvationen f (x) = 0, som ska ha två rötter. Det har ju alltid en andragradsekvation. Håkan Strömberg 11 KTH Syd Haninge
12 KTH: Nej, inte alltid två reella rötter. Dessutom kan det finnas en dubbelrot. TB: Sen då? 3x 2 + 2ax + b = 0 x 2 + 2ax 3 + b 3 = 0 x = a 3 ± a 2 KTH: Hur stor får b vara för att det ska finnas reella rötter? 9 3b 9 TB: 3b får inte vara större än a 2, då blir det negativt under rottecknet. 3b får heller inte vara lika med a 2, för då blir det en dubbelrot, leder till terrasspunkt och endast en extrempunkt. Svaret är alltså a 2 > 3b 3242 b) TB: Den här uppgiften blir inga problem f(x) = 1 x + 1 x f(x) = x 1 + x 1 2 f (x) = x 2 x f (x) = 1 x 2 1 2x x 3243 b) TB: Bara en massa tekniskt manipulerande. f(x) = 5x + 20 x 2 f(x) = 5x + 20x 2 f (x) = 5 40x 3 f (x) = 5 40 x 3 f (x) = 0 då 5 40 x 3 = 0 x 3 = 8 x = 2 Håkan Strömberg 12 KTH Syd Haninge
13 3246 b) TB: f(x) = 15 x KTH: Ska du tolka detta resultat också? f(x) = 15x 1 2 f (x) = 15 2x 1 2 f (x) = 15 2 x f (100) = = 0.75 TB: Då bromsspåren kommer att bli 100 m långa så avtar bilens hastigheten med 0.75 km/tim för varje meter av bromsspåret. Bromsspåren blir 100 m då hastigheten är 150 km/tim. Det här stämmer ju inte! KTH: Nej, f(100) = 150 det är korrekt. Då f(101) Detta betyder att om bromsspåret blir 1 meter längre så har bilen ökat sin hastighet med 0.75 km/tim 3248 TB: Ett enkelt problem. Vi har funktionen som vi ska söka ett minimum för. Vi deriverar Nu ska vi lösa ekvationen g (x) = 0 g(x) = x x g (x) = x x 2 = 0 x 2 = x = ±2000 Den negativa roten förkastar vi och får svaret x = g(2000) = 6. När man tillverkar 2000 knivar kommer kostnaden för en kniv att bli 6 kr. KTH: Det är så riktigt så KTH: Här ska du få en klassisk uppgift som finns i varje matematikbok. Håkan Strömberg 13 KTH Syd Haninge
14 Figur 12: TB: Säger du det! Jag börjar med en figur Jag vet att volymen för en cylinder tecknas V c = hπr 2. Det är bestämt att burken ska rymma 1000 cm 3 (1 liter). Nu blir det lite knepigare, när jag ska teckna burkens totala area A c = 2πr 2 +2πrh. Är det rätt? Den första termen är arean för de två locken och den andra är arean av den rektangel som utgör den tredje delen av burken. En sida i den rektangeln är h och den andra är 2πr, som är lika med lockens omkrets. Eftersom V c = hπr 2 = 1000 kan vi lösa ut h = 1000 πr 2 Detta gör att vi kan substituera bort h och få ett uttryck av arean A c som bara beror av r Jag putsar lite A c (r) = 2πr 2 + 2πr 1000 πr 2 A c (r) = 2πr r Det är den här funktionen vi ska hitta ett minimum för. Då måste jag först derivera A c 2000 (r) = 4πr r 2 Jag börjar kunna derivera funktioner med x i nämnaren ganska bra nu. Vi ska nu lösa ekvationen A c(x) = 0 4πr 2000 r 2 = 0 r 3 = 500 π r = π Jag räknar dessutom ut höjden h Höjden h är alltså dubbelt upp mot radien r, eller diametern är lika med höjden. KTH: Om du vill kan du nu ta reda på hur burkens form ändras om man tar bort ena locket. TB: Jag tror inte jag är så intresserad just nu Håkan Strömberg 14 KTH Syd Haninge
15 TB: En enkel uppgift igen. f(x) = 3 e ax har derivaten f (x) = 3a e ax. Vi kan nu bestämma a eftersom f (0) = 6 som är samma sak som 3a e a 0 = 6 ger a = TB: Här är funktionen T(t) = e t. Temperaturen T som funktion av tiden t. Grafen ser ut så här: Figur 13: Observera origos placering. Det är inte så som det kan se ut, att kaffets temperatur går under noll. Först ska vi besvara frågan: När blir kaffet svalare än 50 C? e t = 50 e t = e ln e t = eln 0.4 e t = eln t = ln 0.4 t = ln Efter minuter har kaffets temperatur sjunkit till 50 C. Det var inte nog med detta, vi ska också ta reda på T (30) och tolka resultatet T(t) = e t T (t) = e t T (30) Detta betyder att efter 30 minuter så sjunker temperaturen med cirka grader/minut. TB: Vilken konstig uppgift, men ganska bra! Jag startar med 2500 kr som jag sätter in på banken till 7% ränta. Hur många år dröjer det innan beloppet har stigit till kr? Håkan Strömberg 15 KTH Syd Haninge
16 3264 TB: Så här ser grafen, som visar bilens värde de närmaste 20 åren, ut: Bilens värde avtar med 15% Figur 14: 3267 per år. V(t) = x V(t) = exln 0.85 V (t) = ln(0.85) e V (5) xln 0.85 Efter 5 år rasar bilens värde med cirka kr/år. I grafen visas detta med en tangent till kurvan i punkten (5,124237). Tangenten har k-värdet TB: Vi har funktionen f(x) = C a x, där C och a är konstanter som ska bestämmas. Vi har två fakta om funktionen: f(0) = 3 och f (x) = 5 f(x). Ur f(0) = C a 0 = 3 får vi omedelbart att C = 3. Den andra ledtråden är svårare att förstå sig på. KTH: Läs bara vad som står och sätt upp ekvationen TB: OK. Jag måste ta fram f (x) och skriver först om f(x) = 3e xln a och får då f (x) = 3lna e xln a Nu får jag ekvationen f (x) = 5 f(x) 3ln a e xln a = 5 3e xln a lna = 5 a = e 5 Nu kan jag skriva funktionen f(x) = 3 e 5x Håkan Strömberg 16 KTH Syd Haninge
Gamla tentemensuppgifter
 Inte heller idag någon ny teori! Gamla tentemensuppgifter 1 Bestäm det andragradspolynom vars kurva skär x-axeln i x = 3 och x = 1 och y-axeln i y = 3 f(x) = (x 3)(x + 1) = x x 3 är en bra start, men vi
Inte heller idag någon ny teori! Gamla tentemensuppgifter 1 Bestäm det andragradspolynom vars kurva skär x-axeln i x = 3 och x = 1 och y-axeln i y = 3 f(x) = (x 3)(x + 1) = x x 3 är en bra start, men vi
Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = 1 x.
 Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = x 8 6 4 2-3 -2-2 3-2 -4-6 -8 Figur : Vi konstaterar följande: Då
Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = x 8 6 4 2-3 -2-2 3-2 -4-6 -8 Figur : Vi konstaterar följande: Då
Egentligen har vi ingen ny teori att presentera idag. Målet för den närmaste framtiden är att nöta in undersökandet av polynomfunktioner.
 Egentligen har vi ingen ny teori att presentera idag. Målet för den närmaste framtiden är att nöta in undersökandet av polynomfunktioner. 1 (Bokens nr 3204) Ett straffkast i basket följer ekvationen h(x)
Egentligen har vi ingen ny teori att presentera idag. Målet för den närmaste framtiden är att nöta in undersökandet av polynomfunktioner. 1 (Bokens nr 3204) Ett straffkast i basket följer ekvationen h(x)
konstanterna a och b så att ekvationssystemet x 2y = 1 2x + ay = b 2 a b
 Tentamen i Inledande matematik för V och AT, (TMV25), 20-0-26. Till denna uppgift skulle endast lämnas svar, men här ges kortfattade lösningar. a) Bestäm { konstanterna a och b så att ekvationssystemet
Tentamen i Inledande matematik för V och AT, (TMV25), 20-0-26. Till denna uppgift skulle endast lämnas svar, men här ges kortfattade lösningar. a) Bestäm { konstanterna a och b så att ekvationssystemet
Dagens tema är exponentialfunktioner. Egentligen inga nyheter, snarare repetition. Vi vet att alla exponentialfunktioner.
 Dagens tema är exponentialfunktioner. Egentligen inga nyheter, snarare repetition. Vi vet att alla exponentialfunktioner f(x) = C a x kan, om man så vill, skrivas om, med basen e, till Vi vet också att
Dagens tema är exponentialfunktioner. Egentligen inga nyheter, snarare repetition. Vi vet att alla exponentialfunktioner f(x) = C a x kan, om man så vill, skrivas om, med basen e, till Vi vet också att
13 Potensfunktioner. Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till
 3 Potensfunktioner 3. Dagens teori Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = x 8 6 4 2-3 -2-2 3-2 -4-6 -8
3 Potensfunktioner 3. Dagens teori Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = x 8 6 4 2-3 -2-2 3-2 -4-6 -8
Teori och teori idag, som igår är det praktik som gäller! 1 (Bokens nr 3216) Figur 1:
 Teori och teori idag, som igår är det praktik som gäller! 1 (Bokens nr 316) Figur 1: a) Bestäm y som funktion av x genom att utnyttja likformiga trianglar. Se figur 1. b) Ange funktionens definitionsmängd
Teori och teori idag, som igår är det praktik som gäller! 1 (Bokens nr 316) Figur 1: a) Bestäm y som funktion av x genom att utnyttja likformiga trianglar. Se figur 1. b) Ange funktionens definitionsmängd
10 Derivator och tillämpningar 1
 10 Derivator och tillämpningar 1 10.1 Dagens Teori Egentligen har vi ingen ny teori att presentera idag. Målet för den närmaste framtiden är att nöta in undersökandet av polynomfunktioner. Övning 10.1
10 Derivator och tillämpningar 1 10.1 Dagens Teori Egentligen har vi ingen ny teori att presentera idag. Målet för den närmaste framtiden är att nöta in undersökandet av polynomfunktioner. Övning 10.1
4-6 Trianglar Namn:..
 4-6 Trianglar Namn:.. Inledning Hittills har du arbetat med parallellogrammer. En sådan har fyra hörn och motstående sidor är parallella. Vad händer om vi har en geometrisk figur som bara har tre hörn?
4-6 Trianglar Namn:.. Inledning Hittills har du arbetat med parallellogrammer. En sådan har fyra hörn och motstående sidor är parallella. Vad händer om vi har en geometrisk figur som bara har tre hörn?
Algebra, polynom & andragradsekvationer en pampig rubrik på ett annars relativt obetydligt dokument
 Algebra, polynom & andragradsekvationer en pampig rubrik på ett annars relativt obetydligt dokument Distributiva lagen a(b + c) = ab + ac 3(x + 4) = 3 x + 3 4 = 3x + 12 3(2x + 4) = 3 2x + 3 4 = 6x + 12
Algebra, polynom & andragradsekvationer en pampig rubrik på ett annars relativt obetydligt dokument Distributiva lagen a(b + c) = ab + ac 3(x + 4) = 3 x + 3 4 = 3x + 12 3(2x + 4) = 3 2x + 3 4 = 6x + 12
Lathund, procent med bråk, åk 8
 Lathund, procent med bråk, åk 8 Procent betyder hundradel, men man kan också säga en av hundra. Ni ska kunna omvandla mellan bråkform, decimalform och procentform. Nedan kan ni se några omvandlingar. Bråkform
Lathund, procent med bråk, åk 8 Procent betyder hundradel, men man kan också säga en av hundra. Ni ska kunna omvandla mellan bråkform, decimalform och procentform. Nedan kan ni se några omvandlingar. Bråkform
Kapitel 6. f(x) = sin x. Figur 6.1: Funktionen sin x. 1 Oinas-Kukkonen m.fl. Kurs 6 kapitel 1
 Kapitel 6 Gränsvärde 6. Definition av gränsvärde När vi undersöker gränsvärdet av en funktion undersöker vi vad som händer med funktionsvärdet då variabeln, x, går mot ett visst värde. Frågeställningen
Kapitel 6 Gränsvärde 6. Definition av gränsvärde När vi undersöker gränsvärdet av en funktion undersöker vi vad som händer med funktionsvärdet då variabeln, x, går mot ett visst värde. Frågeställningen
Pesach Laksman är lärarutbildare i matematik och matematikdidaktik vid Malmö högskola.
 111a Geometri med snöre Pesach Laksman är lärarutbildare i matematik och matematikdidaktik vid Malmö högskola. Areabegreppet När elever får frågan vad area betyder ges mestadels svar som antyder hur man
111a Geometri med snöre Pesach Laksman är lärarutbildare i matematik och matematikdidaktik vid Malmö högskola. Areabegreppet När elever får frågan vad area betyder ges mestadels svar som antyder hur man
Volymer av n dimensionella klot
 252 Volymer av n dimensionella klot Mikael Passare Stockholms universitet Ett klot med radien r är mängden av punkter vars avstånd till en given punkt (medelpunkten) är högst r. Låt oss skriva B 3 (r)
252 Volymer av n dimensionella klot Mikael Passare Stockholms universitet Ett klot med radien r är mängden av punkter vars avstånd till en given punkt (medelpunkten) är högst r. Låt oss skriva B 3 (r)
SF1620 Matematik och modeller
 KTH Teknikvetenskap, Institutionen för matematik 1 SF160 Matematik och modeller 007-09-10 Andra veckan Trigonometri De trigonometriska funktionerna och enhetscirkeln Redan vid förra veckans avsnitt var
KTH Teknikvetenskap, Institutionen för matematik 1 SF160 Matematik och modeller 007-09-10 Andra veckan Trigonometri De trigonometriska funktionerna och enhetscirkeln Redan vid förra veckans avsnitt var
3.1 Linjens ekvation med riktningskoefficient. y = kx + l.
 Kapitel Analytisk geometri Målet med detta kapitel är att göra läsaren bekant med ekvationerna för linjen, cirkeln samt ellipsen..1 Linjens ekvation med riktningskoefficient Vi utgår från ekvationen 1
Kapitel Analytisk geometri Målet med detta kapitel är att göra läsaren bekant med ekvationerna för linjen, cirkeln samt ellipsen..1 Linjens ekvation med riktningskoefficient Vi utgår från ekvationen 1
Institutionen för matematik Envariabelanalys 1. Jan Gelfgren Datum: Fredag 9/12, 2011 Tid: 9-15 Hjälpmedel: Inga (ej miniräknare)
 Umeå universitet Dugga i matematik Institutionen för matematik Envariabelanalys 1 och matematisk statistik IE, ÖI, Stat. och Frist. Jan Gelfgren Datum: Fredag 9/12, 2011 Tid: 9-15 Hjälpmedel: Inga (ej
Umeå universitet Dugga i matematik Institutionen för matematik Envariabelanalys 1 och matematisk statistik IE, ÖI, Stat. och Frist. Jan Gelfgren Datum: Fredag 9/12, 2011 Tid: 9-15 Hjälpmedel: Inga (ej
Snabbslumpade uppgifter från flera moment.
 Snabbslumpade uppgifter från flera moment. Uppgift nr Ställ upp och dividera utan hjälp av miniräknare talet 48 med 2 Uppgift nr 2 Skriv talet 3 8 00 med hjälp av decimalkomma. Uppgift nr 3 Uppgift nr
Snabbslumpade uppgifter från flera moment. Uppgift nr Ställ upp och dividera utan hjälp av miniräknare talet 48 med 2 Uppgift nr 2 Skriv talet 3 8 00 med hjälp av decimalkomma. Uppgift nr 3 Uppgift nr
Övningshäfte Algebra, ekvationssystem och geometri
 Stockholms Tekniska Gmnasium --9 Övningshäfte Algebra, ekvationssstem och geometri Nivå: rätt svårt Fråga : f är ett polnom. Beräkna värdet av f, f och fπ Fråga : Ingångslönen på företaget Börjes Gurkinläggning
Stockholms Tekniska Gmnasium --9 Övningshäfte Algebra, ekvationssstem och geometri Nivå: rätt svårt Fråga : f är ett polnom. Beräkna värdet av f, f och fπ Fråga : Ingångslönen på företaget Börjes Gurkinläggning
Laborativ matematik som bedömningsform. Per Berggren och Maria Lindroth 2016-01-28
 Laborativ matematik som bedömningsform Per Berggren och Maria Lindroth 2016-01-28 Kul matematik utan lärobok Vilka förmågor tränas Problemlösning (Förstå frågan i en textuppgift, Använda olika strategier
Laborativ matematik som bedömningsform Per Berggren och Maria Lindroth 2016-01-28 Kul matematik utan lärobok Vilka förmågor tränas Problemlösning (Förstå frågan i en textuppgift, Använda olika strategier
SF1625 Envariabelanalys
 Modul 2: Derivata Institutionen för matematik KTH 8 september 2015 Derivata Innehåll om derivata (bokens kapitel 2). Definition vad begreppet derivata betyder Tolkning hur man kan tolka derivata Deriveringsregler
Modul 2: Derivata Institutionen för matematik KTH 8 september 2015 Derivata Innehåll om derivata (bokens kapitel 2). Definition vad begreppet derivata betyder Tolkning hur man kan tolka derivata Deriveringsregler
Övningshäfte i matematik för. Kemistuderande BL 05
 Övningshäfte i matematik för Kemistuderande BL 05 Detta häfte innehåller några grundläggande övningar i de delar av matematiken som man har användning för i de tidiga kemistudierna. Nivån är gymnasiematematik,
Övningshäfte i matematik för Kemistuderande BL 05 Detta häfte innehåller några grundläggande övningar i de delar av matematiken som man har användning för i de tidiga kemistudierna. Nivån är gymnasiematematik,
Lokal kursplan för Ängkärrskolan år 9 Rev. 2009-09-22. -Positionssystemet. -Multiplikation och division. (utan miniräknare).
 Lokal kursplan för Ängkärrskolan år 9 Rev. 009-09- Matematik år 9 MOMENT MÅL KRITERIER/EXEMPELl Taluppfattning, aritmetik Repetition av: Skriv med siffror tolv -Positionssystemet. hundradelar. 0,, 0,7
Lokal kursplan för Ängkärrskolan år 9 Rev. 009-09- Matematik år 9 MOMENT MÅL KRITERIER/EXEMPELl Taluppfattning, aritmetik Repetition av: Skriv med siffror tolv -Positionssystemet. hundradelar. 0,, 0,7
Facit åk 6 Prima Formula
 Facit åk 6 Prima Formula Kapitel 3 Algebra och samband Sidan 95 1 a 12 cm (3 4 cm) b Han vet inte att uttrycket 3s betyder 3 s eller s + s + s 2 a 5x b 6y c 12z 3 a 30 cm (5 6 cm) b 30 cm (6 5 cm) Sidan
Facit åk 6 Prima Formula Kapitel 3 Algebra och samband Sidan 95 1 a 12 cm (3 4 cm) b Han vet inte att uttrycket 3s betyder 3 s eller s + s + s 2 a 5x b 6y c 12z 3 a 30 cm (5 6 cm) b 30 cm (6 5 cm) Sidan
Modul 6: Integraler och tillämpningar
 Institutionen för Matematik SF65 Envariabelanalys Läsåret 5/6 Modul 6: Integraler och tillämpningar Denna modul omfattar kapitel 6. och 6.5 samt kapitel 7 i kursboken Calculus av Adams och Essex och undervisas
Institutionen för Matematik SF65 Envariabelanalys Läsåret 5/6 Modul 6: Integraler och tillämpningar Denna modul omfattar kapitel 6. och 6.5 samt kapitel 7 i kursboken Calculus av Adams och Essex och undervisas
KOKBOKEN. Håkan Strömberg KTH STH
 KOKBOKEN Håkan Strömberg KTH STH Hösten 2007 Håkan Strömberg 2 KTH Syd Innehåll Genomsnittlig förändringshastighet...................... 5 Uppgift 1................................. 5 Uppgift 2.................................
KOKBOKEN Håkan Strömberg KTH STH Hösten 2007 Håkan Strömberg 2 KTH Syd Innehåll Genomsnittlig förändringshastighet...................... 5 Uppgift 1................................. 5 Uppgift 2.................................
OM KOMPLEXA TAL. 1 Om a är ett positivt reellt tal så betecknar a det positiva reella tal vars kvadrat är a men det är
 OM KOMPLEXA TAL Inledning. Vilka olika talområden finns det? Jag gör en snabb genomgång av vad ni tidigare stött på, bl.a. för att repetera standardbeteckningarna för de olika talmängderna. Positiva heltal,
OM KOMPLEXA TAL Inledning. Vilka olika talområden finns det? Jag gör en snabb genomgång av vad ni tidigare stött på, bl.a. för att repetera standardbeteckningarna för de olika talmängderna. Positiva heltal,
ATT KUNNA TILL. MA1050 Matte Grund. 2011-06-14 Vuxenutbildningen Dennis Jonsson
 ATT KUNNA TILL MA1050 Matte Grund 2011-06-14 Vuxenutbildningen Dennis Jonsson Sida 2 av 5 Att kunna till prov G1 Kunna ställa upp och beräkna additions-, subtraktions-, multiplikations- och divisuionsuppgifter
ATT KUNNA TILL MA1050 Matte Grund 2011-06-14 Vuxenutbildningen Dennis Jonsson Sida 2 av 5 Att kunna till prov G1 Kunna ställa upp och beräkna additions-, subtraktions-, multiplikations- och divisuionsuppgifter
Lösningar och kommentarer till uppgifter i 3.1
 Lösningar och kommentarer till uppgifter i.1 102 b) TB: Kör de med dessa uppgifter i det här kapitlet också? Det gör inget, jag börjar bli ganska bra på det. Vi har funktionen fx) = x x 2 24x + 1 och man
Lösningar och kommentarer till uppgifter i.1 102 b) TB: Kör de med dessa uppgifter i det här kapitlet också? Det gör inget, jag börjar bli ganska bra på det. Vi har funktionen fx) = x x 2 24x + 1 och man
NATIONELLT KURSPROV I MATEMATIK KURS B HÖSTEN 1998. Tidsbunden del
 Nationellt kursprov i Matematik kurs B ht 1998 sida 1 (av 7) Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap. 3 sekretesslagen. För detta material gäller sekretessen
Nationellt kursprov i Matematik kurs B ht 1998 sida 1 (av 7) Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap. 3 sekretesslagen. För detta material gäller sekretessen
Erfarenheter från ett pilotprojekt med barn i åldrarna 1 5 år och deras lärare
 Erfarenheter från ett pilotprojekt med barn i åldrarna 1 5 år och deras lärare I boken får vi följa hur barn tillsammans med sina lärare gör spännande matematikupptäckter - i rutinsituationer - i leken
Erfarenheter från ett pilotprojekt med barn i åldrarna 1 5 år och deras lärare I boken får vi följa hur barn tillsammans med sina lärare gör spännande matematikupptäckter - i rutinsituationer - i leken
SKOGLIGA TILLÄMPNINGAR
 STUDIEAVSNITT 3 SKOGLIGA TILLÄMPNINGAR I detta avsnitt ska vi titta på några av de skogliga tillämpningar på geometri som finns. SKOGSKARTAN EN MODELL AV VERKLIGHETEN Arbetar man i skogen klarar man sig
STUDIEAVSNITT 3 SKOGLIGA TILLÄMPNINGAR I detta avsnitt ska vi titta på några av de skogliga tillämpningar på geometri som finns. SKOGSKARTAN EN MODELL AV VERKLIGHETEN Arbetar man i skogen klarar man sig
Tankar om elevtankar. HÖJMA-projektet
 Tankar om elevtankar HÖJMA-projektet JAN UNENGE I förra numret av NÄMNAREN påbörjades en redogörelse från ett intressant forsknings- och utvecklingsarbete vid Lärarhögskolan i Jönköping. Den artikeln behandlade
Tankar om elevtankar HÖJMA-projektet JAN UNENGE I förra numret av NÄMNAREN påbörjades en redogörelse från ett intressant forsknings- och utvecklingsarbete vid Lärarhögskolan i Jönköping. Den artikeln behandlade
6 Derivata och grafer
 6 Derivata och grafer 6.1 Dagens Teori När vi plottar funktionen f(x) = x + 1x 99x 8 med hjälp av dosan kan man få olika resultat beroende på vilka intervall man valt. 00000 100000-00 -100 100 00-100000
6 Derivata och grafer 6.1 Dagens Teori När vi plottar funktionen f(x) = x + 1x 99x 8 med hjälp av dosan kan man få olika resultat beroende på vilka intervall man valt. 00000 100000-00 -100 100 00-100000
I den här delen används inte räknare. Motivera alltid din slutsats med matematiska uttryck, figurer, förklaring el.dyl.
 DEL 1 Tid 30 min Poängantal 20 I den här delen används inte räknare. Motivera alltid din slutsats med matematiska uttryck, figurer, förklaring el.dyl. 1. Vilket är det största heltalet, som uppfyller följande
DEL 1 Tid 30 min Poängantal 20 I den här delen används inte räknare. Motivera alltid din slutsats med matematiska uttryck, figurer, förklaring el.dyl. 1. Vilket är det största heltalet, som uppfyller följande
Facit med lösningsförslag kommer att anslås på vår hemsida www.ebersteinska.norrkoping.se. Du kan dessutom få dem via e-post, se nedan.
 Detta häfte innehåller uppgifter från fyra olika områden inom matematiken. Meningen är att de ska tjäna som en självtest inför gymnasiet. Klarar du dessa uppgifter så är du väl förberedd inför gymnasiestudier
Detta häfte innehåller uppgifter från fyra olika områden inom matematiken. Meningen är att de ska tjäna som en självtest inför gymnasiet. Klarar du dessa uppgifter så är du väl förberedd inför gymnasiestudier
Avsikt På ett lekfullt sätt färdighetsträna, utveckla elevers känsla för hur vårt talsystem är uppbyggt samt hitta mönster som uppkommer.
 Strävorna 4A 100-rutan... förmåga att förstå, föra och använda logiska resonemang, dra slutsatser och generalisera samt muntligt och skriftligt förklara och argumentera för sitt tänkande.... grundläggande
Strävorna 4A 100-rutan... förmåga att förstå, föra och använda logiska resonemang, dra slutsatser och generalisera samt muntligt och skriftligt förklara och argumentera för sitt tänkande.... grundläggande
4-3 Vinklar Namn: Inledning. Vad är en vinkel?
 4-3 Vinklar Namn: Inledning I det här kapitlet skall du lära dig allt om vinklar: spetsiga, trubbiga och räta vinklar. Och inte minst hur man mäter vinklar. Att mäta vinklar och sträckor är grundläggande
4-3 Vinklar Namn: Inledning I det här kapitlet skall du lära dig allt om vinklar: spetsiga, trubbiga och räta vinklar. Och inte minst hur man mäter vinklar. Att mäta vinklar och sträckor är grundläggande
Fler uppgifter på andragradsfunktioner
 Fler uppgifter på andragradsfunktioner 1 I grafen nedan visas tre andragradsfunktioner. Bestäm a,b och c för p(x) = ax 2 + bx + c genom att läsa av lämpliga punkter i grafen. 10 5 1 3 5 Figur 1: 2 Vi har
Fler uppgifter på andragradsfunktioner 1 I grafen nedan visas tre andragradsfunktioner. Bestäm a,b och c för p(x) = ax 2 + bx + c genom att läsa av lämpliga punkter i grafen. 10 5 1 3 5 Figur 1: 2 Vi har
Sammanfattning på lättläst svenska
 Sammanfattning på lättläst svenska Utredningen skulle utreda och lämna förslag i vissa frågor som handlar om svenskt medborgarskap. Svenskt medborgarskap i dag Vissa personer blir svenska medborgare när
Sammanfattning på lättläst svenska Utredningen skulle utreda och lämna förslag i vissa frågor som handlar om svenskt medborgarskap. Svenskt medborgarskap i dag Vissa personer blir svenska medborgare när
Sidor i boken f(x) = a x 2 +b x+c
 Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Lösningar och kommentarer till uppgifter i 1.1
 Lösningar och kommentarer till uppgifter i 1.1 1106 d) 1107 d) 5t(t t 1) t (t 3) + t 3 5t 3 10t 5t (t 3 3t ) + t 3 5t 3 10t 5t t 3 + 3t + t 3 6t 3 7t 5t Kommentarer: Starta med att multiplicera in faktorerna
Lösningar och kommentarer till uppgifter i 1.1 1106 d) 1107 d) 5t(t t 1) t (t 3) + t 3 5t 3 10t 5t (t 3 3t ) + t 3 5t 3 10t 5t t 3 + 3t + t 3 6t 3 7t 5t Kommentarer: Starta med att multiplicera in faktorerna
Ekvationssystem, Matriser och Eliminationsmetoden
 Matematiska institutionen Göteborgs universitet och Chalmers tekniska högskola Version 359 Ekvationssystem, Matriser och Eliminationsmetoden - En inledning Ekvationssystem - matrisformulering Vi såg att
Matematiska institutionen Göteborgs universitet och Chalmers tekniska högskola Version 359 Ekvationssystem, Matriser och Eliminationsmetoden - En inledning Ekvationssystem - matrisformulering Vi såg att
Frågorna 1 till 6 ska svaras med sant eller falskt och ger vardera 1
 ATM-Matematik Mikael Forsberg 6-64 89 6 Matematik med datalogi, mfl. Skrivtid:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på ny sida. Använd ej baksidor.
ATM-Matematik Mikael Forsberg 6-64 89 6 Matematik med datalogi, mfl. Skrivtid:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på ny sida. Använd ej baksidor.
Observera att alla funktioner kan ritas, men endast linjära funktioner blir räta linjer.
 1 Matematik som verktyg Antag att vi har en funktion som är en rät linje, y = 1 3x. Eftersom relationen mellan x och y är linjär räcker det med att vi hittar två punkter (två talpar) på linjen för att
1 Matematik som verktyg Antag att vi har en funktion som är en rät linje, y = 1 3x. Eftersom relationen mellan x och y är linjär räcker det med att vi hittar två punkter (två talpar) på linjen för att
Repetition av cosinus och sinus
 Repetition av cosinus och sinus Av Eric Borgqvist, 00-08-6, Lund Syftet med detta dokument är att få en kort och snabb repetition av vissa egenskaper hos de trigonometriska funktionerna sin och cos. Det
Repetition av cosinus och sinus Av Eric Borgqvist, 00-08-6, Lund Syftet med detta dokument är att få en kort och snabb repetition av vissa egenskaper hos de trigonometriska funktionerna sin och cos. Det
var väl Connysson som sade det, att det kändes som vi till och med,
 Det här var ju inte alls vad vi kom överens om. Det här var ju inte alls vad vi kom överens om förra veckan, på vårt möte. Både jag och Connysson upplevde att vi var överens med dig, att vi brainstormade
Det här var ju inte alls vad vi kom överens om. Det här var ju inte alls vad vi kom överens om förra veckan, på vårt möte. Både jag och Connysson upplevde att vi var överens med dig, att vi brainstormade
Nämnarens adventskalendern 2007
 Nämnarens adventskalendern 2007 1 När det närmar sig jul är det kallt. Då behöver de tre tomtenissarna både halsduk och mössa när de leker i snön. I korgen ligger en röd, en blå och en randig halsduk.
Nämnarens adventskalendern 2007 1 När det närmar sig jul är det kallt. Då behöver de tre tomtenissarna både halsduk och mössa när de leker i snön. I korgen ligger en röd, en blå och en randig halsduk.
Presentationsövningar
 Varje möte då temadialog används bör inledas med en presentationsövning. har flera syften. Både föräldrar och ledare har nytta av att gå igenom samtliga deltagares namn och dessutom få en tydlig bild av
Varje möte då temadialog används bör inledas med en presentationsövning. har flera syften. Både föräldrar och ledare har nytta av att gå igenom samtliga deltagares namn och dessutom få en tydlig bild av
Svenska Du kan med flyt läsa texter som handlar om saker du känner till. Du använder metoder som fungerar. Du kan förstå vad du läser.
 Svenska Du kan med flyt läsa texter som handlar om saker du känner till. Du använder metoder som fungerar. Du kan förstå vad du läser. Du berättar på ett enkelt sätt om det du tycker är viktigt i texten.
Svenska Du kan med flyt läsa texter som handlar om saker du känner till. Du använder metoder som fungerar. Du kan förstå vad du läser. Du berättar på ett enkelt sätt om det du tycker är viktigt i texten.
Summan av två tal är 38 och differensen mellan dem är 14. Vilka är talen? 2/0/0
 Del A: Digitala verktyg är tillåtna. Skriv dina lösningar på separat papper. 1) Summan av två tal är 38 och differensen mellan dem är 14. Vilka är talen? 2/0/0 2) Ställ upp ett ekvationssystem för situationen
Del A: Digitala verktyg är tillåtna. Skriv dina lösningar på separat papper. 1) Summan av två tal är 38 och differensen mellan dem är 14. Vilka är talen? 2/0/0 2) Ställ upp ett ekvationssystem för situationen
David Wessman, Lund, 30 oktober 2014 Statistisk Termodynamik - Kapitel 5. Sammanfattning av Gunnar Ohléns bok Statistisk Termodynamik.
 Sammanfattning av Gunnar Ohléns bok Statistisk Termodynamik. 1 Jämviktsvillkor Om vi har ett stort system som består av ett litet system i kontakt med en värmereservoar. Storheter för det lilla systemet
Sammanfattning av Gunnar Ohléns bok Statistisk Termodynamik. 1 Jämviktsvillkor Om vi har ett stort system som består av ett litet system i kontakt med en värmereservoar. Storheter för det lilla systemet
Lösningar och kommentarer till Övningstenta 1
 Lösningar och kommentarer till Övningstenta 1 1 a b b a a b + b a + 2 (a + b) + b a 2 b2 a 2 + b2 + 2 (a + b) + b a 2 b 2 a 2 + b 2 (a + b) + b + 2 a 2 b 2 a 2 + b 2 (a + b) + b + 2 (a b)(a + b)(a + b)
Lösningar och kommentarer till Övningstenta 1 1 a b b a a b + b a + 2 (a + b) + b a 2 b2 a 2 + b2 + 2 (a + b) + b a 2 b 2 a 2 + b 2 (a + b) + b + 2 a 2 b 2 a 2 + b 2 (a + b) + b + 2 (a b)(a + b)(a + b)
Kängurutävlingen Matematikens hopp 2009 Cadet för gymnasiet för elever på kurs A
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Cadet för gymnasiet för elever på kurs A Kängurutävlingen genomförs 9 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Cadet för gymnasiet för elever på kurs A Kängurutävlingen genomförs 9 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
x 2 + px = ( x + p 2 x 2 2x = ( x + 2
 Inledande kurs i matematik, avsnitt P.3 P.3. Bestäm en ekvation för cirkeln med mittpunkt i (0, 0) och radie 4. Med hjälp av kvadratkompletteringsformeln + p = ( + p ) ( p ) En cirkel med mittpunkt i (
Inledande kurs i matematik, avsnitt P.3 P.3. Bestäm en ekvation för cirkeln med mittpunkt i (0, 0) och radie 4. Med hjälp av kvadratkompletteringsformeln + p = ( + p ) ( p ) En cirkel med mittpunkt i (
3. Värmeutvidgning (s. 49 57)
 3. Värmeutvidgning (s. 49 57) Om du vill öppna ett burklock som har fastnat kan du värma det under varmt vatten en stund och sedan lossnar det enklare. Detta beror på att värmen får locket att utvidga
3. Värmeutvidgning (s. 49 57) Om du vill öppna ett burklock som har fastnat kan du värma det under varmt vatten en stund och sedan lossnar det enklare. Detta beror på att värmen får locket att utvidga
Ha det kul med att förmedla och utveckla ett knepigt område!
 Kul med pizzabitar Första gången eleverna får materialet i handen bör dem få sin egen tid till att undersöka det på det viset blir dem bekanta med dess olika delar. Det kan också vara en god idé att låta
Kul med pizzabitar Första gången eleverna får materialet i handen bör dem få sin egen tid till att undersöka det på det viset blir dem bekanta med dess olika delar. Det kan också vara en god idé att låta
Kryssproblem (redovisningsuppgifter).
 Uppsala Universitet Matematiska Institutionen Bo Styf Flervariabelanalys, 5 hp STS, X 2010-03-19 Kryssproblem (redovisningsuppgifter). Till var och en av de åtta lektionerna hör ett par problem, som kallas
Uppsala Universitet Matematiska Institutionen Bo Styf Flervariabelanalys, 5 hp STS, X 2010-03-19 Kryssproblem (redovisningsuppgifter). Till var och en av de åtta lektionerna hör ett par problem, som kallas
NATIONELLA MATEMATIKTÄVLING
 NATIONELLA MATEMATIKTÄVLING PRATA OM SPELS EN KURS I SANNOLIKHET 1 INLEDNING Sannolikhetskursen består av sju olika steg där det sista steget utgörs av själva tävlingsmomentet. Det är upp till pedagogen
NATIONELLA MATEMATIKTÄVLING PRATA OM SPELS EN KURS I SANNOLIKHET 1 INLEDNING Sannolikhetskursen består av sju olika steg där det sista steget utgörs av själva tävlingsmomentet. Det är upp till pedagogen
Omvandla Vinklar. 1 Mattematiskt Tankesätt
 Omvandla Vinklar 1 Mattematiskt Tankesätt (Kan användas till mer än bara vinklar) 2 Omvandla med hjälp av Huvudräkning (Snabbmetod i slutet av punkt 2) 3 Omvandla med Miniräknare (Casio) Läs denna Först
Omvandla Vinklar 1 Mattematiskt Tankesätt (Kan användas till mer än bara vinklar) 2 Omvandla med hjälp av Huvudräkning (Snabbmetod i slutet av punkt 2) 3 Omvandla med Miniräknare (Casio) Läs denna Först
Mål Blå kurs Röd kurs
 Bråk Mål När eleverna har arbetat med det här kapitlet ska de kunna läsa och skriva bråk veta vad som menas med täljare och nämnare känna till och kunna använda begreppen bråkform och blandad form kunna
Bråk Mål När eleverna har arbetat med det här kapitlet ska de kunna läsa och skriva bråk veta vad som menas med täljare och nämnare känna till och kunna använda begreppen bråkform och blandad form kunna
Koll på cashen - agera ekonomicoach!
 För elever Fördjupningsuppgift: Koll på cashen - agera ekonomicoach! Fördjupningsuppgift: Ekonomicoach Så här går det till Börja med att se filmen Koll på cashen. Därefter är ni redo för att komma igång.
För elever Fördjupningsuppgift: Koll på cashen - agera ekonomicoach! Fördjupningsuppgift: Ekonomicoach Så här går det till Börja med att se filmen Koll på cashen. Därefter är ni redo för att komma igång.
a) Ange ekvationen för den räta linjen L. (1/0/0) Varje tal nedan motsvaras av en markerad punkt på tallinjen.
 Delprov B: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet. 1. Ange det uttryck som ska stå i parentesen för att likheten ska gälla. ( ) ( x 5) = x 5 (1/0/0).
Delprov B: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet. 1. Ange det uttryck som ska stå i parentesen för att likheten ska gälla. ( ) ( x 5) = x 5 (1/0/0).
Tentamen i Linjär algebra (TATA31/TEN1) 2013 08 24, 14 19.
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN 8, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst uppgifter
LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN 8, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst uppgifter
Tentamen i matematisk statistik (9MA241/9MA341/LIMAB6, STN2) 2012-01-09 kl 08-13
 LINKÖPINGS UNIVERSITET MAI Johan Thim Tentamen i matematisk statistik (9MA241/9MA341/LIMAB6, STN2) 212-1-9 kl 8-13 Hjälpmedel är: miniräknare med tömda minnen och formelbladet bifogat. Varje uppgift är
LINKÖPINGS UNIVERSITET MAI Johan Thim Tentamen i matematisk statistik (9MA241/9MA341/LIMAB6, STN2) 212-1-9 kl 8-13 Hjälpmedel är: miniräknare med tömda minnen och formelbladet bifogat. Varje uppgift är
Individuellt Mjukvaruutvecklingsprojekt
 Individuellt Mjukvaruutvecklingsprojekt RPG-spel med JavaScript Författare Robin Bertram Datum 2013 06 10 1 Abstrakt Den här rapporten är en post mortem -rapport som handlar om utvecklandet av ett RPG-spel
Individuellt Mjukvaruutvecklingsprojekt RPG-spel med JavaScript Författare Robin Bertram Datum 2013 06 10 1 Abstrakt Den här rapporten är en post mortem -rapport som handlar om utvecklandet av ett RPG-spel
Sammanfattning av kursdag 2, 2013-03-07 i Stra ngna s och 2013-03-12 Eskilstuna
 Sammanfattning av kursdag 2, 2013-03-07 i Stra ngna s och 2013-03-12 Eskilstuna Sammanfattning och genomgång av lektion 1 samt hemläxa. -Hur ta ut en position i sjökortet? Mät med Passaren mellan positionen
Sammanfattning av kursdag 2, 2013-03-07 i Stra ngna s och 2013-03-12 Eskilstuna Sammanfattning och genomgång av lektion 1 samt hemläxa. -Hur ta ut en position i sjökortet? Mät med Passaren mellan positionen
Matematik och modeller Övningsuppgifter
 Matematik och modeller Övningsuppgifter Beräkna a) d) + 6 b) 7 (+) + ( 9 + ) + 9 e) 8 c) ( + (5 6)) f) + Förenkla följande uttryck så långt som möjligt a) ( ) 5 b) 5 y 6 5y c) y 5 y + y y d) +y y e) (
Matematik och modeller Övningsuppgifter Beräkna a) d) + 6 b) 7 (+) + ( 9 + ) + 9 e) 8 c) ( + (5 6)) f) + Förenkla följande uttryck så långt som möjligt a) ( ) 5 b) 5 y 6 5y c) y 5 y + y y d) +y y e) (
Kängurutävlingen Matematikens hopp 2009 Cadet för elever i åk 8 och 9
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs 9 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs 9 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas, däremot
KÄNSLA AV SAMMANHANG. Uppskattad dygnsdos i gr. och preparat (de sista 30 dagarna):
 KÄNSLA AV SAMMANHANG Datum för ifyllandet: Intervjutillfälle nr: Intervjuare: Individens namn: Kön: Födelse år: Antal år i missbruk (med uppehåll): Drogfri dagar (nu): Initiativtagare till kontakt med
KÄNSLA AV SAMMANHANG Datum för ifyllandet: Intervjutillfälle nr: Intervjuare: Individens namn: Kön: Födelse år: Antal år i missbruk (med uppehåll): Drogfri dagar (nu): Initiativtagare till kontakt med
VÄRDERINGSÖVNINGAR. Vad är Svenskt?
 VÄRDERINGSÖVNINGAR Vad är Svenskt? Typ av övning: Avstamp till diskussion. Övningen belyser hur svårt det är att säga vad som är svenskt och att normen vad som anses vara svenskt ändras med tiden och utifrån
VÄRDERINGSÖVNINGAR Vad är Svenskt? Typ av övning: Avstamp till diskussion. Övningen belyser hur svårt det är att säga vad som är svenskt och att normen vad som anses vara svenskt ändras med tiden och utifrån
Elektronen och laddning
 Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
1,2C 4,6C 1A. X-kuber. strävorna
 1,2C 4,6C 1A X-kuber problemlösning begrepp resonemang geometri skala strävorna Avsikt och matematikinnehåll X-kuber är en aktivitet som får olika avsikt och matematikinnehåll beroende på hur och i vilket
1,2C 4,6C 1A X-kuber problemlösning begrepp resonemang geometri skala strävorna Avsikt och matematikinnehåll X-kuber är en aktivitet som får olika avsikt och matematikinnehåll beroende på hur och i vilket
a n = A2 n + B4 n. { 2 = A + B 6 = 2A + 4B, S(5, 2) = S(4, 1) + 2S(4, 2) = 1 + 2(S(3, 1) + 2S(3, 2)) = 3 + 4(S(2, 1) + 2S(2, 2)) = 7 + 8 = 15.
 1 Matematiska Institutionen KTH Lösningar till tentamensskrivning på kursen Diskret Matematik, moment A, för D och F, SF161 och SF160, den juni 008 kl 08.00-1.00. DEL I 1. (p) Lös rekursionsekvationen
1 Matematiska Institutionen KTH Lösningar till tentamensskrivning på kursen Diskret Matematik, moment A, för D och F, SF161 och SF160, den juni 008 kl 08.00-1.00. DEL I 1. (p) Lös rekursionsekvationen
Repetitionsuppgifter i Matematik inför Basår. Matematiska institutionen Linköpings universitet 2014
 Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Handledning för digitala verktyg Talsyntes och rättstavningsprogram. Vital, StavaRex och SpellRight
 Handledning för digitala verktyg Talsyntes och rättstavningsprogram Vital, StavaRex och SpellRight Elevens namn:.. Skola: Datum:.. Varför behövs en handledning? Denna handledning är tänkt att användas
Handledning för digitala verktyg Talsyntes och rättstavningsprogram Vital, StavaRex och SpellRight Elevens namn:.. Skola: Datum:.. Varför behövs en handledning? Denna handledning är tänkt att användas
Finns det någon som kan förklara varför man inte kan använda formeln P=U I rotenur3 cosfi på en pump som sitter i en borrad brunn?
 Räkna ut strömmen på en pump i en borra Postad av Tommy - 15 apr 2015 20:48 Finns det någon som kan förklara varför man inte kan använda formeln P=U I rotenur3 cosfi på en pump som sitter i en borrad brunn?
Räkna ut strömmen på en pump i en borra Postad av Tommy - 15 apr 2015 20:48 Finns det någon som kan förklara varför man inte kan använda formeln P=U I rotenur3 cosfi på en pump som sitter i en borrad brunn?
Gruppenkät. Lycka till! Kommun: Stadsdel: (Gäller endast Göteborg)
 Gruppenkät Du har deltagit i en gruppaktivitet! Det kan ha varit en tjej- / killgrupp, ett läger eller ett internationellt ungdomsutbyte. Eller så har ni kanske ordnat ett musikarrangemang, skött ett café,
Gruppenkät Du har deltagit i en gruppaktivitet! Det kan ha varit en tjej- / killgrupp, ett läger eller ett internationellt ungdomsutbyte. Eller så har ni kanske ordnat ett musikarrangemang, skött ett café,
Förberedelser inför lektion 1 (första övningen läsvecka 1) Lektion 1 (första övningen läsvecka 1)
 Förberedelser inför lektion 1 (första övningen läsvecka 1) Läs kapitel 0.1 0.3. Mycket av detta är nog känt sedan tidigare. Om du känner dig osäker på något, läs detta nogrannare. Kapitel 0.6 behöver inte
Förberedelser inför lektion 1 (första övningen läsvecka 1) Läs kapitel 0.1 0.3. Mycket av detta är nog känt sedan tidigare. Om du känner dig osäker på något, läs detta nogrannare. Kapitel 0.6 behöver inte
DOP-matematik Copyright Tord Persson. Bråktal -3-2 -1 0 1 2 3. Läs av vilka tal på tallinjen, som pilarna pekar på. Uppgift nr 10 -3-2 -1 0 1 2 3
 Bråktal Uppgift nr En limpa delas i 4 lika stora delar. Hur stor del av limpan blir varje del? Uppgift nr 2 Hur många tiondelar behövs för att det skall räcka till en hel? Uppgift nr Hur läser man ut bråket
Bråktal Uppgift nr En limpa delas i 4 lika stora delar. Hur stor del av limpan blir varje del? Uppgift nr 2 Hur många tiondelar behövs för att det skall räcka till en hel? Uppgift nr Hur läser man ut bråket
Kvalitetsrapport Så här går det
 Kvalitetsrapport Så här går det Uppföljning av det systematiska kvalitetsarbetet på Lärkan förskola, Öja Verksamhetsåret 2013/2014 Kort sammanfattning av enhetens kvalitetsarbete under verksamhetsåret
Kvalitetsrapport Så här går det Uppföljning av det systematiska kvalitetsarbetet på Lärkan förskola, Öja Verksamhetsåret 2013/2014 Kort sammanfattning av enhetens kvalitetsarbete under verksamhetsåret
Antal grodor i varje familj Antal hopp tills alla bytt plats Ökning 1 3 5 2 8 7 3 15 9 4 24
 strävorna 1AB Grodhopp problemlösning taluppfattning algebra Avsikt och matematikinnehåll Elever behöver få möta många aktiviteter där de kan se att algebra bland annat är generaliserad aritmetik. För
strävorna 1AB Grodhopp problemlösning taluppfattning algebra Avsikt och matematikinnehåll Elever behöver få möta många aktiviteter där de kan se att algebra bland annat är generaliserad aritmetik. För
Lösningar och kommentarer till uppgifter i 2.3
 Lösningar och kommentarer till uppgifter i 2.3 2303 d) TB: Jaha, nu gäller det att kunna sina deriveringsregler. Polynom kommer man alltid ihåg hur de ska deriveras. f(x) = 4x 2 + 5x 3 ger derivatan f
Lösningar och kommentarer till uppgifter i 2.3 2303 d) TB: Jaha, nu gäller det att kunna sina deriveringsregler. Polynom kommer man alltid ihåg hur de ska deriveras. f(x) = 4x 2 + 5x 3 ger derivatan f
L(9/G)MA10 Kombinatorik och geometri Gruppövning 1
 L(9/G)MA10 Kombinatorik och geometri Gruppövning 1 Lisa och Pelle leker med svarta och vita byggklossar. Deras pedagogiska föräldrar vill att de lär sig matematik samtidigt som de håller på och leker.
L(9/G)MA10 Kombinatorik och geometri Gruppövning 1 Lisa och Pelle leker med svarta och vita byggklossar. Deras pedagogiska föräldrar vill att de lär sig matematik samtidigt som de håller på och leker.
Föreläsning 5: Rekursion
 Föreläsning 5: Rekursion Vi har tidigare sett att man kan dela upp problem i mindre bitar med hjälp av underprogram, vilket är ett utmärkt sätt att lösa problem. Detta är ganska lätt att rita upp för sig
Föreläsning 5: Rekursion Vi har tidigare sett att man kan dela upp problem i mindre bitar med hjälp av underprogram, vilket är ett utmärkt sätt att lösa problem. Detta är ganska lätt att rita upp för sig
När jag har arbetat klart med det här området ska jag:
 Kraft och rörelse När jag har arbetat klart med det här området ska jag: kunna ge exempel på olika krafter och kunna använda mina kunskaper om dessa när jag förklarar olika fysikaliska fenomen, veta vad
Kraft och rörelse När jag har arbetat klart med det här området ska jag: kunna ge exempel på olika krafter och kunna använda mina kunskaper om dessa när jag förklarar olika fysikaliska fenomen, veta vad
2005-01-31. Hävarmen. Peter Kock
 2005-01-31 Hävarmen Kurs: WT0010 Peter Kock Handledare: Jan Sandberg Sammanfattning Om man slår upp ordet hävarm i ett lexikon så kan man läsa att hävarm är avståndet mellan kraften och vridningspunkten.
2005-01-31 Hävarmen Kurs: WT0010 Peter Kock Handledare: Jan Sandberg Sammanfattning Om man slår upp ordet hävarm i ett lexikon så kan man läsa att hävarm är avståndet mellan kraften och vridningspunkten.
Föreläsning 7b. 3329 Längdskalan är L = 2 3
 Föreläsning 7b 3329 Längdskln är L = 2 3 eller 2 : 3 som det oft skrivs i smbnd med krtor. Från teorin får vi tt A, reskln är längdskln i kvdrt det vill säg A = L 2. I denn uppgift ger det A = ( ) 2 2
Föreläsning 7b 3329 Längdskln är L = 2 3 eller 2 : 3 som det oft skrivs i smbnd med krtor. Från teorin får vi tt A, reskln är längdskln i kvdrt det vill säg A = L 2. I denn uppgift ger det A = ( ) 2 2
Föreläsning 8: Räkning. Duvhålsprincipen. Kombinatorik
 Föreläsning 8: Räkning. Duvhålsprincipen. Kombinatorik Summaregeln Om och B är disjunkta mängder så B = + B, ty innehåller inga upprepningar Produktregeln Om och B är disjunkta mängder så är B = B Exempel:
Föreläsning 8: Räkning. Duvhålsprincipen. Kombinatorik Summaregeln Om och B är disjunkta mängder så B = + B, ty innehåller inga upprepningar Produktregeln Om och B är disjunkta mängder så är B = B Exempel:
4-9 Rymdgeometri Namn:.
 4-9 Rymdgeometri Namn:. Inledning Rymden har alltid fascinerat. Men vad menas med rymd i matematisk eller geometrisk mening? Här skall du få studera 3- dimensionella figurer och hur man beräknar volymen
4-9 Rymdgeometri Namn:. Inledning Rymden har alltid fascinerat. Men vad menas med rymd i matematisk eller geometrisk mening? Här skall du få studera 3- dimensionella figurer och hur man beräknar volymen
20 Gamla tentamensuppgifter
 20 Gamla tentamensuppgifter 20.1 Lätta avdelningen Övning 20.1 Beräkna f 0 ( 3) för f(x) = 3x2 2x + 1 med jälp av derivatans definition. Lösning: Här är det allmänna uttrycket för derivatans definition
20 Gamla tentamensuppgifter 20.1 Lätta avdelningen Övning 20.1 Beräkna f 0 ( 3) för f(x) = 3x2 2x + 1 med jälp av derivatans definition. Lösning: Här är det allmänna uttrycket för derivatans definition
Predikan Lyssna! 1 maj 2016
 Predikan Lyssna! 1 maj 2016 Idag är det bönsöndagen en söndag då vi påminns om den fantastiska möjlighet vi har att prata med Gud och att lyssna till honom!! Och det är just det som den tredje vanan i
Predikan Lyssna! 1 maj 2016 Idag är det bönsöndagen en söndag då vi påminns om den fantastiska möjlighet vi har att prata med Gud och att lyssna till honom!! Och det är just det som den tredje vanan i
Väga paket och jämföra priser
 strävorna 2AC 3AC Väga paket och jämföra priser begrepp rutinuppgifter tal geometri Avsikt och matematikinnehåll Den huvudsakliga avsikten med denna aktivitet är att ge elever möjlighet att utveckla grundläggande
strävorna 2AC 3AC Väga paket och jämföra priser begrepp rutinuppgifter tal geometri Avsikt och matematikinnehåll Den huvudsakliga avsikten med denna aktivitet är att ge elever möjlighet att utveckla grundläggande
Tentamen. Makroekonomi NA0133. Juni 2016 Skrivtid 3 timmar.
 Jag har svarat på följande fyra frågor: 1 2 3 4 5 6 Min kod: Institutionen för ekonomi Rob Hart Tentamen Makroekonomi NA0133 Juni 2016 Skrivtid 3 timmar. Regler Svara på 4 frågor. (Vid svar på fler än
Jag har svarat på följande fyra frågor: 1 2 3 4 5 6 Min kod: Institutionen för ekonomi Rob Hart Tentamen Makroekonomi NA0133 Juni 2016 Skrivtid 3 timmar. Regler Svara på 4 frågor. (Vid svar på fler än
Möbiustransformationer.
 224 Om Möbiustransformationer Torbjörn Kolsrud KTH En Möbiustransformation är en komplexvärd funktion f av en komplex variabel z på formen f(z) = az + b cz + d. Här är a b c och d komplexa tal. Ofta skriver
224 Om Möbiustransformationer Torbjörn Kolsrud KTH En Möbiustransformation är en komplexvärd funktion f av en komplex variabel z på formen f(z) = az + b cz + d. Här är a b c och d komplexa tal. Ofta skriver
f(x) = x 2 g(x) = x3 100
 När vi nu ska lära oss att skissa kurvor är det bra att ha en känsla för vad som händer med kurvan när vi sätter in stora tal. Inledningsvis är det ju polynom vi ska studera. Här ska vi se vad som händer
När vi nu ska lära oss att skissa kurvor är det bra att ha en känsla för vad som händer med kurvan när vi sätter in stora tal. Inledningsvis är det ju polynom vi ska studera. Här ska vi se vad som händer
Tentamen TAIU07 Matematiska beräkningar med MATLAB för MI
 TEKNISKA HÖGSKOLAN I LINKÖPING Matematiska institutionen Beräkningsmatematik/Fredrik Berntsson Tentamen TAIU07 Matematiska beräkningar med MATLAB för MI Tid: Provkod: TEN1 Hjälpmedel: Inga. Examinator:
TEKNISKA HÖGSKOLAN I LINKÖPING Matematiska institutionen Beräkningsmatematik/Fredrik Berntsson Tentamen TAIU07 Matematiska beräkningar med MATLAB för MI Tid: Provkod: TEN1 Hjälpmedel: Inga. Examinator:
Sannolikhet och Odds
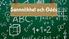 Sannolikhet och Odds Sannolikhet Tärning (Orange) och (Blå) 0 0 0 Om man satsat sina pengar på rätt summa multipliceras oddset med insatsen (pengarna man satsar) Odds Utfall (summan av två tärningar) Sannolikhet
Sannolikhet och Odds Sannolikhet Tärning (Orange) och (Blå) 0 0 0 Om man satsat sina pengar på rätt summa multipliceras oddset med insatsen (pengarna man satsar) Odds Utfall (summan av två tärningar) Sannolikhet
Två konstiga klockor
 strävorna C Två konstiga klockor resonemang geometri Avsikt och matematikinnehåll Det som kan göra det svårt för barn att avläsa en analog klocka är att förstå att den består av två skalor som är beroende
strävorna C Två konstiga klockor resonemang geometri Avsikt och matematikinnehåll Det som kan göra det svårt för barn att avläsa en analog klocka är att förstå att den består av två skalor som är beroende
Boken om Teknik. Boken om Teknik är en grundbok i Teknik för åk 4 6.
 Boken om Teknik Boken om Teknik är en grundbok i Teknik för åk 4 6. PROVLEKTION: Teknikens arbetssätt att göra på riktigt Följande provlektion är ett utdrag ur Boken om Teknik. Uppslaget som är hämtat
Boken om Teknik Boken om Teknik är en grundbok i Teknik för åk 4 6. PROVLEKTION: Teknikens arbetssätt att göra på riktigt Följande provlektion är ett utdrag ur Boken om Teknik. Uppslaget som är hämtat
