EXTRAUPPGIFTER MATEMATISK STATISTIK AK FÖR CDE, FMS 022
|
|
|
- Kurt Bengtsson
- för 7 år sedan
- Visningar:
Transkript
1 LUNDS TEKNISK HÖGSKOL MTEMTIKCENTRUM MTEMTISK STTISTIK EXTRUPPGIFTER MTEMTISK STTISTIK K FÖR CDE, FMS E Betingade sannolikheter. (a) ntag att en tredjedel av alla Volvobilar är röda. Detta kan tolkas som en sannolikhet. Om vi studerar bilar i allmänhet, dvs inte bara Volvo, hur betecknas denna sannolikhet? Ledning: Du behöver definiera två händelser först. (b) Om en femtedel av alla bilar är Volvo, vad är då sannolikheten att en slumpvis vald bil är en röd Volvo? Formulera sannolikheterna mha händelserna i (a). (c) v de bilar som inte är Volvo är en fjärdedel röda. Vad är sannolikheten att en slumpvis vald bil är Röd? Vad heter satsen du använder för att räkna ut detta? (d) En bil visar sig vara röd. Vad är sannolikheten att det är en Volvo? E Låt vara en godtycklig händelse (t.eatten tärning visar en sea) medp() = p. Upprepa försöket och studera om händelsen inträffar eller ej. (a) Vad är sannolikheten, uttryckt i p,atthändelsen inträffar i försök nr k =? (b) Vad är sannolikheten att händelsen inträffar för första gången i försök k =. (dvs inte inträffar en gång och inträffar en gång). (c) Vad är sannolikheten att händelsen inträffar för första gången i försök k = 3. (d) Vad är sannolikheten att händelsen inträffar för första gången i försök nr k,där k är ett godtyckligt heltal? (e) Resultatet i (d) är sannolikhetsfunktionen för en standardfördelning. Vad heter den och hur känns den igen? (f) ntag att p =, dvs kan t.e. vara händelsen att en slantsingling resulterar i krona. Rita upp sannolikhetsfunktionen för k =,, 3, 4. Rita även upp fördelningsfunktionen F X () för 4.5. (g) Om X = ntal slantsinglingar tills man får krona för första gången, hur ser man då P(X ) i de två figurerna i (f) E3 Låt vara en händelse enl. uppgift E, men den här gången upprepas försöket n = 4 ggr. (a) Vad är sannolikheten att händelsen inträffar k = ggr, dvs att alla fyra försöken misslyckas? (b) Vad är sannolikheten att händelsen inträffar precis k = gång? (och således misslyckas n k = 3 ggr). Ledning: Påhurmånga olika sätt kan detta inträffa? (c) Vad är sannolikheten att händelsen inträffar precis k = gånger? Ledning: Samma som i (b). (d) Fortsätt med k = 3, 4. (e) Sammanfatta alla dessa sannolikheter i ett enda uttryck som gäller för ett godtyckligt heltal k. Ledning: ( 4 k) blir,4,6,4,för respektive k =,,, 3, 4. (f) Resultatet i (e) är sannolikhetsfunktionen för en standardfördelning. Vad heter den och hur känner man igen den? (här är n = 4, men det kan naturligtvis vara ett godtyckligt antal). E4 Rita upp fördelningsfunktionen i uppgift 37 samt motsvarande täthetsfunktion i varsitt diagram för. Markera in sannolikheten i 37a i de två figurerna. Detta är en standardfördelning. Vad heter den?
2 Etrauppgifter Matstat K för CDE VT-5 E5 Repetition av dubbelintegraler. Låt {,, y f (, y) =, för övrigt (a) Skissa funktionen f (, y) i en 3d-plot. (b) För att få rätt integrationsgränser vid dubbelintegraler är det användbartmed en skiss av funktionen, men i regel räcker det att rita upp det område i y-planet där funktionen är skild från noll. Gör det. (c) Låt området utgöras av alla (, y) sådana att + y. Ritaindettaområde i figuren du gjorde i (b). Du kan börja med fallet där + y = och sedan välja rätt sida. (d) Beräkna f (, y) ddy dels genom att börja att integrera m.a.p och dels genom att börja m.a.p y. (e) Dubbelintegraler under en konstant funktion kan lösas enbart med geometriska beräkningar. Gör det med integralen i (d). (f) Beräkna f (, y) ddy E6 Repetition av dubbelintegraler. Låt { y, y f (, y) =, för övrigt (a) Skissa upp området där f (, y) = y i y-planet. (b) Beräkna (c) Räkna ut g(y) = f (, y) ddy f (, y) d Glöm inte att ange för vilka värden på y dina resultat gäller. (d) Räkna ut h() = f (, y) dy Glöm inte att ange för vilka värden på dina resultat gäller. (e) Låt området utgöras av alla (, y) sådana att y >. Ritaindettaområde i figuren du gjorde i (a) och lös f (, y) ddy (f) nvänd resultaten i (b) och (e) för att räkna ut f (, y) ddy där utgörs av y
3 Etrauppgifter Matstat K för CDE VT-5 3 E7 Låt X Ep( ). Täthetsfunktionen för Y = X kan härledasiföljande steg. (a) Sätt upp definitionen av Y s fördelningsfunktion F Y (y). (b) Stoppa in Y = X och uttryck F Y (y) som funktion av F X (y). Du behöver inte räkna ut F X () först. (c) Uttryck f Y (y) som funktion av f X (y) genom att derivera resultatet i (b). (d) Skriv upp täthetsfunktionen för X, f X (), mha formelsamlingen samt räkna ut f Y (y) genom att stoppa in resultatet i (c) i f X (). E8 Låt f X () =,. (a) Beräkna P( X < ). (b) Låt k vara ett positivt heltal och bestäm P(k X < k + ). E9 Låt X och Y vara oberoende stokastiska variabler som var och en antar värdena, och med samma sannolikhet. (a) Skriv upp sannolikhetsfunktionerna p X (i)ochp Y (j). (b) Beräkna den simultana sannolikhetsfunktionen p X,Y (i, j) samt markera de värden där p X,Y (i, j) > i(i, j)-planet. (c) Markera in området där i + j = i(i, j)-planet samt beräkna P(X + Y = ). (d) Räkna ut P(X + Y = k) för alla värden på k. Fundera efter hur du har hjälp av figuren över (i, j)-planet. (e) Låt Z = X + Y. Övertyga dig om att du räknat ut p Z (k) i (d), samt att faltningsformeln k p Z (k) = p X (i)p Y (k i) verkarrimlig. i= E Låt X och Y vara oberoende och likformigt fördelade (dvs rektangelfördelade) mellan och a. (a) Sätt Z + = ma(x, Y ). Härled täthetsfunktionen för Z +.Börja med fördelningsfunktionen F Z+ (z) och derivera för att få täthetsfunktionen. Tips: Om den största av X och Y är mindre än eller lika med ett tal z vad kan man då säga om både X och Y? (b) Sätt Z = min(x, Y )ochhärled dess täthetsfunktion. Tips: tt den minsta av X och Y är mindre än z säger inget om både X och Y,mendäremot komplementet; om den minsta är större än z så kan vi uttala oss om både X och Y. (c) Skissa upp täthetsfunktionerna för X (eller Y som ju har samma fördelning) samt Z + och Z. Verkar de rimliga? E I ett lotteri där varje lott kostar 5 öre ingår lotter med vinster enligt tabellen nedan. Låt X vara bruttovinsten på en lott. vinstbelopp (k kr) 5 antal lotter P(X = k) (a) Bestäm bruttovinstens väntevärde, varians och standardavvikelse om man köper en lott. (b) Bestäm nettovinstens väntevärde, varians och standardavvikelse om man köper en lott. E I en börs ligger två enkronor och en femkrona. Man tar slumpmässigt utan återläggning två mynt och sätter X = värdet av första myntet, Y = värdet av andra myntet. För att beräkna korrellationskoefficienten Ö(X, Y ) behövs följande delsteg. (a) Bestäm fördelningen för X, dvs beräkna dess sannolikhetsfunktion.
4 4 Etrauppgifter Matstat K för CDE VT-5 (b) Bestäm fördelningen för Y. Tips: eftersom sannolikheten att Y skall antaett givetvärde beror på vadx blev så är det lämpligt att betinga på X. (c) Beräkna E(X )ochv (X ) samt motsvarande för Y. (d) Bestäm den simultana fördelningen för X och Y, dvs beräkna p X,Y (j, k) för alla värden på j och k. Ledning: betinga på X. (e) nvänd resultatet i (d) för att beräkna E(X Y ) och bestäm slutligen C(X, Y )ochö(x, Y ). Innan du räknar kan du fundera över om du tror att de är positiva, noll eller negativa. E3 I uppgift 53 bestämde du fördelningen för Y = X + då X R(, ). Om man bara är intresserad av Y s väntevärde och varians behöver man inte först bestämma dess fördelning. Beräkna E(Y )ochv (Y ) genom att utnyttja räkneregler för väntevärde och varians för en linjär funktion. Ledning: väntevärde och varians för X kan man bestämma enkelt mha formelsamlingen. E4 De stokastiska variablerna X, X och X 3 är oberoende, alla med väntevärdet och standardavvikelsen 3. Sätt Y = 3X X + X 3 6. Bestäm E(Y )ochd(y ). E5 Träplankors längder varierar slumpmässigt till följd av fel i uppmätningföre tillsågning. Uppmätningarna, som sker med tumstock, kan ses som utfall av oberoende likafördelade stokastiska variabler med väntevärde Ñ = meter och standardavvikelse =.5 meter. Vid ett tillfälle önskar man plankor som skall läggas efter varandra så att den sammanlagda längden blir meter. Man har att såga till de plankorna enligt följande två metoder:. Man mäter upp plankorna och sågar till samtliga plankor påengång såattvarjeplankafår precis samma längd (= X ). Den sammanlagda längden blir då Y = X. Man mäter upp och sågar till varje planka för sig. Den sammanlagda längden blir då Z = i= X i (a) Bestäm E(Y ), D(Y ), E(Z) ochd(z). (b) Vilken metod ger minst spridning (minsta standardavvikelsen)? Varför blir det så? E6 Låt X i R(, a), i =,...,n vara n st. oberoende stokastiska variabler. I statistikteorin skall vi återkomma till denna uppgift och jämföra egenskaperna hos Y, Y och Y 3 nedan. (a) Bestäm väntevärde och varians för X = n X i. n i= (b) Sätt Y = X och bestäm dess väntevärde och varians. (c) Sätt Y = ma(x,...,x n ). Det finns inga färdiga räkneregler för väntevärde och varians för maimum, utan man får härleda dem från grunden. Beräkna först F Y (y) ochf Y (y) och därefter E(Y )oche(y ). nm. Bestämningen av fördelningen för Y är en generalisering av uppgift E(a). (d) nvänd resultatet i (c) för att ge ett uttryck för V (Y ). Du behöver inte förenkla det. (e) Sätt Y 3 = cy och bestäm värdet på konstanten c så atte(y 3 ) = a. E7 X är N (, ). Bestäm (a) P(X.8),
5 Etrauppgifter Matstat K för CDE VT-5 5 (b) P(X.35), (c) P(. < X <.5), (d) a så attp(x > a) = 5%, (e) a så attp( X < a) = 95 %. E8 Denna uppgift är mest av matematisk/programmeringsteknisk karaktär så du kan med gott samvete hoppa över den om du inte tycker att det verkar intressant. En del besvärliga men användbara integraler dyker upp i många olika sammanhang. T.e. den så kallade felfunktionen (eng. error-function) som har uppenbara likheter med N (, )-fördelningens fördelningsfunktion () erf() = Ô e t dt, () = e t / dt Ô Det är ganska vanligt att erf() är implementerad med numeriska metoder i matematiska programbibliotek (t.e i libc som är en grund i olika former av Uni). Man kan alltså utnyttja erf() för att räkna ut () i sitt program. (a) ntag att och visa hur man kan uttrycka () som funktion av erf(). Ledning: () = samt ett enkelt variabelbyte. (b) Det är ganska enkelt att inse att erf( ) = erf(). Utgå från () = ( ) och visa hur ()kanräknas ut som funktion av erf() då <. nm. Funktionen erfc() = erf() är också vanligt förekommande. Etrauppgift: I Statistics Toolbo i Matlab heter normalfördelningens fördelningsfunktion normcdf. Hur är den implementerad? Ledning: type normcdf imatlab. E9 I denna uppgift behöver du inte räkna ut något,utanbarafunderaöver hur man gör. En tillämpning av Centrala gränsvärdessatsen kan dyka upp i någon av deluppgifterna. Låt X i N (, ) och Y i R(, ), alla oberoende av varandra. (a) Hur räknar man ut P(X + X + X 3 < )? (b) Hur räknar man ut P(Y + Y + Y 3 < )? Obs! Lägg inte ner tid påattförsöka räkna ut den. 3 (c) Hur räknar man ut P( X i < )? i= 3 (d) Hur räknar man ut P( Y i < 6)? Varför är detta mycket enklare än (b)? i=
6 6 Etrauppgifter Matstat K för CDE VT-5 Svar till etrauppgifterna E (a) Händelser: R = En bil är röd och V = En bil är en Volvo. P(R V ) = 3. dvs Den betingade sannolikheten att en bil är röd givet att det är en Volvo är en tredjedel. (b) Givet: P(V ) = 5.Sökt: P(R V ) = P(R V )P(V ) = 5. (c) Givet: P(R V ) = 4.Sökt: P(R) = P(R V )P(V ) + P(R V )P(V ) = 4 5.Satsenom total sannolikhet. (d) Sökt: P(V R), dvs Den betingade sannolikheten att en bil är en Volvo givet att den är röd. nvänd def. av betingad slh. två ggr (detta kallas Bayes sats): P(V R) = P(R V )P(V ) P(R) = 4 P(V R) P(R) = E (a) k =, sannolikheten blir p. (b) k =, inte inträffa första ggn, men andra. sannolikheten blir ( p)p. (c) k = 3, sannolikheten blir ( p) p. (d) Sannolikheten i (a) kan skrivas ( p) p,såför k =,, 3,... blir sannolikheten ( p) k p och noll för andra värden på k. (e) För-första-gången-fördelning, eller kortare ffg. p X (k) = pq k, k =,,...och q = p. (ffg är snarlik en geometrisk fördelning. Hur ser den ut, och hur skiljer den sig från ffg?) (f) p X (k) =, 4, 8, 6 för k =,, 3, 4. F X () =, 3 4, 7 8, 5 6 för =,, 3, 4 och konstant enligt figuren..5 Sannolikhetsfunktion Fördelningsfunktion p X (k) F X () k (g) P(X ) är summan av de två första stapelhöjderna i p X (k). I F X () fås samma sannolikhet som funktionsvärdet för =. E3 (a) k =, sannolikheten att inte inträffar i något av de fyra försöken blir ( p) 4. (b) k =, sannolikheten ett händelsen inträffar i ett av försöken och inte i de övriga tre är p( p) 3. Det finns totalt fyra olika sätt som detta kan inträffa påsåsökta slh blir 4p( p) 3. (c) k =. Nu skall händelsen inträffa i två försök och inte i två. Detta kan ske på ( 4 ) = 6olika sätt. Sökt sannolikhet blir alltså 6p ( p). (d) k = 3. Slh 4p 3 ( p). k = 4, slh p 4. (e) lla de uträknade sannolikheterna kan sammanfattas med ( 4 k) p k ( p) 4 k för k =,,, 3, 4. (f) Binomialfördelning. I (e) är det en Bin(4, p)-fördelning. För en Bin(n, p)-fördelning är p X (k) = ( n k) p k q n k för k =,,,...,n och q = p. E4 f X () = d d F X () =.4e.4, samtför <. Eponentialfördelning, bet. Ep(/.4)..4 Täthetsfunktion Fördelningsfunktion f X ().3.. F X () P(X 3) ses som arean under f X ()för 3. I F X () är samma slh funktionsvärdet för = 3.
7 Etrauppgifter Matstat K för CDE VT-5 7 E5 (a) (d) f (, y) ddy = (e) (f) f (, y) dyd = y y= = = y= ddy = dyd = = dy = ( y) dy = [ y y ] = 4 [] y [ y ] y= d = ( ) d = [ ] = 4 f (, y) ddy = [rean av i kvadraten] [Höjden av lådan ] = [ /] = 4 f (, y) ddy = [Volymen av lådan ] = E6 (a) (b) Om vi börjar integrera map fås (prova gärna med y också) y [ y f (, y) ddy = y ddy = (c) Om y fås g(y) = f (, y) d = y= y = y d = för övriga värden på y är g(y) =. (d) Om fås [ y h() = f (, y) dy = y dy = för övriga värden på är h() =. (e) y f (, y) ddy = y ddy = = y= [ y 4 = 4 y3 3 + y 8 ] y dy = [ ] y y = y3, y ] = ] y 3 dy = [ y 4 = ( 3 ), ] y [ y dy = = ).8 ( ] = 8 y(y ) dy = (f) Eftersom och tillsammans täcker y-planet och inte överlappar varandra fås f (, y) ddy = f (, y) ddy f (, y) ddy =
8 j 8 Etrauppgifter Matstat K för CDE VT-5 E7 (a) F Y (y) = P(Y y). (b) F Y (y) = P(Y y) = P( X y) = P(X y ) = F X (y ). (c) f Y (y) = d dy F Y (y) = d dy F X (y ) = yf X (y). (d) f X () = e /,, f Y (y) = yf X (y) = y e y /, y, dvs f Y (y) = y e y /, y E8 (a) P( X < ) = (b) P(k X < k + ) = f X () d = k+ k [ f X () d = ] =. [ ] k+ k = k, k =,,... k + E9 (a) p X (i) = 3, i =,,. p Y (j) = 3, i =,,. (b) p X,Y (i, j) = p X (i)p Y (j) = 9, i =,,, j =,, (c) P(X +Y = ) = P(X = Y = X = Y = ) = p X,Y (, )+p X,Y (, ) = = 9 i + j = i (d) De värden på k som är möjliga är,,, 3 och 4. P(X + Y = ) = p X,Y (, ) = 9 P(X + Y = ) = p X,Y (, ) + p X,Y (, ) = 9 P(X + Y = ) = p X,Y (, ) + p X,Y (, ) + p X,Y (, ) = 3 9 P(X + Y = 3) = p X,Y (, 3) + p X,Y (, ) + p X,Y (, ) + p X,Y (3, ) = = 9 P(X + Y = 4) = p X,Y (, 4) + p X,Y (, 3) + p X,Y (, ) + p X,Y (3, ) + p X,Y (4, ) = 9 E (a) Om ma(x, Y ) z måste både X och Y vara mindre än z. Med hjälp av detta kan man räkna ut F Z+ (z) somilösningen till uppgift 54 (det går naturligtvis att räkna ut som f X ()f Y (y) ddy men det är lite krångligare). Täthetsfunktionen blir ma(,y) z f Z+ (z) = F Z + (z) = z, z a och noll för övriga värden på z. a (b) Här får man utnyttja komplement och det faktum att om min(x, Y ) > z så måste både X och Y vara större än z. Täthetsfunktionen blir f Z (z) = a ( z a ), z a och noll för övriga värden på z. (c) f X () = f Y () f Z+ (z) f Z (z) /a /a /a a a z a z E (a) E(X ) = k E(X ) = k kp X (k) = =.35 kr k p X (k) = =.75 kr V (X ) = E(X ) E(X ) = =.63 kr. D(X ) = V (X ) = 3.55 kr
9 Etrauppgifter Matstat K för CDE VT-5 9 (b) Låt Y vara nettovinsten i kr på en lott. Dåär Y = X.5. E(Y ) = E(X.5) = E(X ).5 =.35.5 =.5 kr V (Y ) = V (X.5) = V (X ) =.63 kr. D(Y ) = 3.55 kr. E (a) X kan anta värdena och 5. Sannolikhetsfunktionens värde i dessa punkter blir p X () = P(X = ) = 3. p X (5) = P(X = 5) = 3. (b) Satsen om total sannolikhet ger: p Y () = P(Y = ) = P(Y = X = )P(X = ) + P(Y = X = 5)P(X = 5) = = 3. Eftersom sannolikhetsfunktionen summeras till fås direkt p Y (5) = p Y () = 3. Observera att X och Y har sammafördelning! (c) E(X ) = kp X (k) = = 7 3. E(X ) = k p X (k) = = 7 3. k k V (X ) = E(X ) E(X ) = 3 9. Eftersom Y har samma fördelning som X så hary samma väntevärde och varians som X. (d) p X,Y (, ) = P(X = Y = ) = P(Y = X = )P(X = ) = 3 = 3. p X,Y (5, ) = P(X = 5 Y = ) = P(Y = X = 5)P(X = 5) = 3 = 3. p X,Y (, 5) = P(X = Y = 5) = P(Y = 5 X = )P(X = ) = 3 = 3. p X,Y (5, 5) =. (e) E(XY ) = j k jk p X,Y (j, k) = = 3.OmX antar ett värde så ökar benägenheten för Y att anta det andra värdet. Därför borde kovariansen och därmed korrellationskoefficienten vara negativa. (E(XY ) är naturligvis positiv eftersom både X och Y bara antar positiva värden). C(X, Y ) = E(XY ) E(X )E(Y ) = = 6 9. Ö(X, Y ) = C(X,Y ) V (X )V (Y ) =. E3 Med hjälp av formelsamlingen fås E(X ) = + = (vilket naturligtvis är mittpunkten i en symmetrisk fördelning). V (X ) = ( ) = X + 3.För Y fås då E(Y ) = E( ) = E(X ) + =. V (Y ) = V ( X + ) = V (X ) + = 4 3 =. Detta stämmer bra för en R(, )-fördelning som ju Y visade sig ha i uppgift 53. E4 Vi har E(X i ) = ochv (X i ) = D(X i ) = 9. E(Y ) = E(3X X + X 3 6) = 3E(X ) E(X ) + E(X 3 ) 6 = = V (Y ) = V (3X X +X 3 6) = 3 V (X )+( ) V (X )+V (X 3 )+ = = 4 9 D(Y ) = V (Y ) = 3 4. E5 (a) E(Y ) = E(X ) = E(X ) = =. V (Y ) = V (X ) = V (X ) =.5. D(Y ) = V (Y ) =.5 =.5. E(Z) = E( i= X i) = i= E(X i) = = V (Z) = V ( i= X i) = i= V (X i) =.5. D(Z) =.5.58 (b) Metod ger minst spridning. Med metod kommer felet man gör i den enda mätingen att tiofaldigas, men med metod kommer en del att vara för korta och en del för långa och felen tar påså vis ut varandra en del. E6 (a) Med hjälp av formelsamlingen fås E(X i ) = a, V (X i) = a E( X ) = E( n X i ) = n E(X i ) = n n n n a = a. i= i= V ( X ) = V ( n X i ) = ( n n n ) V (X i ) = n n a = a n. i= i= (b) E(Y ) = E( X ) = E( X ) = a. V (Y ) = V ( X ) = V ( X ) = a 3n. (c) Repetera gärna uppgift E(a). Då sermanattfördelningsfunktionen blir F Y (y) = ( y a )n för y a (och då y < samtomy > a)..
10 Etrauppgifter Matstat K för CDE VT-5 f Y (y) = d dy F Y (y) = n a ( y a )n = n a n yn, y a. E(Y ) = yf Y (y) dy = n a a n y y n dy = n [ ] y n+ a a n = n ( ) a n+ n + a n = a n n + n +. E(Y ) = y f Y (y) dy = n a a n y y n dy = n [ ] y n+ a a n = n ( ) a n+ n + a n = a n n + n +. (d) V (Y ) = E(Y ) E(Y ) = a n n + a n (n + ) an n+ (e) E(Y 3 ) = E(cY ) = ce(y ) = c n+ = a = c = n. E7 (a) (.8).966 (b) (.35).363 (c) (.5) ( (.)).576 (d) a = Ð.5.64 (e) a = Ð.5.96 E8 (a) För fås () = (b) För < fås = () + = + e t / dt = Ô Ô e t / dt = e t / dt + e t / dt = Ô Ô [ y = t, dt = ] dy t = y = = Ô e y dy = + Ô e y dy = + erf( ) () = ( ) = ( + erf( )) = erf( ) = [erf( ) = erf()] = = + erf( ) dvs samma uttryck gäller för alla värden på. E9 (a) En linjär funktion av normalfördelningar är normalfördelad, i det här fallet X + X + X 3 N (3, 3 ). Så sannolikheten räknas ut som ( 3 ). (b) Genom t.e. f Y (y )f Y (y )f Y3 (y 3 )dy dy dy 3 eller upprepade faltningar för att fåfram y +y +y 3 summans fördelning. lternativt kan man bilda sig en uppfattning om sannolikheten genom attsimulera trer(, )-slumptal ettstor antalgångeroch sehurstorandelavdessa försök som resulterar i att summan av de tre slumptalen är mindre än. (Lite djupare analys kan man göra om man inser att antalet försök som resulterar i en summa mindre än två är Bin(n, p)-fördelat om man gör n simuleringar. p är den sökta sannolikheten. Mer om detta i statistikdelen av kursen). (Sannolikheten blir för övrigt 5 6 ). (c) En linjär funktion av normalfördelningar är normalfördelad, i det här fallet 3 i= X i N (3, 3 ). Så sannolikheten räknas ut som ( 3 ). (d) Enligt Centrala gränsvärdessatsenär en summa av många oberoende likafördelade s.v. ungefär normalfördelad. Det är inte till någon hjälp i (b) men här kan vi anse att 3 är många. Så ett approimativt värde på sannolikheten kan vi få fram genom att 3 i= Y i N ( 3, ( ( 6 3/ ).39). 3/ 3 ).
11 Etrauppgifter Matstat K för CDE VT-5 nm. Med hjälp av t.e. Fourier-transformation kan man visa att täthetsfunktionen för en summa av just n st oberoende R(, )-fördelningar blir n ( ) n f () = ( ) k ( k) n sign( k) (n )! k k= men CGS gäller för alla fördelningar (med ändlig varians).
Tentamen i matematisk statistik (9MA241/9MA341/LIMAB6, STN2) 2012-01-09 kl 08-13
 LINKÖPINGS UNIVERSITET MAI Johan Thim Tentamen i matematisk statistik (9MA241/9MA341/LIMAB6, STN2) 212-1-9 kl 8-13 Hjälpmedel är: miniräknare med tömda minnen och formelbladet bifogat. Varje uppgift är
LINKÖPINGS UNIVERSITET MAI Johan Thim Tentamen i matematisk statistik (9MA241/9MA341/LIMAB6, STN2) 212-1-9 kl 8-13 Hjälpmedel är: miniräknare med tömda minnen och formelbladet bifogat. Varje uppgift är
1. Frekvensfunktionen nedan är given. (3p)
 TENTAMEN I MATEMATIK MED MATEMATISK STATISTIK HF14 TEN 11 kl 1.15-.15 Hjälpmedel: Formler och tabeller i statistik, räknedosa Fullständiga lösningar erfordras till samtliga uppgifter. Lösningarna skall
TENTAMEN I MATEMATIK MED MATEMATISK STATISTIK HF14 TEN 11 kl 1.15-.15 Hjälpmedel: Formler och tabeller i statistik, räknedosa Fullständiga lösningar erfordras till samtliga uppgifter. Lösningarna skall
Datorövning 2 Diskret fördelning och betingning
 Lunds tekniska högskola Matematikcentrum Matematisk statistik FMSF20: MATEMATISK STATISTIK, ALLMÄN KURS, 7.5HP FÖR E, HT-15 Datorövning 2 Diskret fördelning och betingning Syftet med den här laborationen
Lunds tekniska högskola Matematikcentrum Matematisk statistik FMSF20: MATEMATISK STATISTIK, ALLMÄN KURS, 7.5HP FÖR E, HT-15 Datorövning 2 Diskret fördelning och betingning Syftet med den här laborationen
Lunds tekniska högskola Matematikcentrum Matematisk statistik
 Lunds tekniska högskola Matematikcentrum Matematisk statistik FMS0: MATEMATISK STATISTIK AK FÖR V EXEMPEL PÅ DUGGAUPPGIFTER, AVSNITT SANNOLIKHETSTEORI UPPGIFTER Kortare uppgifter. På en arbetsplats skadas
Lunds tekniska högskola Matematikcentrum Matematisk statistik FMS0: MATEMATISK STATISTIK AK FÖR V EXEMPEL PÅ DUGGAUPPGIFTER, AVSNITT SANNOLIKHETSTEORI UPPGIFTER Kortare uppgifter. På en arbetsplats skadas
Tentamen i TMA321 Matematisk Statistik, Chalmers Tekniska Högskola.
 Tentamen i TMA321 Matematisk Statistik, Chalmers Tekniska Högskola. Hjälpmedel: Valfri räknare, egenhändigt handskriven formelsamling (4 A4-sidor på 2 blad) och till skrivningen medhörande tabeller. Fredagen
Tentamen i TMA321 Matematisk Statistik, Chalmers Tekniska Högskola. Hjälpmedel: Valfri räknare, egenhändigt handskriven formelsamling (4 A4-sidor på 2 blad) och till skrivningen medhörande tabeller. Fredagen
Statistik 1 för biologer, logopeder och psykologer
 Innehåll 1 Punktskattning och kondensintervall Innehåll 1 Punktskattning och kondensintervall Population Punktskattning och kondensintervall Vi har en population vars någon mätbar egenskap X vi är intresserade
Innehåll 1 Punktskattning och kondensintervall Innehåll 1 Punktskattning och kondensintervall Population Punktskattning och kondensintervall Vi har en population vars någon mätbar egenskap X vi är intresserade
TT091A, TVJ22A, NVJA02 By, Pu, Ti. 50 poäng
 Matematisk statistik Provmoment: Ladokkod: Tentamen ges för: TT091A, TVJ22A, NVJA02 By, Pu, Ti 7,5 högskolepoäng Namn: (Ifylles av student) Personnummer: (Ifylles av student) Tentamensdatum: 2012-01-11
Matematisk statistik Provmoment: Ladokkod: Tentamen ges för: TT091A, TVJ22A, NVJA02 By, Pu, Ti 7,5 högskolepoäng Namn: (Ifylles av student) Personnummer: (Ifylles av student) Tentamensdatum: 2012-01-11
Föreläsning 9: Hypotesprövning
 Föreläsning 9: Hypotesprövning Matematisk statistik David Bolin Chalmers University of Technology Maj 5, 2014 Statistik Stickprov Ett stickprov av storlek n är n oberoende observationer av en slumpvariabel
Föreläsning 9: Hypotesprövning Matematisk statistik David Bolin Chalmers University of Technology Maj 5, 2014 Statistik Stickprov Ett stickprov av storlek n är n oberoende observationer av en slumpvariabel
4-6 Trianglar Namn:..
 4-6 Trianglar Namn:.. Inledning Hittills har du arbetat med parallellogrammer. En sådan har fyra hörn och motstående sidor är parallella. Vad händer om vi har en geometrisk figur som bara har tre hörn?
4-6 Trianglar Namn:.. Inledning Hittills har du arbetat med parallellogrammer. En sådan har fyra hörn och motstående sidor är parallella. Vad händer om vi har en geometrisk figur som bara har tre hörn?
INLÄMNINGSUPPGIFT 2 (Del 2, MATEMATISK STATISTIK) Kurs: MATEMATIK OCH MATEMATISK STATISTIK 6H3000
 INLÄMNINGSUPPGIFT 2 (Del 2, MATEMATISK STATISTIK) Kurs: MATEMATIK OCH MATEMATISK STATISTIK 6H3000 Lärare: Armin Halilovic armin@syd.kth.se www.syd.kth.se/armin tel 08 790 4810 Inlämningsuppgift 2 består
INLÄMNINGSUPPGIFT 2 (Del 2, MATEMATISK STATISTIK) Kurs: MATEMATIK OCH MATEMATISK STATISTIK 6H3000 Lärare: Armin Halilovic armin@syd.kth.se www.syd.kth.se/armin tel 08 790 4810 Inlämningsuppgift 2 består
Uppgift 2 0 0.10 1 0.25 2 0.40 3 0.20 4 0.05
 Uppgift 1 En grönsaksgrossist har utvecklat ett test för att kontrollera kvaliteten hos tomater. Efter att ha inspekterat ett urval från ett parti tomater, accepteras eller förkastas partiet. Med detta
Uppgift 1 En grönsaksgrossist har utvecklat ett test för att kontrollera kvaliteten hos tomater. Efter att ha inspekterat ett urval från ett parti tomater, accepteras eller förkastas partiet. Med detta
a n = A2 n + B4 n. { 2 = A + B 6 = 2A + 4B, S(5, 2) = S(4, 1) + 2S(4, 2) = 1 + 2(S(3, 1) + 2S(3, 2)) = 3 + 4(S(2, 1) + 2S(2, 2)) = 7 + 8 = 15.
 1 Matematiska Institutionen KTH Lösningar till tentamensskrivning på kursen Diskret Matematik, moment A, för D och F, SF161 och SF160, den juni 008 kl 08.00-1.00. DEL I 1. (p) Lös rekursionsekvationen
1 Matematiska Institutionen KTH Lösningar till tentamensskrivning på kursen Diskret Matematik, moment A, för D och F, SF161 och SF160, den juni 008 kl 08.00-1.00. DEL I 1. (p) Lös rekursionsekvationen
NATIONELLA MATEMATIKTÄVLING
 NATIONELLA MATEMATIKTÄVLING PRATA OM SPELS EN KURS I SANNOLIKHET 1 INLEDNING Sannolikhetskursen består av sju olika steg där det sista steget utgörs av själva tävlingsmomentet. Det är upp till pedagogen
NATIONELLA MATEMATIKTÄVLING PRATA OM SPELS EN KURS I SANNOLIKHET 1 INLEDNING Sannolikhetskursen består av sju olika steg där det sista steget utgörs av själva tävlingsmomentet. Det är upp till pedagogen
Föreläsning 8: Räkning. Duvhålsprincipen. Kombinatorik
 Föreläsning 8: Räkning. Duvhålsprincipen. Kombinatorik Summaregeln Om och B är disjunkta mängder så B = + B, ty innehåller inga upprepningar Produktregeln Om och B är disjunkta mängder så är B = B Exempel:
Föreläsning 8: Räkning. Duvhålsprincipen. Kombinatorik Summaregeln Om och B är disjunkta mängder så B = + B, ty innehåller inga upprepningar Produktregeln Om och B är disjunkta mängder så är B = B Exempel:
Tentamen i Tillämpad matematisk statistik LMA521 för EPI och MI den 14 dec 2011
 Tentamen i Tillämpad matematisk statistik LMA5 för EPI och MI den dec Tentamen består av åtta uppgifter om totalt 5 poäng. Det krävs minst poäng för betyg 3, minst 3 poäng för och minst poäng för 5. Eaminator:
Tentamen i Tillämpad matematisk statistik LMA5 för EPI och MI den dec Tentamen består av åtta uppgifter om totalt 5 poäng. Det krävs minst poäng för betyg 3, minst 3 poäng för och minst poäng för 5. Eaminator:
Lathund, procent med bråk, åk 8
 Lathund, procent med bråk, åk 8 Procent betyder hundradel, men man kan också säga en av hundra. Ni ska kunna omvandla mellan bråkform, decimalform och procentform. Nedan kan ni se några omvandlingar. Bråkform
Lathund, procent med bråk, åk 8 Procent betyder hundradel, men man kan också säga en av hundra. Ni ska kunna omvandla mellan bråkform, decimalform och procentform. Nedan kan ni se några omvandlingar. Bråkform
Modul 6: Integraler och tillämpningar
 Institutionen för Matematik SF65 Envariabelanalys Läsåret 5/6 Modul 6: Integraler och tillämpningar Denna modul omfattar kapitel 6. och 6.5 samt kapitel 7 i kursboken Calculus av Adams och Essex och undervisas
Institutionen för Matematik SF65 Envariabelanalys Läsåret 5/6 Modul 6: Integraler och tillämpningar Denna modul omfattar kapitel 6. och 6.5 samt kapitel 7 i kursboken Calculus av Adams och Essex och undervisas
Kapitel 6. f(x) = sin x. Figur 6.1: Funktionen sin x. 1 Oinas-Kukkonen m.fl. Kurs 6 kapitel 1
 Kapitel 6 Gränsvärde 6. Definition av gränsvärde När vi undersöker gränsvärdet av en funktion undersöker vi vad som händer med funktionsvärdet då variabeln, x, går mot ett visst värde. Frågeställningen
Kapitel 6 Gränsvärde 6. Definition av gränsvärde När vi undersöker gränsvärdet av en funktion undersöker vi vad som händer med funktionsvärdet då variabeln, x, går mot ett visst värde. Frågeställningen
Möbiustransformationer.
 224 Om Möbiustransformationer Torbjörn Kolsrud KTH En Möbiustransformation är en komplexvärd funktion f av en komplex variabel z på formen f(z) = az + b cz + d. Här är a b c och d komplexa tal. Ofta skriver
224 Om Möbiustransformationer Torbjörn Kolsrud KTH En Möbiustransformation är en komplexvärd funktion f av en komplex variabel z på formen f(z) = az + b cz + d. Här är a b c och d komplexa tal. Ofta skriver
SEPARABLA DIFFERENTIALEKVATIONER
 SEPARABLA DIFFERENTIALEKVATIONER En differentialekvation (DE) av första ordningen sägs vara separabel om den kan skrivas på formen P ( y) Q( ) () Den allmänna lösningen till () erhålles genom att integrera
SEPARABLA DIFFERENTIALEKVATIONER En differentialekvation (DE) av första ordningen sägs vara separabel om den kan skrivas på formen P ( y) Q( ) () Den allmänna lösningen till () erhålles genom att integrera
Algebra, polynom & andragradsekvationer en pampig rubrik på ett annars relativt obetydligt dokument
 Algebra, polynom & andragradsekvationer en pampig rubrik på ett annars relativt obetydligt dokument Distributiva lagen a(b + c) = ab + ac 3(x + 4) = 3 x + 3 4 = 3x + 12 3(2x + 4) = 3 2x + 3 4 = 6x + 12
Algebra, polynom & andragradsekvationer en pampig rubrik på ett annars relativt obetydligt dokument Distributiva lagen a(b + c) = ab + ac 3(x + 4) = 3 x + 3 4 = 3x + 12 3(2x + 4) = 3 2x + 3 4 = 6x + 12
Träning i bevisföring
 KTHs Matematiska Cirkel Träning i bevisföring Andreas Enblom Institutionen för matematik, 2005 Finansierat av Marianne och Marcus Wallenbergs Stiftelse 1 Mängdlära Här kommer fyra tips på hur man visar
KTHs Matematiska Cirkel Träning i bevisföring Andreas Enblom Institutionen för matematik, 2005 Finansierat av Marianne och Marcus Wallenbergs Stiftelse 1 Mängdlära Här kommer fyra tips på hur man visar
Pesach Laksman är lärarutbildare i matematik och matematikdidaktik vid Malmö högskola.
 111a Geometri med snöre Pesach Laksman är lärarutbildare i matematik och matematikdidaktik vid Malmö högskola. Areabegreppet När elever får frågan vad area betyder ges mestadels svar som antyder hur man
111a Geometri med snöre Pesach Laksman är lärarutbildare i matematik och matematikdidaktik vid Malmö högskola. Areabegreppet När elever får frågan vad area betyder ges mestadels svar som antyder hur man
Lösningar till Tentamen i Matematisk Statistik, 5p 22 mars, 2001. Beräkna medelvärdet, standardavvikelsen, medianen och tredje kvartilen?
 Lösningar till Tentamen i Matematisk Statistik, 5p 22 mars, 2001 1. Månadslönerna för 10 lärare vid en viss skola är 1 17 700 19 800 19 900 20 200 20 800 16 100 17 000 23 500 19 700 21 100 Beräkna medelvärdet,
Lösningar till Tentamen i Matematisk Statistik, 5p 22 mars, 2001 1. Månadslönerna för 10 lärare vid en viss skola är 1 17 700 19 800 19 900 20 200 20 800 16 100 17 000 23 500 19 700 21 100 Beräkna medelvärdet,
Volymer av n dimensionella klot
 252 Volymer av n dimensionella klot Mikael Passare Stockholms universitet Ett klot med radien r är mängden av punkter vars avstånd till en given punkt (medelpunkten) är högst r. Låt oss skriva B 3 (r)
252 Volymer av n dimensionella klot Mikael Passare Stockholms universitet Ett klot med radien r är mängden av punkter vars avstånd till en given punkt (medelpunkten) är högst r. Låt oss skriva B 3 (r)
Snabbslumpade uppgifter från flera moment.
 Snabbslumpade uppgifter från flera moment. Uppgift nr Ställ upp och dividera utan hjälp av miniräknare talet 48 med 2 Uppgift nr 2 Skriv talet 3 8 00 med hjälp av decimalkomma. Uppgift nr 3 Uppgift nr
Snabbslumpade uppgifter från flera moment. Uppgift nr Ställ upp och dividera utan hjälp av miniräknare talet 48 med 2 Uppgift nr 2 Skriv talet 3 8 00 med hjälp av decimalkomma. Uppgift nr 3 Uppgift nr
DOP-matematik Copyright Tord Persson. Bråktal -3-2 -1 0 1 2 3. Läs av vilka tal på tallinjen, som pilarna pekar på. Uppgift nr 10 -3-2 -1 0 1 2 3
 Bråktal Uppgift nr En limpa delas i 4 lika stora delar. Hur stor del av limpan blir varje del? Uppgift nr 2 Hur många tiondelar behövs för att det skall räcka till en hel? Uppgift nr Hur läser man ut bråket
Bråktal Uppgift nr En limpa delas i 4 lika stora delar. Hur stor del av limpan blir varje del? Uppgift nr 2 Hur många tiondelar behövs för att det skall räcka till en hel? Uppgift nr Hur läser man ut bråket
konstanterna a och b så att ekvationssystemet x 2y = 1 2x + ay = b 2 a b
 Tentamen i Inledande matematik för V och AT, (TMV25), 20-0-26. Till denna uppgift skulle endast lämnas svar, men här ges kortfattade lösningar. a) Bestäm { konstanterna a och b så att ekvationssystemet
Tentamen i Inledande matematik för V och AT, (TMV25), 20-0-26. Till denna uppgift skulle endast lämnas svar, men här ges kortfattade lösningar. a) Bestäm { konstanterna a och b så att ekvationssystemet
FMS012/MASB03: Matematisk statistik 9.0 hp för F+fysiker Föreläsning 1: Sannolikhet
 FMS012/MASB03: Matematisk statistik 9.0 hp för F+fysiker Föreläsning 1: Sannolikhet Anna Lindgren 18 januari 2016 Anna Lindgren anna@maths.lth.se FMS012/MASB03 F1: Sannolikhet 1/27 Tillämpningar Praktiska
FMS012/MASB03: Matematisk statistik 9.0 hp för F+fysiker Föreläsning 1: Sannolikhet Anna Lindgren 18 januari 2016 Anna Lindgren anna@maths.lth.se FMS012/MASB03 F1: Sannolikhet 1/27 Tillämpningar Praktiska
Facit med lösningsförslag kommer att anslås på vår hemsida www.ebersteinska.norrkoping.se. Du kan dessutom få dem via e-post, se nedan.
 Detta häfte innehåller uppgifter från fyra olika områden inom matematiken. Meningen är att de ska tjäna som en självtest inför gymnasiet. Klarar du dessa uppgifter så är du väl förberedd inför gymnasiestudier
Detta häfte innehåller uppgifter från fyra olika områden inom matematiken. Meningen är att de ska tjäna som en självtest inför gymnasiet. Klarar du dessa uppgifter så är du väl förberedd inför gymnasiestudier
L(9/G)MA10 Kombinatorik och geometri Gruppövning 1
 L(9/G)MA10 Kombinatorik och geometri Gruppövning 1 Lisa och Pelle leker med svarta och vita byggklossar. Deras pedagogiska föräldrar vill att de lär sig matematik samtidigt som de håller på och leker.
L(9/G)MA10 Kombinatorik och geometri Gruppövning 1 Lisa och Pelle leker med svarta och vita byggklossar. Deras pedagogiska föräldrar vill att de lär sig matematik samtidigt som de håller på och leker.
Övningshäfte Algebra, ekvationssystem och geometri
 Stockholms Tekniska Gmnasium --9 Övningshäfte Algebra, ekvationssstem och geometri Nivå: rätt svårt Fråga : f är ett polnom. Beräkna värdet av f, f och fπ Fråga : Ingångslönen på företaget Börjes Gurkinläggning
Stockholms Tekniska Gmnasium --9 Övningshäfte Algebra, ekvationssstem och geometri Nivå: rätt svårt Fråga : f är ett polnom. Beräkna värdet av f, f och fπ Fråga : Ingångslönen på företaget Börjes Gurkinläggning
SKOGLIGA TILLÄMPNINGAR
 STUDIEAVSNITT 3 SKOGLIGA TILLÄMPNINGAR I detta avsnitt ska vi titta på några av de skogliga tillämpningar på geometri som finns. SKOGSKARTAN EN MODELL AV VERKLIGHETEN Arbetar man i skogen klarar man sig
STUDIEAVSNITT 3 SKOGLIGA TILLÄMPNINGAR I detta avsnitt ska vi titta på några av de skogliga tillämpningar på geometri som finns. SKOGSKARTAN EN MODELL AV VERKLIGHETEN Arbetar man i skogen klarar man sig
SF1620 Matematik och modeller
 KTH Teknikvetenskap, Institutionen för matematik 1 SF160 Matematik och modeller 007-09-10 Andra veckan Trigonometri De trigonometriska funktionerna och enhetscirkeln Redan vid förra veckans avsnitt var
KTH Teknikvetenskap, Institutionen för matematik 1 SF160 Matematik och modeller 007-09-10 Andra veckan Trigonometri De trigonometriska funktionerna och enhetscirkeln Redan vid förra veckans avsnitt var
Ekvationssystem, Matriser och Eliminationsmetoden
 Matematiska institutionen Göteborgs universitet och Chalmers tekniska högskola Version 359 Ekvationssystem, Matriser och Eliminationsmetoden - En inledning Ekvationssystem - matrisformulering Vi såg att
Matematiska institutionen Göteborgs universitet och Chalmers tekniska högskola Version 359 Ekvationssystem, Matriser och Eliminationsmetoden - En inledning Ekvationssystem - matrisformulering Vi såg att
SANNOLIKHET. Sannolikhet är: Hur stor chans (eller risk) att något inträffar.
 SANNOLIKHET Sannolikhet är: Hur stor chans (eller risk) att något inträffar. tomas.persson@edu.uu.se SANNOLIKHET Grundpremisser: Ju fler möjliga händelser, desto mindre sannolikhet att en viss händelse
SANNOLIKHET Sannolikhet är: Hur stor chans (eller risk) att något inträffar. tomas.persson@edu.uu.se SANNOLIKHET Grundpremisser: Ju fler möjliga händelser, desto mindre sannolikhet att en viss händelse
Tentamen i Linjär algebra (TATA31/TEN1) 2013 08 24, 14 19.
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN 8, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst uppgifter
LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN 8, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst uppgifter
Institutionen för matematik Envariabelanalys 1. Jan Gelfgren Datum: Fredag 9/12, 2011 Tid: 9-15 Hjälpmedel: Inga (ej miniräknare)
 Umeå universitet Dugga i matematik Institutionen för matematik Envariabelanalys 1 och matematisk statistik IE, ÖI, Stat. och Frist. Jan Gelfgren Datum: Fredag 9/12, 2011 Tid: 9-15 Hjälpmedel: Inga (ej
Umeå universitet Dugga i matematik Institutionen för matematik Envariabelanalys 1 och matematisk statistik IE, ÖI, Stat. och Frist. Jan Gelfgren Datum: Fredag 9/12, 2011 Tid: 9-15 Hjälpmedel: Inga (ej
Skriva B gammalt nationellt prov
 Skriva B gammalt nationellt prov Skriva B.wma Då fortsätter vi skrivträningen. Detta avsnitt handlar om att anpassa sin text till en särskild situation, en speciell texttyp och särskilda läsare. Nu ska
Skriva B gammalt nationellt prov Skriva B.wma Då fortsätter vi skrivträningen. Detta avsnitt handlar om att anpassa sin text till en särskild situation, en speciell texttyp och särskilda läsare. Nu ska
HT 2011 FK2004 Tenta Lärare delen 4 problem 6 poäng / problem
 HT 2011 FK2004 Tenta Lärare delen 4 problem 6 poäng / problem Problem 1 (6p) En undersökning utfördes med målet att besvara frågan Hur stor andel av den vuxna befolkningen i Sverige äger ett skjutvapen?.
HT 2011 FK2004 Tenta Lärare delen 4 problem 6 poäng / problem Problem 1 (6p) En undersökning utfördes med målet att besvara frågan Hur stor andel av den vuxna befolkningen i Sverige äger ett skjutvapen?.
Repetition av cosinus och sinus
 Repetition av cosinus och sinus Av Eric Borgqvist, 00-08-6, Lund Syftet med detta dokument är att få en kort och snabb repetition av vissa egenskaper hos de trigonometriska funktionerna sin och cos. Det
Repetition av cosinus och sinus Av Eric Borgqvist, 00-08-6, Lund Syftet med detta dokument är att få en kort och snabb repetition av vissa egenskaper hos de trigonometriska funktionerna sin och cos. Det
Datorövning 2 Statistik med Excel (Office 2007, svenska)
 Datorövning 2 Statistik med Excel (Office 2007, svenska) Denna datorövning fokuserar på att upptäcka samband mellan två variabler. Det görs genom att rita spridningsdiagram och beräkna korrelationskoefficienter
Datorövning 2 Statistik med Excel (Office 2007, svenska) Denna datorövning fokuserar på att upptäcka samband mellan två variabler. Det görs genom att rita spridningsdiagram och beräkna korrelationskoefficienter
Observera att alla funktioner kan ritas, men endast linjära funktioner blir räta linjer.
 1 Matematik som verktyg Antag att vi har en funktion som är en rät linje, y = 1 3x. Eftersom relationen mellan x och y är linjär räcker det med att vi hittar två punkter (två talpar) på linjen för att
1 Matematik som verktyg Antag att vi har en funktion som är en rät linje, y = 1 3x. Eftersom relationen mellan x och y är linjär räcker det med att vi hittar två punkter (två talpar) på linjen för att
Mätningar på op-förstärkare. Del 3, växelspänningsförstärkning med balanserad ingång.
 Mätningar på op-förstärkare. Del 3, växelspänningsförstärkning med balanserad ingång. Denna gång skall vi titta närmare på en förstärkare med balanserad ingång och obalanserad utgång. Normalt använder
Mätningar på op-förstärkare. Del 3, växelspänningsförstärkning med balanserad ingång. Denna gång skall vi titta närmare på en förstärkare med balanserad ingång och obalanserad utgång. Normalt använder
Partnerskapsförord. giftorättsgods görs till enskild egendom 1, 2. Parter 3. Partnerskapsförordets innehåll: 4
 Partnerskapsförord giftorättsgods görs till enskild egendom 1, 2 Parter 3 Namn Telefon Adress Namn Telefon Adress Partnerskapsförordets innehåll: 4 Vi skall ingå registrerat partnerskap har ingått registrerat
Partnerskapsförord giftorättsgods görs till enskild egendom 1, 2 Parter 3 Namn Telefon Adress Namn Telefon Adress Partnerskapsförordets innehåll: 4 Vi skall ingå registrerat partnerskap har ingått registrerat
D A B A D B B D. Trepoängsproblem. Kängurutävlingen 2012 Benjamin
 Kängurutävlingen enjamin Trepoängsproblem. Skrivtavlan i klassrummet är 6 meter bred. Mittdelen är m bred. De båda yttre delarna är lika breda. Hur bred är den högra delen? A: m :,5 m C:,5 m D:,75 m E:
Kängurutävlingen enjamin Trepoängsproblem. Skrivtavlan i klassrummet är 6 meter bred. Mittdelen är m bred. De båda yttre delarna är lika breda. Hur bred är den högra delen? A: m :,5 m C:,5 m D:,75 m E:
Mål Blå kurs Röd kurs
 Bråk Mål När eleverna har arbetat med det här kapitlet ska de kunna läsa och skriva bråk veta vad som menas med täljare och nämnare känna till och kunna använda begreppen bråkform och blandad form kunna
Bråk Mål När eleverna har arbetat med det här kapitlet ska de kunna läsa och skriva bråk veta vad som menas med täljare och nämnare känna till och kunna använda begreppen bråkform och blandad form kunna
Exempel på tentamensuppgifter i LMA100, del 1
 Exempel på tentamensuppgifter i LMA100, del 1 Diskret matematik 1. Givet är de 7 bokstäverna i ordet APPARAT. Hur många olika ord (= bokstavspermutationer) kan man bilda av dem med (a) 7 bokstäver (b)
Exempel på tentamensuppgifter i LMA100, del 1 Diskret matematik 1. Givet är de 7 bokstäverna i ordet APPARAT. Hur många olika ord (= bokstavspermutationer) kan man bilda av dem med (a) 7 bokstäver (b)
Sammanfattning av kursdag 2, 2013-03-07 i Stra ngna s och 2013-03-12 Eskilstuna
 Sammanfattning av kursdag 2, 2013-03-07 i Stra ngna s och 2013-03-12 Eskilstuna Sammanfattning och genomgång av lektion 1 samt hemläxa. -Hur ta ut en position i sjökortet? Mät med Passaren mellan positionen
Sammanfattning av kursdag 2, 2013-03-07 i Stra ngna s och 2013-03-12 Eskilstuna Sammanfattning och genomgång av lektion 1 samt hemläxa. -Hur ta ut en position i sjökortet? Mät med Passaren mellan positionen
Laborativ matematik som bedömningsform. Per Berggren och Maria Lindroth 2016-01-28
 Laborativ matematik som bedömningsform Per Berggren och Maria Lindroth 2016-01-28 Kul matematik utan lärobok Vilka förmågor tränas Problemlösning (Förstå frågan i en textuppgift, Använda olika strategier
Laborativ matematik som bedömningsform Per Berggren och Maria Lindroth 2016-01-28 Kul matematik utan lärobok Vilka förmågor tränas Problemlösning (Förstå frågan i en textuppgift, Använda olika strategier
Laboration 2: Sannolikhetsteori och simulering
 LUNDS TEKNISKA HÖGSKOLA MATEMATIKCENTRUM MATEMATISK STATISTIK LABORATION 2 MATEMATISK STATISTIK AK FÖR CDIFYSIKER, FMS012/MASB03, HT11 Laboration 2: Sannolikhetsteori och simulering Syftet med den här
LUNDS TEKNISKA HÖGSKOLA MATEMATIKCENTRUM MATEMATISK STATISTIK LABORATION 2 MATEMATISK STATISTIK AK FÖR CDIFYSIKER, FMS012/MASB03, HT11 Laboration 2: Sannolikhetsteori och simulering Syftet med den här
Väga paket och jämföra priser
 strävorna 2AC 3AC Väga paket och jämföra priser begrepp rutinuppgifter tal geometri Avsikt och matematikinnehåll Den huvudsakliga avsikten med denna aktivitet är att ge elever möjlighet att utveckla grundläggande
strävorna 2AC 3AC Väga paket och jämföra priser begrepp rutinuppgifter tal geometri Avsikt och matematikinnehåll Den huvudsakliga avsikten med denna aktivitet är att ge elever möjlighet att utveckla grundläggande
Ha det kul med att förmedla och utveckla ett knepigt område!
 Kul med pizzabitar Första gången eleverna får materialet i handen bör dem få sin egen tid till att undersöka det på det viset blir dem bekanta med dess olika delar. Det kan också vara en god idé att låta
Kul med pizzabitar Första gången eleverna får materialet i handen bör dem få sin egen tid till att undersöka det på det viset blir dem bekanta med dess olika delar. Det kan också vara en god idé att låta
3.1 Linjens ekvation med riktningskoefficient. y = kx + l.
 Kapitel Analytisk geometri Målet med detta kapitel är att göra läsaren bekant med ekvationerna för linjen, cirkeln samt ellipsen..1 Linjens ekvation med riktningskoefficient Vi utgår från ekvationen 1
Kapitel Analytisk geometri Målet med detta kapitel är att göra läsaren bekant med ekvationerna för linjen, cirkeln samt ellipsen..1 Linjens ekvation med riktningskoefficient Vi utgår från ekvationen 1
Statistiska metoder för säkerhetsanalys
 F12: Tillförlitlighet och säkerhetsindex Cornell Styrka Säkerhetsindex Ett säkerhetsindex, b: Är ett mått på ett systems tillförlitlighet. Är ett grövre mått än felsannolikheten P f. Används när P f inte
F12: Tillförlitlighet och säkerhetsindex Cornell Styrka Säkerhetsindex Ett säkerhetsindex, b: Är ett mått på ett systems tillförlitlighet. Är ett grövre mått än felsannolikheten P f. Används när P f inte
parametriska test Mätning Ordinalskala: Nominalskala:
 Icke- parametriska test Icke- parametriska test En avgörande skillnad mellan icke-parametriska och s.k. parametriska test, som t.ex. t-test, är att de icke-parametriska testen kräver färre antaganden Icke-parametriska
Icke- parametriska test Icke- parametriska test En avgörande skillnad mellan icke-parametriska och s.k. parametriska test, som t.ex. t-test, är att de icke-parametriska testen kräver färre antaganden Icke-parametriska
10.03.2010. Översikt. Rapport från skolverket. Förändring av matematikprestationerna 1995 2003-2007. Grundtankar bakom Pixel
 Översikt Hur är situationen i Sverige och Norge när det gäller matematik-kompetensen? Är det nödvändigt att undervisa på andra sätt än vi gjort tidigare? Förändring av matematikprestationerna 1995 2003-2007
Översikt Hur är situationen i Sverige och Norge när det gäller matematik-kompetensen? Är det nödvändigt att undervisa på andra sätt än vi gjort tidigare? Förändring av matematikprestationerna 1995 2003-2007
Matematisk statistik för D, I, Π och Fysiker
 max/min Matematisk statistik för D, I, Π och Fysiker Föreläsning 5 Johan Lindström 25 september 218 Johan Lindström - johanl@maths.lth.se FMSF45/MASB3 F5 1/25 max/min Johan Lindström - johanl@maths.lth.se
max/min Matematisk statistik för D, I, Π och Fysiker Föreläsning 5 Johan Lindström 25 september 218 Johan Lindström - johanl@maths.lth.se FMSF45/MASB3 F5 1/25 max/min Johan Lindström - johanl@maths.lth.se
SF1625 Envariabelanalys
 Modul 2: Derivata Institutionen för matematik KTH 8 september 2015 Derivata Innehåll om derivata (bokens kapitel 2). Definition vad begreppet derivata betyder Tolkning hur man kan tolka derivata Deriveringsregler
Modul 2: Derivata Institutionen för matematik KTH 8 september 2015 Derivata Innehåll om derivata (bokens kapitel 2). Definition vad begreppet derivata betyder Tolkning hur man kan tolka derivata Deriveringsregler
Något om permutationer
 105 Något om permutationer Lars Holst KTH, Stockholm 1. Inledning. I många matematiska resonemang måste man räkna antalet fall av olika slag. Den del av matematiken som systematiskt studerar dylikt brukar
105 Något om permutationer Lars Holst KTH, Stockholm 1. Inledning. I många matematiska resonemang måste man räkna antalet fall av olika slag. Den del av matematiken som systematiskt studerar dylikt brukar
Nämnarens adventskalendern 2007
 Nämnarens adventskalendern 2007 1 När det närmar sig jul är det kallt. Då behöver de tre tomtenissarna både halsduk och mössa när de leker i snön. I korgen ligger en röd, en blå och en randig halsduk.
Nämnarens adventskalendern 2007 1 När det närmar sig jul är det kallt. Då behöver de tre tomtenissarna både halsduk och mössa när de leker i snön. I korgen ligger en röd, en blå och en randig halsduk.
Sannolikhet och Odds
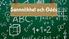 Sannolikhet och Odds Sannolikhet Tärning (Orange) och (Blå) 0 0 0 Om man satsat sina pengar på rätt summa multipliceras oddset med insatsen (pengarna man satsar) Odds Utfall (summan av två tärningar) Sannolikhet
Sannolikhet och Odds Sannolikhet Tärning (Orange) och (Blå) 0 0 0 Om man satsat sina pengar på rätt summa multipliceras oddset med insatsen (pengarna man satsar) Odds Utfall (summan av två tärningar) Sannolikhet
4-3 Vinklar Namn: Inledning. Vad är en vinkel?
 4-3 Vinklar Namn: Inledning I det här kapitlet skall du lära dig allt om vinklar: spetsiga, trubbiga och räta vinklar. Och inte minst hur man mäter vinklar. Att mäta vinklar och sträckor är grundläggande
4-3 Vinklar Namn: Inledning I det här kapitlet skall du lära dig allt om vinklar: spetsiga, trubbiga och räta vinklar. Och inte minst hur man mäter vinklar. Att mäta vinklar och sträckor är grundläggande
Vi skall skriva uppsats
 Vi skall skriva uppsats E n vacker dag får du höra att du skall skriva uppsats. I den här texten får du veta vad en uppsats är, vad den skall innehålla och hur den bör se ut. En uppsats är en text som
Vi skall skriva uppsats E n vacker dag får du höra att du skall skriva uppsats. I den här texten får du veta vad en uppsats är, vad den skall innehålla och hur den bör se ut. En uppsats är en text som
Antal grodor i varje familj Antal hopp tills alla bytt plats Ökning 1 3 5 2 8 7 3 15 9 4 24
 strävorna 1AB Grodhopp problemlösning taluppfattning algebra Avsikt och matematikinnehåll Elever behöver få möta många aktiviteter där de kan se att algebra bland annat är generaliserad aritmetik. För
strävorna 1AB Grodhopp problemlösning taluppfattning algebra Avsikt och matematikinnehåll Elever behöver få möta många aktiviteter där de kan se att algebra bland annat är generaliserad aritmetik. För
Koll på cashen - agera ekonomicoach!
 För elever Fördjupningsuppgift: Koll på cashen - agera ekonomicoach! Fördjupningsuppgift: Ekonomicoach Så här går det till Börja med att se filmen Koll på cashen. Därefter är ni redo för att komma igång.
För elever Fördjupningsuppgift: Koll på cashen - agera ekonomicoach! Fördjupningsuppgift: Ekonomicoach Så här går det till Börja med att se filmen Koll på cashen. Därefter är ni redo för att komma igång.
Matematisk statistik 9 hp Föreläsning 4: Flerdim
 Matematisk statistik 9 hp Föreläsning 4: Flerdim Johan Lindström 3+4 september 26 Johan Lindström - johanl@maths.lth.se FMS2 F4: Flerdim /5 Transformer Inversmetoden Transformation av stokastiska variabler
Matematisk statistik 9 hp Föreläsning 4: Flerdim Johan Lindström 3+4 september 26 Johan Lindström - johanl@maths.lth.se FMS2 F4: Flerdim /5 Transformer Inversmetoden Transformation av stokastiska variabler
1,2C 4,6C 1A. X-kuber. strävorna
 1,2C 4,6C 1A X-kuber problemlösning begrepp resonemang geometri skala strävorna Avsikt och matematikinnehåll X-kuber är en aktivitet som får olika avsikt och matematikinnehåll beroende på hur och i vilket
1,2C 4,6C 1A X-kuber problemlösning begrepp resonemang geometri skala strävorna Avsikt och matematikinnehåll X-kuber är en aktivitet som får olika avsikt och matematikinnehåll beroende på hur och i vilket
Övningshäfte i matematik för. Kemistuderande BL 05
 Övningshäfte i matematik för Kemistuderande BL 05 Detta häfte innehåller några grundläggande övningar i de delar av matematiken som man har användning för i de tidiga kemistudierna. Nivån är gymnasiematematik,
Övningshäfte i matematik för Kemistuderande BL 05 Detta häfte innehåller några grundläggande övningar i de delar av matematiken som man har användning för i de tidiga kemistudierna. Nivån är gymnasiematematik,
Riktlinjer - Rekryteringsprocesser inom Föreningen Ekonomerna skall vara genomtänkta och välplanerade i syfte att säkerhetsställa professionalism.
 REKRYTERINGSPOLICY Upprättad 2016-06-27 Bakgrund och Syfte Föreningen Ekonomernas verksamhet bygger på ideellt engagemang och innehar flertalet projekt där såväl projektledare som projektgrupp tillsätts
REKRYTERINGSPOLICY Upprättad 2016-06-27 Bakgrund och Syfte Föreningen Ekonomernas verksamhet bygger på ideellt engagemang och innehar flertalet projekt där såväl projektledare som projektgrupp tillsätts
Presentationsövningar
 Varje möte då temadialog används bör inledas med en presentationsövning. har flera syften. Både föräldrar och ledare har nytta av att gå igenom samtliga deltagares namn och dessutom få en tydlig bild av
Varje möte då temadialog används bör inledas med en presentationsövning. har flera syften. Både föräldrar och ledare har nytta av att gå igenom samtliga deltagares namn och dessutom få en tydlig bild av
4-9 Rymdgeometri Namn:.
 4-9 Rymdgeometri Namn:. Inledning Rymden har alltid fascinerat. Men vad menas med rymd i matematisk eller geometrisk mening? Här skall du få studera 3- dimensionella figurer och hur man beräknar volymen
4-9 Rymdgeometri Namn:. Inledning Rymden har alltid fascinerat. Men vad menas med rymd i matematisk eller geometrisk mening? Här skall du få studera 3- dimensionella figurer och hur man beräknar volymen
NATIONELLT KURSPROV I MATEMATIK KURS B HÖSTEN 1998. Tidsbunden del
 Nationellt kursprov i Matematik kurs B ht 1998 sida 1 (av 7) Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap. 3 sekretesslagen. För detta material gäller sekretessen
Nationellt kursprov i Matematik kurs B ht 1998 sida 1 (av 7) Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap. 3 sekretesslagen. För detta material gäller sekretessen
Det är bra om även distriktsstyrelsen gör en presentation av sig själva på samma sätt som de andra.
 Modul: Föreningspresentation Ett stort blädderblocksblad delas upp i fyra rutor. Deltagarna, som under detta pass är indelade föreningsvis, får i uppgift att rita följande saker i de fyra rutorna: Föreningsstyrelsen
Modul: Föreningspresentation Ett stort blädderblocksblad delas upp i fyra rutor. Deltagarna, som under detta pass är indelade föreningsvis, får i uppgift att rita följande saker i de fyra rutorna: Föreningsstyrelsen
Idag. Hur vet vi att vår databas är tillräckligt bra?
 Idag Hur vet vi att vår databas är tillräckligt bra? Vad är ett beroende? Vad gör man om det blivit fel? Vad är en normalform? Hur når man de olika normalformerna? DD1370 (Föreläsning 6) Databasteknik
Idag Hur vet vi att vår databas är tillräckligt bra? Vad är ett beroende? Vad gör man om det blivit fel? Vad är en normalform? Hur når man de olika normalformerna? DD1370 (Föreläsning 6) Databasteknik
Kryssproblem (redovisningsuppgifter).
 Uppsala Universitet Matematiska Institutionen Bo Styf Flervariabelanalys, 5 hp STS, X 2010-03-19 Kryssproblem (redovisningsuppgifter). Till var och en av de åtta lektionerna hör ett par problem, som kallas
Uppsala Universitet Matematiska Institutionen Bo Styf Flervariabelanalys, 5 hp STS, X 2010-03-19 Kryssproblem (redovisningsuppgifter). Till var och en av de åtta lektionerna hör ett par problem, som kallas
SF1901 Sannolikhetsteori och statistik I
 SF1901 Sannolikhetsteori och statistik I Jimmy Olsson Föreläsning 6 13 november 2017 1 / 29 Idag Förra gången Mer om väntevärden och varianser (Kap. 5.2 5.3) Beroendemått (Kap. 5.4) Summor, linjärkombinationer
SF1901 Sannolikhetsteori och statistik I Jimmy Olsson Föreläsning 6 13 november 2017 1 / 29 Idag Förra gången Mer om väntevärden och varianser (Kap. 5.2 5.3) Beroendemått (Kap. 5.4) Summor, linjärkombinationer
1 Navier-Stokes ekvationer
 Föreläsning 5. 1 Navier-Stokes ekvationer I förra föreläsningen härledde vi rörelsemängdsekvationen Du j Dt = 1 τ ij + g j. (1) ρ x i Vi konstaterade också att spänningstensorn för en inviskös fluid kan
Föreläsning 5. 1 Navier-Stokes ekvationer I förra föreläsningen härledde vi rörelsemängdsekvationen Du j Dt = 1 τ ij + g j. (1) ρ x i Vi konstaterade också att spänningstensorn för en inviskös fluid kan
Föreläsning 5, Matematisk statistik Π + E
 Repetition Summor max/min Väntevärde Varians Föreläsning 5, Matematisk statistik Π + E Sören Vang Andersen 25 november 2014 Sören Vang Andersen - sva@maths.lth.se FMS012 F5 1/16 Repetition Summor max/min
Repetition Summor max/min Väntevärde Varians Föreläsning 5, Matematisk statistik Π + E Sören Vang Andersen 25 november 2014 Sören Vang Andersen - sva@maths.lth.se FMS012 F5 1/16 Repetition Summor max/min
Storräkneövning: Sannolikhetslära
 UPPSALA UNIVERSITET Matematiska institutionen Jakob Björnberg Sannolikhet och statistik 2012 09 28 Storräkneövning: Sannolikhetslära 1. (Tentamen, april 2009.) Man har efter studier av beredskapen hos
UPPSALA UNIVERSITET Matematiska institutionen Jakob Björnberg Sannolikhet och statistik 2012 09 28 Storräkneövning: Sannolikhetslära 1. (Tentamen, april 2009.) Man har efter studier av beredskapen hos
OM KOMPLEXA TAL. 1 Om a är ett positivt reellt tal så betecknar a det positiva reella tal vars kvadrat är a men det är
 OM KOMPLEXA TAL Inledning. Vilka olika talområden finns det? Jag gör en snabb genomgång av vad ni tidigare stött på, bl.a. för att repetera standardbeteckningarna för de olika talmängderna. Positiva heltal,
OM KOMPLEXA TAL Inledning. Vilka olika talområden finns det? Jag gör en snabb genomgång av vad ni tidigare stött på, bl.a. för att repetera standardbeteckningarna för de olika talmängderna. Positiva heltal,
Två konstiga klockor
 strävorna C Två konstiga klockor resonemang geometri Avsikt och matematikinnehåll Det som kan göra det svårt för barn att avläsa en analog klocka är att förstå att den består av två skalor som är beroende
strävorna C Två konstiga klockor resonemang geometri Avsikt och matematikinnehåll Det som kan göra det svårt för barn att avläsa en analog klocka är att förstå att den består av två skalor som är beroende
SF1901: Sannolikhetslära och statistik
 SF1901: Sannolikhetslära och statistik Föreläsning 5. Kovarians, korrelation, väntevärde och varians för summor av s.v.:er, normalfördelning (del 1) Jan Grandell & Timo Koski 15.09.2008 Jan Grandell &
SF1901: Sannolikhetslära och statistik Föreläsning 5. Kovarians, korrelation, väntevärde och varians för summor av s.v.:er, normalfördelning (del 1) Jan Grandell & Timo Koski 15.09.2008 Jan Grandell &
Lathund till Annonsportalen
 Lathund till Annonsportalen * För uppdrags-/arbetsgivare * www.gu.se/samverkan/annonsportalen/ Snabbvägar: 1. Klicka på För arbetsgivare 2. Sök efter arbetsgivarens namn i sökrutan. a. Om namnet finns
Lathund till Annonsportalen * För uppdrags-/arbetsgivare * www.gu.se/samverkan/annonsportalen/ Snabbvägar: 1. Klicka på För arbetsgivare 2. Sök efter arbetsgivarens namn i sökrutan. a. Om namnet finns
ATT KUNNA TILL. MA1050 Matte Grund. 2011-06-14 Vuxenutbildningen Dennis Jonsson
 ATT KUNNA TILL MA1050 Matte Grund 2011-06-14 Vuxenutbildningen Dennis Jonsson Sida 2 av 5 Att kunna till prov G1 Kunna ställa upp och beräkna additions-, subtraktions-, multiplikations- och divisuionsuppgifter
ATT KUNNA TILL MA1050 Matte Grund 2011-06-14 Vuxenutbildningen Dennis Jonsson Sida 2 av 5 Att kunna till prov G1 Kunna ställa upp och beräkna additions-, subtraktions-, multiplikations- och divisuionsuppgifter
Kvinnor som driver företag pensionssparar mindre än män
 Pressmeddelande 7 september 2016 Kvinnor som driver företag pensionssparar mindre än män Kvinnor som driver företag pensionssparar inte i lika hög utsträckning som män som driver företag, 56 respektive
Pressmeddelande 7 september 2016 Kvinnor som driver företag pensionssparar mindre än män Kvinnor som driver företag pensionssparar inte i lika hög utsträckning som män som driver företag, 56 respektive
Laborationspecifikation
 UMEÅ UNIVERSITET Institutionen för matematik och matematisk statistisk Statistik för tekniska datavetare 5 poäng Per Arnqvist 2007-05-03 Laborationspecifikation Redovisning Ni får gärna jobba parvis och
UMEÅ UNIVERSITET Institutionen för matematik och matematisk statistisk Statistik för tekniska datavetare 5 poäng Per Arnqvist 2007-05-03 Laborationspecifikation Redovisning Ni får gärna jobba parvis och
x 2 + px = ( x + p 2 x 2 2x = ( x + 2
 Inledande kurs i matematik, avsnitt P.3 P.3. Bestäm en ekvation för cirkeln med mittpunkt i (0, 0) och radie 4. Med hjälp av kvadratkompletteringsformeln + p = ( + p ) ( p ) En cirkel med mittpunkt i (
Inledande kurs i matematik, avsnitt P.3 P.3. Bestäm en ekvation för cirkeln med mittpunkt i (0, 0) och radie 4. Med hjälp av kvadratkompletteringsformeln + p = ( + p ) ( p ) En cirkel med mittpunkt i (
Friskoleurval med segregation som resultat
 Friskoleurval med segregation som resultat Rapport februari 2016 Sammanfattning och slutsatser Denna undersökning har tagits fram som en del av projektet Ge alla elever samma chans som är ett samarbete
Friskoleurval med segregation som resultat Rapport februari 2016 Sammanfattning och slutsatser Denna undersökning har tagits fram som en del av projektet Ge alla elever samma chans som är ett samarbete
Svenska Du kan med flyt läsa texter som handlar om saker du känner till. Du använder metoder som fungerar. Du kan förstå vad du läser.
 Svenska Du kan med flyt läsa texter som handlar om saker du känner till. Du använder metoder som fungerar. Du kan förstå vad du läser. Du berättar på ett enkelt sätt om det du tycker är viktigt i texten.
Svenska Du kan med flyt läsa texter som handlar om saker du känner till. Du använder metoder som fungerar. Du kan förstå vad du läser. Du berättar på ett enkelt sätt om det du tycker är viktigt i texten.
2005-01-31. Hävarmen. Peter Kock
 2005-01-31 Hävarmen Kurs: WT0010 Peter Kock Handledare: Jan Sandberg Sammanfattning Om man slår upp ordet hävarm i ett lexikon så kan man läsa att hävarm är avståndet mellan kraften och vridningspunkten.
2005-01-31 Hävarmen Kurs: WT0010 Peter Kock Handledare: Jan Sandberg Sammanfattning Om man slår upp ordet hävarm i ett lexikon så kan man läsa att hävarm är avståndet mellan kraften och vridningspunkten.
Avsikt På ett lekfullt sätt färdighetsträna, utveckla elevers känsla för hur vårt talsystem är uppbyggt samt hitta mönster som uppkommer.
 Strävorna 4A 100-rutan... förmåga att förstå, föra och använda logiska resonemang, dra slutsatser och generalisera samt muntligt och skriftligt förklara och argumentera för sitt tänkande.... grundläggande
Strävorna 4A 100-rutan... förmåga att förstå, föra och använda logiska resonemang, dra slutsatser och generalisera samt muntligt och skriftligt förklara och argumentera för sitt tänkande.... grundläggande
Har du förstått? I De här talen är primtal a) 29,49 och 61 b) 97, 83 och 89 c) 0, 2 och 3.
 PASS 5. FAKTORISERING AV POLYNOM 5. Nyttan av faktorisering och faktorisering av heltal Har vi nytta av att kunna faktorisera polynom? Ja det har vi. Bra kunskaper i faktorisering av polynom möjliggör
PASS 5. FAKTORISERING AV POLYNOM 5. Nyttan av faktorisering och faktorisering av heltal Har vi nytta av att kunna faktorisera polynom? Ja det har vi. Bra kunskaper i faktorisering av polynom möjliggör
[ÖVNINGSBANK] Sollentuna FK. Expressbollen
![[ÖVNINGSBANK] Sollentuna FK. Expressbollen [ÖVNINGSBANK] Sollentuna FK. Expressbollen](/thumbs/41/22376262.jpg) Expressbollen Övning nr. 1 Två lag på varje långlinje i en rektangel på 15x25 meter. o T.ex. Halv gympasal o Viktigt att vara tydlig med mitten, d.v.s. markera mitten med koner Varje spelare har en boll.
Expressbollen Övning nr. 1 Två lag på varje långlinje i en rektangel på 15x25 meter. o T.ex. Halv gympasal o Viktigt att vara tydlig med mitten, d.v.s. markera mitten med koner Varje spelare har en boll.
MRSA. Information till patienter och närstående
 MRSA Information till patienter och närstående I denna folder får Du några svar och dessutom tips om vem Du kan vända Dig till med fler frågor Smittad av MRSA? Vem kan Du fråga och vart kan Du vända Dig?
MRSA Information till patienter och närstående I denna folder får Du några svar och dessutom tips om vem Du kan vända Dig till med fler frågor Smittad av MRSA? Vem kan Du fråga och vart kan Du vända Dig?
De två första korten Tidig position
 De två första korten Tidig position Hold em är ett positionsspel, och förmodligen mer än någon annan form av poker. Det beror på att knappen anger spelarnas turordning under satsningsrundorna. (Enda undantaget
De två första korten Tidig position Hold em är ett positionsspel, och förmodligen mer än någon annan form av poker. Det beror på att knappen anger spelarnas turordning under satsningsrundorna. (Enda undantaget
STATISTIK. Statistik är: 1. Insamling av data 2. Analys av data 3. Presentation av data. tomas.persson@edu.uu.se
 STATISTIK Statistik är: 1. Insamling av data 2. Analys av data 3. Presentation av data tomas.persson@edu.uu.se Insamling av data Tänk efter först! Samla sedan in data. Om du vill att eleverna skall undersöka
STATISTIK Statistik är: 1. Insamling av data 2. Analys av data 3. Presentation av data tomas.persson@edu.uu.se Insamling av data Tänk efter först! Samla sedan in data. Om du vill att eleverna skall undersöka
KTHs Matematiska Cirkel. Sannolikhetsteori. Joakim Arnlind Andreas Enblom
 KTHs Matematiska Cirkel Sannolikhetsteori Joakim Arnlind Andreas Enblom Institutionen för matematik, 2007 Finansierat av Marianne och Marcus Wallenbergs Stiftelse Innehåll 1 Mängdlära 1 1.1 Mängder...............................
KTHs Matematiska Cirkel Sannolikhetsteori Joakim Arnlind Andreas Enblom Institutionen för matematik, 2007 Finansierat av Marianne och Marcus Wallenbergs Stiftelse Innehåll 1 Mängdlära 1 1.1 Mängder...............................
Manpower Work Life: 2014:1. Manpower Work Life. Rapport 2014. Mångfald på jobbet
 Manpower Work Life: 2014:1 Manpower Work Life Rapport 2014 Mångfald på jobbet MÅNGFALD PÅ JOBBET Mångfald diskuteras ständigt i media, men hur ser det egentligen ut på Sveriges arbetsplatser? Hur ser svenska
Manpower Work Life: 2014:1 Manpower Work Life Rapport 2014 Mångfald på jobbet MÅNGFALD PÅ JOBBET Mångfald diskuteras ständigt i media, men hur ser det egentligen ut på Sveriges arbetsplatser? Hur ser svenska
Matematikboken. alfa. Lennart Undvall Christina Melin Jenny Ollén
 Matematikboken alfa Lennart Undvall Christina Melin Jenny Ollén Matematikboken Alfa ISBN 978-91-47-10193-1 Författare: Lennart Undvall, Christina Melin och Jenny Ollén 2011 författarna och Liber AB Illustrationer:
Matematikboken alfa Lennart Undvall Christina Melin Jenny Ollén Matematikboken Alfa ISBN 978-91-47-10193-1 Författare: Lennart Undvall, Christina Melin och Jenny Ollén 2011 författarna och Liber AB Illustrationer:
