UPPGIFT 1 KANINER. Håkan Strömberg 1 Pär Söderhjelm
|
|
|
- Amanda Agneta Åkesson
- för 7 år sedan
- Visningar:
Transkript
1 UPPGIFT 1 KANINER Kaniner är bra på att föröka sig. I den här uppgiften tänker vi oss att det finns obegränsat med hannar och att inga kaniner dör. Vi ska försöka simulera hur många kaninhonor det finns efter varje månad om det vid tiden 0 finns en enda nyfödd kaninhona. Vi antar att det tar x månader innan varje kaninhona är könsmogen och att hon från och med denna ålder (x månader) varje månad föder en kull innehållande y kaninungar av honkön. Indata: Programmet ska fråga efter honornas könsmognadsålder x, 1 x 5, samt antal honor per kull y, 1 y 5. Utdata: Programmet ska skriva en rad för varje månad under totalt 10 månader Könsmognadsålder? 2 Honor per kull? 1 Efter 1 m: 1 Efter 2 m: 2 Efter 3 m: 3 Efter 4 m: 5 Efter 5 m: 8 Efter 6 m: 13 Efter 7 m: 21 Efter 8 m: 34 Efter 9 m: 55 Efter 10 m: 89 Förklaring: Från början finns 1 nyfödd hona, låt oss kalla henne Lisa. Efter 1 månad är Lisa fortfarande ensam. Efter 2 månader har Lisa fått en kull. Efter 3 månader finns 3 honor eftersom Lisa fått ytterligare en kull. Efter 4 månader finns 5 honor eftersom både Lisa och hennes första unge har fått varsin kull med en hona i varje. Håkan Strömberg 1 Pär Söderhjelm
2 UPPGIFT 2 SIFFERTRIANGELN FIGUR 1. De tio siffrorna har i figur 1 ordnats i en triangel. Summan av de fyra talen utefter var och en av triangelns tre sidor är alla 17. Talet 6, i mitten, deltar inte i någon av summorna. Skriv ett program, som för en given centrumsiffra, beräknar antalet sätt på vilket man kan ordna talen i triangeln, så att summorna av talen utefter sidorna alla blir lika. Indata: Programmet frågar efter den siffra, som ska vara placerad i triangelns centrum. Utdata: Antalet möjligheter att placera de övriga 9 siffrorna så att de tre summorna blir lika. Centrumsiffra? 6 Det finns 720 möjligheter Förklaring: Här räknar vi alla arrangemang som olika, även om det finns speglingar eller rotationer som påminner om varandra. Håkan Strömberg 2 Pär Söderhjelm
3 UPPGIFT 3 TELEFONNUMMER FIGUR 2. Så här är siffrorna placerade på Lars telefon Lars ska byta telefonnummer. Telefonbolaget har givit honom en obruten följd av lediga telefonnummer att välja mellan, men han behöver hjälp av dig. Lars tycker nämligen inte om när telefonen ringer så han vill ha det nummer som kräver den längsta förflyttningen av fingret på en knapptelefon, i hopp om att detta ska avskräcka folk från att ringa. Om det finns flera nummer som ger den längsta sträckan vill han ha det nummer som har flest olika siffror, eftersom det då är större chans att folk glömmer bort numret. Knapparnas placering visas i figur 2. För att beräkna den fingerförflyttning som krävs för att slå ett nummer startar vi med fingret på första siffran i numret. För att komma till nästa siffra flyttar vi fingret så få steg som möjligt, där varje steg kan vara en knapp uppåt, enknappneråt, enknappåt höger eller en knapp åt vänster. Den totala förflyttningen för ett n-siffrigt telefonnummer är en summa av n 1 sådana minimala förflyttningar. Exempelvis kräver numret totalt = 10 steg. Indata: Programmet ska fråga efter ett start- och ett slutnummer. Dessa och alla mellanliggande nummer är de lediga numren. Du kan räkna med att start- och slutnumret har samma antal siffror och att inget av dem börjar med 0. Antalet siffror kan variera mellan 2 (i Älgträsk) och 7 (i Stockholm). Utdata: Programmet ska skriva det telefonnummer som kräver flest förflyttningssteg. Om flera olika nummer ger detta maximala antal steg, ska du välja det som innehåller det största antalet olika siffror. Om det finns flera nummer med både maximalt antal steg och maximalt antal olika siffror kan du skriva vilket som helst av dem. Startnummer? 462 Slutnummer? 466 Bästa telefonnumret: 462 Förklaring: Både 462 och 464 kräver 4 steg men 462 innehåller tre olika siffror medan 464 bara innehåller två. De andra numren kräver 3 steg (463 och 465) respektive 2 steg (466) och är sålunda sämre. Håkan Strömberg 3 Pär Söderhjelm
4 UPPGIFT 4 SPEL MED BRICKOR FIGUR 3. Figur 3 ska föreställa två högar av brickor. I den ena finns 7 och i den andra 5. Två spelare turas om att göra drag, där det, för att vinna gäller att ta bort den eller de sista brickorna. I varje drag kan spelaren vid draget, antingen ta bort så många brickor han vill från en hög. Spelaren väljer vilken. eller ta bort så många brickor han vill från båda högarna, mendålika många från varje Skriv ett program som avgör om en given ställning är en vinst- eller förlustställning för den spelare som ska börja, under förutsättning att båda spelarna spelar optimalt. Input: Antalet brickor n ½ och n ¾ idebådahögarna1 n ½,n ¾ 10. Utdata: Texten VINST om inmatad ställning är en vinstställning eller texten FÖRLUST, om det är fråga om en förlustställning för spelaren som ska börja. Antal brickor i den ena högen? 7 Antal brickor i den andra högen? 5 VINST Förklaring: Spelet som presenterats ovan kan inte sluta oavgjort. Detta betyder att varje ställning är en vinst- eller förlustställning för spelaren vid draget. Den som har en vinstställning kan aldrig bli tvingad till ett drag, som leder till en förlustställning för denne, på samma sätt, som att den spelare som har en förlustställning, inte kan finna något drag som leder till en vinstställning för denne. Håkan Strömberg 4 Pär Söderhjelm
5 UPPGIFT 5 GIN RUMMY FIGUR 4. Gin Rummy är ett kortspel för två spelare, där en vanlig kortlek används. Varje spelare får 10 kort i given och målet är att kombinera dessa kort i bilder. Innan vi går vidare i texten definierar vi kortens beteckningar. Varje kort beskrivs med två tecken. Det första betecknar färg och det andra valör. I tredje raden ges kortens belastningsvärde. Spader Hjärter Ruter Klöver Äss Knekt Dam Kung S H D C E T J Q K En bild är något av följande två alternativ: 3 eller 4 kort av samma valör. Till exempel tre kungar, HK SK DK eller fyra femmor S5 C5 D5 H5. 3 eller fler kort i sekvens isammafärg.tillexempelc3 C4 C5, D8 D9 DT DJ eller CE C2 C3 C4 C5. Ässet är det lägsta kortet i en sekvens och Kungen det högsta. Man kan inte gå runt hörnet, HD HK HE är därför ingen giltig sekvens. Spelaren vid tur tar upp ett kort från talongen och har just då 11 kort på handen. Genom att kombinera 10 av dessa kort i bilder på ett så fördelaktigt sätt som möjligt och kasta ett valfritt kort på högen försöker spelaren minimera handens sammanlagda belastningsvärde de sammanlagda belastningsvärdena hos de kort, som inte ingår i bilder och som inte heller är det kastade kortet. Skriv ett program som tar emot uppgift om handens 11 kort och som kombinerar dem på ett sätt som minimerar det sammanlagda belastningsvärdet. Indata: Handens utseende i form av 11 strängar, en för varje kort. Strängarna består av två tecken enligt reglerna ovan. Utdata: Det minsta sammanlagda belastningsvärdet, som kan åstadkommas för inmatad hand. för handen i figur 4, S4 S8 D5 S6 H7 D3 D4 D7 C4 S7 D6 Kort 1? S4 Kort 2? S8... Kort 11? D6 Belastningsvärdet 3 Förklaring: Genom att kasta H7 och kombinera bilderna S4 D4 C4, S6 S7 S8 och D5 D6 D7 blir endast D3 över vilket ger belastningsvärdet 3. Håkan Strömberg 5 Pär Söderhjelm
6 UPPGIFT 6 TÄNDSTICKSFIGURER FIGUR 5. Rad 1: En godkänd tändsticksfigur med 6 stickor. Rad 2: A och B anses identiska i detta problem. Rad 3: C och D är däremot inte identiska. Rad 4: E är grenad och därför ej godkänd. F vidrör sig själv och är därför heller inte godkänd Om man lägger ett antal tändstickor efter varandra som på bilden ovan uppstår ormliknande figurer. I den här uppgiften ska du svara på hur många olika figurer du kan konstruera med ett givet antal tändstickor. Endast räta vinklar får förekomma och figuren får inte vara grenad eller vidröra sig själv. Om det går att rotera en figur så att den blir identisk med en annan anses dessa två figurer vara samma, och ska därför bara räknas en gång (se A och B i figuren). Om man måste spegelvända den ena figuren för att den ska bli identisk med den andra är figurerna däremot olika (se C och D i figuren). Indata: Programmet ska fråga efter antal tändstickor n, där1 n 15 Utdata: Programmet ska skriva ut hur många olika figurer som kan konstrueras med n tändstickor. Detta tal är alltid mindre än en miljon. Antal tändstickor? 3 Möjliga figurer? 6 Håkan Strömberg 6 Pär Söderhjelm
Programmeringsolympiaden 2008 Kvalificering
 Programmeringsolympiaden 2008 Kvalificering TÄVLINGSREGLER Tävlingen äger rum på ett av skolan bestämt datum under sex timmar effektiv tid. Tävlingen består av sex uppgifter som samtliga ska lösas genom
Programmeringsolympiaden 2008 Kvalificering TÄVLINGSREGLER Tävlingen äger rum på ett av skolan bestämt datum under sex timmar effektiv tid. Tävlingen består av sex uppgifter som samtliga ska lösas genom
75059 Stort sorteringsset
 75059 Stort sorteringsset Aktivitetsguide Detta set innehåller: 632 st sorteringsföremål 3 st snurror 6 st sorteringsskålar 1 st sorteringsbricka i plast 1 st siffertärning Detta sorteringsset har tagits
75059 Stort sorteringsset Aktivitetsguide Detta set innehåller: 632 st sorteringsföremål 3 st snurror 6 st sorteringsskålar 1 st sorteringsbricka i plast 1 st siffertärning Detta sorteringsset har tagits
1.5 Vad är sannolikheten för att ett slumpvis draget spelkort ska vara femma eller lägre eller knekt, dam, kung eller äss?
 1 ÖVNINGAR I INDUKTIV LOGIK 1.1 En tärning kastas. Ange sannolikheten för att antalet ögon är a) 3 b) inte 3 c) 3 eller 5 d) jämnt e) mindre än 4 f) jämnt och mindre än 4 g) jämnt eller mindre än 4 h)
1 ÖVNINGAR I INDUKTIV LOGIK 1.1 En tärning kastas. Ange sannolikheten för att antalet ögon är a) 3 b) inte 3 c) 3 eller 5 d) jämnt e) mindre än 4 f) jämnt och mindre än 4 g) jämnt eller mindre än 4 h)
UPPGIFT 2 KVADRATVANDRING
 UPPGIFT 1 LYCKOTAL Lyckotal är en serie heltal, som hittas på följande sätt. Starta med de naturliga talen: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13... Sök upp det första talet i serien, som är större
UPPGIFT 1 LYCKOTAL Lyckotal är en serie heltal, som hittas på följande sätt. Starta med de naturliga talen: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13... Sök upp det första talet i serien, som är större
Problem: BOW Bowling. Regler för Bowling. swedish. BOI 2015, dag 1. Tillgängligt minne: 256 MB. 30.04.2015
 Problem: BOW Bowling swedish BOI 0, dag. Tillgängligt minne: 6 MB. 30.04.0 Byteasar tycker om både bowling och statistik. Han har skrivit ner resultatet från några tidigare bowlingspel. Tyvärr är några
Problem: BOW Bowling swedish BOI 0, dag. Tillgängligt minne: 6 MB. 30.04.0 Byteasar tycker om både bowling och statistik. Han har skrivit ner resultatet från några tidigare bowlingspel. Tyvärr är några
Spelregler. 2-6 deltagare från 10 år. En svensk spelklassiker
 En svensk spelklassiker Spelregler 2-6 deltagare från 10 år Innehåll: 1 spelplan, korthållare, 2 tärningar, 6 spelpjäser, 21 aktier, 20 lagfartsbevis, 12 obligationer, 21 finanstidningar, 40 börstips,
En svensk spelklassiker Spelregler 2-6 deltagare från 10 år Innehåll: 1 spelplan, korthållare, 2 tärningar, 6 spelpjäser, 21 aktier, 20 lagfartsbevis, 12 obligationer, 21 finanstidningar, 40 börstips,
Uppgift 1. Kylskåpstransporter
 Uppgift 1. Kylskåpstransporter 1. Här kan du se de två bilarna lastade med kylskåp på väg mot stormarknaden En fabrik som tillverkar kylskåp ska leverera ett större parti med n, 1 n 1000, kylar till en
Uppgift 1. Kylskåpstransporter 1. Här kan du se de två bilarna lastade med kylskåp på väg mot stormarknaden En fabrik som tillverkar kylskåp ska leverera ett större parti med n, 1 n 1000, kylar till en
Programmeringsolympiaden 2012 Kvalificering
 Programmeringsolympiaden 2012 Kvalificering TÄVLINGSREGLER Tävlingen äger rum på ett av skolan bestämt datum under sex timmar effektiv tid. Tävlingen består av sex uppgifter som samtliga ska lösas genom
Programmeringsolympiaden 2012 Kvalificering TÄVLINGSREGLER Tävlingen äger rum på ett av skolan bestämt datum under sex timmar effektiv tid. Tävlingen består av sex uppgifter som samtliga ska lösas genom
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs B, kapitel 1
 Här presenteras förslag på lösningar och tips till många uppgifter i läroboken Matematik 3000 kurs B som vi hoppas kommer att vara till hjälp när du arbetar dig framåt i kursen. Vi har valt att inte göra
Här presenteras förslag på lösningar och tips till många uppgifter i läroboken Matematik 3000 kurs B som vi hoppas kommer att vara till hjälp när du arbetar dig framåt i kursen. Vi har valt att inte göra
UPPGIFT 1 V75 FIGUR 1.
 UPPGIFT 1 V75 FIGUR 1. Varje lördag året om spelar tusentals svenskar på travspelet V75. Spelet går ut på att finna sju vinnande hästar i lika många lopp. Lopp 1: 5 7 Lopp 2: 1 3 5 7 8 11 Lopp 3: 2 9 Lopp
UPPGIFT 1 V75 FIGUR 1. Varje lördag året om spelar tusentals svenskar på travspelet V75. Spelet går ut på att finna sju vinnande hästar i lika många lopp. Lopp 1: 5 7 Lopp 2: 1 3 5 7 8 11 Lopp 3: 2 9 Lopp
Programmering Grundkurs (6H2950) Grundläggande Programmering (6A2001)
 Programmering Grundkurs (6H2950) Grundläggande Programmering (6A2001) Skrivtid: 8:15-13:15 Datum: Måndagen 2005-03-07 Tentamen består av 7 sidor Hjälpmedel: Förutom dator med installerad Borland C++ 5.02,
Programmering Grundkurs (6H2950) Grundläggande Programmering (6A2001) Skrivtid: 8:15-13:15 Datum: Måndagen 2005-03-07 Tentamen består av 7 sidor Hjälpmedel: Förutom dator med installerad Borland C++ 5.02,
Spelregler för Vira. Åstols Vira- och Bandyklubb 2006
 Spelregler för Vira Åstols Vira- och Bandyklubb 2006 Innehåll 1. Inledning... 3 1.1. Vira...3 2. Speltyper... 4 2.1. Gaskspel...4 2.2. Köpspel...5 2.3. Solospel...7 3. Spelparti... 8 3.1. Medlem...8 3.2.
Spelregler för Vira Åstols Vira- och Bandyklubb 2006 Innehåll 1. Inledning... 3 1.1. Vira...3 2. Speltyper... 4 2.1. Gaskspel...4 2.2. Köpspel...5 2.3. Solospel...7 3. Spelparti... 8 3.1. Medlem...8 3.2.
SPELREGLER. 2-4 deltagare från 10 år
 SPELREGLER 2-4 deltagare från 10 år Fläta samman orden i Alfapet! Med hjälp av bokstavsbrickor och god uppfinningsrikedom bildar ni ord kors och tvärs över spelplanen. Prova gärna spelvarianter där ni
SPELREGLER 2-4 deltagare från 10 år Fläta samman orden i Alfapet! Med hjälp av bokstavsbrickor och god uppfinningsrikedom bildar ni ord kors och tvärs över spelplanen. Prova gärna spelvarianter där ni
Skriv ut korten. Laminera dem gärna. Då håller de längre och kan användas om igen. Klipp ut dem och lägg de röda respektive de gröna i var sin ask.
 RYGG Koppla ihop - Samarbetsövning Ett exempel på kort Förberedelser: Skriv ut korten. Laminera dem gärna. Då håller de längre och kan användas om igen. Klipp ut dem och lägg de röda respektive de gröna
RYGG Koppla ihop - Samarbetsövning Ett exempel på kort Förberedelser: Skriv ut korten. Laminera dem gärna. Då håller de längre och kan användas om igen. Klipp ut dem och lägg de röda respektive de gröna
Problem 1 2 3 4 5 6 7 Svar
 Känguru Cadet, svarsblankett Namn Klass/Grupp Poängsumman Känguruskuttet Ta lös svarsblanketten. Skriv ditt svarsalternativ under numret. Lämna rutan tom om du inte vet svaret. Gissa inte, felaktigt svar
Känguru Cadet, svarsblankett Namn Klass/Grupp Poängsumman Känguruskuttet Ta lös svarsblanketten. Skriv ditt svarsalternativ under numret. Lämna rutan tom om du inte vet svaret. Gissa inte, felaktigt svar
Pernilla Falck Margareta Picetti Siw Elofsdotter Meijer. Matte. Safari. Direkt. Lärarhandledning. Andra upplagan, reviderade sidor
 Matte Direkt Pernilla Falck Margareta Picetti Siw Elofsdotter Meijer Safari 1A Lärarhandledning MS Enhetsdel Sist i varje kapitel finns ett avsnitt som i första hand tar upp enheter. Här i årskurs 1 handlar
Matte Direkt Pernilla Falck Margareta Picetti Siw Elofsdotter Meijer Safari 1A Lärarhandledning MS Enhetsdel Sist i varje kapitel finns ett avsnitt som i första hand tar upp enheter. Här i årskurs 1 handlar
ZÄTA FÄRGCHANSEN CHANSE 58:AN UTSPELET CHANSEN TREKLÖVERN ZÄTA CHANSEN 58:AN. Spelmeny ANGERED - ALINGSÅS. www.idrottensbingo.se
 CHANS TREKLÖVERN ZÄTA FÄRGCHANSEN CHANSEN 58:AN UTSPELET CHANSEN TREKLÖVE ZÄTA FÄRGCH CHANSE 58:AN UTSP Spelmeny ANGERED - ALINGSÅS www.idrottensbingo.se Innehållsförteckning ALLMÄN INFORMATION... sidan
CHANS TREKLÖVERN ZÄTA FÄRGCHANSEN CHANSEN 58:AN UTSPELET CHANSEN TREKLÖVE ZÄTA FÄRGCH CHANSE 58:AN UTSP Spelmeny ANGERED - ALINGSÅS www.idrottensbingo.se Innehållsförteckning ALLMÄN INFORMATION... sidan
UPPGIFT 1 ÖVERSÄTTNING
 UPPGIFT 1 ÖVERSÄTTNING Fikonspråket är ett hemligt språk med gamla anor som till och med har givit upphov till vissa svenska ord, till exempel fimp (fikonspråkets fimpstukon betyder stump). Rövarspråket
UPPGIFT 1 ÖVERSÄTTNING Fikonspråket är ett hemligt språk med gamla anor som till och med har givit upphov till vissa svenska ord, till exempel fimp (fikonspråkets fimpstukon betyder stump). Rövarspråket
Stockholms Wirasällskaps
 Stockholms Wirasällskaps regler för vira Inledning Vira är ett klassiskt svenskt kortspel, som enligt en muntlig tradition uppfanns vid ett vinterting i Vira bruk i Roslagen cirka 1810. Spelet blev en
Stockholms Wirasällskaps regler för vira Inledning Vira är ett klassiskt svenskt kortspel, som enligt en muntlig tradition uppfanns vid ett vinterting i Vira bruk i Roslagen cirka 1810. Spelet blev en
Känguru 2014 Benjamin (Åk 6 och 7) sida 1 / 7 och Pakilan ala-aste
 (Åk 6 och 7) sida 1 / 7 och Pakilan ala-aste NAMN KLASS Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Felaktigt svar ger minus 1/4 poäng av uppgiftens
(Åk 6 och 7) sida 1 / 7 och Pakilan ala-aste NAMN KLASS Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Felaktigt svar ger minus 1/4 poäng av uppgiftens
Nationell simultantävling
 Nationell simultantävling Givsamling 7 oktober 2014 Kommentarer av Bertil G Johnson VENKA BRIDGEFÖRBUNDET Nordisk tandard Kommentarerna till simultantävlingarna baseras på budsystemet Nordisk tandard.
Nationell simultantävling Givsamling 7 oktober 2014 Kommentarer av Bertil G Johnson VENKA BRIDGEFÖRBUNDET Nordisk tandard Kommentarerna till simultantävlingarna baseras på budsystemet Nordisk tandard.
Välkommen till ett Bondespel i tiden.
 2-5 SPELARE FRÅN 10 ÅR Välkommen till ett Bondespel i tiden. Spelplanen och kortillustrationerna i denna jubileumsutgåva kommer från en svunnen tid. Penningsvärdet har däremot räknats upp till en nivå
2-5 SPELARE FRÅN 10 ÅR Välkommen till ett Bondespel i tiden. Spelplanen och kortillustrationerna i denna jubileumsutgåva kommer från en svunnen tid. Penningsvärdet har däremot räknats upp till en nivå
Seriehantering. [En enkel guide för hur du som serieadministratör använder SVEMO TA.]
![Seriehantering. [En enkel guide för hur du som serieadministratör använder SVEMO TA.] Seriehantering. [En enkel guide för hur du som serieadministratör använder SVEMO TA.]](/thumbs/39/18224207.jpg) 2013 Svenska Motorcykel- och Snöskoterförbundet Box 2314 600 02 NORRKÖPING Tel. 011-23 10 80 www.svemo.se Seriehantering [En enkel guide för hur du som serieadministratör använder SVEMO TA.] Innehåll Inledning...
2013 Svenska Motorcykel- och Snöskoterförbundet Box 2314 600 02 NORRKÖPING Tel. 011-23 10 80 www.svemo.se Seriehantering [En enkel guide för hur du som serieadministratör använder SVEMO TA.] Innehåll Inledning...
4-7 Pythagoras sats. Inledning. Namn:..
 Namn:.. 4-7 Pythagoras sats Inledning Nu har du lärt dig en hel del om trianglar. Du vet vad en spetsig och en trubbig triangel är liksom vad en liksidig och en likbent triangel är. Vidare vet du att vinkelsumman
Namn:.. 4-7 Pythagoras sats Inledning Nu har du lärt dig en hel del om trianglar. Du vet vad en spetsig och en trubbig triangel är liksom vad en liksidig och en likbent triangel är. Vidare vet du att vinkelsumman
Lösning till Sommarnötter 2010 Carl Ragnarsson
 till Sommarnötter 2010 Carl Ragnarsson Giv 1 (nivå 1 för nybörjaren) EKDkn109 82 EK2 43 EK 432 K2 E76543 Väst spelar 7, utspel 3. Hur bör spelet läggas upp? Först och främst ska spelföraren räkna sina
till Sommarnötter 2010 Carl Ragnarsson Giv 1 (nivå 1 för nybörjaren) EKDkn109 82 EK2 43 EK 432 K2 E76543 Väst spelar 7, utspel 3. Hur bör spelet läggas upp? Först och främst ska spelföraren räkna sina
Föreläsning 11. Giriga algoritmer
 Föreläsning 11 Giriga algoritmer Föreläsning 11 Giriga algoritmer Användning Växelproblemet Kappsäcksproblemet Schemaläggning Färgläggning Handelsresandeproblemet Uppgifter Giriga algoritmer (Greedy algorithms)
Föreläsning 11 Giriga algoritmer Föreläsning 11 Giriga algoritmer Användning Växelproblemet Kappsäcksproblemet Schemaläggning Färgläggning Handelsresandeproblemet Uppgifter Giriga algoritmer (Greedy algorithms)
Förberedelser: Sätt upp konerna i stigande ordningsföljd (första inlärningen) eller i blandad ordningsföljd (för de elever som kommit längre).
 Räkna till 10 Mål: Eleverna skall kunna räkna till 10, i stigande och sjunkande ordningsföljd. Antal elever: minst 10 elever. Koner med talen 1 till 10.( använd konöverdrag och skriv 10 på en lapp på 0-käglan)
Räkna till 10 Mål: Eleverna skall kunna räkna till 10, i stigande och sjunkande ordningsföljd. Antal elever: minst 10 elever. Koner med talen 1 till 10.( använd konöverdrag och skriv 10 på en lapp på 0-käglan)
I rött och svart. Andreas Sölvebring
 Andreas Sölvebring April 2012 Innehåll Förberedelser 2 Introduktion............................... 2 Om spelet................................ 2 Skapa roller............................... 3 Skapa konflikter.............................
Andreas Sölvebring April 2012 Innehåll Förberedelser 2 Introduktion............................... 2 Om spelet................................ 2 Skapa roller............................... 3 Skapa konflikter.............................
Föreläsning 4: Giriga algoritmer. Giriga algoritmer
 Föreläsning 4: Giriga algoritmer Giriga algoritmer Denna typ av algoritmer arbetar efter följande princip: Gör i varje situation det som är lokalt optimalt, d.v.s. bäst för stunden. Några exempel vi redan
Föreläsning 4: Giriga algoritmer Giriga algoritmer Denna typ av algoritmer arbetar efter följande princip: Gör i varje situation det som är lokalt optimalt, d.v.s. bäst för stunden. Några exempel vi redan
52101 Utforska siffror
 52101 Utforska siffror Innehåll: 1 uppsättning brickor, numrerade från 1 till 24 1 uppsättning räknebrickor 1 uppsättning med 30 stora siffror plastdjur 4 blanka brickor en låda med lock kopieringsbara
52101 Utforska siffror Innehåll: 1 uppsättning brickor, numrerade från 1 till 24 1 uppsättning räknebrickor 1 uppsättning med 30 stora siffror plastdjur 4 blanka brickor en låda med lock kopieringsbara
Kombinatorik. Författarna och Bokförlaget Borken, 2011. Kombinatorik - 1
 Kombinatorik Teori Multiplikationsprincipen..2 Teori Permutationer 3 Teori Kombinationer...5 Modell Dragning utan återläggning & sannolikheter 8 Teori Duvslageprincipen 11 Teori Pascals triangel & Mosertal...13
Kombinatorik Teori Multiplikationsprincipen..2 Teori Permutationer 3 Teori Kombinationer...5 Modell Dragning utan återläggning & sannolikheter 8 Teori Duvslageprincipen 11 Teori Pascals triangel & Mosertal...13
Handbok Kiriki. Albert Astals Cid Eugene Trounev Översättare: Stefan Asserhäll
 Albert Astals Cid Eugene Trounev Översättare: Stefan Asserhäll 2 Innehåll 1 Inledning 5 2 Hur man spelar 6 3 Spelets regler, strategi och tips 8 3.1 Spelregler..........................................
Albert Astals Cid Eugene Trounev Översättare: Stefan Asserhäll 2 Innehåll 1 Inledning 5 2 Hur man spelar 6 3 Spelets regler, strategi och tips 8 3.1 Spelregler..........................................
Kurvlängd och geometri på en sfärisk yta
 325 Kurvlängd och geometri på en sfärisk yta Peter Sjögren Göteborgs Universitet 1. Inledning. Geometrin på en sfärisk yta liknar planets geometri, med flera intressanta skillnader. Som vi skall se nedan,
325 Kurvlängd och geometri på en sfärisk yta Peter Sjögren Göteborgs Universitet 1. Inledning. Geometrin på en sfärisk yta liknar planets geometri, med flera intressanta skillnader. Som vi skall se nedan,
Nummerserie Lediga Vilande Återlämnade 070 (1994/2007) 10 000 200 108 200
 PROMEMORIA Datum Vår referens Sida 2015-12-15 Dnr: 15-11341 1(11) Nätsäkerhetsavdelningen Susanne Chennell 08 678 55 73 susanne.chennell@pts.se Mobilnummerstrategi 1.1 Bakgrund PTS fastställde den 25 november
PROMEMORIA Datum Vår referens Sida 2015-12-15 Dnr: 15-11341 1(11) Nätsäkerhetsavdelningen Susanne Chennell 08 678 55 73 susanne.chennell@pts.se Mobilnummerstrategi 1.1 Bakgrund PTS fastställde den 25 november
Sannolikhetslära. 1 Grundläggande begrepp. 2 Likformiga sannolikhetsfördelningar. Marco Kuhlmann
 Marco Kuhlmann Detta är en kompakt sammanfattning av momentet sannolikhetslära som ingår i kurserna Matematik 1b och 1c på gymnasiet. I slutet av dokumentet hittar du uppgifter med vilka du kan testa om
Marco Kuhlmann Detta är en kompakt sammanfattning av momentet sannolikhetslära som ingår i kurserna Matematik 1b och 1c på gymnasiet. I slutet av dokumentet hittar du uppgifter med vilka du kan testa om
Clicker 5. Lathund kring de vanligaste och mest grundläggande funktionerna för att komma igång med Clicker. Habilitering & Hjälpmedel
 Clicker 5 Lathund kring de vanligaste och mest grundläggande funktionerna för att komma igång med Clicker. Habilitering & Hjälpmedel Vad är Clicker 5? Clicker 5 är ett stöd till personer i behov av extra
Clicker 5 Lathund kring de vanligaste och mest grundläggande funktionerna för att komma igång med Clicker. Habilitering & Hjälpmedel Vad är Clicker 5? Clicker 5 är ett stöd till personer i behov av extra
Uppgift 1 (Oläsliga krypterade meddelanden)
 Uppgift 1 (Oläsliga krypterade meddelanden) Ofta vill man kryptera text för att inte andra skall se vad man skrivit. I den givna filen KRYPTERAD_TEXT.TXT finns en krypterad text som kan vara av intresse
Uppgift 1 (Oläsliga krypterade meddelanden) Ofta vill man kryptera text för att inte andra skall se vad man skrivit. I den givna filen KRYPTERAD_TEXT.TXT finns en krypterad text som kan vara av intresse
Årtalet: 1855. Platsen: Amerikanska västern.
 [pg 1] Claim It! Lycksökarspelet för 2-5 spelare, ålder: från 8 år. Årtalet: 1855. Platsen: Amerikanska västern. Du är en guldgrävare som stakar ut sitt område och försvarar det mot rivaler och andra motståendare.
[pg 1] Claim It! Lycksökarspelet för 2-5 spelare, ålder: från 8 år. Årtalet: 1855. Platsen: Amerikanska västern. Du är en guldgrävare som stakar ut sitt område och försvarar det mot rivaler och andra motståendare.
Användarkort för Business Communications Manager Telefonisttelefon
 Användarkort för Business Communications Manager Telefonisttelefon 2001 Nortel Networks P0941619 Utgåva 01 Använda telefonisttelefonen Din telefon har programmerats som telefonisttelefon för specifika
Användarkort för Business Communications Manager Telefonisttelefon 2001 Nortel Networks P0941619 Utgåva 01 Använda telefonisttelefonen Din telefon har programmerats som telefonisttelefon för specifika
Distriktsfinal. Del 1: 7 uppgifter Tid: 60 min Maxpoäng: 21 (3p/uppgift)
 Distriktsfinal Del 1: 7 uppgifter Tid: 60 min Maxpoäng: 21 (3p/uppgift) Hjälpmedel: Endast skrivmateriel, ingen miniräknare! OBS! Skriv varje uppgift på separat papper och lagets namn på samtliga papper.
Distriktsfinal Del 1: 7 uppgifter Tid: 60 min Maxpoäng: 21 (3p/uppgift) Hjälpmedel: Endast skrivmateriel, ingen miniräknare! OBS! Skriv varje uppgift på separat papper och lagets namn på samtliga papper.
Svar och arbeta vidare med Student 2008
 Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Högskoleverket NOG 2006-10-21
 Högskoleverket NOG 2006-10-21 1. Rekommenderat dagligt intag (RDI) av kalcium är 0,8 g per person. 1 dl mellanmjölk väger 100 g. Hur mycket mellanmjölk ska man dricka för att få i sig rekommenderat dagligt
Högskoleverket NOG 2006-10-21 1. Rekommenderat dagligt intag (RDI) av kalcium är 0,8 g per person. 1 dl mellanmjölk väger 100 g. Hur mycket mellanmjölk ska man dricka för att få i sig rekommenderat dagligt
Nationell simultantävling
 Nationell simultantävling Givsamling 16 oktober 2013 Kommentarer av Bertil G Johnson Nordisk tandard Kommentarerna till simultantävlingarna baseras på budsystemet Nordisk tandard. Det är också det systemet
Nationell simultantävling Givsamling 16 oktober 2013 Kommentarer av Bertil G Johnson Nordisk tandard Kommentarerna till simultantävlingarna baseras på budsystemet Nordisk tandard. Det är också det systemet
Mera ORD! Handledning. till 15 spel med 41varianter ISBN: 978-91-7762-977-1
 C Mera ORD! Handledning till 15 spel med 41varianter ISBN: 978-91-7762-977-1 2012 Nina Melin och SICA Läromedel Tel. 08-93 10 10 Fax. 08-724 60 50 info@smartkids.se www.sica.se Mera ORD! och läroplanerna.
C Mera ORD! Handledning till 15 spel med 41varianter ISBN: 978-91-7762-977-1 2012 Nina Melin och SICA Läromedel Tel. 08-93 10 10 Fax. 08-724 60 50 info@smartkids.se www.sica.se Mera ORD! och läroplanerna.
STÄNG AV FÖNSTER. Regler FLAGGSPECTRUM I FLAGGSPECTRUM II FLAGGSPECTRUM III FLAGGSPECTRUM STJÄRNSPEL
 Sivu 1/5 STÄNG AV FÖNSTER Regler FLAGGSPECTRUM I FLAGGSPECTRUM II FLAGGSPECTRUM III FLAGGSPECTRUM STJÄRNSPEL Ett spännande sätt att lära sig känna igen länder och huvudstäder. Ett utomordentligt kännetecken
Sivu 1/5 STÄNG AV FÖNSTER Regler FLAGGSPECTRUM I FLAGGSPECTRUM II FLAGGSPECTRUM III FLAGGSPECTRUM STJÄRNSPEL Ett spännande sätt att lära sig känna igen länder och huvudstäder. Ett utomordentligt kännetecken
12 roliga rastlekar. från skolor i Halland
 12 roliga rastlekar från skolor i Halland 1 2 Liv & rörelse på rasterna! Barns och ungdomars hälsa och levnadsvanor har stor betydelse för folkhälsan. De senaste åren har den stillasittande leken ökat
12 roliga rastlekar från skolor i Halland 1 2 Liv & rörelse på rasterna! Barns och ungdomars hälsa och levnadsvanor har stor betydelse för folkhälsan. De senaste åren har den stillasittande leken ökat
Semester och arbetstidsförkortning
 Hantverksdata Bilanco 2011-04-01 Semester och arbetstidsförkortning Innehåll SEMESTERUPPDATERING... - 2 - ARBETSTIDSFÖRKORTNING... - 5 - www.hantverksdata.se - 1 - Semesteruppdatering Uppdateringen ska
Hantverksdata Bilanco 2011-04-01 Semester och arbetstidsförkortning Innehåll SEMESTERUPPDATERING... - 2 - ARBETSTIDSFÖRKORTNING... - 5 - www.hantverksdata.se - 1 - Semesteruppdatering Uppdateringen ska
Programmet LastVikt Användarmanual
 Beräkna din maximalt tillåtna last Programmet LastVikt Användarmanual Version 2016-02-17 Sida 1 av 11 Innehåll Inledning... 3 Syfte... 3 Användning... 3 Fast kombination eller enskild bil... 3 Byter ofta
Beräkna din maximalt tillåtna last Programmet LastVikt Användarmanual Version 2016-02-17 Sida 1 av 11 Innehåll Inledning... 3 Syfte... 3 Användning... 3 Fast kombination eller enskild bil... 3 Byter ofta
Årgång 85, 2002. Första häftet
 Elementa Årgång 85, 2002 Årgång 85, 2002 Första häftet 4060. Dorotea, Fredrika, Nora och Ulrika har tillsammans 117 glaskulor. Uppgifterna om hur många kulor var och en äger är ytterst knapphändiga. Man
Elementa Årgång 85, 2002 Årgång 85, 2002 Första häftet 4060. Dorotea, Fredrika, Nora och Ulrika har tillsammans 117 glaskulor. Uppgifterna om hur många kulor var och en äger är ytterst knapphändiga. Man
Lagadministration. 100913 Linda Emterby
 Lagadministration För att lägga till lag ska man stå på organisationssida för en förening. Föreningen hittar man genom organisationsträdet under menyn Organisation eller genom att söka i Snabbsök efter
Lagadministration För att lägga till lag ska man stå på organisationssida för en förening. Föreningen hittar man genom organisationsträdet under menyn Organisation eller genom att söka i Snabbsök efter
Lära känna skrivbordet
 Är det första gången du använder Windows 7? Den här versionen har mycket gemensamt med tidigare versioner av Windows, men du kan behöva hjälp med att få upp farten. Den här guiden innehåller praktisk information
Är det första gången du använder Windows 7? Den här versionen har mycket gemensamt med tidigare versioner av Windows, men du kan behöva hjälp med att få upp farten. Den här guiden innehåller praktisk information
Home Prosafe 1132 GSM larm (Art.nr. 36-2868)
 Snabbstartguide Home Prosafe 1132 GSM larm (Art.nr. 36-2868) 1) Förbereda kontrollpanelen för uppstart a) OBS! innan SIM-kortet Knappbeskrivning monteras i kontrollpanelen - Stegar uppåt i menyn måste
Snabbstartguide Home Prosafe 1132 GSM larm (Art.nr. 36-2868) 1) Förbereda kontrollpanelen för uppstart a) OBS! innan SIM-kortet Knappbeskrivning monteras i kontrollpanelen - Stegar uppåt i menyn måste
OBS - ranking NYTT RANKINGSYSTEM. Jan-Erik Thomasson 2001-01-16 INNEHÅLL
 OBS - ranking NYTT RANKINGSYSTEM Jan-Erik Thomasson 2001-01-16 INNEHÅLL 1 FORMELÄNDRINGAR... 2 1.1 Konvergens mot "rätt" rankingtal... 2 1.2 Höjd konvergenshastighet... 2 2 "CARRY-OVER"... 3 3 METOD...
OBS - ranking NYTT RANKINGSYSTEM Jan-Erik Thomasson 2001-01-16 INNEHÅLL 1 FORMELÄNDRINGAR... 2 1.1 Konvergens mot "rätt" rankingtal... 2 1.2 Höjd konvergenshastighet... 2 2 "CARRY-OVER"... 3 3 METOD...
Kaninen som rymde Lärarmaterial
 sidan 1 Författare: Jessika Berglund Vad handlar boken om? Mia och Shirin vill gärna ha var sitt husdjur men får inte det för sina föräldrar. Varje lördag går de till djuraffären. Där gosar de med kaninerna,
sidan 1 Författare: Jessika Berglund Vad handlar boken om? Mia och Shirin vill gärna ha var sitt husdjur men får inte det för sina föräldrar. Varje lördag går de till djuraffären. Där gosar de med kaninerna,
2. Komma igång Skapa grupper och elever Skriv också ut sidan 13 så att eleverna har en snabbguide till programmet.
 2. Komma igång Skapa grupper och elever Börja med att läsa texten nedan om hur man börjar jobba med programmet efter installationen. Skriv gärna ut sidan och ha bredvid dig tills du känner att du behärskar
2. Komma igång Skapa grupper och elever Börja med att läsa texten nedan om hur man börjar jobba med programmet efter installationen. Skriv gärna ut sidan och ha bredvid dig tills du känner att du behärskar
en femma eller en sexa?
 REPETITION 3 A Du kastar en vanlig tärning en gång. Hur stor är sannolikheten att du får en femma eller en sea? 2 Eleverna i klass C fick ge betyg på en bok som de hade läst. Diagrammet visar resultatet.
REPETITION 3 A Du kastar en vanlig tärning en gång. Hur stor är sannolikheten att du får en femma eller en sea? 2 Eleverna i klass C fick ge betyg på en bok som de hade läst. Diagrammet visar resultatet.
2. (7) Ryck kort i spel. Djurkort. 4 Röda Djur. 4 Grå Djur
 1. (7) Att utmana sina motståndare i detta spel står alla fritt, se till att bli den förste att lägga ett ryck-kort. När alla ryck-kort har vunnits, är den person med flest ryck-kort vinnaren. Detta fartfyllda
1. (7) Att utmana sina motståndare i detta spel står alla fritt, se till att bli den förste att lägga ett ryck-kort. När alla ryck-kort har vunnits, är den person med flest ryck-kort vinnaren. Detta fartfyllda
Nationell simultantävling
 Nationell simultantävling Givsamling 25 september 2014 Kommentarer av Bertil G Johnson VENKA BRIDGEFÖRBUNDET Nordisk tandard Kommentarerna till simultantävlingarna baseras på budsystemet Nordisk tandard.
Nationell simultantävling Givsamling 25 september 2014 Kommentarer av Bertil G Johnson VENKA BRIDGEFÖRBUNDET Nordisk tandard Kommentarerna till simultantävlingarna baseras på budsystemet Nordisk tandard.
Detta prov består av del 1 och 2. Här finns också facit och förslag till poängsättning
 Allmänt om proven Detta prov består av del 1 och. Här finns också facit och förslag till poängsättning och bedömning. Provet finns på lärarwebben, dels som pdf-fil och dels som redigerbar Word-fil. Del
Allmänt om proven Detta prov består av del 1 och. Här finns också facit och förslag till poängsättning och bedömning. Provet finns på lärarwebben, dels som pdf-fil och dels som redigerbar Word-fil. Del
Smygmaskvirkade vantar
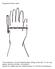 Smygmaskvirkade vantar Virka luftmaskor, och gör luftmaskkedjan så lång, att den når 1 ½ varv runt handen, där den är bredast, vid tumleden. Jag har ett 3-trådigt garn och virknål nummer 5 ½. Det blev
Smygmaskvirkade vantar Virka luftmaskor, och gör luftmaskkedjan så lång, att den når 1 ½ varv runt handen, där den är bredast, vid tumleden. Jag har ett 3-trådigt garn och virknål nummer 5 ½. Det blev
Handbok Fyrkanter. Matt Williams Granskare: Eugene Trounev Översättare: Stefan Asserhäll
 Matt Williams Granskare: Eugene Trounev Översättare: Stefan Asserhäll 2 Innehåll 1 Inledning 5 2 Hur man spelar 6 3 Spelets regler, strategi och tips 7 3.1 Spelregler..........................................
Matt Williams Granskare: Eugene Trounev Översättare: Stefan Asserhäll 2 Innehåll 1 Inledning 5 2 Hur man spelar 6 3 Spelets regler, strategi och tips 7 3.1 Spelregler..........................................
Föreläsning 2 Mer om skyddsjord.
 Föreläsning 2 Mer om skyddsjord. Tänk dig en tvättmaskin som står på gummifötter. Ytterhöljet är en typisk utsatt del. Om fasen pga ett isolationfel kommer i beröring med ytterhöljet får hela tvättmaskinen
Föreläsning 2 Mer om skyddsjord. Tänk dig en tvättmaskin som står på gummifötter. Ytterhöljet är en typisk utsatt del. Om fasen pga ett isolationfel kommer i beröring med ytterhöljet får hela tvättmaskinen
Förslag på. Instruktion för kontrollanter i föreningslotterier
 Förslag på Instruktion för kontrollanter i föreningslotterier Uppdraget Att vara kontrollant innebär att man för tillståndsmyndighetens räkning utför ett uppdrag som ställer stora krav på ordning, noggrannhet
Förslag på Instruktion för kontrollanter i föreningslotterier Uppdraget Att vara kontrollant innebär att man för tillståndsmyndighetens räkning utför ett uppdrag som ställer stora krav på ordning, noggrannhet
Kortleken. Regler Utspel - Tips
 Kortleken Honnörer Hackor E K D kn 10 9 8 7 6 5 4 3 2 Färgernas rangordning Utspelare Träkarl (bordet) Partner till utspelaren Spelförare (handen) Vunna stick Stick: Fyra kort - ett från varje spelare.
Kortleken Honnörer Hackor E K D kn 10 9 8 7 6 5 4 3 2 Färgernas rangordning Utspelare Träkarl (bordet) Partner till utspelaren Spelförare (handen) Vunna stick Stick: Fyra kort - ett från varje spelare.
Doro Secure 580IUP. Användarhandbok. Svenska
 Doro Secure 580IUP Användarhandbok Svenska 3 2 1 4 5 6 7 8 9 14 13 12 11 10 15 16 Obs! Illustrationerna används endast i förklarande syfte och avbildar kanske inte den aktuella enheten korrekt. Svenska
Doro Secure 580IUP Användarhandbok Svenska 3 2 1 4 5 6 7 8 9 14 13 12 11 10 15 16 Obs! Illustrationerna används endast i förklarande syfte och avbildar kanske inte den aktuella enheten korrekt. Svenska
För att använda sifferkrypto använder man en rektangel om 5 gånger 6 bokstäver.
 Nämnarens kryptoskola 8. Sifferkrypto lärarsida För att använda sifferkrypto använder man en rektangel om 5 gånger 6 bokstäver. Siffror från 0 till 5 ovanför och 5 till 9 till vänster om rektangeln anger
Nämnarens kryptoskola 8. Sifferkrypto lärarsida För att använda sifferkrypto använder man en rektangel om 5 gånger 6 bokstäver. Siffror från 0 till 5 ovanför och 5 till 9 till vänster om rektangeln anger
Skolmästerskap. Hur man arrangerar en schacktävling
 Skolmästerskap Hur man arrangerar en schacktävling Det är omvittnat både av pedagoger och i forskning att schack utvecklar barn socialt och intellektuellt. Schack är ett spel, och något av det roligaste
Skolmästerskap Hur man arrangerar en schacktävling Det är omvittnat både av pedagoger och i forskning att schack utvecklar barn socialt och intellektuellt. Schack är ett spel, och något av det roligaste
Bilaga inrikesministeriets förordning SMDno/2012/308 REGLER FÖR VEIKKAUS AB:S PENNINGSPEL
 Bilaga inrikesministeriets förordning SMDno/2012/308 REGLER FÖR VEIKKAUS AB:S PENNINGSPEL 2 Innehåll LOTTO - SPELREGLER... 3 REGLER FÖR EXTRA DRAGNING I LOTTO... 7 REGLER FÖR EXTRA DRAGNING VID FLERVECKORSSPEL
Bilaga inrikesministeriets förordning SMDno/2012/308 REGLER FÖR VEIKKAUS AB:S PENNINGSPEL 2 Innehåll LOTTO - SPELREGLER... 3 REGLER FÖR EXTRA DRAGNING I LOTTO... 7 REGLER FÖR EXTRA DRAGNING VID FLERVECKORSSPEL
Förhandling - praktiska tips och råd
 Förhandling - praktiska tips och råd Tänk på att informationen i detta material inte har uppdaterats sedan januari 2014. Aktuella lagar (inklusive beloppsgränser) har förändrats sedan dess och praxis på
Förhandling - praktiska tips och råd Tänk på att informationen i detta material inte har uppdaterats sedan januari 2014. Aktuella lagar (inklusive beloppsgränser) har förändrats sedan dess och praxis på
Matematik och modeller Övningsuppgifter
 Matematik och modeller Övningsuppgifter Beräkna a) d) + 6 b) 7 (+) + ( 9 + ) + 9 e) 8 c) ( + (5 6)) f) + Förenkla följande uttryck så långt som möjligt a) ( ) 5 b) 5 y 6 5y c) y 5 y + y y d) +y y e) (
Matematik och modeller Övningsuppgifter Beräkna a) d) + 6 b) 7 (+) + ( 9 + ) + 9 e) 8 c) ( + (5 6)) f) + Förenkla följande uttryck så långt som möjligt a) ( ) 5 b) 5 y 6 5y c) y 5 y + y y d) +y y e) (
Tävlingsreglemente för SAM
 Tävlingsreglemente för SAM Tävlingsreglemente av år 1989 för Svenska Akademiska Mästerskapen i dressyr och hoppning (SAR SAM-TR). Reviderade 21 april 2002 Tävlingsreglementets tillämpning: Mom 1 Styrelsen
Tävlingsreglemente för SAM Tävlingsreglemente av år 1989 för Svenska Akademiska Mästerskapen i dressyr och hoppning (SAR SAM-TR). Reviderade 21 april 2002 Tävlingsreglementets tillämpning: Mom 1 Styrelsen
Splitsning av flätade linor gjorda av polyester eller nylon.
 Denna splits är inte lämplig för dubbelflätade linor vars styrka enbart beror på styrkan i kärnan. Öglesplitsen används för att placera en permanent ögla i änden av ett rep, i allmänhet för förtöjning
Denna splits är inte lämplig för dubbelflätade linor vars styrka enbart beror på styrkan i kärnan. Öglesplitsen används för att placera en permanent ögla i änden av ett rep, i allmänhet för förtöjning
2. Registrera en ny medlem
 2. Registrera en ny medlem version 2006-05-10 2.1 2. Registrera en ny medlem Den här dokumentationen beskriver hur man registrerar en ny i SPFs medlemsregister via Internet. Observera att bilderna är exempel
2. Registrera en ny medlem version 2006-05-10 2.1 2. Registrera en ny medlem Den här dokumentationen beskriver hur man registrerar en ny i SPFs medlemsregister via Internet. Observera att bilderna är exempel
En ideal op-förstärkare har oändlig inimedans, noll utimpedans och oändlig förstärkning.
 F5 LE1460 Analog elektronik 2005-11-23 kl 08.15 12.00 Alfa En ideal op-förstärkare har oändlig inimedans, noll utimpedans och oändlig förstärkning. ( Impedans är inte samma sak som resistans. Impedans
F5 LE1460 Analog elektronik 2005-11-23 kl 08.15 12.00 Alfa En ideal op-förstärkare har oändlig inimedans, noll utimpedans och oändlig förstärkning. ( Impedans är inte samma sak som resistans. Impedans
Programmeringsolympiadens final 2009
 Programmeringsolympiadens final 2009 TÄVLINGSREGLER Tävlingen äger rum den 12 mars. Tävlingstiden är sex timmar effektiv tid. Tävlingen består av sju uppgifter som samtliga ska lösas genom datorprogram.
Programmeringsolympiadens final 2009 TÄVLINGSREGLER Tävlingen äger rum den 12 mars. Tävlingstiden är sex timmar effektiv tid. Tävlingen består av sju uppgifter som samtliga ska lösas genom datorprogram.
Fotbollskolan barn födda 2002 Våren 2009
 2009-04-05 Sida 1 av 5 Välkommen till fotbollskolan Fotboll är en meningsfull sysselsättning året runt. För att få ett friskare och roligare liv och inte minst - för att lära sig samarbeta. Drivkraften
2009-04-05 Sida 1 av 5 Välkommen till fotbollskolan Fotboll är en meningsfull sysselsättning året runt. För att få ett friskare och roligare liv och inte minst - för att lära sig samarbeta. Drivkraften
SCHOLA COMAI ELEV WEBBKALENDER / SCHEMA VERSION 1.1. [Skriv text]
![SCHOLA COMAI ELEV WEBBKALENDER / SCHEMA VERSION 1.1. [Skriv text] SCHOLA COMAI ELEV WEBBKALENDER / SCHEMA VERSION 1.1. [Skriv text]](/thumbs/30/14472655.jpg) 20111206 SCHOLA COMAI WEBBKALENDER / SCHEMA VERSION 1.1 ELEV [Skriv text] Innehåll 1 Inledning... 3 1.1 Terminologi... 3 1.2 Teknisk kravspecifikation... 4 1.3 Behörigheter... 4 1.5 Start... 4 1.5.1 Grundinställning
20111206 SCHOLA COMAI WEBBKALENDER / SCHEMA VERSION 1.1 ELEV [Skriv text] Innehåll 1 Inledning... 3 1.1 Terminologi... 3 1.2 Teknisk kravspecifikation... 4 1.3 Behörigheter... 4 1.5 Start... 4 1.5.1 Grundinställning
TDIU Regler
 Regler Student får lämna salen tidigast en timme efter tentans start. Vid toalettbesök eller rökpaus ska pauslista utanför salen fyllas i. All form av kontakt mellan studenter under tentans gång är strängt
Regler Student får lämna salen tidigast en timme efter tentans start. Vid toalettbesök eller rökpaus ska pauslista utanför salen fyllas i. All form av kontakt mellan studenter under tentans gång är strängt
Tentaupplägg denna gång
 Några tips på vägen kanske kan vara bra. Tentaupplägg denna gång TIPS 1: Läs igenom ALLA uppgifterna och välj den du känner att det är den lättaste först. Det kan gärna ta 10-20 minuter. Försök skriva
Några tips på vägen kanske kan vara bra. Tentaupplägg denna gång TIPS 1: Läs igenom ALLA uppgifterna och välj den du känner att det är den lättaste först. Det kan gärna ta 10-20 minuter. Försök skriva
Matematik 92MA41 (15hp) Vladimir Tkatjev
 Matematik 92MA41 (15hp) Vladimir Tkatjev Lite inspiration Går det att konstruera 6 kvadrater av 12 tändstickor? Hur gör man då? (Nämnaren, Nr 2, 2005) Litet klurigt kanske, bygg en kub av stickorna: Uppgift
Matematik 92MA41 (15hp) Vladimir Tkatjev Lite inspiration Går det att konstruera 6 kvadrater av 12 tändstickor? Hur gör man då? (Nämnaren, Nr 2, 2005) Litet klurigt kanske, bygg en kub av stickorna: Uppgift
REGELN: Ett SET består av tre tärningar med samma ELLER olika egenskaper. ANTAL: det finns en, två eller tre av respektive symbol på tärningarna.
 SET CUBED A Curious Game of Clever Connections Instruktioner Para instrucciones en Español por favor visiten www.setgame.com Pour des instructions en Français veuillez visiter www.setgame.com Für Spielanleitungen
SET CUBED A Curious Game of Clever Connections Instruktioner Para instrucciones en Español por favor visiten www.setgame.com Pour des instructions en Français veuillez visiter www.setgame.com Für Spielanleitungen
Uppföljning av de personer som uppnådde maximal tid i sjukförsäkringen under 2010 eller under första och andra kvartalet 2011
 Dnr: 2010/436389 Dnr: 016315-2011 Uppföljning av de personer som uppnådde maximal tid i sjukförsäkringen under 2010 eller under första och andra kvartalet 2011 Återrapportering enligt regleringsbrevet
Dnr: 2010/436389 Dnr: 016315-2011 Uppföljning av de personer som uppnådde maximal tid i sjukförsäkringen under 2010 eller under första och andra kvartalet 2011 Återrapportering enligt regleringsbrevet
Färdtjänsten Dalarna GÄLLER FRÅN 2015-06-01
 Färdtjänsten Dalarna GÄLLER FRÅN 2015-06-01 På uppdrag av Dalarnas kommuner ansvarar Region Dalarna för myndighetsutövningen gällande färdtjänsten i länet. Utredning och prövning av tillstånd för färdtjänst
Färdtjänsten Dalarna GÄLLER FRÅN 2015-06-01 På uppdrag av Dalarnas kommuner ansvarar Region Dalarna för myndighetsutövningen gällande färdtjänsten i länet. Utredning och prövning av tillstånd för färdtjänst
A B C D E. 2 Det står KANGAROO på mitt paraply. Du kan se det på bilden. A B C D E
 N G A RA Kängurutävlingen 2015 Benjamin Trepoängsuppgifter 1 Vilken figur är skuggad till hälften? Slovakien 2 Det står KANGAROO på mitt paraply. Du kan se det på bilden. Vilken av följande bilder är inte
N G A RA Kängurutävlingen 2015 Benjamin Trepoängsuppgifter 1 Vilken figur är skuggad till hälften? Slovakien 2 Det står KANGAROO på mitt paraply. Du kan se det på bilden. Vilken av följande bilder är inte
Diskret matematik: Övningstentamen 4
 Diskret matematik: Övningstentamen 22. Beskriv alla relationer, som är såväl ekvivalensrelationer som partiella ordningar. Är någon välbekant relation sådan? 23. Ange alla heltalslösningar till ekvationen
Diskret matematik: Övningstentamen 22. Beskriv alla relationer, som är såväl ekvivalensrelationer som partiella ordningar. Är någon välbekant relation sådan? 23. Ange alla heltalslösningar till ekvationen
Diskussionsproblem för Statistik för ingenjörer
 Diskussionsproblem för Statistik för ingenjörer Måns Thulin Rolf Larsson rolf.larsson@math.uu.se Jesper Rydén jesper.ryden@math.uu.se Senast uppdaterad 27 januari 2016 Diskussionsproblem till Lektion 3
Diskussionsproblem för Statistik för ingenjörer Måns Thulin Rolf Larsson rolf.larsson@math.uu.se Jesper Rydén jesper.ryden@math.uu.se Senast uppdaterad 27 januari 2016 Diskussionsproblem till Lektion 3
Matematik Åk 9 Provet omfattar stickprov av det centrala innehållet i Lgr-11. 1. b) c) d)
 1. b) c) d) a) Multiplikation med 100 kan förenklas med att flytta decimalerna lika många stg som antlet nollor. 00> svar 306 b) Använd kort division. Resultatet ger igen rest. Svar 108 c) Att multiplicera
1. b) c) d) a) Multiplikation med 100 kan förenklas med att flytta decimalerna lika många stg som antlet nollor. 00> svar 306 b) Använd kort division. Resultatet ger igen rest. Svar 108 c) Att multiplicera
Riksfinal. Del 1: 6 uppgifter Tid: 60 min Maxpoäng: 18 (3p/uppgift) OBS! Skriv varje uppgift på separat papper och lagets namn på samtliga papper.
 Riksfinal Del 1: 6 uppgifter Tid: 60 min Maxpoäng: 18 (3p/uppgift) Hjälpmedel: Endast skrivmateriel, ingen miniräknare OBS Skriv varje uppgift på separat papper och lagets namn på samtliga papper. Fullständiga
Riksfinal Del 1: 6 uppgifter Tid: 60 min Maxpoäng: 18 (3p/uppgift) Hjälpmedel: Endast skrivmateriel, ingen miniräknare OBS Skriv varje uppgift på separat papper och lagets namn på samtliga papper. Fullständiga
Lekar. Namnlekar. Lekens namn Stå i en ring
 Lekar Lek har stor betydelse för barns utveckling och är därför en viktig del av friidrottsskolan. Genom att leka olika typer av rörelselekar utvecklar barn och ungdomar sin rörlighet, balans, koordination
Lekar Lek har stor betydelse för barns utveckling och är därför en viktig del av friidrottsskolan. Genom att leka olika typer av rörelselekar utvecklar barn och ungdomar sin rörlighet, balans, koordination
Netwise CMG Voice. 2002-02-28, Rev 1.0, CJ 1(16)
 Netwise CMG Voice Allmänt... 2 Användargränssnitt... 3 Telefongränssnitt... 3 Aktivitetsinformation... 3 Administration... 3 Inloggning... 4 Huvudmeny...4 Administration av dina röstmeddelanden... 5 Administration
Netwise CMG Voice Allmänt... 2 Användargränssnitt... 3 Telefongränssnitt... 3 Aktivitetsinformation... 3 Administration... 3 Inloggning... 4 Huvudmeny...4 Administration av dina röstmeddelanden... 5 Administration
Nationell simultantävling
 ationell simultantävling Givsamling 9 november 2015 Kommentarer av Daniel Gullberg SVESKA BRIDGEFÖRBUDET ordisk Standard Kommentarerna till simultantävlingarna baseras på budsystemet ordisk Standard. Det
ationell simultantävling Givsamling 9 november 2015 Kommentarer av Daniel Gullberg SVESKA BRIDGEFÖRBUDET ordisk Standard Kommentarerna till simultantävlingarna baseras på budsystemet ordisk Standard. Det
Här kan du välja befintligt upplägg eller skapa ett nytt. Klicka på edit uppe till höger för att redigera och/eller skapat nytt.
 Start-skärmen Här kan du välja befintligt upplägg eller skapa ett nytt. Klicka på edit uppe till höger för att redigera och/eller skapat nytt. Det grå kugghjulet indikerar att du är i redigeringsläge och
Start-skärmen Här kan du välja befintligt upplägg eller skapa ett nytt. Klicka på edit uppe till höger för att redigera och/eller skapat nytt. Det grå kugghjulet indikerar att du är i redigeringsläge och
räkning av antal, första lösandet av räkneuppgifter, matchning språkutveckling genom sortering och hopsamling av träpinnar
 22490 Calculino Nyttigt för: räkning av antal, första lösandet av räkneuppgifter, matchning igenkänning, benämning och sortering av färger finmotorik genom att stoppa träpinnar i hål språkutveckling genom
22490 Calculino Nyttigt för: räkning av antal, första lösandet av räkneuppgifter, matchning igenkänning, benämning och sortering av färger finmotorik genom att stoppa träpinnar i hål språkutveckling genom
Anvisning för ARVI-systemet för dig som matar in personbedömningar 13.4.2015
 Anvisning för ARVI-systemet för dig som matar in personbedömningar 13.4.2015 Innehåll Grunder för ARVI-systemet... 1 Att mata in bedömningen... 2 Att skicka bedömningen till TE-byrån... 5 Att avsluta ARVI...
Anvisning för ARVI-systemet för dig som matar in personbedömningar 13.4.2015 Innehåll Grunder för ARVI-systemet... 1 Att mata in bedömningen... 2 Att skicka bedömningen till TE-byrån... 5 Att avsluta ARVI...
Behandlingen av köpkort och köpkortsbokföringen.
 FOLKFÖRSÖRJNINGSMINISTERIET Helsingfors, den 20 december 1943. Cirkulär 1/7 N:r 374. Till folkförsörjningsnämnderna. Behandlingen av köpkort och köpkortsbokföringen. Sida Antalet köpkort, som tillställes
FOLKFÖRSÖRJNINGSMINISTERIET Helsingfors, den 20 december 1943. Cirkulär 1/7 N:r 374. Till folkförsörjningsnämnderna. Behandlingen av köpkort och köpkortsbokföringen. Sida Antalet köpkort, som tillställes
Problem att fundera över
 Problem att fundera över Här får du öva dig på att formulera en förmodan och försökabevisaden. Jag förväntar mig inte att du klarar av att gå till botten med alla frågorna! Syftet är att ge dig smakprov
Problem att fundera över Här får du öva dig på att formulera en förmodan och försökabevisaden. Jag förväntar mig inte att du klarar av att gå till botten med alla frågorna! Syftet är att ge dig smakprov
Kartövning Lim City. Mål. Material. Förberedelser
 Kartövning Lim City Lim City är en kreativ övning där deltagarna placeras i olika grupper och skall planera ett nytt område på en karta. Varje grupp får en unik förutsättning för sitt arbete tilldelad
Kartövning Lim City Lim City är en kreativ övning där deltagarna placeras i olika grupper och skall planera ett nytt område på en karta. Varje grupp får en unik förutsättning för sitt arbete tilldelad
Räkna med Rutiga Familjen
 Räkna med Rutiga Familjen Ett grafiskt mattespel som behandlar de fyra räknesätten med positiva och negativa tal. Utan siffror och symboler. Med lärande agenter. Saga Http://rutigafamiljen.se 2008-11-06
Räkna med Rutiga Familjen Ett grafiskt mattespel som behandlar de fyra räknesätten med positiva och negativa tal. Utan siffror och symboler. Med lärande agenter. Saga Http://rutigafamiljen.se 2008-11-06
Användarmanual för nya funktioner
 Användarmanual för nya funktioner 070201 Innehåll 1 Introduktion 2 2 Uppdateringar per 2006-06-15 3-5 3 Uppdateringar per 2007-02-01 6 1 Introduktion Detta är en användarmanual för nya funktioner i din
Användarmanual för nya funktioner 070201 Innehåll 1 Introduktion 2 2 Uppdateringar per 2006-06-15 3-5 3 Uppdateringar per 2007-02-01 6 1 Introduktion Detta är en användarmanual för nya funktioner i din
15-03-03. hem ETT. sammanställning Homeparty hos Hanna
 15-03-03 hem ETT sammanställning Homeparty hos Hanna innehåll Homeparty hos Hanna Sammanfattning av workshopen Slutsatser resultat 3 6-10 11 Homeparty hos Hanna Bostadens upplägg och innehåll Vi hade bjudit
15-03-03 hem ETT sammanställning Homeparty hos Hanna innehåll Homeparty hos Hanna Sammanfattning av workshopen Slutsatser resultat 3 6-10 11 Homeparty hos Hanna Bostadens upplägg och innehåll Vi hade bjudit
