Delprov C Innehållet i detta häfte är sekretessbelagt t o m den 30 juni 2007.
|
|
|
- Stina Mattsson
- för 8 år sedan
- Visningar:
Transkript
1 Delprov C Innehållet i detta häfte är sekretessbelagt t o m den 3 juni 7. Efter varje uppgift anges maximala antalet poäng som du kan få för din lösning. T ex betyder (2/1) att uppgiften kan ge 2 g-poäng och 1 vg-poäng. På de -märkta uppgifterna kan du visa MVG-kvaliteter. Till nästan alla uppgifter krävs fullständiga lösningar. För endast korrekt svar ges inga poäng utom för de uppgifter som är markerade med Endast svar krävs. Din redovisning ska vara så tydlig att en annan person ska kunna läsa och förstå vad du menar. Det är viktigt att du redovisar allt ditt arbete. Du kan få poäng för delvis löst uppgift. Hjälpmedel: miniräknare, linjal och formelblad. Provtid: 1 minuter. Namn: Skola: Klass: Födelsedatum: År Månad Dag Kvinna Man Lösningar och svar ska inte skrivas i provhäftet utan på separat papper. Provhäftet ska lämnas in tillsammans med lösningarna.
2 Nya Zeeland 1. Tabellen visar avstånden i kilometer mellan några orter på Nya Zeeland. Dunedin Greymouth Haast Mt Cook Nelson Picton Queenstown Te Anau Wanaka Dunedin Greymouth Haast Mt Cook Nelson Picton Queenstown Te Anau Wanaka a) Hur långt är det mellan Haast och Te Anau? Endast svar krävs. (1/) b) Enligt turistinformationen tar det 7 timmar att köra mellan Haast och Te Anau. Vilken medelfart håller man då? (2/) 2. Daniel och Sara, som semestrar på Nya Zeeland, ska hyra en husbil. De räknar med att köra ca 2 km på 1 dagar. De kan välja mellan två alternativ. Alternativ A: NZD per dag oavsett körsträcka. Alternativ B: 11 NZD per dag och dessutom,5 NZD per kilometer. På Nya Zeeland heter valutan dollar. Den förkortas NZD. Vilket alternativ bör de välja? Motivera ditt svar med resonemang och beräkningar. (2/) 3. Hos kiwifågeln lägger honan ett enda ägg som kan väga 5 g. Det motsvarar en femtedel av kiwifågelns normala kroppsvikt. Detta är rekord bland fåglar. Hur mycket väger en kiwifågel? (2/)
3 4. På Nya Zeeland kan man vaska guld. En dag var det 12 personer som vaskade. Efter en timme vägde de hur mycket guld de hade lyckats vaska per person. Resultatet ser du i tabellen.,15 g 2,96 g,23 g,62 g,43 g,36 g,16 g,28 g,32 g,19 g,26 g,3 g a) Bestäm medelvärde och median för hur mycket guld de vaskade på en timme. (2/1) b) Förklara varför det blir så stor skillnad mellan medianen och medelvärdet. (/1) hittades världens största guldklimp Holtermann s Nugget. Den vägde drygt 285 kg och innehöll 214 kg rent guld. Guldpriset idag är 135 kr/g. Hur mycket skulle guldklimpen vara värd idag? (2/) Källa: Mitchell Library, State Library of New South Wales. 6. Daniel och Sara vaskar guld till Saras förlovningsring. Ringen ska vara 5 mm bred och 2 mm tjock och ha en innerdiameter på 18 mm. 2 mm 2 mm 18 mm 5 mm a) Hur stor volym kommer Saras ring att ha? (1/2) b) Hur många gram rent guld behöver Sara och Daniel vaska fram till Saras ring om den ska innehålla 75 % rent guld? 1 cm 3 guld väger 19,32 g. (1/1)
4 7. Sara ska ringa hem till Sverige med sin mobiltelefon. Hennes kostnad för samtalet kan bestämmas med formeln: K = 9,95 + 1,6x där K är kostnaden i kr och x är samtalstiden i minuter. Hur länge kan hon prata för 2 kr? (1/1) 8. I Auckland på Nya Zeeland finns ett högt torn som kallas Sky Tower. Tornet som är 328 m högt är den högsta byggnaden på södra halvklotet. a) En observationsplattform Main observation level finns på 186 meters höjd. Det är 1 29 trappsteg upp till den. Varje år ordnas en tävling i att springa så fort som möjligt upp för trapporna. Rekordet är 5 min 7 s. Hur många trappsteg tog rekordinnehavaren per sekund? (2/) b) Enligt en turistbroschyr kan man se så långt som 82 km från den högsta utsiktspunkten i Sky Tower (tornet är markerat med ett kryss). Är det i så fall möjligt att se den ö som heter Great Barrier Island? (1/1) Kartan är ritad i skala 1 : 1 5
5 c) Det tar 4 s att åka hiss upp till den observationsplattform som ligger 186 m upp. Den högsta hastighet som hissen kommer upp i under färden är nästan 3 km/h. Vilken av graferna A, B, C eller D visar sambandet mellan tiden och hissens läge? Motivera ditt svar med resonemang och/eller beräkningar A B C D (/2) 9. På Nya Zeelands västkust regnar det mycket. I området faller i genomsnitt 7 5 mm regn per år. En familj 8, m samlar in det vatten som faller på 4, m taket till bostadshuset för att använda 6, m i hushållet. Takets mått kan du se på ritningen. Hur mycket vatten kan familjen samla in på ett år? (1/2) 3, m
6 Foto: H Pettersen På 17-talet var 75 % av Nya Zeelands yta täckt av urskog. Sedan dess har stora delar av urskogen huggits ned för att ge plats för jordbruk och städer. Idag täcker urskogen bara 2 % av landets yta. Hur stor del av urskogen som fanns på 17-talet har huggits ned? (1/2) I mitten på -talet infördes 3 opossumdjur till Nya Zeeland från Australien. Eftersom dessa djur inte har någon naturlig fiende på Nya Zeeland har antalet sedan dess ökat snabbt. Tabellen visar den senaste utvecklingen. År Antal opossumdjur miljoner 5 76 miljoner 21 a) Med hur många procent har antalet djur ökat från 198 till 5? (1/1) b) Man tror att opossumdjuren kommer att fortsätta öka med 6 % per år. Ungefär hur många opossumdjur kommer det att finnas år 21? (1/2)
Del B1 Innehållet i detta häfte är sekretessbelagt t o m den 30 juni 2007.
 Miniräknare ej tillåten Del B1 Innehållet i detta häfte är sekretessbelagt t o m den 30 juni 2007. Denna del består av kortsvarsuppgifter som ska lösas utan miniräknare. Korrekt svar ger 1 g-poäng (1/0)
Miniräknare ej tillåten Del B1 Innehållet i detta häfte är sekretessbelagt t o m den 30 juni 2007. Denna del består av kortsvarsuppgifter som ska lösas utan miniräknare. Korrekt svar ger 1 g-poäng (1/0)
Del B1 Innehållet i detta häfte är sekretessbelagt t o m den 30 juni 2007.
 Miniräknare ej tillåten Del B1 Innehållet i detta häfte är sekretessbelagt t o m den 30 juni 2007. Denna del består av kortsvarsuppgifter som ska lösas utan miniräknare. Korrekt svar ger 1 g-poäng (1/0)
Miniräknare ej tillåten Del B1 Innehållet i detta häfte är sekretessbelagt t o m den 30 juni 2007. Denna del består av kortsvarsuppgifter som ska lösas utan miniräknare. Korrekt svar ger 1 g-poäng (1/0)
Matematik. Delprov B. Vårterminen 2009 ÄMNESPROV. Del B1 ÅRSKURS. Elevens namn
 ÄMNESPROV Matematik ÅRSKURS 9 Prov som ska återanvändas omfattas av sekretess enligt 4 kap. 3 sekretesslagen. Avsikten är att detta prov ska kunna återanvändas t.o.m. 2009-06-30. Vid sekretessbedömning
ÄMNESPROV Matematik ÅRSKURS 9 Prov som ska återanvändas omfattas av sekretess enligt 4 kap. 3 sekretesslagen. Avsikten är att detta prov ska kunna återanvändas t.o.m. 2009-06-30. Vid sekretessbedömning
NATIONELLT KURSPROV I MATEMATIK KURS A HÖSTEN 2000. Del I
 Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap 3 Sekretesslagen. För detta material gäller sekretessen till och med utgången av 010. NATIONELLT KURSPROV I
Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap 3 Sekretesslagen. För detta material gäller sekretessen till och med utgången av 010. NATIONELLT KURSPROV I
NATIONELLT KURSPROV I MATEMATIK KURS A VÅREN 2001. Del II
 Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap 3 Sekretesslagen. För detta material gäller sekretessen till och med utgången av 2011. Anvisningar Provtid
Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap 3 Sekretesslagen. För detta material gäller sekretessen till och med utgången av 2011. Anvisningar Provtid
Komvux/gymnasieprogram:
 Namn: Skola: Komvux/gymnasieprogram: Anvisningar: Tidsbunden del består av två delar, Del I och Del II. Den sammanlagda provtiden är 120 minuter varav högst 30 minuter för Del I. Till uppgifterna i Del
Namn: Skola: Komvux/gymnasieprogram: Anvisningar: Tidsbunden del består av två delar, Del I och Del II. Den sammanlagda provtiden är 120 minuter varav högst 30 minuter för Del I. Till uppgifterna i Del
NATIONELLT KURSPROV I MATEMATIK KURS A VÅREN 2000. Del III
 Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap 3 Sekretesslagen. För detta material gäller sekretessen till och med utgången av 2010. NATIONELLT KURSPROV
Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap 3 Sekretesslagen. För detta material gäller sekretessen till och med utgången av 2010. NATIONELLT KURSPROV
- Nationella prov till eleven -
 - Nationella prov till eleven - Tidigare utgivna ämnesprov för årskurs 9 under kursplan 2000 :: Allmänt Detta kompendium innehåller de skriftliga delarna från fyra tidigare utgivna ämnesprov i matematik
- Nationella prov till eleven - Tidigare utgivna ämnesprov för årskurs 9 under kursplan 2000 :: Allmänt Detta kompendium innehåller de skriftliga delarna från fyra tidigare utgivna ämnesprov i matematik
NATIONELLT KURSPROV I MATEMATIK KURS A VÅREN 2002. Del II
 Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap 3 Sekretesslagen. För detta material gäller sekretessen till och med utgången av juni månad 2002. Anvisningar
Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap 3 Sekretesslagen. För detta material gäller sekretessen till och med utgången av juni månad 2002. Anvisningar
Innehållet i detta häfte är sekretessbelagt t o m den 9 juni 2006.
 Innehållet i detta häfte är sekretessbelagt t o m den 9 juni 2006. Efter varje uppgift anges maximala antalet poäng som du kan få för din lösning. T ex betyder (2/1) att uppgiften kan ge 2 g-poäng och
Innehållet i detta häfte är sekretessbelagt t o m den 9 juni 2006. Efter varje uppgift anges maximala antalet poäng som du kan få för din lösning. T ex betyder (2/1) att uppgiften kan ge 2 g-poäng och
Matematik Åk 9 Provet omfattar stickprov av det centrala innehållet i Lgr-11. 1. b) c) d)
 1. b) c) d) a) Multiplikation med 100 kan förenklas med att flytta decimalerna lika många stg som antlet nollor. 00> svar 306 b) Använd kort division. Resultatet ger igen rest. Svar 108 c) Att multiplicera
1. b) c) d) a) Multiplikation med 100 kan förenklas med att flytta decimalerna lika många stg som antlet nollor. 00> svar 306 b) Använd kort division. Resultatet ger igen rest. Svar 108 c) Att multiplicera
1. 4 + 6 3 = Svar: (1/0) 3. Skriv ett heltal i rutan så att bråket får ett värde mellan 2 och 3. Svar: (1/0)
 1. 4 + 6 3 = Svar: (1/0) 2. Vad är hälften av 1 1 2? Svar: (1/0) 3. Skriv ett heltal i rutan så att bråket får ett värde mellan 2 och 3. Svar: (1/0) 8 4. Andreas har 4 km till skolan. Hur många minuter
1. 4 + 6 3 = Svar: (1/0) 2. Vad är hälften av 1 1 2? Svar: (1/0) 3. Skriv ett heltal i rutan så att bråket får ett värde mellan 2 och 3. Svar: (1/0) 8 4. Andreas har 4 km till skolan. Hur många minuter
Konkretisering av kunskapskraven i matematik år 7-9 (Lgr11)
 Konkretisering av kunskapskraven i matematik år 7-9 (Lgr11) ( www.skolverket.se) Kunskapskraven i matematik kan delas in i följande områden: problemlösning, begrepp, metod, kommunikation och resonemang.
Konkretisering av kunskapskraven i matematik år 7-9 (Lgr11) ( www.skolverket.se) Kunskapskraven i matematik kan delas in i följande områden: problemlösning, begrepp, metod, kommunikation och resonemang.
Innehållet i detta häfte är sekretessbelagt t o m den 9 juni 2006.
 Miniräknare ej tillåten Innehållet i detta häfte är sekretessbelagt t o m den 9 juni 2006. Denna del består av kortsvarsuppgifter som ska lösas utan miniräknare. Korrekt svar ger 1 g-poäng (1/0) eller
Miniräknare ej tillåten Innehållet i detta häfte är sekretessbelagt t o m den 9 juni 2006. Denna del består av kortsvarsuppgifter som ska lösas utan miniräknare. Korrekt svar ger 1 g-poäng (1/0) eller
Ma2bc. Komvux, Lund. Prov 1. 1-Övningsprov.
 Ma2bc. Komvux, Lund. Prov 1. 1-Övningsprov. (Lärare: Ingemar Carlsson) Anvisningar Provtid Hjälpmedel Del A Del B Del C Kravgränser 110 minuter för Del B, C och Del D. Du får påbörja del D (och börja använda
Ma2bc. Komvux, Lund. Prov 1. 1-Övningsprov. (Lärare: Ingemar Carlsson) Anvisningar Provtid Hjälpmedel Del A Del B Del C Kravgränser 110 minuter för Del B, C och Del D. Du får påbörja del D (och börja använda
NATIONELLT ÄMNESPROV I BIOLOGI VÅREN 2009
 Prov som ska återanvändas omfattas av sekretess enligt 4 kap. 3 sekretesslagen. Avsikten är att detta prov ska kunna återanvändas t.o.m. 2009-06-30. Vid sekretessbedömning skall detta beaktas. Delprov
Prov som ska återanvändas omfattas av sekretess enligt 4 kap. 3 sekretesslagen. Avsikten är att detta prov ska kunna återanvändas t.o.m. 2009-06-30. Vid sekretessbedömning skall detta beaktas. Delprov
Nationellt kursprov i MATEMATIK KURS A Våren 2005. Del II
 Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap 3 Sekretesslagen. För detta material gäller sekretessen till och med 10 juni 2005. Anvisningar Provtid Hjälpmedel
Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap 3 Sekretesslagen. För detta material gäller sekretessen till och med 10 juni 2005. Anvisningar Provtid Hjälpmedel
Matematik. Kursprov, vårterminen 2012. Elevhäfte. Del III. Elevens namn och klass/grupp
 Kursprov, vårterminen 2012 Matematik Elevhäfte Del III 1c Elevens namn och klass/grupp Prov som återanvänds omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta prov återanvänds
Kursprov, vårterminen 2012 Matematik Elevhäfte Del III 1c Elevens namn och klass/grupp Prov som återanvänds omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta prov återanvänds
Andreas Sandqvist 2015-04-30 ÖGAT OCH SYNEN
 Andreas Sandqvist 2015-04-30 ÖGAT OCH SYNEN Namn: Klass: 1. Ögats delar Ta reda på vad ögats delar heter som är markerade i bilden. 2. Varför har vi två ögon? I följande försök ska du undersöka om det
Andreas Sandqvist 2015-04-30 ÖGAT OCH SYNEN Namn: Klass: 1. Ögats delar Ta reda på vad ögats delar heter som är markerade i bilden. 2. Varför har vi två ögon? I följande försök ska du undersöka om det
NATIONELLT KURSPROV I MATEMATIK KURS A HÖSTEN 2000. Del II
 Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap 3 Sekretesslagen. För detta material gäller sekretessen till och med utgången av 2010. Anvisningar Provtid
Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap 3 Sekretesslagen. För detta material gäller sekretessen till och med utgången av 2010. Anvisningar Provtid
Matematik. Ämnesprov, läsår 2012/2013. Delprov D. Årskurs. Elevens namn och klass/grupp
 Ämnesprov, läsår 2012/2013 Matematik Delprov D Årskurs 9 Elevens namn och klass/grupp Prov som återanvänds omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta prov återanvänds
Ämnesprov, läsår 2012/2013 Matematik Delprov D Årskurs 9 Elevens namn och klass/grupp Prov som återanvänds omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta prov återanvänds
Delprov C. Innehållet i detta häfte är sekretessbelagt t o m den 30 juni 2008.
 Delprov C Innehållet i detta häfte är sekretessbelagt t o m den 30 juni 2008. Efter varje uppgift anges maximala antalet poäng som du kan få för din lösning. T ex betyder (2/1) att uppgiften kan ge 2 g-poäng
Delprov C Innehållet i detta häfte är sekretessbelagt t o m den 30 juni 2008. Efter varje uppgift anges maximala antalet poäng som du kan få för din lösning. T ex betyder (2/1) att uppgiften kan ge 2 g-poäng
Enkät rörande boende för äldre i Krokoms Kommun
 Enkät rörande boende för äldre i s Kommun 2015-10-14 I din hand håller du just nu en enkät som vi vill att du skall fylla i. Enkäten är helt anonym och skall endast användas för att få fram önskemål om
Enkät rörande boende för äldre i s Kommun 2015-10-14 I din hand håller du just nu en enkät som vi vill att du skall fylla i. Enkäten är helt anonym och skall endast användas för att få fram önskemål om
NATIONELLT KURSPROV I MATEMATIK KURS C HÖSTEN 2009
 Anvisningar Provtid Hjälpmedel Provmaterialet Provet Poäng och betygsgränser NATIONELLT KURSPROV I MATEMATIK KURS C HÖSTEN 009 40 minuter för Del I och Del II tillsammans. Vi rekommenderar att du använder
Anvisningar Provtid Hjälpmedel Provmaterialet Provet Poäng och betygsgränser NATIONELLT KURSPROV I MATEMATIK KURS C HÖSTEN 009 40 minuter för Del I och Del II tillsammans. Vi rekommenderar att du använder
NATIONELLT KURSPROV I MATEMATIK KURS A HÖSTEN 2001. Del II
 Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap 3 Sekretesslagen. För detta material gäller sekretessen till och med utgången av 2011. Anvisningar Provtid
Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap 3 Sekretesslagen. För detta material gäller sekretessen till och med utgången av 2011. Anvisningar Provtid
NATIONELLT KURSPROV I MATEMATIK KURS B VÅREN 2011
 Prov som ska återanvändas omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen (2009:400). Avsikten är att detta prov ska kunna återanvändas t.o.m. 2017-06-30 Vid sekretessbedömning
Prov som ska återanvändas omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen (2009:400). Avsikten är att detta prov ska kunna återanvändas t.o.m. 2017-06-30 Vid sekretessbedömning
Förkunskaper Grundläggande kunskaper om längdmätning med standardiserade mått samt kartkunskaper.
 Strävorna 4B Längdlådor... utvecklar sin förmåga att förstå, föra och använda logiska resonemang, dra slutsatser och generalisera samt muntligt och skriftligt förklara och argumentera för sitt tänkande....
Strävorna 4B Längdlådor... utvecklar sin förmåga att förstå, föra och använda logiska resonemang, dra slutsatser och generalisera samt muntligt och skriftligt förklara och argumentera för sitt tänkande....
Informationskvällar 18, 22 och 24 februari
 Informationskvällar 18, 22 och 24 februari VÄLKOMNA TILL INFORMATION OM NYA HYROR SÅ HÄR ÄR UPPLÄGGET IKVÄLL Del 1 vad blir resultatet för Er Hyresbeloppen 1 april 2016 genomgång av utskickat brev Hur
Informationskvällar 18, 22 och 24 februari VÄLKOMNA TILL INFORMATION OM NYA HYROR SÅ HÄR ÄR UPPLÄGGET IKVÄLL Del 1 vad blir resultatet för Er Hyresbeloppen 1 april 2016 genomgång av utskickat brev Hur
MATEMATIK FÖR KURS B (B-boken version 2)
 NATUR OCH KULTURS PROV VÅRTERMINEN 1997 MATEMATIK FÖR KURS B (B-boken version 2) Provets omfattning: t o m kapitel 4.1 i Matematik 2000 kurs B (version 2). PROVET BESTÅR AV TVÅ DELAR Del 1 testar huvudsakligen
NATUR OCH KULTURS PROV VÅRTERMINEN 1997 MATEMATIK FÖR KURS B (B-boken version 2) Provets omfattning: t o m kapitel 4.1 i Matematik 2000 kurs B (version 2). PROVET BESTÅR AV TVÅ DELAR Del 1 testar huvudsakligen
Hälsoenkät SF-36. Bilaga 1
 Bilaga 1 Hälsoenkät SF-36 Instruktion: Detta formulär innehåller frågor om hur Du ser på Din hälsa. Informationen ska hjälpa till att följa hur Du mår och fungerar i Ditt daglig liv.besvara frågorna genom
Bilaga 1 Hälsoenkät SF-36 Instruktion: Detta formulär innehåller frågor om hur Du ser på Din hälsa. Informationen ska hjälpa till att följa hur Du mår och fungerar i Ditt daglig liv.besvara frågorna genom
OBSERVERA ATT DETTA EXEMPELMATERIAL INTE MOTSVARAR ETT HELT KURSPROV I OMFATTNING OCH INNEHÅLL.
 Matematik kurs b och c - Exempeluppgifter OBSERVERA ATT DETTA EXEMPELMATERIAL INTE MOTSVARAR ETT HELT KURSPROV I OMFATTNING OCH INNEHÅLL. Del I: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv
Matematik kurs b och c - Exempeluppgifter OBSERVERA ATT DETTA EXEMPELMATERIAL INTE MOTSVARAR ETT HELT KURSPROV I OMFATTNING OCH INNEHÅLL. Del I: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv
Tal Räknelagar Prioriteringsregler
 Tal Räknelagar Prioriteringsregler Uttryck med flera räknesätt beräknas i följande ordning: 1. Parenteser 2. Exponenter. Multiplikation och division. Addition och subtraktion Exempel: Beräkna 10 5 7. 1.
Tal Räknelagar Prioriteringsregler Uttryck med flera räknesätt beräknas i följande ordning: 1. Parenteser 2. Exponenter. Multiplikation och division. Addition och subtraktion Exempel: Beräkna 10 5 7. 1.
Den öde ön. Bearbetad av Ingemar Wiklund - http://ingemar-wiklund.se Originalförfattare okänd.
 Den öde ön Av Introduktion 1. Du ska på en resa. Du ska åka med ett skepp långt bort. Beskriv hur skeppet ser ut och vart du ska åka. 2. Det blir storm och skeppet sjunker. bu hamnar på en strand. Skriv
Den öde ön Av Introduktion 1. Du ska på en resa. Du ska åka med ett skepp långt bort. Beskriv hur skeppet ser ut och vart du ska åka. 2. Det blir storm och skeppet sjunker. bu hamnar på en strand. Skriv
Hemtjänsten 2012 2012-08-13. Svarsfrekvens 77 av 130 utdelade = 60 %
 Hemtjänsten 2012 2012-08-13 Svarsfrekvens 77 av 130 utdelade = 60 % Bortfall: 3 av 77 Jag som har hemtjänst är: Bortfall: 1 av 77 Ålder Bortfall: 1 av 77 Jag som svarat på enkäten är: 1. Hur nöjd är du
Hemtjänsten 2012 2012-08-13 Svarsfrekvens 77 av 130 utdelade = 60 % Bortfall: 3 av 77 Jag som har hemtjänst är: Bortfall: 1 av 77 Ålder Bortfall: 1 av 77 Jag som svarat på enkäten är: 1. Hur nöjd är du
Catherine Bergman Maria Österlund
 Lgr 11 Matematik Åk 3 Geometri, mätningar och statistik FA C I T Catherine Bergman Maria Österlund Kan du använda geometriska begrepp? Kan du beskriva figurernas egenskaper, likheter och skillnader? Skriv
Lgr 11 Matematik Åk 3 Geometri, mätningar och statistik FA C I T Catherine Bergman Maria Österlund Kan du använda geometriska begrepp? Kan du beskriva figurernas egenskaper, likheter och skillnader? Skriv
3. Hur vet Max att Allan redan har tjuvstartat med de nybakta bullarna?
 SIDAN 1 Läsförståelse God morgon 1. Vem kommer och sjunger för Max på hans födelsedag? 2. Allan sjöng fel. Vad sjöng Allan som var fel? 3. Hur vet Max att Allan redan har tjuvstartat med de nybakta bullarna?
SIDAN 1 Läsförståelse God morgon 1. Vem kommer och sjunger för Max på hans födelsedag? 2. Allan sjöng fel. Vad sjöng Allan som var fel? 3. Hur vet Max att Allan redan har tjuvstartat med de nybakta bullarna?
HÄR BOR JAG Skogstrollen vt 2013
 HÄR BOR JAG Skogstrollen vt 2013 Fruktstunden (när det startade) Fyra barn och en pedagog satt och åt frukt en förmiddag. Fruktstunden Ett av barnen (Teo 2:10 år) funderar över att pedagogen har sagt att
HÄR BOR JAG Skogstrollen vt 2013 Fruktstunden (när det startade) Fyra barn och en pedagog satt och åt frukt en förmiddag. Fruktstunden Ett av barnen (Teo 2:10 år) funderar över att pedagogen har sagt att
Sid 1 Procent vertikalt SIFO 2010. Boende i lägenhet
 Sid 1 Kön Ålder Ålder - Man Ålder - Kvinna ------ -------------- ---------------------- ---------------------- ---------------------- 15-49 50-64 15-49 50-64 15-49 50-64 Total Man Kvinna år år 65- år år
Sid 1 Kön Ålder Ålder - Man Ålder - Kvinna ------ -------------- ---------------------- ---------------------- ---------------------- 15-49 50-64 15-49 50-64 15-49 50-64 Total Man Kvinna år år 65- år år
Högskoleprovet. Block 4. Anvisningar. Övningsexempel. Delprovet innehåller 22 uppgifter.
 Block 4 2007-03-31 Högskoleprovet Svarshäfte nr. DELPROV 7 NOGd Delprovet innehåller 22 uppgifter. Anvisningar Varje uppgift innehåller en fråga markerad med fet stil. Uppgiften kan även innehålla viss
Block 4 2007-03-31 Högskoleprovet Svarshäfte nr. DELPROV 7 NOGd Delprovet innehåller 22 uppgifter. Anvisningar Varje uppgift innehåller en fråga markerad med fet stil. Uppgiften kan även innehålla viss
Prov Antal uppgifter Uppgiftsnummer Rekommenderad provtid
 2011-10-29 Provpass 2 Svarshäfte nr. Högskoleprovet Kvantitativ del l Provet innehåller 40 uppgifter Instruktion etta provhäfte består av fyra olika delprov. essa är XYZ (matematik), KV (kvantitativa jämförelser),
2011-10-29 Provpass 2 Svarshäfte nr. Högskoleprovet Kvantitativ del l Provet innehåller 40 uppgifter Instruktion etta provhäfte består av fyra olika delprov. essa är XYZ (matematik), KV (kvantitativa jämförelser),
lång och 15 cm bred. Hur stor area har tomten i verkligheten? 4,5 2 l b) 2-2- 3 4
 LÄXA 12 1 Beräkna med huvudräkning a) En kvadrat har arean 81 cm 2. Hur stor är omkretsen? b) Hur mycket kostar 600 g fläskfile, om priset per kilogram är 120 kr? c) En burk energidryck innehåller 200
LÄXA 12 1 Beräkna med huvudräkning a) En kvadrat har arean 81 cm 2. Hur stor är omkretsen? b) Hur mycket kostar 600 g fläskfile, om priset per kilogram är 120 kr? c) En burk energidryck innehåller 200
Luftförvärmare artikel
 Text: Henrik Håkansson Gruppmedlemmar: Henrik Håkansson, Mateusz Gierkowicz, Oscar Ringqvist och William Skarpling. Luftförvärmare är ett smart sätt att värma upp t.ex. hus, det kräver ingen el och är
Text: Henrik Håkansson Gruppmedlemmar: Henrik Håkansson, Mateusz Gierkowicz, Oscar Ringqvist och William Skarpling. Luftförvärmare är ett smart sätt att värma upp t.ex. hus, det kräver ingen el och är
Provkod: TEN1 Exam code: TEN1
 TENTAMEN I TEIE53 INDUSTRIELL EKONOMI IEI, Linköpings Universitet Tid: 14:00-18:00 Sal: SP71 Antal uppgifter: 10 st Antal sidor: 11 st Max poäng: 50 poäng varav 27 p för 3a, 34 p för 4a och 43 p för 5a
TENTAMEN I TEIE53 INDUSTRIELL EKONOMI IEI, Linköpings Universitet Tid: 14:00-18:00 Sal: SP71 Antal uppgifter: 10 st Antal sidor: 11 st Max poäng: 50 poäng varav 27 p för 3a, 34 p för 4a och 43 p för 5a
Komvux/gymnasieprogram:
 Namn: Skola: Komvux/gymnasieprogram: Anvisningar: Tidsbunden del består av två delar, Del I och Del II. Den sammanlagda provtiden är 120 minuter varav högst 30 minuter för Del I. Till uppgifterna i Del
Namn: Skola: Komvux/gymnasieprogram: Anvisningar: Tidsbunden del består av två delar, Del I och Del II. Den sammanlagda provtiden är 120 minuter varav högst 30 minuter för Del I. Till uppgifterna i Del
Övning: Dilemmafrågor
 Övning: Dilemmafrågor Placera föräldrarna i grupper med ca 6-7 st/grupp. Läs upp ett dilemma i taget och låt föräldrarna resonera kring tänkbara lösningar. Varje fråga kan även visas på OH/ppt samtidigt,
Övning: Dilemmafrågor Placera föräldrarna i grupper med ca 6-7 st/grupp. Läs upp ett dilemma i taget och låt föräldrarna resonera kring tänkbara lösningar. Varje fråga kan även visas på OH/ppt samtidigt,
SKOLRESANS KOLDIOXIDAVTRYCK
 SKOLRESANS KOLDIOXIDAVTRYCK Övningens mål Eleverna ska bli medvetna om hur deras resor till skolan bidrar till koldioxidutsläppen beroende på färdmedel. Sammanfattning av övningen På en bestämd dag noterar
SKOLRESANS KOLDIOXIDAVTRYCK Övningens mål Eleverna ska bli medvetna om hur deras resor till skolan bidrar till koldioxidutsläppen beroende på färdmedel. Sammanfattning av övningen På en bestämd dag noterar
Matematik. Ämnesprov, läsår 2014/2015. Delprov C. Årskurs. Elevens namn och klass/grupp
 Ämnesprov, läsår 2014/2015 Matematik Delprov C Årskurs 6 Elevens namn och klass/grupp Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Ämnesprov, läsår 2014/2015 Matematik Delprov C Årskurs 6 Elevens namn och klass/grupp Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
5-1 Avbildningar, kartor, skalor, orientering och navigation
 Namn:. 5-1 Avbildningar, kartor, skalor, orientering och navigation Inledning Nu skall du studera hur man avbildar verkligheten. Vad skall man göra det för? undrar du eftersom du skall ifrågasätta allt.
Namn:. 5-1 Avbildningar, kartor, skalor, orientering och navigation Inledning Nu skall du studera hur man avbildar verkligheten. Vad skall man göra det för? undrar du eftersom du skall ifrågasätta allt.
Läs noggrant informationen nedan innan du börjar skriva tentamen
 Tentamen i Statistik 1: Undersökningsmetodik Ämneskod S0006M Totala antalet uppgifter: Totala antalet poäng Lärare: Mykola Shykula 5 25 Tentamensdatum 2014-05-15 Skrivtid 09.00-14.00 Jourhavande lärare:
Tentamen i Statistik 1: Undersökningsmetodik Ämneskod S0006M Totala antalet uppgifter: Totala antalet poäng Lärare: Mykola Shykula 5 25 Tentamensdatum 2014-05-15 Skrivtid 09.00-14.00 Jourhavande lärare:
Matematik. Delprov C. Vårterminen 2009 ÄMNESPROV ÅRSKURS. Elevens namn
 ÄMNESPROV Matematik ÅRSKURS 9 Prov som ska återanvändas omfattas av sekretess enligt 4 kap. 3 sekretesslagen. Avsikten är att detta prov ska kunna återanvändas t.o.m. 2009-06-30. Vid sekretessbedömning
ÄMNESPROV Matematik ÅRSKURS 9 Prov som ska återanvändas omfattas av sekretess enligt 4 kap. 3 sekretesslagen. Avsikten är att detta prov ska kunna återanvändas t.o.m. 2009-06-30. Vid sekretessbedömning
Världskrigen. Talmanus
 Världskrigen I början av 1900-talet var det två stora krig, första och andra världskriget. Många barn hade det mycket svårt under krigen. Men de som krigade tyckte inte att de hade något ansvar för barnen
Världskrigen I början av 1900-talet var det två stora krig, första och andra världskriget. Många barn hade det mycket svårt under krigen. Men de som krigade tyckte inte att de hade något ansvar för barnen
Låt eleverna öva på att dra slutsatser om textens handling genom att leta ledtrådar i texten.
 Till läraren om kopieringsunderlag: Ledtrådar och bevis Låt eleverna öva på att dra slutsatser om textens handling genom att leta ledtrådar i texten. 1. De börjar med att titta på rubriker och bilder.
Till läraren om kopieringsunderlag: Ledtrådar och bevis Låt eleverna öva på att dra slutsatser om textens handling genom att leta ledtrådar i texten. 1. De börjar med att titta på rubriker och bilder.
WinMore Systems Hippo Hippo Tips
 L-Advantage Solutions AB WinMore Systems Hippo Hippo Tips Hur man gör i Hipposystemet Copyright 2012 Introduktion Välkommen till hur man gör i Hipposystemet. Här kommer vi att ta upp mer anvancerade sätt
L-Advantage Solutions AB WinMore Systems Hippo Hippo Tips Hur man gör i Hipposystemet Copyright 2012 Introduktion Välkommen till hur man gör i Hipposystemet. Här kommer vi att ta upp mer anvancerade sätt
Namn: Det här är jag (Här kan du rita eller skriva)
 Min värld Namn: Det här är jag (Här kan du rita eller skriva) Gramse, Mallo och mamma Gramse är ganska liten med långa öron och bor i en skog i landet Hittapou. Gramse brukar vara lila men byter färg ibland,
Min värld Namn: Det här är jag (Här kan du rita eller skriva) Gramse, Mallo och mamma Gramse är ganska liten med långa öron och bor i en skog i landet Hittapou. Gramse brukar vara lila men byter färg ibland,
SKOLPORTENS NUMRERADE ARTIKELSERIE FÖR UTVECKLINGSARBETE I SKOLAN. Bilagor
 SKOLPORTENS NUMRERADE ARTIKELSERIE FÖR UTVECKLINGSARBETE I SKOLAN Bilagor Gemensamma matematikprov, analysinstrument och bedömningsmatriser för kvalitetshöjningar Författare: Per Ericson, Max Ljungberg
SKOLPORTENS NUMRERADE ARTIKELSERIE FÖR UTVECKLINGSARBETE I SKOLAN Bilagor Gemensamma matematikprov, analysinstrument och bedömningsmatriser för kvalitetshöjningar Författare: Per Ericson, Max Ljungberg
4. Gör lämpliga avläsningar i diagrammet och bestäm linjens ekvation.
 Repetitionsuppgifter inför prov 2 Ma2 NASA15 vt16 E-uppgifter 1. Beräkna sträckan i triangeln nedan. 3,8 m 37 o 2. En seglare ser en fyr på ett berg. Hon mäter höjdvinkeln till fyrljuset till 7,3 o. På
Repetitionsuppgifter inför prov 2 Ma2 NASA15 vt16 E-uppgifter 1. Beräkna sträckan i triangeln nedan. 3,8 m 37 o 2. En seglare ser en fyr på ett berg. Hon mäter höjdvinkeln till fyrljuset till 7,3 o. På
SÄTT DIG NER, 1. KOLLA PLANERINGEN 2. TITTA I DITT SKRIVHÄFTE.
 SÄTT DIG NER, 1. KOLLA PLANERINGEN 2. TITTA I DITT SKRIVHÄFTE. Vad gjorde vi förra gången? Har du några frågor från föregående lektion? 3. titta i ditt läromedel (boken) Vad ska vi göra idag? Optik och
SÄTT DIG NER, 1. KOLLA PLANERINGEN 2. TITTA I DITT SKRIVHÄFTE. Vad gjorde vi förra gången? Har du några frågor från föregående lektion? 3. titta i ditt läromedel (boken) Vad ska vi göra idag? Optik och
BEDÖMNINGSSTÖD. till TUMMEN UPP! matte inför betygssättningen i årskurs 6
 BEDÖMNINGSSTÖD till TUMMEN UPP! matte inför betygssättningen i årskurs 6 Det här är ett BEDÖMNINGSSTÖD som hjälper dig att göra en säkrare bedömning av elevernas kunskaper inför betygssättningen i årskurs
BEDÖMNINGSSTÖD till TUMMEN UPP! matte inför betygssättningen i årskurs 6 Det här är ett BEDÖMNINGSSTÖD som hjälper dig att göra en säkrare bedömning av elevernas kunskaper inför betygssättningen i årskurs
E-post för nybörjare
 E-post för nybörjare Innehåll: Inledning 1 E-post 2 Att skapa ett e-postkonto 3 Skicka och ta emot e-post 5 Övningar 7 Söderköpings stadsbibliotek sep. 2012 2 Inledning Välkommen till Nyfiken på nätet
E-post för nybörjare Innehåll: Inledning 1 E-post 2 Att skapa ett e-postkonto 3 Skicka och ta emot e-post 5 Övningar 7 Söderköpings stadsbibliotek sep. 2012 2 Inledning Välkommen till Nyfiken på nätet
Samhällskunskap Civics
 1 Ämnesprov, läsår 2012/2013 Ersättningsprov Samhällskunskap Civics Delprov A2 Årskurs 6 Elevens namn och klass/grupp Prov som återanvänds omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen.
1 Ämnesprov, läsår 2012/2013 Ersättningsprov Samhällskunskap Civics Delprov A2 Årskurs 6 Elevens namn och klass/grupp Prov som återanvänds omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen.
Matematik. Ämnesprov, läsår 2014/2015. Delprov B. Årskurs. Elevens namn och klass/grupp
 Ämnesprov, läsår 2014/2015 Matematik Delprov B Årskurs 6 Elevens namn och klass/grupp Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Ämnesprov, läsår 2014/2015 Matematik Delprov B Årskurs 6 Elevens namn och klass/grupp Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Veckomatte åk 5 med 10 moment
 Veckomatte åk 5 med 10 moment av Ulf Eskilsson Innehållsförteckning Inledning 2 Utdrag ur kursplanen i matematik 3 Grundläggande struktur i Veckomatte - Åk 5 4 Strategier för Veckomatte - Åk 5 5 Veckomatte
Veckomatte åk 5 med 10 moment av Ulf Eskilsson Innehållsförteckning Inledning 2 Utdrag ur kursplanen i matematik 3 Grundläggande struktur i Veckomatte - Åk 5 4 Strategier för Veckomatte - Åk 5 5 Veckomatte
4. Hur ofta deltar du i föreningsaktiviteter? Ofta Ibland Aldrig 5. I vilken kommun bor du?
 Hej! Jag heter Miri Stryjan, och gör denna enkät för en uppsats i nationalekonomi på Stockholms Universitet. Uppsatsen handlar om globalisering, migration och att skicka pengar till sitt hemland. Enkäten
Hej! Jag heter Miri Stryjan, och gör denna enkät för en uppsats i nationalekonomi på Stockholms Universitet. Uppsatsen handlar om globalisering, migration och att skicka pengar till sitt hemland. Enkäten
Nöjd Hyresgäst Byggebo 2011 Helhetsbedömning
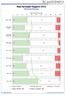 Helhetsbedömning 0 0 0 0 0 0 0 Totalt, n= 1 Kikebo totalt, n= 2 Kristineberg totalt, n= 3 BV 1, n=2 3 BV 2, n= 3 BV 3, n=0 BV, n=3 2 2 BV, n= 3 BV, n= 3 Betyg - "Helnöjda" Betyg 3- - "Varken eller" Betyg
Helhetsbedömning 0 0 0 0 0 0 0 Totalt, n= 1 Kikebo totalt, n= 2 Kristineberg totalt, n= 3 BV 1, n=2 3 BV 2, n= 3 BV 3, n=0 BV, n=3 2 2 BV, n= 3 BV, n= 3 Betyg - "Helnöjda" Betyg 3- - "Varken eller" Betyg
Välkommen till din loggbok!
 Loggbok för: 1 Välkommen till din loggbok! Den här boken är till för dig som ska träna med Minneslek. I loggboken får du information om arbetsminnet, veta hur träningen går till och ett schema där du kan
Loggbok för: 1 Välkommen till din loggbok! Den här boken är till för dig som ska träna med Minneslek. I loggboken får du information om arbetsminnet, veta hur träningen går till och ett schema där du kan
Hörselvetenskap B, Audiologisk rehabilitering, 13,5 hp
 Hörselvetenskap B, Audiologisk rehabilitering, 13,5 hp 2011-05-27 4 timmar Kursansvarig: Sara Båsjö Svaren poängsätts med svarens fullständighet som grund. Besvara varje fråga på separat papper och skriv
Hörselvetenskap B, Audiologisk rehabilitering, 13,5 hp 2011-05-27 4 timmar Kursansvarig: Sara Båsjö Svaren poängsätts med svarens fullständighet som grund. Besvara varje fråga på separat papper och skriv
Matematik. Ämnesprov, läsår 2012/2013. Delprov D. Årskurs. Elevens namn och klass/grupp
 Ämnesprov, läsår 2012/2013 Matematik Delprov D Årskurs 9 Elevens namn och klass/grupp Prov som återanvänds omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta prov återanvänds
Ämnesprov, läsår 2012/2013 Matematik Delprov D Årskurs 9 Elevens namn och klass/grupp Prov som återanvänds omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta prov återanvänds
Ringkontakten. Ett kostnadsfritt erbjudande från frivilligorganisationerna och Hjo kommun
 Ringkontakten Ett kostnadsfritt erbjudande från frivilligorganisationerna och Hjo kommun OM RINGKONTAKTEN Tycker Du att det känns tryggt att veta att någon ringer upp Dig varje vardag? Bara för att höra
Ringkontakten Ett kostnadsfritt erbjudande från frivilligorganisationerna och Hjo kommun OM RINGKONTAKTEN Tycker Du att det känns tryggt att veta att någon ringer upp Dig varje vardag? Bara för att höra
8-1 Formler och uttryck. Namn:.
 8-1 Formler och uttryck. Namn:. Inledning Ibland vill du lösa lite mer komplexa problem. Till exempel: Kalle är dubbelt så gammal som Stina, och tillsammans är de 33 år. Hur gammal är Kalle och Stina?
8-1 Formler och uttryck. Namn:. Inledning Ibland vill du lösa lite mer komplexa problem. Till exempel: Kalle är dubbelt så gammal som Stina, och tillsammans är de 33 år. Hur gammal är Kalle och Stina?
9-1 Koordinatsystem och funktioner. Namn:
 9- Koordinatsystem och funktioner. Namn: Inledning I det här kapitlet skall du lära dig vad ett koordinatsystem är och vilka egenskaper det har. I ett koordinatsystem kan man representera matematiska funktioner
9- Koordinatsystem och funktioner. Namn: Inledning I det här kapitlet skall du lära dig vad ett koordinatsystem är och vilka egenskaper det har. I ett koordinatsystem kan man representera matematiska funktioner
Vad tycker du om sfi?
 Oktober 2012 Vad tycker du om sfi? Skolverket gör under hösten en stor undersökning om vad elever tycker om sin utbildning. Det är första gången undersökningen görs och resultatet kommer att användas till
Oktober 2012 Vad tycker du om sfi? Skolverket gör under hösten en stor undersökning om vad elever tycker om sin utbildning. Det är första gången undersökningen görs och resultatet kommer att användas till
Lärarmaterial. Vad handlar boken om? Mål från Lgr 11: Författare: Morten Dürr
 sidan 1 Författare: Morten Dürr Vad handlar boken om? Boken handlar om Amir som är 9 år och går i andra klass. Amir vill göra saker på sitt eget sätt. I skolan ska de skriva om sitt sommarlov och Amir
sidan 1 Författare: Morten Dürr Vad handlar boken om? Boken handlar om Amir som är 9 år och går i andra klass. Amir vill göra saker på sitt eget sätt. I skolan ska de skriva om sitt sommarlov och Amir
Familjetema: STJÄRNFAMILJEN Vi är alla stjärnor. Allra bäst på att vara just den vi är!
 Familjepaketet Böckerna i Familjepaketet har hög igenkänningsfaktor och koppling till barns vardag och visar samtidigt många olika sätt att leva. Runt 30% av alla barn idag lever i en frånskild familj.
Familjepaketet Böckerna i Familjepaketet har hög igenkänningsfaktor och koppling till barns vardag och visar samtidigt många olika sätt att leva. Runt 30% av alla barn idag lever i en frånskild familj.
dom hem och hämtade en stor badbalja och stoppade mig i den. - vad ska vi kalla den? undrade ett barn. - Då sa ett anat barn kanske Padis. - Ja!
 ÖNSKE BOKEN Önske boken Nu ska ni få höra om när jag var 13 år, 9 månader, 5 dar 3 timmar och 17 sekunder. Jag bodde i Stockholm med min familj. Jag hade två syskon dom heter Erik och Amanda. Min mamma
ÖNSKE BOKEN Önske boken Nu ska ni få höra om när jag var 13 år, 9 månader, 5 dar 3 timmar och 17 sekunder. Jag bodde i Stockholm med min familj. Jag hade två syskon dom heter Erik och Amanda. Min mamma
Skapa utemiljöer i trä Låt dig inspireras!
 Skapa utemiljöer i trä Låt dig inspireras! Kärlek till hållbarhet Från skog till tryckimpregnerat Brunt eller grönt? En smaksak. För att skapa material till en härlig uteplats eller ett stabilt staket
Skapa utemiljöer i trä Låt dig inspireras! Kärlek till hållbarhet Från skog till tryckimpregnerat Brunt eller grönt? En smaksak. För att skapa material till en härlig uteplats eller ett stabilt staket
Trafikskadestöd 020-49 48 00 Måndag-tisdag och torsdag-fredag kl. 9.00-11.30
 En trafikolycka medför många gånger problem för de inblandade och deras anhöriga. Vissa problem kanske kan lösas med ett enkelt telefonsamtal. Detta gäller även för Dig som är anhörig eller vittne. Trafikskadestöd
En trafikolycka medför många gånger problem för de inblandade och deras anhöriga. Vissa problem kanske kan lösas med ett enkelt telefonsamtal. Detta gäller även för Dig som är anhörig eller vittne. Trafikskadestöd
Kursutvärdering Ämne: SO Lärare: Esa Seppälä/Cecilia Enoksson Läsåret 12-13 Klass: SPR2
 8 Mycket bra Bra Dåligt Mycket dåligt EAS 1. Hur var ditt första intryck av denna kurs? Mycket bra 6 21 Bra 21 75 Dåligt - - Mycket dåligt 1 4 EAS - - Antal EAS:. Antal svarande: 28. Mv: (Skala 1) = 78,57
8 Mycket bra Bra Dåligt Mycket dåligt EAS 1. Hur var ditt första intryck av denna kurs? Mycket bra 6 21 Bra 21 75 Dåligt - - Mycket dåligt 1 4 EAS - - Antal EAS:. Antal svarande: 28. Mv: (Skala 1) = 78,57
NATIONELLT PROV I MATEMATIK KURS E HÖSTEN 1996
 Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap. 3 sekretesslagen. För detta material gäller sekretessen till och med utgången av mars 1997. NATIONELLT PROV
Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap. 3 sekretesslagen. För detta material gäller sekretessen till och med utgången av mars 1997. NATIONELLT PROV
Förtest. Hur kan jag arbeta med förtesten? Hur dokumenterar jag elevens kunskapsutveckling? Uppfattar du det som att eleven kan matematikinnehållet
 AB Höst LP 1-2 Flik 02 Förtest (8768) Lev 1.qxd 2004-01-20 18:10 Sida 1 Förtest För alla lärare är det viktigt att skaffa sig en god bild av elevens kunskaper för att veta vad eleven behöver för att gå
AB Höst LP 1-2 Flik 02 Förtest (8768) Lev 1.qxd 2004-01-20 18:10 Sida 1 Förtest För alla lärare är det viktigt att skaffa sig en god bild av elevens kunskaper för att veta vad eleven behöver för att gå
Kryssa för de svarsalternativ som stämmer bäst överens med din uppfattning.
 En del frågor ska besvaras ur två perspektiv: Så här var det för mig och Så här betydelsefullt var det för mig. Kryssa för de svarsalternativ som stämmer bäst överens med din uppfattning. OMT-studien,
En del frågor ska besvaras ur två perspektiv: Så här var det för mig och Så här betydelsefullt var det för mig. Kryssa för de svarsalternativ som stämmer bäst överens med din uppfattning. OMT-studien,
Inledning...5. Bedömningsanvisningar...5 Allmänna bedömningsanvisningar...5 Bedömningsanvisningar Delprov B...6 Bedömningsanvisningar Delprov C...
 Innehåll Inledning...5 Bedömningsanvisningar...5 Allmänna bedömningsanvisningar...5 Bedömningsanvisningar Delprov B...6 Bedömningsanvisningar Delprov C...20 Provbetyg...37 Kopieringsunderlag för resultatsammanställning...38
Innehåll Inledning...5 Bedömningsanvisningar...5 Allmänna bedömningsanvisningar...5 Bedömningsanvisningar Delprov B...6 Bedömningsanvisningar Delprov C...20 Provbetyg...37 Kopieringsunderlag för resultatsammanställning...38
Spöket i Sala Silvergruva
 Spöket i Sala Silvergruva Hej! Jag har hört att du jobbar som smådeckare och jag skulle behöva hjälp av dig. Det är bäst att du får höra vad jag behöver hjälp med. I Sala finns Sala Silvergruva, den har
Spöket i Sala Silvergruva Hej! Jag har hört att du jobbar som smådeckare och jag skulle behöva hjälp av dig. Det är bäst att du får höra vad jag behöver hjälp med. I Sala finns Sala Silvergruva, den har
NATIONELLT KURSPROV I MATEMATIK KURS A VÅREN Del I
 Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap 3 Sekretesslagen. För detta material gäller sekretessen till och med utgången av juni månad 2002. NATIONELLT
Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap 3 Sekretesslagen. För detta material gäller sekretessen till och med utgången av juni månad 2002. NATIONELLT
Övningsmaterial till Pod-utbildningen Förhandlingsteknik
 Övningsmaterial till Pod-utbildningen Förhandlingsteknik Avsnitt 1 Introduktion En förhandling är en process för att tillfredsställa två eller flera parters olika behov. Utifrån definitionen ovan, fundera
Övningsmaterial till Pod-utbildningen Förhandlingsteknik Avsnitt 1 Introduktion En förhandling är en process för att tillfredsställa två eller flera parters olika behov. Utifrån definitionen ovan, fundera
Unghästprojektet på Wången 2010-2012
 Unghästprojektet på Wången 2010-2012 1-3-åriga travhästar fodrade utan kraftfoder och tränade i kortare distanser Den här studien har visat att ettåriga travhästar som utfodras med ett energirikt grovfoder
Unghästprojektet på Wången 2010-2012 1-3-åriga travhästar fodrade utan kraftfoder och tränade i kortare distanser Den här studien har visat att ettåriga travhästar som utfodras med ett energirikt grovfoder
Gruppträning 2011/2012
 Vetlanda Badhus Vecka 51 Gruppträning 2011/2012 Gymmet Varma sängen Myresjö simhall Vecka 51 salen Vetlanda Badhus Vecka 52 Gruppträning 2011/2012 Gymmet Varma sängen Myresjö simhall Vecka 52 salen Gruppträning
Vetlanda Badhus Vecka 51 Gruppträning 2011/2012 Gymmet Varma sängen Myresjö simhall Vecka 51 salen Vetlanda Badhus Vecka 52 Gruppträning 2011/2012 Gymmet Varma sängen Myresjö simhall Vecka 52 salen Gruppträning
Ekegårdsbladet februari 2015 www.ekegarden.nu, styrelsen@ekegarden.se
 Ekegårdsbladet februari 2015 www.ekegarden.nu, styrelsen@ekegarden.se EE-blad Ekegårdsbladet kommer fr.o.m. nu att kunna fås via mail. Gå in på vår hemsida och följ instruktionerna. Stämma 2015, 22 april.
Ekegårdsbladet februari 2015 www.ekegarden.nu, styrelsen@ekegarden.se EE-blad Ekegårdsbladet kommer fr.o.m. nu att kunna fås via mail. Gå in på vår hemsida och följ instruktionerna. Stämma 2015, 22 april.
Statistisk undersökningsmetodik (Pol. kand.)
 TENTAMEN Tentamensdatum 2008-10-02 Statistisk undersökningsmetodik (Pol. kand.) Namn:.. Personnr:.. Tentakod: Obs! Var noga med att skriva din tentakod på varje lösningsblad som du lämnar in. Skrivtid
TENTAMEN Tentamensdatum 2008-10-02 Statistisk undersökningsmetodik (Pol. kand.) Namn:.. Personnr:.. Tentakod: Obs! Var noga med att skriva din tentakod på varje lösningsblad som du lämnar in. Skrivtid
VARGAVINTER JOJO SNÖN DEN FINNS FORTFARANDE KVAR MEN DET FINNS ÄNDÅ DE SOM TROR ATT DET BLIR EN VÅR
 11:ans medlemsblad Brf Stockholmshus nr 11 Gubbängen www.stockholmshus11.se Nummer 1 Våren 2013 VARGAVINTER JOJO SNÖN DEN FINNS FORTFARANDE KVAR MEN DET FINNS ÄNDÅ DE SOM TROR ATT DET BLIR EN VÅR Snön
11:ans medlemsblad Brf Stockholmshus nr 11 Gubbängen www.stockholmshus11.se Nummer 1 Våren 2013 VARGAVINTER JOJO SNÖN DEN FINNS FORTFARANDE KVAR MEN DET FINNS ÄNDÅ DE SOM TROR ATT DET BLIR EN VÅR Snön
Rödebyområdets elevhälsa
 Rödebyområdets elevhälsa Inledning Skolan har två huvuduppdrag; att främja barns lärande och att förankra vårt samhälles värdegrund. Dessa områden hänger nära samman och här ingår också elevhälsan som
Rödebyområdets elevhälsa Inledning Skolan har två huvuduppdrag; att främja barns lärande och att förankra vårt samhälles värdegrund. Dessa områden hänger nära samman och här ingår också elevhälsan som
Moped klass II Kunskapsprov 2
 Moped klass II Kunskapsprov 2 Förnamn Efternamn Adress Postnummer Ort Telefon Mobiltelefon E-postadress Personnummer Provet genomfört den Förrättningsman Lokal Ort Godkänd Ej godkänd Antal rätt Underskrift
Moped klass II Kunskapsprov 2 Förnamn Efternamn Adress Postnummer Ort Telefon Mobiltelefon E-postadress Personnummer Provet genomfört den Förrättningsman Lokal Ort Godkänd Ej godkänd Antal rätt Underskrift
12 Programstege Substantiv
 Det här är en programstege för substantiv. Du kan alltså lära dig om substantiven på ett enkelt sätt, en liten bit i taget. Varje sida innehåller fakta om substantiv, tillsammans med uppgifter som du också
Det här är en programstege för substantiv. Du kan alltså lära dig om substantiven på ett enkelt sätt, en liten bit i taget. Varje sida innehåller fakta om substantiv, tillsammans med uppgifter som du också
NATIONELLT PROV I MATEMATIK KURS A VÅREN 1996. Tidsbunden del
 NATIONELLT PROV I MATEMATIK KURS A VÅREN 1996 Tidsbunden del Anvisningar Provperiod 10 maj - 1 juni 1996. Provtid Hjälpmedel Provmaterialet 120 minuter utan rast. Miniräknare och formelsamling. Formelblad
NATIONELLT PROV I MATEMATIK KURS A VÅREN 1996 Tidsbunden del Anvisningar Provperiod 10 maj - 1 juni 1996. Provtid Hjälpmedel Provmaterialet 120 minuter utan rast. Miniräknare och formelsamling. Formelblad
TENTAMEN KVANTITATIV METOD (100205)
 ÖREBRO UNIVERSITET Hälsoakademin Idrott B, Vetenskaplig metod TENTAMEN KVANTITATIV METOD (205) Examinationen består av 11 frågor, några med tillhörande följdfrågor. Besvara alla frågor i direkt anslutning
ÖREBRO UNIVERSITET Hälsoakademin Idrott B, Vetenskaplig metod TENTAMEN KVANTITATIV METOD (205) Examinationen består av 11 frågor, några med tillhörande följdfrågor. Besvara alla frågor i direkt anslutning
Högskoleverket NOG 2006-10-21
 Högskoleverket NOG 2006-10-21 1. Rekommenderat dagligt intag (RDI) av kalcium är 0,8 g per person. 1 dl mellanmjölk väger 100 g. Hur mycket mellanmjölk ska man dricka för att få i sig rekommenderat dagligt
Högskoleverket NOG 2006-10-21 1. Rekommenderat dagligt intag (RDI) av kalcium är 0,8 g per person. 1 dl mellanmjölk väger 100 g. Hur mycket mellanmjölk ska man dricka för att få i sig rekommenderat dagligt
CUMULUS STEAMER SVENSK BRUKSANVISNING
 CUMULUS STEAMER SVENSK BRUKSANVISNING 11 VÄLKOMMEN TILL THE STEAMERY The Steamery är ett klädvårdsföretag baserat i Stockholm. Vi älskar kläder och vill att de ska hålla länge. Vårt mål är därför att ge
CUMULUS STEAMER SVENSK BRUKSANVISNING 11 VÄLKOMMEN TILL THE STEAMERY The Steamery är ett klädvårdsföretag baserat i Stockholm. Vi älskar kläder och vill att de ska hålla länge. Vårt mål är därför att ge
När Lisa skulle sövas.
 2010 När det var dags att sova fick jag sömnmedel genom plaströret på handen. markusmarkusmarkus När Lisa skulle sövas. Barn- och ungdomsmedicinska kliniken, Jönköping 2010-03-25 Här är jag, jag heter
2010 När det var dags att sova fick jag sömnmedel genom plaströret på handen. markusmarkusmarkus När Lisa skulle sövas. Barn- och ungdomsmedicinska kliniken, Jönköping 2010-03-25 Här är jag, jag heter
Vägen till milen med Metro Mode
 Vägen till milen med Metro Mode 12 veckor till Tjejmilen 2016 Träningsprogram 1: Från 5 till 10 kilometer För dig som är ny i spåret eller som har sprungit runt 5 kilometer tidigare och nu vill ta steget
Vägen till milen med Metro Mode 12 veckor till Tjejmilen 2016 Träningsprogram 1: Från 5 till 10 kilometer För dig som är ny i spåret eller som har sprungit runt 5 kilometer tidigare och nu vill ta steget
Matematik. Kursprov, vårterminen 2012. Elevhäfte. Del I och Del II. Elevens namn och klass/grupp
 Kursprov, vårterminen 2012 Matematik Elevhäfte Del I och Del II 1a Elevens namn och klass/grupp Prov som återanvänds omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta prov
Kursprov, vårterminen 2012 Matematik Elevhäfte Del I och Del II 1a Elevens namn och klass/grupp Prov som återanvänds omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta prov
Ansökan om färdtjänst (egen ansökan)
 Information Ansökan enligt lagen om färdtjänst (http://www.riksdagen.se/sv/dokument-lagar/lagar/ Svenskforfattningssamling/Lag-1997736-om-fardtjanst_sfs-1997-736/) (1997:736). Färdtjänst kan inte erhållas
Information Ansökan enligt lagen om färdtjänst (http://www.riksdagen.se/sv/dokument-lagar/lagar/ Svenskforfattningssamling/Lag-1997736-om-fardtjanst_sfs-1997-736/) (1997:736). Färdtjänst kan inte erhållas
