d) 4 25 e) f) a) b) 679 c) kr. Hur mycket får Magda tillbaka när hon betalar? Ledtråd: Svaret är inte 31 kr.
|
|
|
- Lucas Hellström
- för 9 år sedan
- Visningar:
Transkript
1 Till vart och ett av bokens sex kapitel hör fyra läxor. Varje läxa innehåller 12 uppgifter samt ett veckans problem. I facit kan du kontrollera om du löst uppgifterna rätt. Läxa 1 Efter avsnitt a) b) 72 / 9 c) 7 90 d) 4 25 e) f) Skriv talen med siffror. a) niotusen trettiofem b) två miljoner sextiofemtusen 3 a) b) c) Vilket värde har siffran 7 i talet a) b) 679 c) Magda har 180 kr i sedlar i plånboken. Hon köper en bok som kostar 149 kr. Hur mycket får Magda tillbaka när hon betalar? Ledtråd: Svaret är inte 31 kr. 6 a) 895 / 5 b) c) Centraleuropas högsta berg, Mont Blanc, är m högt. Nordens högsta berg, Galdöpiggen, är m lägre. Afrikas högsta berg, Kilimanjaro, är m högre än Galdöpiggen. Världens högsta berg, Mount Everest, är m. a) Hur hög är Galdöpiggen? b) Hur mycket högre är Mount Everest än Kilimanjaro? 8 Förklara varför siffran 3 är mer värd än siffran 7 i talet
2 År 1909 importerades de första bananerna till Sverige. De blev snabbt populära och idag äter vi varje år i genomsnitt 20 kg bananer per person. 9 Vad kostar bananerna som en familj på fyra personer äter varje år? Räkna med att priset per kilogram är 20 kr. 10 Om man multiplicerar åldern på tre syskon blir produkten 90. Inget av syskonen är över 15 år. Hur gamla är syskonen? Försök komma på så många lösningar som möjligt. 11 Talet 2 3 utläses två upphöjt till tre. Det är ett kortare sätt att skriva Alltså är 2 3 = 8. Hur mycket är a) 5 2 b) c) Multiplikation räknas före addition och subtraktion. 12 Summan av två tal är Det ena talet är sex gånger så stort som det andra. Vilken är differensen mellan de två talen? Veckans problem Vilka siffror ska stå i stället för bokstäverna? a) b) c) A5B + 7C A7 + B5C 1041 A1B 2C
3 Läxa 2 Efter avsnitt a) b) 80 7 c) d) e) 72 / 8 f) Skriv med siffrorna 8, 4, 1 och 2 a) ett så litet tal som möjligt b) det näst största tal som går c) ett tal som ligger så nära som möjligt 3 Vilket tal saknas? 5 1? År 1825 började man gräva en tunnel under floden Themsen. Först efter 18 år var tunneln klar. a) Vilket år var tunneln klar? b) Hur gammal var tunneln vid millennieskiftet, det vill säga år 2000? Tunneln under floden Themsen var från början en gångtunnel. Idag är tunneln en del av Londons tunnelbanesystem. 317
4 5 Skriv talen med siffror. a) en och en halv miljon b) femhundratjugotusen femton 6 Vilka temperaturer saknas? Temp var Temp steg Temp sjönk Temp blev a) 0 ºC 2 ºC 6 ºC? b) 1 ºC 3 ºC? 8 ºC c) 6 ºC? 8 ºC 2 ºC 7 Vilket tal ska stå i rutan? a)? = 701 b) 117 =? 4 c) 5? = Hur vet du att ett bråk är större än 1 2 men mindre än 1? 9 En affär säljer burkar med 4 liter färg. En burk kostar 348 kr. En dag sänker affären priset till 298 kr. Hur mycket sänks priset per liter? 10 Eva arbetar normalt 40 timmar i veckan. Hennes timlön är 160 kr. När Eva arbetar övertid får hon mer betalt. En vecka arbetade hon 42 timmar och tjänade då kr. Hur mycket betalt får Eva för varje timme övertid? 11 Det finns 20 lag i engelska superligan i fotboll. Alla lag möter alla en gång borta och en gång hemma. Om ett lag vinner, får laget 3 poäng. Om en match slutar oavgjort får båda lagen 1 poäng. En säsong fick Arsenal ihop 52 poäng. Då hade laget vunnit 13 matcher. Hur många matcher förlorade Arsenal den säsongen? 12 En burk med tabletter väger 400 g. En tom burk väger 130 g och 10 tabletter väger 60 g. Hur många tabletter finns det i burken? Veckans problem En flaggstång är 12 m hög. En snigel kryper uppför flaggstången. Varje dag kryper den 4 m uppåt men varje natt glider den ner 3 m. Hur lång tid tar det för snigeln att nå toppen? 318
5 Läxa 3 Efter avsnitt a) Hur mycket får du tillbaka på en hundralapp, om du handlar för 65 kr? b) Josefin är 13 år. Hennes morfar är 59 år äldre. Hur gammal är morfar? c) Benny köper tio glassar för 12 kr styck. Hur mycket får han betala? d) Päivi och Sam ska dela lika på 36 kr. Hur mycket får var och en? e) Familjen Ek betalar kr i hyra varje månad. Hur mycket blir det på ett år? f) Hur mycket får man betala för två liter mjölk, om en liter kostar 7,50 kr? 2 a) b) ,7 c) a) Vad kostar apelsinerna per kilogram? b) Vad får Linus tillbaka om han köper två säckar apelsiner och betalar med en 500-lapp? 4 Vilket tal ligger mitt emellan a) 1,1 och 1,15 b) 4 och 2 c) 1 2 och 1 Köp en säck apelsiner (5 kg) för bara 49 kr! 5 a) 5, ,85 b) 9,25 7 c) 24,5 / 5 6 I talet får tiotalssiffran byta plats med hundratalssiffran. a) Vilket blir det nya talet? b) Beräkna summan av de båda talen. 319
6 7 Vilket tal är två tiondelar större än a) 1,6 b) 0,45 c) 0,98 d) 9,95 8 a) Hanna säger att noll komma sjutton är ett större tal än noll komma sju. Har hon rätt? b) Kan man säga på något annat sätt så att det blir tydligare vilket tal som är störst? 9 Av 9 kg äpplen kan man få 4 liter äppelmust. Hur många kilogram äpplen behövs för att få 100 liter must? 10 Varje lördagsmorgon säljer Magnus, Mustafa och Sepideh frallor för att tjäna ihop pengar till klasskassan. En morgon säljer Magnus 27 stycken och Mustafa 43 stycken. För varje fralla de säljer tjänar de 2 kr. Den här morgonen tjänar de sammanlagt 218 kr. Hur många frallor sålde Sepideh? 11 Stina har en Barbiedocka som är 30 cm lång. Dockans fötter är endast 1,7 cm långa. Stina själv är 150 cm lång och har 22 cm långa fötter. Hur långa fötter borde egentligen Barbiedockan ha för att mer likna Stina? Den första Barbiedockan såg dagens ljus Barbieklubben i Sverige startades redan 1964 av socialdemokraten Mona Sahlin. 12 Ur en lärobok från 1800-talet: En handelsman köpte 28 tunnor sill. Han sålde dem sedan för sammanlagt 420 riksdaler. På den affären tjänade handelsmannen 56 riksdaler. Hur mycket kostade en silltunna i inköp? Veckans problem Anna har några femkronor och tre gånger så många tiokronor. Sammanlagt har Anna 140 kr. Hur många femkronor har hon? 320
7 Läxa 4 Efter avsnitt a) 45 / 5 b) c) d) 10 0,2 e) Hur mycket är a) summan av termerna 14 och 17 b) differensen av termerna 87 och 29 c) produkten av faktorerna 7 och ,1 f) Sofia, Fredrik och Alexandra fick tillsammans 750 kr av sin farmor. De delade lika på pengarna. För sin del köpte Fredrik en flygplansmodell för 199 kr. Hur mycket hade han sedan kvar av sina pengar? 4 Byt plats på tiondelssiffran och tiotalssiffran i talet 543,21. a) Vilket tal får du då? b) Beräkna differensen av de båda talen. < betyder är mindre än > betyder är större än = betyder är lika med 5 Sätt ut rätt tecken mellan talen. Välj mellan >, < och =. a) 1 4 0,25 b) 0,299 0,3 c) Vilka tal hör ihop med vilka bokstäver? , ,76 a b c d e f 0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 7 Vilka tal är utelämnade? 1,8 1,2? 0? 8 På en provräkning skulle eleverna avrunda talet 3,2499 till tiondelar. Merwin svarade 3,2 och Julius svarade 3,3. Vem fick rätt på uppgiften? Vilket fel tror du att den andre kan ha gjort? 321
8 9 Vad kostar det att röka ett och ett halvt paket om dagen i ett år? Räkna med att ett paket kostar 49 kr. Avrunda till tusental kronor. 10 Hur många människor i världen dör i genomsnitt per minut på grund av rökning? Avrunda till heltal. Man tror att 3,5 miljoner människor i världen dör varje år på grund av rökning. I Sverige orsakar rökningen ungefär dödsfall per år. Det kan jämföras med att det dör cirka 500 personer per år i trafikolyckor. 11 När man skalar ett äpple kan man få långa band av skalet. Världsrekordet är 57 yards och 1 foot. Hur många meter motsvarar det? Avrunda till tiondels meter. 1 yard = 3 feet 1 foot = 30,5 cm (feet är pluralformen till foot) 12 Emma tankar sin bil full. Hon kör 383 km och fyller sen på fullt med etanol igen. Då går det i 49,5 liter. a) Hur mycket etanol drar bilen per mil? Avrunda till tiondels liter. b) Bilens tank rymmer 75 liter. Hur långt kan Emma köra på en full tank? Avrunda till hela mil. Veckans problem När en digital klocka visar till exempel så är summan av de fyra siffrorna 16. Vilket klockslag ger den största siffersumman? 322
9 Läxa 5 Efter avsnitt a) 5,6 100 b) 72 / 10 c) d) 1 0,3 e) 1,8 + 0,7 f) ,18 2 Avrunda talen till hundradelar. a) 7,627 b) 0,193 c) 2, d) 0, Vilket tal är störst? a) 0 eller 5 b) 0,189 eller 0,19 c) 3 eller 0,8 4 4 Vilket tal ska stå i stället för n? a) = n b) 1 + 0,3 + n + 0,008 = 1,358 5 a) 72,5 + 6,75 b) 0,78 4 c) 84,6 / 6 6 Maria köper sex bakelser för 108 kr. Hur mycket kostar åtta bakelser? 7 Beräkna med överslagsräkning. a) b) 19 9,2 c) 7, När ett tal multipliceras med 10 ser det ut som om decimaltecknet flyttas ett steg åt höger. Förklara varför. 9 Från en ko får man ungefär liter mjölk per år. Till hur många familjer med fyra personer räcker mjölken som en ko ger under ett år. Avrunda på lämpligt sätt. 10 Hur många sockerbitar per person får vi i genomsnitt i oss under ett år genom läsken? En liter läsk innehåller 100 g socker och en sockerbit väger 4 g. Vi dricker mycket mjölk och läsk i Sverige. Varje person dricker i genomsnitt 103 liter mjölk och 74 liter läsk per år. 323
10 11 I en slalomtävling ledde André Myhrer efter första åket på tiden 44,68 s. Tvåa låg österrikaren Hirscher, fjorton hundradelar efter. I andra åket hade Hirscher tiden 43,73 s. a) Vilken tid hade Hirscher i första åket? b) Vilken blev Hirschers sammanlagda tid? c) Myhrer vann tävlingen, tre tiondelar före Hirscher. Vilken tid hade André Myhrer i andra åket? I slalomtävlingar läggs tiderna för båda åken ihop, och det är den med kortast sammanlagd tid som vinner. 12 Ett träd blir fullvuxet efter ungefär 80 år. Det kan då ge 60 kg papper. I skolan förbrukar vi mycket papper bland annat genom kopiering. Ett kopieringspapper väger cirka 5 g. På Nybyggeskolan finns ett läsår 400 elever. Vi antar att varje elev får 6 kopior i veckan i genomsnitt och att läsåret har 40 veckor. Hur många fullvuxna träd behövs för att tillverka allt kopieringspapper som används på Nybyggeskolan det läsåret? Veckans problem I en kasse finns ett antal äpplen. Det är färre än 30 stycken. Om man låter fyra personer få lika många äpplen var, så blir det tre äpplen över. Om man låter fem personer dela på äpplena, så blir det fyra över. Hur många äpplen finns det i kassen? 324
11 Läxa 6 Efter avsnitt a) 10 0,2 b) 0,7 0,2 c) / 3 d) 0, e) 45 / 100 f) ,24 2 Avrunda talen till tiotal. a) 39,5 b) 123 c) 237 d) 63,2 3 Skriv talen i decimalform. a) 9 b) c) d) a) b) ,5 c) 24, 60 d) 0, Hur mycket billigare blir det per nummer med erbjudandet i annonsen? LEK & AKTIVERA Prova-på-erbjudande 5 nummer för 195: (Ordinarie pris: 59: per nummer.) 6 Beräkna med överslagsräkning. a) 48,7 + 83,5 + 66,8 b) 61, 5 695, c) 7,2 293,4 325
12 Bilden är från en dinosauriepark i Kina. Vid utgrävningar i landet har man funnit många fossiler av dinosaurier, bland andra Erketu Ellisoni. 7 Dinosaurien Erketu Ellisoni hade en hals som var dubbelt så lång som resten av kroppen. Hur lång var dinosaurien om halsen var 7,5 m lång? Avrunda till hela meter. 8 Förklara varför 25, 8 30 är lika med 258, 3. 9 Vilket tal ligger mitt emellan a) 1,2 och 1,7 b) 1 och 0,35 c) 7 och 2, Hyran för Pernilla och Fredriks lägenhet på 94 kvadratmeter var kr per månad. Hyran höjdes med 2,50 kr per kvadratmeter. Hur mycket får Pernilla och Fredrik betala i hyra per år efter höjningen? 11 År 1903 köpte handelsman Flink 123 m siden för 493 kr. Han sålde det sedan för 5 kr per meter. Hur stor blev hans förtjänst för hela tyget? 12 Josefin och Danwei spelar på V75 varje vecka. Josefin satsar 60 kr och Danwei 90 kr. En vecka vinner de kr. Hur mycket av vinsten får var och en? Veckans problem Lisa står i matkön på skolan. Hon står som åttonde elev framifrån och som elfte bakifrån. Hur många elever står i matkön? 326
13 Läxa 7 Efter avsnitt a) 10 0,235 b) 420 / 70 c) 20 0,5 d) 1,3 + 4,7 e) 2 / 0,1 f) 0, Avrunda talen till hundratal. a) 288 b) 417 c) 792 d) Skriv talen med siffror. a) etthundrafemtusen trettio b) fyrtiofem tusendelar 4 Beräkna med överslagsräkning. a) 47,5 + 19,2 + 63,6 b) 2,9 411 c) Vilket tal ska stå i rutan? a) 10? = 9,75 b) 6 =? 0,3 c)? 200 = 0,03 6 Vilken pil pekar på talet a) 1 3 b) c) 3 2 d) 3 4 A B C D E 0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 7 Talen 8, 10 och 12 är exempel på jämna tal som följer på varandra. Summan av de tre talen är 30. Tre andra jämna tal som följer på varandra har summan 444. Vilka är de tre talen? 8 En bil använder 7,5 liter bensin på 10 mils körning. Bensinpriset är 13 kr per liter. Bensintanken rymmer 75 liter. Förklara med ord vad som räknas ut med uttrycket a) 75, 10 b) 13 7,5 c) , 9 För en säck som innehåller 15 kg gödsel får man vid ett tillfälle betala 108 kr. För en säck som väger 25 kg är priset 60 öre lägre per kilogram. Hur mycket kostar den större säcken? 327
14 10 Från januari 2002 till december 2009 minskade lejonstammen i Masai Mara med 800 lejon. Antag att lejonstammen skulle minska i samma takt i fortsättningen. Hur många år till dröjer det i så fall innan lejonen i Masai Mara är helt utrotade? Naturreservatet Masai Mara ligger i Kenya och har en stor lejonpopulation. År 2002 fanns det lejon i parken. Åker man dit på safari finns det alltså en god chans att få se dem. 11 Ett av världens giftigaste djur är pilgiftsgrodan. Giftet i en enda groda kan ta livet av personer. För att döda en människa räcker det med 0,01 mg av giftet. Hur mycket gift finns det i en groda? Avrunda till hundradels gram. 1 g = mg 12 År 1881 köpte en handlare 36 hattar av samma modell till sin affär. Han sålde hattarna för 180 kr sammanlagt och tjänade då 1,50 kr per hatt. Hur mycket kostade varje hatt i inköp? Veckans problem På en parkeringsplats fanns ett antal bilar och motorcyklar. Magnus lillebror gick runt och räknade hur många fordon det fanns sammanlagt. Han räknade också hur många hjul bilarna och motorcyklarna hade sammanlagt. Han kom fram till att antalet fordon var 31 och antalet hjul var 98. Hur många motorcyklar och hur många bilar stod på parkeringen? 328
15 Läxa 8 Efter avsnitt a) Skriv 9 4 i blandad form. b) Vilket tal saknas? 1? = 3 5 c) Skriv i bråkform. d) Hur mycket är 1 2 0,45? 2 Skriv vikterna i hektogram. a) 450 g b) 0,2 kg c) 50 g d) 1,5 kg 3 Avrunda talen till tiondelar. a) 8,219 b) 11,877 c) 0, d) 21, a) Vilket tal är störst, tre komma tolv eller tre komma sju? b) Beräkna differensen av de båda talen. 5 Ett strutsägg väger ungefär 1,8 kg och ett kolibriägg ungefär 400 mg. Hur många kolibriägg behövs för att de sammanlagt ska väga lika mycket som ett strutsägg? 1 g = mg Det är bara i Afrika som strutsen lever i det vilda, men det förekommer många strutsfarmer runt om i världen. I Sverige finns det till exempel en strutsfarm i Stigtomta utanför Nyköping. Där kan man bland annat köpa strutssalami och strutsbiff. 329
16 6 a) Skriv volymerna i centiliter. b) 0, c) 8 004, a) 85 ml b) 1,2 liter c) 3,2 dl d) 5 ml 8 När August ska räkna ut 52 gör han så här: = 26 8 = 13 4 = 3,25 a) Förklara hur han tänker. b) Räkna ut 88 på samma sätt En människa innehåller tillräckligt med kol för att tillverka ungefär 900 blyerts pennor. En penna väger 7 g och består till fem sjundedelar av grafit (kol). Ungefär hur många kilogram kol innehåller en människa? 10 Socker används ofta i recept. Ibland anges mängden i deciliter och ibland i gram. Lovisa läser i ett recept att 2 dl socker väger 170 g. a) Hur mycket väger 1 liter socker? Svara i gram. b) Hur stor volym har 1 kg socker? Avrunda till tiondels liter. 11 Hur mycket har man sänkt priset per kilogram? 400 g, 10:50 12:90 ord pris 12 På 20 dagar beräknar man att 30 personer ska hinna bygga en stuga. När de har arbetat två dagar bestäms att arbetet måste vara klart tre dagar tidigare än vad man sa från början. Man måste därför anställa fler personer. Hur många fler? Utgå från att alla arbetar lika snabbt. Veckans problem En flaska och en kork väger tillsammans 56 g. Flaskan väger 50 g mer än korken. Hur mycket väger flaskan och hur mycket väger korken? 330
17 Läxa 9 Efter avsnitt Skriv med siffrorna 3, 5, 7 och 9 det tal som a) är näst störst b) ligger så nära som möjligt 2 Vilket tal är störst? a) 0,19 eller 0,2 b) 1,9 eller 1,89 c) 0,7 eller 0,699 3 Skriv längderna i centimeter. a) 7,2 dm b) 3 mm c) 1,3 m d) 78 mm 4 Vilka tal pekar pilarna på? a b c d Skriv vikterna i kilogram. a) 1,5 ton b) 35 hg c) g d) 700 g 6 a) 23,2 7,65 b) 30 1,18 c) 4,14 / 0,3 7 En burk med vitamintabletter kostar 72 kr och innehåller 200 tabletter. Varje tablett väger 0,3 g. a) Hur många gram väger alla tabletterna? b) Skriv vikten i kilogram. c) Vad kostar tabletterna per styck? 8 Förklara hur du tänker när du ska omvandla a) liter till milliliter b) decimeter till meter 9 En jeansaffär köper in 200 par jeans för 225 kr styck. Man säljer sedan 160 av dem för 595 kr styck. De jeans som blir kvar säljs på rea för 349 kr styck. Hur mycket tjänar affären sammanlagt på jeansen? 331
18 10 Vad kostar diskmedlet per liter? 70 cl, 35: 11 I ett recept står det att 1 ½ dl valnötskärnor väger 100 g. Hur mycket väger 1 liter valnötskärnor? Avrunda till tiotal gram. 12 En swimmingpool fylls på 8 timmar genom ett rör där det kan rinna 50 liter per minut. Hur lång tid tar det att fylla poolen med ett rör som ger 2,5 liter per sekund? Veckans problem Vad är A / B om A + B = 27, A B = 9 och A B = 162? 332
19 Läxa 10 Efter avsnitt a) Vad kostar 10 kg äpplen om priset per kilogram är 12,90 kr? b) En förpackning med fyra batterier kostar 48 kr. Vad kostar batterierna per styck? c) Mustafa har 500 kr i tiokronor. Hur många tiokronor har han? d) I en aula finns 244 platser. Vid ett tillfälle lyssnar 192 elever och 6 lärare på en konsert i aulan. Hur många platser är tomma? e) En påse med 10 kg apelsiner kostar 119 kr. Vilket är priset per kilogram? f) En film på TV börjar kl Filmen är en timme och trettio minuter lång. Hur mycket är klockan när filmen är slut? 2 Hur lång tid har det gått mellan följande klockslag? a) b) c) Skriv vikterna i hektogram. a) b) c) d) 160 g 1,2 kg 15 g 210 g 4 Beräkna med överslagsräkning. a) 57,8 + 71,9 + 89,5 b) 3,78 42,5 c) 6,1 392,5 5 Skriv volymerna i deciliter. a) 75 ml b) 1,2 liter c) 65 cl d) 5 ml 6 Åsa köper äpplen som sammanlagt väger 700 g. Åsa betalar med en tjugokronorssedel. Hur mycket får hon tillbaka? 19,90 kr/kg 7 Ursain Bolt tog VM-guld 2009 på 200 m när han sprang på tiden 19,19 s. Beräkna medelhastigheten i meter per sekund. Avrunda till en decimal. 8 Förklara vad som menas med medelhastighet. 333
20 9 Vilka tal saknas? a) 0,5 h =? min b)? min = 0,75 h c) 1,1 h =? min 10 Tabellen visar hur mycket tid man tjänar på att öka hastigheten om man kör bil en viss sträcka. Sätt dig in i hur tabellen är uppbyggd och lös sedan uppgifterna. a) Hur lång tid tar det att köra 20 mil med hastigheten 90 km/h? b) Hur lång tid tar det att köra 30 mil med hastigheten 80 km/h? c) Hur mycket tid tjänar man om man kör 10 mil och ökar hastigheten från 90 km/h till 100 km/h? d) Hur mycket tid tjänar man om man kör 60 mil och ökar hastigheten från 75 km/h till 90 km/h? Så lite tid sparar fortköraren Att köra 110 km/tim i 10 mil tar 54 minuter. Kör man samma sträcka i 130 km/tim sparar man bara in 8 minuter. 10 mil 20 mil 30 mil 40 mil 50 mil 60 mil 1:25 2:51 4:17 5:42 7:08 8:34-0:05-0:11-0:17-0:22-0:28-0:34-0:10-0:21-0:33-0:42-0:53-0:64-0:15-0:30-0:46-1:00-1:16-1:31-0:19-0:38-0:57-1:16-1:35-1:54 10 mil 20 mil 30 mil 40 mil 50 mil 60 mil 1:03 2:13 3:20 4:26 5:33 6:40-0:03-0:07-0:11-0:14-0:18-0:22-0:06-0:13-0:20-0:26-0:33-0:40-0:09-0:19-0:29-0:38-0:48-0:58-0:12-0:24-0:37-0:48-1:01-1:13 11 Den snabbaste snigel som finns kan röra sig med hastigheten 2,3 mm/s. Hur långt hinner den på ett dygn med den hastigheten? Avrunda till hundratal meter. 12 Det svenska rekordet på 100 m är 10,18 s. Hur lång tid skulle det ta att springa en mil med samma hastighet? mil 20 mil 30 mil 40 mil 50 mil 60 mil 0:54 1:49 2:43 3:38 4:33 5:27-0:04-0:09-0:13-0:18-0:23-0:27-0:08-0:17-0:25-0:33-0:42-0:50 Veckans problem För fem år sen var tvillingarna Matilda och Julia och deras storebror Oscar 37 år tillsammans. Oscar är 4 år äldre än tvillingarna. Hur gammal är Oscar idag? 334
21 Läxa 11 Efter avsnitt Hur lång tid har det gått mellan klockslagen? a) b) Eftermiddag Förmiddag 2 Skriv volymerna i centiliter. a) b) c) d) 57 ml 1,2 liter 1 ml 7,5 dl 3 a) 65,4 + 8,7 + 23,9 b) 58,1 26,7 c) 114, En film är 1 h 40 min lång. När började filmen om den slutar 20.15? 5 a) 12,3 / 10 b) c) 1 4 0,1 d) 8 60 e) 15 05, f) / En flaska hostmedicin innehåller 600 ml. Hur många dygn räcker flaskan om man ska ta en matsked två gånger per dygn? 1 msk (matsked) = 15 ml 7 Tabellen visar temperaturen utomhus under en vecka. Mån Tis Ons Tors Fre Lör Sön Visa hur temperaturen varierade i ett linjediagram. 335
22 8 Stolp- och stapeldiagram ser ganska lika ut. Men de används i olika sammanhang. Ge exempel på när man använder de olika diagrammen. 9 Fem udda tal som följer på varandra har summan 155. Vilka är talen? 10 I en flock med 40 elefanter är 17 honor. Hur många ton väger hela flocken? Avrunda till tiotal. En elefanthona väger i genomsnitt kg och en hane kg. En elefant äter ungefär 200 kg mat om dagen och dricker mer än 100 liter vatten. 11 Magda och Anna säljer lotter för att få pengar till sitt fotbollslag. För varje lott de säljer tjänar laget 3,50 kr. Magda säljer 240 och Anna 360 lotter. Hur mycket pengar ger det till laget? 12 Världens snabbaste vanliga flygplan är ett spionplan som kan flyga med hastigheten 980 m/s. Hur lång tid tar det för planet att flyga ett varv runt jorden? Anta att det flyger längs ekvatorn där jordens omkrets är mil. Avrunda till hela timmar. Veckans problem En beduin har både kameler och dromedarer. Sammanlagt har djuren 44 pucklar och 112 ben. Hur många djur av varje sort är det? (Ledtråd: En kamel har två pucklar och en dromedar har en puckel.) 336
23 Läxa 12 Efter avsnitt Avrunda talen till hundratal. a) 785 b) c) d) Gebro köper en burk vit målarfärg och en stol och betalar med två 500 krsedlar. Hur mycket får han tillbaka? 195 kr 595 kr 3 Hur mycket väger den kattunge som väger a) mest b) minst c) Hur många gram är skillnaden mellan de två katternas vikter? 0,5 kg 0,499 kg 0,41 kg 0,419 kg 0,489 kg 4 Ulrika och Anders har ätit mat på Crazy Cow. Ulrika betalade 89 kr kontant och Anders 165 kr med sitt kort. Hur mycket är Ulrika skyldig Anders om de ska betala lika mycket var? 5 I ett höghus undersökte hyresvärden hur många som bodde i varje lägenhet. Han fick följande resultat: 1, 4, 3, 2, 5, 3, 3, 2, 1, 4, 1, 6, 4, 1, 4, 2, 3, 2, 6, 3, 2, 3, 3, 4, 2, 5, 3, 2, 1, 4 Sammanställ undersökningen i en frekvenstabell. Visa resultatet i ett stolpdiagram. 6 Beräkna med överslagsräkning. a) 49, 8 b) 18,7 7,1 c) 129, ,8 + 95,3 61, 337
24 7 Under tio dagar i juli uppmäter man följande regnmängder i Gällivare: 8 mm 12 mm 0 mm 0 mm 3 mm 6 mm 9 mm 0 mm 0 mm 2 mm Vilket är a) typvärdet b) medelvärdet c) medianen 8 Ibland ger medianen en bättre bild än medelvärdet av ett statistiskt material. Ge ett exempel. 9 En teatergrupp har tio medlemmar. Medelåldern är 19,5 år. a) Hur gamla är de tio medlemmarna sammanlagt? b) En medlem som är 27 år slutar i teatergruppen och samtidigt börjar en 15-åring. Vilken blir nu medelåldern i gruppen? 10 Bilden visar en vandringskarta med avstånden angivna i meter. Krister startar från parkeringsplatsen och går därifrån den nedre vägen till D. Därifrån går han till E och sedan närmaste vägen till B. Hur långt har då Krister gått sammanlagt? Svara i kilometer och avrunda till en decimal D C B E 1090 A 1640 P 11 Vasaloppet är en skidtävling som går varje år första söndagen i mars. Loppet är 90 km långt. Ernst Alm vann det allra första Vasaloppet år Hans tid blev 7 h 32 min 49 s. Vilken var Ernsts medelhastighet? Avrunda till tiondels meter per sekund. 12 En pool som rymmer 12 kiloliter fylls med två kranar. Ur den ena kranen rinner det 15 liter vatten på 50 s och ur den andra kranen rinner 154 liter på 7 min. Hur lång tid tar det att fylla poolen? Veckans problem En person var 78 år när han dog. Summan av hans födelseår och dödsår är Vilket år var han född? 338
25 Läxa 13 Efter avsnitt Diagrammet visar hur priset på äpplen i en butik beror på antalet kilogram man köper. a) Hur mycket kostar 1 kg äpplen? b) Hur mycket äpplen får man för 50 kr? kr kg 2 Skriv volymerna i liter. a) 6 dl b) ml c) 25 cl d) 900 ml 3 a) b) (9 + 6) / 3 c) 9 (6 3) d) 9 / e) 9 / (3 + 6) f) 9 / Avrunda talen till hundradelar. a) 0, b) 2, c) 42, Vilka tal saknas? ?? 6 Mellan London och Newcastle är det ungefär 40 svenska mil. Hur många engelska mil är det? Avrunda till tiotal. 1 km 0,62 engelska mil 339
26 7 Jesper gör en undersökning i sin klass om vilken skostorlek som klasskamraterna har. Han redovisar sin undersökning i ett diagram. a) Vilken sorts diagram är det? b) Hur många elever går i Jespers klass? c) Vad är medianen och typvärdet? st antal skostorlek 8 Visa med ett exempel varför man räknar multiplikation före addition. 9 Att åka taxi kostar vid ett tillfälle 45 kr i grundavgift. Man får sedan betala 12 kr per kilometer. Hur mycket kostar en taxiresa på 1,5 mil? 10 Tio träd står i rad. Mellan varje träd är det 4,5 m. Trädens stammar är 1,5 dm tjocka. Hur lång är hela raden med träd? 11 På en vägsträcka som är 2 km lång sänks högsta tillåtna hastighet från 90 km/h till 70 km/h. Det kommer att ta flera minuter längre tid att komma till jobbet säger Jonatan till sin fru. Har han rätt? 12 När Jill Smith föddes vägde hon 8 pounds 6 ounces. Med våra mått motsvarar det 3 798,9 g. Hur många ounces går det på ett pound? 1 ounce = 28,35 g Veckans problem Arton tändstickor kan läggas så att man får sex kvadrater på det sätt som bilden visar. Försök nu flytta på två stickor så att det istället bildas fem kvadrater. 340
27 Läxa 14 Efter avsnitt a) Linda köper ett par handskar för 169 kr. Hur mycket får hon tillbaka på två hundralappar? b) Adam väger 42 kg. Hans pappa väger dubbelt så mycket. Vad visar vågen om de båda ställer sig på den samtidigt? c) Vad kostar tio wienerbröd om priset per styck är 9,50 kr? d) Petter är 1,5 dm längre än sin syster Pia. Hur lång är Petter om Pia är 158 cm? e) Hur mycket är klockan tre kvart efter 16.50? f) Hur många sekunder är två och en halv minut? 2 a) Hur många tåg finns det att välja på, om du åker en söndag? b) Hur lång tid tar resan om du åker från Västerås kl 18.40? 3 Vilka av bråken här nedanför har ett värde som är a) större än 1 b) lika med 1 c) mindre än Avg M-L Dagl M-F Dagl Dagl M-F,S S Dagl S Från Till Karlstad C Ank Dagar Byten Anm 9.26 M-L 22 aug-12jun 16 aug-21 aug 4 I en stafett i en skola sprang man en bana som var m lång. I varje lag deltog 15 elever. Hur lång sträcka sprang var och en i genomsnitt? Avrunda till tiotal meter. Västerås C Hallsberg Hallsberg Katrineholm C Hallsberg Flen Hallsberg Hallsberg Laxå Hallsberg Hallsberg Tåg Tåg Tåg Tåg Tåg X 2000 Tåg Tåg Tåg Tåg Tåg Tåg Tåg X 2000 Tåg Tåg Tåg Tåg Tåg Tåg 5 a) 0,1 + 0,01 b) 0,1 0,01 c) 0,1 0,01 d) 0,1 / 0,01 6 Beräkna värdet av uttrycket a 3 b 4 för a) a = 12 och b = 16 b) a = 9 och b =
28 7 Tabellen visar antalet blixtnedslag på jorden i genomsnitt per minut. jan feb mar apr maj jun a) Hur många gånger slog blixten ner per minut i genomsnitt detta halvår? b) Hur många blixtnedslag var det i genomsnitt per dygn? Avrunda till tiondels miljoner. 8 I familjen Johnson är medelåldern 19,5 år. Familjen består av mamma, pappa och två barn. Ge ett exempel på hur gamla familjemedlemmarna kan vara. 9 Förr mätte man längd i enheterna famn, aln och fot. I en gammal bok står att läsa om en sjö som var 60 famnar djup. Hur djup var sjön i meter? 1 famn = 3 alnar 1 aln = 2 fot 1 fot = 30 cm 10 Det kostar 3/4 miljard kronor att bygga 25 km motorväg. Vad kostar det per meter? 11 Du ska laga köttfärssås för nio personer enligt receptet. Hur mycket behöver du av varje ingrediens? 1 tsk = 15 ml 1 krm = 1 ml 12 Den första människan i rymden var ryssen Yuri Gagarin. År 1961 åkte han ett varv runt jorden på 1 h 48 min i en rymdkapsel. Rymdkapseln färdades 30 mil över jordens yta. Omkretsen runt jorden på den höjden är ungefär km. Vilken var medelhastigheten uttryckt i kilometer per timme? Avrunda till tusental. Köttfärssås 4 port 500 g köttfärs 1 gul lök (120 g hackad) 1 vitlöksklyfta 1/2 dl tomatpuré 1 tsk salt 2 krm nymald vitpeppar 4 1 x Veckans problem Lista ut hur talen i rutorna hänger ihop. När du gjort det kan du lätt räkna ut vilka tal som ska stå istället för x och y y
29 Läxa 15 Efter avsnitt Skriv längderna i meter. a) 0,7 km b) 14 dm c) 765 cm d) 500 mm 2 Vilken enhet passar? a) Jordens omkrets är ungefär 4 000?. b) Till en klänning köpte Malin 2,5? av ett tyg. c) Bensintanken i Evas bil rymmer 72?. d) En miniräknare väger 160?. 3 Vilket tal saknas? a) 11 18? b) ? 4 a) Vad är summan av talen A och C? b) Vad är differensen av talen F och B? c) Vad är produkten av talen D och E? d) Vad är kvoten av talen F och A? A B C D E F 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 5 a) 45,3 13,9 1,8 b) 2,35 70 c) 4,35 / 5 6 Tabellen visar hur en omgång i elitserien i ishockey slutade. Rögle Leksand 3 5 Brynäs Luleå 6 2 HV 71 Djurgården 1 3 Linköping Södertälje 5 0 MoDo Västra Frölunda 7 4 Timrå Färjestad 3 3 Räkna ut antalet mål per match. Beräkna sedan a) medelvärdet b) medianen c) typvärdet 343
30 7 Jonas har a kr. Han köper fem bullar. Varje bulle kostar b kr. Vilket uttryck visar hur många kronor Jonas har kvar efter köpet? a 5 b 5 b a a b 5 (a b) 5 8 Fanny och hennes 10 innebandykompisar åker tillsammans med sina två tränare på cup. Fanny är 13 år och tränarna är i 50 års-åldern. Vilket lägesmått beskriver bäst gruppens ålder? Förklara hur du tänker. 9 Rekordet i snabb rakning med rakkniv sattes 1887 av Teddy Wick då han rakade 77 män på 59 min 53 s. Hur många hela sekunder tog varje rakning i genomsnitt? 10 Ulrika ska skicka iväg fyra paket. Medelvärdet av paketens vikt är 8,4 hg. Två av paketen har samma innehåll och väger 630 g vardera. Av de två återstående paketen väger det ena dubbelt så mycket som det andra. Hur många kilogram väger det paket som väger mest? 11 Hur många mil kördes varje bil i genomsnitt det här året? Avrunda till tiotal mil. 12 Världens största bordsduk är 200 m lång och 1,8 m bred. Duken används av ett kungligt hov i Mellersta Östern. När duken inte används viks den först en gång på bredden och sedan sex gånger på längden. När den viks på längden, viks den på mitten varje gång. a) Hur lång och hur bred blir den hopvikta duken? Svenskar körde bil 8,1 miljarder mil I vårt land fanns förra året 6,5 miljoner bilar. Bilarna kördes sammanlagt 8,1 miljarder mil. Det visar en databas som Statistiska Centralbyrån tagit fram tillsammans med bilprovningen. n b) Hur tjock blir den hopvikta duken om tyget är 0,7 mm tjockt? Avrunda till hela millimeter. Veckans problem Vilket av talen nedan passar inte ihop med de övriga? Förklara varför
31 Läxa 16 Efter avsnitt a) b) 19,9 + 9,9 c) d) 7,5 / 100 e) 0,95 + 0,5 f) 10 0,1 2 Skriv längderna i millimeter. a) 0,4 dm b) 24 cm c) 1,2 m d) 3,5 cm 3 Skriv talen med siffror i decimalform. a) tjugosju tusendelar b) en hel och två hundradelar 4 Lös ekvationerna. a) 4x + 1 = 21 b) z 5 1 = 4 c) 17 3y = 5 5 Skriv talen i bråkform. a) 0,7 b) c) 0,03 d) Jonas kastar en tärning ett antal gånger. Resultatet visas i diagrammet. a) Hur många kast gjorde Jonas? b) Vilket antal prickar var typvärdet? c) Vilken är medianen? antal kast f 7 Hur många tändstickor är det i varje ask om det är lika många i varje? 1 Teckna en ekvation som passar till bilden. Lös sedan ekvationen prickar x + + = x x 345
32 8 Hur kan du kontrollera om du löst en ekvation rätt om du inte har något facit? Visa med ett exempel. 9 a) Teckna ett uttryck för hur mycket du får betala för x biobiljetter och y kartonger med popcorn. b) Förklara vad som menas med uttrycket x 25y. 25 kr 10 Det största antal flygtimmar som någon pilot kommit upp till är h. Hur många hela år i luften motsvarar det? 11 I den 508 m höga byggnaden Taipei 101 i Taiwan finns världens snabbaste hiss. Den åker 381 m upp till 89:e våningen på bara 30 s. Med vilken hastighet går hissen? Svara i kilometer per timme. Avrunda till heltal. 12 Ett franskt snabbtåg har på en kort sträcka kommit upp i hastigheten 574,8 km/h. Hur lång tid skulle det ta att åka med ett sådant tåg mellan Stockholm och Göteborg? Avståndet mellan de båda städerna är 484 km. Avrunda till hela minuter. Veckans problem En brandman står på den mittersta pinnen på en brandstege. Han klättrar upp 12 steg. Men eftersom elden är så kraftig blir han tvungen att backa 7 steg. Efter en stund klättrar brandmannen upp 11 steg och står då på stegens näst översta pinne. Hur många pinnar har stegen? 346
33 Läxa 17 Efter avsnitt a) 8 40 b) 2 0,05 c) d) e) 0,7 0,3 f) 15 dl =? liter 2 Skriv vikterna i kilogram. a) 2,7 ton b) 7 hg c) g d) 50 g 3 Pröva om y = 10 är lösning till följande ekvationer. a) 5y 10 = 40 b) y = 11 c) y = 0 4 Skriv talen i storleksordning med det största först. 0,99 1, , Hur många grader vrider du dig när du snurrar a) ett halvt varv b) tre varv c) ett och ett fjärdedels varv 6 När Viktoria var sjuk tog hon tempen varje morgon. Hon ritade sen ett diagram över hur tempen hade varierat. a) Vilken sorts diagram är det här? b) Vilken dag hade Viktoria högst temperatur? c) Beräkna medeltemperaturen för de fem dagar då Viktoria hade feber, det vill säga de dagar då tempen var över 37. C temperatur må ti on to fr lö 7 a) ,78 b) 1,6 3 4 c) ,
34 8 En vanlig gradskiva går bara till 180. Hur kan man då ta reda på storleken på en vinkel som är större än 180? 9 Det bor i genomsnitt 20 personer per kvadratkilometer i Sverige. Jordens tätast befolkade område är Macao på Kinas sydkust. Där bor personer på ett område som är 16 km 2. Hur många gånger fler människor bor det per kvadratkilometer i Macao än i Sverige? 10 På våra huvuden har vi ungefär hårstrån. De växer ungefär 0,4 mm per dygn. a) Hur många veckor dröjer det innan ett hårstrå har blivit 2 cm längre? Avrunda till heltal. b) Hur mycket växer hårstråna sammanlagt på ett år? Svara i kilometer och avrunda till heltal. 11 Den första flygningen med luftballong jorden runt utan uppehåll genomfördes På 22 dygn flög man ungefär mil. Beräkna luftballongens medelhastighet uttryckt i kilometer per timme. Avrunda till tiotal. 12 Några studenter vid Luleå tekniska universitet har byggt en bil som går 152 km på en liter bensin. Hur många deciliter bensin drar bilen per mil? Avrunda till hundradelar. Veckans problem I en tall satt några kråkor. I granen bredvid satt fler kråkor än i tallen. Om en av er flyger över till oss så blir vi lika många. Om en av er flyger över till oss så blir vi dubbelt så många som ni. Hur många kråkor satt i tallen och hur många satt i granen? 348
35 Läxa 18 Efter avsnitt a) 145 cm =? m b) c) 45 dl =? liter 2 d) 0, e) 100 0,135 f) , 2 Beräkna storleken av vinkeln v. a) b) c) v v v 17 3 Lös ekvationerna. a) 4x + 12 = 32 b) y 1 = 2 c) 13 = 3z a) Mät triangelns sidor i hela och halva centimeter. Beräkna sedan omkretsen. b) En kvadrat har samma omkrets som den här triangeln. Hur långa sidor har kvadraten? C 5 a) 66,8 / 4 b) 14,5 0,8 12, c) 0, 004 A 6 Tabellen visar Lindas vikt under det första året. a) Visa viktökningen i ett linjediagram. b) Avläs ur ditt diagram hur mycket Linda vägde efter 5 månader. B Månader Vikt i gram
36 7 Skriv det tal som är en hundradel större än a) 0,77 b) 0,4 c) 1,214 d) 0,99 8 Förklara varför en triangel inte kan ha två räta vinklar. 9 Vinkeln B är dubbelt så stor som vinkeln A. Hur stor är vinkeln C? C A 33,7 B 10 Diagrammet visar hur många rätt några elever hade vid en tips promenad med 12 frågor. Vad är a) typvärdet b) medianen c) medelvärdet antal elever f x antal rätt 11 Vilket är priset per liter för deodoranten? 50 ml 45: 12 En tom hink väger 1,8 kg. När hinken är fylld till hälften med vatten så väger den 5,8 kg. Hur mycket väger hinken när den är fylld till 3/4 med vatten? Veckans problem Linus går upp till toppen av ett berg med medelhastigheten 3 km/h. På vägen nerför samma berg blir medelhastigheten dubbelt så hög. Det tar en timme längre tid att gå upp än ner. Hur lång är sträckan upp till bergets topp? 350
37 Läxa 19 Efter avsnitt a) Jenny betalar två räkningar genom sin internetbank. Den ena räkningen är på 299 kr och den andra på 95 kr. Hur mycket betalar Jenny sammanlagt? b) Två vinklar i en triangel är 65 vardera. Hur stor är den tredje vinkeln? c) Vilket är priset per kilogram om 1/2 kg vindruvor kostar 19 kr? d) Hur stor andel av blommorna är röda? Svara i bråkform. e) En bunt med tio julkort kostar 39 kr. Vad kostar korten per styck? f) En cirkel har diametern 7 cm. Vilket värde stämmer bäst på cirkelns omkrets? 14 cm 18 cm 22 cm 26 cm 2 Ett flygplan lyfter från Östersunds flygplats kl Fyrtiofem minuter senare landar planet på Arlanda utanför Stockholm. Vad är klockan då? 3 Vilket av talen är a) störst b) minst c) Hur stor är differensen mellan det största och det minsta talet? 75/ ,795 0,79 0, Mät i hela och halva centimeter och beräkna omkrets och area av rektanglarna. a) b) 351
38 5 Vilka tal saknas? a) 1,5 kg =? g b)? km = 700 m c) 2,5 dl =? cl d) 1 4 liter =? ml e) m =? mm f)? dygn = 8 h 6 Eiffeltornet i Paris invigdes år 1889 och hade det året 1,9 miljoner besökare. När tornet fyllde hundra år besöktes det av personer. Hur många fler besökare hade tornet 1989 jämfört med när det invigdes? Svara i miljoner. Eiffeltornet skapades av Gustave Eiffel och är gjort av stål. Tornet väger cirka ton och metallkonstruktionen består av balkar som är ihopsatta med 2,5 miljoner nitar. 7 Lös ekvationerna. a) 8x 16 = 40 b) y = 11 c) 15 3z = 0 8 Förklara varför det är rätt att säga att a) alla kvadrater är rektanglar b) alla rektanglar är parallellogrammer 352
39 9 Andreas åkte på en bilfärd. Diagrammet visar hur långt han hade kommit vid olika tidpunkter. Sammanlagt skulle han köra 20 mil. a) Vilken var medelhastigheten under den första halvtimmen? b) Efter pausen höll Andreas medelhastigheten 100 km/h. Rita av diagrammet och rita in Andreas fortsatta biltur. c) Vilken tid var Andreas framme? km sträcka kl 10 Beräkna figurens area. 32 (cm) En äkta persisk matta är 3,5 m lång och 1,8 m bred. Vid en rea sänktes priset från kr till kr. Med hur mycket sänktes priset per kvadratmeter? 12 Ett skogsområde är 56 hektar stort, vilket motsvarar m 2. Skogsägaren vill veta ungefär hur många träd det finns i området. Han räknar därför antalet träd i tjugo kvadratiska områden med storleken 10 m gånger 10 m. I genomsnitt finns det 5 träd i ett sådant område. Ungefär hur många träd bör det finnas i hela skogsområdet? 55 Veckans problem Fyll i plustecken och gångertecken mellan siffrorna så att det som står är sant =
40 Läxa 20 Efter avsnitt Mät i triangeln i hela och halva centimeter. Beräkna sedan triangelns a) omkrets b) area 2 a) 24,5 6 b) 36,4 / 8 c) 2,7 + 14,9 3 Hur många minuter har gått när a) timvisaren på en klocka vridit sig ett fjärdedels varv b) minutvisaren har vridit sig två och ett halvt varv 4 En karta över Stockholm är i skala 1 : På kartan är det 6,6 cm fågelvägen mellan Haga slott och Drottningholms slott. Hur många kilometer är det i verkligheten? Sedan 1981 har kungafamiljen bott på Drottningholms slott. År 2010 flyttade kronprinsessan Viktoria hemifrån till Haga slott i Solna. 354
41 5 Tre liter mjölk kostar 23,25 kr. Vad kostar fyra liter mjölk? 6 Lös ekvationerna. a) x 9 = 1 2 b) 6y + 5 = 17 c) 12 3z = 3 7 Minna köper en ostbit som väger 700 g och kostar 69,30 kr/kg. Hon betalar med en femtiokronorssedel. Hur mycket får hon tillbaka? 8 Rita en parallellogram som har arean 12,5 cm 2. 9 I början av 1600-talet emigrerade tusentals personer med båt från England till Virginia i USA personer överlevde den farliga båtfärden medan tre fjärdedelar dog i sjukdomar och svält. Hur många var det som åkte från England? 10 En dag var temperaturen vid Kebnekajses fjällstation 12 C. Högre upp var temperaturen lägre. Man kan räkna med att temperaturen sjunker med en hundradels grad per meter. a) Teckna ett uttryck för vilken temperaturen var på höjden x m ovanför fjällstationen. b) Räkna ut vilken temperaturen var på Kebnekajses topp? Toppen ligger m ovanför fjällstationen. c) Hur högt ovanför fjällstationen var temperaturen 5 C? 11 Triangeln ABC är likbent. Sidorna AB och AC är lika långa. Vinkeln A är 44,8. Hur stora är vinklarna B och C? 12 Beräkna arean av det blåa området. Räkna med att varje ruta har arean 1 cm 2. Veckans problem Huvudet på en fisk är en tredjedel av fiskens hela längd. Fiskens stjärt är lika lång som huvudet och kroppen tillsammans. Kroppen är 8 cm. Hur lång är hela fisken? 355
42 Läxa 21 Efter avsnitt Hur lång är pennan, mattan och bokhyllan i verkligheten? Mät i hela och halva centimeter. a) b) c) Skala 1:3 Skala 1:100 Skala 1:50 2 Förkorta a) 10 med 5 b) med 3 c) 7 28 med 7 3 På en ritning är Tunaskolan 8,5 cm lång. Skalan är 1 : Hur lång är skolan i verkligheten? 4 a) / 6 b) ( ) / 6 c) 18 / Lös ekvationerna. a) y = 10 b) 3z + 7 = 22 c) 18 4x = 2 6 En deciliter vetemjöl väger 60 g. I ett recept står det att man ska använda 165 g vetemjöl. Hur många deciliter motsvarar det? Svara med ett bråk i blandad form och med så liten nämnare som möjligt. 7 a) Rita en triangel som har arean 6 cm 2. b) Mät längden av sidorna på din triangel och beräkna omkretsen. 356
43 8 Om man förkortar ett bråk så blir det mindre, säger Oscar. Visa med en bild att Oscar har fel. 9 En ny idé till en rymdfärja ser ut som en rektangulär flygande matta. Hela ovan sidan på rymdfärjan är m 2 och täckt av solceller. Vilken omkrets har färjan om den är 20 m bred? 10 På en tipstävling med fem frågor fick deltagarna så här många rätt: 4, 2, 5, 4, 1, 4, 5, 3, 2, 5, 3, 4, 1, 3, 2, 4, 2, 3, 4, 5 a) Gör i ordning en frekvenstabell och visa resultatet i ett lämpligt diagram. b) Vilket är medelvärdet? c) Vilken är medianen? d) Vilket är typvärdet? 11 Hur stor area har det gula området? 3 (cm) Jessicas rum är 3,6 m långt och 3,2 m brett. Rita en bild av rummet i skala 1 : 50. Veckans problem Tänk dig att du har 12 stickor som alla är 1 dm långa. Stickorna kan läggas som en triangel med arean 6 dm 2 på det sätt som bilden visar. Flytta nu på fyra stickor så att den nya figuren har hälften så stor area, det vill säga 3 dm
44 Läxa 22 Efter avsnitt Hur många procent av figuren är blå? a) b) c) d) 2 Mät i hela och halva centimeter och beräkna sedan triangelns a) omkrets b) area 3 Vilket tal är störst och vilket är minst? a) 7 0,69 0, b) 1 4 0, ,19 4 Du har talet a) Hur mycket mer värd är siffran 5 än siffran 6? b) Kasta om siffrorna så att du får det näst största tal som är möjligt. 5 Klass 7B hade samlat returburkar. Klassen hade 30 elever. Hur många burkar hade varje elev samlat i genomsnitt? 6 I en tunnelbanevagn åker x män och y kvinnor. Förklara vad som menas med uttrycket a) x + y b) y x 7 Till en kurs i matlagning hade tio personer anmält sig. Åldern på deltagarna var: 22 år, 68 år, 31 år, 27 år, 42 år, 25 år, 33 år, 72 år, 29 år, 35 år Vad är a) medelåldern b) medianåldern c) typvärdet 8 Förklara varför 25 % kan vara mindre än 20 %. 358
45 Tabellerna visar hur vi använder vårt vatten i Sverige och hur mycket vatten det går åt för att tillverka en del mat och produkter. Lös uppgifterna nedan med hjälp av tabellerna. Vatten till Liter vatten per person och dag bad och dusch 60 wc 60 tvätt 20 disk 20 mat 7 trädgård 7 annat 26 Totalt 200 Produkter Liter vid tillverkning 1 kg bomull en hamburgare liter mjölk kg ost en kopp kaffe cl läsk Hur många procent av vattnet använder vi till a) bad och dusch b) mat 10 Sveriges befolkning är cirka 9,5 miljoner. Hur mycket väger allt vatten som vi använder i Sverige under ett år? Avrunda till tiotal miljoner ton. 1 liter vatten väger 1 kg. 11 Ett par jeans innehåller ungefär 600 g bomull och en t-shirt ungefär 300 g bomull. Antag att du under ett år köper två par jeans och fem t-shirts. Hur mycket väger det vatten som har använts vid tillverkningen? Svara i ton. 12 Varje år äter vi i genomsnitt 18 kg ost och dricker koppar kaffe. Hur mycket vatten förbrukar vi i genomsnitt per dag för kaffe och ost? Avrunda till hundratal liter. 1 3 Veckans problem Rita av figuren. Skriv sedan in talen 4, 5, 6, 7, 8 och 9 i ringarna så att summan av talen längs alla sidor blir
46 Läxa 23 Efter avsnitt a) b) 2 5 =? % c) 1/3 av 600 kr d) 0,7 0,05 e) ,9 f) 5 02, 2 Hur många procent är a) 15 kr av 50 kr b) 60 cl av 200 cl c) 12 kg av 25 kg 3 Lös ekvationerna. a) 5x + 11 = 21 b) 20 3y = 5 c) z = 12 4 Skriv tiderna i minuter. a) 1 h 4 b) 0,1 h c) h d) 1 6 h 5 Jättemammuten levde i Nordamerika för ungefär 1 miljon år sen. Den vägde 15 ton och åt 300 kg växter varje dag. Hur stor andel av sin vikt åt mammuten per dag? Svara i procent. 6 a) Du har talet x. Ett annat tal är 20 större än x. Teckna ett uttryck för det talet. b) Summan av talet y och ett annat tal är 20. Teckna ett uttryck för det andra talet. 7 Vid sekelskiftet år 2000 passerade jordens befolkning sex miljarder invånare. Europa hade då 750 miljoner invånare och Asien miljoner invånare. a) Skriv jordens befolkning år 2000 med siffror. Hur många procent av jordens befolkning bodde i b) Europa c) Asien Avrunda till hela procent. På bilden ser du en pygmémammut som står framför en träskulptur. Skulpturen är gjord i verklig storlek och visar bakifrån en mammut, en afrikansk elefant och en amerikansk mastodont. 360
47 8 Jag håller med dig till 110 %, sa Jesper till sin kompis. Kan man hålla med någon till 110 %? 9 I vissa sammanhang använder man tum som längdenhet. Hur mycket längre är en skruv med längden 1 1 tum än 4 en med längden 3 cm? Svara i tiondels millimeter. 1 tum 2,5 cm invaderades Australien av gräshoppor. En svärm med gräshoppor var 170 m bred och sex kilometer lång. Hur många fotbollsplaner motsvarade det? En fotbollsplan har arean m 2. Avrunda till tiotal. 11 Under en friluftsdag åkte tre femtedelar av skolans elever till Sälen för att åka skidor. Resterande nittiosex elever stannade hemma och åkte skridskor eller pulka istället. Hur många elever gick i den skolan? År 2004 blev Kanarieöarna plötsligt invaderade av gräshoppor. På bilden ser du några badgäster som flyr från en strand i Corralejo. Man uppskattar att svärmen, som kom från västra Afrika, innehöll ungefär 100 miljoner gräshoppor. 12 Andelen guld i smycken anges i karat. 1 karat innebär att guld. Om en ring är på 21 karat så innebär det alltså att 21/24 av vikten är rent guld. a) Hur stor andel guld är det i ett halsband på 18 karat? 1 24 är rent b) Antag att ett halsband väger 30 g och består av 18 karats guld. Hur mycket är guldet i halsbandet värt, om guldpriset är kr per kilogram? Veckans problem En gammal dam säger till sitt barnbarns barn så här: Om du tar nio år från min ålder, så är 3/4 av resten lika med 60 år? Hur gammal är jag? 361
48 Läxa 24 Efter avsnitt a) ,5 b) 150 0,2 c) 05, 2 d) 0,7 0,9 e) ,2 f) 2 3 h =? min 2 Hur mycket är a) 2 av 90 kr 3 b) 20 % av 250 kg c) 3 av m 5 3 a) Hur stor är sänkningen? b) Vad kostar jackan? REA 25% kr (ord pris) 4 Evas hyra höjs med 5 %. Före höjningen var hyran kr. a) Hur stor blir höjningen? b) Hur stor blir Evas nya hyra? 5 Vilka tal ska stå i rutorna för att det ska stämma? a) =? % b)? % av 500 kr = 100 kr c) 10 % av? kr = 65 kr 6 Lös ekvationerna. a) x + 2 = 7 b) 6y 1 = 41 c) z + 2z 7 = Hur många glaskulor är det i vardera påsen om det är lika många i varje? Teckna en ekvation och lös den. + + = x x 362
49 8 Du ska räkna ut hur många procent 12 liter är av 20 liter. Ge flera förslag på hur du kan göra. 9 En rektangels sidor är 8 cm och 5 cm. Om vi ökar längden med 25 % och bredden med 30 % så får vi en ny rektangel. Hur mycket större area har den nya rektangeln än den första? 10 En flaska väger 500 g när den är tom. Fylld med vatten väger flaskan 1,3 kg. Hur stor andel av flaskan är fylld med vatten om flaskan väger 950 g? Svara i a) bråkform med så liten nämnare som möjligt b) hela procent 11 Indonesien är världens fjärde folkrikaste land med mer än 213 miljoner invånare. 5 % av landets befolkning är kristna. Hälften av dem bor på Java och en femtedel på Sumatra. Hur många miljoner kristna bor det på Sumatra? Avrunda till heltal. 12 En bit ut i vattnet står en stolpe. 0,75 m av stolpen är ovanför vattenytan. 2/3 av stolpens hela längd står i vatten och 1/4 är nedslagen i sjöbotten. Hur lång är stolpen? Veckans problem Tänk dig att du placerar vita möss vid start. Vid varje vägskäl finns angivet hur många procent som väljer den ena eller den andra vägen. Hur många möss kommer fram till mål? Start 50 % 50 % 70 % 30% 10% 90% 40% 60% 40% 80% 20% 60% 35% 25% 75% 65% 25% 75% Mål 363
5 Beräkna med huvudräkning
 2 Beräkna a) Hur mycket får man tillbaka på en hundralapp, om man handlar för 65 kr? b) Kristina är 13 år. Morfar är 63 år äldre. Hur gammal är morfar? c) Benny köper tio kolor. De kostar 50 öre styck.
2 Beräkna a) Hur mycket får man tillbaka på en hundralapp, om man handlar för 65 kr? b) Kristina är 13 år. Morfar är 63 år äldre. Hur gammal är morfar? c) Benny köper tio kolor. De kostar 50 öre styck.
Arbetsblad 1. Addition och subtraktion i flera steg 1 524 + 162 = 2 374 + 424 = 3 762 + 218 = 4 257 + 431 = 5 287 + 372 = 6 415 + 194 = 7 665 58 =
 Arbetsblad NAMN: Addition och subtraktion i flera steg + 3 + 3 + + 3 + 3 + 9 3 3 9 9 9 39 3 3 + 39 3 + 99 0 3 Kopiering tillåten Matematikboken Författarna och Liber AB Arbetsblad Addition och subtraktion
Arbetsblad NAMN: Addition och subtraktion i flera steg + 3 + 3 + + 3 + 3 + 9 3 3 9 9 9 39 3 3 + 39 3 + 99 0 3 Kopiering tillåten Matematikboken Författarna och Liber AB Arbetsblad Addition och subtraktion
Sammanfattningar Matematikboken X
 Sammanfattningar Matematikboken X KAPITEL 1 TAL OCH RÄKNING Naturliga tal Med naturliga tal menas talen 0, 1,,, Jämna tal 0,,, 6, 8 Udda tal 1,,, 7 Tallinje Koordinater En tallinje kan t ex användas för
Sammanfattningar Matematikboken X KAPITEL 1 TAL OCH RÄKNING Naturliga tal Med naturliga tal menas talen 0, 1,,, Jämna tal 0,,, 6, 8 Udda tal 1,,, 7 Tallinje Koordinater En tallinje kan t ex användas för
Läxa 9 7 b) Dividera 84 cm med π för att få reda på hur lång diametern är. 8 1 mm motsvarar 150 / 30 mil = = 5 mil. Omvandla till millimeter.
 LEDTRÅDAR LÄXOR Läa Förläng så att du får ett heltal i nämnaren. Använd division. Varje sekund klipper Karin, m =, m. Läa 0 ml = 0,0 liter Använd sambandet s = v t. Räkna ut hur mycket vattnet väger när
LEDTRÅDAR LÄXOR Läa Förläng så att du får ett heltal i nämnaren. Använd division. Varje sekund klipper Karin, m =, m. Läa 0 ml = 0,0 liter Använd sambandet s = v t. Räkna ut hur mycket vattnet väger när
Läxa 11. Läxa T ex kan en sida vara 4 cm. Hur lång är då höjden mot den sidan? 8 b) Flytta andra stickan i översta raden ett steg åt höger.
 ledtrådar LäxOr Läxa Rita en bild med de lyktstolparna. Hur många mellanrum är det? Läxa 8 På nedre halvan ska talen adderas tv å och två och på den övre halvan ska talen subtraheras. Läxa 6 7 Rita en
ledtrådar LäxOr Läxa Rita en bild med de lyktstolparna. Hur många mellanrum är det? Läxa 8 På nedre halvan ska talen adderas tv å och två och på den övre halvan ska talen subtraheras. Läxa 6 7 Rita en
a) 29 + 7 b) 83 5 c) 7 9 d) 4 25 e) 10 + 1,5 f) 103 95 a) niotusen trettiofem b) två hela och tjugofem hundradelar 0,5 kg 0,41 kg
 .... Laxor Laxor LÄXA 1 Efter avsnitt 1.2 a) 29 + 7 b) 83 5 c) 7 9 d) 4 25 e) 10 + 1,5 f) 103 95 2 Skriv med siffror a) niotusen trettiofem b) två hela och tjugofem hundradelar 3 Beräkna utan räknare a)
.... Laxor Laxor LÄXA 1 Efter avsnitt 1.2 a) 29 + 7 b) 83 5 c) 7 9 d) 4 25 e) 10 + 1,5 f) 103 95 2 Skriv med siffror a) niotusen trettiofem b) två hela och tjugofem hundradelar 3 Beräkna utan räknare a)
Addition och subtraktion. Vilka uträkningar visas på tallinjerna nedan? Beräkna med huvudräkning 1 3 5 = 2 2 2 + 5 = 3 3 7 + 3 = 4 4 1 4 = 5 7 2 + 7 5
 OH 1 Addition och subtraktion Vilka uträkningar visas på tallinjerna nedan? 1 = 7 6 1 0 1 + = 7 6 1 0 1 7 + = 7 6 1 0 1 1 = 7 6 1 0 1 Beräkna med huvudräkning 8 6 6 8 7 + 7 8 9 7 9 1 8 10 1 + 0 Kopiering
OH 1 Addition och subtraktion Vilka uträkningar visas på tallinjerna nedan? 1 = 7 6 1 0 1 + = 7 6 1 0 1 7 + = 7 6 1 0 1 1 = 7 6 1 0 1 Beräkna med huvudräkning 8 6 6 8 7 + 7 8 9 7 9 1 8 10 1 + 0 Kopiering
Repetitionsuppgifter 1
 Repetitionsuppgifter 1 1 Vilka tal pekar pilarna på? a) b) Skriv talen med siffror 2 a) trehundra sju b) femtontusen fyrtiofem c) tvåhundrafemtusen tre 3 a) fyra tiondelar b) 65 hundradelar c) 15 tiondelar
Repetitionsuppgifter 1 1 Vilka tal pekar pilarna på? a) b) Skriv talen med siffror 2 a) trehundra sju b) femtontusen fyrtiofem c) tvåhundrafemtusen tre 3 a) fyra tiondelar b) 65 hundradelar c) 15 tiondelar
a) trettiotvåtusen femhundrasju b) femhundratusen åttiotre a) ett udda tal b) det största jämna tal som är möjligt A B C A B C 3,1 3,2
 Alternativdiagnos 1 1 Skriv med siffror a) trettiotvåtusen femhundrasju b) femhundratusen åttiotre 2 Använd siffrorna 2, 3, 4 och 5 och skriv a) ett udda tal b) det största jämna tal som är möjligt 3 Vilka
Alternativdiagnos 1 1 Skriv med siffror a) trettiotvåtusen femhundrasju b) femhundratusen åttiotre 2 Använd siffrorna 2, 3, 4 och 5 och skriv a) ett udda tal b) det största jämna tal som är möjligt 3 Vilka
Repetition 1A. Del I. a) 0,3 eller 0,13 b) 1,19 eller 1,2 c) eller. a) b) c) a) fem tiondelar = b) = c) tre hundradelar =
 Repetition A Del I a) 976 + 2 = b) 07 233 = c) 6 = 2 Vilket av talen är störst? a) 0,3 eller 0,3 b),9 eller,2 c) 7 0 3 Hur stor andel av figuren är vit? a) b) c) eller 7 00 Skriv talen i decimalform. a)
Repetition A Del I a) 976 + 2 = b) 07 233 = c) 6 = 2 Vilket av talen är störst? a) 0,3 eller 0,3 b),9 eller,2 c) 7 0 3 Hur stor andel av figuren är vit? a) b) c) eller 7 00 Skriv talen i decimalform. a)
Facit Läxor. Tal. Tian Siffrans värde blir tio gånger mindre. 40 till 04 11 67, 69 och 71 12 a) 10, 22 och 15, 14 b) 15, 27 och 10, 9
 Tal Läxa 1 1 a) 307 b) 55 c) 00 003 a) 131 > 113 b) 1 > 1 c) 99 < 9 99 3 a) 1 170 b) 5 75 c) 91 a) 3 hundra b) 3 ental c) 3 tusen 5 a) 370 b) 0 a) 31 b) 1 3 c) 1 3 7 a) 99 b) 13 a) 37 b) 19 00 9 5 15 50
Tal Läxa 1 1 a) 307 b) 55 c) 00 003 a) 131 > 113 b) 1 > 1 c) 99 < 9 99 3 a) 1 170 b) 5 75 c) 91 a) 3 hundra b) 3 ental c) 3 tusen 5 a) 370 b) 0 a) 31 b) 1 3 c) 1 3 7 a) 99 b) 13 a) 37 b) 19 00 9 5 15 50
x kr y kr a) 7 dm b) 325 mm c) 1,2 km d) cm 2 Hur mycket är a) b) ( ) / 4 c) 10 / (14 4)
 REPETITION 2 A Del I 1 Skriv i meter. a) 7 dm b) 32 mm c) 1,2 km d) 1 20 cm 2 Hur mycket är a) + 1 b) ( + 1) / c) / (1 ) 3 Hur lång tid är det mellan klockslagen? a) 13.3 1. b).2 11.37 c) 1. 21.32 Teckna
REPETITION 2 A Del I 1 Skriv i meter. a) 7 dm b) 32 mm c) 1,2 km d) 1 20 cm 2 Hur mycket är a) + 1 b) ( + 1) / c) / (1 ) 3 Hur lång tid är det mellan klockslagen? a) 13.3 1. b).2 11.37 c) 1. 21.32 Teckna
1 Skriv med siffror a) tolvtusen femton b) fem hela och fyra hundradelar. b) 1000 0,04. 3 Skriv i kilogram a) 0,2 ton b) 4 hg c) 6400 g
 1 Skriv med siffror a) tolvtusen femton b) fem hela och fyra hundradelar 2 Beräkna a) 0,7 50 d) 45110 b) 1000 0,04 e) 78,2/100 c) 0,08 0,5 f) 555511000 3 Skriv i kilogram a) 0,2 ton b) 4 hg c) 6400 g 4
1 Skriv med siffror a) tolvtusen femton b) fem hela och fyra hundradelar 2 Beräkna a) 0,7 50 d) 45110 b) 1000 0,04 e) 78,2/100 c) 0,08 0,5 f) 555511000 3 Skriv i kilogram a) 0,2 ton b) 4 hg c) 6400 g 4
150 cm 2 m 70 dm. 280 cm 3,5 m 40 dm 3,50 0,50. 200 cm 1,5 2,5. 6 m. 30 cm 4 dm 500 mm. 2 m. 70 dm. 150 cm. 3,5 m. 40 dm. 280 cm.
 Skriv sträckorna i storleksordning. Längdenheter: meter (m), decimeter (dm), centimeter (cm) och millimeter (mm). Längden 15 cm kan skrivas på olika sätt: 15 cm = 1 m 5 cm = 1,5 m eller 15 dm cm eller
Skriv sträckorna i storleksordning. Längdenheter: meter (m), decimeter (dm), centimeter (cm) och millimeter (mm). Längden 15 cm kan skrivas på olika sätt: 15 cm = 1 m 5 cm = 1,5 m eller 15 dm cm eller
lång och 15 cm bred. Hur stor area har tomten i verkligheten? 4,5 2 l b) 2-2- 3 4
 LÄXA 12 1 Beräkna med huvudräkning a) En kvadrat har arean 81 cm 2. Hur stor är omkretsen? b) Hur mycket kostar 600 g fläskfile, om priset per kilogram är 120 kr? c) En burk energidryck innehåller 200
LÄXA 12 1 Beräkna med huvudräkning a) En kvadrat har arean 81 cm 2. Hur stor är omkretsen? b) Hur mycket kostar 600 g fläskfile, om priset per kilogram är 120 kr? c) En burk energidryck innehåller 200
Matematik A Testa dina kunskaper!
 Testa dina kunskaper! Försök i största möjliga mån att räkna utan hjälp av boken, skriv små noteringar i kanten om ni tycker att ni kan uppgifterna, att ni löste dem med hjälp av boken etc. Facit kommer
Testa dina kunskaper! Försök i största möjliga mån att räkna utan hjälp av boken, skriv små noteringar i kanten om ni tycker att ni kan uppgifterna, att ni löste dem med hjälp av boken etc. Facit kommer
Namn: Hundradelar. 4 tiondelar 0, 4 17 tiondelar 1, tiondelar 298 hundradelar. Hundradelar. 98 hundradelar 875 hundradelar
 arbetsblad 1:1 Positionssystemet > > Skriv talen med siffror. Glöm inte decimaltecknet. Ental Tiondelar Hundradelar 1 tiondel 0, 1 52 hundradelar 0, 5 2 tiondelar 0, 17 tiondelar 1, 7 9 tiondelar 0, 9
arbetsblad 1:1 Positionssystemet > > Skriv talen med siffror. Glöm inte decimaltecknet. Ental Tiondelar Hundradelar 1 tiondel 0, 1 52 hundradelar 0, 5 2 tiondelar 0, 17 tiondelar 1, 7 9 tiondelar 0, 9
Arbetsblad 1:1. 1 Svara i bråkform hur stor andel av den stora rutan som är. 2 Svara i decimalform hur stor andel av den stora rutan som är.
 Arbetsblad 1:1 Tal i bråkform och i decimalform Grundbok: grundkurs s. 8 blåkurs s. 0 1 Svara i bråkform hur stor andel av den stora rutan som är a) grå b) kryssad c) prickad d) vit 2 Svara i decimalform
Arbetsblad 1:1 Tal i bråkform och i decimalform Grundbok: grundkurs s. 8 blåkurs s. 0 1 Svara i bråkform hur stor andel av den stora rutan som är a) grå b) kryssad c) prickad d) vit 2 Svara i decimalform
I addition adderar vi. Vi kan addera termerna i vilken ordning vi vill: 1 + 7 = 7 + 1
 BEGREPP ÅR 3 Taluppfattning och tals användning ADDITION 3 + 4 = 7 term + term = summa I addition adderar vi. Vi kan addera termerna i vilken ordning vi vill: 1 + 7 = 7 + 1 SUBTRAKTION 7-4 = 3 term term
BEGREPP ÅR 3 Taluppfattning och tals användning ADDITION 3 + 4 = 7 term + term = summa I addition adderar vi. Vi kan addera termerna i vilken ordning vi vill: 1 + 7 = 7 + 1 SUBTRAKTION 7-4 = 3 term term
1. Tina köper en joggingdress som kostar 186 kr. Hon betalar med två hundralappar. Hur mycket får hon tillbaka? Svar:
 8. MATEMATIK ÅK 5 8.1. Elevhäfte 8.1.1. Problemlösning 1 1. Tina köper en joggingdress som kostar 186 kr. Hon betalar med två hundralappar. Hur mycket får hon tillbaka? Svar: 2. Storleken av bildrutan
8. MATEMATIK ÅK 5 8.1. Elevhäfte 8.1.1. Problemlösning 1 1. Tina köper en joggingdress som kostar 186 kr. Hon betalar med två hundralappar. Hur mycket får hon tillbaka? Svar: 2. Storleken av bildrutan
Repetitionsuppgifter 1
 Repetitionsuppgifter 1 Beräkna 1 a) 0,5 + 0,7 b) 0,45 + 1,6 c) 2,76 0,8 2 a) 4,5 10 b) 30,5 10 c) 0,45 1 000 3 Vilka av produkterna är a) större än 6 1,09 6 0,87 6 1 6 4,3 6 0,08 6 b) mindre än 6 4 Skriv
Repetitionsuppgifter 1 Beräkna 1 a) 0,5 + 0,7 b) 0,45 + 1,6 c) 2,76 0,8 2 a) 4,5 10 b) 30,5 10 c) 0,45 1 000 3 Vilka av produkterna är a) större än 6 1,09 6 0,87 6 1 6 4,3 6 0,08 6 b) mindre än 6 4 Skriv
Välkommen till Borgar!
 Välkommen till Borgar! Välkommen till Borgar! Vi ser fram emot att snart träffa en ny årskull med naturettor och hoppas att du kommer att trivas mycket bra hos oss. Studier i naturvetenskapliga ämnen förutsätter
Välkommen till Borgar! Välkommen till Borgar! Vi ser fram emot att snart träffa en ny årskull med naturettor och hoppas att du kommer att trivas mycket bra hos oss. Studier i naturvetenskapliga ämnen förutsätter
Facit till Tema Matematik 5
 Facit till Tema Matematik 5 Till dig som använder detta facit: Sidnumren hänvisar till sidan i arbetsboken. På en del frågor står det Elevens eget svar i facit. Det beror på att man kan svara på olika
Facit till Tema Matematik 5 Till dig som använder detta facit: Sidnumren hänvisar till sidan i arbetsboken. På en del frågor står det Elevens eget svar i facit. Det beror på att man kan svara på olika
Tankenötter. från a till e
 Tankenötter från a till e H O L M S T R Ö M S M E D H A M R E Matematikserier av Holmström och smedhamre Kära Läsare Det här är den 4:e boken med tankenötter. Vissa nötter är enkla att knäcka, medan andra
Tankenötter från a till e H O L M S T R Ö M S M E D H A M R E Matematikserier av Holmström och smedhamre Kära Läsare Det här är den 4:e boken med tankenötter. Vissa nötter är enkla att knäcka, medan andra
Catherine Bergman Maria Österlund
 Lgr 11 Matematik Åk 3 Geometri, mätningar och statistik FA C I T Catherine Bergman Maria Österlund Kan du använda geometriska begrepp? Kan du beskriva figurernas egenskaper, likheter och skillnader? Skriv
Lgr 11 Matematik Åk 3 Geometri, mätningar och statistik FA C I T Catherine Bergman Maria Österlund Kan du använda geometriska begrepp? Kan du beskriva figurernas egenskaper, likheter och skillnader? Skriv
Matematikpärmen 4-6. 105 fullmatade arbetsblad i matematik för åk 4-6. Massor med extrauppgifter.
 M A T E M A T I K P Ä R M E N - 6 Matematikpärmen -6 Arbetsblad med fri kopieringsrätt! 05 fullmatade arbetsblad i matematik för åk -6. Massor med extrauppgifter. Materialet är indelat i 7 områden per
M A T E M A T I K P Ä R M E N - 6 Matematikpärmen -6 Arbetsblad med fri kopieringsrätt! 05 fullmatade arbetsblad i matematik för åk -6. Massor med extrauppgifter. Materialet är indelat i 7 områden per
4 Dividera höjningen (0,5 %) med räntesatsen från början (1 %). 7 Du kan pröva dig fram till exempel så här: Från Till Procent- Procent enheter
 ledtrådar LäOr Läa 8 Räkna först ut hur mycket tiokronorna och enkronorna är värda sammanlagt. Läa 8 Räkna först ut hur mycket allt vatten i hinken väger när den är full. Läa MGN = 8 Tänk dig att näckrosen
ledtrådar LäOr Läa 8 Räkna först ut hur mycket tiokronorna och enkronorna är värda sammanlagt. Läa 8 Räkna först ut hur mycket allt vatten i hinken väger när den är full. Läa MGN = 8 Tänk dig att näckrosen
REPETITION 3 A. a) b) a) 1 4 av 200 kr b) 10 % av 750 kr c) 2 3. av 60 kg. a) b) c) b) a) 6 8. a) b) b) 0,075 c) d) 0,9.
 DEL I 1 Mät vinklarna. Gradtalen ska sluta på 0 eller 5. 2 Hur mycket är a) 1 4 av 200 kr b) 10 % av 750 kr c) 2 3 av 60 kg 3 Mät sidorna i hela och halva centimeter. Beräkna sedan omkrets och area av
DEL I 1 Mät vinklarna. Gradtalen ska sluta på 0 eller 5. 2 Hur mycket är a) 1 4 av 200 kr b) 10 % av 750 kr c) 2 3 av 60 kg 3 Mät sidorna i hela och halva centimeter. Beräkna sedan omkrets och area av
Arbetsblad 1:1. 1 Svara i bråkform hur stor andel av den stora rutan som är. 2 Svara i decimalform hur stor andel av den stora rutan som är.
 Arbetsblad 1:1 Tal i bråkform och i decimalform Grundbok: grundkurs s. 8 blåkurs s. 0 1 Svara i bråkform hur stor andel av den stora rutan som är a) grå b) kryssad c) prickad d) vit 2 Svara i decimalform
Arbetsblad 1:1 Tal i bråkform och i decimalform Grundbok: grundkurs s. 8 blåkurs s. 0 1 Svara i bråkform hur stor andel av den stora rutan som är a) grå b) kryssad c) prickad d) vit 2 Svara i decimalform
Förtest. Hur kan jag arbeta med förtesten? Hur dokumenterar jag elevens kunskapsutveckling? Uppfattar du det som att eleven kan matematikinnehållet
 AB Vår LP (8766) Flik 0 Förtest (Lev vc).qxd 00-0-6 :5 Sida Förtest För alla lärare är det viktigt att skaffa sig en god bild av elevens kunskaper för att veta vad eleven behöver för att gå vidare i sin
AB Vår LP (8766) Flik 0 Förtest (Lev vc).qxd 00-0-6 :5 Sida Förtest För alla lärare är det viktigt att skaffa sig en god bild av elevens kunskaper för att veta vad eleven behöver för att gå vidare i sin
Mattestegens matematik
 höst Decimaltal pengar kr 0 öre,0 kr Rita 0,0 kr på olika sätt. räkna,0,0 storleksordna decimaltal Sub för lite av två talsorter 7 00 0 tallinjer heltal 0 0 Add med tiotalsövergångar 0 7 00 0 Sub för lite
höst Decimaltal pengar kr 0 öre,0 kr Rita 0,0 kr på olika sätt. räkna,0,0 storleksordna decimaltal Sub för lite av två talsorter 7 00 0 tallinjer heltal 0 0 Add med tiotalsövergångar 0 7 00 0 Sub för lite
Matematik klass 1 Problemlösning nummer 1
 Matematik klass 1 Problemlösning nummer 1 ditt eget matteproblem Skriv ditt namn här Anneli Weiland, HepPed A och O Matematik åk 1 Problemlösning 1 Kalle hade fem gamla böcker i sin låda. Nu fick han tre
Matematik klass 1 Problemlösning nummer 1 ditt eget matteproblem Skriv ditt namn här Anneli Weiland, HepPed A och O Matematik åk 1 Problemlösning 1 Kalle hade fem gamla böcker i sin låda. Nu fick han tre
sträckan = tiden. hastigheten hastigheten = sträckan tiden 210 hastigheten = 3 = 70 Bilisten kör 70 km/h. tiden =
 Enheter och skala I det här kapitlet kan du lära dig mer om hastighet att skriva minuter som del av timme att räkna om km/h till m/s något om hastigheter till sjöss om volymenheterna cm 3, dm 3 och m 3
Enheter och skala I det här kapitlet kan du lära dig mer om hastighet att skriva minuter som del av timme att räkna om km/h till m/s något om hastigheter till sjöss om volymenheterna cm 3, dm 3 och m 3
1 a) 8,3 b) 5,4. 2 a) 16,38 b) 20, m. 4 a) 6 cm 2 b) 5 cm 2. 5 a) m 2 b) m c) dm 2. 6 a) 12 m 2 b) 27 cm 2
 epetition Facit epetition a) 9, 7, 2 a),, a),,7 A,2 B,9 C,7 a),,0 c) 0,2 2,0 m 2, m 2,2 m, m 7 a) 0, m 0,0 m c) 0, m a) 9 a) 0 2 a) 7 a) st st 2 a) 7 0 a),0 kr,0 kr,7 m,7 km T.ex. 7 valpar dl 9 0, m 20
epetition Facit epetition a) 9, 7, 2 a),, a),,7 A,2 B,9 C,7 a),,0 c) 0,2 2,0 m 2, m 2,2 m, m 7 a) 0, m 0,0 m c) 0, m a) 9 a) 0 2 a) 7 a) st st 2 a) 7 0 a),0 kr,0 kr,7 m,7 km T.ex. 7 valpar dl 9 0, m 20
!TIE - 1,5 10,8 LÄXA a) omkrets b) area. 7,5 a) 0,6 700 b) 200. c) 0,05. c) (-7) + (-3) f) (-7)'3. a) 181 b) 12, 16,01-1,6
 LÄXA. 1 1 En fönsterruta har måtten 0,8 m x 1,5 m. Vilken är rutans a) omkrets b) area 2 Räkna utan miniräknare 62000 7,5 a) 0,6 700 b) 200 c) 0,05 3 Beräkna a) 7 + (-3) d) (-7) (-3) b) 7 (-3) e) (-7)
LÄXA. 1 1 En fönsterruta har måtten 0,8 m x 1,5 m. Vilken är rutans a) omkrets b) area 2 Räkna utan miniräknare 62000 7,5 a) 0,6 700 b) 200 c) 0,05 3 Beräkna a) 7 + (-3) d) (-7) (-3) b) 7 (-3) e) (-7)
4 Sätt in punkternas koordinater i linjens ekvation och se om V.L. = H.L. 5 Räkna först ut nya längden och bredden.
 Läxor Läxa 7 En sådan timme skulle ha 00 00 s = 0 000 s. 8 a) O = π d och A = π r r. 0 Beräkna differensen mellan hela triangelns area och arean av den vita triangeln i toppen. Läxa 9 Hur stor andel målar
Läxor Läxa 7 En sådan timme skulle ha 00 00 s = 0 000 s. 8 a) O = π d och A = π r r. 0 Beräkna differensen mellan hela triangelns area och arean av den vita triangeln i toppen. Läxa 9 Hur stor andel målar
ARBETSBLAD FACIT. 1 Skriv med siffror Träna huvudräkning. 10 Multiplikation med uppställning De fyra räknesätten 1.
 FACIT Skriv med siffror 0 0 0 0 0 8 0 8 0 0 0 008 0 00 8 0 00 0 000 00 000 08 000 00 00 8 0 000 0 000 000 0 00 000 00 8 Addition med uppställning 08 88 8 8 0 0 80 0 8 88 0 0 0 Subtraktion med uppställning
FACIT Skriv med siffror 0 0 0 0 0 8 0 8 0 0 0 008 0 00 8 0 00 0 000 00 000 08 000 00 00 8 0 000 0 000 000 0 00 000 00 8 Addition med uppställning 08 88 8 8 0 0 80 0 8 88 0 0 0 Subtraktion med uppställning
Eva Björklund Heléne Dalsmyr. matematik. Koll på. Skriva Facit
 Eva Björklund Heléne Dalsmyr 5B matematik Koll på Skriva Facit 6Ekvationer, uttryck och mönster 1 a) b) = c) d) 2 a) = b) c) = d) 3 a) < b) < c) < d) > 4 a) < b) < c) > d) < 5 a) < b) > c) < d) > Talet
Eva Björklund Heléne Dalsmyr 5B matematik Koll på Skriva Facit 6Ekvationer, uttryck och mönster 1 a) b) = c) d) 2 a) = b) c) = d) 3 a) < b) < c) < d) > 4 a) < b) < c) > d) < 5 a) < b) > c) < d) > Talet
Förord. Innehåll. 1 Tal 4. 4 Algebra 42. 2 Bråk och procent 18. 5 Statistik och sannolikhet 54. 6 Tid, hastighet och skala 60.
 Förord Det här häftet är tänkt som ett komplement till kapitel 5, Genrepet, i läroboken Matte Direkt år 9. Häftet vänder sig främst till de elever som har svårigheter att klara Genrepets nivå i boken och
Förord Det här häftet är tänkt som ett komplement till kapitel 5, Genrepet, i läroboken Matte Direkt år 9. Häftet vänder sig främst till de elever som har svårigheter att klara Genrepets nivå i boken och
Eva Björklund Heléne Dalsmyr. matematik. Koll på. Skriva Facit
 Eva Björklund Heléne Dalsmyr 5A matematik Koll på Skriva Facit 1 Tal i decimalform,3 1 a) 0,5 b) 0,7 c) 0, a) 4, b),1 c) 9,4 3 a) 35,8 b) 41, c) 0,9 4 a) 1,1 b) 4, c) 7,3 5 a) 13,4 b) 3,5 c) 91,7 a) 40,8
Eva Björklund Heléne Dalsmyr 5A matematik Koll på Skriva Facit 1 Tal i decimalform,3 1 a) 0,5 b) 0,7 c) 0, a) 4, b),1 c) 9,4 3 a) 35,8 b) 41, c) 0,9 4 a) 1,1 b) 4, c) 7,3 5 a) 13,4 b) 3,5 c) 91,7 a) 40,8
PROVUPPGIFTER. Steg 9 10 Bråk och procent. Godkänd 9 10 1 Skriv 0,03 i procentform. 2 Skriv i blandad form.
 Steg 9 10 Bråk och procent Godkänd 9 10 1 Skriv 0,03 i procentform. 16 2 Skriv i blandad form. 5 3 Vilket eller vilka av talen är lika med en åttondel? 0,8 2 8 2 16 0,12 1,8 4 Skriv 7 % i decimalform.
Steg 9 10 Bråk och procent Godkänd 9 10 1 Skriv 0,03 i procentform. 16 2 Skriv i blandad form. 5 3 Vilket eller vilka av talen är lika med en åttondel? 0,8 2 8 2 16 0,12 1,8 4 Skriv 7 % i decimalform.
a) 4a + a b) 4a 3a c) 4(a + 1)
 REPETITION 2 A 1 Förenkla uttrycken. a) 4a + a b) 4a 3a c) 4(a + 1) 2 Johannas väg till skolan är a m lång. a) Robins skolväg är 200 m längre än Johannas. Teckna ett uttryck för hur lång skolväg Robin
REPETITION 2 A 1 Förenkla uttrycken. a) 4a + a b) 4a 3a c) 4(a + 1) 2 Johannas väg till skolan är a m lång. a) Robins skolväg är 200 m längre än Johannas. Teckna ett uttryck för hur lång skolväg Robin
REPETITION 2 A. a) 4a + a b) 4a 3a c) 4(a + 1)
 REPETITION 2 A 1 Förenkla uttrycken. a) 4a + a b) 4a 3a c) 4(a + 1) 2 Johannas väg till skolan är a m lång. a) Robins skolväg är 200 m längre än Johannas. Teckna ett uttryck för hur lång skolväg Robin
REPETITION 2 A 1 Förenkla uttrycken. a) 4a + a b) 4a 3a c) 4(a + 1) 2 Johannas väg till skolan är a m lång. a) Robins skolväg är 200 m längre än Johannas. Teckna ett uttryck för hur lång skolväg Robin
Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning
 Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning Eleven skall år 1 Begrepp Jämförelse- och storleksord, t.ex. stor, större, störst. Positionssystemet
Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning Eleven skall år 1 Begrepp Jämförelse- och storleksord, t.ex. stor, större, störst. Positionssystemet
Arbetsblad 3:1. Tolka uttryck. 1 Kajsa är a år gammal. Para ihop varje påstående med rätt uttryck.
 Arbetsblad :1 sid 78, 92 Tolka uttryck 1 Kajsa är a år gammal. Para ihop varje påstående med rätt uttryck. a) Karin är tre gånger så gammal: b) Katta är år yngre: a + a c) Kristina är en tredjedel så gammal:
Arbetsblad :1 sid 78, 92 Tolka uttryck 1 Kajsa är a år gammal. Para ihop varje påstående med rätt uttryck. a) Karin är tre gånger så gammal: b) Katta är år yngre: a + a c) Kristina är en tredjedel så gammal:
Lokala mål i matematik
 Lokala mål i matematik År 6 År 7 År 8 År 9 Taluppfattning (aritmetik) förstår positionssystemets uppbyggnad med decimaler ex: kan skriva givna tal adderar decimaltal ex: 15,6 + 3,87 subtraherar decimaltal
Lokala mål i matematik År 6 År 7 År 8 År 9 Taluppfattning (aritmetik) förstår positionssystemets uppbyggnad med decimaler ex: kan skriva givna tal adderar decimaltal ex: 15,6 + 3,87 subtraherar decimaltal
Procent 1, 50 % är hälften
 Innehåll Procent -7 Bråkform decimalform procentform 8-9 Sannolikhet 10-1 Kombinatorik 13-1 Medelvärde, median och typvärde 1-16 Negativa tal 17-18 Koordinatsystem 19- Proportionella samband 3- Geometriska
Innehåll Procent -7 Bråkform decimalform procentform 8-9 Sannolikhet 10-1 Kombinatorik 13-1 Medelvärde, median och typvärde 1-16 Negativa tal 17-18 Koordinatsystem 19- Proportionella samband 3- Geometriska
Addera. Skriv mellanled. Subtrahera Skriv mellanled. 532-429 1685-496 1 1 10 10 10
 Namn: Hela och halva tusental till 00 000 Addera och subtrahera. 000+ 000= 000 000+ 00 = 00 000-000= 000 000-00 = 00 Skriv talen i fallande ordningsföljd. 000 0 00 0 00 0 00 00 0 000 0 00 0 00 0 00 0 00
Namn: Hela och halva tusental till 00 000 Addera och subtrahera. 000+ 000= 000 000+ 00 = 00 000-000= 000 000-00 = 00 Skriv talen i fallande ordningsföljd. 000 0 00 0 00 0 00 00 0 000 0 00 0 00 0 00 0 00
Steg dl. 3 a) 12 b) eller 5 = = 6 a) 100% b) 75% 7 7 gröna rutor. Steg 5. 2 a) 600 b) 6% c) 270
 Förtest Bråk och procent Steg a) b) dl Pizzadeg vatten jäst olja salt vetemjöl personer dl / paket msk / tsk / dl I den högra är störst del skuggad. a) T ex ruta av b) T ex rutor av Steg dl a) b) eller
Förtest Bråk och procent Steg a) b) dl Pizzadeg vatten jäst olja salt vetemjöl personer dl / paket msk / tsk / dl I den högra är störst del skuggad. a) T ex ruta av b) T ex rutor av Steg dl a) b) eller
Södervångskolans mål i matematik
 Södervångskolans mål i matematik Mål som eleverna lägst ska ha uppnått i slutet av det första skolåret beträffande tal och taluppfattning kunna läsa av en tallinje mellan 0-20 kunna läsa och ramsräka tal
Södervångskolans mål i matematik Mål som eleverna lägst ska ha uppnått i slutet av det första skolåret beträffande tal och taluppfattning kunna läsa av en tallinje mellan 0-20 kunna läsa och ramsräka tal
'. '.,.':p ~~~?t:~~;s:!l
 LÄXA 7 1 Avrunda till två decimaler a) 0,098 b) 13,574999 c) 0,0051 d) 1,7051 2 Skriv i grundpotensform a) 8000 b) 0,0005 c) 0,012 d) 675000 3 Hur mycket får man betala för 4 hg rökt korv, om priset per
LÄXA 7 1 Avrunda till två decimaler a) 0,098 b) 13,574999 c) 0,0051 d) 1,7051 2 Skriv i grundpotensform a) 8000 b) 0,0005 c) 0,012 d) 675000 3 Hur mycket får man betala för 4 hg rökt korv, om priset per
Sammanfattningar Matematikboken Y
 Sammanfattningar Matematikboken Y KAPitel 1 TAL OCH RÄKNING Numeriska uttryck När man beräknar ett numeriskt uttryck utförs multiplikation och division före addition och subtraktion. Om uttrycket innehåller
Sammanfattningar Matematikboken Y KAPitel 1 TAL OCH RÄKNING Numeriska uttryck När man beräknar ett numeriskt uttryck utförs multiplikation och division före addition och subtraktion. Om uttrycket innehåller
Läxa nummer 1 klass 3
 Läxa nummer 1 klass 3 Skriv ditt namn i triangeln som ett konstverk! Det här är din läxbok för klass 3. Du kommer att få en läxa i veckan. Där det står X skriver du vilket tal X är under eller över X:et.
Läxa nummer 1 klass 3 Skriv ditt namn i triangeln som ett konstverk! Det här är din läxbok för klass 3. Du kommer att få en läxa i veckan. Där det står X skriver du vilket tal X är under eller över X:et.
ARBETSBLAD FACIT. 1 Skriv med siffror Träna huvudräkning. 10 Multiplikation med uppställning De fyra räknesätten 1.
 Skriv med siffror 0 0 0 0 0 0 0 0 0 00 0 00 0 00 0 000 00 000 0 000 00 00 0 000 0 000 000 0 00 000 00 Addition med uppställning 0 0 0 0 0 0 0 0 Subtraktion med uppställning 0 0 0 0 0 Multiplikation med
Skriv med siffror 0 0 0 0 0 0 0 0 0 00 0 00 0 00 0 000 00 000 0 000 00 00 0 000 0 000 000 0 00 000 00 Addition med uppställning 0 0 0 0 0 0 0 0 Subtraktion med uppställning 0 0 0 0 0 Multiplikation med
Bok: X (fjärde upplagan) Kapitel : 3 Längd, tid och samband Kapitel : 4 Algebra och mönster
 PLANERING MATEMATIK - ÅK 7 Bok: X (fjärde upplagan) Kapitel : 3 Längd, tid och samband Kapitel : 4 Algebra och mönster Elevens namn: markera med kryss vilka uppgifter du gjort Avsnitt: sidor ETT ETT TVÅ
PLANERING MATEMATIK - ÅK 7 Bok: X (fjärde upplagan) Kapitel : 3 Längd, tid och samband Kapitel : 4 Algebra och mönster Elevens namn: markera med kryss vilka uppgifter du gjort Avsnitt: sidor ETT ETT TVÅ
Decimaltal. Matteord hela tal decimaltal tiondel hundradel. tusendel decimal decimaltecken
 Decimaltal Mål När du har arbetat med det här kapitlet ska du kunna > förstå vad som menas med ett decimaltal > storleksordna decimaltal > multiplicera och dividera med 10, 100 och 1 000 > räkna med överslagsräkning
Decimaltal Mål När du har arbetat med det här kapitlet ska du kunna > förstå vad som menas med ett decimaltal > storleksordna decimaltal > multiplicera och dividera med 10, 100 och 1 000 > räkna med överslagsräkning
Matematik. Mål att sträva mot. Mål att uppnå. År 1 Mål Kriterier Eleven ska kunna. Taluppfattning koppla ihop antal och siffra kan lägga rätt antal
 Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Matematik. Ämnesprov, läsår 2014/2015. Delprov B. Årskurs. Elevens namn och klass/grupp
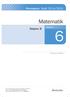 Ämnesprov, läsår 2014/2015 Matematik Delprov B Årskurs 6 Elevens namn och klass/grupp Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Ämnesprov, läsår 2014/2015 Matematik Delprov B Årskurs 6 Elevens namn och klass/grupp Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Volym liter och deciliter
 Volym liter och deciliter Måla så volymen stämmer. Skriv så volymen stämmer. : l och dl l dl l och 8 dl 0 l 9 dl dl l dl Hur många dl ska du hälla i för att få l? 7 9 dl dl dl dl dl Hur mycket? Skriv.
Volym liter och deciliter Måla så volymen stämmer. Skriv så volymen stämmer. : l och dl l dl l och 8 dl 0 l 9 dl dl l dl Hur många dl ska du hälla i för att få l? 7 9 dl dl dl dl dl Hur mycket? Skriv.
Innehåll. 1 Allmän information 5. 4 Formativ bedömning 74. 5 Diagnoser och tester 90. 6 Prov och repetition 107. 2 Kommentarer till kapitlen 18
 Innehåll 1 Allmän information Seriens uppbyggnad Lärobokens struktur 6 Kapitelinledning 7 Avsnitten 7 Pratbubbleuppgifter Aktivitet Taluppfattning och huvudräkning 9 Resonera och utveckla 9 Räkna och häpna
Innehåll 1 Allmän information Seriens uppbyggnad Lärobokens struktur 6 Kapitelinledning 7 Avsnitten 7 Pratbubbleuppgifter Aktivitet Taluppfattning och huvudräkning 9 Resonera och utveckla 9 Räkna och häpna
Träningsuppgifter, gamla nationella prov i matematik(del B1) från Taluppfattning. Hashem Rezai, S:t Ilians skola, Västerås
 Taluppfattning 1. Vilket av följande tal är minst? Ringa in ditt svar. 2,9 2,98 2,998 2,889 2,89 (1/0) 2. Hur många miljoner visar miniräknaren? Svar: (1/0) 3. Vilket tal pekar pilen på? 31 32 33 Svar:
Taluppfattning 1. Vilket av följande tal är minst? Ringa in ditt svar. 2,9 2,98 2,998 2,889 2,89 (1/0) 2. Hur många miljoner visar miniräknaren? Svar: (1/0) 3. Vilket tal pekar pilen på? 31 32 33 Svar:
Svikten. enheter. Innehåll Tid och temperatur Längd Vikt Volym Problemlösning Kan du? Hur gick det?
 Svikten enheter Innehåll Tid och temperatur Längd Vikt Volym Problemlösning Kan du? Hur gick det? 2 11 12 17 18 23 24 29 30 31 7, 9, 11, 15, 17, 21, 23, 27, 29 11, 17, 23, 29, 32 På sidorna 11, 17, 23,
Svikten enheter Innehåll Tid och temperatur Längd Vikt Volym Problemlösning Kan du? Hur gick det? 2 11 12 17 18 23 24 29 30 31 7, 9, 11, 15, 17, 21, 23, 27, 29 11, 17, 23, 29, 32 På sidorna 11, 17, 23,
parallellogram pentagon hexagon parallelltrapets
 geometriska former och figurer Vad heter figurerna? Välj bland orden nedan. hexagon parallellogram parallelltrapets pentagon figur namn parallellogram pentagon hexagon parallelltrapets Hur många hörn och
geometriska former och figurer Vad heter figurerna? Välj bland orden nedan. hexagon parallellogram parallelltrapets pentagon figur namn parallellogram pentagon hexagon parallelltrapets Hur många hörn och
Välkommen till Borgar!
 Välkommen till Borgar! Välkommen till Borgar! Vi ser fram emot att snart träffa en ny årskull med ettor och hoppas att du kommer att trivas mycket bra hos oss. Din första termin på gymnasiet kommer att
Välkommen till Borgar! Välkommen till Borgar! Vi ser fram emot att snart träffa en ny årskull med ettor och hoppas att du kommer att trivas mycket bra hos oss. Din första termin på gymnasiet kommer att
GEOMETRISKA TILLÄMPNINGAR
 INNEHÅLL GEOMETRISKA TILLÄMPNINGAR GEOMETRISKA TILLÄMPNINGAR 251 252 GEOMETRISKA TILLÄMPNINGAR I samband med ett åskväder regnade det enligt en regnmätare 38 mm. Hur många liter vatten kom det a) på en
INNEHÅLL GEOMETRISKA TILLÄMPNINGAR GEOMETRISKA TILLÄMPNINGAR 251 252 GEOMETRISKA TILLÄMPNINGAR I samband med ett åskväder regnade det enligt en regnmätare 38 mm. Hur många liter vatten kom det a) på en
Facit Träningshäfte 9:2
 Kapitel 1 1 a) 4 800 000 b) 300 200 c) 25 085 d) 0,8 e) 0,25 f) 0,785 2 a) 2 miljoner 35 tusen: 2 035 000 235 tusen: 235 000 tjugotretusen femhundra: 23 500 b) 12 tiondelar: 1,2 12 hundradelar: 0,12 12
Kapitel 1 1 a) 4 800 000 b) 300 200 c) 25 085 d) 0,8 e) 0,25 f) 0,785 2 a) 2 miljoner 35 tusen: 2 035 000 235 tusen: 235 000 tjugotretusen femhundra: 23 500 b) 12 tiondelar: 1,2 12 hundradelar: 0,12 12
REPETITION 3 A. en femma eller en sexa?
 REPETITION 3 A 1 Du kastar en vanlig tärning en gång. Hur stor är sannolikheten att du får en femma eller en sexa? 2 Eleverna i klass 8C fick ge betyg på en bok som de hade läst. Diagrammet visar resultatet.
REPETITION 3 A 1 Du kastar en vanlig tärning en gång. Hur stor är sannolikheten att du får en femma eller en sexa? 2 Eleverna i klass 8C fick ge betyg på en bok som de hade läst. Diagrammet visar resultatet.
Övningsblad 1.1 A. Bråkbegreppet. 1 Skugga. 2 Hur stor andel av figuren är skuggad? 3 Ringa in 2 av stjärnorna.
 Övningsblad 1.1 A Bråkbegreppet 1 Skugga 1 6 av figuren b) 2 3 av figuren 3 av figuren 4 2 Hur stor andel av figuren är skuggad? b) 3 Ringa in 2 av stjärnorna. 4 Skriv 20 valfria bokstäver och låt 1 av
Övningsblad 1.1 A Bråkbegreppet 1 Skugga 1 6 av figuren b) 2 3 av figuren 3 av figuren 4 2 Hur stor andel av figuren är skuggad? b) 3 Ringa in 2 av stjärnorna. 4 Skriv 20 valfria bokstäver och låt 1 av
Läxa nummer 1 klass 2
 Läxa nummer 1 klass 2 Rita hur det ser ut när du gör matteläxan! Skriv ditt namn också. Det här är din läxbok för klass 2. Du kommer i regel att få en läxa i veckan hela året. Skriv vilket tal som är X
Läxa nummer 1 klass 2 Rita hur det ser ut när du gör matteläxan! Skriv ditt namn också. Det här är din läxbok för klass 2. Du kommer i regel att få en läxa i veckan hela året. Skriv vilket tal som är X
Start Matematik facit
 FACIT Start Matematik facit Årskurs 4-9 Facit till Start Matematik 47-60-0 Liber AB Får kopieras 2 Kapitel Siffror och tal a) 9-42 a) 9-42 c) 84 d) 555 e) -6 f) 7 400 c) 84 d) 555 e) -6 f) 7 400 g) 985
FACIT Start Matematik facit Årskurs 4-9 Facit till Start Matematik 47-60-0 Liber AB Får kopieras 2 Kapitel Siffror och tal a) 9-42 a) 9-42 c) 84 d) 555 e) -6 f) 7 400 c) 84 d) 555 e) -6 f) 7 400 g) 985
7 Använd siffrorna 0, 2, 4, 6, 7 och 9, och bilda ett sexsiffrigt tal som ligger så nära 700 000 som möjligt.
 Steg 9 10 Numerisk räkning Godkänd 1 Beräkna. 15 + 5 3 Beräkna. ( 7) ( 13) 3 En januarimorgon var temperaturen. Under dagen steg temperaturen med fyra grader och till kvällen sjönk temperaturen med sex
Steg 9 10 Numerisk räkning Godkänd 1 Beräkna. 15 + 5 3 Beräkna. ( 7) ( 13) 3 En januarimorgon var temperaturen. Under dagen steg temperaturen med fyra grader och till kvällen sjönk temperaturen med sex
Lärandemål E-nivå årskurs 9
 Lärandemål E-nivå årskurs 9 Detta är vad ni behöver kunna för att nå E för kunskapskraven om begrepp och rutinuppgifter i matematik när ni slutar nian. Ni behöver klara av alla dessa moment. För att nå
Lärandemål E-nivå årskurs 9 Detta är vad ni behöver kunna för att nå E för kunskapskraven om begrepp och rutinuppgifter i matematik när ni slutar nian. Ni behöver klara av alla dessa moment. För att nå
Språkstart Matematik Facit. Matematik för nyanlända. Jöran Petersson
 Språkstart Matematik Facit Matematik för nyanlända Jöran Petersson Positionssystem hela tal s. 4-5 3. Skriv med siffror. 52 502 5002 65 665 6665 31 131 3131 4. Skriv hur mycket siffran är värd. 300 4 1000
Språkstart Matematik Facit Matematik för nyanlända Jöran Petersson Positionssystem hela tal s. 4-5 3. Skriv med siffror. 52 502 5002 65 665 6665 31 131 3131 4. Skriv hur mycket siffran är värd. 300 4 1000
Nästan allt omkring dig har underliggande matematik. En del anser att den bara ligger där och väntar
 Matematikplanering 7B Läsår 15/16 Nästan allt omkring dig har underliggande matematik. En del anser att den bara ligger där och väntar på att bli upptäckt. Mönster, statistik, överlevnad, evolution, mopeder
Matematikplanering 7B Läsår 15/16 Nästan allt omkring dig har underliggande matematik. En del anser att den bara ligger där och väntar på att bli upptäckt. Mönster, statistik, överlevnad, evolution, mopeder
kunna använda ett lämpligt mått, tex. mugg till vätska. Geometri
 Studieplan och bedömningsgrunder i Matematik för åk F-1 Stor-liten, framför - bakom, större än osv. kunna visa att du förstår ordens förhållande till varandra, tex. med hjälp av olika saker eller genom
Studieplan och bedömningsgrunder i Matematik för åk F-1 Stor-liten, framför - bakom, större än osv. kunna visa att du förstår ordens förhållande till varandra, tex. med hjälp av olika saker eller genom
Facit till Mattespanarna 6B Lärarboken. Facit till Mattespanarna 6B Lärarboken best.nr Får kopieras Författarna och Liber AB 1/9
 Facit till Mattespanarna 6B Lärarboken 1/9 KOPIERINGSBLAD 1.1 Övningar med stora tal Skriv följande tal med siffror. 2 000 000 2 400 000 2 490 000 490 000 5 050 000 50 000 1 a) 2 miljoner b) 2,4 miljoner
Facit till Mattespanarna 6B Lärarboken 1/9 KOPIERINGSBLAD 1.1 Övningar med stora tal Skriv följande tal med siffror. 2 000 000 2 400 000 2 490 000 490 000 5 050 000 50 000 1 a) 2 miljoner b) 2,4 miljoner
KW ht-17. Övningsuppgifter
 Övningsuppgifter Ht-2017 1 Innehållsförteckning: Taluppfattning, positionssystem s. 3 4 Räkning, prioriteringsregler s. 4 6 Tvåbassystemet s. 6-7 Avrundning och noggrannhet s. 8-11 Bråk s. 12-17 Decimaltal
Övningsuppgifter Ht-2017 1 Innehållsförteckning: Taluppfattning, positionssystem s. 3 4 Räkning, prioriteringsregler s. 4 6 Tvåbassystemet s. 6-7 Avrundning och noggrannhet s. 8-11 Bråk s. 12-17 Decimaltal
Högstadiets matematikorientering
 Högstadiets matematikorientering STARTKORT MATEMATIKORIENTERING KONTROLLER FYLL I DINA SVAR FRÅN DE OLIKA KONTROLLERNA. HITTA OCH LÖS SÅ MÅNGA KONTROLLER DU HINNER. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Högstadiets matematikorientering STARTKORT MATEMATIKORIENTERING KONTROLLER FYLL I DINA SVAR FRÅN DE OLIKA KONTROLLERNA. HITTA OCH LÖS SÅ MÅNGA KONTROLLER DU HINNER. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Eva Björklund Heléne Dalsmyr. matematik. Koll på. Skriva Facit
 Eva Björklund Heléne Dalsmyr 4A matematik Koll på Skriva Facit 1Taluppfattning och problemlösning 1 253 1 a) 3 579 b) 1 286 c) 4 819 2 a) 1 280 b) 5 470 c) 2 093 3 a) 4 884 b) 1 763 c) 4 884 d) 6 431 4
Eva Björklund Heléne Dalsmyr 4A matematik Koll på Skriva Facit 1Taluppfattning och problemlösning 1 253 1 a) 3 579 b) 1 286 c) 4 819 2 a) 1 280 b) 5 470 c) 2 093 3 a) 4 884 b) 1 763 c) 4 884 d) 6 431 4
STARTAKTIVITET 2. Bråkens storlek
 STARTAKTIVITET 2 Bråkens storlek Arbeta gärna två och två. Rita en stjärna över de bråk som är mindre än 1 2. Sätt ett kryss över de bråk som är lika med 1 2. Rita en ring runt de bråk som är större än
STARTAKTIVITET 2 Bråkens storlek Arbeta gärna två och två. Rita en stjärna över de bråk som är mindre än 1 2. Sätt ett kryss över de bråk som är lika med 1 2. Rita en ring runt de bråk som är större än
Problem 1 I en familj fanns fem barn. När barnen väger sig flera åt gången får de följande resultat:
 EXTRA PROBLEM TILL ALMA Problem 1 I en familj fanns fem barn. När barnen väger sig flera åt gången får de följande resultat: Ann + Carolina = 65 kg Erik + David = 75 kg David + Ann = 85 kg Ann + Magnus
EXTRA PROBLEM TILL ALMA Problem 1 I en familj fanns fem barn. När barnen väger sig flera åt gången får de följande resultat: Ann + Carolina = 65 kg Erik + David = 75 kg David + Ann = 85 kg Ann + Magnus
Procent 1, 50 % är hälften
 Innehåll (Facit) Procent -7 Bråkform decimalform procentform 8-9 Sannolikhet 10-1 Kombinatorik 13-1 Medelvärde, median och typvärde 1-16 Negativa tal 17-18 Koordinatsystem 19- Proportionella samband 3-
Innehåll (Facit) Procent -7 Bråkform decimalform procentform 8-9 Sannolikhet 10-1 Kombinatorik 13-1 Medelvärde, median och typvärde 1-16 Negativa tal 17-18 Koordinatsystem 19- Proportionella samband 3-
Matematik. Ämnesprov, läsår 2013/2014. Delprov B. Årskurs. Elevens namn och klass/grupp
 Ämnesprov, läsår 2013/2014 Matematik Delprov B Årskurs 6 Elevens namn och klass/grupp Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Ämnesprov, läsår 2013/2014 Matematik Delprov B Årskurs 6 Elevens namn och klass/grupp Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Torskolan i Torsås Mars 2007. Matematik. Kriterier för betyget godkänd. Metoder: Arbetssätt. Muntligt. Problemlösning
 Torskolan i Torsås Mars 2007 Matematik Kriterier för betyget godkänd Metoder: Arbetssätt Ta ansvar för sin egen inlärning. Göra läxor. Utnyttja lektionstiden (lyssna, arbeta). Utnyttja den hjälp/stöd som
Torskolan i Torsås Mars 2007 Matematik Kriterier för betyget godkänd Metoder: Arbetssätt Ta ansvar för sin egen inlärning. Göra läxor. Utnyttja lektionstiden (lyssna, arbeta). Utnyttja den hjälp/stöd som
Högskoleverket. Delprov NOG 2002-10-26
 Högskoleverket Delprov NOG 2002-10-26 1. Det ordinarie priset på en skjorta, som såldes på rea, var 600 kr. Inför slutrean sänktes priset till halva ursprungliga reapriset. Vad var det ursprungliga reapriset
Högskoleverket Delprov NOG 2002-10-26 1. Det ordinarie priset på en skjorta, som såldes på rea, var 600 kr. Inför slutrean sänktes priset till halva ursprungliga reapriset. Vad var det ursprungliga reapriset
b) kg c) 900 g 1071 a) g b) kg c) 800 g 1072 a) 500 g b) kg 1073 a) 5 kg b) 4,5 kg c) 1,1 kg
 BASHÄFTE X Kapitel a) b) c) a) 9 b) 9 c) 9 a) b) c) d) a), b),8 c), d) 9, a) b) 9 a) 9 b) a), b), 8 a), b), 9 Störst: 8 Minst: 88 Störst: 8, Minst:,8 a) 89 a) b) 8 kr kr a) 8 9 kr a) b) 8 kr 9 9 kr kr
BASHÄFTE X Kapitel a) b) c) a) 9 b) 9 c) 9 a) b) c) d) a), b),8 c), d) 9, a) b) 9 a) 9 b) a), b), 8 a), b), 9 Störst: 8 Minst: 88 Störst: 8, Minst:,8 a) 89 a) b) 8 kr kr a) 8 9 kr a) b) 8 kr 9 9 kr kr
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 4. b) = 3 1 = 2
 Kapitel.1 101, 102 Exempel som löses i boken 10 a) x= 1 11+ x= 11+ 1 = 2 c) x= 11 7 x= 7 11 = 77 b) x= 5 x 29 = 5 29 = 6 d) x= 2 26 x= 26 2= 1 10 a) x= 6 5+ 9 x= 5+ 9 6= 5+ 5= 59 b) a = 8a 6= 8 6= 2 6=
Kapitel.1 101, 102 Exempel som löses i boken 10 a) x= 1 11+ x= 11+ 1 = 2 c) x= 11 7 x= 7 11 = 77 b) x= 5 x 29 = 5 29 = 6 d) x= 2 26 x= 26 2= 1 10 a) x= 6 5+ 9 x= 5+ 9 6= 5+ 5= 59 b) a = 8a 6= 8 6= 2 6=
TAL OCH RÄKNING HELTAL
 1 TAL OCH RÄKNING HELTAL Avsnitt Heltal... 6 Beräkningar med heltal...16 Test Kan du?... 1, 27 Kapiteltest... 28 Begrepp addition avrundning bas differens division exponent faktor kvadratroten ur kvot
1 TAL OCH RÄKNING HELTAL Avsnitt Heltal... 6 Beräkningar med heltal...16 Test Kan du?... 1, 27 Kapiteltest... 28 Begrepp addition avrundning bas differens division exponent faktor kvadratroten ur kvot
PRIMA MATEMATIK EXTRABOK 3 FACIT
 PRIMA MATEMATIK EXTRABOK FACIT t.ex. Dela upp talet. = + + = + + = + + Dela upp talet i lika stora delar. = +, +++ = ++ = +, ++ = ++++ = + = + + Skriv alla uppdelningar du kan av talet, lika stora delar.,
PRIMA MATEMATIK EXTRABOK FACIT t.ex. Dela upp talet. = + + = + + = + + Dela upp talet i lika stora delar. = +, +++ = ++ = +, ++ = ++++ = + = + + Skriv alla uppdelningar du kan av talet, lika stora delar.,
sex miljoner tre miljarder femton miljoner trehundratusen 6 000 000 520 000 > 50 200 40 000 500 > 40 000 050 5 505 050 < 5 505 500
 Namn: Förstå och använda stora tal som miljoner och miljarder Skriv talen med siffror. sex miljoner tre miljarder femton miljoner trehundratusen Läs talen först. Använd sedan > eller > < Vilket tal
Namn: Förstå och använda stora tal som miljoner och miljarder Skriv talen med siffror. sex miljoner tre miljarder femton miljoner trehundratusen Läs talen först. Använd sedan > eller > < Vilket tal
c) a) b) c) tre och en halv miljon
 REPETITION 1 A 1 Hur många procent av figurerna är gula a) b) c) 2 Hur mycket är a) 10 % av 7 kr b) 30 % av 600 kr c) 7 % av 20 000 kr 3 Skriv bråken i enklaste form. a) 4 28 b) 1 2 c) 16 40 4 Skriv i
REPETITION 1 A 1 Hur många procent av figurerna är gula a) b) c) 2 Hur mycket är a) 10 % av 7 kr b) 30 % av 600 kr c) 7 % av 20 000 kr 3 Skriv bråken i enklaste form. a) 4 28 b) 1 2 c) 16 40 4 Skriv i
Högskoleverket. Delprov NOG
 Högskoleverket Delprov NOG 2004-10-23 2 1. Caroline hyrde en flyttbil och fick då betala en fast grundkostnad och en kostnad per körd mil. Hur hög var grundkostnaden som Caroline fick betala? (1) Caroline
Högskoleverket Delprov NOG 2004-10-23 2 1. Caroline hyrde en flyttbil och fick då betala en fast grundkostnad och en kostnad per körd mil. Hur hög var grundkostnaden som Caroline fick betala? (1) Caroline
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 1
 Här presenteras förslag på lösningar och tips till många uppgifter i läroboken Matematik 3000 kurs A som vi hoppas kommer att vara till hjälp när du arbetar dig framåt i kursen. Vi har valt att inte göra
Här presenteras förslag på lösningar och tips till många uppgifter i läroboken Matematik 3000 kurs A som vi hoppas kommer att vara till hjälp när du arbetar dig framåt i kursen. Vi har valt att inte göra
Matematik Formula, kap 3 Tal och enheter
 Matematik Formula, kap 3 Tal och enheter Nedan berättar jag i punktform hur du ska arbeta och lite av det vi gör tillsammans. Listan kommer att fyllas på allteftersom vi arbetar. Då och då hittar du blå
Matematik Formula, kap 3 Tal och enheter Nedan berättar jag i punktform hur du ska arbeta och lite av det vi gör tillsammans. Listan kommer att fyllas på allteftersom vi arbetar. Då och då hittar du blå
Övningsblad 3.1 A. Omkrets och area. 1 Beräkna figurernas omkrets och area. Varje ruta har arean 1 cm 2.
 Övningsblad 3.1 A Omkrets och area 1 Beräkna figurernas omkrets och area. Varje ruta har arean 1 cm 2. a) b) O = A = O = A = 2 Skugga rektangelns area och markera triangelns omkrets. (m) (m) 25 80 80 70
Övningsblad 3.1 A Omkrets och area 1 Beräkna figurernas omkrets och area. Varje ruta har arean 1 cm 2. a) b) O = A = O = A = 2 Skugga rektangelns area och markera triangelns omkrets. (m) (m) 25 80 80 70
Förtest. Hur kan jag arbeta med förtesten? Hur dokumenterar jag elevens kunskapsutveckling? Uppfattar du det som att eleven kan matematikinnehållet
 AB Höst LP 1-2 Flik 02 Förtest (8768) Lev 1.qxd 2004-01-20 18:10 Sida 1 Förtest För alla lärare är det viktigt att skaffa sig en god bild av elevens kunskaper för att veta vad eleven behöver för att gå
AB Höst LP 1-2 Flik 02 Förtest (8768) Lev 1.qxd 2004-01-20 18:10 Sida 1 Förtest För alla lärare är det viktigt att skaffa sig en god bild av elevens kunskaper för att veta vad eleven behöver för att gå
Fundera tillsammans. Victor är 5 år och Åsa är 8 år. Hur gammal kommer Victor att vara när Åsa är dubbelt så gammal som hon är nu?
 STARTAKTIVITET 5 Fundera tillsammans Victor är 5 år och Åsa är 8 år. Hur gammal kommer Victor att vara när Åsa är dubbelt så gammal som hon är nu? 13 år Nils är född den 20 mars. Linus är född samma år
STARTAKTIVITET 5 Fundera tillsammans Victor är 5 år och Åsa är 8 år. Hur gammal kommer Victor att vara när Åsa är dubbelt så gammal som hon är nu? 13 år Nils är född den 20 mars. Linus är född samma år
8 a) 670. b) a) 0,11. b) 0, a) 0,45. b) 0, a) 0,5. b) 0,2. 12 a) 0,004. b) 0, a) 0,95. b) 1,2. 14 a) 9,95. b) 0,5.
 Arbetsblad a) 8 a) 0 a), a) 0 00 a) 0 00 00 000 a) 0,8 0,0 a) 0,0, a), 0,, d), Störst: 0, Minst: 0, Störst: 8, Minst: 8,0 8 Störst:, Minst:,0 Störst: 0,8 Minst: 0,0 0 a) 0 0 80 d) 0 a) 0 0, 0 d), a) 00
Arbetsblad a) 8 a) 0 a), a) 0 00 a) 0 00 00 000 a) 0,8 0,0 a) 0,0, a), 0,, d), Störst: 0, Minst: 0, Störst: 8, Minst: 8,0 8 Störst:, Minst:,0 Störst: 0,8 Minst: 0,0 0 a) 0 0 80 d) 0 a) 0 0, 0 d), a) 00
Högskoleprovet. Block 1. Anvisningar. Övningsexempel. Delprovet innehåller 22 uppgifter.
 Block 1 2008-10-25 Högskoleprovet Svarshäfte nr. DELPROV 1 NOGe Delprovet innehåller 22 uppgifter. Anvisningar Varje uppgift innehåller en fråga markerad med fet stil. Uppgiften kan även innehålla viss
Block 1 2008-10-25 Högskoleprovet Svarshäfte nr. DELPROV 1 NOGe Delprovet innehåller 22 uppgifter. Anvisningar Varje uppgift innehåller en fråga markerad med fet stil. Uppgiften kan även innehålla viss
rektangel cirkel triangel 4 sidor 3 sidor 4 sidor
 geometriska former och figurer Vad heter figurerna? figur namn rektangel cirkel triangel Hur många sidor har varje figur? 4 sidor 3 sidor 4 sidor Para ihop varje föremål med en eller flera geometriska
geometriska former och figurer Vad heter figurerna? figur namn rektangel cirkel triangel Hur många sidor har varje figur? 4 sidor 3 sidor 4 sidor Para ihop varje föremål med en eller flera geometriska
