Basbyte (variabelbyte)
|
|
|
- Ingegerd Fredriksson
- för 8 år sedan
- Visningar:
Transkript
1 Basbyte (variabelbyte) En vektors koordinater beror på valet av bas! Tänk på geometriska vektorer här. v har längden 2 och pekar rakt uppåt i papprets plan. Kan vi då skriva v (, 2)? Om vi valt basvektorer e x och e y som har längden och som pekar till höger resp. uppåt ja. Men, omt.ex.e x pekar uppåt och e y till vänster, så v (2, ). Med ett annat val av basvektorer kan v få koord. (, ) ja, koordinatvektorn kan se ut hur som helst! Precis som saker och ting heteer olika på olika språk, har vektorer olika koordinater beroende på valet av bas. Kom ihåg: v (5, 2) är ett förkortat skrivsätt för v 5e x +2e y, där e x, e y är någon underförstådd bas Icke-geometriska vektorer (talmultiplar) kan också betraktas som koordinater relativt ett koord.- system av någon koordinatsystemoberoende storhet. Säg att vi utför en sociologisk undersökning och för olika grupper av människor antecknar antalet män resp. antalet kvinnor som ingår. Då har vi för varje grupp v ett par av tal (v x,v y ): v x antalet män i v, v y antalet kvinnor i v. Inga pilar syns på långa vägar ändå kan vi tänka oss att (v x,v y ) är koordinater m.a.p. en viss bas: I stället för antal män/kvinnor kunde vi antecknat t.ex. (vi hade då haft precis lika mycket information!) bv x v x + v y totala antalet människor bv y v x v y överskottet av män På matrisform kan detta skrivas µ µ b bv y µ v y och motsvarar bv S V i högerspalten. Wahde använder termen komponenter, men koordinater går också bra. Samband mellan koordinater relativt olika baser Ibland vill man byta från en gammal bas e x, e y till en ny bas be x, be y. Vad är sambandet mellan de olika koordinaterna av v, (v x,v y ) resp. (bv x, bv y )? Alltså: v v x e x + v y e y v bv x be x + bv y be y Låt oss uttrycka alla vektorer med koordinater med avseende på e x, e y och skriva dem som kolonnmatriser. Då är v v x e x + v y e y µ µ v v x + v y µ v y v bv x be x + bv y be y µ µ # % v bv x + bv # y % µ µ # % b # % bv y varvid # och % symboliserar be x :sresp. be y :skoordinater med avseende på den gamla basen. Alltså µ µ µ # % b v y # % bv y µ # % eller kortare V ScV med S # % Den s.k. transformationsmatrisen 2 (basbytesmatrisen) S har som kolonner koordinaterna av de nya basvektorerna med avseende på de gamla. Vill vi ha de nya koordinaterna som funktioner av de gamla i stället får vi multiplicera med S : bv S V (Inversen måste finnas, annars skulle be x, be y vara parallella och inte utgöra någon bas!) Ett viktigt specialfall: när båda baserna är ortonormerade, är S ortogonal, d.v.s. S T S I SS T vilket är ekvivalent med S S T. Övertyga dig om att S T S I Kolonnerna i S bildar ON-system SS T I Raderna i S bildar ON-system 2 I Wahde, kap.5, heter denna matris P. 9
2 Linjära avbildningar: Avbildningsmatrisen beror på basvalet! Precis som vektorernas koordinater, är matrisrepresentationen av en linjär avbildninig avhängig av basvalet. Ex. Matrisen för spegling i planet med ekvationen ger x + Projektionsformeln, d.v.s att ortogonala projektionen av en vektor u på en vektor n är u n n 2 n y y 2 y 3 x x ( ) x En helt annan (och betydligt enklare!) matris hade vi fått, om vi valt koordinatsystemet så att det speglande planet sammanfaller med, säg, xy-planet! Då hade nämligen avbildningsmatrisen varit (2) (Vi kan antingen skriva upp sambanden mellan bildens och urbildens koordinater direkt: y x y 2 y 3 eller resonera så här: Spegling är en linjär avbildning. Det räcker då att bestämma bilderna av basvektorerna och sätta ihop dessa som kolonner i en matris. De två första basvektorerna (,, ) och (,, ) liggerkvarpå sin plats medan den tredje (,, ) avbildas på (,, ). Ger samma matris som ovan!) Hur avbildningsmatrisen transformeras vid basbyten Om man gör ett basbyte, vad blir sambandet mellan den gamla avbildningsmatrisen A och den nya A? (Vi inskränker oss här till avbildningar mellan ett och samma rum, och därmed kvadratiska avbildningsmatriser.) Låt S beteckna transformationsmatrisen som ovan. Vi har då Y AX, X S bx, Y SY b och söker ba sådan att by ba bx En rättfram räkning ger by S Y S AX S AS bx således A b S AS Ex.: Speglingsmatrisen (3) kunde vi fått med följande räkning (inte enklare dock!): Gör ett basbyte, så att de två första basvektorerna är parallella med speglingsplanet och den tredje är vinkelrät mot det, t.ex. alltså S be 3 (,, ) / 3 be (,, ) / 2 be 2 be 3 be (,, 2) / 6 / 2 / 6 / 3 / 2 / 6 / 3 2/ 6 / 3 Med avseende på denna nya bas ges avbildningsmatrisen av (2), d.v.s. S AS och därmed A S S som ger (3) (S är ortogonal till följd av konstruktionen, så S S T ).
3 Diagonalmatriser lättast att analysera Ovan har vi bestämt avbildningsmatriser för givna linjära avbildningar. Ofta förekommer det omvända problemet (om än i diverse förklädnader): Givet en matris, lista ut vad avbildningen, som den motsvarar, gör! Då vore det ju bra om vi kunde göra ett basbyte så att avbildningsmatrisen blir så enkel som möjligt en diagonalmatris (tänk hur enkelt det är att multiplicera diagonalmatriser!). Säg att en avbildning har, relativt en viss bas e, e 2, e 3, matrisen λ λ 2 λ 3 Detta innebär att avbildas på avbildas på λ λ 2 e λ e 2 λ 2 λ e λ 2 e 2 Egenvärden och egenvektorer Vektorer som avbildas (av en linjär avbildning) på sig själva, så när som på multiplikation med en konstant Av λv, v 6 kallas egenvektorer till avbildningen och motsvarande λ kallas egenvärden. (Utesluter fallet v, som ointressant.) Diagonalisering Att göra ett basbyte så att en given avbildning blir representerad av en diagonalmatris, kallas att diagonalisera avbildningen. Tyvärr kan inte alla avbildningar diagonaliseras egenvektorerna räcker inte alltid till för att bilda en bas. Men det finns en stor och viktig klass av avbildningar som alltid går att diagonalisera de symmetriska, d.v.s. de som representeras av symmetriska matriser. Avbildningar kontra matriser I och med att linjära avbildningar representeras med matriser, brukar man tala om egenvektorer/egenvärden/diagonalisering till/av en matris, men det är bättre att tänka i termer av avbildningar egenvektorer och egenvärden är något som alltid finns, men hur tydligt de syns beror på vårt val av bas. etc. D.v.s. avbildningen kan på sin höjd sträcka ut (λ > ), pressa ihop ( λ < ) och ev. kasta om riktningen på en basvektor (λ < ), men inte vrida den, vilket förenklar analysen betydligt! Allmänt råd för matrisproblem Ofta är svårigheten den att matrisens element utanför diagonalen är 6, vilket gör att variabler är kopplade till varandra. Undersök om man inte kan genomföra ett basbyte/variabelbyte så att den urspr. matrisen ersätts av en diagonalmatris!
4 Analys av en linjär avbildning Vad gör den linjära avbildningen y y y x? Försök att diagonalisera! Mankanräknafram skasenaresehur att i) Alla vektorer av typen t (,, ),t6, 3 är egenvektorer med egenvärdet. (Innebörden av detta är att vilket lätt kontrolleras stämma.) ii) Alla vektorer 6, som är vinkelräta mot (, 3, ) 4, är egenvektorer med egenvärdet, t.ex. är (3, 2, 3) (, 3, ) och Vi kan då bilda en bas av egenvektorer: be (,, ) be 2 (,, ) be 3 (3,, ) (Jag tar som be 2 och be 3 två icke-parallella vektorer, vars skalärprodukt med (, 3, ) är.) I denna nya bas har avbildningen matrisen Men detta är ju ingenting annat än en sned projektion: på det plan som spänns upp av be 2, och be 3 (d.v.s. x 3y + z ), parallellt med be. (Projektioner behöver inte alltid vara vinkelräta!) System av linjära differentialekvationer Vi klarar av differentialekvationer av typen y (t) ky(t), Alla lösningar är av formen k given konstant, y(t) obekant funktion y(t) Ce kt, C konstant ( y ()) Ofta ställs man inför ett system av sådana: y (t) y (t)+y 2 (t) y 2(t) 3y (t) y 2 (t) Om man nu dels tar 3 ekv.()+ekv.(2), dels subtraherar ekvationerna, så fås 3y + y 2 2(3y + y 2 ) y y2 2(y y 2 ) Om vi alltså gör variabelbytet ½ by 3y + y 2 by 2 y y 2 (4) så får vi två frikopplade ekvationer som löses snabbt: by 2by by 2 2by 2 by C e 2t by 2 C 2 e 2t Sedan är det bara att lösa ut y (t) och y 2 (t) ur (4): y 4 (by + by 2 ) C e 2t + C 2 e 2t 4 y 2 4 (by 3by 2 ) C e 2t 3C 2 e 2t 4 C och C 2 godtyckliga konstanter Men hur komma på radoperationerna ovan? 3 D.v.s. alla vektorer 6, som är parallella med (,, ), vilket jag ibland förkortar med k (,, ) 4 Förkortas: (, 3, ) 2
5 Variabelbyte är detsamma som basbyte! Våra ekvationer kan på matrisform skrivas: µ Y AY, A 3 Försök med variabelbyte Y S by, då blir Y S by Y AY SY b ASY b by S AS by Att ekvationerna by S AS by blir frikopplade som ovan är ekvivalent med att S AS är diagonal. Försök därför att hitta en bas av egenvektorer till A! Man kan räkna fram att i) egenvärden är 2 och 2 (Koefficienterna i de frikopplade ekvationerna!) ii) Motsv. egenvektorer är t (, ) resp. t (, 3),t6. S µ 3, by S Y 4 µ 3 Y System av linjära differensekvationer (linjära rekursionsekvationer) som y (n +)y (n)+y 2 (n) y 2 (n +)3y (n) y 2 (n),n,, 2,... kan behandlas på samma sätt. I och med att en enkel rekursionsekvation som y(n +)ky(n), k given konstant har den allmänna lösningen y(n) Ck n,ckonstant ( y ()) så blir den enda skillnaden jämfört med behandlingen av differentialekvationerna att e λt ersätts av λ n vilket är detsamma som ovan bortsett från den konstanta faktorn 4. Till slut går vi tillbaka till µ y (t) Y S by y 2 (t) µ µ C e 2t 3 C 2 e 2t µ µ C e 2t + C 2 3 e 2t vilket är precis det vi fick förut! Här kan vi se en anledning till varför egenvärdena ensamma kan vara viktiga. Det är mycket stor skillnad om vi har en term e 2t eller e 2t det förstnämnda, den andra växer explosionsartat! (Vad konstanterna C och C 2 är, brukar, däremot, vara av underordnad betydelse.) Antag att våra ekvationer och funktionerna y (t) och y 2 (t) skall beskriva något fysikaliskt förlopp. Skulle något egenvärde vara >, har vi en katastrof att vänta!). Linjära system av differential ekvationer går också att klara av med Laplacetransformation. Testapåsystemetovan! Det är något bökigare att Laplacetransformera, om man inte har fixa begynnelsevärden, så testa för specialfallet då y () 3, y 2 (), vilket svarar mot C 2,C Linjära system av differensekvationer går också att klara av med z-transformation. Testa på systemet ovan, förslagsvis i spec.fallet y () 3, y 2 (). 3
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Vektorer i planet och i rummet III Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Vektorer i planet och i rummet III Innehåll
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
LINJÄRA AVBILDNINGAR
 LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Egenvärden och egenvektorer. Linjär Algebra F15. Pelle
 Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
LÖSNINGAR LINJÄR ALGEBRA LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2016-05-10 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 2016-05-10 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
där β R. Bestäm de värden på β för vilka operatorn är diagonaliserbar. Ange även för respektive av dessa värden en bas av egenvektorer till F.
 MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Examinator: Lars-Göran Larsson TENTAMEN I MATEMATIK MMA9 Linjär algebra Datum: 7 januari 04 Skrivtid:
MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Examinator: Lars-Göran Larsson TENTAMEN I MATEMATIK MMA9 Linjär algebra Datum: 7 januari 04 Skrivtid:
Version 0.82. Linjär algebra kapiltet från ett ODE-kompendium. Mikael Forsberg
 Version.8 Linjär algebra kapiltet från ett ODE-kompendium Mikael Forsberg 8 Den här boken är typsatt av författaren med hjälp av L A TEX. Alla illustrationer är utförda av Mikael Forsberg med hjälp av
Version.8 Linjär algebra kapiltet från ett ODE-kompendium Mikael Forsberg 8 Den här boken är typsatt av författaren med hjälp av L A TEX. Alla illustrationer är utförda av Mikael Forsberg med hjälp av
Dagens ämnen. Repetition basbyten och linjära avbildningar Diagonalisering Kvadratiska former. Andragradskurvor
 Seminarium 25 Dagens ämnen Repetition basbyten och linjära avbildningar Diagonalisering Kvadratiska former Matrisform Diagonalisering av kvadratiska former Andragradskurvor De olika kurvtyperna Rita graferna
Seminarium 25 Dagens ämnen Repetition basbyten och linjära avbildningar Diagonalisering Kvadratiska former Matrisform Diagonalisering av kvadratiska former Andragradskurvor De olika kurvtyperna Rita graferna
Linjära avbildningar. Definition 1 En avbildning mellan två vektorrum, F : V U, kallas linjär om. EX. Speglingar, rotationer, projektioner i R 3.
 Linjära avbildningar Definition 1 En avbildning mellan två vektorrum, F : V U, kallas linjär om F (v +v ) = F (v)+f (v ) och F (cv) = cf (v) för alla v, v V och alla skalärer c. EX. Speglingar, rotationer,
Linjära avbildningar Definition 1 En avbildning mellan två vektorrum, F : V U, kallas linjär om F (v +v ) = F (v)+f (v ) och F (cv) = cf (v) för alla v, v V och alla skalärer c. EX. Speglingar, rotationer,
ax + y + 4z = a x + y + (a 1)z = 1. 2x + 2y + az = 2 Ange dessutom samtliga lösningar då det finns oändligt många.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
Självkoll: Ser du att de två uttrycken är ekvivalenta?
 ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 2014
 SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 214 Skrivtid: 14.-19. Tillåtna hjälpmedel: inga Examinator: Roy Skjelnes Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 214 Skrivtid: 14.-19. Tillåtna hjälpmedel: inga Examinator: Roy Skjelnes Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
1 som går genom punkten (1, 3) och är parallell med vektorn.
 KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
Crash Course Algebra och geometri. Ambjörn Karlsson c januari 2016
 Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Inför tentamen i Linjär algebra TNA002.
 Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
Linjär algebra kurs TNA002
 Linjär algebra kurs TNA002 Lektionsanteckningar klass ED1 I detta dokument finns ett utdrag av de tavelanteckningar som uppkommit under lektionstid under kursen TNA002. Alltså kan detta dokument långt
Linjär algebra kurs TNA002 Lektionsanteckningar klass ED1 I detta dokument finns ett utdrag av de tavelanteckningar som uppkommit under lektionstid under kursen TNA002. Alltså kan detta dokument långt
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
Linjär algebra på några minuter
 Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
ANDRAGRADSKURVOR Vi betraktar ekvationen
 ANDRAGRADSKURVOR Vi betraktar ekvationen Ax + Bxy + Cy + Dx + Fy + G 0 (ekv) där minst en av A,B, eller C är skild från 0 En andragradskurva är mängden av alla punkter vilkas koordinater satisfierar en
ANDRAGRADSKURVOR Vi betraktar ekvationen Ax + Bxy + Cy + Dx + Fy + G 0 (ekv) där minst en av A,B, eller C är skild från 0 En andragradskurva är mängden av alla punkter vilkas koordinater satisfierar en
Vektorerna är parallella med planet omm de är vinkelräta mot planets normal, dvs mot
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
November 24, Egenvärde och egenvektor. (en likformig expansion med faktor 2) (en rotation 30 grader moturs)
 Fö : November 4, 7 Egenvärde och egenvektor Definition s 9: Låt A resp T : R n R n vara en n n-matris resp en linjär avbildning En icke-trivial vektor v R n kallas en egenvektor till A resp till T med
Fö : November 4, 7 Egenvärde och egenvektor Definition s 9: Låt A resp T : R n R n vara en n n-matris resp en linjär avbildning En icke-trivial vektor v R n kallas en egenvektor till A resp till T med
LÖSNINGAR TILL LINJÄR ALGEBRA kl 8 13 LUNDS TEKNISKA HÖGSKOLA MATEMATIK. 1. Volymen med tecken ges av determinanten.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
Stöd inför omtentamen i Linjär algebra TNA002.
 LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
LYCKA TILL! kl 8 13
 LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
17. Övningar ÖVNINGAR Låt F och G vara avbildningar på rummet, som i basen e = {e 1,e 2,e 3 } ges av. x 1 x 2 2x 2 + 3x 3 2x 1 x 3
 192 17 ÖVNINGAR 17. Övningar 17.1. Låt F och G vara avbildningar på rummet, som i basen e = {e 1,e 2,e 3 } ges av F(eX) = ey = e x 1 x 2 2x 2 + 3x 3 2x 1 x 3, G(eX) = e x 1 x 2 x 2 2 x 2 + x 3 Undersök
192 17 ÖVNINGAR 17. Övningar 17.1. Låt F och G vara avbildningar på rummet, som i basen e = {e 1,e 2,e 3 } ges av F(eX) = ey = e x 1 x 2 2x 2 + 3x 3 2x 1 x 3, G(eX) = e x 1 x 2 x 2 2 x 2 + x 3 Undersök
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng. Använd bifogat formulär för dessa 6 frågor.
 TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
EXEMPEL OCH LÖSNINGAR I LINJÄR ALGEBRA II
 EXEMPEL OCH LÖSNINGAR I LINJÄR ALGEBRA II PER ALEXANDERSSON Sammanfattning. Detta är en samling kompletterande uppgifter till Linjär Algebra II för lärare. Exemplen är av varierande svårighetsgrad och
EXEMPEL OCH LÖSNINGAR I LINJÄR ALGEBRA II PER ALEXANDERSSON Sammanfattning. Detta är en samling kompletterande uppgifter till Linjär Algebra II för lärare. Exemplen är av varierande svårighetsgrad och
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
SKRIVNING I VEKTORGEOMETRI Delkurs
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng.
 ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
Lite Linjär Algebra 2017
 Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
TMV166 Linjär algebra för M, vt 2016
 TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
19. Spektralsatsen Spektralsatsen SPEKTRALSATSEN
 9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
Facit/lösningsförslag
 Facit/lösningsförslag 06-08- Låt l vara linjen med parameterform x, y, z 0 s, mellan planet x y z och planet z 0 och låt l vara skärningslinjen a) Skriv l på parameterform b) Beräkna avståndet mellan l
Facit/lösningsförslag 06-08- Låt l vara linjen med parameterform x, y, z 0 s, mellan planet x y z och planet z 0 och låt l vara skärningslinjen a) Skriv l på parameterform b) Beräkna avståndet mellan l
6.1 Skalärprodukt, norm och ortogonalitet. TMV141 Linjär algebra E VT 2011 Vecka 6. Lärmål 6.1. Skalärprodukt. Viktiga begrepp
 6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
Lösningar till utvalda uppgifter i kapitel 8
 Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
Egenvektorer och egenvärden
 Egenvektorer och egenvärden Diagonalmatriser Tidigare (Sparr, kap.8) har vi bestämt avbildningsmatriser för givna linjära avbildningar. Ofta förekommer det omvända problemet (om än i diverse förklädnader):
Egenvektorer och egenvärden Diagonalmatriser Tidigare (Sparr, kap.8) har vi bestämt avbildningsmatriser för givna linjära avbildningar. Ofta förekommer det omvända problemet (om än i diverse förklädnader):
Institutionen för Matematiska Vetenskaper TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F1/TM1, TMA671 2014-05-26
 Institutionen för Matematiska Vetenskaper Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F/TM, TMA67 4-5-6 DAG: Måndag 6 maj 4 TID: 4. - 8. SAL: V Ansvarig: Ivar Gustafsson, tel: 75-33545 Förfrågningar:
Institutionen för Matematiska Vetenskaper Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F/TM, TMA67 4-5-6 DAG: Måndag 6 maj 4 TID: 4. - 8. SAL: V Ansvarig: Ivar Gustafsson, tel: 75-33545 Förfrågningar:
AB2.1: Grundläggande begrepp av vektoranalys
 AB2.1: Grundläggande begrepp av vektoranalys En vektor är en storhet som dels har icke-negativ storlek dels har riktning i rummet. Två vektorer a och b är lika, a = b, om de har samma storlek och samma
AB2.1: Grundläggande begrepp av vektoranalys En vektor är en storhet som dels har icke-negativ storlek dels har riktning i rummet. Två vektorer a och b är lika, a = b, om de har samma storlek och samma
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Prov i matematik F2, X2, ES3, KandFys2, Lärare, Frist, W2, KandMat1, Q2 LINJÄR ALGEBRA II
 UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Bo Styf Prov i matematik F, X, ES, KandFys, Lärare, Frist, W, KandMat1, Q LINJÄR ALGEBRA II 010 08 4 Skrivtid: 1400 1900 Tillåtna hjälpmedel:
UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Bo Styf Prov i matematik F, X, ES, KandFys, Lärare, Frist, W, KandMat1, Q LINJÄR ALGEBRA II 010 08 4 Skrivtid: 1400 1900 Tillåtna hjälpmedel:
Basbyten och linjära avbildningar
 Föreläsning 11, Linjär algebra IT VT2008 1 Basbyten och linjära avbildningar Innan vi fortsätter med egenvärden så ska vi titta på hur matrisen för en linjär avbildning beror på vilken bas vi använder.
Föreläsning 11, Linjär algebra IT VT2008 1 Basbyten och linjära avbildningar Innan vi fortsätter med egenvärden så ska vi titta på hur matrisen för en linjär avbildning beror på vilken bas vi använder.
Linjär Algebra F14 Determinanter
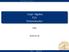 Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
UPPSALA UNIVERSITET Matematiska institutionen Styf. Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 2004
 UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
Linjär algebra på 2 45 minuter
 Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Isometrier och ortogonala matriser
 Isometrier och ortogonala matriser (Delvis resultat som kunde kommit tidigare i kursen) För att slippa parenteser, betecknas linära avbildningar med A och bilden av x under en lin avbildn med Ax i stället
Isometrier och ortogonala matriser (Delvis resultat som kunde kommit tidigare i kursen) För att slippa parenteser, betecknas linära avbildningar med A och bilden av x under en lin avbildn med Ax i stället
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
Multiplicera 7med A λ 1 I från vänster: c 1 (Av 1 λ 1 v 1 )+c 2 (Av 2 λ 1 v 2 )+c 3 (Av 3 λ 1 v 3 ) = 0
 Diagonalisering Anm. Begreppet diagonaliserbarhet är relevant endast för linjära avbildningar mellan rum av samma dimension, d.v.s. sådana som representeras av kvadratiska matriser. När vi i fortsättningen
Diagonalisering Anm. Begreppet diagonaliserbarhet är relevant endast för linjära avbildningar mellan rum av samma dimension, d.v.s. sådana som representeras av kvadratiska matriser. När vi i fortsättningen
Föreläsningsanteckningar i linjär algebra
 1 Föreläsningsanteckningar i linjär algebra Per Jönsson och Stefan Gustafsson Malmö 2013 2 Innehåll 1 Linjära ekvationssystem 5 2 Vektorer 11 3 Linjer och plan 21 4 Skalärprodukt 27 5 Vektorprodukt 41
1 Föreläsningsanteckningar i linjär algebra Per Jönsson och Stefan Gustafsson Malmö 2013 2 Innehåll 1 Linjära ekvationssystem 5 2 Vektorer 11 3 Linjer och plan 21 4 Skalärprodukt 27 5 Vektorprodukt 41
Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4.
![Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4. Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4.](/thumbs/93/112939298.jpg) LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 8-- kl 4-9 a) Triangelns area är en halv av parallellograms area som spänns upp av tex P P (,, ) och P P (,, ), således area av P P P (,, ) (,,
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 8-- kl 4-9 a) Triangelns area är en halv av parallellograms area som spänns upp av tex P P (,, ) och P P (,, ), således area av P P P (,, ) (,,
Omtentamen i DV & TDV
 Umeå Universitet Institutionen för Datavetenskap Gunilla Wikström (e-post wikstrom) Omtentamen i Teknisk-Vetenskapliga Beräkningar för DV & TDV Tentamensdatum: 2005-06-07 Skrivtid: 9-15 Hjälpmedel: inga
Umeå Universitet Institutionen för Datavetenskap Gunilla Wikström (e-post wikstrom) Omtentamen i Teknisk-Vetenskapliga Beräkningar för DV & TDV Tentamensdatum: 2005-06-07 Skrivtid: 9-15 Hjälpmedel: inga
e = (e 1, e 2, e 3 ), kan en godtycklig linjär
 Linjära avbildningar II Förra gången visade vi att givet en bas i rummet, e = (e 1, e 2, e 3 ), kan en godtycklig linjär avbildning F : R 3 R 3 representeras av en matris: Om vi betecknar en vektor u:s
Linjära avbildningar II Förra gången visade vi att givet en bas i rummet, e = (e 1, e 2, e 3 ), kan en godtycklig linjär avbildning F : R 3 R 3 representeras av en matris: Om vi betecknar en vektor u:s
SF1624 Algebra och geometri Tentamen Torsdag, 9 juni 2016
 SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
1. (a) Bestäm alla värden på c som gör att matrisen A(c) saknar invers: 1 0 1. 1 c 1
 ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
TMV142/186 Linjär algebra Z/TD
 MATEMATIK Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Chalmers tekniska högskola Datum: 2018-08-27 kl 1400 1800 Tentamen Telefonvakt: Anders Hildeman ank 5325 TMV142/186 Linjär algebra Z/TD Skriv
MATEMATIK Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Chalmers tekniska högskola Datum: 2018-08-27 kl 1400 1800 Tentamen Telefonvakt: Anders Hildeman ank 5325 TMV142/186 Linjär algebra Z/TD Skriv
4x az = 0 2ax + y = 0 ax + y + z = 0
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
SF1624 Algebra och geometri Lösningsförsag till modelltentamen
 SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
Tentamen i Linjär algebra (TATA31/TEN1) 2013 08 24, 14 19.
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN 8, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst uppgifter
LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN 8, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst uppgifter
6. Matriser Definition av matriser 62 6 MATRISER. En matris är ett rektangulärt schema av tal: a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A =
 62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
LÖSNINGAR TILL LINJÄR ALGEBRA kl LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2017-08-24 kl 14 19 1. Vi får ū = 1 2 + 1 2 + 0 2 = 2, v = 1 2 + 2 2 + 2 2 = 3 och ū v = 1 1+1 2+0 2 = 3. Om φ är vinkeln mellan ū och v
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2017-08-24 kl 14 19 1. Vi får ū = 1 2 + 1 2 + 0 2 = 2, v = 1 2 + 2 2 + 2 2 = 3 och ū v = 1 1+1 2+0 2 = 3. Om φ är vinkeln mellan ū och v
MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET MED MATRISINVERSER = = =
 Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
n = v 1 v 2 = (4, 4, 2). 4 ( 1) + 4 ( 1) 2 ( 1) + d = 0 d = t = 4 + 2s 5 t = 6 + 4s 1 + t = 4 s
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 7-8-4 kl 4 9 a) Triangelns sidor ges av vektorerna v OP OP (,, ) och v OP 3 OP (,, 4) som även blir riktningsvektorer till planet En normal
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 7-8-4 kl 4 9 a) Triangelns sidor ges av vektorerna v OP OP (,, ) och v OP 3 OP (,, 4) som även blir riktningsvektorer till planet En normal
Del 1: Godkäntdelen. TMV142 Linjär algebra Z
 MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 130313 kl 0830 1230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV142 Linjär algebra Z Tentan
MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 130313 kl 0830 1230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV142 Linjär algebra Z Tentan
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
För studenter på distans och campus Linjär algebra ma014a 2014 02 10. ATM-Matematik Mikael Forsberg 0734-41 23 31
 ATM-Matematik Mikael Forsberg 734-4 3 3 För studenter på distans och campus Linjär algebra maa Skrivtid: 9:-:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
ATM-Matematik Mikael Forsberg 734-4 3 3 För studenter på distans och campus Linjär algebra maa Skrivtid: 9:-:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
SF1624 Algebra och geometri
 Föreläsning 10 Institutionen för matematik KTH 21 november 2016 Dagens och veckans ämnen Idag: Allmänna vektorrum, baser, koordinater, kap 4.1-4.4: Vektorrum och delrum, igen Bas, igen Koordinater med
Föreläsning 10 Institutionen för matematik KTH 21 november 2016 Dagens och veckans ämnen Idag: Allmänna vektorrum, baser, koordinater, kap 4.1-4.4: Vektorrum och delrum, igen Bas, igen Koordinater med
SF1624 Algebra och geometri
 SF1624 Algebra och geometri Tjugofemte föreläsningen Mats Boij Institutionen för matematik KTH 10 december, 2009 Tentamens struktur Tentamen består av tio uppgifter uppdelade på två delar, Del A och Del
SF1624 Algebra och geometri Tjugofemte föreläsningen Mats Boij Institutionen för matematik KTH 10 december, 2009 Tentamens struktur Tentamen består av tio uppgifter uppdelade på två delar, Del A och Del
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Provräkning 3, Linjär Algebra, vt 2016.
 LINK OPINGS UNIVERSITET Matematiska Institutionen Provräkning, Linjär Algebra, vt 6. Lämna in lösningar för rättning senast 8. onsdagen den 7 april 6. Lämnas in antigen i mitt fack på MaI eller direkt
LINK OPINGS UNIVERSITET Matematiska Institutionen Provräkning, Linjär Algebra, vt 6. Lämna in lösningar för rättning senast 8. onsdagen den 7 april 6. Lämnas in antigen i mitt fack på MaI eller direkt
0 Allmänt. Följande delar behöver man kunna utöver avsnitten som beskrivs senare i dokumentet.
 Linja r algebra TATA (del) Allmänt Följande delar behöver man kunna utöver avsnitten som beskrivs senare i dokumentet. Matrisekvationer och Gauss-elimination o Parameterform Allmänt om vektorer o Räknelagar
Linja r algebra TATA (del) Allmänt Följande delar behöver man kunna utöver avsnitten som beskrivs senare i dokumentet. Matrisekvationer och Gauss-elimination o Parameterform Allmänt om vektorer o Räknelagar
SF1624 Algebra och geometri Tentamen Onsdag, 13 januari 2016
 SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
SF1624 Algebra och geometri Tentamen Torsdag, 17 mars 2016
 SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
Egenvärden och egenvektorer
 Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
SF1624 Algebra och geometri Bedömningskriterier till tentamen Tisdagen den 15 december, 2009
 SF1624 Algebra och geometri Bedömningskriterier till tentamen Tisdagen den 15 december, 2009 Allmänt gäller följande: Om lösningen helt saknar förklarande text till beräkningar och formler ges högst två
SF1624 Algebra och geometri Bedömningskriterier till tentamen Tisdagen den 15 december, 2009 Allmänt gäller följande: Om lösningen helt saknar förklarande text till beräkningar och formler ges högst två
Här är ett antal uppgifter, en del tagna från gamla tentamina, som handlar om basbyte. respektive B = uttryckta i basen A
 Problem om asbyte Mikael Forsberg, 8 februari 0 Här är ett antal uppgifter, en del tagna från gamla tentamina, som handlar om basbyte.. Vi har baserna A och, givna som kolonnerna till matriserna T-00 A
Problem om asbyte Mikael Forsberg, 8 februari 0 Här är ett antal uppgifter, en del tagna från gamla tentamina, som handlar om basbyte.. Vi har baserna A och, givna som kolonnerna till matriserna T-00 A
1. (a) (1p) Undersök om de tre vektorerna nedan är linjärt oberoende i vektorrummet
 1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
. b. x + 2 y 3 z = 1 3 x y + 2 z = a x 5 y + 8 z = 1 lösning?
 Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
TMV166 Linjär Algebra för M. Tentamen
 MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 8 kl 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Olof Giselsson, ankn
MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 8 kl 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Olof Giselsson, ankn
