Grafisk Teknik. Färg. Övningar med lösningar/svar. Sasan Gooran (HT 2013)
|
|
|
- Joakim Henriksson
- för 5 år sedan
- Visningar:
Transkript
1 Grafisk Teknik Färg Övningar med lösningar/svar Det här lilla häftet innehåller ett antal räkneuppgifter med svar och i vissa fall med fullständiga lösningar De här uppgifterna täcker en del av kursen som handlar om färg De grundläggande teorier som behövs för att kunna lösa dessa uppgifter gås igenom under kursens föreläsningar och även finns i kursmaterialen som distribueras under kursen Sasan Gooran (HT 3)
2 Övningar: Belysnigens spektralfördelning beskrivs med funktionen l(λ), där λ är våglängdsvariabeln Reflektansegenskaperna beskrivs med r(λ) och kamerans tre kanaler med c R (λ), c G (λ), c B (λ) a) Hur beräknas kamerans (RGB)-vektor som funktion av l(λ), r(λ) och c R (λ), c G (λ), c B (λ)? b) Approximera l, r och c med 5-D vektorer: c R (λ) = (,,,, ) c G (λ) = (, /3, /3, /3, ) c B (λ) = (,,,, ) Beskriv (RGB)-vektorn som en funktion av l och r c) Vilken färg har belysningen som ges av vektorn l = (,,,, )? d) Beräkna (RGB)-vektorn för kombinationen l,, där reflektansvektorn, = ( /, /, /, /, / ) e) Konstruera en fördelning r så att (l, ) och (l,r ) ger samma RGB-vektor Färgmatchningsfunktionerna ges av: x(λ) = ( ) y(λ) = ( ) z(λ) = ( 8 5 ) En belysningskälla ges av: L(λ) = ( ) Två objektpunkters reflektansegenskaper ges av: O (λ) = ( /4 /4 / /8 ) O (λ) = ( /3 /3 ) Ingen normalisering krävs a) Beräkna -koordinater för O och O under belysning L b) Är O och O metameriska under belysning L? 3 Nedan följer en förenklad version av CIEs färgmatchningsfunktioner: x(λ) = ( 5 5 ) y(λ) = ( ) z(λ) = ( 6 8 ) a) Beräkna CIE koordinater för följande spektralfördelningar (belysning och reflektansegenskaper ingår): s (λ) = ( ) s (λ) = ( 3 ) b) Beskriv alla spektra av formen s(λ) = ( a b c ) som är metameriska
3 4 Raderna i matrisen M = [ ; ; ] definierar 3 färgmatchningsfunktioner x(λ), y(λ) och z(λ), tex x = ( ) Spektralfördelningarna för två ljuskällor är: L(λ)=[ ] och L(λ)=[ ] Reflektansegenskaperna för en objektpunkt beskrivs med vektorn R(λ) = ( r, r, r3, r4 ) a) Beräkna färgkoordinaterna för R under belysning L(λ) respektive L(λ) b) Beskriv alla metameriska färger under belysningen L(λ) Ge exempel på två metameriska färger under L c) Beskriv alla metameriska färger under belysningen L(λ) Ge exempel på två metameriska färger under L 5 Följande matriser beskriver en -kanals kamera K, en belysningskälla L och två reflektansspektra (objektpunkter) O Som det framgår av matriserna har vi delat in det synliga våglängdsintervallet i 4 delintervall K = [ ; ] L = [ 3 4] O = [ ; ]/ a) Beräkna den resulterande pixelvektorn (numeriska värden) för de två objektpunkterna b) Anta att vitt ljus representeras med en vektor V = [ ] Använd den kamera som beskrivs mha matrisen K ovan Konstruera två reflektansspektra R och R så att R och R är metameriska under L (lampan ovan) men inte under vitt ljus (V) 6 Nedan följer en förenklad version av CIEs färgmatchningsfunktioner x(λ) = [ 5 5 ] y(λ) = [ ] z(λ) = [ 6 8 ] a) Beräkna CIE koordinater för följande spektralfördelning R (λ) under I (λ) = [ ] (Ingen normalisering behövs för denna deluppgift) R (λ) = [ ] b) Vilken normaliseringsfaktor bör användas för att ljuskällans vitpunkt ska ha -värdet =? Svara för ljuskällan i uppgift a, dvs för I (λ) c) Beskriv alla spektra av formen R(λ) = ( a a a 3 ) som är metameriska under I (λ) 3
4 Lösningar och Svar a) Anta att alla fördelningar kan reprsenteras med vektorer av längd N, dvs l(λ) = [l,l,,l N ], r(λ) = [,r,, r N ], c R (λ) = [c R,c R,,c RN ], c G (λ) = [c G, c G,, c GN ] och c B (λ) = [c B, c B,, c BN ] man kan beräkna RGB vektorerna på två olika sätt, Metod : genom summan av punktvis multiplikation mellan vektorerna Metod : Matrismultiplikation Metod : R kan beräknas enligt, R = l C R + l r C R + + l N r N C RN vilket kan skrivas som, R = sum(l*r*c R ), där (*) betecknar elementvis multiplikation och sum betyder summan av alla element i vektorn G och B kan beräknas på motsvarande sätt: G = sum(l*r*c G ) och B = sum(l*r*c B ) Metod : Man kan bilda matriser först enligt, C R C G C B l C R C G C B l C =, L = och RR = C RN C GN C BN l N r r N C är en N x 3 matris L är en N x N diagonal matris och RR är en N x matris RGB vektorn kan nu direkt beräknas genom följande matrismultiplikation (T betyder transponat): R G B = C T L R b) R G B = l + l r 3 (l r + l r + l r ) l 4 r 4 + l 5 r 5 c) Färgen på belysningen är neutral, och om vi antar att är det största värdet ljusintensiteten kan anta då är färgen på belysningen vit 4
5 5 d) R G B = e) Anta att vi har två skilda reflektansspektra och r enligt, = a a a 3 a 4 a 5 och r = b b b 3 b 4 b 5 För att dessa två spektra ska ge samma RGB-vektor måste vi ha, a + a 3 (a + a 3 + a 4 ) a 4 + a 5 = b + b 3 (b + b 3 + b 4 ) b 4 + b 5 Det finns oändligt många skilda spektra som kan uppfylla detta, exempelvis följande två: = och r = a) för O under L : = för O under L : = b) Nej eftersom:
6 3 a) för S : = för S : = b) Anta att vi har följande två skilda spektralfördelningar s och p av formen som nämndes i uppgiften: s = a a a 3 och p = b b b 3 för att dessa två ska vara metameriska måste vi ha: a + 5a + a 3 = b + 5b + b 3 3a = 3b 6a = 6b Förenklar vi ekvationerna ovan får vi, a = b a = b a 3 = b 3, vilket innebär att för att s och p ska vara metameriska måste de vara lika, vilket betyder att det inte finns metameriska spektra av formen s = a a a 3 4 a) Färgkoordinaterna för R under L: Färgkoordinaterna för R under L: r 3 + r 4 = r + r = b) Anta att vi har två fördelningar R = [ r r 3 r 4 ] och R' = [ r' r' r' 3 r' 4 ] För att de ska vara metameriska under L måste vi ha: r 3 + r 4 = r' 3 + r' 4 r = r' + r = r' + r' Förenklar vi ekvationerna får vi: r 3 + r 4 = r' 3 + r' 4 r = r' = r' Exempel på två fördelningar som är metameriska under L: [ ] och [ ] 6
7 c) Anta att vi har två fördelningar R = [ r r 3 r 4 ] och R' = [ r' r' r' 3 r' 4 ] För att de ska vara metameriska under L måste vi ha: = = = r' Förenklar vi ekvationerna får vi: = r' Exempel på två fördelningar som är metameriska under L: [ ] och [ ] 5 a) för o (rad i O)à (3, ) för o (rad i O)à (, 5) b) K = [ ; ] L = [ 3 4] V=[ ] För att R= a a a 3 a 4 ha: och R = b b b 3 b 4 ska vara metameriska under L, bör vi a + a = b + b 3a 3 + 4a 4 = 3b 3 + 4b 4 och för att inte vara metameriska under V bör vi ha antingen a + a b + b eller a 3 + a 4 b 3 + b 4 Exempel: R=(/, /4, /3, /4) och R=(/4, 3/8, /, /8) 6 a) = = =4 b) normaliseringsfaktorn: sum(y* I) = 3 c) Om (a,,,, a, a3) och (b,,,, b, b3) är metameriska, då gäller: 7
8 a+ a = b+ b a = b 6a+8a = 6b+8b à a= b a = b a3 b3 kan vara godtyckliga 8
DIGITAL FÄRGRASTRERING
 DIGITAL FÄRGRASTRERING Sasan Gooran (HT 2003) 2006-08-18 Grafisk teknik 1 FÄRG Det mänskliga ögat kan uppfatta ljus, elektromagnetiska strålningar, med vågländer mellan 380 till 780 nm. Ett exempel: Spectral
DIGITAL FÄRGRASTRERING Sasan Gooran (HT 2003) 2006-08-18 Grafisk teknik 1 FÄRG Det mänskliga ögat kan uppfatta ljus, elektromagnetiska strålningar, med vågländer mellan 380 till 780 nm. Ett exempel: Spectral
DIGITAL FÄRGRASTRERING FÄRG. SPD Exempel. Sasan Gooran (HT 2003) En blåaktig färg
 DIGITAL FÄRGRASTRERING Sasan Gooran (HT 2003) 2006-08-18 Grafisk teknik 1 FÄRG Det mänskliga ögat kan uppfatta ljus, elektromagnetiska strålningar, med vågländer mellan 380 till 780 nm. Ett exempel: Spectral
DIGITAL FÄRGRASTRERING Sasan Gooran (HT 2003) 2006-08-18 Grafisk teknik 1 FÄRG Det mänskliga ögat kan uppfatta ljus, elektromagnetiska strålningar, med vågländer mellan 380 till 780 nm. Ett exempel: Spectral
DIGITAL FÄRGRASTRERING
 DIGITAL FÄRGRASTRERING Sasan Gooran 1/8/15 Grafisk teknik 1 FÄRG Det mänskliga ögat kan uppfatta ljus, elektromagnetiska strålningar, med vågländer mellan ca 380 till ca 780 nm. Ett exempel: Spectral Power
DIGITAL FÄRGRASTRERING Sasan Gooran 1/8/15 Grafisk teknik 1 FÄRG Det mänskliga ögat kan uppfatta ljus, elektromagnetiska strålningar, med vågländer mellan ca 380 till ca 780 nm. Ett exempel: Spectral Power
DIGITAL FÄRGRASTRERING FÄRG. Färg. Sasan Gooran
 DIGITAL FÄRGRASTRERING Sasan Gooran 1 FÄRG Det mänskliga ögat kan uppfatta ljus, elektromagnetiska strålningar, med vågländer mellan ca 380 till ca 780 nm. Ett exempel: Spectral Power Distribution (SPD).
DIGITAL FÄRGRASTRERING Sasan Gooran 1 FÄRG Det mänskliga ögat kan uppfatta ljus, elektromagnetiska strålningar, med vågländer mellan ca 380 till ca 780 nm. Ett exempel: Spectral Power Distribution (SPD).
FÄRG. Färg. SPD Exempel FÄRG. Stavar och Tappar. Ögats receptorer. Sasan Gooran (HT 2003) En blåaktig färg
 FÄRG Färg Sasan Gooran (HT 2003) Det mänskliga ögat kan uppfatta ljus, elektromagnetiska strålningar, med vågländer mellan 380 till 780 nm. Ett exempel: Spectral Power Distribution (SPD). Se nästa bild.
FÄRG Färg Sasan Gooran (HT 2003) Det mänskliga ögat kan uppfatta ljus, elektromagnetiska strålningar, med vågländer mellan 380 till 780 nm. Ett exempel: Spectral Power Distribution (SPD). Se nästa bild.
DIGITAL FÄRGRASTRERING
 DIGITAL FÄRGRASTRERING Sasan Gooran (HT 2003) 2005-03-31 Grafisk teknik 1 FÄRG Det mänskliga ögat kan uppfatta ljus, elektromagnetiska strålningar, med vågländer mellan 380 till 780 nm. Ett exempel: Spectral
DIGITAL FÄRGRASTRERING Sasan Gooran (HT 2003) 2005-03-31 Grafisk teknik 1 FÄRG Det mänskliga ögat kan uppfatta ljus, elektromagnetiska strålningar, med vågländer mellan 380 till 780 nm. Ett exempel: Spectral
Grafisk Teknik. Rastrering. Övningar med lösningar/svar. Sasan Gooran (HT 2013)
 Grafisk Teknik Rastrering Övningar med lösningar/svar Det här lilla häftet innehåller ett antal räkneuppgifter med svar och i vissa fall med fullständiga lösningar. Uppgifterna är för det mesta hämtade
Grafisk Teknik Rastrering Övningar med lösningar/svar Det här lilla häftet innehåller ett antal räkneuppgifter med svar och i vissa fall med fullständiga lösningar. Uppgifterna är för det mesta hämtade
FÄRG DIGITAL FÄRGRASTRERING FÄRG. Ögats receptorer. SPD Exempel. Stavar och Tappar. Sasan Gooran (HT 2003) En blåaktig färg
 FÄRG DIGITAL FÄRGRASTRERING Sasan Gooran (HT 2003) Newton: Indeed rays, properly expressed, are not colored. Han hade rätt. SPD existerar i den fysiska världen, men färg existerar bara i ögat och hjärnan.
FÄRG DIGITAL FÄRGRASTRERING Sasan Gooran (HT 2003) Newton: Indeed rays, properly expressed, are not colored. Han hade rätt. SPD existerar i den fysiska världen, men färg existerar bara i ögat och hjärnan.
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
 RÄKNEOPERATIONER MED VEKTORER LINJÄRA KOMBINATIONER AV VEKTORER ----------------------------------------------------------------- Låt u vara en vektor med tre koordinater, u = x, Vi säger att u är tredimensionell
RÄKNEOPERATIONER MED VEKTORER LINJÄRA KOMBINATIONER AV VEKTORER ----------------------------------------------------------------- Låt u vara en vektor med tre koordinater, u = x, Vi säger att u är tredimensionell
6. Matriser Definition av matriser 62 6 MATRISER. En matris är ett rektangulärt schema av tal: a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A =
 62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
Egenvärden och egenvektorer
 Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
1 Reducerat faktorförsök rf f
 1 REDUCERAT FAKTORFÖRSÖK RF F 1 Reducerat faktorförsök rf f Vi skall med tre faktorer och således 2 3 försök reducera till ett fullständigt 2 2 försök. 1.1 Tre faktorer Vi repeterar med ett tidigare fullständigt
1 REDUCERAT FAKTORFÖRSÖK RF F 1 Reducerat faktorförsök rf f Vi skall med tre faktorer och således 2 3 försök reducera till ett fullständigt 2 2 försök. 1.1 Tre faktorer Vi repeterar med ett tidigare fullständigt
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Sida 1 av Låt VV = RR nn där RR nn är mängden av alla reella n-tipplar (ordnade listor med n reella tal) dvs
 Sida av 7 ALLMÄNNA VEKTORRUM VEKTORRUM Definition Mängden V sägs vara ett reellt vektorrum om det finns i) en additionsoperation som till varje uu VV och vv VV ordnar uu vv VV ii) en operation kallad multiplikation
Sida av 7 ALLMÄNNA VEKTORRUM VEKTORRUM Definition Mängden V sägs vara ett reellt vektorrum om det finns i) en additionsoperation som till varje uu VV och vv VV ordnar uu vv VV ii) en operation kallad multiplikation
Lösningar till MVE021 Linjär algebra för I
 Lösningar till MVE Linjär algebra för I 7-8-9 (a Vektorer är ortogonala precis när deras skalärprodukt är Vi har u v 8 5h + h h 5h + 6 (h (h När h och när h (b Låt B beteckna basen {v, v } Om vi sätter
Lösningar till MVE Linjär algebra för I 7-8-9 (a Vektorer är ortogonala precis när deras skalärprodukt är Vi har u v 8 5h + h h 5h + 6 (h (h När h och när h (b Låt B beteckna basen {v, v } Om vi sätter
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
15 september, Föreläsning 5. Tillämpad linjär algebra
 5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
TNM011 Grafisk teknik Laboration 3 - Färg
 TNM011 Grafisk teknik Laboration 3 - Färg Martin Solli marso@itn.liu.se ITN, Linköpings Universitet HT 2006 Introduktion Laborationen handlar om sambandet mellan reflektansspektran, belysningar och den
TNM011 Grafisk teknik Laboration 3 - Färg Martin Solli marso@itn.liu.se ITN, Linköpings Universitet HT 2006 Introduktion Laborationen handlar om sambandet mellan reflektansspektran, belysningar och den
TAMS79: Föreläsning 10 Markovkedjor
 TAMS79: Föreläsning 0 Markovkedjor Johan Thim december 08 0. Markovkedjor Vi ska nu betrakta en speciell tidsdiskret diskret stokastisk process, nämligen Markovkedjan. Vi börjar med en definition Definition.
TAMS79: Föreläsning 0 Markovkedjor Johan Thim december 08 0. Markovkedjor Vi ska nu betrakta en speciell tidsdiskret diskret stokastisk process, nämligen Markovkedjan. Vi börjar med en definition Definition.
10.4. Linjära höljet LINJÄRA RUM
 98 LINJÄRA RUM.4. Linjära höljet Definition.37. Mängden av alla linjärkombinationer av M = {v, v,...,v n } iett linjärt rum V kallas för linjära höljet av M betecknas [M], dvs [M] ={u V : u = λ v + λ v
98 LINJÄRA RUM.4. Linjära höljet Definition.37. Mängden av alla linjärkombinationer av M = {v, v,...,v n } iett linjärt rum V kallas för linjära höljet av M betecknas [M], dvs [M] ={u V : u = λ v + λ v
Moment 6.1, 6.2 Viktiga exempel Övningsuppgifter T6.1-T6.6
 Moment 6., 6. Viktiga exempel 6.-6. Övningsuppgifter T6.-T6.6 Matriser Definition. En matris är ett schema med m rader och n kolonner eller kolumner, som vi kallar dem i datalogin innehållande m n element.
Moment 6., 6. Viktiga exempel 6.-6. Övningsuppgifter T6.-T6.6 Matriser Definition. En matris är ett schema med m rader och n kolonner eller kolumner, som vi kallar dem i datalogin innehållande m n element.
5 Linjär algebra. 5.1 Addition av matriser 5 LINJÄR ALGEBRA
 5 LINJÄR ALGEBRA 5 Linjär algebra En kul gren av matematiken som inte fått speciellt mycket utrymme i gymnasiet men som har många tillämpningsområden inom t.ex. fysik, logistik, ekonomi, samhällsplanering
5 LINJÄR ALGEBRA 5 Linjär algebra En kul gren av matematiken som inte fått speciellt mycket utrymme i gymnasiet men som har många tillämpningsområden inom t.ex. fysik, logistik, ekonomi, samhällsplanering
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
Geometriska vektorer
 Föreläsning 1, Linjär algebra IT VT2008 1 Geometriska vektorer De begrepp som linjär algebra kretsar kring är vektorer och matriser Dessa svarar mot datorernas fält (`arra') av dimension ett respektive
Föreläsning 1, Linjär algebra IT VT2008 1 Geometriska vektorer De begrepp som linjär algebra kretsar kring är vektorer och matriser Dessa svarar mot datorernas fält (`arra') av dimension ett respektive
Grafisk Teknik. Rastrering. Övningar med lösningar/svar. Sasan Gooran (HT 2004)
 Grafisk Teknik Rastrering Övningar med lösningar/svar Sasan Gooran (HT 24) Det här lilla häftet innehåller ett antal räkneuppgifter med svar och i vissa fall med fullständiga lösningar. Uppgifterna är
Grafisk Teknik Rastrering Övningar med lösningar/svar Sasan Gooran (HT 24) Det här lilla häftet innehåller ett antal räkneuppgifter med svar och i vissa fall med fullständiga lösningar. Uppgifterna är
SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 2014
 SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 214 Skrivtid: 14.-19. Tillåtna hjälpmedel: inga Examinator: Roy Skjelnes Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 214 Skrivtid: 14.-19. Tillåtna hjälpmedel: inga Examinator: Roy Skjelnes Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
SF1624 Algebra och geometri
 Föreläsning 10 Institutionen för matematik KTH 21 november 2016 Dagens och veckans ämnen Idag: Allmänna vektorrum, baser, koordinater, kap 4.1-4.4: Vektorrum och delrum, igen Bas, igen Koordinater med
Föreläsning 10 Institutionen för matematik KTH 21 november 2016 Dagens och veckans ämnen Idag: Allmänna vektorrum, baser, koordinater, kap 4.1-4.4: Vektorrum och delrum, igen Bas, igen Koordinater med
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
3 1 = t 2 2 = ( 1) ( 2) 1 2 = A(t) = t 1 10 t
 SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
29 november, 2016, Föreläsning 21. Ortonormala baser (ON-baser) Gram-Schmidt s ortogonaliseringsprocess
 29 november, 2016, Föreläsning 21 Tillämpad linjär algebra Innehåll: Ortonormala baser (ON-baser) Gram-Schmidt s ortogonaliseringsprocess Minsta-kvadratmetoden - exempel 1. Uppgift. Tentamen 19/1-15, uppgift
29 november, 2016, Föreläsning 21 Tillämpad linjär algebra Innehåll: Ortonormala baser (ON-baser) Gram-Schmidt s ortogonaliseringsprocess Minsta-kvadratmetoden - exempel 1. Uppgift. Tentamen 19/1-15, uppgift
14 september, Föreläsning 5. Tillämpad linjär algebra
 14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
TNM059 Grafisk teknik
 TNM059 Grafisk teknik Färg Fö 1(2) VT 2015 Fysik: Ljus, ytor och sensorer Färgseende - hur ögat ser färg Colorimetry att mäta färg Färgperception hur hjärnan ser färg Färgreproduktion Färgstyrning Färg
TNM059 Grafisk teknik Färg Fö 1(2) VT 2015 Fysik: Ljus, ytor och sensorer Färgseende - hur ögat ser färg Colorimetry att mäta färg Färgperception hur hjärnan ser färg Färgreproduktion Färgstyrning Färg
Logik och Jämförelser. Styrsatser: Villkorssatsen if och repetitonssatsen for. Scriptfiler. Kommentarer. Tillämpningar: Ett enkelt filter.
 TAIU07 Föreläsning 3 Logik och Jämförelser. Styrsatser: Villkorssatsen if och repetitonssatsen for. Scriptfiler. Kommentarer. Tillämpningar: Ett enkelt filter. 27 januari 2016 Sida 1 / 21 Logiska variabler
TAIU07 Föreläsning 3 Logik och Jämförelser. Styrsatser: Villkorssatsen if och repetitonssatsen for. Scriptfiler. Kommentarer. Tillämpningar: Ett enkelt filter. 27 januari 2016 Sida 1 / 21 Logiska variabler
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
1 som går genom punkten (1, 3) och är parallell med vektorn.
 KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
Enhetsvektorer. Basvektorer i två dimensioner: 1 1 Basvektorer i tre dimensioner: Enhetsvektor i riktningen v: v v
 Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
2 = 3 = 1. ekvationssystem är beskriven som de vektorer X = 2 0 1 2. 1 1 0 2
 . Tisdagen 35 Igår visade vi att lösningsmängden W R 5 till ekvationssystemet 3x + x 2 + 3x 3 + 2x 4 x 5 = (..) 2x 2 + x 3 + 4x 4 + 2x 5 = 3x 3x 2 + x 3 6x 4 5x 5 = har bas u och u 2 och u 3 där 5 2 6
. Tisdagen 35 Igår visade vi att lösningsmängden W R 5 till ekvationssystemet 3x + x 2 + 3x 3 + 2x 4 x 5 = (..) 2x 2 + x 3 + 4x 4 + 2x 5 = 3x 3x 2 + x 3 6x 4 5x 5 = har bas u och u 2 och u 3 där 5 2 6
Lösningsforslag till tentamen i SF1624 den 22/ e x e y e z = 5e x 10e z = 5(1, 0, 2). 1 1 a a + 2 2a 4
 Institutionen för matematik, KTH Serguei Shimorin Lösningsforslag till tentamen i SF64 den /0 007 Eftersom planet går genom punkten (,, 0, det har ekvation a(x + b(y + + cz = 0, där a, b, c är koefficienter
Institutionen för matematik, KTH Serguei Shimorin Lösningsforslag till tentamen i SF64 den /0 007 Eftersom planet går genom punkten (,, 0, det har ekvation a(x + b(y + + cz = 0, där a, b, c är koefficienter
DIAGONALISERING AV EN MATRIS
 DIAGONALISERING AV EN MATRIS Definition ( Diagonaliserbar matris ) Låt A vara en kvadratisk matris dvs en matris av typ n n. Matrisen A är diagonaliserbar om det finns en inverterbar matris P och en diagonalmatris
DIAGONALISERING AV EN MATRIS Definition ( Diagonaliserbar matris ) Låt A vara en kvadratisk matris dvs en matris av typ n n. Matrisen A är diagonaliserbar om det finns en inverterbar matris P och en diagonalmatris
4x az = 0 2ax + y = 0 ax + y + z = 0
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
Numerisk Analys, MMG410. Exercises 2. 1/33
 Numerisk Analys, MMG410. Exercises 2. 1/33 1. A är en kvadratisk matris vars alla radsummor är noll. Visa att A är singulär. Låt e vara vektorn av ettor. Då är Ae = 0 A har icke-trivialt nollrum. 2/33
Numerisk Analys, MMG410. Exercises 2. 1/33 1. A är en kvadratisk matris vars alla radsummor är noll. Visa att A är singulär. Låt e vara vektorn av ettor. Då är Ae = 0 A har icke-trivialt nollrum. 2/33
Hemuppgift 1, SF1861 Optimeringslära, VT 2017
 Hemuppgift 1, SF1861 Optimeringslära, VT 2017 Examinator: Krister Svanberg, tel: 790 7137, krille@math.kth.se. Labassistent: David Ek, daviek@kth.se, Lämnas i Matematiks svarta postlåda (SF) för inlämningsuppgifter,
Hemuppgift 1, SF1861 Optimeringslära, VT 2017 Examinator: Krister Svanberg, tel: 790 7137, krille@math.kth.se. Labassistent: David Ek, daviek@kth.se, Lämnas i Matematiks svarta postlåda (SF) för inlämningsuppgifter,
tal. Mängden av alla trippel av reella tal betecknas med R 3 och x 1 x 2 En sekvens av n reella tal betecknas med (x 1, x 2,, x n ) eller
 Augusti, 5 Föreläsning Tillämpad linjär algebra Innehållet: linjen R, planet R, rummet R, oh vektor rummet R n Matriser punkter oh vektorer i planet, rummet, oh R n Linjen, planet, rummet, oh vektor rummet
Augusti, 5 Föreläsning Tillämpad linjär algebra Innehållet: linjen R, planet R, rummet R, oh vektor rummet R n Matriser punkter oh vektorer i planet, rummet, oh R n Linjen, planet, rummet, oh vektor rummet
. b. x + 2 y 3 z = 1 3 x y + 2 z = a x 5 y + 8 z = 1 lösning?
 Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 17 april 2010 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
ANDRAGRADSKURVOR Vi betraktar ekvationen
 ANDRAGRADSKURVOR Vi betraktar ekvationen Ax + Bxy + Cy + Dx + Fy + G 0 (ekv) där minst en av A,B, eller C är skild från 0 En andragradskurva är mängden av alla punkter vilkas koordinater satisfierar en
ANDRAGRADSKURVOR Vi betraktar ekvationen Ax + Bxy + Cy + Dx + Fy + G 0 (ekv) där minst en av A,B, eller C är skild från 0 En andragradskurva är mängden av alla punkter vilkas koordinater satisfierar en
MVE022 Urval av bevis (på svenska)
 MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
Vi definierar addition av två vektorer och multiplikation med en reell skalär (tal) λλ enligt nedan
 ORTOGONALA VEKTORER OCH ORTONORMERADE (ORTONORMALA) BASER I R n INLEDNING ( repetition om R n ) Låt RR nn vara mängden av alla reella n-tipplar (ordnade listor med n reella tal) dvs RR nn {(aa, aa,, aa
ORTOGONALA VEKTORER OCH ORTONORMERADE (ORTONORMALA) BASER I R n INLEDNING ( repetition om R n ) Låt RR nn vara mängden av alla reella n-tipplar (ordnade listor med n reella tal) dvs RR nn {(aa, aa,, aa
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
SF1624 Algebra och geometri Tentamen Onsdag, 13 januari 2016
 SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
Laboration 1. Grafisk teknik (TNM059) Introduktion till Matlab. R. Lenz och S. Gooran (VT2007)
 Laboration 1 Grafisk teknik (TNM059) Introduktion till Matlab R. Lenz och S. Gooran (VT2007) Introduktion: Denna laboration är en introduktion till Matlab. Efter denna laboration ska ni kunna följande:
Laboration 1 Grafisk teknik (TNM059) Introduktion till Matlab R. Lenz och S. Gooran (VT2007) Introduktion: Denna laboration är en introduktion till Matlab. Efter denna laboration ska ni kunna följande:
KPP053, HT2016 MATLAB, Föreläsning 2. Vektorer Matriser Plotta i 2D Teckensträngar
 KPP053, HT2016 MATLAB, Föreläsning 2 Vektorer Matriser Plotta i 2D Teckensträngar Vektorer För att skapa vektorn x = [ 0 1 1 2 3 5]: >> x = [0 1 1 2 3 5] x = 0 1 1 2 3 5 För att ändra (eller lägga till)
KPP053, HT2016 MATLAB, Föreläsning 2 Vektorer Matriser Plotta i 2D Teckensträngar Vektorer För att skapa vektorn x = [ 0 1 1 2 3 5]: >> x = [0 1 1 2 3 5] x = 0 1 1 2 3 5 För att ändra (eller lägga till)
Laboration 1. Grafisk teknik Rastrering. Sasan Gooran (HT 2004)
 Laboration 1 Grafisk teknik ------------------------------------- Rastrering Sasan Gooran (HT 2004) Introduktion 1.0 Introduktion Den här laborationen måste förberedas innan laborationstillfället. Ett
Laboration 1 Grafisk teknik ------------------------------------- Rastrering Sasan Gooran (HT 2004) Introduktion 1.0 Introduktion Den här laborationen måste förberedas innan laborationstillfället. Ett
LÖSNINGAR LINJÄR ALGEBRA LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem.
 Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
SF1900 Sannolikhetsteori och statistik, HT 2017 Laboration 1 för CINEK2
 Matematisk Statistik SF1900 Sannolikhetsteori och statistik, HT 2017 Laboration 1 för CINEK2 1 Introduktion Denna laboration är inte poänggivande utan är till för den som vill bekanta sig med MATLAB. Fokusera
Matematisk Statistik SF1900 Sannolikhetsteori och statistik, HT 2017 Laboration 1 för CINEK2 1 Introduktion Denna laboration är inte poänggivande utan är till för den som vill bekanta sig med MATLAB. Fokusera
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604 för D, den 5 juni 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF164 för D, den 5 juni 21 kl 9.- 14.. Examinator: Olof Heden. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen.
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF164 för D, den 5 juni 21 kl 9.- 14.. Examinator: Olof Heden. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen.
TSBB14 Laboration: Intro till Matlab 1D
 TSBB14 Laboration: Intro till Matlab 1D Utvecklad av Maria Magnusson med mycket hjälp av Lasse Alfredssons material i kursen Introduktionskurs i Matlab, TSKS08 Avdelningen för Datorseende, Institutionen
TSBB14 Laboration: Intro till Matlab 1D Utvecklad av Maria Magnusson med mycket hjälp av Lasse Alfredssons material i kursen Introduktionskurs i Matlab, TSKS08 Avdelningen för Datorseende, Institutionen
A = x
 Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
P Q = ( 2, 1, 1), P R = (0, 1, 0) och QR = (2, 2, 1). arean = 1 2 P Q P R
 1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
14. Minsta kvadratmetoden
 58 MINSTA KVADRATMETODEN. Minsta kvadratmetoden Eempel.. Det är inte så svårt att komma åt en trasig lampa på golvet för att byta den. Det är bara att gå fram till den. Hur är det om lampan hänger i taket?
58 MINSTA KVADRATMETODEN. Minsta kvadratmetoden Eempel.. Det är inte så svårt att komma åt en trasig lampa på golvet för att byta den. Det är bara att gå fram till den. Hur är det om lampan hänger i taket?
Tentamen 1 i Matematik 1, HF okt 2018, Skrivtid: 14:00-18:00 Examinator: Armin Halilovic
 Tentamen i Matematik, HF9 4 okt 8, Skrivtid: 4:-8: Examinator: Armin Halilovic För godkänt betyg krävs av max 4 poäng Betygsgränser: För betyg A, B, C, D, E krävs, 9, 6, respektive poäng Komplettering:
Tentamen i Matematik, HF9 4 okt 8, Skrivtid: 4:-8: Examinator: Armin Halilovic För godkänt betyg krävs av max 4 poäng Betygsgränser: För betyg A, B, C, D, E krävs, 9, 6, respektive poäng Komplettering:
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra, SF1604, den 15 mars 2012 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF604, den 5 mars 202 kl 08.00-3.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF604, den 5 mars 202 kl 08.00-3.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
e 3 e 2 e 1 Kapitel 3 Vektorer i planet och i rummet precis ett sätt skrivas v = x 1 e 1 + x 2 e 2
 Kapitel 3 Vektorer i planet och i rummet B e 3 e 2 A e 1 C Figur 3.16 Vi har ritat de riktade sträckor som representerar e 1, e 2, e 3 och v och som har utgångspunkten A. Vidare har vi skuggat planet Π
Kapitel 3 Vektorer i planet och i rummet B e 3 e 2 A e 1 C Figur 3.16 Vi har ritat de riktade sträckor som representerar e 1, e 2, e 3 och v och som har utgångspunkten A. Vidare har vi skuggat planet Π
GRAM-SCHMIDTS METOD ... Med hjälp av Gram-Schmidts metod kan vi omvandla n st. linjäroberoende vektorer. samma rum dvs som satisfierar
 Armin Halilovic: EXTRA ÖVNINGAR GRAM-SCHMIDTS METOD Med hjälp av kan vi omvandla n st linjäroberoende vektorer vv vv nn i ett vektorrum till n st ortonormerade vektorer ff ff nn som spänner upp samma rum
Armin Halilovic: EXTRA ÖVNINGAR GRAM-SCHMIDTS METOD Med hjälp av kan vi omvandla n st linjäroberoende vektorer vv vv nn i ett vektorrum till n st ortonormerade vektorer ff ff nn som spänner upp samma rum
Hemuppgift 1, SF1861 Optimeringslära för T
 Hemuppgift 1, SF1861 Optimeringslära för T Examinator: Per Enqvist, tel: 790 6298, penqvist@math.kth.se. Assistenter: Amol Sasane, sasane@math.kth.se, Mikael Fallgren, werty@kth.se. Lämnas in till någon
Hemuppgift 1, SF1861 Optimeringslära för T Examinator: Per Enqvist, tel: 790 6298, penqvist@math.kth.se. Assistenter: Amol Sasane, sasane@math.kth.se, Mikael Fallgren, werty@kth.se. Lämnas in till någon
Dagens ämnen. Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer
 Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
September 13, Vektorer En riktad sträcka P Q, där P Q, är en pil med foten i P och med spetsen i Q. Denna har. (i) en riktning, och
 Fö : September 3, 205 Vektorer En riktad sträcka P Q, där P Q, är en pil med foten i P och med spetsen i Q. Denna har i en riktning, och ii en nollskild längd betecknad P Q. Man använder riktade sträckor
Fö : September 3, 205 Vektorer En riktad sträcka P Q, där P Q, är en pil med foten i P och med spetsen i Q. Denna har i en riktning, och ii en nollskild längd betecknad P Q. Man använder riktade sträckor
Laboration 2. Grafisk teknik (TNM059) Digital Rastrering. S. Gooran (VT2007)
 Laboration 2 Grafisk teknik (TNM059) Digital Rastrering S. Gooran (VT2007) Introduktion Denna laboration handlar om rastrering och är tänkt att fungera som komplement till rastreringsföreläsningar och
Laboration 2 Grafisk teknik (TNM059) Digital Rastrering S. Gooran (VT2007) Introduktion Denna laboration handlar om rastrering och är tänkt att fungera som komplement till rastreringsföreläsningar och
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
Föreläsning 13 Linjär Algebra och Geometri I
 Föreläsning 13 Linjär Algebra och Geometri I Se slide 1: det är i rymden oftast lättast att jobba med parametrar för linjer och ekvationer för plan. Exempel: Låt l : (x, y, z) = (1 t, 3 + t, 4t), t R och
Föreläsning 13 Linjär Algebra och Geometri I Se slide 1: det är i rymden oftast lättast att jobba med parametrar för linjer och ekvationer för plan. Exempel: Låt l : (x, y, z) = (1 t, 3 + t, 4t), t R och
FÖ: MVE045, Riemann integral, grunder Zoran Konkoli, HT 2018
 FÖ: MVE045, Riemann integral, grunder Zoran Konkoli, HT 2018 VIKTIG: Vi hinner inte gå igenom allt som ni skall kunna under föreläsningar. Varje föreläsning är alltid en tolkning av ADAMS boken, och ibland
FÖ: MVE045, Riemann integral, grunder Zoran Konkoli, HT 2018 VIKTIG: Vi hinner inte gå igenom allt som ni skall kunna under föreläsningar. Varje föreläsning är alltid en tolkning av ADAMS boken, och ibland
x 2y + z = 1 (1) 2x + y 2z = 3 (2) x + 3y z = 4 (3)
 TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 74-4 kurser:: Linjär Algebra ma4a Matematik för ingenjörer maa 8 5 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta
TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 74-4 kurser:: Linjär Algebra ma4a Matematik för ingenjörer maa 8 5 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta
Laboration 0: Del 2. Benjamin Kjellson Introduktion till matriser, vektorer, och ekvationssystem
 Laboration 0: Del 2 Benjamin Kjellson 2016 03 21 Introduktion till matriser, vektorer, och ekvationssystem I den här filen får ni en kort introduktion till hur man hanterar och räknar med matriser i R,
Laboration 0: Del 2 Benjamin Kjellson 2016 03 21 Introduktion till matriser, vektorer, och ekvationssystem I den här filen får ni en kort introduktion till hur man hanterar och räknar med matriser i R,
Vektorerna är parallella med planet omm de är vinkelräta mot planets normal, dvs mot
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Dagens program. Linjära ekvationssystem och matriser
 Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
LYCKA TILL! kl 8 13
 LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
Datorlaboration :: 1 Problembeskrivning ::
 Datorlaboration :: Ett hyrbilsföretags problem Laborationen går ut på att lösa Labbuppgift 1 till 5. Laborationen redovisas individuellt genom att skicka laborationens Mathematicafil till Mikael Forsberg
Datorlaboration :: Ett hyrbilsföretags problem Laborationen går ut på att lösa Labbuppgift 1 till 5. Laborationen redovisas individuellt genom att skicka laborationens Mathematicafil till Mikael Forsberg
u av funktionen u = u(x, y, z) = xyz i punkten M o = (x o, y o, z o ) = (1, 1, 1) i riktningen mot punkten M 1 = (x 1, y 1, z 1 ) = (2, 3, 1)
 ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
= ( 1) ( 1) = 4 0.
 MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
SF1624 Algebra och geometri Tentamen med lösningsförslag onsdag, 11 januari 2017
 SF64 Algebra och geometri Tentamen med lösningsförslag onsdag, januari 7. (a) För vilka värden på k har ekvationssystemet (med avseende på x, y och z) kx + ky + z 3 x + ky + z 4x + 3y + 3z 8 en entydig
SF64 Algebra och geometri Tentamen med lösningsförslag onsdag, januari 7. (a) För vilka värden på k har ekvationssystemet (med avseende på x, y och z) kx + ky + z 3 x + ky + z 4x + 3y + 3z 8 en entydig
TAIU07 Matematiska beräkningar med Matlab
 TAIU07 Matematiska beräkningar med Matlab Datorlektion 2. Villkor och Repetition 1 Logiska uttryck Uppgift 1.1 Låt a=3 och b=6 Vad blir resultatet av testerna ab? Uppgift 1.2 Låt a, b,
TAIU07 Matematiska beräkningar med Matlab Datorlektion 2. Villkor och Repetition 1 Logiska uttryck Uppgift 1.1 Låt a=3 och b=6 Vad blir resultatet av testerna ab? Uppgift 1.2 Låt a, b,
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
Självkoll: Ser du att de två uttrycken är ekvivalenta?
 ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
1 Grundläggande kalkyler med vektorer och matriser
 Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
TMV206: Linjär algebra
 Matematiska vetenskaper Lösningsförslag till tentamen Chalmers tekniska högskola 2018-06-07, 14:00 18:00 TMV206: Linjär algera Uppgift 1 Linjerna skär varandra om det finns någon punkt (x,y, z) som uppfyller
Matematiska vetenskaper Lösningsförslag till tentamen Chalmers tekniska högskola 2018-06-07, 14:00 18:00 TMV206: Linjär algera Uppgift 1 Linjerna skär varandra om det finns någon punkt (x,y, z) som uppfyller
MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET MED MATRISINVERSER = = =
 Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
x 1 x 2 T (X) = T ( x 3 x 4 x 5
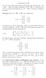 Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
8(x 1) 7(y 1) + 2(z + 1) = 0
 Matematiska Institutionen KTH Lösningsförsök till tentamensskrivningen på kursen Linjär algebra, SF60, den juni 0 kl 08.00-.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Matematiska Institutionen KTH Lösningsförsök till tentamensskrivningen på kursen Linjär algebra, SF60, den juni 0 kl 08.00-.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
