Repetitionsuppgifter inför Matematik 1. Matematiska institutionen Linköpings universitet 2013
|
|
|
- Elisabeth Pålsson
- för 8 år sedan
- Visningar:
Transkript
1 Repetitionsuppgifter inför Matematik Matematiska institutionen Linköpings universitet 0
2 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Facit 4
3 Repetitionsuppgifter inför Matematik Repetitionsuppgifter i matematik Inför studierna i vår det lämpligt att fräscha upp räknefärdigheterna. Det är kanske något år sedan du läste gymnasiematematiken, och när du kommer till Linköping och Norrköping sätter vi igång med full fart från första början! I skolan används numera räknare (bl.a. grafritare) flitigt. Detta har många fördelar. Rutinberäkningar går snabbt och man kan därigenom ägna mer tid åt verksamhet som utvecklar begreppsförståelse och problemlösningsförmåga. Det finns dock risker med att använda miniräknare alltför flitigt. Många moment i matematiken är av den karaktären att man förstår dem bättre om man vänjer sig vid att hantera dem genom att räkna för hand, med penna och papper. Alla uppgifter i detta häfte skall lösas helt utan tekniska hjälpmedel. De fyra räknesätten.. Bestäm de tal på tallinjen, som är markerade med A, B och C. a) b).. Vilket tal ligger mitt emellan a) 0, och 0, b) 0,6 och 0, 0,7 och 0,8 d) 0,8 och 0,8.. Beräkna a) + 6 b) ( + 6 ) ( + 6) d) ( + 6).4. Beräkna a) 40 0 b) ( 0) d) 4 + ( ) e) 6 ( 0) f) 0 ( 0).. Beräkna a) + 8 b) 8 + ( 0) ( ) d) ( 0) + ( 00) Det är inte tillåtet att skriva två operationssymboler intill varandra. Ett vanligt fel är gånger minus, dvs att man får se något sådant som. Detta är förbjudet; man måste sätta parentes om den andra faktorn: ( )..6. Beräkna a) ( ) ( ) ( 4) b) 8 ( ) ( ) ( 6) ( ) 7 + ( ) ( 4) d) ( ) ( 0) 6 ( ) e) (4 7 ) + ( 6 7 )/
4 4 När man arbetar med bråkuttryck är det mycket viktigt att bråkstrecket står på samma nivå som tecknet = och symboler som + och (om dessa inte själva ingår i bråket). Exempelvis är det fel, ja direkt förbjudet, att skriva a + b = c när man menar a + b = c..7. Beräkna 7 a) ( ) b) + ( 0) ( ) ( ) Beräkna a) 0 0, b) 0, ,7, 0, d) 0 (0,8 0,).. Beräkna a) 0, 0, b) 0,08 0,7 0,7 0,0 d) 0, 0,00.0. Beräkna a) 4 0, + 0, b) 0,7 0, 0, 4, 0, d) 0,8 + 0, 6.. Beräkna a) 0, + 0, b) 6 0, + 6 0, 0,4 + 0, 0, d) 0,7 0, 0,.. Beräkna a) 0,6 0, 0,4 0,7 b) 0,7 0,08 0,04 0,6 d) 0,6 + 0, 0, 0,06 0,4 0, 0, 0,00.. Vilket tal skall talet, multipliceras med för att resultatet skall bli:.4. Beräkna a) b) 0,0 a) 0,8 + 0, b) 0, 0, 0,07 0,07 d) 0,8 0,0.. Summan av två tal är 0,6. Det ena talet är 0,04. Vilket är det andra?.6. Produkten av två tal är 0,04. Det ena talet är 0,. Vilket är det andra?.7. Vad kostar det att köpa 0, kg köttfärs, om köttfärsen kostar 4 kr/kg?.8. För en viss kopieringsmaskin är kostnaden 0 öre per kopia. Hur många kopior har en kund tagit, om hon får betala 67,0 kr?
5 Repetitionsuppgifter inför Matematik Räkning med tal i bråkform Förkortning (med 7) 4 = /7 4/7 = 7 Förlängning (med 7) = 7 7 = 6 Multiplikation 4 7 = Addition och subtraktion + 6 = = = = = 7/ 0/ = 0 Division = 7 = 0 = 0 = 0 Om man förlänger dubbelbråket med nämnaren) får man talet i nämnaren. (det inverterade talet till den ursprungliga.. Förkorta så långt som möjligt a) 0 b) Bestäm det tal, som skall stå på den tomma platsen: a) = b) 7 = 8 d) 7 6 = d) = 7.. Skriv upp de tal mellan 0 och, som i enklaste bråkform skrivs med nämnaren... Vilket tecken (=, < eller >) skall stå mellan talen? a) 4 b) Vilket tecken (< eller >) skall stå mellan talen? a) b) d) 4 d) 0.4. Skriv följande tal i enklaste bråkform: a) 0,00 b) 0,0 0,07 d) 0, Beräkna a) b) d) e) 6 ( 4) ( ) f) 6+( )+ ( 0)+( ) ( ) ( ) 8.6. Summan av två tal är 0. Det ena talet är. Vilket är det andra? 6 4 0
6 6.7. Produkten av två tal är. Bestäm den andra faktorn, om den ena faktorn är a) 7 b) 6.8. Vilket tal skall 6 multipliceras med för att produkten skall bli 8?.. Beräkna a) Bestäm det bråk som ligger mitt emellan b) d) ( ) ( 7 + ) 7 + a) 4 och b) 8 och.. Beräkna medelvärdet av, 4 och... Beräkna a) ( ) 8.. Beräkna a) d) b) 4 e) / g) + 8 ( ) ( ) ( ) b) ) d) ( f) 4 ( ) / ( ) 4.4. Av en tygrulle skall man klippa till 40 cm långa stycken till dukar. Hur många dukar får man om tygrullen är 40 m lång?.. Vilket är kilopriset för jäst om 0 g kostar,7 kr?.6. I Sverige kastas i genomsnitt 00 kg sopor per person och år. Hur stor mängd sopor blir det under ett år i ett samhälle med invånare? Svara i ton..7. Vid en regnskur föll mm regn. Hur många liter föll på en rektangulär gräsmatta, som är m lång och 0 m bred?
7 Repetitionsuppgifter inför Matematik 7 Potenser och rötter Uttrycket a x kallas för en potens med basen a och exponenten x. Följande räknelagar för potenser förutsätts vara kända (a, b > 0): a x a y = a x+y ( a ) x a x = b a x a y = ax y (a x ) y = a x y (a b) x = a x b x b x a x = a x a 0 = a m n = n a m.. Beräkna a) b) 0,008 0, d) Beräkna a) b) ( ) d) ( ).. Beräkna a) 4 6 b) 0 + d).4. Beräkna a) b) d).. Förenkla så långt som möjligt: a) 4 b) ( ) / d) 0 e) 000 / f) 6 /4 g) 4/ 6 x+y h) x y i) /7 7 ( ) 6/7 j) 0 7/ (/0) 4 0 /.6. Beräkna a) b) d) Skriv i potensform med basen :.8. Beräkna a) 8 b) 4 a) 0, b) 0, e) 0,07 0, , d) d) 8 0,.. Beräkna a) ( ) b) ( 7) ( ) 6 d) ( 0).0. Beräkna a) ( ) + ( ) b) (0) + ( ) ( ) + ( ) d) ( 4) + ( ) ( 0) e) ( ) + ( ) 4 ( )
8 8.. Ordna följande tal efter storlek, från det minsta till det största ( ) 87 0 ; ( 0,) ; ; ( 0,) ; (0,) 4 ; Beräkna a) 0, b), , d) 0, Beräkna a) b) d) e) 0 0 f) Skriv i potensform med basen det tal som är a) dubbelt så stort som 0 b) hälften så stort som 0.. Skriv som en enda potens av : a) 7 b) 6 d) ( ).6. Beräkna a) 6 4 b) d) ( 4) 6.7. Skriv som en enda potens av : a) 4 b).8. Beräkna a) b) ( 4) ( ).. Skriv som en enda potens av :.0. Förkorta a) 7 b) 4 a) 4 b).. Skriv som en potens med basen 4 d) ( ) ( 0 4) 0 7 ( ) ( 4) a) b) d) 6 8 (6 ) d).. Beräkna a) 7 b) d) +.. Beräkna a) 0, b) 0, 0, + 0,6 d) 0, + 0,.4. Beräkna och svara i grundpotensform (dvs. på formen a 0 n, där a < 0): a) 0 0 b) d)
9 Repetitionsuppgifter inför Matematik.. Med hur många siffror skrivs följande tal om de skrivs utan potenser? a),7 0 8 b) 8, d) 0, Beräkna och svara i grundpotensform: a) 0 b) , 0 d).7. Beräkna och svara i grundpotensform: a) ( 4 0 4) b) ( 0 ) ( 0 ).8. a = och b = 0. Beräkna och svara i grundpotensform: a) ab b) a/b b/a d) ( 0 ) Ett rotuttryck kan ibland förenklas genom att man faktoriserar under rotmärket efter följande modell: 7 = 8 = = ( ) = = 6.. Följande tio tal är parvis lika. Para ihop de tal som är lika 8,,,,, 8, 7, 4,,.0. Snygga till följande uttryck enligt ovanstående idé: a) 8 b) 0 48 d) + 8 e) f) Beräkna och förenkla följande uttryck: a) 8 b) 0 d) e) f) Ett bråk med kvadratrotsuttryck i nämnaren brukar inte anses som förenklat. Kvadratrötter i nämnare kan avlägsnas genom att man förlänger med det s.k. konjugatuttrycket: = ( ) ( ) = ( ) = + = +.. Skriv om följande uttryck utan kvadratrötter i nämnaren: + a) b) d) Förenkla så långt som möjligt följande tal: a) ( ) b) 6 6 d) 6
10 0 Algebra Förenklingar och omskrivningar Produkten av två polynom innebär multiplikation av två parentesuttryck, som visas i exemplet nedan. Teckenregeln lika tecken ger plus; olika tecken ger minus tillämpas. Exempel: (x 4) (x ) = x x 8x + 0 = x x + 0 Vi fortsätter med några räknelagar: (a + b) = a + ab + b () (a b) = a ab + b () (a b) (a + b) = a b () De två första, ekvationerna () och (), kallas kvadreringsreglerna och den tredje, (), kallas konjugatregeln. Samtliga dessa räknelagar kan kontrolleras genom att man utför multiplikationen i vänsterledet. Den första kvadreringsregeln kan vi även se på följande geometriska sätt, i alla fall då a och b är positiva. Vänsterledet i den översta ekvationen är arean av hela kvadraten med sidan a + b, högerledet är summan av arean av de fyra delar som kvadraten består av. Konjugatregeln och andra kvadreringsregeln kan på motsvarande sätt ges en geometrisk tolkning. Konjugatregeln är för övrigt ofta användbar, då det gäller att förenkla uttryck som innehåller rotuttryck i nämnaren, vilket illustrerades på sida. Faktorisering genom utbrytning xy x y = x y x x y = xy ( x) = xy( x) (x + y) + xz + yz = (x + y) + z(x + y) = (x + y)( + z) Faktorisering genom användning av konjugat- och kvadreringsreglerna 4s t = (s + t)(s t) 8a + a + = ( a + 6a + ) = (a + ) (x + ) 4y = (x + + y) (x + y)
11 Repetitionsuppgifter inför Matematik Ekvationslösning är vad det låter som. Det handlar om att finna samtliga tal som uppfyller en given ekvation. Exempel Lös ekvationen x = 4 ( x) Ekvationen kan skrivas x = 0 x. Vi möblerar om, så att alla x hamnar på ena sidan och alla konstanter på den andra sidan om likhetstecknet, och får ekvationen 4x = d.v.s. x = 4. Exempel Lös ekvationen x + = Samla konstanterna på högra sidan och gör liknämnigt, så fås x = = = Detta ger lösningen x =. Exempel Lös ekvationen (x ) (x 4) = (x 4) ( x) Vi observerar att faktorn (x 4) finns med i båda leden. Om x = 4 så blir alltså såväl höger- som vänsterled 0, d.v.s. x = 4 är en lösning. Om x 4 kan vi dividera båda leden med (x 4) och då erhålla ekvationen x = x, vilken har lösningen x =. Svaret blir att x = eller att x = 4. (Ett mycket vanligt fel är att man direkt dividerar båda leden med den gemensamma faktorn och erhåller ekvationen x = x. Då har man dock dessvärre tappat bort en lösning. Division med (x 4) förutsätter ju att x 4.).. Förenkla a) (x y) (4x+y) (6x 0y) (x+y) b) 6 ( x y ( y + 8 ) 6 x ).. Lös ekvationerna a) x = x b) 7z + = z (x + ) = 6 (x + ) d) x x = 0 e) 800 = f) x = Lös ekvationen (x + 8) (6 x) (4 x) (x + ) = 44
12 Andragradsekvationer Betrakta en allmän andragradsekvation x + px + q = 0 där p och q är konstanter. För att härleda en formel för ekvationens rötter, använder man sig av en omskrivning, som är mycket vanlig, då man arbetar med andragradsuttryck, nämligen kvadratkomplettering. Detta innebär att man samlar alla uttryck som innehåller x i en kvadrat, vilket kan ses geometriskt i nedanstående figur. Vi kan även se det algebraiskt genom att använda oss av första kvadreringsregeln: x + px + q = x + p x + q = x + p ( p ( p ) ( ) x + + q = x + p ) ( (p ) q ) ( Med denna omskrivning kan ekvationen x + px + q = 0 tecknas x + p ) ( p ) = q under ( p ) förutsättning att q 0. Då har ekvationen lösningarna x + p (p ) = ± p (p ) q, d.v.s. x = ± q.4. Tre på varandra följande positiva heltal (konsekutiva tal) har summan 4. Vilka är talen?.. Lös ekvationerna a) x + + x x 8 = b) x 4 = x + x 8 + x = d) x + x + x 4 x 6 = När man skall lösa ekvationen 6 ( x) = 48 nedan, är det enklast att först lösa ut ( x) och inte att multiplicera in i parentesen..6. Lös ekvationerna a) 6 ( x) = 48 b) 7 (x 7) = 4 4 x x 4 4 x =.7. Faktorisera följande uttryck så långt som möjligt: a) x 4 b) x 8x x d) x 0x +
13 Repetitionsuppgifter inför Matematik.8. Förenkla följande uttryck ) a) x y (y + x) b) z ( z.. Utför multiplikationerna a) (4y ) (y ) b) (x ) (4x x 6).0. Förenkla följande uttryck och beräkna därefter uttryckets värde för det angivna x- värdet. ( x a) 6 ) ( x 4 8 ) och x = 6 b) (x + ) (x 4x + ) (x x + ) och x =.. π betecknar ett tal som anger omkretsen av en cirkel med radien r =. π =,4... En cirkel med radien r har alltså omkretsen O = πr och dess area ges av A = πr. Beräkna en cirkels omkrets och area om a) r = b) r = r = π.. Utveckla och förenkla a) (x + 7) (x 7) b) (x + y) d) (x + ) + (x ) e) (4a + b) (4a b).. Uttrycket döljer ett heltal. Vilket?.4. Förenkla genom att förkorta a) 0a6 a.. Lös ekvationerna ( ) ( ) ( + 4 ) ( 4 + ) b) x + 6x x + 8a 4a + 8 a) x = b) (x ) = x = 6x d) (x ) + (x+) (x ) = (x+) (x+) (x+).6. Lös följande ekvationer: a) x + 4x + 4 = 0 b) x x 6 = 0 x x 8 = 0 d) x + x 0 = 0 e) x 0x + 8 = 0.7. Faktorisera följande uttryck så långt som möjligt: a) x x b) x + x + 0 x + x 7 d) 4 x x Kom ihåg följande regel: Om en produkt av två eller flera faktorer är noll, så måste minst en av faktorerna vara noll..8. Lös följande ekvationer: a) x (x + ) = 0 b) (x ) (x + ) = 0 x (x ) = 0 d) (x ) (x + 8) = 0.. Ekvationen x 4x + a = 0 har en rot x =. Bestäm a och den andra roten.
14 4 4 Facit. Facit: Räknesätt.. a) A = 0,7, B = 0,0, C = 0, b) A = 0,8, B =,0, C = 0,.. a) 0, b) 0,8 0,7 d) 0,8.. a) 8 b) 00 0 d) a) 0 b) 8 d) 0 e) 8 f) 0.. a) 0 b) 6 0 d) 6.6. a) b) 4 d) 8 e).7. a) 4 b) a) 0 b) d) 4.. a) 0,06 b) 0,06 8 d) 0.0. a) 0, b) 0,0, d).. a) 0, b) 0 d) 0,0.. a) 0,0 b) 7 0,0 d).. a) b) 0,00.4. a) 0,8 b) 0, 0,00 d) 0,77.. Det andra talet är 0,6..6. Den andra talet är 0,0..7.,0 kronor.8. kopior.. a) b) 7 7 d).0. a) b) 4 d) 7.. a) b) d).. a) = b) > > d) <.. a) > b) > < d) > 7.4. a) b) d) a) b) d) e) f) 0.6. Det andra talet är /.7. Andra faktorn är a) 7 b) 6.8. Talet är /0.. a) 7 0 b) 6 d) 7
15 Repetitionsuppgifter inför Matematik.0. a) a) a) 40 b) b) 6 48 b) 6 e) 6 f) dukar.. kronor per kilo ton sopor liter regn föll på gräsmattan g) d) 0 d) 0. Facit: Potenser och rötter.. a) 70 b) 0,0 0, d) 0.. a) b) d).. a) 0 b) 8 d).4. a) 00 b) 7 00 d) 7.. a) b) d) e) 0 f) 8 g) 0, h) x y i) 0, j) 0,.6. a) 00 b) d) a) b) 6 d) 7.8. a) 0,0 b) 0, d) e) 0.. a) 7 b) 4 64 d) a) b) 7 d) 4 e) 8 (.. 0, ( 0,) ), 0,0 ( 0 ) (, 0,008 (0,) 4) (, 0,0 ( 0,) ), 0,8 ((/0) ), 0,87 ( 87 0 ).. a) 000 b) d) 00.. a) 00 b) d) 000 e) 0,0 f) 0,0.4. a) b).. a) 4 b) 8 d) 6.6. a) = b) = 7 0 = d) = 4.7. a) b) 6 6 d)
16 6.8. a) 7 = 4 b) = 0 = 0 d) 6 = 6.. a) 0 b) 7 d) 6.0. a) b).. a) b).. a) 6 b) 7.. a) b) 00 0 d) 7 7 d).4. a), 0 b) 0 0,4 0 d) a) siffror b) siffror siffror d) 7 siffror.6. a) 0 8 b) d), a),6 0 b), d) a),6 0 7 b) 4 0 0, =, 8 =, =, 4 =, 7 =.0. a) b) 4 d) e) 4 f) 7.. a) 4 b) 6 0 d) 77 e) f).. a) ( ) + b) 6 + d) a) + b) d) ( ). Facit: Algebra.. a) 0 b) 0.. a) x = 4 b) z = 0 x = d) x = e) x = 600 f) x =.. x =.4. Talen är 7, 8 och.. a) x = b) x = x = 7 d) x =.6. a) x = 0 b) x = x =.7. a) (x 7) (x + 7) b) (x ) (x+) x ( x) (+x) d) (x ) 7.8. a) 0y b) z 6 = 7z.. a) 8y 6y + b) 8x 6x +x+0.0. a) Det förenklade uttrycket är x och antar värdet 0 då x =. b) Det förenklade uttrycket är x och antar värdet då x =... a) O = 4π, A = 4π b) O = 4π, A = 4π O = 6, A = π
17 Repetitionsuppgifter inför Matematik 7.. a) x 4 b) 4x +y +0xy d) 8x + 8 e) 80ab a) 4a b) x (a ).. a) x = ± b) x = 7 eller x = x = 0 eller x = 6 d) x = 7.6. a) x = eller x = b) x = eller x = x = 4 eller x = 7 d) x = eller x = e) x = eller x = 4.7. a) (x ) (x + ) b) (x + ) (x + 4) (x ) (x + 7) d) (x ) (x + 8).8. a) x = 0 eller x = b) x = eller x = x = 0 eller x =.. a = och den andra roten är x = 7 d) x = 8 eller x =
Repetitionsuppgifter inför Matematik 1-973G10. Matematiska institutionen Linköpings universitet 2014
 Repetitionsuppgifter inför Matematik - 7G0 Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 4 Facit Repetitionsuppgifter inför
Repetitionsuppgifter inför Matematik - 7G0 Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 4 Facit Repetitionsuppgifter inför
Repetitionsuppgifter i Matematik inför Basår. Matematiska institutionen Linköpings universitet 2014
 Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Algebra och rationella uttryck
 Algebra och rationella uttryck - 20 Uppgift nr Förenkla x0 y 6 z 5 25 y 2 Uppgift nr 2 Uppgift nr 3 ab b 5a - a² 9a där a 0. där b 0. Uppgift nr 4 Multiplicera in i parentesen 2x(4 + 2x 3 ) Uppgift nr
Algebra och rationella uttryck - 20 Uppgift nr Förenkla x0 y 6 z 5 25 y 2 Uppgift nr 2 Uppgift nr 3 ab b 5a - a² 9a där a 0. där b 0. Uppgift nr 4 Multiplicera in i parentesen 2x(4 + 2x 3 ) Uppgift nr
Repetitionsuppgifter i matematik
 Repetitionsuppgifter i matematik De fyra enkla räknesätten Här övar vi på de fyra räknesätten för hela tal (positiva och negativa), tal i bråkform och tal i decimalform Bestäm de tal på tallinjen, som
Repetitionsuppgifter i matematik De fyra enkla räknesätten Här övar vi på de fyra räknesätten för hela tal (positiva och negativa), tal i bråkform och tal i decimalform Bestäm de tal på tallinjen, som
Algebra, exponentialekvationer och logaritmer
 Höstlov Uppgift nr 1 Ge en lösning till ekvationen 0 434,2-13x 3 Ange både exakt svar och avrundat till två decimalers noggrannhet. Uppgift nr 2 Huvudräkna lg20 + lg50 Uppgift nr 3 Ge en lösning till ekvationen
Höstlov Uppgift nr 1 Ge en lösning till ekvationen 0 434,2-13x 3 Ange både exakt svar och avrundat till två decimalers noggrannhet. Uppgift nr 2 Huvudräkna lg20 + lg50 Uppgift nr 3 Ge en lösning till ekvationen
TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor
 TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor Johan Thim 22 augusti 2018 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför Q
TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor Johan Thim 22 augusti 2018 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför Q
Sammanfattningar Matematikboken Y
 Sammanfattningar Matematikboken Y KAPitel 1 TAL OCH RÄKNING Numeriska uttryck När man beräknar ett numeriskt uttryck utförs multiplikation och division före addition och subtraktion. Om uttrycket innehåller
Sammanfattningar Matematikboken Y KAPitel 1 TAL OCH RÄKNING Numeriska uttryck När man beräknar ett numeriskt uttryck utförs multiplikation och division före addition och subtraktion. Om uttrycket innehåller
Övning log, algebra, potenser med mera
 Övning log, algebra, potenser med mera Uppgift nr 1 Förenkla uttrycket x 3 + x 3 + x 3 + x 3 + x 3 Uppgift nr 2 Förenkla x x x+x x x Uppgift nr 3 Skriv på enklaste sätt x 2 x x x 8 x x x Uppgift nr 4 Förenkla
Övning log, algebra, potenser med mera Uppgift nr 1 Förenkla uttrycket x 3 + x 3 + x 3 + x 3 + x 3 Uppgift nr 2 Förenkla x x x+x x x Uppgift nr 3 Skriv på enklaste sätt x 2 x x x 8 x x x Uppgift nr 4 Förenkla
Studieplan och bedömningsgrunder i Matematik för åk 7 Moment Bedömningsgrunder för uppnåendemålen Begreppsbildning Tal och räkning
 Moment Begreppsbildning Mätningar och enheter Algebra och ekvationer Studieplan och bedömningsgrunder i Matematik för åk 7 Bedömningsgrunder för uppnåendemålen känna igen naturliga tal kunna positiva heltal:
Moment Begreppsbildning Mätningar och enheter Algebra och ekvationer Studieplan och bedömningsgrunder i Matematik för åk 7 Bedömningsgrunder för uppnåendemålen känna igen naturliga tal kunna positiva heltal:
Matematik EXTRAUPPGIFTER FÖR SKOLÅR 7-9
 Matematik EXTRAUPPGIFTER FÖR SKOLÅR 7-9 Matematik Extrauppgifter för skolår 7-9 Pärm med kopieringsunderlag. Fri kopieringsrätt inom utbildningsenheten! Författare: Mikael Sandell Copyright 00 Sandell
Matematik EXTRAUPPGIFTER FÖR SKOLÅR 7-9 Matematik Extrauppgifter för skolår 7-9 Pärm med kopieringsunderlag. Fri kopieringsrätt inom utbildningsenheten! Författare: Mikael Sandell Copyright 00 Sandell
TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter
 TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter Johan Thim 15 augusti 2015 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför
TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter Johan Thim 15 augusti 2015 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför
DOP-matematik Copyright Tord Persson Potenser. Matematik 1A. Uppgift nr 10 Multiplicera
 Potenser Uppgift nr Skriv 7 7 7 i potensform Uppgift nr 2 Vilket tal är exponent och vilket är bas i potensen 9 6? Uppgift nr 3 Beräkna värdet av potensen (-3) 2 Uppgift nr 4 Skriv talet 4 i potensform
Potenser Uppgift nr Skriv 7 7 7 i potensform Uppgift nr 2 Vilket tal är exponent och vilket är bas i potensen 9 6? Uppgift nr 3 Beräkna värdet av potensen (-3) 2 Uppgift nr 4 Skriv talet 4 i potensform
DOP-matematik Copyright Tord Persson. Potensform. Uppgift nr 10. Uppgift nr 11 Visa varför kan skrivas = 4 7
 Potensform Uppgift nr Vad menas i matematiken med skrivsättet 3 6? (Skall inte räknas ut.) Uppgift nr 2 värdet av potensen 3 2 Uppgift nr 3 Skriv 8 8 8 i potensform Uppgift nr 4 Skriv 4 3 som upprepad
Potensform Uppgift nr Vad menas i matematiken med skrivsättet 3 6? (Skall inte räknas ut.) Uppgift nr 2 värdet av potensen 3 2 Uppgift nr 3 Skriv 8 8 8 i potensform Uppgift nr 4 Skriv 4 3 som upprepad
1 Addition, subtraktion och multiplikation av (reella) tal
 Omstuvat utdrag ur R Pettersson: Förberedande kurs i matematik Addition, subtraktion och multiplikation av (reella) tal För reella tal gäller som bekant bl.a. följande räkneregler: (a + b) + c = a + (b
Omstuvat utdrag ur R Pettersson: Förberedande kurs i matematik Addition, subtraktion och multiplikation av (reella) tal För reella tal gäller som bekant bl.a. följande räkneregler: (a + b) + c = a + (b
Algebra, kvadreringsregler och konjugatregeln
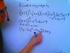 Algebra, kvadreringsregler och Uppgift nr 1 Multiplicera in i parentesen x(9 + 2y) Uppgift nr 2 Multiplicera in i parentesen 3x(7 + 5y) Uppgift nr 3 x² + 3x Uppgift nr 4 xy + yz Uppgift nr 5 5yz + 2xy
Algebra, kvadreringsregler och Uppgift nr 1 Multiplicera in i parentesen x(9 + 2y) Uppgift nr 2 Multiplicera in i parentesen 3x(7 + 5y) Uppgift nr 3 x² + 3x Uppgift nr 4 xy + yz Uppgift nr 5 5yz + 2xy
Lokala mål i matematik
 Lokala mål i matematik År 6 År 7 År 8 År 9 Taluppfattning (aritmetik) förstår positionssystemets uppbyggnad med decimaler ex: kan skriva givna tal adderar decimaltal ex: 15,6 + 3,87 subtraherar decimaltal
Lokala mål i matematik År 6 År 7 År 8 År 9 Taluppfattning (aritmetik) förstår positionssystemets uppbyggnad med decimaler ex: kan skriva givna tal adderar decimaltal ex: 15,6 + 3,87 subtraherar decimaltal
= a) 12 b) -1 c) 1 d) -12 [attachment:1]räkneoperation lektion 1.odt[/attachment] = a) 0 b) 2 c) 2 d) 1
![= a) 12 b) -1 c) 1 d) -12 [attachment:1]räkneoperation lektion 1.odt[/attachment] = a) 0 b) 2 c) 2 d) 1 = a) 12 b) -1 c) 1 d) -12 [attachment:1]räkneoperation lektion 1.odt[/attachment] = a) 0 b) 2 c) 2 d) 1](/thumbs/88/115435209.jpg) Lektion. + 8= 0 0. := 0 0. : = 8. : ( )= 8. 0/0 = 8. +(+ ) = 8. + = 0 8. ( )+0= 0 8. 8/ = - 0 8 0 0. = - - [attachment:]räkneoperation lektion.odt[/attachment]. = 0. /( )= - -. ( )= 0. 0 (0 0: )+ = 0.
Lektion. + 8= 0 0. := 0 0. : = 8. : ( )= 8. 0/0 = 8. +(+ ) = 8. + = 0 8. ( )+0= 0 8. 8/ = - 0 8 0 0. = - - [attachment:]räkneoperation lektion.odt[/attachment]. = 0. /( )= - -. ( )= 0. 0 (0 0: )+ = 0.
Matematik Uppnående mål för år 6
 Matematik Uppnående mål för år 6 Allmänt: Eleven ska kunna förstå, lösa samt redovisa problem med konkret innehåll inom varje avsnitt. Ha en grundläggande taluppfattning som omfattar naturliga tal och
Matematik Uppnående mål för år 6 Allmänt: Eleven ska kunna förstå, lösa samt redovisa problem med konkret innehåll inom varje avsnitt. Ha en grundläggande taluppfattning som omfattar naturliga tal och
Dra streck. Vilka är talen? Dra pil till tallinjen. Skriv på vanligt sätt. Sätt ut <, > eller =
 n se ta l l ta al u at sen nt al rat l r l d d n iotu se hun tiot a ent a hu t tu + + 7 tiotusental tusental 7 tiotal 7 7 7 7 Ju längre till höger, desto större är talet. 7 > 7 Siffran betyder tiotusental
n se ta l l ta al u at sen nt al rat l r l d d n iotu se hun tiot a ent a hu t tu + + 7 tiotusental tusental 7 tiotal 7 7 7 7 Ju längre till höger, desto större är talet. 7 > 7 Siffran betyder tiotusental
Blandade uppgifter om tal
 Blandade uppgifter om tal Uppgift nr A/ Beräkna värdet av (-3) 2 B/ Beräkna värdet av - 3 2 Uppgift nr 2 Skriv (3x) 2 utan parentes Uppgift nr 3 Multiplicera de de två talen 2 0 4 och 4 0 med varandra.
Blandade uppgifter om tal Uppgift nr A/ Beräkna värdet av (-3) 2 B/ Beräkna värdet av - 3 2 Uppgift nr 2 Skriv (3x) 2 utan parentes Uppgift nr 3 Multiplicera de de två talen 2 0 4 och 4 0 med varandra.
Uppfriskande Sommarmatematik
 Uppfriskande Sommarmatematik Matematiklärarna på Bäckängsgymnasiet genom Johan Espenberg juni 206 Välkommen till Naturvetenskapsprogrammet GRATTIS till din plats på Naturvetenskapsprogrammet på Bäckängsgymnasiet!
Uppfriskande Sommarmatematik Matematiklärarna på Bäckängsgymnasiet genom Johan Espenberg juni 206 Välkommen till Naturvetenskapsprogrammet GRATTIS till din plats på Naturvetenskapsprogrammet på Bäckängsgymnasiet!
Sammanfattningar Matematikboken Z
 Sammanfattningar Matematikboken Z KAPitel procent och statistik Procent Ordet procent betyder hundradel och anger hur stor del av det hela som något är. Procentform och 45 % = 0,45 6,5 % = 0,065 decimalform
Sammanfattningar Matematikboken Z KAPitel procent och statistik Procent Ordet procent betyder hundradel och anger hur stor del av det hela som något är. Procentform och 45 % = 0,45 6,5 % = 0,065 decimalform
Sammanfattningar Matematikboken X
 Sammanfattningar Matematikboken X KAPITEL 1 TAL OCH RÄKNING Naturliga tal Med naturliga tal menas talen 0, 1,,, Jämna tal 0,,, 6, 8 Udda tal 1,,, 7 Tallinje Koordinater En tallinje kan t ex användas för
Sammanfattningar Matematikboken X KAPITEL 1 TAL OCH RÄKNING Naturliga tal Med naturliga tal menas talen 0, 1,,, Jämna tal 0,,, 6, 8 Udda tal 1,,, 7 Tallinje Koordinater En tallinje kan t ex användas för
Sidor i boken 110-113, 68-69 2, 3, 5, 7, 11,13,17 19, 23. Ett andragradspolynom Ett tiogradspolynom Ett tredjegradspolynom
 Sidor i boken 110-113, 68-69 Räkning med polynom Faktorisering av heltal. Att primtalsfaktorisera ett heltal innebär att uppdela heltalet i faktorer, där varje faktor är ett primtal. Ett primtal är ett
Sidor i boken 110-113, 68-69 Räkning med polynom Faktorisering av heltal. Att primtalsfaktorisera ett heltal innebär att uppdela heltalet i faktorer, där varje faktor är ett primtal. Ett primtal är ett
Sidor i boken V.L = 8 H.L. 2+6 = 8 V.L. = H.L.
 Sidor i boken 119-11 Andragradsekvationer Dagens tema är ekvationer, speciellt andragradsekvationer. Men först några ord om ekvationer i allmänhet. En ekvation är en likhet som innehåller ett (möjligen
Sidor i boken 119-11 Andragradsekvationer Dagens tema är ekvationer, speciellt andragradsekvationer. Men först några ord om ekvationer i allmänhet. En ekvation är en likhet som innehåller ett (möjligen
Ekvationer och system av ekvationer
 Modul: Undervisa matematik utifrån problemlösning Del 4. Strategier Ekvationer och system av ekvationer Paul Vaderlind, Stockholms universitet Ekvationslösning är ett av de viktiga målen i skolmatematiken.
Modul: Undervisa matematik utifrån problemlösning Del 4. Strategier Ekvationer och system av ekvationer Paul Vaderlind, Stockholms universitet Ekvationslösning är ett av de viktiga målen i skolmatematiken.
Matematik Betygskriterier i matematik år 9 Ekholmsskolan i Linköping
 Enhet 591 Ekholmen Matematik Betygskriterier i matematik år 9 Ekholmsskolan i Linköping Fakta Förståelse Färdighet Förtrogenhet De olika formerna samspelar och utgör varandras förutsättningar. För att
Enhet 591 Ekholmen Matematik Betygskriterier i matematik år 9 Ekholmsskolan i Linköping Fakta Förståelse Färdighet Förtrogenhet De olika formerna samspelar och utgör varandras förutsättningar. För att
Kap 1: Aritmetik - Positiva tal - " - " - " - " - - " - " - " - " -
 År Startvecka Antal veckor 2013 34 18 Planering för ma 1b/c - ma 5000- boken OBS: För de i distansgruppen, meddela lärare innan prov. (justeringar för 1c ännu ej genomförda) Vecka Lektio n (2h) Datum Kapitel
År Startvecka Antal veckor 2013 34 18 Planering för ma 1b/c - ma 5000- boken OBS: För de i distansgruppen, meddela lärare innan prov. (justeringar för 1c ännu ej genomförda) Vecka Lektio n (2h) Datum Kapitel
8-3 Kvadreringsreglerna och konjugatregeln. Namn:
 8-3 Kvadreringsreglerna och konjugatregeln. Namn: Inledning I kapitlet med matematiska uttryck lärde du dig hur man förenklade ett uttryck med en faktor framför en parentes genom att multiplicera varje
8-3 Kvadreringsreglerna och konjugatregeln. Namn: Inledning I kapitlet med matematiska uttryck lärde du dig hur man förenklade ett uttryck med en faktor framför en parentes genom att multiplicera varje
Konsten att lösa icke-linjära ekvationssystem
 Konsten att lösa icke-linjära ekvationssystem Andreas Axelsson Vi beskriver här de grundläggande teknikerna för att lösa icke-linjära ekvationssystem. Detta är en nödvändig kunskap för att kunna lösa diverse
Konsten att lösa icke-linjära ekvationssystem Andreas Axelsson Vi beskriver här de grundläggande teknikerna för att lösa icke-linjära ekvationssystem. Detta är en nödvändig kunskap för att kunna lösa diverse
FÖRBEREDANDE KURS I MATEMATIK 1
 FÖRBEREDANDE KURS I MATEMATIK 1 Till detta kursmaterial finns prov och lärare på Internet Ger studiepoäng Kostnadsfritt Fortlöpande anmälan på wwwmathse Eftertryck förbjudet utan tillåtelse 2007 MATHSE
FÖRBEREDANDE KURS I MATEMATIK 1 Till detta kursmaterial finns prov och lärare på Internet Ger studiepoäng Kostnadsfritt Fortlöpande anmälan på wwwmathse Eftertryck förbjudet utan tillåtelse 2007 MATHSE
Uppföljning av diagnostiskt prov HT-2016
 Uppföljning av diagnostiskt prov HT-0 Avsnitt Ungefärligen motsvarande uppgifter på diagnosen. Räknefärdighet. Algebra, ekvationer, 8 0. Koordinatsystem, räta linjer 8 0. Funktionerna ln och e.. Trigonometri
Uppföljning av diagnostiskt prov HT-0 Avsnitt Ungefärligen motsvarande uppgifter på diagnosen. Räknefärdighet. Algebra, ekvationer, 8 0. Koordinatsystem, räta linjer 8 0. Funktionerna ln och e.. Trigonometri
Lokal studieplan Matematik 3 8 = 24. Centrum för tvåspråkighet Förberedelseklass
 Lokal studieplan Matematik 3 8 = 24 Centrum för tvåspråkighet Förberedelseklass 1 Mål att sträva mot Skolan skall i sin undervisning i matematik sträva efter att eleven S11 utvecklar intresse för matematik
Lokal studieplan Matematik 3 8 = 24 Centrum för tvåspråkighet Förberedelseklass 1 Mål att sträva mot Skolan skall i sin undervisning i matematik sträva efter att eleven S11 utvecklar intresse för matematik
TAL OCH RÄKNING HELTAL
 1 TAL OCH RÄKNING HELTAL Avsnitt Heltal... 6 Beräkningar med heltal...16 Test Kan du?... 1, 27 Kapiteltest... 28 Begrepp addition avrundning bas differens division exponent faktor kvadratroten ur kvot
1 TAL OCH RÄKNING HELTAL Avsnitt Heltal... 6 Beräkningar med heltal...16 Test Kan du?... 1, 27 Kapiteltest... 28 Begrepp addition avrundning bas differens division exponent faktor kvadratroten ur kvot
Utvidgad aritmetik. AU
 Utvidgad aritmetik. AU Delområdet omfattar följande tio diagnoser som är grupperade i tre delar, negativa tal, potenser och närmevärden: AUn1 Negativa tal, taluppfattning AUn Negativa tal, addition och
Utvidgad aritmetik. AU Delområdet omfattar följande tio diagnoser som är grupperade i tre delar, negativa tal, potenser och närmevärden: AUn1 Negativa tal, taluppfattning AUn Negativa tal, addition och
Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning
 Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning Eleven skall år 1 Begrepp Jämförelse- och storleksord, t.ex. stor, större, störst. Positionssystemet
Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning Eleven skall år 1 Begrepp Jämförelse- och storleksord, t.ex. stor, större, störst. Positionssystemet
Planering för kurs A i Matematik
 Planering för kurs A i Matematik Läromedel: Holmström/Smedhamre, Matematik från A till E, kurs A Antal timmar: 90 (80 + 10) I nedanstående planeringsförslag tänker vi oss att A-kursen studeras på 90 klocktimmar.
Planering för kurs A i Matematik Läromedel: Holmström/Smedhamre, Matematik från A till E, kurs A Antal timmar: 90 (80 + 10) I nedanstående planeringsförslag tänker vi oss att A-kursen studeras på 90 klocktimmar.
Avsnitt 1, introduktion.
 KTHs Sommarmatematik Introduktion 1:1 1:1 Kvadratkomplettering Avsnitt 1, introduktion. Det här är en viktig teknik som måste tränas in. Poängen med kvadratkomplettering är att man direkt kan se om andragradsfunktionen
KTHs Sommarmatematik Introduktion 1:1 1:1 Kvadratkomplettering Avsnitt 1, introduktion. Det här är en viktig teknik som måste tränas in. Poängen med kvadratkomplettering är att man direkt kan se om andragradsfunktionen
Matematik Steg: Bas. Mål att sträva mot Mål Målkriterier Omdöme Åtgärder/Kommentarer
 Matematik Steg: Bas ha en grundläggande taluppfattning som omfattar naturliga tal och enkla tal i talområdet 0-10 bråk- och decimalform ordningstal upp till 5 ha en grundläggande rumsuppfattning och kunna
Matematik Steg: Bas ha en grundläggande taluppfattning som omfattar naturliga tal och enkla tal i talområdet 0-10 bråk- och decimalform ordningstal upp till 5 ha en grundläggande rumsuppfattning och kunna
Planering för matematik 2a OBS: Provdatumen är endast förslag, kontakta läraren innan du kommer och vill ha prov
 År Startvecka 2013 2 Planering för matematik 2a OBS: Provdatumen är endast förslag, kontakta läraren innan du kommer och vill ha prov Vecka Lektion (2h) Datum Kapitel Avsnitt 2 Ti 08-jan Kap 1: Räta linjen
År Startvecka 2013 2 Planering för matematik 2a OBS: Provdatumen är endast förslag, kontakta läraren innan du kommer och vill ha prov Vecka Lektion (2h) Datum Kapitel Avsnitt 2 Ti 08-jan Kap 1: Räta linjen
Tal Räknelagar Prioriteringsregler
 Tal Räknelagar Prioriteringsregler Uttryck med flera räknesätt beräknas i följande ordning: 1. Parenteser 2. Exponenter. Multiplikation och division. Addition och subtraktion Exempel: Beräkna 10 5 7. 1.
Tal Räknelagar Prioriteringsregler Uttryck med flera räknesätt beräknas i följande ordning: 1. Parenteser 2. Exponenter. Multiplikation och division. Addition och subtraktion Exempel: Beräkna 10 5 7. 1.
Södervångskolans mål i matematik
 Södervångskolans mål i matematik Mål som eleverna lägst ska ha uppnått i slutet av det första skolåret beträffande tal och taluppfattning kunna läsa av en tallinje mellan 0-20 kunna läsa och ramsräka tal
Södervångskolans mål i matematik Mål som eleverna lägst ska ha uppnått i slutet av det första skolåret beträffande tal och taluppfattning kunna läsa av en tallinje mellan 0-20 kunna läsa och ramsräka tal
Block 1 - Mängder och tal
 Block 1 - Mängder och tal Mängder Mängder och element Venndiagram Delmängder och äkta delmängder Union och snittmängd Talmängder Heltalen Z Rationella talen Q Reella talen R Räkning med tal. Ordning av
Block 1 - Mängder och tal Mängder Mängder och element Venndiagram Delmängder och äkta delmängder Union och snittmängd Talmängder Heltalen Z Rationella talen Q Reella talen R Räkning med tal. Ordning av
Linnéuniversitetet Institutionen för datavetenskap, fysik och matematik Per-Anders Svensson
 Linnéuniversitetet Institutionen för datavetenskap, fysik och matematik Per-Anders Svensson Tentamen i Matematikens utveckling, 1MA163, 7,5hp fredagen den 28 maj 2010, klockan 8.00 11.00 Tentamen består
Linnéuniversitetet Institutionen för datavetenskap, fysik och matematik Per-Anders Svensson Tentamen i Matematikens utveckling, 1MA163, 7,5hp fredagen den 28 maj 2010, klockan 8.00 11.00 Tentamen består
Uppdaterad 2003-10-14 Allmänt Läroplanens mål för matematik finns att ta del av för elever och målsmän på webbadressen: http://www.skolverket.se.
 Matematik Uppdaterad 2003-10-14 Allmänt Läroplanens mål för matematik finns att ta del av för elever och målsmän på webbadressen: http://www.skolverket.se. ADDITION, SUBTRAKTION, DIVISION OCH MULTIPLIKATION.
Matematik Uppdaterad 2003-10-14 Allmänt Läroplanens mål för matematik finns att ta del av för elever och målsmän på webbadressen: http://www.skolverket.se. ADDITION, SUBTRAKTION, DIVISION OCH MULTIPLIKATION.
Kunskapsmål och betygskriterier för matematik
 1 (1) 2009-0-12 Kunskapsmål och betygskriterier för matematik För betyget G i matematik skall eleven kunna utföra beräkningar, lösa problem samt se enklare samband utifrån de kunskapsmål som anges under
1 (1) 2009-0-12 Kunskapsmål och betygskriterier för matematik För betyget G i matematik skall eleven kunna utföra beräkningar, lösa problem samt se enklare samband utifrån de kunskapsmål som anges under
8-1 Formler och uttryck. Namn:.
 8-1 Formler och uttryck. Namn:. Inledning Ibland vill du lösa lite mer komplexa problem. Till exempel: Kalle är dubbelt så gammal som Stina, och tillsammans är de 33 år. Hur gammal är Kalle och Stina?
8-1 Formler och uttryck. Namn:. Inledning Ibland vill du lösa lite mer komplexa problem. Till exempel: Kalle är dubbelt så gammal som Stina, och tillsammans är de 33 år. Hur gammal är Kalle och Stina?
Ansvarig lärare: Maria Lindström eller , Camilla Sjölander Nordin eller
 Skolmatematiktenta LPGG05 Kreativ Matematik 21 april 2016 8.15 13.15 Hjälpmedel: - Ansvarig lärare: Maria Lindström 054-7002146 eller 070-5699283, Camilla Sjölander Nordin 054-7002313 eller 070-2907171
Skolmatematiktenta LPGG05 Kreativ Matematik 21 april 2016 8.15 13.15 Hjälpmedel: - Ansvarig lärare: Maria Lindström 054-7002146 eller 070-5699283, Camilla Sjölander Nordin 054-7002313 eller 070-2907171
Torskolan i Torsås Mars 2007. Matematik. Kriterier för betyget godkänd. Metoder: Arbetssätt. Muntligt. Problemlösning
 Torskolan i Torsås Mars 2007 Matematik Kriterier för betyget godkänd Metoder: Arbetssätt Ta ansvar för sin egen inlärning. Göra läxor. Utnyttja lektionstiden (lyssna, arbeta). Utnyttja den hjälp/stöd som
Torskolan i Torsås Mars 2007 Matematik Kriterier för betyget godkänd Metoder: Arbetssätt Ta ansvar för sin egen inlärning. Göra läxor. Utnyttja lektionstiden (lyssna, arbeta). Utnyttja den hjälp/stöd som
KW ht-17. Övningsuppgifter
 Övningsuppgifter Ht-2017 1 Innehållsförteckning: Taluppfattning, positionssystem s. 3 4 Räkning, prioriteringsregler s. 4 6 Tvåbassystemet s. 6-7 Avrundning och noggrannhet s. 8-11 Bråk s. 12-17 Decimaltal
Övningsuppgifter Ht-2017 1 Innehållsförteckning: Taluppfattning, positionssystem s. 3 4 Räkning, prioriteringsregler s. 4 6 Tvåbassystemet s. 6-7 Avrundning och noggrannhet s. 8-11 Bråk s. 12-17 Decimaltal
Tema: Pythagoras sats. Linnéa Utterström & Malin Öberg
 Tema: Pythagoras sats Linnéa Utterström & Malin Öberg Innehåll: Introduktion till Pythagoras sats! 3 Pythagoras sats! 4 Variabler! 5 Potenser! 5 Att komma tillbaka till ursprunget! 7 Vi bevisar Pythagoras
Tema: Pythagoras sats Linnéa Utterström & Malin Öberg Innehåll: Introduktion till Pythagoras sats! 3 Pythagoras sats! 4 Variabler! 5 Potenser! 5 Att komma tillbaka till ursprunget! 7 Vi bevisar Pythagoras
FÖRBEREDANDE KURS I MATEMATIK 1. Till detta kursmaterial finns prov och lärare på Internet.
 FÖRBEREDANDE KURS I MATEMATIK Till detta kursmaterial finns prov och lärare på Internet. Detta material är en utskrift av det webbaserade innehållet i wiki.math.se/wikis/forberedandematte Studiematerialet
FÖRBEREDANDE KURS I MATEMATIK Till detta kursmaterial finns prov och lärare på Internet. Detta material är en utskrift av det webbaserade innehållet i wiki.math.se/wikis/forberedandematte Studiematerialet
Andragradsekvationer. + px + q = 0. = 3x 7 7 3x + 7 = 0. q = 7
 Andragradsekvationer Tid: 70 minuter Hjälpmedel: Formelblad. Alla andragradsekvationer kan skrivas på formen Vilket värde har q i ekvationen x = 3x 7? + E Korrekt svar. B (q = 7) x + px + q = 0 (/0/0)
Andragradsekvationer Tid: 70 minuter Hjälpmedel: Formelblad. Alla andragradsekvationer kan skrivas på formen Vilket värde har q i ekvationen x = 3x 7? + E Korrekt svar. B (q = 7) x + px + q = 0 (/0/0)
Röd kurs. Multiplicera in i parenteser. Mål: Matteord. Exempel. 1 a) 4(x- 5) b) 5(3 + x) 3 Om 3(a + 4) = 36, vad är då 62 2 FUNKTIONER OCH ALGEBRA
 Röd kurs Mål: I den här kursen får du lära dig att: ~ multiplicera parenteser ~ använda kvadreringsregler ~ använda konjugatregeln ~ uttrycka formler på olika sätt Matteord första kvadreringsregeln andra
Röd kurs Mål: I den här kursen får du lära dig att: ~ multiplicera parenteser ~ använda kvadreringsregler ~ använda konjugatregeln ~ uttrycka formler på olika sätt Matteord första kvadreringsregeln andra
Tal och polynom. Johan Wild
 Tal och polynom Johan Wild 14 augusti 2008 Innehåll 1 Inledning 3 2 Att gå mellan olika typer av tal 3 3 De hela talen och polynom 4 3.1 Polynom........................... 4 3.2 Räkning med polynom...................
Tal och polynom Johan Wild 14 augusti 2008 Innehåll 1 Inledning 3 2 Att gå mellan olika typer av tal 3 3 De hela talen och polynom 4 3.1 Polynom........................... 4 3.2 Räkning med polynom...................
1Mer om tal. Mål. Grunddel K 1
 Mer om tal Mål När eleverna har studerat det här kapitlet ska de: kunna multiplicera och dividera med positiva tal mi ndre än veta vad ett negativt tal är kunna addera och subtrahera negativa tal kunna
Mer om tal Mål När eleverna har studerat det här kapitlet ska de: kunna multiplicera och dividera med positiva tal mi ndre än veta vad ett negativt tal är kunna addera och subtrahera negativa tal kunna
Manipulationer av algebraiska uttryck
 Manipulationer av algebraiska uttryck Valentina Chapovalova SMaL-kursen i Mullsjö 19 juni 2018 Kluring 1 Bestäm produkten (x a) (x b) (x c)... (x z) Lösning kluring 1 Bestäm produkten (x a) (x b) (x c)..
Manipulationer av algebraiska uttryck Valentina Chapovalova SMaL-kursen i Mullsjö 19 juni 2018 Kluring 1 Bestäm produkten (x a) (x b) (x c)... (x z) Lösning kluring 1 Bestäm produkten (x a) (x b) (x c)..
Delkursplanering MA Matematik A - 100p
 Delkursplanering MA1201 - Matematik A - 100p som du skall ha uppnått efter avslutad kurs Du skall kunna formulera, analysera och lösa matematiska problem av betydelse för vardagsliv och vald studieinriktning
Delkursplanering MA1201 - Matematik A - 100p som du skall ha uppnått efter avslutad kurs Du skall kunna formulera, analysera och lösa matematiska problem av betydelse för vardagsliv och vald studieinriktning
Övningshäfte 2: Komplexa tal
 LMA100 VT007 ARITMETIK OCH ALGEBRA DEL Övningshäfte : Komplexa tal Övningens syfte är att bekanta sig med komplexa tal. De komplexa talen, som är en utvidgning av de reella talen, kom till på 1400 talet
LMA100 VT007 ARITMETIK OCH ALGEBRA DEL Övningshäfte : Komplexa tal Övningens syfte är att bekanta sig med komplexa tal. De komplexa talen, som är en utvidgning av de reella talen, kom till på 1400 talet
Block 1 - Mängder och tal
 Block 1 - Mängder och tal Mängder Mängder och element Venndiagram Talmängder Heltalen Z Rationella talen Q Reella talen R Räkning med tal. Ordning av talen i R Intervall Absolutbelopp Olikheter 1 Prepkursen
Block 1 - Mängder och tal Mängder Mängder och element Venndiagram Talmängder Heltalen Z Rationella talen Q Reella talen R Räkning med tal. Ordning av talen i R Intervall Absolutbelopp Olikheter 1 Prepkursen
DIAMANT. NaTionella DIAgnoser i Matematik. Ett diagnosmaterial i matematik för skolåren årskurs F- 9. Anpassat till Lgr 11. Löwing januari 2013
 DIAMANT NaTionella DIAgnoser i Matematik Ett diagnosmaterial i matematik för skolåren årskurs F- 9 Anpassat till Lgr 11 Diamantmaterialets uppbyggnad 6 Områden 22 Delområden 127 Diagnoser Till varje Område
DIAMANT NaTionella DIAgnoser i Matematik Ett diagnosmaterial i matematik för skolåren årskurs F- 9 Anpassat till Lgr 11 Diamantmaterialets uppbyggnad 6 Områden 22 Delområden 127 Diagnoser Till varje Område
Tal Räknelagar. Sammanfattning Ma1
 Tal Räknelagar Prioriteringsregler I uttryck med flera räknesätt beräknas uttrycket i följande ordning: 1. Parenteser 2. Potenser. Multiplikation och division. Addition och subtraktion Exempel: 5 22 1.
Tal Räknelagar Prioriteringsregler I uttryck med flera räknesätt beräknas uttrycket i följande ordning: 1. Parenteser 2. Potenser. Multiplikation och division. Addition och subtraktion Exempel: 5 22 1.
Övningsblad 1.1 A. Bråkbegreppet. 1 Skugga. 2 Hur stor andel av figuren är skuggad? 3 Ringa in 2 av stjärnorna.
 Övningsblad 1.1 A Bråkbegreppet 1 Skugga 1 6 av figuren b) 2 3 av figuren 3 av figuren 4 2 Hur stor andel av figuren är skuggad? b) 3 Ringa in 2 av stjärnorna. 4 Skriv 20 valfria bokstäver och låt 1 av
Övningsblad 1.1 A Bråkbegreppet 1 Skugga 1 6 av figuren b) 2 3 av figuren 3 av figuren 4 2 Hur stor andel av figuren är skuggad? b) 3 Ringa in 2 av stjärnorna. 4 Skriv 20 valfria bokstäver och låt 1 av
Nästan allt omkring dig har underliggande matematik. En del anser att den bara ligger där och väntar
 Matematikplanering 7B Läsår 15/16 Nästan allt omkring dig har underliggande matematik. En del anser att den bara ligger där och väntar på att bli upptäckt. Mönster, statistik, överlevnad, evolution, mopeder
Matematikplanering 7B Läsår 15/16 Nästan allt omkring dig har underliggande matematik. En del anser att den bara ligger där och väntar på att bli upptäckt. Mönster, statistik, överlevnad, evolution, mopeder
Moment 1.15, 2.1, 2.4 Viktiga exempel 2.2, 2.3, 2.4 Övningsuppgifter Ö2.2ab, Ö2.3. Polynomekvationer. p 2 (x) = x 7 +1.
 Moment.5, 2., 2.4 Viktiga exempel 2.2, 2.3, 2.4 Övningsuppgifter Ö2.2ab, Ö2.3 Ett polynom vilket som helst kan skrivas Polynomekvationer p(x) = a 0 +a x+a 2 x 2 +...+a n x n +a n x n Talen a 0,a,...a n
Moment.5, 2., 2.4 Viktiga exempel 2.2, 2.3, 2.4 Övningsuppgifter Ö2.2ab, Ö2.3 Ett polynom vilket som helst kan skrivas Polynomekvationer p(x) = a 0 +a x+a 2 x 2 +...+a n x n +a n x n Talen a 0,a,...a n
Utdrag ur Sommarmatte
 Utdrag ur Sommarmatte Matematiska Vetenskaper 21 augusti 2008 Innehåll 1 Aritmetik och Algebra 3 1.1 Räkning med naturliga tal och heltal.................. 3 1.1.1 Naturliga tal..........................
Utdrag ur Sommarmatte Matematiska Vetenskaper 21 augusti 2008 Innehåll 1 Aritmetik och Algebra 3 1.1 Räkning med naturliga tal och heltal.................. 3 1.1.1 Naturliga tal..........................
Bråk. Introduktion. Omvandlingar
 Bråk Introduktion Figuren till höger föreställer en tårta som är delad i sex lika stora bitar Varje tårtbit utgör därmed en sjättedel av hela tårtan I nästa figur är två av sjättedelarna markerade Det
Bråk Introduktion Figuren till höger föreställer en tårta som är delad i sex lika stora bitar Varje tårtbit utgör därmed en sjättedel av hela tårtan I nästa figur är två av sjättedelarna markerade Det
lim 1 x 2 lim lim x x2 = lim
 Moment 8.-8. Viktiga eempel 8.,8.4-6,8.8,8.-,8.5,8.0 Övningsuppgifter Ö8.a, Ö8.cdef,Ö8.a,e,f, Ö8.4cde, Ö8.5d, Ö8.0- Gränsvärden Definition. Funktionen f har gränsvärdet G då går mot om vi kan få f) att
Moment 8.-8. Viktiga eempel 8.,8.4-6,8.8,8.-,8.5,8.0 Övningsuppgifter Ö8.a, Ö8.cdef,Ö8.a,e,f, Ö8.4cde, Ö8.5d, Ö8.0- Gränsvärden Definition. Funktionen f har gränsvärdet G då går mot om vi kan få f) att
PASS 2. POTENSRÄKNING. 2.1 Definition av en potens
 PASS. POTENSRÄKNING.1 Definition av en potens Typiskt för matematik är ett kort, lätt och vackert framställningssätt. Den upprepade additionen går att skriva kortare i formen där anger antalet upprepade
PASS. POTENSRÄKNING.1 Definition av en potens Typiskt för matematik är ett kort, lätt och vackert framställningssätt. Den upprepade additionen går att skriva kortare i formen där anger antalet upprepade
ÖVNINGAR I MATEMATIK. Göran Forsling. 14 april 2011
 ÖVNINGAR I MATEMATIK Göran Forsling 4 april 0 Förord. Tänker du börja studera på ett tekniskt/naturvetenskapligt program till hösten? Vill du ge dina studier en flygande start? I stort sett vilken teknisk/naturvetenskaplig
ÖVNINGAR I MATEMATIK Göran Forsling 4 april 0 Förord. Tänker du börja studera på ett tekniskt/naturvetenskapligt program till hösten? Vill du ge dina studier en flygande start? I stort sett vilken teknisk/naturvetenskaplig
Talmönster och algebra. TA
 Talmönster och algebra. TA Diagnoserna i området avser att kartlägga om eleverna kan upptäcka talmönster samt på olika sätt bearbeta algebraiska uttryck och ekvationer. Förståelse av koordinatsystem och
Talmönster och algebra. TA Diagnoserna i området avser att kartlägga om eleverna kan upptäcka talmönster samt på olika sätt bearbeta algebraiska uttryck och ekvationer. Förståelse av koordinatsystem och
Övningsblad 1.1 A. Tallinjer med positiva tal. 1 Skriv det tal som motsvaras av bokstaven på tallinjen.
 Övningsblad 1.1 A Tallinjer med positiva tal 1 Skriv det tal som motsvaras av bokstaven på tallinjen. A B C D E F 0 5 10 0 10 20 A = B = C = D = E = F = G H I J K L 30 40 50 100 G = H = I = J = K = L =
Övningsblad 1.1 A Tallinjer med positiva tal 1 Skriv det tal som motsvaras av bokstaven på tallinjen. A B C D E F 0 5 10 0 10 20 A = B = C = D = E = F = G H I J K L 30 40 50 100 G = H = I = J = K = L =
Lösa ekvationer på olika sätt
 Lösa ekvationer på olika sätt I denna aktivitet ska titta närmare på hur man kan lösa ekvationer på olika sätt. I kurserna lär du dig att lösa första- och andragradsekvationer exakt med algebraiska metoder.
Lösa ekvationer på olika sätt I denna aktivitet ska titta närmare på hur man kan lösa ekvationer på olika sätt. I kurserna lär du dig att lösa första- och andragradsekvationer exakt med algebraiska metoder.
Sidor i boken
 Sidor i boken 0- Dagens mängdträning gäller ekvationer. Med den algebraträning vi nu har i ryggen bör även de mest komplicerade ekvationerna gå att reda ut. Tillsammans med övningarna i föreläsning 6 täcker
Sidor i boken 0- Dagens mängdträning gäller ekvationer. Med den algebraträning vi nu har i ryggen bör även de mest komplicerade ekvationerna gå att reda ut. Tillsammans med övningarna i föreläsning 6 täcker
Avsnitt 3, introduktion.
 KTHs Sommarmatematik Introduktion 3:1 3:1 Avsnitt 3, introduktion. Teckenstudium Här tränas teckenstudium av polynom och rationella funktioner (som är kvoter av polynom). Metoden går ut på att man faktoriserar
KTHs Sommarmatematik Introduktion 3:1 3:1 Avsnitt 3, introduktion. Teckenstudium Här tränas teckenstudium av polynom och rationella funktioner (som är kvoter av polynom). Metoden går ut på att man faktoriserar
Faktorisering av polynomuttryck har alltid utgjort en väsentlig del av algebran.
 Per-Eskil Persson Visst kan man faktorisera x 4 +1 Att faktorisera polynom är inte alltid helt enkelt men inte dess mindre en väsentlig del av den algebra som elever möter i slutet av högstadiet och senare
Per-Eskil Persson Visst kan man faktorisera x 4 +1 Att faktorisera polynom är inte alltid helt enkelt men inte dess mindre en väsentlig del av den algebra som elever möter i slutet av högstadiet och senare
Ordlista 5A:1. term. faktor. täljare. nämnare. Dessa ord ska du träna. Öva orden
 Ordlista 5A:1 Öva orden Dessa ord ska du träna term Talen som du räknar med i en addition eller subtraktion kallas termer. faktor Talen som du räknar med i en multiplikation kallas faktorer. täljare Talet
Ordlista 5A:1 Öva orden Dessa ord ska du träna term Talen som du räknar med i en addition eller subtraktion kallas termer. faktor Talen som du räknar med i en multiplikation kallas faktorer. täljare Talet
Övningar i ekvationer
 i ekvationer Innehåll A. Addition och subtraktion B. Multiplikation och division C. Blandade räknesätt - prioritet D. Enkla förenklingar E. Parenteser F. Tillämpningar Detta häfte är till dig som läser
i ekvationer Innehåll A. Addition och subtraktion B. Multiplikation och division C. Blandade räknesätt - prioritet D. Enkla förenklingar E. Parenteser F. Tillämpningar Detta häfte är till dig som läser
Addition och subtraktion. Vilka uträkningar visas på tallinjerna nedan? Beräkna med huvudräkning 1 3 5 = 2 2 2 + 5 = 3 3 7 + 3 = 4 4 1 4 = 5 7 2 + 7 5
 OH 1 Addition och subtraktion Vilka uträkningar visas på tallinjerna nedan? 1 = 7 6 1 0 1 + = 7 6 1 0 1 7 + = 7 6 1 0 1 1 = 7 6 1 0 1 Beräkna med huvudräkning 8 6 6 8 7 + 7 8 9 7 9 1 8 10 1 + 0 Kopiering
OH 1 Addition och subtraktion Vilka uträkningar visas på tallinjerna nedan? 1 = 7 6 1 0 1 + = 7 6 1 0 1 7 + = 7 6 1 0 1 1 = 7 6 1 0 1 Beräkna med huvudräkning 8 6 6 8 7 + 7 8 9 7 9 1 8 10 1 + 0 Kopiering
BASPROBLEM I ENDIMENSIONELL ANALYS 1 Jan Gustavsson
 Matematikcentrum Matematik BASPROBLEM I ENDIMENSIONELL ANALYS Jan Gustavsson. Algebraiska förenklingar.. Reella andragradsekvationer.. Enkla rotekvationer - eventuellt med falsk rot.. Enkla absolutbeloppsproblem.
Matematikcentrum Matematik BASPROBLEM I ENDIMENSIONELL ANALYS Jan Gustavsson. Algebraiska förenklingar.. Reella andragradsekvationer.. Enkla rotekvationer - eventuellt med falsk rot.. Enkla absolutbeloppsproblem.
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 4. b) = 3 1 = 2
 Kapitel.1 101, 102 Exempel som löses i boken 10 a) x= 1 11+ x= 11+ 1 = 2 c) x= 11 7 x= 7 11 = 77 b) x= 5 x 29 = 5 29 = 6 d) x= 2 26 x= 26 2= 1 10 a) x= 6 5+ 9 x= 5+ 9 6= 5+ 5= 59 b) a = 8a 6= 8 6= 2 6=
Kapitel.1 101, 102 Exempel som löses i boken 10 a) x= 1 11+ x= 11+ 1 = 2 c) x= 11 7 x= 7 11 = 77 b) x= 5 x 29 = 5 29 = 6 d) x= 2 26 x= 26 2= 1 10 a) x= 6 5+ 9 x= 5+ 9 6= 5+ 5= 59 b) a = 8a 6= 8 6= 2 6=
Träningsuppgifter, gamla nationella prov i matematik(del B1) från Taluppfattning. Hashem Rezai, S:t Ilians skola, Västerås
 Taluppfattning 1. Vilket av följande tal är minst? Ringa in ditt svar. 2,9 2,98 2,998 2,889 2,89 (1/0) 2. Hur många miljoner visar miniräknaren? Svar: (1/0) 3. Vilket tal pekar pilen på? 31 32 33 Svar:
Taluppfattning 1. Vilket av följande tal är minst? Ringa in ditt svar. 2,9 2,98 2,998 2,889 2,89 (1/0) 2. Hur många miljoner visar miniräknaren? Svar: (1/0) 3. Vilket tal pekar pilen på? 31 32 33 Svar:
Introduktion. Exempel Övningar Lösningar 1 Lösningar 2 Översikt
 KTHs Sommarmatematik 2002 Exempel Övningar Lösningar 1 Lösningar 2 Översikt 1.1Introduktion Introduktion Avsnitt 1 handlar till att börja med om hantering av bråkstreck. Samtidigt ges exempel och övningar
KTHs Sommarmatematik 2002 Exempel Övningar Lösningar 1 Lösningar 2 Översikt 1.1Introduktion Introduktion Avsnitt 1 handlar till att börja med om hantering av bråkstreck. Samtidigt ges exempel och övningar
Repetitionsuppgifter 1
 Repetitionsuppgifter 1 Beräkna 1 a) 0,5 + 0,7 b) 0,45 + 1,6 c) 2,76 0,8 2 a) 4,5 10 b) 30,5 10 c) 0,45 1 000 3 Vilka av produkterna är a) större än 6 1,09 6 0,87 6 1 6 4,3 6 0,08 6 b) mindre än 6 4 Skriv
Repetitionsuppgifter 1 Beräkna 1 a) 0,5 + 0,7 b) 0,45 + 1,6 c) 2,76 0,8 2 a) 4,5 10 b) 30,5 10 c) 0,45 1 000 3 Vilka av produkterna är a) större än 6 1,09 6 0,87 6 1 6 4,3 6 0,08 6 b) mindre än 6 4 Skriv
Mallisivuja. Framåt med matematiken. Raimo Seppänen Tytti Kiiski
 Raimo Seppänen Tytti Kiiski Framåt med matematiken REPETITION OCH FÖRDJUPNING INFÖR LÅNG MATEMATIK I GYMNASIET OCH MATEMATIK FÖR KRÄVANDE UTBILDNING VID YRKESINSTITUT MFKA-KUSTANNUS OY HELSINKI 2010 Beställningar
Raimo Seppänen Tytti Kiiski Framåt med matematiken REPETITION OCH FÖRDJUPNING INFÖR LÅNG MATEMATIK I GYMNASIET OCH MATEMATIK FÖR KRÄVANDE UTBILDNING VID YRKESINSTITUT MFKA-KUSTANNUS OY HELSINKI 2010 Beställningar
4-5 Kvadrater och rotuttryck Namn:...
 4-5 Kvadrater och rotuttryck Namn:... Inledning Du har nu lärt dig en hel del om kvadrater i kapitlet om ytorparallellogrammer. Du lärde dig bland annat att om kvadratens sida var given, säg 5 cm så kan
4-5 Kvadrater och rotuttryck Namn:... Inledning Du har nu lärt dig en hel del om kvadrater i kapitlet om ytorparallellogrammer. Du lärde dig bland annat att om kvadratens sida var given, säg 5 cm så kan
Matematiska uppgifter
 Elementa Årgång 67, 984 Årgång 67, 984 Första häftet 3340. a) Vilket av talen A = 984( + + 3 + + 984 ) är störst? b) Vilket av talen B 3 = 3 + 3 + 3 3 + + 984 3 är störst? A / = 984( + + 3 + + 984) B =
Elementa Årgång 67, 984 Årgång 67, 984 Första häftet 3340. a) Vilket av talen A = 984( + + 3 + + 984 ) är störst? b) Vilket av talen B 3 = 3 + 3 + 3 3 + + 984 3 är störst? A / = 984( + + 3 + + 984) B =
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Språkstart Matematik Facit. Matematik för nyanlända. Jöran Petersson
 Språkstart Matematik Facit Matematik för nyanlända Jöran Petersson Positionssystem hela tal s. 4-5 3. Skriv med siffror. 52 502 5002 65 665 6665 31 131 3131 4. Skriv hur mycket siffran är värd. 300 4 1000
Språkstart Matematik Facit Matematik för nyanlända Jöran Petersson Positionssystem hela tal s. 4-5 3. Skriv med siffror. 52 502 5002 65 665 6665 31 131 3131 4. Skriv hur mycket siffran är värd. 300 4 1000
Föreläsning 3: Ekvationer och olikheter
 Föreläsning 3: Ekvationer och olikheter En ekvation är en likhet som innehåller en flera obekanta storheter. Exempel: x = 9, x är okänd. t + t + 1 = 7, t är okänd. Vi säger att ett värde på den obekanta
Föreläsning 3: Ekvationer och olikheter En ekvation är en likhet som innehåller en flera obekanta storheter. Exempel: x = 9, x är okänd. t + t + 1 = 7, t är okänd. Vi säger att ett värde på den obekanta
Ekvationer och olikheter
 Kapitel Ekvationer och olikheter I kapitlet bekantar vi oss med första och andra grads linjära ekvationer och olikheter. Vi ser också på ekvationer och olikheter med absolutbelopp och kvadratrötter. När
Kapitel Ekvationer och olikheter I kapitlet bekantar vi oss med första och andra grads linjära ekvationer och olikheter. Vi ser också på ekvationer och olikheter med absolutbelopp och kvadratrötter. När
Talmängder. Målet med första föreläsningen:
 Moment 1..1, 1.., 1..4, 1..5, 1.. 1..5, 1..6 Viktiga exempel 1.7, 1.8, 1.8,1.19,1. Handräkning 1.7, 1.9, 1.19, 1.4, 1.9 b,e 1.0 a,b Datorräkning 1.6-1.1 Målet med första föreläsningen: 1 En första kontakt
Moment 1..1, 1.., 1..4, 1..5, 1.. 1..5, 1..6 Viktiga exempel 1.7, 1.8, 1.8,1.19,1. Handräkning 1.7, 1.9, 1.19, 1.4, 1.9 b,e 1.0 a,b Datorräkning 1.6-1.1 Målet med första föreläsningen: 1 En första kontakt
Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen.
 Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
Matematik CD för TB = 5 +
 Föreläsning 4 70 a) Vi delar figuren i två delar, en triangel (på toppen) och en rektangel. Summan av dessa två figurers area ger den eftersökta. Vi behöver följande formler: A R = b h A T = b h Svar:
Föreläsning 4 70 a) Vi delar figuren i två delar, en triangel (på toppen) och en rektangel. Summan av dessa två figurers area ger den eftersökta. Vi behöver följande formler: A R = b h A T = b h Svar:
5.6 MATEMATIK. Hänvisning till punkt 7.6 i Lpgr 16.1.2004
 5.6 MATEMATIK Hänvisning till punkt 7.6 i Lpgr 16.1.2004 Undervisningen i matematik skall hos eleverna utveckla det matematiska tänkandet, ge matematiska begrepp samt de mest använda lösningsmetoderna.
5.6 MATEMATIK Hänvisning till punkt 7.6 i Lpgr 16.1.2004 Undervisningen i matematik skall hos eleverna utveckla det matematiska tänkandet, ge matematiska begrepp samt de mest använda lösningsmetoderna.
LÖSNINGAR TILL ÖVNINGAR I FÖRBEREDANDE KURS I MATEMATIK 1. Till detta kursmaterial finns prov och lärare på Internet.
 LÖSNINGAR TILL ÖVNINGAR I FÖRBEREDANDE KURS I MATEMATIK Till detta kursmaterial finns prov och lärare på Internet. Detta material är en utskrift av delar av det webbaserade innehållet i wiki.math.se/wikis/forberedandematte
LÖSNINGAR TILL ÖVNINGAR I FÖRBEREDANDE KURS I MATEMATIK Till detta kursmaterial finns prov och lärare på Internet. Detta material är en utskrift av delar av det webbaserade innehållet i wiki.math.se/wikis/forberedandematte
Matematik. Ämnesprov, läsår 2013/2014. Bedömningsanvisningar Delprov B, C, D, E. Årskurs
 Ämnesprov, läsår 2013/2014 Matematik Bedömningsanvisningar Delprov B, C, D, E Årskurs 6 Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Ämnesprov, läsår 2013/2014 Matematik Bedömningsanvisningar Delprov B, C, D, E Årskurs 6 Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Avsnitt 2, introduktion.
 KTHs Sommarmatematik Introduktion 2:1 2:1 Bråkstreck Avsnitt 2, introduktion. Gemensamt bråkstreck. Två fall: Ingen gemensam faktor i nämnarna (Ex: ) Se Exempel 1 Gemensam faktor i nämnarna (Ex: ) Se Exempel
KTHs Sommarmatematik Introduktion 2:1 2:1 Bråkstreck Avsnitt 2, introduktion. Gemensamt bråkstreck. Två fall: Ingen gemensam faktor i nämnarna (Ex: ) Se Exempel 1 Gemensam faktor i nämnarna (Ex: ) Se Exempel
MA2047 Algebra och diskret matematik
 MA2047 Algebra och diskret matematik Något om komplexa tal Mikael Hindgren 17 oktober 2018 Den imaginära enheten i Det finns inga reella tal som uppfyller ekvationen x 2 + 1 = 0. Vi inför den imaginära
MA2047 Algebra och diskret matematik Något om komplexa tal Mikael Hindgren 17 oktober 2018 Den imaginära enheten i Det finns inga reella tal som uppfyller ekvationen x 2 + 1 = 0. Vi inför den imaginära
