Vardagsnära matematik i gymnasiet
|
|
|
- Sven Bergman
- för 8 år sedan
- Visningar:
Transkript
1 Institutionen för matematik och fysik Vardagsnära matematik i gymnasiet Mathematics with everyday applications Maria Carlsäter Ekdahl Examensarbete för lärarexamen I kunskapsområdet matematik VT Handledare: Hillevi Gavel Examinator: Sten Lindstam
2 Institutionen för matematik och fysik Examensarbete för lärarexamen i kunskapsområdet matematik MY1030, 10 poäng Sammanfattning Författarens namn: Maria Carlsäter Ekdahl Titel på examensarbetet: Vardagsnära matematik i gymnasiet Årtal: 2006 Antal sidor: 22 Examensarbetet fokuserar på användbarheten av vardagsnära eller verklighetsförankrad matematik, som ett sätt att göra skolmatematiken roligare, mer motiverande samt mer lättförståelig. För att fånga upp elevers och lärares intresse för samt syn på vardagsnära/verklighetsanknuten matematik har enkätundersökningar i fem gymnasieklasser samt fyra matematiklärarintervjuer genomförts. Undersökningarna är utförda i estetiska och samhällsvetenskapliga program. Eleverna som deltog i undersökningen läser gymnasieskolans A- eller B-kurs i matematik, på Carlforsska gymnasiet i Västerås. Resultaten visar att majoriteten av gymnasieeleverna löser matematiska problem mer eller mindre mekaniskt och accepterar resultatet om det överensstämmer med matematikbokens facit. En tydlig önskan från eleverna om mer varierande matematiklektioner samt en verklighetsförankring av matematiken framkom ur intervjuerna. 60% av killarna och 40% av tjejerna uppgav att de skulle kämpa mer för att förstå matematiken om de förstod vad de skulle använda den till i sin egen vardag. Nyckelord: Verklighetsförankrad, vardagsnära, matematik, gymnasiet 2
3 Innehållsförteckning Sammanfattning...2 Innehållsförteckning Introduktion Frågeställning och syfte Bakgrund Litteratur och teori Begreppet vardagsnära matematik Analys av litteraturen Metodologi Enkätundersökning Lärarintervjuer Sammanställning av resultaten Resultat Resultat från elevenkäterna Lärarprofiler Specialpedagog i matematik på gymnasiet (M1, man) Matematiklärare på gymnasiet (M2, man) Matematiklärare på gymnasiet (M3, man) Matematiklärare på gymnasiet (Q1, kvinna) Diskussion Trial-and-error en populär metod Tidsbrist begränsar undervisningen Prata matematik Verklighetsförankrad/vardagsnära matematik Elevers tro på nyttan av matematik Slutsatser Förslag till framtida forskning Förslag till förbättringar...21 Referenser...22 Bilaga 1. Elevenkäten Bilaga 2. Guide för lärarintervju
4 1. Introduktion Jag har vid flera tillfällen, under min verksamhetsförlagda del av lärarutbildningen, stött på elever i skolan som tappat lusten att lära sig matematik. Ett stort antal elever har uppvisat ett dåligt självförtroende beträffande skolmatematiken. Med en bristande tilltro till sin egen förmåga blir det självfallet också svårare att klara av uppgifterna. Under praktikperioder ute i skolan väcktes mitt intresse för att arbeta med matematik laborativt, praktiskt eller med verkliga problem. Genom att använda alternativa metoder till skolboken, kunde elevernas självkänsla och glädje inför matematik stärkas. Jag insåg att den klassiskt teoretiska skolmatematiken inte var den enda vägen att lära ut matematik. Kanske är den inte heller alltid den bästa? I mitt examensarbete har jag valt att fokusera runt en av dessa alternativa metoder att arbeta med matematik, för att göra matematiken mer lättförståelig, rolig och motiverande, nämligen vardagsanknuten eller verklighetsförankrad matematik. Jag är speciellt intresserad av att titta på förståelsen av matematik. Blir det enklare, roligare och/eller mer motiverande för eleverna att arbeta med matematik om den relateras till deras egen vardag? Kan vardagsanknuten matematik vara ett sätt att få eleverna att se samband mellan talen i boken och den verklighet vi lever i? Samtidigt uppstår problem runt frågor som vad vardagsanknuten matematik är och var gränsen går mellan abstrakt skolboksmatematik och praktisk matematik? För att få svar på dessa frågor har jag dels letat bland tidigare forskning, dels genomfört en undersökning i fem gymnasieklasser samt intervjuat fyra gymnasiematematiklärare. I litteraturdelen i bakgrunden till min uppsats går jag igenom en del av dessa frågor, med stöd av tidigare författares arbeten om vardagsnära matematik. Begreppet vardagsnära matematik behandlas särskilt under en egen rubrik. Därefter följer en kort genomgång av metodologin för mina studier, efter detta resultaten som framkommit ur mina studier. I diskussionsdelen återknyter jag resultaten från undersökningen till mina egna frågeställningar samt litteraturen och försöker binda samman uppsatsen och utvärdera vad som framkommit. 2. Frågeställning och syfte Frågeställningen uppsatsen bygger på är riktad till gymnasiet. Den skulle lika gärna kunna vara ställd till grundskolan, men jag har valt att titta på gymnasiet eftersom min uppfattning är att det är på gymnasiet som det i störst utsträckning lärs ut strikt skolboksbunden matematik. Uppsatsen fokuserar på frågan om vardagsanknuten och verklighetsnära matematik kan vara ett sätt att öka elevernas förståelse, motivation och glädje inför matematiken. Syftet med uppsatsen är följaktiligen att få ett svar på frågan. 4
5 3. Bakgrund Kursplanerna för matematik i gymnasiet har flera mål där vardagsanknytning av matematiken betonas. Därför kan inte användandet av metoder som gynnar förståelsen av hur matematiken kan användas i vardagen ifrågasättas. Frågan om användande av verklighetsförankrad/vardagsnära matematik är givetvis också relevant och viktig, i en tid då resultaten i matematik blir allt sämre. Går det att hitta en väg att göra matematiken roligare och mer lättförstådd för eleverna är det positivt. Verklighetsförankrad/vardagsnära matematik kan vara ett sätt att nå fram till fler elever, ett sätt att lyckas fördjupa kunskaperna inom matematik och öka förståelsen. Eftersom det är en viktig fråga finns det ett flertal artiklar runt ämnet. Litteratursammanfattningen nedan bygger på ett urval av de artiklar som jag ansåg var relevanta för min uppsats. 3.1 Litteratur och teori Traditionellt har skolmatematiken till stor del undervisats genom den akademiska matematiken (Riesbeck 2000). Även idag undervisas vanligen matematik strikt teoretiskt, vanligen så teoretiskt att eleverna mister förankringen av matematik till verkligheten (Wistedt 1992). Direkta tillämpningar av matematiken i skolans värld har förekommit sparsamt genom historien (läs t.ex. Wistedt, 1992, s.8-15). I en rapport från Skolverket (2003) framgår det att eleverna lär sig bäst när matematiken är relevant, begriplig och verklighetsanknuten. Dessutom ska den vara varierad, flexibel och undvika monoton räkning. Läroplanen för grundskolan talar om att Undervisningen i matematik skall utgå från elevernas erfarenheter och behov och den ska vara så konkret, att varje elev kan förankra begreppen och förstå användningen i praktiska situationer (Lgr 80). Kursplanen för Matematik A på gymnasiet innehåller elva olika mål som eleverna skall ha uppnått efter avslutad kurs. Fyra av dessa betonar en vardagsanknytning av matematiken: Eleven skall kunna formulera, analysera och lösa matematiska problem av betydelse för vardagsliv och vald studieinriktning. Eleven skall med och utan tekniska hjälpmedel med omdöme kunna tillämpa sina kunskaper i olika former av numerisk räkning med anknytning till vardagsliv och studieinriktning. Eleven skall ha fördjupat kunskaperna om geometriska begrepp och kunna tillämpa dem i vardagssituationer och i studieinriktningens övriga ämnen. Eleven skall kunna tolka och hantera algebraiska uttryck, formler och funktioner som krävs för problemlösning i vardagslivet och i studieinriktningens övriga ämnen. Uppenbarligen följer inte den traditionella undervisningen skolverkets riktlinjer eller läroplanens mål. Ytterligare aspekter på en traditionell skolboksundervisning, kontra andra former av matematikundervisning, lyfts fram av andra författare. Greer (1997) belyser hur svårt det är för eleverna att relatera en matematisk skoluppgift till verkligheten. Eleverna svarar ofta matematiskt korrekt utan att fundera över om svaret är tillämpbart i verkligheten. För att komma runt detta kan en lösning vara att ställa frågor som tvingar eleverna att fundera (Greer 1997). Exempel kan vara frågor som har flera lösningar eller frågor som innehåller fler eller färre faktorer än det behövs för att lösa problemet. Ett annat sätt kan vara att flytta ut 5
6 matematiken utanför klassrummet. Wänström (2003) visade på positiva resultat av detta som en djupare förståelse och att eleverna får använda flera sinnen. Samtidigt fanns negativa resultat t.ex. att det kan upplevas förvirrande för både lärare och elever att arbeta med matematik i en utomhusmiljö då de är vana att arbeta med matematiken traditionellt, samt att det är mer resurskrävande. Greer (1997) menar att eleverna tacklar ett matematiskt problem på ett realistiskt sätt i en verklig situation men inte i klassrummet. I klassrummet behövs det 3,25 bussar till 80 personer om varje buss tar 20 elever. I verkligheten behövs det fyra. Butterworth (1999) betonar att avancerad matematik ofta används i verkligheten. När sedan samma personer kommer till skolans artificiella miljö och frågan presenteras med en skolboksalgoritm kan de inte längre lösa den. Fördelen med en verklig miljö är att det är lättare att föreställa sig eller modellera situationen (Butterworth 1999). Det matematiska symbolspråket som traditionellt används inom matematiken gör det svårare för eleverna att anknyta matematiken till verkligheten (Riesbeck 2000). Det matematiska språket skapar på sätt och vis en värld för sig skild från elevernas vardag. Sammanhanget påverkar också hur en elev angriper ett matematiskt problem (Riesbeck 2000) Om eleverna får ett problem på en matematiklektion så antar de att de ska lösa uppgiften genom att räkna. Får de däremot uppgiften på en samhällsvetenskaplig lektion så löser de den ofta på ett helt annat sätt (Riesbeck 2000). Genom att integrera matematiken i andra ämnen eller arbeta tematiskt så uppmuntras flera olika sätt hos eleverna att lösa matematiska problem. Butterworth (1999) belyser ytterligare en aspekt med skolboksmatematik, nämligen att det alltför ofta inom skolmatematiken finns ett sätt att lösa uppgiften som är rätt och ett sätt som är fel. Den rätta är oftast lärarens effektiva, eleganta lösning och den felaktiga elevens lösning. Butterworth (1999) menar att detta minskar elevens lust att lära samt tilltro till sin egen förmåga. I Lusten att lära - med fokus på matematik (Skolverket 2003) lyfts det fram att matematikundervisningen och kunnande inom matematik skall bidra till självförtroende, kompetens och reella möjligheter att påverka och delta i vårt samhälle. Wistedt et. al. (1992) lyfter fram att det finns en bred enighet inom forskarvärlden att individernas vardagliga matematiska aktiviteter bör lyftas fram och utgöra grunden för matematikundervisningen. I Wistedts bok Att vardagsanknyta matematikundervisningen (1992) lyfter författaren fram flera olika argument för att knyta an matematiken till vardagen: Individers erfarenheter bör tas tillvara i skolan. Eleverna har rätt att känna igen sig i skolmiljön. Inlärningsteoretiska argument (Piaget 1941, Kegan 1968). Kegan (1968) skriver att all inlärning som inte har sin grund i redan förvärvade kunskaper är dömd att bli ylig och meningslös I debatten hävdas ofta att matematik lärs in bäst genom tillämpning. Kunskaper som utvecklats i ett sammanhang kan vara svåra att föra över till ett annat sammanhang om det inte finns en förankring till en vardaglig/verklig situation. Eleverna använder fler metoder att lösa ett problem än den strikt matematiskt korrekta. Samtidigt tar Wistedt (1992) upp en del av de motargument som finns mot vardagsanknuten matematik: 6
7 Det är önskvärt men inte alltid lätt att omsätta den teoretiska matematiken i praktiken. Eleverna bär inte nödvändigtvis med sig kunskap från vardagen som går att använda i undervisningssituationen. Wheat (1946) menar att det är naivt att tro att barnet ser matematiken i vardagen och menar att det är att förväxla den vuxnes och barnets situation. Problem kan dyka upp som att eleverna fastnar i vardagen och den matematiska diskussionen går förlorad. Eleverna kan fastna i praktiska moment av övningen och därmed missa övningen syfte. Ett exempel kan vara hur laboratorieutrustningen fungerar. Att en elev har kunskap i ett ämne betyder inte att eleven har lättare att förstå matematiken som exemplifieras genom just detta ämne. Wistedt menar att lärarna för att undkomma problemet med otillräckliga förkunskaper, inte kan ta elevernas förkunskaper för givna utan måste fråga efter vilka erfarenheter de enskilda eleverna faktiskt har och därefter bygga sin undervisning på en faktisk grund. Lärarna kan exempelvis knyta an till en situation i skolan så alla elever får samma förutsättningar (slöjdsalen, matematiklaboration, studiebesök etc.). Därmed får alla elever samma möjlighet att vinna erfarenheter med relevans för matematiken (Wistedt 1992). 3.2 Begreppet vardagsnära matematik Wistedt (1992) lyfter fram att det finns många olika begrepp ( konkretion, laborativ undervisning, vardagsanknytning, åskådliggöra ) för en vilja att åstadkomma samma sak, nämligen knyta ämnesstoffet till elevernas egna erfarenheter. Ord som vardag och verklighet används flitigt i den pedagogiska debatten runt matematikundervisning t.ex. vardagsanknuten eller verklighetsförankring (Wistedt et. al., 1992) och är också de ord jag valt att använda i min uppsats. Begreppen är dock problematiska som Wistedt (1992) lyfter fram. Ordet vardagskunskaper t.ex. är ett tvetydigt begrepp eftersom det används i två innebörder i debatten, dels för de kunskaper som individen formar i sitt vardagsliv men också för de kunskaper, färdigheter och kompetenser som individen anses behöva i sitt vardagsliv. Begreppet inkluderar därmed både kunskaper vunna i vardagen och kunskaper önskvärda i vardagen (Wistedt 1992). Ordet vardagsanknytning är ytterligare problematiskt genom att det dels kan beskriva hur enskilda elever använder sina vardagserfarenheter i undervisningen, dels kan det beskriva lärares ambitioner att knyta an till elevens kunskaper när de lär ut matematik (Wistedt 1992). Ordet har alltså både en inlärnings- och undervisningsaspekt. Perttu och Rondhal (2005) lyfter fram en ytterligare aspekt på begreppsförvirringen: Vems verklighet och vardag är det vi utgår från? Elevernas verklighet/vardag ser säkerligen inte likadan ut som lärarens! I min uppsats använder jag ordet vardagsanknuten när jag menar kunskapen är knuten till elevens egen vardag. Verklighetsförankrad använder jag som ett vidare begrepp när jag menar att kunskapen kan förankras till miljön utanför skolan, på ett enkelt och påtagligt sätt. 3.3 Analys av litteraturen I den litteratur som jag har läst och funnit relevant för mitt arbete framstår författarna eniga om att den traditionella skolboksmatematiken inte enbart bör nyttjas i undervisningen. Skolverkets riktlinjer och läroplanens mål stämmer väl överens med författarnas åsikter. En varierad, verklighetsanknuten undervisning framstår som bättre än en ensidig undervisning hårt knuten till skolboken. 7
8 Ett av motargumenten till tillämpad, verklighetsanknuten matematik som Wistedt (1992) och Wänström (2003) lyfter fram är att den matematiska diskussionen kan gå förlorad bland de mer praktiska momenten. Wistedt (1992) tog vidare upp problemet med elever som oreflekterat använder sitt vardagstänkande för att lösa problem och missar den matematiska diskussionen - eleverna fastnar i sin egen vardag. Wistedt (1992) menar dock att det måste gå att hitta en medelväg där det matematiska resonemanget inte går förlorat i en alltför praktiskt anpassad undervisning. Wistedt uttrycker detta som att vi bör skilja mellan vardagsmatematik och vardagsanknuten matematikundervisning. I det först fallet förblir undervisningen i vardagen där kunskaper används på ett oreflekterat sätt. I det senare fallet används vardagskunskaperna för att lära sig matematik. Vardagsanknuten matematik ska utgöra en brygga mellan det intuitiva tänkandet och det matematiska tänkandet (Wistedt 1992). Givetvis förekommer lärare som använder vardagen för mycket och hamnar vid sidan om ämnet (Wistedt 1992). Det är således en skör balansgång mellan att utnyttja det praktiska, verklighetsnära men inte förlora den renodlade matematiken! Lärarna kan med vardagliga uppgifter komma att ställas inför alternativa tolkningar av ett problem. Gränsen mellan rätt och fel svar blir mer diffus. En vardaglig tolkning av ett matematiskt problem kanske t.o.m. i vissa situationer är mer trolig i verkligheten. En löpare kan bli trött eller bryta foten efter halva loppet. En bil kan köra av vägen. Wistedt (1992) lyfter fram att det måste finnas utrymme för alternativa tolkningar av de vardagsnära matematiska problemen samt utrymme till diskussioner om lösningar. Det finns inom den vardagsanknutna matematiken inte längre strikt rätt och fel sätt att lösa en uppgift som det gör inom den traditionella skolboksmatematiken (Butterworth, 1999). Wistedt (1992) lyfter fram att det är viktigt att ta tillvara på elevernas egna intressen vid matematiklektioner, samtidigt som det inte nödvändigtvis betyder att det går lättare för eleverna att förstå matematiken. Att döma av de artiklar jag läst, gynnas nog ändå majoriteten av eleverna av en mer varierad och verklighetsförankrad matematikundervisning (Piaget 1941, Kegan 1968, Butterworth 1999, Wänström 2003 m.fl.). En förhoppning är ju att eleverna i alla fall tycker att det är roligare när de lär sig något som de kan relatera till sin egen vardag. Riesbeck (2000) lyfter också fram att eleverna löser samma uppgifter på olika sätt beroende på inom vilket skolämne de arbetar. Det borde vara en fördel att presentera matematikuppgifter i en annan miljö än den traditionella skolboksmiljön för att uppmuntra eleverna till att tänka i nya tankebanor. Greer (1997) belyser också hur svårt det är för eleverna att lösa en matematikuppgift i skolmiljön på ett reflekterande, vardagsnära sätt. Oftast, menade Greer (1997), löser eleverna uppgifterna matematiskt korrekt men oreflekterat medan de i vardagen löser samma problem genomtänkt. När jag läst igenom artiklarna inser jag att ett mål för matematikläraren under matematikundervisningen borde vara att rycka eleverna ur sina gamla, inlärda sätt att arbeta med matematik och tvinga eleverna att fundera på vad de egentligen gör. Ett sätt kan vara att som Greer (1997) beskriver i sin artikel Modelling reality in mathematics classrooms: the case of word problems att t.ex. använda ofullständiga frågor eller frågor med fler än en lösning eller att flytta matematiken ut utanför klassrummet. 8
9 4. Metodologi Metoderna som användes för att genomföra undersökningen var dels enkätundersökningar, dels friare intervjuer med fyra lärare. Undersökningsmetodiken behandlas mer detaljerat under följande rubriker. 4.1 Enkätundersökning En kvantitativ studie i form av en enkätundersökning utformades (bil. 1) och lämnades till fem utvalda klasser på Carlforsska gymnasiet (Västerås). Syftet med en enkätundersökning var att på en begränsad tid lyckas samla in en tillräckligt stor mängd data för att ha möjlighet att kunna dra vissa statistiska slutsatser (se ex. Cohen et. al. 2000). Enkäten testades först på en försöksgrupp, för att se om frågorna besvarades på det sätt jag förväntade mig. Efter testet modifierades en del frågor något för att bättre passa målgruppen. Utrymmen lämnades t.ex. på flera av frågorna för att ge möjlighet till unika svar från eleverna och därmed en kvalitativ vinkling på enkätundersökningen. Avsiktligen valdes samhällsvetenskapliga och estetiska klasser som oftast inte stötte på matematik i andra ämnen än just matematikämnet. Detta för att undvika elevgrupper som redan hade en naturlig förankring mellan skolboksmatematiken och en annan verklighet, t.ex. genom ett ämne som fysik. Klasserna som enkäterna besvarades av läste antingen A- eller B- kursen i matematik. I enkäterna samt i texten som behandlar resultat och diskussion har jag valt att använda mig av beteckningarna kille och tjej, eftersom jag bedömde det vara de beteckningar eleverna i denna ålderskategori föredrar. 4.2 Lärarintervjuer Som komplement till enkätundersökningen genomfördes också en kvalitativ studie i form av intervjuer med fyra gymnasiematematiklärare (varav en speciallärare). Intervjun skedde i en mer informell form (Cohen et. al. 2000), för att ge möjlighet att ställa följdfrågor och fånga upp intressanta frågor och svar som dök upp. De ämnen och frågor som behandlades i intervjun följde en intervjuguide (bil. 2). Jag skrev ner svaren och lät sedan den intervjuade läsa igenom svaren för att försäkra mig om att jag uppfattat henne/honom korrekt och att mina egna värderingar inte lyste igenom. Lärarna som intervjuades fick ut de frågor som skulle diskuteras en vecka innan studien genomfördes för att de skulle få en möjlighet att tänka igenom frågorna och sina egna ståndpunkter. Tre av de intervjuade lärarna hade jag haft kontakt med tidigare vilket bidrog till en avslappnad och naturlig intervjusituation (läs ex. Cohen et. al. 2000). 4.3 Sammanställning av resultaten Enkätundersökningens kvantitativa del sammanställdes i tabell- och diagramformat. I de kvalitativa delarna av enkätundersökningen försökte jag plocka ut och beskriva det som förenade eleverna samt särdragen. Lärarintervjuerna behandlades på samma sätt. I diskussionen analyseras och diskuteras det som framkommit med stöd av litteraturen. 9
10 5. Resultat Resultatet presenteras under två huvudrubriker, en som behandlar elevenkäterna och en som behandlar lärarintervjuerna. Resultatet från elevenkäterna presenteras främst i tabellformat, med en kort förklaring i text. Dessutom tillkommer elevkommentarerna, samt avvikande svar i texten. Lärarintervjuerna presenteras var för sig, där det som framkom under intervjun har skrivits ner. 5.1 Resultat från elevenkäterna Totalt svarade 133 elever på enkäten, fördelat på 5 olika program. Tre av klasserna gick på samhällsvetenskapliga program och de resterande på estetiska program. Resultaten presenteras i den ordning de besvarades i enkäten och kommenteras direkt under tabellen i de fall det krävs. 120 Svarsfrekvens Jag brukar använda den metod vi lärt oss använda för att lösa uppgiften Jag funderar på vad det står, vad uppgiften betyder i verkligheten och vilket sätt som är bäst att använda för att lösa uppgiften. Sedan räknar jag ut den på det sättet. Killar Tjejer 2 2 En annan strategi, nämligen: Figur 1. Frågan löd Hur brukar du vanligen lösa en uppgift i din matematikbok?. Två tjejer och två killar uppgav för den första frågan att de använde andra strategier än de angivna för att lösa uppgifter i matematikboken. De andra strategierna var att fråga en kompis eller titta på grannen, räkna i huvudet samt använda andra metoder som jag lärt mig tidigare. Som kommentarer hade tre elever dessutom skrivit kan även bli att man enbart kollar i facit om talet är svårt, kollar i facit, sen hittar en strategi för att räkna ut talet samt oftast den metod vi lärt oss i skolan, dock vid vissa tillfällen annan metod. 10
11 Svarsfrekvens När jag löst ett tal När jag räknat ut funderar jag på om uppgiften så tittar jag i svaret är rimligt. Om facit för att se om jag det verkar rimligt går har räknat rätt. Om det jag vidare till nästa tal. stämmer går jag vidare till nästa tal Killar Tjejer 2 Jag använder en annan strategi nämligen: * På frågan om hur eleverna kontrollerar sina lösta tal (fig. 2) uppgav två tjejer och två killar att de använde andra strategier än de angivna för att lösa uppgifter i matematikboken (fig. 2). De alternativa strategierna var att lösa talet och fundera på om det var rimligt först och därefter titta i facit (3 st.) samt att titta på grannen. Figur 2. Hur elever kontrollerar sina lösta tal. Frågan löd När du löst ett tal i matematikboken, hur försäkrar du dig om att det är rätt och rimligt svar?. Den tredje frågan (fig. 3) var följaktligen varför de valde detta sätt för att lösa matematikproblem. Noteras ska att det var möjligt att kryssa för flera svarsalternativ på denna fråga. Två Svarsfrekvens Det går fortast Jag förstår bäst då Det är roligast Jag har lärt mig göra så/vanesak Killar Tjejer Killar Tjejer Annan anledning,nämli gen: elever hade svarat en annan anledning, nämligen så slipper man göra fel på andra, har man rätt så går det enklare och räkna ut andra tal också samt osäkerhet. En elev hade kommenterat frågan med att hon löser ofta med facit, lär mig dock bättre genom att titta och se om det är rimligt. Figur 3. Varför använder eleverna den strategi de angav i uppgift 1 och 2 för att lösa talen? Svarsfrekvens Jag förstår oftast inte vad det betyder i verkligheten, men jag försöker lösa uppgifterna ändå med de metoder vi har lärt oss Det är olika. Killar Tjejer Jag brukar förstå uppgifterna i boken och ser ofta ett samband mellan uppgifter i matteboken och "verkligheten". I fråga fyra (fig. 4) fick eleverna svara på om de brukade se ett samband mellan talen i boken och verkligheten. Majoriteten av eleverna svarade att det var olika. Ett par av dessa elever kommenterade dock att de oftast inte förstod vad uppgifterna betydde i verkligheten men försökte lösa dem ändå. Figur 4. Om eleverna anser att de brukar se ett samband mellan uppgiften i matematikboken och verkligheten. 11
12 70 60 Svarsfrekvens Ja Kanske Nej Förstår redan det Killar Tjejer Figur 5. Anser eleverna att en förståelse av matematikens användbarhet i vardagen skulle göra matematiken roligare? På den femte frågan fick eleverna svara på om de trodde att de skulle tycka att det vara roligare med matematik om de förstod vad de skulle använda den till i sin egen vardag, samt om de skulle kämpa mer för att försöka förstå matematiken då (fig. 5 och 6). En absolut majoritet av eleverna ansåg att matematiken skulle vara roligare om de förstod vad de skulle använda matematiken till i sin vardag (fig. 5). Ett fåtal svarade på denna fråga att de förstod matematikens användbarhet i vardagen (6 resp. 9 % av killarna resp. tjejerna), vilket kan jämföras med 17 % i föregående fråga (fig. 5). Svarsfrekvens Ja Kanske Nej Förstår redan det Killar Tjejer På följdfrågan om eleverna skulle kämpa mer för att förstå matematiken om de förstod vad de skulle använda den till i sin egen vardag (fig. 6) var 60 % av killarna och 40 % av tjejerna positiva (siffrorna inkluderar de som svarat kanske ). Figur 6. Tror eleverna att de skulle kämpa mer för att förstå matematiken om de visste vad de skulle använda den till i sin egen vardag. 120 Svarsfrekvens Ja, ofta Ja, ofta Ibland Ibland Inte vad jag kan Jag tror inte det. Serie Figur 7. Om eleverna anser att de haft nytta av sina matematik-kunskaper i sin vardag (gråa staplar) eller tror att de kommer att ha nytta av dem i fram-tiden (vita staplar). 12
13 I fråga sex och sju (fig. 7) efterfrågades om eleverna tycker att de har haft (gråa staplar) eller tror att de kommer att ha (vita staplar) nytta av sina matematikkunskaper. Majoriteten av de svarande eleverna kryssade för ibland/i vissa situationer för båda alternativen (stapel 3 och 4). Eftersom det var jämnt fördelat mellan könen på denna fråga redovisas endast den totala siffran. Svarsfrekvens Undervisningen var mer varierad Tycker det är bra som det är Jag var bättre på matte Killar Tjejer Jag förstod användbarheten i vardagen 2 Jag vågade fråga mer om hjälp! 2 1 Övrigt Den näst sista frågan (fig. 8) handlade om vilka faktorer som eleverna ansåg vara de främsta för att göra matematiken roligare i vardagen. Här ska noteras att eleverna hade möjlighet att välja fler än ett svar. Figur 8. Vilka faktorer eleverna anser vara de främsta för att göra matematiken roligare i skolan. I enkäten hade också en del av eleverna lämnat kommentarer eller funderingar, speciellt under fråga nio, där jag efterfrågade deras egna synpunkter. Jag har valt ut ett antal kommentarer som jag anser är särskilt belysande eller representativa för enkätundersökningen. På övriga kommentarer hade flera elever kommenterat verklighetsförankring av matematik: Jag tror inte att jag kommer att använda matten, som vi läser nu, i vardagslivet (kille) Vi använder aldrig matten i vår vardag (kille) Använda matten praktiskt, inte bara räkna (tjej) Få exempel på hur matte används i vardagen då man kanske minst anar det (tjej) Ta exempel som vi ungdomar kan relatera till (kille) Vanligt var också kommentarer om att försöka göra matematiken roligare och mer varierad: Att göra matten lite mer praktisk och varierande så att det blir roligare (tjej) Ge exempel på olika sätt att lösa tal och variera undervisningen (tjej) En mattelärare måste kunna vara pedagogisk. Han/hon måste kunna förklara på många olika sätt! (tjej) Man ska göra lektionerna roliga, annars sitter eleverna bara och pratar. Men om man kan göra mattelektionerna roliga, tror jag att eleverna kommer uppskatta matte mera. Och inte skolka från lektionerna, dom kommer tycka om att gå dit. (tjej) Andra arbetssätt kanske skulle leda till roligare lektioner (kille) En annan vanlig kategori var förståelsen av matematik: Se till att alla förstår (tjej) Viktigt att inte ha krav att eleverna ska göra för många tal på lektionerna. Man lär sig inte då. (kille) 13
14 Jag brukar inte fråga efter hjälp nu. Jag är ganska dålig i matte. Men på grundskolan fick jag specialhjälp, då var matte roligare. Och specialhjälp får jag inte nu! (tjej) Matte är oftast roligast när man förstår. Så fort man kör fast tappar man lusten, hamnar efter i planeringen och blir ännu mer stressad. Mer individuella planer tycker jag vore bra (tjej) 5.2 Lärarprofiler Specialpedagog i matematik på gymnasiet (M1, man) M1 betonade vikten av samtalet, kontakten med eleverna och av att bygga upp relationer med eleverna. Eftersom han arbetar med små grupper har han möjlighet att arbeta med relationsskapande verksamhet och att samtala mycket med eleverna runt matematiska problem. M1 tyckte att det var viktigt för de elever han mötte att avdramatisera matematiken som ämnesområde. Positivt vore menade M1 om matematiken kunde lyftas in i andra ämnen eller att lyfta in vardagsmatematiken i klassrummet. M1 betonade hur många olika lärarpersonligheter det fanns och att eleverna framförallt var individer. Viktigt i hans egen undervisning tyckte M1 var kontakt och respekt byggd på förtroende och tillit. För att öka elevernas motivation trodde han att en väg kunde vara att få in så många sinnen som möjligt i undervisningen, t.ex. genom att arbeta med laborativt material. M1 själv arbetade mycket med laborativt material inom geometrin. Nackdelen menade han var att det tar mera tid vilket ofta är en bristvara både för eleverna och lärarna. M1 ansåg att färdigheter inom matematik övas upp genom att träna, öva, arbeta mycket och ofta även hemma. Han funderade på när förståelsen skulle komma in i bilden. M1 menade att matematiken från början måste grundas med övning, träning och inlärning av det matematiska språket. I detta skede menade han att förståelsen kanske inte var det mest centrala. M1 menade att många elever inte ser något användningsområde för den matematik de lär sig i skolan. Samtidigt trodde han att de matematiska färdigheterna skulle utvecklas när en elev väl hamnade i en situation där de behövdes. Verklighetsförankrad matematik såg han som något självklart positivt men något som dock kan vara svårt att realisera i klassrumsituationer. M1 såg det som en krydda i matematikundervisningen att förankra tal etc. till verkliga situationer men menade att det inte är säkert att det når fram till alla. Tvärtom kan en del elever tycka att det krånglar till det bara. Han menade att man måste använda olika språk för olika elever. Det största problemet han såg med dagens matematikundervisning var tidsbristen. M1 menade att det inte finns möjlighet att förklara för alla tillräckligt ingående i de storas grupper som råder i skolan idag. Han tryckte också på hur viktig elevernas egen motivation är för att klara kurserna Matematiklärare på gymnasiet (M2, man) M2 ansåg att det var bra att variera matematikundervisningen eftersom det var olika elevpersonligheter. Han menade också att det handlar mycket om elevernas vilja att förstå. M2 brukade vanligen lägga upp lektionen med en inledande genomgång och därefter fick eleverna själva öva. Han menade att ibland tvingas matematiklärarna blunda för förståelsen eftersom tiden är så begränsad. Som han uttryckte det: när man blir van i situationen kommer ibland förståelsen. 14
15 I sin undervisning tyckte han att det viktigaste var att så många elever som möjligt fick en grunduppfattning, en förståelse för det matematiska språket. Kurserna var för tighta menade han och han ansåg också att det därför rådde en brist på tillämpningar av matematiken. Tillämpad matematik tar mer tid ansåg han. Det var också svårt att hitta bra verklighetsförankrade exempel inom de teoretiska programmen menade han. M2 ansåg därför att det skulle vara bra och önskvärt att använda matematiken i andra kurser (bättre samarbete mellan ämnen) men att det är svårt i praktiken. Eleverna kunde inte inse användbarheten. För att öka elevernas motivation trodde han att en väg kunde vara att bryta den traditionella matematikundervisningen med tillämpade övningar. Då skulle eleverna också kunna inse användbarheten av matematik. Samtidigt betonade han att vissa elever känner motivation för abstrakt matematik medan andra inte gör det. M2 menade därför att det var viktigt med verklighetsförankrade problem men lika viktigt med problem som inte var det. M2 menade att majoriteten av hans elever angrep ett matematiskt problem genom trial-anderror tekniken. Vidare ansåg han att de flesta eleverna inte hade någon djupare förståelse för matematik samtidigt som han menade att det kunde vara svårt att få eleverna att arbeta om man betonade förståelsen. M2 betonade också att eleverna kunde ha nytta av matematiken även om de inte förstod alla tal eftersom de övade upp det logiska tänkandet Matematiklärare på gymnasiet (M3, man) M3 menade att många av gymnasieeleverna saknade en grund från grundskolan. Denna måste börja läggas redan i förskolan eller allra helst i hemmet, menade han. M3 hyste en rädsla för att lärare för de tidiga åldrarna inte var tillräckligt utbildade, intresserad och engagerade i skolämnet matematik. M3 tryckte på att eleverna ofta är intresserade av matematik i de lägre stadierna och måste fångas upp här så de inte förlorar sin motivation. M3 ansåg att många av de elever han undervisat saknar taluppfattning och använder miniräknare utan att fundera över rimligheten i det de räknar ut. Han saknade också tiden för den individuella hänsynen, som han uttryckte det, vid helklassundervisning. M3 hade föredragit nivågruppering, eftersom det då är lättare att anpassa sin undervisning till gruppen. I sin egen undervisning skulle han gärna blanda den teoretiska undervisningen med praktiska och laborativa inslag, gärna utanför klassrumsmiljön om han bara hade haft den tiden! M3 hade tidigare arbetat på ett annat sätt, under en period när han haft mer tid och mindre grupper. Då hade han varvat med laborativa, praktiska och verklighetsanpassade inslag. M3 menade att det hade ökat elevernas förståelse. En nackdel som han kunde se var att dagens elever var så vana att alltid arbeta mot skolboken att de kunde uppleva det svårt att arbeta på något annat sätt. Idag lade han vanligen upp sina lektioner med en teoretisk genomgång och därefter tid för eleverna att öva själva i skolboken. M3 hade önskat att läromedlet de använde innehöll uppgifter som eleverna lättare kunde relatera till. Idag menade han att det läromedel de använde var väldigt abstrakt för majoriteten av eleverna. M3 trodde att den absoluta majoriteten av eleverna löste matematiska problem genom trialand-error -metoden. Han menade att den främsta anledningen nog var att eleverna kände sig tidspressade. De ska hinna klart så många tal under varje lektion att det inte finns tid till eftertanke eller reflektion. M3 trodde inte att de elever som han undervisade hade någon förståelse för hur de kunde använda den matematik de lärde sig i sin vardag. Anledningen trodde han var att de inte sett det i undervisningen som är alltför abstrakt. 15
16 5.2.4 Matematiklärare på gymnasiet (Q1, kvinna) Q1 tryckte inledningsvis på hur svårt det var att ändra elevers attityder till matematik. Eleverna har så inpräntat i sig att matematik är svårt. Därför trodde hon att det var viktigt med ett resonemang runt matematik, i mindre grupper. Inte bara för att avdramatisera matematiken utan även för att få se var eleverna egentligen ligger och hur de resonerar kring matematik. Viktigast i sin egen undervisning tycket hon var först och främst att få mera tid! Om hon haft mer tid hade hon önskat genomföra fler praktiska övningar. Det hon betonade var ändå en bas, en grund för eleverna att stå på, att i alla fall kunna uppnå vissa delmål. Just nu kämpade hon med att lära en klass hela multiplikationstabellen (!). Q1 menade att det kanske skulle öka elevernas motivation om undervisningen innehöll fler praktiska moment, fler gruppövningar och problemlösning i grupp. Samtidigt berättade hon att hon använt mycket verklighetsanpassade problem i en Hv/mode-klass (som att räkna ut omkrets och area på tyg, dukar etc.). Q1 menade att det inte gett någon större motivation i klassen. Hon ansåg att det berodde mycket på klassens sammansättning vilken undervisning som fungerade. Q1 hade noterat att praktiska moment i undervisningen gagnade de medelduktiga och duktiga eleverna men oftast bara gjorde de svaga eleverna ännu mer förvirrade. De upplevde att hon bara krånglade till undervisningen. Q1 menade att vissa elever vill arbeta mot skolboken och att eleverna överlag var väldigt bundna till skolboken. Q1 brukade själv använda sig av olika läromedel för eleverna. T.ex. upplevde hon att vissa elever tyckte det var jobbigt med matematikböcker som innehöll för mycket text. Q1 trodde att majoriteten av eleverna angrep ett problem med trial-and-error metoden. Hon såg två orsaker till detta. Den först var att eleverna inte hade någon träning i att arbeta på andra sätt. Det andra att de inte har tid att reflektera över talen eftersom de oftast känner sig tidspressade under matematiklektionerna. Q1 tryckte också på att miniräknaren tar död på mycket av reflekterandet och rimlighetsantaganden i matematikinlärningen idag. Q1 hade inte ambitionen att eleverna ska förstå vad de ska använda matematiken till i vardagen utan att de ska lära sig hur man gör. Förståelsen, menade hon, kan komma senare. Q1 brukade ändå använda exempel ur vardagen som procent i affären, ränta på banken eller inom geometrin. Q1 trodde trots detta inte att eleverna själva kunde se nyttan av matematik i deras vardag. 16
17 6. Diskussion 6.1 Trial-and-error en populär metod Det viktigaste målet för matematiken måste vara att lära eleverna att tillämpa matematiken i verkligheten, inte ett meningslöst formelrabblande. Detta oavsett om eleverna ska fortsätta med matematiska/naturvetenskapliga studier på högre nivå eller väljer en annan bana. Ett problem med dagens matematikinlärning i skolan, som tydligt framkom i studien är att eleverna ofta löser övningar i läroboken mer eller mindre mekaniskt utan att diskutera eller fundera över slutsatserna från uppgiften. Ca 70 % av eleverna i studien angav att de löste matematikuppgifter med den metod de lärt sig i skolan (fig. 1) utan att reflektera vidare över alternativa metoder eller uppgiften som sådan. Eleverna löser uppgifterna för att få det svar som står angivet i facit (83 % av tjejerna, 73 % av killarna) inte för att förstå vägen dit (fig. 2). Från lärarintervjuerna var M2, M3 och Q1 också eniga om att de flesta eleverna löste talen oreflekterat genom trial-and-error tekniken! M2 ansåg att de flesta eleverna inte hade någon djupare förståelse för matematik samtidigt som M2 menade att det kunde vara svårt att få eleverna att arbeta om man betonade förståelsen. Det framstod för mig som att elevernas sätt att hantera matematikuppgifterna var ett utbrett men ganska accepterat problem. M1 och Q1 hade noterat att praktiska moment oftast bara gjorde de svaga eleverna ännu mer förvirrade. De upplevde att M1 och Q1 krånglade till undervisningen. Wänström (2003) belyser också denna förvirring som uppstår när elever som är vana att arbeta med matematik traditionellt plötsligt ska arbeta på ett annat sätt. Jag kan tänka mig att det säkert är svårt att helt plötsligt tvingas försöka förstå vad det är man egentligen gör! M3 hade under en tidigare, lugnare period varvat den traditionella undervisningen med laborativa, praktiska och verklighetsanpassade inslag. M3 menade att det hade ökat elevernas förståelse, men att eleverna var så vana att alltid arbeta mot skolboken att de kunde uppleva det svårt att arbeta på något annat sätt. Lärarna uppgav flera anledningar till att eleverna arbetade genomgående så oreflekterat med matematiken. De manliga lärarna framhävde i intervjuerna att den främsta anledningen nog var att eleverna kände sig tidspressade. De ska hinna klart så många tal under varje lektion att det inte finns tid till eftertanke eller reflektion. M3 menade att det också berodde på att eleverna inte hade någon träning i att arbeta på andra sätt. Q1 tryckte på att miniräknaren tar död på mycket reflekterande och rimlighetsantagande i matematikinlärningen idag. Jag tror också att ett problem för den matematiska förståelsen idag kan vara dagens datorsamhälle. Det är lätt att stoppa in siffror i en dator och få ut svaret eller att på högre nivå mata in vissa faktorer, låta datorn göra alla avancerade beräkningar och få ut en färdig modell. Men varför ser det ut som det gör? Vad var det som hände inne i datorn? Miniräknaren tar säkert död på en del av den matematiska förståelsen för gymnasister, liksom mer avancerade datorer säkerligen gör även på högre nivå! 6.2 Tidsbrist begränsar undervisningen När jag läser igenom lärarintervjuerna samt elevenkäterna inser jag hur tidspressad matematikundervisningen är. En fjärdedel av eleverna valde att lösa uppgifterna genom att räkna enligt den modell de lärt sig på lektionen, kontrollera mot facit och därefter angripa nästa tal för att det gick fortast (fig. 3). Samtliga lärare var rörande överens om att det största 17
18 problemet i matematikundervisningen var tidsbristen. Tre av lärarna (M1, M3 och Q1) önskade mer tid för att kunna genomföra verklighetsnära och tillämpad matematik. M2 instämde i uppfattningen att det tog mer tid om de lämnade matematikboken och använde mer praktiska exempel, men höll i högre grad fast vid nyttan av det traditionella sättet att arbeta. Under de matematiklektioner jag varit med på (tillsammans med M2 och Q1) har både lärarna och eleverna var pressade av att hinna igenom talen i kapitlet för att kunna fortsätta på nästa kapitel osv. Jag undrar om det viktiga egentligen är att göra många tal eller att göra några tal och förstå dem? Vitsen med matematik är ju egentligen inte att klara av att lösa en given uppgift med givna metoder att använda för att lösa den utan att utifrån en situation kunna göra vissa välgrundade antaganden och utifrån detta konstruera en modell för verkligheten. Läroplanen (Lgr80) talar också om att matematiken ska vara så konkret, att varje elev kan förankra begreppen och förstå användningen i praktiska situationer. En elev uttryckte just detta: Viktigt att inte ha krav att eleverna ska göra för många tal på lektionerna. Man lär sig inte då.. En annan elev påpekade att hon inte fick extra hjälp, fast hon behövde det. En tredje elev önskade fler individuella planer för att slippa känna stressen när man halkar efter i den allmänna planeringen. Jag tycker det verkar som att tidsbristen bidrar till att eleverna skyndar på i en så hög grad att deras förståelse för matematiken blir lidande. 6.3 Prata matematik För att lärarna ska lyckas öka elevernas förståelse för sambandet mellan matematik och verklighet tror jag att det krävs ett annat sätt att tackla matematiken. Den traditionella skolboksmatematiken kan vara bra för de repetitiva steg som krävs inom matematiken men bör kombineras med andra metoder. Gärna metoder som tar ner matematiken på jorden. Diskussionen runt matematiken i klassrummet är sådant viktigt inslag tror jag. Exempel på diskussionsämnen kan vara att låta eleverna att fundera över problem och inte bara lösa dem utan förståelse eller att lära eleverna att ställa sig kritiska frågor som: vad betyder detta i verkligheten? eller är det rimligt?. Greer (1997) tar upp vikten av att diskutera och ställa frågor som tvingar eleverna att fundera. Q1 betonade i intervjun hur viktigt det var med ett resonemang runt matematik. Q1 menade att detta var viktigt av två orsaker, dels för att avdramatisera matematiken som många anser är svår men också för att få en möjlighet att se vid vilken nivå eleverna egentligen befinner sig samt hur de resonerar kring matematik. M1 betonade också vikten av samtalet för att avdramatisera matematiken som ämnesområde men också för att bygga upp relationer till eleverna. Matematiken som sådan är ett eget språk som behöver behärskas för att kunna använda matematiken som ett verktyg och hjälpmedel till att hantera och förstå verkligheten. Riesbeck (2000) betonar hur det matematiska symbolspråket gör det svårare för eleverna att anknyta matematiken till verkligheten och därmed ytterligare avgränsar matematiken från elevernas vardag. Därför kan ju diskussionen runt matematik och matematiska problem fungera som ett sätt för eleverna att komma in i det matematikens värld. 6.4 Verklighetsförankrad/vardagsnära matematik Tre av de lärare jag intervjuat (M2, M3, Q1) arbetade idag väldigt traditionellt med matematik; först en genomgång, därefter fick eleverna arbeta självständigt med uppgifterna i matematikboken medan läraren gick runt i klassrummet och försökte hjälpa alla framåt. M1 18
19 arbetade inte speciellt bundet till boken, p.g.a. att M1 fungerade som speciallärare som eleverna själva fick söka upp honom under vissa tider för att få hjälp med tal. M1 arbetade mycket med laborativt material, försökte diskutera med eleverna samt ansträngde sig för att få in så många sinnen som möjligt i undervisningen. M1 såg verklighetsförankrad matematik som en krydda i matematikundervisningen, men menade att det inte är säkert att det når fram till alla. M1 skulle gärna integrera matematiken i andra ämnen eller lyfta in vardagsmatematiken i klassrummet. M2 ansåg också att det skulle vara önskvärt att integrera matematiken i andra ämnen, men att det var svårt i praktiken. Riesbeck (2000) påpekar att flera olika sätt hos eleverna att lösa matematiska problem uppmuntras genom att integrera matematiken i andra ämnen. Q1 menade att det kanske skulle öka elevernas motivation om undervisningen innehöll fler praktiska moment, fler gruppövningar och problemlösning i grupp, trots att det inte var Q1: s erfarenhet. M2 trodde att en väg att öka elevernas motivation kunde vara att bryta den traditionella matematikundervisningen med tillämpade övningar. Samtidigt betonade M2 att vissa elever känner motivation för abstrakt matematik medan andra inte gör det och att det var viktigt med verklighetsförankrade problem men lika viktigt med problem som inte var det. Jag kan instämma i detta men menar att problemet är att den abstrakta delen av undervisningen dominerar så totalt idag. I elevenkäten kom flera åsikter fram som antydde att eleverna önskade mer verklighetsförankrad/vardagsnära matematik. En tjej önskade använda matten praktiskt, inte bara räkna, en annan ville få exempel på hur matte används i vardagen då man kanske minst anar det och en kille önskade att läraren skulle ta exempel som vi ungdomar kan relatera till. Samtidigt var det bara en knapp femtedel av tjejerna och en fjärdedel av killarna som ansåg att en vardagsanknytning var en av de främsta orsakerna till att öka lusten till matematik (fig. 8). För tjejerna var den dominerande orsaken till olust att de ansåg sig vara dåliga på matematik, medan killarna främst efterfrågade mer varierade matematiklektioner. Mer varierande matematiklektioner efterfrågades som en nära tvåa för tjejerna (fig. 8). På frågan om vardagsnära matematik överhuvudtaget skulle vara roligare (fig. 5) svarade majoriteten av eleverna ja. 60 % av killarna och 40 % av tjejerna svarade dessutom att de troligen skulle kämpa mer för att förstå matematiken om det förstod vad de skulle använda den till i sin vardag (fig. 6), siffrorna inkluderar de som svarat kanske. Ungefär hälften av tjejerna och en tredjedel av killarna svarade dock att det inte skulle få dem att kämpa mer med matematiken. Slutsatsen kan ändå dras att om resultaten stämmer så skulle en vardagsnära matematik vara klart prestationshöjande i klassrummet. Q1 ansåg att det berodde mycket på klassens sammansättning vilken undervisning som fungerade. Q1 brukade själv använda sig av olika läromedel för eleverna, samt exempel ur vardagen som procent i affären, ränta på banken eller inom geometrin. M2 tyckte däremot att det var svårt att hitta bra verklighetsförankrade exempel inom de teoretiska programmen. M3 skulle gärna ha blandat den teoretiska undervisningen med praktiska och laborativa inslag om M3 bara hade haft den tiden! M3:s erfarenhet var att mer laborativa, praktiska och verklighetsanpassade inslag ökade elevernas förståelse. M3 hade önskat att läromedlet de använde innehöll uppgifter som eleverna lättare kunde relatera till. Idag menade M3 att det läromedel de använde var väldigt abstrakt för majoriteten av eleverna. I fråga fyra (fig. 4) i elevenkäten framkommer också att eleverna ofta anser att matematiken är alltför abstrakt och svår att relatera till verkligheten. En knapp femtedel av eleverna svarade att de brukade förstå uppgifterna i boken och ofta såg ett samband mellan uppgifterna och verkligheten. En väg att tillmötesgå elevernas önskan om en mer vardagsnära matematik kunde vara att ett läromedel togs fram som förankrade uppgifterna bättre till elevernas verklighet. Jag tror att ett sätt att klara av det kunde vara att ha speciella läromedel beroende på vilka program eller 19
20 kurser eleverna gick, samt att erbjuda eleverna att välja mellan flera olika läromedel på lektionerna. 6.5 Elevers tro på nyttan av matematik M1 menade att många elever inte ser något användningsområde för den matematik de lär sig i skolan och tryckte på hur viktig elevernas egen motivation är för att klara kurserna. M2 instämde i vikten av elevernas egen vilja att försöka förstå. M1 trodde att de matematiska färdigheterna skulle utvecklas när en elev väl hamnade i en situation där de behövdes. M2 och Q1 instämde i att den matematiska förståelsen kan komma senare i livet. M2 förklarade att matematiklärarna ibland tvingas blunda för förståelsen, eftersom tiden är så begränsad och menade att det t.o.m. kunde vara svårt att få eleverna att arbeta om man betonade förståelsen. Q1 hade inte överhuvudtaget ambitionen att eleverna skulle förstå vad de ska använda matematiken till i vardagen utan bara att de ska lära sig hur man gör. Varken M2, M3 eller Q1 trodde att eleverna själva kunde se nyttan av matematik i deras vardag eller hade någon förståelse för hur de kunde använda den matematik de lärde sig i sin vardag. M3 trodde att detta berodde på undervisningen är alltför abstrakt. M2 betonade dock att eleverna kunde ha nytta av matematiken även om de inte förstod alla tal eftersom de övade upp det logiska tänkandet. Eleverna instämde i lärarnas farhågor. En kille skrev vi använder aldrig matten i vår vardag. En annan kille drog det ännu längre: jag tror inte att jag kommer att använda matten, som vi läser nu, i vardagslivet. I elevenkäten var dock resultaten lite svårtolkade eftersom majoriteten av eleverna svarade att de trodde att de hade haft/kommer att ha nytta av matematik ibland/i vissa situationer (fig. 7). En knapp tiondel svarade att de använt matematiken ofta i sin egen vardag (fig.7), medan en knapp femtedel (17 %) svarade att de inte, vad de kunde minnas, hade haft nytta av matematiken i sin egen vardag. En femtedel trodde dock att de skulle få nytta av matematiken i framtiden, medan enbart 7 % svarade att de inte trodde att de skulle få nytta av matematiken i framtiden. Sammanfattningsvis verkar eleverna inte se hur de kan använda den matematik de lär sig i sin egen vardag, men hoppas kunna göra det i framtiden! 7. Slutsatser Jag har valt att summera de tydligaste och viktigaste slutsatserna från undersökningen punktvis, för att det ska bli så lättöverskådligt som möjligt. Majoriteten av eleverna löser matematikuppgifter mer eller mindre mekaniskt, utan att reflektera över vad de egentligen gör. Lärarna är medvetna om detta, men känner sig liksom eleverna oftast tidspressade vilket leder till att de ofta sätter förståelsen åt sidan till förmån för alla tal och moment som ska hinnas med. Lärarna upplever att det tar mer tid när de frångår boken och arbetar med mer verklighetsnära eller vardagsanknutna exempel. Lärarna menar också att ett arbetssätt som skiljer mycket från det traditionella skolboksbundna arbetssättet kan göra en del elever mer förvirrade. Eleverna efterfrågar mer varierande matematiklektioner, med inslag av praktiska och laborativa moment samt exempel de kan relatera till. 20
Kursplan för Matematik
 Sida 1 av 5 Kursplan för Matematik Inrättad 2000-07 SKOLFS: 2000:135 Ämnets syfte och roll i utbildningen Grundskolan har till uppgift att hos eleven utveckla sådana kunskaper i matematik som behövs för
Sida 1 av 5 Kursplan för Matematik Inrättad 2000-07 SKOLFS: 2000:135 Ämnets syfte och roll i utbildningen Grundskolan har till uppgift att hos eleven utveckla sådana kunskaper i matematik som behövs för
Rapport av genomförd "Lesson study" av en lektion med temat ekvationer i gymnasiets B-kurs. Bultar, muttrar och brickor
 Rapport av genomförd "Lesson study" av en lektion med temat ekvationer i gymnasiets B-kurs Bultar, muttrar och brickor Vågad problemlösning Förberedelser Ekvationssystem i matematik B ger progression från
Rapport av genomförd "Lesson study" av en lektion med temat ekvationer i gymnasiets B-kurs Bultar, muttrar och brickor Vågad problemlösning Förberedelser Ekvationssystem i matematik B ger progression från
När vi läste Skolverkets rapport Svenska elevers matematikkunskaper
 Florenda Gallos Cronberg & Truls Cronberg Två perspektiv på att utveckla algebraiska uttryck Svenska elever påstås ha svårt med mönstertänkande. Eller är det så att de inte får lärarledd undervisning i
Florenda Gallos Cronberg & Truls Cronberg Två perspektiv på att utveckla algebraiska uttryck Svenska elever påstås ha svårt med mönstertänkande. Eller är det så att de inte får lärarledd undervisning i
Matematikundervisning genom problemlösning
 Matematikundervisning genom problemlösning En studie om lärares möjligheter att förändra sin undervisning Varför problemlösning i undervisningen? Matematikinlärning har setts traditionell som en successiv
Matematikundervisning genom problemlösning En studie om lärares möjligheter att förändra sin undervisning Varför problemlösning i undervisningen? Matematikinlärning har setts traditionell som en successiv
Pedagogisk dokumentation kring Matematikverkstaden på Bandhagens skola.
 Pedagogisk dokumentation kring Matematikverkstaden på Bandhagens skola. Åh, nu förstår jag verkligen sa en flicka på 10 år efter att ha arbetat med bråk i matematikverkstaden. Vår femåriga erfarenhet av
Pedagogisk dokumentation kring Matematikverkstaden på Bandhagens skola. Åh, nu förstår jag verkligen sa en flicka på 10 år efter att ha arbetat med bråk i matematikverkstaden. Vår femåriga erfarenhet av
Verksamhetsrapport. Skolinspektionen. efter kvalitetsgranskning av undervisningen i matematik kurs 3c vid IT-gymnasiet Södertörn i Huddinge kommun
 Bilaga 1 Verksam hetsrapport 2015-02-18 Dnr 400-2014:2725 efter kvalitetsgranskning av undervisningen i matematik kurs 3c vid IT-gymnasiet Södertörn i Huddinge kommun 1 (8) Innehåll Inledning Bakgrundsuppgifter
Bilaga 1 Verksam hetsrapport 2015-02-18 Dnr 400-2014:2725 efter kvalitetsgranskning av undervisningen i matematik kurs 3c vid IT-gymnasiet Södertörn i Huddinge kommun 1 (8) Innehåll Inledning Bakgrundsuppgifter
Inkludering, utan exkludering, eller tack vare?
 Inkludering, utan exkludering, eller tack vare? Sedan en tid tillbaka pågår det livliga diskussioner kring inkludering och exkludering i samband med att man funderar kring särskilda undervisningsgrupper
Inkludering, utan exkludering, eller tack vare? Sedan en tid tillbaka pågår det livliga diskussioner kring inkludering och exkludering i samband med att man funderar kring särskilda undervisningsgrupper
Variation i matematikundervisningen
 Stefan Löfwall Karlstads universitet Variation i matematikundervisningen Idag diskuterar man mycket behovet av att variera matematikundervisningen. Inte minst betonas detta i Skolverkets rapport Lusten
Stefan Löfwall Karlstads universitet Variation i matematikundervisningen Idag diskuterar man mycket behovet av att variera matematikundervisningen. Inte minst betonas detta i Skolverkets rapport Lusten
Matematikutveckling med stöd av alternativa verktyg
 Matematikutveckling med stöd av alternativa verktyg Vad ska man ha matematik till? Vardagslivet Yrkeslivet Skönheten och konsten Underbart att veta att det finns räcker inte det+ LGR11 Undervisningen ska
Matematikutveckling med stöd av alternativa verktyg Vad ska man ha matematik till? Vardagslivet Yrkeslivet Skönheten och konsten Underbart att veta att det finns räcker inte det+ LGR11 Undervisningen ska
Tummen upp! Matte ÅK 6
 Tummen upp! Matte ÅK 6 Tummen upp! är ett häfte som kartlägger elevernas kunskaper i förhållande till kunskapskraven i Lgr 11. PROVLEKTION: RESONERA OCH KOMMUNICERA Provlektion Följande provlektion är
Tummen upp! Matte ÅK 6 Tummen upp! är ett häfte som kartlägger elevernas kunskaper i förhållande till kunskapskraven i Lgr 11. PROVLEKTION: RESONERA OCH KOMMUNICERA Provlektion Följande provlektion är
Pedagogisk planering i matematik; Tal i bråkform, decimalform och procentform. Ur Lgr 11 Kursplan i matematik.
 Pedagogisk planering i matematik; Tal i bråkform, decimalform och procentform. Ur Lgr 11 Kursplan i matematik. Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl
Pedagogisk planering i matematik; Tal i bråkform, decimalform och procentform. Ur Lgr 11 Kursplan i matematik. Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl
Ämnesblock matematik 112,5 hp
 2011-12-15 Ämnesblock matematik 112,5 hp för undervisning i grundskolans år 7-9 Ämnesblocket omfattar ämnesstudier inklusive ämnesdidaktik om 90 hp, utbildningsvetenskaplig kärna 7,5 hp och VFU 15 hp.
2011-12-15 Ämnesblock matematik 112,5 hp för undervisning i grundskolans år 7-9 Ämnesblocket omfattar ämnesstudier inklusive ämnesdidaktik om 90 hp, utbildningsvetenskaplig kärna 7,5 hp och VFU 15 hp.
Constanta Olteanu, Linnéuniversitetet och Anna-Lena Ekdahl, Högskolan i Jönköping
 Modul: Algebra Del 3: Bedömning för utveckling av undervisningen i algebra Intervju Constanta Olteanu, Linnéuniversitetet och Anna-Lena Ekdahl, Högskolan i Jönköping I en undervisning kan olika former
Modul: Algebra Del 3: Bedömning för utveckling av undervisningen i algebra Intervju Constanta Olteanu, Linnéuniversitetet och Anna-Lena Ekdahl, Högskolan i Jönköping I en undervisning kan olika former
Teknik gör det osynliga synligt
 Kvalitetsgranskning sammanfattning 2014:04 Teknik gör det osynliga synligt Om kvaliteten i grundskolans teknikundervisning Sammanfattning Skolinspektionen har granskat kvaliteten i teknikundervisningen
Kvalitetsgranskning sammanfattning 2014:04 Teknik gör det osynliga synligt Om kvaliteten i grundskolans teknikundervisning Sammanfattning Skolinspektionen har granskat kvaliteten i teknikundervisningen
Observationsschema. Bakgrundsuppgifter. Skola: Observation nr: Årskurs/-er: Datum: Total lektionstid enligt schema (min):
 1 (7) akgrundsuppgifter Skola: Årskurs/-er: Observation nr: Datum: Total lektionstid enligt schema (min): Lärarens utbildning: ehörig lärare: J/N Lärarerfarenhet (antal år): ntal elever i klassen/gruppen:
1 (7) akgrundsuppgifter Skola: Årskurs/-er: Observation nr: Datum: Total lektionstid enligt schema (min): Lärarens utbildning: ehörig lärare: J/N Lärarerfarenhet (antal år): ntal elever i klassen/gruppen:
Samhället och skolan förändras och matematikundervisningen som den
 Saman Abdoka Elevens bakgrund en resurs De senaste tjugo åren har inneburit stora förändringar för såväl samhälle som skolmatematik. Ur en lång erfarenhet av att undervisa i mångkulturella klassrum ger
Saman Abdoka Elevens bakgrund en resurs De senaste tjugo åren har inneburit stora förändringar för såväl samhälle som skolmatematik. Ur en lång erfarenhet av att undervisa i mångkulturella klassrum ger
Lgr 11 matriser i Favorit matematik 4 6
 Lgr 11 matriser i Favorit matematik 4 6 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla förmågan att De matematiska förmågor
Lgr 11 matriser i Favorit matematik 4 6 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla förmågan att De matematiska förmågor
Vad skall en matematiklärare kunna? Översikt. Styrdokument. Styrdokument. Problemlösning
 Vad skall en matematiklärare kunna? Andreas Ryve Stockholms universitet och Mälardalens Högskola. Översikt 1. Vad skall en elev kunna? 2. Matematik genom problemlösning ett exempel. 3. Skapa matematiska
Vad skall en matematiklärare kunna? Andreas Ryve Stockholms universitet och Mälardalens Högskola. Översikt 1. Vad skall en elev kunna? 2. Matematik genom problemlösning ett exempel. 3. Skapa matematiska
Matematikundervisning för framtiden
 Matematikundervisning för framtiden Matematikundervisning för framtiden De svenska elevernas matematikkunskaper har försämrats över tid, både i grund- och gymnasieskolan. TIMSS-undersökningen år 2003 visade
Matematikundervisning för framtiden Matematikundervisning för framtiden De svenska elevernas matematikkunskaper har försämrats över tid, både i grund- och gymnasieskolan. TIMSS-undersökningen år 2003 visade
Enkäten inleds med några frågor om demografiska data. Totalt omfattar enkäten 85 frågor. 30-40 år. 41-50 år. 51-60 år. > 60 år. 6-10 år.
 1 av 15 2010-11-03 12:46 Syftet med den här enkäten är att lära mer om hur lärare tänker och känner när det gäller matematikundervisningen, särskilt i relation till kursplanen och till de nationella proven.
1 av 15 2010-11-03 12:46 Syftet med den här enkäten är att lära mer om hur lärare tänker och känner när det gäller matematikundervisningen, särskilt i relation till kursplanen och till de nationella proven.
Ungdomars kommentarer om patientjournalen på nätet Våren 2014
 Ungdomars kommentarer om patientjournalen på nätet Våren 2014 Önskas mer information om hur Landstinget Kronoberg arbetar med kontaktklasser eller om innehållet i denna rapport, kontakta: Susann Swärd
Ungdomars kommentarer om patientjournalen på nätet Våren 2014 Önskas mer information om hur Landstinget Kronoberg arbetar med kontaktklasser eller om innehållet i denna rapport, kontakta: Susann Swärd
Olika sätt att lösa ekvationer
 Modul: Algebra Del 5: Algebra som språk Olika sätt att lösa ekvationer Cecilia Kilhamn, Göteborgs Universitet och Lucian Olteanu, Linnéuniversitetet Att lösa ekvationer är en central del av algebran, det
Modul: Algebra Del 5: Algebra som språk Olika sätt att lösa ekvationer Cecilia Kilhamn, Göteborgs Universitet och Lucian Olteanu, Linnéuniversitetet Att lösa ekvationer är en central del av algebran, det
Paper från lärgruppen i matematik. S:t Olofsskolan vt 13
 Paper från lärgruppen i matematik S:t Olofsskolan vt 13 Agneta Sillman Karlsson Carolina Strömberg Katrin Lingensjö Ulla Sjöstedt Bakgrund: Många elever tycker matte är att enbart räkna i en mattebok.
Paper från lärgruppen i matematik S:t Olofsskolan vt 13 Agneta Sillman Karlsson Carolina Strömberg Katrin Lingensjö Ulla Sjöstedt Bakgrund: Många elever tycker matte är att enbart räkna i en mattebok.
Enkätresultat. Kursenkät, Flervariabelanalys. Datum: 2010-03-29 08:47:04. Aktiverade deltagare (MMGF20, V10, Flervariabelanalys) Grupp:
 Enkätresultat Enkät: Status: Kursenkät, Flervariabelanalys stängd Datum: 2010-03-29 08:47:04 Grupp: Besvarad av: 13(40) (32%) Aktiverade deltagare (MMGF20, V10, Flervariabelanalys) Helheten Mitt helhetsomdöme
Enkätresultat Enkät: Status: Kursenkät, Flervariabelanalys stängd Datum: 2010-03-29 08:47:04 Grupp: Besvarad av: 13(40) (32%) Aktiverade deltagare (MMGF20, V10, Flervariabelanalys) Helheten Mitt helhetsomdöme
30-40 år år år. > 60 år år år. > 15 år
 1 av 14 2010-11-02 16:21 Namn: Skola: Epostadress: 1. Kön Kvinna Man 2. Ålder < 30 år 30-40 år 41-50 år 51-60 år > 60 år 3. Har varit verksam som lärare i: < 5 år 6-10 år 11-15 år > 15 år 4. Har du en
1 av 14 2010-11-02 16:21 Namn: Skola: Epostadress: 1. Kön Kvinna Man 2. Ålder < 30 år 30-40 år 41-50 år 51-60 år > 60 år 3. Har varit verksam som lärare i: < 5 år 6-10 år 11-15 år > 15 år 4. Har du en
Elevernas uppfattningar om alltmer digitaliserad undervisning
 Resultat Elevernas uppfattningar om alltmer digitaliserad undervisning Fråga 1 Mycket inspirerande (6) till mycket tråkigt (1) att arbeta med etologisidan Uppfattas som mycket inspirerande eller inspirerande
Resultat Elevernas uppfattningar om alltmer digitaliserad undervisning Fråga 1 Mycket inspirerande (6) till mycket tråkigt (1) att arbeta med etologisidan Uppfattas som mycket inspirerande eller inspirerande
1. Skollagen 2. Läroplanen Lpo 94 / Lpf Grundskole- / Gymnasieförordningen
 Olika styrdokument har olika dignitet 1. Skollagen 2. Läroplanen Lpo 94 / Lpf 94 3. Grundskole- / Gymnasieförordningen Riksdagen Regeringen Utskott SOU Departement (utbildnings-) Statliga verk (Skolverket)
Olika styrdokument har olika dignitet 1. Skollagen 2. Läroplanen Lpo 94 / Lpf 94 3. Grundskole- / Gymnasieförordningen Riksdagen Regeringen Utskott SOU Departement (utbildnings-) Statliga verk (Skolverket)
Under min praktik som lärarstuderande
 tomoko helmertz Problemlösning i Japan och Sverige Japansk matematikundervisning skiljer sig på många sätt från svensk. Vilka konsekvenser får det för hur elever i respektive länder löser problem? Tomoko
tomoko helmertz Problemlösning i Japan och Sverige Japansk matematikundervisning skiljer sig på många sätt från svensk. Vilka konsekvenser får det för hur elever i respektive länder löser problem? Tomoko
Ungdomars kommentarer om skolk Hösten 2013
 Ungdomars kommentarer om skolk Hösten 2013 Önskas mer information om hur Landstinget Kronoberg arbetar med kontaktklasser eller om innehållet i denna rapport, kontakta: Susann Swärd Barnrättsstrateg 0709-844
Ungdomars kommentarer om skolk Hösten 2013 Önskas mer information om hur Landstinget Kronoberg arbetar med kontaktklasser eller om innehållet i denna rapport, kontakta: Susann Swärd Barnrättsstrateg 0709-844
Under höstterminen 2015 arbetade lärare på mellan- och högstadiet på
 Per Berggren Födelsedagstårtan en språkutvecklande uppgift Efter att skolans lärare genomfört Matematiklyftets modul Språk i matematik provade författaren att fokusera på kommunikationen i klassrummet
Per Berggren Födelsedagstårtan en språkutvecklande uppgift Efter att skolans lärare genomfört Matematiklyftets modul Språk i matematik provade författaren att fokusera på kommunikationen i klassrummet
Nationella medieprogrammet Obligatoriska kärnämnen
 Nationella medieprogrammet Obligatoriska kärnämnen Engelska (A) 100p Estetisk verksamhet 50p Idrott och hälsa (A) 100p Matematik (A) 100p Naturkunskap (A) 50p Religionskunskap (A) 50p Samhällskunskap (A)
Nationella medieprogrammet Obligatoriska kärnämnen Engelska (A) 100p Estetisk verksamhet 50p Idrott och hälsa (A) 100p Matematik (A) 100p Naturkunskap (A) 50p Religionskunskap (A) 50p Samhällskunskap (A)
2013-08-27. Gymnasielärare Doktorand, Linköpings universitet
 Gymnasielärare Doktorand, Linköpings universitet Simon Hjort Från forskningsöversikt till undervisningspraktik: Hur förbättra elevers studieresultat i skolan? Vilka faktorer påverkar elevers studieprestationer
Gymnasielärare Doktorand, Linköpings universitet Simon Hjort Från forskningsöversikt till undervisningspraktik: Hur förbättra elevers studieresultat i skolan? Vilka faktorer påverkar elevers studieprestationer
Färdighet med förståelse
 Färdighet med förståelse DAGMAR NEUMAN Är det möjligt att lära "räkneomogna" nybörjare den logik som är basen för matematisk förståelse? "Mognad" anses av många vara omöjlig att påverka genom undervisning
Färdighet med förståelse DAGMAR NEUMAN Är det möjligt att lära "räkneomogna" nybörjare den logik som är basen för matematisk förståelse? "Mognad" anses av många vara omöjlig att påverka genom undervisning
Tummen upp! Matte Kartläggning åk 5
 Tryck.nr 47-11064-3 4711064_t_upp_ma_5_omsl.indd Alla sidor 2014-01-27 12.29 TUMMEN UPP! Ç I TUMMEN UPP! MATTE KARTLÄGGNING ÅK 5 finns övningar som är direkt kopplade till kunskapskraven i åk 6. Kunskapskraven
Tryck.nr 47-11064-3 4711064_t_upp_ma_5_omsl.indd Alla sidor 2014-01-27 12.29 TUMMEN UPP! Ç I TUMMEN UPP! MATTE KARTLÄGGNING ÅK 5 finns övningar som är direkt kopplade till kunskapskraven i åk 6. Kunskapskraven
LPP för årskurs 2, Matte V.46-51 HT12
 LPP för årskurs 2, Matte V.46-51 HT12 Värdegrund och uppdrag Skolan ska vara öppen för skilda uppfattningar och uppmuntra att de förs fram. Den ska framhålla betydelsen av personliga ställningstaganden
LPP för årskurs 2, Matte V.46-51 HT12 Värdegrund och uppdrag Skolan ska vara öppen för skilda uppfattningar och uppmuntra att de förs fram. Den ska framhålla betydelsen av personliga ställningstaganden
Jag tror att alla lärare introducerar bråk
 RONNY AHLSTRÖM Variabler och mönster Det är viktigt att eleverna får förståelse för grundläggande matematiska begrepp. Ett sätt att närma sig variabelbegreppet är via mönster som beskrivs med formler.
RONNY AHLSTRÖM Variabler och mönster Det är viktigt att eleverna får förståelse för grundläggande matematiska begrepp. Ett sätt att närma sig variabelbegreppet är via mönster som beskrivs med formler.
Observationsprotokoll för lektionsbesök
 Observationsprotokoll för lektionsbesök Datum och tidpunkt för observationen: Observerad lärare: Skola: Antal närvarande elever i klassen/gruppen: Årskurs/årskurser: Lektionens ämne: Lektionens huvudsakliga
Observationsprotokoll för lektionsbesök Datum och tidpunkt för observationen: Observerad lärare: Skola: Antal närvarande elever i klassen/gruppen: Årskurs/årskurser: Lektionens ämne: Lektionens huvudsakliga
Högskolepedagogisk utbildning-modul 3-perspektivkurs nov 2004
 Genus och programmering av Kristina von Hausswolff Inledning Under läsåret 3/ var jag med i ett projekt om Genus och datavetenskap lett av Carin Dackman och Christina Björkman. Under samma tid, våren,
Genus och programmering av Kristina von Hausswolff Inledning Under läsåret 3/ var jag med i ett projekt om Genus och datavetenskap lett av Carin Dackman och Christina Björkman. Under samma tid, våren,
Provmoment: Tentamen Matematik och matematikdidaktik, 3 hp, tillfälle 1
 Matematik med didaktisk inriktning för grundlärare i förskoleklass och grundskolans a rskurs 1-3, III, VT18 7,5 högskolepoäng Provmoment: Tentamen Matematik och matematikdidaktik, 3 hp, tillfälle 1 Ladokkod:
Matematik med didaktisk inriktning för grundlärare i förskoleklass och grundskolans a rskurs 1-3, III, VT18 7,5 högskolepoäng Provmoment: Tentamen Matematik och matematikdidaktik, 3 hp, tillfälle 1 Ladokkod:
Boken Förstå och använda tal en handbok behandlar 22 områden av elevers
 Marie Mäkiranta Att diagnostisera elevers kunskaper och missuppfattningar Författaren har i ett fördjupningsarbete under en kurs i Lärarlyftet arbetat med boken Förstå och använda tal en handbok av Alistair
Marie Mäkiranta Att diagnostisera elevers kunskaper och missuppfattningar Författaren har i ett fördjupningsarbete under en kurs i Lärarlyftet arbetat med boken Förstå och använda tal en handbok av Alistair
Rapport av genomförd lesson study av en lektion med temat geometri i gymnasiets A-kurs
 Rapport av genomförd lesson study av en lektion med temat geometri i gymnasiets A-kurs Förberedelser Geometri visade sig vara det svåraste området att planera utifrån tanken om en progression genom skolans
Rapport av genomförd lesson study av en lektion med temat geometri i gymnasiets A-kurs Förberedelser Geometri visade sig vara det svåraste området att planera utifrån tanken om en progression genom skolans
Hanna Melin Nilstein. Lokal pedagogisk plan för verklighetsbaserad och praktisk matematik Årskurs 3 1+1=?
 Hanna Melin Nilstein Lokal pedagogisk plan för verklighetsbaserad och praktisk matematik Årskurs 3 1+1=? Lpp (Lokal pedagogisk plan) för verklighetsbaserad och praktisk matematik Bakgrund och beskrivning
Hanna Melin Nilstein Lokal pedagogisk plan för verklighetsbaserad och praktisk matematik Årskurs 3 1+1=? Lpp (Lokal pedagogisk plan) för verklighetsbaserad och praktisk matematik Bakgrund och beskrivning
Sandåkerskolans plan för elevernas utveckling av den metakognitiva förmågan
 1(7) 2011-08-29 s plan för elevernas utveckling av den metakognitiva förmågan 18 august-20 december Steg 1: Ämnesläraren dokumenterar Syfte synliggöra utvecklingsbehov Ämnesläraren dokumenterar elevens
1(7) 2011-08-29 s plan för elevernas utveckling av den metakognitiva förmågan 18 august-20 december Steg 1: Ämnesläraren dokumenterar Syfte synliggöra utvecklingsbehov Ämnesläraren dokumenterar elevens
Matematiklektionen i fokus. Några klassrum öppnar dörren
 Matematiklektionen i fokus Några klassrum öppnar dörren Brister i matematikundervisningen Lusten att lära med fokus på matematik (Skolverkets rapport nr 221) Den dominerande undervisningen är genomgång
Matematiklektionen i fokus Några klassrum öppnar dörren Brister i matematikundervisningen Lusten att lära med fokus på matematik (Skolverkets rapport nr 221) Den dominerande undervisningen är genomgång
KURSUTVÄRDERING AV UPPSATSARBETE OCH HANDLEDNING AVDELNINGEN FÖR PSYKOLOGI
 KURSUTVÄRDERING AV UPPSATSARBETE OCH HANDLEDNING AVDELNINGEN FÖR PSYKOLOGI Med detta frågeformulär vill vi få mer kunskap kring hur uppsatsarbete och handledning upplevs och fungerar vid ämnet psykologi.
KURSUTVÄRDERING AV UPPSATSARBETE OCH HANDLEDNING AVDELNINGEN FÖR PSYKOLOGI Med detta frågeformulär vill vi få mer kunskap kring hur uppsatsarbete och handledning upplevs och fungerar vid ämnet psykologi.
Vårt projekt genomfördes under vårterminen Självreglering
 Carlsson, Dalsjö, Ingelshed & Larsson Bjud in eleverna att påverka sin matematikundervisning Fyra lärare beskriver hur deras elever blev inbjudna till att få insikt i och makt över sina egna lärandeprocesser
Carlsson, Dalsjö, Ingelshed & Larsson Bjud in eleverna att påverka sin matematikundervisning Fyra lärare beskriver hur deras elever blev inbjudna till att få insikt i och makt över sina egna lärandeprocesser
Rapport av genomförd lesson study av en lektion med temat bråk i gymnasiets A-kurs
 Rapport av genomförd lesson study av en lektion med temat bråk i gymnasiets A-kurs Klippa gräset Jenny klipper gräsmattan hos Bo på 2 timmar. Måns gör det på 4 timmar. Förberedelser Utifrån en diskussion
Rapport av genomförd lesson study av en lektion med temat bråk i gymnasiets A-kurs Klippa gräset Jenny klipper gräsmattan hos Bo på 2 timmar. Måns gör det på 4 timmar. Förberedelser Utifrån en diskussion
2012-01-12 FÖRSLAG TILL KURSPLAN INOM KOMMUNAL VUXENUTBILDNING GRUNDLÄGGANDE NIVÅ
 Matematik, 600 verksamhetspoäng Ämnet handlar bland annat om mängder, tal och geometriska figurer. Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl ur praktiska
Matematik, 600 verksamhetspoäng Ämnet handlar bland annat om mängder, tal och geometriska figurer. Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl ur praktiska
DIGITALA KOMPETENSER OCH PROGRAMMERING
 Pilotutvärdering 7 juli 2017 DIGITALA KOMPETENSER OCH PROGRAMMERING En utvärdering av samverkan mellan Uddevallas grundskolor och Innovatum Science Center När och var? Läsåret 16/17 har Uddevalla kommun
Pilotutvärdering 7 juli 2017 DIGITALA KOMPETENSER OCH PROGRAMMERING En utvärdering av samverkan mellan Uddevallas grundskolor och Innovatum Science Center När och var? Läsåret 16/17 har Uddevalla kommun
Studenter i lärarprogrammet GF(11GF20) 46 p G: 28 p VG: 38 p
 11GF20 MaI Provmoment: Ladokkod: Tentamen ges för: Matematik 0,5 hp Studenter i lärarprogrammet GF(11GF20) 15 högskolepoäng TentamensKod: Tentamensdatum: 18-05-22 Tid: 09.00-13.00 Hjälpmedel: Inga hjälpmedel
11GF20 MaI Provmoment: Ladokkod: Tentamen ges för: Matematik 0,5 hp Studenter i lärarprogrammet GF(11GF20) 15 högskolepoäng TentamensKod: Tentamensdatum: 18-05-22 Tid: 09.00-13.00 Hjälpmedel: Inga hjälpmedel
3OM218. Examinator. Monica Christianson. 58% (14 av 24 möjliga personer) Muntlig utvärdering 2013-05 06
 Institutionen för omvårdnad Sammanställning [2013-06-13] [OM 218vt13] Sid 1 (1) Kursutvärdering Kursnamn och poäng Kvinno- och familjehälsa I, 7,5 hp Kurs inom program (ange program)/fristående Barnmorskeprogrammet,
Institutionen för omvårdnad Sammanställning [2013-06-13] [OM 218vt13] Sid 1 (1) Kursutvärdering Kursnamn och poäng Kvinno- och familjehälsa I, 7,5 hp Kurs inom program (ange program)/fristående Barnmorskeprogrammet,
/////// // ///////// / // /
 Utvärdering matematikämnet hösten 2010 Dessa grupper är inskrivna: Åk 7 Petra & Malins grupp Åk 8 Malins grupp Åk 9 Petras grupp Åk 7 Jörgens grupp Åk 8 Jonas & Petras grupp Åk 9 Jonas grupp Åk 7 Evas
Utvärdering matematikämnet hösten 2010 Dessa grupper är inskrivna: Åk 7 Petra & Malins grupp Åk 8 Malins grupp Åk 9 Petras grupp Åk 7 Jörgens grupp Åk 8 Jonas & Petras grupp Åk 9 Jonas grupp Åk 7 Evas
ATT ANVÄNDA SPRÅK FÖR ATT LÄRA SIG OCH ATT LÄRA SIG ANVÄNDA SPRÅK
 ATT ANVÄNDA SPRÅK FÖR ATT LÄRA SIG OCH ATT LÄRA SIG ANVÄNDA SPRÅK Liisa Suopanki Carin Söderberg Margaretha Biddle Framtiden är inte något som bara händer till en del danas och formges den genom våra handlingar
ATT ANVÄNDA SPRÅK FÖR ATT LÄRA SIG OCH ATT LÄRA SIG ANVÄNDA SPRÅK Liisa Suopanki Carin Söderberg Margaretha Biddle Framtiden är inte något som bara händer till en del danas och formges den genom våra handlingar
kultursyn kunskapssyn elevsyn 2014 Ulla Wiklund
 kultursyn kunskapssyn elevsyn Pedagogik förmågan att inte ingripa? Kultursyn Inlärning perception produktion Kunskapssyn perception Lärande produktion reflektion inre yttre Estetik gestaltad erfarenhet
kultursyn kunskapssyn elevsyn Pedagogik förmågan att inte ingripa? Kultursyn Inlärning perception produktion Kunskapssyn perception Lärande produktion reflektion inre yttre Estetik gestaltad erfarenhet
Det övergripande syftet med kompetensutvecklingen beskrivs som:
 Elisabeth Rystedt, Madeleine Löwing & Lena Trygg Matematikundervisning för nyanlända elever del 2 I en artikel i förra numret beskrevs planeringsarbetet mellan NCM och tre skolor i Borås inför pilotprojektet
Elisabeth Rystedt, Madeleine Löwing & Lena Trygg Matematikundervisning för nyanlända elever del 2 I en artikel i förra numret beskrevs planeringsarbetet mellan NCM och tre skolor i Borås inför pilotprojektet
Känner elever lust att lära matematik?
 Malmö högskola Lärarutbildningen Natur Miljö Samhälle Examensarbete 10 poäng Känner elever lust att lära matematik? Do students feel any desire for learning mathematics? Beata Blankberg Lärarexamen 140
Malmö högskola Lärarutbildningen Natur Miljö Samhälle Examensarbete 10 poäng Känner elever lust att lära matematik? Do students feel any desire for learning mathematics? Beata Blankberg Lärarexamen 140
Muntlig kommunikation på matematiklektioner
 LÄRARPROGRAMMET Muntlig kommunikation på matematiklektioner Enkätundersökning med lärare som undervisar i årskurs 7-9 Margareta Olsson Examensarbete 15hp Höstterminen 2008 Handledare: Maria Bjerneby Häll
LÄRARPROGRAMMET Muntlig kommunikation på matematiklektioner Enkätundersökning med lärare som undervisar i årskurs 7-9 Margareta Olsson Examensarbete 15hp Höstterminen 2008 Handledare: Maria Bjerneby Häll
Elevernas lust att lära matematik
 Lärarutbildningen Natur, miljö, samhälle Examensarbete 15 högskolepoäng, grundnivå Elevernas lust att lära matematik Fem lärares syn på undervisningsutformning och elevdelaktighet i denna utformning Students
Lärarutbildningen Natur, miljö, samhälle Examensarbete 15 högskolepoäng, grundnivå Elevernas lust att lära matematik Fem lärares syn på undervisningsutformning och elevdelaktighet i denna utformning Students
Stjärneboskolan Läsåret 2007-2008. Kvalitetsredovisning
 Stjärneboskolan Läsåret 2007-2008 Kvalitetsredovisning STJÄRNEBOSKOLAN Skolan ligger vid norra infarten till Kisa, mellan Kisasjön och ett närliggande skogsområde. I detta skogsområde finns skolans uteklassrum
Stjärneboskolan Läsåret 2007-2008 Kvalitetsredovisning STJÄRNEBOSKOLAN Skolan ligger vid norra infarten till Kisa, mellan Kisasjön och ett närliggande skogsområde. I detta skogsområde finns skolans uteklassrum
Elevers utvärdering av Evolutionstrappan. Skola: Solängsskolan, Gävle Lärare: Gunilla Djuvfelt Antal elever: sex st. Metod.
 Elevers utvärdering av Evolutionstrappan Skola: Solängsskolan, Gävle Lärare: Gunilla Djuvfelt : sex st Metod De elever som skulle delta i utvärdering av Evolutionstrappan fick information att ta hem till
Elevers utvärdering av Evolutionstrappan Skola: Solängsskolan, Gävle Lärare: Gunilla Djuvfelt : sex st Metod De elever som skulle delta i utvärdering av Evolutionstrappan fick information att ta hem till
DD2458-224344 - 2014-12-19
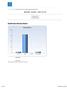 KTH / KURSWEBB / PROBLEMLÖSNING OCH PROGRAMMERING UNDER PRESS DD2458-224344 - 2014-12-19 Antal respondenter: 26 Antal svar: 18 Svarsfrekvens: 69,23 % RESPONDENTERNAS PROFIL (Jag är: Man) Det var typ en
KTH / KURSWEBB / PROBLEMLÖSNING OCH PROGRAMMERING UNDER PRESS DD2458-224344 - 2014-12-19 Antal respondenter: 26 Antal svar: 18 Svarsfrekvens: 69,23 % RESPONDENTERNAS PROFIL (Jag är: Man) Det var typ en
1. Hur många timmar per vecka har du i genomsnitt lagt ner på kursen (inklusive schemalagd tid)?
 Vattenresursteknik MV0190, 30056.1314 5 Hp Studietakt = 35% Nivå och djup = Avancerad Kursledare = Abraham Joel Värderingsresultat Värderingsperiod: 2014-03-05-2014-04-04 Antal svar 8 Studentantal 52 Svarsfrekvens
Vattenresursteknik MV0190, 30056.1314 5 Hp Studietakt = 35% Nivå och djup = Avancerad Kursledare = Abraham Joel Värderingsresultat Värderingsperiod: 2014-03-05-2014-04-04 Antal svar 8 Studentantal 52 Svarsfrekvens
Kurskod: GRNMAT2 Verksamhetspoäng: 600
 Kurs: Matematik Kurskod: GRNMAT2 Verksamhetspoäng: 600 lust att utforska matematiken som sådan. Matematisk verksamhet är till sin lad till den samhälleliga, sociala och tekniska utvecklingen. Kunskaper
Kurs: Matematik Kurskod: GRNMAT2 Verksamhetspoäng: 600 lust att utforska matematiken som sådan. Matematisk verksamhet är till sin lad till den samhälleliga, sociala och tekniska utvecklingen. Kunskaper
Teori och praktik. Vilket bör komma först?
 Miniprojekt, pedagogisk grundkurs III, ht Martina Tedenborg, Avd för samhällsfarmaci Teori och praktik. Vilket bör komma först? En diskussion kring den pedagogiska betydelsen av praktiken och dess placering
Miniprojekt, pedagogisk grundkurs III, ht Martina Tedenborg, Avd för samhällsfarmaci Teori och praktik. Vilket bör komma först? En diskussion kring den pedagogiska betydelsen av praktiken och dess placering
På vilket sätt kan man få elever i år 9 mer intresserade av schack?
 Lärande och samhälle. Schack som pedagogiskt verktyg På vilket sätt kan man få elever i år 9 mer intresserade av schack? - Kan man få elever i år 9 att vilja spela på fritiden med kompisar eller via tekniska
Lärande och samhälle. Schack som pedagogiskt verktyg På vilket sätt kan man få elever i år 9 mer intresserade av schack? - Kan man få elever i år 9 att vilja spela på fritiden med kompisar eller via tekniska
Algebra och Ekvationer År 7
 Undervisning Algebra och Ekvationer År 7 Lärandemål (konkretisering av syfte och centralt innehåll ur Lgr 11) Rimlighetsbedömning vid uppskattningar och beräkningar i vardagliga och situationer och inom
Undervisning Algebra och Ekvationer År 7 Lärandemål (konkretisering av syfte och centralt innehåll ur Lgr 11) Rimlighetsbedömning vid uppskattningar och beräkningar i vardagliga och situationer och inom
ämnesområden. Funktioner och räta linjens ekvation. Hur funktioner kan användas för att undersöka förändring, förändringstakt och andra samband.
 MATEMATIK Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl ur praktiska behov som ur människans nyfikenhet och lust att utforska matematiken som sådan. Matematisk
MATEMATIK Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl ur praktiska behov som ur människans nyfikenhet och lust att utforska matematiken som sådan. Matematisk
I arbetet hanterar eleven flera procedurer och löser uppgifter av standardkaraktär med säkerhet, både utan och med digitala verktyg.
 Kunskapskrav Ma 2a Namn: Gy Betyg E D Betyg C B Betyg A 1. Begrepp Eleven kan översiktligt beskriva innebörden av centrala begrepp med hjälp av några representationer samt översiktligt beskriva sambanden
Kunskapskrav Ma 2a Namn: Gy Betyg E D Betyg C B Betyg A 1. Begrepp Eleven kan översiktligt beskriva innebörden av centrala begrepp med hjälp av några representationer samt översiktligt beskriva sambanden
Skolenkäten hösten 2018
 Skolenkäten hösten 2018 Huvudmannarapport/Skolenhetsrapport Enkätresultat Vänersborgs kommun Elever Total antal Antal svar Svarsfrekvens Årskurs 5 grundskola 463 433 94% Årskurs 9 grundskola 393 310 79%
Skolenkäten hösten 2018 Huvudmannarapport/Skolenhetsrapport Enkätresultat Vänersborgs kommun Elever Total antal Antal svar Svarsfrekvens Årskurs 5 grundskola 463 433 94% Årskurs 9 grundskola 393 310 79%
Förmågor i naturvetenskap, åk 1-3
 Förmågor i naturvetenskap, åk 1-3 I Lgr11 betonas att eleverna ska använda sina naturvetenskapliga kunskaper på olika sätt. Det formuleras som syften med undervisningen och sammanfattas i tre förmågor.
Förmågor i naturvetenskap, åk 1-3 I Lgr11 betonas att eleverna ska använda sina naturvetenskapliga kunskaper på olika sätt. Det formuleras som syften med undervisningen och sammanfattas i tre förmågor.
Att arbeta med skrivmallar och uppgiftsmatriser en pilotstudie om ett språkutvecklande projekt i samhällsvetenskapliga ämnen i åk 8
 Att arbeta med skrivmallar och uppgiftsmatriser en pilotstudie om ett språkutvecklande projekt i samhällsvetenskapliga ämnen i åk 8 Inledning Marie Olsson I flera av kunskapskraven i de samhällsvetenskapliga
Att arbeta med skrivmallar och uppgiftsmatriser en pilotstudie om ett språkutvecklande projekt i samhällsvetenskapliga ämnen i åk 8 Inledning Marie Olsson I flera av kunskapskraven i de samhällsvetenskapliga
Elevenkät Viljan Friskola Vt. 2014
 Elevenkät Viljan Friskola Vt. 2014 Sammanställning av Elevenkäterna på Viljan Friskola. Det är 19 av 21 elever som har besvarat enkäten. Kommentarer från ungdomarna är skrivna med röd text och resultatet
Elevenkät Viljan Friskola Vt. 2014 Sammanställning av Elevenkäterna på Viljan Friskola. Det är 19 av 21 elever som har besvarat enkäten. Kommentarer från ungdomarna är skrivna med röd text och resultatet
Del ur Lgr 11: kursplan i matematik i grundskolan
 Del ur Lgr 11: kursplan i matematik i grundskolan 3.5 Matematik Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl ur praktiska behov som ur människans nyfikenhet
Del ur Lgr 11: kursplan i matematik i grundskolan 3.5 Matematik Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl ur praktiska behov som ur människans nyfikenhet
Verksamhetsrapport. Skoitnst.. 7.1,ktion.en
 Skoitnst.. 7.1,ktion.en Bilaga 1 Verksamhetsrapport Verksamhetsrapport efter kvalitetsgranskning av undervisningen i matematik kurs 3c vid den fristående gymnasieskolan JENSEN gymnasium Uppsala i Uppsala
Skoitnst.. 7.1,ktion.en Bilaga 1 Verksamhetsrapport Verksamhetsrapport efter kvalitetsgranskning av undervisningen i matematik kurs 3c vid den fristående gymnasieskolan JENSEN gymnasium Uppsala i Uppsala
Det finns mycket kritik som förs fram om skolan i allmänhet samtidigt
 Joakim Samuelsson Expert i matematikklassrummet Vad är det som kännetecknar skickliga matematiklärare? Artikelförfattaren har följt en erkänt duktig matematiklärare och sett hur han bedriver sin undervisning.
Joakim Samuelsson Expert i matematikklassrummet Vad är det som kännetecknar skickliga matematiklärare? Artikelförfattaren har följt en erkänt duktig matematiklärare och sett hur han bedriver sin undervisning.
Elevsamtal med eleverna kring deras lärande
 Grundskoleavdelningen Goda exempel Sida 1 (7) Elevsamtal med eleverna kring deras lärande Hämtad från Tallkrogens skola Uppdaterad: 2017-08-22 Pedagogerna i Tallkrogens skola har arbetat fram frågeställningar
Grundskoleavdelningen Goda exempel Sida 1 (7) Elevsamtal med eleverna kring deras lärande Hämtad från Tallkrogens skola Uppdaterad: 2017-08-22 Pedagogerna i Tallkrogens skola har arbetat fram frågeställningar
Dokumentera och följa upp
 Modul: Förskoleklass Del 8: Dokumentera och följa upp Dokumentera och följa upp Ola Helenius, Maria L. Johansson, Troels Lange, Tamsin Meaney, Eva Riesbeck, Anna Wernberg, Malmö högskola, Luleå tekniska
Modul: Förskoleklass Del 8: Dokumentera och följa upp Dokumentera och följa upp Ola Helenius, Maria L. Johansson, Troels Lange, Tamsin Meaney, Eva Riesbeck, Anna Wernberg, Malmö högskola, Luleå tekniska
Lära matematik med datorn. Ulrika Ryan, projektledare för Matematik för den digitala generationen Byskolan, Södra Sandby
 Lära matematik med datorn Ulrika Ryan, projektledare för Matematik för den digitala generationen Byskolan, Södra Sandby Innehåll Varför undervisar jag som jag gör? Lärarens roll i det digitala klassrummet
Lära matematik med datorn Ulrika Ryan, projektledare för Matematik för den digitala generationen Byskolan, Södra Sandby Innehåll Varför undervisar jag som jag gör? Lärarens roll i det digitala klassrummet
Bedömning av Examensarbete (30 hp) vid Logopedprogrammet Fylls i av examinerande lärare och lämnas i signerad slutversion till examinator
 version 2014-09-10 Bedömning av Examensarbete (30 hp) vid Logopedprogrammet Fylls i av examinerande lärare och lämnas i signerad slutversion till examinator Studentens namn Handledares namn Examinerande
version 2014-09-10 Bedömning av Examensarbete (30 hp) vid Logopedprogrammet Fylls i av examinerande lärare och lämnas i signerad slutversion till examinator Studentens namn Handledares namn Examinerande
Centralt innehåll. I årskurs 1.3
 3.5 Matematik Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl ur praktiska behov som ur människans nyfikenhet och lust att utforska matematiken som sådan.
3.5 Matematik Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl ur praktiska behov som ur människans nyfikenhet och lust att utforska matematiken som sådan.
Bilaga till ansökan om bidrag för utveckling av undervisningen
 1 (7) Bilaga till ansökan om bidrag för utveckling av undervisningen i matematik Matematiksatsningen 2011 Ha riktlinjerna och blankettstödet tillhands då denna ansökningsbilaga fylls i. Bakgrundsinformation
1 (7) Bilaga till ansökan om bidrag för utveckling av undervisningen i matematik Matematiksatsningen 2011 Ha riktlinjerna och blankettstödet tillhands då denna ansökningsbilaga fylls i. Bakgrundsinformation
Förbättra din studieteknik med Matematik 5000! 12 praktiska tips!
 Förbättra din studieteknik med Matematik 5000! 12 praktiska tips! ik Hej! Det är jag som är Daniel Nilsson. Jag är utbildad matematik- och historielärare och även speciallärare med inriktning mot matematik.
Förbättra din studieteknik med Matematik 5000! 12 praktiska tips! ik Hej! Det är jag som är Daniel Nilsson. Jag är utbildad matematik- och historielärare och även speciallärare med inriktning mot matematik.
Statistik, sannolikhet, algebra och funktioner, 3 hp. Studenter i lärarprogrammet F-3 III, 12F380 ht17 Varberg
 Grundläggande matematik II 7,5 högskolepoäng Provmoment: Ladokkod: Tentamen ges för: Statistik, sannolikhet, algebra och funktioner, 3 hp Studenter i lärarprogrammet F-3 III, 12F380 ht17 Varberg TentamensKod:
Grundläggande matematik II 7,5 högskolepoäng Provmoment: Ladokkod: Tentamen ges för: Statistik, sannolikhet, algebra och funktioner, 3 hp Studenter i lärarprogrammet F-3 III, 12F380 ht17 Varberg TentamensKod:
Syfte. Malmö stad Komvux Malmö Södervärn PRÖVNING. prövning grundläggande matematik
 prövning grundläggande matematik Malmö stad Komvux Malmö Södervärn PRÖVNING Kurs: Matematik Kurskod: GRNMAT2 Verksamhetspoäng: 600 Matematiken har en flertusenårig historia med bidrag från många kulturer.
prövning grundläggande matematik Malmö stad Komvux Malmö Södervärn PRÖVNING Kurs: Matematik Kurskod: GRNMAT2 Verksamhetspoäng: 600 Matematiken har en flertusenårig historia med bidrag från många kulturer.
Bedömning av Examensarbete (30 hp) vid Logopedprogrammet Fylls i av examinerande lärare och lämnas till examinator
 version 2017-08-21 Bedömning av Examensarbete (30 hp) vid Logopedprogrammet Fylls i av examinerande lärare och lämnas till examinator Studentens namn Handledares namn Examinerande lärare Uppsatsens titel
version 2017-08-21 Bedömning av Examensarbete (30 hp) vid Logopedprogrammet Fylls i av examinerande lärare och lämnas till examinator Studentens namn Handledares namn Examinerande lärare Uppsatsens titel
Kursplanen i ämnet matematik
 DISKUSSIONSUNDERLAG FÖR GRUNDSKOLAN Diskutera Kursplanen i ämnet matematik Läsåret 2011/12 införs en samlad läroplan för var och en av de obligatoriska skolformerna grundskolan, grundsärskolan, sameskolan
DISKUSSIONSUNDERLAG FÖR GRUNDSKOLAN Diskutera Kursplanen i ämnet matematik Läsåret 2011/12 införs en samlad läroplan för var och en av de obligatoriska skolformerna grundskolan, grundsärskolan, sameskolan
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Matematik. Mål som eleverna skall ha uppnått i slutet av det fjärde skolåret. Mål som eleverna skall ha uppnått i slutet av det femte skolåret
 Balderskolan, Uppsala musikklasser 2009 Matematik Mål som eleverna skall ha uppnått i slutet av det fjärde skolåret läsa och skriva tal inom talområdet 0 10 000 räkna de fyra räknesätten med olika metoder
Balderskolan, Uppsala musikklasser 2009 Matematik Mål som eleverna skall ha uppnått i slutet av det fjärde skolåret läsa och skriva tal inom talområdet 0 10 000 räkna de fyra räknesätten med olika metoder
Aha-upplevelser och tidsbrist
 maria nordlund Aha-upplevelser och tidsbrist Vad är det som är glädjen och vad är svårigheten med att undervisa i matematik? Här redovisas några av de upplevelser som lärarna i åk 5 och 9 redovisade i
maria nordlund Aha-upplevelser och tidsbrist Vad är det som är glädjen och vad är svårigheten med att undervisa i matematik? Här redovisas några av de upplevelser som lärarna i åk 5 och 9 redovisade i
Exempel på ämnen för examensarbete inom kurserna UÖÄ007, HOA400, UÖÄ008: (Se också DIVA: http://mdh.diva-portal.org/smash/search.
 MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Exempel på ämnen för examensarbete inom kurserna UÖÄ007, HOA400, UÖÄ008: (Se också DIVA: http://mdh.diva-portal.org/smash/search.jsf)
MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Exempel på ämnen för examensarbete inom kurserna UÖÄ007, HOA400, UÖÄ008: (Se också DIVA: http://mdh.diva-portal.org/smash/search.jsf)
Ekvationen. www.grul.se
 Ekvationen Ekvationen Speldesign: Niklas Lindblad Carl Heath Version 1.0 Tack till: Alexander Hallberg Tidsåtgång: Ca 50 minuter inklusive efterdiskussion Antal deltagare Fungerar bäst i grupper om 2-4
Ekvationen Ekvationen Speldesign: Niklas Lindblad Carl Heath Version 1.0 Tack till: Alexander Hallberg Tidsåtgång: Ca 50 minuter inklusive efterdiskussion Antal deltagare Fungerar bäst i grupper om 2-4
Riktlinjer för bedömning av examensarbeten
 Fastställda av Styrelsen för utbildning 2010-09-10 Dnr: 4603/10-300 Senast reviderade 2012-08-17 Riktlinjer för bedömning av Sedan 1 juli 2007 ska enligt högskoleförordningen samtliga yrkesutbildningar
Fastställda av Styrelsen för utbildning 2010-09-10 Dnr: 4603/10-300 Senast reviderade 2012-08-17 Riktlinjer för bedömning av Sedan 1 juli 2007 ska enligt högskoleförordningen samtliga yrkesutbildningar
Tänka, resonera och räkna i förskoleklass, Gävle kommun lå 15/16
 Tänka, resonera och räkna i förskoleklass, Gävle kommun lå 15/16 Sammanfattning av lärares synpunkter 1. På vilket sätt är lärarguiden ett stöd för undervisningen om tal och räkning? Det finns en tydlig
Tänka, resonera och räkna i förskoleklass, Gävle kommun lå 15/16 Sammanfattning av lärares synpunkter 1. På vilket sätt är lärarguiden ett stöd för undervisningen om tal och räkning? Det finns en tydlig
Vad kan vi i Sverige lära av Singapores matematikundervisning?
 Vad kan vi i Sverige lära av Singapores matematikundervisning? Singapore tillhör sedan länge toppnationerna i internationella undersökningar som Pisa och TIMSS. Deras framgångar har gjort att många andra
Vad kan vi i Sverige lära av Singapores matematikundervisning? Singapore tillhör sedan länge toppnationerna i internationella undersökningar som Pisa och TIMSS. Deras framgångar har gjort att många andra
Skolenkäten hösten 2018
 Skolenkäten hösten 2018 Huvudmannarapport/Skolenhetsrapport Enkätresultat Vendestigens skola, Vendestigens Förskola och Skola AB Elever Total antal Antal svar Svarsfrekvens Årskurs 5 grundskola 9 9 100%
Skolenkäten hösten 2018 Huvudmannarapport/Skolenhetsrapport Enkätresultat Vendestigens skola, Vendestigens Förskola och Skola AB Elever Total antal Antal svar Svarsfrekvens Årskurs 5 grundskola 9 9 100%
Min man kommer ursprungligen från
 t í m e a d a n i Varför räknar du just så? Denna artikel bygger på ett examensarbete för lärarutbildningen. I arbetet undersöktes skillnader mellan lärares, svenska föräldrars och invandrarföräldrars
t í m e a d a n i Varför räknar du just så? Denna artikel bygger på ett examensarbete för lärarutbildningen. I arbetet undersöktes skillnader mellan lärares, svenska föräldrars och invandrarföräldrars
Information om bedömning av reell kompetens
 Information om bedömning av reell kompetens Reell kompetens Det är möjligt att söka till Lernia Yrkeshögskola på reell kompetens och få denna bedömd i förhållande till den grundläggande behörigheten för
Information om bedömning av reell kompetens Reell kompetens Det är möjligt att söka till Lernia Yrkeshögskola på reell kompetens och få denna bedömd i förhållande till den grundläggande behörigheten för
Matematik 92MA41 (15hp) Vladimir Tkatjev
 Matematik 92MA41 (15hp) Vladimir Tkatjev Projektarbete: bakgrund och idéer Etymologi Proicio: kasta fram, sträcka fram (latin) Projektarbetets historia Historiskt sätt har projektarbetet som arbetsform
Matematik 92MA41 (15hp) Vladimir Tkatjev Projektarbete: bakgrund och idéer Etymologi Proicio: kasta fram, sträcka fram (latin) Projektarbetets historia Historiskt sätt har projektarbetet som arbetsform
Prata matematik. Bengt Drath. Stöpenskolan i Skövde kommun
 Prata matematik Bengt Drath Högskolan i Skövde Stöpenskolan i Skövde kommun Matematikkunnande Vad ingår i begreppet matematikkunnande? eller som elever skulle tänka: Hur skall en duktig elev i matte vara?
Prata matematik Bengt Drath Högskolan i Skövde Stöpenskolan i Skövde kommun Matematikkunnande Vad ingår i begreppet matematikkunnande? eller som elever skulle tänka: Hur skall en duktig elev i matte vara?
Exempel på observation
 Exempel på observation 1 Jag gjorde en ostrukturerad, icke deltagande observation (Bell, 2005, s. 188). Bell beskriver i sin bok ostrukturerad observation som något man tillämpar när man har en klar uppfattning
Exempel på observation 1 Jag gjorde en ostrukturerad, icke deltagande observation (Bell, 2005, s. 188). Bell beskriver i sin bok ostrukturerad observation som något man tillämpar när man har en klar uppfattning
